1、引　言

高分辨率遥感是衡量一个国家光电技术水平的重要标志，具有巨大的商业与军事价值。微纳卫星以造价低、周期短、发射灵活等优点成为遥感技术发展趋势之一。然而由于受到体积和重量的限制，微纳卫星的成像载荷难以通过大口径、长焦距的常规方式实现高分辨率观测。

提高微纳卫星对地观测分辨率的途径主要有3种：(1)为降低轨道高度，但是会大幅缩短卫星的寿命；(2)为使用轻型材料，如基于衍射薄膜的光子筛成像，但这类光学系统研制难度大，目前尚无法应用；(3)为使用超分辨率成像体制的载荷，通过提取多帧影像构成的图像序列之间的亚像元信息，以图像重建的方式提高分辨率。

在航天遥感领域，超分辨率成像最早应用于法国的大型卫星SPOT 5，它实现了在800 km轨道从5—2.5 m的分辨率提升(Jacobsen，2005)；后又应用于美国100 kg的SkySat系列微卫星，实现了在600 km轨道从1.1—0.87 m的分辨率提升(Murthy 等，2014)。中国于2016年12月22日发射的创新六号02微纳卫星(以下简称CX-6(02)星)整星重量66 kg，由中国科学院微小卫星创新研究院和中国科学院计算光学成像技术重点实验室联合研制，实现了在700 km轨道从2.8—1.4 m的分辨率提升，是中国首个超分辨率成像体制的微纳卫星。

超分辨率成像的设计主要包含亚像元信息获取方式设计和图像重建算法设计两方面的内容。

亚像元信息获取方式是针对探测器的成像采样而言，主要有线阵CCD错位拼接采样(Latry 等，2003)和高帧频CMOS画幅式重采样两类，CCD错位拼接是指将线阵CCD行与行之间错开一定的亚像元距离进行拼接，再对错位距离进行标定，这样就可直接获得亚像元信息，而避免了图像配准的步骤；高帧频CMOS画幅式重采样是指通过运动驱动机构，使高帧频CMOS探测器可以对同一地物目标进行多次成像采样，任意两次成像结果包含一定的旋转位移和平移位移，位移包含亚像元信息，如果运动驱动机构的位移不能精确测得，还需要通过图像配准算法获得亚像元信息。这两种方式都已经取得了航天应用，SPOT 5卫星采用的是线阵CCD拼接方式，SkySat卫星采用的是CMOS方式。

超分辨重建算法包含图像配准和图像复原，图像配准主要用于提取多帧图像之间的亚像元信息；图像复原主要是从成像场景、点扩散函数、探测器采样函数、亚像元信息投影函数、以及噪声函数，5者耦合中求解超分辨重建结果，属于反卷积运算，具有病态性(邹谋炎，2001)。目前多帧图像超分辨算法主要包括频域差值法(谭政 等，2017)、投影凸集法(Chen，2010)、迭代反投影法(Nitta 等，2006)、Tikhonov正则化法(Farsiu 等，2004；沈焕锋 等，2005)、最大后验法(Shen 等，2007)、变分贝叶斯法等，其中变分贝叶斯法将配准参数建模为高斯分布，将先验信息建模为L1范数模型(Villena 等，2009)或全变分模型(Babacan 等，2011；Woods和Katsaggelos，2017)，在一步迭代中对建模涉及的所有变量进行求解，一定程度上阻止了误差的传播，获得了较好的超分辨率重建效果，然而，该种方法采用的L1范数先验模型和全变分先验模型都具有较强的稀疏性，这会导致算法对图像的非边缘区域约束较弱而影响重建效果，特别是对于遥感影像来说，由于受大气的不均匀性和各种噪声的影响，图像的非边缘区域信噪比较低，从而限制了该类算法在遥感影像超分辨率重建上的应用，因此，还需要针对遥感图像的特性对算法进行改进。

本文结合CX-6(02)星超分辨率成像设计和成像结果，阐述了一种星载超分辨成像的设计方法。首先，在图像获取方面，为获得同一区域的多帧图像就要通过卫星姿态控制图像相对于地面的运动速度，由于卫星姿态控制偏差客观存在，就可以利用这个随机偏差来获得亚像元位移信息，而无需再在卫星上安装其他位移发生装置；其次，在超分辨重建算法设计方面，在变分贝叶斯超分辨求解框架下，基于马尔可夫随机场模型建立每个像元点4邻域之间的不一致关系，提出加权双向差分先验模型，进一步约束观测方程的解空间，削弱求解的病态性。CX-6(02)星成像数据实验结果表明，本文的设计方法能够获得较好的超分辨率重建效果。

2、基本原理     (2.1) 图像序列获取方式

获得具有亚像元位移信息的多帧图像是进行超分辨率成像的先决条件。由于CCD探测器具有较好的感光能力和较高的调制传递函数，使CCD探测器在航天遥感中取得了非常广泛的应用，但是CCD探测器像元尺寸较大，特别是线阵CCD的像元尺寸通常在10 μm以上(https://camera-finder.e2v.com [2018-01-11])，而光学系统的焦距与探测器像元尺寸成反比，这就意味着要实现相同的成像分辨率，若使用10 μm像元的CCD探测器的系统焦距比5—6 μm像元CMOS探测器的系统焦距要长一倍，因此，由于体积的限制，线阵CCD拼接的方式难以应用于微纳卫星。此外，卫星固有的姿态控制误差会使相机光轴指向呈一定频率的偏转，所以就可以利用这个姿态控制偏差，并与CMOS探测器的帧频相配合，来获得不同大小的亚像元位移，从而不必专门设计快反镜、压电陶瓷等微扫描驱动装置来产生亚像元位移，进一步的简化了系统，节约了成本。

综合以上分析，CX-6(02)星载荷采用CMOS探测器画幅式重采样来获得图像序列，探测器最大帧频为35帧/s。卫星相对于地面的运动速度较快，为了能够对同一地物目标多次成像，要通过控制卫星姿态来降低CMOS探测器在地面上的投影沿轨道方向的运动速度，以下对这种成像补偿方式简称为地速补偿，补偿前后探测器投影相对于地面的运动速度之比称为地速补偿比，记为 $R$ 。卫星姿态控制误差引起的俯仰、偏航、滚转的姿态稳定度为±8×10^–3(°)/s，这3个轴的控制偏差是产生亚像元位移的主要因素。

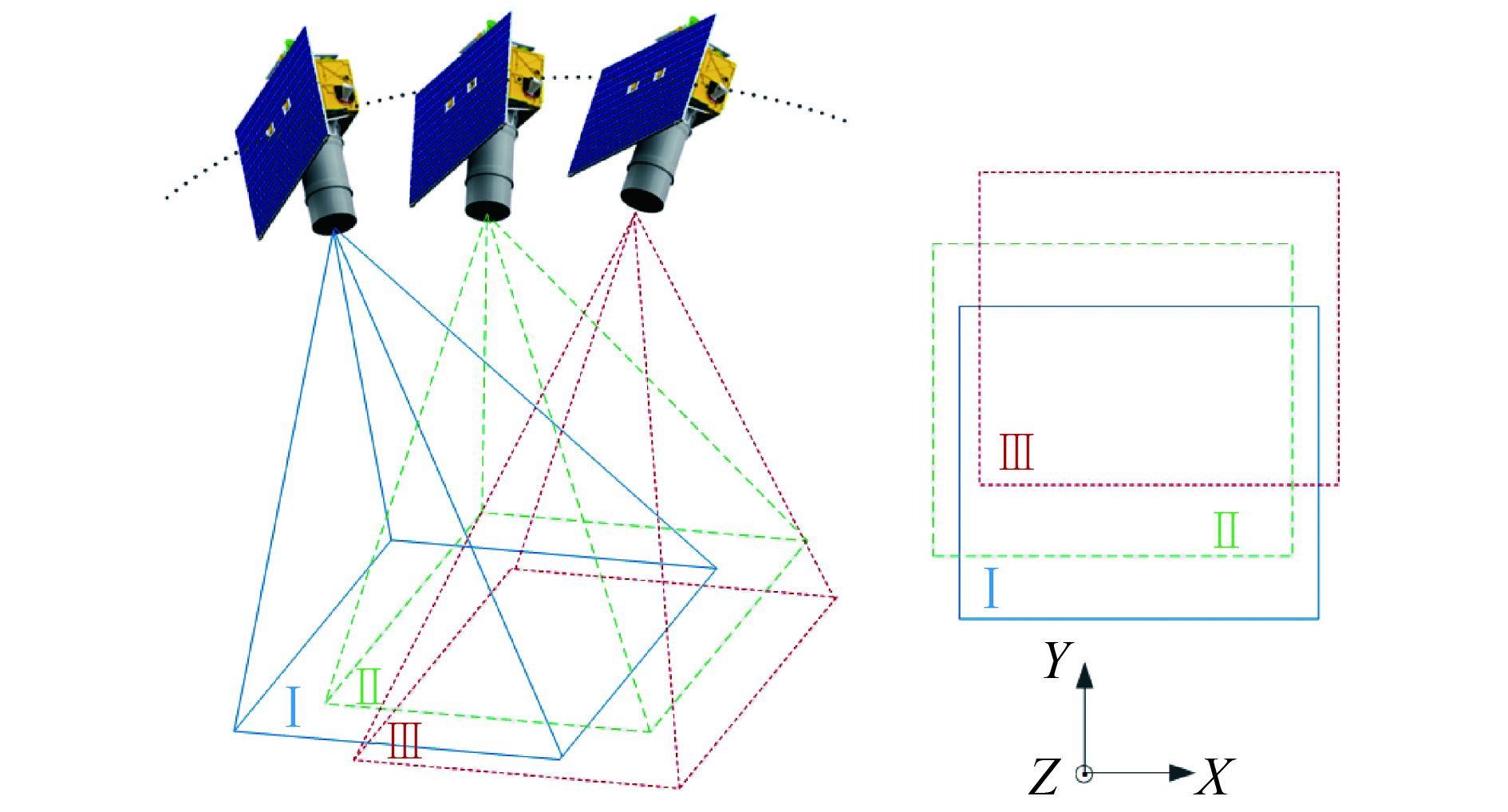
如图1所示，以3帧图像为例，第Ⅰ、Ⅱ、Ⅲ帧图像重叠区域就构成了目标多次采样的图像序列。图像之间的相对位移可以分解为图像坐标系下的X方向位移和Y方向位移，以及光轴指向方向Z的旋转位移。若对同一目标区域观测 $K$ 次， $k = 1, 2, \cdots, K$ ，将图像序列的第1帧图像作为参考图像，则第k帧图像的旋转位移为

${\theta _k} = {D_{{\textit{z}}k}} - {D_{{\textit{z}}1}}$

(1)

式中， ${D_{{\textit{z}}1}}$ 为参考图像的旋转角度，一般为0， ${D_{{\textit{z}}k}}$ 表示第 $K$ 帧图像的由偏航角控制偏差导致的图像旋转，由于其最大仅为8×10^–3°，因此在成像分析时可暂时忽略。X方向的位移主要表现为在卫星滚转稳定度范围内的随机摆动，第 $k$ 帧图像相对于图像序列的第1帧图像的沿X方向的位移为

${c_k} = H\left( {\tan ({D_{{\rm{x}}k}}) - \tan ({D_{{\rm{x}}1}})} \right)/GSD$

(2)

式中， $H$ 表示轨道高度， $GSD$ 表示地面像元分辨率， ${D_{{\rm{x}}k}}$ 为第 $K$ 帧图像对应的滚转姿态控制偏差角。Y方向的位移表现为沿轨方向的前向运动，第 $k$ 帧图像相对于第1帧沿Y方向的位移为

${d_K} = \frac{{(K - 1)v/R}}{{GSD \cdot {f_{\rm{p}}}}} + \frac{H}{{GSD}}\left( {\sum\limits_{k = 2}^K {\tan ({D_{yk}})} - \tan ({D_{y1}})} \right)$

(3)

式中， $v$ 表示卫星沿轨运动速度， ${f_{\rm{p}}}$ 为帧频， ${D_{yk}}$ 和 ${D_{y1}}$ 表示第 $k$ 帧图像及参考图像对应的俯仰姿态控制偏差角。由公式(3)可知重采样目标区域的像元行数 ${m_{{\rm{OY}}}}$ 为

${m_{{\rm{OY}}}} = {m_Y} - {d_K}$

(4)

式中， ${m_Y}$ 为Y方向图像的行数。由于 ${D_{zk}}$ 、 ${D_{xk}}$ 、 ${D_{yk}}$ 会在–8×10^–3°到8×10^–3°随机变化，因此图像序列的位移 ${\theta _k}$ 、 ${c_k}$ 和 ${d_K}$ 具有较强的随机性。

在X或Y方向的位移可以表示为 $[m({b / a})]$ 个像元，其中分数部分 $({b / a})$ 即为亚像元位移。对于超分辨率重建来说，如果分数部分 $({b / a}) = 0$ ，整数部分 $m$ 无论如何变化都是无效的；而如果几帧图像相对于基准图像位移的分数部分都相等，那么即便它们的整数部分不同，也相当于只有一个有效的亚像元位移值，因此，为了提高计算效率，可通过配准结果对无效亚像元位移图像进行剔除，考虑到配准本身的误差，在实际执行时剔除的阈值选为0.05像元。

    (2.2) 超分辨率重建算法

对目标区域 $K$ 次观测构成的图像序列记为 ${{{y}}_k}$ ，每帧图像像元数为 $N$ ， ${{x}}$ 为目标的高分辨率图像，像元数为 $P$ ，根据成像链路，观测方程可以表示为

${{{y}}_k} = {{A}} {{HC}}({{{s}}_k}) {{x}} + {{{n}}_k}$

(5)

式中， ${{A}}$ 为探测器下采样函数， ${{H}}$ 为大气等外界环境和光学系统共同导致的点扩散函数， ${{C}}({{{s}}_k})$ 为包含亚像元信息的位移函数， ${{{s}}_k} = {({\theta _k}, {c_k}, {d_k})^{\rm{T}}}$ ， ${{A}}$ 、 ${{H}}$ 、 ${{C}}({{{s}}_k})$ 、 ${{x}}$ 四者之间为卷积关系， ${{{n}}_k}$ 为加性噪声。根据贝叶斯公式，可以写出式(5)的概率形式解为

$p({{x}}|{{{y}}_k}) = {{p({{{y}}_k}|{{x}})p({{x}})} / {p({{{y}}_k})}}$

(6)

式中，等号左侧的条件概率为要求的超分辨率重建结果；等号右侧第1项和第3项与获取的图像数据 ${{{y}}_k}$ 有关；等号右侧第2项与重建结果 ${{x}}$ 的解空间有关，是 ${{x}}$ 的先验概率。超分辨率重建就是对等号右边的3项分别进行建模并迭代求解建模参数。

若噪声 ${{{n}}_k}$ 服从高斯分布，则条件概率 $p({{{y}}_k}{{|x}})$ 可以建模为

$p({{{y}}_k}{\rm{|}}{{x}},{{{s}}_k},{\beta _k}) \propto \beta _k^{N/2}\exp \left( { - \frac{{{\beta _k}}}{2}{{\left\| {{{{y}}_k} - {{AHC}}({{{s}}_k}){{x}}} \right\|}^2}} \right)$

(7)

式中， $\,{\beta _k}$ 为高斯分布方差的倒数，服从Gamma分布： $p(\,{\beta _k}) \propto \Gamma (\,{\beta _k}|a_\beta , b_\beta )$ ；为抑制配准误差， ${{{s}}_k}$ 服从均值 ${{\bar{ s}}_k}$ 、方差 ${{{S}}_k}$ 的高斯分布。则 $p({{{y}}_k}|{{x}})$ 可以表示为

$p({{{y}}_k}{{|x}}) \propto p({{{y}}_k}|{{x}}, {{{s}}_k}, \alpha, {\beta _k})p({{{s}}_k})p(\,{\beta _k})$

(8)

图像中每个像元点可以用马尔可夫模型描述，则先验概率 $p({{x}})$ 可表示为吉布斯分布

$p({{x}}|\alpha ) = Z(\alpha )\exp \left( { - \alpha U({{x}})} \right)$

(9)

式中， $Z(\alpha)$ 为关于常数 $\alpha $ 的配分函数， $U({{x}})$ 为对重建结果 ${{x}}$ 具有约束作用的能量函数，需具有较强的空间约束性。L1范数模型或全变分模型均通过建立图像中每个像元点相邻水平和垂直的两个点的关系来对方程的求解空间进行约束，这种建模方式有利于重建图像的边缘信息，但是对图像非边缘区域约束较差，而大气扰动等因素会降低遥感图像非边缘区域的信噪比并体现出一定的不均匀性，如果先验模型仅对图像边缘信息进行约束就会放大图像非边缘区域的噪声或非均匀性，导致超分辨率重建结果产生较大的异常值。作为改进，在CX-6(02)星的超分辨率重建中采用如下形式的加权双向差分先验模型

$p({ x}|\alpha ) = {(\alpha )^{\frac{P}{2}}}\exp \left( { - \alpha \sum\limits_{i = 1}^P {\left( {\sqrt {{\Lambda _i}({{x}})} } \right)} } \right)$

(10)

$\begin{split} {\Lambda _i}({{x}}) = & {\left( {\Delta _{hi}^ \leftarrow ({{x}})} \right)^2} + {\left( {\Delta _{vi}^ \uparrow ({{x}})} \right)^2} + \\ & {\textit{λ}} \left( {{{\left( {\Delta _{hi}^ \to ({{x}})} \right)}^2} + {{\left( {\Delta _{vi}^ \downarrow ({{x}})} \right)}^2}} \right) \end{split}$

(11)

式中，“箭头”符号表示沿着该方向向 ${x_i}$ 相邻的像元点取一阶差分， ${\Delta _{hi}}$ 和 ${\Delta _{vi}}$ 分别表示水平和垂直方向的差分矩阵算子，引入常数权值 ${\textit{λ}} $ 作为约束强度因子，从差分方向来讲，该先验函数相当于沿着像元 ${x_i}$ 水平和垂直的正负两个方向做差分。该模型通过建立每个像元点和其周围4个像元点的不一致关系对高频噪声加以约束，进一步增强了先验模型的空间约束性，更能削弱反卷积本身造成的噪声放大和传播等缺点，使算法在重建图像边缘信息的同时能够保证较高的信噪比，从而进一步的减轻成像方程求解的病态性。参数 $\alpha $ 服从与参数 ${\beta _k}$ 形式相同的Gamma分布，则先验概率模型为

$p({{x}}) = p({{x}}|\alpha)p(\alpha)$

(12)

将式(8)和式(12)代入式(6)得

$\begin{split} p({{x}},{{{s}}_k},\alpha ,{\beta _k}|{{{y}}_k}) = & p({{{y}}_k}|{{x}},{{{s}}_k},{\beta _k})p({{{s}}_k}) \times \\ & p({\beta _k})p({{x}}|\alpha )p(\alpha )/p({{{y}}_k}) \end{split}$

(13)

由于难以对分布 $p({{{y}}_k})$ 进行建模，因此引入变分贝叶斯模型(Heinrich和Goesele，2009)解决该问题，如下式所示

$\begin{split} \hat q(\Theta ) = & \arg \min {C_{{\rm{KL}}}}(q(\Theta )\left\| {p(\Theta |{{y}})} \right.)\approx \\ & \arg \min \left( {\int q(\Theta )\log (\frac{{q(\Theta )}}{{p(\Theta ,{{y}})}}){\rm{d}}\Theta } \right) \end{split}$

(14)

通过使分布 $q(\Theta)$ 与联合分布 $p{\rm{(}}\Theta |{{y}})$ 之间的相对熵 ${C_{{\rm{KL}}}}$ 最小来获得分布 $p{\rm{(}}\Theta |{{y}})$ 的近似分布 $\hat q(\Theta)$ 。根据最大最小方法，求式(14)的最小值就是要求 $p{\rm{(}}\Theta, {{y}})$ 下边界的最大值，即

$\max \left( {\inf \left( {p({{{y}}_k}|{{x}},{{{s}}_k},{\beta _k})p({{{s}}_k})p({\beta _k})p({{x}}|\alpha )p(\alpha )} \right)} \right)$

(15)

式(15)下边界的最大值由先验分布 $p({{x}}|\alpha)$ 决定，根据几何均值不等式，引入辅助向量 ${{w}}$ ，可得 $p({{x}}|\alpha)$ 最大值

$\gamma ({{x}},\alpha ,{{w}}) = {(\alpha )^{P/2}}\exp \left( { - \alpha \sum\limits_i {\frac{{{\Lambda _i}({{x}}) + {w_i}}}{{2\sqrt {{w_i}} }}} } \right)$

(16)

因此，式(14)变为

$\hat q(\Theta) = \arg \min \int {{q} (\Theta)\log \frac{{{q} (\Omega)}}{{p(\Omega)\varUpsilon ({ x}, \alpha, { w})}}} {\rm{d}}\Theta $

(17)

集合 ${{\varOmega}} = \{ {{x}}, {\beta _k}, {{{s}}_k}, \alpha \} $ ，各未知量之间相互独立：

${q} (\varTheta) = {q} ({ x})\prod\limits_{k = 1}^K {{q} ({\beta _k})} {q} ({{{s}}_k}){q} (\alpha)$

(18)

再对式(17)分别对分布 ${q} ({{x}})$ 、 ${q} ({\beta _k})$ 、 ${q} ({{{s}}_k})$ 、 ${q} (\alpha)$ 求导并取值为零，即可求出各未知量的解析表达式。

$\begin{split} q({{x}}) \propto \exp & \left( { - \frac{1}{2}\left\langle \alpha \right\rangle \sum\limits_{i = 1}^P {\frac{{{\Lambda _i}({{x}}) + {w_i}}}{{\sqrt {{w_i}} }}} - } \right.\\ & \left. {\frac{1}{2}\sum\limits_k {\left\langle {{\beta _k}} \right\rangle {E_{{{{s}}_k}}}\left[ {{{\left\| {{{{y}}_k} - {\bf{AHC}}({{{s}}_k}){{x}}} \right\|}^2}} \right]} } \right) \end{split}$

(19)

式中，符号 $\left\langle \cdot \right\rangle $ 和 ${E_{{{{s}}_k}}}[ \cdot ]$ 表示数学期望，对函数 ${{C}}({{{s}}_k})$ 在均值 ${{\bar{ s}}_k}$ 处进行一阶泰勒展开

$\begin{split} & {E_{{{{s}}_k}}}\left[ {{{\left\| {{{{y}}_k} - {\bf{AHC}}({{{s}}_k}){{x}}} \right\|}^2}} \right] \approx{\left\| {{{{y}}_k} - {\bf{AHC}}({{{\bar{ s}}}_k}){{x}}} \right\|^2}+\\ & \sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {{\zeta _{kij}}{{{x}}^{\rm{T}}}{{{O}}_{ki}}{{({{{\bar{ s}}}_k})}^{\rm{T}}}{{{O}}_{kj}}({{{\bar{ s}}}_k}){{x}}} } \end{split}$

(20)

式中， ${\zeta _{kij}}$ 为协方差矩阵 ${{S}}_k$ 的元素。表达式 ${{{O}}_{ki}}({{\bar{ s}}_k}) = $ $ {\bf{AH}}{{\bf{N}}_i}({{\bar{ s}}_k})$ ， ${{{N}}_i}({{\bar{ s}}_k})$ 为

$\begin{split} [{{{N}}_1}({{{\bar{ s}}}_k}){{x}}, &{{{N}}_2}({{{\bar{ s}}}_k}){{x}},{{{N}}_3}({{{\bar{ s}}}_k}){{x}}] = [({{{P}}_1}({{{\bar{ s}}}_k}){{{M}}_1}({{{\bar{ s}}}_k}) + \\ & {{{P}}_2}({{{\bar{ s}}}_k}){{{M}}_2}({{{\bar{ s}}}_k})){{x}},{{{M}}_1}({{{\bar{ s}}}_k}){{x}},{{{M}}_2}({{{\bar{ s}}}_k}){{x}}] \end{split}$

(21)

${{{P}}_1}({{\bar{ s}}_k})$ 、 ${{{P}}_2}({{\bar{ s}}_k})$ 、 ${{{M}}_1}({{\bar{ s}}_k})$ 、 ${{{M}}_2}({{\bar{ s}}_k})$ 分别为

${{{P}}_1}({{\bar{ s}}_k}) = diag(- u\sin ({\theta _k}) - v\cos ({\theta _k}))$

(22)

${{{P}}_2}({{\bar{ s}}_k}) = diag(u\cos ({\theta _k}) - v\sin ({\theta _k}))$

(23)

$\begin{split} {{{M}}_1}({{{\bar{ s}}}_k}) = & ({{I}} - {{{V}}_{{{\bar s}_k}}})({{{L}}_{tr({{\bar s}_k})}} - {{{L}}_{tl({{\bar s}_k})}}) + \\ & {{{V}}_{{{\bar s}_k}}}({{{L}}_{br({{\bar s}_k})}} - {{{L}}_{bl({{\bar s}_k})}}) \end{split}$

(24)

$\begin{split} {{{M}}_2}({{{\bar{ s}}}_k}) = & ({{I}} - {{{U}}_{{{\bar s}_k}}})({{{L}}_{bl({{\bar s}_k})}} - {{{L}}_{tl({{\bar s}_k})}}) + \\ & {{{U}}_{{{\bar s}_k}}}({{{L}}_{br({{\bar s}_k})}} - {{{L}}_{tr({{\bar s}_k})}}) \end{split}$

(25)

式(24)和(25)中， ${{{U}}_{{{\bar s}_k}}}$ 、 ${{{V}}_{{{\bar s}_k}}}$ 分别表示配准投影转换矩阵， ${{{L}}_{bl({s_k})}}$ 、 ${{{L}}_{br({s_k})}}$ 、 ${{{L}}_{tl({s_k})}}$ 、 ${{{L}}_{tr({s_k})}}$ 分别表示双线性插值权重算子(He 等，2007)。

将式(20)代入到(19)中，则 ${q} ({{x}})$ 服从均值为 ${\hat{ x}}$ ，协方差为 ${{{\Sigma }}_{{\hat{ x}}}}$ 的多变量高斯分布(Babacan 等，2011)， ${\hat{ x}}$ 可通过下式求解

${\left[ {{{{\Sigma }}_{{\hat{ x}}}}} \right]^{ - 1}}{\hat{ x}} = \sum\limits_k {\left\langle {{\beta _k}} \right\rangle {{[{\bf{AHC}}({{{\bar{ s}}}_k})]}^{\rm{T}}}{{{y}}_k}} $

(26)

其中，

$\begin{split} {\left[ {{{{\Sigma }}_{\hat x}}} \right]^{ - 1}} = & \sum\limits_k {\left\langle {{\beta _k}} \right\rangle {{[{\bf{AHC}}({{{\bar{ s}}}_k})]}^{\rm{T}}}} {\bf{AHC}}({{{\bar{ s}}}_k}) + \\ & \sum\limits_k {\sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {\left\langle {{\beta _k}} \right\rangle {\zeta _{kij}}{{{x}}^{\rm{T}}}{{{O}}_{ki}}{{({{{\bar{ s}}}_k})}^{\rm{T}}}{{{O}}_{kj}}({{{\bar{ s}}}_k})} } } + \\ & \left\langle \alpha \right\rangle {[{\Lambda _i}({{x}})]^{\rm{T}}}\sqrt {{w}} [{\Lambda _i}({{x}})] \end{split}$

(27)

辅助变量矩阵表示为 ${{w}} = diag({1 / {{\Lambda _i}(x)}})$ 。参数 $\alpha = P\sum\limits_i {{{(\sqrt {{w_i}})}^{ - 1}}} /2$ ； $\, \beta = P/||{{{y}}_k} - {\bf{AHC}}({{{s}}_k}){{x}}|{|^2}$ 。

对于配准参数分布 ${q} ({{{s}}_k})$ ，服从高斯分布 $N({{{s}}_k}|{{\bar{ s}}_k}, {{{S}}_k})$ ，可通过如下迭代过程对配准参数进行求解

$\begin{split} {\left[ {{{{\bar{ s}}}_k}} \right]_{n + 1}} = & {{{S}}_k}[{({{S}}_k^p)^{ - 1}}{\bar{ s}}_k^p + \\ & \left\langle {{\beta _k}} \right\rangle ({{{\varGamma }}_k}{\left[ {{{{\bar{ s}}}_k}} \right]_n} + {{{\varPsi }}_k}{\left[ {{{{\bar{ s}}}_k}} \right]_n} + {{{Q}}_k} - {{{\varPhi }}_k})] \end{split}$

(28)

式中， ${\left[ {{{{\bar{ s}}}_k}} \right]_{n + 1}}$ 表示第n+1次迭代， ${\left[ {{{{\bar{ s}}}_k}} \right]_n}$ 表示第n次迭代结果， ${{{S}}_k} = {({{S}}_k^p)^{ - 1}} + \left\langle {{\beta _k}} \right\rangle ({{{\varPsi }}_k} + {{{\varGamma }}_k})$ ； ${{{\varPhi }}_k}$ 和 ${{{Q}}_k}$ 为3×1维向量，元素分别为

${{{\varPhi}} _{ki}} = trace[{({\bf{AHC}})^{\rm{T}}}{{{O}}_{ki}}({{\bar{ s}}_k}){{{\Sigma }}_{{\hat{ x}}}}]$

(29)

${{{Q}}_{ki}} = {[{y_k}{{ - }}{\bf AHC}({s_k})x]^{\rm{T}}}{{{\psi }}_{ki}}$

(30)

${{{\varPsi }}_k} = [{{{O}}_{k1}}({{\bar{ s}}_k}){\hat{ x}}, {{{O}}_{k2}}({{\bar{ s}}_k}){\hat{ x}}, {{{O}}_{k3}}({{\bar{ s}}_k}){\hat{ x}}]$

(31)

式(29)、式(30)、式(31)中，下标 $i = 1, 2, 3$ 。

${{{\varPsi }}_k}$ 和 ${{{\varGamma }}_k}$ 为3×3维矩阵，元素分别为

${{{\varPsi}} _{kij}} = trace[{{{O}}_{ki}}{({{\bar{ s}}_k})^{\rm{T}}}{{{O}}_{kj}}({{\bar{ s}}_k}){\Sigma _{{\hat{ x}}}}]$

(32)

${{{\varGamma}} _{kij}} = \psi _{ki}^{\rm{T}}{\psi _{kj}}$

(33)

式中，下标 $i, j = 1, 2, 3$ 。

将式(27)、式(28)代入到式(26)中，利用共轭梯度等方法即可求出超分辨率重建结果 ${\hat{ x}}$ 。

3、超分辨结果与分析     (3.1) 亚像元位移分析

对中国包头遥感定标场区域的图像序列进行分析，提取25帧图像X方向和Y方向的亚像元信息，并分别按从小到大的顺序重新排序，如图2所示，图像序列可覆盖0.1像元量级的亚像元信息，可保证为重建算法提供充分的亚像元参数，因此，本文中利用卫星姿态控制偏差来获得随机亚像元信息的方式是有效可行的。

    (3.2) 算法对比分析

对该组图像序列进行超分辨率重建，并分别与基于L1范数先验模型和全变分先验模型的变分贝叶斯方法重建结果进行对比，扇形分辨率靶标和刃边靶标的原始成像以及3种算法的超分辨率重建结果如图3所示。首先，通过对扇形分辨率靶标的测量来分析算法对分辨率的提升效果，由于难以测量图像的绝对几何分辨率，因此，用相对分辨率的方式来对靶标进行测量，具体判定方法为：设扇形靶标半径为 $L$ ，靶标共包含16根白色靶标线和15根黑色靶标线，沿扇形靶标的圆心向圆周做同心圆弧，考查所做圆弧上各点对应的图像上的灰度值。

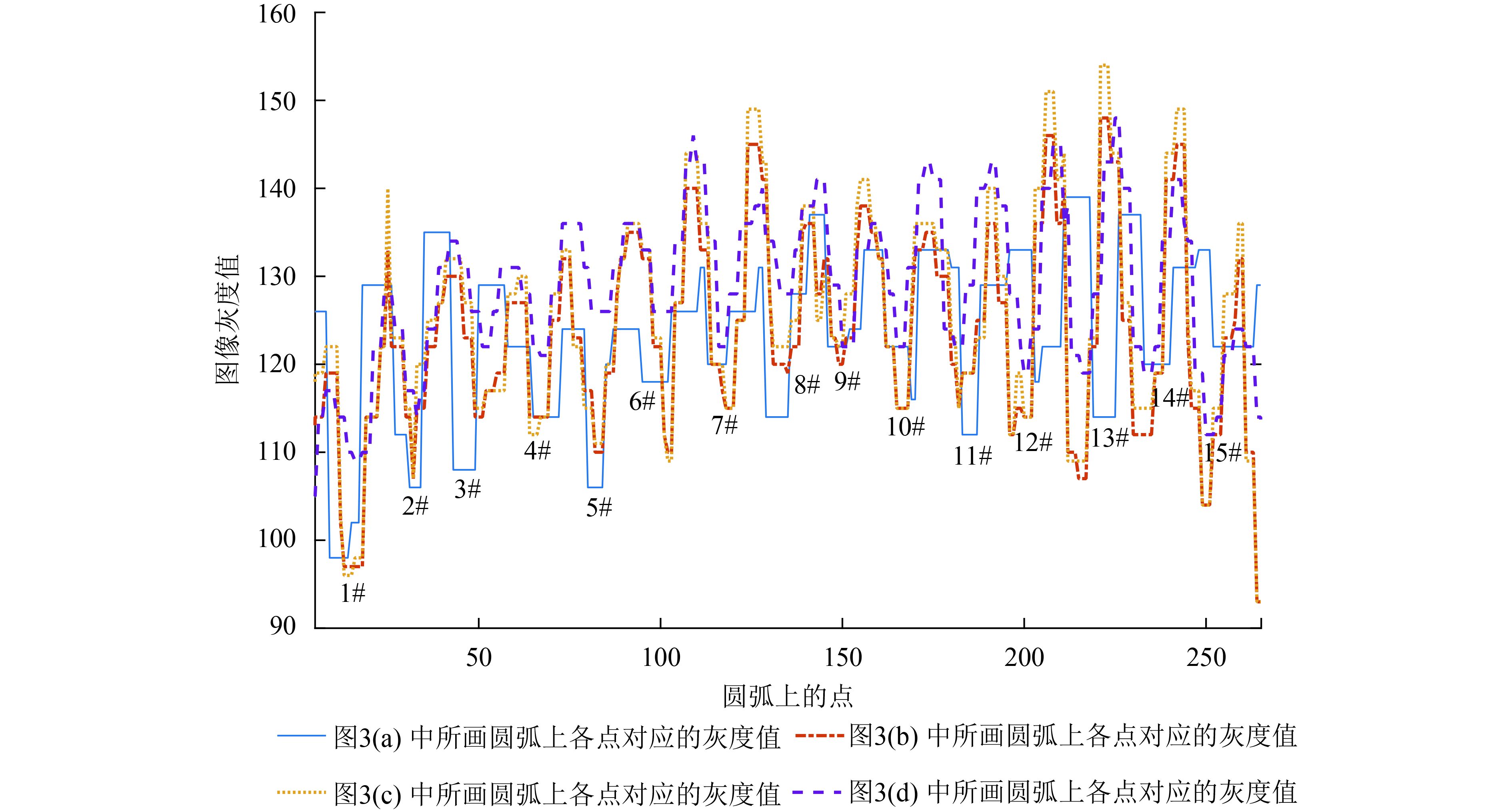
当黑白线对恰能分辨时，圆弧各点对应的图像灰度值构成的曲线应有15个能够清晰识别的“波谷”，此时，所画圆弧的半径记为 $R$ ，那么图像的相对分辨率为 $({{L - R)} / L}$ 。扇形靶标沿圆心的最大半径对应的圆弧如图3(a)中虚线“--”标识所示，对应半径 $L$ 约为70.0个像元。分别对图3(a)、(b)、(c)、(d)的扇形靶标按以上方法在图中画圆弧进行分辨率测量，如各图中实线“-”标识所示。

图3(a)、(b)、(c)、(d)中圆弧对应的像元灰度值如图4所示，图4中的标注的1#—15#即为扇形靶标恰能分辨时对应的15根黑色靶标线。图3(a)圆弧对应半径为52.5个像元，图3(b)、(c)、(d)的圆弧对应半径均为33.5个像元，因此基于全变分先验、基于L1范数先验、基于加权双向差分先验的变分贝叶斯算法重建结果的相对分辨率都为0.52，原图的相对分辨率为0.25，那么，算法对于分辨率的提升约为2倍。

其次，从对噪声的抑制作用来看，视觉上本文方法的重建结果要明显优于其他两种方法，采用如图3(a)中标注的A、B、C 3个灰阶靶标来量化的评价算法对噪声的抑制效果，计算方法为：在图3(a)的灰阶靶标A处选取一块灰度分布较为均匀的ROI区域，然后在图3(b)、(c)、(d)的灰阶靶标A上选取与图3(a)所选区域坐标相同的ROI区域，这4块ROI区域都记为区域A，用区域内所有像元灰度均值与方差之比来估算该区域的信噪比 (朱博 等，2010)。灰阶靶标B和C信噪比的计算方式与A相同。估算结果如表1所示，本文方法重建结果在A、B、C区域的信噪比估算值均高于原始图像和其他两种算法，对原始图像噪声和计算噪声均有较好的抑制作用。

因此，基于L1范数先验和基于全变分先验的算法重建结果对于图像非边缘信息的约束均劣于本文算法，特别如灰阶靶标这样灰度均匀且面积较大的地物目标上体现的更为明显，从视觉上这两种算法的结果均具有一定的“布纹”感，且随着算法迭代次数的增加这种现象也会逐渐增强，导致信噪比下降。这就说明L1先验模型和全变分先验模型均未对观测方程的解空间起到较好的约束作用，在计算中引入了新的噪声，反卷积运算导致的强病态性未得以解决。而与原图相比，本文提出的基于加权双向差分先验模型的变分贝叶斯算法在图像的分辨率和信噪比上都保持了较好的像质提升，且在获得最优解后随迭代次数的增加像质保持不变，没有引入明显的计算噪声，从而对方程的解空间起到了更好的约束作用，削弱了反卷积的病态性。

CX-6(02)星除可获得全色波段的超分辨率图像外，还可获得同一地物目标区域的红、绿、蓝、及两个近红外，共5个多光谱波段的图像，从而可利用全色增强(Pan-Sharpening)算法(Sun 等，2017)进行超分辨图像与多光谱图像的融合，提高多光谱伪彩色合成图像的空间分辨率，卫星对鸟巢和水立方区域的伪彩色合成结果如图5(a)所示，图5(b)为图5(a)中鸟巢和水立方的局部放大结果，图5(c)为图5(b)表示区域的全色波段超分辨率重建结果与红、绿、蓝波段伪彩色图像的融合结果，融合后图5(c)的灰度平均梯度GMG(Gray Mean Gradient)是图5(b)的1.43倍，因此图5(c)具有更多的纹理特征，视觉上鸟巢和水立方的顶部细节表现力明显增强，进一步提高了卫星数据的应用价值。

4、结　论

本文提出一种星载超分辨率成像方案：图像获取设计上，将高帧频面阵CMOS探测器与卫星地速补偿相结合，通过姿态控制随机偏差来获得同一区域的多帧具有亚像元位移的图像；超分辨率重建算法设计方面，在变分贝叶斯框架下，提出了加权双向差分先验模型，进一步削弱反卷积运算的病态性。经CX-6(02)微纳卫星真实成像数据验证，本文图像获取方法可得到分布较为充分的亚像元位移信息，与同为变分贝叶斯框架的L1范数和全变分先验算法相比，本文重建算法具有较好的噪声抑制作用，可实现2倍分辨率的提升，为高分辨率对地遥感提供了一定的理论和试验支撑。

超分辨算法的初衷是解除因探测器奈奎斯特采样频率低于光学截止频率导致的频谱混叠，因此，超分辨率重建的效能与光学系统设计参数密切相关，需要围绕算法效能参数对成像系统进行整体优化；另外，还需在本文提出的先验模型基础上，结合图像的边缘特征和非边缘特征进一步对变分贝叶斯超分辨重建算法进行优化。这都是未来研究工作的重要方向。

志 谢 CX-6(02)星图像数据的存储和传输获得了中国科学院遥感与数字地球研究所中国遥感卫星地面站卫星数据技术部的大力支持，在此致以诚挚的感谢。