| 资源三号卫星影像无控制区域网平差 |
收稿日期: 2018-02-09
2. Chinese Academy Surveying & Mapping, Beijing 100830,China
3. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
近些年来,国产卫星的空间分辨率、辐射分辨率得到了跨越式提高。通过“资源三号”等系列立体测图卫星的研制和应用,中国在测绘卫星传感器设计、制造与几何标定等方面的技术水平大幅提高。但由于成像系统一般采用CCD线阵成像技术,长焦距和窄视场角导致其几何模型具有近似空间3维平行投影的特点,严密在轨几何检校后仍会存在残余系统误差,为满足遥感监测、测图等应用需求,仍需进行区域网平差处理。因此,无需地面控制信息的卫星影像精准对地定位成为获取全球地理和资源环境信息,监测全球资源环境变化等的先决条件。
在进行高分辨率光学卫星影像的高精度无控制定位时,由于缺少控制点的约束,直接将待平差参数作为自由未知数会导致法方程矩阵的病态(秩亏),使得平差精度不稳定且误差容易过度累积而引起网的扭曲变形。为了提高定位的精度,研究人员开展了一系列相关的研究。将高分辨率光学卫星影像的高精度无控制区域网平差总结为在无地面控制情况下,引入特定约束(距离、角度等)的多源光学卫星影像联合区域网平差处理。其中一类方法是影像经过在轨几何标定,获得处于同一数量级的对地定位精度(如50 m左右)后,针对传感器成像特点,选择特定的后续区域网平差模型进行影像的区域网平差处理(李德仁和王密,2012;唐新明 等,2017;王任享 等, 2013, 2015, 2016);或利用待平差影像的初始RPC模型生成均匀分布的虚拟控制点,并将其作为带权观测值引入平差模型实现无控制区域网平差(龚健雅 等,2017;王密 等,2017;杨博 等,2017)。另一类方法则通过引入多源控制信息(SAR影像、高精度的光学卫星影像)来进行“无控制”区域网平差(刘楚斌 等, 2015, 2016;陈源源 等,2015);或采用独立模型法、最小高差(LZD)法等直接通过待处理影像与公众地理信息数据控制基准自动匹配一定数量的所谓的“控制点”作为虚拟控制点进行卫星影像的无控制定位(汪韬阳 等,2014;张浩 等,2016;陈小卫 等,2016)。综上所述,理论上有控制平差与无控制平差本质的区别在于,有控制平差中使用的是外业实测控制点,精度高且一致性好;而大多数无控制平差中使用的是一种虚拟控制点,这些虚拟控制点的精度较低(含有不同程度的系统误差)且精度在测区中是不一致的,所以无控制平差是不等精度控制下的区域网平差,其误差传播规律更加复杂,粗差检测与定位难度较大。
针对以上问题,本文提出了一种基于“平均值”虚拟控制点的大规模高分辨率光学卫星影像无控制区域网平差方法GISIBA(GCP-Independent Satellite Imagery Block Adjustment)。该方法在自动可靠地获取分布均匀的影像连接点的基础上,综合利用航空摄影测量中熟知的“交替趋近法”(王之卓,2007;Boyd 等,2011)和基于RFM的最小二乘平差算法来实现大区域卫星影像的联合平差处理。首先,利用交替趋近法实现并行处理平台基础上的待平差未知数初值的解算、中等尺度以上粗差的自动检测与剔除,并根据计算结果赋予所有未知数一定的先验权值;然后通过最小二乘法实现大规模改化法方程的解算,获得满足高精度影像产品生产制作需求的高精度定向参数。通过构建虚拟的“平均值”控制点进行区域网平差,既解决了无控制平差中遇到的“秩亏”问题,改善了区域网平差系统的法方程状态从而有利于区域网的稳定和快速收敛;同时便于从理论上分析卫星影像无控制区域网平差结果与数据的覆盖次数及时相之间的关系。另外,为保证区域网平差的效率,基于OMP并行的方式实现了交替趋近未知数解算的并行处理及基于RFM的最小二乘平差的多线程并行计算。本文利用多组境内外典型试验区域的资源三号卫星(ZY-3)影像数据进行无控制区域网平差试验,验证所提方法的精度和实际性能。
2、GISIBA无控区域网平差模型 (2.1) 基于有理函数模型(RFM)的卫星影像区域网平差基于RFM的区域网平差模型可采用RFM模型配合其模型变换基础上的像方平移、仿射变换来实现(Dial和Grodecki,2003;张力 等,2009;Zhang 等,2012;Li 等,2017)。
本文采用在像方空间的变换方法,即像点的改正数用仿射变换表示
| $\begin{gathered} x + \Delta x = x + {a_0} + {a_1}x + {a_2}y = {{\rm RP{C}}_x}(\phi, \lambda, h) \\ y + \Delta y = y + {b_0} + {b_1}x + {b_2}y = {{\rm RP{C}}_y}(\phi, \lambda, h) \\ \end{gathered} $ | (1) |
式中,(x, y)为像点坐标,
| $\left[ {\begin{array}{*{20}{c}} {{{{v}}_{{{\rm TP}}}}}\\ {{{{v}}_{{{\rm GCP}}}}} \end{array}} \right]{{ = }}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{{A}}_{{{\rm TP}}}}}\\ 0 \end{array}} \right]}&{{{T}}{\rm{ + }}\left[ {\begin{array}{*{20}{c}} {{{{B}}_{{{\rm TP}}}}}\\ {{{{B}}_{{{\rm GCP}}}}} \end{array}} \right]} \end{array}{{X}} - \left[ {\begin{array}{*{20}{c}} {{{{l}}_{{{\rm TP}}}}}\\ {{{{l}}_{{{\rm GCP}}}}} \end{array}} \right]}&{\left[ {\begin{array}{*{20}{c}} {{{{P}}_{{{\rm TP}}}}}&0\\ 0&{{{{P}}_{{{\rm GCP}}}}} \end{array}} \right]} \end{array}$ | (2) |
式中,BTP, BGCP表示连接点、控制点地面坐标改正数系数矩阵;ATP表示仿射变换参数改正数系数矩阵,lTP, lGCP表示连接点观测和控制点观测的常数项矩阵,PTP, PGCP表示连接点、控制点的权阵。T为像方仿射变换参数改正数矩阵,X为地面点坐标改正数矩阵。
| $\begin{gathered} {{{T}}} = {\left[ \!\!\!\!\!\!{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\Delta {a_0}}&{\Delta {a_1}}&{\Delta {a_2}} \end{array}}&{\begin{array}{*{20}{c}} {\Delta {b_0}}&{\Delta {b_1}}&{\Delta {b_2}} \end{array}} \end{array}}\!\!\!\!\!\! \right]^{\rm T}} \\ {{X}} = {\left[\! {\begin{array}{*{20}{c}} {\Delta \varphi }&{\Delta \lambda }&{\Delta h} \end{array}} \! \right]^{\rm T}} \\ \end{gathered} $ | (3) |
依据最小二乘原理,相对应的法方程矩阵为
| $\left[ {\begin{array}{*{20}{c}} {{{A}}_{{{\rm TP}}}^{\rm{T}}{{{P}}_{{{\rm TP}}}}{{{A}}_{{{\rm TP}}}}}&{{{A}}_{{{\rm TP}}}^{\rm{T}}{{{P}}_{{{\rm TP}}}}{{{B}}_{{{\rm TP}}}}} \\ {{{B}}_{{{\rm TP}}}^{\rm{T}}{{{P}}_{{{\rm TP}}}}{{{A}}_{{{\rm TP}}}}}&{{{B}}_{{{\rm TP}}}^{\rm{T}}{{{P}}_{{{\rm TP}}}}{{{B}}_{{{\rm TP}}}}{{ + B}}_{{{\rm GCP}}}^{\rm{T}}{{{P}}_{{{\rm GCP}}}}{{{B}}_{{{\rm GCP}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{T}} \\ {{X}} \end{array}} \right]{{ = }}\left[ {\begin{array}{*{20}{c}} {{{A}}_{{\rm{TP}}}^{\rm{T}}{{{P}}_{{\rm{TP}}}}{{{l}}_{{\rm{TP}}}}} \\ {{{B}}_{{\rm{TP}}}^{\rm{T}}{{{P}}_{{\rm{TP}}}}{{{l}}_{{\rm{TP}}}}{{ + B}}_{{\rm{GCP}}}^{\rm{T}}{{{P}}_{{\rm{GCP}}}}{{{l}}_{{\rm{GCP}}}}} \end{array}} \right]$ | (4) |
式(4)可以简化为
| $\left[ {\begin{array}{*{20}{r}} {{{{N}}_{11}}}&{{{{N}}_{12}}}\\ {{{N}}_{12}^{\rm T}}&{{{{N}}_{22}}} \end{array}} \right]\left[ {\frac{{{T}}}{{{X}}}} \right] = \left[ {\begin{array}{*{20}{r}} {{{{u}}_1}}\\ {{{{u}}_2}} \end{array}} \right]$ | (5) |
式(5)所述的法方程矩阵为一对称带状矩阵。因此,区域网平差实际解算过程中,由于未知数较多,需将定向参数与待定点坐标未知数分开求解,即先消去一类未知数(一般消去待定点未知数X),得到仅含有一类未知数的改化法方程式
| $\left[ {{{{N}}_{11}} - {{{N}}_{12}}{{N}}_{22}^{ - 1}{{N}}_{12}^{\rm T}} \right]{{T }}= {{{u}}_1} - {{{N}}_{12}}{{N}}_{22}^{ - 1}{{{u}}_2}$ | (6) |
式(6)可利用循环分块法解算,当解算出一类未知数后,将其代入式(2)中解算另外一类未知数。区域网平差为一循环迭代过程,每次迭代时解算待定未知数的改正量并更新,将其用于下一次迭代,如此反复循环,直至整个平差系统满足预先设定的收敛条件为止。
(2.2) 基于“平均值”虚拟控制点的光学卫星影像无控制区域网平差方法GISIBA高分辨率光学卫星影像通常需要利用地面几何检校场进行规模化和定期化在轨几何检校恢复星上成像几何参数,即针对卫星平台的不稳定性及星载光学相机的结构特性采用高精度传感器校正方法,消除影像内部畸变,得到(单景)内部精度一致性良好且初始无控定位精度较好的影像数据。但即使影像产品经在轨几何检校修正系统误差及稳态重成像处理优化内部精度后,仍会存在因星载GPS/惯导的漂移误差、姿轨与行时之间的不同步等因素引起的残余系统误差,仍无法实现定位的可靠性,且影像间存在较显著的配准、拼接误差(唐新明 等,2017;龚健雅 等,2017)。一般情况下,这类残余系统误差在同一轨道或短时间间隔内成像的邻轨影像中呈现明显的系统性,即在不同的点位上,残余系统误差的大小和方向基本保持一致;但在覆盖同一区域的不同时相、较长时间间隔内成像的不同轨道影像中这些系统误差大小和方向是不同的,表现出一定的随机性,甚至可部分相互抵消(张过,2016)。
通过以上对影像残余系统误差特性的分析,同时考虑到区域网平差计算量巨大、且实际数据中存在的局部低重叠度、短基线、不规则区域网结构等影响区域网平差计算的效率和稳定性的问题,本文综合使用在交替趋近法和基于RFM的最小二乘平差方法,分两步来实现超大规模卫星影像的无控制区域网平差处理。
“交替趋近法”的基本思想是将大的全局最优化(凸优化)问题分解为多个较小(可并行化)、较容易求解的局部子问题,并通过协调子问题的解而得到大的全局问题的解(王之卓,2007)。首先,假定式(1)中每景影像的仿射变换参数(a0, a1, a2)和(b0, b1, b2)是已知的,则可计算出所有连接点的物方坐标值,即所谓的“前方交会”,该步骤对于每个连接点其法方程仅为一个3×3矩阵;其次,假定所有连接点的物方坐标已知,则可解算出每景影像的仿射变换参数(a0, a1, a2)和(b0, b1, b2),即所谓的“后方交会”,该步骤对于每景影像其法方程仅为一个6×6矩阵;通过反复循环上述两个步骤,直到所有未知数改正数的迭代变化值小于预先设定的阈值为止。交替趋近法的优点是适合于并行处理,因为每景影像仿射变换参数的解算、每个连接点物方坐标的计算是相互独立的,缺点是趋近迭代的次数较多,但用于本文中获得所有待平差未知数的初值已经符合要求了。
在交替趋近平差过程中,如果连接点k在n个立体像对中,则对n个地面坐标取平均作为该点的地面坐标,相当于通过“交替趋近法”构建了一种“平均值”虚拟控制点来解决无控平差时遇到的法方程矩阵的病态(秩亏)问题,该方法一方面可以利用并行计算来快速计算出待平差未知数初值,另一方面也利用“好”的初值最终进行最小二乘法平差。理论上该方法可以充分利用影像残余系统误差特性的分析,提高平差后卫星影像的定位精度,且方便的进行平差结果的精度分析。
具体可以表述为,对于出现在n(n≥2)个像对上的连接点k,假设连接点k通过第i(i=1, 2, ···, n)个立体像对的定向参数经前方交会计算得到的物方坐标为
| ${\left[ {\begin{array}{*{20}{c}} {{\varphi _{\rm k}}}&{{\lambda _{\rm k}}}&{{h_{\rm k}}} \end{array}} \right]^{\rm T}} = {\left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\sum\limits_{i = 1}^n {\varphi _{\rm k}^i} }}{n}}&{\displaystyle\frac{{\sum\limits_{i = 1}^n {\lambda _{\rm k}^i} }}{n}}&{\displaystyle\frac{{\sum\limits_{i = 1}^n {h_{\rm k}^i} }}{n}} \end{array}} \right]^{\rm T}}$ | (7) |
设该连接点的物方坐标真值为
| $\overrightarrow {{{r}}_{\rm{k}}^{{i}}} = {\left[ {\begin{array}{*{20}{c}} {\varphi _{\rm k}^i - \varphi _{\rm k}^o}&{\lambda _{\rm k}^i - \lambda _{\rm k}^o}&{h_{\rm k}^i - h_{\rm k}^o} \end{array}} \right]^{\rm T}}$ | (8) |
相应地,该连接点的“平均值”物方坐标的误差矢量为
| $\overrightarrow {{{{r}}_{\rm{k}}}} = {\left[ {\begin{array}{*{20}{c}} {{\varphi _{\rm k}} - \varphi _{\rm k}^o}&{{\lambda _{\rm k}} - \lambda _{\rm k}^o}&{{h_{\rm k}} - h_{\rm k}^o} \end{array}} \right]^{\rm T}}$ | (9) |
通过式(7)—式(9)可以得出
| $\overrightarrow {{{{r}}_{\rm k}}} = \frac{{\sum\limits_{{ i} = 1}^n {\overrightarrow {{{r}}_{\rm{k}}^{{i}}} } }}{n}$ | (10) |
假设连接点最大误差为
| $\left| {\overrightarrow {{{{r}}_{\rm{k}}}} } \right| = \left| {\frac{{\sum\limits_{i = 1}^n {\overrightarrow {{{r}}_{\rm{k}}^{{i}}} } }}{n}} \right| \leqslant \frac{{\sum\limits_{i = 1}^n {\overrightarrow {\left| {{{r}}_{\rm{k}}^{{i}}} \right|} } }}{n} \leqslant \left| {\overrightarrow {{{r}}_{\rm k}^{\max }} } \right|$ | (11) |
显然,利用式(11)可以方便地对GISIBA无控平差法的精度进行如下的精度分析。
(1) 假设参与处理的卫星影像的初始无控定位精度在同一数量级(如50 m左右),那么使用“平均值”虚拟控制点进行无控制区域网平差后,影像最终的定位精度一定会得到改善,最不利的情况下也不会弱于原有影像的最差初始定位精度;
(2) 假设卫星影像的初始无控定位精度在同一数量级,增加卫星影像的覆盖数不一定总是使无控定位精度得到快速提高,但在统计意义上可以认为覆盖同一区域的高分辨率卫星影像景数越多,其最终无控制区域网平差后定位精度改善的越多。
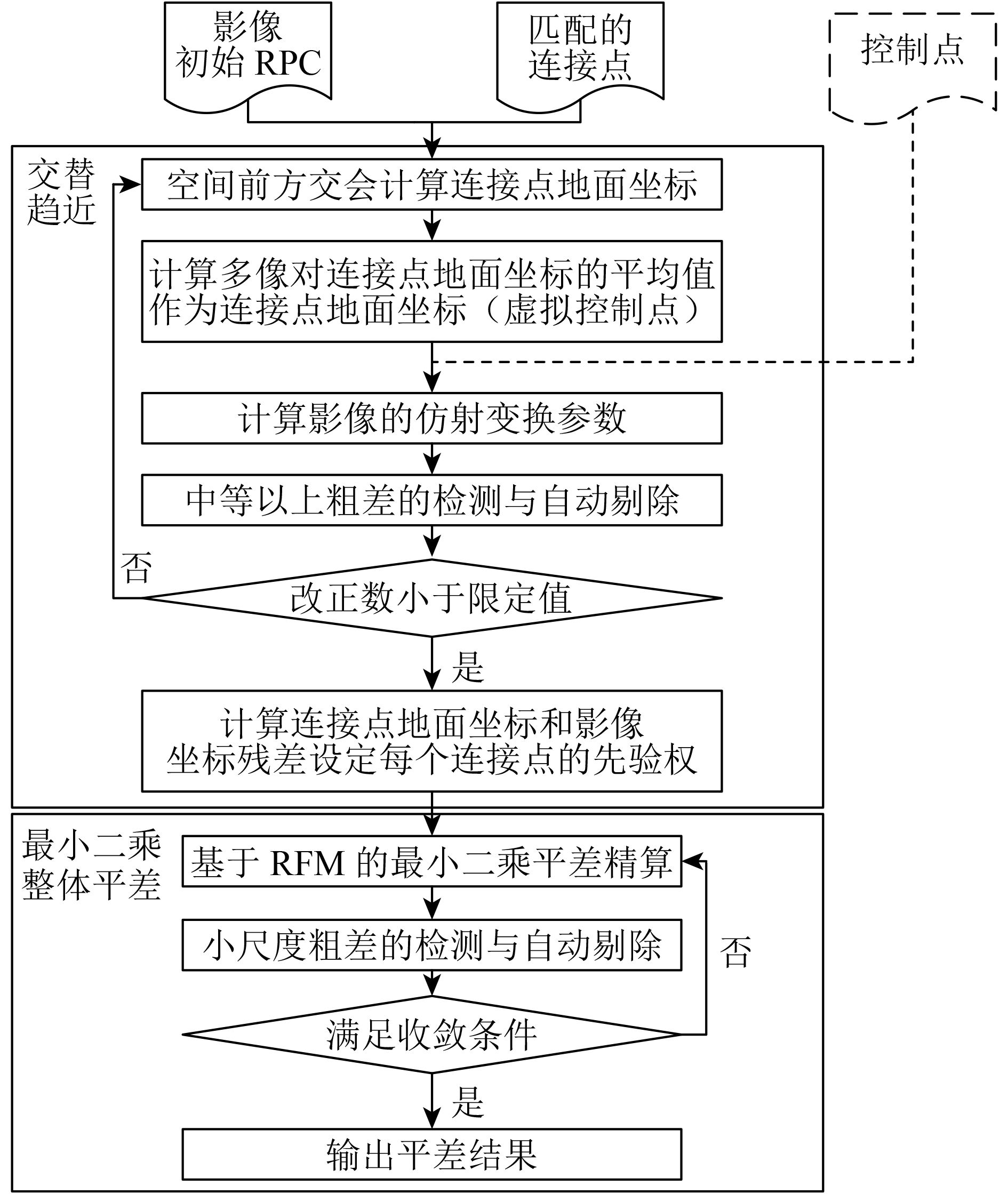
综上所述,本文采用的GISIBA光学卫星影像立体无控制区域网平差方法流程图如图1所示。
|
| 图 1 GISIBA光学卫星影像立体无控制区域网平差方法流程 Figure 1 Flow chart of GCP-Independent Satellite Imagery Block Adjustment (GISIBA) |
流程主要步骤可以总结为:
(1) 假设所有影像的仿射变换参数已知(每张影像的像方仿射变换参数改正数初值为0),根据连接点在多景影像上的像方坐标,以立体像对为基本单元,通过前方交会解算出连接点在该立体像对中的地面坐标
(2) 假设位于每景影像上连接点的地面坐标已知,可解算出该景影像的仿射变换参数,此过程中理论上需要至少3个点。该步骤对于每景影像涉及到一个法方程为6×6矩阵的平差计算步骤,根据平差后的单位权中误差
(3) 重复步骤(1)—(2),直至各影像仿射变换参数和连接点的地面坐标改正值小于某个限定值为止(本文选择0.2像素),迭代结束;
(4) 利用影像的仿射变换参数,针对每个连接点通过前方交会计算出其地面坐标和在相关影像上的像点坐标残差(vx, vy)i, i=1, ···, n,其中n为该连接点的“光线束”,即该点出现在n景影像中。令vi=sqrt(vx2+vy2),vmax=max(vi, i=1, ···, n),对每个连接点设定先验权p=1.0/
(5) 根据各连接点已经得出的地面坐标和相应的先验权,依据式(1)—式(4)执行基于RFM的最小二乘平差,并通过迭代选权策略剔除仍然存在的小尺度粗差(小尺度粗差的检测与自动剔除)(王之卓,2007;张力 等,2017)。
从上述描述可看出,本文算法的核心是通过构建“平均值”虚拟控制点进行完全不依赖于第3方地理空间数据和地面控制点的无控制区域网平差,目的是充分利用覆盖同一成像区域的长时间序列立体卫星影像残余系统误差所表现出的随机性,达到较高的最小二乘平差精度。考虑到算法的通用性,如果平差时有一定数量的地面控制点,控制点的地面坐标在迭代过程中保持不变。
3、试验数据与结果分析 (3.1) 试验数据与方案ZY-3是中国高分辨率立体测图卫星,主要目标是获取三线阵立体影像和多光谱影像;资源三号01星、02星分别于2012年、2016年发射成功,两星已形成有效互补,实现双星在轨稳定运行。ZY-3影像经过检校场在轨几何标定后单景无控制精度达到15 m,内部精度优于1个像素,经过后续无地面控制区域网平差处理后,影像的平面和高程精度可进一步提高到5 m(中误差)(李德仁和王密,2012;唐新明 等,2017;龚健雅 等,2017;王密 等,2017;杨博 等,2017)。
为了验证本文提出GISIBA无控制平差方法的平差精度及实际生产性能,特别针对该方法在不同平差区域的接边处理的适用性,在全球范围内选取4组ZY-3影像数据(两组境内、两组境外)依次对GISIBA方法的精度和实际生产时相邻区域接边处理的适用性进行了3组试验验证(具体数据情况及试验目的见表1)。
|
|
表 1 试验中使用的数据概况 Table 1 Description of different data sets for experiment |
试验以团队搭建的集群计算环境为基础(包括4个高性能计算节点,每个计算节点均配置了一个8核Intel Xeon E5-4650L的CPU和64GB的内存,存储系统为SAS接口的500 G×2硬盘系统),分连接点自动匹配和无控制区域网平差(基于VC++2015开发,64位OS)两个步骤进行试验数据的处理。
具体试验方案为:首先,使用团队自主研发的光学卫星影像连接点全自动匹配方法(张力 等,2017),采用由粗到精的多层金字塔逐级影像匹配策略(Zhang 等,2011, 2017)进行影像连接点的自动提取;然后使自动匹配获取连接点,进行GISIBA无控制区域网平差计算,获得高精度的影像定向参数(包括仿射变换参数改正数和连接点的地面坐标改正数);最后,以外业GPS实测控制点及自动匹配辅助的半自动手段量测的地面点作为平差精度评定的检查点,检查提出方法的适用性及精度。
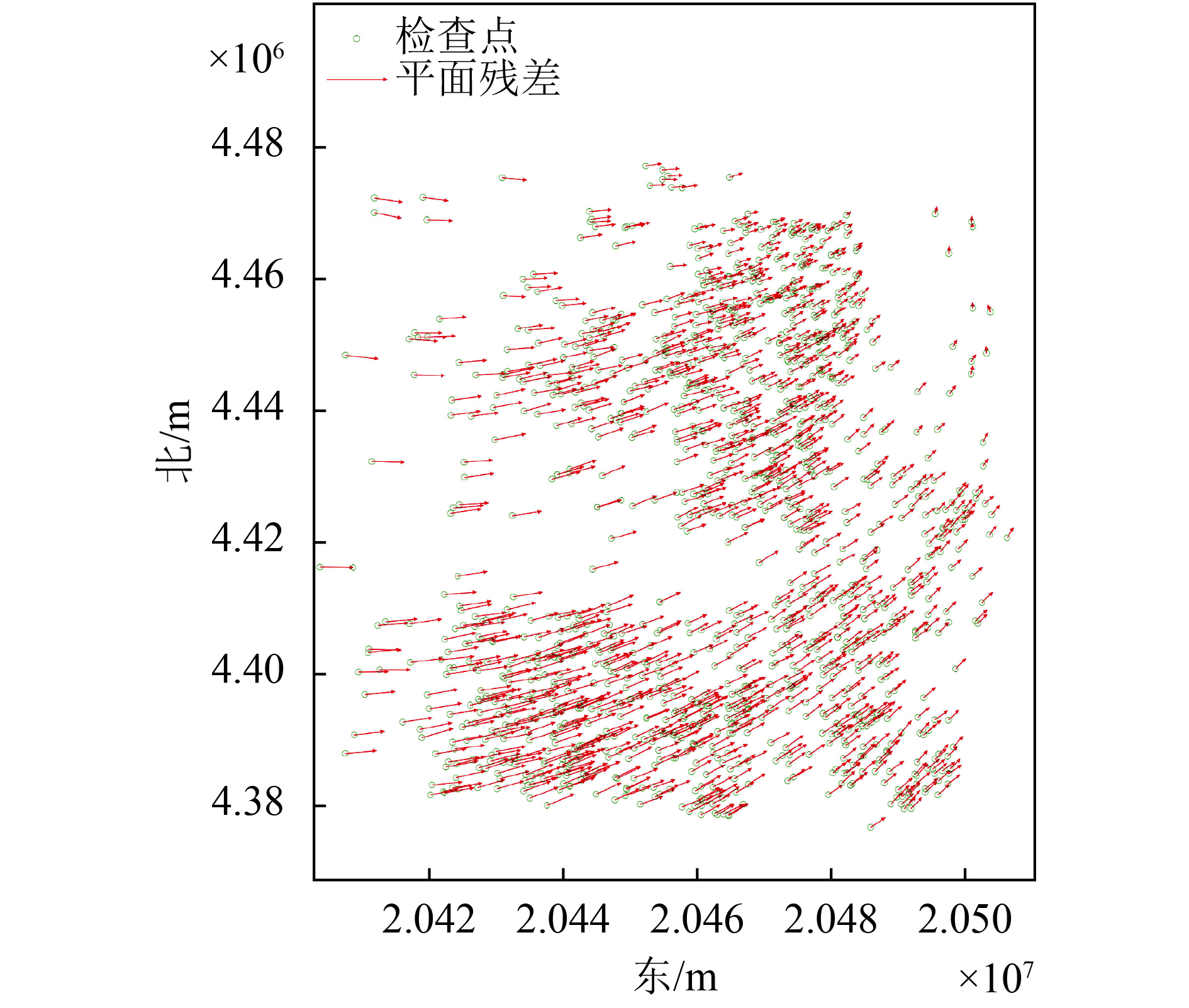
(3.2) 试验结果与分析 3.2.1. 试验1 不同覆盖次数多时相立体影像无控制区域网平差试验数据1-1:包含23景ZY-3数据(8个三线阵和立体影像对,详见表1),50%以上区域影像仅覆盖1次,原始数据无控制定位误差最大为29.0 m。数据处理过程共提取29661个连接点,GISIBA平差后单位权中误差
|
| 图 2 23景ZY-3数据(8个三线阵和立体影像对)1300个检查点上的平面误差分布(误差矢量的尺度为10 m) Figure 2 Horizontal error distribution from 1300 check points about 23 ZY-3 satellite images (8 three-line array and stereo images) (scale of error vector is 10 m) |
|
|
表 2 两组试验数据平差精度评估结果对比 Table 2 Accuracy comparison between two groups of test data |
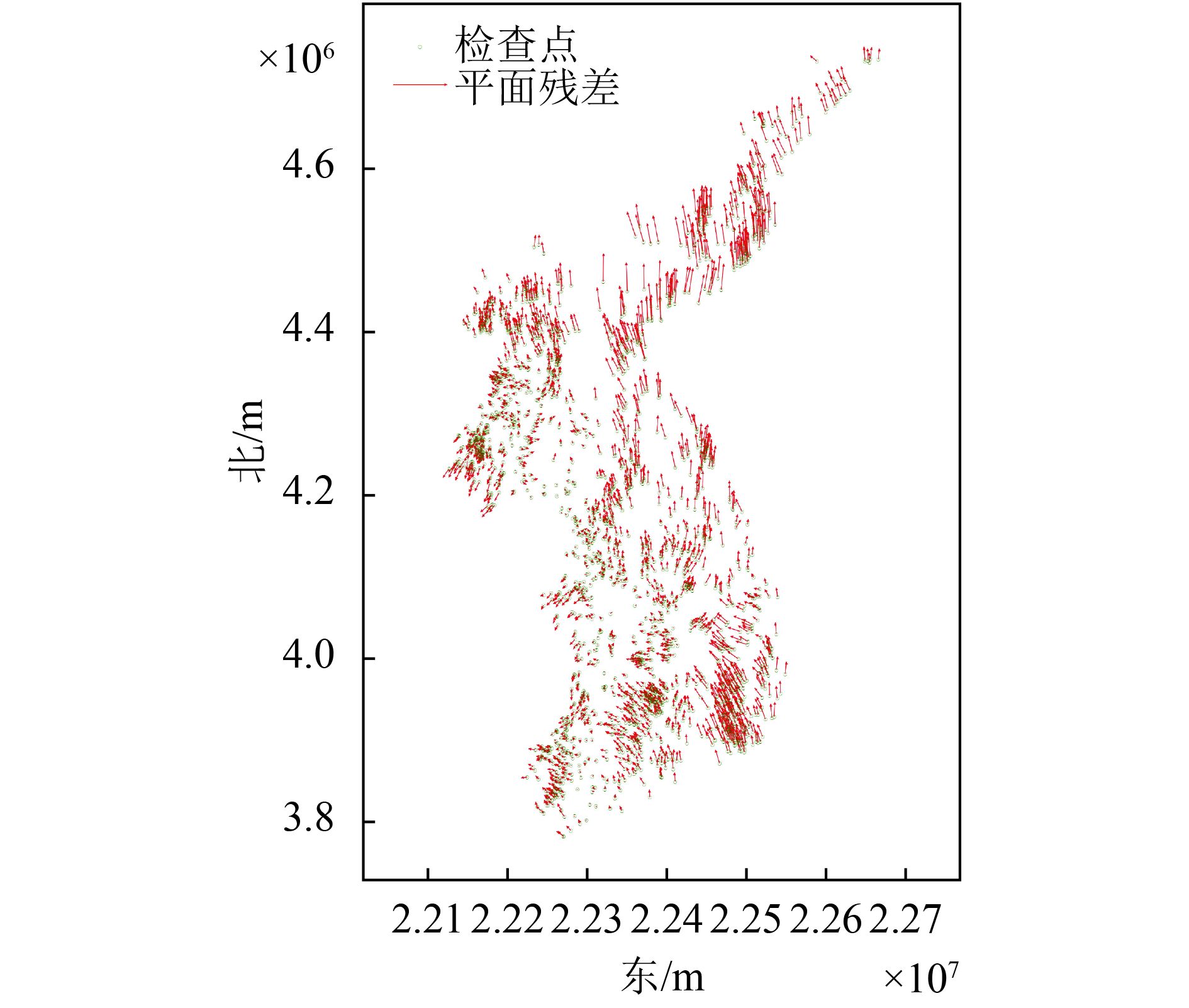
数据1-2:包含1815景ZY-3数据(505个三线阵和立体影像对,详见表1),绝大部分区域有约5次三线阵和立体影像对覆盖,原始数据无控制定位误差最大为24.9 m。数据处理过程共提取903244个连接点,区域网平差后单位权中误差
|
| 图 3 1815景ZY-3数据(605个三线阵和立体影像对)2200个检查点上的平面误差分布(误差矢量的尺度为1 m) Figure 3 Horizontal error distribution from 2200 check points about 1815 ZY-3 satellite images (605 three-line array and stereo images) (scale of error vector is 1 m) |
上述两组结果表明:
(1) 利用本文提出的GISIBA平差后单位权中误差
(2) 数据1-2试验结果使用时相跨度为5年的5次覆盖试验区域的卫星影像进行无控制区域网平差,可以达到优于6.0 m的平面精度和2 m的高程精度,从图3显示的误差矢量(图3中矢量的尺度仅为图2的0.1)的分布也可以看出平差结果基本上是无偏的;对比数据1-2的结果,数据1-1因仅仅使用了不到1年时间跨度的覆盖次数较少的数据,其无控制平差结果虽然也达到了优于15 m的平面精度,但平差结果中存在明显的系统误差。
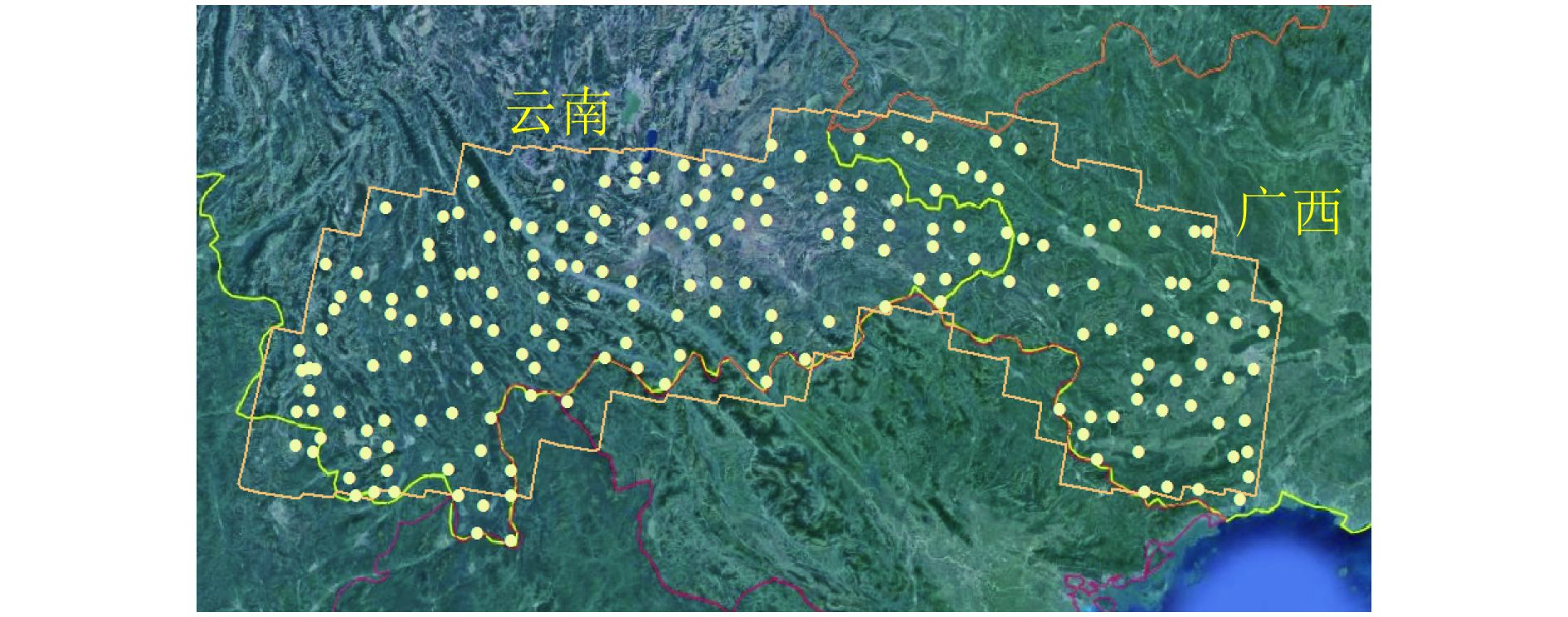
3.2.2. 试验2 立体影像无控制区域网平差实际精度验证试验试验区包括中国云南南部及广西西部区域,包含1026景ZY-3影像数据(264个三线阵和立体影像对,详见表1)。数据处理过程中删除1个立体影像对(该区域大部分被云覆盖),试验共提取2581578个连接点,自动剔除粗差后剩余1574435个连接点,平差计算耗时小于4 min。试验中使用191个均匀分布的GPS实测控制点进行GISIBA无控制平差精度分析(图4),精度分析结果见表3。
|
| 图 4 云南广西区域实测控制点分布图 Figure 4 Distribution of GCPs in Yunnan and Guangxi regions |
|
|
表 3 基于191个实测控制点的云南广西区域无控制平差精度结果 Table 3 Adjustment accuracy analysis with 191 GCPs in Yunnan and Guangxi regions |
实测控制点精度分析结果表明:使用时相跨度为近5年的3次覆盖试验区域的ZY-3影像进行无控制区域网平差,经191个实测控制点进行精度检查,可以达到优于6.0 m的平面精度和优于5.0 m的高程精度,充分验证了GISIBA无控制平差方法的可靠性及精度。
3.2.3. 试验3 立体影像无控制区域网平差与区域接边试验试验区包含5241景资源三号卫星数据(1382个三线阵和立体影像对,详见表1)。原始数据无控制定位误差最大为29.7 m(存在两景异常数据,误差在100像素以上)。为说明区域网接边的问题,将试验区数据分为东、西两个分区,东部分区包含653个立体影像对,西部区域包含808个立体影像对,两个分区之间存在三轨数据的重叠,使用1100个检查点精度分析结果见表4。
|
|
表 4 东部西部两区与整体区域无控制平差精度评估结果对比 Table 4 Adjustment accuracy comparison of east, west and whole teat areas without control |
试验结果显示:
(1) 由于使用了时相跨度为6年的多次覆盖试验区域的资源三号卫星影像进行无控制区域网平差,在东、西两个分区都获得了优于6.0 m的平面精度,且无明显的系统性;
(2) 整个试验区的无控制区域网平差处理自动连接点提取总共耗时49 h,自动提取了1千多万个连接点;区域网平差步骤耗时仅7.5 min,平差后在整个区域获得了优于5.0 m的无控制平面精度,且无明显的系统性,高程精度稍差,达到了6.0 m的中误差。
考虑到算法的适用性,如果在实际生产中需要进行东、西两个分区的接边处理,特别是在进行高程接边时,会存在很大困难。为解决东、西分区平差结果的接边问题,且上述试验已经分析验证了GISIBA无控制平差方法的计算速度及稳定性,这里尝试在试验中引入4.5 m分辨率Google DOM和30 m SRTM DEM作为具有一定精度的平面和高程几何约束(张祖勋和陶鹏杰,2017),通过自动匹配算法将部分均匀分布的连接点与这些带有地理空间信息的数据进行配准并内插出相应的地面坐标,然后在GISIBA区域网平差过程中,这些连接点将在平差中作为带权“参考点”观测值引入平差,其权值按平面50 m、高程20 m确定。仍使用在整个试验区选取的1100个检查点进行精度评价,在区域网平差过程中引入这些几何约束条件后的区域网平差结果见表5。
|
|
表 5 引入平面高程约束的东、西部两区与整体区域平差精度评估结果对比 Table 5 Adjustment accuracy comparison of east, west and whole teat areas with geometric constraints of horizontal and vertical |
实验结果表明:在引入这些平面和高程几何约束条件后,在整个区域以及东、西两个分区都获得了相对于第3方地理信息数据平面优于1 m、高程优于3 m的精度,且无系统性误差,解决了东、西区域的平差结果接边问题。
在实际生产中需要注意的是:引入平面/高程几何约束条件后的区域网平差结果显示了对参考数据的很好地“拟合”精度,虽然参考数据中大的误差会在平差过程中作为“粗差”被自动剔除,但在生产中仍建议尽量使用“精度已知/精度可验证”的第3方地理信息数据作为平面和高程几何约束。
4、结 论本文针对ZY-3影像成像几何的特点及影像的无控制精准定位技术存在的问题,以“交替趋近法”和基于RFM的最小二乘区域网平差为基础,提出了一种易于并行化、高效的大规模高分辨率光学卫星影像无控制联合区域网平差方法GISIBA。
利用多组典型区域的ZY-3影像数据试验结果表明:(1) 该方法将航空摄影测量中熟知的“交替趋近法”和最小二乘平差用于国产高分辨率卫星影像的无控制平差处理可以充分地发挥其对初值的依赖性小、计算速度快、精度分布均匀一致的优势,且方法稳定可靠。(2) 该方法通过构建“平均值”虚拟控制点,一方面解决了无控制区域网平差中不收敛导致的“秩亏”问题,另一方面充分利用覆盖同一成像区域的长时间序列立体卫星影像残余系统误差所表现出的随机性,可以进行完全不依赖于第3方地理空间数据和地面控制点的无控制区域网平差,达到了优于6.0 m的平面精度和优于5.0 m的高程精度。(3) 在GISIBA平差方法中引入“精度已知/精度可验证”第3方地理信息数据等平面和高程几何约束作为弱辅助控制,可以有效解决实际生产中遇到的不同区域平差结果接边等问题。
本文提出的方法已经集成为自主知识产权的软件系统,可以广泛应用于困难地区和境外地区大区域卫星影像高精度无控制几何定位。软件系统在2016年、2017年全球测图试生产中得到实际应用和改进,为全球地理信息资源建设工程、国产光学卫星影像高精度影像产品生产提供了技术保障。
| [1] | Boyd S, Parikh N, Chu E, Peleato B and Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3 (1) : 1 –122. DOI: 10.1561/2200000016 |
| [2] | 陈小卫, 张保明, 张同刚, 郭海涛, 岑敏仪. 公开DEM辅助无地面控制点国产卫星影像定位方法[J]. 测绘学报, 2016, 45 (11) : 1361 –1370. Chen X W, Zhang B M, Zhang T G, Guo H T and Cen M Y. Public DEM-assisted positioning method for Chinese satellite imagery without ground control points[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45 (11) : 1361 –1370. DOI: 10.11947/j.AGCS.2016.20160317 |
| [3] | 陈源源, 汤志强, 吴芳. 基于" 谷歌+SAR”卫星影像开展联合无控测图的方法研究[J]. 测绘技术装备, 2015, 17 (4) : 17 –19. Chen Y Y, Tang Z Q and Wu F. Research of surveying and mapping methods without control based on " Google Earth + SAR” images[J]. Geomatics Technology and Equipment, 2015, 17 (4) : 17 –19. DOI: 10.3969/j.issn.1674-4950.2015.04.005 |
| [4] | Dial G and Grodecki J. 2003. IKONOS stereo accuracy without ground control//Proceedings of ASPRS 2003 Conference. Anchorage Alaska: [s.n.] |
| [5] | 龚健雅, 王密, 杨博. 高分辨率光学卫星遥感影像高精度无地面控制精确处理的理论与方法[J]. 测绘学报, 2017, 46 (10) : 1255 –1261. Gong J Y, Wang M and Yang B. High-precision geometric processing theory and method of high-resolution optical remote sensing satellite imagery without GCP[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46 (10) : 1255 –1261. DOI: 10.11947/j.AGCS.2017.20170307 |
| [6] | Li C, Liu X J, Zhang Y J and Zhang Z X. A stepwise-then-orthogonal regression (STOR) with quality control for optimizing the rfm of high-resolution satellite imagery[J]. Photogrammetric Engineering & Remote Sensing, 2017, 83 (9) : 611 –620. DOI: 10.14358/PERS.83.9.611 |
| [7] | 李德仁, 王密. " 资源三号”卫星在轨几何定标及精度评估[J]. 航天返回与遥感, 2012, 33 (3) : 1 –6. Li D R and Wang M. On-orbit geometric calibration and accuracy assessment of ZY-3[J]. Spacecraft Recovery & Remote Sensing, 2012, 33 (3) : 1 –6. DOI: 10.3969/j.issn.1009-8518.2012.03.001 |
| [8] | 刘楚斌, 张永生, 范大昭, 雷蓉. 资源三号卫星境外高精度定位方法研究[J]. 测绘通报, 2015 (9) : 6 –8, 27. Liu C B, Zhang Y S, Fan D Z and Lei R. Research on the geometrical positioning evaluation of ZY-3 satellite at abroad[J]. Bulletin of Surveying and Mapping, 2015 (9) : 6 –8, 27. DOI: 10.13474/j.cnki.11-2246.2015.0266 |
| [9] | 刘楚斌, 张永生, 田野, 范大昭, 雷蓉. 天绘一号卫星境外几何定位精度初步验证[J]. 辽宁工程技术大学学报(自然科学版), 2016, 35 (6) : 657 –660. Liu C B, Zhang Y S, Tian Y, Fan D Z and Lei R. First results of geometrical positioning evaluation of TH-1 satellite at abroad[J]. Journal of Liaoning Technical University (Natural Science), 2016, 35 (6) : 657 –660. DOI: 10.11956/j.issn.1008-0562.2016.06.019 |
| [10] | 唐新明, 王鸿燕, 祝小勇. 资源三号卫星测绘技术与应用[J]. 测绘学报, 2017, 46 (10) : 1482 –1491. Tang X M, Wang H Y and Zhu X Y. Technology and applications of surveying and mapping for ZY-3 satellites[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46 (10) : 1482 –1491. DOI: 10.11947/j.AGCS.2017.20170251 |
| [11] | 王密, 杨博, 李德仁, 龚健雅, 皮英冬. 资源三号全国无控制整体区域网平差关键技术及应用[J]. 武汉大学学报(信息科学版), 2017, 42 (4) : 427 –433. Wang M, Yang B, Li D R, Gong J Y and Pi Y D. Technologies and applications of block adjustment without control for ZY-3 images covering China[J]. Geomatics and Information Science of Wuhan University, 2017, 42 (4) : 427 –433. DOI: 10.13203/j.whugis20160534 |
| [12] | 王任享, 胡莘, 王建荣. 天绘一号无地面控制点摄影测量[J]. 测绘学报, 2013, 42 (1) : 1 –5. Wang R X, Hu X and Wang J R. Photogrammetry of mapping satellite-1 without ground control points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42 (1) : 1 –5. |
| [13] | 王任享, 王建荣. 无地面控制点卫星摄影测量探讨[J]. 测绘科学, 2015, 40 (2) : 3 –12. Wang R X and Wang J R. Discussion on satellite photogrammetry without ground control point[J]. Science of Surveying and Mapping, 2015, 40 (2) : 3 –12. DOI: 10.16251/j.cnki.1009-2307.2015.02.001 |
| [14] | 王任享, 王建荣, 胡莘. 天绘一号03星定位精度初步评估[J]. 测绘学报, 2016, 45 (10) : 1135 –1139. Wang R X, Wang J R and Hu X. Preliminary location accuracy assessments of 3rd satellite of TH-1[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45 (10) : 1135 –1139. DOI: 10.11947/j.AGCS.2016.20160373 |
| [15] | 汪韬阳, 张过, 李德仁, 江万寿, 唐新明, 刘学林. 资源三号测绘卫星影像平面和立体区域网平差比较[J]. 测绘学报, 2014, 43 (4) : 389 –395, 403. Wang T Y, Zhang G, Li D R, Jiang W S, Tang X M and Liu X L. Comparison between plane and stereo block adjustment for ZY-3 satellite images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43 (4) : 389 –395, 403. DOI: 10.13485/j.cnki.11-2089.2014.0058 |
| [16] | 王之卓. 2007. 摄影测量原理. 武汉: 武汉大学出版社: 138–139 Wang Z Z. 2007. Principle of photogrammetry. Wuhan: Wuhan University Press: 138–139 |
| [17] | 杨博, 王密, 皮英冬. 仅用虚拟控制点的超大区域无控制区域网平差[J]. 测绘学报, 2017, 46 (7) : 874 –881. Yang B, Wang M and Pi Y D. Block-adjustment without GCPs for large-scale regions only based on the virtual control points[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46 (7) : 874 –881. DOI: 10.11947/j.AGCS.2017.20160588 |
| [18] | 张过. 2016. 线阵推扫式光学卫星几何高精度处理. 北京: 科学出版社 Zhang G. 2016. Geometric high precision processing of a linear array pushbrow optical satellite. Beijing: Science Press |
| [19] | 张浩, 张过, 蒋永华, 汪韬阳. 以SRTM-DEM为控制的光学卫星遥感立体影像正射纠正[J]. 测绘学报, 2016, 45 (3) : 326 –331. Zhang H, Zhang G, Jiang Y H and Wang T Y. A SRTM-DEM-controlled ortho-rectification method for optical satellite remote sensing stereo images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45 (3) : 326 –331. DOI: 10.11947/j.AGCS.2016.20150358 |
| [20] | 张力, 张继贤, 陈向阳, 安宏. 基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J]. 测绘学报, 2009, 38 (4) : 302 –310. Zhang L, Zhang J X, Chen X Y and An H. Block-adjustment with SPOT-5 imagery and sparse GCPs based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38 (4) : 302 –310. DOI: 10.3321/j.issn:1001-1595.2009.04.004 |
| [21] | 张力, 艾海滨, 许彪, 孙钰珊, 董友强. 基于多视影像匹配模型的倾斜航空影像自动连接点提取及区域网平差方法[J]. 测绘学报, 2017, 46 (5) : 554 –564. Zhang L, Ai H B, Xu B, Sun Y S and Dong Y Q. Automatic tie-point extraction based on multiple-image matching and bundle adjustment of large block of oblique aerial images[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46 (5) : 554 –564. DOI: 10.11947/j.AGCS.2017.20160571 |
| [22] | Zhang Y J, Lu Y H, Wang L and Huang X. A new approach on optimization of the rational function model of high-resolution satellite imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50 (7) : 2758 –2764. DOI: 10.1109/TGRS.2011.2174797 |
| [23] | Zhang Z X, Lu L P, Tao P J, Zhang Y and Zhang Y J. 2011. Registration of CBERS-02B Satellite Imagery in quick GIS Updating. Proceedings of the 7rd SPIE international symposium multispectral image processing and pattern recognition. Guilin: SPIE [DOI: 10.1117/12.901652] |
| [24] | 张祖勋, 陶鹏杰. 谈大数据时代的" 云控制”摄影测量[J]. 测绘学报, 2017, 46 (10) : 1238 –1248. Zhang Z X and Tao P J. An overview on " Cloud Control” photogrammetry in big data era[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46 (10) : 1238 –1248. DOI: 10.11947/j.AGCS.2017.20170337 |

