| 激光测高数据辅助卫星成像几何模型精化处理 |
收稿日期: 2017-06-26
在卫星测绘应用中,高程是制约卫星影像测图精度的关键因素之一(周平 等,2016)。随着美国2003年搭载有地球科学激光测高系统GLAS(Geoscience laser altimeter system)的ICESat卫星的成功发射,星载激光对地测高技术逐步成为研究热点(Wang 等,2011;于真真 等,2013;赵双明 等,2014)。Abshire等人(2005)对ICESat卫星搭载的GLAS进行了详细的说明,卫星在轨运行期间获取垂直分辨率3 cm数据4600余轨。ICESat-2作为ICESat卫星的后续卫星已有明确计划。激光雷达作为一种高精度测距仪器,因具有方向性好、测距精度高等特点,在航天航空摄影测量领域被广泛应用于获取高精度高程信息。2016年5月30号发射的资源三号02星上搭载了中国首个对地观测试验性激光测高试验载荷,卫星在轨检校期间共获取44轨激光测高数据。唐新明等人(2017),Xie等人(2017)针对资源三号02星激光测高仪特点,构建了一套严密的激光足印位置预报模型,通过在轨几何检校试验,预报误差与捕获足印最大误差小于150 m,并提出一种基于地面探测器的在轨几何检校方法。通过以指向、测距为系统误差的严密几何检校模型,实现了高精度在轨几何检校,经验证,坡度小于2°区域激光精度约为2—3 m,平坦地区绝对精度优于1 m。目前,光学遥感卫星数据的成像几何模型主要包括严密成像几何模型(RSM)和有理函数模型(RFM)两种,其处理理论也集中在基于严密成像几何模型的区域网平差方法和基于有理函数模型的区域网平差方法。高分辨率遥感卫星大多采用CCD线阵推扫成像模式,因此每一行影像都有一组外方位元素,这意味着基于严密成像几何模型的区域网平差需要解算每一行影像方位元素的补偿参数。Poli (2007)详细论述了严密成像几何模型对线阵传感器影像的优化理论,并对RFM和RSM做了对比。Teo(2011)利用不同高分辨率卫星影像对RSM和RFM的精度做了对比试验,结果表明轨道空间的严密成像几何模型呈现略高的几何精度,像空间RSM和RFM呈现较一致的结果。Zhang等人(2015)等利用严密成像几何模型对最大长度3000 km的大范围ZY-3三线阵立体数据进行无控制条件下的区域网平差处理,经过两测区的对比试验,平面和高程均达到13—15 m精度。有理函数模型作为一种更通用的表达方式,从数学角度更容易应用。有理函数模型对严密成像几何模型的替代精度较高(巩丹超和张永生,2003;Tao和Hu,2001),且目前影像供应商多将有理函数模型系数(RPC)作为影像元数据的一部分提供给用户。近年来,基于有理函数模型的区域网平差研究和应用十分广泛和深入。Dial和Grodecki(2002)详细阐述了基于有理函数模型的区域网平差模型,其利用像方多项式作为补偿模型对IKONOS影像进行试验,结果表明有理函数模型组合多项式模型可有效消除影像的系统偏移误差;文献(曹宁 等,2014;汪韬阳 等,2014;Teo 等,2010;Zhang 等,2016)等针对直下视卫星影像轨道间几何强度不足的问题,利用DEM内插连接点高程,有效避免了因影像间交会角度过小导致的平差计算无法收敛问题。Zhou等人(2016)利用SRTM数据在平坦地区高程精度远高于其标称精度的特点,通过设计无控制条件下以SRTM作为高程约束的立体区域网平差方法,结果表明该方法可达到中国1∶2.5万比例尺测图应用的高程精度要求;Wu等人(2011)将嫦娥一号卫星上的立体影像数据和激光测高数据进行联合平差处理,有效减小了影像和激光数据在像方的不符值。李国元等人(2014)将GLAS激光测高数据作为广义高程控制点辅助资源三号三线阵影像进行区域网平差,结果表明可达到1:5万立体测图高程精度要求。综上研究方法,大区域测图、减少控制点使用数量是众多学者研究的方向,利用已有地理信息资源辅助卫星影像数据处理达到提高精度的目的成为众多学者考虑的方法。激光测高数据处理技术的日趋成熟,其高程精度的逐步提高正可为大范围测图借鉴使用。
基于以上研究现状,探讨及完善激光测高数据辅助卫星影像成像几何模型精化处理的理论将进一步提高卫星数据的几何精度,为后续数据处理提供更加可靠的精度支撑。但从目前研究情况来看,利用激光测高数据辅助立体测图的技术水平还有待提高,对于激光数据的使用理论急需完善。结合较成熟的卫星影像区域网平差处理理论及激光测高数据自身无点之记、平面精度较好的特点,本文将在激光测高数据辅助立体影像几何模型精化处理通用理论、激光测高数据使用策略及影响激光测高数据使用的主要因素等方面开展研究,并利用相关数据进行试验验证。
2、激光测高数据辅助区域网平差原理 (2.1) 基于RFM的区域网平差模型RFM是多种传感器模型的一种更通用的表达方式,适用于各类传感器包括最新的航空和航天传感器,可以理解为一种广义、通用的传感器模型(曹宁 等,2014)。从数学角度,可将RFM理解为以物方3维坐标为自变量和以影像像方坐标为因变量的函数关系,如式(1)所示。
| $ \left. {\begin{aligned} &{Y = \frac{{Nu{m_L}\left( {P,L,H} \right)}}{{De{n_L}\left( {P,L,H} \right)}}}\\ & {X = \frac{{Nu{m_S}\left( {P,L,H} \right)}}{{De{n_S}\left( {P,L,H} \right)}}} \end{aligned}} \right\} $ | (1) |
式中,因变量(X, Y)分别表示影像扫描行方向和飞行方向的归一化坐标,自变量(P, L, H)表示任一地面位置的归一化物方3维坐标,归一化系数共10个。NumL, DenL, NumS, DenS为关于(P, L, H)不同组合的一般多项式。多项式中每分项自变量的幂不多于3,自变量幂总和不多于3,因此,每一多项式为20种自变量不同组合的和。4个多项式的系数及归一化系数共同组成有理函数模型系数(RPC)。式中一次项用于描述由光学投影引起的变形,二次项用于描述由地球曲率、大气折射及镜头畸变引起的变形,三次项用于描述传感器振动以及其他未知因素所造成的误差(曹宁 等,2014)。
由于平台特点,卫星影像几何模型较为稳定,一般影像供应商提供给用户的均为消除影像内畸变后且带有有理函数模型参数的数据产品。而基于有理函数模型的区域网平差多采用在函数模型的基础上,以像方多项式模型对其误差进行补偿。区域网平差数学模型可用下式表示
| $ \left. {\begin{aligned} & {Line = \Delta p + p\left( {Latitude,Longitude,Height} \right)}\\ & {Sample = \Delta r + r\left( {Latitude,Longitude,Height} \right)} \end{aligned}} \right\} $ | (2) |
式中,Sample、Line分别为影像扫描行和飞行方向的像方坐标。Δr、Δp分别为像方不同坐标方向的补偿函数,Latitude、Longitude、Height为任一地面位置的3维坐标。r、p为原成像几何模型通过归一化参数计算所得的影像像方坐标。其数值由下式计算所得,LINE_SCALE、LINE_OFF、SAMPLE_SCALE、SAMPLE_OFF为像方坐标归一化系数。
| $ \left. {\begin{aligned} &{p\left( {Latitude,Longitude,Height} \right) = Y \cdot {\rm{LINE}}\_{\rm{SCALE}} + {\rm{LINE}}\_{\rm{OFF}}}\\ & {r\left( {Latitude,Longitude,Height} \right) = X \cdot {\rm{SAMPLE}}\_{\rm{SCALE}} + {\rm{SAMPLE}}\_{\rm{OFF}}} \end{aligned}} \right\} $ | (3) |
若将多项式最高次幂取至1,补偿模型即为仿射变换模型,如下式所示
| $ \left. {\begin{aligned} & {\Delta p = {a_0} + {a_s} \cdot Sample + {a_L} \cdot Line}\\ & {\Delta r = {b_0} + {b_S} \cdot Sample + {b_L} \cdot Line} \end{aligned}} \right\} $ | (4) |
式中,a0、as、aL、b0、bS、bL即为有理函数模型补偿模型的6个参数,其中a0、b0主要用于补偿因模型漂移而造成的系统偏移误差,as、bS可近似认为用于消除因姿态滚动而造成的模型扫描方向的误差,aL、bL用于消除因姿态俯仰而造成的飞行方向的误差。因卫星平台成像特点,姿态补偿值均较小。通过连接点对模型进行连接,并设置控制点对区域网绝对位置进行确定,基于有理函数模型的区域网平差误差方程如式(5)所示。
| $ {{V}} = {{A}}{{{X}}_1} + {{B}}{{{X}}_2} - {{l}},{{P}} $ | (5) |
式中,
在平差过程中,有两类未知数需要求解,分别是每景影像的仿射变换补偿参数以及每个连接点、控制点的物方3维坐标改正数。由式(1)可知,有理函数模型是关于物方3维坐标的非线性方程组,式(5)列出了对误差方程线性化形式,文献(Grodecki和Dial,2003;曹宁,2014)对误差方程线性化进行了详细的阐述。根据光束法区域网平差原理,通过各个光束在空间的旋转和平移,使模型之间公共点的光线实现最佳交会,并使整个区域最佳地纳入到已知的控制点坐标系统中去,以实现优化影像定向模型参数的目的。
本文中激光测高数据作为高程控制辅助光学影像,进行区域网平差并达到优化几何模型的效果,在组建误差方程过程中,控制数据的权值一般设定高于单位权值多个数量级,而在实际区域网平差计算过程中控制数据的权重一般由其自身精度确定,由文献(唐新明 等,2017)可知,经联合检校后资源三号02星激光测高数据平面精度优于10 m,高程精度优于0.7 m。因此在对激光测高数据组建误差方程时,按照实际精度比例设置权重(通过下文的试验,对于资源三号02星激光测高数据,按照其自身精度将高程权值设置为平面的10—15倍比较合理,对于其他数据本文未涉及实际数据结果,在此仅将此作为参考使用),顾及影像间的相对关系,通过优化模型参数将测区高程维最大限度地拟合到高程坐标中,以起到高程控制的作用。通过迭代计算,获取最终优化后的模型参数。
(2.2) 激光测高数据辅助区域网平差方案地形平坦且地物单一区域的激光测高数据拥有较高的高程精度(Xie 等,2017),可将其作为区域网平差的高程控制点。传统的摄影测量处理中,控制点的使用需要根据实测坐标和点之记将其人工刺在影像数据上,由于资源三号02星激光测高载荷没有配备足印相机,控制数据的点之记也无从获取。因此传统的控制数据使用方法不能适用于激光测高数据。
对于立体影像的摄影测量处理,一般的连接点匹配策略是首先提取参考影像上的特征点,通过成像几何模型正变换预测目标同名点的初始影像位置,然后根据影像匹配原理,基于参考影像点位特征进行匹配进而获得同名点坐标。本文拟采用此思路获取激光测高数据像方坐标以保证影像间的相对关系。利用激光测高数据辅助卫星数据的区域网平差处理流程如下图1所示。
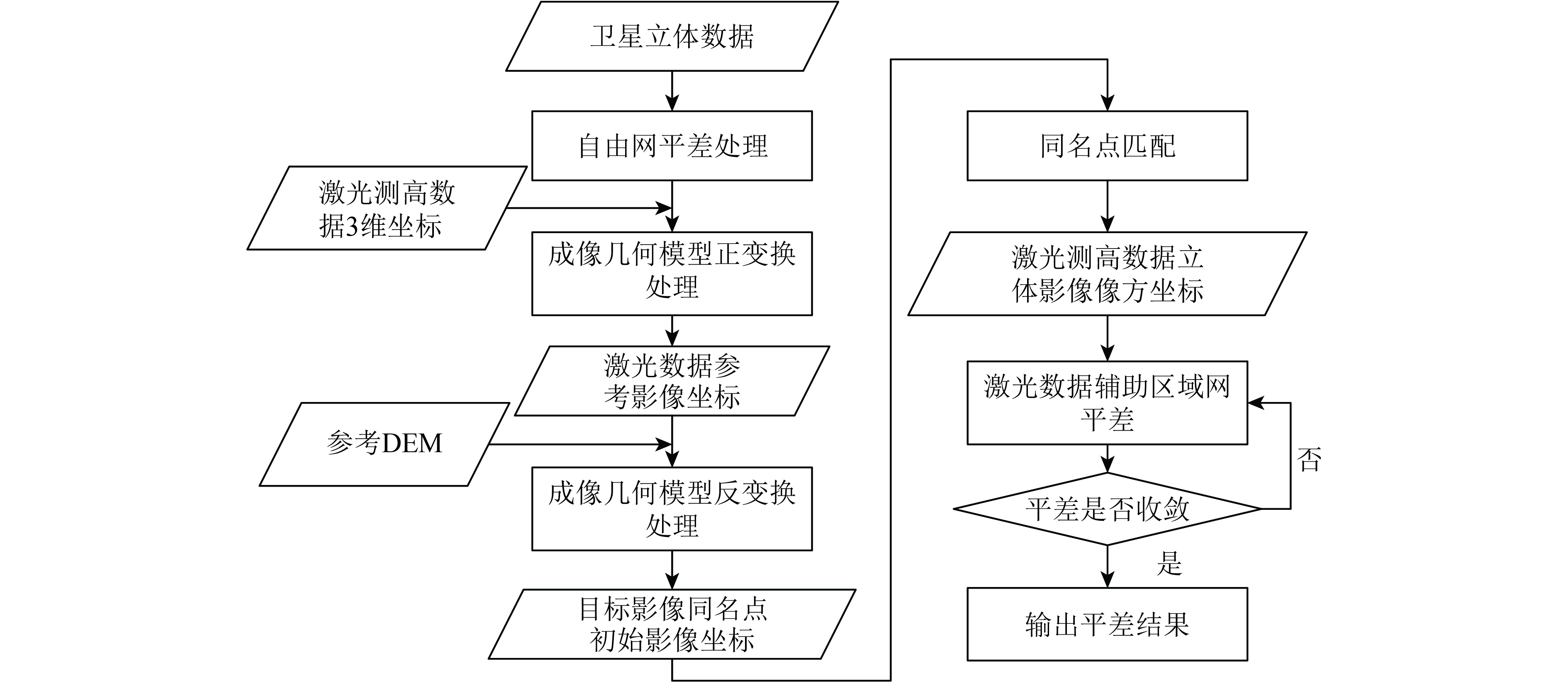
|
| 图 1 激光测高数据辅助光学影像区域网平差流程图 Figure 1 Flowchart of laser altimetry data aided optical satellite stereo image block adjustment |
如图1所示,首先,对测区内立体卫星数据进行连接点匹配处理,然后进行无控制条件下的自由网平差处理,精化后的成像几何模型具备精度较高的相对位置关系,并且通过在测区中设定虚拟控制点可保证自由网定向后模型绝对精度不亚于原始精度(该步骤可有效提高激光测高数据参考像方坐标的精度,并且良好的相对关系可提高同名点匹配效率);其次,根据激光测高数据3维坐标、自由网平差优化后的模型参数,经模型正变换获取激光数据参考影像像方坐标,由参考像方坐标、测区DEM通过光线追踪法(曹宁 等,2014)获取物方3维坐标,并通过模型映射获取同名点目标影像初始坐标;第三,对同名点以参考影像为基准进行影像匹配,通过设定相关阈值获取同名点高精度坐标;第四,将获取到的立体影像中激光数据的同名点坐标和物方3维坐标作为高程控制进行卫星数据区域网平差迭代处理直到平差计算收敛,在平差过程中激光测高数据的高程维数值不做修改;最后,输出平差结果,完成激光测高数据辅助区域网平差计算的流程。
由于激光测高数据没有点之记信息,因此其参考影像点位坐标就十分重要。若参考影像初始成像几何模型精度较差或者立体影像姿态和位置相对精度较差,将造成激光测高数据像方坐标匹配成功率较低或者匹配点位与实际位置高差较大,也就不能保证或者降低激光测高数据辅助平差的精度。因此本文首先对卫星数据进行自由网平差计算,经过自由网平差后影像间具备较好的相对位置关系,且通过在测区内设定虚拟控制点的方法可保证影像成像几何模型优于或不亚于原始精度,这一方面可以减小匹配代价以提高匹配效率,另一方面经匹配获取的控制数据同名点具备更优的相对位置关系。
影响激光测高数据应用精度的因素主要包含两方面:(1)因地形起伏原因导致的参考影像点位高程精度较差,通过激光数据物方坐标和成像几何模型可获取其参考位置,若地形起伏较大,较小的几何模型误差将造成较明显的参考位置高程误差(因平面偏移导致)。(2)激光测高控制点的匹配代价及准确率,通过自由网平差后,目标影像点位与参考影像较为接近可有效提高匹配效率和降低因重复纹理等原因造成的误匹配率。
此外,激光测高数据包含平面和高程坐标两类信息,将两类信息分别对待,可看作高程信息关于平面位置的唯一函数关系,设H为激光测高数据的高程值,X、Y为平面坐标,设H0为平面位置(X、Y)下的高程真值,ΔZ为真值与激光测高数据高程间的差值,ΔZ可以用式(6)表示,因此,激光测高数据的精度由两方面数值决定,一是平面位置(X、Y)的精度,二是平面位置(X、Y)处实际高程真值。
| $ \Delta Z = H - {H_0} $ | (6) |
资源三号02星激光测高数据平面精度约为10 m(唐新明 等,2017),若辅助平差的激光测高数据在影像数据上的点位与实际点位偏移较大,可能引起因地形起伏因素造成的高程误差(图2)。
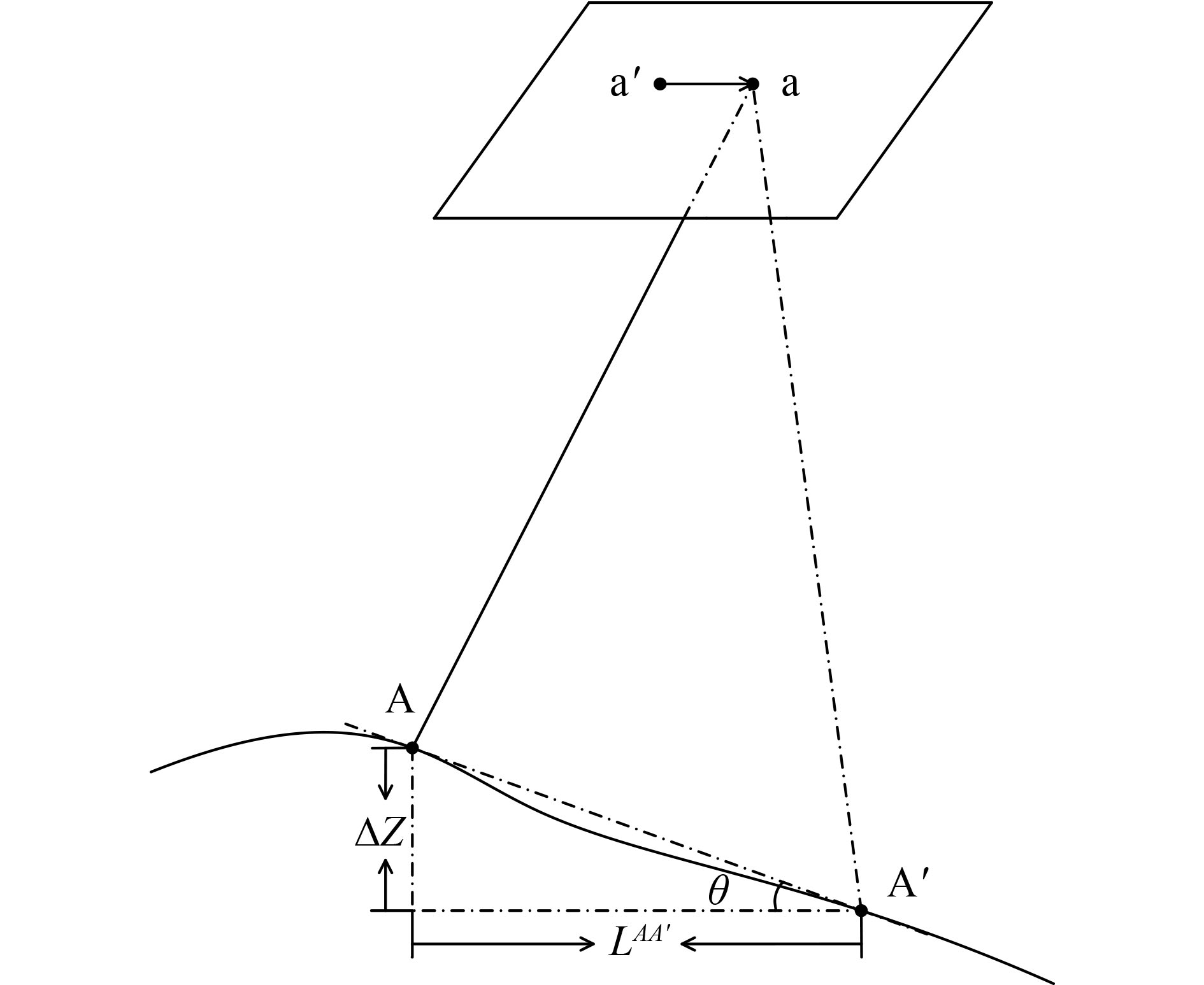
|
| 图 2 平面位置对高程精度影响分析示意图 Figure 2 Diagrammatic sketch of vertical accuracy impact analysis by plan position |
图2中A点为激光测高数据3维点位,通过几何模型正变换可以得到其在参考影像上的坐标a,并可进一步获取其同名点位。但因卫星影像存在一定的平面偏移量,点位A的实际像方坐标位置应为a′,像点a的实际物方位置则为A′,物方点A、A′的平面偏移量为LAA′,高程偏移量为ΔZ,因存在地形起伏,两点在高程维上存在大小为θ的角度。在平差过程中A′的真实高程值与点A高程值的差值将会引起影像高程的偏差ΔZ。由上图分析得到高程偏差可由式(7)计算得到。
| $ \Delta Z = {L^{AA'}} \cdot \tan \theta $ | (7) |
对于资源三号卫星影像其平面精度为5—25 m(Tang 等,2015),若地面存在10°夹角,由式(7)计算可得,其将引起高程0.9—4.4 m的误差。因此,对于激光测高数据的使用应尽量保证其位于地势平坦区域,以避免因平面偏移而造成的控制高程偏差。本文为保证激光测高数据的控制精度,在应用激光测高数据前首先通过数字高程模型对测区地形进行分析。具体做法是:首先,获取实验测区数字高程模型数据,并得到激光测高数据平面位置精度限差数值范围内高程值;其次,对该范围内高程值进行曲面拟合,计算激光测高数据平面位置处不同方向(宜选用东、南、西、北及其夹角等方位)的坡度值;最后,判断坡度值小于6°位置为可利用控制数据,否者不予应用。如前文所述,因地形起伏因素,激光数据高程精度受制于其实际平面位置环境,为保证激光测高数据精度,应尽量排除其影响。资源三号02星激光数据平面精度约为10 m,按照误差限差理论,要分析其周围地形应至少考虑其2—3倍的精度空间范围(空间范围可扩大以保证其精度),因此,进行地形分析的数字高程模型格网间隔至少应为10 m来进行坡度的计算(两格网进行线性计算,三格网以上可进行曲线拟合获取平面位置的切线斜率)。若无相关DEM辅助可通过相对定向后对影像进行局部密集匹配获取其地形数据。为进一步排除地形环境对激光精度的影像可对匹配获取的像方激光数据进行目视判读,排除点位限差空间范围复杂地物环境的影响,如20—30 m范围内存在明显人工地物、地形起伏物应舍去。
3、试验与分析 (3.1) 试验数据及方案试验共选取湖北、青海两个测区作为试验区域,搜集整理了两测区的资源三号卫星三线阵立体影像。湖北测区位于湖北省中部,地势平坦,平均海拔约100 m。青海测区位于青海省中部,平均海拔高约4000 m,测区南部为山地,北部相对地势平坦,最大高差约1900 m。两测区所有试验影像辐射质量优良,云量小于2%。
试验共搜集到测区内资源三号02星激光测高数据112个,内容包括大地坐标及大地高。此外,每个测区搜集到外业测量数据作为每种平差模式的控制或检查数据,大地基准为WGS-84坐标系,高程基准为WGS-84大地高,数据包括点位3维物方坐标、点之记影像片和点位描述信息等内容。外业测量数据主要为道路交叉口,地物明显,易于转刺。控制或检查数据通过点之记在影像上人工量测所得,刺点精度优于0.5个像素。
各试验测区影像分布情况及激光测高数据、检查点数据分布情况见图3和图4。
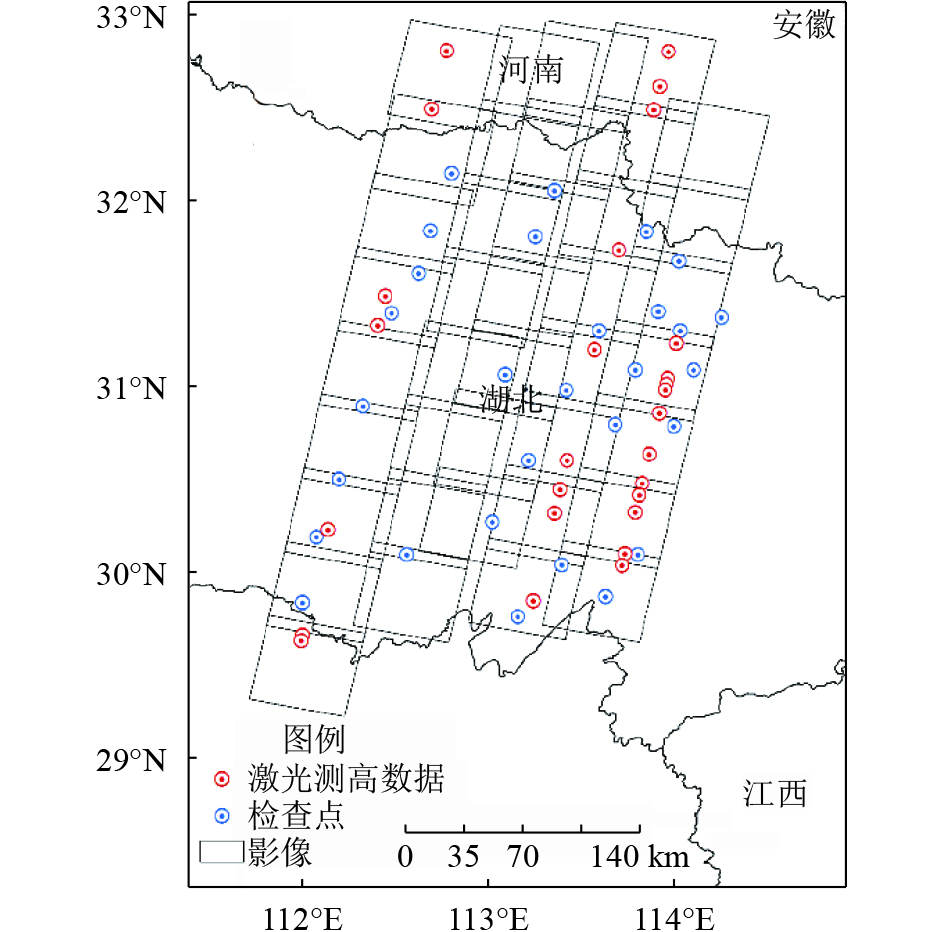
|
| 图 3 湖北试验测区影像、激光测高数据、检查点分布图 Figure 3 The laser altimetry data and check points in Hubei experiment area |
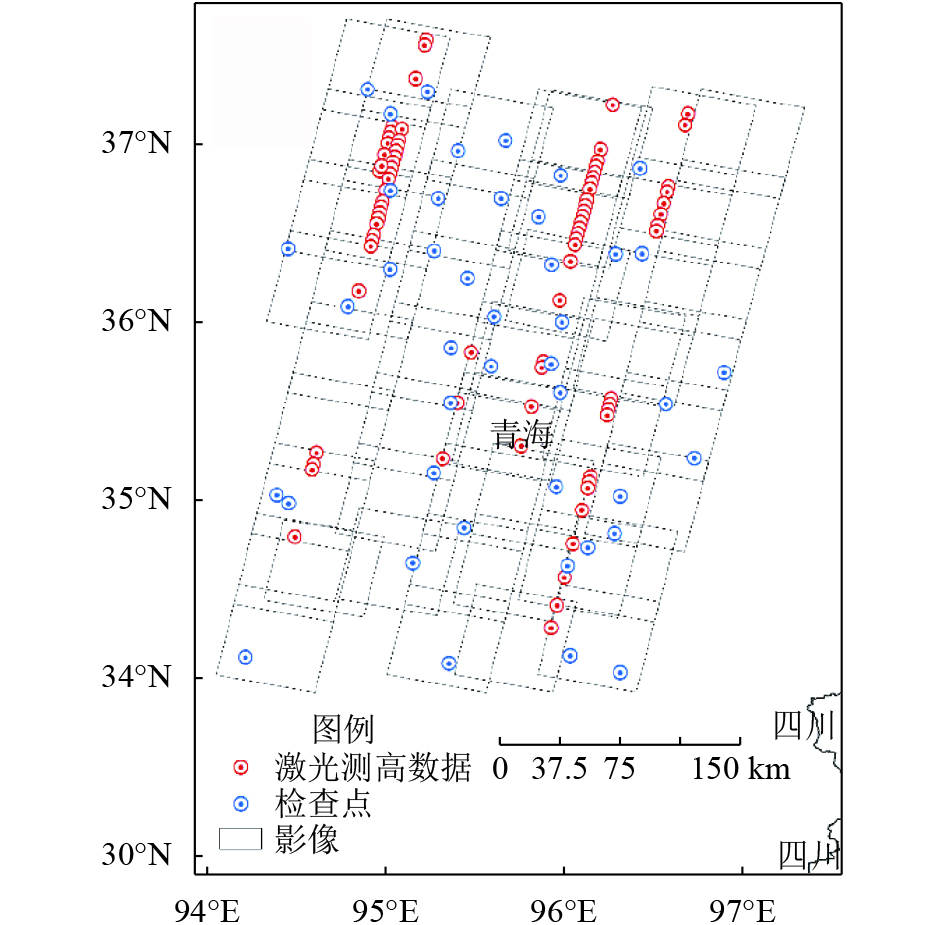
|
| 图 4 青海试验测区影像、激光测高数据、检查点分布图 Figure 4 The laser altimetry data and check points in Qinghai experiment area |
试验所用数据各项信息见表1。
|
|
表 1 试验数据信息表 Table 1 Experiment data infomation |
试验主要包括以下内容和对比方案:
(1) 对立体影像原始几何模型进行前方交会,利用外业数据对几何模型精度进行评定;
(2) 对测区内试验影像进行连接点自动匹配,并进行无控制条件的自由网平差,利用外业测量数据对无控平差结果进行精度评定;
(3) 根据外业测量数据实际分布情况,选取4周加中心位置的5个控制点布控方案进行有控条件下的区域网平差,利用剩余外业测量数据对区域网平差结果进行精度评定;
(4) 按照上文中提到的资源三号02星激光测高数据辅助光学卫星影像区域网平差的方案,首先对测区地形进行坡度计算,剔除落在坡度大于6°的激光数据;其次,在自由网平差的基础上,通过激光参考位置获取、待匹配位置计算、同名点匹配等步骤获取激光像方位置坐标,最后,将激光测高数据作为控制数据,在自由网平差结果的基础上进行影像几何模型精化处理,并利用外业测量数据对平差结果进行精度评定。
为保证每种平差模式因连接强度不同带来不必要的误差,试验中每种平差模式均采用同一套连接点,且同一地理位置处的所有分布影像均有连接。此外,有控模式控制点的刺点由具有多年数据处理经验的作业员完成处理,以排除刺点误差引起的处理问题。并对匹配获取的激光控制像方坐标进行人工目视检查同名点相符性,排除因匹配误差而引起的控制误差。
(3.2) 试验结果及分析按照以上试验方案,湖北、青海测区试验精度评定结果如表2。
|
|
表 2 湖北和青海测区试验结果统计表 Table 2 The statistics of Hubei and Qinghai experiment area |
湖北测区不同平差方案残差分布见图5。
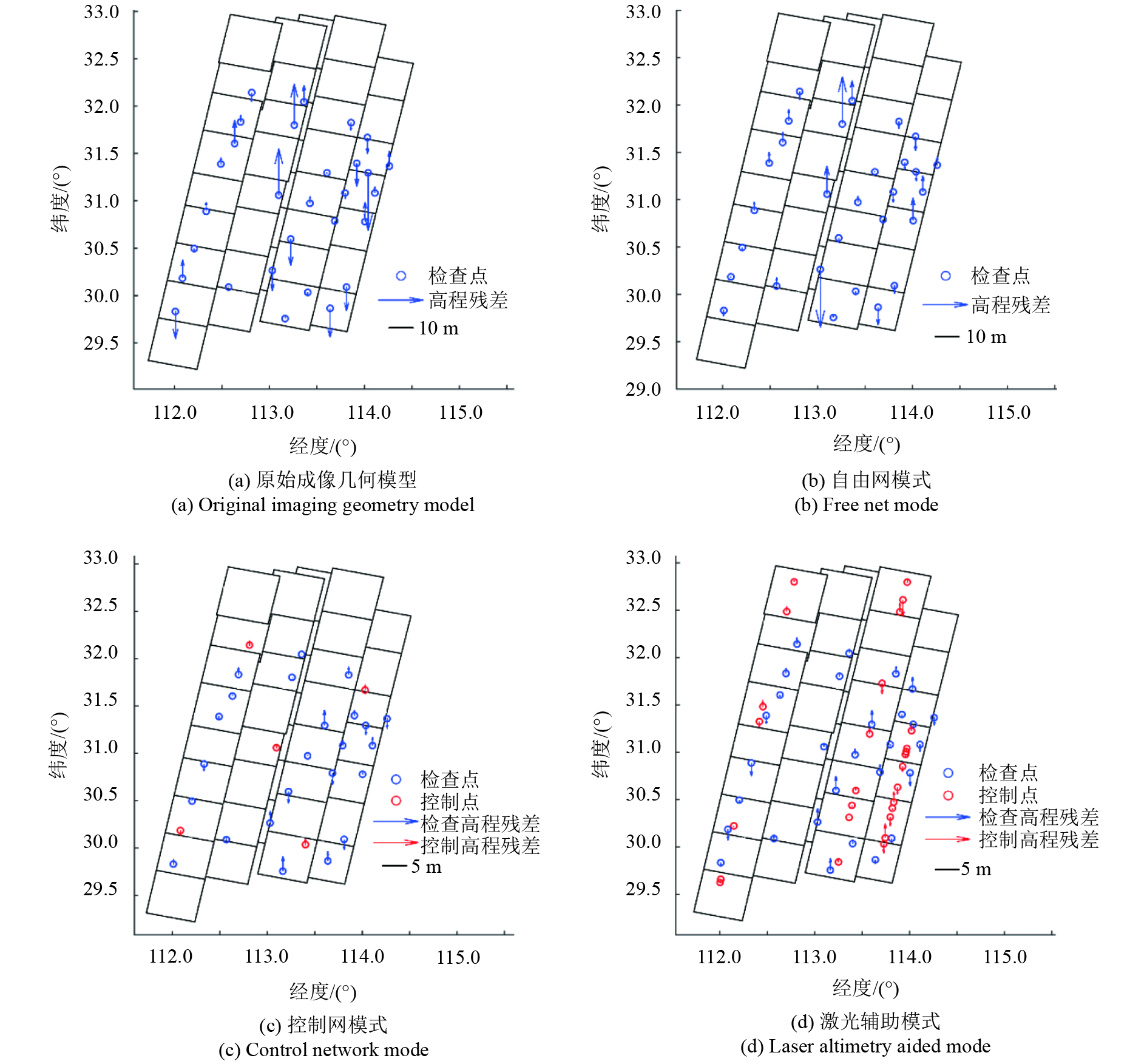
|
| 图 5 湖北测区不同平差模式残差分布图 Figure 5 Residual distribution of different adjustment modes in Hubei area |
由图5及表2可以看出,影像原始成像几何模型前方交会高程中误差为11.38 m,且无系统性分布。在无控模式下,检查点高程残差呈现出局部系统性分布特征,中误差为10.11 m,最大误差为21.87 m,这与资源三号三线阵卫星影像高程精度结论是一致的(Tang 等,2015)。在控制网平差模式下,影像高程几何精度较无控模式约提升了4倍,检查点残差明显减小,高程中误差为2.47 m,最大误差为4.65 m。在激光数据辅助平差模式下,控制数据分布较为均匀,高程中误差为1.97 m,最大误差为3.13 m。
通过对影像原始几何模型模式与无控相对定向模式进行对比,结果验证了通过相对定向可获取优于或不亚于原始几何模型精度的结论。通过无控模式与有控模式结果对比分析可得,在有控模式下,有效消除了无控模式中存在的局部系统性残差(测区西北部及中部较为明显),达到了较高的几何精度。经激光测高数据辅助的平差模式与有控模式对比分析可得,其残差与控制网模式呈现出几乎一致的分布规律,检查点残差大小、方向均无明显系统性,且单点的残差值也与控制网模式接近。从湖北测区的地形特点出发,由于其地势较为平缓,综合激光测高数据平面位置对高程精度影响的分析可知,在该区域,平面位置对高程精度影响较小,激光测高数据能对该区域几何模型进行较好的拟合。结果表明按照本文提出的平差方案可有效降低测区系统性误差,提高影像几何模型精度。
按照同样的试验方案,青海测区不同平差模式的残差分布见图6。

|
| 图 6 青海测区不同平差模式残差分布图 Figure 6 Residual distribution of different adjustment modes in Qinghai area |
从图6及表2的数据结果可以看出,原始成像几何模型前方交会高程中误差为13.25 m,与湖北测区一样,无系统性分布特征。在无控平差模式下,检查点高程中误差为10.41 m,最大误差为20.01 m。在控制网模式下,检查点高程中误差为2.88 m,最大误差为9.82 m。在激光数据辅助平差模式下高程中误差分别为3.23 m,最大误差分别为7.34 m,高程精度与控制网模式相当。
结合湖北测区试验结果,资源三号卫星原始几何模型高程精度为11—14 m,无系统性分布特征。经无控相对定向后,几何模型精度略有提高,为10—11 m。在无控平差模式下,两测区结果基本相当,湖北测区在测区西北部及中部呈现出一定的系统性偏差,而青海测区的西部及中部均呈现出较为明显的系统性残差,两测区整体高程精度较差,约为10 m。在控制网模式下,青海测区较无控模式精度约提升3倍,略差于湖北测区。初步分析,该结果与测区地形有关,青海测区南部山地较多,测区整体高差较明显,高程精度不如地势较为平坦的湖北测区。但在此模式下,两测区均呈现了一致的现象,均有效消除了无控模式下的局部系统性残差。在激光测高数据辅助平差模式下,两测区均呈现出与有控模式一致的残差分布特征。所不同的是青海测区激光模式精度略差于有控模式,而湖北测区激光模式精度略优于有控模式。初步分析,整体上激光数据高程精度要差于外业GPS数据。在地形起伏明显区域,平面位置对高程影响因素较大,虽然本文已经做了应对地形起伏因素的措施,但较平缓区域,其精度仍有所下降,因此青海测区山地区域激光数据精度的下降导致了整体精度较有控模式有所下降(残差图中,激光模式南部山区残差值较大)。而湖北测区因地势较为平缓,激光测高数据精度较高,且激光数据数量较有控模式控制点数据多出很多,因此测区整体精度呈现出激光模式下高于控制模式。
(3.3) 激光测高数据控制区域试验在上述试验的基础上,本文对激光测高数据控制范围进一步进行研究,选取湖北、新疆两个测区进行模型精化处理并进行精度评定,对于湖北测区分两组试验进行,分别是使用最外侧两轨激光数据作为高程控制(湖北1)和在原有影像数据的基础上对东西两侧各增加一轨数据(湖北2)进行激光数据辅助模式下的区域网平差试验;对于新疆测区,共搜集资源三号卫星三线阵立体影像42景125幅。该测区位于新疆西北部,邻接国界线,南端和北端为山地,中部地势相对平缓,平均海拔约1000 m,最大高差约1500 m。选择在该测区中部区域布设两轨激光测高数据,测区西侧约两轨、东侧一轨影像无高程控制数据。
新疆测区共搜集资源三号02星激光测高数据60个,高精度GPS检查点113个。试验中连接点、控制点、激光测高控制数据等的处理要求与上试验相同。按照激光数据辅助平差方案,湖北、新疆两测区激光测高数据控制区域试验结果如表3。
|
|
表 3 激光测高数据控制区域试验平差结果 Table 3 The adjustment results of laser altimetry data control area experiment |
各测区平差结果残差分布如图7。

|
| 图 7 激光测高数据控制区域试验残差分布图 Figure 7 The experiment residuals of Laser altimetry data control area |
对比湖北1测区与上实验中湖北激光测高辅助平差模式试验(以下简称原湖北测区)结果,在湖北1中,没有布设控制的中部区域(约两轨数据)虽然残差比较小,但仍呈现出一定的系统性偏离。测区整体中误差为3.01 m,较原湖北测区有一定下降。对比湖北2测区与原湖北测区试验结果,新增加的两轨影像上的检查点呈现出偏离激光控制区域越远残差越大的明显系统性分布特征,位于激光测高数据分布的影像及激光测高数据分布之间影像上的检查点高程残差与原湖北测区保持一致,测区整体精度明显下降,中误差为6.41 m。对比新疆测区与湖北2测区实验结果,两测区呈现出一致的残差分布特征,即偏离激光测高数据越远高程残差越大的系统性分布。从新疆测区残差图可以看出,在激光数据的西侧分布有两轨影像,残差的系统性也更加明显。
由光束法区域网平差理论结合2.1节高程控制区域网平差的原理可知,影像的区域定向精度依赖于测区中控制数据的精度及其分布,控制数据精度越高,分布越均匀,测区定向精度也就越高。由本试验激光测高数据分布特征可知,湖北1测区为在测区两侧布设高程控制数据,分布较合理,但由于激光测高数据本身精度较GPS控制数据较低,其控制强度较弱,该测区依旧呈现出离控制数据越远残差越大的系统性误差。而湖北2和新疆两测区控制数据分布于测区的中部区域,在测区的两侧区域控制数据无分布,均匀性较差。位于控制数据较远区域,通过连接点的传递未能实现有效的控制,因此其精度呈现出明显的下降趋势,而激光测高数据分布区域达到了较高的几何精度。
综上所有试验结果,从激光数据和影像分布特征来看,若在测区的最外侧及最多隔一轨影像的区域布设激光测高数据,均达到了较好的高程精度。若隔一轨以上或在测区的中间轨布设激光数据的方案,几何模型均呈现出不同程度的系统偏差。由于激光测高数据量的限制,本试验未能从精细数量级上分析高程控制数据的控制范围,只呈现了因激光测高数据分布不均匀和控制强度较弱而导致的残差系统性分布现象,初步给出了激光测高数据布设指导性建议,该试验可在高程控制数据量充足的情况下进一步分析。
4、结 论从本文的试验结果结合激光数据辅助卫星影像几何模型精化的理论可以得出以下结论:
(1) 本文提出的激光测高数据辅助立体卫星数据进行几何模型精化处理理论是切实可行的,通过使用资源三号02星激光测高数据进行试验验证,湖北、青海测区分别达到1.97 m和3.23 m的高程精度;
(2) 激光测高数据的应用对地形起伏有一定的敏感性。在地势平坦区域激光辅助模型精化精度可达到甚至优于有控模式,而位于山地区域,激光数据的使用应根据地形特征进行筛选,处理后,可达到与有控模式相当的几何精度。
(3) 激光测高数据因其本身精度限制,其控制强度有一定的局限性。通过本文试验结果,在实际应用中,应保证激光数据尽可能均匀且测区最外侧数据应有激光数据分布,从量级上建议至多每隔一轨影像数据应有激光数据分布。
(4) 本文提出的激光数据辅助模型精化的理论有一定的通用性,无点之记而又具备较高物方精度的几何数据同样适用此策略。
基于本文的研究方法和结论,建议在以下两方面继续开展研究工作:
(1) 激光测高数据与立体影像上的位置确认算法,可依据其他参考数据进一步研究更精确的位置预测算法及匹配算法;
(2) 待激光数据丰富后可进一步开展激光数据控制强度量化方面的研究,对激光数据的应用价值提供更可靠的依据。
| [1] | Abshire J B, Sun X L, Riris H, Sirota J M, McGarry J F, Palm S, Yi D H and Liiva P. Geoscience Laser Altimeter System (GLAS) on the ICEsat Mission: on-orbit measurement performance[J]. Geophysical Research Letters, 2005, 32 (21) : L21S02 . DOI: 10.1029/2005GL024028 |
| [2] | 曹宁. 2014. 以DEM为高程辅助的弱交会卫星影像的区域网平差. 兰州: 兰州交通大学 Cao N. 2014. DEM-Aided Block Adjustment for Satellite Images with Weak Convergence Geometry. Lanzhou: Lanzhou Jiaotong University |
| [3] | 曹宁, 张力, 杜全叶. 以DEM为高程辅助的弱交会卫星影像的区域网平差[J]. 遥感信息, 2014, 29 (6) : 21 –24. Cao N, Zhang L and Du Q Y. DEM-aided block adjustment for satellite images with weak convergence geometry[J]. Remote Sensing Information, 2014, 29 (6) : 21 –24. DOI: 10.3969/j.issn.1000-3177.2014.06.005 |
| [4] | Dial G and Grodecki J. 2002. Block adjustment with rational polynomial camera models//Proceeding of ASCM-ASPRS Annual Conventions. Washington, DC: [s.l.] |
| [5] | 巩丹超, 张永生. 有理函数模型的解算与应用[J]. 测绘学院学报, 2003, 20 (1) : 39 –42, 46. Gong D C and Zhang Y S. The solving and application of rational function model[J]. Journal of Institute of Surveying and Mapping, 2003, 20 (1) : 39 –42, 46. DOI: 10.3969/j.issn.1673-6338.2003.01.012 |
| [6] | Grodecki J and Dial G. Block adjustment of high-resolution satellite images described by rational polynomials[J]. Photogrammetric Engineering and Remote Sensing, 2003, 69 (1) : 59 –68. DOI: 10.14358/PERS.69.1.59 |
| [7] | 李国元, 唐新明, 王华斌, 张重阳, 高小明. 2014. GLAS激光测高数据辅助的资源三号三线阵区域网平差研究//第三届高分辨率对地观测学术年会优秀论文集. 北京: 中国科学院高分重大专项管理办公室 Li G Y, Tang X M, Wang H B, Zhang C Y and Gao X M. 2014. Research on the ZY-3 block adjustment supported by the GLAS laser altimetry data//China High Resolution Earth Observation Conference. Beijing |
| [8] | Poli D. A rigorous model for spaceborne linear array sensors[J]. Photogrammetric Engineering and Remote Sensing, 2007, 73 (2) : 187 –196. DOI: 10.14358/PERS.73.2.187 |
| [9] | 唐新明, 谢俊峰, 付兴科, 莫凡, 李少宁, 窦显辉. 资源三号02星激光测高仪在轨几何检校与试验验证[J]. 测绘学报, 2017, 46 (6) : 714 –723. Tang X M, Xie J F, Fu X K, Mo F, Li S N and Dou X H. ZY3-02 Laser Altimeter On-orbit Geometrical Calibration and Test[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46 (6) : 714 –723. DOI: 10.11947/j.AGCS.2017.20160597 |
| [10] | Tang X M, Zhou P, Zhang G, Wang X and Pan H B. Geometric accuracy analysis model of the Ziyuan-3 satellite without GCPs[J]. Photogrammetric Engineering and Remote Sensing, 2015, 81 (12) : 927 –934. DOI: 10.14358/PERS.81.12.927 |
| [11] | Tao C V and Hu Y. A comprehensive study of the rational function model for photogrammetric processing[J]. Photogrammetric Engineering and Remote Sensing, 2001, 67 (12) : 1347 –1357. |
| [12] | Teo T A. Bias compensation in a rigorous sensor model and rational function model for high-resolution satellite images[J]. Photogrammetric Engineering and Remote Sensing, 2011, 77 (12) : 1211 –1220. DOI: 10.14358/PERS.77.12.1211 |
| [13] | Teo T A, Chen L C, Liu C L, Tung Y C and Wu W Y. DEM-aided block adjustment for satellite images with weak convergence geometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48 (4) : 1907 –1918. DOI: 10.1109/TGRS.2009.2033935 |
| [14] | 汪韬阳, 张过, 李德仁, 江万寿, 唐新明, 刘学林. 资源三号测绘卫星影像平面和立体区域网平差比较[J]. 测绘学报, 2014, 43 (4) : 389 –395, 403. Wang T Y, Zhang G, Li D R, Jiang W S, Tang X M and Liu X L. Comparison between Plane and stereo block adjustment for ZY-3 satellite images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43 (4) : 389 –395, 403. DOI: 10.13485/j.cnki.11-2089.2014.0058 |
| [15] | Wang X W, Cheng X, Gong P, Huang H B, Li Z and Li X W. Earth science applications of ICESat/GLAS: a review[J]. International Journal of Remote Sensing, 2011, 32 (23) : 8837 –8864. DOI: 10.1080/01431161.2010.547533 |
| [16] | Wu B, Guo J, Zhang Y S, King B A, Li Z L and Chen Y Q. Integration of Chang’E-1 imagery and laser altimeter data for precision lunar topographic modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49 (12) : 4889 –4903. DOI: 10.1109/TGRS.2011.2153206 |
| [17] | Xie J F, Tang X M, Mo F, Li G Y, Zhu G B, Wang Z M, Fu X K, Gao X M and Dou X H. ZY3-02 laser altimeter footprint geolocation prediction[J]. Sensors, 2017, 17 (10) : 2165 . DOI: 10.3390/s17102165 |
| [18] | 于真真, 侯霞, 周翠芸. 星载激光测高技术发展现状[J]. 激光与光电子学进展, 2013, 50 (2) : 020006 . Yu Z Z, Hou X and Zhou C Y. Progress and current state of space-borne laser altimetry[J]. Laser and Optoelectronics Progress, 2013, 50 (2) : 020006 . DOI: 10.3788/lop50.020006 |
| [19] | Zhang Y J, Wan Y, Huang X H and Ling X. DEM-assisted RFM block adjustment of pushbroom nadir viewing HRS imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54 (2) : 1025 –1034. DOI: 10.1109/TGRS.2015.2472498 |
| [20] | Zhang Y J, Zheng M T, Xiong X D and Xiong J X. Multistrip bundle block adjustment of ZY-3 satellite imagery by rigorous sensor model without ground control point[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12 (4) : 865 –869. DOI: 10.1109/LGRS.2014.2365210 |
| [21] | 赵双明, 冉晓雅, 付建红, 郭秋燕. CE-1立体相机与激光高度计数据联合平差[J]. 测绘学报, 2014, 43 (12) : 1224 –1229. Zhao S M, Ran X Y, Fu J H and Guo Q Y. Combined adjustment of CE-1 stereo camera image and laser altimeter data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43 (12) : 1224 –1229. DOI: 10.13485/j.cnki.11-2089.2014.0178 |
| [22] | 周平, 唐新明, 曹宁, 王霞, 李国元, 张恒. SRTM约束的无地面控制立体影像区域网平差[J]. 测绘学报, 2016, 45 (11) : 1318 –1327. Zhou P, Tang X M, Cao N, Wang X, Li G Y and Zhang H. SRTM-aided stereo image block adjustment without ground control points[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45 (11) : 1318 –1327. DOI: 10.11947/j.AGCS.2016.20160219 |

