| 联合EEMD-KECA算法的InSAR干涉相位时频滤波 |
收稿日期: 2017-08-10
2. College of Computer, Hubei University of Education, Wuhan 430205, China
3. Beijing Key Laboratory of Resources Environment and Geographic Information System, Capital Normal University, Beijing 100048, China
4. College of Resource Environment and Tourism, Capital Normal University, Beijing 100048, China
InSAR干涉测量中大量存在的相位噪声,降低干涉条纹的周期性及连续度,为后续相位解缠带来困难,影响形变解算精度。
为消除相位噪声的影响,国内外研究者开展了大量研究工作。目前InSAR干涉图的滤波方法主要分为3大类:空间域滤波方法、频率域滤波方法以及时频分析的滤波方法。基于空间域和频率域分析的滤波方法,主要有Goldstein滤波法(Goldstein和Werner,1998;李佳 等,2011)、圆周期均/中值法(Eichel和Ghiglia,1993;Lanari 等,1996)、加权圆周期种植滤波法(段克清 等,2005)、自适应滤波方法(Lee 等,1998;廖明生 等,2003;于晶涛和陈鹰,2004;孙豆 等,2017)等。由于单一算法存在不足,研究者也相继提出一些组合滤波算法,如Song等人(2015)针对Goldstein算法进行改进,结合自适应滤波器提出改进的滤波方法,并结合傅里叶变换进行自适应噪声分离。Wang等人(2015)将Baran和自适应滤波器进行结合提出双控滤波算法,在干涉性较低区域可以获得较好滤波效果。但由于InSAR干涉图数据本身的特点,基于空间域和时间域的滤波方法,虽然引入自适应滤波思想,干涉图依旧存在噪声抑制性能和边缘细节无法同步的矛盾。
近年来,针对干涉相位为非平稳信号这一特征,研究者提出一系列基于时频分析的滤波方法(俞晓莹,2012;Li 等,2013;Abdallah和Abdelfattah,2015),根据干涉图中真实形变信号和噪声相位分布特性的差异,通过构造相应的规则,进行信号和噪声分离剔除,在干涉相位边缘区域具有较好噪声滤除和细节保持能力。基于经验模态分解方法EMD(Empirical Mode Decomposition)的InSAR干涉图滤波方法是基于时频分析的经典代表,它根据信号的尺度特性,完全由数据驱动进行自适应盲信号分解,获取隐含的振动模态,适合非平稳信号分离,有较好的InSAR干涉图滤波效果,如黄长军等人(2013)基于信号和噪声分布差异,利用EMD算法进行干涉相位经验模态分解,获取去除噪声且边缘及条纹细节保持较好的干涉相位。Song等人(2014a, 2014b)分别利用EMD以及基于EMD改进Goldstein方法对干涉图进行滤波,获得优于Godstein滤波及圆周期的滤波效果。已有基于EMD时频分析的干涉图滤波方法,多直接将部分高频模态分量作为噪声进行剔除,缺乏对高频模态分量是否为噪声的客观分析和评估;另外由于EMD算法本身固有缺陷,模态分解时易出现模态混叠现象,噪声分离与信号分量无法有效区分,对滤波效果会产生一定影响。
在分析已有InSAR干涉图滤波方法的基础上,针对EMD时频相位滤波方法的不足,本文提出一种EEMD-KECA滤波方法,该方法首先利用增强经验模态分解算法EEMD(Ensemble EMD)分离干涉相位中不同模态分量,降低分量间的模态混叠现象;然后采用适应于非线性信号分析的核熵成分分析KECA(Kernel Entropy Component Analysis)算法客观评估模态分量中的噪声成分,并加以去除,完成干涉相位的时频滤波,以期在有效抑制相位噪声的同时,较好地保持干涉图边缘细节信息。
2、EEMD总体经验模态分解算法EEMD算法是Wu和Huang(2009)针对EMD模态混叠现象提出的一种改进算法。它在EMD分解前,为待分解信号引入白噪声辅助分析,不仅能为待分解信号提供均匀的随机尺度,且可以平滑间歇性异常干扰,改善EMD分解的本征模分量IMF (Intrinsic Mode Function)包含不同时间尺度特征成分导致的模态混叠。对加入白噪声的待分解信号,重复多次利用EMD进行经验模态分解,把每次得到的IMF进行集合平均,以削弱均匀分布的白噪声影响,分解得到较传统EMD更为合理的IMF分量及趋势项。
以给定时序信号
(1) 向待分解信号中添加归一化的随机白噪声
| ${\hat { {s}}}({ t}) = {{s}}({ t}) + {\rm{noise}}({ t})$ | (1) |
(2) 参考EMD分解流程(Song 等,2014a),对添加均匀分布白噪声后的信号
| ${\hat { {s}}({ t})} = \sum\limits_{k = 1}^k {{{im}}{{{f}}_{{{{ kj}}}}}{{({ t})}}} + {{{y}}_{{{ j}}}}{{({ t})}}$ | (2) |
(3) 重复
(4) 将
| $\begin{array}{l} {{im}}{{{\hat{ {f}}}}_{ i}}({ t}) = \displaystyle\sum\limits_{j = 1}^n {{{im}}{{{f}}_{{ ij}}}({ t})} \\ {{{\hat{ {y}}}}_{ i}}({ t}) = \displaystyle\sum\limits_{j = 1}^n {{{{y}}_{ j}}} ({ t}) \end{array}$ | (3) |
EEMD算法通过给信号添加随机均匀分布的白噪声,进行多次重复分解,将多次分解得到的对应尺度的均值作为该尺度的本征模态分量,解决了EMD存在的模态混叠问题,而且分解得到的IMF更为合理,周期性更为显著,抗干扰能力更强。
在将EEMD等经验模态分解方法扩展到2维图像处理时,Wu和Huang(2009)提出对2维图像按照列/行方向进行一维经验模态分解,得到
| ${{{C}}_{{i}}} = \sum\limits_{k = i}^N {{{{h}}_{{{i, k}}}}} + \sum\limits_{j = i + i}^N {{{{h}}_{{{j, i}}}}} $ | (4) |
本文在利用EEMD算法对2维InSAR干涉图开展时频信号分解时,首先将干涉图分解为实部2维图和虚部2维图,然后利用EEMD算法分解对实部和虚部图的行列方向分别进行经验模态分解。
3、KECA干涉噪声评估识别利用EEMD对干涉图的实部和虚部分别进行2维分解之后,得到的行向及列向的本征模态分量IMF均有不同程度的噪声分布,需通过降维及客观评估,将各层IMF中隐含的噪声识别并加以去除。
已有研究表明(Flandrin 等,2004;王文波 等,2012),EEMD分解后得到的各时间尺度的模态分量中,IMF1中包含主要的高频成分,从第2层开始,该层模态分量的高频成分几乎是其下一层分量的2倍。如果按照直接以某一层或者几层高频IMF分量为噪声,不经过定量噪声评估,会导致噪声滤除不完全,且部分干涉图细节信息可能被误当作噪声滤除。有研究者提出利用主分量分析方法PCA(Principle Component analysis)对IMF集进行主分量分析(郭际明 等,2014),根据特征分量的大小识别噪声,但PCA算法主要适用于线性变换,对非线性复杂数据分析能力不足。
KECA算法(Jenssen,2010)以熵值(Renyi熵)最大为原则进行数据投影和转化,无需对待分解数据进行分布假设,直接以信息熵为评价指标进行投影转换,具有很好的非线性处理能力,较PCA具有更好的普适性,且在较低维度时仍有较好的降维效果(黄丽瑾 等,2012),可更好保持高维数据的原始特性。本文为有效评估并剔除噪声,采用KECA算法对IMF集合进行分析,并根据噪声能量分布模型,自适应选择保留的核熵成分分量。
KECA核熵成分分析基本原理为:
对于概率密度函数为
| $H(p) = - \lg \int {{p^2}} ({{x}})d{{x}} = - \lg ({{v}}(p))$ | (5) |
为求取Renyi熵,采用Parzen窗概率密度估计算子
| $\hat V(p) = \frac{1}{{{N^2}}}{{{I}}^{\rm T}}{{KI}}$ | (6) |
由于核矩阵可以分解为特征值组成的对角阵与特征向量乘积的表达
| ${{K}} = {{E}}{{{D}}_\lambda }{{{E}}^{\rm T}}$ | (7) |
则Renyi熵可转化为
| $\hat V(p) = \frac{1}{N^2}\sum\limits_{i = 1}^N {\left(\sqrt {{{\lambda _i}} } {{e}}_i^{\rm T}{{I}}\right)}^2$ | (8) |
在KECA特征分量选取时,以熵值贡献大小原则代替KPCA特征值大小,进行主分量选取。熵值越大,成为主分量的可能性越大。经过数据映射转化,KECA问题可以转化为最小化求解问题
| $\begin{array}{l} \mathop {\min }\limits_{{\lambda _{1,}}{e_1},\cdots{\lambda _{n,}}{e_{n1}}} \displaystyle\frac{1}{{{N^2}}}{{{I}}^{\rm T}}({{K}} - {{{K}}_{\rm{ECA}}}){{I}}=\\ \mathop {\min }\limits_{{\lambda _{1,}}{e_1},\cdots{\lambda _{n,}}{e_{n1}}} \hat V(p) - {{\hat V}_k}(p) \end{array}$ | (9) |
在利用KECA对IMF进行去噪时,按照式(10)计算应保留的核熵主份个数
| $\sum\limits_{i = H + 1}^N {{\lambda _i}} /\sum\limits_{i = 1}^N {{\lambda _i}} \leqslant \sum\limits_{i = \beta }^N {{\lambda _i}} /\sum\limits_{i = 1}^N {{\lambda _i}} $ | (10) |
本文在进行KECA本征模态分量分解时,利用式(11)所示的高斯核函数将低维的模态分量转换到高维空间
| ${{K}}({{x}}, {{y}}) = - \exp ({\left\| {{{x}} - {{y}}} \right\|^2}/2{\delta ^2})$ | (11) |
识别和剔除的IMF中噪声分量后,对残余信号分量进行重构,通过对无噪声分量累加以求解无噪声的干涉相位。
4、EEMD-KECA干涉相位滤波方法基于EMD时频干涉相位滤波方法存在模态混叠及噪声评价不客观的问题。本文提出一种改进的EEMD-KECA滤波方法,通过EEMD经验模态分解和KECA噪声相位评估分离,识别剔除干涉相位中的噪声信息,以期在有效抑制相位噪声的同时,较好地保持干涉图边缘细节信息。
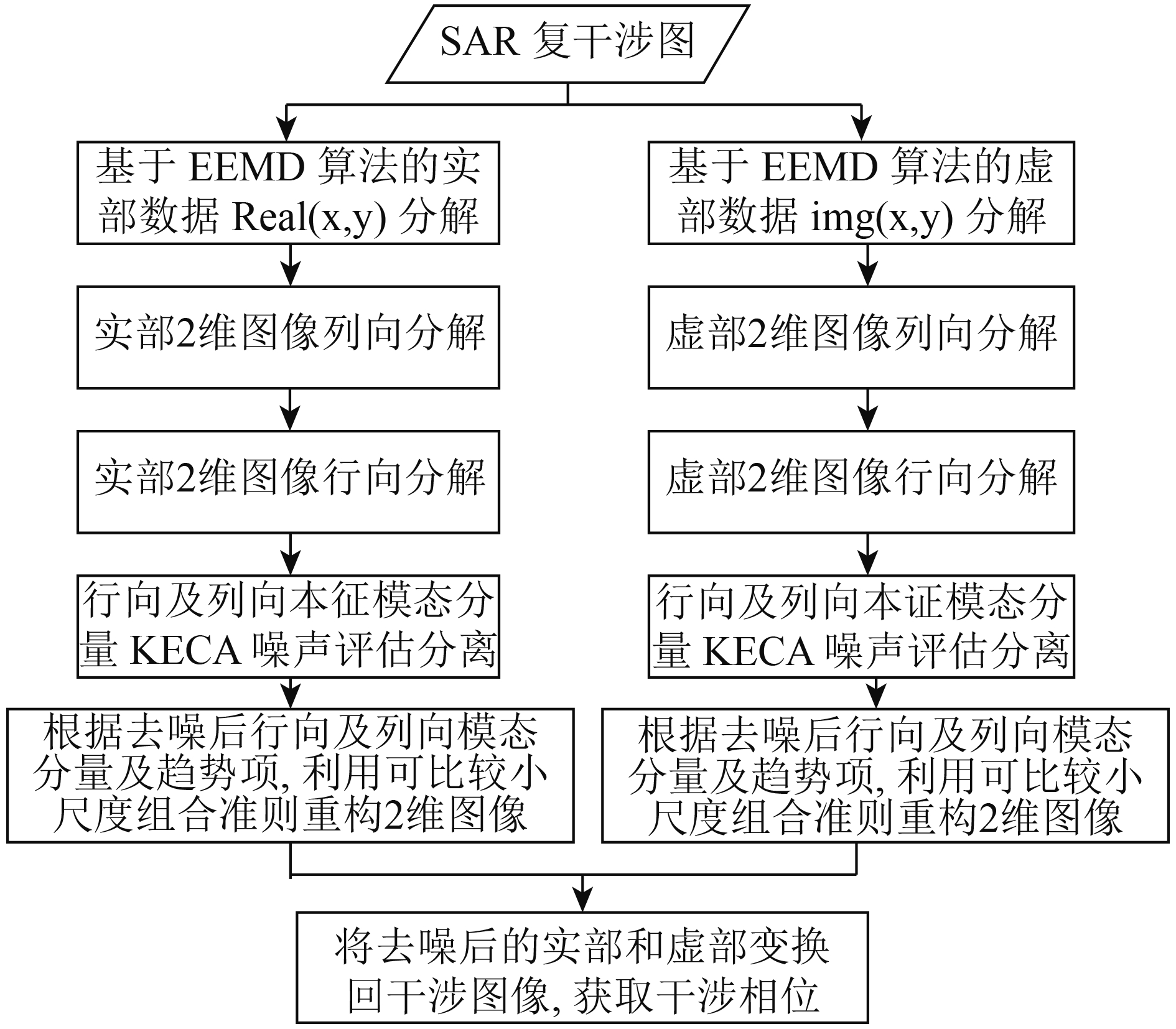
本文EEMD-KECA干涉相位时频滤波的流程如图1所示。
|
| 图 1 EEMD-KECA干涉相位滤波流程 Figure 1 Flow chart of the presented EEMD-KECA method |
为对本文提出的干涉相位滤波方法进行有效性验证,选取模拟干涉相位及北京地区真实差分干涉相位分别进行滤波试验,并与在干涉相位滤波领域应用较多的经典滤波方法进行对比验证,包括圆周期均值、圆周期中值、Goldstein滤波方法、EMD滤波方法、EMD-PCA滤波方法。为了评价不同方法的滤波效果,采用滤波前后的相位剖线,以及定量评价指标如RMS指标、相位差和值、相位标准差及边缘保持指数EPI(Song 等,2014b)对不同方法的滤波结果进行对比分析。
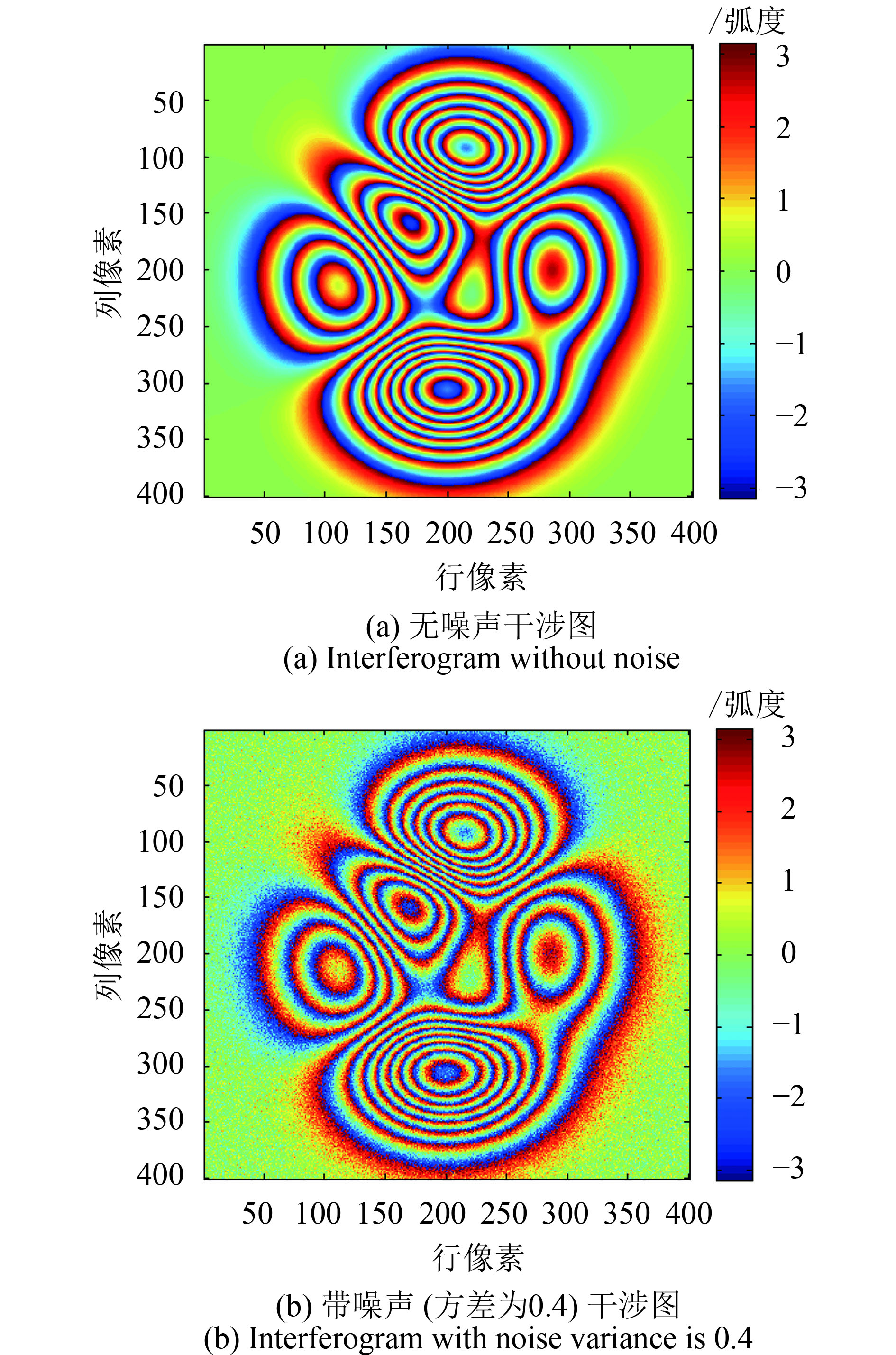
(5.1) 模拟数据滤波试验对图2所示的大小为400像素×400像素的2维模拟干涉相位进行滤波试验,其中图2(a)为原始无噪声相位,图2(b)为带噪声干涉图。
|
| 图 2 模拟的干涉图 Figure 2 Simulated interferogram |
分别采用经典圆周期均值/中值滤波算法、Goldstein滤波方法、常规EMD算法、EMD-PCA降维以及本文滤波方法,对含有噪声的模拟相位进行滤波。由于Goldstein滤波、EMD滤波、EMD-PCA滤波及本文方法,需要对干涉相位对应的复干涉图进行操作,利用式(10)计算将缠绕相位转换为复干涉图。滤波时,为了既能去除噪声又尽可能不降低原始相位的分辨率,圆周期均值及中值算法滤波窗口选择5×5;Goldstein滤波的平滑强度因子
| ${\rm{int}} \,\, {{erf }} = \exp ({{i }}\cdot{{\varphi }})$ | (12) |
图3—图8分别为不同方法的滤波结果及滤波后与原始无噪声相位之差。为了充分对比不同方法的滤波效果,计算了不同方法滤波后与滤波前的相位之差,及滤波后相位与原始无噪声相位之差。
|
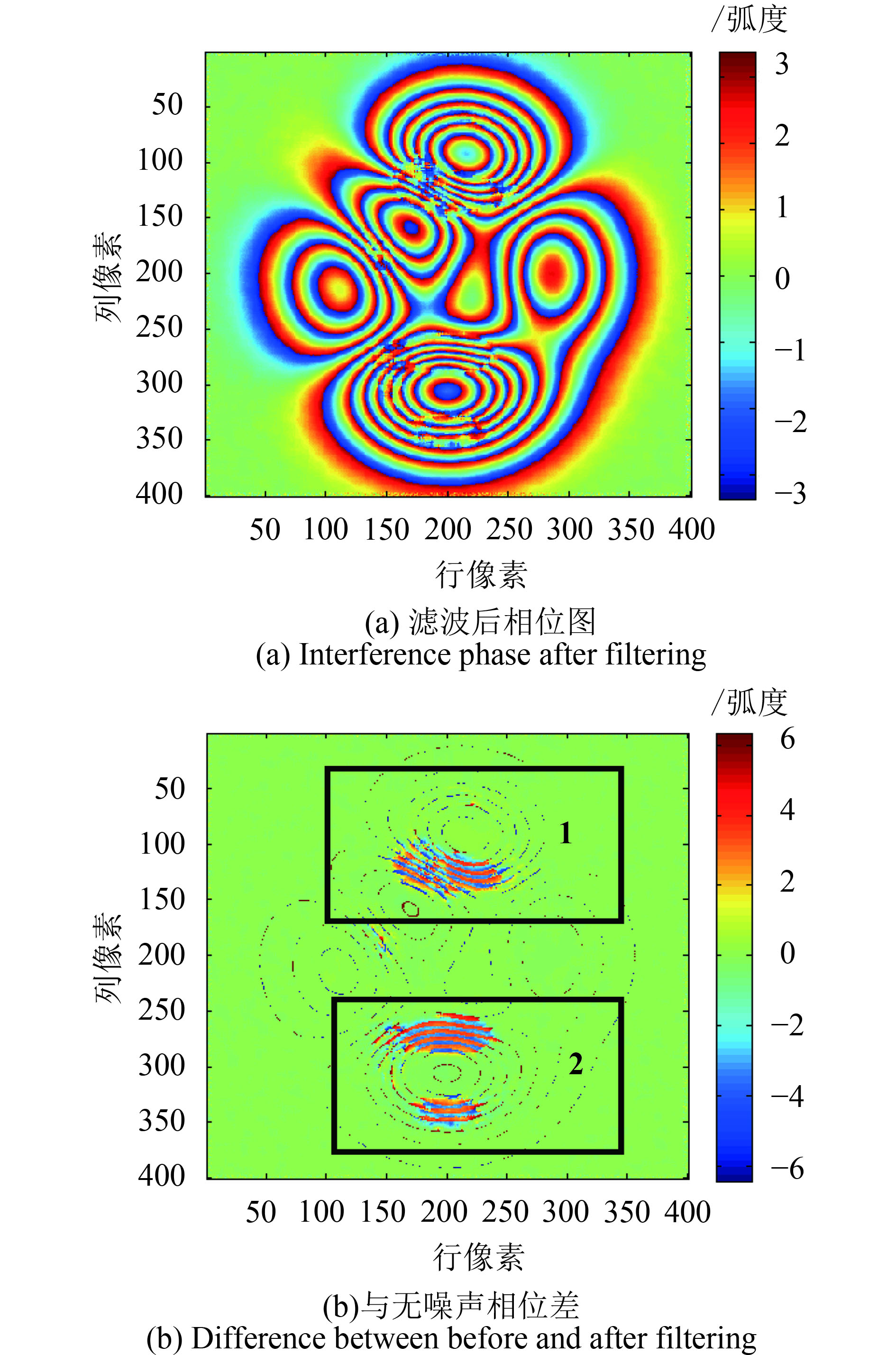
| 图 3 圆周期均值滤波结果 Figure 3 The Circular periodic mean filter result |
|
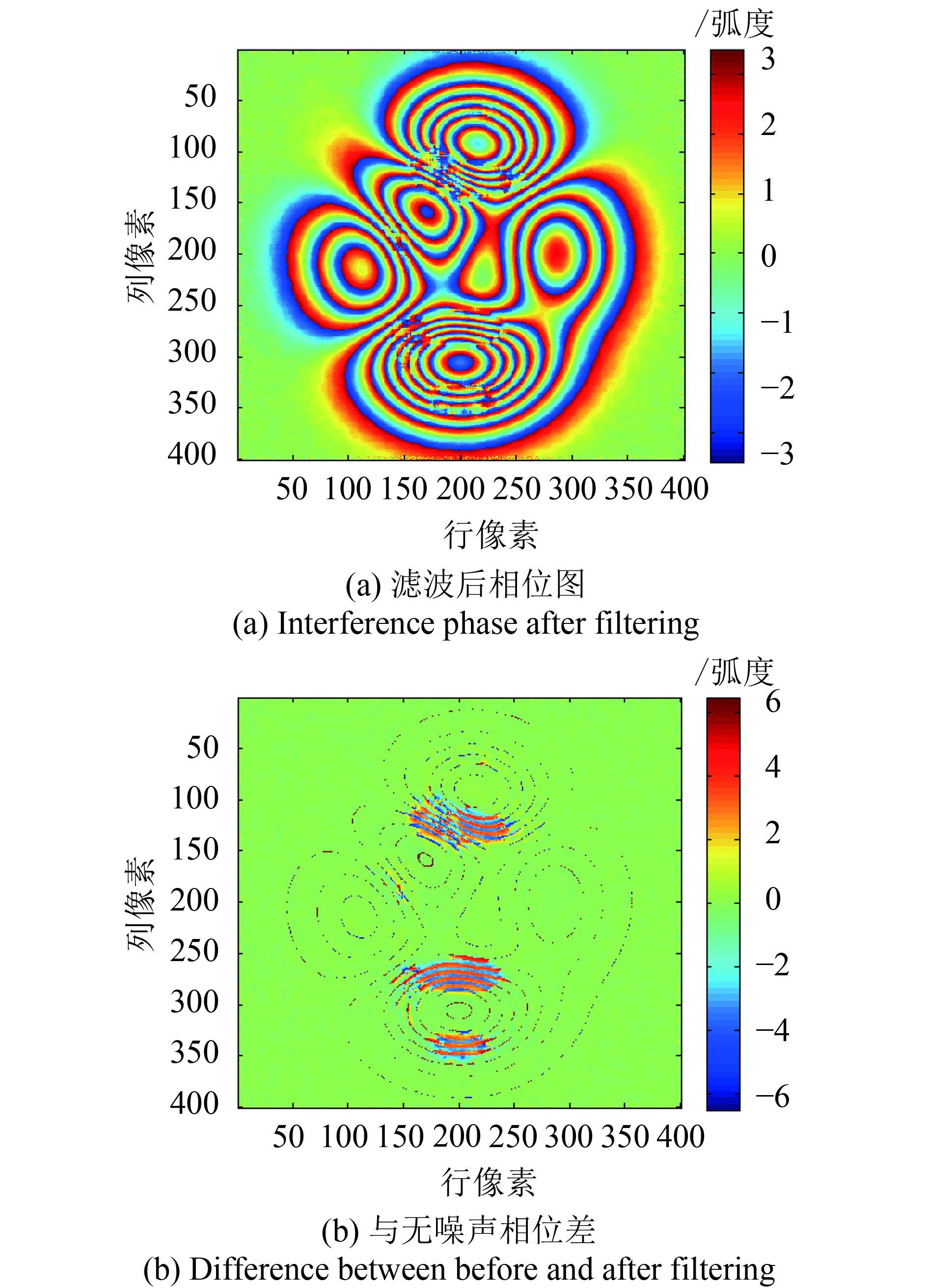
| 图 4 圆周期中值滤波结果 Figure 4 The Circular periodic median filter result |
|
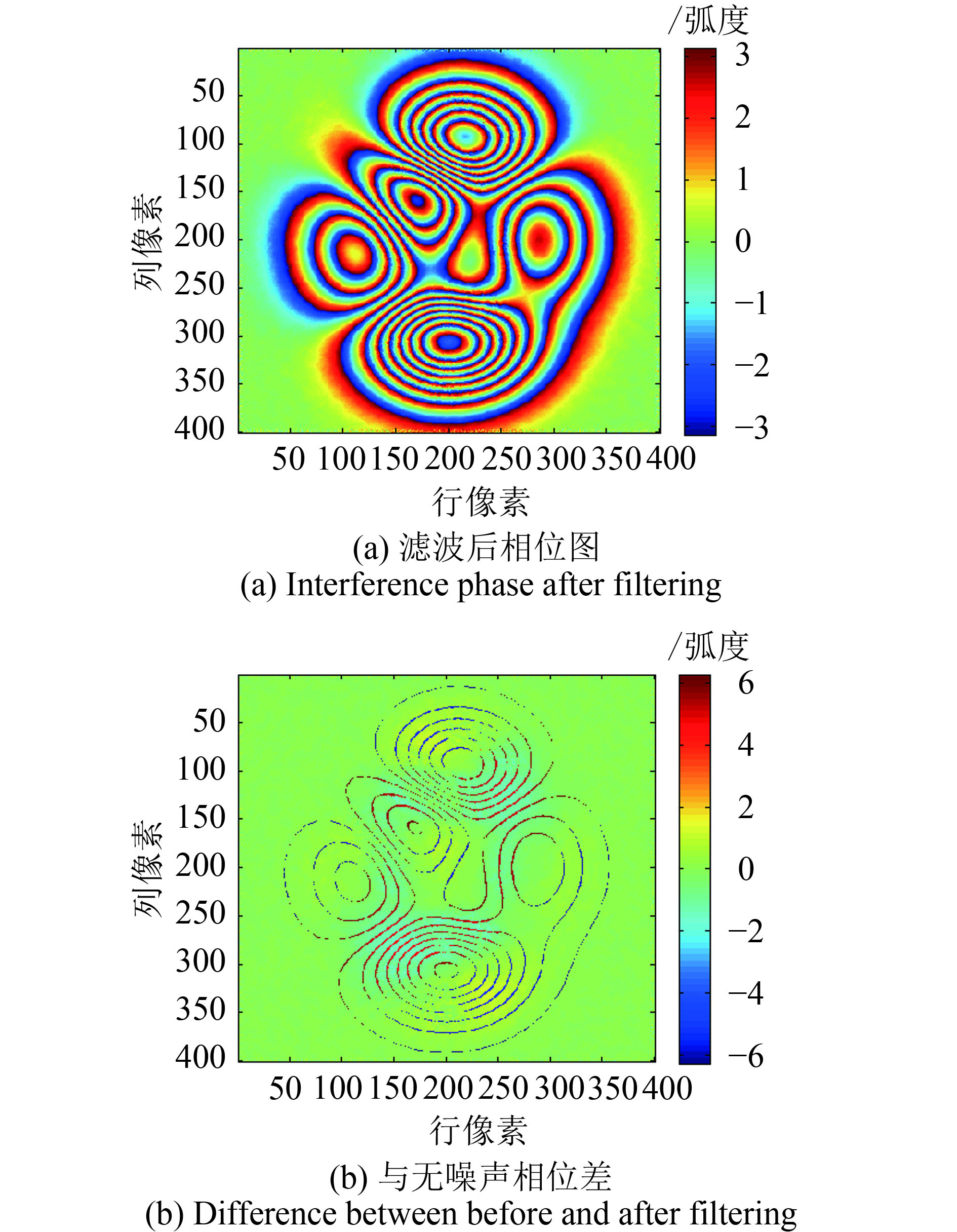
| 图 5 Goldstein滤波结果 Figure 5 The Goldstein filter result |
|
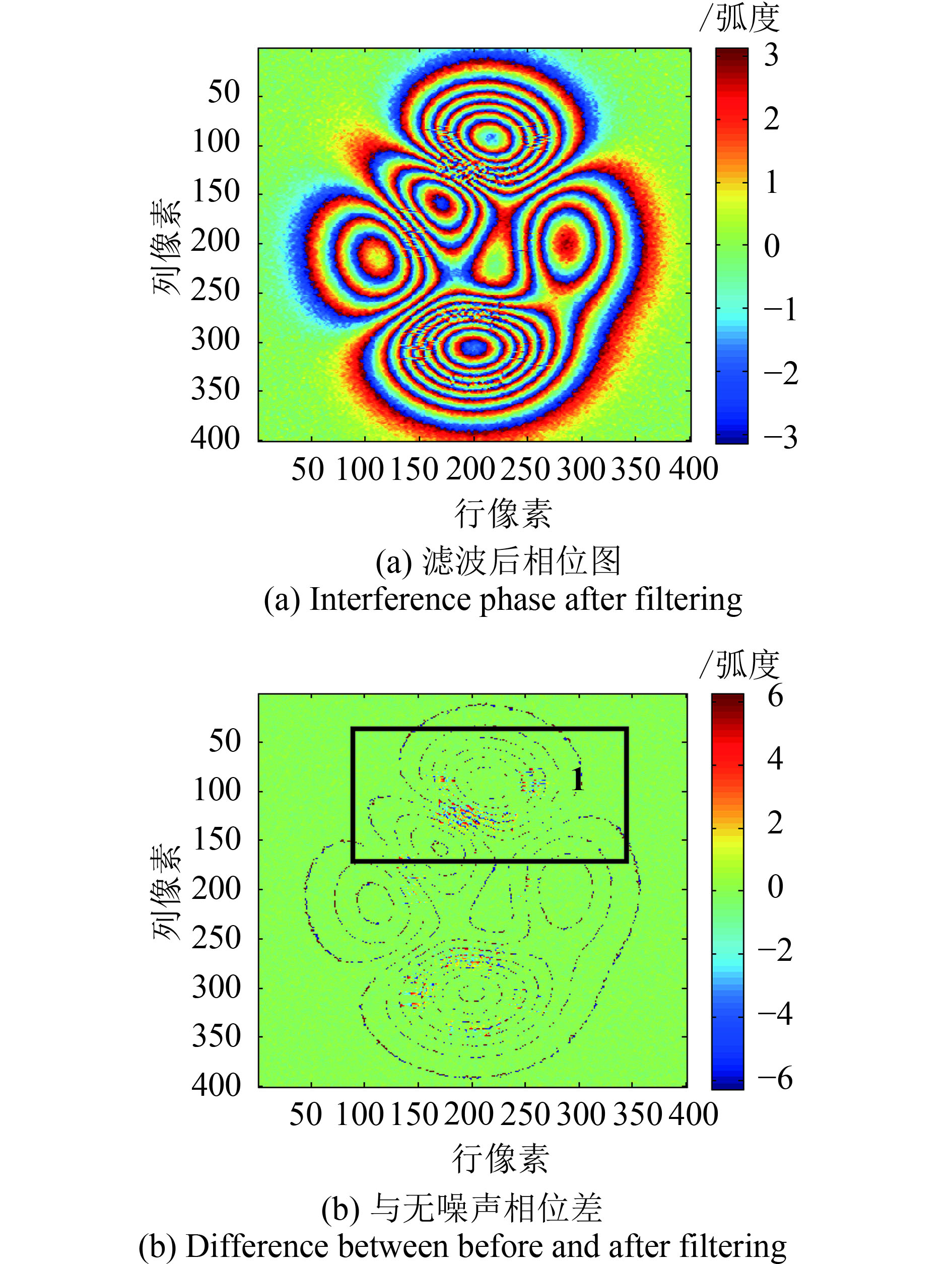
| 图 6 EMD滤波结果 Figure 6 EMD filter result |
|
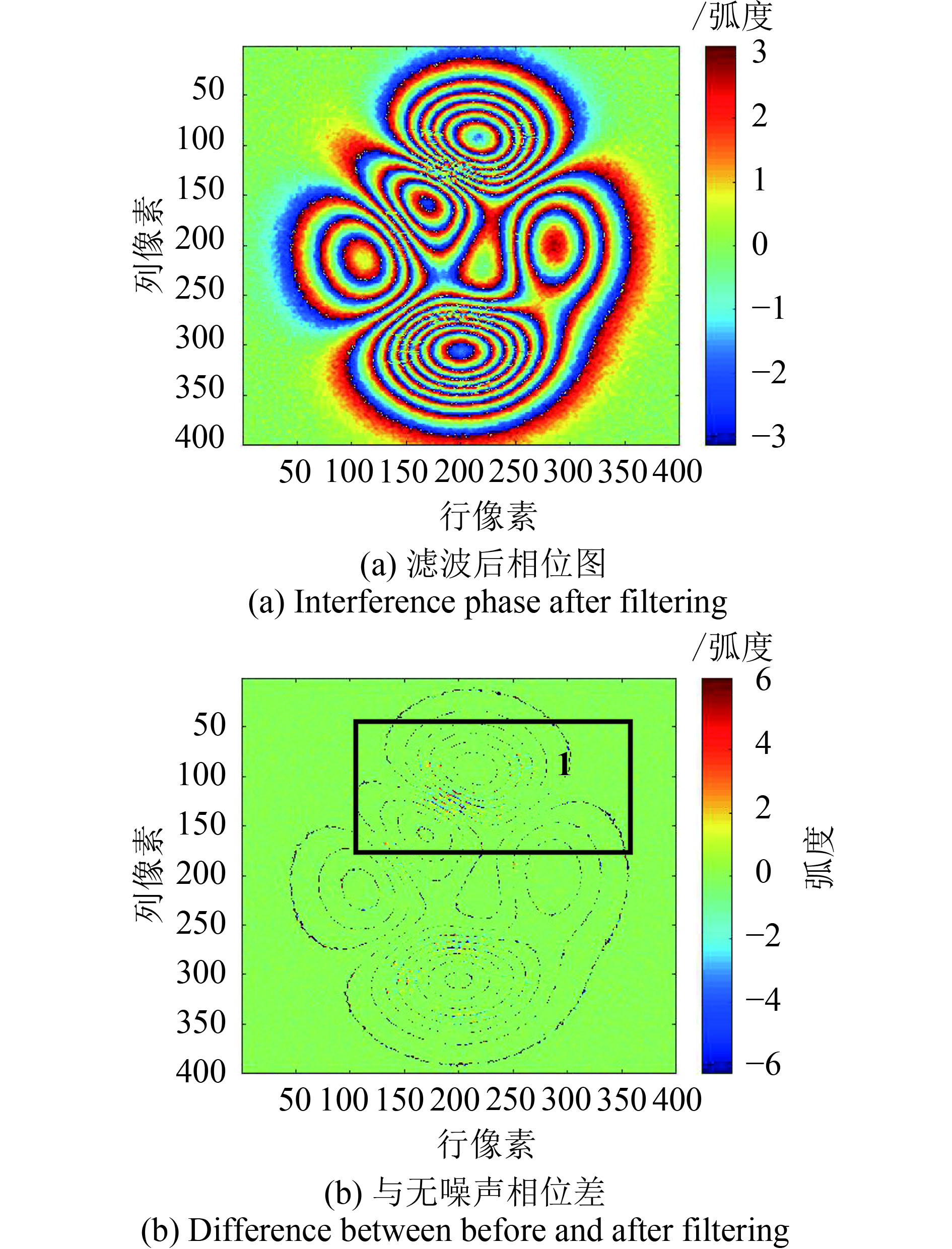
| 图 7 EMD-PCA滤波结果 Figure 7 EMD-PCA filter result |
|
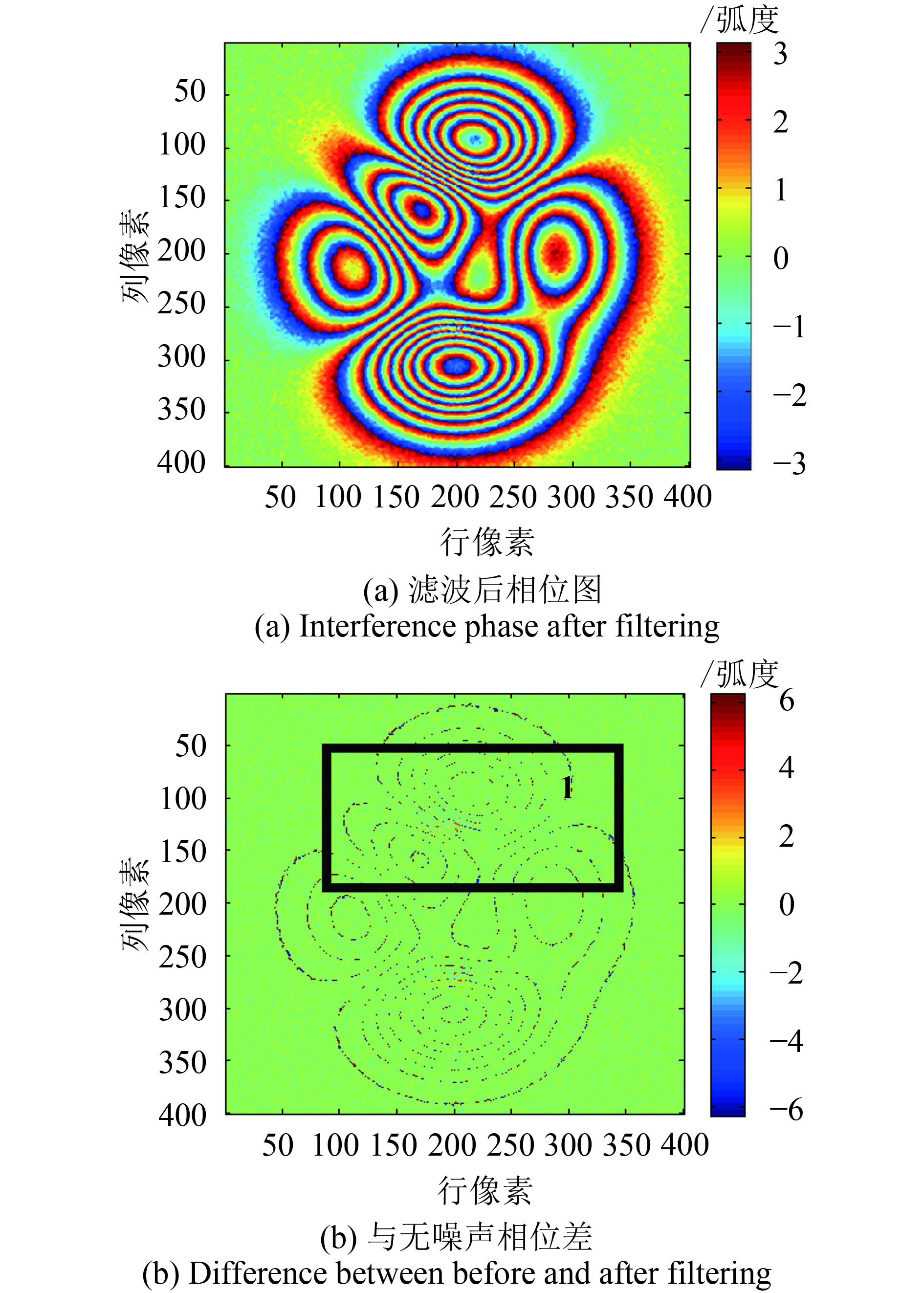
| 图 8 本文EEMD-KECA方法滤波结果 Figure 8 The proposed EEMD-KECA filter result |
从图3—图8(a)发现,6种滤波方法均能一定程度上降低干涉相位图的斑点噪声,滤波后的干涉条纹具有一定的连续性。滤波后干涉相位与原始无噪声相位差值越小,表明相位恢复能力越强、滤波效果越好。由图3—图8(b),不同方法滤波前后的相位差异图发现,不同方法的滤波效果差异明显。由图3(a)及图4(a)的滤波结果发现,圆周期均值及中值滤波方法在条纹相对不密集的地方,总体滤波效果不错,但对于条纹密集区,滤波效果较差,滤波后的相位干涉条纹断裂,滤波后引入的虚假信号,破坏了条纹的连续性,这可能是由于圆周期的滤波滑动窗口大于密集区的条纹宽度,导致的条纹混叠和失真;由图3及图4(b),圆周期均值及中值滤波后的相位差图发现,在区域1和区域2处,滤波后与原始无噪声相位存在较大的相位失真;由图5(a),Goldstein方法滤波后虽条纹连续性较好,这是由于Goldstein滤波是将干涉图通过傅里叶变换转换到频域进行噪声平滑,所以在条纹密集区也可获得连续性较好的干涉条纹,滤波效果均优于圆周期均值及中值滤波方法。但从图5(b)的滤波后相位与无噪声相位的差值图发现,相位差图中条纹边界明显,边界上较多像素的相位差的绝对值接近
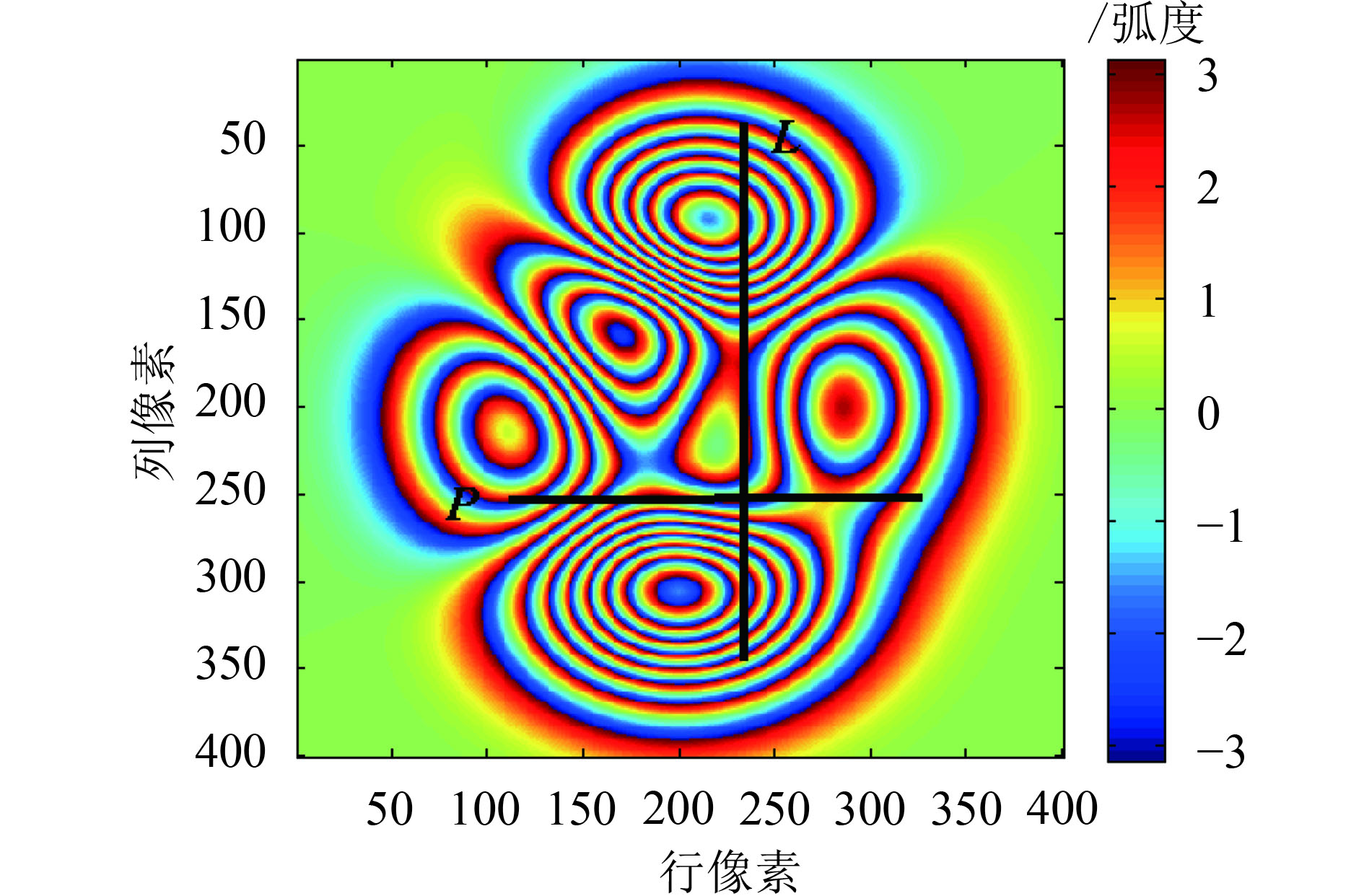
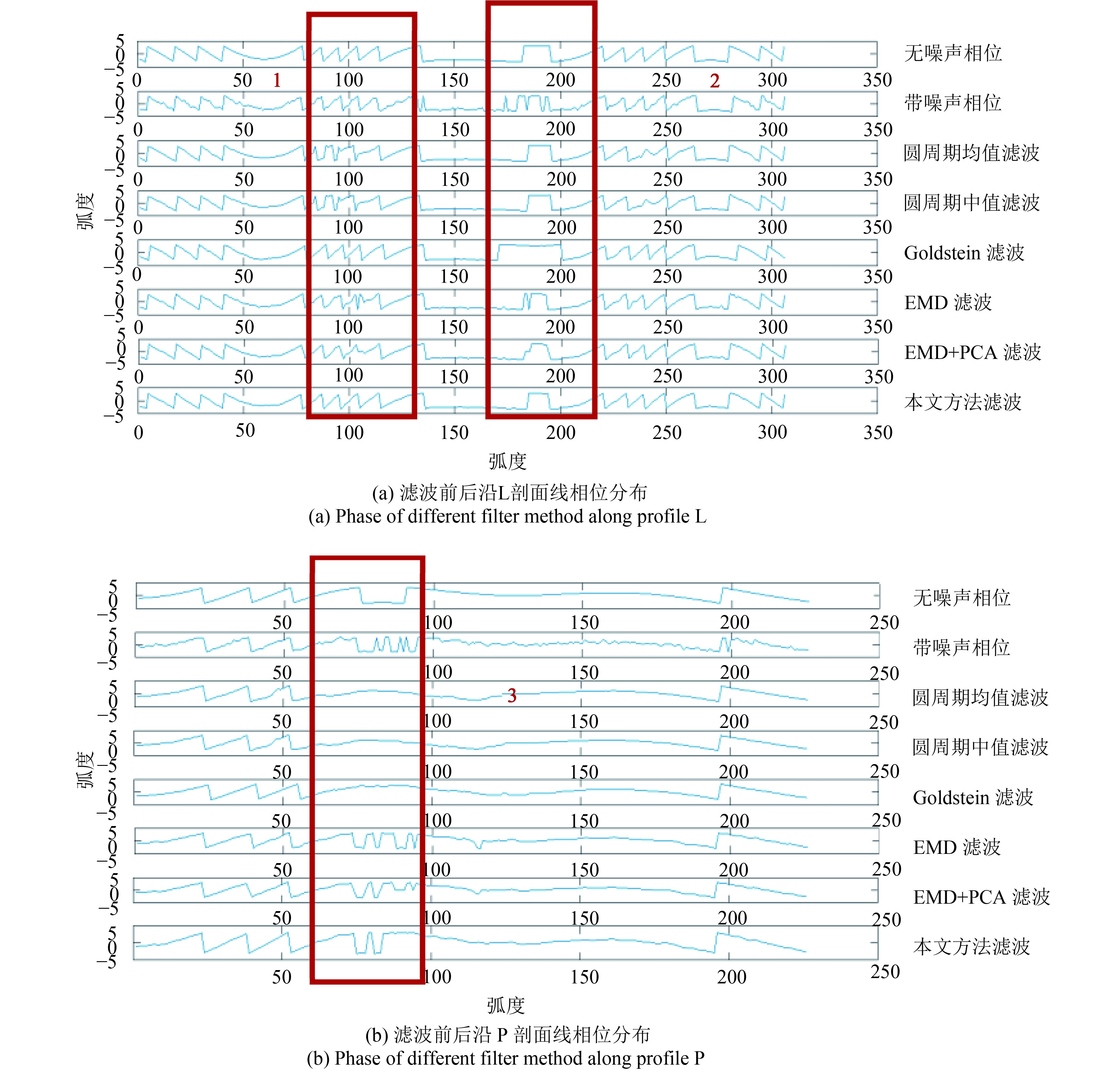
为了进一步比较不同方法的滤波效果,选取无噪声干涉相位、含噪声相位以及6种方法滤波结果,沿如图9所示的线段L及P绘制剖面线,剖面上相位分布分别如图10(a)及图10(b)所示。
|
| 图 9 剖面线L及P分布示意图 Figure 9 Distribution of cross section lines L and P |
|
| 图 10 不同方法滤波结果剖面相位分布 Figure 10 Cross section over the filtered interferograms |
对比剖线L上各滤波方法得到相位图,结合红框1和2所示区域,表明本文方法的滤波结果与原始无噪声相位分布较为一致,有效滤除了添加的噪声相位;而其他5种方法的滤波结果,各自存在一定的误差。对于剖线P上的各滤波方法的相位分布,对于红框3所示区域,虽然6种滤波方法均未能完全恢复原始无噪声相位,但较其他5种方法而言,本文EEMD-KECA滤波方法相位恢复效果最优。
以上分析表明,本文方法较其他5种方法而言,由于根据噪声及信号的时频分布特性差异进行噪声识别,无需设定滑动窗口,所以滤波结果不受干涉条纹疏密及噪声变化方向的影响,滤波结果最接近初始无噪声相位,在条纹边缘区较其他5种方法有更好的保持效果。
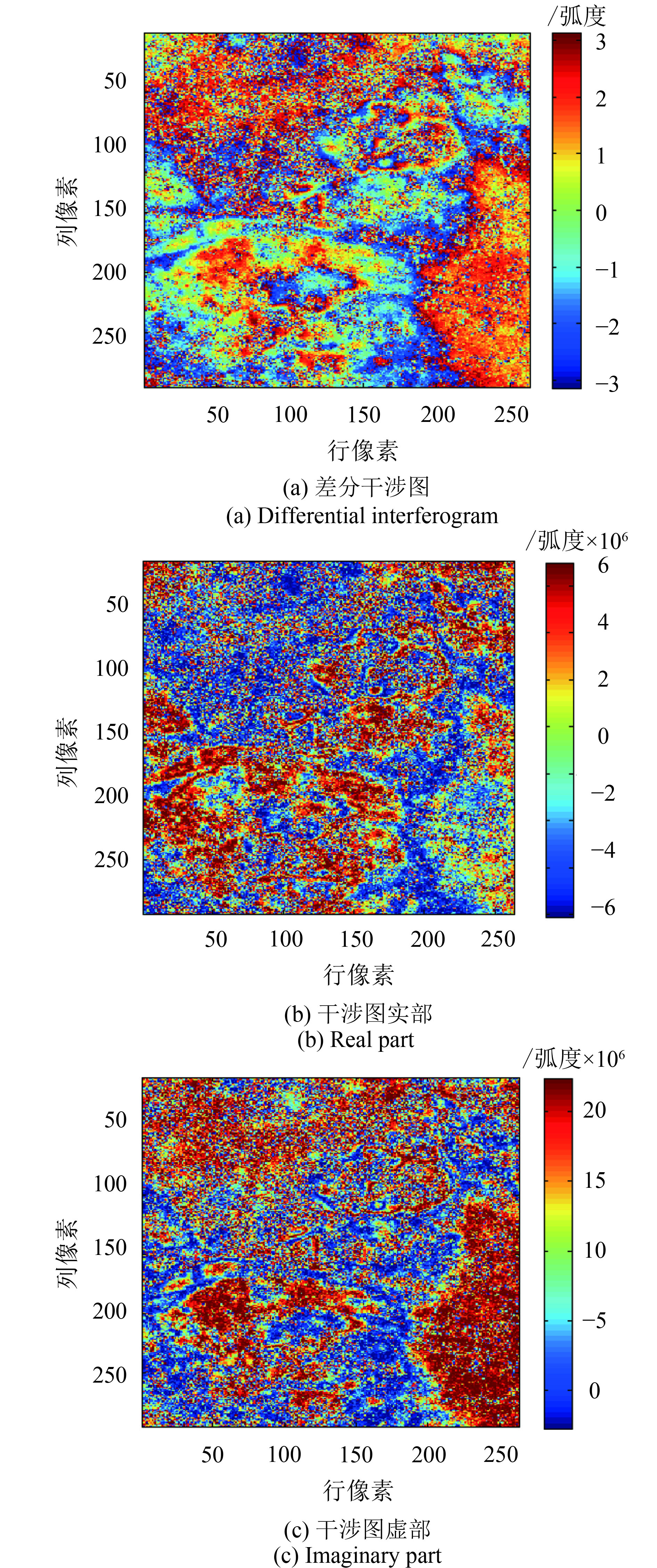
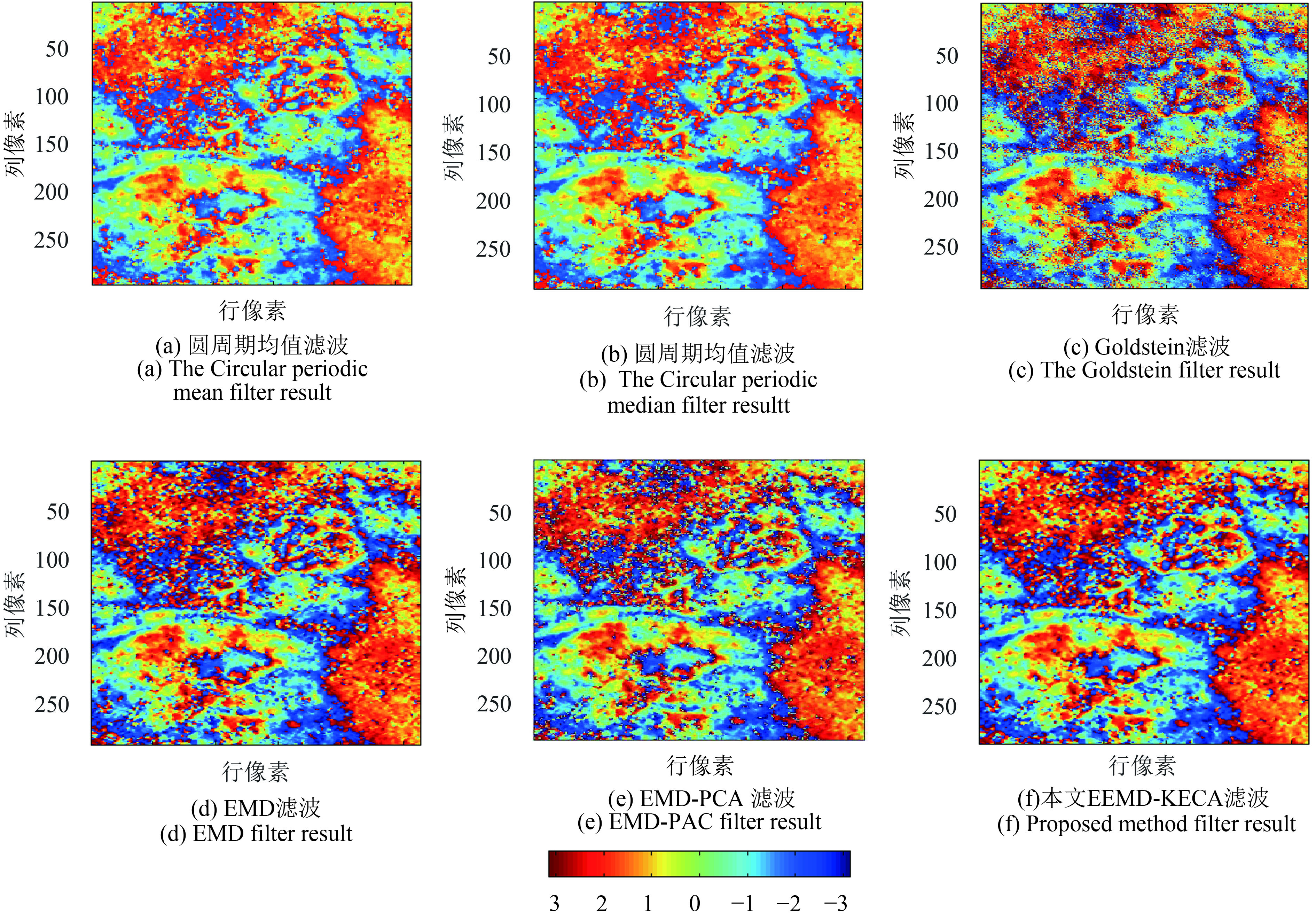
(5.2) 真实差分干涉相位滤波试验采用北京地区2007-10-10与2008-02-27获取的Envisat ASAR影像进行差分共轭干涉计算,利用5种方法,经典圆周期均值/中值滤波算法、Goldstein滤波方法、常规EMD算法、EMD-PCA滤波以及本文滤波方法分别对真实差分干涉图进行滤波试验,研究区大小为295像素×263像素。原始差分干涉相位图、复干涉图实部及虚部见图11。对图11所示的真实差分干涉图进行滤波处理,滤波结果如图12所示。
|
| 图 11 真实差分干涉图 Figure 11 Real differential Interferogram |
|
| 图 12 真实差分干涉图不同方法滤波结果 Figure 12 Differential Interferogram filtered by different filters |
由原始干涉相位图及不同方法的滤波结果图发现,不同的滤波方法均能一定程度上降低干涉图上的噪声,滤波后干涉相位图连续性较原始图像变好。由圆周期均值/中值滤波结果图12(a)及图12(b)发现,由于圆周期属于空域滤波,计算过程的滑动窗口导致相位图分辨率下降,干涉相位较原始干涉相位,均被过度平滑,导致干涉相位失真;而图12(c) Goldstein滤波结果,相位保真能力相对较强,但整体而言,滤波后干涉相位残余的噪声较多,散布的斑点导致干涉条纹连续性不佳;而基于EMD及本文滤波方法,相位保真能力较好,与Goldstein类似,且整体滤波效果明显优于Goldstein滤波方法;而EMD-PCA方法较EMD滤波效果有所改善;此外本文方法滤波结果干涉条纹的连续性较好。6种滤波结果的目视效果表明,本文滤波方法不但具有较好的相位保真能力,而且滤波之后干涉条纹连续性更优,说明本文方法滤波效果优于其他5种方法。
对不同方法滤波结果进行指标评价,结果见表1。其中,边缘保持指数EPI的值越接近1越好,相位残差点越少越好。由于对于真实差分干涉图,没有无噪干涉相位作为对比,所以在真实数据滤波结果定量评价中,没有计算“相位差绝对值和”和相位均方根误差RMS这两项指标。
|
|
表 1 真实数据不同方法滤波效果定量评价 Table 1 Quantitative evaluation of differential interferogram filtered results |
真实差分干涉图滤波结果目视效果及表1的定量评价,可得到与模拟数据滤波试验相同的结论,即本文方法较其他5种方法具有更好的滤波性能,在修正剔除干涉图噪声的同时,较好地保持了干涉条纹连续性及边缘细节信息。
6、结 论本文针对传统基于EMD算法的InSAR干涉相位滤波存在模态混叠及噪声相位未进行有效客观评估的问题,提出一种改进的联合EEMD-KECA的干涉相位滤波方法。通过模拟数据及真实差分干涉数据的滤波试验,对比本文方法与经典圆周期均值、圆周期中值、Goldstein滤波方法、EMD滤波及EMD-PCA方法的滤波效果,目视分析及指标定量评价均表明了本文方法的有效性及优势。本文方法不仅保留了EMD时频滤波不会造成相位平滑且边缘细节保持能力较强的优点,而且改善了因模态混叠导致的噪声滤除不彻底及部分图像信息被误滤除的问题,获得更优的滤波效果。试验结果表明,该方法不仅在条纹变化缓慢区域表现出较好的滤波性能,在干涉条纹密集区及相位边缘细节处,也具有较好的滤波效果和较强的相位保真度,对于具有不同疏密干涉条纹具有较好的适用性。
利用EEMD分解干涉图信号和噪声时,是通过先行向再列向分解的方式进行,对于某些具有方向性的噪声而言,适应性和扩展性相对受限。因此在进行干涉相位分解时,如何针对具有不同方向特征的噪声进行有效滤波是下一步研究目标。
| [1] | Abdallah W B and Abdelfattah R. Two-dimensional wavelet algorithm for interferometric synthetic aperture radar phase filtering enhancement[J]. Journal of Applied Remote Sensing, 2015, 9 (1) : 096061 . DOI: 10.1117/1.JRS.9.096061 |
| [2] | 段克清, 向家彬, 汪枫. InSAR相位条纹图的加权圆周期中值滤波算法[J]. 空军雷达学院学报, 2005, 19 (1) : 4 –6. Duan K Q, Xiang J B and Jiang F. An algorithm of weighted periodic pivoting median filtering for InSAR phase fringe[J]. Journal of Air Force Radar Academy, 2005, 19 (1) : 4 –6. |
| [3] | Eichel P H and Ghiglia D C. 1993. Spotlight SAR interferometry for terrain elevation mapping and interferometric change detection. Sand: Sandia National Labs Technology: 2529–2546 |
| [4] | Flandrin P, Rilling G and Goncalves P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters, 2004, 11 (2) : 112 –114. DOI: 10.1109/LSP.2003.821662 |
| [5] | Goldstein R M and Werner C L. Radar interferogram filtering for geophysical applications[J]. Geophysical Research Letters, 1998, 25 (21) : 4035 –4038. DOI: 10.1029/1998GL900033 |
| [6] | 郭际明, 黄长军, 喻小东, 聂智平. 利用BEMD-自适应滤波去除SAR干涉图噪声[J]. 武汉大学学报•信息科学版, 2014, 39 (4) : 422 –427. Guo J M, Huang C J, Yu X D and Nie Z P. Interferogram denoising method based on BEMD and adaotive filter[J]. Geomatics and Information Science of Wuhan University, 2014, 39 (4) : 422 –427. |
| [7] | 黄长军, 郭际明, 喻小东, 袁长征. 干涉图EMD-自适应滤波去噪法[J]. 测绘学报, 2013, 42 (5) : 707 –714. Huang C J, Guo J M, Yu X D and Yuan C Z. The study of interferogram denoising method based on EMD and adaptive filter[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42 (5) : 707 –714. |
| [8] | 黄丽瑾, 施俊, 钟瑾. 基于核熵成分分析的数据降维[J]. 计算机工程, 2012, 38 (2) : 175 –177. Huang L J, Shi J and Zhong J. Data dimension reduction based on kernel entropy component analysis[J]. Computer Engineering, 2012, 38 (2) : 175 –177. DOI: 10.3969/j.issn.1000-3428.2012.02.057 |
| [9] | Jenssen R. Kernel entropy component analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32 (5) : 847 –860. DOI: 10.1109/TPAMI.2009.100 |
| [10] | Lanari R, Fornaro G, Riccio D, Migliaccio M, Papathanassiou K P, Moreira J R, Schwabisch M, Dutra L, Puglisi G, Franceschetti G and Coltelli M. Generation of digital elevation models by using SIR-C/X-SAR multifrequency two-pass interferometry: the Etna case study[J]. IEEE Transaction on Geoscience and Remote Sensing, 1996, 34 (5) : 1097 –1114. DOI: 10.1109/36.536526 |
| [11] | Lee J S, Papathanassiou K P, Ainsworth T L, Grunes M R and Reigber A. A new technique for noise filtering of SAR interferometric phase images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36 (6) : 1456 –1465. DOI: 10.1109/36.718849 |
| [12] | Li F F, Hu D H and Ding C B. InSAR Phase Noise Reduction Based on Empirical Mode Decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10 (5) : 1180 –1184. |
| [13] | 李佳, 李志伟, 丁晓利, 朱珺和汪长城. 强噪声SAR干涉图的等值线中值——Goldstein二级滤波[J]. 遥感学报, 2011, 15 (4) : 750 –765. Li J, Li Z W, Ding X L, Zhu J and Wang C C. Filtering strong noisy synthetic aperture radar (SAR) interferogram with integrated Contoured Median[J]. Journal of Remote Sensing, 2011, 15 (4) : 750 –765. |
| [14] | 廖明生, 林珲, 张祖勋, 杨文和张力. INSAR干涉条纹图的复数空间自适应滤波[J]. 遥感学报, 2003, 7 (2) : 98 –105. Liao M S, Lin H, Sun Z X, Yang W and Zhang L. Adaptive algorithm for filtering interferometric phase noise[J]. Journal of Remote Sensing, 2003, 7 (2) : 98 –105. |
| [15] | Song R, Guo H D, Liu G, Perski Z and Fan J H. Improved Goldstein SAR interferogram filter based on empirical mode decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2014a, 11 (2) : 399 –403. DOI: 10.1109/LGRS.2013.2263554 |
| [16] | Song R, Guo H D, Liu G, Perski Z, Yue H Y, Han C M and Fan J H. SAR interferometric phase filtering technique based on bivariate empirical mode decomposition[J]. Remote Sensing Letters, 2014b, 5 (8) : 743 –752. DOI: 10.1080/2150704X.2014.963894 |
| [17] | Song R, Guo H D, Liu G, Perski Z, Yue H Y, Han C M and Fan J H. Improved Goldstein SAR interferogram filter based on adaptive-neighborhood technique[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12 (1) : 140 –144. DOI: 10.1109/LGRS.2014.2329498 |
| [18] | 孙豆, 邢世其, 李永帧和代大海. SAR稀疏成像模型参数自适应选择[J]. 遥感学报, 2017, 21 (4) : 579 –587. Sun D, Xing S Q, Li Y Z and Dai D H. Adaptive parameter selection of SAR sparse imaging model[J]. Journal of Remote Sensing, 2017, 21 (4) : 579 –587. |
| [19] | 王文波, 赵攀, 张晓东. 利用经验模态分解和主成分分析的SAR图像相干斑抑制[J]. 测绘学报, 2012, 41 (6) : 838 –843. Wang W B, Zhao P and Zhang X D. Research on SAR image speckle reduction using EMD and principle component analysis[J]. Acta Geodaetica et Cartographical Sinca, 2012, 41 (6) : 838 –843. |
| [20] | Wang Y, Huang H F, Dong Z and Wu M Q. A dual-domain interferometric phase filter[J]. Remote Sensing Letters, 2015, 6 (12) : 962 –971. DOI: 10.1080/2150704X.2015.1093669 |
| [21] | Wu Z H and Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1 (1) : 1 –41. DOI: 10.1142/S1793536909000047 |
| [22] | 杨晨, 黄丽亚, 文念, 杨俊宇. 基于二维集合经验模式分解的稳态视觉诱发电位目标检测研究[J]. 生物医学工程学杂志, 2015, 32 (3) : 508 –513. Yang C, Huang L Y, Wen N and Yang J Y. Study on steady state visual evoked potential target detection based on two-dimensional ensemble empirical mode decomposition[J]. Journal of Biomedical Engineering, 2015, 32 (3) : 508 –513. DOI: 10.7507/1001-5515.20150093 |
| [23] | 于晶涛, 陈鹰. 一种新的INSAR干涉条纹图滤波方法[J]. 测绘学报, 2004, 33 (2) : 121 –126. Yu J T and Chen Y. A new filter on INSAR interferogram fringe[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33 (2) : 121 –126. DOI: 10.3321/j.issn:1001-1595.2004.02.006 |
| [24] | 俞晓莹.2012.改进的SBAS地表形变监测及地下水应用研究.长沙: 中南大学 Yu X Y. 2012. Improved SBAS Technology for Land Deformation Detection and Groundwater Applicaton.Changsha: Central South University |

