| 激光测距对静态重力场恢复精度的影响分析 |
收稿日期: 2017-06-29
2. Qian Xuesen Laboratory of Space Technology, Beijing 100094, China
3. College of Earth Science, University of Chinese Academy of Sciences, Beijing 100049, China
高精度的地球重力场模型对经济、军事以及地球科学研究等具有十分重要的作用。为此,国外发射了多颗具有重力场探测效能的地球观测卫星,如CHAMP、GRACE、GOCE以及海洋测高卫星等。其中,CHAMP、GRACE和GOCE统称为重力卫星,GRACE卫星相对于CHAMP和GOCE卫星有更加广泛的应用前景,如海洋、南极冰盖、陆地水等地球科学方面的应用(许厚泽 等,2012)。GRACE卫星已于2017年10月坠落,其后续卫星GRACE Follow-on已于2018年5月发射,近期Earth system mass transport mission(e.motion)和Next Generation satellite Gravimetry Mission(NGGM)卫星计划正在设计研究阶段(Panet 等,2013;Roland和Thomas,2015)。该类卫星的基本原理是通过高低跟踪和低低跟踪距离测量来探测地球重力场所引起的卫星星间距离的变化,并以此来反演地球重力场,其中高低跟踪测量主要通过星载GPS接收机来完成,低低跟踪则主要依靠微波测距完成。对于GRACE卫星而言,卫星低低跟踪数据的精度对重力场模型的精度起着至关重要的作用,因此在新的卫星计划中,除了微波测距外,还将搭载高精度的激光测距来进行更高精度的测距实验。由此,便产生这样的问题:激光测距对重力场模型恢复精度的提升会带来多大帮助,特别是当其他载荷的精度没有提升时。
事实上,关于以上问题,当前已有不少研究和结论。Loomis等人(2012)通过模拟仿真讨论了块质量异常体所引起的重力场变化的探测精度问题,其结论表明:激光测距对块质量异常体的探测精度的提升帮助有限,只有背景场的时变误差得到削弱后,才会明显改善该文所提出的质量异常体的探测精度。显然该文主要讨论的对象为时变重力场。Elsaka等人(2014)讨论了7种不同轨道构型下的重力场模型探测精度,其中一种构型(该文中以GRACE Follow-on表示)用激光来进行测距,其余载荷和GRACE一样,另外的区别是将轨道降低了40 km,此种情况下的重力场恢复精度和GRACE相比精度提高了约10倍,由于该结论受到了轨道降低的影响,因此难以估计激光单独的贡献占多大量级。此外多篇国外文献讨论了采用激光后的重力卫星计划,如Panet等人(2013)、Gruber等人(2014)和Sheard等人(2012),但少有文献单独评估激光的贡献。
围绕下一代的低低跟踪重力卫星,国内多家单位进行了相应的指标论证研究。庞振兴等人(2012)利用谱分析方法估计了GRACE Follow-On的空间分辨率,该文指出后者比前者能够以更高的空间分辨率和至少高一个量级的精度来恢复地球的时变重力场和静态重力场,后者所采用的技术除了激光测距之外,还采用了无拖曳技术,并且提高了定轨、定速及加速度计的精度,因此此文中重力场精度的提升是各类因素的一个综合效应,而不是激光测距单独的贡献;郑伟等人(2010)利用解析法估计了GRACE Follow-On的地球重力场精度,但该文将定轨、定速误差与星间测距误差及加速度计误差作了等权处理,这与实际的重力场解算不符,很显然定轨定速数据的权重应低于星间测距和加速度计数据的权重;赵倩等人(2014)利用仿真分析讨论了观测误差对新一代重力卫星任务的影响,指出定轨精度主要影响重力场模型低阶项的反演精度,星间距变率主要影响中高阶。
综合以上的文献,发现已有文献很少单独评估激光测距精度本身的贡献,很多结论是各类新技术的综合效应,同时不同文献讨论的对象不同,有的关注的是时变重力场,而有的结论则主要针对的是静态重力场。时变重力场强调实时性,一般需要以较短的时间为单位来解算重力场,如以月为单位,这就对各类时变背景场模型的精度提出了更高的要求。例如:当前所有的GRACE时变重力场模型均存在南北条带误差问题,而静态重力场则不存在,这表明静态重力场由于能够使用更多的数据,因此能够降低对各类背景场模型的精度要求。另外一点也需要注意的是定轨定速数据的权重问题,本文认为二者与星间距变率数据和加速度计数据的权重应该有所区别,对于不同的解算方法也会有差别。针对以上问题,本文限制了相应的前提,即:(1)主要讨论地球静态重力场模型的精度,而不考虑重力场解算过程中的时变误差;(2)主要评估采用激光测距后,相对已有的GRACE卫星而言,其余载荷和轨道均不变的情况,重力场模型的精度提升有多大。在以上约束条件下,本文主要通过高精度的数值反演方法讨论本文开头所提出的问题。
2、基本原理 (2.1) 动力学法原理GRACE卫星反演重力场的方法主要有Kaula线性摄动法、动力学法、基线法、能量守恒法、加速度法和短弧长法等。从理论上讲动力学方法来自于对卫星轨道方程组的线性化,理论上相对是严密的,精度相对其他方法更高,因此本研究采用动力学方法进行模拟计算。
动力学积分法(Tapley,1989)的基本原理是基于牛顿运动方程,将卫星轨道数据线性化表达成状态转移矩阵(即任意时刻的状态向量(卫星或速度)对初始时刻状态向量的偏导数矩阵)和参数敏感矩阵(即任意时刻的状态向量对未知参数的偏导数,如引力场位系数、加速度校正参数和力模型未知参数)的形式,来建立卫星跟踪数据与重力场位系数间的关系式,然后基于最小二乘准则解算引力场位系数。动力学定轨的微分方程可用以下形式表示:
| $\left\{ \begin{gathered} \frac{{{\rm{d}}{{r}}\left(t \right)}}{{{\rm{d}}t}} = {\dot{ r}}(t) \\ \frac{{{\rm{d}}{\dot{ r}}\left(t \right)}}{{{\rm{d}}t}} = {{f}}\left(t \right) \\ {{r}}\left({{t_0}} \right) = {{{r}}_0} \\ {\dot{ r}}\left({{t_0}} \right) = {{{\dot{ r}}}_0} \\ \end{gathered} \right.$ | (1) |
式中,
| ${{X}}\left(t \right) = {{X}}\left({{t_0}} \right) + \int\limits_t {{{F}}\left(t \right)} {\rm{d}}t$ | (2) |
| $\left\{ \begin{gathered} \frac{{{\rm{d}}{{X}}\left(t \right)}}{{{\rm{d}}t}} = {{F}}\left(t \right) \\ {{X}}\left({{t_0}} \right) = {{{X}}_0} \\ \end{gathered} \right.$ | (3) |
对式(2)进行积分,可以得到任意时刻的状态向量
| ${{X}}\left(t \right) = {{{X}}_ {\rm{ref}}}\left(t \right) + {{S}}\left(t \right)\delta {{p}} + {{Q}}\left(t \right)\delta {{X}}\left({{t_0}} \right)$ | (4) |
其矩阵形式为
| $\delta {{X}}\left(t \right) = \left({{{Q}}\left(t \right) {{S}}\left(t \right) } \right)\left(\begin{gathered} \delta {{X}}\left({{t_0}} \right) \\ \delta {{p}} \\ \end{gathered} \right)$ | (5) |
式中,
GRACE卫星主要测量两颗卫星之间的速度在两颗卫星的水平线上的分速度,即星间变率。星间变率测量的精度高于GPS测量位置差分得到的速度。相比于卫星精密轨道数据,星间变率的优势是对地球重力场中高阶次较为敏感,并且能够减少SST测量系统振荡器的不稳定性。但星间变率与重力场位系数等参数之间是非线性的,本文在于锦海等人(2017)推导的轨道扰动方程组的形式上进行星间变率公式线性化的推导,现直接给出卫星轨道扰动方程推导得到的式(6)和式(7),分别用A和B来表示GRACE的两颗卫星,方程如下:
| ${{{r}}^{\rm{A}}}(t) = {{r}}_ {\rm{ref}}^{\rm{A}}(t) + {{{\varPhi }}^{\rm{A}}}(t)\delta {{{X}}^{\rm{A}}}\left({{t_0}} \right) + {{{{B}}}^{\rm{A}}}\left(t \right)\delta {{p}}$ | (6) |
| ${{{r}}^{\rm{B}}}(t) = {{r}}_ {\rm{ref}}^{\rm{B}}(t) + {{{\varPhi }}^{\rm{B}}}(t)\delta {{{X}}^{\rm{B}}}\left({{t_0}} \right) + {{{{B}}}^{\rm{B}}}\left(t \right)\delta {{p}}$ | (7) |
其导数可以写为
| ${{\dot{ r}}^{\rm{A}}}(t) = {\dot{ r}}_ {\rm{ref}}^{\rm{A}}(t) + {{\dot{ \varPhi }}^{\rm{A}}}(t)\delta {{{X}}^{\rm{A}}}\left({{t_0}} \right) + {{\dot{ { B}}}^{\rm{A}}}\left(t \right)\delta {{p}}$ | (8) |
| ${{\dot{ r}}^{\rm{B}}}(t) = {\dot{ r}}_ {\rm{ref}}^{\rm{B}}(t) + {{\dot{ \varPhi }}^{\rm{B}}}(t)\delta {{{X}}^{\rm{B}}}\left({{t_0}} \right) + {{\dot{ {B}}}^{\rm{B}}}\left(t \right)\delta {{p}}$ | (9) |
式中,
| $ \begin{aligned}{{\rho }}(t) = & {{{\rho }}_0}(t) + {{{\varPhi }}^{\rm{A}}}\left(t \right)\delta {{{X}}^{\rm{A}}}\left({{t_0}} \right) - {{{\varPhi }}^{\rm{B}}}\left(t \right)\delta {{{X}}^{\rm{B}}}\left({{t_0}} \right) + \\ & \left({{{{B}}^{\rm{A}}}\left(t \right) - {{{B}}^{\rm{B}}}\left(t \right)} \right)\delta {{p}}\end{aligned}$ | (10) |
| $\begin{aligned}{\dot{ \rho }}(t) = & {{\dot{ \rho }}_0}(t) + {{\dot{ \varPhi }}^{\rm{A}}}\left(t \right)\delta {{{X}}^{\rm{A}}}\left({{t_0}} \right) - {{\dot{ \varPhi }}^{\rm{B}}}\left(t \right)\delta {{{X}}^{\rm{B}}}\left({{t_0}} \right) + \\ & \left({{{{\dot{ {B}}}}^{\rm{A}}}\left(t \right) - {{{\dot{ {B}}}}^{\rm{B}}}\left(t \right)} \right)\delta {{p}}\end{aligned}$ | (11) |
式中,
| $\begin{aligned}{{\varepsilon }}(t) = & {{{\varPhi }}^{\rm{A}}}\left(t \right)\delta {{{X}}^{\rm{A}}}\left({{t_0}} \right) - {{{\varPhi }}^{\rm{B}}}\left(t \right)\delta {{{X}}^{\rm{B}}}\left({{t_0}} \right) + \\ & \left({{{{B}}^{\rm{A}}}\left(t \right) - {{{ B}}^{\rm{B}}}\left(t \right)} \right)\delta {{p}}\end{aligned}$ | (12) |
| $\begin{aligned}{\dot{{ \varepsilon }}}(t) = & {\dot{{ \varPhi }}^{\rm{A}}}\left(t \right)\delta {{{X}}^{\rm{A}}}\left({{t_0}} \right) - {{\dot{ \varPhi }}^{\rm{B}}}\left(t \right)\delta {{{X}}^{\rm{B}}}\left({{t_0}} \right) + \\ & \left({{{{\dot{ {B}}}}^{\rm{A}}}\left(t \right) - {{{\dot{ {B}}}}^{\rm{B}}}\left(t \right)} \right)\delta {{p}}\end{aligned}$ | (13) |
而
| ${{\rho }}(t) = {{{\rho }}_0}(t) + {{\varepsilon }}(t)$ | (14) |
| ${\dot{ \rho }}(t) = {{\dot{ \rho }}_0}(t) + {\dot{ \varepsilon }}(t)$ | (15) |
由星间距矢量和星间距标量的关系及式(12)可以得
| ${d ^2} = {{{\rho }}^2}(t) = {[{{{\rho }}_0}(t) + {{\varepsilon }}(t)]^2} = d _0^2(t) + 2{{{\rho }}_0}(t) \cdot {{\varepsilon }}(t) + {\varepsilon ^2}$ | (16) |
根据式(11)可知
| $d (t) = {d _0}(t) + \frac{{{{{\rho }}_0}(t)}}{{{d _0}(t)}}{{\varepsilon }}(t)$ | (17) |
由式(17)变形可得
| $\frac{1}{{d (t)}} = \frac{1}{{{d _0}(t)}}\left[ {1 - \frac{{{{{\rho }}_0}(t) \cdot {{\varepsilon }}(t)}}{{d _0^2(t)}}} \right]$ | (18) |
代回观测值
| $D(t) = \frac{{[{{{\dot{ \rho }}}_0}(t) + {\dot{ \varepsilon }}(t)] \cdot [{{{\rho }}_0}(t) + {{\varepsilon }}(t)]}}{{{d _0}(t)}}\left[ {1 - \frac{{{{{\rho }}_0}(t) \cdot {{\varepsilon }}(t)}}{{d _0^2(t)}}} \right]$ | (19) |
在式(18)中再进一步地舍去
| $\begin{aligned} D(t) = & {D_0}(t) + \frac{{{{{\dot{ \rho }}}_0}(t) \cdot {{\varepsilon }}(t) + {{{\rho }}_0}(t) \cdot {\dot{ \varepsilon }}(t)}}{{{d _0}(t)}} - \\ & \frac{{[{{{\dot{ \rho }}}_0}(t) \cdot {{{\rho }}_0}(t)][{{{\rho }}_0}(t) \cdot {{\varepsilon }}(t)]}}{{d _0^3(t)}} {\text{ = }} \\ &{D_0}(t) + \left({\frac{{{{{\dot{ \rho }}}_0}(t)}}{{{d _0}(t)}} - \frac{{[{{{\dot{ \rho }}}_0}(t) \cdot {{{\rho }}_0}(t)]{{{\rho }}_0}(t)}}{{d _0^3(t)}}} \right) \cdot \\ & {{\varepsilon }}(t) + \frac{{{{{\dot{ \rho }}}_0}(t)}}{{{d _0}(t)}} \cdot {\dot{ \varepsilon }}(t) \end{aligned}$ | (20) |
这里
由于两颗卫星在同一轨道上一前一后分别运行,若单独使用星间变率数据,则势必会造成局部法方程的欠定问题。因此必须要将卫星精密轨道数据与星间变率数据一起参与计算才可解算正确模型。一方面有卫星精密轨道数据提供卫星位置信息来降低局部法方程欠定的问题。另一方面轨道观测值对卫星重力场的低阶项较为敏感,能够提供一定精度的重力场信息。由于轨道的相对误差比较大,因此会将误差传递到法方程中。因此必须加相应的权比降低其对方程的影响,综上所述,必须融合卫星精密轨道数据及星间变率观测值来反演GRACE卫星的重力场,而实质是通过一定的比例关系将精密轨道方程与星间变率方程相加后进行求解,因此可以直接建立起两个法方程之间的关系。本文直接给出星间变率和精密轨道最终的法方程可以写为式(21)和式(22):
| ${{{N}}_ {\rm{kbrr}}}{{x}} = {{{L}}_ {\rm{kbrr}}}$ | (21) |
| ${{{N}}_ {\rm{orbit}}}{{x}} = {{{L}}_ {\rm{orbit}}}$ | (22) |
式中,
| $\left({\alpha {N_ {\rm{kbrr}}} + {N_ {\rm{orbit}}}} \right)x = \alpha {L_ {\rm{kbrr}}} + {L_ {\rm{orbit}}}$ | (23) |
由于星间变率测量精度要高于GPS测量轨道的精度,如果选取不恰当的权,则高精度的重力场的计算精度一定会被污染或者由于法方程条件数过高而使方程欠定,而权比的确定实质上是由卫星的观测精度决定。本文不加推导的利用王长青(2015)提供的轨道与星间变率的权比
通过数值实验来讨论论文开头提出的问题。(1)首先来验证有关程序的正确性;(2)讨论不同情况下反演精度。
(1)先用数值积分方法模拟出GRACE 1个月的轨道数据,模拟GRACE的轨道参数与真实轨道参数相同,然后并进一步得到星间距变率数据,再利用上节所述的方法进行反演计算。为了减小计算量,模拟轨道使用EGM08模型前60阶完整阶次来当作真实场,数值积分方法我们使用Adam预测校正方法,所使用的软件为Intel FORTRAN 64位软件。在解算时不加入任何误差,得到了一组重力场参数,将真实的重力场与反演计算得到的重力场相减,即式(24)画出了KUALA曲线误差图(Kaula,1966),误差量级越小代表计算的精度越高,结果如图1所示。
| ${\varsigma _n} = \sqrt {\frac{1}{{2n + 1}}\sum\limits_{m = 0}^n {\left[ {{{\left({{C_{nm}} - C_{nm}^{\rm{ref}}} \right)}^2} + {{\left({{S_{nm}} - S_{nm}^{\rm{ref}}} \right)}^2}} \right]} } $ | (24) |
式中,n代表重力场计算阶数,
图1中,“EGM08”代表真实重力场EGM08模型的KUALA曲线,“EGM08-EGM96”代表真实重力场EGM08模型减去参考模型EGM96以后得到的曲线,即不同重力场模型之间的误差曲线,“Error-free”代表利用动力学方法反演得到的重力场与模型EGM08相减后的误差曲线,该曲线表明了本实验计算程序的正确性,能够满足本研究的计算精度要求。
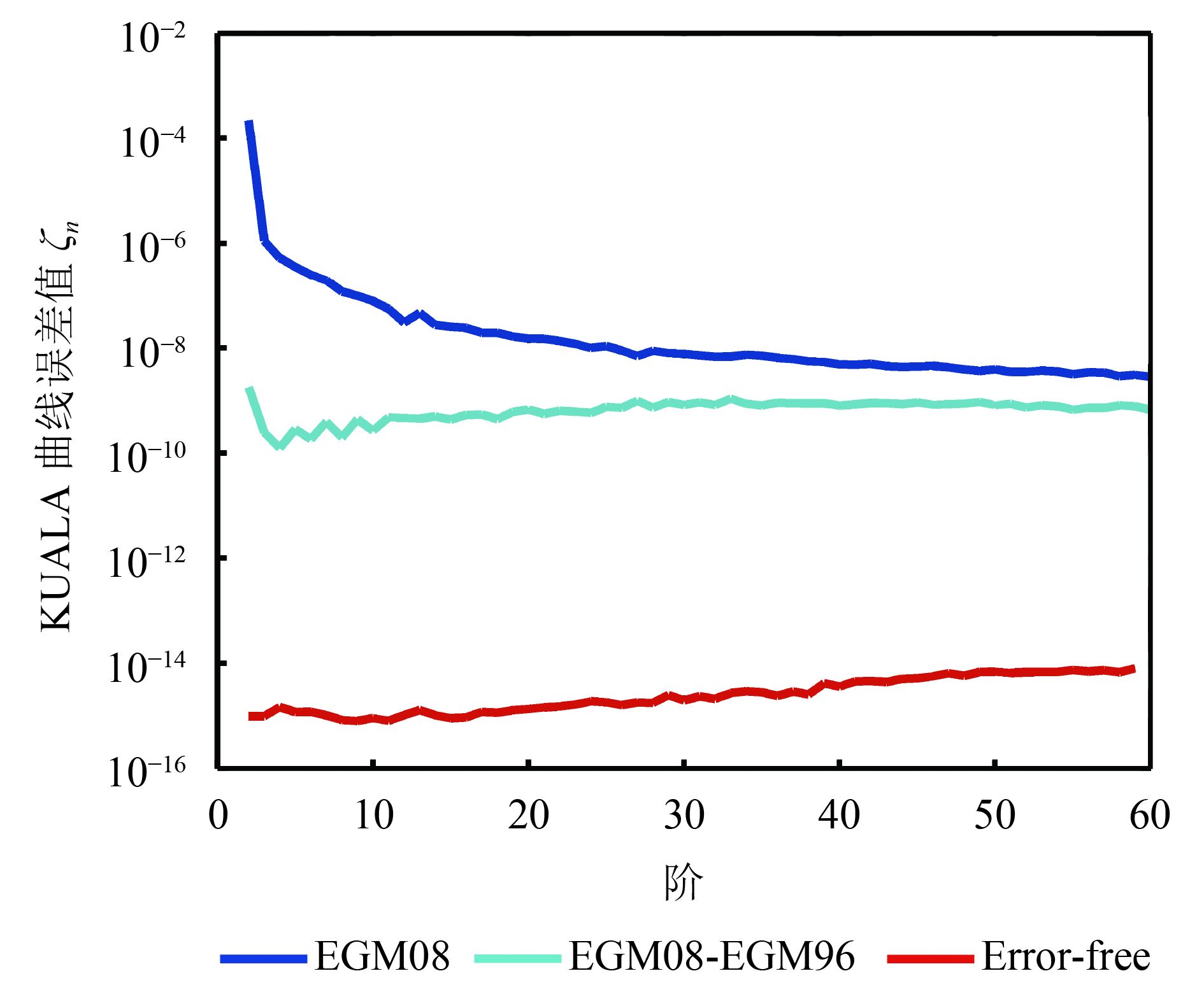
|
| 图 1 计算精度验证试验结果 Figure 1 Verification testing of the computational accuracy |
(2)解算流程与计算方法与(1)一致。区别在于首先将重力场的阶数增加到120阶。然后对观测数据加入几组误差,误差如表1所示,即GRACE卫星的设计精度指标,以及GRACE Follow On 的测量精度指标,主要是提高了星间变率的测量精度,结果如图2所示。
|
|
表 1 精度指标设计 Table 1 Precision index design |
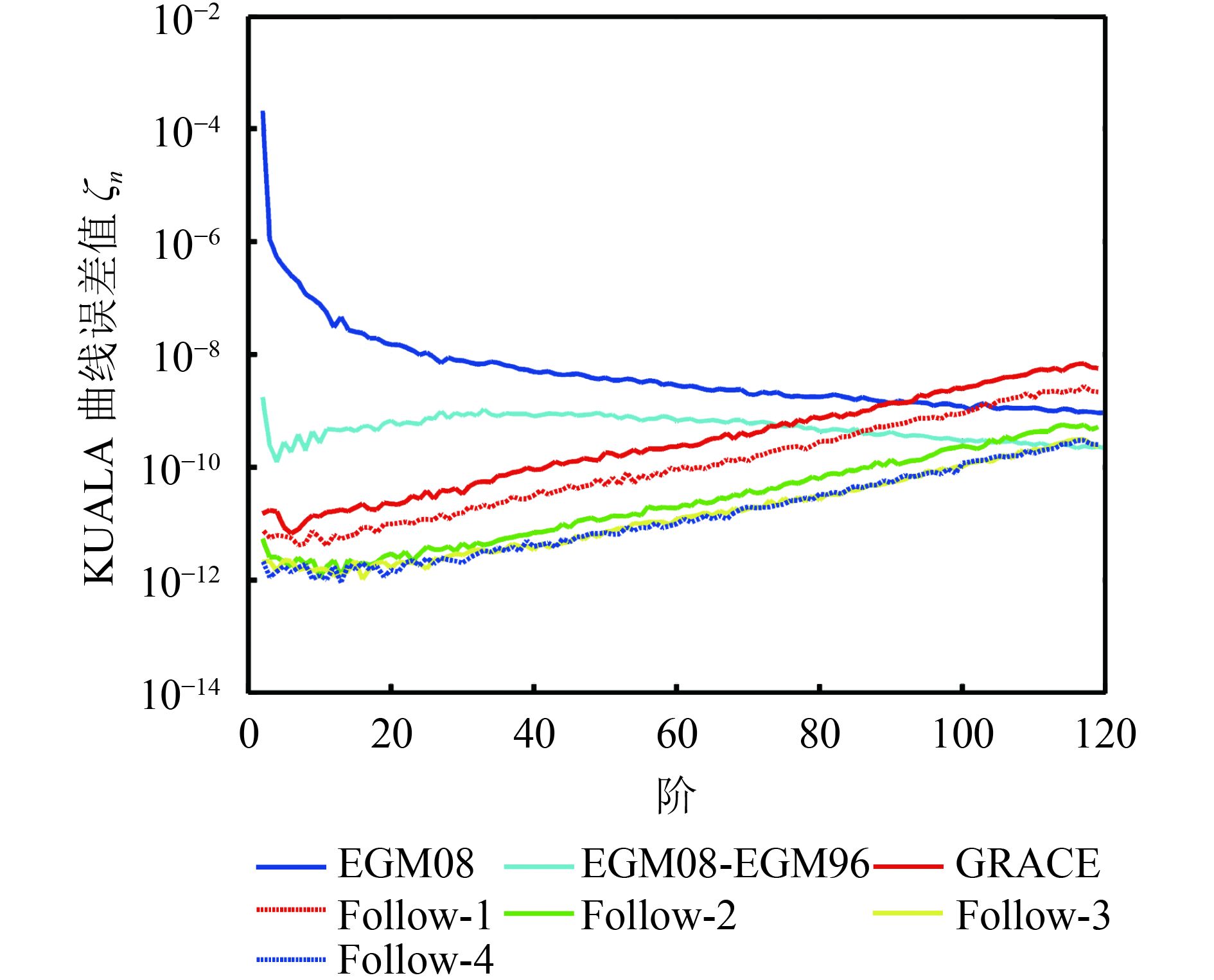
|
| 图 2 不同的星间变率精度对重力场位系数恢复精度的影响 Figure 2 Influence of different inter satellite variability accuracy on the recovery of geopotential coefficients |
图2中“EGM08”代表重力场模型EGM08的KUALA曲线,“GRACE”代表GRACE卫星的设计精度指标,“Follow-1、Follow-2、Follow-3、Follow-4”分别代表星间变率计算精度提高到5.0×10–7 m/s、1.0×10–7 m/s、5.0×10–8 m/s、1.0×10–8 m/s。该计算结果表明当星间距变率提高到1.0×10–8 m/s时,相对于GRACE现有的精度指标,重力场恢复精度能够提高1个量级。
本文将图2中的误差曲线图转换为图3的累计大地水准面误差图,各曲线的表示与图2一致。通过分析图3可知:保持GRACE现有的轨道和其他载荷精度,当星间变率精度依次从1.0×10–6 m/s提高到5.0×10–7 m/s、1.0×10–7 m/s、5.0×10–8 m/s、1.0×10–8 m/s时,累积大地水准面误差则在120阶时从85.14 cm依次降低为33.09 cm、7.33 cm、3.70 cm、3.59 cm。这表明当采用高精度的激光测距后,采用低低卫卫跟踪模式,地球静态重力场模型的探测精度有望比GRACE提高1个量级。上述结论与冉将军等人(2012,2015)的结论一致。但星间变率精度为5.0×10–8 m/s和1.0×10–8 m/s大地水准面累积误差和KUALA曲线图几乎无差别。
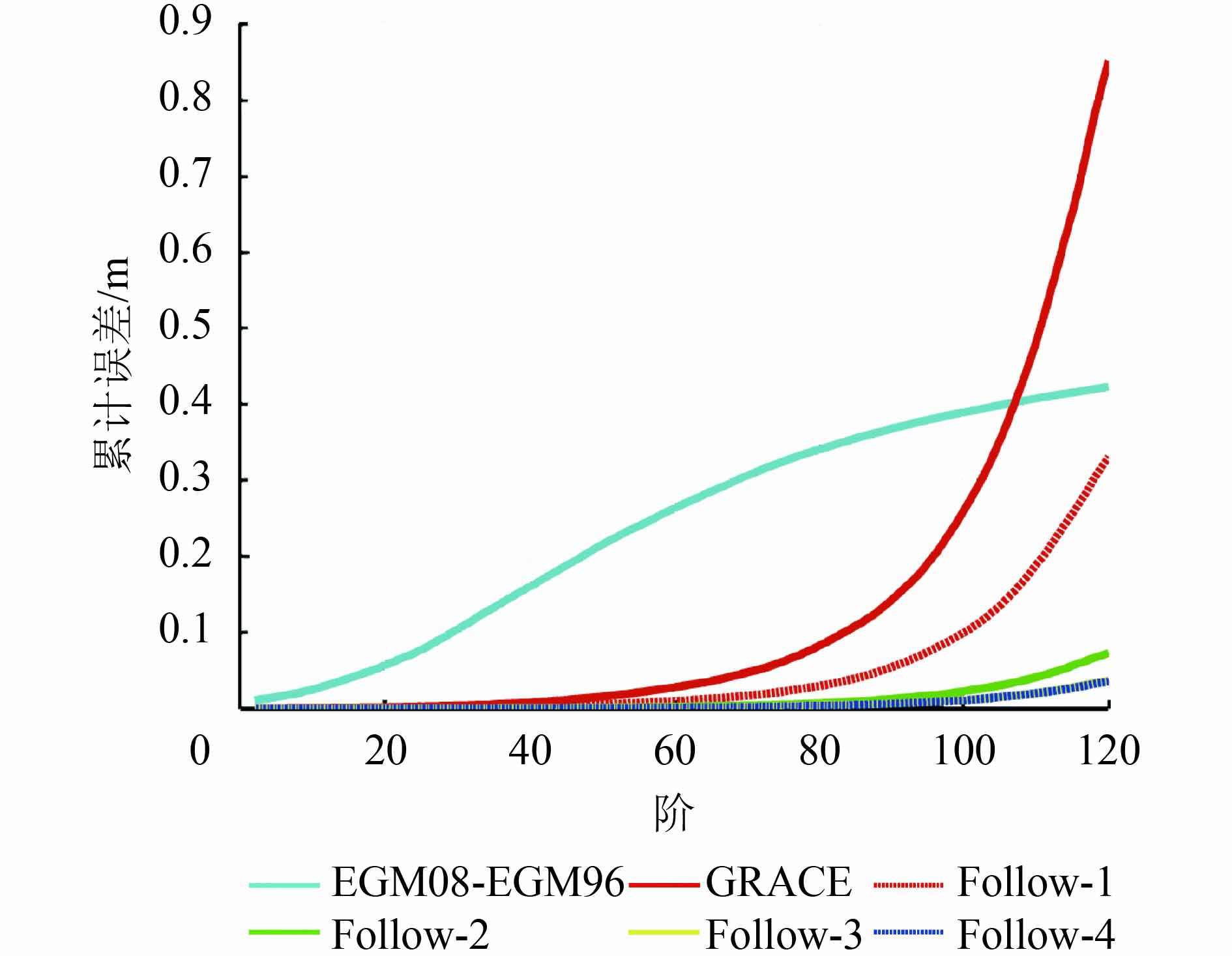
|
| 图 3 累积大地水准面误差图 Figure 3 Accumulative geoid error map |
本文主要讨论了基于轨道扰动方程对星间变率进行了线性化的推导,并通过一定的权值将线性化的星间变率方程组与精密轨道方程组融合,通过实例验证了公式及程序的正确性。通过仿真计算验证了激光测距对静态重力场恢复精度提升的贡献。结果表明:当激光测距的精度达到50 nm/s时,轨道和其余指标与GRACE卫星相同时,静态重力场的恢复精度可提高约1个量级。但当激光测距精度提高至10 nm/s时,计算结果与精度为50 nm/s的计算结果无明显差别,这表明过高的星间变率测量精度相对于其他指标而言精度有冗余。因此,建议在其他测量技术精度未有提高的前提下,只需将激光测距的精度提高至50 nm/s即可。
值得说明的是:以上工作所讨论的对象为地球静态重力场,而非时变重力场。静态重力场反演可利用多年的数据,如1年甚至5年,因此部分时变误差可被大大削弱和平滑。而对于时变重力场,由于其解算以月甚至更短时间为单位,对时变环境误差的扣除提出了更高的要求(例如:固体潮、海潮、大气潮等),因此仅仅提高星间测距,对于时变重力场的解算不如静态重力场的帮助明显。时变重力场的解算除了提高测距精度外,还需发射多颗不同轨道倾角的卫星来提供观测数据。而无论是对于静态重力场,还是时变重力场的解算,通过激光测距来提高星间距离测量精度,是提高下一代重力卫星反演精度的关键因素之一。因此,及时开展基于激光测距技术的下一代重力卫星关键技术研究具有重要意义。
本文未能对时变重力场的精度提升问题进行系统的分析,下一步可对重力卫星测量的其他精度指标以及背景场模型(如海潮、大气潮等)误差对时变重力场恢复精度的影响进行研究,从而为大幅提升时变重力场的精度提供可行的卫星设计方案。
| [1] | Elsaka B, Raimondo J C, Brieden P, Reubelt T, Kusche J, Flechtner F, Pour S I, Sneeuw N and Müller J. Comparing seven candidate mission configurations for temporal gravity field retrieval through full-scale numerical simulation[J]. Journal of Geodesy, 2014, 88 (1) : 31 –43. DOI: 10.1007/s00190-013-0665-9 |
| [2] | Gruber T, Murböck R, Mark B, Brieden P, Danzmann K, Daras I, Doll B, Feili D and Flechtner F. 2014. Earth System Mass Transport Mission: Concept for A Next Generation Gravity Field Mission. 1–199 |
| [3] | 许厚泽, 陆洋, 钟敏, 郑伟, 张子占. 卫星重力测量及其在地球物理环境变化监测中的应用[J]. 中国科学: 地球科学, 2012, 42 (6) : 843 –853. Hsu H Z, Lu Y, Zhong M, Zheng W and Zhang Z Z. Satellite gravity and its application to monitoring geophysical environmental change[J]. Scientia Sinica Terrae, 2012, 42 (6) : 843 –853. |
| [4] | Kaula W M and Street R E. 1966. Theory of satellite geodesy: Applications of satellites to geodesy. Blaisdell Pub. Co. |
| [5] | Loomis B D, Nerem R S and Luthcke S B. Simulation study of a follow-on gravity mission to GRACE[J]. Journal of Geodesy, 2012, 86 (5) : 319 –335. DOI: 10.1007/s00190-011-0521-8 |
| [6] | Panet I, Flury J, Biancale R, Gruber T, Johannessen J, van den Broeke M R, van Dam T, Gegout P, Hughes C W, Ramillien G, Sasgen I, Seoane L and Thomas M. Earth system mass transport mission (e[J]. motion): a concept for future earth gravity field measurements from space. Surveys in Geophysics, 2013, 34 (2) : 141 –163. DOI: 10.1007/s10712-012-9209-8 |
| [7] | 庞振兴, 姬剑锋, 肖云, 李迎春. 利用谱分析法估计GRACE Follow-On地球重力场的空间分辨率[J]. 测绘学报, 2012, 41 (3) : 333 –338. Pang Z X, Ji J F, Xiao Y and Li Y C. Estimation of the resolution of earth’s gravity field for GRACE follow-on using the spectrum method[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41 (3) : 333 –338. |
| [8] | 冉将军, 许厚泽, 沈云中, 钟敏, 张兴福. 新一代GRACE重力卫星反演地球重力场的预期精度[J]. 地球物理学报, 2012, 55 (9) : 2898 –2908. Ran J J, Xu H Z, Shen Y Z, Zhong M and Zhang X F. Expected accuracy of the global gravity field for next GRACE satellite gravity mission[J]. Chinese Journal of Geophysics, 2012, 55 (9) : 2898 –2908. DOI: 10.6038/j.issn.0001-5733.2012.09.009 |
| [9] | 冉将军, 钟敏, 许厚泽, 周泽兵, 万晓云. 模拟分析低低跟踪模式重力卫星反演地球重力场的精度[J]. 地球物理学报, 2015, 58 (10) : 3487 –3495. Ran J J, Zhong M, Xu H Z, Zhou Z B and Wan X Y. Analysis of the gravity field recovery accuracy from the low-low satellite-to-satellite tracking mission[J]. Chinese Journal of Geophysics, 2015, 58 (10) : 3487 –3495. DOI: 10.6038/cjg20151005 |
| [10] | Roland P and Thomas G. 2015. Future gravity missions: an integral component of the global geodetic observing system. Österreichischer Geodätentag: Veldenam Wörthersee |
| [11] | Sheard B S, Heinzel G, Danzmann K, Shaddock D A, Klipstein W M and Folkner W M. Intersatellite laser ranging instrument for the GRACE follow-on mission[J]. Journal of Geodesy, 2012, 86 (12) : 1083 –1095. DOI: 10.1007/s00190-012-0566-3 |
| [12] | Tapley B D. 1989. Fundamentals of orbit determination//Sansò F and Rummel R. Theory of Satellite Geodesy and Gravity Field Determination. Lecture Notes in Earth Sciences. Berlin, Heidelberg: Springer, 25: 235–260 [DOI: 10.1007/BFb0010553] |
| [13] | 王长青. 2015. GRACE时变重力场反演与相关问题研究. 北京: 中国科学院大学 Wang C Q. 2015. Time-variable gravity field determination from GRACE mission and some related issues. Beijing: University of Chinese Academy of Sciences. |
| [14] | 于锦海, 朱永超, 孟祥超. CHAMP型卫星定轨顾及非线性改正的轨道扰动方程[J]. 地球物理学报, 2017, 60 (2) : 514 –526. Yu J H, Zhu Y C and Meng X C. The orbital perturbation differential equations with the non-linear corrections for CHAMP-like satellite[J]. Chinese Journal of Geophysics, 2017, 60 (2) : 514 –526. DOI: 10.6038/cjg20170207 |
| [15] | 郑伟, 许厚泽, 钟敏, 员美娟, 周旭华, 彭碧波. 利用解析法有效快速估计将来GRACE Follow-On地球重力场的精度[J]. 地球物理学报, 2010, 53 (4) : 796 –806. Zheng W, Xu H T, Zhong M, Yuan M J, Zhou X H and Peng B B. Efficient and rapid estimation of the accuracy of future GRACE Follow-On Earth’s gravitational field using the analytic method[J]. Chinese Journal of Geophysics, 2010, 53 (4) : 796 –806. DOI: 10.3969/j.issn.0001-5733.2010.04.004 |

