| 电磁监测试验卫星(张衡一号)高精度磁强计研制与标定 |
收稿日期: 2017-06-16
地球磁场是地球重要物理场之一。地球磁场以地球本底磁场为主,形式上接近偶极子磁场,同时地球圈层内部的地幔、地壳中有或大或小的磁异常区,海洋中洋流运动也会形成大尺度磁场,外部的地球电离层磁层电流也会对地球磁场产生随时干扰磁场,这些使得地球磁场的组成非常复杂,同时也为通过地磁场进行各个领域的研究创造了条件(白春华 等,2008)。描述全球地球磁场主要是通过球谐函数模型,早期的地磁模型利用大量地磁台站的数据进行建模,效率和精度都很低,从1980年第一颗以地球矢量磁场测绘为目的的卫星MAGSAT(Thomas 等,1980)的成功运行后,开始基于卫星磁场探测数据建立地磁模型,精度得到了大大的提高。欧洲空间局1999年发射的ORSTED(Nielsen 等,1995)、2000年发射的CHAMP和目前在轨运行的SWARM卫星,几个任务接续运行持续提供高准确度矢量磁场探测数据,使得近几年的地磁场模型保持高水平的迭代更新。这些磁场探测数据对于地质构造、洋流运动和电离层空间物理等方面研究来说也是非常有效的工具,依靠这些数据取得了大量的科学成果,可见利用卫星对地球磁场进行精确探测是非常具有科学价值的。
电磁监测试验卫星CSES(China Seiso-Electomagnetic Satellite)是中国第一颗近地轨道电场磁场监测试验卫星,地球磁场矢量的准确探测是其重要的任务之一。它可以填补中国在近地轨道进行精确矢量磁场探测的空白,为国际地磁模型的建立提供数据,并以此为基础建立中国自主全球地磁模型,为空间物理、地磁导航、地震前兆等多领域研究一手数据(王兰炜 等,2016)。本文将介绍电磁监测试验卫星为实现磁场探测方案而部署的高精度磁强计HPM(High Precision Magnetometer)的研制和标定成果。
2、高精度矢量磁场探测方案卫星探测地球磁场与地面探测地球磁场有很大差异。电磁监测试验卫星运行轨道高度约为507 km,轨道倾角97°,卫星姿态为三轴稳定(王兰炜 等,2016)。卫星轨道高度,整体上地球磁场强度呈现的分布是两极强、赤道弱,磁场方向在两极区域近似垂直地面,赤道区域近似水平,图1是根据IGRF模型计算的的磁场分布。
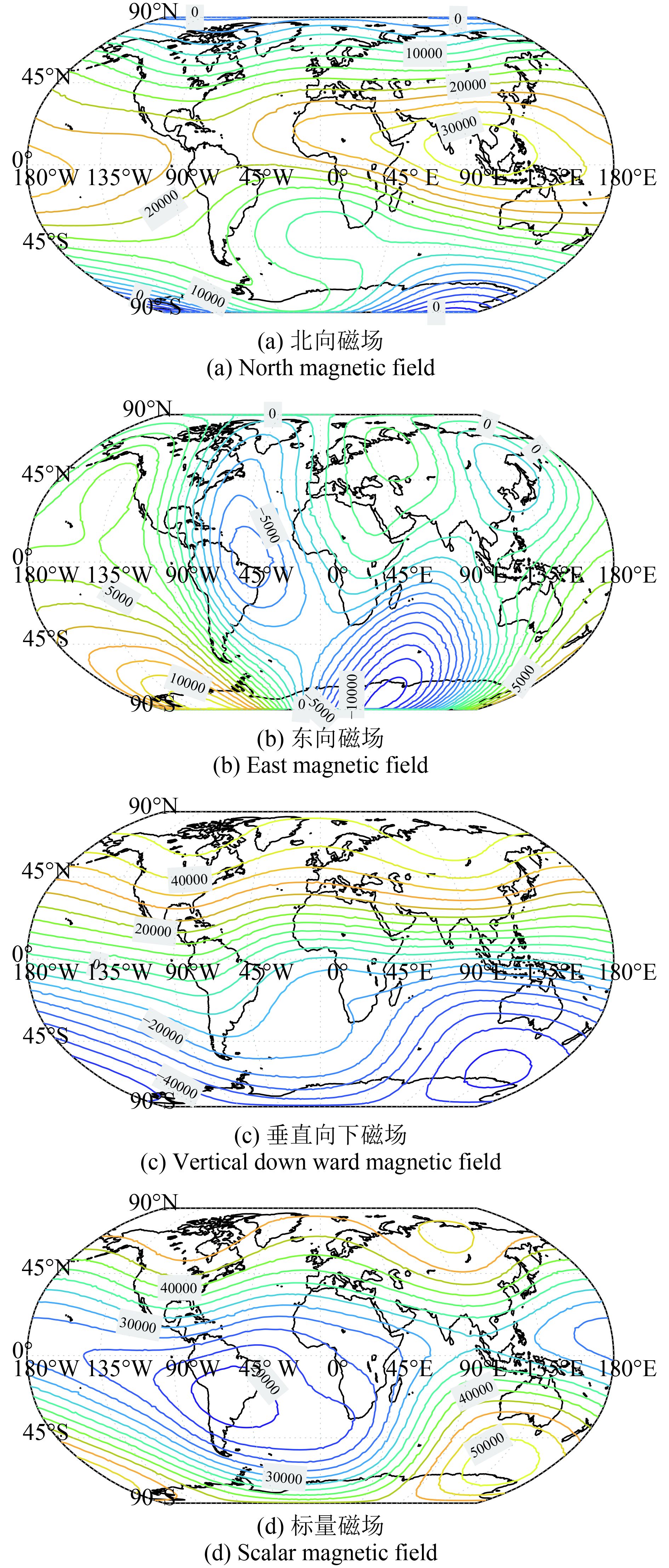
|
| 图 1 地球磁场等值图 Figure 1 The Earth magnetic field contour map |
卫星运动速度接近8 km/s,以卫星坐标系下观察地磁场,卫星飞行一轨观察到的信号如图2所示。可见卫星对地(Bz)和飞行方向(Bx)的磁场变化非常剧烈,垂直飞行方向(By)上的磁场强度和相对变化都较小,如表1所示。这还仅仅是在地磁场主磁模型下的模拟结果,考虑到局部磁异常,以及空间事件在短时间内对地球磁场的剧烈扰动,磁场的变化率会更大。
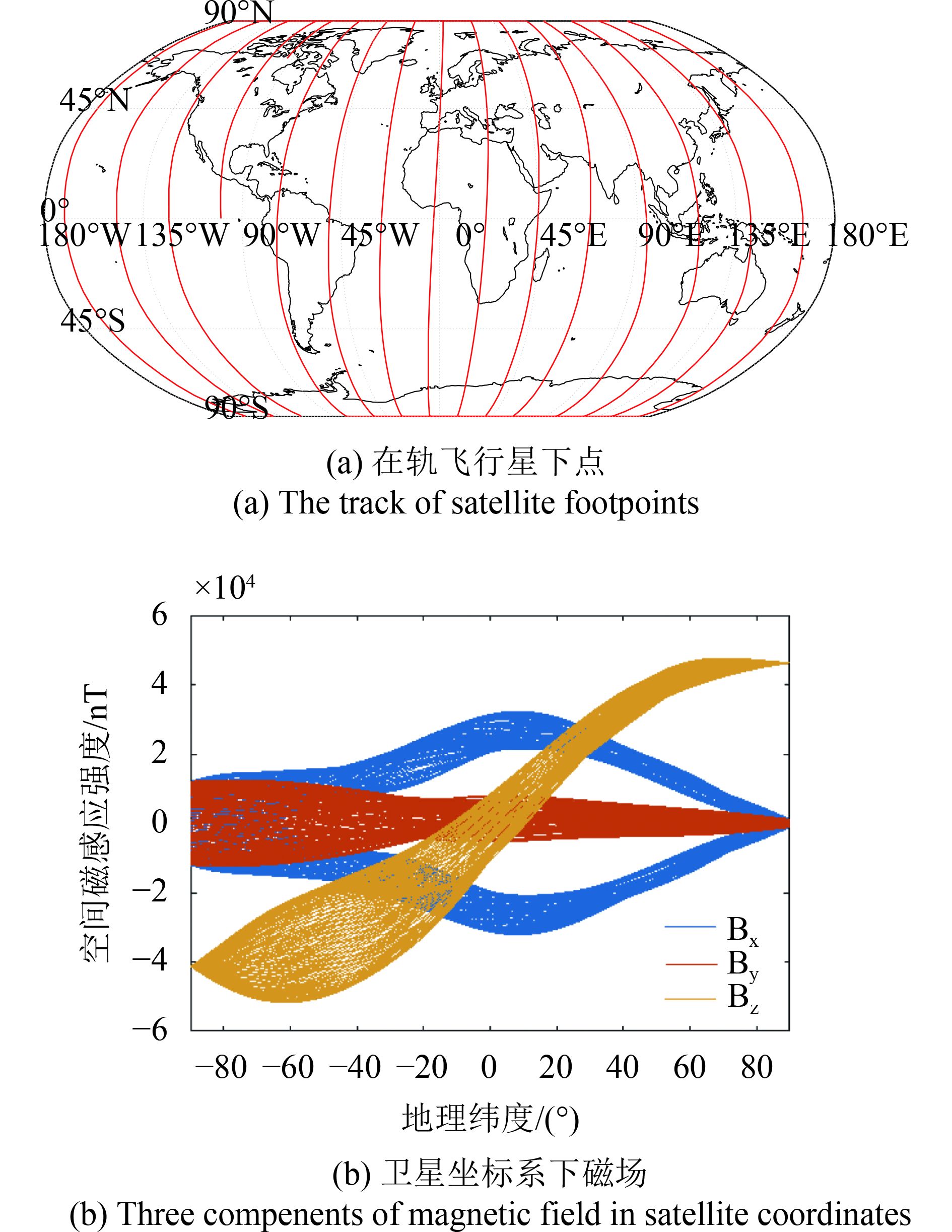
|
| 图 2 模拟卫星在轨飞行星下点和在卫星坐标系下磁场 Figure 2 Simulation of magnetic field in the satellite coordination system |
|
|
表 1 卫星平台观察到的磁场信号特征 Table 1 Characteristics of magnetic field signals observed by satellite platform |
根据磁场信号的特点,设计高精度磁强计的量程设计为±65000 nT和采样率60 Hz,同时分辨率设计为0.15 nT,HPM具备稳定性和准确性。
磁通门磁强计FGM(Fluxgate Magnetometer)是目前空间矢量磁场探测最为成熟的载荷,它的相对误差很小,随机噪声可以控制10 pT以下(周斌 等,2014)。但这种原理的仪器不能作为绝对基准,它的零点和转换系数受电子学探头的设计、工艺、生产等各个方面的影响,地面上虽然可以进行标定,但在轨运行不可避免受到空间环境温度、辐照等影响导致线性偏差。为了解决这一问题,在磁场探测方案中设计了一个CPT(Coherent Population Trapping)原理的CDSM(Coupled Dark State Magnetometer)传感器,作为绝对磁场校准装置。它是利用Rb87原子的塞曼效应对标量磁场进行测量,从原理上具有准确度。在轨对空间磁场的标量和矢量进行同时探测,可以实现对矢量磁场的绝对校正,国际上其他的地球磁场探测项目也都采用类似的方法确保矢量磁场的准确度(Mioara,2006)。它的基本原理如式(1)所示,矢量磁场线性校正后,等式必然成立。一组矢量和标量的联立方程是无法解算的,但卫星在轨运行时,磁场方向在卫星坐标系内是旋转的,就产生了多个组量和矢量的联立方程,通过拟合算法可以将线性误差系数计算出来(张镇琦 等,2014)。
| $B_{{\rm{scale}}}^2{\rm{ = }}B_x^2 + B_y^2 + B_z^2$ | (1) |
式中,Bx、By和Bz是矢量磁场正交三分量,Bscale是这个矢量的大小。
3、高精度磁强计的设计与实现电磁监测试验卫星高精度磁强计包括3个传感器探头和一个电子学箱。两个FGM探头,同时探测矢量磁场,一方面可以实现工程上的备份提高可靠性,另一方面用于通过差分的方法评估平台剩磁干扰的长期变化。这3个探头安装在卫星的4.5 m伸杆上,CDSM部署在顶端,后面紧接两个FGM探头(图3)。
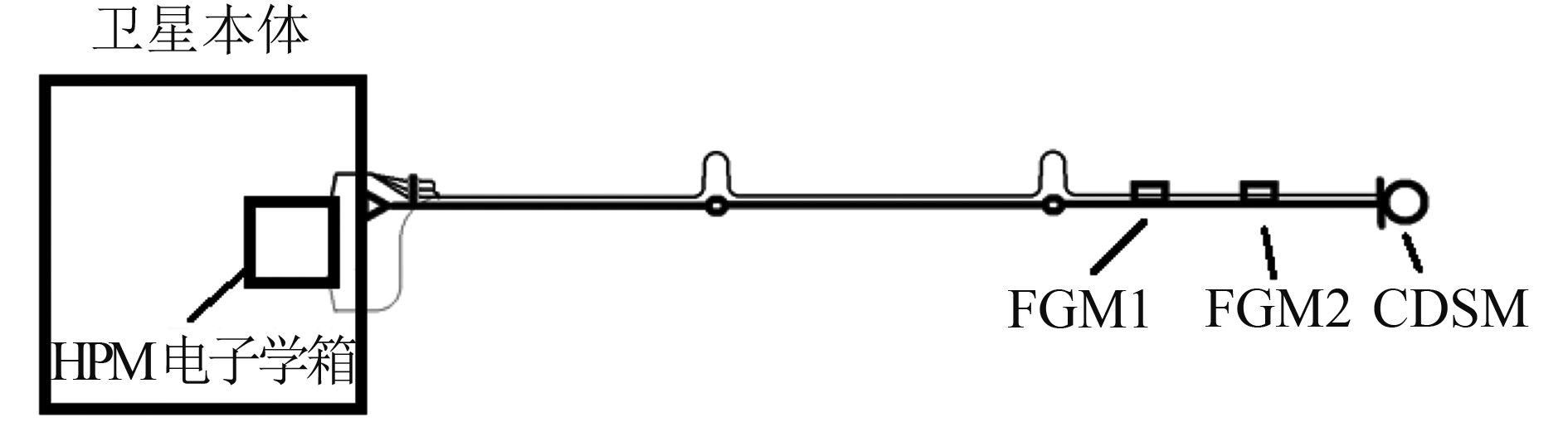
|
| 图 3 HPM在卫星上的安装布局示意图 Figure 3 The deployment of HPM on the satellite |
每个FGM探头由3个独立的单分量FGM传感器组成,3个独立单分量传感器设计为正交安装(图4),考虑到结构的可靠性工艺上不进行微调,在固化后通过标定实现正交探测。每个探头内部安装温度传感器,用于进行在轨温度校正(周斌 等,2014)。
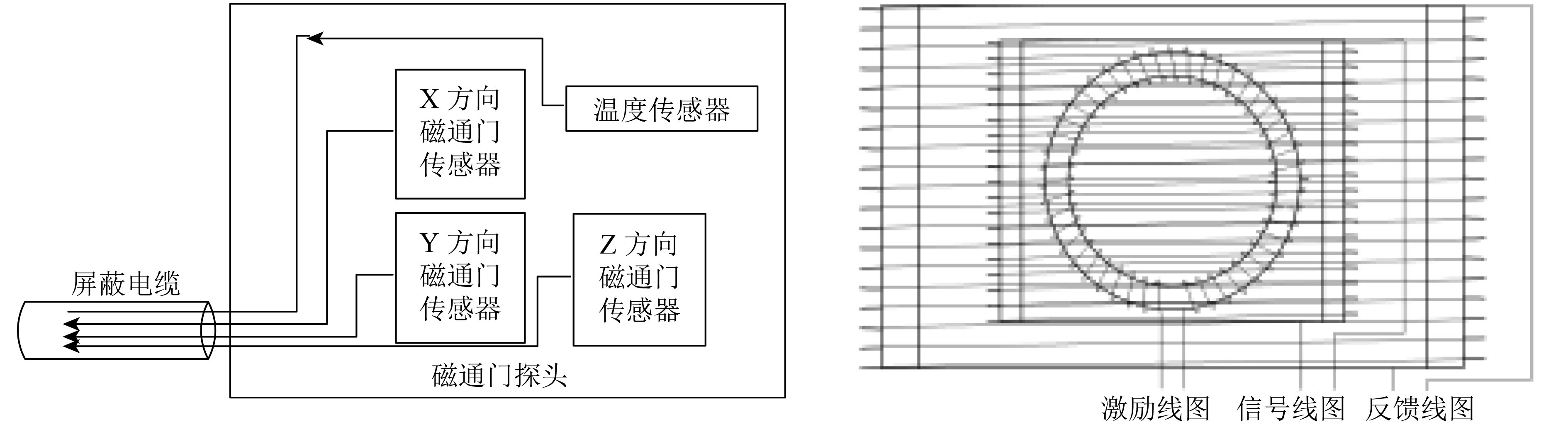
|
| 图 4 FGM探头内部结构和传感器线圈组示意图 Figure 4 The interior structure diagram of FGM sensor and schematic diagram of sensor coil group |
CDSM探头主要有奥地利空间研究所研制,探头内部主体是一个Rb87吸收室,内部充满惰性气体。微波调制的激光穿过吸收室,通过频率扫描过程中找到CPT效应的频率点,并通过闭环控制锁定。这一频率与探头所在磁场标量的比例与Rb87的原子磁旋比相关。在进行充分的频率扫描后,可以看到能够获取到多个CPT效应的信号,有一些在磁场方向与激光方向一致时信号最强,有一些在两者相互垂直时信号最强,选取其中两个作为两种工作模式,同向和垂直工作模式。这两种工作模式在轨实现自动切换以达到最佳探测效果。
HPM电子学箱包括了FGM传感器模拟信号处理电路,CDSM信号处理电路,用于数据采集处理的数字控制电路如图5所示。磁通门磁强计每一个传感器都配有一套激励、前置放大、调制解调、滤波反馈电路,采用低噪声高稳定性的电子元器件保证磁通门磁强计的信号质量。CDSM信号处理电路包括激光器及温度控制,微波调制,光电信号采集和数字信号处理等电路模块。数字控制单元采集磁通门的模拟信号和CDSM的数字通讯信号,对数据进行简单处理后形成数据包,通过数传和遥测通道将数据发送给卫星其他分系统,并最终送回地面。
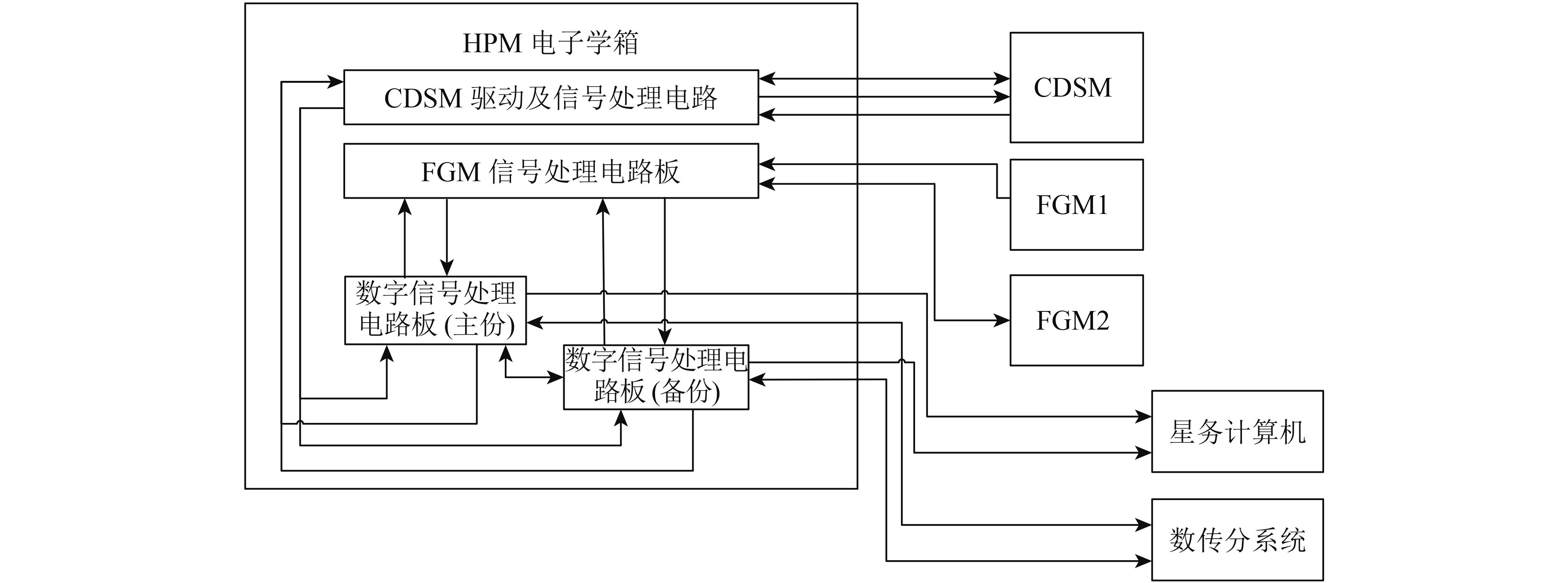
|
| 图 5 HPM电子学结构示意图 Figure 5 The schematic diagram of HPM electronics |
HPM最终为用户提供的数据是在地理坐标系下空间矢量磁强。从各个传感器探测到的数据到空间矢量磁场之间需要4个主要的处理步骤,单个传感器校正,绝对矢量磁场校正,剩磁干扰消除和坐标系转换。
(4.1) 单物理量传感器校正HPM共有6个FGM传感器和1个CDSM传感器,从探测值到物理量之间的关系理论上是一阶线性关系:
| $B = aX + b$ | (2) |
式中,a为转换系数,b为零点偏差,X是探测值,B是物理量。FGM传感器由于自身特点,它的线性系数受到电子学箱和探头温度的影响。数据处理是,除了基本的线性处理,还需要根据温度值对线性系数进行校正。CDSM理论上它的一阶线性系数是固定的,但是这种传感器在激光与磁场的夹角不同时,会有一定探测偏差,需要根据在轨的磁场方向进行校正。所以,式(2)针对FGM和CDSM在处理时应演化为式(3)和式(4)。线性系数的校正依据要根据地面标定试验来获取。
| ${B_{{\rm{FGM}}}} = a\left( {{t_{\rm{e}}},{t_{\rm{p}}}} \right){a_0}X + \left( {{b_0} + b\left( {{t_{\rm{e}}},{t_{\rm{p}}}} \right)} \right)$ | (3) |
| ${B_{{\rm{CDSM}}}} = {a_0}X + {b_0} + b\left( D \right)$ | (4) |
式中,tp、te分别是电子学箱温度和探头温度,D是激光与磁场方向夹角,地面还需要标定基准线性系数a0和b0。
(4.2) 绝对矢量磁场校正绝对矢量磁场校正,就是利用标量磁场的数据校正矢量磁场的线性误差,它的基本等式如式(1)所示。三分量磁场探头的线性误差,可以理解为一阶线性系数a、b和三轴正交度。当三轴不正交时,可以利用两个角度将其转换到一个正交坐标系上。如图6所示,可以将非正交的3个轴转换到z轴和y/z平面保持不变的正交轴。那么对于矢量数据来说一共有9个线性系数需要计算,ax,ay,az,bx,by,bz,θ11,θ31,θ32。
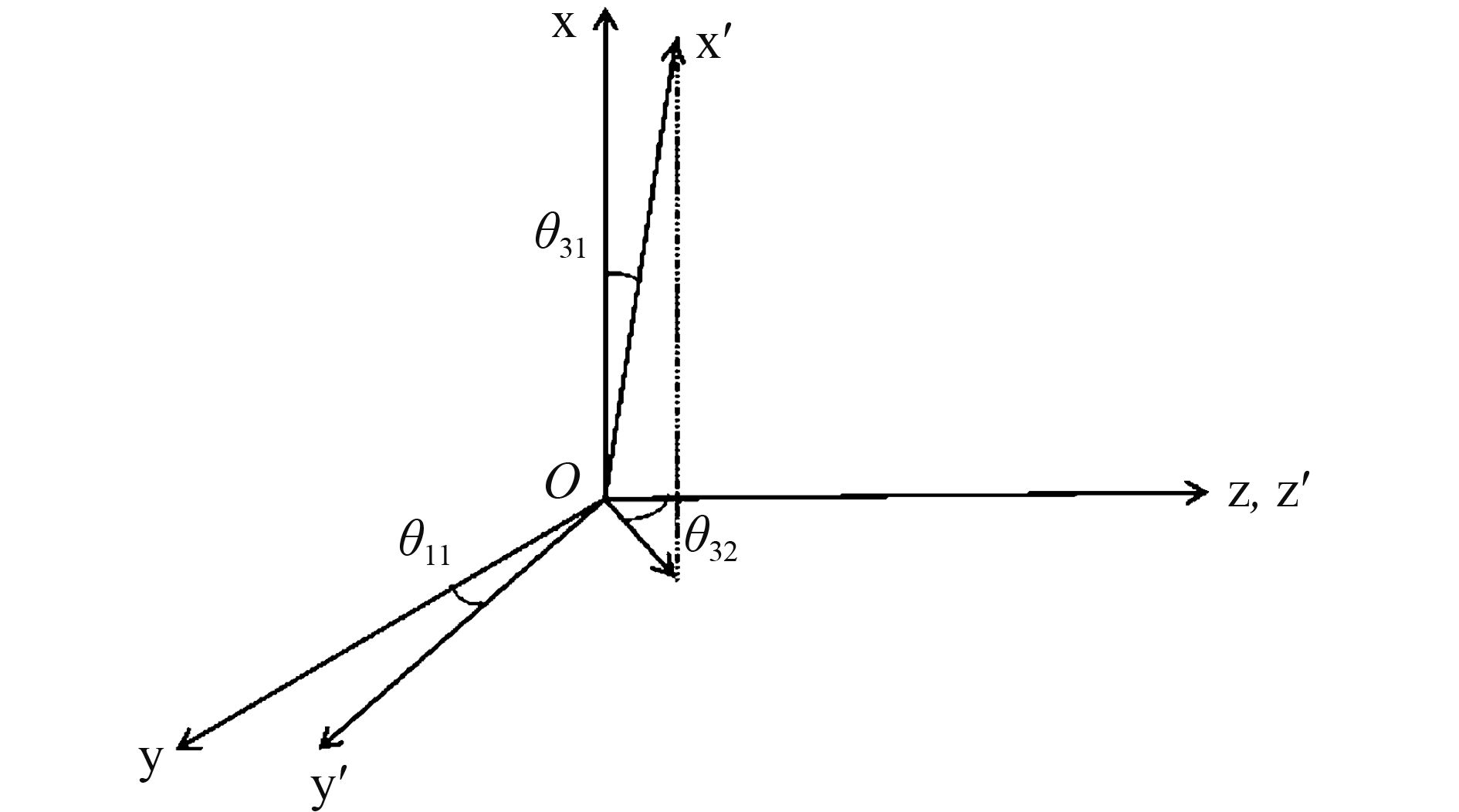
|
| 图 6 非正交系到正交系的关系示意图 Figure 6 The relations between nonorthogonal system and orthogonal system |
| ${{M}}\left( {{\theta _1},{\theta _{31}},{\theta _{32}}} \right)\left[ \begin{array}{l}\!\! B_x' \!\! \\\!\! B_y' \!\! \\\!\! B_z' \!\! \end{array} \right] = \left[ {\begin{array}{*{20}{c}}\!\! {{a_x}} & 0 & 0 \!\! \\\!\! 0 & {{a_y}} & 0 \!\! \\\!\! 0 & 0 & {{a_z}} \!\! \end{array}} \right]\left[ \begin{array}{l}\!\! {B_x} \!\! \\\!\! {B_y} \!\! \\\!\! {B_z} \!\! \end{array} \right] + \left[ \begin{array}{l}\!\! {b_x} \!\! \\\!\! {b_y} \!\! \\\!\! {b_z} \!\! \end{array} \right]$ | (5) |
式中,非正交系下的矢量B经过校正后得到的正交系矢量B′,M是非正交校正矩阵。
将式(5)代入式(1)完全展开,得到多项式式(6),mi是多项式系数。利用一轨或者多轨的数据,进行拟合和方程解算,可以得到所有的线性系数。用这种方式可以克服FGM可能的长期漂移问题。
| $\begin{split}B_{{\rm{scal}}}^2 = & {m_1}B_x^2 + {m_2}B_y^2 + {m_3}B_z^2 + {m_4}{B_x}{B_y} + {m_5}{B_x}{B_z} +\\ & {m_6}{B_y}{B_z} + {m_7}{B_x} + {m_8}{B_y} + {m_9}{B_z} + {m_{10}}\end{split}$ | (6) |
卫星平台的磁场干扰始终是困扰空间磁场探测的主要因素之一,国内外大多数空间探测任务都要进行事先的平台磁洁净控制和事后的消除平台干扰的数据处理工作(陈斯文,2009;Narvaez,2004;Lohr 等,1998)。电磁监测试验卫星在研制过程中充分考虑了这一问题,并进行了严格的磁洁净控制程序。在地面上定量的测定了影响磁场探测的因素。
| ${{{B}}_{{\rm{sat}}}} = {{{A}}_{{\rm{sat}}}}{{{B}}_{\rm{E}}} + {{{B}}_{{\rm{sat}}0}} + {{{C}}_{{\rm{sat}}}}{I_{{\rm{sat}}}}$ | (7) |
式中,Bsat0指的是卫星平台的固有剩磁,这是不变的干扰。Asat是卫星平台的感磁系数,平台中的一些金属材料具有一定的感磁特性,在外部磁场发生变化时,干扰随之变化,要根据FGM探测磁场BE计算感磁大小。Csat是磁力矩器断点状态干扰。磁力矩器是卫星平台上最大的磁源,它的中心包括磁感应系数很大的磁性材料,在南北纬65°以外要加强电流工作,它停止工作时电流的方向Isat决定了它在不工作时的磁场干扰。以上这些因素共同决定了卫星平台干扰Bsat。
在绝对矢量磁场校准后,得到的矢量磁场等价于CDSM位置的矢量磁场,平台的剩磁干扰标定结果也是在CDSM位置上的,所以可以进行消除处理。
(4.4) 坐标系变换矢量磁场校正后的所处的坐标系是传感器的磁轴坐标系,在卫星平台出厂前会精测探头的基准棱镜通过伸杆基准棱镜、卫星基准棱镜到卫星本体坐标系的转换关系。这个环节中磁轴到探头基准棱镜的坐标系转换关系需要在载荷交付前进行标定测量。在得到所有的转换关系后,可以将磁轴坐标系下的磁场转换到卫星平台坐标系下,再根据在轨实时测量的姿态信息转换到惯性坐标系和地理坐标系下。最终得到用户需要的空间矢量磁场数据,这一坐标转换过程如图7所示。
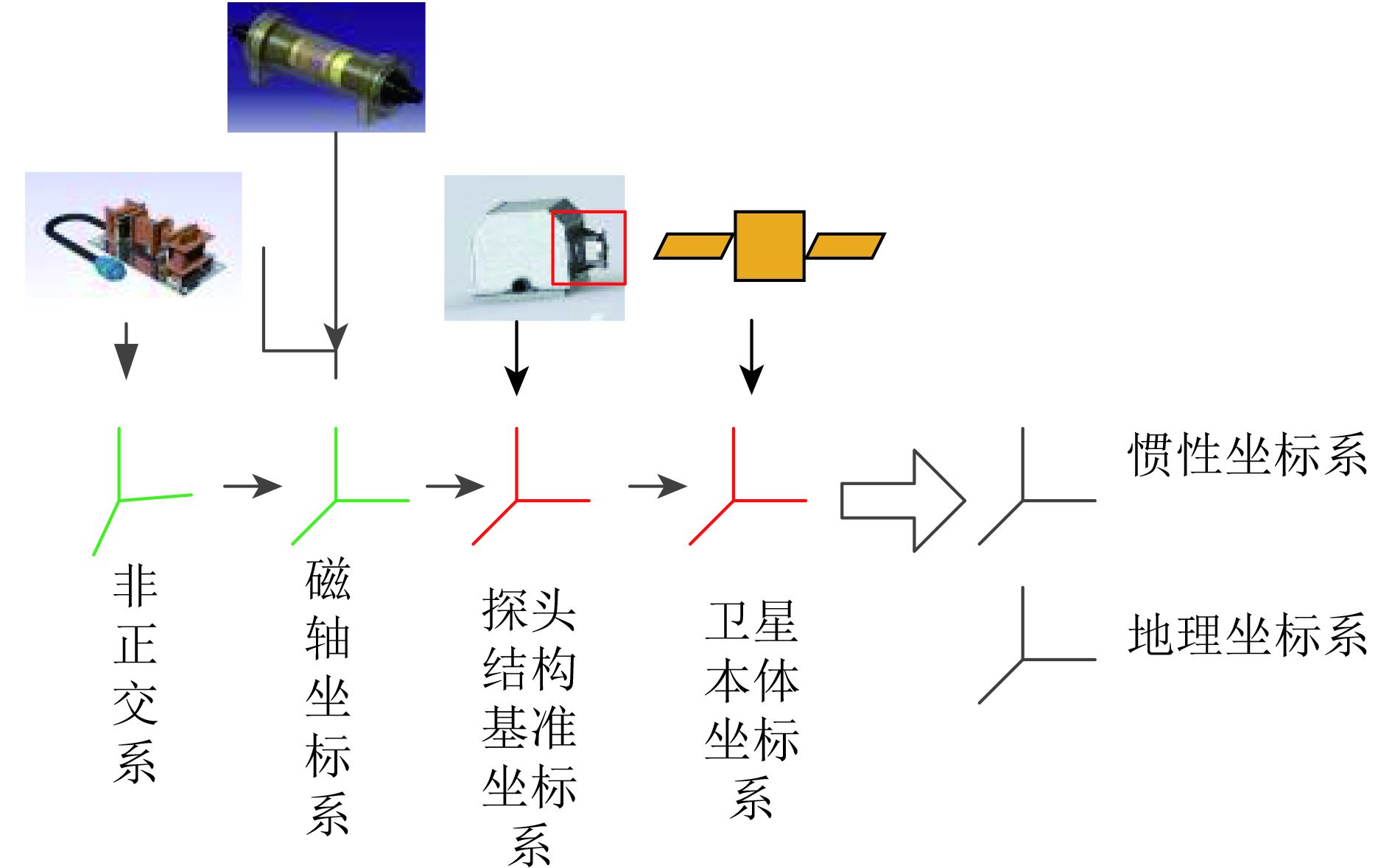
|
| 图 7 坐标系转换关系示意图 Figure 7 The transformational relations of several coordination systems |
根据载荷的探测方案、仪器设计和数据处理方法的研究结果,实现空间矢量磁场探测目标,除了高质量的在轨探测数据还需要严谨精确的地面标定结果。HPM的标定试验设计了线性度试验、温度试验、传感器和结构坐标转换试验、CDSM转向差,得到的参数可以为前面讨论的数据处理算法提供支持,另外还设计了正交试验、频响试验、分辨率试验等,验证了仪器的性能指标。
(5.1) 线性度试验线性度试验验证的是传感器的一阶线性关系的基准线性系数。试验在三轴亥姆霍斯线圈内进行,利用光泵锁定稳场技术(王晓峰 等,2004),可以将线圈内的标量磁场稳定在几个pT以内。在试验过程中,当与待测方向垂直的两个方向磁场补偿到接近0 nT,每个分量的试验时间只有20 min,在这样的时间里垂直待测方向的磁场最大不会超过10 nT量级,待测方向的磁场误差小于0.3 nT。
对CDSM进行线性度试验时,采用计量用Overhauser磁力仪进行交替测量的方式读取更为准确的磁场数据。由于线圈内的磁场极为稳定,FGM传感器的探测数据还可以用来评估传感器的噪声水平。
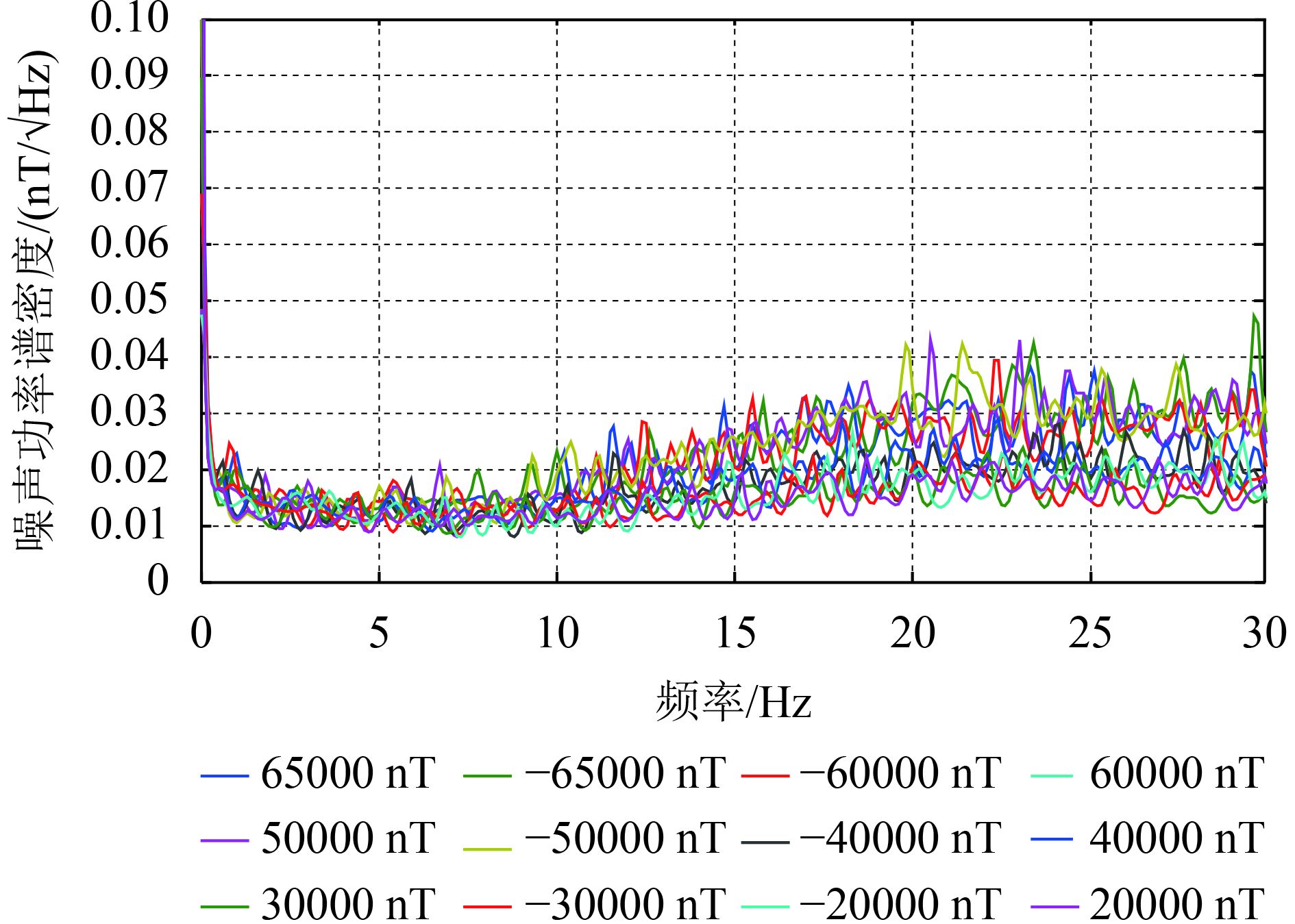
CDSM标定的线性误差只有0.15 nT,线性度达到了0.0004%这已经达到了试验系统能力的极限。CDSM的线性度和FGM的噪声评估结果如图8、图9所示。
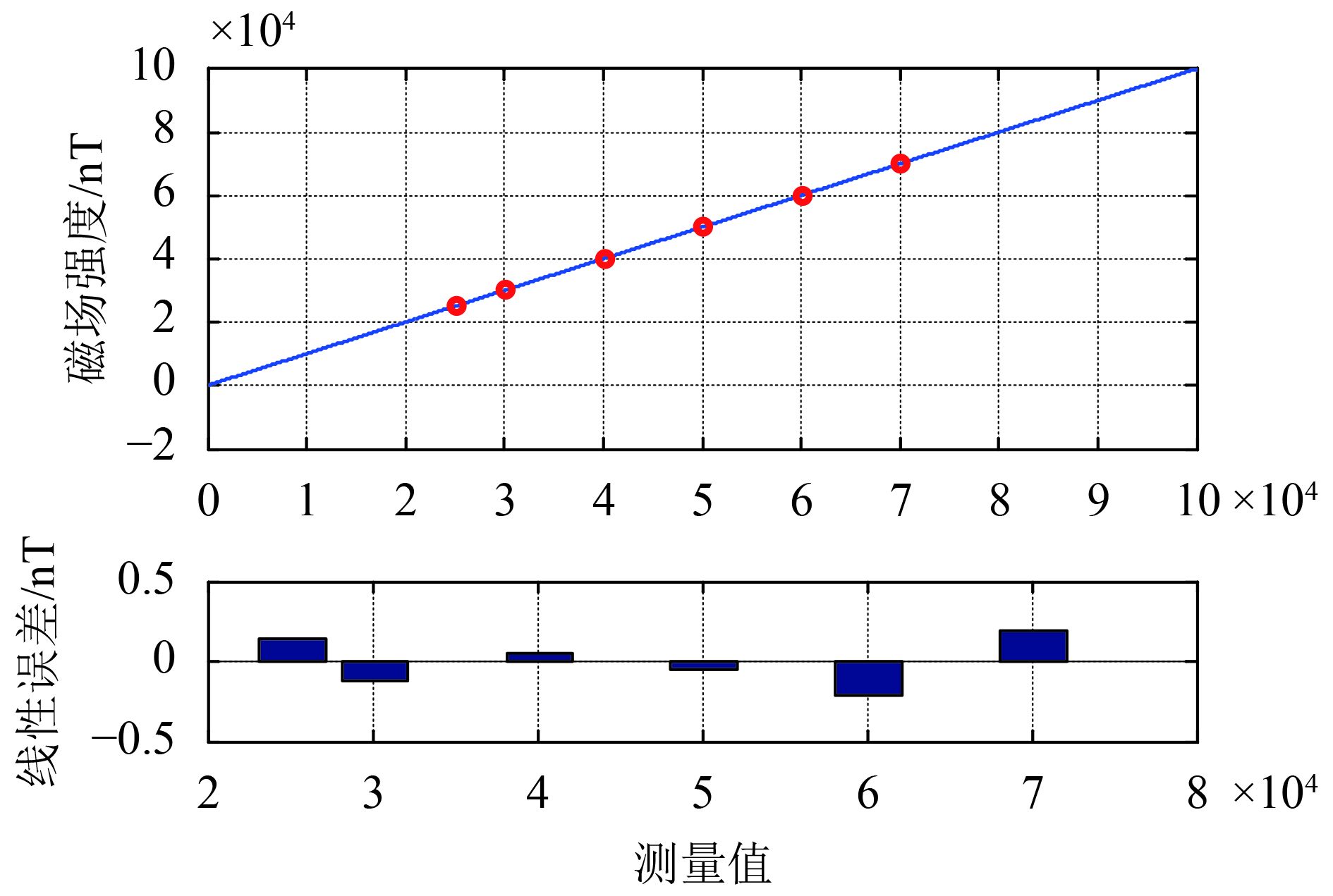
|
| 图 8 CDSM线性度试验结果(n=3) Figure 8 Linearity results of CDSM |
|
| 图 9 磁通门探头1 Y分量在不同磁场下的噪声谱 Figure 9 The noises of FGM1-Y axis under different magnetic field values |
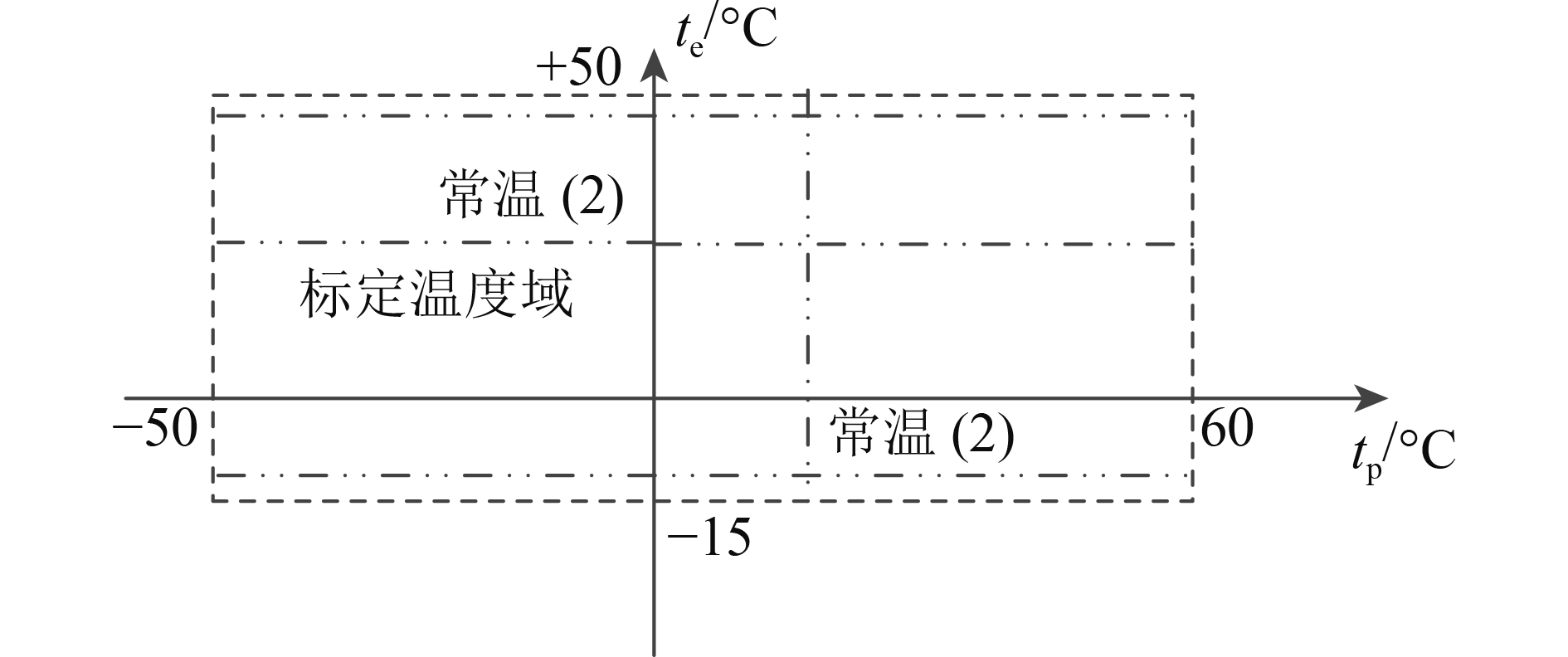
温度试验标定FGM传感器线性系数随温度的变化量。HPM电子学和FGM探头温度都会影响FGM传感器的线性系数,需要掌握整个温度域线性系数的变化。根据目前的试验条件,设计通过标定4条曲线再插值得到整个温度域线性系数变化的方案,如图10所示。
|
| 图 10 温度标定曲线在温度域的覆盖示意图 Figure 10 The temperature range of thermal drift calibration test |
FGM探头和HPM电子学箱分别放置在两个无磁温度可控的设备中,将其中一个保持恒定温度,对另一个进行变温实现这4条标定曲线的测量。
零点偏差b的试验在零磁场空间进行,FGM探头连同温控设备放置在零场环境中。转换系数a的试验在外部标准磁场的环境中进行试验,FGM他体内连同温控装置放置在三轴线圈内,并保证初始的轴向对正,在特定温度连续施加3个方向的正反标准磁场,在后续处理时需要校正探头在变温过程中的变形,移位对试验带来的干扰。
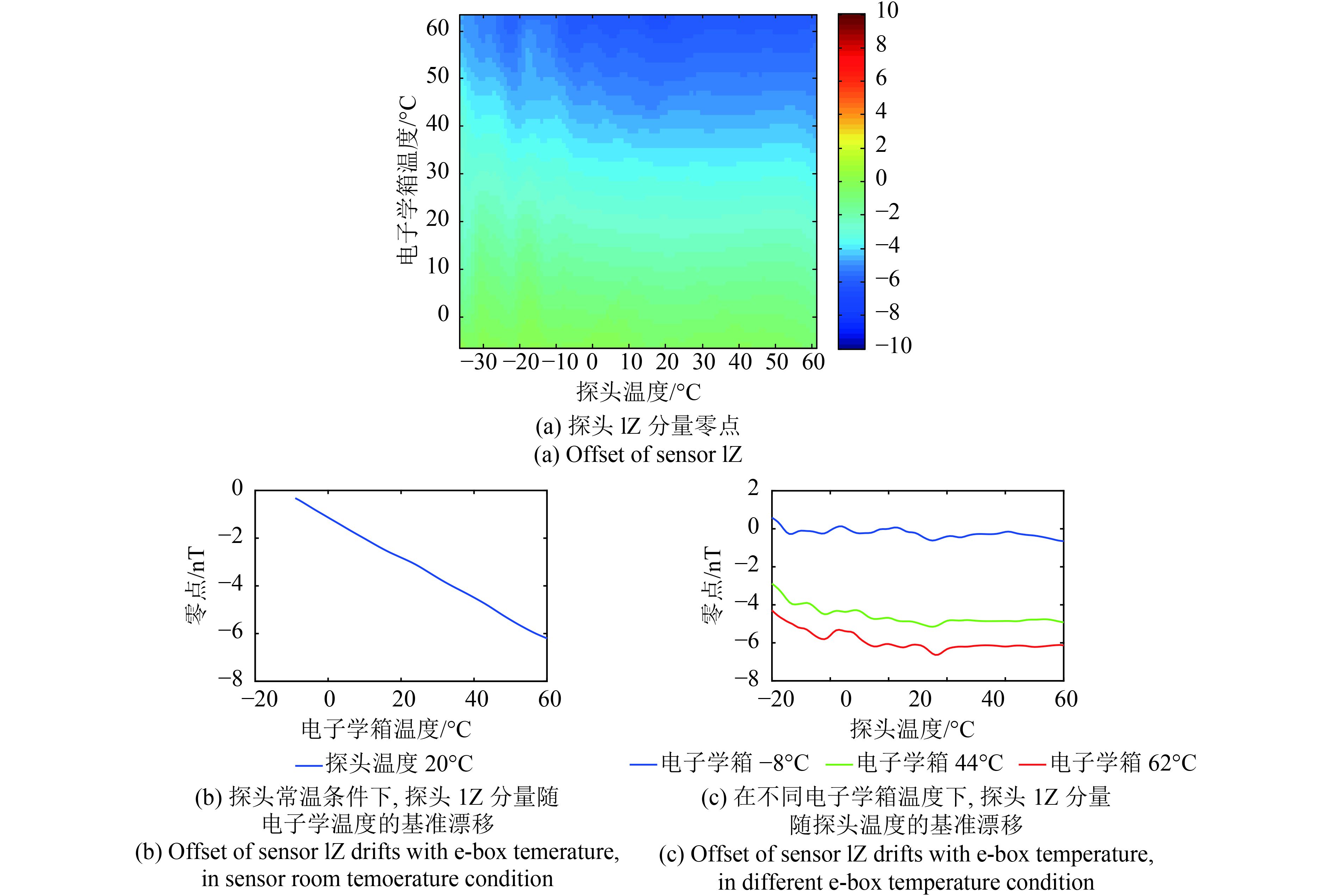
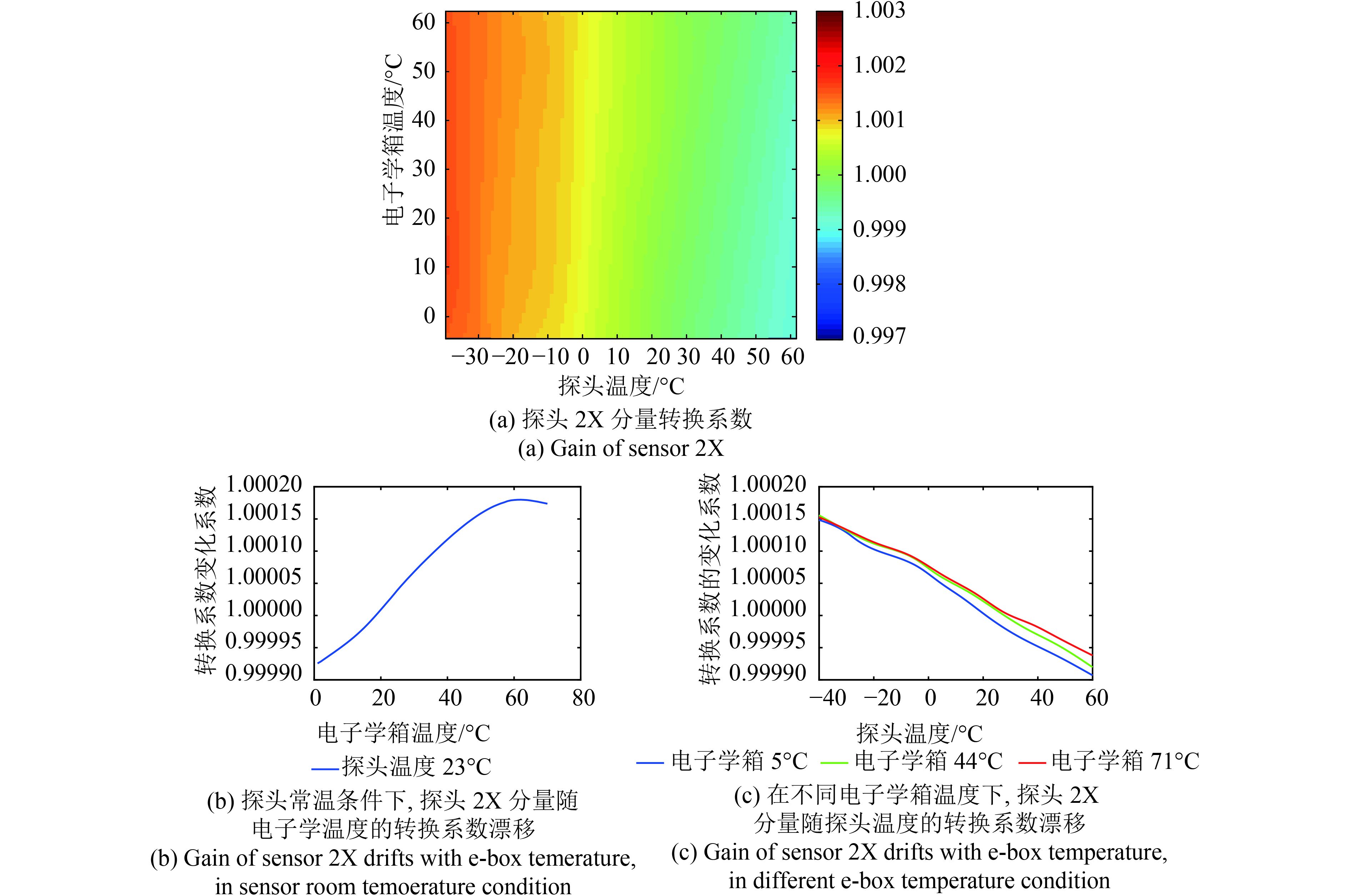
温度试验的结果如下图11和图12所示,可见探头的温度对于线性系数a和b的影响要大于电子学温度变化的干扰。
|
| 图 11 零点温漂标定结果 Figure 11 Offset drift of sensor 1Z with temperature |
|
| 图 12 转换系数温漂标定结果 Figure 12 Gain drift of sensor 2X with temperature |
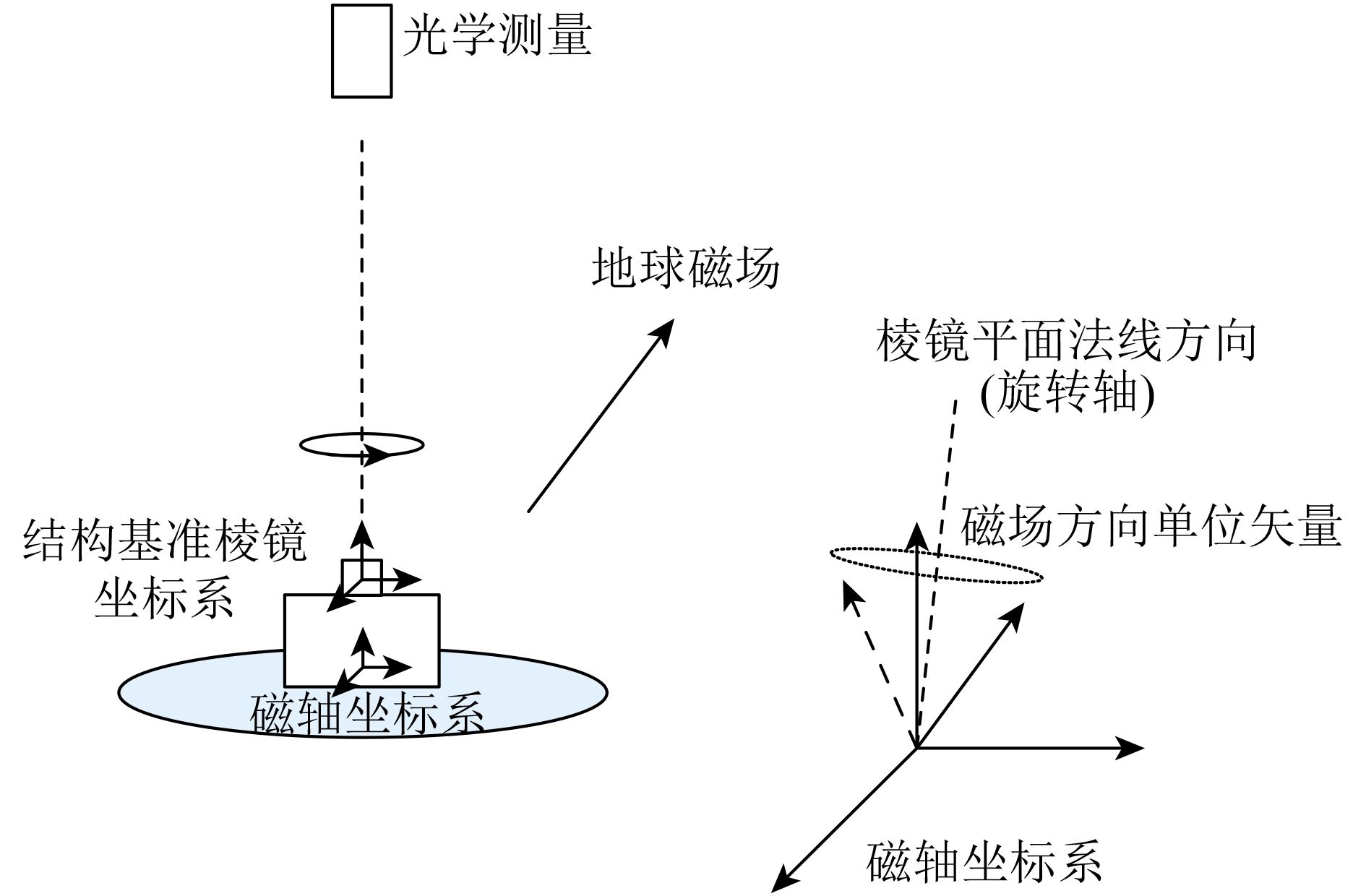
FGM探头在进行正交校正后处于磁轴坐标系中,它与探头基准棱镜之间的关系是未知的。标定的过程就是确定基准棱镜的法线方向与磁轴的角度关系,从而得到两者之间的转换矩阵。
地球磁场在短时间内是稳定的,可以用来作为标定过程中的参考矢量。如图13所示,标定试验将旋转探头,通过光学观测的方式保证棱镜法线方向不变,探头的旋转等效于磁场矢量在磁轴坐标系中的旋转。那么旋转中归一化的磁场矢量画出了一个圆,它所在平面的法线方向就是棱镜法线方向在探头磁轴坐标系中的方向,这样就可以计算磁轴坐标轴与棱镜法线的夹角。当得到两个棱镜面法线在磁轴坐标系的表达后,就能确定棱镜法线构成的结构坐标系与磁轴坐标系之间的关系。
|
| 图 13 传感器和结构坐标转换试验示意图 Figure 13 The diagram of sensor and structure coordination transformation |
HPM的3个探头在伸杆上的安装间距约为400 mm,FGM的工作原理是反馈控制的,反馈线圈在工作时在传感器内部产生与外界磁场相等的磁场,那么同时它对于传感器外部的磁场也是一种干扰,在近距离内不可忽略。
将传感器模拟伸杆上的安装方式进行安装,然后分别在传感器中通过电流模拟实际工作的反馈状态,另一个探头进行探测。试验结果表明,当探头2的3分量传感器全部工作在60000 nT时,对探头1的3分量干扰分别为[1.39, –3.66, 2.68] nT,对CDSM探头的干扰分别为[5.1, –4.05, 2.99] nT。试验同时表明这种干扰线性度很好,试验已经精确测量的FGM探头1对FGM探头2、CDSM探头,FGM探头2对FGM探头1、CDSM的干扰矩阵,根据探测数据可以精确地将这种干扰消除。
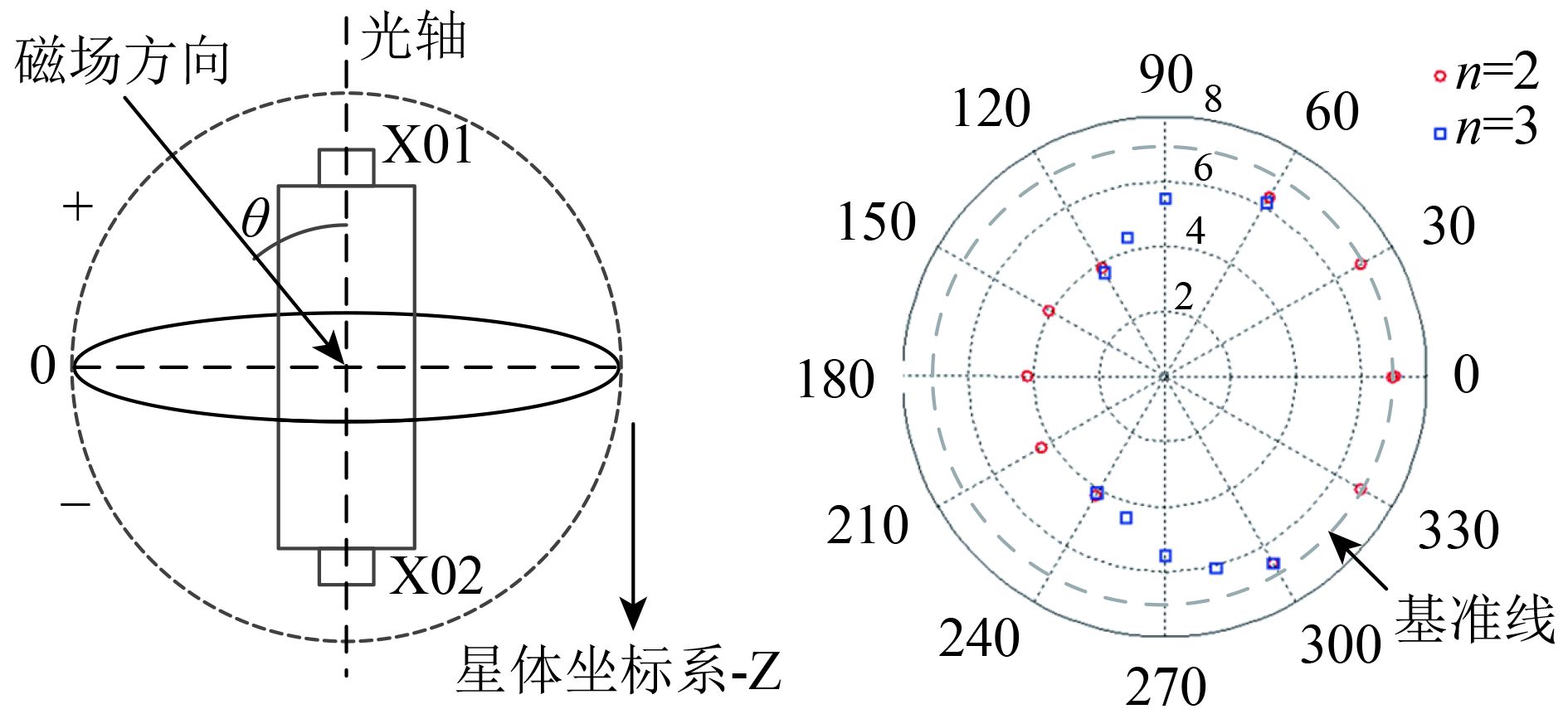
(5.5) CDSM转向差试验CDSM转向差试验在大型的三轴亥姆霍斯线圈中进行,试验前需要对线圈内部磁场进行再次补充提高均匀区。通过测试,中国计量院香山弱磁实验室能够实现在20000—100000 nT稳场环境下,实现±10 cm球型空间内磁场变化小于0.1 nT。这就可以确保CDSM在工装上旋转的过程中,工作介质所在磁场以及磁场梯度保持一致,从而确保测量到的是转向差是磁场方向引起的而不是环境的干扰。
测试是在50000 nT磁场下进行的,磁场方向与光轴方向一致时为0°,相反时为180°。CDSM在旋转360°过程中,同向和垂直两种工作模式各自优势区域工作,一致性良好,最大转向差3.3 nT,如图14所示。载荷在轨运行时,根据FGM测量到的磁场方向,可以将这一专项差消除。
|
| 图 14 CDSM转向差试验示意图 Figure 14 The results of CDSM heading error |
HPM在通过一系列的标定和性能测试后,对最终在轨执行任务的正样产品的性能进行了全面地评估,见表2。
|
|
表 2 HPM地面测试性能 Table 2 The performance of HPM calibration |
电磁监测试验卫星磁场探测方案是根据近地轨道矢量磁场探测的特点而设计的。高精度磁强计配备FGM探头和CDSM探头可以实现传感器优势互补,同时根据两种传感器的特点设计了有针对性的数据处理方法。在发射前对高精度磁强计进行标定试验,一方面验证了载荷性能,另一方面为在轨数据处理提供依据。随着卫星在轨运行后对数据分析的深入,数据处理方法可能需要进一步的优化和改进,地面标定的一些参数也将通过在轨标定的形式进行修正。通过这一探测方案的实施,电磁监测试验卫星可获取的高精度的近地轨道矢量磁场数据,这在地球物理、空间环境、海洋科学、导航定位等领域都有重要的意义和广泛的应用前景。
| [1] | 白春华, 徐文耀, 康国发. 地球主磁场模型[J]. 地球物理学进展, 2008, 23 (4) : 1045 –1057. Bai C H, Xu W Y and Kang G F. Main geomagnetic field models[J]. Progress in Geophysics, 2008, 23 (4) : 1045 –1057. |
| [2] | Thomas A P, Frederick F M and Lewis D E. The geomagnetic field and its measurement: introduction and magnetic field satellite (MAGSAT) glossary[J]. Johns Hopkins APL TECHNICAL DIGEST, 1980, 1 (3) : 161 –170. |
| [3] | 陈斯文. 卫星磁洁净的控制和测量[J]. 地球物理学进展, 2009, 24 (2) : 797 –800. Chen S W. Control and measure of satellite magnetic cleanliness[J]. Progress in Geophysics, 2009, 24 (2) : 797 –800. DOI: 10.3969/j.issn.1004.2903.2009.02.061 |
| [4] | Lohr D A, Zanetti L J, Anderson B J, Potemra T A and Acuña M H. The NEAR magnetic field instrument[J]. Johns Hopkins APL Technical Digest, 1998, 19 (2) : 136 –141. |
| [5] | Mioara M. Magnetic satellite missions: where have we been and where are we going[J]. Comptes rendus geoscience, 2006, 338 : 1002 –1011. DOI: 10.1016/j.crte.2006.05.011 |
| [6] | Narvaez P. The magnetostatic cleanliness program for the Cassini spacecraft[J]. Space Science Reviews, 2004, 114 (1/4) : 385 –394. DOI: 10.1007/s11214-004-1433-1 |
| [7] | Nielsen O V, Petersen J R, Primdahl F, Brauer P, Hernando B, Fernandez A, Merayo J M G and Ripka P. Development, construction and analysis of the ‘OErsted’ fluxgate magnetometer[J]. Measurement Science and Technology, 1995, 6 (8) : 1099 –1115. DOI: 10.1088/0957-0233/6/8/004 |
| [8] | 王兰炜, 申旭辉, 张宇, 张兴国, 胡哲, 颜蕊, 袁仕耿, 朱兴鸿. 中国电磁监测试验卫星工程研制进展[J]. 地震学报, 2016, 38 (3) : 376 –385. Wang L W, Shen X H, Zhang Y, Zhang X G, Hu Z, Yan R, Yuan S G and Zhu X H. Developing progress of China seismo-electromagnetic satellite project[J]. Acta Seismologica Sinica, 2016, 38 (3) : 376 –385. DOI: 10.11939/jass.2016.03.005 |
| [9] | 王晓峰, 韩晓东, 杨昌茂. Cs光泵磁强计补偿地磁变化的方法[J]. 传感器技术, 2004, 23 (7) : 47 –49. Wang X F, Han X D and Yang C M. Method of earth’s magnetic field fluctuation compensated by Cs magnetometer[J]. Journal of Transducer Technology, 2004, 23 (7) : 47 –49. DOI: 10.3969/j.issn.1000-9787.2004.07.016 |
| [10] | 张镇琦, 李磊, 周斌, 张艺腾. 基于绝对磁场测量的磁通门磁强计在轨标定方法[J]. 空间科学学报, 2014, 34 (2) : 235 –241. Zhang Z Q, Li L, Zhou B and Zhang Y T. A method of in-orbit calibration of fluxgate magnetometer based on the measurement of absolute scalar magnetometer satellite[J]. Chinese Journal of Space Science, 2014, 34 (2) : 235 –241. DOI: 10.11728/cjss2014.02.235 |
| [11] | 周斌, 程炳钧, 张艺腾, 张镇祁, 王劲东, 李磊. 电磁监测试验卫星矢量磁场探测方法[J]. 空间科学学报, 2014, 34 (6) : 843 –848. Zhou B, Cheng B J, Zhang Y T, Zhang Z Q, Wang J D and Li L. Magnetic field detection method of China seismo-electromagnetic satellite[J]. Chinese Journal of Space Science, 2014, 34 (6) : 843 –848. DOI: 10.11728/cjss2014.06.843 |

