| 电磁监测试验卫星(张衡一号)数据处理方法和流程 |
收稿日期: 2017-06-16
2. Beijing Engineering Research Center of Earthquake Observation, Beijing 100085, China
电磁监测试验卫星(CSES)设计在轨寿命5年,其目的是建立一个监测全球空间电磁场、电磁波、电离层等离子、高能粒子沉降等物理量的空间试验平台,对中国及其周边地区开展准实时监测和跟踪,开展全球7级以上、中国6级以上地震电磁信息分析研究,探索地震电离层响应变化的信息特征及其机理,为大震预测提供有价值的前兆信息。同时为空间环境监测预报和地球系统科学研究提供新的技术手段服务,为未来建立地震前兆电磁监测卫星业务化系统奠定技术基础。
国际上,利用卫星进行空间电磁环境观测最早开始于20世纪60年代,随着前苏联INTERCOSMOS系列卫星的发射,得到了大量的空间电磁场观测数据,并显示了空间对地观测技术在地震预测研究中的应用前景(Gokhberg 等,1982;Parrot,1994;Hayakawa 等,1996;Liu 等,2004;Pulinets和Boyarchuk,2004)。近年来,电磁监测卫星有关的技术与应用发展迅速。法国2004年发射了专用于地震监测的DEMETER卫星,其主要目的是探测与地震、火山活动相关的电离层电磁异常,该卫星在轨运行6年,观测到了较为明显的震前电磁扰动信息(Parrot 等,2006b;Zlotnicki 等,2010;朱涛和王兰炜,2011)。
自1966年中国发射第一颗人造卫星以来,发射的卫星几乎全部都是成像遥感卫星,电磁监测试验卫星是中国第一颗非成像遥感卫星。共搭载3类8种有效载荷。一是电磁场有效载荷,包括高精度磁强计(含磁通门磁力仪和标量磁力仪)、电场探测仪和感应式磁力仪,用于测量直流和交变电磁场及其变化信息;二是电离层原位参数测量有效载荷,包括等离子体分析仪、朗缪尔探针和高能粒子探测器,用于测量等离子体的电子和离子的密度、温度,漂移速度以及带电高能粒子通量与运动方向;三是电离层结构层析成像载荷,包括GNSS掩星接收机和三频信标机,用于测量电离层2维、3维等离子体精细结构及其变化(王兰炜 等,2016)。
张衡一号是中国发射的第一颗电磁卫星,其数据处理方法和以前的成像遥感卫星数据处理方法完全不同,是一个全新的领域,科学、有效的数据处理方法是数据产出和数据应用的前提。
本文针对中国电磁监测试验卫星不同科学载荷观测数据,在介绍电磁卫星科学数据种类和分级定义的基础上,详细描述各个科学载荷观测数据的处理方法、流程及相应的关键算法。
2、科学数据产品及分级 (2.1) 科学数据产品种类电磁监测试验卫星科学数据产品按照类型分为电磁类数据、电离层原位探测数据、电离层结构类数据以及相应的监测应用和科学应用产品。其中:
电磁类数据包括不同频段的电场三分量波形、功率谱数据、不同频段的磁场三分量波形、功率谱数据(包括感应式磁力仪和磁通门磁力仪观测数据),以及标量地磁场观测数据。
电离层原位探测数据包括电子密度、电子温度、离子密度、离子温度、离子总含量、离子漂移速度、离子涨落、高能电子计数/通量/投掷角、高能质子计数/通量/投掷角、X射线通量。
电离层结构类数据包括相对总电子含量TEC(Total Electron Content)、绝对TEC、峰值密度(NmF2)和峰值高度(HmF2)等。
监测应用产品是在2、2A或3级数据的基础上,产出包括中国6级、全球7级以上地震的电离层扰动震例研究数据,主要用于地震监测预测研究。科学应用产品基于2、2A或3级数据产品,开展各物理参量的背景场特征分析及建模工作,产出地磁场、电离层模型及其扰动等相关科学研究成果。
(2.2) 科学数据分级及定义电磁监测试验卫星是在充分调研国内外相关卫星数据分级的基础上,结合电磁卫星的特点进行分级和定义的。
电磁监测试验卫星科学观测数据分为0—4级标准科学数据产品。各级数据产品具体定义为
0级数据产品:经过帧同步、解扰、纠错、去重、按时间排列得到的各个载荷的科学数据和工程参数;三频信标地面站接收到的观测数据。
1级数据产品:对0级数据进行格式转换、定标处理后得到的按时间排列的物理量数据。
2级数据产品:对1级数据进行坐标变换、反演后生成的带有地理和地磁坐标系、时间、位置和姿态信息的物理量数据。
2A级数据产品:对于电场仪观测数据,是在2级卫星坐标系电场波形数据基础上,去除由于卫星在磁场中高速运动产生的附加电场影响后生成的数据;对于GNSS掩星观测数据,是对1级数据进行精密定轨、反演后生成有地理和地磁坐标系、时间、位置和姿态信息的物理量数据。
3级数据产品:在2级或2A级数据的基础上,进行重采样生成重访轨道指定区域的时序数据,或反演得到的电离层、大气层2维结构数据。
4级数据产品:在2级或2A级数据的基础上,进行空间插值处理后生成某个区域的空间演化数据。
3、总体数据处理流程根据数据分级定义和各级数据的产出,电磁监测试验卫星科学数据处理总体流程见图1。

|
| 图 1 科学数据处理总体流程图 Figure 1 General data processing procedure of scientific data |
其中,0—1级数据主要是格式转换、数据定标和物理量校正等。电磁类数据包括高精度磁强计、感应式磁力仪和电场探测仪3个载荷的观测数据,其0—1级数据处理主要是将观测的电压量通过进制转换和数据定标,获得电磁场波形或谱数据,包括基本磁场、10 Hz—20 kHz交变磁场,DC~3.5 MHz交变电场的波形数据、分频段频谱数据等。
电离层原位探测类数据,包括朗缪尔探针、等离子体分析仪和高能粒子探测器3个载荷的观测数据,0级数据的处理主要是基于标定文件将观测的电压量转变为物理量,然后通过拟合的方式得到需要的物理量,包括离子温度和密度、电子温度和密度、高能粒子的电子和质子通量、电子和质子能谱等。
电离层结构类数据,包括掩星接收机和三频信标机两个载荷的探测数据,1级数据主要有掩星观测载波相位、码伪距和信噪比,以及三频信标接收机观测的甚高频VHF(Very High Frequency)、UHF(Ultra High Frequency, 特高频)、L(1—2 GHz的无线电波波段)3个频段的差分相位数据和幅度数据。
1—2级数据产品的处理过程主要为坐标系变换或反演过程。对于电磁类数据,主要是将1级观测数据进行坐标系转换,从卫星坐标系到地理坐标系(地磁坐标系)的坐标变换;对于原位类数据,主要是对1级数据增加相应的地理坐标信息;对于结构类数据,主要在1级数据的基础上,通过计算反演获得相对TEC。
2—3级数据产品的处理过程,对电磁类和原位类主要是在2级数据的基础上,基于当前轨道以及之前若干个重访周期的重访轨道数据,给出不同规格轨道的连续数据随时间的变化;对结构类数据,主要是生成电子剖面和获取绝对TEC及其他参量,提取NmF2异常特征。
2—4级数据处理过程,对电磁类和原位类是利用全球以及中国区域的当前轨道以及之前若干个重访周期的重访数据,给出不同区域的空间变化数据。
4、载荷数据处理流程和关键算法根据电磁监测试验卫星数据分级定义,2级科学数据产品即探测的物理量数据,3—4级科学数据产品为在2级数据基础上对重访轨道数据进行的重采样,从而生成指定区域的时间序列或者是空间变化,3—4级数据产品是对2级数据产品在时间或空间的重新排列,不涉及特殊的算法和处理。因此,本文仅对1—2级科学数据产品的处理过程和关键算法进行讨论。
(4.1) 高精度磁强计 4.1.1. 数据处理流程高精度磁强计数据产品包括两个磁通门磁力仪(FGM1和FGM2)和CSDM总场仪的观测数据,其0—2级数据产品见表1。
|
|
表 1 高精度磁强计0—2级数据产品 Table 1 Level 0—2 data products of high precision magnetometer |
高精度磁强计数据处理流程如下:
对于接收的0级数据,经过二进制到十进制的转换后得到磁通门磁力仪(FGM)的电压量数据、CDSM总场仪的频率量数据。其中FGM数据经过线性校正以及温度校正,CDSM经过线性校正以及转向差校正等处理过程,得到三分量磁场和总场强度1级数据产品。1级数据再经过时标对齐,正交校正,消除卫星及矢量探头磁干扰,坐标变换等过程后得到2级数据产品,具体的处理流程如图2所示。

|
| 图 2 高精度磁强计1—2级数据处理流程 Figure 2 Level 1 and level 2 data processing procedure of high precision magnetometer |
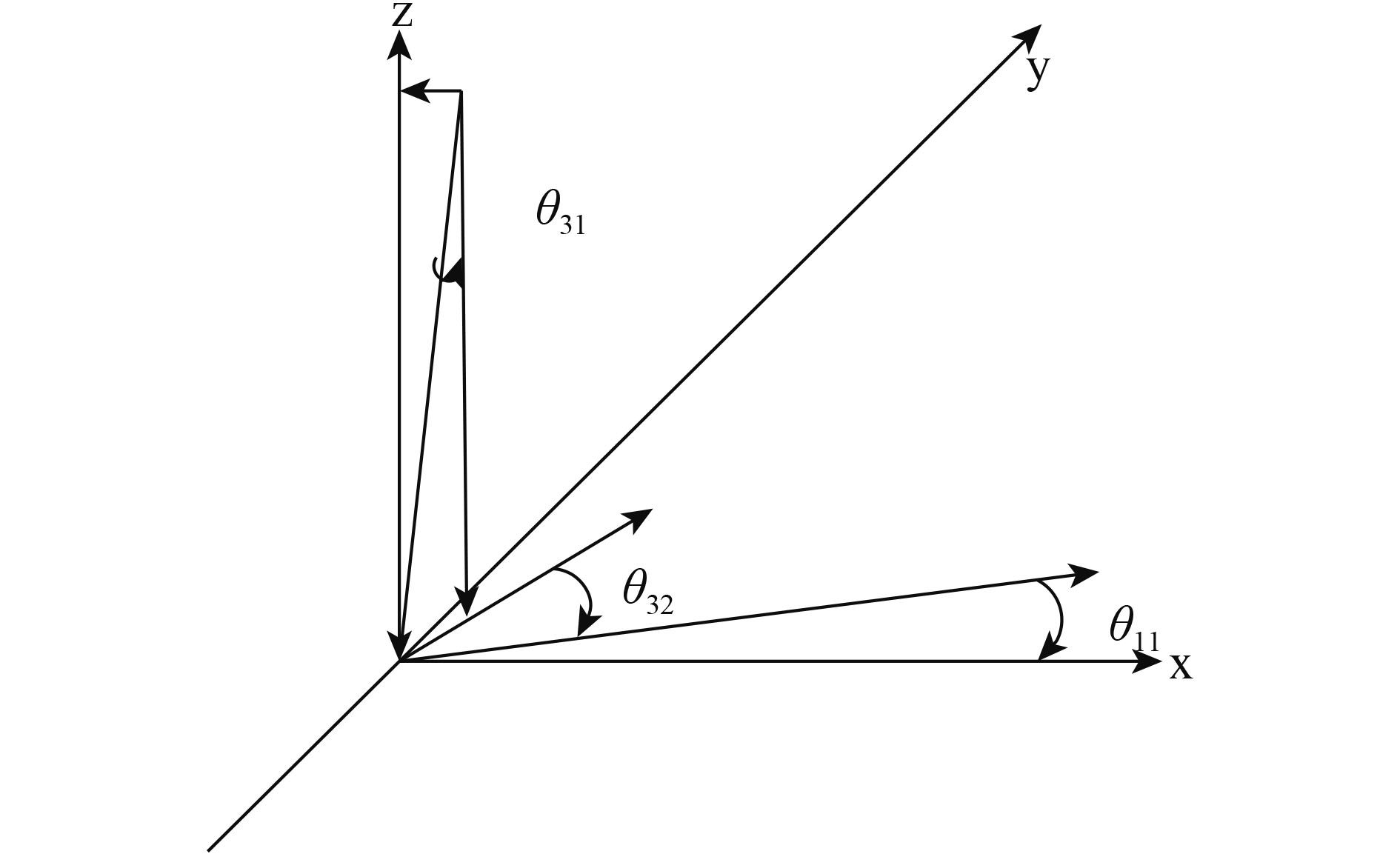
在高精度磁强计的数据处理中正交校正是其关键算法。正交校正是通过标量磁场数据对矢量磁场进行正交校正,采用多于一轨数据拟合的方式获取磁通门探头正交矩阵和零点偏差的绝对矢量磁场校准算法,其基本原理是标量磁场数据平方等于矢量磁场分量数据平方和,利用在轨运行磁场相对方向旋转一周的特点,实现拟合磁通门探头的解算正交矩阵和零点。图3是正交关系的示意图。式(1)是正交校正算法的计算。
|
| 图 3 正交变换角度关系示意图 Figure 3 Schematic diagram of angle relation in orthogonal transformation |
| $\begin{split}& \left[ {\begin{array}{*{20}{c}}1&0&0\\ {\sin {\theta _{11}}}&{\cos {\theta _{11}}}&{0}\\\!\!\! {\sin {\theta _{31}}\sin {\theta _{32}}}&{\sin {\theta _{31}}\cos {\theta _{32}}}&{\cos {\theta _{31}}} \!\!\! \end{array}} \right]\left[ {\begin{array}{*{20}{c}}\!\!\! {{B_{{\rm{x}}\_2}}} \!\!\! \\\!\!\! {{B_{{\rm{y}}\_2}}} \!\!\! \\\!\!\! {{B_{{\rm{z}}\_2}}} \!\!\! \end{array}} \right] = \\ & \qquad\left[ {\begin{array}{*{20}{c}}{{\alpha _{\rm{x}}}}&0&0\\0&{{\alpha _{\rm{y}}}}&0\\0&0&{{\alpha _{\rm{z}}}}\end{array}} \right]\left( {\left[ {\begin{array}{*{20}{c}}{{B_{\rm{x}}}}\\{{B_{\rm{y}}}}\\{{B_{\rm{z}}}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{{b_{\rm{x}}}}\\{{b_{\rm{y}}}}\\{{b_{\rm{z}}}}\end{array}} \right]} \right)\end{split}$ | (1) |
式中,
经过一系列转换后,可以得到:
| $\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{{B_{{\rm{x}}\_2}}}\\{{B_{{\rm{y}}\_2}}}\\{{B_{{\rm{z}}\_2}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}1&0&0\\{{k_{21}}}&{{k_{22}}}&0\\{{k_{31}}}&{{k_{32}}}&{{k_{33}}}\end{array}} \right] \times \\\left[ {\begin{array}{*{20}{c}}{{\alpha _{\rm{x}}}}&0&0\\0&{{\alpha _{\rm{y}}}}&0\\0&0&{{\alpha _{\rm{z}}}}\end{array}} \right]\left( {\left[ {\begin{array}{*{20}{c}}{{B_{\rm{x}}}}\\{{B_{\rm{y}}}}\\{{B_{\rm{z}}}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{{b_{\rm{x}}}}\\{{b_{\rm{y}}}}\\{{b_{\rm{z}}}}\end{array}} \right]} \right)\end{array}$ | (2) |
式中,
| $\begin{array}{c}{k_{21}} = -\displaystyle \frac{{\sin {\theta _{11}}}}{{\cos {\theta _{11}}}},{k_{22}} = \frac{1}{{\cos {\theta _{11}}}},{k_{31}} = - \frac{{\sin {\theta _{31}}\sin {\theta _{32}}}}{{\cos {\theta _{31}}}} +\\\displaystyle\frac{{\sin {\theta _{11}}\sin {\theta _{31}}\cos {\theta _{32}}}}{{\cos {\theta _{11}}\cos {\theta _{31}}}}\\{k_{32}} = - \displaystyle\frac{{\sin {\theta _{31}}\cos {\theta _{32}}}}{{\cos {\theta _{11}}\cos {\theta _{31}}}},{k_{33}} = \frac{1}{{\cos {\theta _{31}}}}\end{array}$ |
最后得到校正后的矢量磁场
电场探测仪3个分量的观测数据按照4个频段划分,包括DC—16 Hz(ULF),6 Hz—2.2 kHz(ELF),1.8—20 kHz(VLF)和18 kHz—3.5 MHz(HF),其0—2级数据产品见表2。
|
|
表 2 电场探测仪0—2级数据产品 Table 2 Level 0—2 data products of electric field detector |
电场探测仪的0级数据是4个传感器的电位,经过物理量生成、传递函数修正、电场值计算、正交性校正以及功率谱密度计算得到1级数据,其中的物理量生成包括,二进制电位值到十进制的转化,4个传感器的电位值经过两两差分,变为两个传感器之间的电位差值,电位差除以两个传感器之间的距离,即可得到此两个传感器连线方向的电场值。
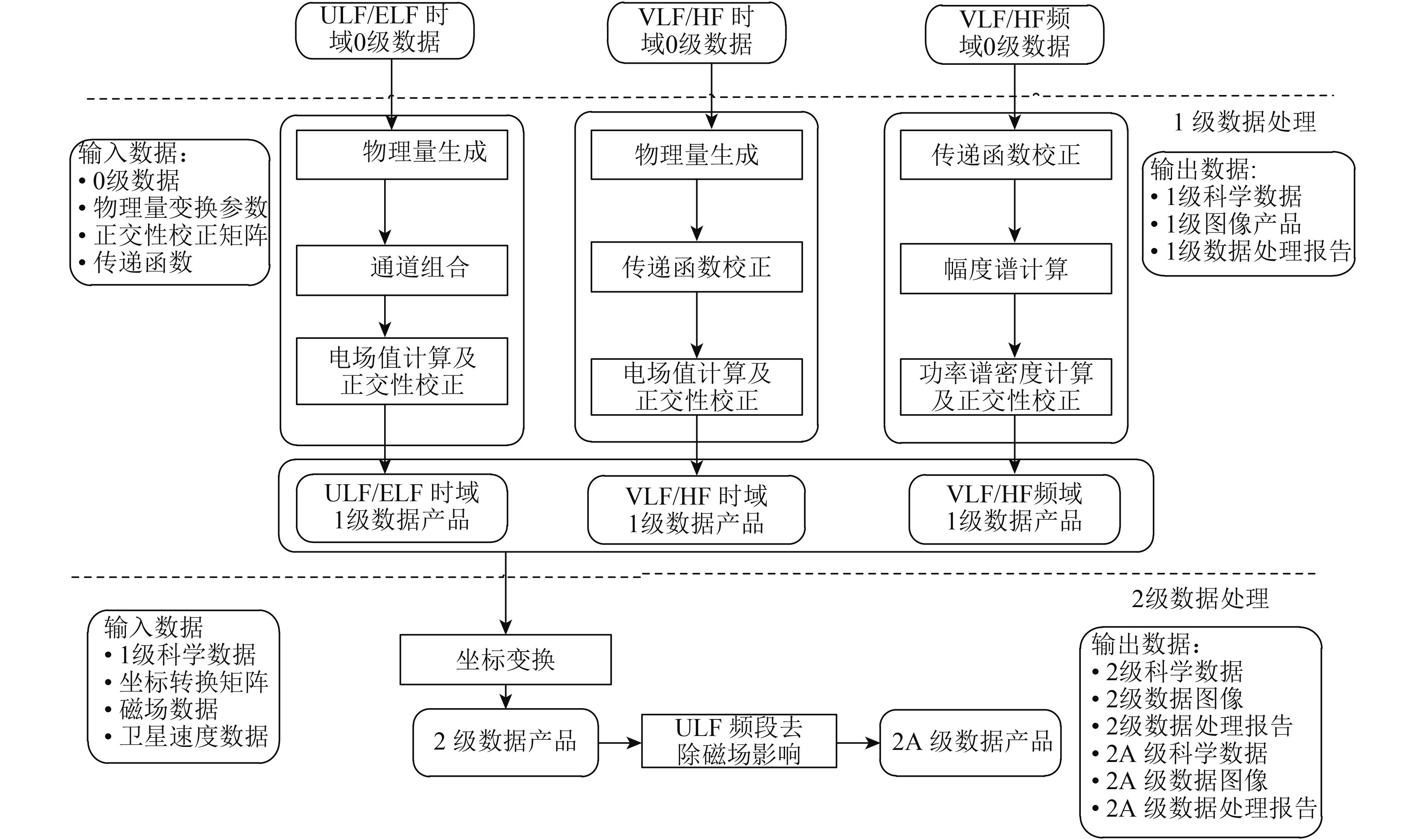
在1级数据生成2级数据的过程中,通过坐标变换得到地理坐标系下的2级数据。对于ULF频段的2级数据,消除由于卫星在磁场中的高速运动而产生的附加感生电动势可得到2A级数据,具体的处理流程见图4。
|
| 图 4 电场探测仪1—2级数据处理流程 Figure 4 Level 1 and level 2 data processing procedure of electric field detector |
在电场探测仪的数据处理流程中,其关键的算法是正交性校正算法。由于电场仪的实际测量结果为各通道的传感器之间的表面电势差,除以探头间距离,得到各通道传感器之间的电场值,此时得到的电场值为非正交系下电场值,需要转换到正交坐标系,然后再转换到卫星本体坐标系,该算法主要实现从电场值非正交坐标系到正交坐标系的转换。
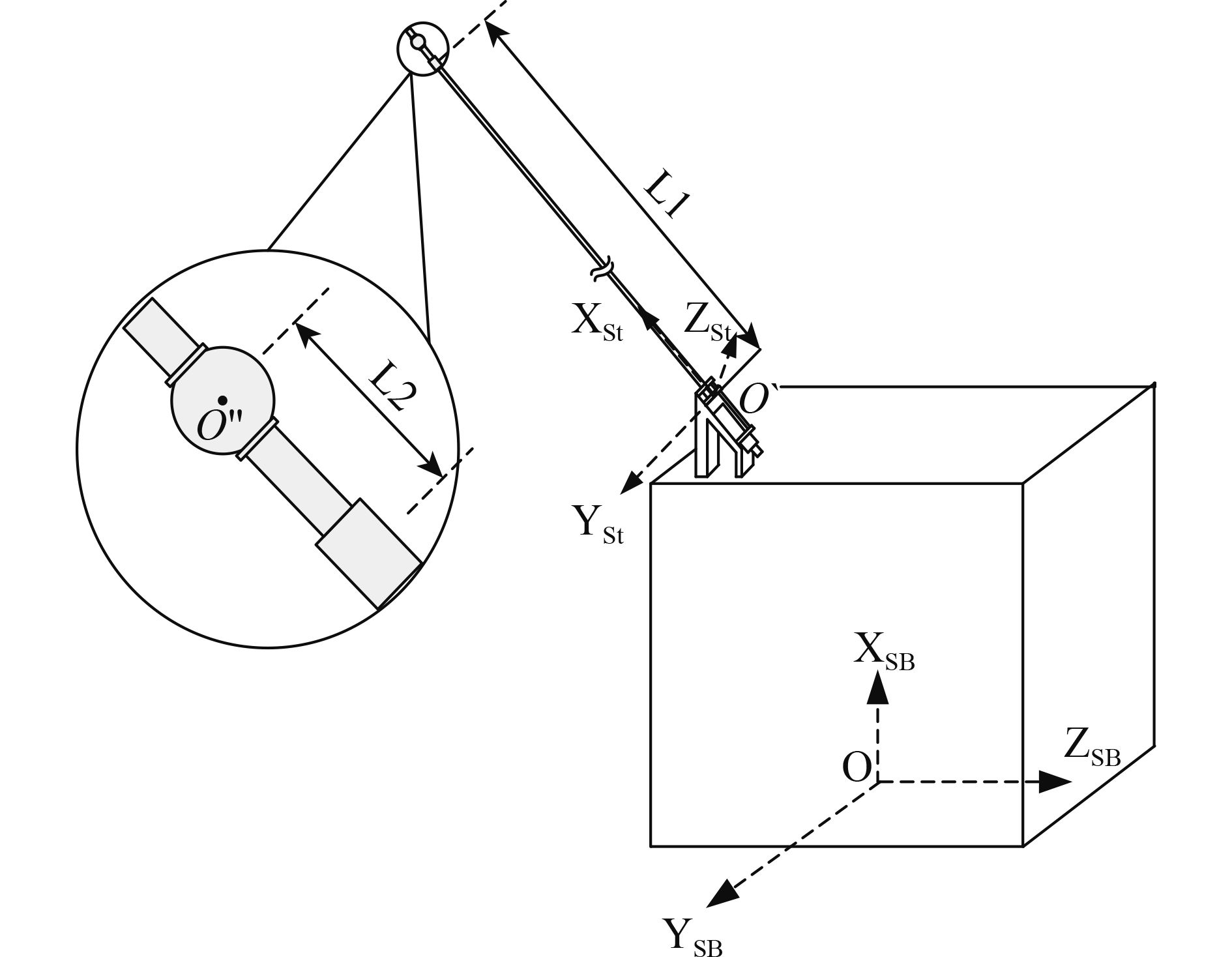
假设单个球形传感器与伸杆组合后的坐标关系如图5所示。
|
| 图 5 单个球形传感器与伸杆组合后的坐标关系示意图 Figure 5 Schematic diagram of coordinate between ball-shaped sensor and booom |
卫星坐标系为O(XSB,YSB,ZSB),卷筒式伸杆坐标系为
| $\begin{split}& \qquad {\left[ {\begin{array}{*{20}{c}} {x_{\rm{o}}^{''}} \\ {y_{\rm{o}}^{''}} \\ {z_{\rm{o}}^{''}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} {{L_1} + {L_2}} \\ 0 \\ 0 \end{array}} \right]^{\rm{T}}} \times \\ & \left[ {\begin{array}{*{20}{c}} {\cos \alpha 1}&{\cos \beta 1}&{\cos \gamma 1} \\ {\cos \alpha 2}&{\cos \beta 2}&{\cos \gamma 2} \\ {\cos \alpha 3}&{\cos \beta 3}&{\cos \gamma 3} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {x_{{\rm{oo}}}'} \\ {y_{{\rm{oo}}}'} \\ {z_{{\rm{oo}}}'} \end{array}} \right]\end{split}$ | (3) |
式中,
α1、β1、γ1为伸杆坐标系O′XSt轴与卫星坐标系OXSB、OYSB、OZSB轴的夹角;
α2、β2、γ2为伸杆坐标系O′YSt轴与卫星坐标系OXSB、OYSB、OZSB轴的夹角;
α3、β3、γ3为伸杆坐标系O′ZSt轴与卫星坐标系OXSB、OYSB、OZSB轴的夹角。
设4个球形传感器,其球心在卫星坐标系中的位置分别为a、b、c、d,其坐标分别为
电场仪的测量通道组合方式如下:通道1:a-b;通道2:c-d;通道3:a-d。
各通道传感器球心连线矢量在卫星坐标系中的归一化矢量的坐标矩阵为
| $\left[ {\begin{array}{*{20}{c}} {{x_{{\rm{ab}}}}}&{{y_{{\rm{ab}}}}}&{{z_{{\rm{ab}}}}} \\ {{x_{{\rm{cd}}}}}&{{y_{{\rm{cd}}}}}&{{z_{{\rm{cd}}}}} \\ {{x_{{\rm{ad}}}}}&{{y_{{\rm{ad}}}}}&{{z_{{\rm{ad}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \displaystyle{\frac{{{x_{\rm{a}}} - {x_{\rm{b}}}}}{{{d_{{\rm{ab}}}}}}}&\displaystyle{\frac{{{y_{\rm{a}}} - {y_{\rm{b}}}}}{{{d_{{\rm{ab}}}}}}}&\displaystyle{\frac{{{z_{\rm{a}}} - {z_{\rm{b}}}}}{{{d_{{\rm{ab}}}}}}} \\ \displaystyle {\frac{{{x_{\rm{c}}} - {x_{\rm{d}}}}}{{{d_{{\rm{cd}}}}}}}&\displaystyle{\frac{{{y_{\rm{c}}} - {y_{\rm{d}}}}}{{{d_{{\rm{cd}}}}}}}&\displaystyle{\frac{{{z_{\rm{c}}} - {z_{\rm{d}}}}}{{{d_{{\rm{cd}}}}}}} \\ \displaystyle{\frac{{{x_{\rm{a}}} - {x_{\rm{d}}}}}{{{d_{{\rm{ad}}}}}}}&\displaystyle{\frac{{{y_{\rm{a}}} - {y_{\rm{d}}}}}{{{d_{{\rm{ad}}}}}}}&\displaystyle{\frac{{{z_{\rm{a}}} - {z_{\rm{d}}}}}{{{d_{{\rm{ad}}}}}}} \end{array}} \right]$ | (4) |
式中,
| $\begin{array}{c} {d_{{\rm{ab}}}} = \sqrt {{{\left({{x_{\rm{a}}} - {x_{\rm{b}}}} \right)}^2} + {{\left({{y_{\rm{a}}} - {y_{\rm{b}}}} \right)}^2} + {{\left({{z_{\rm{a}}} - {z_{\rm{b}}}} \right)}^2}} \\ {d_{{\rm{cd}}}} = \sqrt {{{\left({{x_{\rm{c}}} - {x_{\rm{d}}}} \right)}^2} + {{\left({{y_{\rm{c}}} - {y_{\rm{d}}}} \right)}^2} + {{\left({{z_{\rm{c}}} - {z_{\rm{d}}}} \right)}^2}} \\ {d_{{\rm{ad}}}} = \sqrt {{{\left({{x_{\rm{a}}} - {x_{\rm{d}}}} \right)}^2} + {{\left({{y_{\rm{a}}} - {y_{\rm{d}}}} \right)}^2} + {{\left({{z_{\rm{a}}} - {z_{\rm{d}}}} \right)}^2}} \\ \end{array} $ |
则沿卫星坐标系的电场分量与沿各测量通道的电场分量之间,有以下关系:
| $\begin{array}{*{20}{l}}{{x_{{\rm{ab}}}}{E_{\rm{x}}} + {y_{{\rm{ab}}}}{E_{\rm{y}}} + {z_{{\rm{ab}}}}{E_{\rm{z}}} = {E_{{\rm{CH}}1}}}\\{{x_{{\rm{cd}}}}{E_{\rm{x}}} + {y_{{\rm{cd}}}}{E_{\rm{y}}} + {z_{{\rm{cd}}}}{E_{\rm{z}}} = {E_{{\rm{CH}}2}}}\\{{x_{{\rm{ad}}}}{E_{\rm{x}}} + {y_{{\rm{ad}}}}{E_{\rm{y}}} + {z_{{\rm{ad}}}}{E_{\rm{z}}} = {E_{{\rm{CH}}3}}}\end{array}$ | (5) |
式中,
式(4)即为坐标转换矩阵,利用它就可实现电场仪坐标系与卫星坐标系的转换,即将非正交坐标系转换为卫星坐标系。
(4.3) 感应式磁力仪 4.3.1. 数据处理流程感应式磁力仪(SCM)3个分量的观测数据按照3个频段进行划分,包括10—200 Hz(ULF),200 Hz—2.2 kHz(ELF)和1.8 kHz—20 kHz(VLF),其0—2级数据产品见表3。
|
|
表 3 感应式磁力仪0—2级数据产品 Table 3 Level 0—2 data products of search coie magnetometer |
感应式磁力仪0级数据首先进行二进制到十进制的数据格式转换,此时生成的是电压量数据,分为波形数据和频谱数据两种,对于波形数据,经过傅里叶变换到频域内进行定标参数校正(即传输函数校正),再进行傅里叶逆变换生成校正后的波形数据,此时得到的是三分量的交变磁场强度的波形数据。而频谱数据直接在频域内进行传输函数校正,生成校正后的功率谱数据,得到1级数据产品。对于1级数据,根据星下点的位置、卫星姿态等信息,利用坐标变换生成带有地理和地磁坐标信息的三分量波形和功率谱物理量数据,并标注地震、磁情指数等辅助信息,生成2级数据产品。具体处理流程见图6。

|
| 图 6 感应式磁力仪1—2级数据处理流程 Figure 6 Level 1 and level 2 data processing procedure of search coie magnetometer |
在感应式磁力仪的数据处理中,其关键的算法是传输函数校正。其具体步骤包括傅里叶变换、传输函数校正和傅里叶反变换(Lagoutte 等,2005)。
(1) 傅里叶变换。首先要对其进行傅里叶变换,按照式(6)将其由时间域转换到频率域。
| $\begin{array}{c}X(k) = \displaystyle\sum\limits_{n = 0}^{N - 1} {x(n){{\rm{e}}^{ - j\frac{{2{\rm{\text{π} }}}}{N}kn}}} ,\;\;k = 0,1,2, \cdots ,N - 1\end{array}$ | (6) |
式中,
(2) 传输函数校正。传输函数校正是利用在频率域一个系统的输出等于输入与系统传输函数的乘积的原理进行:
| $Y(K) = X(K) \times H(K)$ | (7) |
式中,
(3) 傅里叶反变换。通过傅里叶反变换将信号从频域变换到时域:
| ${\rm{x}}(n) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {{\rm{X}}(k)} {{\rm{e}}^{j\frac{{2\text{π} }}{N}kn}},\;\;n = 0,1,2, \cdots ,N - 1$ | (8) |
式中,X(K)为频域幅度值,x(n)是经过校正的时间序列,N为参与计算的数据个数。
(4.4) 朗缪尔探针 4.4.1. 数据处理流程朗缪尔探针观测数据经过处理得到电离层等离子体环境的电子密度、电子温度等数据。其0—2级数据产品见表4。
|
|
表 4 朗缪尔探针0—2级数据产品 Table 4 Level 0—2 data products of langmuir probe |
朗缪尔探针的基本原理是将一根金属电极(传感器)伸入到等离子体中,通过测量电极的电压和其收集的等离子体电流关系,来反演等离子体的特性参数。其数据处理流程是首先对0级数据进行十进制转换,然后进行增益和零漂等参数修正,生成扫描电压和输出电流。根据扫描电压和输出电流,可以生成I-V曲线,经过对I-V曲线的拟合反演,得到电子密度、电子温度等物理量,从而生成1级标准数据。
对于1级数据,利用坐标变换生成带有地理和地磁坐标信息的电子密度、电子温度,获取地震记录、磁情指数等辅助信息,对应叠加至1级数据,生成2级标准数据。具体处理流程见图7。

|
| 图 7 朗缪尔探针1—2级数据处理流程 Figure 7 Level 1—2 data processing procedure of langmuir probe |
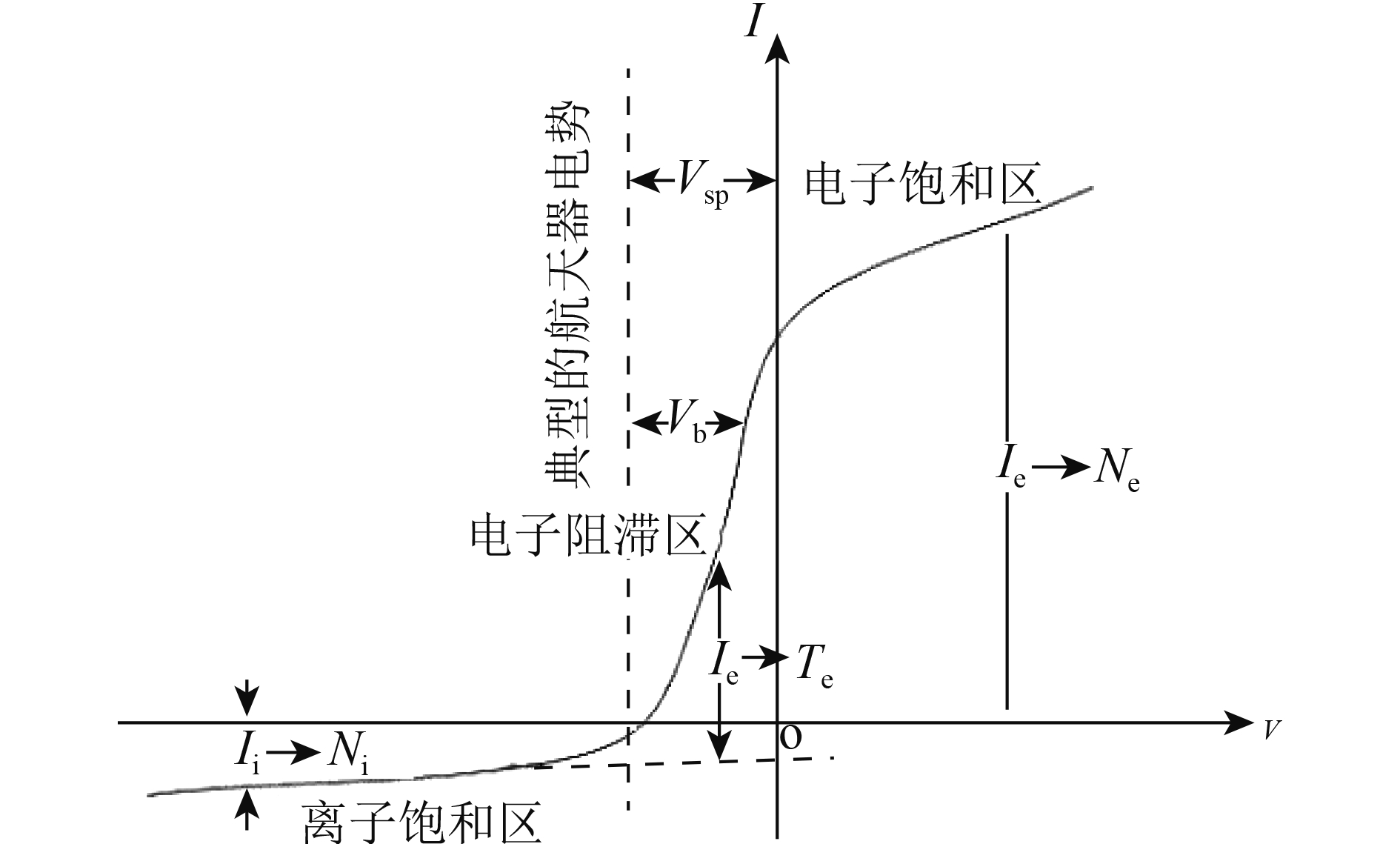
朗缪尔探针数据处理中关键算法是I-V曲线的拟合和反演计算。该算法包括了悬浮电位的确定、空间等离子体电位确定、电子电流点Ie0和Ii0确定以及电子温度和密度的计算,图8是朗缪尔探针理想的I-V曲线示意图。
|
| 图 8 朗缪尔探针理想的I-V曲线示意图 Figure 8 Ideal I-V curve of langmuir probe |
(1) 确定悬浮电位点Vf。悬浮电位点是朗缪尔探针伏安特性曲线中电流为0的点,当探针扫描电压Vs=Vf时,探针收集的电子电流Ie和离子电流Ii异号相等,探针收集的总电流I为0,即I=Ie+Ii=0。
(2) 拟合离子电流和电子电流。确定Vf后,理论上,在离子饱和区(V<Vf–4k·Te·e–1区域,k为玻尔兹曼常数1.38×10–23),可以认为朗缪尔探针收集的电流仅由离子电流贡献(电子电流的贡献小于1%)。这样就可以据实际电离层温度情况,先给定Te,然后拟合出离子饱和区和离子电流Ii,并利用Ii反推电子阻滞区和电子饱和区。
将朗缪尔探针的总电流I减去拟合的离子电流Ii,即可获得探针收集的电子电流Ie,即Ie=I–Ii。
(3) 找出空间等离子体电位点Vp。等离子体电位Vp点是朗缪尔探针电位(Vb)和空间等离子体电位(Vp)相等的点,是伏安特性曲线中电子阻滞区和电子饱和区的转折点。Vp可以通过式(9)计算(Chen和Chang,2002):
| ${V_{\rm{f}}} = {V_{\rm{s}}} - \frac{{K{T_{\rm{e}}}}}{{2e}}\ln \left(\frac{{2M}}{{{\text{π}}m}}\right)$ | (9) |
对于式(9),找到Ie开始偏离指数增长的点,也就是Ie(V)一阶导数最大,或者Ie(V)二阶导数为0的点即为Vp。由于各种干扰因素的影响,电子阻滞区和电子饱和区的转折点并不明显,求取的空间等离子离子体电位Vp会有所偏差,因此需要对电子阻滞电流和电子饱和电流多次拟合迭代,修正得到最佳的空间等离子体电位。
(4) 找到Vp点所对应的电子电流点Ie0和Ii0。电子电流以等离子体电位点为分界点可以分为电子阻滞电流和电子饱和电流(加速电流)两个部分。当Vs=Vp时,探针收集的电子电流为电子热随机电流Ie0为和离子电流Ii0为
| ${I_{{\rm{e}}0}} = {N_{\rm{e}}}eA\sqrt {\frac{{k{T_{\rm{e}}}}}{{2{\text{π}}{m_{\rm{e}}}}}} $ | (10) |
| ${I_{{\rm{i}}0}} = {N_{\rm{i}}}e{A_{\rm{s}}}\sqrt {\frac{{k{T_{\rm{i}}}}}{{2{\text{π}}{m_{\rm{i}}}}}} $ | (11) |
式中,A和As分别为朗缪尔探针传感器的表面积和横截面积;Ne和Ni为等离子体的电子密度和离子密度;k为玻尔兹曼常量;e为基本电荷常量;me为电子的质量,mi为离子质量。
(5) 计算电子温度Te。在电子阻滞区,电子电流随朗缪尔探针的电压呈指数变化:
| ${I_{\rm{e}}} = {I_{{\rm{e}}0}}\exp \left(\frac{{e{V_{\rm{p}}}}}{{k{T_{\rm{e}}}}}\right) = {I_{{\rm{e}}0}}\exp \left(\frac{{e({V_{\rm{b}}} - {V_{{\rm{sc}}}})}}{{k{T_{\rm{e}}}}}\right)$ | (12) |
两边求对数可得:
| $\ln {I_{\rm{e}}} = \ln {I_{{\rm{e}}0}} + \frac{{e{V_{\rm{p}}}}}{{k{T_{\rm{e}}}}} = C + \frac{{e{V_{\rm{p}}}}}{{k{T_{\rm{e}}}}}$ | (13) |
式中,Vb是朗缪尔探针的扫描电压,Vsc是航天器的电位;C为常数。
由式(13)可以看出,阻滞区的(ln(Ie1)–ln(Ie2/))/(Vp1–Vp2)正比于1/Te,在半对数坐标下,求取电子阻滞电流的斜率
| ${T_e} = \frac{e}{{k \times \tan \varphi }} \approx \frac{{11600}}{{\tan \varphi }}$ | (14) |
(6) 计算电子密度及离子密度。在朗缪尔探针伏安特性曲线中找出等离子体电位Vp所对应的电子电流,即是电子热随机电流Ie0。可求得等离子体的电子密度和离子密度。
| ${N_{\rm{e}}} = \frac{{{I_{{\rm{e}}0}}}}{{e \times A}}\sqrt {\frac{{2{\text{π}}{m_{\rm{e}}}}}{{k{T_{\rm{e}}}}}} $ | (15) |
| ${N_{\rm{i}}} = \frac{{I{e_{\rm{i}}}}}{{e \times A}}\sqrt {\frac{{2{\text{π}}{m_{\rm{i}}}}}{{k{T_{\rm{i}}}}}} $ | (16) |
等离子体分析仪(PAP)包括阻滞式分析仪(RPA)、离子漂移计(IDM)和离子捕获计(ICM)3个部分,观测数据经过处理可得到电离层等离子体环境的离子密度、温度等数据。其0—2级数据产品见表5。
|
|
表 5 等离子体分析仪0—2级数据产品 Table 5 Level 0—2 data products of plasma analyzer package |
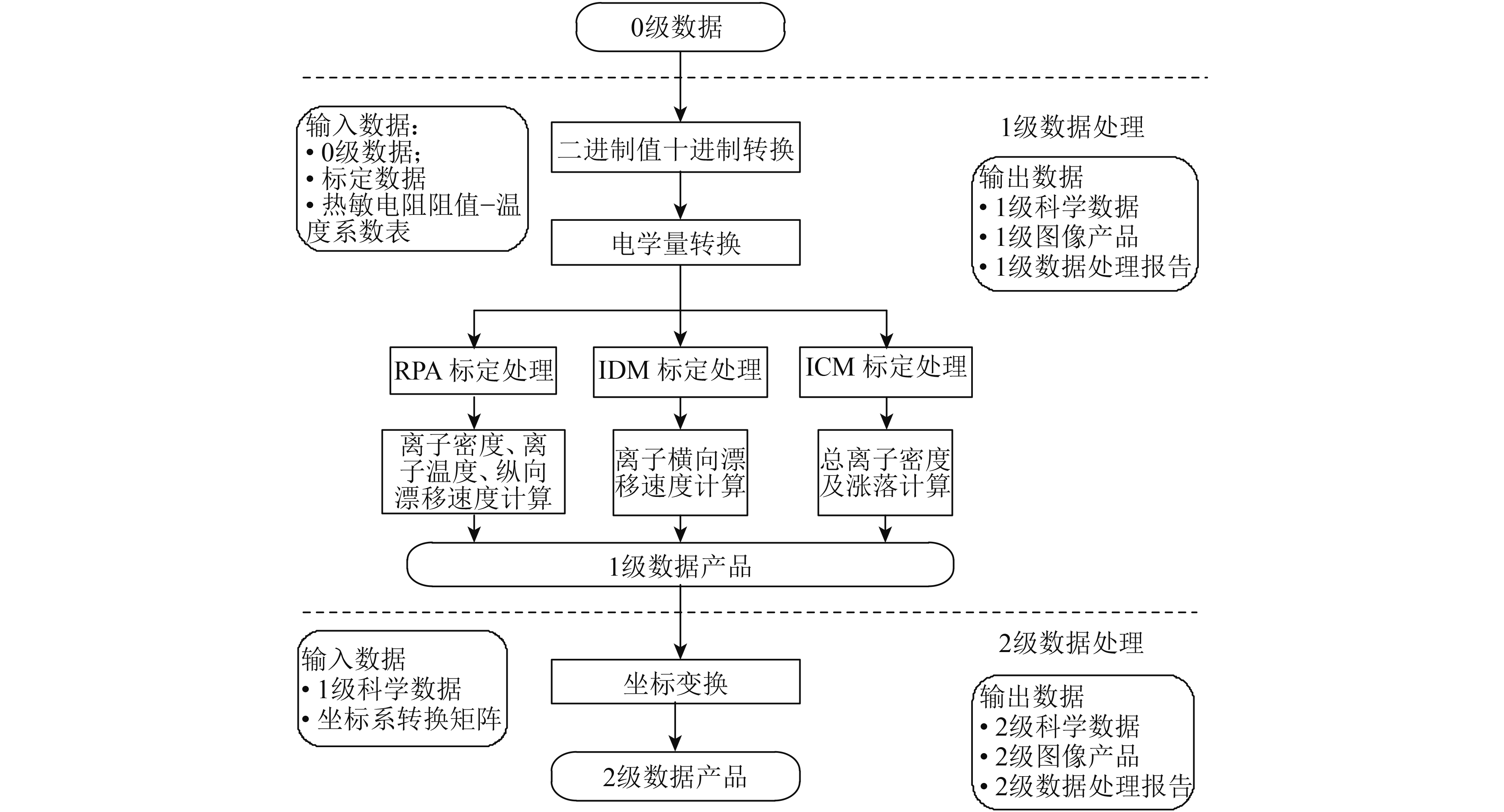
数据处理过程中,将二进制数据转换为十进制数据,然后进行电学量数值转换,并进行标定参数修正,生成若干组扫描电压和输出电流。其中RPA的扫描电压和输出电流,经过伏安特性曲线反演计算,可以生成H+、He+、O+的密度、离子温度Ti、离子纵向漂移速度Vx。IDM的输出电流值经过计算可以生成离子横向漂移速度Vy和Vz。ICM的输出电流值经过计算可以生成总离子密度及其涨落从而得到按时间顺序排列的1级数据产品。从星务数据包中获取星下点的位置信息,经过坐标变换处理,对应叠加至1级数据,生成带有时间和地理坐标信息的2级数据产品。等离子体分析仪的1—2级数据处理流程见图9。
|
| 图 9 等离子体分析仪1—2级数据处理流程 Figure 9 Level 1 and level 2 data processing procedure of plasma analyzer package |
等离子分析仪的数据处理算法中,关键是阻滞式分析器(RPA)的数据处理,通过对RPA的数据处理,最终计算得到H+密度NH+、He+密度NHe+、O+离子密度NO+、离子温度
(1) 读取由朗缪尔探针测量的卫星结构地相对等离子体的绝对电位(
(2) 设置初值,假设5个求解量的初始值分别为
(3) 最小二乘拟合。利用粒子速度分布积分关系
| $I = \frac{1}{2}K{V_{\rm{r}}}Ae\sum\limits_{\rm{i}} {{N_{\rm{i}}}[1 + erf({\beta _{\rm{i}}}{f_{\rm{i}}}) + \frac{1}{{{V_{\rm{r}}}\sqrt {\text{π}} {\beta _{\rm{i}}}}}\exp (- {\beta _{\rm{i}}}^2{f_{\rm{i}}}^2)]} $ | (17) |
式中,
将观测值(包括125个扫描偏压值Vn和125个电流值In,n=1, 2,
掩星接收机的各级数据产品见表6。
|
|
表 6 掩星接收机0—3数据产品 Table 6 Level 0—3 data products of GNSS occultation receiver |
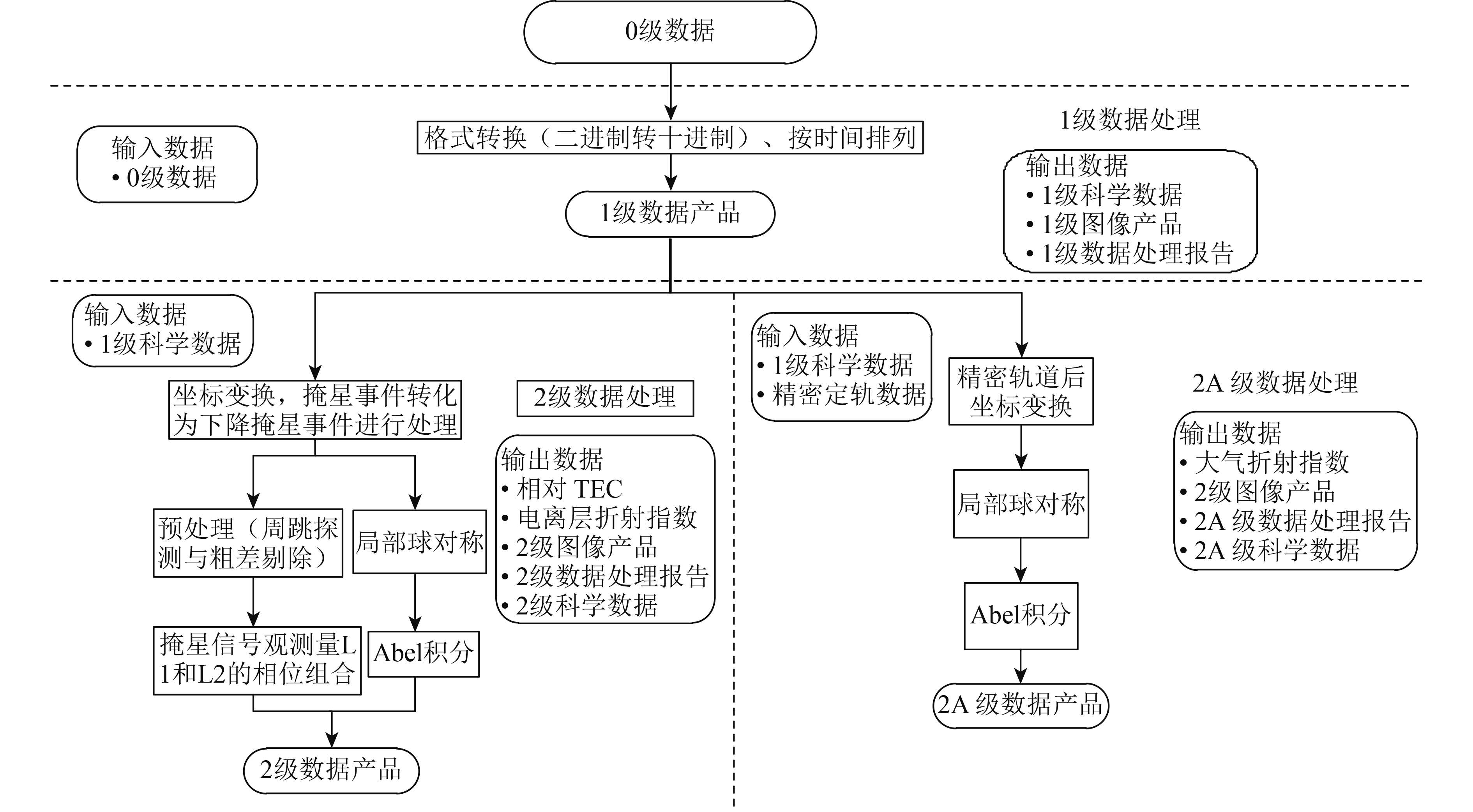
根据掩星接收机的0级数据,经过进制变换、去周跳和粗差处理,得到信号的载波相位和码伪距等1级数据产品。对于1级数据,基于Abel积分或洋葱分层等方法计算改正TEC和电离层折射指数,得到2级数据。掩星接收机同时还有2A级数据,2A级数据是在1级数据的基础上,利用精密定轨数据,计算得到大气折射指数。随后,在2级数据的基础上,通过硬件延迟计算绝对TEC,并基于球对称假设理论,通过改正TEC获得电离层电子密度剖面,建立NmF2时间序列,得到3级数据。掩星接收机数据处理流程见图10。
|
| 图 10 GNSS掩星接收机1—2级数据处理流程 Figure 10 Level 1 and level 2 data processing procedure of GNSS occultation receiver |
在掩星接收机(GNSS)数据处理过程中,数据预处理(粗差的剔除和周跳探测与修复)是一项非常重要的工作,也是最后能得到高精度的反演结果的重要保证。其关键的算法就是修复周跳和剔除粗差。具体的方法如下。
GNSS伪距和载波的差观测方程可表示为
| $P_{\rm{i}}^{\rm{k}} = \rho _{\rm{i}}^{\rm{k}} + cd{t_{\rm{i}}} - cd{t^{\rm{k}}} + I_{\rm{i}}^{\rm{k}} + Tr_{\rm{i}}^{\rm{k}} + c({b_{\rm{i}}} + {b^{\rm{k}}}) + {\varepsilon _{\rm{P}}}$ | (18) |
| $L_{\rm{i}}^{\rm{k}} = \rho _{\rm{i}}^{\rm{k}} + cd{t_{\rm{i}}} - cd{t^{\rm{k}}} - I_{\rm{i}}^{\rm{k}} + Tr_{\rm{i}}^{\rm{k}} + \lambda B_{\rm{i}}^{\rm{k}} + {\varepsilon _L}$ | (19) |
式中,i表示频率,k表示卫星,
周跳的探测与修复和粗差剔除可采用双频GPS观测值线性组合的方式来进行,常用的线性组合包括无电离层延迟组合、无几何距离组合、宽巷组合和M-W组合等方法。电磁监测试验卫星数据处理中选择M-W组合方法来进行,见式(20)。其优点是消除了电离层、对流层、钟差和几何距离的影响,并且具有较长的波长,约为86 cm。
| ${L_6} = \frac{1}{{{f_1} - {f_2}}}({f_1}{L_1} - {f_2}{L_2}) - \frac{1}{{{f_1} + {f_2}}}({f_1}{P_1} + {f_2}{P_2})$ | (20) |
按照式(20)组成M-W组合观测值,其观测噪声为
| $\begin{split}{v_{{\rm{L}}6}}(i) = & \displaystyle \frac{1}{{{f_1} - {f_2}}}\left({{f_1}{v_{{\rm{L}}1}}(i) - {f_2}{v_{{\rm{L}}2}}(i)} \right) -\\ &\displaystyle\frac{1}{{{f_1} + {f_2}}}\left({{f_1}{v_{{\rm{P}}1}}(i) + {f_2}{v_{{\rm{P}}2}}(i)} \right)\end{split}$ | (21) |
式中,VL1、VL2为L1和L2载波波相位的观测噪声,VP1、VP2为码伪距观测噪声。
方差为
| $\begin{aligned}\sigma _{{\rm{L}}6}^2(i) = & \frac{1}{{{{({f_1} - {f_2})}^2}}}\left({f_1^2\sigma _{{\rm{L}}1}^2(i) - f_2^2\sigma _{{\rm{L}}2}^2(i)} \right) +\\ &\frac{1}{{{{({f_1} + {f_2})}^2}}}\left({f_1^2\sigma _{{\rm{P}}1}^2(i) + f_2^2\sigma _{{\rm{P}}2}^2(i)} \right)\end{aligned}$ | (22) |
组合观测值的整周模糊度为
| $\begin{aligned}&{b_{\rm{w}}}(i) = \\ & \left({\frac{1}{{{f_1} - {f_2}}}\left({{f_1}{L_1}(i) - {f_2}{L_2}(i)} \right) - \frac{1}{{{f_1} + {f_2}}}\left({{f_1}{P_1}(i) + {f_2}{P_2}(i)} \right)} \right)/{{\textit{λ}} _{\rm{w}}}\end{aligned}$ | (23) |
整周模糊度的方差为
| $\begin{aligned} & \sigma _{{\rm{bw}}}^2(i) =\frac{{\sigma _{{\rm{L}}6}^2}}{{\lambda _{\rm{w}}^2}} =\\ & \left({\frac{{f_1^2\sigma _{{\rm{L}}1}^2(i) - f_2^2\sigma _{{\rm{L}}2}^2(i)}}{{{{({f_1} - {f_2})}^2}}} + \frac{{f_1^2\sigma _{{\rm{P}}1}^2(i) + f_2^2\sigma _{{\rm{P}}2}^2(i)}}{{{{({f_1} + {f_2})}^2}}}} \right)/{\textit{λ}} _{\rm{w}}^2\end{aligned}$ | (24) |
由于在M-W组合观测值中已消除了电离层延迟、对流层延迟、钟误差和几何距离的影响,而且具有较长的波长(λw约为86 cm),较小的量测噪声等特点,因此适合用于非差周跳的探测和修复。采用递推的方法计算每一历元
| ${\left({{b_{\rm{w}}}} \right)_{{i}}} = \frac{{i - 1}}{i}{\left({{b_{\rm{w}}}} \right)_{i - 1}} + \frac{1}{i}{b_{\rm{w}}}(i)$ | (25) |
| $\sigma _{{i}}^2 = \frac{{i - 1}}{i}\sigma _{i - 1}^2 + \frac{1}{i}{({b_{\rm{w}}}(i) - {\left({{b_{\rm{w}}}} \right)_{i - 1}})^2}$ | (26) |
对于第i历元的观测数据,若
弧段与弧段之间的周跳大小
| $\Delta {b_{\rm{w}}} = \Delta {n_1} - \Delta {n_2}$ | (27) |
式中,
三频信标机是通过地面接收机接收星上三频信标发射机发射的UHF、VHF和L频段的信号,并进行计算得到电离层的相关参数。三频信标的0—2级数据产品见表7。
|
|
表 7 三频信标接收机0—2级数据产品 Table 7 Level 0—2 data products of tri-band-beacon |
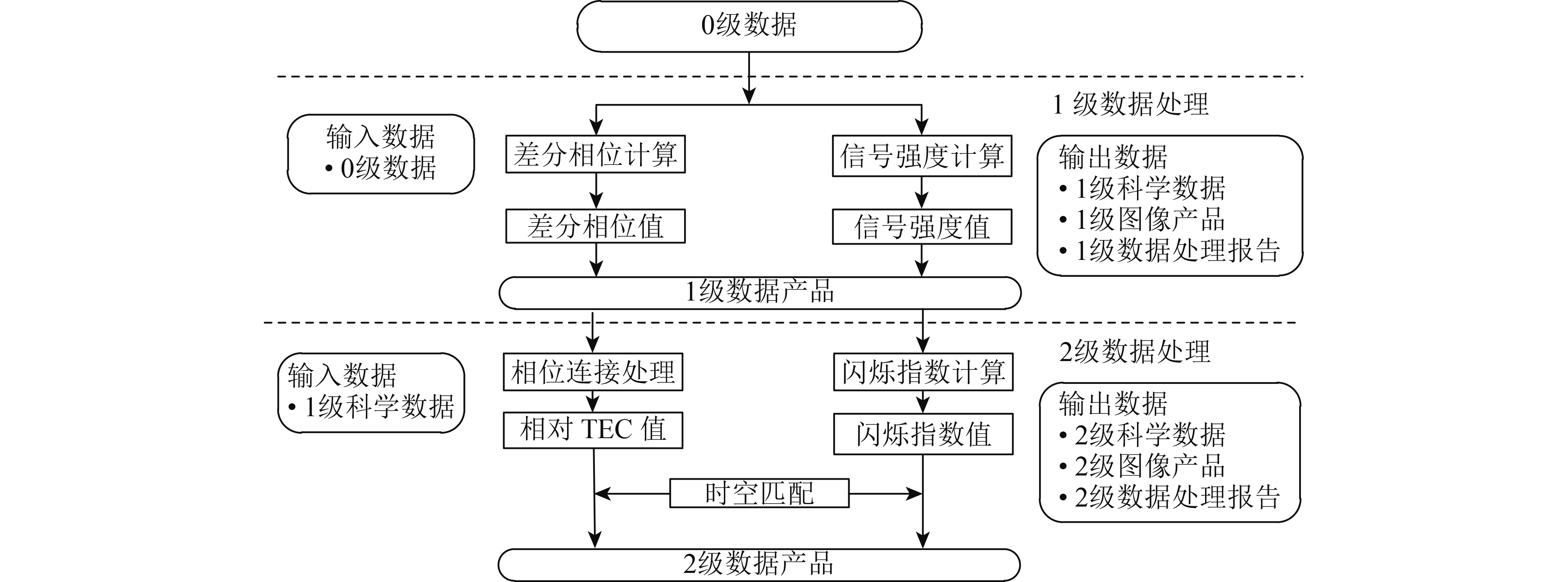
地面三频信标接收机跟踪锁定星载三频信标信号后,输出3个频段信号的两路正交分量(I和Q)的观测数据和信噪比数据,即0级数据。对0级数据3个频段的相位进行差分计算,可计算得到VHF和UHF、UHF和L的差分相位值,得到1级数据。对计算得到的差分相位值进行相位连接处理,每秒计算出一组相对电离层总电子含量TEC值。同时对根据信号强度值进行闪烁指数计算,每1秒计算出一组闪烁指数,得到2级数据。最后通过对多个台站的观测数据进行集中处理,利用多站法,每秒钟计算一个电离层绝对TEC数据,再利用层析成像算法对单个链路进程反演得到二维电子密度剖面数据,得到3级数据。其具体数据处理流程见图11。
|
| 图 11 三频信标接收机1—2级数据处理流程 Figure 11 Level 1 and level 2 data processing procedure of tri-band-beacon |
在三频信标1—2级数据处理中,关键算法是相对TEC的计算,具体的步骤包括差分相位计算、相位翻转个数计算、相位连接处理、计算最小相位值计算以及相对TEC值计算等。
(1) 差分相位计算。对于观测到的n个点的相位数据,按照式(28)所示对相位数据进行差分计算。
| $\Delta (t) = \varPhi (t + 1) - \varPhi (t),\;\;t = 1,2,\cdots,n - 1$ | (28) |
(2) 相位翻转个数计算。将各数据点的
| $k = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {k - 1}& {\Delta > D} \end{array} \\ \begin{array}{*{20}{c}} {k + 1}&{\Delta < - D} \end{array} \\ \begin{array}{*{20}{c}} k& \quad \,\,\, {\left| \Delta \right| \leqslant D} \end{array} \\ \end{array} \right.$ | (29) |
(3) 相位连接处理。依次对各数据点的差分相位序列进行相位连接。
| $\varPhi _{\rm{c}}'(t) = \varPhi (t) + 2k{\text{π}}$ | (30) |
(4) 计算最小相位值。在连接完成后,按式(31)和(32)计算相位序列中的最小相位值Z和多普勒相位序列。
| $Z = \min (\varPhi _{\rm{c}}'(t))$ | (31) |
| ${\varPhi _{\rm{c}}}(t) = \varPhi _{\rm{c}}'(t) - Z$ | (32) |
式中,
(5)计算相关系数CD
| ${C_{\rm{D}}} = \frac{{c{f_{\rm{r}}}}}{{2{\text{π}} \times 40.31}} \times \frac{{m_1^2m_2^2}}{{m_2^2 - m_1^2}}$ | (33) |
按照式(33)计算相关系数CD。其中,c=299792458 m/s,fr=16.668 MHz,mi表示倍频数,如果取VHF/UHF组合,则取m1=9,m2=24;如果取UHF/L组合,则取m1=24,m2=64。
(6) 计算相对TEC值。按照式(34)可计算得到电离层相对TEC值。TEC值的单位为TECU(1TECU=1016 el·m–2)。
| ${\rm{TE}}{{\rm{C}}_{\rm{r}}} = {C_{\rm{D}}} \times {\varPhi _{\rm{c}}}(t)$ | (34) |
高能粒子探测器的数据产出为高能带电粒子种类、能量以及入射方向。主要能量范围为高能段电子(2—50 MeV)、质子(15—200 MeV),低能段电子(0.1—3 MeV)、质子(2—20 MeV)及太阳X射线(1—20 keV),并实现带电粒子投掷角度的测量。高能粒子探测器(HEPP)的0—2级数据产品见表8。
|
|
表 8 高能粒子探测器0—2级数据产品 Table 8 Level 0—2 data products of high energy particle package |
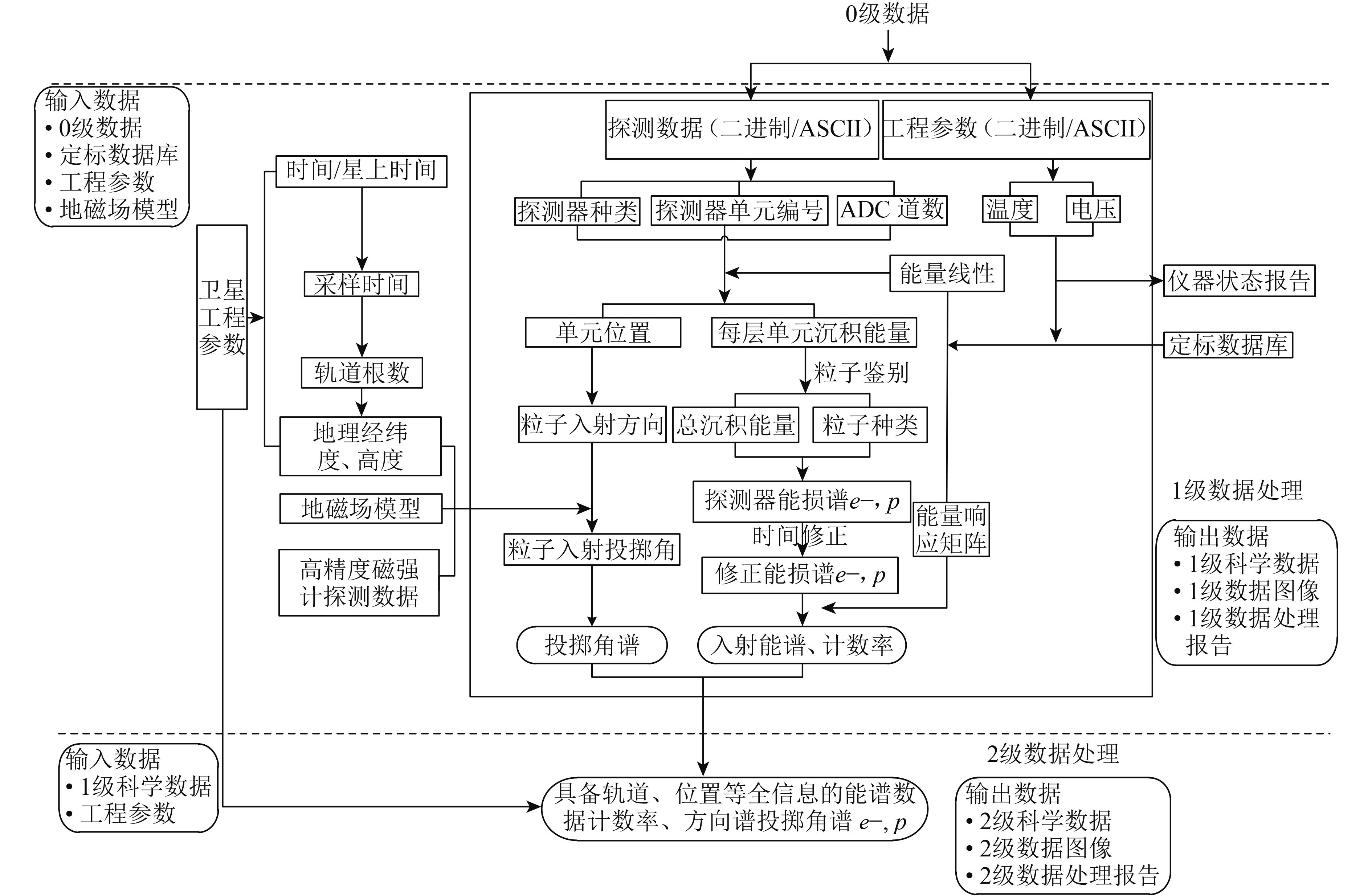
高能粒子探测器的0级数据首先通过十进制转换,然后根据定标参数进行粒子种类鉴别、能谱重建、能谱反演以及投掷角反演等,得到中间结果和最终的物理量,从而生成1级标准数据。从星务数据包中获取星下点位置等信息,通过电磁场模型(或者高精度磁强计)得到磁场数据,获取地震记录、空间天气指数等辅助信息,对应叠加至1级数据,生成2级标准数据。具体的流程图见图12。
|
| 图 12 高能粒子1—2级数据处理流程 Figure 12 Level 1 and level 2 data processing procedure of high energy particle package |
在高能粒子1—2级数据处理流程中,需要经过粒子种类初步鉴别、能谱重建、死时间修正、能谱反演和入射角判定得到1级高能粒子数据,其关键的算法是能谱重建和粒子入射角判定。
能谱重建能谱重建的流程见图12,具体实现过程如下:
(1) 数据读取。对于每个事例按高能单事例表格顺序读取5个反符合、2个DSSD、5个量能器的二进制数据,分别换算成十进制数据;如果反符合的读数为1,此数据是不可使用的;
(2) 粒子种类初步鉴别。通过读取探测器的双层能道值,根据质子和电子在两层探测器中的能量沉积情况不同,初步判定入射的粒子种类是电子还是质子。
(3) 能量反演。按照粒子种类的判定结果,利用能量线性标定数据,对应每个探测器的能量重建为Energy_i=A·CHN_i+B,A为斜率,B为截距,CHN_i 表示每个探测器的ADC道数,i=1,2,
(4) 能谱重建。将各探测单元各个探测能谱对应的计数率累积计算出来,得到总的计数;根据粒子种类按秒累积分别得到电子和质子的探测能谱。
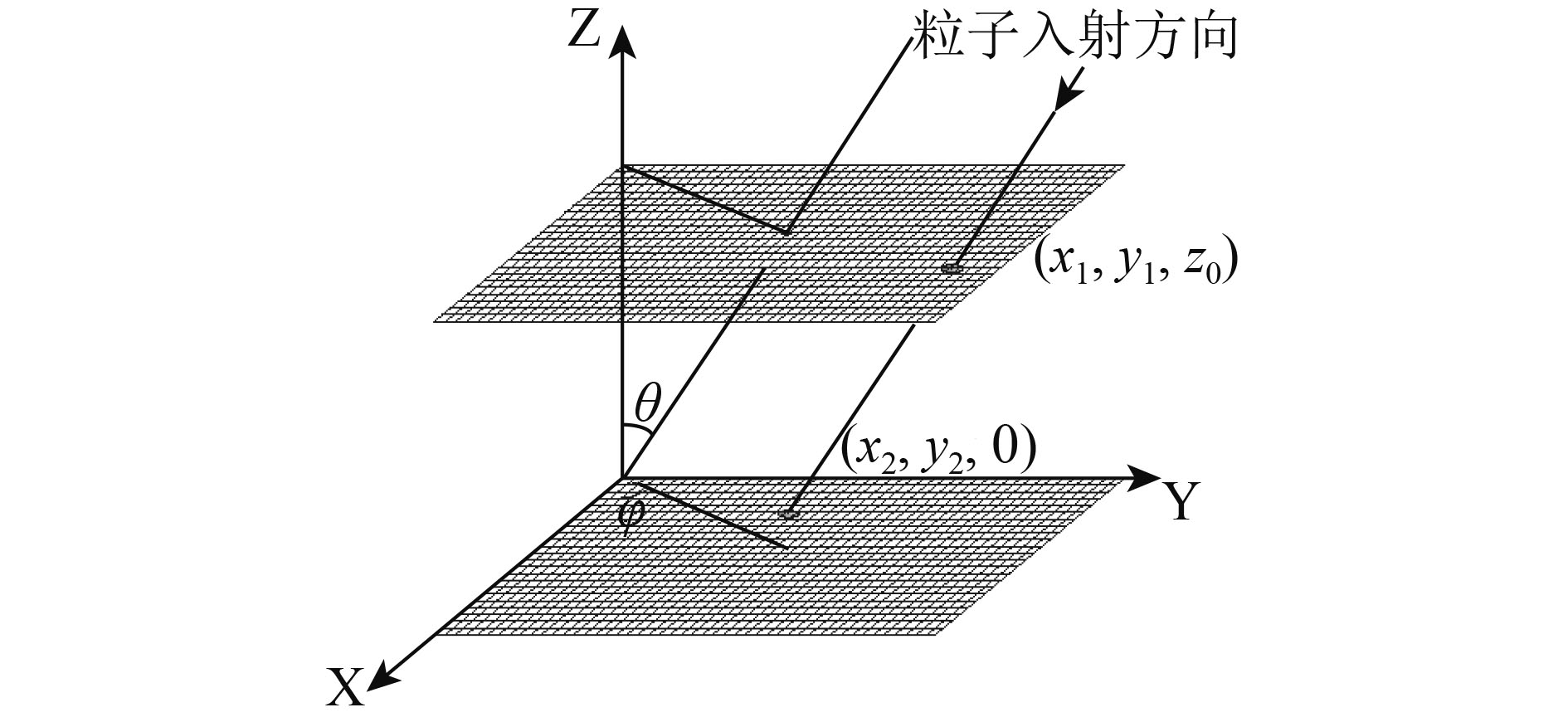
粒子入射角判定在探测器坐标系当中,假设两层探测器之间的间距为z0,粒子击中上下两层的坐标位置分别为(x1, y1)和(x2, y2),坐标值根据探测器所记录的探测单元位置计算得到,如图13所示。
|
| 图 13 粒子击中探测器前两层硅条探测器方向重建示意图 Figure 13 Schematic diagram of direction reconstruction when particle hit first two layer silicon strip detector |
则入射粒子相对与探测器指向的极角θ、方位角φ为
| $\left\{ \begin{array}{l}\theta = arctg\displaystyle\frac{{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} }}{{{z_0}}}\\\varphi = arctg\left( {\displaystyle\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)\end{array} \right.$ | (35) |
根据此计算结果,可以通过与通用坐标系之间的坐标变换计算得到入射粒子方向的天顶角和方位角。
5、结 论电磁监测试验卫星是中国地震立体观测体系第一个天基平台,也是中国地球物理场探测卫星计划首发星,相应的数据处理方法也是近十年来随着中国电磁监测试验卫星工程的研制发展起来的。在数据处理方法研究方面中国地震局电磁卫星团队利用法国DEMETER卫星的观测数据,在前期开展了多方面的研究工作,包括其数据从原始观测数据到物理量观测数据的处理,并取得了很多的成果(Berthelier 等,2006;Sauvaud 等,2006;Parrot 等,2006;Lebreton 等,2006;Santolík 等,2006),这些成果对于电磁卫星数据的处理工作奠定了很好的基础。目前电磁卫星的8种科学载荷的数据处理方法和流程的方案设计已经完成,并已应用到电磁监测试验卫星应用系统的相关工作中,这是电磁监测试验卫星观测数据能够用好、好用的关键。
事实上,对于电磁卫星观测数据处理,特别是电磁场观测数据的处理,无论是国际还是国内迄今为止还没有完整、确定的理论和方法,随着数据的积累和研究的深入,会有更完善、更好的数据处理方法。本文介绍的电磁监测试验卫星的数据处理方法,也仅是针对该卫星观测的特点,提出了初步的数据分析、处理方法,随着后期观测数据的不断积累,以及在观测机理、观测模型、数据应用等方面研究的不断深入,必将对这些方法进行更进一步的完善和优化,进一步提升卫星观测数据分析、处理水平以及在地震科学中的研究水平。
志 谢 感谢中国地震局电磁卫星团队以及航天科技集团东方红卫星有限公司、510所、503所,中国科学院空间技术应用研究中心、中国科学院高能物理研究所,北京航空航天大学、中国电子科技电集团第22研究所相关人员在数据处理方法和流程研究中给予的大力支持和帮助。
| [1] | Berthelier J J, Godefroy M, Leblanc F, Malingre M, Menvielle M, Lagoutte D, Brochot J Y, Colin F, Elie F, Legendre C, Zamora P, Benoist D, Chapuis Y, Artru J and Pfaff R. ICE, the electric field experiment on DEMETER[J]. Planetary and Space Science, 2006, 54 (5) : 456 –471. DOI: 10.1016/j.pss.2005.10.016 |
| [2] | Chen F F and Chang J P. 2002. Lecture Notes on Principles of Plasma Processing. New York: Plenum/Kluwer Publishers |
| [3] | Gokhberg M B, Morgounov V A, Yoshino T and Tomizawa I. Experimental measurement of electromagnetic emissions possibly related to earthquakes in Japan[J]. Journal of Geophysical Research: Solid Earth, 1982, 87 (B9) : 7824 –7828. DOI: 10.1029/JB087iB09p07824 |
| [4] | Hayakawa M, Kawate R, Molchanov O and Yumoto K. Results of ultra-low-frequency magnetic field measurements during the Guam earthquake of 8 August 1993[J]. Geophysical Research Letters, 1996, 23 (3) : 241 –244. DOI: 10.1029/95GL02863 |
| [5] | Lebreton J P, Stverak S, Travnicek P, Maksimovic M, Klinge D, Merikallio S, Lagoutte D, Poirier B, Blelly P L, Kozacek Z and Salaquarda M. The ISL Langmuir probe experiment processing onboard DEMETER: scientific objectives, description and first results[J]. Planetary and Space Science, 2006, 54 (5) : 472 –486. DOI: 10.1016/j.pss.2005.10.017 |
| [6] | Liu J Y, Chuo Y J, Shan S J, Tsai Y B, Chen Y I, Pulinets S A and Yu S B. Pre-earthquake ionospheric anomalies registered by continuous GPS TEC measurements[J]. Annales Geophysicae, 2004, 22 (5) : 1585 –1593. DOI: 10.5194/angeo-22-1585-2004 |
| [7] | Parrot M. Statistical study of ELF/VLF emissions recorded by a low-altitude satellite during seismic events[J]. Journal of Geophysical Research: Space Physics, 1994, 99 (A12) : 23339 –23347. DOI: 10.1029/94JA02072 |
| [8] | Parrot M, Benoist D, Berthelier J J, Błęcki J, Chapuis Y, Colin F, Elie F, Fergeau P, Lagoutte D, Lefeuvre F, Legendre C, Lévêque M, Pinçon J L, Poirier B, Seran H C and Zamora P. The magnetic field experiment IMSC and its data processing onboard DEMETER: scientific objectives, description and first results[J]. Planetary and Space Science, 2006a, 54 (5) : 441 –455. DOI: 10.1016/j.pss.2005.10.015 |
| [9] | Parrot M, Berthelier J J, Lebreton J P, Sauvaud J A, Santolik O and Blecki J. Examples of unusual ionospheric observations made by the DEMETER satellite over seismic regions[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2006b, 31 (4/9) : 486 –495. DOI: 10.1016/j.pce.2006.02.011 |
| [10] | Pulinets S and Boyarchuk K. 2004. Ionospheric Precursors of Earthquakes. Berlin Heidelberg: Spring [DOI: 10.1007/6137616] |
| [11] | Santolík O, Němec F, Parrot M, Lagoutte D, Madrias L and Berthelier J J. Analysis methods for multi-component wave measurements on board the DEMETER spacecraft[J]. Planetary and Space Science, 2006, 54 (5) : 512 –527. DOI: 10.1016/j.pss.2005.10.020 |
| [12] | Sauvaud J A, Moreau T, Maggiolo R, Treilhou J P, Jacquey C, Cros A, Coutelier J, Rouzaud J, Penou E and Gangloff M. High-energy electron detection onboard DEMETER: the IDP spectrometer, description and first results on the inner belt[J]. Planetary and Space Science, 2006, 54 (5) : 502 –511. DOI: 10.1016/j.pss.2005.10.019 |
| [13] | 王兰炜, 申旭辉, 张宇, 张兴国, 胡哲, 颜蕊, 袁仕耿, 朱兴鸿. 中国电磁监测试验卫星工程研制进展[J]. 地震学报, 2016, 38 (3) : 376 –385. Wang L W, Shen X H, Zhang Y, Zhang X G, Hu Z, Yan R, Yuan S G and Zhu X H. Developing progress of China Seismo-Electromagnetic Satellite project[J]. Acta Seismologica Sinica, 2016, 38 (3) : 376 –385. DOI: 10.11939/jass.2016.03.005 |
| [14] | 朱涛, 王兰炜. DEMETER卫星观测到的与汶川地震有关的LF电场异常[J]. 地球物理学报, 2011, 54 (3) : 717 –727. Zhu T and Wang L W. LF electric field anomalies related to Wenchuan earthquake observed by DEMETER satellite[J]. Chinese Journal of Geophysics, 2011, 54 (3) : 717 –727. DOI: 10.3969/j.issn.0001-5733.2011.03.011 |
| [15] | Zlotnicki J, Li F and Parrot M. Signals recorded by DEMETER satellite over active volcanoes during the period 2004 August–2007 December[J]. Geophysical Journal International, 2010, 183 (3) : 1332 –1347. DOI: 10.1111/j.1365-246X.2010.04785.x |

