常规遥感传感器通过测量植被冠层反射或散射的入射辐射来量化植被的光学特性，其由于非接触、大面积等特点，被广泛应用于植被监测、辐射收支和全球气候变化等研究中。随着卫星传感器分辨率的提高与地面测量、模型构建等同步技术的进步，对于植被更高精度监测与组分反演的需求与日俱增。

Ollinger和Knyazikhin两位科学家团队自2008年起在美国科学院院刊PNAS(Proceedings of the National Academy of Sciences of the United States of America)上对于利用植被反射光谱进行氮含量反演的争论引起广泛关注。Ollinger等人(2008，2013)提出植被在近红外的反射率与氮含量之间存在正相关关系，Townsend等人(2013)指出该正相关关系并不包含氮含量的信息，而是由冠层结构与叶片光学特征造成，并提出需要偏振手段研究冠层结构与表面反射(Knyazikhin 等，2013a, 2013b, 2013c)。以Ollinger为代表的研究团队从宏观的生态学角度出发，将植被看作一个对入射辐射直接反射的整体；而Knyazikhin团队从遥感光学角度出发考虑了植被的立体特性，即光子在植被中微小的反射、透射、折射等特征，这与前者存在本质上的区别。这些特征会体现在植被的偏振反射特性上，因此偏振探测手段有利于从冠层角度更精细地刻画植被反射的光学特征，从而为甄别PNAS上引出的争议提供手段。偏振效应在植被冠层结构与高分辨率定量遥感反演中的重要性日渐凸显，对植被偏振特性的研究也成为丰富植被遥感体系的基础性工作。

目前，国内外利用偏振手段进行的遥感反演研究主要集中于大气方面，实现了气溶胶和多种云光学参数的遥感反演(Guo 等，2014；Dubovik 等，2011；Sano，2004)。利用偏振信息进行参数反演的研究较少，主要存在于实验室条件或利用卫星影像进行大区域研究。例如以单叶片偏振BRDF模型模拟其偏振反射特性，并利用实测值有效反演叶片漫反射率和表面粗糙度等结构参数(Xie 等，2010)；利用POLDER卫星数据结合偏振信息和辐射强度信息构建模型，可以同时反演大区域大气气溶胶和地表反射率的区域分布(Duan和Lü，2008)。对于植被的偏振遥感研究则多集中于其偏振反射特性与对叶片和冠层结构的模拟和经验、物理模型的构建方面。较早期的植被偏振测量和物理特性分析(Egan，1970；Curran, 1981, 1982；Fitch 等，1984)以及后来分别对叶片和植被冠层的偏振信息提取(Grant 等，1993；Vanderbilt 等，1985；Woessner和Hapke，1987)集中地得出了一些一致性结论，即植被的散射特性由辐射在植被结构中的多次散射造成，叶表的镜面反射是导致反射光具有偏振态的直接原因(Grant，1987；Grant 等，1987)，并且偏振特性会随入射观测几何的改变而改变(Rondeaux和Herman，1991；Vanderbilt and Grant, 1985；Yang 等，2016)。这些结论为光在叶片和植被内部的传输、散射和偏振特性研究提供了理论基础，利用菲涅尔反射折射定律所构建的诸多模型也广泛地用来模拟计算植被的偏振二向反射值(Rondeaux和Herman，1991；Waquet 等，2009；Nadal和Breon，1999；Maignan 等，2009；Xie 等，2017)，与实验室和野外测量的多种植被类型偏振反射实测值相比较均产生了相近的结果(Sun 等，2016)。随着仪器和测量手段的发展，更高精度、更高的角度和光谱分辨率的实测数据和现存模型的验证和改进工作越来越多(Suomalainen 等，2009b；Wu和Zhao，2005；Puttonen 等，2009)，从而扩展了利用偏振信息进行植被遥感研究的应用范围，并不断证明了其巨大潜能。此外，利用偏振信息还可以对岩石、水体、雪等地表典型地物开展多种研究(Zhao 等，2004；Shen 等，2016；Suomalainen 等，2009a；Peltoniemi 等，1994)。

多种偏振反射率二向分布模型精细刻画了光在植被冠层中的辐射传输过程。从理论上来说，冠层反射的偏振特性主要由冠层结构决定(Myneni和Ross，1991)，即叶片在冠层内部的分布对光子—冠层作用的影响及冠层内的叶倾角状况。Vanderbilt和Grant(1985)提出了一种模型，利用叶面积指数LAI(Leaf Area Index)，叶倾角分布函数LIDF(Leaf Inclination Distribution Function)，粗糙度因子和逃逸概率来描述植被在2π空间内的偏振反射分布，并指出偏振信息有助于区分树种。之后，Rondeaux和Herman(1991)基于均匀冠层提出了一个更简单的偏振反射率模型。基于Rondeaux-Herman模型，Breon等人(1995)推导了裸土和植被的偏振反射模型。随着POLDER数据的获取，Nadal和Breon(1999)建立了地表双参数经验双向偏振分布模型。一些研究考虑阴影效应，提出了具有阴影函数的偏振反射率模型(Waquet 等，2009；Litvinov 等，2011)。Maignan等人(2009)还引入了结合归一化差分植被指数(NDVI)和地表偏振的单参数模型。基于以上研究成果，Xie等人(2017)提出了城市地区的偏振反射率模型，取得了较高精度结果，这个模型对于植被也具有适用性。实际上，Rondeaux-Herman模型之后的大多数模型均基于叶片球形分布的假设构建，并没有严格考虑不同叶倾角分布函数的影响。

基于上述研究，本文从理论推导出发，介绍光子—叶片—冠层的相互作用，即植被的叶片光学特征与冠层立体结构，分析其对于植被偏振光效应的影响，以期甄别PNAS上关于植株氮含量反演的争议，并在Rondeaux-Herman模型的基础上，通过引入不同叶倾角分布来研究叶倾角对植被偏振光效应的影响，以完善偏振反射模型，实现植被叶倾角分布的反演，并探索由叶倾角产生的多角度偏振信息的更多应用价值。

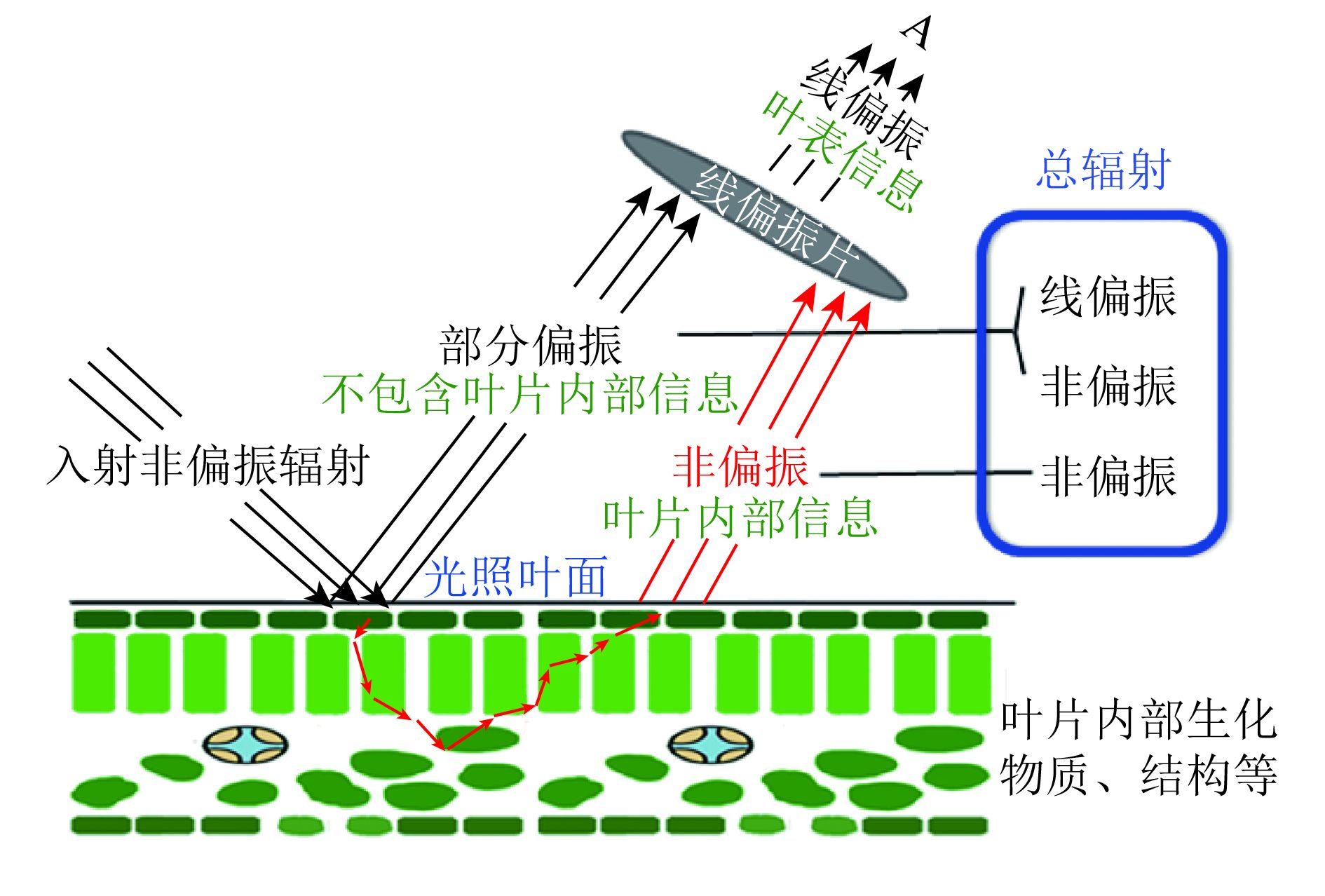
植被反射辐射具有偏振特性的本质原因是光子—叶片的单次散射，多次散射具有褪偏作用而在探测到的偏振反射率中忽略不计。光子—叶片的单次散射可描述如下：被叶片散射的入射辐射包括两部分，第1部分是在空气和叶面分界处发生镜面反射，这部分反射辐射没有进入叶片内部，是部分偏振的(Grant 等，1993)。第2部分进入叶片，与叶片内部的生化物质相互作用后被传感器接收，这部分通常是非偏振的(图1)。基于强度的常规遥感可以探测到这两部分的总和，但不能对二者进行有效区分(Vanderbilt和Grant，1985)。利用偏振探测能够提取其中的线偏振部分，实现二者有效区分。

图 1 传感器接收到的来自叶片的两部分辐射 Figure 1 Two-part radiation from the leaf received by the sensor

由图1(Yang 等，2016)，可以假设叶表的散射反照率为 $\omega $ ，入射辐射在叶表直接被反射的概率为 ${r_{\rm{s}}}$ ，在叶片内部向上散射的概率为 $\beta $ ，向下散射的概率为 $\tau $ 。根据菲涅尔原理，可以知道在叶表直接被反射的辐射是部分偏振的，也就是说 ${r_{\rm{s}}}$ 可以进一步分解为

式中， ${r_{{\rm{sp}}}}$ 代表线偏振部分，而 ${\rm{r\_snp}}$ 代表非偏振部分。

进入到叶片内部，与其相互作用后，辐射被向上散射的总概率为

则辐射被吸收的概率 ${a_{\rm{i}}}$ 以及向下透射的概率 ${t_{\rm{i}}}$ 为

传感器接收到的辐射与叶表及内部相互作用后的总能量则可以简单表述为

则传感器探测到的偏振度p为

而一般情况下， ${r_{{\rm{sp}}}}$ 可以认为是常量，即是与波长无关的量。当叶片的反射率较低时，即 $\omega \beta $ 表现为较小值，从视觉效果来看，目标会显得很暗，则偏振度 $p$ 表现为较大值，则实现了“弱光强化”的过程；反之，当地表的反射率较大时，即 $\omega \beta $ 表现为较大值，从视觉效果来看，目标会显得很亮，则偏振度 $p$ 表现为较小值，则实现了“强光弱化”的过程。这是偏振光能够敏感植被冠层立体结构精细的透射反射再出射的物理基础，也是偏振具有“强光弱化，弱光强化”的光学遥感特性的通用物理表征。

上述光子—叶片的单次散射造成的偏振特性在叶片尺度可较为明显的探测与分辨。而在冠层尺度，这种直接探测得到的偏振特性与冠层结构是相互耦合的。

在可见光—近红外范围内，尽管冠层的吸收过程与波长相关，但是光子与冠层相互作用的概率却是仅仅由冠层结构决定，与波长无关，称之为光谱不变量理论(Knyazikhin 等，1998)。利用光谱不变量理论可以精确描述冠层结构及光子与冠层的相互作用。

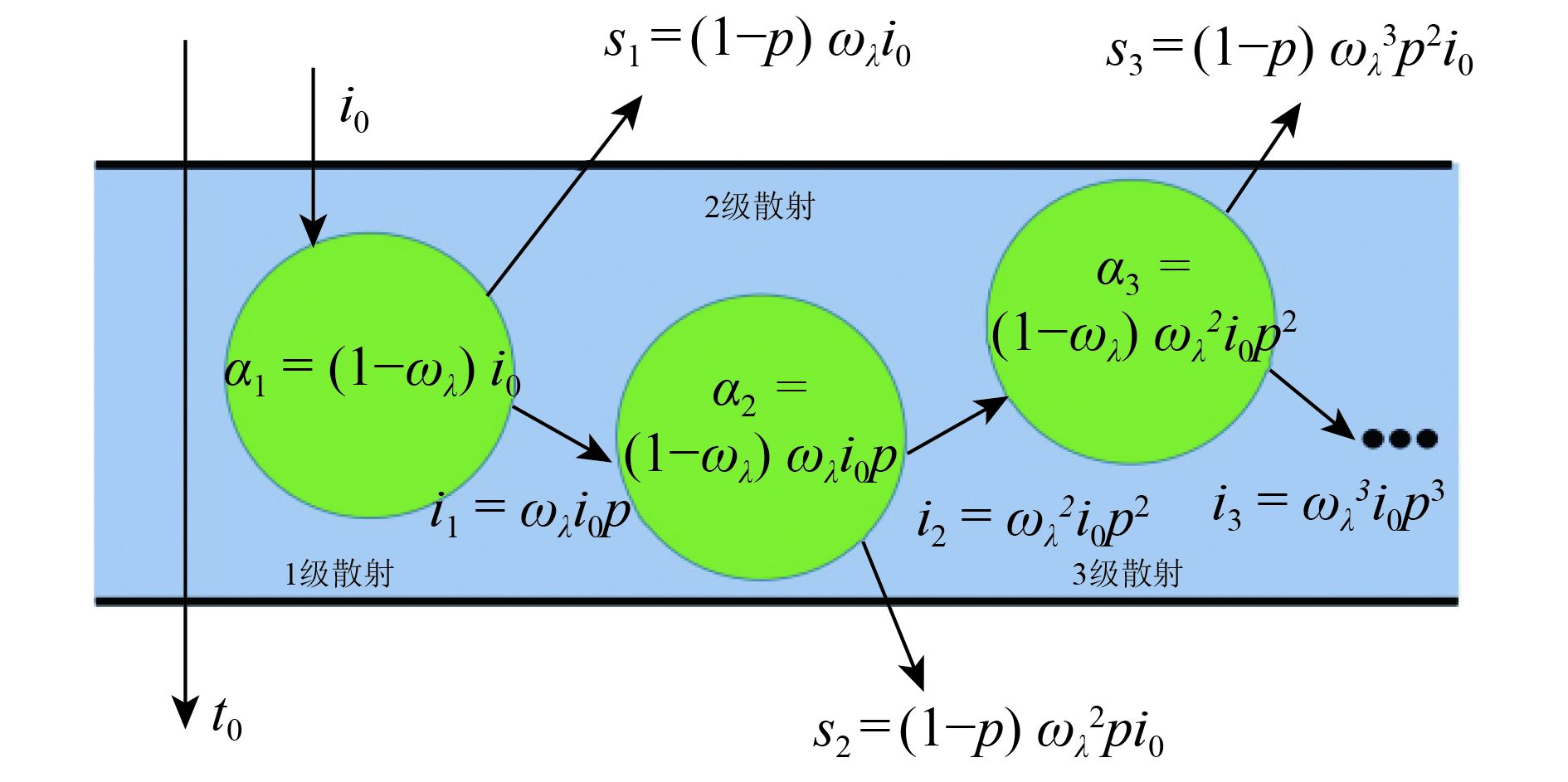
如图2，假设冠层底部为不反射任何辐射的黑体，辐射入射到冠层后，被冠层截获的概率为截获率i₀。没有被截获的那部分辐射将直接透过冠层，到达冠层底部，这一部分的概率为透过率t₀=1–i₀。被截获的辐射与叶片第一次相互作用后，有a₁=(1–ω_λ)i₀部分辐射被吸收，其中ω_λ为叶片单次散射反照率。光子与冠层内部的散射体相互作用后再次与其他散射体相互作用的概率定义为再碰撞概率p，则有i₁=ω_λi₀p部分辐射会与冠层内部的其他叶片相互作用，另外有s₁=(1–p)ωi₀的辐射会被散射出冠层。i₁部分会激发与叶片的第二次相互作用，分解为吸收、散射出冠层和继续与其他叶片相互作用3部分，以此类推，发生多次散射。从辐射多次散射后的分布可以发现，每次散射的吸收和逃逸能量呈现等比数列关系。

假设冠层底部是不反射辐射的黑体，且再碰撞概率在各散射级数保持不变，则冠层与辐射相互作用的吸收a( $ \lambda$ )和散射s( $\lambda$ )分别为

图 2 光子在冠层内的多次散射与多次吸收 Figure 2 Multiple scattering and multiple absorption of photons in the canopy

若将逃逸概率(1–p)分解到空间各个方向，并用ρ表示(即ρ( $ \varOmega $ )表示光子与叶片碰撞后从方向 $ \varOmega $ 逃逸出冠层的概率)，则可以得到如图2所示的光子多次散射与逃逸关系，基于此可以获得冠层双向反射率因子BRF(Bidirectional Reflectance Factor)

这样，冠层的散射和吸收以及光子逃逸关系可以通过光谱不变量精确描述，利用光谱不变量理论构建结构参数并进行冠层结构—叶片光学特性解耦至关重要。利用光谱不变量理论可以建立起方向散射面积因子DASF和散射系数W $ _\lambda$ 的概念(Knyazikhin 等，2013c)。DASF是冠层沿某方向的可视叶面积比例，是一个光谱不变量。对于浓密植被，DASF可直接通过710—790 nm的反射率获得，并在此基础上获得冠层的光学因子，即散射系数W $ _\lambda$ 。W $_\lambda$ 可由BRF通过与DASF的比值直接获得，相比于BRF，散射系数与叶片内部的信息(叶绿素含量、化学成分等)更相关，因而使得从遥感高精度反演叶片内部信息成为可能。

由上述分析可以看出，遥感传感器观测到的BRF同时受叶片表面反射与冠层结构影响，这两种影响是紧密耦合的。冠层的立体结构使得植被在各角度上的BRF出现不同值，而引入冠层结构的考虑是为了描述光子在冠层内部的二次碰撞与逃逸过程。考虑这些因素计算得到的散射系数(即上述散射系数的计算过程)可以帮助恢复各个观测角度下植被冠层的反射率光谱，使其归化到同一值上。因此冠层结构的解耦为研究植被的多角度(尤其是大角度)偏振特性提供了必要条件，而偏振特性的精细研究也为实现传感器大角度观测、给出精确解算结果提供了可能。

针对引言中提到的争议，一方面从植物冠层出发(Yang 等，2017a)刻画反射特征，另一方面从2009年开始进行大量地面和实验室试验，于2016年在对针叶叶簇样本的研究中发现，植被冠层与叶片表面反射(部分偏振)特性对探测到的叶簇反射率均会产生误差，而只有偏振探测能够敏感出上述作用带来的微弱光线变化导致的误差；在40°天顶角进行观测时，若不考虑此误差，则测算得到的叶簇样本的散射系数在蓝光波段可产生140%的误差(Yang 等，2016)。现阶段，遥感对地观测对于多角度(尤其是大倾角)、多时相观测需求巨大，越来越多的观测平台上开始搭载多角度传感器，因此偏振效应在多角度观测上带来的误差不可忽略。由此看出，考虑光子在冠层内多次碰撞与逃逸的细微过程进行冠层结构的解耦，使得表面反射对植被光谱的影响占据了主导地位，而利用偏振手段可敏感出表面反射产生的变化，从而将表面反射与内部散射部分有效分离，实现对遥感反演参量的精确刻画。

光子—叶片与光子—冠层的相互作用效应最直观地体现在偏振反射率上。偏振反射率二向分布模型BPDF(Bidirectional Polarized Reflectance Distribution Function)描述了理想情况下经地物反射后的偏振辐射在2π空间中的分布，目前已存在包括物理模型和半物理—半经验模型在内的十余种BPDF模型，这些模型起初均以植被中光子—叶片—冠层的相互作用为物理基础进行构建，并将其应用于其他地物分析。作者基于偏振传感器POLDER的全球尺度地表偏振反射率数据，针对5种IGBP分类地物，对6种常用模型进行了拟合精度对比(Yang 等，2017b)，表1归纳了整体结果。显然，6种模型的精度均处于较高水平(Cor普遍大于0.86，RMSE普遍小于0.3%)，且其中模型对植被(表1中第一、二列)的拟合精度最高。这说明，现存的BPDF模型由光子—叶片—冠层的相互作用精确刻画，这种相互作用可以作为植被遥感定量化的依据，为植被辐射传输过程以及高分辨率定量反演提供理论基础。

表 1(Table 1)

表 1 6种BPDF模型拟合结果比较 Table 1 Comparison of six BPDF model results 模型 参数 IGBP 混合森林 IGBP 农田 IGBP 建成区 IGBP 冰雹 IGBP 稀疏植被 Nadal-Breon RMSE/% 0.168 0.147 0.231 0.367 0.106 Cor 0.922 0.955 0.934 0.948 0.987 Waquet RMSE/% 0.209 0.213 0.253 0.461 0.154 Cor 0.886 0.917 0.920 0.925 0.974 Maignan RMSE/% 0.175 0.156 0.269 0.423 0.130 Cor 0.915 0.949 0.910 0.934 0.981 Litvinov RMSE/% 0.155 0.150 0.201 0.408 0.109 Cor 0.934 0.953 0.950 0.936 0.986 Diner RMSE/% 0.233 0.277 0.342 0.666 0.296 Cor 0.871 0.881 0.863 0.863 0.918 Xie-Cheng RMSE/% 0.174 0.155 0.227 0.386 0.104 Cor 0.916 0.950 0.935 0.942 0.987 　注：RMSE为均方根误差，Cor为模型值与实测值的拟合相关系数。

表 1 6种BPDF模型拟合结果比较 Table 1 Comparison of six BPDF model results

由上述分析可知，光子与叶片和冠层的相互作用是产生植被偏振光效应的本质原因。偏振具有角度敏感特征，因而对植被叶倾角分布可以实现精密计量，因此相对于传统光学遥感，偏振对叶倾角具备更有效的探测能力。因此基于上节偏振对叶片光学特性与冠层结构的精密探测模型，本节将采用偏振手段进一步实现不同种类植被叶倾角的反演。

偏振传感器能够将传感器接收的辐射分为偏振部分和非偏振部分(Rondeaux和Herman，1991)，使得更精细化的对地观测成为可能。研究型扫描式偏振辐射仪RSP(Research Scanning Polarimeter)可以提供机载和地面的高精度偏振测量。RSP具有9个波段410 nm(30)，470 nm(20)，550 nm(20)，670 nm(20)，865 nm(20)，960 nm(20)，1590 nm(60)，1880 nm(90)和2250 nm(120)(Cairns 等，1999)。括号内的数字是对应波段的半峰全宽(FWHM)。RSP数据空间分辨率高，覆盖了具有不同叶倾角分布的多种植被类型，是研究植被偏振特性对叶倾角分布灵敏性的最合适的数据库之一。

本文利用2005年9月16日俄克拉荷马州实验的RSP低空数据(Knobelspiesse 等，2008)。表2展示了本文中用到的航带信息。RSP的观测天顶角(VZA)具有[–40°, 80°]大范围，由于较大VZA可能引入更多的不确定性，本文只利用[–40°, 60°]的VZA范围。θ_s, θ_v, φ_s, φ_v可以确定入射观测几何，分别代表太阳天顶角、观测天顶角、太阳方位角和观测方位角。由于RSP数据包含了大气和土壤偏振信息，为有效实现叶倾角分布对植被偏振特性研究，需要进行大气校正及浓密植被提取。

表 2(Table 2)

表 2 测量航带信息 Table 2 Measurement parameters 类别 参数 日期 2005年9月16日 获取时间，UTC 16:32:25 飞行高度(海平面)/m 511.3 (均值)，15.3 (标准差) 飞行高度(地面)/m 318 太阳—传感器几何 θs: 42.6° (均值)，0.1° (标准差) φs: 136.8° (均值)，0.3° (标准差) θv: –40°—60° φv: 91.4° (均值)，1.7° (标准差) AERONET τa(λ=670 nm) 0.04 (quite clear)

表 2 测量航带信息 Table 2 Measurement parameters

本文选取的RSP数据的获取高度为318 m，传感器获取的上行辐射数据包含了地表和大气的信息。假设传感器在距地高程为z处探测到的上行偏振反射率为 $R_{{\rm{p}}{\rm{ }}}^{{\rm{meas}}}$ ，则(Waquet 等，2009, Wang 等，2014)：

式中， $R_{\rm{p}}^{{\rm{atm}}}$ 和 $R_{\rm{p}}^{{\rm{surf}}}$ 分别代表大气偏振反射率和地表偏振反射率，φ_r代表相对方位角。T^↓(θ_s)和T^↑(θ_v)分别代表大气下行和上行透过率。偏振反射率 $R_{\rm{p}}^{{\rm{atm}}}$ 可由6SV模型精确估算(Kotchenova和Vermote，2007)。下行、上行透过率T^↓(θ_s)和T^↑(θ_v)可由Waquet(2009)提出的方法计算，地表偏振反射率 $R_{\rm{p}}^{{\rm{surf}}}$ 则可通过式(1)获得。

本文研究对象为植被地表，为有效降低土壤背景的影响，需要选取浓密植被作为研究对象。本文选用抗气溶胶植被指数(ARVI)作为浓密植被选取参数，ARVI对大气效应不敏感(Kaufman和Tanré，1992)，可以通过对其设置阈值来提取浓密植被像元。ARVI的表达式为

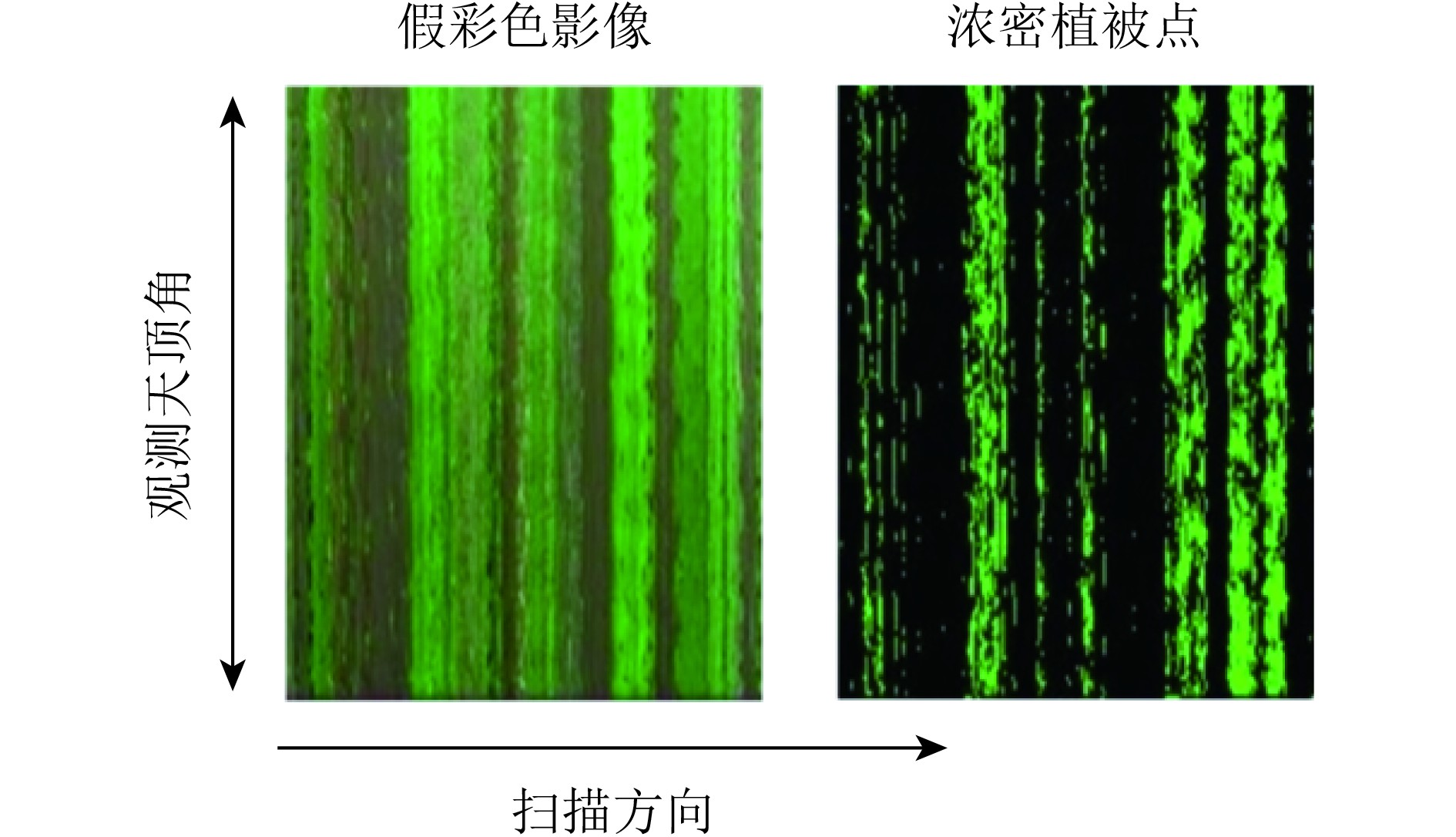
式中，R_NIR，R_red和R_blue是近红外与红、蓝波段的反射率。对于RSP，波段5(865 nm)、4(670 nm)和2(470 nm)分别被用来作为R_NIR，R_red和R_blue。γ取决于气溶胶类型，对于大陆型气溶胶，其值为0.9。在本文中，ARVI值介于0.600和0.775之间的像元被标记为候选浓密植被像元。在沿传感器扫描方向上超过50%的像元被标记为候选浓密植被像元时，该地面点被标记为浓密植被，如图3所示。其中水平轴线表示传感器扫描方向，垂直轴线表示观测天顶角方向。图3(b)中的每一个绿色点代表该方向的ARVI在[0.600, 0.775]范围内。

图 3 RSP数据的假彩色影像与筛选得到的浓密植被点 Figure 3 False color image of RSP data (R (670 nm), G (865 nm), B (470 nm)) and the selected dense vegetation

在去除了大气影响和提取浓密植被区域之后，可以获取浓密植被的偏振反射率分布。Rondeaux与Herman指出，对于单位体积内的叶面积S(z)均匀并且土壤贡献可忽略的冠层而言，其偏振反射率分布表达式为

式中，坐标系和太阳—传感器几何定义如图4。μ=cosθ(θ_i是入射天顶角，θ_r是反射天顶角)，R(ω)是菲涅尔反射系数。f(θ_n)是LIDF，G(θ)是G函数(Ross，1981)。

图 4 坐标系与太阳—传感器几何定义 Figure 4 The coordinate system and sun—sensor geometry definition

LIDF比较复杂，不容易精确估算。Goel和Strebel(1984)提出了双参数Beta分布模型来描述叶倾角分布。然而Beta分布需要叶倾角的平均值和方差，不易估算。Rondeaux和Herman(1991)则采用高斯函数替代之，但是这种估算方法精度低。在本文中，采用SAIL模型的“图形法”(Verhoef和Bunnik, 1981, Zhao 等，2010)确定两个参数去描述冠层结构，运用的两个参数为a和b，其中a控制平均叶倾角，b反映分布形状。a与b之间满足：

平均叶倾角 $\overline {{\theta _n}} $ 为

通过设置叶倾角分布函数中的参数，即可实现不同叶倾角分布情况下的植被偏振反射率模拟，在已知偏振反射率的情况下，也可通过数据拟合，实现叶倾角分布函数的反演。本节在分析RSP数据的基础上，进一步探讨不同叶倾角情况下的植被偏振反射率分布及叶倾角反演，将在3.2节中具体讨论。

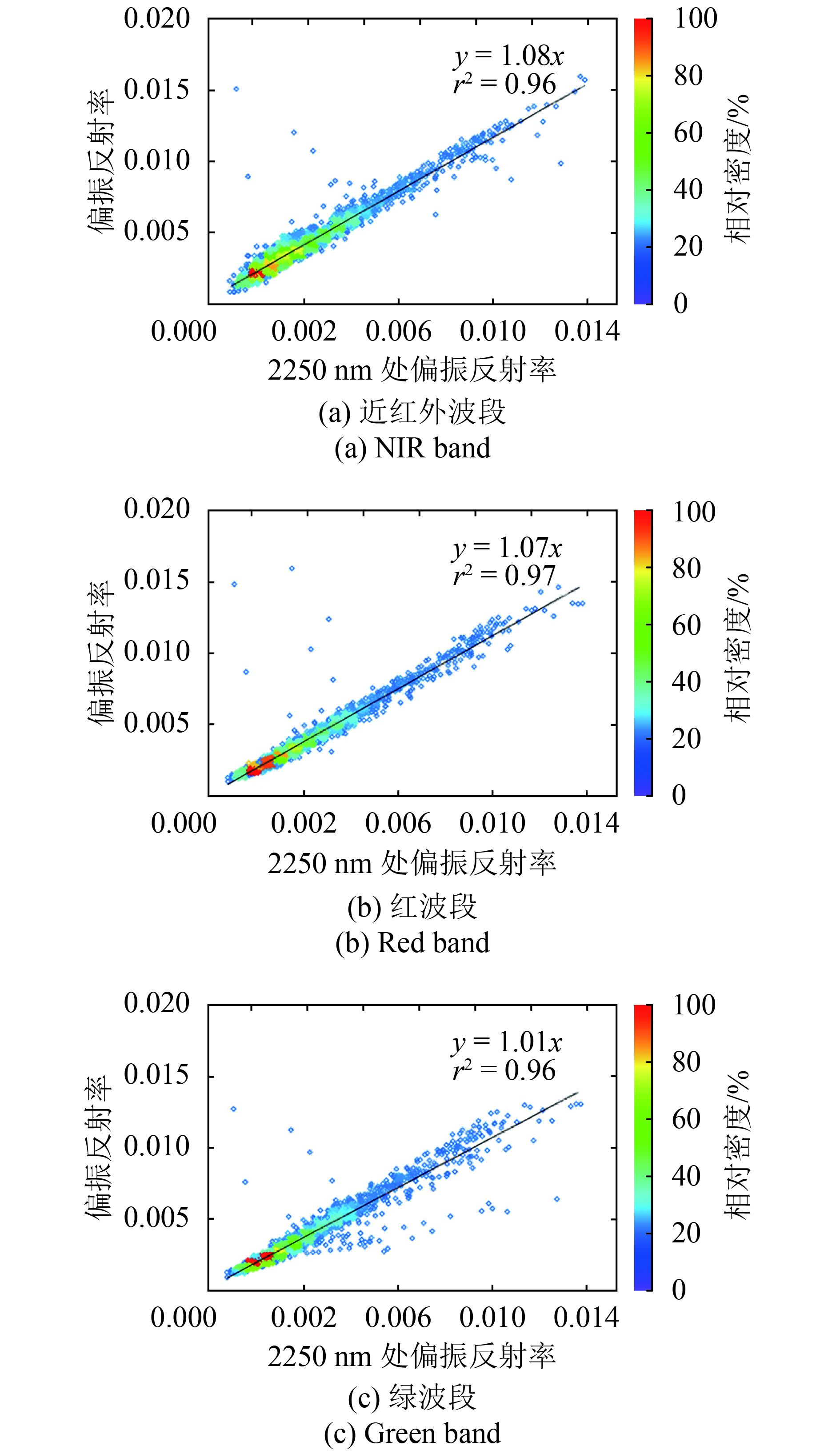
将NIR(865 nm)，红(670 nm)和绿(555 nm)波段与2250 nm的偏振反射率对比分析(图5和表3)，可以发现不同波长偏振反射率之间高度相关，决定系数很接近于1.0，截距很小(在10^–4量级)。对于给定的冠层结构和入射观测几何，折射率在 (400 nm，2500 nm)波段范围内有略微降低(Jacquemoud和Baret，1990)，说明偏振特性和波长之间仅有微弱相关性。另外，由于大气校正在555 nm的不确定性大于865 nm和670 nm，斜率随着波长的减小而略微减小。

图 5 浓密植被在NIR(865 nm)，红(670 nm)和绿(555 nm)波段的偏振反射率分别与2250 nm偏振反射率相关性分析 Figure 5 Surface polarimetric reflectances over dense vegetation at NIR band(865 nm), red band(670 nm) and green band(555 nm) are regressed as a function of that of 2250 nm respectively

表 3(Table 3)

表 3 线性回归参数 Table 3 Parameters of the liner regression 两个波段线性拟合 0.865 mm/2.25 μm 0.67 mm/2.25 μm 0.555 mm/2.25 μm 斜率 1.08 1.07 1.01 截距 3×10–4 3×10–4 –1×10–4 r2 0.96 0.97 0.96

表 3 线性回归参数 Table 3 Parameters of the liner regression

偏振反射率具有的光谱不变特性，使得利用偏振手段研究植被冠层结构相对于常规光学遥感而言具有更大优势。常规光学传感器获取的BRF同时包含光谱与结构信息，即BRF为波长与结构的函数，二者耦合在一起，为研究冠层结构带来了困难；而利用偏振探测时，由于偏振反射率与光谱无关，则获取到的值仅为结构信息的函数，从而可以更容易地开展植被冠层结构研究。偏振的光谱不变特性在遥感反演中具有诸多优势，利用其反射率发掘其更有效的价值有待深化。

为了模拟不同叶倾角分布情况下的偏振反射率，选择3种类型的植被：平展型，直立型和球形。表4所示即为描述这些分布的参数。

表 4(Table 4)

表 4 叶倾角分布模拟 Table 4 Simulations of leaf inclination distribution 分布型 参数 a b ${\overline {{\theta }} }_{\rm n}$ 平展型 0.8 0.1 74° 直立性 –0.8 0.1 16° 球形 –0.35 –0.15 58° 　注：a、b为拟合参数。

表 4 叶倾角分布模拟 Table 4 Simulations of leaf inclination distribution

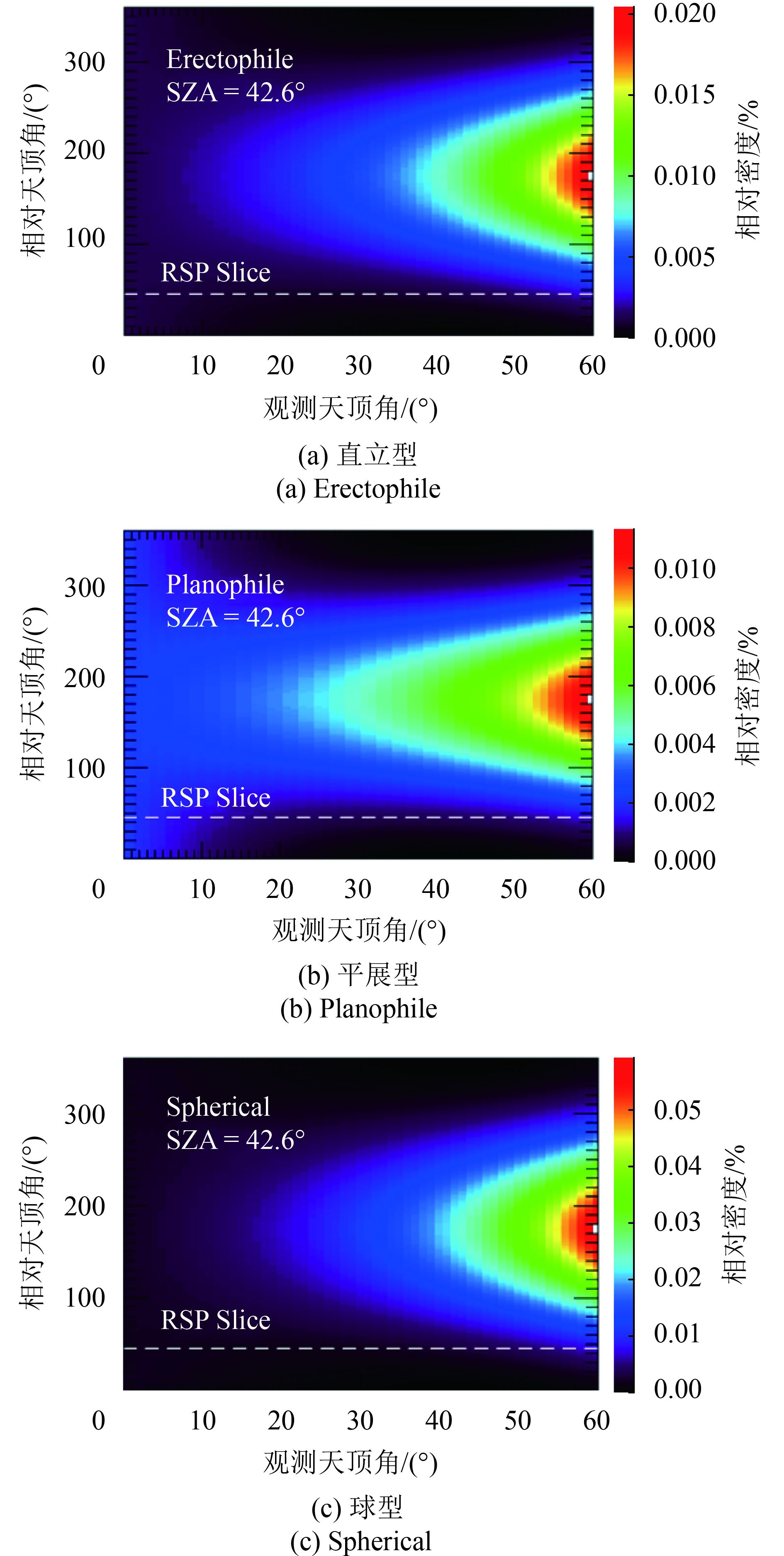
基于式(4)的模拟结果表明，对于直立型，平展型和球型3种叶倾角分布类型，偏振反射率分布具有一定的相似性，但是均随入射—观测几何有显著的变化。图6(a)—(c)为3种LIDF的植被偏振反射率模拟结果，白色虚线代表RSP的观测。可以看出：(1)植被偏振反射存在于上半球空间各个方向，叶片在冠层内部的不同取向具有不同的概率分布，从而将入射辐射以对应概率向各方向镜面反射。(2)偏振反射率随着散射相位角(太阳和传感器之间的角度)的增大而增加。(3)当太阳入射方向和观测方向一致时，偏振反射率达到最小值，即在热点方向没有偏振现象。图7表示NIR波段RSP的偏振反射率数据，其中的相对密度是与最大密度相比时的归一化密度。结果表明，在传感器观测平面上，偏振特性随观测天顶角变化，在观测平面各个方向都大于0，在接近最小相位角的过程中降低，然后随相位角的增大而增大。

图 6 直立型，平展型和球型植被的偏振反射率模拟 Figure 6 Polarimetric reflectance simulations of three types of distribution: erectophile, planophile and spherical

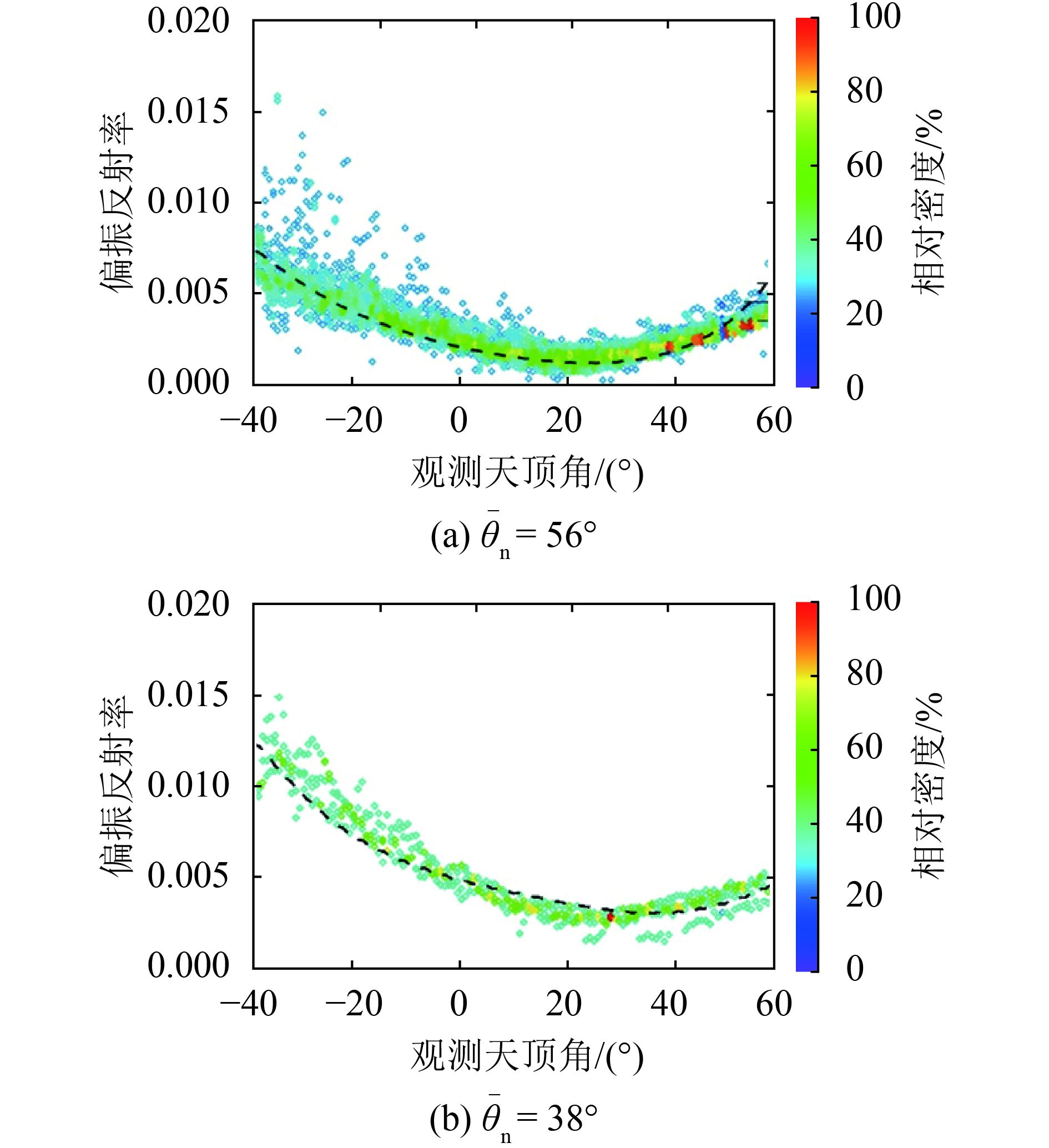
本文研究区域与Knobelspiesse等人(2008)的研究相同，该区域被草地和农作物覆盖。本文结果同样表明该区域存在两种不同类型的植被。根据不同的密度分布，将图7所示数据分为两组结果如图8所示，其中虚线是Rondeaux模型对数据集拟合最佳时的结果。平均叶倾角 \normalsize$\overline {{\theta }}_{\rm{n}} $ 分别是56°(a= –0.3, b= –0.1)和38°(a=0.2, b= –0.3)，表明存在两个包含不同叶倾角分布函数的不同植被类型，符合该场景的真实情况(Knobelspiesse 等，2008)。当观测天顶角为–40°时，模型拟合结果表明偏振反射率可分别达到0.0078和0.0125，偏振反射率差异较大。由于植被偏振特性对叶倾角分布十分灵敏，特别是在大相位角条件下，因此采用偏振测量方法进行地表分类是可行的。且借助叶倾角分布类型和其他辅助信息共同确定植被种类，则是一个更有应用价值的工作。这也将是日后研究工作的重点之一。

图 7 NIR波段(865 nm)的偏振特性随RSP观测天顶角的变化规律 Figure 7 Polarimetric signatures of dense vegetation at NIR (865 nm) varies with view zenith angle from RSP

图 8 RSP数据在NIR波段的两种类型浓密植被的偏振特性随观测天顶角的变化规律 Figure 8 Polarimetric signatures of dense vegetation at NIR (865 nm) varies with view zenith angle from RSP dataset

利用偏振方法系统分析了植被精细反演的两个要素，即冠层结构中光子—冠层的相互作用和叶倾角分布。在对分子与冠层结构相互作用的分析中，引入方向散射面积因子即结构因子DASF，用偏振观测方法去除冠层结构对散射透射再反射光的耦合作用，以及由此在植被散射系数上产生的误差；在对叶倾角分布的分析中，选择Rondeaux-Herman模型，利用偏振RSP数据集综合分析了植被偏振特性对叶倾角分布的灵敏性，采用SAIL模型中的双参数法来描述模型中的叶倾角分布函数，利用大气校正和ARVI准则提取浓密植被，进行植被偏振特性分析，并利用真实偏振探测数据获得了模型拟合结果。

主要结论有：(1)植被冠层与叶片表面反射特性对冠层BRF均有作用并产生误差，偏振探测能够敏感出这种变化导致的误差；若不利用偏振手段对此误差进行甄别，植被冠层的散射系数最高可产生140%的误差。考虑偏振观测对冠层立体结构的灵敏探测能力和对植被生化含量的高精度反演作用，有助于甄别植被氮含量与遥感反演正负相关的国际争议。(2)在多角度、多时相遥感中，偏振探测能够灵敏感知大角度观测中光辐射传输路径和强度的微弱变化，有助于剔除常规传感器大倾角地表探测的误差，从而提升遥感反演精度，因此相比于限制在±15°天顶角内观测的常规遥感探测而言，偏振探测可将传感器有效观测天顶角扩大到±40°—60°，为低约束条件下更大角度的遥感观测提供了可能。(3)在给定的入射观测几何条件下，偏振反射率在400—2500 nm范围内具有光谱不变特性，不同波段之间的偏振反射率决定系数>0.96，偏振的这种光谱不变特性可以有效分离植被反射的光谱与结构信息，从而可以利用偏振手段更好地研究植被冠层结构；由于叶片倾角的分布，冠层对于入射辐射的镜面反射存在于各个方向上，且偏振反射率随着相位角的增大而增大。(4)偏振对叶倾角分布的变化非常灵敏，特别是在大相位角条件下，这有助于获得更丰富的多角度植被反射信息，使得利用偏振遥感对物种进行分类和获取冠层结构参数成为可能。