| 大气中性点区域偏振效应的地—气参量研究 |
收稿日期: 2017-09-03
2. Beijing Key Laboratory of Spatial Information Integration and 3S Engineering Applications, School of Earth and Space Science, Peking University, Beijing 100871, China
3. Institute of Remote Sensing and Digital Earth, Beijing 100101, China
4. Helsinki Universit, Helsinki, Finland 00014
5. Institute of Space Optics, Xi’an Jiaotong Univeristy, Xi’an 710049, China
对目标进行偏振遥感探测起源于1929年法国科学家Lyot对月球进行的偏振测量(Lyot, 1964);20世纪60年代末有学者开始利用偏振对地球的遥感研究(Talmage和Curran, 1986)。大量的对地表目标偏振反射定性特征的研究表明,地表物体具有比较强烈的偏振特性,可以作为遥感的信息源(Chen和Rao, 1968),然而,在大气的偏振辐射过程中,大气粒子表现出非常强烈的偏振效应。这导致了星载遥感器无法用于地表目标的偏振探测(Nadal和Bréon, 1999)。因此,如何对大气与地表偏振信号进行有效分离是是偏振对地观测的一个现实问题与难点问题。
太阳辐射经过大气散射后,就具有一定的偏振性,如果大气散射多为一次散射时,此时就在天空中就形成了一个稳定的偏振分布,称之为天空偏振模式图。对天空偏振信息的测量和应用,近几十年来,求解向量辐射传输方程的各种数值解法日趋成熟(周秀骥 等, 1991),并逐步应用到对地气系统中天光、反射光偏振特性的研究上来,从而对辐射偏振特性有了定性到半定量的认识。Bullrich等人(1966)在Coulson等人(1959)发展的分子大气向量辐射传输模式的基础上,模拟了天光偏振特征;Tanaka(1971)计算和分析了混浊大气漫反射和漫透射的偏振度分布特征;Coulson(1988)对Hawaii地区天光偏振度进行了分子大气下天光偏振的模拟分析,比较全面地总结了人们对天光特性的研究成果,进一步加深了对最大偏振点与观测波长、太阳高度角、大气浑浊度之间关系的认识。通过这些研究成果,人们认识到对漫透射辐射,在围绕太阳的一个区域是极小偏振区,也即为大气偏振中性点,是天空中大气偏振度为零的点(或区域)。
本文拟利用大气粒子散射的物理性质,探讨大气偏振中性点区域的地表—大气偏振信息分离的可行性与方法。分析了大气偏振效应及其模式,通过对大气中性点在上行辐射和下行辐射中的计算,得出Babinet大气中性点的偏振效应以及基于Babinet中性点进行偏振对地观测的基本方法,着重从航空遥感和航天遥感两个层面对如何将大气中性点应用于遥感观测进行了讨论。
2、大气偏振效应对于Rayleigh粒子散射占优势的天空散射而言,在入射光为自然光的条件下偏振度为
| $P\left(\theta \right) = \displaystyle\frac{{{{\sin }^2}\theta }}{{1 + {{\cos }^2}\theta }}{P_{\max }}$ | (1) |
式中,在散射角θ为90°和270°时,偏振度最大为Pmax,理想状况下最大偏振是100%,散射出射的光线为完全线偏振光;在散射角为0°和180°时,为无偏振,出射光线仍是自然光;其他位置是部分线偏振光。然而,由于分子和粒子的多次散射以及地表反射,在白天无云的天空中亦存在很多中性点,并且不会有偏振度为100%的点出现。
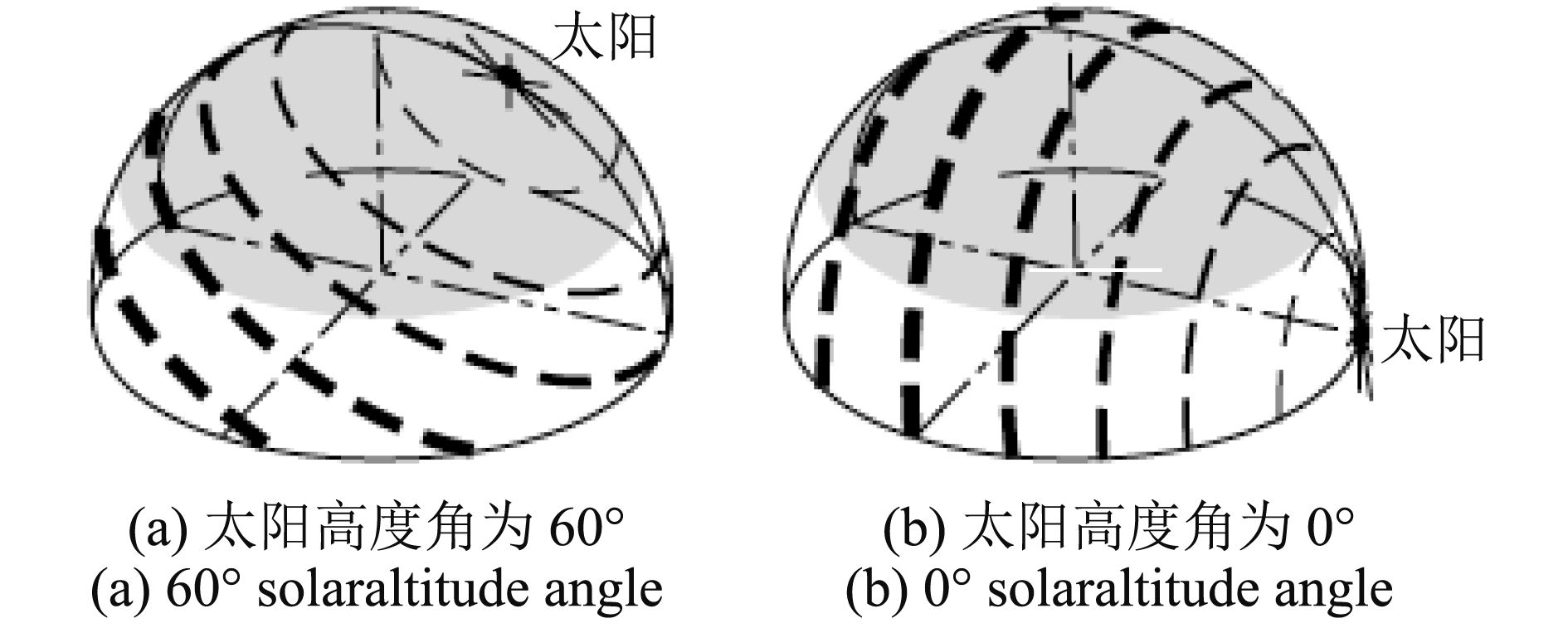
图1(a)、(b)分别表示太阳高度角为60°和0°时天空偏振光分布情况,其中黑色条棒的方向表示的是偏振方向,而条棒的宽度表示的是偏振度,即偏振强度的大小,阴影部分表示的是人眼可观测到的天空部分。天空中的偏振模式图与太阳高度角(即时刻)密切相关,不同太阳高度角其偏振模式图各不相同,偏振光的强度与方向都有差异,太阳高度角低的时候,天空中的偏振强度比较大,也就是说傍晚或早晨的时候天空中偏振强度比中午时大。显然,偏振模式图有两条鲜明的对称线:一条是与太阳或反太阳点相距90°角距的大圆,在该圆上偏振度最大;另一条是太阳与反太阳点的连线,在这条对称线上,偏振角垂直的。
|
| 图 1 不同时刻天空中的偏振模式图 Figure 1 Polarization pattern in the sky at different times |
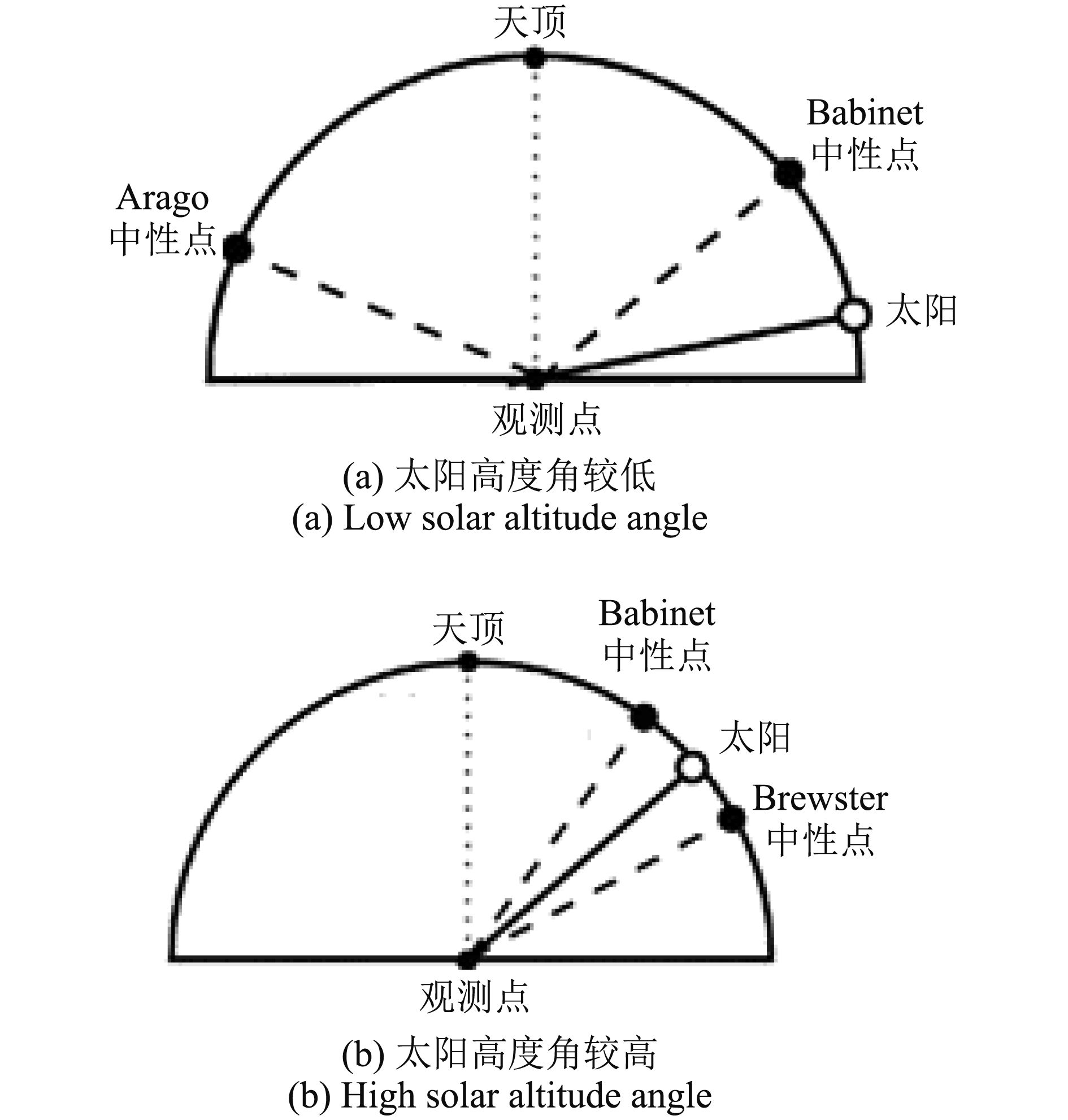
1809年法国天文学家Dominique Francois Jean Arago发现了天空偏振的现象,并随后发现天空中有一个零偏振的点,这个点今天称之为Arago中性点;约30年后,法国气象学家Jacques Babinet发现了第2个中性点;其后苏格兰物理学家David Brewster发现了第3个中性点。正常的晴空的天气条件下,在太阳的垂直面上,天空中会出现这3个大气中性点(周秀骥 等, 1991, McConteny, 1988)。Arago点位于反太阳点上方20°—30°的位置,Babinet点位于太阳上方约20°的位置,由于与太阳在同一方向。Brewster点位于太阳下方25°—30°的位置。具体分布详见图2。太阳和地平线之间的部分是天空中最亮的区域,同时地平线附近的雾霾也常产生低的偏振值,所以Brewster点最难被看到。在正常的大气条件下,只有Babinet点和Arago点或者Babinet点和Brewster点能够在同一时间被看到。当太阳升得比较高时,Babinet点和Brewster点之间比较接近,当太阳达到天顶时它们差不多就合并为一个点。
|
| 图 2 不同太阳高度角主平面上天空中性点的位置 Figure 2 The relative positions of neutral points to sun on the main plane |
对于大气中性点的产生的一个合理解释是这样的(Coulson, 1988, Horváth 等, 1998):单次散射条件下,天空光的偏振一般为正值,但大气粒子的多次散射造成负偏振。正负偏振交叉处的天空偏振度为零,就产生了大气中性点。一般处于太阳与天顶所在的主平面上。多次散射越强烈,大气中就有越多的负偏振,同时中性点位置就会离理想状态的位置更远。
3、偏振遥感中大气中性点上下行辐射计算对分子大气天光的光谱强度和偏振状态的大部分工作都是基于Chandrasekhar和Elbert (1951)及Chandrasekhar和Elbert (1954)在提出的Stokes参数方法。Coulson等人(1960)给出了考虑多次散射后天光强度和偏振度的详细数值表。这些数值表包括的参数有7个光学厚度(0.02—1.00)、7个太阳天顶角、16个观测天顶角、6个相对方位角(0°—180°间隔30°)以及3个地面反射率(0,0.25,0.80)。基于上述参数的组合,计算了Stokes参数[I, Q, U, V]、偏振度(P)与偏振角(θ),给出了上行辐射和下行辐射的共142688种组合的数值表。由于遥感主要考虑下行辐射,下面是大气中性点下行辐射的计算过程。
Ie、Ir分别表示通过偏振器为垂直方向和平行方向上的光强度,则有:
| $\begin{gathered} {I_{{\text{e}},{\text{r}}}}\left( {\tau ;\mu ,\varphi } \right) = I_{{\text{e}},{\text{r}}}^{\left( 0 \right)}\left( {\tau ;\mu ,{\mu _0}} \right) + I_{{\text{e}},{\text{r}}}^{\left( 1 \right)}\left( {\tau ;\mu ,{\mu _0}} \right) \hfill \\ \cos \varphi + I_{{\text{e}},{\text{r}}}^{\left( 2 \right)}\left( {\tau ;\mu ,{\mu _0}} \right)\cos 2\varphi \hfill \\ \end{gathered} $ | (2) |
式中,τ是大气光学厚度,μ=conθ, θ 是观测天顶角, φ 是相对方位角。
大气顶的散射辐射为
| $\left\{ {\begin{array}{*{20}{l}}\!\!\!\!{I_{\rm{e}}^{\left(0 \right)}\left({0,\mu, - {\mu _0}} \right) = \displaystyle\frac{C}{{\mu + {\mu _0}}}\left[ {K\psi \left(\mu \right) + L\phi \left(\mu \right) - M\xi \left(\mu \right) - N\eta \left(\mu \right)} \right]}\\\!\!\!\!{I_{\rm{r}}^{\left(0 \right)}\left({0,\mu, - {\mu _0}} \right) = \displaystyle\frac{C}{{\mu + {\mu _0}}}\left[ {K\chi \left(\mu \right) + L\zeta \left(\mu \right) - M\sigma \left(\mu \right) - N\theta \left(\mu \right)} \right]}\end{array}} \right.$ | (3) |
式中,
| $\left\{ {\begin{array}{*{20}{l}}{K = \psi \left({{\mu _0}} \right) + \chi \left({{\mu _0}} \right), \;L = 2\left( {\phi \left({{\mu _0}} \right) + \zeta \left({{\mu _0}} \right)} \right)}\\{M = \xi \left({{\mu _0}} \right) + \sigma \left({{\mu _0}} \right), \;N = 2\left( {\theta \left({{\mu _0}} \right) + \eta \left({{\mu _0}} \right)} \right)}\end{array}} \right.$ | (4) |
| $C = \displaystyle\frac{2}{{32}}{\mu _0}{F_0}$ | (5) |
式中,
| $\left. {\begin{array}{*{20}{l}} {{X_i}\left( \mu \right) = 1 + \mu \int_0^1 {{\psi _i}} \left( {\mu '} \right)\left( {{X_i}\left( \mu \right){X_i}\left( {\mu '} \right)} \right) - {\rm{ }}}\\ {\quad \quad \quad \;\;\left( {{Y_i}\left( \mu \right){Y_i}\left( {\mu '} \right)} \right)\frac{{{\rm{d}}\mu '}}{{\mu + \mu '}}{\rm{ }}}\\ {\rm{ }}\\ {{\rm{ }}{Y_i}\left( \mu \right) = {{\rm{e}}^{ - \tau /\mu }} + \mu \int_0^1 {{\psi _i}} \left( {\mu '} \right)\left( {{Y_i}\left( \mu \right){X_i}\left( {\mu '} \right)} \right) - {\rm{ }}}\\ {\quad \quad \quad \;\left( {{X_i}\left( \mu \right){Y_i}\left( {\mu '} \right)} \right)\frac{{{\rm{d}}\mu '}}{{\mu - \mu '}}{\rm{ }}}\\ {} \end{array}} \right\}\left( {i = {\rm{e}},{\rm{r}}} \right)$ | (6) |
式中,
则大气顶的散射辐射有:
| $\left\{ \begin{array}{l}I_{\rm{e}}^{\left(1 \right)}\left(\!{0,\mu, - {\mu _0}} \right) \!= \!\! - \displaystyle\frac{{4C}}{{\mu + {\mu _0}}}\mu {\mu _0}{\left({1 - {\mu ^2}} \right)^{\frac{1}{2}}}{\left({1 \!-\! \mu _0^2} \right)^{\frac{1}{2}}}\!{M^{\left(1 \right)}\!}\left({\mu, {\mu _0}} \right)\\I_{\rm{r}}^{\left(1 \right)}\left({0,\mu, - {\mu _0}} \right) = 0\\I_{\rm{e}}^{\left(2 \right)}\left({0,\mu, - {\mu _0}} \right) = - \displaystyle\frac{C}{{\mu + {\mu _0}}}{\mu ^2}\left({1 - \mu _0^2} \right){M^{\left(2 \right)}}\left({\mu, {\mu _0}} \right)\\I_{\rm{r}}^{\left(2 \right)}\left({0,\mu, - {\mu _0}} \right) = \displaystyle\frac{C}{{\mu + {\mu _0}}}\left({1 - \mu _0^2} \right){M^{\left(2 \right)}}\left({\mu, {\mu _0}} \right)\end{array} \right.$ | (7) |
式中,
| $\begin{gathered}\left\{ {\begin{array}{*{20}{l}} {{W^{\left( j \right)}}\left( {\mu ,{\mu _0}} \right) = {X^{\left( j \right)}}\left( {{\mu _0}} \right){Y^{\left( j \right)}}\left( \mu \right) - {Y^{\left( j \right)}}\left( {{\mu _0}} \right){X^{\left( j \right)}}\left( \mu \right)} \\ {{M^{\left( j \right)}}\left( {\mu ,{\mu _0}} \right) = {X^{\left( j \right)}}\left( {{\mu _0}} \right){X^{\left( j \right)}}\left( \mu \right) - {Y^{\left( j \right)}}\left( {{\mu _0}} \right){Y^{\left( j \right)}}\left( \mu \right)} \end{array}} \right. \hfill \\ \left( {j = 1,2} \right) \hfill \\ \end{gathered} $ | (8) |
式中,
| ${\psi ^{\left(1 \right)}}\left(\mu \right) = \displaystyle\frac{3}{8}\left({1 - {\mu ^2}} \right)\left({1 + 2{\mu ^2}} \right), {\psi ^{\left(2 \right)}}\left(\mu \right) = \displaystyle\frac{3}{{16}}{\left({1 + {\mu ^2}} \right)^2}$ | (9) |
Stokes参量的U分量可以表示为
| $\begin{array}{*{20}{l}} {U\left( {\tau , - \mu ,\varphi } \right) = \displaystyle\frac{{2C}}{{\mu - {\mu _0}}}\left[ \begin{gathered} 2{\mu _0}{\left( {1 - {\mu ^2}} \right)^{\frac{1}{2}}}{\left( {1 - \mu _0^2} \right)^{\frac{1}{2}}}{W^{\left( 1 \right)}}\left( {\mu ,{\mu _0}} \right) \hfill \\ \sin \varphi - \mu \left( {1 - \mu _0^2} \right){W^{\left( 2 \right)}}\left( {\mu ,{\mu _0}} \right)\sin 2\varphi \hfill \\ \end{gathered} \right]} \\ \end{array}$ | (10) |
| $U\left( {\tau , - \mu ,\varphi } \right) = \displaystyle\frac{{2C}}{{\mu + {\mu _0}}}\left[ \begin{gathered} 2{\mu _0}{\left( {1 - {\mu ^2}} \right)^{\frac{1}{2}}}{\left( {1 - \mu _0^2} \right)^{\frac{1}{2}}}{M^{\left( 1 \right)}}\left( {\mu ,{\mu _0}} \right) \hfill \\ \sin \varphi + \mu \left( {1 - \mu _0^2} \right){M^{\left( 2 \right)}}\left( {\mu ,{\mu _0}} \right)\sin 2\varphi \hfill \\ \end{gathered} \right]$ | (11) |
Stokes中的入射光总光强I和第二分量Q为
| $I = {I_{\rm{e}}} + {I_{\rm{r}}}$ | (12) |
| $Q = {I_{\rm{r}}} - {I_{\rm{e}}}$ | (13) |
入微光的偏振度(P)与偏振角(θ)为
| $P = \displaystyle\frac{{\sqrt {{Q^2} + {U^2} + {V^2}} }}{I}$ | (14) |
| $\theta = \displaystyle\frac{1}{2}\arctan \left({U/Q} \right)$ | (15) |
根据式(14)、(15)可分别计算出下行辐射的偏振度和偏振角。
4、偏振遥感大气中性点地—气分离方法 (4.1) Babinet大气偏振中性点性质对于天空中的3个偏振中性点,其在天空中出现的位置及物理性质是不同的,其受外界条件如太阳位置、大气状况、地面反照率以及观测波段等的影响都较大,要选取适用于对地偏振遥感观测的中性点,其条件是首先其位置便于遥感观测,其次受外界干扰或影响较小。对于Arago点,只有当太阳天顶角较大时(一般为70°—90°)时才会在天空中出现,也就是在早晚的时候才能观测到Arago点,它与太阳之间的角距离几乎是保持一致的。在可见光—近红外波段的遥感探测中,为了获取充足的光照条件,一般情况下卫星过境或航空遥感飞行都选择在太阳高度角比较高,光照条件较好的情况下进行,Arago点只能在早晚观测到,而且其位置较低,不适合用于对地偏振遥感观测。对于Brewster中性点,当太阳高度角约为20°时Brewster点出现,当太阳向天顶方向移动时,Brewster点的位置与太阳的位置近乎成线性相关,表现一致。Brewster中性点出现在太阳一侧,其位置总是比太阳低,其位置较低的劣势跟Arago点类似。另外,Brewster点在上行辐射时受大气状况和地表反射的影响也比较大,故Brewster点也不适用于对地偏振遥感。
相对而言,Babinet中性点是对地偏振遥感的理想选择,原因如下:
(1) Babinet中性点位于太阳的同一侧,在太阳高度角为零,即太阳升起时,其位置大概在太阳上方18°;然后随着太阳的升起,其位置也在慢慢升起,在太阳高度角为90°时与太阳的位置重合,Babinet点伴随着太阳升起到落下的全过程,且始终处于太阳的上方。Babinet中性点这种全天都可以观测,且高度角较大,在遥感应用中有利于获取较好的光照条件,也方便遥感观测。
(2)Babinet中性点受大气状况的影响较小,在上行辐射中,Babinet中性点在光学厚度增大时向天顶方向移动,在光学厚度约为1的时候其位置不再随光学厚度的增大而变化。也就是说Babinet中性点在光学厚度小于1的时候位置有些微变化,光学厚度大于1时的变化则无影响。也就是说Babinet中性点对大气状况不敏感,在大气状况变化时其位置比较稳定。
(3) Babinet中性点的位置受观测波段的变化也小于Brewster中性点的位置,在Babinet中性点观测对于多光谱遥感更有意义。
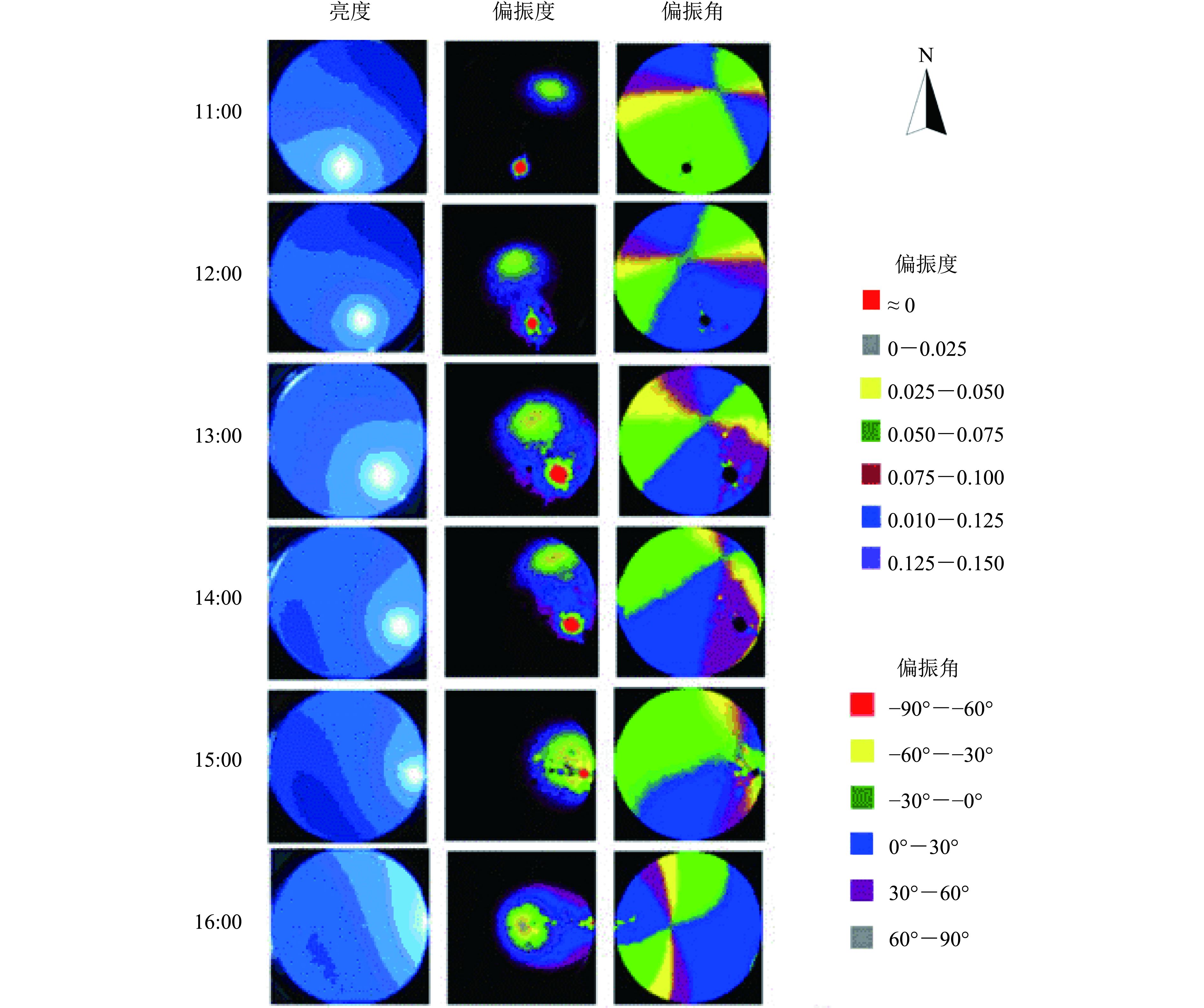
图3是Babinet中性点一天中随太阳高度角变化的情况。在2008-09-01 T 11:00—2008-09-01 T 16:00于北京大学遥感楼5楼平台进行了连续观测实验,实验时天空晴好,实验中每隔1小时对全天空拍摄1组数据。图3是实时拍摄的照片亮度、偏振度及偏振方位角的分布对比图。图3中偏振度图中红色圆点以及偏振角度图中黑色圆点为太阳位置,偏振度图中紫色环形中心区域的灰色区域以及偏振角度图中各种颜色交叉区域为中性点位置。
|
| 图 3 Babinet中性点分布的连续观测图 Figure 3 Daily continuous observation of the Babinet neutral distribution in the sky |
从图3的实验结果中可以得出Babinet中性点随太阳高度角(时间)变化的规律。首先,从各个时间的太阳位置及偏振度的分布情况可以知道,全天空的偏振度分布以及Babinet中性点位置并不是固定不变的,而是随着太阳位置的变化而变化的;其次从偏振度分布图上可以明显的看到Babinet中性点偏振度呈环状分布,在太阳高度角较高即接近中午的时候,天空中可以观测到一个环状分布,而随着时间的推移可以发现出现了另外一个环形分布,而整个天空的偏振度分布是这两个环状分布的叠加;综合看各幅偏振方位角分布图可以看出Babinet中性点与偏振方位角的分布也有着一定的分布规律,主要与太阳的位置有关。
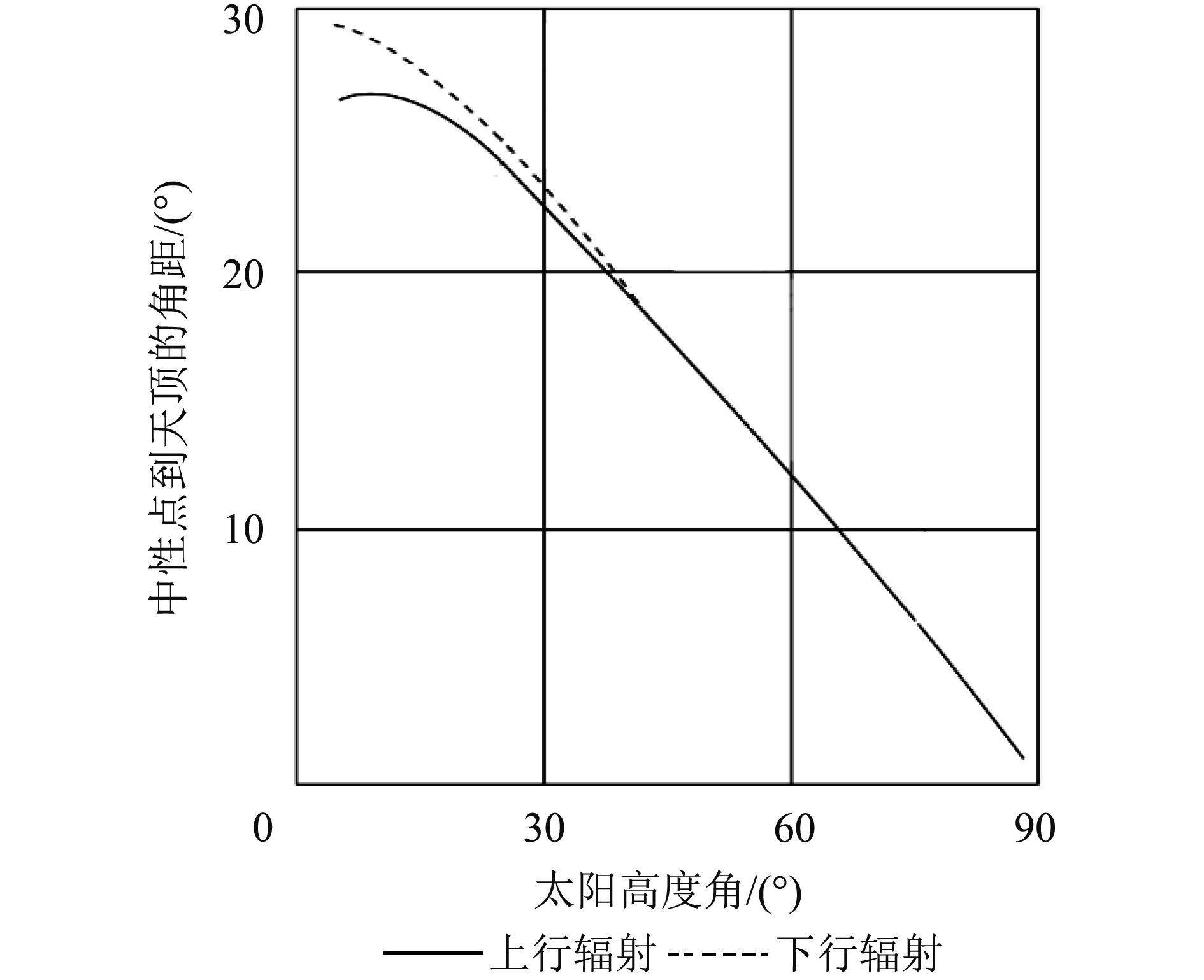
图4是Coulson(1959)利用平面平行大气模型计算得到的大气下行辐射的Babinet偏振中性点曲线图,表示的是大气光学厚度为0.1时,中性点到天顶的角度距离与太阳高度角的函数曲线。图4表明当太阳高度角在32°—90°时,Babinet中性点的上行辐射与下行辐射的中性点位置完全一致,即此时大气中性点与在地面观测到的大气中性点的位置在太阳高度角较高时一致;当太阳高度角在5°—25°时,上行辐射与下行辐射的中性点位置开始出现不同,太阳高度角小于5°时,上、下行辐射都没有Babinet中性点出现。一般情况下,在利用卫星对地进行资源探测时,卫星过境的太阳高度角都比较高,这时的上行辐射和下行辐射的中性点位置与行为相差不大。
|
| 图 4 Babinet中性点到天顶的角距与太阳高度角的关系曲线 Figure 4 The relationship curves between the angle of the Babinet neutral point to the zenith and the solar elevation angle |
将大气中性点应用于航空遥感探测中,也就是在Babinet中性点区域对地表进行观测,根据Babinet中性点在大气偏振模式中的特征,太阳高度角是其主要影响因素,因此,研究其太阳高度角也即是观测时间是该方法的关键。
如图4所示,Babinet中性点与太阳出现在同一个主平面上,在大气光学条件一定的情况下,其到天顶角的角度距离与太阳高度角具有一定的定量关系。图4的曲线可以拟合为如下的线性函数,即
| $y = - 0.3x + 30$ | (19) |
式中,x为太阳高度角,y为中性点到天顶的角距。其中当地(已知经纬度)某一时刻的太阳高度角可以通过太阳高度角公式来求得。
通过地面验证,证明利用中性点进行地—气偏振效应分离方法具有一定的可行性(吴太夏 等, 2013)。另外,在航空遥感平台验证方面,研究团队进行了一次专门的航空遥感飞行实验。实验地点为珠海。飞行前的准备工作包括飞机联系、航迹规划、相机定制、空域申请等一系列工作。2012年6月18日,利用偏振相机,搭载在运12型飞机上,进行了两个航带的飞行,获取了中性点区域与非中性点区域的对比偏振影像。
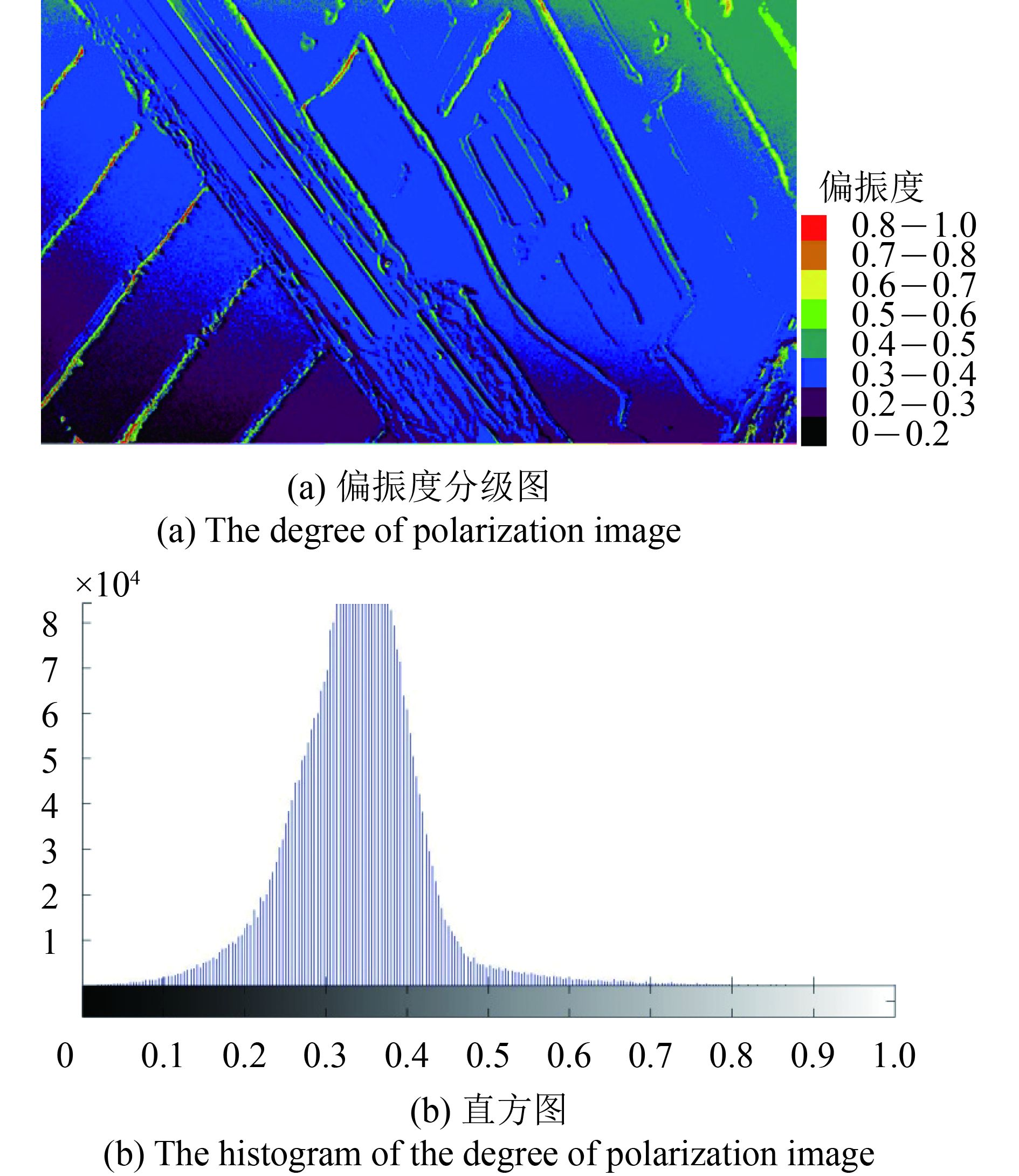
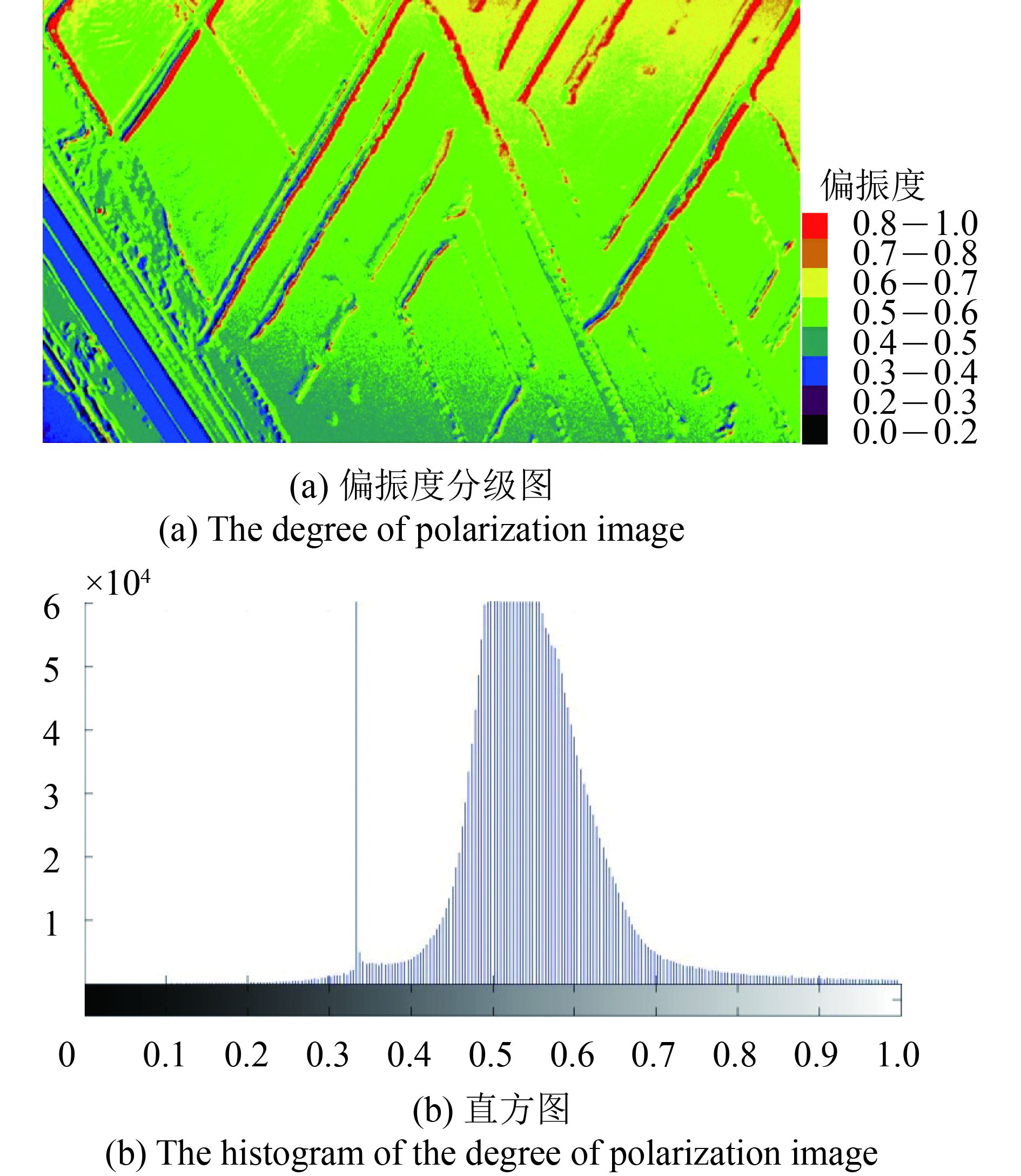
图5为在中性点位置,利用所得3幅影像计算得到的影像偏振度分级图和偏振度直方图。图6为在非中性点位置,利用所得3幅影像计算得到的影像偏振度分级图和偏振度直方图。通过对比可以看出,中性点位置影像偏振度绝大部分小于0.4,而在非中性点位置偏振度绝大部分大于0.5,并且中性点位置地物影像细节要明显多于非中性点位置地物影像。经统计,中性点位置影像偏振度小于0.4所占比例为84.45%,非中性点位置影像偏振度小于0.4所占比例为5.17%。由于大气偏振是强偏振,这说明在中性点位置进行遥感探测确实可以有效消除大气偏振,以突出地物偏振信息(Yang 等, 2013)。
|
| 图 5 中性点位置影像偏振度分级图及偏振度直方图 Figure 5 The degree of polarization image and the histogram of the degree of polarization image taken at neutral point position |
|
| 图 6 非中性点位置影像偏振度分级图及偏振度直方图 Figure 6 The degree of polarization image and the histogram of the degree of polarization image taken at non-neutral point position |
要使在卫星遥感平台上的偏振遥感器能够观测到大气中性点,要满足两个条件:(1)偏振遥感器与太阳在同一个平面上,即二者的相对方位角为0°或180°;(2)太阳的高度角应该满足式(19)。
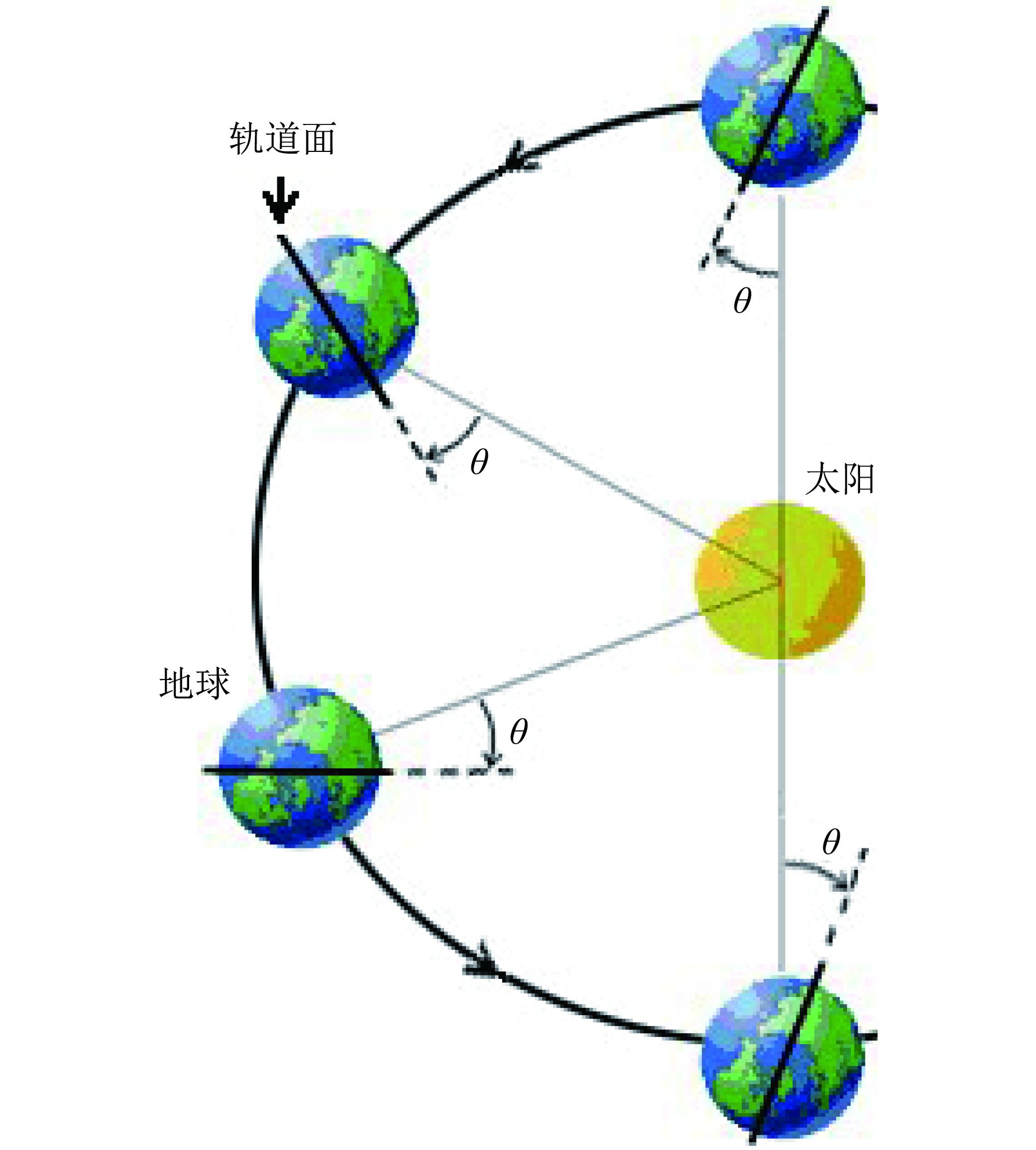
POLarization and Directionality of the Earth’s Reflectances(POLDER)是由法国空间中心(CNES)研制,是世界上第一个可进行多角度偏振成像观测的卫星载荷,于1996年搭载在日本国家空间发展局的高级地球观测卫星(ADEOS)上飞行。ADEOS是一颗太阳同步轨道卫星,高度为797 km,倾斜角为98°,降交点的地方太阳时间为上午10:15与10:45。太阳同步轨道的太阳照射轨道面的方向在一年内基本保持不变,即轨道平面法线与太阳方向在赤道平面上的投影之间的夹角保持不变,卫星通过赤道节点的地方时不变。在太阳同步轨道上,卫星于同一纬度的地点,每天在同一地方时同一方向上通过,因此太阳光的入射角几乎是固定的,这对利用太阳反射光的被动式遥感器来说就具备了观测条件固定的优点。太阳同步轨道的这种太阳入射角度基本固定的轨道性质使中性点在偏振遥感对地观测中成为可能。图7是太阳同步轨道的示意图。θ角是太阳同步轨道的光照角,在卫星运动的过程中始终保持不变。
|
| 图 7 太阳同步轨道示意图 Figure 7 Schematic diagram of the sun synchronous orbit |
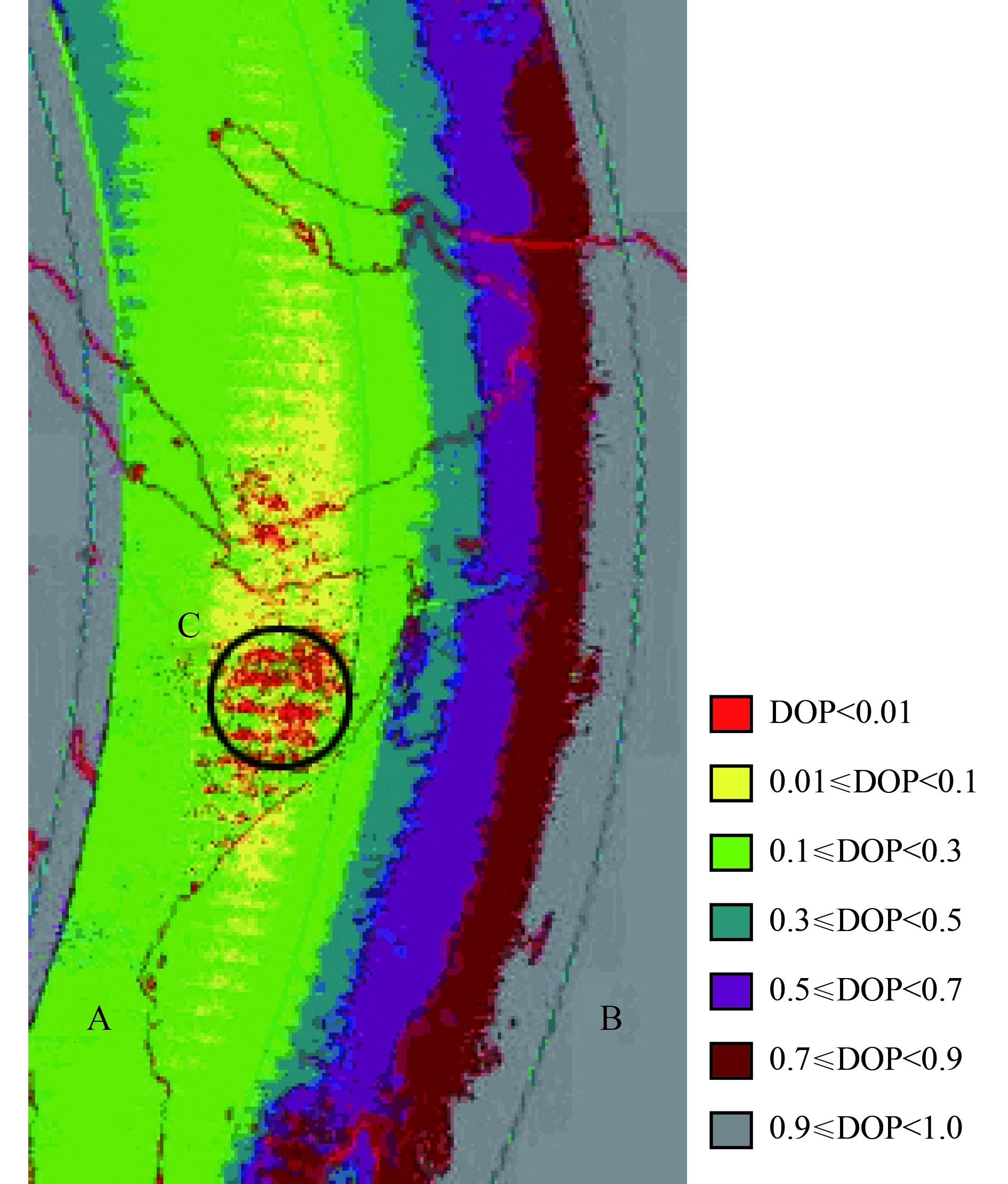
图8为POLDER偏振传感器遥感影像的偏振度分布图,图像取自POLDER 2003年10月5日的一个序列(Pass No.034, level-1数据),波段为443 nm,近似垂直方向探测。区域A,B分别为陆地和海洋。如图8所示,偏振度在影像中呈现有规律的分布,中间部分(区域C)的偏振度较小,向图像的两侧偏振度慢慢变大,这跟图3在地面观测的结果类似。图8中区域C的偏振度小于等于0.01,接近于零,可以认为是偏振中性点区域。图9表示的是偏振中性点区域的太阳与POLDER传感器的相对方位角为180°,结合该地区的经纬度以及卫星经过该区域的时间,可以确定当地当时的太阳高度角以及理论的中性点区域。
|
| 图 8 POLDER偏振传感器遥感影像的偏振度分布图 Figure 8 The degree of polarization distribution of the POLDER image |

|
| 图 9 太阳与POLDER传感器相对位置 Figure 9 Relative position of the sun with the POLDER sensor |
本文研究了天空的偏振分布以及大气中性点的偏振效应,对利用大气中性点区域进行地表—大气偏振效应分离的可行性进行了论证,解决偏振遥感对地观测过程中大气偏振信息对地表偏振信号干扰的问题。通过对大气中性点在辐射传输过程中的数值模拟与计算,得出Babinet大气中性点的在不同太阳高度角情况下的性质,并分析了基于该点所在的区域进行航空偏振对地观测的基本方法,并进行了航天遥感进行大气中性点区域的观测验证。结果表明:(1)Babinet中性点相比于其他两个中性点,其在不同观测条件下位置更稳定,更适合于偏振对地观测中地—气偏振参量分离;(2)航空遥感搭载偏振传感器在Babinet中性点区域进行地表探测的实验可以得出,该区域的遥感影像中可以更有效地消除大气偏振,从而突出地物偏振信息;(3)在太阳同步轨道的卫星偏振遥感影像上能够识别偏振中性点区域,验证中性点在卫星高度的可观测性。成果将偏振遥感中最大的大气误差源降到尽可能降低,形成偏振遥感物理的大气窗口,以提升偏振遥感中地表目标的探测精度,形成偏振遥感物理的大气窗口,提升偏振遥感中地表目标的探测精度。
| [1] | Bullrich, K., R. Eiden and W. Nowak.. Sky radiation, polarization and twilight radiation in Greenland[J]. Pure and Applied Geophysics, 1966, 64 (1) : 220 –242. DOI: 10.1007/BF00875549 |
| [2] | Chandrasekhar S and Elbert D. Polarization of the sunlit sky[J]. Nature, 1951, 167 (4237) : 51 –55. DOI: 10.1038/167051a0 |
| [3] | Chandrasekhar S and Elbert D D. The illumination and polarization of the sunlit sky on Rayleigh scattering[J]. Transactions of the American Philosophical Society, 1954, 44 (6) : 643 –728. DOI: 10.2307/1005777 |
| [4] | Chen H S and Rao C R N. Polarization of light on reflection by some natural surfaces[J]. Journal of Physics D: Applied Physics, 1968, 1 (9) : 1191 –1200. DOI: 10.1088/0022-3727/1/9/312 |
| [5] | Coulson K L. Characteristics of the radiation emerging from the top of a rayleigh atmosphere. 1. Intensity and polarization[J]. Planetary and Space Science, 1959, 1 (4) : 265 –276. DOI: 10.1016/0032-0633(59)90031-5 |
| [6] | Coulson K L. 1988. Polarization and intensity of light in the atmosphere. Hampton, VA., USA: A Deepak Pub. |
| [7] | Coulson, K. L., J. V. Dave and Z. Sckera. 1960. Tables related to radiation emerging from a planetary atmosphere with Rayleigh scattering.Berkeley, CA., USA:University of California Press. |
| [8] | Horváth G, Gál J, Pomozi I and Wehner R. Polarization portrait of the Arago point: video-polarimetric imaging of the neutral points of skylight polarization[J]. Naturwissenschaften, 1998, 85 (7) : 333 –339. DOI: 10.1007/s001140050510 |
| [9] | Lyot B. 1964. Research on the polarization of light from planets and from some terrestrial substances. Washington: National Aeronautics and Space Administration. |
| [10] | Nadal F and Bréon F M. Parameterization of surface polarized reflectance derived fromPOLDER spaceborne measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37 (3) : 1709 –1718. DOI: 10.1109/36.763292 |
| [11] | Talmage D A and Curran P J. Remotesensing using partially polarized light[J]. International Journal of Remote Sensing, 1986, 7 (1) : 47 –64. DOI: 10.1080/01431168608954660 |
| [12] | Tanaka M. Radiative transfer in turbid atmospheres[J]. Journal of the Meteorological Society of Japan, 1971, 49 (5) : 321 –332. DOI: 10.2151/jmsj1965.49.5_321 |
| [13] | 杨尚强, 关桂霞, 赵海盟, 赵红颖, 杨彬, 张文凯, 谭翔, 吴太夏, 晏磊. 基于大气中性点的地—气分离方法空基验证探究[J]. 光谱学与光谱分析, 2013, 33 (9) : 2525 –2531. Yang S Q, Guan G X, Zhao H M, Zhao H Y, Yang B, Zhang W K, Tan X, WuT X and Yan L. Airborne validation of ground-object detection from polarized neutral-point atmosphere[J]. Spectroscopy and Spectral Analysis, 2013, 33 (9) : 2525 –2531. DOI: 10.3964/j.issn.1000-0593(2013)09-2525-07 |
| [14] | 麦卡特尼. 1988. 大气光学——分子和粒子散射. 北京: 科学出版社 McContney E J. 1988. Optics of the atinosphere-molecular and particle scattering. Beijing: Science Press |
| [15] | 吴太夏, 张立福, 岑奕, 黄长平, 赵恒谦, 孙雪剑. 偏振遥感的中性点大气纠正方法研究[J]. 遥感学报, 2013, 17 (2) : 235 –247. Wu T X, Zhang L F, Cen Y, Huang C P, Zhao H Q and Sun X J. Neutral point consideration for atmospheric correction in polarization remote sensing[J]. Journal of Remote Sensing, 2013, 17 (2) : 235 –247. DOI: 10.11834/jrs.20132156 |
| [16] | 周秀骥, 陶善昌, 姚克亚. 1991. 高等大气物理学. 北京: 气象出版社 Zhou X J, Tao S C and Yao K Y. 1991. Advanced atmospheric physics. Beijng: China Meteorological Press |

