孙仲秋, 赵云升, 卢珊, 吕云峰
Function of polarization on the bidirectional reflectance factor of vegetation samples
SUN Zhongqiu, ZHAO Yunsheng, LU Shan, LYU Yunfeng
1. School of Geographical Science, Northeast Normal University, Changchun 130024, China
2. College of Urban and Environmental Science, Changchun Normal University, Changchun 130032, China
1、引 言 被动光学遥感主要是利用反射光与地表参数之间的关系实现反演与监测,光强度信息在遥感应用当中被广泛关注,但是偏振信息却很少用在研究地面自然目标的特性 (Talmage和Curran,1986)。20世纪70年代末至今,研究者们已经证明了偏振测量技术在大气探测,材料鉴定以及目标识别方面具有重要的科学价值 (Tyo 等,2006)。尤其是伴随着机载与星载探测器的出现,使偏振遥感技术在表征地表参数研究中变成了可能。其中,RSP (Research Scanning Polarimeter) (Cairn 等,1999)与POLDER (Polarization and Directionality of the Earth’s Reflectances) (Deschamps 等,1994) 是非常具有代表性的偏振探测器。虽然这些研究的主要目的是为了消除地表偏振对大气偏振遥感反演应用中的贡献,但是也为地表偏振特性的研究提供了依据。众多科学机构利用这些偏振信息结合地表偏振反射模型来描述与解释自然地物的偏振特性,其中主要包括植被,土壤以及积雪 (Breon 等,1995;Nadal和Breon,1999;Ottaviani 等,2015)。
关于地表偏振的研究主要得益于众多研究者使用地基平台测量过程中发现了偏振信息与自然地物特征属性之间的关系。其中,关于植被偏振特性的研究备受关注,早期的研究分别从叶片与植被冠层两个层面来测量植被的偏振特性(Curran,1981;Grant,1987;Vanderbilt和Grant,1985),测量结果说明了偏振信息与叶片和冠层的生物特性具有一定的联系:研究发现叶片的漫反射分量来源于叶片内部结构,偏振信息是由叶片表面所产生的镜面反射引起的,同时也发现,植被冠层的几何特征也会改变其偏振信息。上述结论帮助研究者们从经验上了解到植物叶片与植被冠层是如何产生偏振信息的(Vanderbilt 等,1985)。基于偏振是由镜面反射产生的假设,研究者们利用菲涅尔公式建立偏振解析模型对植被的偏振反射进行模拟计算。结果发现偏振反射模型可以很好的评估测量结果,并且具有分析植被冠层结构特征的能力 (Vanderbilt和Grant,1985)。而非偏振部分完全是由叶片内部产生的,因此具有反映植被生理特征的潜力 (Vanderbilt 等,1985)。
然而,在随后的研究中,星载偏振探测器的出现并没有促进偏振遥感技术在植被特征参数反演方面的研究 (Deschamps 等,1994)。一方面,星载偏振探测器获取的偏振信息主要是用来反演气溶胶参数,而将地面植被背景的偏振信息作为影响因素考虑 (Tanré 等,2011);另外一方面,受到大气偏振的影响,低分辨率的星载探测器很难将地面的偏振信息与植被的特征参数建立关系。即使在这样的背景下,研究者们指出仍然需要系统地开展植被多角度偏振特性的研究 (Litvinov 等,2011;Maignan 等,2009),这不仅可以将植被对大气偏振的贡献解释清楚,而且能阐明植被自身的偏振传输过程,从而确定偏振遥感在植被监测中的作用。
与此同时,基于地面偏振测量平台对植被偏振反射特性的研究也一直被广泛开展 (Peltoniemi 等,2015;Sun 等,2017;Suomalainen 等,2009),这些测量结果在20世纪八、九十年代研究的基础上考虑了更多的光谱信息,使研究者们对植被多角度偏振光谱反射特性有了更多的了解。无论是机载还是地面平台开展的研究,都为利用偏振信息反演地物的特征参数提供了潜在的数据源。但是,由于偏振信息与植被特征参数之间的关系尚不清晰,仍然无法利用偏振信息反映出植被的特征参数。如果要量化偏振信息与植被特征参数之间的关系,应该以地基平台开展研究,例如:野外与实验室测量。这样才能获取植被最本质的偏振反射特性,进而反演植被的结构特征参数。此外,偏振信息在众多植被双向反射模型研究中并没有被单独考虑,那么它是否会对双向反射模型的计算结果有所影响。
本研究基于多角度偏振测量,分析了信息对植被反射模型的影响以及偏振信息对植被反射模型的影响以及偏振信息在植被结构特征参数表达方面的潜力,发挥偏振测量在植被遥感研究中的作用。
2、植被多角度偏振反射原理 (2.1) 偏振测量基本原理 自然地物反射过程所产生的偏振信息可以通过斯托克斯参量表达出来,其中地表反射过程的V分量通常可以忽略(Talmage和Curran,1986):
|
$\left\{ \begin{aligned} I = &({L_{0}} + {L_{90}} + {L_{45}} + {L_{135}})/2 \\ &Q = {L_{0}} - {L_{90}} \\ &U = {L_{45}} - {L_{135}} \\ &V = {L_{\rm{r}}} - {L_{\rm{l}}} \\ \end{aligned} \right.$
|
(1) |
式中,Lx是偏振片透光轴在不同方向(Lr为右方向,Ll为左方向)获得的偏振反射辐射亮度值。本研究中主要考虑测量的偏振反射比BPRF(Bidirectional Polarized Reflectance Factor),偏振反射比值可以表示为在相同入射与探测环境下,目标偏振反射光与理想朗伯体反射光之间的比值 (Sun 等,2017b):
|
$\left\{ \begin{array}{l}{\rm{BPR}}{F_Q} =\displaystyle \frac{{{L_0} - {L_{90}}}}{L} =\displaystyle \frac{{{L_Q}}}{L}\\{\rm{BPR}}F =\displaystyle \frac{{{L_{\rm{p}}}}}{L} =\displaystyle \frac{{\sqrt {{Q^2} + {U^2}} }}{L}\end{array} \right.$
|
(2) |
式中,L为理想漫反射白板的反射辐射亮度值,Lp为测量目标的偏振反射辐射亮度值,两者是在完全相同的环境中获取的。此外,双向反射系数BRF(Bidirectional Reflectance Factor)的定义可以表示为
|
${\rm{BRF}} = \frac{{{L_{{\rm{sample}}}}({\theta _{\rm{s}}}, {\theta _{\rm{v}}};{\phi _{\rm{s}}}, {\phi _{\rm{v}}})}}{{L({\theta _{\rm{s}}}, {\theta _{\rm{v}}};{\phi _{\rm{s}}}, {\phi _{\rm{v}}})}}$
|
(3) |
式中,θs表示入射天顶角,θv为探测天顶角,φs为入射方位角,φv为探测方位角,Lsample为测量目标的反射辐射亮度值,这里面需要注意的是,双向反射系数与偏振反射系数都是与入射测量几何相关的参量。
(2.2) 植被偏振反射理论 本研究中,将使用偏振反射模型对单叶与植被覆被的偏振信息进行计算。根据研究者们得出的结论,菲涅尔偏振反射系数(Fp(α, n))可以表征植被的偏振反射特性(Litvinov 等,2011;Maignan 等,2009;谢东海 等, 2012):
|
${F_{\rm{p}}}(\alpha, n) = 0.5\left({\frac{{{{\sin }^2}({\alpha _t} - \alpha)}}{{{{\sin }^2}({\alpha _t} + \alpha)}} - \frac{{{{\tan }^2}({\alpha _t} - \alpha)}}{{{{\tan }^2}({\alpha _t} + \alpha)}}} \right)$
|
(4) |
|
$\sin {\alpha _t} = \sin \alpha /n$
|
(5) |
|
$\begin{array}{l}\cos 2\alpha {\rm{ = }}\cos \xi = \cos {\theta _{\rm{s}}}\cos {\theta _{\rm{v}}} + \\\sin {\theta _{\rm{s}}}\sin {\theta _{\rm{v}}}\cos ({\phi _{\rm{s}}} - {\phi _{\rm{v}}})\end{array}$
|
(6) |
式中,α为反射角,是相角的一半,ξ 表示相角,αt表示折射角,n代表植被的折射率,取值1.5。本文使用由Diner等人(2012)提出的偏振反射模型来计算单个叶片以及植被覆被的偏振反射比值,选择这个模型是由于该模型可以用来模拟平整表面所产生的偏振信息:
|
$\begin{array}{l}BPR{F_\lambda }({\theta _{\rm{s}}}, {\theta _{\rm{v}}};{\phi _{\rm{s}}}, {\phi _{\rm{v}}}) = {f_{\lambda, {\rm{volumetric}}}}({\theta _{\rm{s}}}, {\theta _{\rm{v}}};{\phi _{\rm{s}}}, {\phi _{\rm{v}}})+\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {f_{\lambda, {\rm{microfacet}}}}({\theta _{\rm{s}}}, {\theta _{\rm{v}}};{\phi _{\rm{s}}}, {\phi _{\rm v}})\end{array}$
|
(7) |
式中,体散射部分表示为
|
$\begin{array}{l}{f_{\lambda, {\rm{volumetric}}}}({\theta _{\rm{s}}}, {\theta _{\rm{v}}};{\phi _{\rm{s}}}, {\phi _{\rm{v}}}) =\displaystyle \frac{{{a_\lambda }}}{{\text{π}}}[(\cos {\theta _{\rm{v}}} + \cos {\theta _{\rm{s}}})\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cos {\theta _{\rm{v}}}\cos {\theta _{\rm{s}}}{]^{k - 1}}\exp (b\cos \gamma){D}\end{array}$
|
(8) |
式中,aλ,b,k为拟合参数,D为消偏矩阵,本文中等于1。第二部分可以表示为
|
$\begin{split}{f_{\lambda, {\rm{microfacet}}}}({\theta _{\rm{s}}}, - {\theta _{\rm{v}}}, {\phi _{\rm{v}}}) =& \zeta \frac{{f(\sigma, \beta)}}{{4\cos ({\theta _{\rm{s}}})\cos ({\theta _{\rm{v}}})\cos \beta }}\\&{M}(- m){PM}({m_0})\end{split}$
|
(9) |
|
$\text{式中,}f(\sigma, \beta) = \frac{1}{{{\text{π }}{{\cos }^3}\beta 2{\sigma ^2}}}\exp \left({ - \frac{{{{\tan }^2}\beta }}{{2{\sigma ^2}}}} \right)$
|
(10) |
式中,f(σ, β)表示小平面分布,式(9)中ζ和σ为需要拟合的参数。
|
$\cos \beta = \frac{{\cos {\theta _{\rm{v}}} + \cos {\theta _{\rm{s}}}}}{{2\cos \alpha }}$
|
(11) |
式(9)中的菲涅尔反射矩阵P以及旋转矩阵M的详细介绍请参照Diner等人(2012)的文献。
(2.3) 植被样品与测量过程 本研究中包括3个样本,一个单叶片和两个植株样本,如图1所示。其中为了模拟不同植被样本结构特征,图1(b)表示平展型植被样本,图1(c)表示直立性植被样本。其中,单叶为橡皮树叶片样本a(图1(a)),叶片平整,表面无毛,厚蜡质;样本b为豆叶九里香(图1(b)),冠层平整,叶片平展分布,无毛;样本c为菜豆树(图1(c)),叶片近似直立分布,无毛。选择这3种样品是由于它们为阔叶树,而且它们的叶片无毛,有较厚的蜡质层覆盖,在研究过程中不用考虑叶片绒毛引起的反射差异。
本研究在实验室内进行测量,所使用的多角度偏振测量系统为东北师范大学偏振光遥感实验室自行研发设计的装置(Sun 等,2014),测量当中入射天顶角为40与50°,方位角为15°间隔,探测天顶角间隔为10°,每个方位从0°开始,60°探测天顶角结束。偏振测量过程每个方向进行10次测量,随后求平均,用于表示样本的偏振信息。由于本研究中假设测量目标的反射以入射主平面呈对称分布,因此,测量方向的总数量为78个。测量示意图如图2所示,图2中180°方位表示前向散射探测方向,0°表示后向散射方向,实线为测量方向。进行测量时,为了保证测量面积相同,通过调整载物台,确保所有植被样品的表面与仪器的测量基准面相同。本研究将选择560 nm,670 nm以及865 nm的偏振与反射信息进行分析,这是由于RSP与POLDER传感器可以在这3个波段对地进行观测。
3、偏振信息对植被双向反射模型结果的影响 (3.1) 植被反射模型 本部分主要研究双向反射模型在计算植被覆被反射特性中的效力,这是由于研究过程中发现植被b在可见光波段的反射具有明显的前向散射峰值。这归结于平展的叶片分布特性产生了镜面反射,从而将植被具有的后向热点效应所掩盖(Sandmeier 等,1998)。因此,本研究选择了两个常用的线性核驱动BRF反射模型来说明这些模型是否可以有效的计算出植被的反射信息。因为Ross-Roujean 模型和Ross-Li dense 模型分别被用在了POLDER和MODIS星载探测器上,更具有实际应用价值。其中,线性模型表示如下
|
${\rm{BRF}} = {k_0} + {k_1}{F_1}({\theta _{\rm{s}}}, {\theta _{\rm{v}}}, \phi) + \cdots + {k_n}{F_n}({\theta _{\rm{s}}}, {\theta _{\rm{v}}}, \phi)$
|
(12) |
式中,kn为反演参数,Fn表示核,一般研究中,线性模型中包含3个参数,即n=2。本研究所使用的第一个模型为Ross-Roujean模型(Roujean 等,1992),表达式为
|
$\begin{array}{l}{F_1} =\displaystyle \frac{1}{{2{\text{π }}}}\left[ {({\text{π }} - \phi)\cos \phi + \sin \phi } \right]\tan {\theta _{\rm{s}}}\tan {\theta _{\rm{v}}} - \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\displaystyle\frac{1}{{\text{π }}}\left[ {\tan {\theta _{\rm{s}}} + \tan {\theta _{\rm{v}}} + \Delta ({\theta _{\rm{s}}}, {\theta _{\rm{v}}}, \phi)} \right]\end{array}$
|
(13) |
|
$\Delta ({\theta _{\rm{s}}}, {\theta _{\rm{v}}}, \phi) = \sqrt {{{\tan }^2}{\theta _{\rm{s}}} + {{\tan }^2}{\theta _{\rm{v}}} - 2\tan {\theta _{\rm{s}}}\tan {\theta _{\rm{v}}}\cos \phi } $
|
(14) |
|
${F_2} = \frac{{(0.5{\text{π }} - \xi)\cos \xi + \sin \xi }}{{\cos {\theta _{\rm{s}}} + \cos {\theta _{\rm{v}}}}} - \frac{{\text{π}}}{4}$
|
(15) |
第二个模型为Ross-Li致密核模型(Li和Strahler,1992),与Ross-Roujean不同的是,两个模型的F1核有所差异,Li致密核可以表示为
|
${F_1} = \frac{{(1 + \cos \theta ')\sec \theta _{\rm{s}}'\sec \theta _{\rm{v}}'}}{{\sec \theta _{\rm{s}}' + \sec \theta _{\rm{v}}' - O({\theta _{\rm{s}}}, {\theta _{\rm{v}}}, \phi)}}$
|
(16) |
|
$O({\theta _{\rm{s}}}, {\theta _{\rm{v}}}, \phi) = \frac{1}{{\text{π }}}(t - \sin t\cos t)(\sec \theta _{\rm{s}}' + \sec \theta _{\rm{v}}')$
|
(17) |
|
$\cos t = \frac{h}{b}\frac{{\sqrt {{D^2} + {{(\tan \theta _{\rm{s}}'\tan \theta _{\rm{v}}'\sin \phi)}^2}} }}{{\sec \theta _{\rm{s}}' + \sec \theta _{\rm{v}}'}}$
|
(18) |
|
$D = \sqrt {{{\tan }^2}\theta _{\rm{s}}' + {{\tan }^2}\theta _{\rm{v}}' - 2\tan \theta _{\rm{s}}'\tan \theta _{\rm{v}}'\cos \phi } $
|
(19) |
|
$\cos {\theta '} = \cos \theta _{\rm{s}}'\cos \theta _{\rm{v}}' + \sin \theta _{\rm{s}}'\sin \theta _{\rm{v}}'\cos \phi $
|
(20) |
|
$\theta _{\rm{s}}' = {\tan ^{ - 1}}\left({\frac{b}{r}\tan {\theta _{\rm{s}}}} \right), \theta _{\rm{v}}' = {\tan ^{ - 1}}\left({\frac{b}{r}\tan {\theta _{\rm{v}}}} \right)$
|
(21) |
致密核中包含两个参数h/b与b/r,通常赋值为2和1。
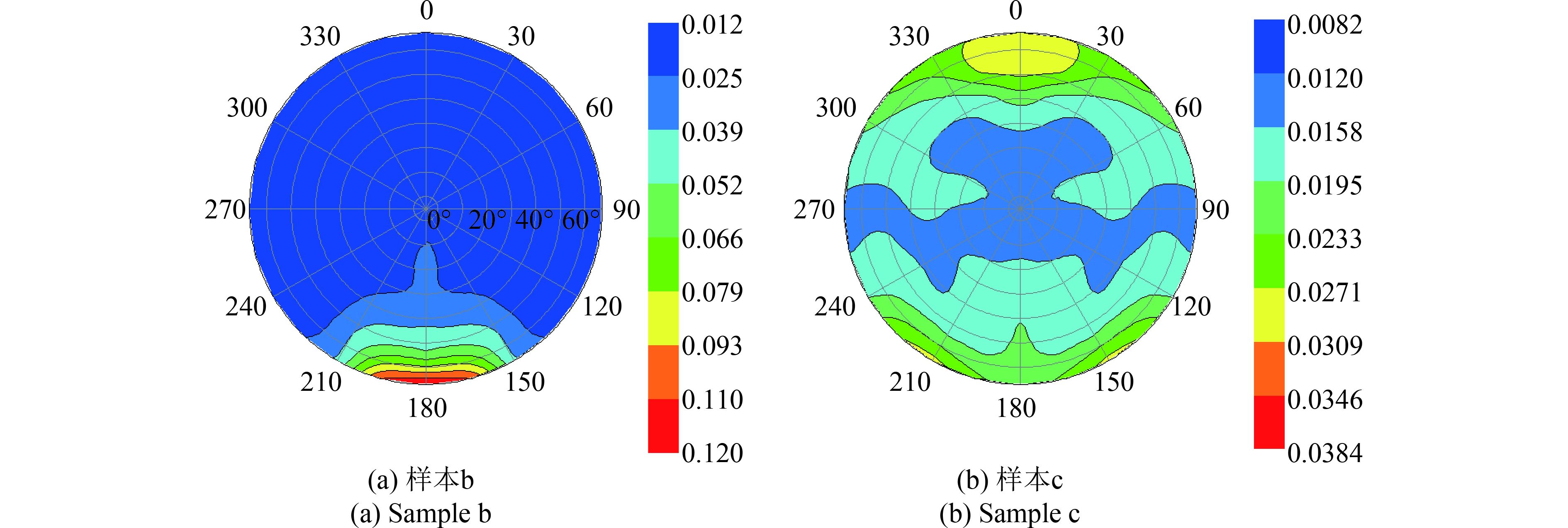
(3.2) 植被覆被反射特性 图3给出了不同植被覆被在670 nm处BRF的分布图,入射天顶角为50°。从图3中可以发现样本b与样本c的反射分布特性具有显著差异。其中,具有平展型的样本b具有明显的前向散射峰值,如图3(a)所示;而直立型冠层的样本c则具有典型的后向反射峰值,如图3(b)所示。以往的研究已经表明(Sun 等,2017a, b),由于镜面反射在670 nm波段的贡献大,平展型植被在该波段处的反射出现前向反射峰值,因此会出现图3(a)的结果。随后,本研究利用两个BRF模型来模拟平展型与直立型植被覆被的双向反射信息。表1与表2分别给出了样本b与样本c在不同波段所反演的模型参数,以及均方根误差(RMSE),同时包括模拟值与测量之间的平均差异的绝对值(ARD) (Sun 等,2017a)。其中,ARD是用来评价模型有效性的一个重要指标,根据Goel(1988)的研究表明,如果有一个模型的模拟结果与测量值之间的差异在20%以内,那么这个模型是有效的。从表1中的结果可以发现,两个常用的BRF模型在670 nm波段的计算结果与测量结果之间的差异达到了30%,而在其他波段的差异均在20%之内;表2中样本c在各个波段的测量结果与模拟值之间的差异均小于20%。这些结果表明,在670 nm波段处,BRF模型不能有效地计算样本b的反射值。出现这种结果是由于样本b在670 nm是以镜面反射按为主,而本研究所使用的BRF模型在计算植被反射过程中没有考虑镜面反射 (Sun 等,2017a)。因此,如果能将镜面反射从总反射当中分离,则可以利用现有的BRF模型对漫反射部分信息进行计算。
表 1(Table 1)

表 1 植被b在不同波段反演的最优模型参数,入射天顶角为50°
Table 1 Best fitted parameters of vegetation b at selected wavelengths while the incident zenith angle was 50°
| 波长 |
Ross-Roujean 模型 |
|
Ross-Li dense 模型 |
| k0 |
k1 |
k2 |
RMSE |
ARD |
|
k0 |
k1 |
k2 |
RMSE |
ARD |
| 560 nm |
0.0493 |
–0.0003 |
0.0171 |
0.013 |
0.16 |
|
0.0697 |
–0.062 |
0.0448 |
0.012 |
0.19 |
| 670 nm |
0.0228 |
–0.0017 |
–0.0091 |
0.013 |
0.29 |
|
0.0627 |
–0.1209 |
0.0693 |
0.011 |
0.32 |
| 865 nm |
0.4467 |
0.0181 |
0.1408 |
0.06 |
0.11 |
|
0.2139 |
0.7015 |
–0.3656 |
0.045 |
0.091 |
|
表 1 植被b在不同波段反演的最优模型参数,入射天顶角为50°
Table 1 Best fitted parameters of vegetation b at selected wavelengths while the incident zenith angle was 50°
|
表 2(Table 2)

表 2 植被c在不同波段反演的最优模型参数,入射天顶角为50°
Table 2 Best fitted parameters of vegetation c at selected wavelengths while the incident zenith angle was 50°
| 波长 |
Ross-Roujean 模型 |
|
Ross-Li dense 模型 |
| k0 |
k1 |
k2 |
RMSE |
ARD |
|
k0 |
k1 |
k2 |
RMSE |
ARD |
| 560 nm |
0.0484 |
–0.0012 |
0.168 |
0.0072 |
0.11 |
|
0.0606 |
–0.0368 |
0.0936 |
0.0069 |
0.1 |
| 670 nm |
0.0155 |
–0.0006 |
0.0406 |
0.0028 |
0.12 |
|
0.0227 |
–0.0217 |
0.0304 |
0.0026 |
0.11 |
| 865 nm |
0.3109 |
–0.0011 |
0.6183 |
0.02 |
0.047 |
|
0.3154 |
–0.0131 |
0.2704 |
0.02 |
0.046 |
|
表 2 植被c在不同波段反演的最优模型参数,入射天顶角为50°
Table 2 Best fitted parameters of vegetation c at selected wavelengths while the incident zenith angle was 50°
|
(3.3) 偏振信息计算镜面反射 由于偏振反射主要是由镜面反射引起的,因此,研究者们提出利用偏振反射信息计算镜面反射。首先,将总的双向反射分成两部分,镜面部分BRFspecular与漫反射部分BRFdiffuse
|
${\rm BRF} = {\rm BR{F}_{{\rm{specular}}}} + {\rm BR{F}_{{\rm{diffuse}}}}$
|
(22) |
镜面反射部分则可以根据测量的偏振信息与式(23)计算得到(Vanderbilt 等,1985)
|
$F(\alpha, n){\rm{ = }}\frac{{{{\sin }^2}({\alpha _t} - \alpha){{\tan }^2}({\alpha _t} + \alpha) - {{\sin }^2}({\alpha _t} + \alpha){{\tan }^2}({\alpha _t} - \alpha)}}{{{{\sin }^2}({\alpha _t} - \alpha){{\tan }^2}({\alpha _t} + \alpha) + {{\sin }^2}({\alpha _t} + \alpha){{\tan }^2}({\alpha _t} - \alpha)}}$
|
(23) |
随后,将计算得到的镜面反射从总反射中减去,得到漫反射部分;最后,利用BRF模型对漫反射部分进行模拟计算,得到的结果如表3所示 (Sun 等,2017a)。通过表3可以发现,利用现有的BRF模型可以很好的模拟植被b的漫反射部分。其中在670 nm处的ARD已经从原来的30%降低到20%以内,而在其他波段,模型计算值与测量之间的差异也有不同程度的降低。这说明,将镜面反射从总反射中排出,有助于提高现有双向反射模型对植被覆被反射特性计算的精度。
表 3(Table 3)

表 3 植被b在不同波段漫反射部分反演的最优模型参数,入射天顶角为50°
Table 3 Best fitted parameters of vegetation b inverted by the diffuse portion of BRF at selected wavelengths while the incident zenith angle was 50°
| 波长 |
Ross-Roujean 模型 |
|
Ross-Li dense 模型 |
| k0 |
k1 |
k2 |
RMSE |
ARD |
|
k0 |
k1 |
k2 |
RMSE |
ARD |
| 560 nm |
0.0321 |
0.001 |
0.0397 |
0.005 |
0.13 |
|
0.0216 |
0.0316 |
–0.0023 |
0.0046 |
0.12 |
| 670 nm |
0.0096 |
0.0001 |
0.0285 |
0.0029 |
0.19 |
|
0.0084 |
0.0036 |
0.0099 |
0.003 |
0.20 |
| 865 nm |
0.4059 |
0.0153 |
0.1575 |
0.055 |
0.11 |
|
0.1824 |
0.6742 |
–0.3418 |
0.039 |
0.085 |
|
表 3 植被b在不同波段漫反射部分反演的最优模型参数,入射天顶角为50°
Table 3 Best fitted parameters of vegetation b inverted by the diffuse portion of BRF at selected wavelengths while the incident zenith angle was 50°
|
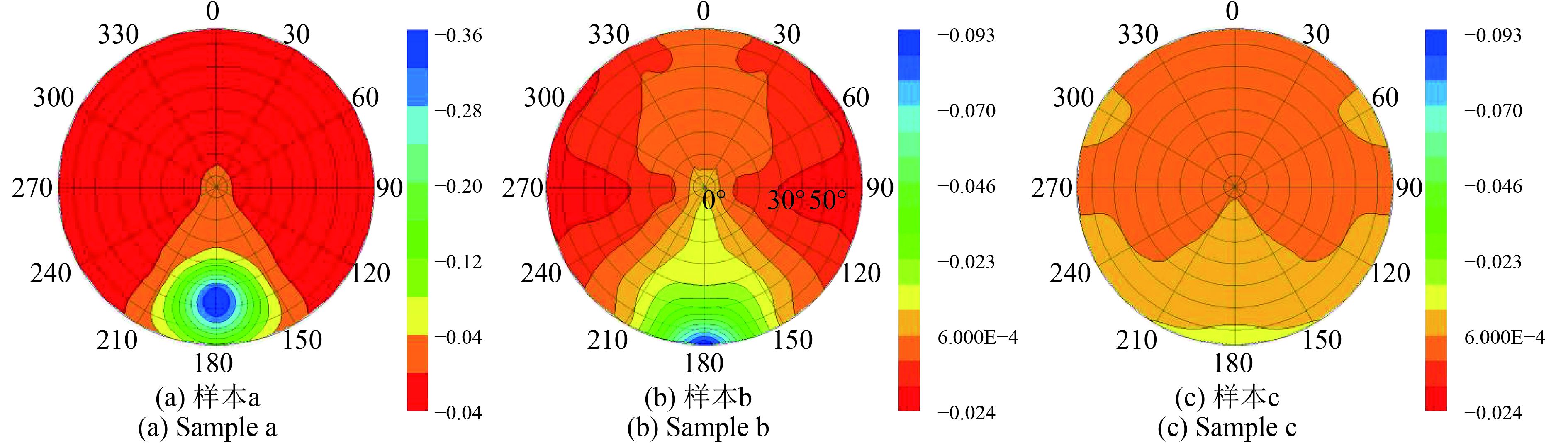
4、植被结构特征与偏振反射比之间关系 (4.1) 不同植被的偏振反射特性 大部分研究者用线偏振度作为指标来描述植被的偏振反射特性,并提出利用偏振度可以不需要对测量结果进行归一化处理。这是由于偏振度是偏振反射比与双向反射比的比值,而两个分量的定义都是用标准白板进行归一化计算的,所以在直接计算线偏振度时可以忽略归一化过程。为了说明本论文中偏振信息的准确性,图4给出了不同植被样品的线偏振度光谱曲线,该结果是在前向散射方向主平面测量的,入射天顶角为40°。从图4中可以发现,植被样品的偏振度曲线与植被反射光谱曲线呈现反比例关系(Breon 等,1995;Maignan 等,2009),这一现象被研究者们解释为偏振反射比与波长无关(王涵 等,2014;相坤生 等,2015;谢东海 等,2012),所以低反射波段对应高的偏振度,高反射波段对应低偏振度值。为了进一步说明不同植被样品的偏振差异,在图5中给出了它们的偏振度分布特性,入射天顶角为40°。在图5中表示方位角过程中,180表示前向散射方向,0表示后向散射方向。从图5中可以发现,所有样品的最大偏振均出现在前向散射方向,这一规律可以通过式(4)的菲涅尔偏振反射系数来解释。然而,在图5中发现,最大偏振度值不是出现在单叶的测量结果中,而是样本b的偏振度最大。这进一步说明,偏振度是两个反射系数的比值,它不能完全代表植被的偏振特性。因此,这里用BPRF来表示植被样本的偏振特性,一方面由于BPRF是直接获取的偏振信息;另一方面现有的偏振反射模型可以直接用来计算植被的BPRF (Diner 等,2012)。
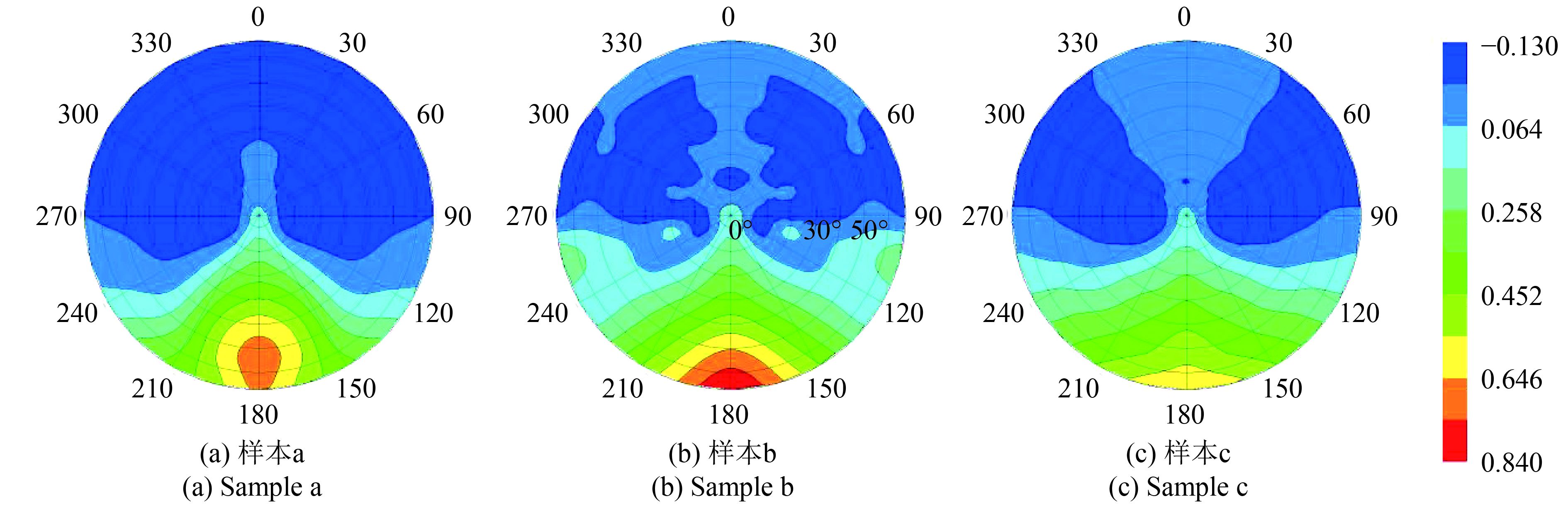
(4.2) 植被结构与偏振反射比的关系 本研究中将植被样品的粗糙度按照逐渐增加的程度依次分为样本a、样本b和样本c,进而分析植被结构特征与偏振反射比之间的关系。同时利用Diner等人(2012)的模型对3个样本进行模拟计算,进一步说明菲涅尔反射系数可以要来表征植被样品的偏振特性。反演得到的模型参数如表4所示。在这里本研究没有给出偏振反射模型计算结果与测量结果的相对差异,这是由于偏振反射比值本身较小,一部分BPRF值在10–3左右。非常小的差异值就会引起较大的相对差异。因此也就意味着RMSE越小,说明偏振反射模型与测量的BPRF值之间的拟合程度越高。在偏振反射模型当中,包含一个粗糙度参数σ,通过分析表4的结果可以发现,在波段相同的情况下,粗糙度参数σ增加的顺序为单叶,平展植被(b),直立型植被(c)。这表明,粗糙度参数可以在一定程度上反映出植被样品的结构特征,即σ值越大,植被冠层越粗糙,或者说叶片越接近直立状态。这是由于叶片的分布状态会直接影响其产生镜面反射的多少,从而影响偏振信号的大小。为了进一步说明偏振反射比的产生于植被样品的结构特征有关,图6给出了不同植被样品在865 nm处BPRFQ(式(2))的分布特性,与图5的方位相同,这里面考虑了Q参量自身的符号,在前向为负,后向为正。选择BPRFQ是由于Q参量可以表示植被反射过程中所产生的大部分偏振信息,另一方面Q参量正负值的变化可以体现出植被偏振信息或者以垂直分量为主,或者以平行分量为主。从图6中可以发现,无论是单叶还是植被覆被,均在所有方向都产生了偏振反射比值,其中,图6(b)与(c)共用一个图例。根据以往的研究结果表明,平整的单叶除了前向散射方向之外,在其他方向不会有镜面反射发生(Bousquet 等,2005)。那么没有镜面反射的区域所产生的偏振信息则是由其他物理机制所产生的。近期的研究表明,多重散射也可以产生偏振信息 (Kallel和Gastellu-Etchegorry,2017)。这里需要注意的是,图6(a)是植被单叶在865 nm处的偏振反射比结果,在非前向散射方向的反射值都是由叶片内部所产生的多重散射所引起的,本研究虽然没有利用模型计算多重散射结果,但是也从实验结果角度说明:除了镜面反射之外,多重散射也是产生偏振的一个原因,而多重散射产生的偏振是以平行分量为主的。
表 4(Table 4)

表 4 不同植被拟合Diner偏振反射模型的参数结果,入射天顶角为40°
Table 4 Best fitted parameters of Diner model for vegetation samples while the incident zenith angle was 40°
| 样品 |
波长/nm |
aλ
|
b
|
k
|
σ
|
ζ
|
RMSE |
| 单叶 |
560 |
0.0012 |
6.2544 |
–6.009 |
0.1234 |
5.8737 |
0.009 |
| 670 |
0.0019 |
6.1068 |
–5.229 |
0.1246 |
6.7455 |
0.0088 |
| 865 |
0.074 |
0.1203 |
–0.449 |
0.1087 |
6.7737 |
0.01 |
| 植被b |
560 |
0.0697 |
2.2339 |
0.7741 |
0.1528 |
–0.9291 |
0.0048 |
| 670 |
0.0743 |
2.3248 |
0.6188 |
0.149 |
–0.9685 |
0.0048 |
| 865 |
0.0563 |
0.0617 |
0.1134 |
0.1464 |
–0.752 |
0.0053 |
| 植被c |
560 |
0.0598 |
2.194 |
0.8512 |
0.2505 |
0.0816 |
0.00084 |
| 670 |
0.0767 |
2.387 |
1.079 |
0.1764 |
0.0773 |
0.00066 |
| 865 |
0.0306 |
0.6855 |
0.529 |
0.1524 |
–0.0754 |
0.0012 |
|
表 4 不同植被拟合Diner偏振反射模型的参数结果,入射天顶角为40°
Table 4 Best fitted parameters of Diner model for vegetation samples while the incident zenith angle was 40°
|
5、结 论 本文系统地分析了地表偏振光多角度反射物理效应,并且研究了不同植被样品的多角度偏振反射信息对双向反射的影响,以及利用偏振信息反映植被的结构特征参数:植被覆被的粗糙度。研究发现,多角度偏振反射可以根据菲涅尔偏振反射理论进行解释,并且可以直接利用偏振反射信息或者将其从总反射中移除。通过本研究总结出以下结论,可以作为植被偏振测量方法以及植被偏振特性规律研究所参考。
首先,地表测量是详细了解植被偏振特性的最有效方法,因为可以获得植被最本质的偏振反射信息;这不仅对建立偏振信息与植被参数之间的关系至关重要,同时也可以为下垫面对大气偏振研究提供支持。在测量过程中应在尽可能多的方向均匀获取植被偏振信息,这样才能完整地表达偏振分布特性。
其次,植被偏振反射比可以用来计算镜面反射部分,如果将这部分镜面反射部分从总反射中减去,那么现有的双向反射模型可以以更高的精度来模拟漫反射部分。这种提升对镜面反射为主的植被覆被具有明显的效果。同时,也为未来的研究提供了一个参考,即,把偏振反射比当成一种“噪声”排出来提升植被遥感的精度,可以将BRF模型计算误差从原来的30%减少到20%,从而使模型在可见光波段有效的计算植被反射信息。
最后,研究中发现,偏振反射比还可以直接应用在对植被的研究当中,因为偏振反射模型可以有效的计算植被的偏振反射比,同时,不同粗糙度的植被覆被可以通过模型参数的大小来表示出来。但是这一结论需要后续对更多类型植被偏振特性的研究来证明。这些结果表明,偏振反射比本身也具有研究植被的结构特征参数的潜能。
本研究不仅证明了偏振信息自身具有的独特能力,而且还可以把偏振信息排出,提升基于反射强度信息可为主的研究。这进一步说明偏振遥感作为一种非常有效的探测手段,可以用于地表植被监测研究。从地表研究来看,偏振探测技术已经发挥了其特有的作用,但是在未来机载与星载应用中,还需要研究者们开展大量的研究来实现偏振遥感在地表监测中的应用,因为像元尺度上植被异质性以及与地面测量范围的差异会对反射信息产生影响。本研究可以为后续关于植被偏振遥感测量以及规律的研究提供一些参考,同时也说明了偏振遥感技术是遥感领域中非常有效的一种反演与估算植被特征参数的手段。