高光谱遥感依托成像光谱仪设备，利用数百个波段来采集地表地物的细微光谱响应信息(童庆禧 等，2016；张良培和李家艺，2016)。获取的高光谱遥感影像利用目标探测技术来区分低概率且细小地物与主要背景信息，并用于军事侦察、公共安全和生态监测等实践中(王跃明 等，2016；杜培军 等，2016)。作为非监督的目标探测技术，异常探测不需要目标地物的光谱特征信息和复杂的影像预处理工作(如大气校正和辐射定标等)，因此在高光谱遥感领域中应用更为广泛(Zhang 等，2010；Zhao 等，2014；Wu 等，2016)。异常探测假定影像场景中的主要地物为背景信息，细小且低概率的地物为异常信息，目的是有效区分异常信息与背景信息所占的像元。

常规的异常探测方法大多利用背景像元和异常像元的统计特性差异来探测异常信息。经典的RX(Reed-Xiaoli)方法假设背景信息满足多变量正态分布的统计特性，利用背景信息的概率分布密度来确定某一像元是否属于背景或异常信息(Reed和Yu，1990)。然而高光谱遥感影像并不一定满足正态分布假设，尤其在较为复杂的地物分布场景中(Nasrabadi，2014)。后来，学者提出许多针对RX方法的改进模型包括核RX、加权RX和子空间RX等(Nasrabadi，2014)，以及一些更为先进的基于统计的异常探测算法，如基于双窗口的本征分离转换DWEST(Dual Window-based Eigen Separation Transform)(Kwon 等，2003)和多重窗口异常探测器MWAD(Multiple-Window Anomaly Detection)(Liu和Chang，2013)。以上这些方法通过压制背景信息来更好实现背景和异常信息的有效区分。然而，这些方法在估计背景统计特性时并未排除异常信息的影响，导致探测结果可能会混杂一些背景像元进而影响结果的准确性和可靠性(Sun 等，2014)。

近年来，随着压缩感知和稀疏理论的兴起，鲁棒主成分分析方法逐渐被应用于解决高光谱的异常探测问题。鲁棒主成分分析RPCA(Robust Principal Component Analysis)于2009年提出，目的为更好解决传统主成分分析中背景信息容易受到噪声和粗差影响的问题(Candes 等，2009)，其目前广泛应用于视频监控、人脸识别和潜在语义索引等方面。在高光谱遥感领域，鲁棒主成分分析将高光谱遥感影像数据看作2维矩阵，采用矩阵分解的思想将其分解为一个低秩的背景矩阵和一个稀疏异常组分矩阵(以下简称稀疏矩阵)，其中稀疏矩阵的非零元素包含影像的异常信息(Sun 等，2014)。目前已有学者利用鲁棒主成分分析来研究高光谱遥感的异常探测问题。如低秩和稀疏分解方法LSD(Low-rank and Sparse Decomposition)将高光谱影像划分为一系列的影像子块来分别构建鲁棒主成分分析模型，通过排列所有像元估计得到的稀疏系数的范数值来探测异常像元(Cui 等，2014)。低秩稀疏矩阵分解方法LRaSMD(Low-rank and sparse decomposition based anomaly detector)考虑高光谱遥感中的噪声问题来改进传统的鲁棒主成分分析模型，利用矩阵分解将原始高光谱遥感影像数据分解为低秩背景组分，噪声组分和稀疏异常组分，进而排列所有像元的稀疏异常组分的二阶范数值来探测异常信息(Sun 等，2014)。随后马氏距离被考虑来更好融合背景信息到LRaSMD模型中以进一步提升其探测结果的可靠性(Zhang 等，2015)。后来，低秩稀疏表达LRASR(Low-Rank And Sparse Representation)(Xu 等，2016)方法引入低秩表达模型来表达背景信息的低秩特性，利用重构背景组分的稀疏残差信息来探测异常像元。相比常规的基于统计的异常探测方法，基于RPCA的模型无须背景信息的任何统计假设，能够更好应用于高光谱遥感影像来实现异常信息的有效估计。然而，上述RPCA模型假定稀疏矩阵为非低秩且非零元素在稀疏矩阵中呈现随机分布特性，非零元素没有明显的结构特征(Candes 等，2009)。这导致稀疏矩阵的非零元素同样影响低秩背景矩阵的列元素估计(Rahmani和Atia，2015；Xu 等，2010)，进而降低背景信息估计与异常信息的探测结果。

因此，本文提出列式鲁棒主成分分析方法CWRPCA(Column-Wise RPCA)来尝试解决传统RPCA模型应用于高光谱遥感异常探测时存在的上述问题，采用非精确增强拉格朗日乘子算法IALM(Inexact Augmented Lagrange Multipliers)来优化求解CWRPCA模型，进而有效探测得到异常信息。采用PaviaC(Pavia City)和Cri两个高光谱数据集，对比5种主流的异常探测方法来验证方法的有效性。

传统RPCA模型认为高光谱影像背景信息构成的矩阵具有低秩特性，异常信息在稀疏矩阵中具有随机分布特性。CWRPCA改进传统RPCA模型，认为异常信息在稀疏矩阵中为少数非零列即稀疏矩阵呈现列稀疏的特性，即稀疏矩阵中每一非零列对应于异常像元。另一方面，CWRPCA假设所有背景像元存在于一个低维的背景列子空间中，背景列子空间可以通过随机采样背景像元来构建得到；同时假设稀疏矩阵中的异常信息对应的非零列不存在于该子空间中。稀疏矩阵中的非零列与部分背景像元对应列不相关，这使得低秩背景矩阵的部分列元素的估计并不受到稀疏矩阵中非零列的影响，进而改善背景信息与异常信息的分离结果(Rahmani和Atia，2015)。假设高光谱影像数据形成2维矩阵 ${ Y} = \left\{ {{{{y}}_i}} \right\}_{i = 1}^N \in {{\bf{R}} ^{D \times N}}$ ，式中，D为波段数量，N为像素个数， ${{{y}}_i}$ 为任一像元的光谱向量。考虑到高光谱遥感成像过程中的高斯随机噪声，CWRPCA将原始高光谱2维矩阵 ${ Y}$ 分解为一个低秩背景矩阵 ${ B} \in {{\bf{R}} ^{D \times N}}$ ，一个噪声矩阵 ${ E} \in {{\bf{R}} ^{D \times N}}$ 和一个列稀疏异常矩阵 ${ S} \in {{\bf{R}}^{D \times N}}$ 。

式中， ${\rm{rank}}({ B}) = r > 0$ 是为限定背景矩阵的低秩特性， ${\left\| { S} \right\|_{{\rm{column}},0}} \leqslant K$ 是为保证列稀疏异常矩阵 $ S$ 中非零列的数量不超过K。可以看出，稀疏列矩阵中 $ S$ 的的非零列对应于高光谱影像中的异常信息，同时这些异常信息在背景矩阵 $ B$ 的对应位置应该为0。式(1)可转换为以下目标函数的优化求解问题

式中， ${\left\| \cdot \right\|_{\rm F}}$ 代表弗罗贝尼乌斯范数(Frobenius范数)， ${\left\| { S} \right\|_{0,2}}$ 为稀疏矩阵中非零列的约束项， ${\textit{λ}} $ 为正则化参数以平衡低秩约束和列稀疏约束的贡献大小， $\varepsilon $ 为设定的逼近误差值或噪声范数约束值。

式(2)是一个NP-hard的非凸优化问题，因此较难求解得到低秩背景矩阵 $ B$ 和列稀疏矩阵 $ S$ 的全局最优解。理论证明，核范数能够很好地逼近低秩约束项 ${\rm{rank}}({ B})$ (Sun 等，2017)，同时 ${{\rm{L}}_{1,2}}$ 混合范数可以作为矩阵 ${{\rm{L}}_{0,2}}$ 范数的最佳近似(Liu 等，2013)。因此式(2)被松弛为以下凸优化问题

式中， ${\left\| \cdot \right\|_ * }$ 为矩阵核范数运算符， ${\left\| { S} \right\|_{1,2}} \!=\!\! \sum\limits_{i = 1}^N {({{\left\| {{ S}(:,i)} \right\|}_2})} $ 为 ${{\rm{L}}_{1,2}}$ 混合范数，表示S中每一列向量 ${{\rm{L}}_2}$ 的范数之和。前项 ${\left\| { B} \right\|_ * }$ 限定背景矩阵的低秩特性，后项 ${\left\| { S} \right\|_{1,2}}$ 保证异常矩阵的列稀疏特性。式(3)的求解可以采用离群值追踪算法(Xu 等，2010)、调制器追踪算法(Chen 等，2011)和加速邻近梯度算法(Lin 等，2009)等。本文中，考虑到计算简单和方便，采用非精确增强拉格朗日乘子(IALM)算法(Lin 等，2010)来求解得到式(3)的全局优化解。IALM通过引入辅助变量来增强式(3)的约束条件，转换式(3)为一系列优化主变量和拉格朗日乘子的目标子方程来依次进行迭代求解。首先，引入辅助变量 ${ J} = { B}$ ，式(3)转换为

进一步，引入两个拉格朗日乘子 ${{ Z}_1}$ 和 ${{ Z}_2}$ ，式(4)可以转换为如下问题

式中， ${\rm{tr}}( \cdot )$ 为矩阵的迹运算符， $\displaystyle\frac{\beta }{2}(\left\| {{ Y} - { B} - { S}} \right\|_{\rm F}^2 + $ $ \left\| {{ J} - { B}} \right\|_{\rm F}^2)$ 为惩罚项以增强目标函数的凸特性且并不影响其全局最优解估计， $\, \beta $ 为设定的惩罚正则化参数，其随着迭代过程而发生改变。假设初始条件为 ${{ J}^{(0)}} = {{ B}^{(0)}} = 0$ ， ${{ S}^{(0)}} = 0$ ， ${ Z}_1^{(0)} = 0$ ， ${ Z}_2^{(0)} = 0$ 和 $\, {\beta ^{(0)}} = {10^{ - 6}}$ 。在t+1次迭代中，当固定其他变量时，变量 ${{ J}^{(t + 1)}}$ 可以通过求解以下目标子式(6)来实现

进一步，当固定其他变量时，变量 ${B^{(t + 1)}}$ 可以通过求解以下目标子式(7)来实现

接下来，固定其他变量，变量 ${{ S}^{(t + 1)}}$ 可以通过求解以下目标子式(8)来实现

最后，两个拉格朗日乘子 ${ Z}_1^{(t{\rm{ + }}1)}$ 和 ${ Z}_2^{(t{\rm{ + }}1)}$ 及惩罚正则化参数 ${\beta ^{(t{\rm{ + }}1)}}$ 分别通过式(9)—(11)来依次进行更新

上述迭代过程持续更新直至满足以下条件： ${\left\| {{{ B}^{(t + 1)}} - {{ J}^{(t + 1)}}} \right\|_\infty } < \tau $ 和 ${\left\| {{ Y} - {{ B}^{(t + 1)}} - {{ S}^{(t + 1)}}} \right\|_\infty } < \tau $ ；或者最大迭代次数 ${t_{\max }} > {10^6}$ ， ${\left\| \cdot \right\|_\infty }$ 表示无穷范数， $\tau $ 为设定的逼近误差。迭代结束，最终得到低秩背景矩阵和列稀疏异常矩阵的最优解 ${ B} = {{ B}^{(t + 1)}}$ 和 ${ S} = $ ${{ S}^{(t + 1)}}$ 。

由式(1)可知，求解得到的列稀疏异常矩阵S非零列对应于原始高光谱影像中的异常信息，其每一列对应一个异常像元。然而，实际计算过程中，由于噪声等因素的影响，非零列的数量会往往大于实际异常像元的个数。因此，采用列稀疏矩阵S的每一列向量的L₂范数来求解得到各个像元的异常值，通过设定阈值η来分割得到异常像元集合 ${ Y}(:,C)$

在此基础上得到CWRPCA的2维异常探测结果。

基于CWRPCA的高光谱异常探测流程如图1所示，包括以下步骤：

图 1 CWRPCA用于异常探测的流程 Figure 1 The process of hyperspectral anomaly detection using CWRPCA

(1) 将3维高光谱影像数据立方体转换为2维矩阵 ${ Y} \in {{\bf{R}} ^{D \times N}}$ ，式中D为波段数量，N为像素个数；

(2) 利用式(2)来构造CWRPCA模型，并通过范数松弛转换为凸优化问题(3)；

(3) 采用IALM算法，利用式(5)—(11)迭代更新各个变量，求解得到背景矩阵和列稀疏异常矩阵的最优解 ${ B} = {{ B}^{(t + 1)}}$ 和 ${ S} = {{ S}^{(t + 1)}}$ ；

(4) 采用式(12)来求解稀疏矩阵S中各个列向量的L₂范数并通过阈值分割得到异常探测图。

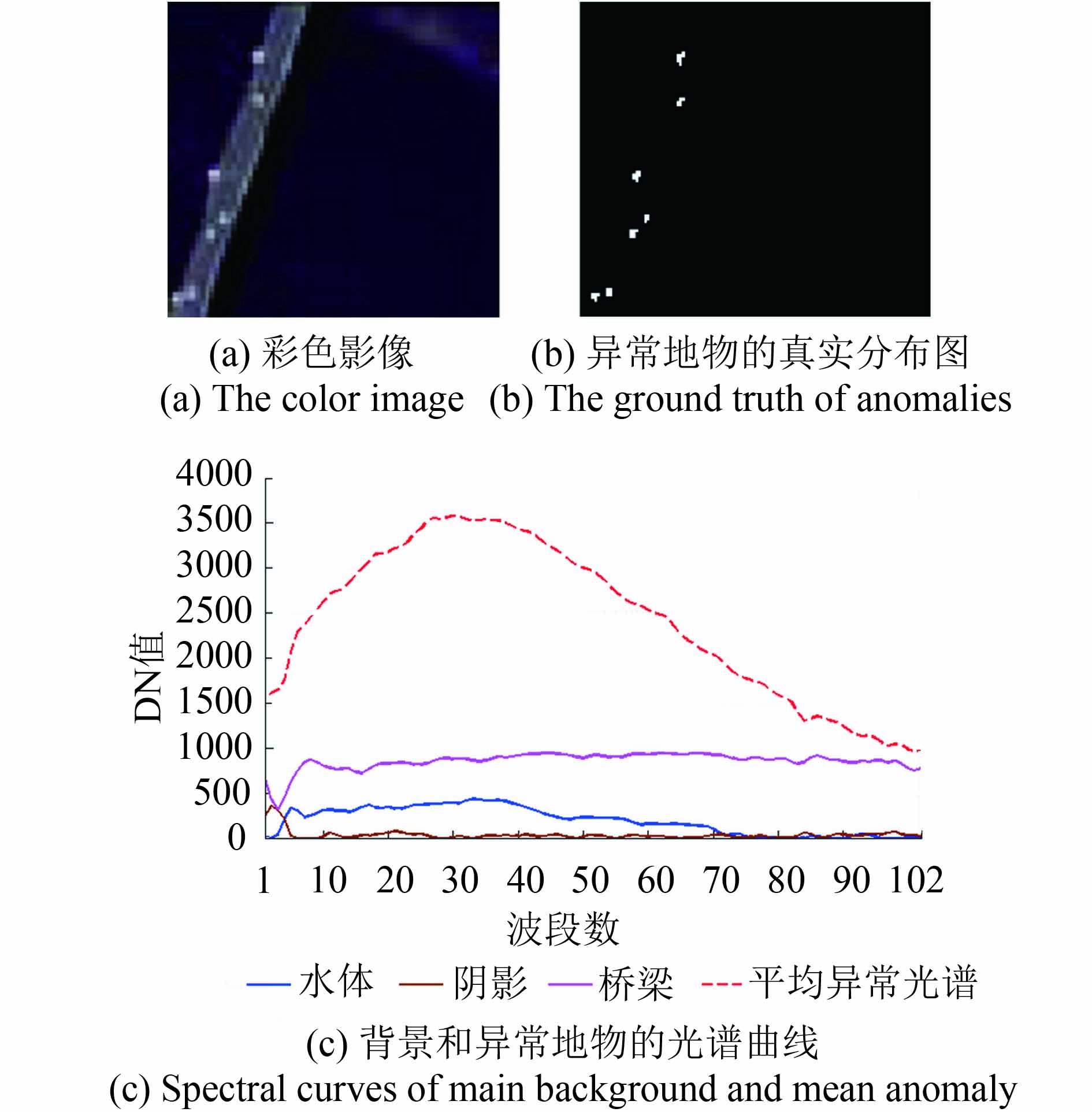
PaviaC数据由ROSIS光学系统成像光谱仪采集得到，影像覆盖意大利北部的帕维亚大学区域，具有准确的真实地物空间分布信息(Sun 等，2014；Zhang 等，2015)。PaviaC数据的原始波段数为115，光谱范围为430—860 nm，空间分辨率为1.3 m。实验采用原始影像中较小的一块区域，大小为108×120像素；对原始115波段进行预处理，移除13个低信噪比的波段，剩余102波段。图2(a)中3种主要地物构成影像场景的背景信息：桥、水体和阴影。代表桥上车辆的47个像元被认为是场景中的异常信息，因为车辆的光谱特征曲线与背景地物差异较大。图2(b)展示异常像元的实际分布情况，图2(c)展示异常像元和背景像元的光谱响应曲线信息。

图 2 PaviaC数据信息 Figure 2 The information of PaviaC dataset

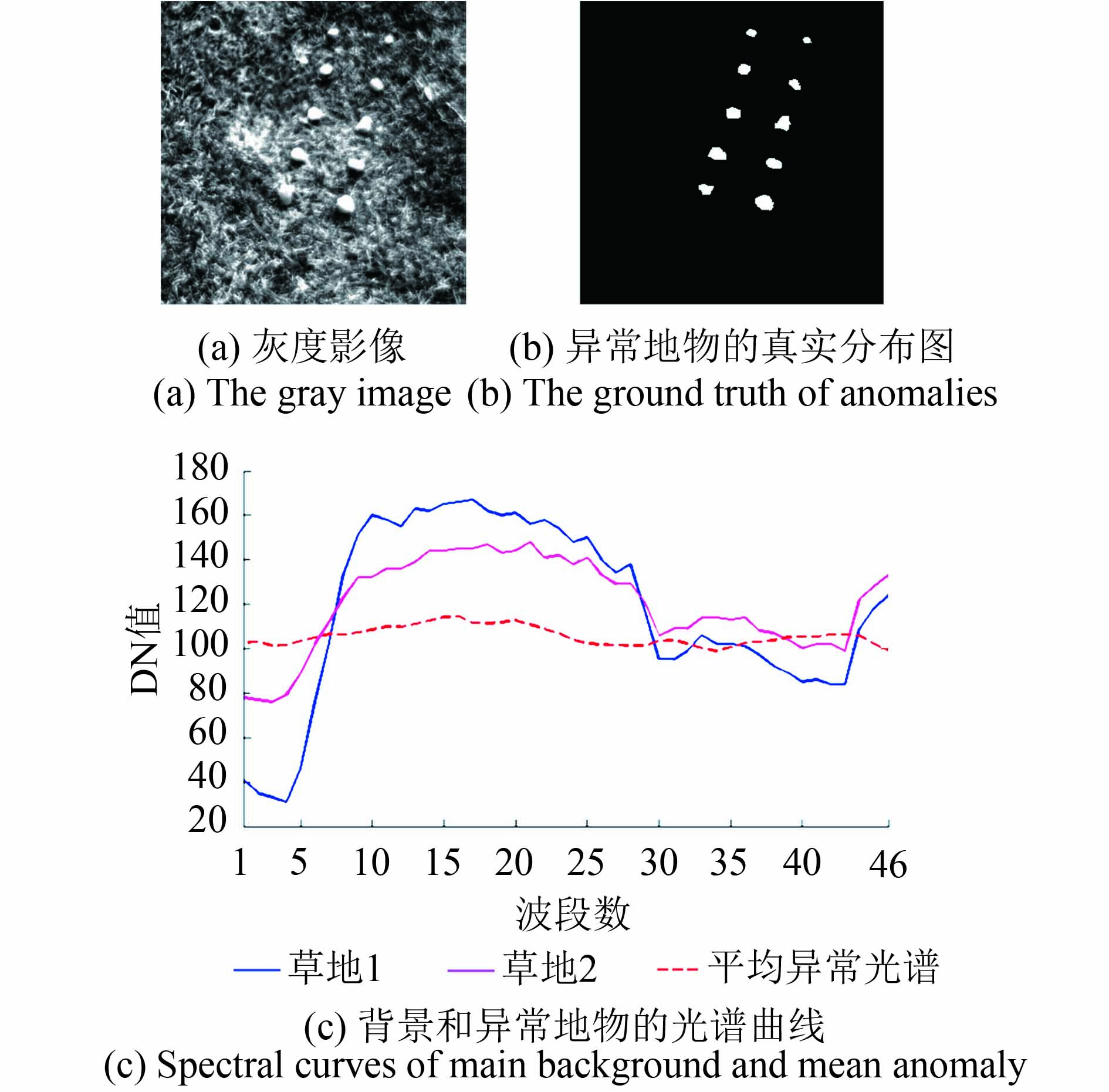
Cri数据由Nuance Cri成像光谱仪采集得到，具有46个光谱波段，覆盖光谱区间为650—1100 nm(Zhang 等，2015)。实验采用原始影像中较小的一块区域，大小为400×400像素(图3(a))。10块石头散落在草地中，占据图像2216个像元。这些石块与主要背景地物的光谱特征差异很大，被认为是场景中的异常信息。图3(b)展示异常像元的实际分布情况，图3(c)展示异常像元和背景像元的光谱响应曲线信息。

图 3 Cri数据信息 Figure 3 The information of Cri dataset

本节利用以上两个高光谱影像数据集来设计两组实验以验证提出的CWRPCA异常探测方法的有效性。第一组实验探讨不同的正则化参数λ对CWRPCA的异常探测性能的影响，试图为后续应用中选取合适的正则化参数λ提供依据。第二组实验对比CWRPCA与5种主流的异常探测方法的探测结果。对比方法包括全局RX算法GRX(Global RX)、两种局部方法双窗口的本征分离转换算法(DWEST)(Kwon 等，2003)和协同表达探测算法CRD(Collaborative Representation based Detector)(Li和Du，2015)，基于传统RPCA模型的低秩稀疏矩阵分解的异常探测算法(LRaSMD)(Sun 等，2014)，以及低秩稀疏表达方法(LRASR)(Xu 等，2016)。采用受试者工作特征ROC(Receiver Operating Characteristic)曲线和ROC曲线的线下面积AUC(Area Under Curve)来定量评价异常探测结果。ROC曲线能够同时描述探测概率和虚警概率，而AUC能够定量评价ROC曲线偏离其理想ROC曲线(AUC=1)的程度。

(1)正则化参数λ对CWRPCA的影响分析

本实验通过改变不同的正则化参数λ来分析其对CWRPCA的探测性能的影响。PaviaC和Cri数据中，正则化参数λ的选择区间人为设定为[0.001, 0.005, 0.01, 0.02, 0.05]。

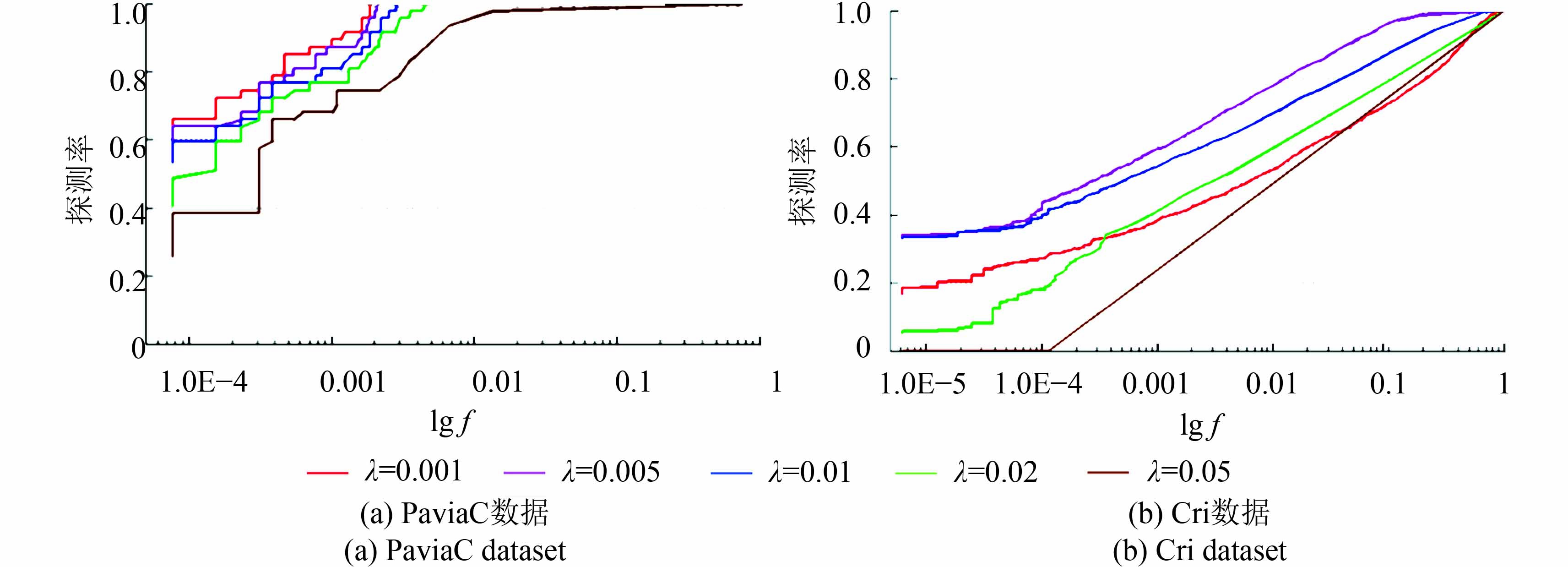
图4展示不同正则化参数λ情况下的CWRPCA在PaviaC和Cri数据中得到的ROC曲线。从图4(a)可以看出，随着λ从0.001增大至0.05，CWRPCA的ROC曲线所表现的探测性能逐渐下降。当λ=0.05时ROC曲线表现最差，达到100%的探测率时具有最大的虚警率(f)。类似地，图4(b)中，ROC曲线所表现出来的CWRPCA探测性能总体呈现下降趋势。当λ从0.001升至0.005时，ROC曲线性能明显提升；在λ=0.005时表现最佳，达到100%的探测率时具有最小的虚警率(f)。随着λ持续增大至0.05时，CWRPCA的探测性能逐渐下降。当λ=0.05时，ROC曲线表现最差。另一方面，表1列出不同λ情况下CWRPCA的ROC曲线的AUC值。可以看出，AUC随着λ的增加整体呈下降趋势，与ROC曲线的结果变化情况一致。因此，可以得出如下结论：正则化参数λ的选取对CWRPCA的探测性能影响较大；较小的λ能够保证CWRPCA能够得到较好的探测结果。

图 4 不同正则化参数λ情况下的ROC曲线 Figure 4 The ROC curves of CWRPCA with different choices of regularized parameter λ

表 1(Table 1)

表 1 不同正则化参数λ情况下的AUC值 Table 1 The AUC values of CWRPCA with different choices of λ 高光谱影像 线下面积AUC λ=0.001 λ=0.005 λ=0.01 λ=0.02 λ=0.05 PaviaC数据 0.9997 0.9996 0.9994 0.9992 0.9878 Cri数据 0.8890 0.9836 0.9626 0.8724 0.4999

表 1 不同正则化参数λ情况下的AUC值 Table 1 The AUC values of CWRPCA with different choices of λ

(2)CWRPCA的探测性能分析

本实验对比CWRPCA与其他5种主流异常探测方法的探测性能。利用交叉验证方法，PaviaC和Cri数据中，DWEST方法的最大窗口大小设置分别为9×9和21×21。利用交叉验证方法，CRD方法中，PaviaC数据的外窗和内窗大小分别设置为5×5和3×3；Cri数据的外窗和内窗大小分别设置为17×17和3×3。利用交叉验证方法，LRaSMD方法中，PaviaC数据的秩数和正则化参数分别设置为2和0.4；Cri数据的秩数和正则化参数分别设置为3和0.6。PaviaC和Cri数据中，LRASR的正则化参数都设置为0.1。利用交叉验证，PaviaC和Cri数据中，CWRPCA的正则化参数分别设置为0.001和0.005。

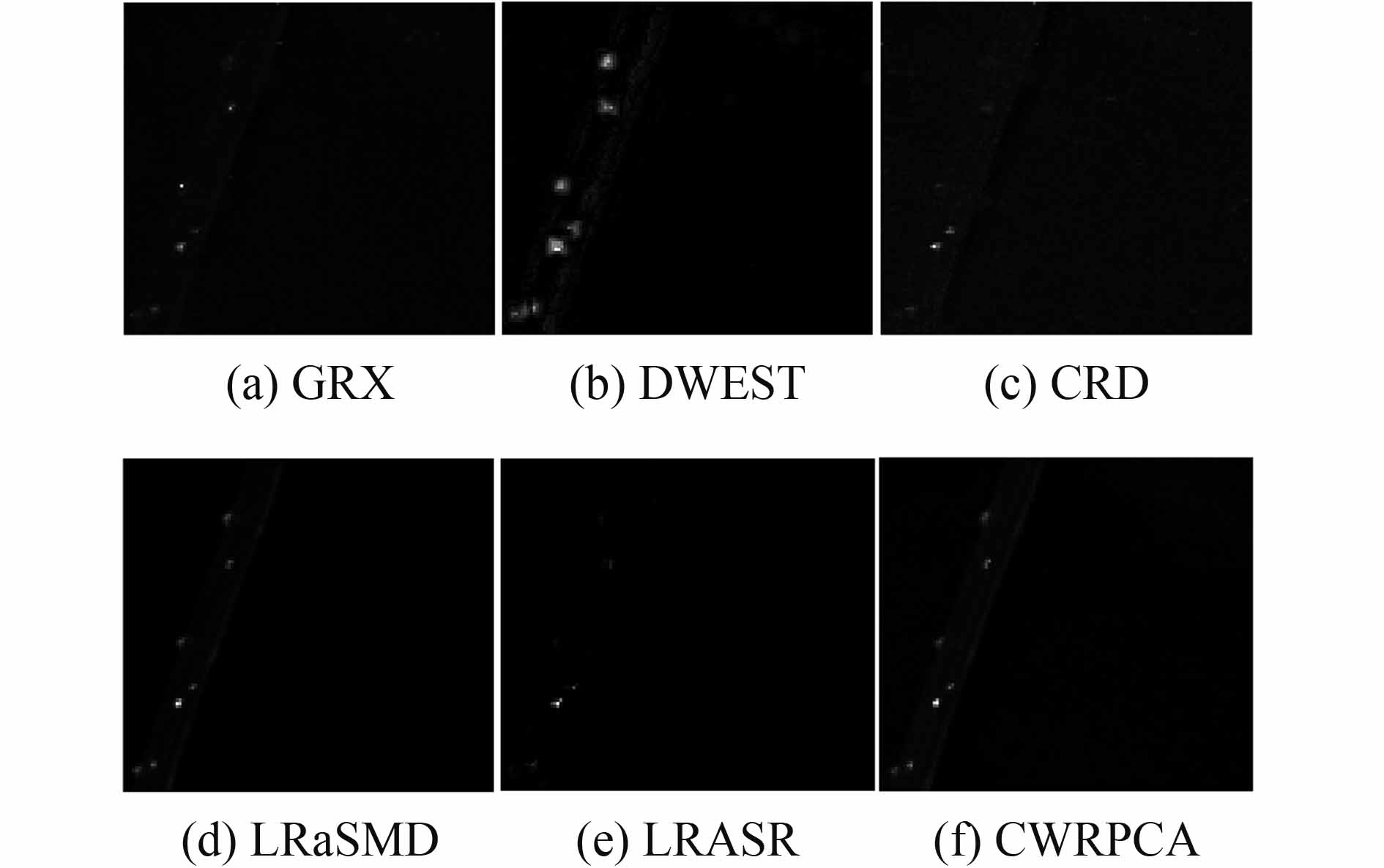
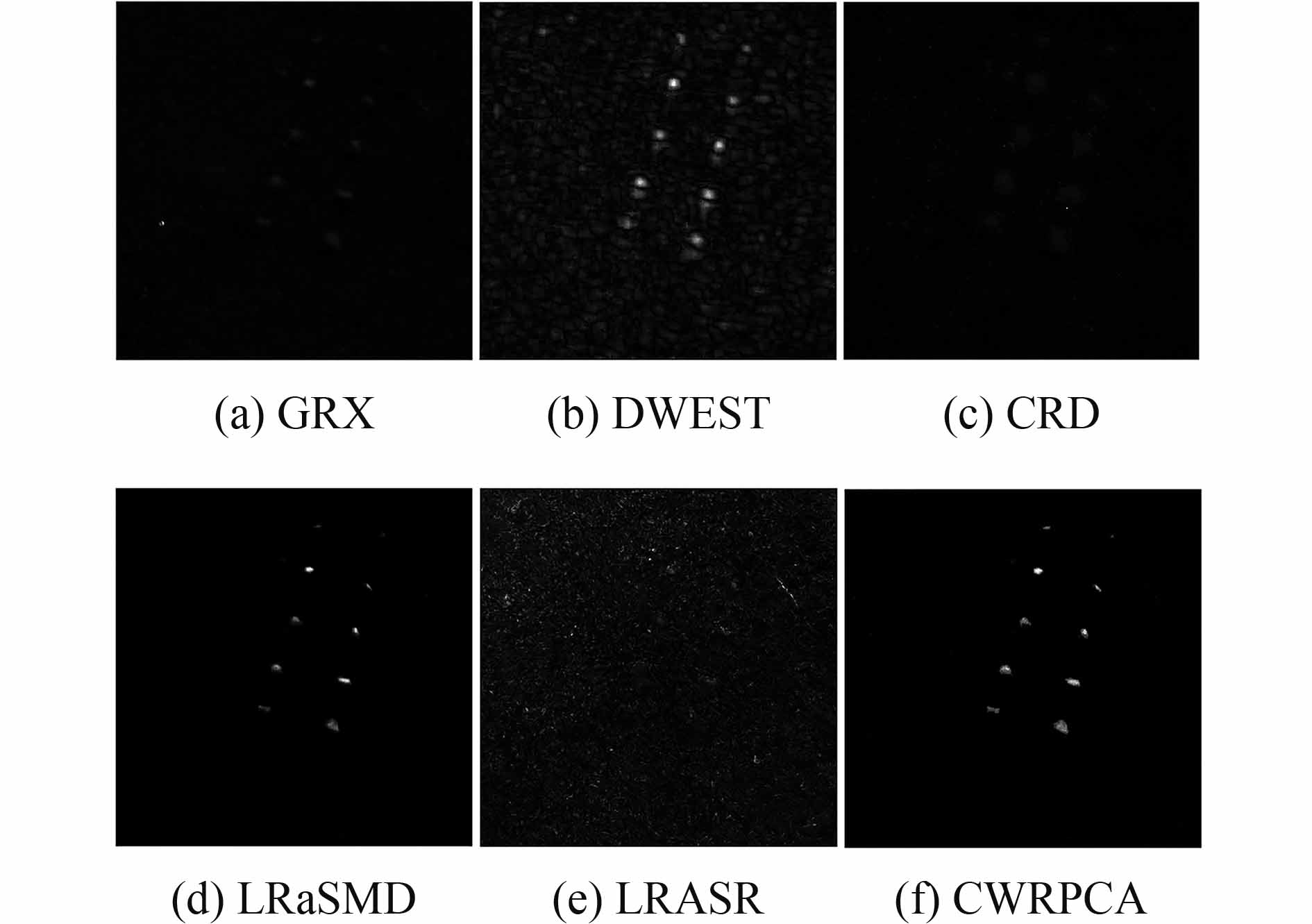
图5为CWRPCA和其他5种方法在PaviaC和Cri数据中得到的ROC曲线。图5(a)中，CWRPCA的ROC曲线明显优于其他5种方法，在同样的虚警率(f)条件下始终具有最高的探测率。LRaSMD方法的ROC优于DWEST、CRD、GRX和LRASR。GRX的ROC曲线优于两种局部方法DWEST和CRD。DWEST和CRD表现不佳的原因解释如下。47个像元的异常信息位于细长的桥梁中部或边界，邻域窗口内背景地物较为复杂，导致其并不满足高斯空间分布假设。6种异常探测方法中，LRASR方法表现最差，探测性能明显低于其他5种方法。图5(b)中，CWRPCA同样优于其他5种方法，在达到100%的探测率时具有最低的虚警率(f)。DWEST方法的ROC曲线优于GRX、LRASR和LRaSMD。表2列出6种异常探测方法在PaviaC和Cri数据中的AUC值。表2中可以看出，CWRPCA方法获得最大的AUC值；LRaSMD方法的AUC大于GRX和LRASR。尤其CWRPCA的ROC曲线和AUC优于LRaSMD，这说明CWRPCA模型能够改善背景信息与异常信息的估计，进而提升异常探测的性能。图6和图7列出6种方法在PaviaC和Cri数据中得到的阈值分割前的2维探测图。

图 5 6种异常探测方法的ROC曲线对比 Figure 5 The contrast in ROC curves from six anomaly detection methods

表 2(Table 2)

表 2 6种异常探测方法的线下面积AUC对比 Table 2 The contrast in AUC from six anomaly detection methods 数据集 异常探测方法 GRX DWEST CRD LRaSMD LRASR CWRPCA PaviaC数据 0.9946 0.9871 0.9822 0.9979 0.9643 0.9997 Cri数据 0.9135 0.9206 0.9612 0.9158 0.7057 0.9836

表 2 6种异常探测方法的线下面积AUC对比 Table 2 The contrast in AUC from six anomaly detection methods

图 6 PaviaC数据的阈值分割前的2维探测图 Figure 6 The detection maps on PaviaC data without thresholding segmentation from GRX, DWEST, CRD, LRaSMD, LRASR, CWRPCA

图 7 Cri数据的阈值分割前的2维探测图 Figure 7 The detection maps on Cri data without thresholding segmentation from GRX, DWEST, CRD, LRaSMD, LRASR, CWRPCA

此外，表3列出6种异常探测方法在PaviaC和Cri数据上的运行时间。6种异常探测方法都通过MALTAB 2014a编程实现，运算环境为Inter(R) CORE(TM) i5-3230M双核处理器，内存为8 GB和Windows 10操作系统。可以看出，GRX的计算效率最高，所需的计算时间最短。LRaSMD计算效率高于CWRPCA、DWEST、LRASR和CRD。LRASR由于包含过多迭代过程，导致计算效率最低。DWEST和CRD的计算效率较低，这是由于遍历所有像元的局部背景信息统计所需的计算时间较长。因此，可以得出如下结论：5种异常探测方法中，CWRPCA的探测性能最优，优于基于传统RCPA的LRaSMD方法；CWRPCA的计算效率适中，LRASR的计算效率最低。

表 3(Table 3)

表 3 6种异常探测方法的计算时间对比 Table 3 The contrast in computation times from six anomaly detection methods 数据集 异常探测方法 GRX DWEST CRD LRaSMD LRASR CWRPCA PaviaC数据 0.144 87.418 29.802 14.116 578.52 60.369 Cri数据 1.902 1271.722 2371.417 85.243 3242.503 364.591

表 3 6种异常探测方法的计算时间对比 Table 3 The contrast in computation times from six anomaly detection methods

本文提出列式鲁棒主成分分析CWRPCA模型来解决传统RPCA用于异常探测时的不足，降低稀疏异常矩阵中非零元素对背景信息估计的影响，增强背景信息和异常信息的分离程度以提升异常探测效果。CWRPCA将非凸优化问题松弛为拉格朗日函数的优化求解问题，采用非精确增强拉格朗日乘子算法IALM来求解得到列稀疏的异常矩阵，进而通过其列向量的L₂范数值的阈值分割来实现异常探测。基于PaviaC和Cri数据来设计两组实验以验证CWRPCA的探测性能。实验结果表明，CWRPCA的探测性能明显优于基于LRaSMD和其他4种方法GRX，DWEST，LRASR与CRD，且所需的计算时间适中。此外，一个较小的正则化参数λ能够使CWRPCA具有较好的异常探测结果。