| 顾及大气延迟效应的YG-13A斜距标定 |
收稿日期: 2017-05-05
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
3. Liaoning Technical University, Fuxin 123000, China
2015年11月,中国发射了一颗高分辨率的星载合成孔径雷达SAR(Synthetic Aperture Radar)卫星——YG-13A,主要用于科学试验、国土资源普查、农作物估产和防灾减灾等领域。与国际上先进的SAR卫星TerraSAR-X(Mittermayer 等,2010)一样,YG-13A有聚束、条带、扫描多种成像模式,且分辨率最高可达0.5 m,它的发射标志着中国雷达遥感卫星分辨率进入了亚米时代。SAR卫星的高分辨率成像不仅受限于卫星的硬件水平,地面处理手段的作用也不可忽视。随着星载SAR影像成像分辨率的不断提高,斜距精度对调频率计算精度的影响越来越大,从而会在成像过程中引入二次相位误差和分辨率的展宽(Cumming和Wong,2007)。另外,斜距精度对定位的影响主要是斜距误差引入了距离向定位误差,制约着SAR影像无控定位精度的提高(刘秀芳 等,2006)。因此,不管是影像的高分辨率成像还是高精度定位,都对SAR系统的斜距精度提出了更高的要求。
SAR系统斜距精度主要受雷达系统收发通道延迟和大气折射延迟的影响(魏钟铨,2001)。对于SAR卫星来说,要实现高的斜距精度,有效的途径就是建立斜距标定模型,利用控制数据标定出斜距测量中的系统误差,从而在成像过程中,对斜距测量值进行修正(Bräutigam 等,2006)。在YG-13A发射之前,国内开展了已有SAR卫星的斜距在轨标定工作。定标数据的处理结果表明,由于系统收发通道延迟等因素的影响,辅助数据给出的斜距值比真实斜距值要大几十米。虽然这几颗卫星都对斜距值进行了标定,但是最终标定出的斜距精度仍然停留在数米量级,与TerraSAR-X卫星厘米级的斜距测量精度相差甚远(Schubert 等,2010;Eineder 等,2011)。
究其主要原因,是在之前国产SAR卫星的斜距标定过程中并没有考虑大气延迟效应的影响,星载SAR在对地面点进行成像时,雷达观测信号穿过大气,大气会反射、折射、散射、吸收雷达观测信号(赵欣 等,2011),导致雷达观测信号的延迟以及相位、振幅的不规则变化等(李松 等,2013)。星载SAR系统是通过记录从卫星平台天线相位中心发射的雷达观测信号在天线相位中心与地面目标点之间的渡越时间来计算斜距的,雷达观测信号在大气中的传播延迟会带来斜距测量的误差,由于大气时空的复杂性和变化性,SAR系统每次对地面成像时,大气折射效应引起的测距延迟都会变化(Noerdlinger,1999),其变化值随着雷达信号入射角和大气环境的改变能达数米量级(Li 等,2016),从而导致标定出的斜距改正值杂糅了大气延迟引起的时变误差。在早期分辨率不高的SAR卫星,例如ERS-1/2的定标过程中,这一影响往往被忽略(Mohr和Madsen,2001),但是新近发射的SAR卫星,随着分辨率的提高,大气延迟效应在斜距标定过程中都会加以考虑(Schwerdt 等,2016)。
目前,星载测距系统主要采用基于外部数据的大气延迟改正方法来计算大气延迟改正值,利用外部数据获取测距时刻的气象数据,并结合大气天顶延迟模型构建卫星测距的距离改正模型(Herring和Quinn,2001;Jehle 等,2008;Doin 等,2009;陈钦明 等,2012)。因此,本文通过构建大气延迟改正模型,在斜距标定过程中,计算出标定景的大气延迟改正量,在此基础上,进行YG-13A斜距测量系统误差量的标定,将该斜距标定精度与未考虑大气延迟时变误差的斜距标定精度进行了对比分析,利用定标场标定出的斜距改正参数对验证区域的影像进行斜距改正,利用检查点检查YG-13A斜距精度。试验结果证明了本文所提出的顾及大气延迟时变误差的斜距标定模型的有效性。
2、斜距标定方法 (2.1) 大气延迟改正模型大气延迟改正模型多写成高度角相关映射函数和大气天顶延迟的乘积(Davis 等,1985):
| $\Delta L{\rm{ = }}m{\rm{(}}\varepsilon {\rm{)}}\int_z^\infty {\left( {n(z) - 1} \right){\rm{d}}z} $ | (1) |
式中,
映射函数模型有多种,其中精度较高的映射函数包括Saastamoinen映射函数、Marini映射函数(Marini 等,1972)、Chao映射函数和CfA2.2模型(Chao,1974)、VMF1映射函数模型(王纯和张捍卫,2009)。映射函数还可近似表示成简单形式:
大气天顶延迟的计算主要分为两部分,包括对流层延时和电离层延时,需要构建大气模型,以此获取大气折射率的空间分布模式。大量的统计表明,大气折射率在垂直方向上的变化比水平方向上的变化大1—3个数量级。因此在构建大气折射率分布模型时,经常忽略大气折射率水平方向的变化,将大气折射率差简化为随高度z变化的量。常用的大气折射率计算模型如下:
| $\left\{ \begin{aligned}& (n(z) - 1) = {10^{ - 6}}N\\ & N = {k_1}\frac{{{P_{\rm{d}}}}}{T} + {k_2}\frac{e}{T} + {k_3}\frac{e}{{{T^2}}} + {k_4}{W_{{\rm{cloud}}}} + {k_5}\frac{{ne}}{{{f^2}}}\end{aligned} \right.$ | (2) |
式中,
SAR具有测距和测多普勒频率的能力。SAR影像每个像素包含了SAR天线到目标的距离信息和天线与目标之间相对运动的多普勒信息,这些信息可以很精确地将影像像素坐标和目标地面位置通过如下3个方程相联系(费文波,2012)。
(1) 距离方程F1
| $\left| {{{{R}}_{\rm{s}}} - {{{R}}_{\rm{t}}}} \right| = {R_{{\rm{near}}}} + {N_{\rm{i}}} \times c \cdot f_{\rm{s}}^{ - 1} \cdot 0.5$ | (3) |
(2) 多普勒方程F2
| ${f_{\rm{d}}} = - \frac{2}{{\lambda \left| {{{{R}}_{\rm{s}}} }- {{{R}}_{\rm{t}}} \right|}}{{{V}}_{\rm{s}}}\left( {{{{R}}_{\rm{s}}}} - {{{R}}_{\rm{t}}} \right)$ | (4) |
(3) 地球模型方程F3
| $\frac{{{x_{\rm{t}}}^2 + {y_{\rm{t}}}^2}}{{{{({R_{\rm{e}}} + {h_{\rm{t}}})}^2}}} + \frac{{{z_{\rm{t}}}^2}}{{{R_{\rm{p}}}^2}} = 1$ | (5) |
式中,
SAR图像的近距
因此,在考虑斜距测量误差情况下,方程F1应写为如下的形式:
| $\left| {{{{R}}_{\rm{s}}} - {{{R}}_{\rm{t}}}} \right| = {R_{{\rm{near}}}} + {N_{\rm{i}}} \times c \cdot f_{\rm{s}}^{ - 1} \cdot 0.5 + \Delta R$ | (6) |
式中,
由于大气引起的斜距延迟具有随时间变化的特性,将这种时变误差与系统误差区分开来,式(6)可以表示为
| $\left| {{{{R}}_{\rm{s}}} - {{{R}}_{\rm{t}}}} \right| = {R_{{\rm{near}}}} + {N_{\rm{i}}} \times c \cdot f_{\rm{s}}^{ - 1} \cdot 0.5 + \Delta {R_{{\rm{delay}}}} + \Delta {R_{{\rm{sys}}}}$ | (7) |
式中,
从而得到,
| $\Delta {R_{{\rm{sys}}}} = \left| {{{{R}}_{\rm{s}}} - {{{R}}_{\rm{t}}}} \right| - ({R_{{\rm{near}}}} + {N_{\rm{i}}} \times c \cdot f_{\rm{s}}^{ - 1} \cdot 0.5) - \Delta {R_{{\rm{delay}}}}$ | (8) |
通过已知地面坐标和像素坐标的角反射器点基于SAR影像距离多普勒方程即可求出斜距测量的系统误差量
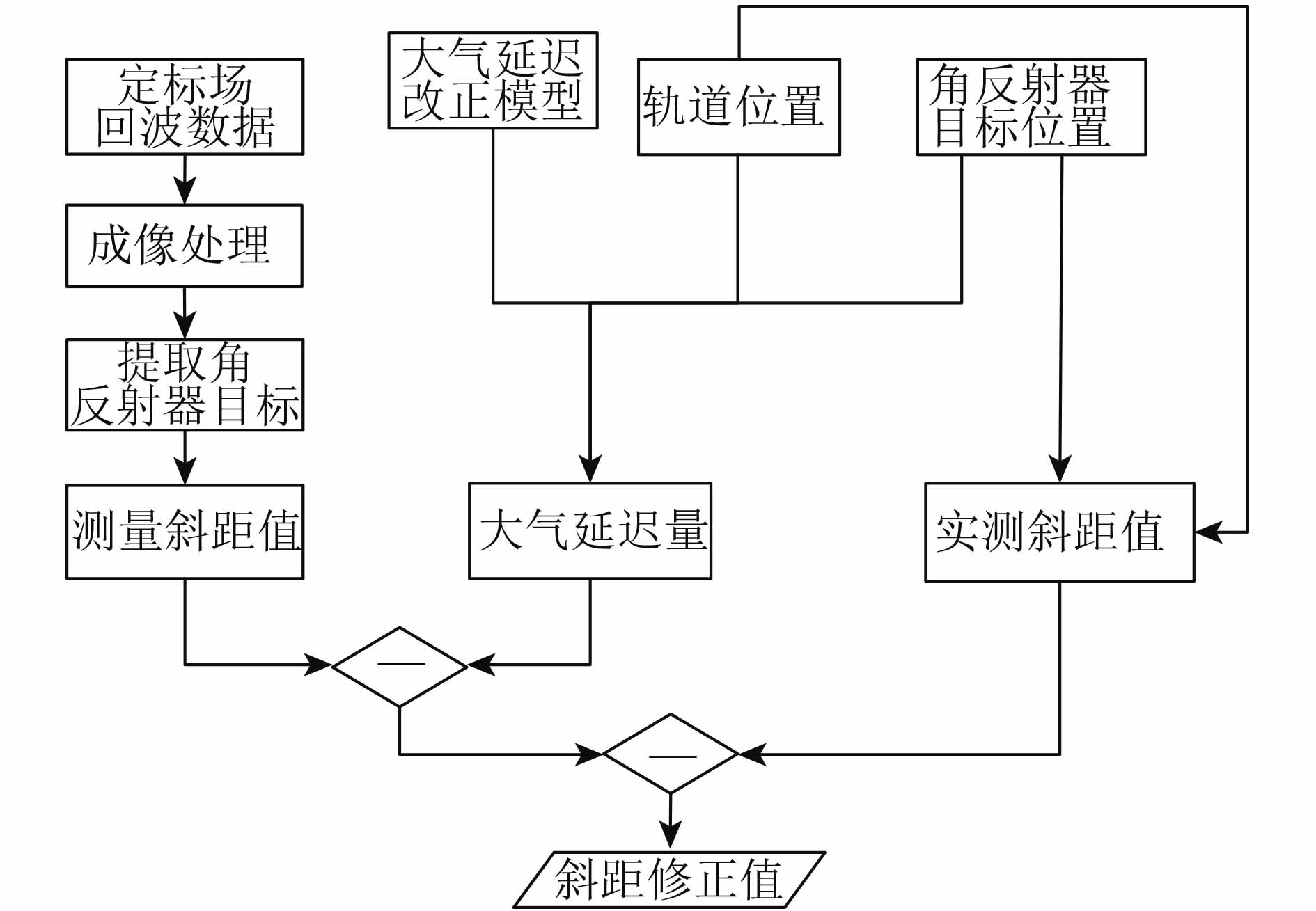
|
| 图 1 算法流程图 Figure 1 Algorithm flow chart |
采用YG-13A的1B级数据产品作为试验数据,包含影像数据和对应的辅助测量数据。收集嵩山定标场区域的试验数据,嵩山定标场位于河南登封嵩山地区。嵩山定标场的范围为112.811°E—113.356°E,34.255°E—34.634°E,区域内海拔高度在100—1500 m。该区域内现布设有6个高精度的角反射器装备,可用作SAR影像的高精度地面控制,自动角反射器在嵩山定标场内的分布情况如图2所示。
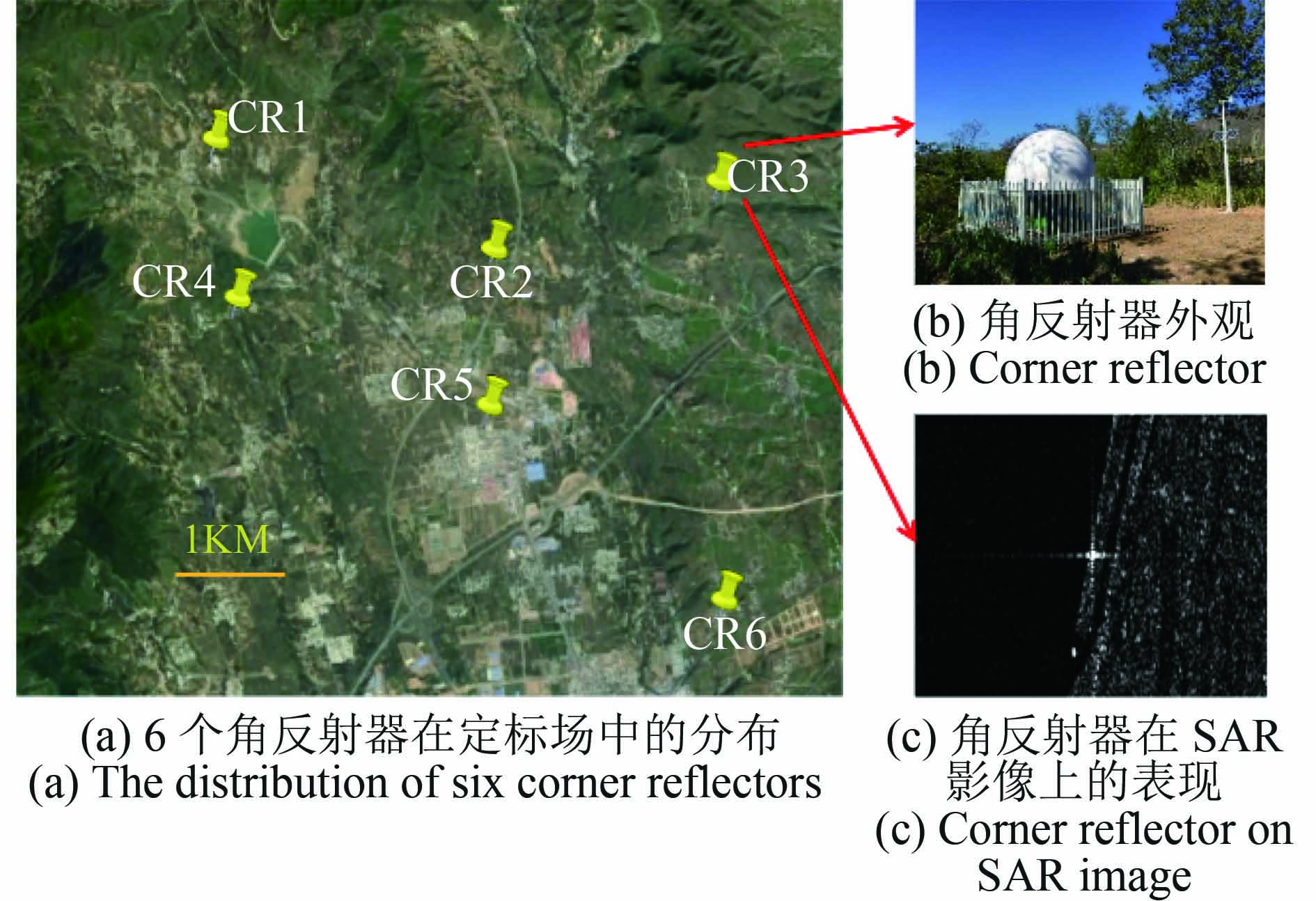
|
| 图 2 嵩山定标场 Figure 2 Songshan test site |
共收集了该定标场区域14景条带模式的数据。从雷达信号特性的角度出发,雷达系统以脉冲信号的前沿记为发射时刻,而接收时刻通过对相应的接收通路脉冲压缩,并分析脉压后峰值相对零时刻的时间得到,因此不同带宽时宽下的系统时延会略有差异,按照时宽带宽将试验样本分为A/B两组,A组(200 Mhz&24.4 us),B组(150 Mhz&24.4 us)
另外,由于SAR卫星成像时,需要根据卫星轨道类型以及左右侧视调整地面角反射器的朝向,从而会引入角反射器像点坐标误差,因此根据卫星轨道类型的不同将A组分为A1组(200 Mhz&24.4 us&升轨右侧视)、A2组(200 Mhz&24.4 us&降轨右侧视),将B组分为B1组(150 Mhz&24.4 us&升轨右侧视)、B2组(150 Mhz&24.4 us&降轨右侧视), 这样使得同一组内数据获取时角反射器的摆放姿态较为一致,减少了角反射器点位误差对实验结果的干扰。
(3.2) 试验方案设计为了验证大气延迟改正模型在斜距标定中的有效性,主要采用以下两种方案进行对比试验。
方案一:不顾及雷达观测信号在大气中传播时变误差的存在,利用高精度的地面角反射器控制点,直接分别计算A1、A2、B1、B2 4组数据中的斜距改正值,统计A1、A2、B1、B2 4组斜距改正值的均值和标准差;顾及雷达观测信号在大气中传播时变误差的存在,先分别计算出每一标定景的大气延迟改正值,在此基础上,利用高精度的地面角反射器控制点,分别计算A1、A2、B1、B2 4组数据中的斜距改正值,统计A1、A2、B1、B2 4组斜距改正值的均值和标准差。对比两种情况下4组数据斜距改正值的均值和标准差。
方案二:选取验证区域的YG-13A影像,采用定标场标定出的相应成像模式系统时延和相应区域的大气和电离层数据进行斜距校正,通过已知像平面坐标和地面坐标的检查点来检验斜距改正后的YG-13A影像斜距精度。
(3.3) 斜距标定对比试验采用3.2节所设计的试验方案,进行了YG-13A斜距标定的对比试验。在不顾及大气延迟时变误差的情况下,A1、A2、B1、B2 4组数据斜距改正值如表1、表2、表3、表4所示,其中∆Rsys表示斜距改正值,Stddev表示该组数据标准差,Mean表示该组数据均值。
|
|
表 1 不顾及大气时变误差的A1组斜距改正值 Table 1 Group A1 range correction value without regard for atmosphere path delay |
|
|
表 2 不顾及大气时变误差的A2组斜距改正值 Table 2 Group A2 range correction value without regard for atmosphere path delay |
|
|
表 3 不顾及大气时变误差的B1组斜距改正值 Table 3 Group B1 range correction value without regard for atmosphere path delay |
|
|
表 4 不顾及大气时变误差的B2组斜距改正值 Table 4 Group B2 range correction value without regard for atmosphere path delay |
分别对比表1和表2以及表3和表4可知,在同一时宽带宽情况下,不同轨道类型的斜距改正均值略有差异,说明不同拍摄状态下SAR斜距的系统误差并不完全相同。
基于大气延迟改正模型,计算各标定景斜距改正值,实时大气数据来自美国NCEP(National Centers for Environmental Prediction)发布的气象资料,时间间隔为6 h,空间间隔为1°(经度)×1°(纬度)。电离层电子密度数据采用欧洲定轨中心(CODE)提供的全球TEC数据,时间间隔为2 h,空间间隔为5°(经度)×2.5°(纬度)。A1、A2、B1、B2 4组数据各标定景大气延迟改正值如表5、表6、表7、表8所示,其中∆Rdelay表示大气延迟改正值。
|
|
表 5 A1组数据大气延迟改正值 Table 5 Group A1 atmosphere path delay value |
|
|
表 6 A2组数据大气延迟改正值 Table 6 Group A2 atmosphere path delay value |
|
|
表 7 B1组数据大气延迟改正值 Table 7 Group B1 atmosphere path delay value |
|
|
表 8 B2组数据大气延迟改正值 Table 8 Group B2 atmosphere path delay value |
结合表5、表6、表7、表8来看,各标定景大气延迟改正值主要受入射角大小的影响,随着入射角变大,雷达观测信号在大气中传播的距离越长,大气延迟效应越明显。在入射角为54.5°时,大气延迟改正值达到了5.02 m。
在修正了各标定景大气延迟改正值的基础上,再进行斜距标定,A1、A2、B1、B2 4组数据斜距改正值如表9、表10、表11、表12所示。
|
|
表 9 顾及大气时变误差的A1组斜距改正值 Table 9 Group A1 range correction value with considering of atmosphere path delay |
|
|
表 10 顾及大气时变误差的A2组斜距改正值 Table 10 Group A2 range correction value with considering of atmosphere path delay |
|
|
表 11 顾及大气时变误差的B1组斜距改正值 Table 11 Group B1 range correction value with considering of atmosphere path delay |
|
|
表 12 顾及大气时变误差的B2组斜距改正值 Table 12 Group B2 range correction value with considering of atmosphere path delay |
同样,分别对比表9和表10以及表11和表12,在同一时宽带宽情况下,不同轨道类型的斜距改正均值略有差异,与未消除大气时变延迟的标定结果体现出来的规律一致,因此在对YG-13A进行斜距标定过程中,应根据雷达信号时宽带宽、卫星轨道类型以及左右侧视分别进行标定,得出各拍摄模式下的斜距改正参数。
分别对比A1、A2、B1、B2 4组数据未消除大气时变误差和消除大气时变误差两种情况下的斜距标定结果,如表13所示。
|
|
表 13 斜距标定结果对比 Table 13 Comparison of slant range calibration results |
从表13中可以看出,在顾及大气延迟效应情况下,A1、A2、B1、B2 4组数据斜距标定值标准差变小,说明斜距标定值离散程度减小,验证了顾及大气延迟效应的YG-13A斜距标定方法的有效性。
收集了3景验证区域的影像验证斜距校正后的YG-13A斜距精度。验证景的信息如表14所示。
|
|
表 14 验证影像信息 Table 14 Test image information |
根据实时大气延迟改正模型计算出各标定景大气延迟改正值,再结合标定出的各相应拍摄模式下斜距系统误差对验证景影像进行斜距校正,天津区域利用1∶2000的DOM和DEM作为检查数据,太原地区利用1∶5000的DOM和DEM作为检查数据,检查斜距校正后的YG-13A斜距精度。斜距校正精度如表15所示。
校正后的影像斜距精度主要受4个方面的因素影响,包括卫星轨道位置误差、大气延迟改正误差、斜距标定误差、检查点点位误差。从表15中可以看出,3景验证影像的斜距精度最小值为0.55 m,最大值为0.91 m,均值为0.70 m。考虑到YG-13A搭载的是单频GPS,其卫星轨道位置处理之后的标称精度为0.3 m以内,加上1个像素左右的选点误差,说明本试验结果是合理的。
|
|
表 15 斜距校正精度 Table 15 Slant range correction accuracy |
斜距精度一直是制约国产SAR卫星几何精度提升的主要因素,本文通过分析大气对星载SAR观测信号传播的延迟影响,建立大气延迟改正模型,并将其应用于YG-13A斜距标定模型中;实验利用YG-13A数据对顾及了大气延迟时变误差的斜距标定模型加以验证,得到以下结论:
(1) 雷达观测信号在大气中的传播延迟误差与雷达视角相关,视角越大,雷达观测信号在大气中传播的路径越长,大气折射效应引起的雷达观测信号传播延迟值越大。对于高分辨率SAR卫星来说,高达数米的大气折射延迟量必须加以改正。
(2) 在顾及大气延迟时变误差的前提下,获取YG-13A多个拍摄模式下的斜距改正参数,利用太原、天津区域的影像进行斜距精度验证,三景验证影像的斜距精度最小值为0.55 m,最大值为0.91 m,均值为0.70 m。说明本文提出的顾及大气延迟时变误差的YG-13A斜距标定方法是有效的。
(3) 由于YG-13A搭载的是单频GPS,其轨道精度在0.3 m左右,而搭载了双频GPS的TerraSAR-X卫星其轨道精度在厘米量级,因此TerraSAR-X的斜距测量精度可达厘米量级。排除检查点选点误差的影响,本文的试验结果也表明轨道精度是限制YG-13A斜距测量精度的最主要因素。分米级的斜距测量精度使得YG-13A影像在不依赖地面控制设备情况下的控制点获取、目标定位等方面有广阔的应用前景。
(4) 随着国产星载SAR卫星定轨精度的提高,厘米级斜距测量精度的实现指日可待,但是厘米级的斜距测量精度也将会对地面角反射器的定位精度以及像点坐标提取精度等提出新的挑战。如何获取高精度的控制数据来进行斜距精度的提升与验证是值得考虑的研究角度。
本文利用YG-13A条带模式的数据验证了顾及大气延迟时变误差的斜距标定模型的正确性,后续将增加其他成像模式的斜距标定试验以进一步验证该方法的适用性。
| [1] | Bräutigam B, Schwerdt M and Bachmann M. 2006. The external calibration of TerraSAR-X, a multiple mode SARSystem//Proceedings of the 6th European Conference on Synthetic Aperture Radar. Dresden, Germany: VDE |
| [2] | Chao C C. 1974. The Tropospheric Calibration Model for MARINER MArs 1971. Technical Report 32–1587. Pasadena, California: JPL: 61–76. |
| [3] | 陈钦明, 宋淑丽, 朱文耀. 亚洲地区ECMWF/NCEP资料计算ZTD的精度分析[J]. 地球物理学报, 2012, 55 (5) : 1541 –1548. Chen Q M, Song S L and Zhu W Y. An analysis of the accuracy of zenith tropospheric delay calculated from ECMWF/NCEP data over Asian area[J]. Chinese Journal of Geophysics, 2012, 55 (5) : 1541 –1548. DOI: 10.6038/j.issn.0001-5733.2012.05.011 |
| [4] | Cumming I G, Wong F H. 2007. 合成孔径雷达成像——算法与实现. 洪文, 胡东辉, 译. 北京: 电子工业出版社 Cumming I G and Wong F H. 2007. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation. Hong W and Hu D H, trans. Beijing: Electronic Industries Press: 155–191 |
| [5] | Davis J L, Herring T A, Shapiro I I, Rogers A E E and Elgered G. Geodesy by radio interferometry: effects of atmospheric modeling errors on estimates of baseline length[J]. Radio Science, 1985, 20 (6) : 1593 –1607. DOI: 10.1029/RS020i006p01593 |
| [6] | Doin M P, Lasserre C, Peltzer G, Cavalié O and Doubre C. Corrections of stratified tropospheric delays in SAR interferometry: validation with global atmospheric models[J]. Journal of Applied Geophysics, 2009, 69 (1) : 35 –50. DOI: 10.1016/j.jappgeo.2009.03.010 |
| [7] | Eineder M, Minet C, Steigenberger P, Cong X Y and Fritz T. Imaging geodesy—toward centimeter-level ranging accuracy with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49 (2) : 661 –671. DOI: 10.1109/TGRS.2010.2060264 |
| [8] | 费文波. 2012. RPC模型在星载SAR与星载InSAR几何处理中的研究与应用. 武汉: 武汉大学: 20–22 Fei W B. 2012. Research and Application of the RPC Model Geometry Processing for Spaceborne SAR and Spaceborne InSAR. Wuhan: Wuhan University: 20–22 |
| [9] | Herring T A and Quinn K. 2001. Atmospheric Delay Correction to GLAS Laser Altimeter Ranges. http://www.csr.utexas.edu/glas/atbd-tropo.pdf |
| [10] | Jehle M, Perler D, Small D, Schubert A and Meier E. Estimation of atmospheric path delays in TerraSAR-X data using models vs[J]. measurements. Sensors (Basel), 2008, 8 (12) : 8479 –8491. DOI: 10.3390/s8128479 |
| [11] | 李松, 肖建明, 马跃, 周辉, 郭想. 星载激光测高系统的大气折射延迟改正模型研究[J]. 光学与光电技术, 2013, 11 (1) : 7 –11. Li S, Xiao J M, Ma Y, Zhou H and Guo X. Study on atmospheric refraction delay correction for satellite laser altimeter system[J]. Optics and Optoelectronic Technology, 2013, 11 (1) : 7 –11. DOI: 1672-3392(2013)01-0007-05 |
| [12] | Li S N, Zhang G, Tang X M and Huang W C. A method for detecting the atmospheric refraction effect using satellite remote sensing[J]. Remote Sensing Letters, 2016, 7 (10) : 985 –993. DOI: 10.1080/2150704X.2016.1199082 |
| [13] | 刘秀芳, 刘佳音, 洪文. 星载SAR图像的定位精度分析研究[J]. 遥感学报, 2006, 10 (1) : 76 –81. Liu X F, Liu J Y and Hong W. The analysis of the precision in spaceborne SAR image location[J]. Journal of Remote Sensing, 2006, 10 (1) : 76 –81. DOI: 10.11834/jrs.2006011 |
| [14] | Marini J W. Correction of satellite tracking data for an arbitrary tropospheric profile[J]. Radio Science, 1972, 7 (2) : 223 –231. DOI: 10.1029/RS007i002p00223 |
| [15] | Mittermayer J, Younis M, Metzig R, Wollstadt S, Martinez J M and Meta A. TerraSAR-X System performance characterization and verification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48 (2) : 660 –676. DOI: 10.1109/TGRS.2009.2026742 |
| [16] | Mohr J J and Madsen S N. Geometric calibration of ERS satellite SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39 (4) : 842 –850. DOI: 10.1109/36.917909 |
| [17] | Nitti O D, Bovenga F, Nutricato R, Refice A, Bruno M F, Petrillo A F and Chiaradia M T. 2013. On the use of numerical weather models for improving SAR geolocation accuracy//Proceedings of the 10th European Conference on Synthetic Aperture Radar. Berlin, Germany: IEEE: 1–4 |
| [18] | Noerdlinger P D. Atmospheric refraction effects in earth remote sensing[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54 (5/6) : 360 –373. DOI: 10.1016/S0924-2716(99)00030-1 |
| [19] | Schubert A, Jehle M, Small D and Meier E. Influence of atmospheric path delay on the absolute geolocation accuracy of TerraSAR-X high-resolution products[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48 (2) : 751 –758. DOI: 10.1109/TGRS.2009.2036252 |
| [20] | Schwerdt M, Schmidt K, Ramon N T, Alfonzo G C, Döring B J, Zink M and Prats-Iraola P. Independent verification of the sentinel-1A system calibration[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9 (3) : 994 –1007. DOI: 10.1109/JSTARS.2015.2449239 |
| [21] | 王纯, 张捍卫. 大气折射延迟映射函数的比较[J]. 地理空间信息, 2009, 7 (6) : 85 –87. Wang C and Zhang H W. Comparison of atmospheric refraction delay mapping function[J]. Geospatial Information, 2009, 7 (6) : 85 –87. DOI: 10.3969/j.issn.1672-4623.2009.06.027 |
| [22] | Wang X W, Cheng X, Gong P, Huang H B, Li Z and Li X W. Earth science applications of ICESat/GLAS: a review[J]. International Journal of Remote Sensing, 2011, 32 (23) : 8837 –8864. DOI: 10.1080/01431161.2010.547533 |
| [23] | 魏钟铨. 2001. 合成孔径雷达卫星. 北京: 科学出版社: 17–22 Wei Z Q. 2001. Synthetic Aperture Radar Satellite. Beijing: Science Press: 17–22 |
| [24] | 赵欣, 张毅, 赵平建, 涂碧海. 星载激光测高仪大气传输延迟对测距精度的影响[J]. 红外与激光工程, 2011, 40 (3) : 438 –442. Zhao X, Zhang Y, Zhao P J and Tu B H. Influence of atmospheric transmission delay of satellite laser altimeter on ranging precision[J]. Infrared and Laser Engineering, 2011, 40 (3) : 438 –442. DOI: 10.3969/j.issn.1007-2276.2011.03.012 |
| [25] | 朱陶业, 朱建军, 张学庄, 郭云开. 大气折射的映射函数与神经网络拟合比较分析[J]. 测绘学报, 2007, 36 (3) : 290 –295. Zhu T Y, Zhu J J, Zhang X Z and Guo Y K. Atmospheric refraction numerical fitting research based on mapping function and neural network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36 (3) : 290 –295. DOI: 10.3321/j.issn:1001-1595.2007.03.009 |

