高光谱遥感采用数十个乃至数百个很窄光谱波段对地物进行遥感成像，从而获取高光谱分辨率的影像(张春森 等，2015)。相比于其他影像，高光谱的特性使其在地物鉴别及影像分类上更具优势。随着高光谱影像在很多相关领域应用越来越广泛，处理方法也越来越多。主要处理步骤包括影像的特征提取或特征选择，其目的是在保留影像中主要特征的同时尽可能移除高光谱影像的冗余信息(Quesada-Barriuso 等，2014)。

由于高光谱影像往往还具有较高的空间分辨率，将空间及光谱特征结合应用于高光谱影像分类中已经成为高光谱影像解译主要方法之一(Mura 等，2011)。本文中所指“空间特征”是指由像素及其邻域内像素通过数学运算获取的反映影像局部空间特性的数值。如Ji等人(2014)提出使用空间光谱约束的方法进行影像分类。Shen等人(2011)将多频段和方向的Gabor纹理特征与光谱特征融合用于高光谱影像分类，分类精度得到提升。Huang等人(2007)从多个窗口提取基于灰度共生矩阵的特征，并加以特征融合，实现了全色影像的高效分类。Benediktsson等人(2005)提出应用拓展形态特征与光谱特征结合的分类方法，其分类结果要优于纯光谱分类方法。刘纯等人(2015)通过分割得到多尺度区域特征，融合光谱及像元形状指数，输入支持向量机分类器，优化了影像分类结果。郑晨等人(2013)提出一种多尺度区域粒度特征，能够从大尺度上提取出地物整体信息，从小尺度上获取地物细节特征。季江等人(2015)提出一种多尺度窗口的噪声平滑方法，对光谱有良好的平滑效果。

综合来看，影像空间特征主要包含区域形状特征(刘纯 等，2015；黄昕 等，2007)、纹理特征(Huang 等，2007；刘萌萌 等，2014；余旭初 等，2014；尹明 等，2015)及形态滤波特征(Benediktsson 等，2005；Licciardi 等，2012)等。其中，形态滤波利用事先定义好形状及大小的结构元素对影像进行开或闭运算，能够较好地滤除噪声和保留地物空间结构特征，近年获得了广泛的关注。但是，这类多尺度滤波方法多采用多向同性的滤波器，不能同时实现地物平滑和有效地保留地物的结构信息。

引导滤波建立了引导影像和输出的局部线性模型，并通过输入与输出影像间差异函数的求解，隐式地完成对输入影像的滤波(He 等，2013)。除了能实现基本的平滑滤波功能，引导滤波还能将引导影像中的空间边缘信息较完整的转移到输出影像中。引导滤波算法已在影像融合(Li 等，2013；Zhao 等，2015)和影像增强(He 等，2013)等方面报道了应用。考虑引导滤波的这一特性，同时考虑到单一尺度特征难以表达高分辨率高光谱遥感影像中地物的多尺度结构信息的不足，本文提出一种基于引导滤波的多尺度空间特征提取方法，并采用多种分类器进行分类验证。该方法利用引导滤波提取影像中地物不同尺度的空间信息，可有效提高分类精度。

本节首先介绍引导滤波的原理，然后提出基于引导滤波的多尺度特征提取和影像分类方法。

引导滤波是近年来出现的一种性能优异的边缘保存滤波器，能够使输出影像同时保留被滤波影像特征和较好的载入引导影像的边缘信息(He 等，2013)。

本质上，引导滤波影像处理建立在引导影像和输入影像之间的局部线性关系模型之上。假设引导影像为 ${{I}}$ ，输入影像为 ${{p}}$ ，则滤波输出影像 ${{q}}$ 由一个以像素k为中心以 $r$ 为半径的窗口 ${{\omega} _k}$ 内的局部线性模型获得，即

式中， ${{\omega}_k}$ 是以像素 $k$ 为中心，长宽为 $2 \times r + 1$ 的正方形窗口； ${{{a}}_k}$ 和 ${b_k}$ 均是线性模型的待估参数，在窗口 ${{\omega}_k}$ 内保持不变， ${{{a}}_k}$ 是维数与引导影像 ${{I}}$ 波段数一致的向量， ${b_k}$ 为标量。

然后，为估计线性模型的参数 ${{{a}}_k}$ 和 ${b_k}$ ，基于输入影像 ${{p}}$ 与输入影像 ${{q}}$ 之间的差值，建立代价函数

式中， $\varepsilon $ 是一个避免 ${{{a}}_k}$ 过大的正则化参数。

最后，采用岭回归技术(Hastie 等，2009) 进行参数估计。通过最小化代价函数式(2)，可求解出系数 ${{{a}}_k}$ 和 ${b_k}$

式中, ${{{\mu }}_k}$ 和 $\sigma _k^2$ 分别表示引导影像 ${{I}}$ 在窗口中的均值和方差， $\left| \omega \right|$ 是窗口内的像素数， ${\overline p _k}$ 是输入影像 ${{p}}$ 在窗口内的均值。

由于同一个像素i可位于多个不同的窗口内，导致 $\left\{ {{{{a}}_k}, {b_k}} \right\}$ 和q_i的值会发生变化，需计算出以像素 $i$ 为中心窗口内 $\left\{ {{{{a}}_k}, {b_k}} \right\}$ 的均值，进而计算出q_i的平均值(He 等，2013)

通过式(1)可以看出在窗口中输出影像与输入影像是线性关系，即 $\Delta {q_i} = {a_k}\Delta {I_i}$ 。因此，当引导影像I中包含边缘信息时，输出影像 $q$ 就会保留相应位置上的边缘信息。在采取上述平均化策略后，式(6)仍有 $\Delta {q_i} \approx \overline {{a_i}} \Delta {{{I}}_i}$ ，即引导滤波输出仍能保存引导影像中的主要边缘信息。

由上述估计过程式(2)—(6)可知，引导滤波计算过程中涉及两个重要参数：滤波半径大小 $r$ 和正则化参数 $\varepsilon $ 。其中，滤波半径大小 $r$ 控制滤波窗口大小。窗口越大，平滑的效果越明显，体现的影像细节越少。正则化参数 $\varepsilon $ 决定了待估计参数 $\left\{ {{{{a}}_k}, {b_k}} \right\}$ 的范围。 $\varepsilon $ 越大，正则化效果越强。 $\varepsilon $ 的作用类似于局部块的方差阈值(He 等，2013)，即大于方差的局部块将被平滑，否则加以保留。之前的研究发现 $\varepsilon $ 取值对滤波结果的影响较小(Li 等，2013)，故本研究设置该参数为固定值10^–4。

理论上，由于地物本身具有尺度属性，其空间特征也往往需要在不同尺度上加以度量。特征提取的多尺度可以通过不同频率和方向的滤波器模板(Shen和Jia，2011；张刚和马宗民，2010)，不同大小的提取窗口(Huang 等，2007)，不同大小的结构元素(Benediktsson 等，2005, 2003)以及不同大小的分割区域(刘纯 等，2015；Wang 等，2015)实现。

受其启发，本文采用不同大小的窗口序列进行引导滤波，实现多尺度的影像平滑滤波，以表征不同尺度的影像细节。由于引导滤波具有良好的局部梯度保持特性，因此相比现有方法，基于引导滤波的空间特征能更好的保持地物的边界信息。

具体来说，由于第一主成分(PC₁)包含了原始影像中最主要的信息，保留了原始影像中绝大部分的边界，故以其作为引导影像，对多个波段进行滤波处理。引导滤波多尺度特征集的获取过程如下：

对波段B_i分别采用半径为1–r的窗口进行引导滤波，获得的多尺度引导滤波特征MGFF(Multi-scale guided filter features)可表示为

式中， $W_G^r\left({{{B}_i}} \right)$ 表示以波段G(第1主成分)为引导影像，以r为半径对 ${{{B}}_i}$ 波段进行处理，获得的滤波特征。

在得到所有d个波段的MGFF后，通过特征向量的堆叠可以组合成整幅影像的多尺度引导滤波特征集，即

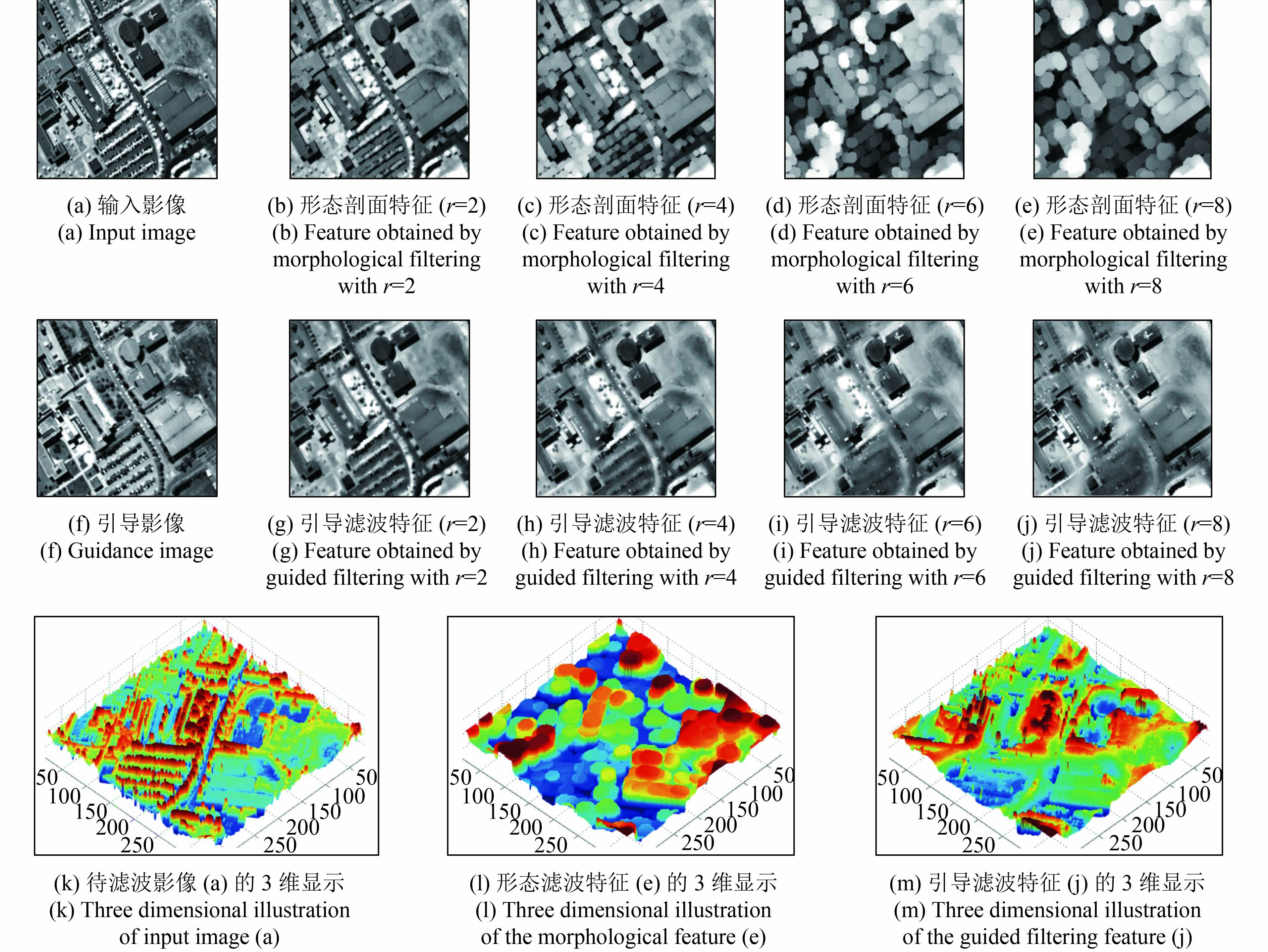
以高光谱数据Pavia University(Gamba 等，2016)的第二主成分(PC₂)为输入图像(图1(a))，图1给出了拓展形态滤波特征(Benediktsson 等，2005)和多尺度引导滤波特征的对比。采用窗口半径分别为2，4，6，8的圆形结构元素，形态滤波特征如图1(b)—(e)。采用窗口半径r为2，4，6，8的方形窗口，以第一主成分(PC₁)为引导影像(图1(f))，引导滤波特征如图1(g)—(i)。图1(k)—(m)以3维显示的方式，对比了采用相似尺度滤波后地物结构的保留情况。其中，X，Y坐标为影像的行列号，Z坐标为影像像元的灰度值。

由图1可见：半径为2和4的两种滤波影像基本都能够较好的提取出地物的结构特征，而半径为6和8的滤波影像中地物结构特征差别较大；仅用单一尺度不能有效的提取出不同大小地物的结构特征。对比原影像和滤波结果的3维图中还可以看出：引导滤波后的影像保留了原影像的主要边缘信息，而半径为8的形态滤波仅能识别地物的大致轮廓。因此，相比形态滤波，引导滤波具有更好地保留影像结构信息的能力。

图 1 多尺度引导滤波特征与多尺度形态剖面特征(Benediktsson 等，2005)的对比 Figure 1 Comparison between Multi-scale Guided Filtering Features (MGFF) and Extended Morphological Profiles (EMPs)

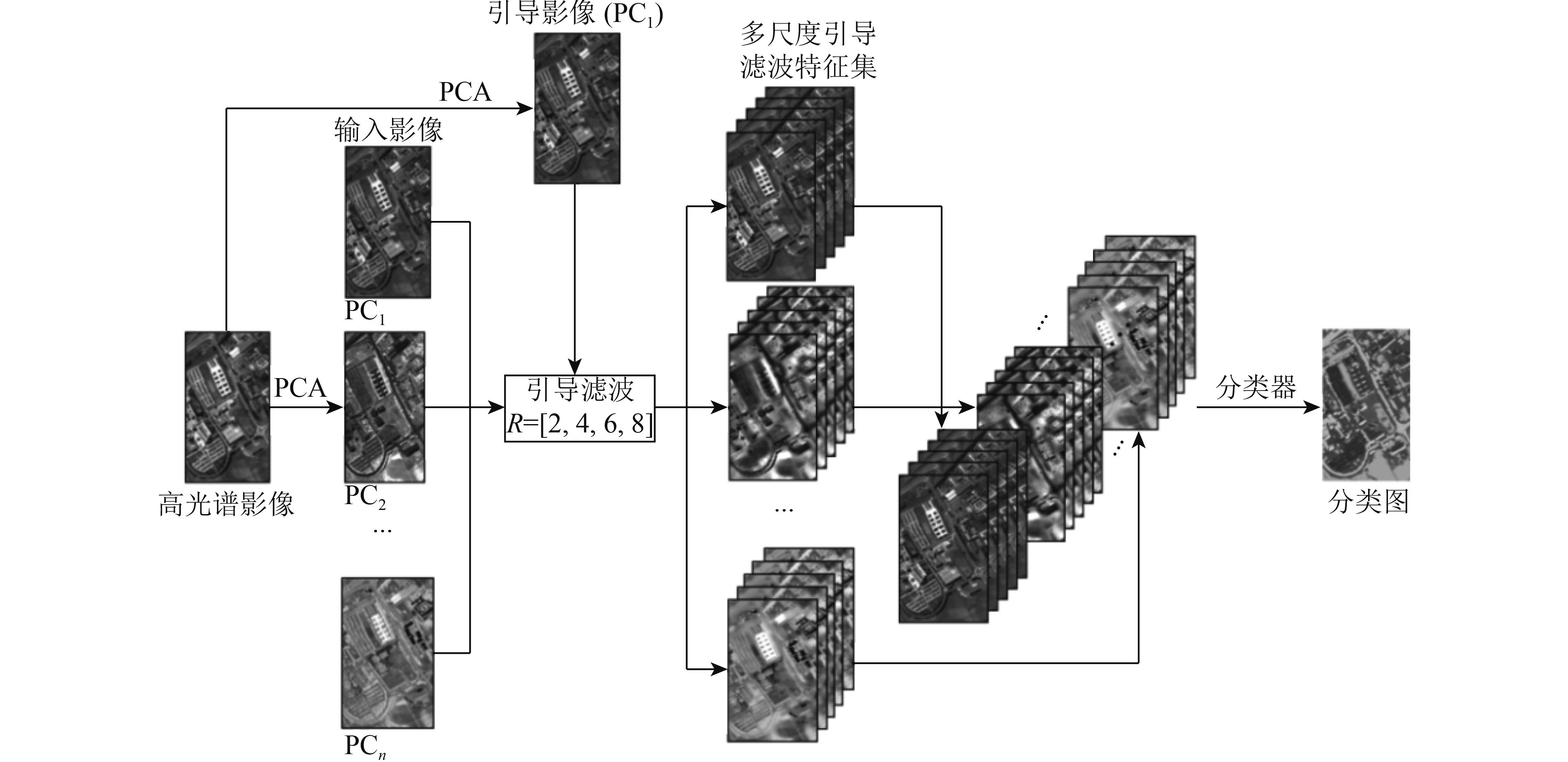
基于上述多尺度引导滤波特征，整体分类流程如图2所示。首先，对高维度的高光谱影像原始数据进行主成分变换(PCA)，得到包含98%以上信息的若干个主成分波段PC₁—PC_n；然后，将包含信息最多的第1主成分波段PC₁作为引导影像，将PC₁—PC_n分别作为输入影像，分别采用[2, 4, 6, 8]4种不同的窗口进行引导滤波运算得到各个尺度下的滤波特征向量，将所有向量与各主成分波段进行堆叠组成多尺度引导滤波特征集；最后，将特征及其对应的类别信息输入分类器中进行模型训练及结果预测。

为验证特征提取方法的效果，本研究采用一组仿真数据和3幅高光谱数据进行了实验。除了本文提出的多尺度引导滤波特征(MGFF)，研究还提取了主成分、多尺度灰度共生矩阵纹理特征MSTF(Multi-Scale Textural Features)(Baraldi和Parmiggiani，1995)和基于拓展形态滤波的多尺度特征EMP(Extended Morphological Profiles)(Benediktsson 等，2003)，用于对比。其中，MSTF采用长宽均为[3, 5, 7, 9]的4种正方形窗口，从各主成分的灰度共生矩阵中依次提取。由于实验发现灰度共生矩阵的同质性纹理特征的分类精度在所有提取的纹理属性中分类精度最高，本文提取多尺度同质性纹理特征进行对比实验。EMP通过采用不同大小的结构元素对原始影像进行开闭运算，实现多尺度结构提取。之前的研究结果表明：半径大小相同时，使用圆形结构元素提取特征的分类精度要高于其他类型结构元素的精度(Cao 等，2015)。因此，本研究采用半径为[2, 4, 6, 8]的圆形结构元素提取多尺度空间结构特征。为使得结果具有可比性，本文提出的MGFF也采用相同的半径设置[2, 4, 6, 8]。

图 2 基于多尺度引导滤波特征的分类流程 Figure 2 Flow chart of the proposed multi-scale guided filtering based classification method

4种特征提取后，被输入到支持向量机SVM(Support Vector Machine)(张学工，2010；Chang 等，2011)、随机森林RF(Random Forests)(方匡南 等，2011)和K近邻KNN(K-Nearest Neighbor)(Altman，1992)3种分类器。其中，随机森林分类器通过randomforest-matlab工具箱(Ho，1998)实现，实验中均建立500颗树进行决策，每个节点处选取的特征数则采用该工具包的默认参数。KNN分类器由Matlab2013a中KNN函数实现，近邻数k设置为9，其他参数均采用默认值。评价特征对于地物描述能力通过分类结果的整体精度OA(Overall Accuracy)，Kappa系数等分类精度指标，结合目视解译进行整体评价。

如图3所示，仿真数据是大小为 $558 \times 524$ 像素的单波段含噪声影像，包含圆形、三角形、不规则及背景对象4个类别。实验中，每类300个训练样本从测试样本中随机选择获得。按照第2节所述设置好相应的参数，采用EMP和提出的MGFF方法对仿真数据提取特征后，分别输入RF分类器，得到两种分类结果。因仿真数据为单波段影像，所以MGFF方法提取特征时采用的引导和待滤波影像均原始单波段含噪声影像。

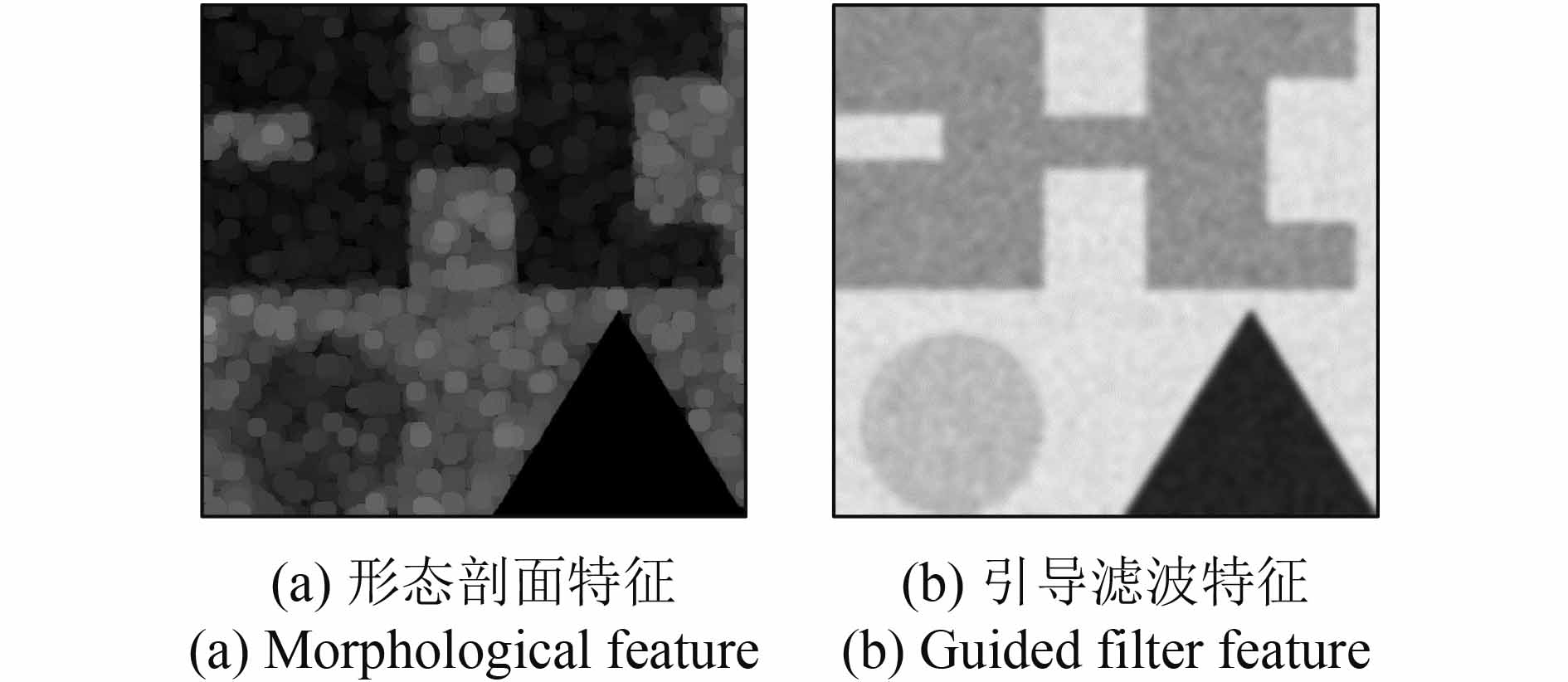
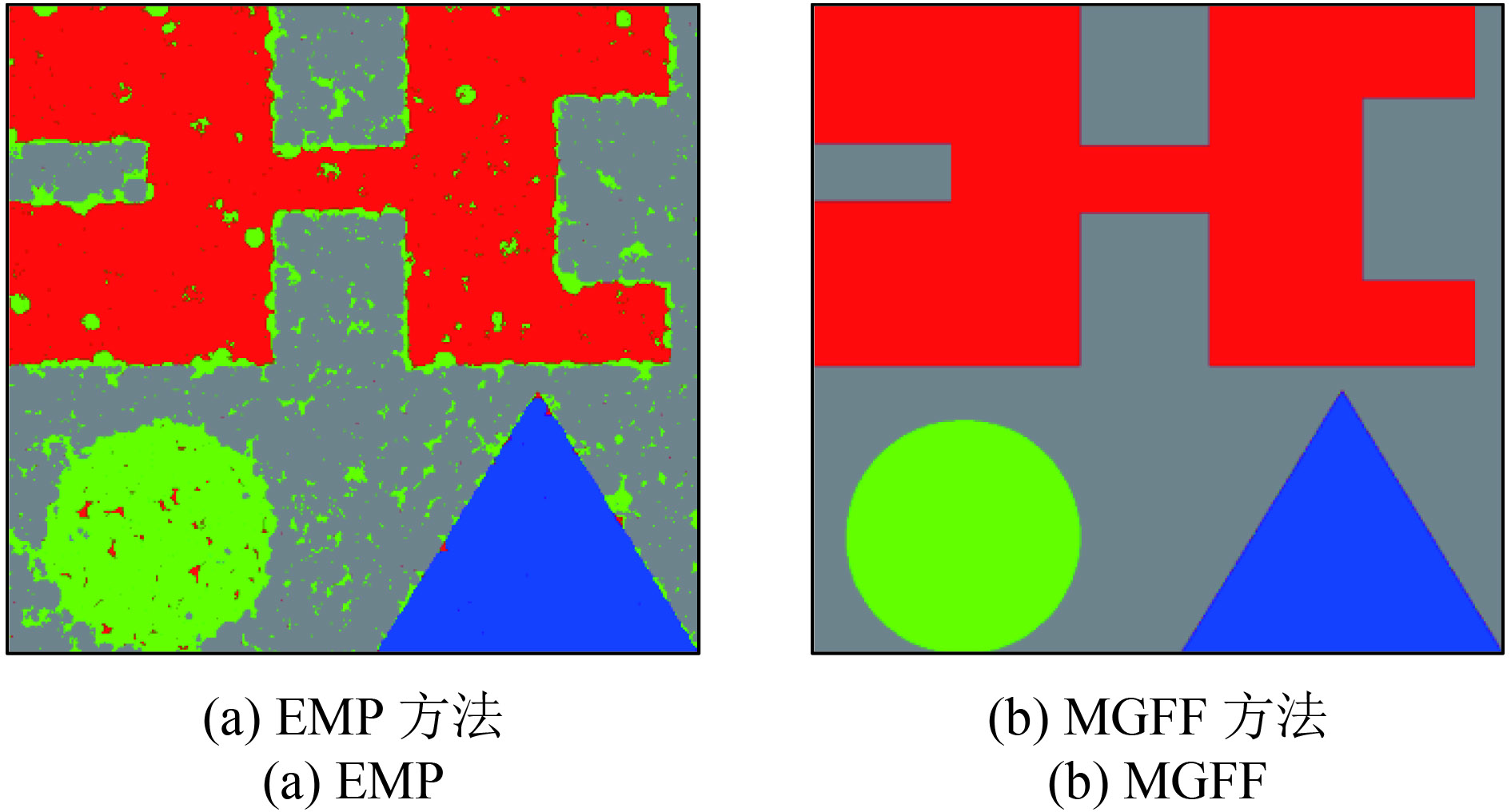
图4给出了当半径为8时，获得的形态剖面特征和引导滤波特征。显然，引导滤波特征滤除了对象内部噪声，同时更好的保留了影像中的对象边缘信息。图5所示的EMP和MGFF分类结果对比也显示出MGFF在对象边界上有更好的表现，且具有更好的抗噪能力。

图 3 仿真数据 Figure 3 Synthetic data set

图 4 形态剖面特征与引导滤波特征对比 Figure 4 Comparison of Morphological and guided filter features

图 5 仿真数据采用EMP和MGFF特征的分类结果对比 Figure 5 Comparison of EMP and MGFF Classification results with synthetic data

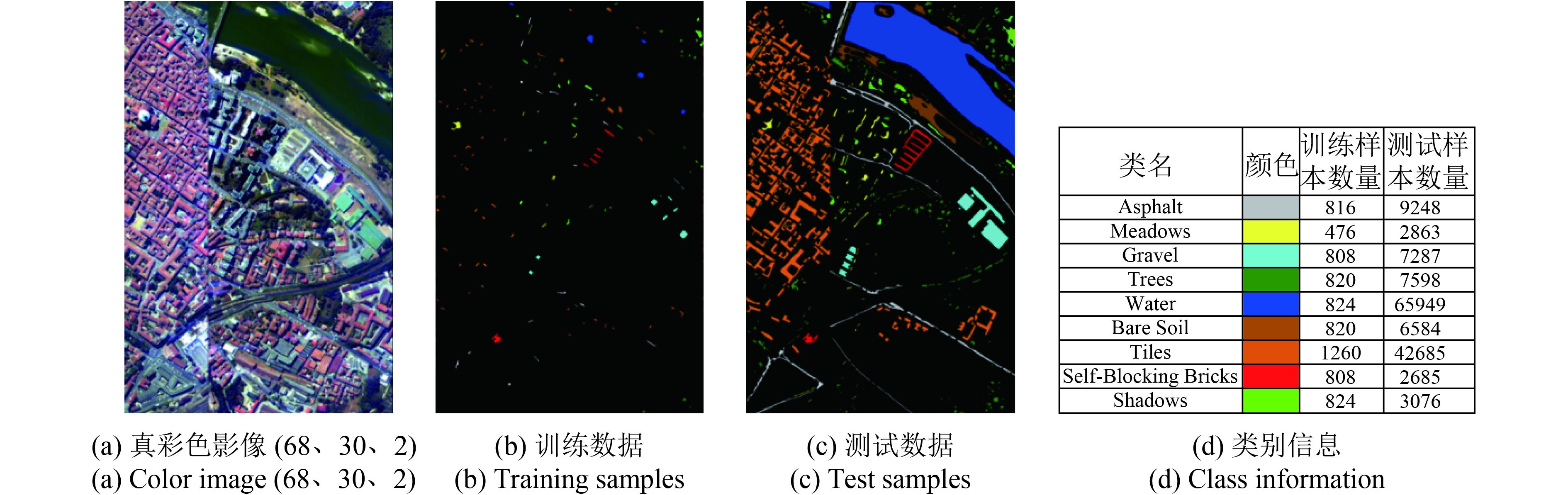
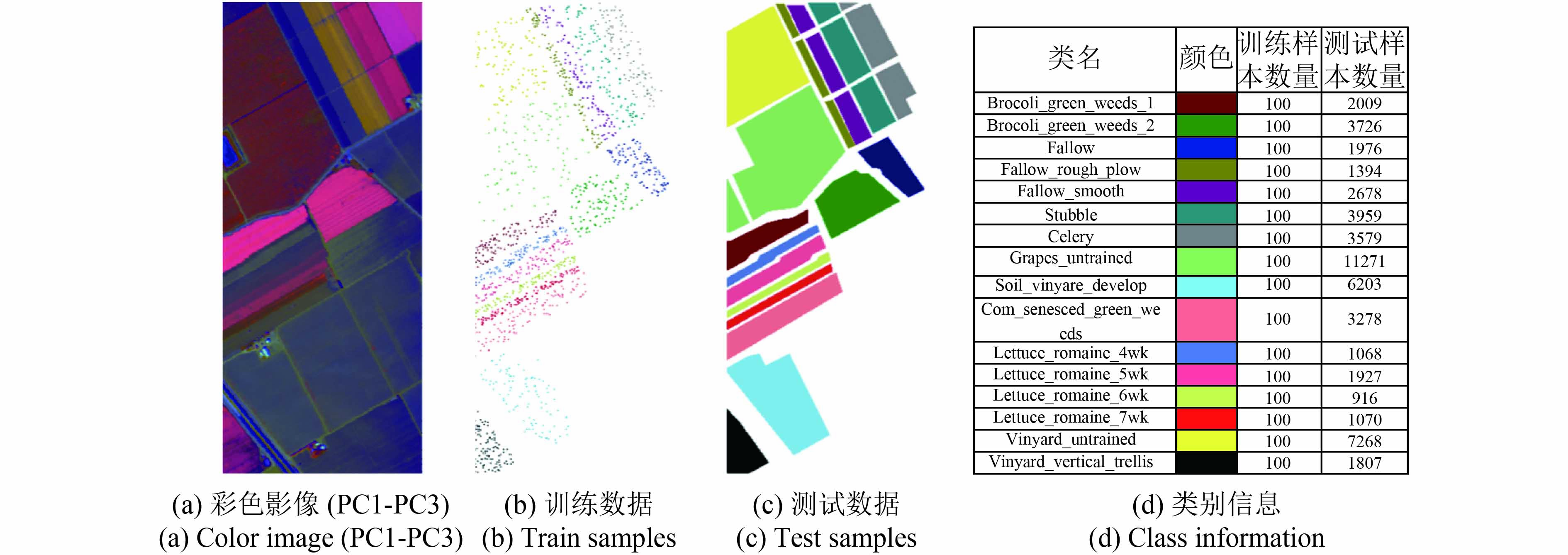
实验采用了3幅广泛用于高光谱遥感影像分类算法测试的公开数据。数据的详细信息可参考网址：http://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes[2016-09])。图6—图8给出了3幅数据Pavia University，Pavia Centre和Salinas的彩色合成影像、训练和测试样本标记及数目等信息。其中，Pavia University和Pavia Centre原始数据集均包含独立训练样本；Salina数据的每类100个训练样本从原始测试样本中随机选择获得。

图 6 Pavia University实验数据 Figure 6 Pavia University data set

图 7 Pavia Centre实验数据 Figure 7 Pavia Centre data set

图 8 Salinas实验数据 Figure 8 Salinas data set

对3幅实验影像分别进行PCA变换时，因前3个主成分均包含原始影像98%以上信息，所以均采用前3个主成分作为基础光谱特征，用于后续多种空间特征的提取。表2给出了各种特征组合的特征维数信息。

表 1(Table 1)

表 1 不同提取方法获得的特征维数 Table 1 The dimensions of features obtained by different methods PCA MSTF EMP MGFF University 3 15 27 15 Centre 3 15 27 15 Salinas 3 15 27 15

表 1 不同提取方法获得的特征维数 Table 1 The dimensions of features obtained by different methods

表3给出了基于SVM分类器的多特征分类精度结果。多数情况下，相较于仅仅采用3个主成分的PCA方法，空间特征的加入均显著地提升了分类精度。3种加入空间特征的方法中，MGFF方法的分类精度最高，EMP方法次之，MSTF方法最差。其中，基于MGFF方法的OA及Kappa系数提升最为明显；相比次优的EMP方法，MGFF在Pavia University、Pavia Centre和Salinas数据的OA上的提升分别达到了6.57%、2.97%和4.06%。结合表2，15维MGFF特征获得了比27维EMP特征更高的分类精度；MSTF方法与MGFF方法虽提取出相同维数的特征集，MGFF方法的精度高于MSTF方法。

表 3(Table 3)

表 3 不同特征+RF分类器的精度对比 Table 3 Accuracy evaluation of different features based on RF classifier PCA MSTF EMP MGFF Pavia University OA/% 65.46 81.59 84.72 89.75 Kappa 0.6208 0.7754 0.8105 0.8745 Pavia Centre OA/% 96.43 94.48 97.1 98.09 Kappa 0.9502 0.9242 0.9593 0.9732 Salinas OA/% 84.47 86.08 95.97 95.84 Kappa 0.8337 0.8506 0.9557 0.9543 　注：OA为总体精度。

表 3 不同特征+RF分类器的精度对比 Table 3 Accuracy evaluation of different features based on RF classifier

图9中是Salinas影像采用不同特征输入SVM获得的分类结果。从影像整体分类效果上可以看出EMP和MGFF方法的分类效果优于PCA和MSTF方法。在结果中，区域1地物的边缘信息保存比较完整，内部像素所属类别一致性较好，与其他方法相比也更符合彩色影像中地物的真实分布情况。区域2也可以得到类似的结论。因此，针对形状及边界明显的地物，MGFF方法有着较好的识别效果。

图 9 Salinas影像基于不同特征的分类结果(采用SVM分类器) Figure 9 Classification results of Salinas according to different features(with SVM classifier)

图10还给出Pavia University影像采用不同方法的各类别分类精度对比图。从图10中可以看出：Asphalt(沥青马路)、Gravel(碎石砂砾)和Bare Soil(裸土)3类地物基于MGFF方法的分类精度相对其他3种方法提高的比较明显。考虑到这些类别在影像中均具有较为明显的边界，这体现了引导滤波在具有规则边界的地物的特征提取中具有的优势：很好地保留影像中主要地物空间边缘信息并适当对地物内部进行滤波。

图 10 不同特征的逐类别分类精度对比：PaviaUniversity+SVM Figure 10 Class-specific accuracies of different features over the configuration PaviaUniversity+SVM

将提取的多种特征分别用于RF分类器时，OA及Kappa精度评价如表3。从表3中可知：对于Pavia University和Centre影像，MGFF方法的OA及Kappa均为最高，OA分别达到89.75%和98.09%，Kappa分别为0.8745和0.9732；而Salinas影像采用MGFF方法的OA值虽然不是最高，为95.84%，但与最高的EMP方法的OA值非常接近，仅相差0.13%，并且明显高于MSTF和PCA方法。这表明，MGFF在包含地物对象结构相对复杂的影像分类中具有优势。

表 4(Table 4)

表 4 不同特征+KNN分类器的精度对比 Table 4 Accuracy evaluation of different features based on KNN classifier PCA MSTF EMP MGFF Pavia University OA/% 67.17 68.66 80.96 85.21 Kappa 0.6342 0.6389 0.7738 0.8207 Pavia Centre OA/% 96.07 82.76 97.22 97.62 Kappa 0.9452 0.7756 0.961 0.9667 Salinas OA/% 85.1 66.97 92.29 93.69 Kappa 0.84 0.6529 0.9162 0.9311 注：OA为总体精度。

表 4 不同特征+KNN分类器的精度对比 Table 4 Accuracy evaluation of different features based on KNN classifier

图11为Pavia Centre影像采用EMP和MGFF分类结果及细节对比图。从中可以看出：MGFF方法的在区域1中地物的空间细节及轮廓保存完好，也符合该影像真实地表地物；区域2细节图中也反映出Gravel(碎石砂砾)类别的边界保持最好。因此，采用MGFF方法的分类结果无论是精度评价还是视觉效果都要比EMP要好。

图 11 Pavia Centre影像基于EMP和MGFF特征的分类结果(采用RF分类器) Figure 11 Classification results of Pavia Centre according to EMP and MGFF features (with RF classifier)

不同特征采用KNN分类器，OA及Kappa精度评价如表4。与其他两种分类器情况类似，MGFF方法对于Pavia University 、Centre和Salinas3幅影像的分类精度也是最高的。

对比MGFF特征用于不同分类器的情况，无论是仿真或是真实影像实验中，本文提出的MGFF特征均获得了最佳或次佳的分类精度。相比形态滤波方法，在地物结构比较复杂，场景空间异质性较强的区域(如城区影像)，MGFF体现出它较大的优势，能够有效地提高分类精度和改善目视效果。

本研究针对高光谱遥感影像分类中单一尺度特征无法有效表达地物类间差异和区分地物边界的不足，提出采用引导滤波算法提取出多尺度引导滤波特征。该方法充分利用引导滤波的优势，采用第一主成分作为引导影像，将包含信息量最多的若干主成分分别作为输入影像，应用依次增加的滤波半径分别进行引导滤波处理提取多个尺度的特征，获得影像不同尺度的结构信息。相比典型的形态滤波特征和纹理特征，引导滤波将引导影像中空间结构信息保存到滤波后的影像中，在滤除地物内部细节的同时，保留了影像中的地物边界；同时，通过选取不同大小的窗口进行滤波，表征出影像中不同尺度下的结构信息，更好地将光谱及空间信息结合。采用合成及真实高光谱影像，城区、郊区及农地多种地物场景的实验均验证了提出的特征在提高影像整体分类精度和改善地物边界的完整性的效果。实验结果标明本文方法提取出的特征能够更好的将空间与光谱信息结合，增强类间的可分性，较大幅度提高影像分类精度，特别适用地表结构比较复杂的场景分析。

本文方法中的不足之处在于提取多尺度特征时参数需要手动调整滤波窗口参数，因此在后期研究工作中需要考虑自适应或者基于参数学习的参数确定算法。

志 谢 感谢意大利帕维亚大学P.Gamb教授和F. Dell’Acqua教授提供Pavia University和Centre数据，普渡大学D.Landgrebe教授提供Salinas数据。