| 月球目标监测风云二号静止气象卫星可见光辐射响应变化 |
收稿日期: 2016-12-26
2. Key Laboratory of Radiometric Calibration and Validation for Environmental Satellite, China Meteorological Administration, Beijing 100081, China
准确的辐射定标是星载遥感仪器观测资料定量化应用的前提与保证。受在轨工作环境变化、探测器响应率与光学系统效率衰减等因素的影响,遥感仪器的定标参数在不断变化。根据其他遥感器的在轨性能表现,遥感器在轨运行一段时间,其辐射响应均有不同程度的衰减(Xiong和Barnes,2006;Hu 等,2012;Chen 等,2013;Wu 等,2013)。为了保证数据高质量的定量应用,需要及时监测并评估这种衰减的大小和趋势。
大多数业务运行的静止气象卫星没有搭载星上的可见光通道定标器,而是使用替代辐射定标目标来进行定标,如沙漠和深对流云DCC (Deep Convective Cloud)(Hu 等,2010;Chen 等,2013, 2017)。沙漠可以同时用于可见光和近红外辐射定标,但是大多数沙漠对于风云二号静止卫星(FY-2)而言观测角过大,因此引起的BRDF效应较大,计算时会引起较大误差。深对流云的目标要求首先保证红外通道的辐射定标精度。月球作为辐射定标基准具有许多优点,月球具有纪年级的稳定性,不受大气的影响,而且辐射能量处于大多数星载设备动态范围内,月球反射率光谱变化平缓,因此它是可用的最稳定的辐射目标之一(Kieffer和Wildey,1996;Kieffer,1997),特别在遥感器的长期辐射响应衰减跟踪中具有明显的优势。由于它的绝对辐射稳定性,也常常被用作除星上定标器外最值得参考的辐射定标源(Sun 等,2007;Xiong 等,2008;Eplee 等,2011)。
目前,很多星载光学载荷都具备观测月球的能力,如MODIS、SeaWiFS、GOES、Hyperion等国外卫星载荷(Eplee 等,2004, 2011;Wu 等,2006;Sun 等,2007;Xiong 等,2008;Shao 等,2014),及国内风云三号(FY-3)光学载荷也具有月球观测模式(吴荣华 等,2016)。卫星载荷的观月模式一般分为两种:一种是被动模式,即月球通过轨道运动随机进入仪器的冷空视场或者对地观测视场,被仪器所观测得到,如几乎所有的静止卫星和部分极轨卫星均存在这种情况;另一种是主动模式,即当需要观测月球时,卫星主动进行机动观测,调整仪器视场指向月球完成观测,如MODIS的大部分对月观测数据即采用这种模式获取的。
基于月球的辐射定标响应跟踪已经成为监测仪器辐射响应变化的重要方法之一,在MODIS(Sun 等,2007;Xiong 等,2008)、VIIRS(Shao 等,2014)等极轨气象环境卫星和GOES(Wu 等,2006)静止气象卫星上得到了广泛应用。利用月球目标进行中国风云气象卫星遥感仪器辐射定标工作相对较少。吴荣华等人(2016)利用FY-3C/MERSI冷空观测月球数据,采用与稳定通道比值的方法,获取了FY-3C/MERSI的仪器辐射衰减。因为FY-3C具有多个通道,且通道不在一个焦平面上,因此采用通道比值的方法更容易实现仪器衰减分析,但该方法首先需要假设一个稳定通道。FY-2由于只有一个可见光通道,不能采用基于月球观测的通道比值法。因此本文采用了国际月球辐射照度模型作为辐射参考基准。
FY-2系列卫星是中国第一代地球同步轨道气象观测卫星。它采用自旋稳定工作方式,星上主要气象探测仪器——可见红外自旋扫描辐射计(VISSR),具备从可见光到热红外的多波段探测能力(许健民 等,2014)。受整体结构的限制,FY-2的可见光波段未设计星上定标器,也无全口径全光路的星上定标装置(陈福春和陈桂林,2007)。虽然FY-2是第一代静止气象卫星,但是月球有时能够进入对地观测窗口并被观测到。FY-2作为静止气象卫星,其角分辨能力明显优于相同对地分辨率的极轨气象卫星,因此其“看到”的月球更“清晰”,使得利用月球目标对FY-2可见光波段辐射定标响应跟踪成为可能。FY-2E是风云二号系列卫星02批中的最后一颗星,从2008年12月23日发射以来,在轨运行时间已有8年,目前仍然在轨观测。相较于其后发射的FY-2(03)批的F星和G星,FY-2E在轨时间长,更适合作为研究仪器辐射响应变化的数据源。本文利用2010年—2014年FY-2E/VISSR所观测得到的月球数据,通过与月球辐射照度模型的比较,获取5年间FY-2E/VISSR可见光通道的辐射响应衰减率,并与深对流云监测结果进行比较,探索实现利用月球目标进行静止气象卫星辐射响应变化跟踪的方法。
2、FY-2E/VISSR观测月球数据 (2.1) FY-2E/VISSR仪器特性FY-2E/VISSR有5个通道,其中1个可见光通道,4个红外通道。可见光通道星下点空间分辨率为1.25 km,红外通道星下点空间分辨率5 km。FY-2E/VISSR主要特性见表1。它的对地观测视场约20°,由于月球绕地球运动的关系,月球会在卫星的对地观测视场内出现,并和地球目标一起被记录下来。因为处于高轨道,同等对地观测分辨率条件下,静止气象卫星的角分辨率能力明显优于极轨气象卫星,因此获取的月球图像像素较高。如FY-2E/VISSR对月面的分辨率约为10 km,FY-3/MERSI的250 m分辨率通道对月面的分辨率约100 km。
|
|
表 1 FY-2E-VISSR主要特性指标 Table 1 The main characteristics of FY-2E-VISSR |
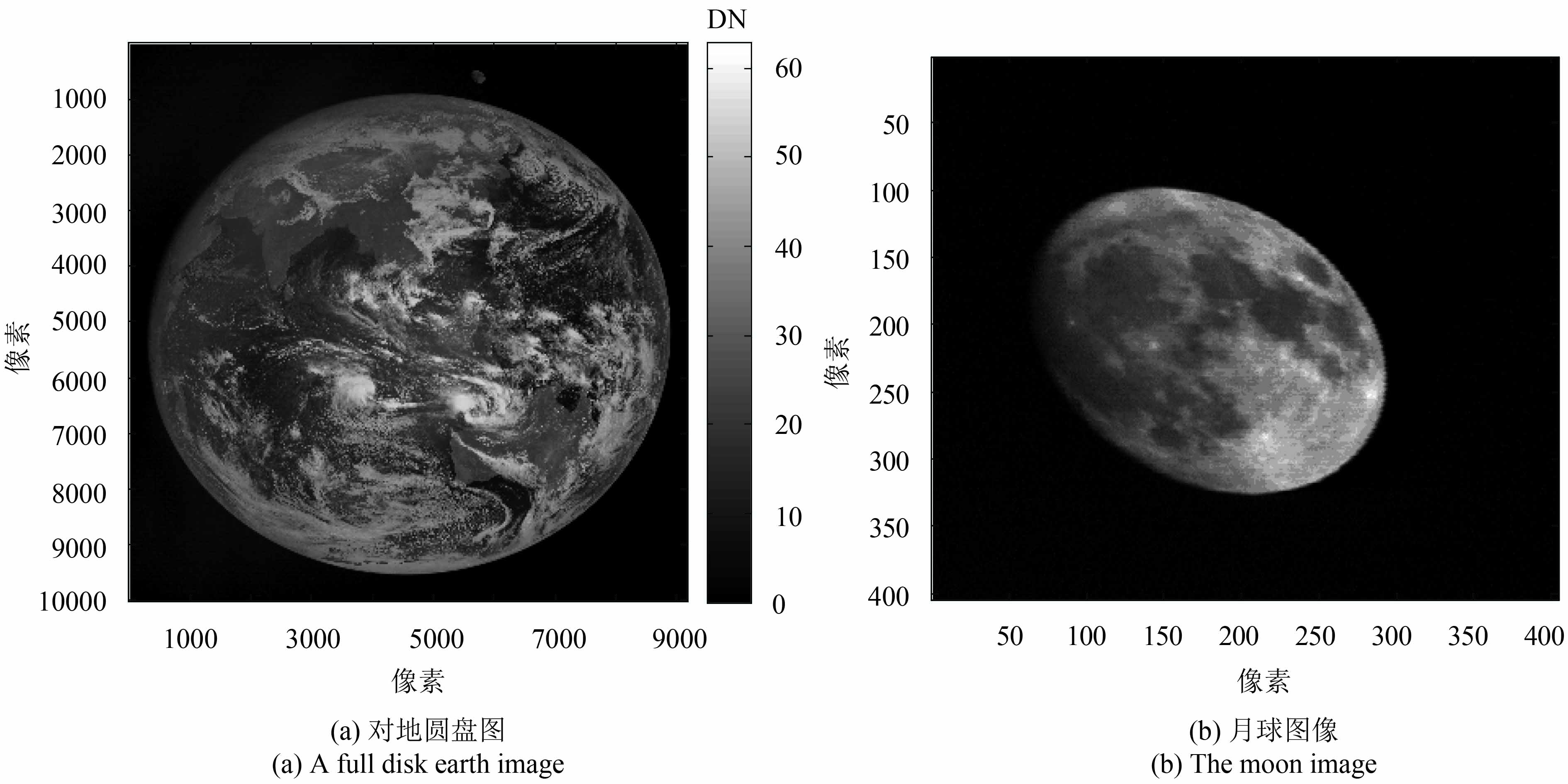
由于月、地、日、星在不同的运动中,FY-2静止气象卫星做圆盘扫描时,将会观测到不同月相条件下的月球,而这种对月观测事件是可以被精确预报出来的。通过几何计算和预报方法(详见3.3节),获取了2010年1月—2014年10月可识别的月球观测事件。图1为FY-2E在2013年2月24日04:00时观测到圆盘图和月球。由于月球的相对运动速度与仪器扫描时间不匹配,造成月球图像不是正圆形,在后续的辐照度计算中需要进行校正。
|
| 图 1 FY-2E观测到的对地圆盘图及月球图像(月球在圆盘图上方) Figure 1 A full disk earth image observed by FY-2E on 04:00 UTC February 24, 2003 and the moon image (in the upper of the full disk image) |
由于静止气象卫星观测的月球出现位置和月相大小的不确定性,无法从固定区域内寻找和识别月球图像,故采用了一种图像识别的方式来进行月球图像的自动提取。主要原理是采用FY-2E的红外图像和图像处理中的联通域来帮助进行月球的提取。因为对地观测和月球观测的温度相对于冷空间高许多,红外图像上其亮温远大于冷空间,所以用红外阈值能够容易区分对地图像、月球图像和冷空间。对于FY-2E而言,设定11 μm红外亮温大于等于180 K且存在大于500像素的次联通区域(主联通区域为地球)为月球图像。然后通过红外与可见光图像的匹配,找到FY-2E可见光图像的月球图像,找其中的中心区域,将月球图像置中,形成400×400像素大小的包含有月球观测的数据文件。
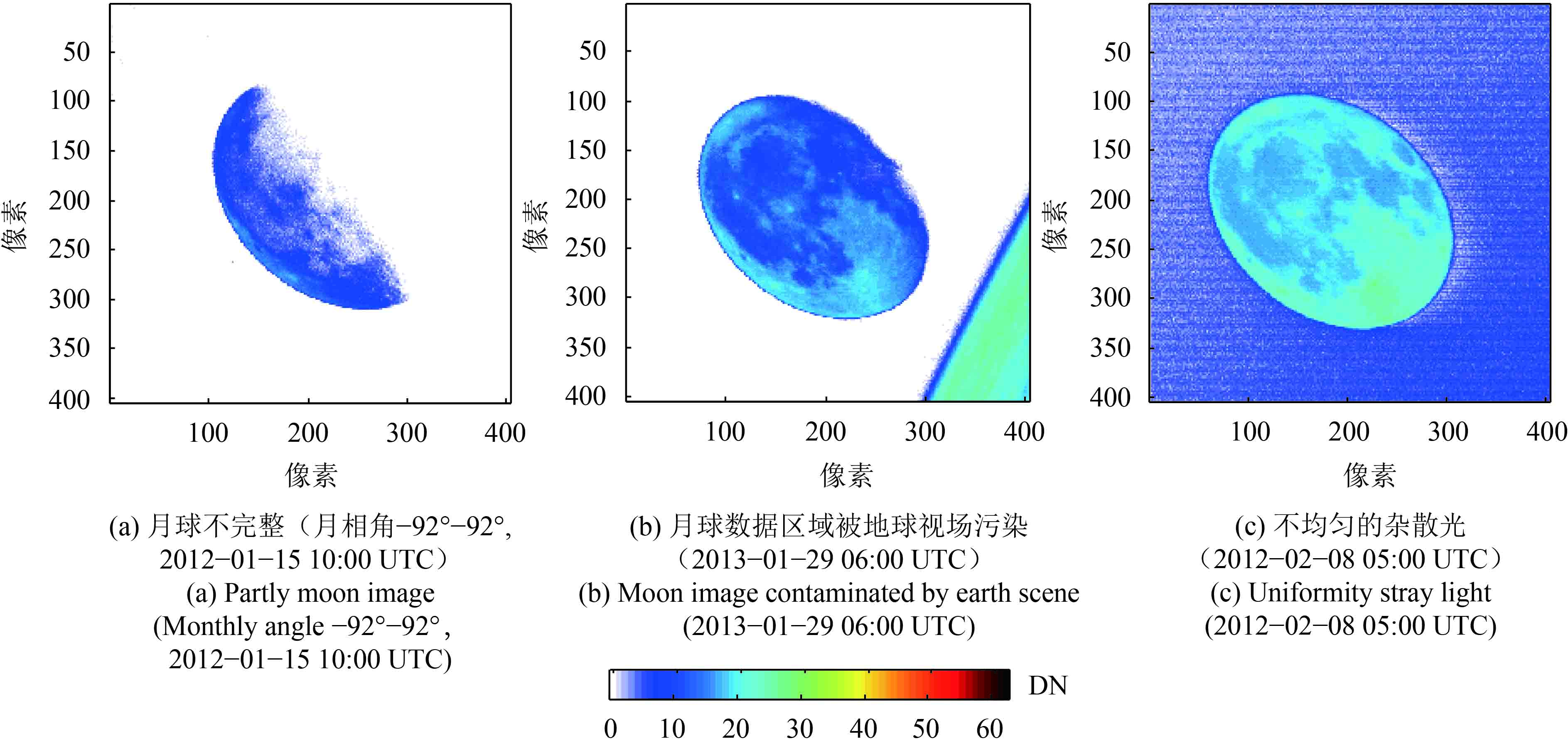
(2.4) FY-2E观测月球的有效性分析FY-2E扫描辐射计在实际对月成像观测中会存在以下问题:(1)月球表面分布有月山和月海,其反射特性不一致,月海的反射率较低。这些实际问题造成了目前获取的FY-2E扫描辐射计对月观测事件中,有部分时刻观测到的月球不完整,不能满足月球辐照度计算条件。(2)当月球与地球靠的很近时,地球图像也出现在了对月成像观测窗口中,影响月球照度的计算。(3)FY-2E有杂散光现象,且杂散光的分布随时间和位置分布不均匀。图2给出了自动提取数据文件中出现了几种月球图像。根据月相角的阈值,可以用来作为判断月球完整性的判据,当月相角不在–92°—92°,认为月球观测不完整。当对月观测的400×400窗口内出现地球图像时,也一般将其剔除。杂散光的情况最难以判断,本文采用剔除方法是在对月观测的400×400窗口中,取窗口4个角点各20×20的小区域,对其信号进行积分,并都除以最大的信号值进行归一化处理,然后计算4个角点区域积分值的标准差,若标准差大于0.05,则剔除该数据。
因此在实际应用中采用以上的原则剔除了部分观测数据,最终获取时间段内有效月球观测数据为33个。
|
| 图 2 几种不能作为定标使用的月球图像 Figure 2 Some lunar image examples which cannot be used for calibration |
稳定的月球表面为地球观测成像仪的校准提供了可靠的目标。为了校准在轨卫星成像仪辐射定标,美国地质调查局(USGS)在美国航空航天局(NASA)对地观测系统项目资助下,进行了名为“自动月球观测ROLO (RObotic Lunar Observatory)”计划的月球地基观测,通过8年的观测发展了ROLO月球辐射照度模型(Kieffer和Stone,2005)。ROLO模型目前是度量月球辐射的基准模型,卫星观测到的月球辐射经过日、月、星距离等观测几何的校正后与月球辐射基准相比,可以反映星载遥感仪器的辐射响应变化情况,已被广泛用于遥感仪器的辐射定标检验和辐射响应衰减监测。
(3.1) 月球辐射模型ROLO计划在亚立桑那大学弗拉格斯塔夫(Flagstaff,32°12′52.9″N,111°38′5.0″E,海拔2148 m)开展了8年多的地基望远镜对月自动观测,在350—2450 nm的光谱范围内32个波段上获取了晴朗夜空、月相角约±90°范围内的83000幅月球图像,得到了各种条件下月球辐照度周期性变化的大量数据。以此为基础数据,考虑月相角、空间变化、天平动、低相角时的强后向散射等因素,建立了以几何参数为变量、基于经验方程反演的月球等效反射率及照度ROLO模型(Kieffer和Stone,2005)。ROLO照度模型可以给出有效月相角几何范围(±92°)之内的月球照度(Kieffer和Stone,2005),见式(1)
| ${I_{{{ROLO}},}}_{\textit{λ}} = {A_{\textit{λ}} } \cdot {E_{{{sun}},{\textit{λ}} }} \cdot {\varOmega _{{m}}}/{{\text{π}}}$ | (1) |
式中,
| $\begin{aligned}\ln {A'_{k}} = & \sum\limits_{i = 0}^3 {{a_{ik}}{g^i}} + \sum\limits_{j = 1}^3 {{b_{jk}}{\varPhi ^{2j - 1}}} {c_1}\theta + {c_2}\phi + \\ &{c_3}\varPhi \theta + {c_4}\varPhi \phi + {d_{1k}}{{{e}}^{ - g/{p_1}}} + {d_{2k}}{{{e}}^{ - g/{p_2}}} + \\ &{d_{3k}} \cos [(g - {p_3})/{p_4}]\end{aligned}$ | (2) |
式中,g为月相绝对值,ϕ和θ分别为月面经度和纬度,Φ为太阳月面经度。其他参数都为模型拟合系数,通过83000次月球观测,ROLO给出了32个波段的328个系数(Kieffer和Stone,2005)。
根据式(1)和式(2),任意时刻处的月球辐射照度Iλ为
| ${I_{\textit{λ}} } = {I_{{{ROLO}},\,\,{\textit{λ}} }} \cdot {\left(\frac{{384400}}{{{d_{{{mp}}}}}}\right)^2} \cdot {\left(\frac{1}{{{d_{{{ms}}}}}}\right)^2}$ | (3) |
式中,dmp为该时刻处月球和卫星的距离,dms为该时刻月球和太阳的距离与标准日地距离(AU)的比值。
(3.2) 观测几何计算如上所述,为了得到任意时刻的月球辐射照度,需要进行月—星、月—日距离校正,需要得到月相角度、月面经纬度等几何信息。此外,为了获取卫星观测的月球数据,需要对月球出现在卫星冷空视场进行预报,在预报可能出现月球的时段的卫星数据中进行查找和提取。这些工作都涉及精确的卫星、月球和太阳位置的计算。本文使用了JPL开发的SGP4模型,结合JPL星历表文件DE430和卫星两行报文件,得到J2000(2000年春分时刻地球天球坐标系)历元下的卫星、月球、地球、太阳位置信息,根据仪器坐标转换矩阵和地、月、卫星的几何关系,预报出月球出现在卫星冷空视场的时间(刁宁辉 等,2012)。月相角在月球照度模型中是一个重要的参数,它定义为月球和观测点连线与月球和太阳连线所成角。如果定义月球满月时月相角为0°,月圆后月相角为负值,ROLO模型的适用月相角范围是–92°—92°。
(3.3) 卫星观测月球辐照度计算FY-2E扫描辐射计观测得到的辐射单位为辐亮度,月球的辐照度为其各点的辐亮度在立体角上的积分,如式(4)
| ${I_{{{lunar}}}} = \frac{{{\varOmega _{{s}}} \cdot \sum\limits_{i = 1}^N {{L_{{{lunar}}}}(i)} }}{{fi}}$ | (4) |
式中,Ilunar为FY-2E观测到的月球辐照度,Llunar(i)为每个像元的月球辐亮度值,Ωs是FY-2E扫描辐射计像元的立体角,fi是过采样系数,对于FY-2E对月观测图像,fi取1。
由于FY-2E扫描辐射计可见光采用的是反射率定标,由定标查找表得到的是反射率,因此需要将反射率乘以通道太阳常数(通过卷积标准太阳辐照度光谱和FY-2E扫描辐射计可见光通道的光谱响应得到),从而计算出观测辐亮度Llunar。
(3.4) FY-2E扫描辐射计辐射响应衰减计算以ROLO模型计算得到的卫星观测时刻和位置处的月球辐照度为参考基准,扫描辐射计对月观测辐照度与之相比的结果即表征了扫描辐射计的定标偏差。ROLO模型的绝对辐射不确定度在5%—10%,用其绝对值在来评估定标偏差的误差较大,但其相对稳定性可以达到1%—2% (Velikodsky 等,2011)。因此将这种定标偏差归一化可以用来评估仪器辐射响应的衰减程度。MODIS、VIIRS/NPP等仪器均采用此方法来监测仪器辐射响应的衰减,并作为一种独立检验方法检验星上定标器获取的辐射响应衰减规律。因此,t时刻处的仪器辐射响应变化D(t)可以用式(5)表示
| $D(t) = \frac{{{I_{{{lunar}}}}(t)}}{{{I_{{{ROLO}}}}(t)}} \cdot \frac{{{I_{{{ROLO}}}}({t_0})}}{{{I_{{{lunar}}}}({t_0})}} \cdot 100{{\text{\% }}}$ | (5) |
式中,Ilunar(t0)和Ilunar(t)分别是起始时刻t0和t时刻卫星观测得到的月球辐射照度,IROLO(t0)和IROLO(t)分别是起始时刻t0和t时刻ROLO模型观测得到的月球辐射照度。
采用线性拟合公式来计算仪器辐射响应衰减、年衰减率。并将响应值与线性拟合线差值的标准差作为稳定性指标(σ),其主要公式如下
总辐射响应衰减Dtotal公式表达为
| ${D_{{{total}}}} = \frac{{(f({t_{{{end}}}}) - f({t_1}))}}{{f({t_1})}} \cdot 100 \text{\%} $ | (6) |
式中,f为线性拟合公式,t1为序列的第一天,tend为序列的最后一天。
辐射响应年衰减率Dannual公式表达为
| ${D_{{{annual}}}} = ({D_{{{total}}}}/({t_{{{end}}}} - {t_{{1}}})) \cdot 365$ | (7) |
稳定性指标σ用来表示辐射响应变化与拟合公式之间的偏离程度,公式表达为
| $\sigma = {\left( {\displaystyle\frac{1}{n}\sum\limits_{{t_i} = 1}^n {{{\left( {(D({t_i}) - f({t_i}))/f({t_1}) - \overline {({{D}}({t_i}) - f({t_i}))/f({t_1})} } \right)}^2}} } \right)^{\frac{1}{2}}}$ | (8) |
式中,ti表示某一天,D(ti)表示这一天的响应变化值,f(ti)表示这一天线性拟合的响应变化值。
4、结果分析利用以上的处理方法,可以得到基于月球目标的FY-2E扫描辐射计辐射响应变化及拟合趋势线(图3(a))。为了观察辐射响应变化是否与月相角相关,还将月相角变化分布与辐射响应变化一并给出,见图3(b)。从图3(a)可以直观的看出,试验数据期间,FY-2E可见光通道有明显的辐射响应衰变情况,衰变大体呈线性衰变的趋势,2010年—2014年共5年FY-2E/VISSR可见光有近10%的衰减。月相角与辐射响应变化来看,没有明显相关性,说明月相的变化没有对响应变化的结果产生影响。
为了与月球目标得到的FY-2E辐射定标响应跟踪结果进行验证,采用同时间段的深对流云目标进行辐射定标跟踪结果比对。由于DCC具有反射率高、朗伯性好、受大气影响小且能连续跟踪等优势(陈林 等,2016),已被多种业务气象卫星采用为辐射定标方法之一,也和月球定标方法一起被世界气象组织下属的全球天基卫星交叉定标系统(WMO/GSICS)列为优先采用的可见光辐射定标方案。

|
| 图 3 基于月球观测的FY-2E可见光通道辐射响应变化 Figure 3 The radiometric respond change of FY-2E/VISSR visible band based on lunar observation |
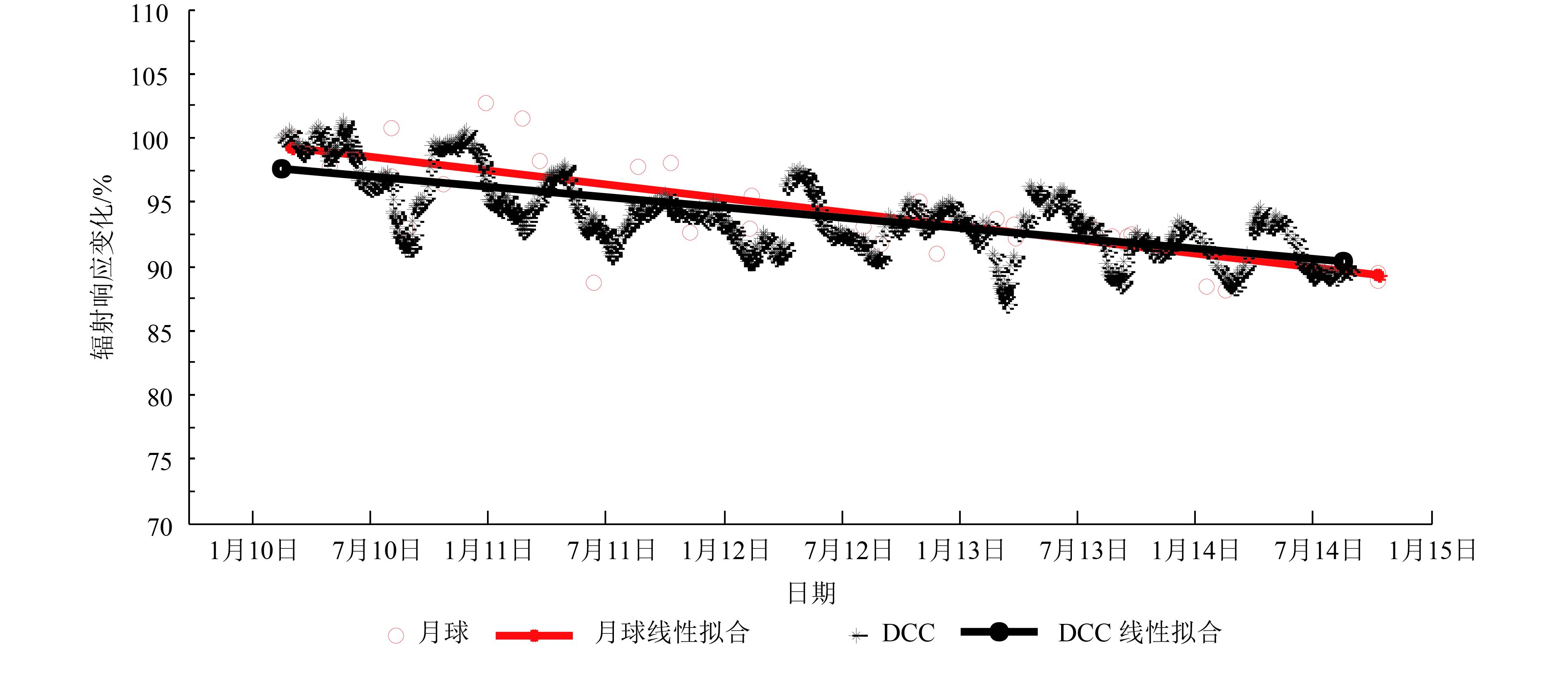
采用陈林等人(2016)方法,给出利用DCC方法得到的FY-2E扫描辐射计的辐射响应变化结果与月球辐射定标方法结果进行比较。图4是基于月球和DCC目标给出的FY-2E扫描辐射计的辐射响应变化时间序列图,相关参数列于表2。在试验数据期间,基于月球和DCC的FY-2E辐射响应衰减分别为9.2%和8.1%,年衰减率分别为1.96%和1.72%,并计算95%的置信度区间(费业泰,2010),不确定度分别为±0.79%和±0.09%。稳定性的指标分别为2.66(月球)和2.25(DCC)。月球目标是低端目标,DCC目标是高端目标,FY-2E扫描辐射计可见光通道是多段线性定标模式,两个独立的目标得到的结果较为一致,且大部分情况下的高值和低值的对应性也较好,充分说明了利用月球目标作为稳定定标源进行辐射定标跟踪的可行性和结果的可靠性。但从不确定度和稳定性指标来看,月球的方法要略低于DCC的方法,可能有以下几个原因:(1)与DCC高亮度目标相比,月球是低反射率目标,对仪器的观测噪声更加敏感,仪器噪音对月球定标结果的影响更大;(2)在月相绝对值较大时(1/2月盘),观测的图像不能包含完整月球辐射信息,月球图像边缘像素在计算总辐照度时的贡献影响较大;(3)FY-2E存在杂散光的影响,对于高端目标杂散光的相对影响较小,而对低端目标的影响较大。此外,通过月球目标和DCC目标的辐射响应跟踪对比都发现FY-2E的辐射响应具有一定的周期性震荡的特点。这种震荡可能与静止卫星星体一年中受光照条件的周期性变化相关联,如每年进入地影期间,会对星上温度造成一定的影响,而仪器的辐射响应存在温度依赖关系。这种周期性变化能从星上遥测温度中反映出来。每年3月—4月中旬以及9月—10月中旬卫星处于地影期,昼夜温差大,星上状态不稳定。从3月、4月到9月、10月遥测温度有一个明显的周期趋势变化。顶点或低点的位置在7月前后。这与可见光响应在7月前后有一个低点的周期变化相吻合。未来需要更多的数据,特别是星上状态数据来定量化说明这种关联性。
|
|
表 2 基于月球目标和DCC目标的FY-2E/VISSR辐射响应变化统计结果 Table 2 The statistic results of FY-2E/VISSR radiometric respond change based on lunar and DCC targets |
|
| 图 4 基于月球和DCC观测的FY-2E可见光通道辐射响应变化及线性趋势拟合线 Figure 4 The radiometric respond change and the linearity regression line of FY-2E/VISSR visible band based on lunar observation and DCC |
月球目标是除了太阳以外,张角最大的地外目标,除了极少数的可分辨的陨石撞击造成的月面状态的改变,可以保证长期的辐射光度稳定性,因此适合作为稳定的辐射基准目标对气象卫星开展辐射定标工作。FY-2E静止卫星能够在地球圆盘观测的同时也观测到月球。基于月球辐射照度模型计算,获取了FY-2E扫描辐射计可见光通道2010年1月—2014年10月时间序列的辐射响应变化,并且与深对流云结果进行了比较,结果表明(1)基于月球目标能够发现FY-2E在试验数据期间存在辐射响应衰变的情况,总衰减率为9.2%,说明了月球辐射定标跟踪方法的有效性;(2)通过与DCC方法的比较,两者获取的总衰减率相近,分别为9.2%和8.1%,95%置信区间的不确定度分别为±0.79%和±0.09%;(3)两种方法都能发现,FY-2E辐射响应变化存在年际周期性震荡的现象,这种现象可能与卫星光照角变化从而引起星体温度变化相关联。也要注意到,因为月球目标处于辐射响应的低端,FY-2可见光通道较低的量化等级、圆盘外杂散光等现象对利用月球进行辐射响应跟踪监测存在一定的不利影响。
中国第二代静止气象卫星风云四号(FY-4)已于2016年12月11日发射,与风云二号相比其产品定量化要求更高,对辐射定标精度也提出了更高要求。本方法也是作为FY-4辐射定标的一项预研工作,探索了利用月球目标进行辐射定标的可能性,得到的结果充分表明基于月球目标的辐射定标方法能够作为辐射定标方法的一种,有助于实现高精度辐射定标,进一步提升遥感产品定量化水平。同时也要看到,月球照度模型的精度是制约这一方法的关键因素,因此建立和发展一个高精度的月球照度模型将是下一步工作的重点。
| [1] | 陈福春, 陈桂林. FY-2C发射前后可见光星上定标的比较[J]. 量子电子学报, 2007, 24 (6) : 709 –713. Chen F C, Chen G L. Comparison between pre-launch and in-orbit visible onboard calibrations[J]. Chinese Journal of Quantum Electronics, 2007, 24 (6) : 709 –713. DOI: 10.3969/j.issn.1007-5461.2007.06.010 |
| [2] | Chen L, Hu X Q, Xu N, Zhang P. The application of deep convective clouds in the calibration and response monitoring of the reflective solar bands of FY-3A/MERSI (Medium Resolution Spectral Imager)[J]. Remote Sensing, 2013, 5 (12) : 6958 –6975. DOI: 10.3390/rs5126958 |
| [3] | 陈林, 徐娜, 胡秀清, 陆风, 张鹏. 基于深对流云目标的风云二号可见光通道辐射定标[J]. 光谱学与光谱分析, 2016, 36 (8) : 2639 –2645. Chen L, Xu N, Hu X Q, Lu F, Zhang P. Study on orbit radiometric calibration for FY-2 visible band based on deep convective cloud[J]. Spectroscopy and Spectral Analysis, 2016, 36 (8) : 2639 –2645. DOI: 10.3964/j.issn.1000-0593(2016)08-2639-0 |
| [4] | Chen L, Zhang P, Lv J Y, Xu N, Hu X Q. Radiometric calibration evaluation for RSBs of Suomi-NPP/VIIRS and Aqua/MODIS based on the 2015 Dunhuang Chinese radiometric calibration site in situ measurements [J]. International Journal of Remote Sensing, 2017, 38 (20) : 5640 –5656. DOI: 10.1080/01431161.2017.1343514 |
| [5] | 刁宁辉, 刘建强, 孙从容, 孟鹏. 基于SGP4模型的卫星轨道计算[J]. 遥感信息, 2012, 27 (4) : 64 –70. Diao N H, Liu J Q, Sun C R, Meng P. Satellite orbit calculation based on SGP4 model[J]. Remote Sensing Information, 2012, 27 (4) : 64 –70. DOI: 10.3969/j.issn.1000-3177.2012.04.011 |
| [6] | Eplee R E, Barnesa R A, Patta F S, Meisterb G, Mccain C R. SeaWiFS lunar calibration methodology after six years on orbit[J]. Earth Observing Systems IX, Proc. of SPIE, 2004, 5542 : 1 –13. DOI: 10.1117/12.556408 |
| [7] | Eplee R E Jr, Sun J Q, Meister G, Patt F S, Xiong X X, McClain C R. Cross calibration of SeaWiFS and MODIS using on-orbit observations of the Moon[J]. Applied Optics, 2011, 50 (2) : 120 –133. DOI: 10.1364/AO.50.000120 |
| [8] | 费业泰. 2010. 误差理论与数据处理. 6版. 北京: 机械工业出版社: 132–139 Fei Y T. 2010. Error theory and data processing. 6th ed. Beijing: China Machine Press: 132–139 |
| [9] | Hu X Q, Liu J J, Sun L, Rong Z G, Li Y, Zhang Y, Zheng Z J, Wu R H, Zhang L J, Gu X F. Characterization of CRCS Dunhuang test site and vicarious calibration utilization for Fengyun (FY) series sensors[J]. Canadian Journal of Remote Sensing, 2010, 36 (5) : 566 –582. DOI: 10.5589/m10-087 |
| [10] | Hu X Q, Sun L, Liu J J, Ding L, Wang X H, Li Y, Zhang Y, Xu N, Chen L. Calibration for the solar reflective bands of medium resolution spectral imager onboard Fy-3A[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50 (12) : 4915 –4928. DOI: 10.1109/TGRS.2012.2214226 |
| [11] | Kieffer H H. Photometric stability of the lunar surface[J]. Icarus, 1997, 130 (2) : 323 –327. DOI: 10.1006/icar.1997.5822 |
| [12] | Kieffer H H, Stone T C. The spectral irradiance of the Moon[J]. The Astronomical Journal, 2005, 129 (6) : 2887 –2901. DOI: 10.1086/430185 |
| [13] | Kieffer H H, Wildey R L. Establishing the moon as a spectral radiance standard[J]. Journal of Atmospheric and Oceanic Technology, 1996, 13 (2) : 360 –375. DOI: 10.1175/1520-0426(1996)013<0360:ETMAAS>2.0.CO;2 |
| [14] | Shao X, Cao C Y, Uprety S, Padula F, Choi T. Comparing Hyperion Lunar Observation with model calculations in support of GOES-R Advanced Baseline Imager (ABI) calibration//Proceedings of the SPIE Volume 9218, Earth Observing Systems XIX, SPIE Optical Engineering + Applications[J]. San Diego, California, United States: SPE, 2014, 9218 : 92181X . DOI: 10.1117/12.2062250 |
| [15] | Sun J Q, Xiong X X, Barnes W L, Guenther B. MODIS reflective solar bands on-orbit lunar calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45 (7) : 2383 –2393. DOI: 10.1109/TGRS.2007.896541 |
| [16] | Thuillier G, Hersé M, Labs D, Foujols T, Peetermans W, Gillotay D, Simon P C, Mandel H. [J]. Solar Physics, 2003, 214 (1) : 1 –12. DOI: 10.1023/A:1024048429145 |
| [17] | Velikodsky Y I, Opanasenko N V, Akimov L A, Korokhin V V, Shkuratov Y G, Kaydash V G, Videen G, Ehgamberdiev S A, Berdalieva N E. New Earth-based absolute photometry of the Moon[J]. Icarus, 2011, 214 (1) : 30 –45. DOI: 10.1016/j.icarus.2011.04.021 |
| [18] | Wu A S, Xiong X X, Doelling D R, Morstad D, Angal A, Bhatt R. Characterization of terra and aqua MODIS VIS, NIR, and SWIR spectral bands’ calibration stability[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51 (7) : 4330 –4338. DOI: 10.1109/TGRS.2012.2226588 |
| [19] | 吴荣华, 张鹏, 杨忠东, 胡秀清, 丁雷, 陈林. 基于月球反射的遥感器定标跟踪监测[J]. 遥感学报, 2016, 20 (2) : 278 –289. Wu R H, Zhang P, Yang Z D, Hu X Q, Ding L, Chen L. Monitor radiance calibration of the remote sensing instrument with reflected lunar irradiance[J]. Journal of Remote Sensing, 2016, 20 (2) : 278 –289. DOI: 10.11834/jrs.20165155 |
| [20] | Wu X Q, Stone T C, Yu F F, Han D J. Vicarious calibration of GOES Imager visible channel using the Moon//Proceedings of the SPIE Volume 6296, Earth Observing Systems XI[J]. San Diego, California, United States: SPE, 2006, 6296 : 62960Z . DOI: 10.1117/12.681591 |
| [21] | Xiong X X, Barnes W. An overview of MODIS radiometric calibration and characterization[J]. Advances in Atmospheric Sciences, 2006, 23 (1) : 69 –79. DOI: 10.1007/s00376-006-0008-3 |
| [22] | Xiong X X, Sun J Q, Barnes W. Intercomparison of on-orbit calibration consistency between Terra and Aqua MODIS reflective solar bands using the moon[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5 (4) : 778 –782. DOI: 10.1109/LGRS.2008.2005591 |
| [23] | 许健民, 郭强, 陆其峰, 陆风, 张晓虎. 风云气象卫星数据处理算法的若干创新[J]. 气象学报, 2014, 72 (5) : 1023 –1038. Xu J M, Guo Q, Lu Q F, Lu F, Zhang X H. Innovations in the data processing algorithm for Chinese FY meteorological satellites[J]. Acta Meteorologica Sinica, 2014, 72 (5) : 1023 –1038. DOI: 10.11676/qxxb2014.086 |

