高光谱遥感图像中包含了丰富的光谱和空间信息，被广泛应用于岩矿物质识别(张成业 等，2015)、海洋遥感(陆应诚 等，2016)、环境监测(Roberts 等，2012)、精准农业(Gevaert 等，2014)以及军事目标检测(张朝阳 等，2008)等多个邻域。高光谱遥感图像的分类有利于挖掘图像中丰富的信息，目前新兴的一些分类方法，如神经网络(NN)(Tiwari 等，2015；高红民 等，2016)、支持向量机(SVM)(梁亮 等，2010；Kuo 等，2014；谭熊 等，2014)等均能在高光谱遥感图像分类中取得不错的效果。然而，高光谱遥感图像的高维性通常需要采用主成分分析(PCA)、独立成分分析(ICA)或最小噪声分离变换(MNF)等降维算法从原始数据中提取具有代表性的波段进行分类。尽管这些算法有效避免了“Hughes现象”，提升了分类效率，但是却在一定程度上丢失了原数据中所蕴含的丰富信息，而图像物理信息的改变会导致分类精度的下降。

20世纪以来，深度学习在自然语言处理、语音识别和图像识别等领域取得了显著的进展，如Lecun等人(1988)成功地将CNN应用于手写数字的识别；Krizhevsky等人(2012)使用深度CNN对ImageNet数据库图像进行分类，并取得了突破性的成果；以及不久前产生了轰动效应的一场AlphaGo人机围棋大战等。因此，将深度学习的理论和技术应用于高光谱遥感图像分类存在着巨大的潜在价值，它可以将光谱信息转化为灰度图像信息，以尽可能保留原有图像的数据信息，而又有效地避免“Hughes现象”。近年来，越来越多的研究者采用基于深度学习的方法对高光谱遥感图像进行分类。Chen等人(2014)构建了堆栈自动编码器(SAE)，以无监督的方式提取图像的深层特征，然后将像元的光谱矢量以及对光谱维度上高光谱数据进行PCA操作所获得的对应空间矢量共同作为SAE的输入，最后对高光谱遥感图像进行分类，虽然该方法较传统方法取得了较大突破，但SAE网络的各层都是全连接，会产生较多参数，因而需要较多样本用于训练。而相较于非监督分类方法，CNN作为监督分类方法能够依据标签样本数据提取更多利于图像分类的特征，Hu等人(2015)首次利用深度CNN网络模型对高光谱遥感图像进行分类，它通过获取每个像元的光谱矢量，再利用CNN卷积层提取光谱矢量上的局部光谱信息，并将卷积操作生成的特征图作为全连接层的输入，最后完成高光谱遥感图像的分类，该方法利用CNN的局部连接、权值共享等特性，从而大大减少了模型参数和降低了训练难度，进一步提高了分类性能，但未能充分利用高光谱遥感图像的空间信息，此外，构建的CNN模型仅包含单一卷积层，降低了其特征学习的能力。随后，Chen等人(2016)采用包含像元光谱信息和空间信息的CNN分类方法，并研究了空间信息对于CNN高光谱遥感图像分类的重要性，使得分类精度得到进一步提升。

然而，CNN的输入信息量与分类效果并不是完全正相关。一定模型下，太过复杂的输入不仅仅会使得训练时间、分类时间变长，甚至会导致精度不增反减。因此有必要对CNN分类前的特征选择问题进入深入的研究，同时构造适合于高光谱遥感图像分类的CNN模型。基于此，本文提出了一种将变异系数与CNN结合的方法，用于对高光谱遥感图像中的像元进行分类。首先采用基于变异系数的方法对高光谱遥感图像进行低效波段的剔除，随后获取每个像素的光谱矢量和空间矢量，并将其转化为2维灰度图像作为CNN模型的输入，从而完成高光谱遥感图像的分类任务。该方法对于进一步提升分类精度、推广CNN在高光谱遥感图像分类上的应用具有重要意义。

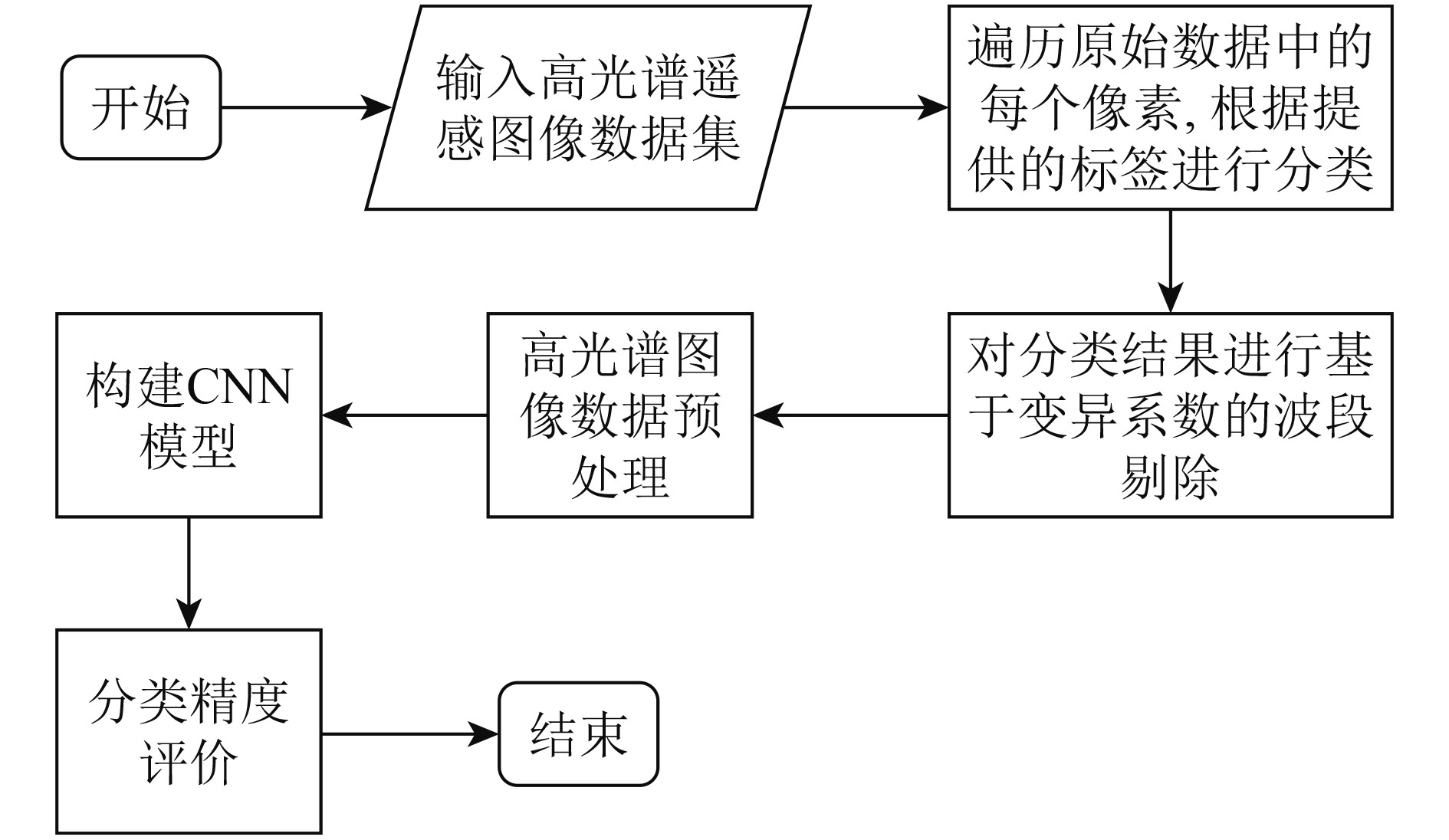
根据遥感图像的成像原理，图像的光谱分辨率和空间分辨率往往不可兼得，通常表现为高光谱遥感图像的空间分辨率低于普通遥感图像。因此，针对于高光谱遥感图像的分类问题，研究者们常使用基于像元的分类方法(Bioucas-Dias 等，2013)。本文基于像元分类的CV-CNN方法整体流程如图1。

图 1 CV-CNN方法整体流程图 Figure 1 The overall flowchart of CV-CNN method

CNN作为有监督分类方法，需要对原始数据按照样本标签进行分类，通过分别遍历原始数据和标签数据的每个像素，从而按照标签数据对每个像素进行分类，并将结果分别存入至特定的类别当中。

得益于光谱技术的发展和成熟，相比于多光谱遥感图像，高光谱图像中包含了更加丰富的光谱信息，甚至包含了数百个波段。虽然高光谱图像为地物的精准分类提供了更多的依据，但也不可避免地包含了一些受大气影响、有噪声的冗余波段，导致分类性能受到影响；数据的波段数量有时不便于转化成高宽比例合适的CNN输入矩阵，导致输入不合适或者需要resize函数对图像进行压缩使其转换为高度和宽度一致的图像，而压缩过程中有可能存在一定的特征损失。因此，本文提出了一种基于变异系数的高光谱遥感图像中低效波段的剔除方法。

变异系数(CV)(Feng和Brown，1998)是指标准差和平均数的比值，主要是用于衡量总体数据相对离散程度的数字特征，其优势在于变异系数是无量纲的，不受数据取值大小的影响。变异系数的计算过程如下

式中，σ表示样本的标准偏差，μ表示样本均值。设C_v表示第v类样本(v=1, 2, $ \cdots $ , C)，B_k表示高光谱遥感图像中的第k个波段(k=1, 2, $ \cdots $ , B)。随后定义两种变异系数，分别是类内变异系数CVIA (Coefficient of Variation for Intraclass)和类间变异系数CVIE (Coefficient of Variation for Interclass)。B_k的类内变异系数用来衡量该波段下的类内差异性，通过计算某一类别下B_k的均值和标准差求得B_k在该类别下的变异系数，然后求解所有类别下此变异系数的均值即可得到B_k的CVIA值。CVIA越大说明类内差异性越大，不利于分类，所以越应该舍弃。该计算过程如式(2)

式中， $\mathit{\boldsymbol{X}}_k^v = \left[ {x_{1, k}^v, x_{2, k}^v, \cdots \! , x_{t, k}^v} \right]$ 表示第v类第k个波段的所有像素点，t表示第v类的像素总数，std(·)表示求标准差操作，mean(·)表示求均值操作。

B_k的类间变异系数用来衡量该波段下的类间相似性，首先计算每类中B_k的均值 $M_k^v\left({v = 1, 2, \cdots \! , C} \right)$ ，然后求解所有类别(即v=1, 2, $ \cdots $ , C)的 $M_k^v$ 的均值和 $M_k^v$ 的标准差，最后用得到的 $M_k^v$ 的标准差除以 $M_k^v$ 的均值得到变异系数，即为此B_k的CVIE。CVIE越小则说明类间相似性越大，不利于分类，所以越应该舍弃。该计算过程如式(3)

通过引入变异系数来衡量不同波段的类间相似性以及类内差异性。同时考虑到CVIE是影响分类精度的最直接原因，而类内差异性大不一定就难以区分，并且在很多时候一种类别中本身就包含了多种实际地物，普遍存在类内差异性，所以剔除波段的原则为：CVIE为主要因素，CVIA为次要因素，因此本文剔除波段时的判别依据为(CVIE)²/CVIA值。考虑到剔除波段主要是3个目的：1是剔除掉干扰波段；2是减少波段个数，加快训练和分类；3是尽量使CNN输入为方阵，有利于训练和分类。故剔除波段的个数没有限定要求，一般根据数据集的不同以及后继CNN处理的方便性和分类效果来适宜的确定。

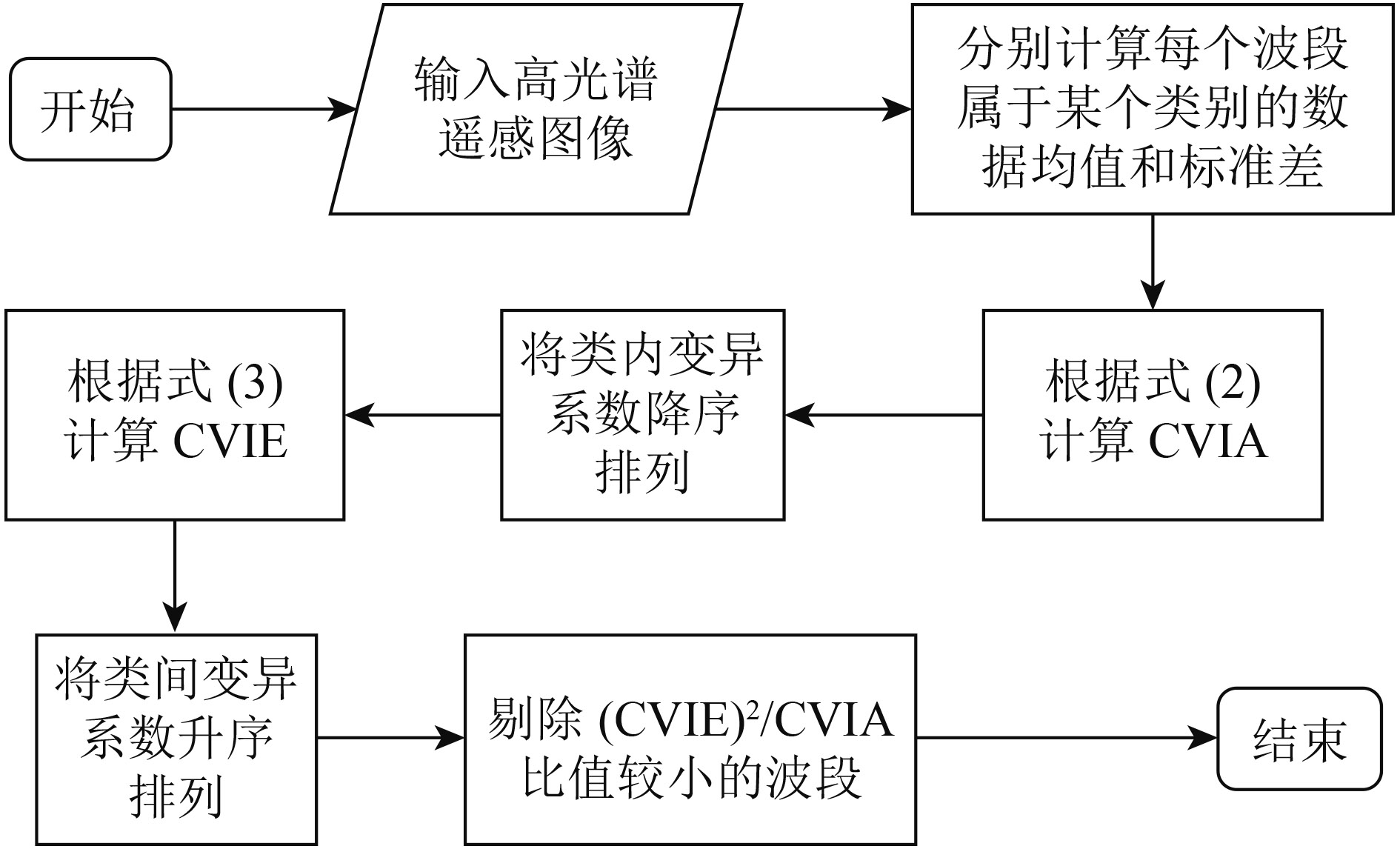
本文利用变异系数的方法来剔除高光谱遥感图像中低效波段的具体流程如图2。

图 2 基于变异系数方法剔除波段的流程图 Figure 2 The flow chart of removing bands based on CV method

使用变异系数方法剔除波段后的各像素点的高光谱数据还需要经过一定的预处理操作才能得到CNN的标准输入。

由于高光谱遥感图像不同波段的数据范围不一致，为了降低不同数据范围对高光谱遥感图像分类精度的影响，在训练CNN模型之前需要对高光谱遥感图像数据按波段分别进行归一化操作，计算公式如下

式中， $1 \leqslant i \leqslant H$ ， $1 \leqslant j \leqslant W$ ， $1 \leqslant k \leqslant B$ ， ${\mathit{\boldsymbol{x}}^k}$ 表示第k个波段的所有像素点， $x_{i, j}^k$ 表示第k个波段中第i行、第j列的像素，W表示图像宽度，H表示图像的高度，B表示高光谱遥感图像的波段总数。

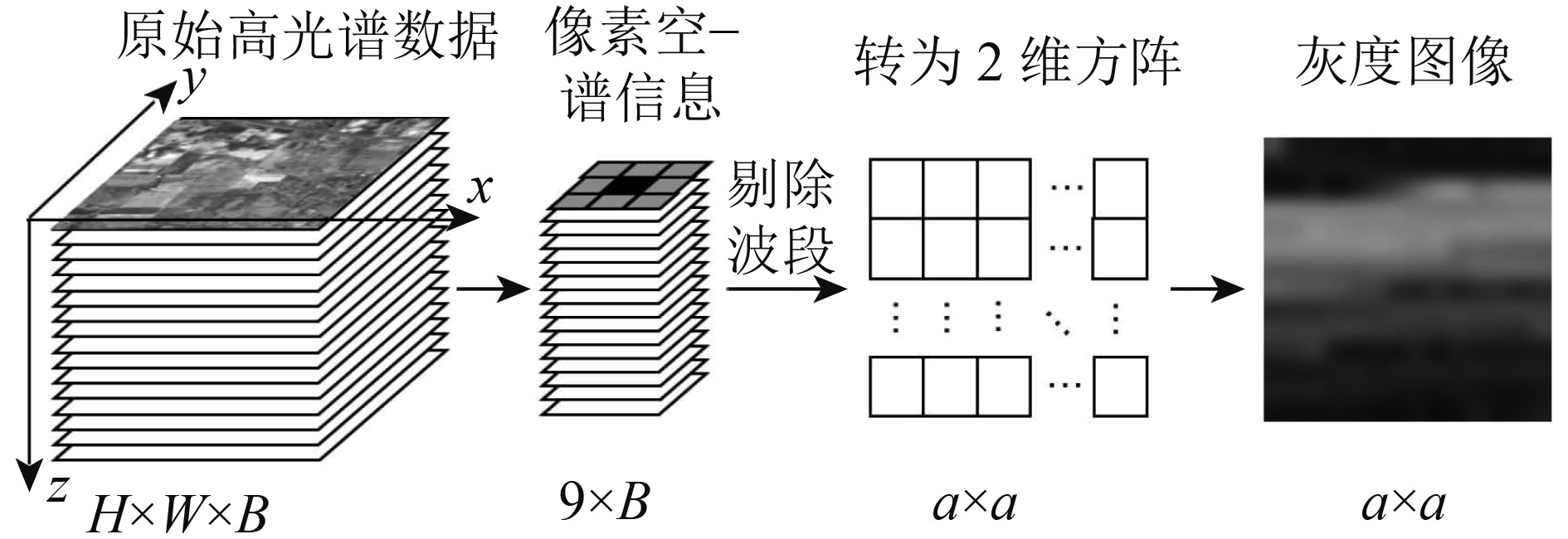
在高光谱遥感图像中，一个像素与其周围像素的光谱信息往往表现为高度的相关性，结合光谱信息和空间信息能够有效地改善高光谱的分类精度(田彦平 等，2015)。为了改善CNN下高光谱遥感图像的分类精度，需要提取每个像素的空—谱信息，然后经过剔除波段操作使得其接下来能被转化为2维方阵。如图3，像素的空—谱信息中的黑色区域为目标像素，而其周围的灰色区域为该目标像素的8个邻域像素，将目标像元与其8个邻域像素的高光谱数据经过波段剔除后一并转化为一个2维方阵(a表示剔除最少波段能达到的最大方阵大小)，最后将该矩阵保存为灰度图像作为该像元在CNN模型中的输入。

图 3 高光谱遥感图像的空–谱信息预处理 Figure 3 Spatial-spectral information preprocessing of HSI

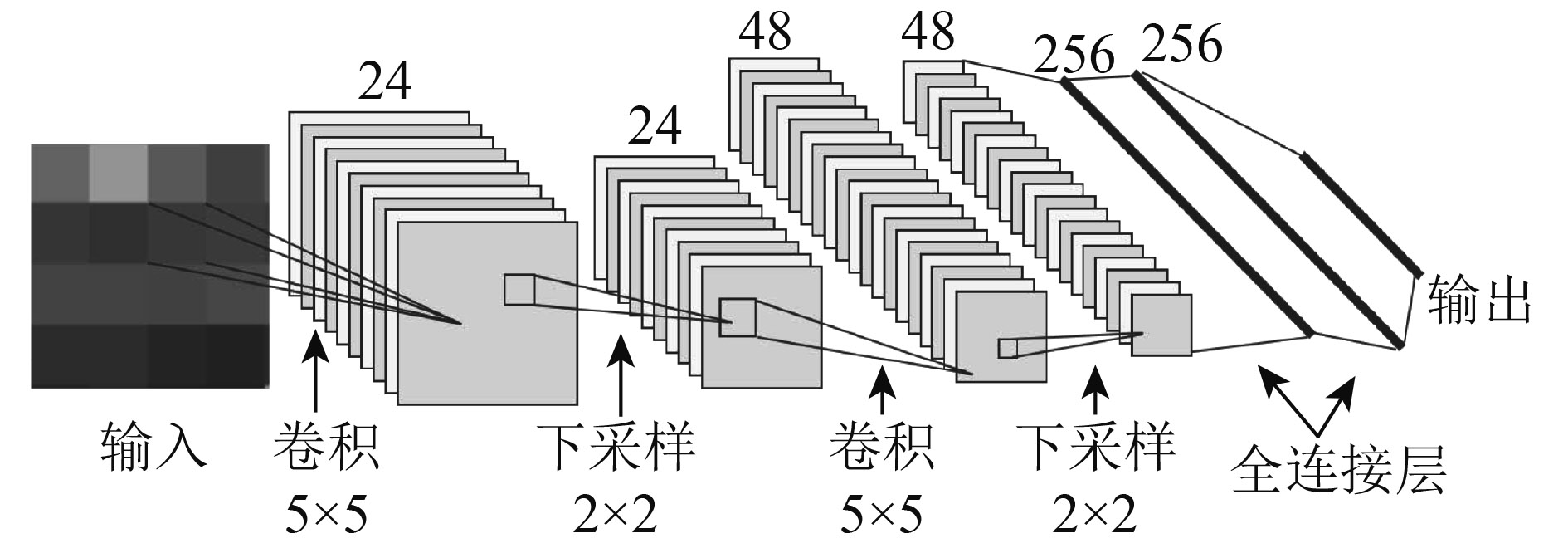
在构建CNN模型的过程中，需要重点考虑的因素主要为模型的深度(层数)、滤波器的大小和滤波器的数量，其中模型的深度是影响分类精度的主要因素，在设计适用于高光谱遥感图像分类的CNN模型时，实验研究表明，当构建一定层数的模型时，进一步增加CNN模型的层数，分类精度没有提高反而出现降低的情况，且还会花费更多时间(He和Sun 等，2015)。因此针对高光谱遥感图像的特性，本文构建了一个由两个卷积层、两个最大池化层、两个全连接层以及一个Softmax层组成的7层CNN模型，如图4。在滤波器选择问题上，考虑到对高光谱遥感图像分类时，CNN中的输入通常为每个像素的空谱信息通过矩阵化转换的2维图像，而这些图像通常较小，所以滤波器不宜过大，且(He和Sun，2015)实验研究也表明，在构建更深层次的模型时，可以适当降低滤波器大小或减少滤波器的数量来弥补深层次模型的时间成本，但是过度降低滤波器大小或减少滤波器数量同样也会损害分类精度。因此本文CNN模型中的第1个卷积层由24个5×5的卷积核对输入图像进行步长为1的滤波操作所得，第2个卷积层由48个5×5的卷积核对特征图进行步长为1的滤波操作所得，卷积层特征提取时步长选择为1，这既能够较为全面的提取图像的特征信息，又不至于特征过多、训练时间过长。

图 4 CNN模型总体结构 Figure 4 The whole structure of CNN model

在图像识别中，图像的特征点和其相对的位置对图像的正确识别很重要，而特征点的精确位置却不是很重要，下采样既能降低特征的维度又能保留特征点的大体位置，这是卷积神经网络具有一定的平移、缩放和旋转不变性的重要原因。所以考虑到与滤波器大小选择时的相同原因，确定使用大小为2×2的下采样区域进行最大值采样(Max-Pooling)，由于下采样区域本身就时非常小了，因此不考虑再进行重复采样，故选择采样的步长为2。

在CNN模型的最后采用ReLu(Rectified Linear Units)函数作为神经元的激活函数，以解决使用传统的Sigmoid、Tanh等激活函数易出现梯度弥散等问题，其输出作为第2个全连接层的输入。第2个全连接层同样经过ReLu激活函数，然后将其输出作为Softmax层(分类器)的输入。

将上述CNN模型应用于Indian Pines数据时过程如下：首先第1个卷积层使用24个5×5大小的卷积核对42×42的灰度图像进行步长为1的滤波操作，生成24个38×38(计算过程：42−5+1=38)的特征图；然后对产生的特征图进行Max-Pooling操作，产生24个19×19(计算过程：(38−2)/2+1=19)的特征图；第2个卷积层使用48个5×5大小的卷积核对19×19的特征图进行步长为1的滤波操作，生成48个15×15(计算过程：19−5+1=15)的特征图，同样紧接着进行Max-Pooling操作，产生48个8×8(计算过程： $\left\lceil {\left({{\rm{15}} - {\rm{2}}} \right)/2} \right\rceil {\rm{ + 1 = 8}}$ )的特征图；然后经过第1个全连接层，产生256个神经元，再将经过ReLu激活函数产生的神经元作为第2个全连接层的输入；第2个全连接层共产生256个神经元，同样将ReLu激活函数产生的神经元作为Softmax层的输入，最终输出结果即为14类的概率结果。应用于Pavia University数据时过程如下：首先第1个卷积层使用24个5×5大小的卷积核对30×30的灰度图像进行步长为1的滤波操作，生成24个26×26(计算过程：30−5+1=26)的特征图；然后对产生的特征图进行Max-Pooling操作，产生24个13×13(计算过程：(26−2)/2+1=13)的特征图；第2个卷积层使用48个5×5大小的卷积核对13×13的特征图进行步长为1的滤波操作，生成48个9×9(计算过程：13−5+1=9)的特征图，同样紧接着进行Max-Pooling操作，产生48个5×5(计算过程： $\left\lceil {\left({{\rm{9}} - {\rm{2}}} \right)/2} \right\rceil {\rm{ + 1 = 5}}$ )的特征图；然后经过第1个全连接层，产生256个神经元，再将经过ReLu激活函数产生的神经元作为第2个全连接层的输入；第2个全连接层共产生256个神经元，同样将ReLu激活函数产生的神经元作为Softmax层的输入，最终输出结果即为9类的概率结果。

分别针对Indian Pines和Pavia University高光谱遥感图像数据展开实验研究，以验证方法的有效性。实验环境是一台PC机，配置为Intel(R) Core(TM)i7-6500U CPU @2.5 GHz 2.59 GHz，8 G内存。

Indian Pines由机载可见光/红外成像光谱仪(AVIRIS)获取，覆盖了美国印第安纳州的整个西北部地区，其原始图像大小为145×145像素，空间分辨率为20 m，包含220个波段和16种地物，由于部分地物类别的样本数量过低，因此本文实验时仅保留其中的14类地物；Pavia University数据是由反射光学系统成像光谱仪(ROSIS)传感器在意大利帕维亚市的帕维亚大学上空拍摄获取的，其原始图像大小为610×320像素，空间分辨率为1.3 m，包含103个波段和9种地物。

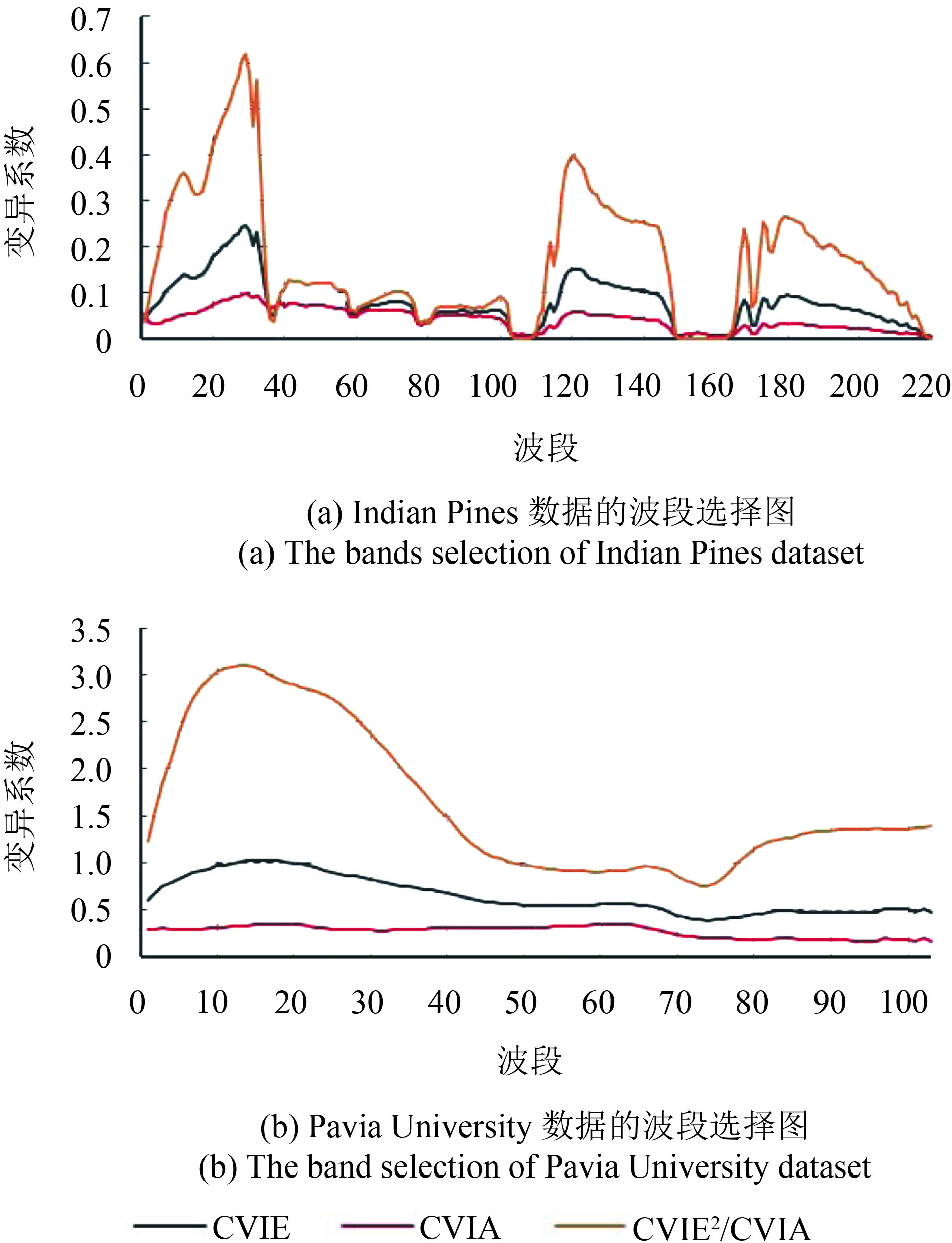
如图5，在对Indian Pines使用基于变异系数的波段剔除法时，为方便高光谱遥感图像的空—谱信息易于转换为高度和宽度一致的灰度图像，剔除(CVIE)²/CVIA最小的24个波段(第104—109、149—164、219、220波段)，然后保留剩余的196个波段，值得注意的是这种方法剔除的24个波段中正好包含了该数据受水气噪声影响的所有20个波段(104—108、150—163和220波段(Li 等，2014))，这20个波段指标值是最差的，从而从侧面印证了变异系数法的有效性；同理剔除Pavia University中的第72—74等3个波段。

图 5 数据的波段选择图 Figure 5 The bands selection of two datasets

在剔除波段后，Indian Pines的像元空—谱信息维度大小为9×196，通过reshape函数进行矩阵化可得到42×42像素的灰度图像；Pavia University的像素空—谱信息维度大小为9×100，通过reshape函数进行矩阵化可得到30×30像素的灰度图像。然后根据两组数据的已知标签信息对灰度图像进行分类，并将分类后的图像按照8∶2的比例随机分为训练集和测试集数据，Indian Pines和Pavia University数据的配置详情分别如表1和表2。

表 1(Table 1)

表 1 Indian Pines数据配置 Table 1 The allocation of Indian Pines data 编号 类别名称 训练集/个 测试集/个 1 Alfalfa 17 5 2 Building-Grass-Tree-Drives 212 54 3 Corn 126 32 4 Corn-mintill 440 112 5 Corn-notill 820 204 6 Grass/Pasture 266 70 7 Grass/Tree 412 104 8 Hay-windrowed 319 80 9 Soybean-clean 318 80 10 Soybeans-mintill 1572 393 11 Soybeans-notill 558 140 12 Stone-steel towers 36 10 13 Wheat 111 30 14 Woods 838 210 总计 6045 1524

表 1 Indian Pines数据配置 Table 1 The allocation of Indian Pines data

表 2(Table 2)

表 2 Pavia University数据配置 Table 2 The allocation of Pavia University data 编号 类别名称 训练集/个 测试集/个 1 Asphalt 5262 1316 2 Meadows 14623 3656 3 Gravel 1661 415 4 Trees 2442 610 5 Painted-metal-sheets 1076 269 6 Bare-Soil 4023 1006 7 Bitumen 1064 266 8 Self-Blocking-Bricks 2946 736 9 Shadows 758 189 总计 33854 8464

表 2 Pavia University数据配置 Table 2 The allocation of Pavia University data

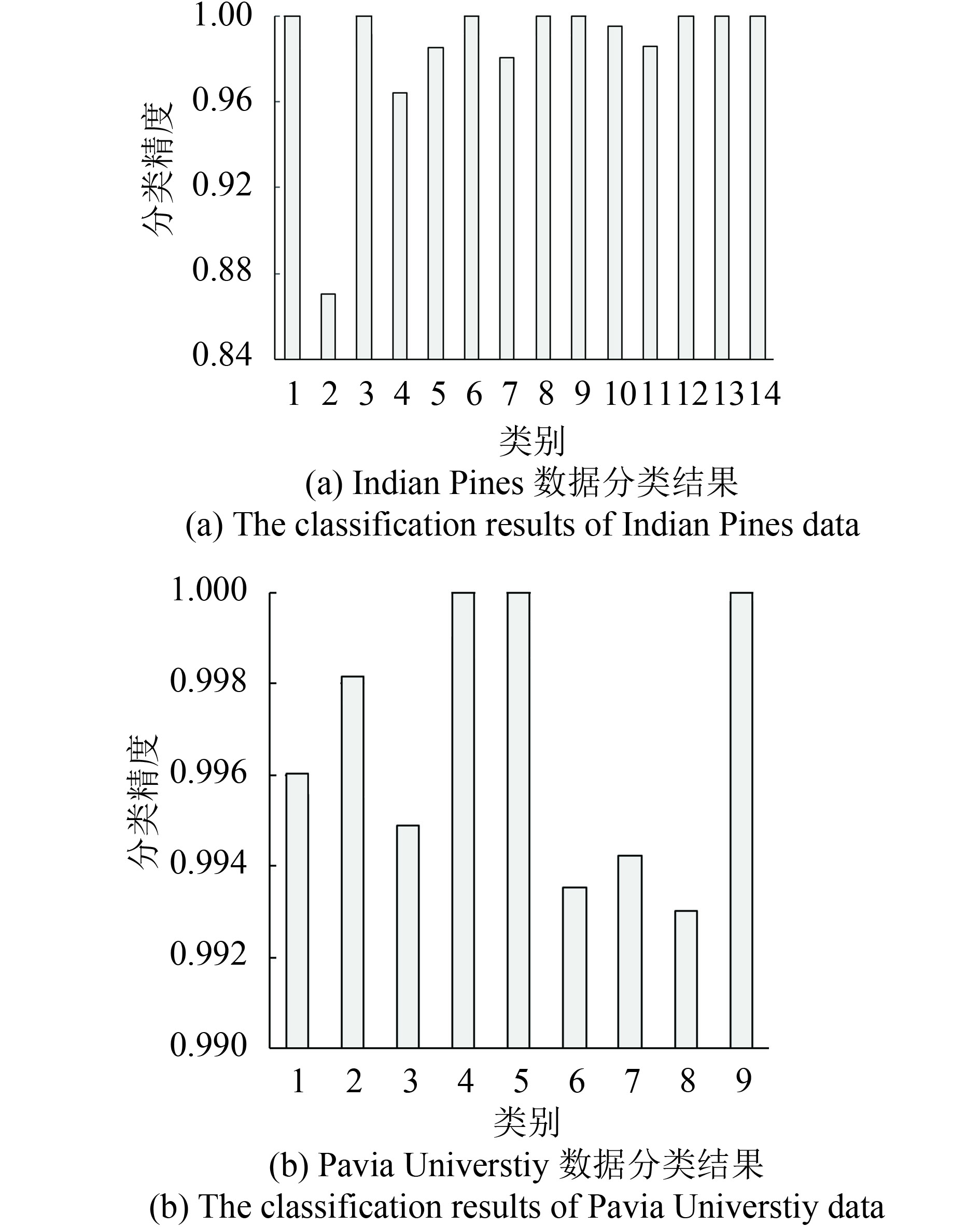
使用CV-CNN方法对两组测试数据集的分类结果如图6，其展示了两组数据测试集中每一类的分类精度。Indian Pines测试集的大多类别精度保持96%以上，尤其是第2类的分类精度较总体偏低，仅达到87%，主要原因在于第2类的复杂性，它包含了建筑物、草地、树木以及车辆等多个目标，分类时干扰信息较多，从而导致分类精度较低；Pavia University相比于Indian Pines拥有更高的空间分辨率，大大降低了混合像元情况的产生，因此该数据的测试集的任意类分类精度均保持在99%以上。

图 6 两个数据集的分类结果 Figure 6 The classification results of two datasets

表3和表4对比了本文CV-CNN方法与近两年文献中使用的CNN方法(Hu 等，2015；Chen 等，2016；Leng 等，2016；Mei 等，2016)。对于表3的Indian Pines数据，方法1既未考虑空间信息也未考虑剔除波段的特征选择；方法4仅考虑了空间信息但未考虑剔除波段的特征选择；方法2、方法3和方法5既考虑了空间信息也考虑了剔除波段的特征选择；方法6—10为本文CNN方法对照，都考虑了8邻域的空间信息，区别在于方法6未考虑剔除波段，方法9剔除了20个波段，方法7，8，10剔除了24个波段。对于表4的Pavia University数据，该数据的103个波段本身已经剔除了大量受影响的波段，所以方法1—5在未研究特征选择情况下，都未考虑剔除波段的情况；此外，方法1未考虑空间信息；方法2—5都考虑了像素的邻域空间信息，区别主要是邻域空间区域的大小；方法6—9为本文CNN方法对照，都考虑了8邻域的空间信息，区别在于方法6未考虑剔除波段，方法7—9剔除了3个波段。根据不同方法下的总体分类精度的比较可以得到以下结论：

表 3(Table 3)

表 3 使用Indian Pines数据不同的CNN方法对比 Table 3 Comparison of different CNN methods using Indian Pines dataset 方法 编号 方法 名称 空间 信息 剔除低 效波段 总体分 类精度/% 1 CNN(Hu 等，2015) 未考虑 无 90.16 2 CNN(Mei 等，2016) 8邻域 剔除20个水气波段 93.70 3 CNN(Mei 等，2016) 24邻域 剔除20个水气波段 95.70 4 CNN(Leng 等，2016) 8邻域 无 95.29 5 CNN(Chen 等，2016) 27×27–1邻域 剔除20个水气波段 97.56 6 本文CNN 8邻域 无 97.90 7 本文CNN 8邻域 PCA变换(降为196维) 97.31 8 本文CNN 8邻域 MNF变换(降为196维) 98.25 9 本文CV-CNN 8邻域 CV法剔除20个波段 (等同于剔除20个水气波段) 98.30 10 本文CV-CNN 8邻域 CV法剔除24个波段 (刚好包含20个水气波段) 98.69

表 3 使用Indian Pines数据不同的CNN方法对比 Table 3 Comparison of different CNN methods using Indian Pines dataset

表 4(Table 4)

表 4 使用Pavia University数据进行不同的CNN方法对比 Table 4 Comparison of different CNN methods using Pavia University dataset 方法 编号 方法名称 空间信息 剔除低效波段 总体分类 精度(%) 1 CNN(Hu 等，2015) 未考虑 无 92.56 2 CNN(Mei 等，2016) 8邻域 无 99.20 3 CNN(Mei 等，2016) 24邻域 无 99.60 4 CNN(Leng 等，2016) 8邻域 无 96.74 5 CNN(Chen 等，2016) 27×27–1邻域 无 99.54 6 本文CNN 8邻域 无 99.60 7 本文CNN 8邻域 PCA变换 (降为100维) 96.40 8 本文CNN 8邻域 MNF变换 (降为100维) 97.83 9 本文CV-CNN 8邻域 CV法剔除 3个波段 99.66

表 4 使用Pavia University数据进行不同的CNN方法对比 Table 4 Comparison of different CNN methods using Pavia University dataset

(1) 对比表3和表4，在使用同一的方法的基础上，Pavia University数据集的分类效果优于Indian Pines数据集。正如上文所提到的，Pavia University的空间分辨率为1.3 m，在很大的程度上避免了混合像元的产生，因此图像质量更高，最终的分类精度也越高。

(2) 对比方法1与方法4，可以发现相比于仅利用高光谱遥感图像的光谱信息进行分类，考虑像素的空间信息能够有效地改善最终的分类精度；对比方法2、方法3和方法5，可以发现空间邻域大小的选择也能一定程度上影响高光谱遥感图像的分类精度。

(3) 对比方法4和方法6，可以发现在仅考虑8邻域并且未剔除波段的情况下，本文构建的CNN模型(方法6)与目前较优的CNN(方法4)相比，Indian Pines分类精度提高了2.61%，Pavia University分类精度提高了2.86%，从而说明本文构建的CNN模型的有效性。

(4) 对比方法6、方法9和方法10(Pavia University仅有方法6和方法9)，使用CV法剔除波段，不仅能将空—谱信息尽可能转化为方阵以简化CNN模型滤波器大小的设置，此外也能剔除更多的冗余波段，提高模型分类性能。在Indian Pines数据集中，CV方法剔除24个波段相比于不剔除波段提升了0.79%的分类精度，相比于剔除20个水气波段，提升了0.39%的分类精度；在Pavia University数据集中，CV方法剔除3个波段相比于不剔除波段提升了0.06%的分类精度。Pavia University数据集的精度提升有限主要是因为不剔除波段时分类精度已经达到很高的99.6%了。

(5) 对比表3中的方法7、方法8、方法10以及表4中的方法7、方法8和方法9，可以发现在CNN模型相同且保留相同维度数据时，本文的CV方法在Indian Pines数据中较PCA、MNF方法分别提升了1.38%和0.44%，在Pavia University数据中较PCA、MNF方法分别提升了3.26%和1.83%。

总而言之，通过Indian Pines和Pavia University两组数据的实验结果表明，本文提出的CV-CNN方法能够有效地改善高光谱遥感图像的分类精度。

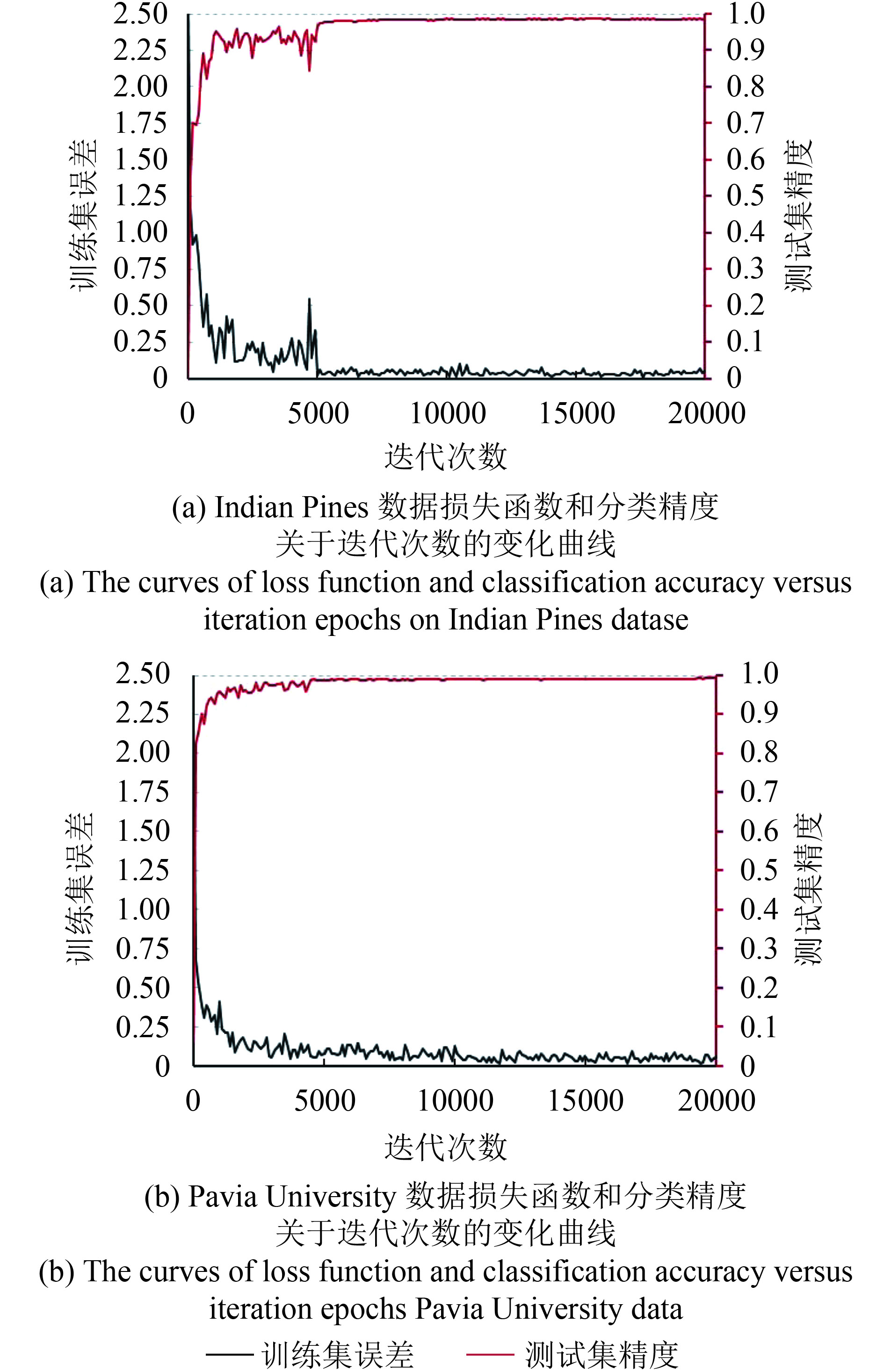
为了进一步评价CV-CNN模型的性能，图7分别给出了使用Indian Pines和Pavia University训练集数据来训练本文构建的CNN模型的损失函数变化曲线以及对测试集数据分类的精度变化曲线。其中训练集的损失函数变化曲线能够反映出模型的预测结果与实际结果的误差，因此损失函数越小，说明该模型被训练的越好；测试集的总体精度变化曲线能够反映模型泛化能力的好坏，因此，测试集精度越高，说明该模型的泛化能力越好。从图7中可以看出，在迭代次数超过5000次的时候，训练集的损失函数和测试集的总体精度变化曲线都趋于比较稳定的较优水平。

图 7 损失函数和分类精度关于迭代次数的变化曲线 Figure 7 The curves of loss function and classification accuracy versus iteration epochs

本文提出了一种适用于高光谱遥感图像分类的CV-CNN方法。该方法采用变异系数的方式来剔除高光谱中的低效波段，从而减少其对分类性能的影响，且便于将空—谱信息尽量转换为方阵，最终提高分类精度、减少分类时间；同时提取高光谱遥感图像中各个像素的空—谱信息，增加空间信息相比于单独的光谱信息能够获得更好的分类效果。此外，在构建CNN模型时需要考虑高光谱遥感图像分类特点，合理设置CNN模型的层数、滤波器的大小和数量以及操作的步长。实验结果表明，本文所提出的CV-CNN方法能够有效地改善高光谱遥感图像的分类精度，有助于推广CNN在高光谱遥感图像分类中的实际应用。在后继的研究中，可以进一步研究CV-CNN方法剔除波段的定量化，即类内变异系数值大于多少的波段或类间变异系数值小于多少的波段是一定要剔除，从而进一步优化CV-CNN方法的分类效果。此外，研究不同的归一化方式对CV-CNN方法的影响也具有一定的意义，因为不同的归一化方式会在一定程度上改变数据的一些特性，如变异系数等。另外，目前基于像素的CNN方法泛化能力还有待提升，往往适应了一个数据集的CNN模型在另一数据集上表现不尽如人意，如何利用CV-CNN方法，去实现一定波段的任意目标像素的准确分类，仍是需要长期探索研究的重要问题，也是制约CNN在高光谱遥感图像中推广应用的关键所在。