20世纪80年代初期，随着成像光谱概念和技术的出现，光学遥感在经历了全色、彩色摄影、多光谱成像阶段之后出现了高光谱成像质的飞跃，对地物的光谱属性及特征的研究也不断深入，大量隐藏在狭窄光谱信息内的地物特性被人类逐一挖掘，使得高光谱技术发展、应用研究在国际领域中一直处于研究热点，引起广大从事遥感技术人士的高度重视。

高光谱遥感是指在电磁波谱的紫外、可见光、近红外和中红外区域，利用成像光谱仪获取的许多非常窄且光谱连续的图像数据。高光谱遥感图像不仅包含了全色及彩色摄影丰富的空间信息，同时相对于多光谱图像其拥有更多更精细的光谱信息，使得图像中每一个像元都对应一条平滑而完整的光谱曲线。由于不同地物光谱曲线属性不同，利用高光谱遥感技术充分挖掘不同物质的光谱特征及形态特征，为地物的精细探测奠定基础。

高光谱遥感对地观测技术受到研究学者的普遍关注，也相继研发出大量高光谱成像仪系统，包括航空成像光谱仪以及航天成像光谱仪系统。成像光谱仪的出现突破了传统科学领域中“成像无光谱”以及“光谱不成像”的历史性瓶颈问题(童庆禧 等，2006b)。具有代表性的航空高光谱成像光谱仪有美国的AVIRIS、HYDICE、Probe、MIVIS、DAIS-7915等，澳大利亚的HyMap，加拿大ITRES公司的系列产品等(张兵，2011)，星载的美国Hyperion以及欧空局的CHRIS、APEX影响较大。此外，一些基于太空的地球观测仪器，如HERO、EnMAP、Flora、HyspIRI、PRISMA、FLEX、SpectraSat、MEOS等航天高光谱传感器在未来几年将会投入使用(Schaepman 等，2009；Bioucas-Dias 等，2013)。中国一直紧跟国际高光谱成像技术的发展前沿，先后研制了MAIS、PHI、OMIS等航空高光谱遥感(童庆禧 等，2006a)，以及HJ-1A、天宫一号、天宫二号等航天遥感，目前高分五号星载高光谱传感器也处于积极研发中。因此，研究者可以充分利用高光谱数据进行分析，并广泛应用于地表分类、冰雪应用、森林资源清查、岩矿识别、农业监测、食品安全检测、环境管理等领域(赵少华 等，2013；吴见和彭道黎，2011；王润生 等，2011；张达和郑玉权，2013；Thomas 等，2016)。

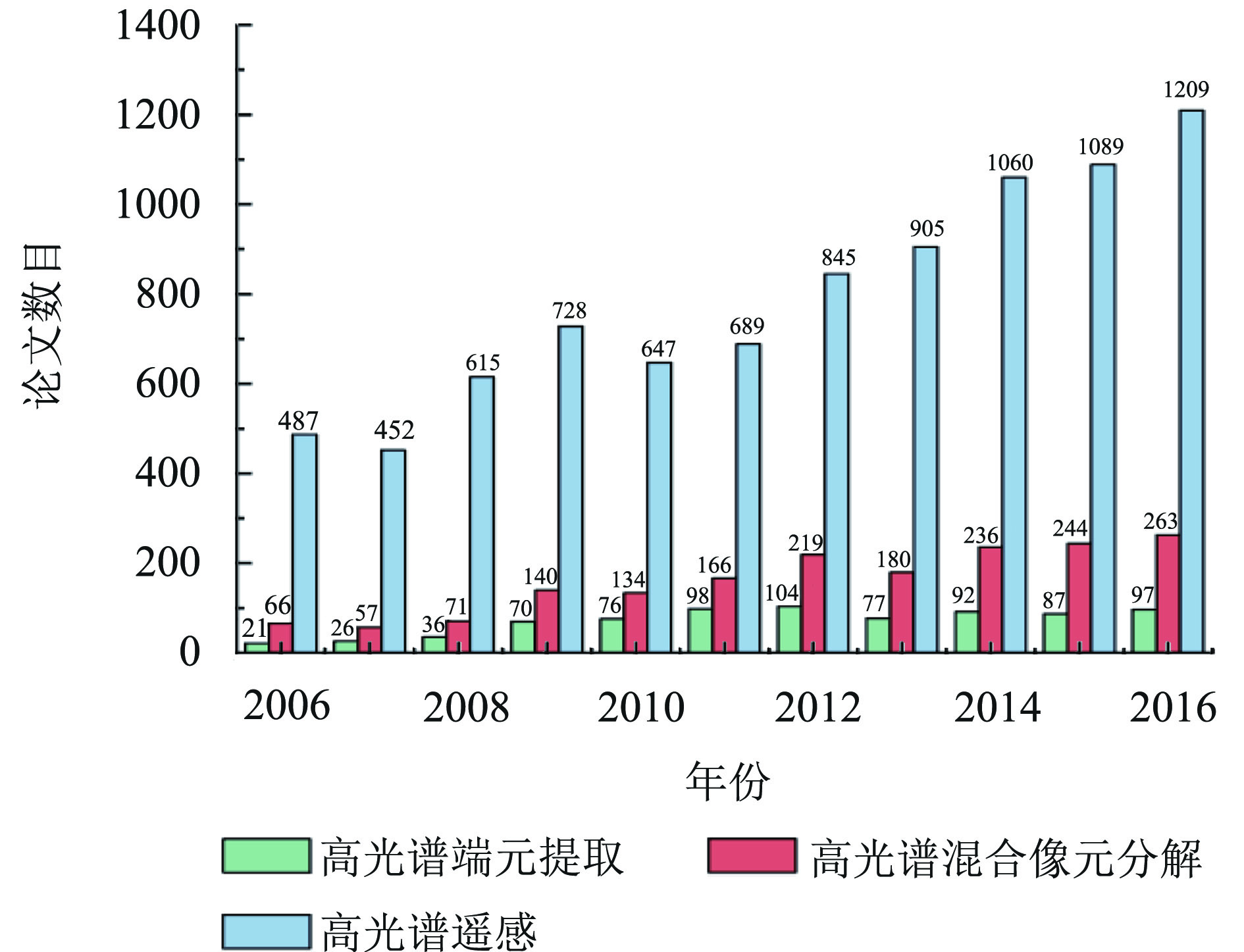
然而相对于多光谱遥感，高光谱在光谱分辨率提高的同时却制约着空间分辨率。由于高光谱遥感图像空间分辨率限制和地物分布的复杂多样性，混合像元广泛存在于图像中，影响遥感图像的分类精度以及目标探测效果，制约定量高光谱遥感的发展与应用。混合像元是指一个像元中包含多种地物，像元光谱信号的组成成分即为端元。由于高光谱数据自带几十至上百个波段光谱信息，使得高光谱遥感图像在混合像元分解、亚像元级处理方面较全色、多光谱图像更具有优势。图1是2006年以来近10年高光谱应用的部分发表论文统计，数据来源于SCI-Expanded数据库，可以直观看出高光谱遥感越来越受关注，其中对于高光谱数据混合像元分解与端元提取的研究也逐年增多。由此可见，高光谱混合像元分解技术是高光谱遥感影像处理和应用中一项重要研究内容，相对于分类是在赋以每个像元一种类别，解混的最终目标是在亚像元级上得到各个端元的比例或者亚像元级目标的探测与识别。因此，研究高光谱混合像元分解技术，充分结合高光谱图像像元的光谱特性及空间特征，了解其中的端元组成及成分，能够为提高精细化分类及目标探测提供可能，从而提高高光谱遥感定量化应用水平。

图 1 高光谱遥感的部分论文统计 Figure 1 Partial paper statistics of hyperspectral remote sensing

本文总结了高光谱遥感影像混合像元分解技术中端元数目估计、端元提取以及丰度估计的常用方法，阐述了当前高光谱遥感混合像元分解面临的挑战、尚待解决的问题以及解决途径，并对高光谱遥感影像混合像元分解技术的应用前景提出展望。

高光谱混合像元分解主要依赖于3种混合模型，线性模型、非线性模型以及正态组分模型，其中线性混合是指大尺度的光谱混合且入射光仅与一种地物发生作用；非线性混合则是由多种地物之间的相互作用形成，可以是经典的、近距离的、微观尺度或者多层次的。但由于非线性混合模型需要事先了解端元的先验知识或者相应的特征信息，且模型在多种地物间相互作用普适性差，即解决近距离混合的模型不能应用于多层次混合，虽然研究者对非线性模型(如广义双线性模型)做了大量的研究工作包括引入机器学习、神经网络等算法，但仍然无法实现盲分解，算法相对于线性模型不够成熟。正态组分模型则是将高光谱图像中的每个像元视为由端元线性混合而成的随机变量(Eismann和Stein，2007)，可以看成线性模型的一种扩展，但相对于线性模型，正态组分模型考虑到端元变异性，对高光谱数据描述的更为详细。然而由于引入模型位置变量增加了求解复杂度，目前尚未有直接求解的方法。相反，3种模型中线性模型提出最早，且在大部分场景下能够很好的近似反映光散射机理，具有易于理解、实施简单且适应性高的特点，因此也是研究的最广泛的。

高光谱混合像元分解的步骤一般分为端元数目估计、端元提取以及丰度估计，具体技术路线如图2所示。

图 2 高光谱混合像元分解技术路线图 Figure 2 The flow chart of hyperspectral unmixing

端元数目的估计影响后续高光谱混合像元分解的精度，如果端元数目估计过少则导致端元提取精度不纯，提取的光谱仍是混合信息，且增大了原始图像与反演图像的均值误差，反之端元数目估计过多则引起重复端元的提取，且易受噪声、大气、光谱变异等干扰，导致丰度估计误差增大。目前端元数目可以依据先验知识或者端元数目估计算法获得。其中端元数目估计算法主要包括：基于本征维度算法、基于似然函数算法、基于特征值分析算法以及基于几何学的端元数目估计算法等。

(1) 基于本征维度算法(ID)(Fukunaga，1982)，即寻找用于描述观测数据特性所需参数的最小数目。较为经典的方法是利用主成分分析(PCA) (Jolliffe，1986)和最大噪声分数(MNF)(Green 等，1988)进行端元数目估计，实质上就是将端元数目等同于本征维度。PCA是通过求解每个主成分的方差贡献率寻找图像中的主成分信息，该方法能够去除数据中的冗余，尽可能减少信息损失并使之成为互不相关的成分，更适合处理多波段数据，但是当高光谱遥感图像波段数远大于端元数目时，特别是有小目标存在图像数据时，利用PCA会丢弃子空间的端元，容易忽略细微光谱信息而导致较大误差；MNF与PCA相似，相当于连续两次PCA，都是对数据进行线性变换，不同之处是MNF变换之后各个波段是按照信噪比顺序排序，逐级减少，而PCA是按照信息量排序逐级减少。由于两种算法都是基于线性模型，认为端元为互不相关的信号，因此可以近似认为信噪比较大的波段数据即为端元数目。后期也有研究者利用入度分布统计方法(IDD)(Heylen 等，2017)，在本征维度的基础上分析寻找目标高光谱图像与合成图像最佳匹配图像，从而确定端元数目，实验结果表明能够获得较好的效果，但算法依赖光谱库及部分先验知识，不能自动确定端元。

(2) 基于似然函数算法的有利用Akaike信息准则(AIC)(Akaike，1974)、最小描述长度(MDL) (Rissanen，1978)等算法，由于算法需要混合模型或似然函数的先验知识，端元数目估计结果可能会由于不正确的先验信息导致的模型不匹配错误。此外，当AIC和MDL应用于高光谱数据时，估计结果往往比真实值大。

(3) 基于特征值方法，是分析图像相关矩阵与协方差矩阵特征值从而对端元数目进行判定。最具代表性的算法是虚拟维度(VD)(Bajorski，2011)算法，该算法将光谱差异信号数目的最小值作为最终的端元数目，但需要计算图像的相关矩阵及协方差矩阵，计算量较大，且对噪声比较敏感，计算结果易受误警率影响；可以用来估计VD得方法有很多，除了PCA，文献(Chang和Du，2004)利用AIC、MDL以及HFC算法辅助估计，并得出使用HFC达到的效果最好。HFC算法基于Neyman-Pearson理论，分别使用相关特征值和协方差特征值表示由样本相关矩阵和样本协方差矩阵产生的特征值，通过相关特征值与协方差特征值差异性确定端元数量，但该算法会因阈值的选择不同导致结果出现随机性波动，且没有考虑噪声白化过程，使得弱信号往往被噪声所淹没，为此后续研究者针对此类问题又提出基于噪声白化的HFC方法(NWHFC)、噪声子空间投影方法(NSP)(Chang和Du，2004)。其中，NSP兼具HFC和NWHFC优点，并且适用于小样本情况下的数据处理；特征值极大似然函数(ELM)(Luo 等，2013)算法是基于VD算法的改进，利用相关特征值与协方差特征值之差的分布函数来估计端元数量，不需调整任何参数及噪声估计，能够在信噪比低的条件下，依然给出较为准确的估计，但是极大似然函数会受噪声影响使得极值不明显、峰值波动不大，导致端元数目估计偏小(汪国平 等，2016)。Eches等人(2010)利用正态组分模型(NCM)及分层贝叶斯算法实现端元数目估计，该算法适用于端元数目及数据量较小的情况下使用。最小误差高光谱信号辨识(Hysime)(Bioucas-Dias和Nascimento，2008)算法是通过估计信号与噪声的相关矩阵，寻找满足最小均值误差的条件下最能够代表信号子空间的一个特征向量子集，由于该方法理论考虑到高光谱图像相邻波段的高度相关性，因而能够较好的估计噪声。不足之处是需要估计样本噪声的协方差矩阵，计算量较大，且端元数目估计结果往往比实际偏大。

(4) 基于几何学的端元数目估计算法(Ambikapathi 等，2013)有几何—凸包算法(GENE-CH)和几何—仿射包算法(GENE-AH)，认为所有观测像元向量都位于端元特征的凸包和仿射包内，即后提取的端元向量会存在于之前提取的端元所构成的凸包或仿射包内，因此基于几何学的端元数目估计算法本质上算是为逐次提取端元算法提供一个算法终止的判定法则。算法主要适用于图像中包含纯净像元以及无噪声条件，而且无须随机设定初始端元都能够达到稳定的端元估计结果，具体计算量则依端元提取算法而定。Andreou和Karathanassi(2014)提出异常点检测算法(ODM)，对高光谱图像数据进行噪声估计与白化预处理，认为信号位于噪声超球面异常点，从而提取端元，得到较好的结果。

除此之外，还有研究者结合端元提取算法与光谱角等方法，在端元数目未知的条件下实现端元数目的估计。Song等人(2015)利用迭代误差法与光谱约束条件，将端元数目由大到小自动调整到最优端元数目，但由于需要多次迭代及计算均值误差，使得计算量大，运行速度较慢。

端元提取旨在从高光谱遥感图像中提取相对含量高的地物光谱向量，并将此向量作为图像端元。目前已有大量研究者针对端元提取提出多种算法，然而对于端元提取的分类至今并没有一个明确详细的划分。按照端元已知与未知可分为监督光谱分解与非监督光谱分解；按照端元与丰度值是否同时获得或者解混前是否需要降维分为两类等。在本文中根据算法主要特点将端元提取算法分为6大类：几何单形体体积法、统计误差法、空间投影法、融合空间信息的端元提取算法、稀疏回归算法以及其他智能端元提取算法等。

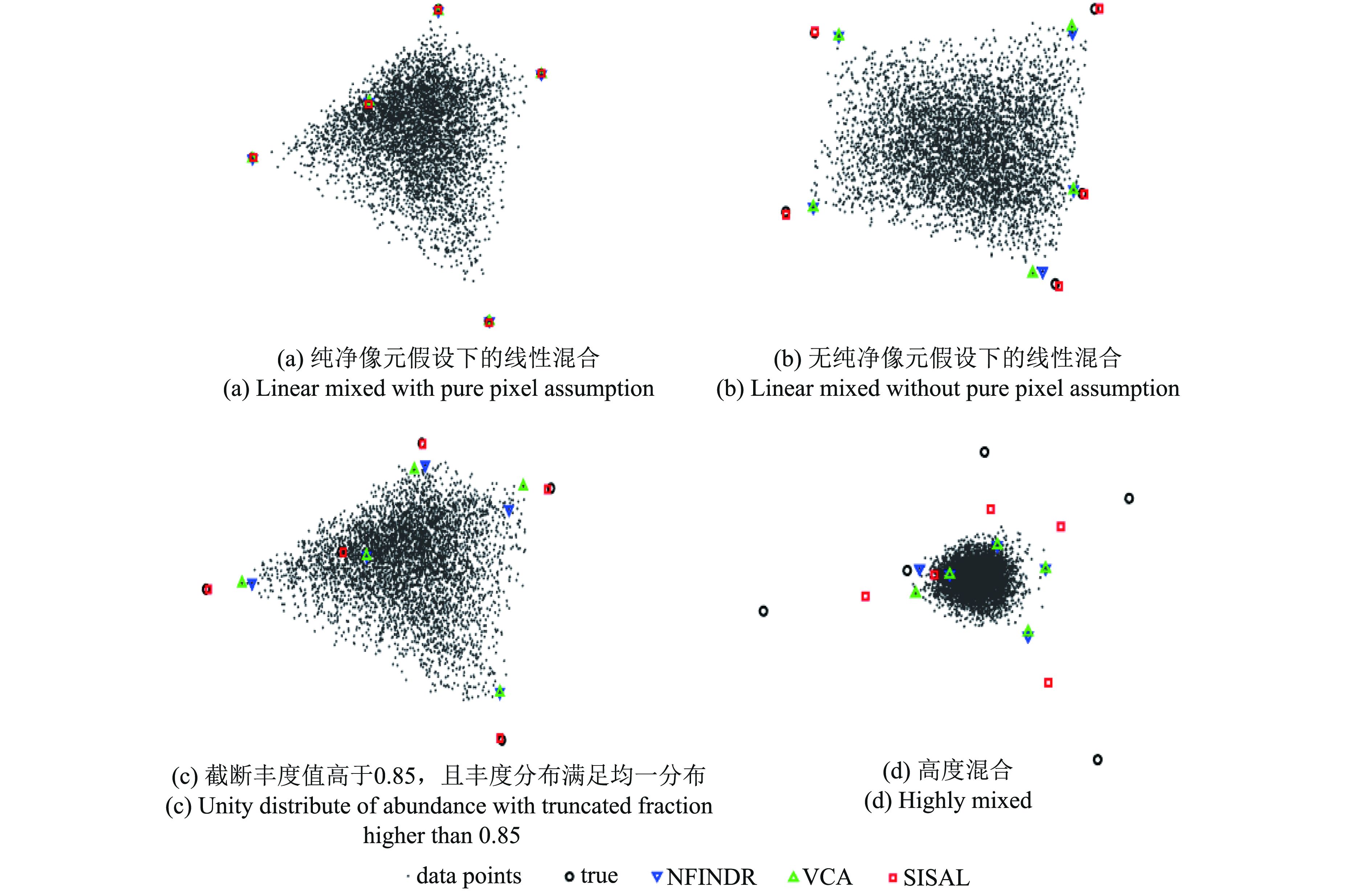
(1) 基于几何单形体端元提取方法是目前研究者研究最多、较成熟的算法，包含最小体积变换(MVT)(Craig，1994)、内部最大体积分析(N-FINDR)(Winter，1999)、迭代误差法(IEA)(Neville 等，1999)、外包单形体收缩法(SSWA)(Fuhrmann，1999)、顺序最大角凸锥法(SMACC)(Gruninger 等，2004)、迭代限制端元法(ICE)(Berman 等，2004)、顶点成分分析(VCA) (Nascimento和Dias，2005)、最小体积约束下的非负矩阵分解(MVC-NMF)(Miao和Qi，2007)、最小体积单形体分析(MSVA)(Li和Bioucas-Dias，2008)、基于分裂增广拉格朗日的单纯形识别(SISAL)(Bioucas-Dias，2009)等。这些方法都是基于凸面几何体理论，利用高光谱点云数据在特征空间中呈现出凸面单形体的特殊结构，高光谱图像中的端元对应单形体的顶点，纯净像元则出现在单形体的表面上并接近顶点，因此通过寻找单形体的外接最小体积或者内接最大体积寻找顶点从而得到所需端元。但这些方法在求解过程中都存在非线性规划，容易陷入局部极小点，因此对于寻找最优解的要求比较高。此外大部分基于几何学端元提取的方法需要图像中包含纯净像元，本文参考Bioucas-Dias等人(2012)做了4组模拟数据对比实验，结果如图3，由图3可见在包含纯净像元线性混合条件下，基于纯净像元的VCA和N-FINDR以及不依托纯净像元的SISAL均能达到良好效果，但在满足均匀分布前提下去除纯净像元甚至丰度值高于0.85的部分也去除掉时，只有不依托纯净元的SISAL方法能保持较好的鲁棒性，当模拟数据丰度值为Dirichlet分布高度混合时，此时3种方法都无法得到满意的端元结果。因此，基于几何学端元提取的另一个弊端是当高光谱图像中所对应地面的数据为高度混合时，该方法将不再适用。

图 3 不同数据集N-FINDR、VCA、SISAL端元提取结果 Figure 3 Endmember extraction results of N-FINDR，VCA and SISAL on different data sets

(2) 基于统计误差法也有很多算法，如独立成分分析(ICA)(Bayliss 等，1998)、非负矩阵分解(NMF) (Miao和Qi，2007)、依赖成分分析(DECA) (Nascimento和Bioucas-Dias，2007)、贝叶斯分析(Bayesian approaches)(Dobigeon 等，2009)、鲁棒性协同非负矩阵分解(RC-NMF)(Li 等，2016b)等。其算法原理主要通过引入几何约束等，统计分析计算得到最小误差从而得到光谱解混结果。这些方法相对于几何法在处理高度混合的高光谱图像中能够得到较好的效果，不过以计算复杂性高为代价。由于在大部分情况下，图像中的端元数目及反射率都是未知的，此时进行光谱解混即为所谓的盲信号分离。独立成分分析就是一种盲信号分离的方法，但由于其算法模型需要源信号输入完全独立，这与高光谱数据丰度间含约束相矛盾，因此在某些情况下只能作为端元解混的近似解。在构建高光谱数据线性模型中，将最大后验概率估计引入到贝叶斯分析方法中，可以得知之前被分类到基于几何学的最小体积约束下的非负矩阵分解和迭代限制端元法也可以划分到统计误差法中。

(3) 空间投影法包括纯净像元指数(PPI)(Boardman，1993；Boardman 等，1995)、子空间投影(OSP)(Harsanyi和Chang，1994)、逐次投影算法(SPA)(Araújo 等，2001)、支持向量机(SVM)(吴波等，2004，2006)等算法，根据单形体向量投影进行端元提取。前3种算法是将高光谱数据通过投影变换或由高维向低维方向投影，能够大大减少计算时间与复杂度、提高信噪比，但对于混合像元分解求逆过程的求解病态问题并没有改善。支持向量机则是将低维空间的非线性问题转化为高维空间线性表示，具有较强的泛化能力，但在核函数以及最优化参数组合的选择上仍是待解决的难点。

融合空间信息法(孔祥兵 等，2013)，代表性方法有自动形态学端元提取(AMEE)(Plaza 等，2002)、全变量—分离和增广拉格朗日的稀疏解混算法(SUVSAL-TV)(Rudin 等，1992)、空间光谱端元提取法(SSEE)(Rogge 等，2007)、空间预处理算法(SPP)(Zortea和Plaza，2009)等。与前面几类混合像元分解的方法区别之处是融合空间信息法能够将高光谱图像数据的空间信息引入到求解过程目标函数的约束中，充分考虑相邻像素之间丰度变化的连续平滑特性及空间相关性，能够更合理的体现地物含量变化，避免不同像元间丰度值差异变化大的问题。由于在光谱信息的提取过程中引入空间信息的约束，大大提高算法的计算复杂程度，因此需要研究并行算法以提高算法的运行速度。

基于稀疏回归的端元提取算法，由于能够同时获取端元及丰度信息矩阵，具体算法会在2.3节“丰度估计”中详细介绍。

除了以上几类还有研究者提出了智能端元提取算法如离散粒子群优化端元提取(DPSO)(Gao 等，2016)、蚁群优化端元提取(ACO-EE)(Gao 等，2015)、自适应布谷鸟端元提取算法(ACSEE)(Zhao 等，2016)等算法，实现混合像元解混。尽管能够得到较好的结果，但通常计算复杂且需要调整多个参数。

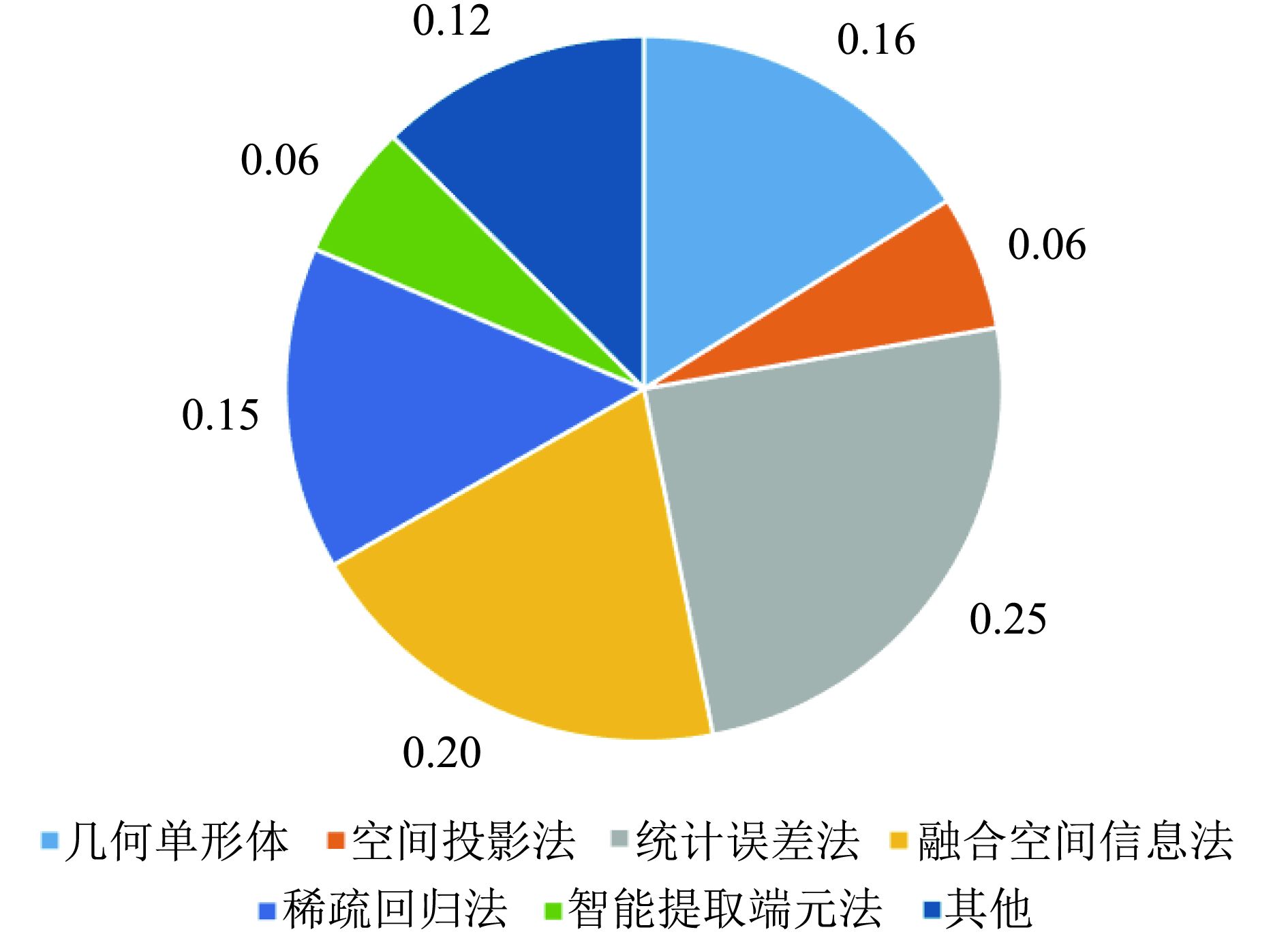
图4是2016年高光谱端元提取方法类别的部分统计，检索词为hyperspectral endmember extraction，根据检索结果划分方法类别，可以看出基于统计误差的端元提取算法(尤其是基于非负矩阵分解)研究最多，其次是融合空间信息的端元提取算法，这是由于高光谱图像空间分辨率的不断提高，充分利用空间信息约束有助于提高解混精度；近年来引入的稀疏回归算法也是当前研究者重点研究方向，而最经典的几何单形体体积模型的算法由于模型简单易实施的优势仍占据较大的比例；图4中的其他指的是融合多种算法以及未归类的算法，可以看出该部分占有很大比例，由此推断融合多种算法及引入新型模型算法也将是今后端元提取技术重点研究方向之一。

图 4 2016年高光谱端元提取方法类别的部分统计 Figure 4 Parital paper statistics of endmember extraction of hyperspectral in 2016

丰度估计是指对混合像元中各端元比例进行估计。对于非线性模型中广义双线性混合模型的丰度估计算法主要有基于贝叶斯方法、梯度下降法(GDA)(Halimi 等，2011)、半—非负矩阵分解法(semi-NMF)(Yokoya 等，2014)等，但贝叶斯方法计算量复杂程度较大，semi-NMF容易陷入局部极小且对初始化要求较高，而GDA算法只适用于数据量较小的情况。对于线性模型的丰度估计算法，由于部分算法能够将端元矩阵与丰度估计矩阵同时获取，如非负矩阵法、独立成分分析、迭代误差分析算法(2.2节(1)已经介绍)、稀疏回归算法等，本节中主要介绍稀疏回归算法以及在获得端元矩阵之后进行丰度估计的算法。

(1) 基于稀疏回归算法能够同时获取端元矩阵和对应丰度信息，代表方法有基于稀疏策略的迭代约束端元提取算法(SPICE)(Zare和Gader，2007)、约束稀疏回归问题(CSR)、分离和增广拉格朗日光谱解混算法(SUNSAL)、约束性基追踪去噪法(CBPDN) (Bioucas-Dias和Figueiredo，2010)、L1/2稀疏约束非负矩阵分解算法(L1/2-NMF)(Qian 等，2011)、双加权稀疏回归像元分解算法(DRSR)(Zheng 等，2016)、局部协同稀疏回归法(LC-SR)(Zhang 等，2016)。近几年在高光谱混合像元分解中除了监督与非监督，又涌现出半监督式解混法，稀疏回归法就是半监督式解混的一类方法。通过假设图像中的光谱信息是由预先已知的几种纯净像元的光谱线性组合而成，并从光谱库中寻找与图像中每一个混合像元的光谱最接近的光谱子集。与前述的几种方法不同的是，稀疏回归法是先建立一个含有大量光谱样本的光谱库，结合先验知识利用库中的光谱曲线线性混合，再与给定的高光谱图像中的每个像元光谱进行匹配拟合寻找最优子集，不仅能够估计出图像中包含的端元个数，还能够同时得到端元提取及丰度估计的结果，算是近年来高光谱混合像元分解的前沿算法之一。如果将丰度和为一约束引入到稀疏回归算法时，在求解最优解过程中就相当于全限制性最小二乘可行性问题。但是在实际问题当中，很难满足丰度和为一的约束条件，再加上图像存在噪声或者构建模型再加上图像存在噪声或者构建模型与图像不匹配的问题，使用稀疏回归算法在解混效果方面要优于约束最小二乘和全约束性最小二乘。基于稀疏回归算法的高光谱图像解混的成功性关键在于确定混合物质的数目及如何构建合适的光谱库，由于光谱库中会存在一定的互相关性，在数据集相同的条件下很难获取，且光谱库获取过程又需要消耗大量的时间和步骤，还需考虑光谱库与数据集之间的校准。为解决这一问题引入字典学习(Elad和Aharon，2006)，直接从数据集中学习，无需考虑先验知识。此外，稀疏回归算法仅适用于线性混合模型，对于高度混合高光谱数据并不能达到较好的结果，且空间信息利用不足，为此Qu等人(2014)将稀疏回归算法从线性模型扩展至双线性混合模型，建立线性字典库和双线性字典库，并提出广义低秩表示(LRR)模型充分考虑空间信息，能够有效估计针对双线性混合模型的高光谱图像丰度，但也只适用于双线性混合模型，而且对于线性字典及双线性字典建立大小有限制，对丰度条件和为一约束的正则化参数敏感；Feng等人(2015)提出空间自相似正则化方法能够有效利用空间高阶结构信息，但其巨大的计算量制约了实际应用潜力。

(2) 在获得端元矩阵之后进行丰度估计的算法主要包括最小二乘法、人工神经网络法等。其中最小二乘算法为最经典的丰度估计算法，通过计算误差平方和的最小值的思想得到丰度估计矩阵，算法包括无约束最小二乘法(LS)、和为一约束最小二乘法(SCLS)、非负约束最小二乘法(NCLS)、全约束性最小二乘法(FCLS)，可以看出这4种最小二乘算法逐级增加丰度代数约束，虽然增加了计算量，但总体分解精度逐级提高(Heinz 等，1999)。然而最小二乘算法的不足之处是：当端元数目较大时，算法收敛速度较慢；对于端元矩阵的精度要求很高，端元矩阵中较少比例的噪声或变动都可能会引起丰度估计值较大的偏差(Gong和Zhang，1999)；未能利用波段之间的高阶相关性，不能够适应非线性混合的影像数据。因此，后期也有研究者利用离散小波变换(DWT)(Li，2004)、遗传算法与最小均方误差端元估计算法(GA-LSEM)(Farzam 等，2008)、核全约束最小二乘(Broadwater 等，2007)、图像空间重构算法(ISRA)(Gonzalez 等，2012)、初始双内点约束(Chouzenoux 等，2014)、空间正则化约束的非线性解混算法(Chen 等，2014)、有界投影最佳梯度法(BPOGM)(Li 等，2016a)、向量化代码投影梯度下降法(VCPGD)(Kizel 等，2017)来提高最小二乘丰度估计结果。人工神经网络法包括RBF(Guilfoyle 等，2001)、结合Hopfield神经网络与多层感知器(HNN/MLP)(Plaza 等，2004)，计算结果相对于使用线性分解方法，在处理线性混合数据与非线性混合数据获取较好的结果。

表1为高光谱图像典型混合像元分解算法分类总结。

表 1(Table 1)

表 1 高光谱典型混合像元分解算法及其优缺点 Table 1 Advantage and disadvantage of classical algorithms for hyperspectral umixing 分类依据 典型算法 优缺点 端元数目 估计算法 本征维度算法 主成分分析(PCA)、最大噪声分数(MNF)、入度分布统计方法(IDD) 优点：能够去除数据冗余，尽可能减少信息损失 缺点：更适合处理多波段数据 似然函数算法 Akaike信息准则(AIC)、最小描述长度(MDL) 优点：统计模型识别的通用方法 缺点：算法需要先验知识，端元数目估计结果偏大 特征值方法 虚拟维度(VD)、HFC、基于噪声白化的HFC方法(NWHFC)、噪声子空间投影方法(NSP)、特征值极大似然函数(ELM)、最小误差高光谱信号辨识(Hysime) 优点：能给出较为准确的估计 缺点：需要计算图像的相关矩阵及协方差矩阵，计算量大；部分算法对噪声敏感 几何学的端元数目估计算法 几何—凸包算法(GENE-CH)、几何—仿射包算法(GENE-AH)、异常点检测算法(ODM) 优点：无需随机设定初始端元都能达到稳定的端元估计结果 缺点：对图像质量要求较高，包含纯净像元及高信噪比条件 端元提取 算法 几何单形体法 最小体积变换(MVT)、内部最大体积分析(N-FINDR)、顶点成分分析(VCA)、迭代误差法(IEA)、最小体积单形体分析(MSVA)、顺序最大角凸锥法(SMACC)、迭代限制端元法(ICE)、外包单形体收缩法(SSWA)、基于分裂增广拉格朗日的单纯形识别(SISAL) 优点：通过寻找单形体的外接最小体积或者内接最大体积寻找顶点从而得到所需端元，算法模型简单，易实施 缺点：求解过程存在非线性规划，容易陷入局部极小点，不适用于高光谱图像中对应地面数据为高度混合的情况，精度较低 统计误差法 独立成分分析(ICA)、非负矩阵分解(NMF)、贝叶斯分析(Bayesian approaches)、依赖成分分析(DECA)、鲁棒性协同非负矩阵分解(RC-NMF)、最小体积约束下的非负矩阵分解(MVC-NMF) 优点：处理高度混合的高光谱图像效果较好 缺点：计算复杂性较高，运算量大 空间投影法 纯净像元指数(PPI)、主成分分析法(PCA)、逐次投影算法(SPA)、子空间投影(OSP)、支持向量机(SVM)、有界投影最佳梯度法(BPOGM)(Li 等，2016a) 优点：寻找高光谱数据代表子空间，能够大大减少计算时间与复杂度、提高信噪比 缺点：通常需要先验知识，不能改善混合像元分解求逆病态问题，核函数和最优化参数组合选择困难 融合空间信息法 自动形态学端元提取(AMEE)、全变量—分离和增广拉格朗日的稀疏解混算法(SUnSAL-TV)、空间光谱端元提取法(SSEE)、空间预处理算法(SPP)、多维SURF算法(MD-SURF)(杨可明 等，2016) 优点：能够合理的体现地物含量变化，避免不同像元间丰度值差异变化大的问题，精度较高 缺点：算法的计算复杂度高，运行速度慢 智能提取端元法 蚁群优化端元提取(ACO-EE)、离散粒子群优化端元提取(DPSO)、自适应布谷鸟搜索算法(ACS-EE) 优点：混合像元解混效果较好 缺点：计算复杂，需要调整多个参数 稀疏回归法 基于稀疏策略的迭代约束端元提取算法(SPICE)、约束稀疏回归问题(CSR)、双加权稀疏回归像元分解算法(DRSR)、分离和增广拉格朗日光谱解混算法(SUnSAL)、约束性基追踪去噪法(CBPDN)、正交匹配追踪(OMP)、局部协同稀疏回归法(LC-SR) 优点：无需假设纯像元存在，不仅能够估计出图像中包含的端元个数，还能够同时得到端元提取及丰度估计的结果 缺点：难以满足丰度和为一的约束条件，光谱库获取困难，需要花费大量时间，而且光谱间高相关性会降低结果精度 丰度估计算法 最小二乘算法 无约束最小二乘(LS)、非负约束最小二乘(NCLS)、和为一约束最小二乘(SCLS)、全约束最小二乘算法(FCLS) 优点：结构模型简单，对于端元数目少时计算速度快 缺点：随着端元数目增多，计算速度较慢，对端元提取精度要求较高，不适用于非线性混合数据

表 1 高光谱典型混合像元分解算法及其优缺点 Table 1 Advantage and disadvantage of classical algorithms for hyperspectral umixing

高光谱遥感影像混合像元分解技术在各行业领域均有初步的应用，但尚未实现系统化工程推广。今后高光谱混合像元分解技术所面临的挑战及未来发展方向主要包括：

(1) 维数灾难。高光谱图像数据在光谱维上具有较高的分辨率，增加了地物的细节特征，但同时由于各个波段之间的高度相关性，导致光谱间存在冗余信息和数据处理难度加大的问题，再加上图像在产生及传输过程易受噪声的影响，无疑降低了混合像元分解的精度。

(2) 高精度遥感混合反演模型的建立。高光谱混合像元分解实际上就是求逆问题，通过解混求出每个混合像元光谱对应的端元及丰度比例。由于环境条件、观测噪声、端元可变以及算法模型不精确都导致端元提取结果精度差、不稳定等问题。对于地形复杂，地物碎细的地区，在高光谱图像上往往呈现的是非线性混合，包括经典的、多层次、微观层面及近距离混合。虽然目前很多研究者针对非线性模型提出相应算法，但往往只能解决某一类混合，无法做到一种模型算法适应多种混合效果。若建立完全基于物理模型的非线性混合像元分解算法，那么在求解过程中往往引入辐射传输理论(RTT)求逆过程，该过程是个完全病态问题，其中的参数也难于甚至不能获取。而且在很多情况下，图像中既包含线性混合又包含非线性混合，因此需要建立适当的算法模型，研究空间及光谱信息相结合，利用多个模型簇近似混合模型，提高解混精度。其中完全非监督的非线性模型是最近提出的解混算法模型，一直是高光谱解混方面的迫切解决的问题，能够在不需要先验知识条件下直接从图像中获取端元与丰度。此外，阵列信号处理也将是今后另一个研究方向，例如在稀疏表达回归解混算法中，有效的整理光谱库数据，从而提高算法精度。

(3) 同物异谱、异物同谱。以矿物信息为例，其光谱信息除了由矿物晶体结构与化学成分决定外，还依赖于颗粒度形状、表面状态、在岩石中的赋存状态以及矿物混合等因素，导致同一种矿物光谱信息复杂多变。同时由于光照等其他因素影响，存在不同地物的光谱信息相同的问题，在这种情况下无疑加大了端元提取及后续的矿物填图与矿物识别的难度。目前的高光谱数据，无论是机载还是航天，在不同航带数据间同一位置光谱都难以保证一致性，常常会造成航带间信息的不连续导致误识别。因此，需要深入研究光谱产生机理，逐步提高高光谱遥感定量化应用。研究者可以针对同类端元光谱出现差异即端元光谱变异性提出采用基于光谱特征方法或基于多端元思想的方法减少分解误差，从而提高混合像元分解精度(陈晋 等，2016)。

(4) 遥感产品的业务化。当前大多数算法都是针对于高光谱图像数据模型的角度提出，在改进传统算法不足的基础上，大量新型算法也不断涌现，但围绕应用角度而提出具体解决技术方案研究较少。高光谱遥感数据处理的应用应以用户的需求为牵引，目前高光谱遥感主要用户为农业、林业与矿业等。从各用户在高光谱处理使用方法来看，大多是采用经典的算法，没有将新生代算法应用其中，因此高光谱遥感数据混合像元分解技术面临的挑战与用户应用需求密切相关，如何将新型算法与应用需求更好的结合并用于解决实际问题是未来高光谱混合像元分解技术的发展方向。在农业方面多光谱图像应用比较成熟，在多光谱应用几个波段就将农作物在绿光、红光和近红外的敏感波段体现，而在使用高光谱数据时该波段范围拓展成几十个波段(杜培军 等，2016)，因此如何充分应用高光谱图像丰富的光谱信息发挥敏感波段的特性而抑制其他波段影响，突出主要信息，有效提取端元信息是亟需解决的问题之一；林业方面由于受地形、坡度坡向、气候等因子影响显著，且混交林广泛，在低空间分辨率的图像上混合像元严重，在进行图像树种组识别方面研究尚属于发展阶段，未得到广泛应用；矿业方面矿物识别、蚀变信息提取等主要依赖于近红外波长，仅能识别一些有限的蚀变矿物，且由于矿物光谱信息的复杂性导致了某些具有微小光谱差异的矿物端元提取与识别区分能力有待提高。在矿物填图方面从技术的角度上已经具备工程化应用能力与条件，但数据源问题是其推广及规模化应用的主要限制条件(甘甫平 等，2014)。因此随着高分五号的发射，大量的高光谱数据将满足用户工程化应用对数据的需求，在研究新型算法的同时，以用户应用需求为牵引，更贴近实际的解决问题，实现高光谱遥感数据工程化与业务化应用。可以预期，在未来高光谱混合像元分解技术不断更新的趋势下，不同行业用户在获得大量高性能的高光谱遥感数据，算法软件业务化应用指日可待。

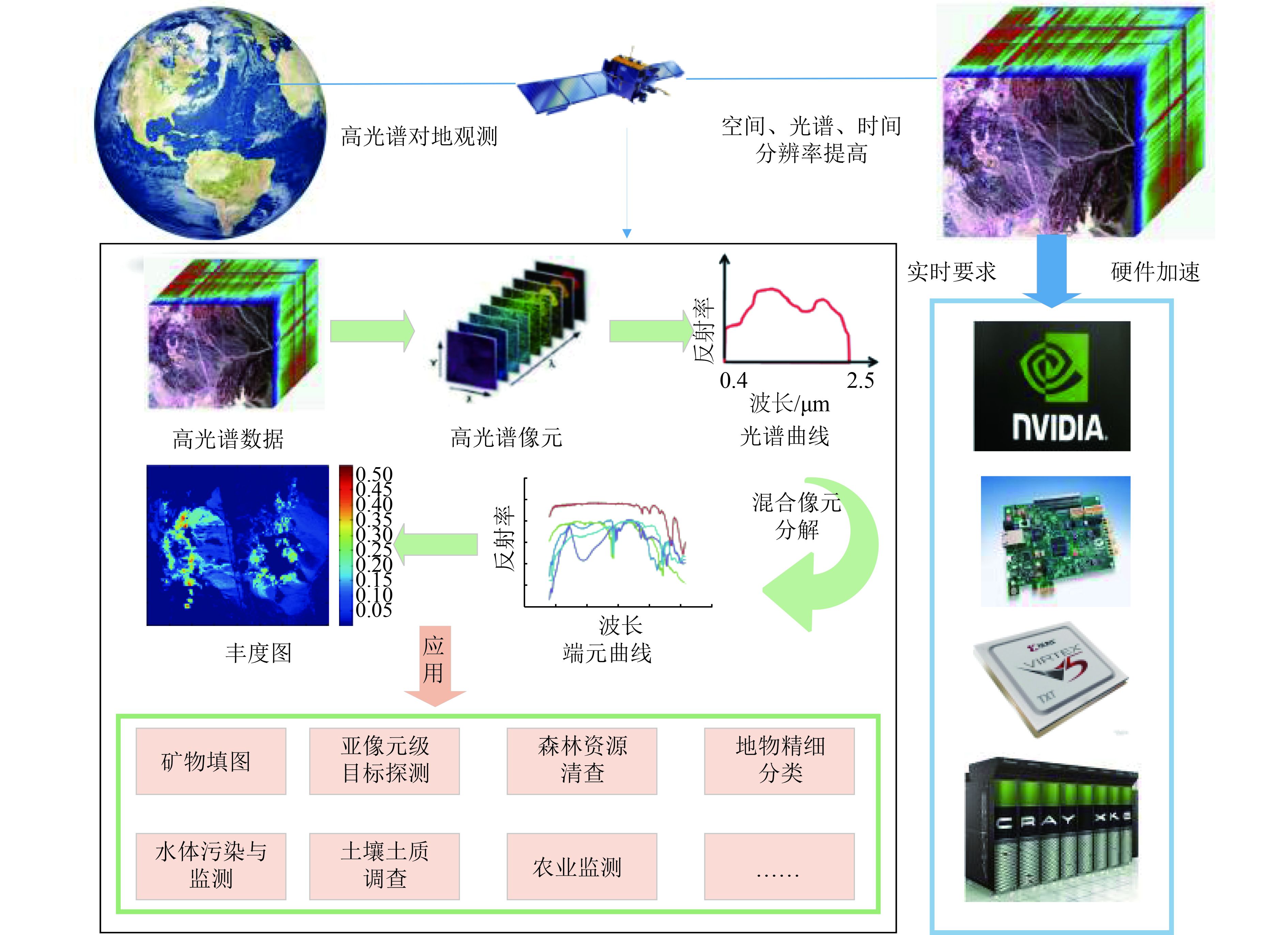
(5) 算法实时性。高光谱成像仪的迅速发展，空间分辨率、光谱分辨率都有了明显的提升，这使得在大数据处理方面普通计算机以及小型计算机难以有效快速处理。为此除了在使用并行FPGA、GPU等硬件处理平台，美国NASA、密西西比大学都采用高性能超计算机(HPC)并行处理器专门用于处理高光谱数据(Lee 等，2011；Gonzalez 等，2012；Bioucas-Dias 等，2013)。中国也有研究者应用DSP或者FPGA搭建的高光谱数据处理的硬件平台，但主要是用于异常探测或者数据降维，对混合像元分解处理较少。因此，为提高利用高光谱混合像元分解技术实现亚像元级目标探测或环境实时监测等应用，今后在引入新型HPC的基础上(包括GPU、FPGA、DSP等)，可以对高光谱数据进行分块处理，并优化算法提高算法的实时性，是高光谱混合像元分解技术的重点发展方向，对环境灾害、亚像元级目标识别等应用实时处理具有重要意义。高光谱遥感混合像元分解发展趋势及应用如图5。

图 5 高光谱混合像元分解发展趋势及应用 Figure 5 The development trend and application of hyperspectral unmixing

随着科学技术水平的提升，未来高光谱成像仪的性能会不断提高，更多的管理部门应用高光谱数据进行推广化业务应用是高光谱遥感未来发展的趋势之一。因此，如何合理有效地选择高光谱数据与用户需求密切相关。针对不同的业务应用需求，应选择适当的高光谱数据分析，往往能够达到较好的预期处理效果，而不是一味的追求空间分辨率更高、光谱分辨率更精细、波长覆盖范围更广的数据。同时，高光谱数据性能的提高无疑增大数据处理的运行时间，在当前数据无法满足应用需求的基础上，可以进一步研究高光谱混合像元分解技术，或者结合多光谱高空间分辨率以高光谱数据精细光谱分辨率的优势，采用数据融合等方法实现应用预期目标。此外，大数据及云计算等新兴技术的涌现，以“互联网+”为驱动，推进高光谱数据处理应用云服务平台的设计与研制，有利于推动高光谱遥感应用服务于大众。

高光谱遥感影像混合像元分解技术在高光谱遥感图像处理解译方面具有巨大潜力，并已经取得显著进步。本文主要介绍当前混合像元分解中端元数目估计、端元提取以及丰度估计的主要算法，总结并分析各类算法的优缺点，进一步阐述了高光谱混合像元分解技术的后续发展过程中所面临的挑战以及未来发展趋势。由于本文的篇幅有限，还有许多算法没有列入文中，但总体上可以从各研究者工作量反映出在高光谱混合模型的建立、数据处理计算量以及精度方面都明显提高，对现有技术手段综合是混合像元分解算法的一个趋势之一。然而对于混合像元中不同端元之间光谱可能具有一定相似性以及端元变异性问题，限制了分解精度，目前仍未得到彻底解决。此外在遥感产品方面，由于很多算法都是基于模拟数据，对于真实数据验证也大都采用较为经典的数据，形成可直接利用遥感产品的较少，此外地面测量数据的不足严重影响了反演算法的研发和产品的验证，因此，发展新的计算和验证方法，提高野外测量的精度是未来的研究方向。随着高光谱卫星各方面的快速发展和“一带一路”建设的实施，在加强对地监测与管理进程中对高光谱遥感影像混合像元分解技术提出了更高的要求，也对混合像元分解算法的工程化应用以及算法的实时性问题提出了紧迫性的需求。总之，混合像元分解技术应在引进新型模型、研究具有泛化能力强、稳定性好的混合像元分解算法的基础上，需要密切结合应用需求，进而对不同行业领域进行推广业务化应用，对提高高光谱遥感定量化应用具有重要意义。