收稿日期: 2016-11-24
2. Key Laboratory of Space Ocean Remote Sensing and Applications, State Oceanic Administration, People’s Republic of China, Beijing 100081, China
星载微波散射计是目前获取全球海洋风矢量最主要的微波遥感器。自1978年美国发射第一个搭载业务化运行散射计的卫星Seasat以来(Grantham 等,1977),卫星遥感海面风矢量观测技术得到长足发展,已有包括ERS-1/SCAT(1991年7月—1996年6月)、ERS-2(1995年4月—2001年1月)、ADEOS-I/NSCAT(1996年8月—1997年6月)、QuikSCAT(1999年6月—2009年11月)、ADEOS-II/SeaWinds(2002年12月—2003年10月)、Metop-A/ASCAT(2006年10月至今)、Oceansat-2/OSCAT(2009年9月—2014年2月)、海洋二号微波散射计(HY-2/SCAT,2011年8月至今)、Metop-B/ASCAT(2012年9月至今)等在内的多个星载散射计投入业务化运行(Attema,1991;Naderi 等,1991;Wu 等,2003;Figa-Saldaña 等,2002;Zou 等,2014;Gohil 等,2013),极大地提高了全球海面风矢量观测能力。
对散射计测量数据的处理得到海面风矢量结果,通常要经过地理定位、辐射定标、面元匹配、风矢量反演、模糊解去除等关键步骤。由于后向散射系数(sigma0)对风向的关系具有双余弦分布特征,对风矢量的反演需要不少于3个不同方位角/入射角的sigma0观测结果(简称“观测结果”),才能准确反演出风速和风向。因此,需要在一定空间尺度的面元(即风矢量面元)上对散射计的观测结果进行重采样,才能满足风场反演所需的多个sigma0的要求。对风矢量的反演是以风矢量面元为单位进行的,通过反演所得的风矢量反映了该风矢量面元的风矢量平均值。面元匹配就是将经过地理定位和辐射定标所获得的按观测时序存储的sigma0,以及与sigma0对应的观测几何等参数,重采样到风矢量面元,以期为后续风矢量反演提供输入参数。在散射计数据处理中,面元匹配非常重要,直接影响到最终的风矢量反演精度。根据散射计的观测特点,设计了不同的面元匹配方案。
ERS散射计将风矢量面元设计成网格形式,其观测结果需要插值到单元网格大小为25 km×25 km的网格中。sigma0测量节点的位置通过下面的方法来确定:在中部天线指向线、卫星与地心连线共同确定的平面与由GEM6定义的椭球面的交线上,以中部天线的指向线与椭球面的交点作为刈幅的中心结点,由中心结点沿交线向两侧方向每隔25 km设置一个新的结点。由于地表是扁平状的,这些节点所形成的网格线并不是严格平行的。对每个天线,每个结点处的sigma0由结点周围sigma0观测样本加权平均后获得。平均过程中离结点越远的观测样本,权重越低;越近的样本,权重越高(Lecomte,1998)。
JPL则采用Snyder的空间倾斜墨卡托投影(SOM)算法来对Quikscat观测结果进行面元匹配。地面网格划分以星下点轨迹为中心,以顺轨向及交轨向坐标来表示指定位置。由于地球自转,卫星星下点轨迹并非一个完整的圆形。如两个连续的升交点并非在地球上的同一点,因此从大地坐标向地面轨迹坐标转换时需考虑这些因素的影响。这种投影方式首先是为Landsat映射而发展的,适合于相对较窄的近圆轨道的应用。“完全SOM”多用于制图,它采用傅里叶变换将球面坐标转换到笛卡尔坐标地图。为简化计算,JPL算法仅对角坐标进行转化(Dunbar 等,2001)。
随着对散射计研究的发展,陆续对面元匹配方法开展了研究。针对神舟4号多模态微波遥感器散射计分系统,为得到每个面元的4次测量,张云华等人(2005)在面元匹配中将测量区域划分为50 km×50 km的区域,因此在垂直航线的方向可以划分为8个面元,并根据40 min的有效观测数据,成功反演获得海面风场(Zhang 等,2005;Wang和Jiang,1997)。邹巨洪等人(2009)在JPL的面元匹配方法的基础上,提出了Quikscat风矢量快速反演的sigma0预处理算法,通过对Quikscat风矢量面元sigma0进行分组压缩预处理,取每组sigma0平均值作为对应组的观测结果,再将平均结果代入反演流程中,有效提高了运算速度。
中国于2011年8月发射了海洋二号卫星微波散射计(HSCAT)。为从HSCAT观测结果中准确反演出风速和风向,有必要设计相应的可业务化运行的面元匹配方法。本文在借鉴Quikscat和神舟4号多模态微波遥感器散射计分系统面元匹配方法的基础上,根据HSCAT的观测特点,设计了一种可业务化运行的HSCAT面元匹配方法。
2、HSCAT简介2011年8月发射的海洋二号卫星,搭载中国第一个可业务化运行的微波散射计HSCAT。HSCAT主要用于全球海面风矢量观测,测风风速范围为4—24 m/s,风速精度为2 m/s或10%;风向测量范围为0°—360°,风向精度为±20°。HSCAT工作频率为13.256 GHz,采用笔形波束圆锥扫描方式,通过笔形波束以固定仰角围绕天底方向旋转,在卫星平台顺轨方向的运动中形成一定的地面覆盖刈幅(图1(a));散射计系统包括VV和HH两个极化方式,分别以不同入射角进行观测,在平台的运动过程中对同一分辨单元可获取不同极化方式、不同入射角度的多次观测结果,以克服海面风场方向反演的多值模糊问题(图1(b))。其中内波束采用HH极化方式,入射角为41°,对应地面足印大小约为23 km×31 km,刈幅宽度为1350 km。外波束采用VV极化方式,入射角为48°,对应地面足印大小约为25 km×38 km,刈幅宽度为1700 km(Zou 等,2014)。
海洋二号卫星微波散射计数据产品分为L1B级产品数据产品、L2A级数据产品、L2B级数据产品和L3级数据产品。本文采用L1B数据作为面元匹配的输入数据,该数据以遥测帧的时间为顺序进行存储的HSCAT观测数据,每个L1B数据文件包含绕一轨完整的卫星地球飞行一圈HSCAT所观测到的观测数据。每个遥测帧包含一个观测时间信息,与该帧数据所对应的星下点的经纬度信息,以及96个散射计测量脉冲对应的观测结果与相关的几何观测信息。散射计的脉冲重复频率(PRF)为181 Hz,每帧数据时间间隔约为0.54 s,即每隔0.54 s将获得一组遥测帧包信息。每个测量脉冲包括观测结果、每个脉冲足迹的地理位置、用来描述测量数据的质量和不确定性等信息的参数。

|
| 图 1 海洋二号卫星微波散射计观测几何 Figure 1 HY-2A/SCAT measurement geometry |
为满足风矢量反演所需的多个sigma0的要求,在风矢量反演之前,需要通过面元匹配,在合适的空间尺度下,将L1B数据中按观测时序存储的sigma0,以及与sigma0对应的观测几何等参数进行重采样,以期为后续风矢量反演提供输入。面元大小,以及重采样的质量,将直接影响到最终的风矢量反演精度。面元的大小一方面要满足数值气象预报等应用对空间分辨率提出的要求;另一方面,需要考虑散射计的观测条件,即满足一个面元内不少于3个不同方位角sigma0观测的要求。因此,本文设计的面元匹配方法将主要包括地面网格划分和观测结果重采样两个关键步骤。
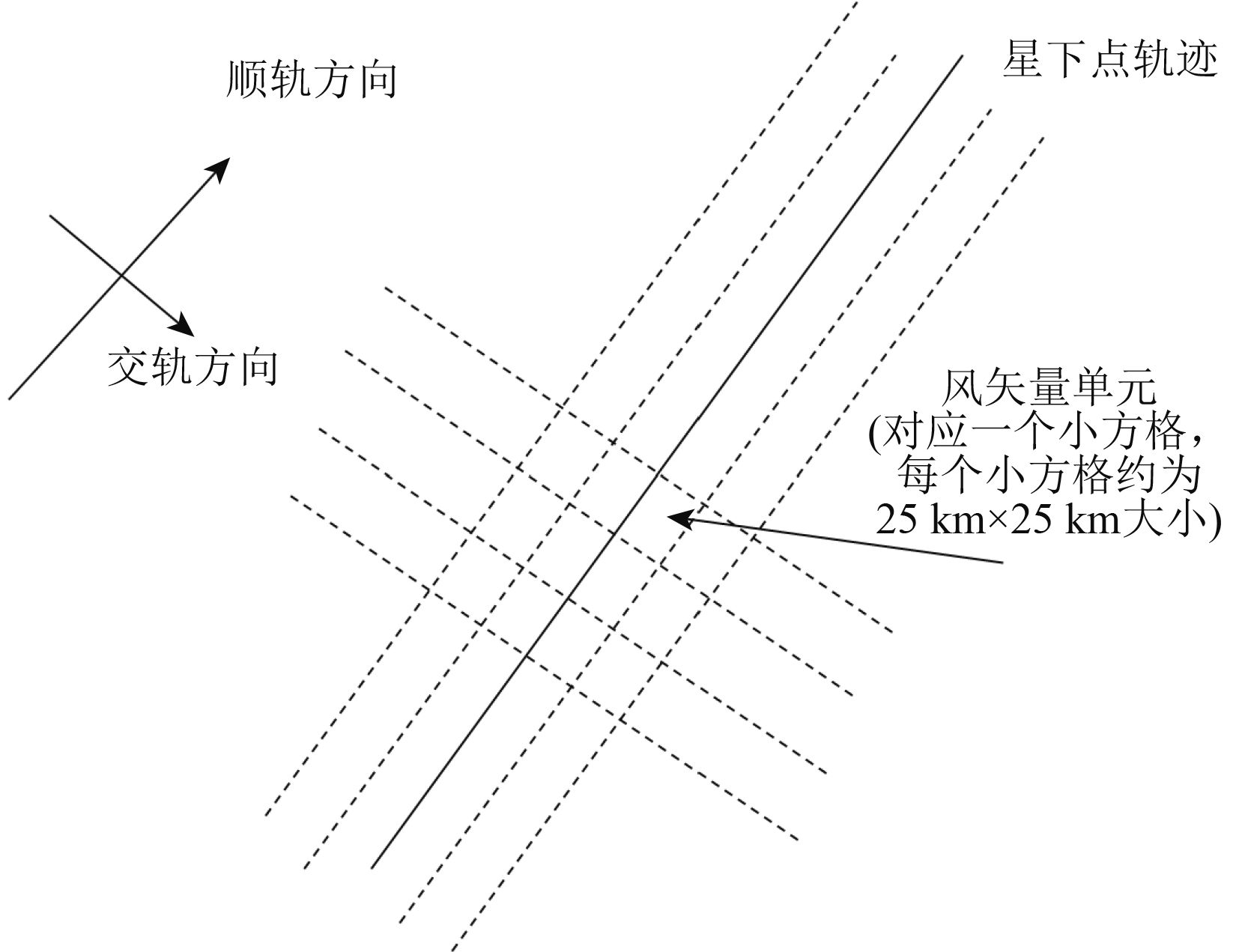
(3.1) 地面网格划分观测结果的面元匹配方法要求能够简化计算,因此HSCAT采用了如图2所示的一种较为方便的网格模型,以星下点轨迹为中心,以顺轨向及交轨向坐标来表示指定位置,采用25 km×25 km的分辨率进行重采样。该坐标系的原点设置为HSCAT轨道的边界,即纬度最南端星下点的对应点。由于HSCAT的刈幅足够窄,因此可忽略“经度”在刈幅边缘的压缩。该模型可视为一个严格的矩形网格,这样处理也可简化计算。为描述方便,将该网格坐标体系记为地面网格。
|
| 图 2 HSCAT风矢量面元及其坐标空间示意图 Figure 2 The map of wind vector cell and its coordinate space for HSCAT |
面元匹配输入的L1B数据中,观测结果以时间为序,因此由时间边界来定义。风矢量面元是按空间位置进行排列,因此由空间边界来定义。为确保所有的数据都能实现从输入产品到输出产品的转换,地面网格的设计必须考虑HY-2A散射计的旋转天线数据获取模式。当卫星接近并经过一个轨道边界时,散射计在该边界的两侧获取数据。因此,地面网格必须包括位于两个边界点以外的一部分风矢量面元行。为了覆盖超过轨道边界的sigma0测量值,地面网格产品在每个轨道的开始边界之前和结束边界之后各增加39个附加的风矢量面元行。这样,地面网格一般包括1702个风矢量面元行。
根据HY-2A卫星的轨道参数,散射计的标称测量刈幅宽度是以卫星天底点为中心向两边各延伸约850 km。因此,天底点轨迹两边各有34个,共计68个风矢量面元,几乎能够容纳每个sigma0测量值。但是,HY-2A卫星的姿态与地球的形状将会影响到每个后向散射测量足迹在地球表面上的最终位置。由于这些变化因素,某些sigma0单元有可能会落在850 km仪器测量刈幅之外。因此,地面网格每个风矢量面元行在两侧各增加了附加的4个风矢量面元列,以确保所有的观测结果都能落在地面网格中。这样,地面网格一般包括76个风矢量面元列。
(3.2) 观测结果重采样观测结果重采样算法将按时序排列的观测结果投影到地面轨道网格坐标系下的风矢量面元,并同时记录sigma0测量的方位角、入射角、sigma0测量方差Kp等参数。
为了将观测结果准确的投影到相应的地面网格单元(即风矢量面元),重采样算法需要精确地将观测结果的经纬度位置信息转换到地面网格坐标。在地面网格划分完成之后,重采样实际是求解按时序排列的每个观测结果在顺轨—交轨坐标网格体系下所对应的风矢量面元(即行列号)。本文利用L1B级数据产品中提供的卫星星下点数据,搜索与每个观测结果球面距离最近的卫星星下点,并利用该最近球面距离计算获得交轨方向的标号,同时沿星下点轨迹计算该星下点距离起始星下点的距离,并以此距离计算顺轨方向的标号,从而确定该观测结果在顺轨—交轨坐标网格体系下所对应的风矢量面元,达到重采样的目的。

|
| 图 3 HSCAT观测结果重采样流程图 Figure 3 Resampling flow chart of HSCAT observations |
图3给出了HSCAT观测结果重采样的流程图,具体步骤如下:
步骤1提取L1B级数据产品中提供的卫星星下点地面经纬度信息,以及卫星经过各星下点对应的时间,分别记
步骤2计算每个星下点轨迹数据元素在地面网格空间中对应的行号。具体操作如下:
(1)从
(2)以
| $D_{{\rm{sum}}}^{{i_{{\rm{sub}}}}} = \sum\limits_{i = 1}^{{i_{{\rm{sub}}}}} {D_{{\rm{sub}}}^{{i_{{\rm{sub}}}}}} $ | (1) |
(3)计算每个星下点数组元素在地面网格空间中对应的风矢量面元行号(沿轨向面元号),并记第
| $N_{{\rm{sub\_along\_track}}}^{{i_{{\rm{sub}}}}} = floor(D_{{\rm{sum}}}^{{i_{{\rm{sub}}}}}/25) + 1$ | (2) |
式中,等式右边的25代表地面网格空间分辨率取25 km。
步骤3后向散射系数观测结果对应的风矢量面元行列号计算与风矢量面元赋值。
对L1B级数据产品中的观测结果进行循环,计算获得当前观测结果对应的风矢量面元在地面网格空间中的行列号。该步骤包括粗搜素、精搜索、计算行列号等几个部分。为描述方便,记当前循环指针为
(1) 粗搜素。对每个观测结果,以100的搜索步长对星下点轨迹进行遍历,并计算各星下点与当前观测结果位置之间的球面距离,记为
(2) 精搜索。以1为步长,在以粗搜索确定的“最小距离星下点”
(3) 计算行列号。根据精搜索确定的“最小距离星下点”标号
| $N_{{\rm{cell\_cross\_track}}}^{{i_{{\rm{cell}}}},{j_{{\rm{cell}}}}} = fix(D_{{\rm{cell\_min}}}^{{i_{{\rm{cell}}}},{j_{{\rm{cell}}}}}/25) + 1$ | (3) |
(4) 风矢量面元赋值。对每个观测结果进行循环,将sigma0观测结果以及相应的几何观测参数赋值到相应的风矢量面元。具体来说,记当前sigma0观测点标记为
(5) 将距当前观测点球面距离最近的星下点标号
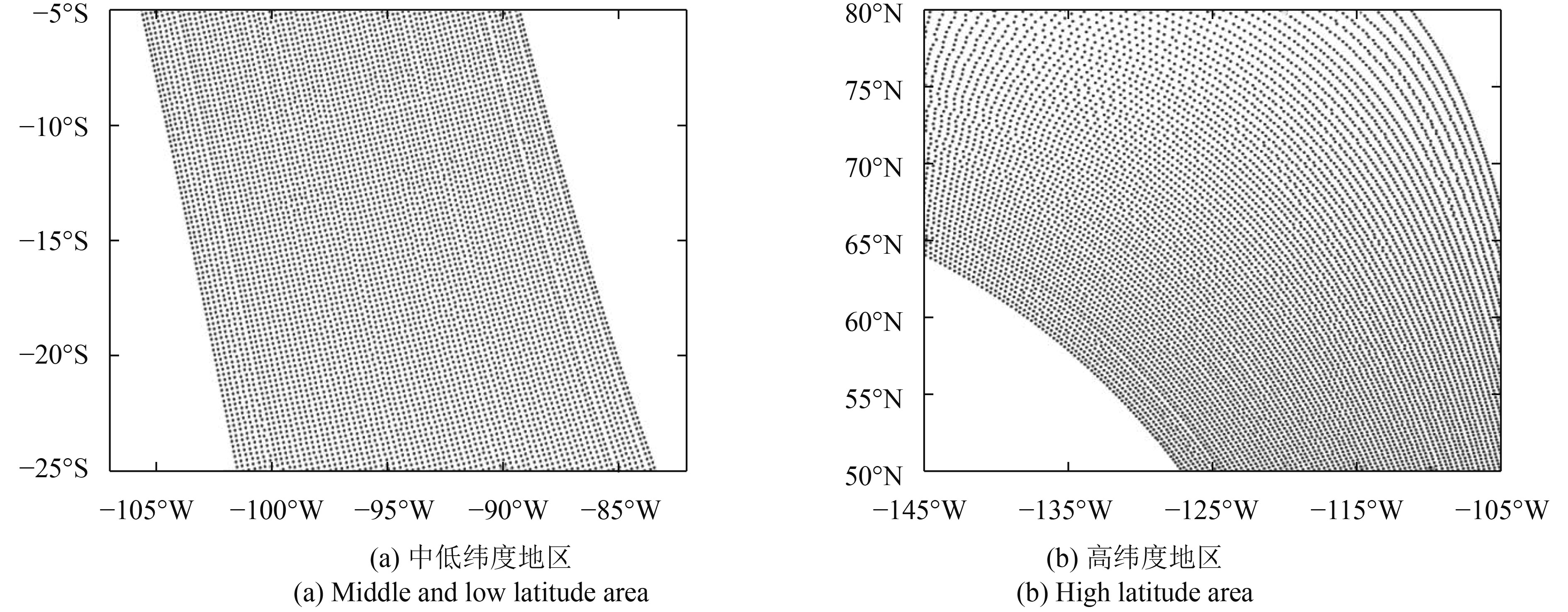
采用本文提出的面元匹配方法,对HSCAT观测数据进行处理,并对面元匹配结果进行分析。为验证面元匹配算法的有效性,首先对2013年5月30日HSCAT第8368轨数据匹配结果的风矢量面元位置分布、每个风矢量面元的观测数量空间分布进行分析,所得结果如图4、图5所示。对每个风矢量面元,计算落入该风矢量面元的所有观测结果的几何分布重心,并以该重心位置代表风矢量面元的位置。图4(a)和图4(b)分别给出了通过上述处理所得的面元匹配后风矢量面元重心位置在中低纬度和高纬度地区的分布图。图5(a)和图5(b)则给出了与图4对应区域每个风矢量面元所获得的独立观测结果的次数空间分布结果。从图4和图5可以看出,通过本文提出的面元匹配算法,在高纬度和中低纬度地区均可对sigma0进行有效的重采样,风矢量面元的位置分布均匀,每个风矢量面元均有足够数量的独立观测sigma0,可以满足风矢量反演的需求。
|
| 图 4 风矢量面元重心位置分布图 Figure 4 Distribution of gravity centre for wind vector cell |

|
| 图 5 每个面元的不同方位角观测结果数量分布图 Figure 5 Total numbers of independent looks for each Wind Vector Cell (WVC) |
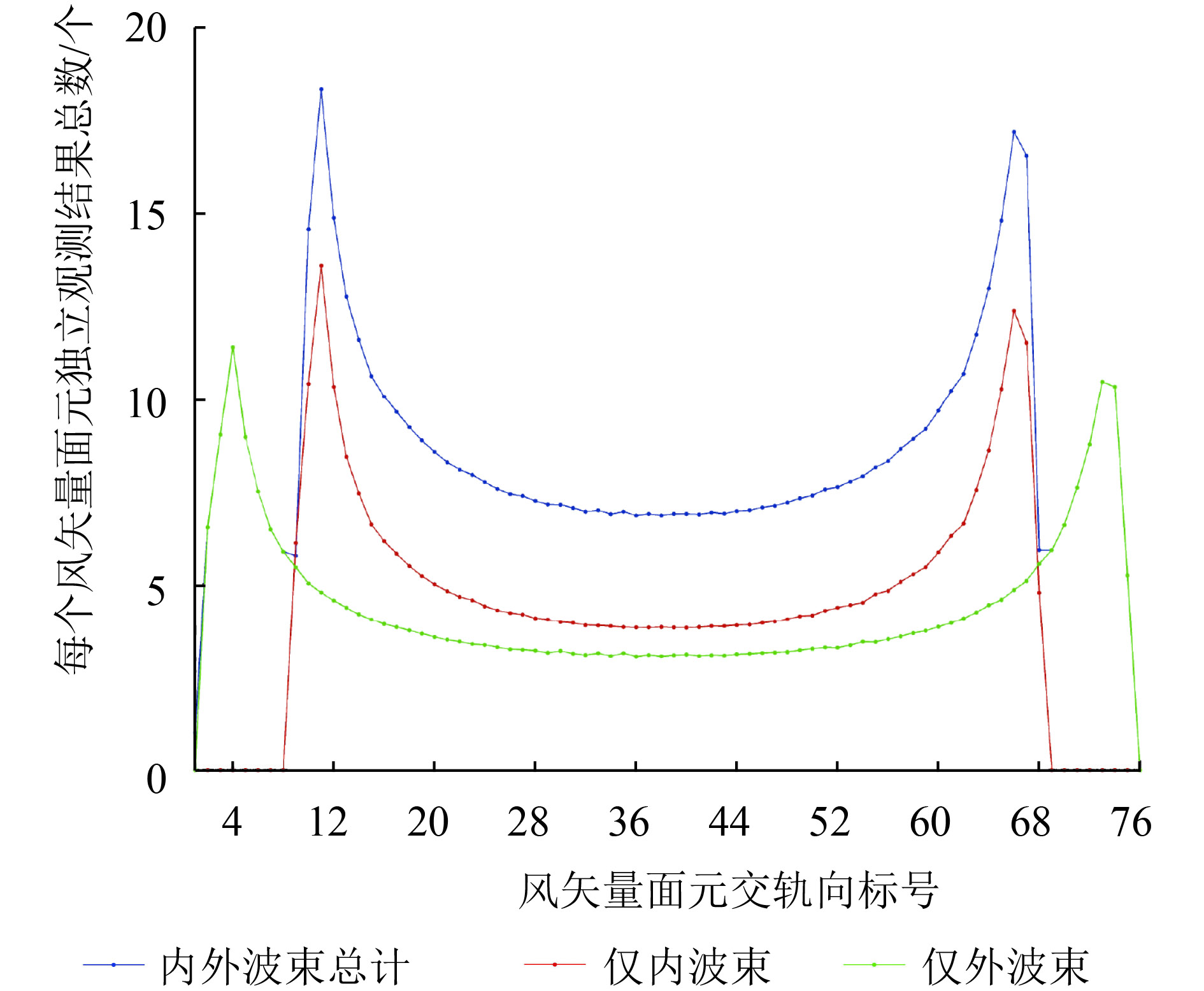
在此基础上,利用2013年1月1日到1月31日HSCAT面元匹配结果,对每个面元的后向散射系数独立观测数量随距离星下点的距离变化情况进行统计分析,结果如图6所示。由于交轨向面元号与面元距星下点的距离直接相关,标号为38和39的面元距星下点距离最近;以38、39标号为中心,标号越靠近两边的面元距星下点越远。因此,面元的后向散射系数独立观测数量随距离星下点的距离变化,可以等价于面元的后向散射系数独立观测数量随面元交轨向标号的变化。图6中红色曲线代表内波束后向散射系数独立观测数量随交轨向面元号的变化情况,绿色曲线为外波束后向散射系数独立观测数量随交轨向面元号的变化情况,蓝色曲线为两个波束独立观测数量之和随交轨向面元号的变化情况。通过图5可以看出,HSCAT每个面元的后向散射系数独立观测数量,随面元到星下点距离的变化近似为以星下点为对称轴的轴对称分布。在刈幅的任何位置的面元,内外波束刈幅内独立观测样本数最小值为3次,且内波束独立观测样本数在面元标号为11和66处(距内波束刈幅边缘3个面元距离,对应约75 km处)取得极大值12次,外波束独立观测样本数在面元标号为4和73处取得极大值(距离外波束边缘3个面元距离,约75 km处)14次。
|
| 图 6 每个面元的后向散射系数独立观测数量随交轨向面元分布图 Figure 6 Distributions for total numbers of independent looks for each WVC according to cross-track WVC index |
面元匹配的最终目标是为风矢量反演准备满足要求的sigma0观测数据,因此,通过面元匹配划分的风矢量面元网格,以及匹配到每个风矢量面元对应的观测结果,能否有效地反演得出风矢量,将是评判面元匹配方法是否有效的重要指标。结合最大似然估计算法和圆中数滤波方法,对本文面元匹配所得的sigma0进行反演,所得结果如图7、图8所示。从图7、图8中可以看出,本文的面元匹配方法,可在全球范围内对观测结果进行有效的重采样,同时通过反演所得台风风向呈现明显的涡旋状分布,风眼位置明显可见,符合台风的基本分布特征,说明本文的面元匹配结果可以满足高质量海面风场反演的要求。

|
| 图 7 HSCAT风矢量反演结果(2014年10月31日) Figure 7 Retrieved HSCAT wind vector (October 31, 2014) |

|
| 图 8 HSCAT台风鹦鹉风场反演结果(October 31, 2014) Figure 8 Retrieved HSCAT wind vector for typhoon Nuri (October 31, 2014) |
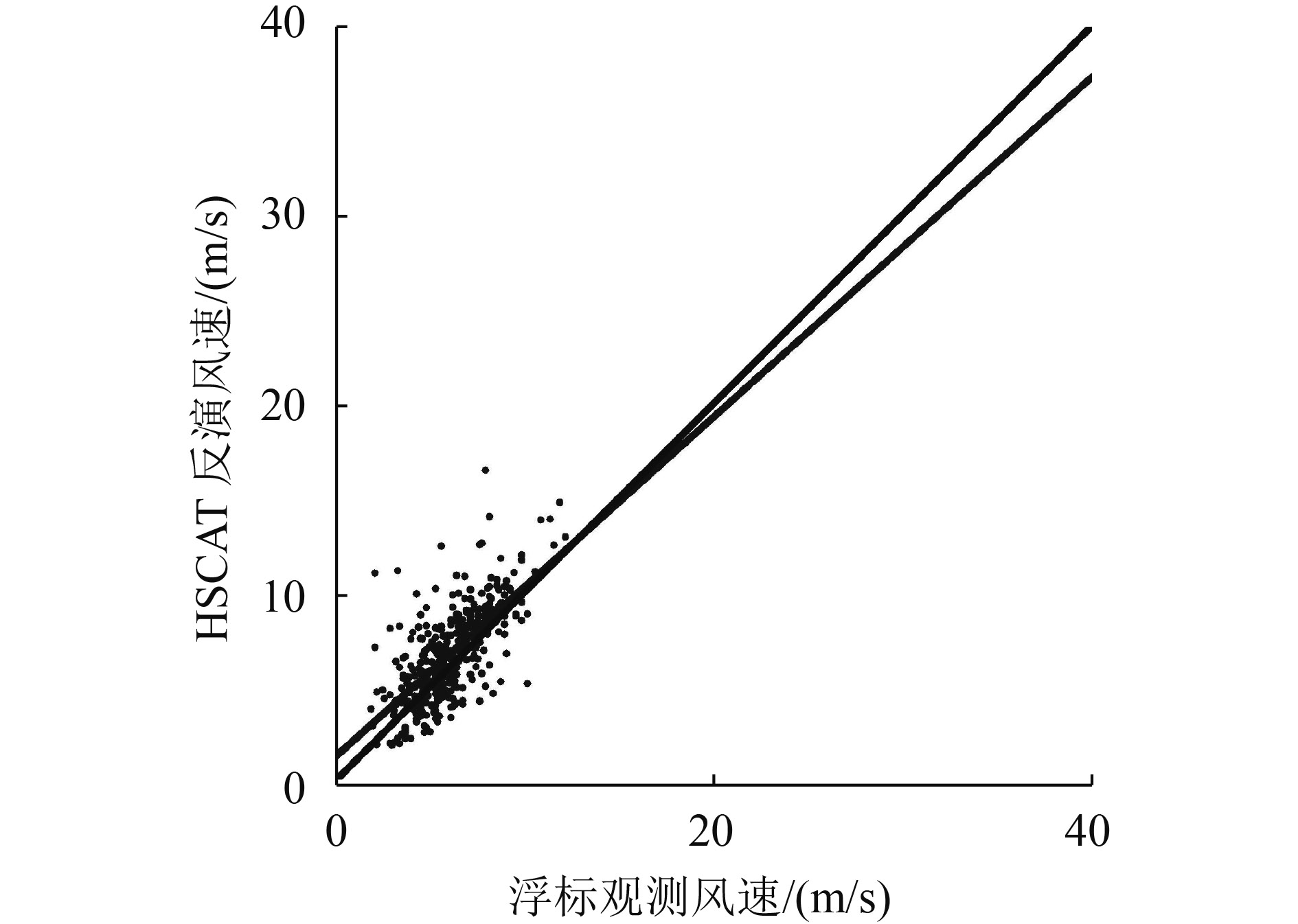
利用NDBC浮标实测数据,对采用本文算法所得的HSCAT海面风矢量进行验证。所采用的浮标位置分布如图9所示,采用10 min平均的浮标观测海面风场数据,取匹配的时间窗口为2 h,空间窗口为25 km,通过3 sigma法进行质量控制以剔除部分异常数据,并同时剔除离岸距离小于100 km的数据。从2013年5月1日到5月31日,共获得396组同步观测数据,其中风速均方根误差为1.7 m/s,风向均方根误差为23.4°。同步观测数据对比分析结果如图10、图11所示,说明通过本文方法所得HSCAT海面风矢量具有较高的精度,进一步印证了本文的面元匹配结果可以满足高质量海面风场反演的要求。

|
| 图 9 NDBC浮标位置分布图 Figure 9 Location of NDBC buoy |
|
| 图 10 风速对比散点图 Figure 10 Scatter plot of retrieved HSCAT wind speed vs. buoy wind speed |

|
| 图 11 风向对比散点图 Figure 11 Scatter plot of retrieved HSCAT wind direction vs. buoy wind direction |
本文结合HSCAT工作特点,提出了一种可业务化运行的HSCAT面元匹配方法。该方法采用以星下点轨迹为中心,以顺轨向及交轨向为坐标轴的网格划分方式,简化网格划分。同时利用L1B级数据产品中提供的卫星星下点数据,对每个观测结果,搜索与之球面距离最近的卫星星下点数据,并利用该最近球面距离计算获得交轨方向的标号,同时计算该星下点与起始点沿星下点轨迹的球面累加距离,并以此距离计算顺轨方向的标号,从而确定该观测结果在顺轨—交轨坐标网格体系下所对应的风矢量面元,达到重采样的目的。在计算搜索sigma0与各星下点球面距离的最小值时,采用了粗搜索和精搜索两级搜索策略,以提高计算效率。该方法充分利用了L1B级数据产品提供的星下点位置信息,且整个过程只涉及两点之间球面距离计算等简单操作,避免了常用的面元匹配算法中所用到的投影变换等较为烦琐的计算,因此具有计算过程简单,易于业务化应用等优点。对面元匹配结果的风矢量面元位置分布、每个风矢量面元的观测数量空间分布分析结果表明,通过本文给出的面元匹配算法,在高纬度和中低纬度地区均可对sigma0进行有效的重采样,风矢量面元的位置分布均匀,每个风矢量面元均有足够数量的独立观测sigma0,可以满足风矢量反演的需要。对每个面元的后向散射系数独立观测数量随距离星下点的距离变化情况进行统计分析结果表明,HSCAT每个面元的后向散射系数独立观测数量随面元到星下点距离的变化近似为以星下点为对称轴的轴对称分布,且独立观测数在距刈幅边缘3个面元处取得极大值,说明通过本文算法所得的面元匹配结果可以满足风场反演所要求的每个风矢量单元不少于3个独立观测样本的条件,同时也验证了HSCAT观测时序和观测几何等系统设计的合理性。利用NDBC浮标实测数据,对采用本文算法所得的HSCAT海面风矢量进行验证,所得风速均方根误差为1.7 m/s,风向均方根误差为23.4°,说明通过本文方法所得HSCAT海面风矢量具有较高的精度,进一步印证了本文的面元匹配结果可以满足高质量海面风矢量反演的要求。当然,本文提出的面元匹配方法对于HSCAT星下点位置信息的连续性有一定的依赖,如何避免星下点信息出现缺失或者数据异常等情况对面元匹配结果的影响是下一步要研究的内容。
| [1] | Attema E P W. The active microwave instrument on-board the ERS-1 satellite[J]. Proceedings of the IEEE, 1991, 79 (6) : 791 –799. DOI: 10.1109/5.90158 |
| [2] | Dunbar R S, Hsiao S V, Kim Y J, Pak K S, Weiss B H and Zhang A. 2001. Science Algorithm Specification for SeaWinds on QuikSCAT and SeaWinds on ADEOS-II. Pasadena, California: JET Propulsion Laboratory California Institute of Technology: 209–239 |
| [3] | Figa-Saldaña J, Wilson J J W, Attema E, Gelsthorpe R, Drinkwater M R, Stoffelen A. The advanced scatterometer (ASCAT) on the meteorological operational (MetOp) platform: a follow on for European wind scatterometers[J]. Canadian Journal of Remote Sensing, 2002, 28 (3) : 404 –412. DOI: 10.5589/m02-035 |
| [4] | Gohil B S, Sikhakolli R, Gangwar R K. Development of geophysical model functions for oceansat-2 scatterometer[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10 (2) : 377 –380. DOI: 10.1109/LGRS.2012.2207369 |
| [5] | Grantham W, Bracalente E, Jones W, Johnson J. The SeaSat—a satellite scatterometer[J]. IEEE Journal of Oceanic Engineering, 1977, 22 (2) : 200 –206. DOI: 10.1109/JOE.1977.1145338 |
| [6] | Lecomte P. 1998. The ERS scatterometer instrument and the on-ground processing of its data//Proceedings of Workshop on Emerging Scatterometer Applications: From Research to Operations. Noordwijk, The Netherlands: European Space Agency, Special Publication 424: 241–260 |
| [7] | Naderi F M, Freilich M H, Long D G. Spaceborne radar measurement of wind velocity over the ocean—an overview of the NSCAT scatterometer system[J]. Proceedings of the IEEE, 1991, 79 (6) : 850 –866. DOI: 10.1109/5.90163 |
| [8] | 王新中, 姜景山. 旋转扫描散射计海面风场检测仿真研究[J]. 遥感学报, 1997, 1 (3) : 185 –191. Wang X Z, Jiang J S. Study of ocean surface wind field detection of scan-scatterometer[J]. Journal of Remote Sensing, 1997, 1 (3) : 185 –191. DOI: 10.11834/jrs.19970304 |
| [9] | Wu C, Liu Y, Kellogg K H, Pak K S, Glenister R L. Design and calibration of the SeaWinds scatterometer[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39 (1) : 94 –109. DOI: 10.1109/TAES.2003.1188896 |
| [10] | 张云华, 姜景山, 张祥坤, 孙波, 付文君. 神舟4号多模态微波遥感器散射计分系统[J]. 遥感技术与应用, 2005, 20 (1) : 58 –63. Zhang Y H, Jiang J S, Zhang X K, Sun B, Fu W J. SZ-4 scatterometer mode of multimode microwave sensors (CNSCAT/M3RS) [J]. Remote Sensing Technology and Application, 2005, 20 (1) : 58 –63. DOI: 10.3969/j.issn.1004-0323.2005.01.010 |
| [11] | 邹巨洪, 林明森, 潘德炉, 陈正华, 杨乐. QuikSCAT风矢量快速反演的后向散射系数预处理算法[J]. 热带海洋学报, 2009, 28 (2) : 36 –41. Zou J H, Lin M S, Pan D L, Chen Z H, Yang L. A quick-look wind-vector retrieval algorithm for QuikSCAT[J]. Journal of Tropical Oceanography, 2009, 28 (2) : 36 –41. DOI: 10.3969/j.issn.1009-5470.2009.02.006 |
| [12] | Zou J H, Xie X T, Zhang Y and Lin M S. 2014. Wind retrieval processing for HY-2A microwave scatterometer//Proceeding of 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Quebec City, QC: IEEE: 5160–5163 [DOI: 10.1109/IGARSS.2014.6947660] |

