|
收稿日期: 2016-05-30; 修改日期: 2016-06-03;
优先数字出版日期: 2016-09-25
基金项目: 高分辨率对地观测系统重大专项(编号:03-Y20A04-9001-15116);中国科学院遥感与数字地球研究所“一三五规化”培育方向
第一作者简介:
唐娉(1968-), 女, 研究员, 研究方向为遥感图像处理、信息提取和数据挖掘技术。E-mail:tangping@radi.ac.cn
中图分类号: TP701
文献标识码: A
文章编号: 1007-4619(2016)05-1126-12
|
摘要
全球变化研究需要将多种传感器光谱波长接近的图像波段一起使用,以满足遥感应用对时间分辨率和区域覆盖的要求,这给遥感图像处理提出了新要求,涉及多传感器多时相数据几何定位一致性问题、辐射归一化问题及地类属性标识一致性问题以及高度自动化处理的问题。针对上述几方面问题,提出了一个基于“不变特征点集”IFPs(Invariant Feature Points set)作为控制数据集的区域级遥感图像自动化处理框架,将图像的几何空间、辐射值空间和类别属性值空间的时空对齐问题纳入到统一框架,提供了一种间接快速处理的手段和理念,并对构建IFPs的关键技术进行了综述。
关键词
遥感图像处理 , 不变特征点集 , 控制数据集 , 图像控制点 , 伪不变特征 , 主动学习 , 深度学习
Abstract
Global change research consistently requires the combined use of cross-sensor images with similar spectral wavelengths. To meet the temporal resolution and coverage requirements of remote sensing applications, new requirements are proposed for remote sensing image processing technology. Such technology requirements are related to how to obtain geometric consistency between cross-sensor/multi temporal data, how to obtain radiometric normalization, and how to obtain land cover class labels that are consistent between cross-sensor/multi temporal data. They are also related to highly automated processing. For the above requirements, we propose a framework for the automatic processing of remote sensing images with "an invariant feature point set" (IFPs) as the control data set. Specifically, we combine the spatial and temporal alignment in geometry space, radiation space, and land cover class space into a unified framework and thereby provide an indirect means to achieve fast processing. The key technologies for building IFPs are also reviewed.
Key words
remote sensing image processing , invariant feature point set , control point set , image controt point , Pseudo-In variant features , active learning , deep learning
1 何谓“不变特征点集”
“不变”是相对“变”存在的。图像变换是一类比较规则的“变”的方式。不变性是相对“变”保持不变的属性,不变特征是相对“变”而保持不变的特征。
如果把图像函数表示为f(x,y),g(f)(x,y)为定义在图像点(x,y)的特征函数,H(f)表示图像的某种变换。假如
| $ g\left( f \right)\left( x,y \right)=g\left( H\left( f \right) \right)\left( x,y \right) $ | (1) |
则g(f)(x,y)是图像在点(x,y)针对变换H的不变特征。如果特征g与图像点(x,y)相关,则这种不变特征就是局部不变特征,否则就是全局不变的。g(f)(x,y)所表示的图像在(x,y)的特征函数可以是1维或多维函数。H(f)所表示的图像变换可以是几何变换、光度变换或光谱变换、卷积变换、视角变换,甚至是分类变换等。
几何变换涉及空间坐标变换,与图像函数的定义域变化相关;与图像函数值域相关的变换是辐射变换、光谱变换或卷积变换,如图像增强、图像融合等;还有一类变换涉及图像像元的属性,与像元语义相关,如图像分类,是按照图像像元属性对像元进行归类的变换。从变换取值的意义上,几何变换、辐射变换可以认为是连续变换,图像分类是离散变换。
应用非常广泛的平移不变、尺度不变、旋转不变特征(Lindeberg,1994,1998,2012)及仿射不变特征SIFT(Lowe,1999,2004)都是针对某一类几何变换的不变特征。平移、尺度、旋转、仿射不变特征都是针对平移变换、尺度变换、选装变换及仿射变换不变的特征。如果图像点(x,y)的局部特征是平移不变的、尺度不变的、旋转不变的或仿射不变的特征,则点(x,y)就是具有某不变特征的点,这样的点集就是具有某不变特征的点集IFPs。平移、尺度、旋转变换都是仿射变换的特殊情况。
针对辐射变换、分类变换的IFPs,含义是类似的。遥感图像针对几何变换、辐射变换、分类变换的IFPs在区域级遥感图像的自动化处理中发挥着重要作用,架起了一条实现自动化处理的桥梁。
2 区域级遥感图像应用对遥感图像处理的新要求
全球变化问题研究通常需要将多种传感器波长接近的图像波段一起应用,以满足遥感应用对时间分辨率和区域覆盖的要求。如Chen等人(2015)、Gong等人(2013)在全球地表覆盖遥感制图中由卫星传感器Landsat TM/ETM+图像和HJ-1A/B CCD图像形成了2000年和2010年两个基准年度覆盖全球陆地的数据集。该数据集共2万余景图像需要做辐射校正,1千多景HJ-1 A/B CCD图像需要几何精校正和辐射校正(唐娉 等,2014),而且要求两个基准年度的数据在几何定位上具有一致性;Hansen等人(2013)在进行全球森林覆盖变化制图时,所用数据涵盖从2000年—2012年共12年Landsat 4、Landsat 5、Landsat 7和Landsat 8的TM/ETM+图像,合计130万景,这些数据需要几何处理形成几何定位一致的时间序列图像集,需要辐射处理使辐射差异对图像分类错分的影响尽可能小,需要对每年的数据分类,使得每年的分类结果是合理、可比的。这种多个传感器数据综合应用的例子,给区域级遥感图像的处理提出了新的要求,新的要求中除大规模数据的自动化快速处理能力是共性要求外,主要包括:
要求1 多传感器数据或多时相数据间的几何定位应尽可能保有一致性;
要求2 同一地理位置多传感器数据或多时相数据使用时存在的辐射差异应在合理可控范围内,或存在变换关系;
要求3 同一地理位置和一定的时间、分辨率尺度约束下,多传感数据或多时相数据的地物属性标记应有一致性。
本文暂且抛开从计算机软件角度如何自动化快速处理大规模遥感图像的技术问题,单纯从上述3个要求出发来讨论。
3 以“不变特征点集”为控制数据集的遥感图像自动化处理框架
对于第2节的3个要求,通常有各自不同的解决思路。
要求1的解决思路:对图像分别进行几何精纠正或正射校正,依赖图像的绝对定位精度自然实现多传感器多时相数据之间几何定位的一致性。缺点是因校正精度存在差异,所以不一定能够保证图像之间几何定位的一致性,也不能保证自动化实现。可选方案是利用图像配准方法直接解决图像间几何定位的一致性问题。该方法需要在图像间确定锚点或控制点CPs(Control Points),然后基于控制点建立图像之间的变换关系,实现图像间几何定位的一致性。如果匹配所用的基准图像是经过几何绝对定位的,则配准后的图像间其绝对定位也是有一致性。
要求2的解决思路:利用交叉辐射定标方法(Zhong等,2014)建立不同传感器之间的光谱辐射关系,再对图像进行全流程的绝对辐射校正,提供给用户地表反射率图像。在全流程的绝对辐射校正中,大气校正仍旧是最具不确定性的步骤(Schroeder等,2006)。Schroeder等人(2006)指出,理论上单个图像的绝对辐射校正应当有效消除大气效应,使谱段接近的图像有比较一致的辐射特性,然而已有证据表明即使绝对辐射校正方法,如6S,仍然会使时间序列中图像间的光谱存在一定程度的不相似。另一方面,有一些卫星传感器数据缺乏用于大气校正的充足信息,如国产卫星GF-1/GF-2、HJ-1、CBERS等的多光谱图像均只有4个波段,缺少Landsat TM大气校正所具有的2.1 μm的波段,因此常用的大气校正方法,如暗目标法。这种情况下需要有新的方法对图像进行辐射校正。
要求3的解决思路:对应遥感数据尺度确定类别体系,然后人工分别建立来自不同传感器图像的地物类别训练样本集,再利用机器学习算法分别对不同的传感器数据实现对所有像元分类。该方法的缺点是同一类别不同传感器图像的训练样本集不一定相同,对同一地理位置的像元,即使时相相同,分类结果也可能不同。
本文提出的满足上述3个要求实现遥感图像自动处理的框架是基于IFPs的解决框架。该框架的基本思路是:借鉴图像配准的CPs思路,在同一区域两个图像(不同传感器或不同时相)的定义域(几何或地理空间)、值域(辐射值空间)、地物属性空间分别构建控制点集,利用控制点集建立图像在地理空间、辐射值空间和属性空间的关联或对齐,从而保有某种一致性。这种思路是可行性,因为面对同一个地球同一个地表,多传感器多时相数据集之间必然存在着这样紧密关联的点集。如果构建了控制点集,则自动处理水到渠成。
进一步,要求控制点集是具有不变特征的点集IFPs,因为不同传感器不同时相图像间在上述的3个空间存在诸多变化,只有面对这些变化不变、稳定的特征点才能始终存在、被检测,构成稳定的控制点集,为遥感图像的自动化处理架起桥梁。
4 检测和对齐IFPs关键技术
在图像不同的空间里:几何空间、辐射值空间、属性值空间,面对不同的变换,IFPs检测和对齐的关键技术是不同的。
4.1 几何空间IFPs自动检测和对齐的关键技术
在几何空间里,图像间的CPs早先是常用的地面控制点GCP(Ground Control Point)。GCP一般取地标点,更准确地,是用精密测量仪器测定了平面位置和高程的地标点。很多时候地面控制点也泛指在图像上容易识别和定位明确的点。GCP在低空间分辨率图像上一般取道路的交叉点、人工设施的拐点等。但随着空间分辨率的提高,道路交叉点已经不适合做GCP,GCP更多时候取的是地表标志物的拐点,是那些容易精确定位的点。发展到现在,很多GCP不是实地采集而是从正射图像上采集的,更准确地应该称为图像控制点ICP(Image Control Point)。因此,可以说ICP是随着时间变化仍然容易精确定位的图像上的锚点。
ICP作为图像局部特征的一种,并非单纯指只有空间位置没有空间范围的点。实际上为了定位ICP,需要分析ICP的局部邻域,因此所有的ICP均隐含着一个空间范围,就是ICP的某种形状的邻域。
通过人工在图像上分析选择控制点,是费时费力的工作,为了减少重复的工作量,提高应用效率,控制点选择技术的发展经历了几个不同的阶段:
(1) 控制点库模式。将人工选择的ICPs建库存储,使这些控制点可重复使用(张继贤和马瑞金,2000)。控制点库中存储以控制点为中心的图像片和控制点的坐标高程信息以及控制点图像分辨率、来源、获取时间等信息。应用时将控制点片与图像进行匹配即可。
控制点库方法唯一的问题是,控制点片与图像的匹配不一定能很好实现,一方面控制点特征是人眼容易识别的,不一定是计算机容易识别的,另一方面控制点库中控制点片的获取时相、辐射特性、几何特性、空间分辨率(尺度)与待匹配的图像可能存在差异,对匹配算子的要求很高。
(2) 伴随各种特征点自动提取算子和描述子发展而来的动态控制点模式。特征点提取算子有时也称兴趣点(interest point)提取算子,“兴趣点”的概念最早是Moravec(1981)提出的,一般刻画为具有以下性质的点(Lindeberg,2013):
● 有清楚的,最好是从数学基础上清晰定义的点;
● 在图像空间中有明确定义的位置;
● 兴趣点周围的局部图像结构丰富;
● 在图像空间对局部和全局扰动稳定,如图像的光照/亮度变化,兴趣点能够可靠地检测,重复率高;
● 可选的特性:兴趣点的概念应该包括尺度属性,使现实中的图像在尺度变化时仍然可检测出兴趣点。
兴趣点提取算子重要的部分是角点(Corner)提取算子,目的是自动提取出感兴趣的点特征并进行特征描述(描述子),以便在图像匹配时能找到对应点,即使图像在时相、辐射特性、几何特性、空间分辨率等方面均存在差异。
角点提取算子应该包括两个部分:检测算子和描述子,检测算子的任务是检出角点,描述子的任务是对检出的点的邻域性质或特征进行描述,这种描述一般都是定量的描述,可以作为后续特征点确认和特征点匹配的基础。描述子通常计算角点的邻域特征作为对角点的刻画。最简单的邻域特征是邻域本身。
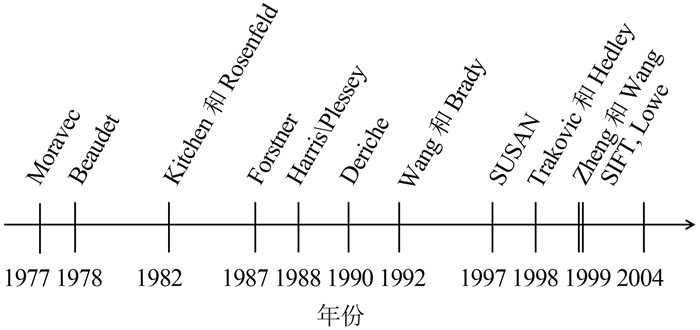
事实上,早先的角点提取算子通常只包括检测角点的部分,当角点检测完成,在具体应用时再构建描述子。早先图像匹配时直接提取兴趣点的邻域作为描述子。这样的描述子必然会影响图像匹配的效果。各种角点提取算子的研究经历了一个比较长的发展历程,如图 1所示。
角点的提取方法有基于灰度的方法、基于轮廓的方法和基于模型的方法。其中,基于灰度的方法应用非常广泛,一般与图像的局部自相关、图像局部的一阶或二阶梯度相关。
Moravec算子作为第1个广泛应用的角点检测算法,开创了角点检测的新纪元,后续的很多角点检测算子都是在其基础上通过扩展得到的。Moravec检测算子是基于灰度自相关获得的,它在像素邻域窗口和几个方向的平移窗口间测量图像灰度间的差值,大于某阈值的最小差值认为是兴趣值。
给定一个平移(△x,△y)和像元点(x,y),图像I的自相关函数定义为
| $ f\left(x{\text{,}}y \right)={{\sum\limits_{W}{\left(I\left({{x}_{k}}{\text{,}}{{y}_{k}} \right)-I\left({{x}_{k}}+\Delta x{\text{,}}{{y}_{k}}+\Delta y \right)\right)}}^{2}} $ | (2) |
式中,(xk,yk)是中心在(x,y)的窗口w中的点。
检测算子使用图像的二阶微分计算测度DET=IxxIyy–Ixy2,DET是Hessian矩阵的行列式和图像的Gaussian曲率相关。该测量是旋转不变的,DET最大值对应的点就是兴趣点。
有几个兴趣点检测算子都与自相关函数的矩阵相关。这个矩阵的在像元点(x,y)的窗口W内对图像I的微分进行平均处理
| $ {\boldsymbol{A}}\left( {x{\rm{,}}y} \right) = \!\! \left[ {\begin{array}{*{20}{c}} {{{\sum\limits_W {\left( {{I_x}\left( {{x_k}{\rm{,}}{y_k}} \right)} \right)} }^2}} & \!\!\!\!\!\!\!\!{{{\sum\limits_W {\left( {{I_x}\left( {{x_k}{\rm{,}}{y_k}} \right){I_y}\left( {{x_k}{\rm{,}}{y_k}} \right)} \right)} }^2}}\\ {\sum\limits_W {{I_x}\left( {{x_k},{y_k}} \right){I_y}\left( {{x_k}{\rm{,}}{y_k}} \right)} } & {{{\sum\limits_W {\left( {{I_y}\left( {{x_k}{\rm{,}}{y_k}} \right)} \right)} }^2}} \end{array}} \right] $ | (3) |
该矩阵获得了像元邻域的结构。如果上面矩阵的秩是2,则其两个特征值都比较大,检测出的就是兴趣点;秩为1的矩阵代表边缘点,秩为0的矩阵代表平坦区域。
矩阵A(x,y)和图像的局部自相关是有关联的,具体关联为
| $ \begin{array}{*{20}{l}} {f\left( {x,y} \right) = \sum\limits_W {{{\left( {{I_x}\left( {{x_k},{y_k}} \right) - I\left( {{x_k} + \Delta x,{y_k} + \Delta y} \right)} \right)}^2}} = }\\ {\sum\limits_W {{{\left( {\left( {{I_x}\left( {{x_k},{y_k}} \right){I_y}\left( {{x_k},{y_k}} \right)} \right)\left( {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right)} \right)}^2}} = }\\ \begin{array}{l} \left( {\Delta x\;\Delta y} \right)\left[ {\begin{array}{*{20}{c}} {{{\sum\limits_W {\left( {{I_x}\left( {{x_k},{y_k}} \right)} \right)} }^2}{{\sum\limits_W {\left( {{I_x}\left( {{x_k},{y_k}} \right){I_y}\left( {{x_k},{y_k}} \right)} \right)} }^2}}\\ {\sum\limits_W {{I_x}\left( {{x_k}.{y_k}} \right){I_y}\left( {{x_k}.{y_k}} \right)} {{\sum\limits_W {\left( {{I_y}\left( {{x_k}.{y_k}} \right)} \right)} }^2}} \end{array}} \right]\\ \left( {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right) = \left( {\Delta x\;\Delta y} \right){\boldsymbol{A}}\left( {x,y} \right)\left( {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right) \end{array}\\ {} \end{array} $ | (4) |
检测算子SUSAN(Smallest Univalue Segment Assimilating Nucleus)(Smith和Brady,1997)及Trajković和Hedley(1998)给出的是另外的思路,即不使用对噪声敏感的局部梯度,使用形态学方法:计算圆形邻域和中心像元灰度相似的像元的比例,角点是满足某种阈值的局部极小点。
在自动获得特征点之后,伴随其后的重要内容是不同图像上特征点的匹配,特征点的匹配本质上是特征点描述子的相似度比较,相似度高就认为是匹配的。这中间涉及两方面的问题:特征点如何描述,对应的相似度如何度量。特征点的描述与相似性度量依据描述子的不同通常使用的有两大类:
(1) 邻域模板和基于模板的各种相似性度量。邻域模板直接取角点的邻域作为角点的描述,相似性度量取交叉相关性系数(Rosenfeld和Kak,1982)或相关系数(Svedlow等,1976),绝对值差(Barrow等,1977),相位相关(Anuta,1970; De Castro和Morandi,1987; Chen等,1994; Reddy和Chatterji,1996; Lucchese等,2002),互信息(Viola和Wells,1997; Thévenaz和Unser,1998; Rangarajan等,1999),图匹配,(Aguilar等,2009;Izadi和Saeedi,2012)等。
(2) 各种具有不变特征的局部描述子与对应的相似性度量。角点的邻域构成兴趣区域,对兴趣区域的局部描述子已经在宽基线的图像匹配、目标识别、纹理识别、图像检索、视频数据挖掘等邻域有成功的应用。
各种不变特征的描述子可以构成特征矢量或特征直方图,对应于特征矢量的相似性度量主要是欧氏距离或其他距离;对应于特征直方图的相似性度量主要是基于分布的距离。
现在应用最广泛的特征描述子是尺度不变特征变换SIFT类(Scale-Invariant Feature Transform)的描述子(Lowe,1999,2004),如RIFT(Lazebnik等,2004),G-RIF(Kim等,2006),SURF(Bay等,2006),PCA-SIFT(Ke和Sukthankar,2004),Gauss-FIFT(Lindeberg,2015),GLOH(Gradient Location and Orientation Histogram,Mikolajczyk和Schmid,2005),SIFT-Rank(Toews和Wells,2009)。其他的描述子还有形状内容(shapecontext,Belongie等,2002),可控滤波器(steerable Filters,Freeman和Adelson,1991),微分不变量(differential invariants,Koenderink和Van Doorn,1987),复合滤波器(complexfilters,Schaffalitzky和Zisserman,2002),矩不变量(moment invariants,Van Gool等,1996)。其中形状内容描述子与SIFT类似,只是它是基于边缘建立的,是关于边缘点定位和定向的3维直方图。
SIFT是计算机视觉中用于检测和描述局部特征的算法,它组合了一个尺度不变的斑点检测算子和斑点区域梯度分布的描述子一起。描述子是一个关于梯度位置和方向的3维直方图,SIFT描述子对图像域的平移、旋转和尺度变换不变,而且对中度的透视变换和照明变化是鲁棒的,对遮挡也鲁棒。SIFT的描述子已经被实验证明是非常有用的图像匹配和目标识别工具。SIFT描述子也被扩展从灰度图像到彩色图像,从2维图像空间到3维时空视频领域。
图像间的匹配点找到后,利用匹配点可以建立图像间的建立形变模型,最终完成图像在几何空间的对齐。几何空间IFPs的自动提取、对齐及应用技术已相对比较成熟,已有很多的应用。单小军等人(2014)利用Landsat TM图像作为基准,动态提取图像控制点,自动实现了HJ-1 A/BCCD图像的几何精纠正;赵涌泉等人(2014)将MODIS图像作为基准,动态提取图像控制点,将多源低分辨率图像与其进行空间对齐,获得了高时间频率的全球陆地图像集,为全球变化研究提供了数据支撑。甚至在无人机图像拼接中(Lucieer等,2011)广泛使用的大区域网平差也是以相邻图像间动态提取的尺度不变、仿射不变控制点集为基础实现3维点云提取及相关校正和拼接的。
4.2 辐射值空间IFPs自动检测的关键技术及应用
辐射值空间的IFPs是辐射值空间具有某种不变特征的控制点集。
辐射值空间是遥感图像的值域空间。辐射值会受地物属性、成像几何、光照、地形等的影响。这里的IFPs指对线性或一些非线性光谱变换保持不变的像元,其中对线性变换保持不变的像元也称为具有伪不变特征PIFs(Pseudo-Invariant Features)的像元。早先Schott等人(1988)提出的PIFs指的是一些具体的地物,这些地物的反射特性随时间和光照的变化不大,如沥青和水泥路面。一般,PIFs可以是不透水的路面、干燥地表,如停车场、大面积的屋顶(Schott等,1988; Berger,1989; Caselles和García,1989; Hall等,1991)等,PIFs在有些文献中也称为辐射控制点集(Hall等,1991)。Eckhardt等人(1990)给出的人工选择PIFs的准则包括:
(1) PIFs中应当既有亮的地物,也有暗的地物;
(2) PIFs应当尽可能是均值的;
(3) PIFs应当是光滑的和水平的,可以假设为朗伯体,这样成像几何和光照引起的误差最小;
(4) PIFs尺寸不能太小,这样临近效应小,而且在不同的图像和地面上容易确认。
当标记出不同时相图像中的PIFs时,可以依据这些PIFs建立线性回归关系对图像进行辐射归一化。
由于人工标记PIFs费事费力,PIFs的精度依赖于用户的精度和知识,会导致比较主观的变换。因此PIFs的选择也逐渐由人工标记发展到了自动标记的阶段。
基于樱帽变换在亮度绿度散点图上从低绿、低亮和低绿高亮部分选择“未变”像元从而选择PIFs;Elvidge等人(1995)提出了一种自动散点控制回归法ASCR(Automatic Scattergram Control Regression)的算法,余晓敏和陈云浩(2007)提出了改进的自动散点控制回归算法(改进的ASCR算法);Du等人(2002)提出基于PCA变换在主轴方向结合统计方法选择PIFs。这些方法的实质都是选择某线性变换后“未变”像元,但很难做到完全自动。直到Nielsen等人(1998)提出了多元统计方法MAD(Multiva-riate Alteration Detection),Canty和Nielsen(2008)利用它自动提取PIFs用于辐射归一化并提出了优化算法IR-MAD(Iteratively Re-weighted modificationof the MAD),该算法不受总体的大气状况和传感器标定导致的线性与仿射变换的影响,可提取两不同时相图像的特征不变像素。相对于手工选取时不变特征的方法,该方法简单、快速、自动,而且迭代的算法进一步优化改进了算法的精度、稳定性与鲁棒性。
Hu和Tang(2012)推导了由原始图像DN值直接计算到地表反射率的近似线性关系,将MAD算法用于不同传感器具有不同量纲的图像Landsat TM和HJ-1CCD图像,Landsat TM是地表反射率图像(值域0—1)为参考图像,HJ-1CCD图像(值域0—255)是DN值的原始图像,从两幅图像上自动提取PIFs,通过辐射归一化得到HJ-1 CCD图像的地表反射率,实现了对HJ-1CCD图像的大气校正。
MAD算法的实质是典型相关分析CCA(Canonical Correlation Analysis)。典型相关依据相关性最大的约束得到新的变量,新的变量中的点按照一定的条件筛选后就是伪不变图像特征点。这些点的实质是对线性变换后不变。利用找到的点通过最小二乘方法构建线性关系就获得了使图像间辐射值对齐的连续映射函数。基于典型相关的MAD的基本原理如下:设随机向量X和Y分别为对地表同一区域不同时相的两幅原始多光谱卫星影像,总体{X,Y}的协方差矩阵为
| $\sum = \left[ {\begin{array}{*{20}{c}} \displaystyle{\sum\limits_{11} }&\displaystyle{\sum\limits_{12} }\\ \displaystyle{\sum\limits_{21} }&\displaystyle{\sum\limits_{22} } \end{array}} \right]$ |
考虑如下的线性变换:
| $ \left[ \begin{array}{l} {\boldsymbol{X}}\\ {\boldsymbol{Y}} \end{array} \right] \to \left[ \begin{array}{l} {\boldsymbol{U}}\\ {\boldsymbol{V}} \end{array} \right] $ |
| $ {\boldsymbol{U}} = {{\boldsymbol{a}}^{\rm{T}}}{\boldsymbol{X}}{\text{,}}{\boldsymbol{V}} = {{\boldsymbol{b}}^{\rm{T}}}{\boldsymbol{Y}} $ |
典型变换就是寻找一个线性变换,求定义为线性变换,即求向量$\boldsymbol{a}$和b,满足
| $ {{\boldsymbol{a}}^{\rm{T}}}\displaystyle\sum\limits_{11} {{\boldsymbol{a}} = 1} , \,\,\,{{\boldsymbol{b}}^{\rm{T}}}\displaystyle\sum\limits_{22} {{\boldsymbol{b}} = 1} \\ Corr\left\{ {{\boldsymbol{U}},\,\,\,{\boldsymbol{V}}} \right\} = {{\boldsymbol{a}}^{\rm{T}}}\displaystyle\sum\limits_{12} {{\boldsymbol{b}} = \max } $ |
相应的U和V称为X和Y的典型变量,它们之间的相关系数Corr{U,V}称为典型相关系数。因为U、V任意改变一个常数倍,并不改变它们之间的相关系数,简单起见,姑且限定典型变量具有标准方差,也就是$Var${U}=$Var${V}=1。
MAD变换在典型变换的基础上稍有变化Nielsen等人(1998),即用线性变换的差定义MAD变量
| $ {\rm{MAD}}={{{\boldsymbol \alpha} }^{\rm T}}{\boldsymbol X}-{{{\boldsymbol\beta} }^{\rm T}}{\boldsymbol Y} $ | (5) |
在条件$Var${αTX}=$Var${βTY}=1下使得
$Var${MAD}=max
而$Var${MAD}=max等价于Corr{αTX–βTY}=min,因为$Var${MAD}=$Var${αTX–βTY}=2(1–Corr{αTX–βTY})
MAD变换的一个重要的性质是MAD变量是线性变换的不变量,MAD变换对图像值的值域范围和增益不敏感,因而这种变换没有对图像数据X和Y值域的一致性提出任何要求,理论上适用于PIFs筛选时,原始图像为DN值,参考图像为地表反射率的情况。
一般,因时间差异引起的变化信息都集中在前几个MAD变量中。而Canty和Nielsen(2008)将MAD变换应用到线性相对辐射校正时,是寻找具有线性不变的信息,此时需要的信息都集中在最后几个MAD变量中。MAD方法后续得到改进变成迭代实现的IR-MAD,在迭代的过程中不断更新MAD变量,以便得到更准确的PIFs。
需要说明的是,MAD或IR-MAD算法提取的像元点集称为特征不变点集,是一个纯数学意义上的点集,不是基于物理含义的点集筛选,而早先PIFs的定义是包含物理机理的,是对那些光谱特性随时间变换不敏感的个别的地物类型。一般可以认为MAD或IR-MAD算法筛选出的具有线性不变特性的不变特征点集,即包含了PIFs,也包含其他非PIFs。因此可以使用多种方法从不变特征点集中筛选PIFs用于线性相对辐射校(胡昌苗 等,2014)。也可以认为PIFs的定义经过了扩展,从早先单纯包含物理机理的点扩展到了一般的特征不变点集,具体应用需要选择具有特定辐射特性的辐射控制点集。
当需要考虑针对非线性变换不变的特征点集时,上述基于典型相关的技术可采用核典型相关技术来替代。利用核典型相关分析(kernel cano-nical correlation analysis,Nielsen,2011)自动获得的不变特征点集是非线性变换下的不变点。核映射是一个强大的映射,很多方法在这个映射下可以直接推广到核空间。核函数的作用就是隐含着一个从低维空间到高维空间的映射,而这个映射可以把低维空间中线性不可分的两类点变成线性可分的。
引入核函数后的变量为
| $ {\boldsymbol{U}}={{\boldsymbol{c}}^{\rm{T}}}{{\boldsymbol\phi }_{x}}\left({\boldsymbol{X}} \right),{\boldsymbol{V}}={{\boldsymbol{d}}^{\rm T}}{{\boldsymbol\phi }_{y}}\left({\boldsymbol{Y}} \right) $ |
式中,
| $ {\boldsymbol{k}}\left({{x}_{i}},{{y}_{i}} \right)=<\boldsymbol\phi \left({{x}_{i}} \right),\boldsymbol\phi \left({{x}_{j}} \right)> $ |
为构建核矩阵,利用拉格朗日公式,可得
| $ \begin{array}{l} {\boldsymbol{U}} = \displaystyle\sum\limits_i {{\alpha _i}} < {{\boldsymbol \phi} _x}\left( {{x_i}} \right),{{\boldsymbol \phi} _x}\left( {{x_x}} \right) > \\ {\boldsymbol{V}} = \displaystyle\sum\limits_i {{\beta _i}} < {{\boldsymbol \phi} _y}\left( {{y_i}} \right),{{\boldsymbol \phi} _y}\left( {{y_y}} \right) > \end{array} $ | (7) |
令
| $Corr\left\{ {\boldsymbol{U}}{\text{,}}{\boldsymbol{V}} \right\}=\frac{{{\boldsymbol\alpha }^{{\rm{T}}}}{{{\boldsymbol{k}}}_{x}}{{{\boldsymbol{k}}}_{y}}\boldsymbol\beta }{\sqrt{{{\boldsymbol\alpha }^{{\rm{T}}}}{{{\boldsymbol{k}}}_{x}}{{{\boldsymbol{k}}}_{y}}\boldsymbol\alpha }\sqrt{{{\boldsymbol\beta }^{{\rm{T}}}}{{{\boldsymbol{k}}}_{x}}{{{\boldsymbol{k}}}_{y}}\boldsymbol\beta }}$ | (10) |
式中,
| $ {{\boldsymbol{k}}_x} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol\phi _x^{\rm{T}}\left( {{x_1}} \right)}\\ {\boldsymbol\phi _x^{\rm{T}}\left( {{x_2}} \right)}\\ \vdots \\ {\boldsymbol\phi _x^{\rm{T}}\left( {{x_n}} \right)} \end{array}} \right] $ |
类似于典型相关分析,确定α和β的值使得Corr{U,V}最大,便可得到高维空间中的特征不变点集。继而可以在点集中进行筛选获得需要的不变特征点集并进行应用。
进一步的应用可在如下方面扩展,包括:
(1) 提取时间序列的光谱变化轨迹,基于光谱变化轨迹进行变化检测(Kennedy等,2007);
(2) 以大气校正后类似谱段的图像作为参考图像,通过提取伪不变特征点集,对图像进行绝对—辐射归一化(Schroeder等,2006);
(3) 提取非线性变换不变的辐射控制点集,通过非线性变换实现色彩迁移或光谱特性的转移(Reinhard等,2001; Wang等,2011);
(4) 航空图像同样受大气的影响,基于重叠区域的辐射控制点集形成的三角网可有效实施对航空图像的辐射校正(Chandelier和Martinoty,2009)。
4.3 地表覆盖属性空间不变特征点集构建的关键技术
相似尺度不同传感器的地表覆盖分类在同一个分类体系下同一时相的分类应该有唯一的标记。这个问题在目前的分类工作中很少直接涉及。只有一些间接的工作与此相关,主要通过对同一区域甚至同样的影像进行分类,然后评价分类精度。地表覆盖分类的属性是随时间和空间变换不变的。监督分类精度的高低主要取决于以下3方面的因素:训练样本集、监督训练得到的类别特征的表达能力和分类器的分类能力。其中,不同尺度不同传感器数据的分类训练样本集对遥感图像的分类作用类似于分类的控制数据集。
直到目前,类别的训练样本都是人工选取的。训练样本选择最重要的原则是“代表性”,但“代表性”如何定量衡量是比较困难的。早先的样训练样本选择不只选择单一样本,更多是选择训练样区,要求训练样区是齐次的,即每个样本都在同一个类别,还要求样区包含该类的各种变化。
训练样本选择重要的一步是训练像素类别的事先认定。认定的途径可能包括昂贵的场地调查,也可能是判读员使用地形图及航空图片、高分辨率卫星影像等参考数据来确定。监督分类的“监督”有两个含义:训练样本的类别是事先已知的;监督训练的特征是根据分类器确定的,训练过程是监督的特征学习过程。
训练过程或学习过程,本质是找到特征和类别标签间的关系(mapping),这样当有特征而无标签的数据输入时,就可以通过已有的关系得到未知数据标签。因此,训练样本集作为控制数据集,关键是能否从中提取出表达类别的特征,从而建立类别特征与类别标签之间的关系,而提取的类别特征能否有足够的类别表达能力,不仅与训练样本集相关也与分类器的性能相关。
当训练样本数据的选择不是穷尽的(不全)/或者代表性不足的时候,若采用最小距离或者最大似然的分类器,必须谨慎使用阈值限制,以确保不能被很好表征的像素不会被错误地标记。如果一个像素与最近均值的距离在标准差的数倍之内,可以通过最小距离的限制正确分类。对于最大似然分类,可以通过对判决函数的阈值约束进行分类。分类器一旦有了这样的限制,则训练数据中不能被很好表示的图像像素则不会被正确分类。这一方面表明训练数据集选择时的不足,需要修正训练集,重新分类;另一方面表明提取的特征不能完全表达该类别。
从训练数据中提取哪些特征取决于所采用的分类器的类型。由训练数据产生的特征具有不同的形式,这主要取决于所采用的分类器的类型。如,对于平行六面体分类器,类特征是每个谱带中亮度的上下限;对于最小距离分类器,特征是每一训练数据的均值矢量;对于最大似然分类,类均值矢量和协方差矩阵构成了特征;对于神经网络和支持向量机来说,权值集合定义了类别之间的边界。它们都是分类器的固有特性,由训练数据学习生成,目标是使类别可分。与训练样本全不全、代表性如何关联的问题是训练样本数量多少是足够的,而对这些问题一直没有绝对的答案。
对于基于统计的分类器,训练样本的数量问题有一些研究(Rosenfield等,1982)。一位学者建议的原则是每类训练样本的数量至少是所用特征数量或待估计参数个数的30倍。
关联样本质量与数量的研究中,主动学习是一类重要的方法,主动学习的目标获得数量少且对分类精度有重要影响的样本,一定程度上回答应该选择什么样的样本增加到训练样本集中的问题。主动学习(active learning)是一种机器学习方法,该方法试图在小训练样本的情况下,通过上一次分类结果预测出哪些样本对分类有重要影响,一般是位于分类器边界的样本,用户对这些样本进行标记后,重新进行分类,依次迭代的过程(Tuia等,2009;Demir等,2011)。这里选择样本的依据有两个:不确定性(uncertainty)准则及相异性(diversity)准则。不确定性准则基于对未标记样本的信息度来度量,未标记样本的不确定性越大,说明对样本的分类越是不准,对下次的分类越是有信息量的;具体的不确定准则根据不同的分类方法,有不同的构造方法。为了保证批处理模式的主动学习所选择的多个样本在足够有信息量的前提下不是相似冗余的样本,还需要这些样本之间有足够的“不同”,以便能给分类模型提供更多的信息。这种批处理模式的主动学习过程中样本之间的“不同”的度量,就是样本的相异性准则。至此结合具体的分类器,样本的不确定性和相异性都是可以定量衡量的,如结合SVM的主动学习分类器的算法有MS(Margin Sampling)类(Tong和Koller,2000; Huo和Tang,2014; Settles,2010)等。主动学习算法中用到的各种选择样本的策略可以参考Settles(2010)的综述文章。
同时,半监督学习(Yarowsky,1995;)采用完全不同的方法试图解决同一个问题,它将未标记样本中认为预测标记置信度最高的样本加入到训练样本中去,迭代训练分类的过程。这与主动学习中选择不确定性最大的样本进行询问用户确定类别,是完全不同的思路(Settles,2010)。
近些年,随着机器学习技术的进一步发展,学习模型从浅层模型发展到深度学习,浅层学习如支持向量机SVM(Support Vector Machines)、Boosting、最大熵方法,这些模型结构基本上可以看成带有一层隐层节点或没有隐层节点的模型(余凯 等,2013)。而有很多隐层的人工神经网络具有优异的特征学习能力,学习得到的特征对数据有更本质的刻划,更加有利于分类。
从特征学习角度看,浅层模型的一个重要特点是靠人工经验来抽取样本的特征,分类模型一旦确定,特征的好坏是分类精度的瓶颈。因此结合图像分割技术,研究更好的类别表示特征,是很多遥感图像分类的主要工作之一(Benz等,2004;Camps-Valls等,2006)。
深度学习的实质,是通过构建具有隐层机器学习模型和海量的训练数据,学习更有用的特征,最终提升分类或预测的准确性。“深度模型”是手段,“特征学习”是目的。区别于浅层学习,深度学习的不同在于:(1)强调了模型结构的深度,通常有5层、6层、甚至10多层的隐层节点;(2)明确突出了特征学习的重要性,即通过逐层特征变换,将样本在原空间的特征表示变换到一个新特征空间,使分类或预测更加容易。与人工规则构造特征的方法相比,自学习的特征,更能够刻画数据的丰富内在信息,避免了人工特征抽取的时间消耗,大大提升了准确性。深度神经网络在训练上的难度,可通过“逐层初始化”(layer-wise pre-training)有效克服,逐层初始化通过无监督学习实现。其中卷积神经网络CNN(Convolution Neural Networks)是适合图像分类识别的网络结构,它的权值共享网络结构降低了网络模型的复杂度,减少了权值的数量;而图像或训练样本子图像可以直接作为网络输入,在网络结构中进行非监督特征学习;卷积网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。
作为新的方法,目前深度学习在遥感图像分类中并未有广泛应用,相信很快会有大量应用出现,大大提高遥感图像分类的精度。
用深度模型进行遥感图像分类,首先面临的问题是:对训练样本集有怎样的要求;深度模型有非常好的可表示性,但可表示性不代表可学习性,需要多少训练样本才能学习到足够好的深度模型,这也是深度学习目前没有解决的理论问题之一(余凯 等,2013)。结合深度学习方法的框架,对于训练样本集的构建,目前可采用通用的原则:
(1) 尽可能选择具有信息量大的、具有代表性的类别数据作为训练样本,必要时与主动学习相结合,增加同类样本的相异性,增加样本的数量。深度学习模型涉及上万特征,直观上需要大量的样本以避免过拟合。如果数据量不够或代表数据不足,得到的模型不容易形成对整个数据的描述,泛化能力不够,就是过拟合。
(2) 尽可能多地收集样本的好处:如果不知道哪些是具有代表性的数据,增加训练数据样本,包含代表性数据的概率自然增加;足够大的样本数据集可能会覆盖所有可能的情况,令每种情况总能找到一个或多个相同或相近的样本,当样本数据多到能对问题的样本空间进行充分覆盖,从而减弱对理论和模型的依赖时,这样的样本数据就足够大了。
5 结语
建立更加严格、细致精确的几何成像模型获得更高精度更自动化的正射校正影像仍然是几何校正最关注的问题。不断研究细化不同电磁波段的成像机理,建立精确的辐射校正模型,获得精确地表物理生化参量也仍然是遥感的辐射处理研究最关注的问题;以训练样本为媒介,不断提高类别特征表达能力和分类器识别能力,对地表覆盖和土地利用进行适宜于应用的分类,也仍然是图像分类所关注的。这些是几何校正、辐射校正、图像分类本身技术发展需要进一步得到发展的。
但随着遥感技术的快速发展,遥感以其宏观、快速提供全球和区域地表信息的优势,在全球变化研究中起着越来越重要、不可或缺的作用。遥感数据作为增长最快的一类数据,已在全球现有数据中至少占有一半的份额,而这些由多种卫星传感器在不同的时间、空间获得的数据,区域级的综合应用前首先要解决问题就是不同数据时空对齐、属性对齐的问题。对齐是要有基准的,本文给出的利用某种不变特征点集作为控制数据集实现时空对齐、属性对齐的统一框架,该框架将图像间的几何空间、辐射值空间和类别属性值空间的对齐,纳入到一起,提供了一种间接快速处理的手段和理念,这对大数据时代遥感图像的快速处理和信息挖掘将发挥重要作用。
参考文献(References)
-
Aguilar W, Frauel Y, Escolano F, Martinez-Perez M E, Espinosa-Romero A, Lozano M A.2009.A robust graph transformation matching for non-rigid registration. Image and Vision Computing, 27 (7): 897–910. DOI: 10.1016/j.imavis.2008.05.004.
-
Barrow H G, Tenenbaum J M, Bolles R C and Wolf H C.1977.Parametric correspondence and chamfer matching:two new techniques for image matching//Proceedings of the 5th International Joint Conference in Artificial Intelligence.San Francisco, CA, USA:Morgan Kaufmann Publishers Inc.:659-663
-
Bay H, Tuytelaars T and Van Gool L.2006.SURF:speeded up robust features//Proceedings of the 9th European Conference on Computer Vision.Graz, Austria:Springer:404-417 [DOI:10.1007/11744023_32].
-
Belongie S, Malik J, Puzicha J.2002.Shape matching and object recognition using shape contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24 (4): 509–522. DOI: 10.1109/34.993558.
-
Benz U C, Hofmann P, Willhauck G, Lingenfelder I, Heynen M.2004.Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS Journal of Photogrammetry and Remote Sensing, 58 (3/4): 239–258. DOI: 10.1016/j.isprsjprs.2003.10.002.
-
Berger H F.1989.Multi-temporal analysis of forest areas in the surroundings of Innsbruck, Austria//Guyenne T D, Calabresi G, eds.European Coordinated effort for Monitoring the Earth's Environment:A Pilot Project Campaign on Landsat Thematic Mapper Applications.Noordwijk, Netherlands:ESA Publications Division:293-298
-
Camps-Valls G, Gomez-Chova L, Muñoz-Marí J, Vila-Frances J, Calpe-Maravilla J.2006.Composite kernels for hyperspectral image classification. IEEE Geoscience and Remote Sensing Letters, 3 (1): 93–97. DOI: 10.1109/LGRS.2005.857031.
-
Canty M J, Nielsen A A.2008.Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted MAD transformation. Remote Sensing of Environment, 112 (3): 1025–1036. DOI: 10.1016/j.rse.2007.07.013.
-
Caselles V, García M J L.1989.An alternative simple approach to estimate atmospheric correction in multitemporal studies. International Journal of Remote Sensing, 10 (6): 1127–1134. DOI: 10.1080/01431168908903951.
-
Chandelier L, Martinoty G.2009.A radiometric aerial triangulation for the equalization of digital aerial images and orthoimages. Photogrammetric Engineering & Remote Sensing, 75 (2): 193–200. DOI: 10.14358/PERS.75.2.193.
-
Chen J, Chen J, Liao A P, Cao X, Chen L J, Chen X H, He C Y, Han G, Peng S, Lu M, Zhang W W, Tong X H, Mills J.2015.Global land cover mapping at 30 m resolution:a POK-based operational approach. ISPRS Journal of Photogrammetry and Remote Sensing, 103 : 7–27. DOI: 10.1016/j.isprsjprs.2014.09.002.
-
Chen Q S, Defrise M, Deconinck F.1994.Symmetric phase-only matched filtering of Fourier-Mellin transforms for image registration and recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 16 (12): 1156–1168. DOI: 10.1109/34.387491.
-
De Castro E, Morandi C.1987.Registration of translated and rotated images using finite Fourier transforms. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-9 (5): 700–703. DOI: 10.1109/TPAMI.1987.4767966.
-
Demir B, Persello C, Bruzzone L.2011.Batch-mode active-learning methods for the interactive classification of remote sensing images. IEEE Transactions on Geoscience and Remote Sensing, 49 (3): 1014–1031. DOI: 10.1109/TGRS.2010.2072929.
-
Du Y, Teillet PM, Cihlar J.2002.Radiometric normalization of multitemporal high-resolution satellite images with quality control for land cover change detection. Remote Sensing of Environment, 82 (1): 123–134. DOI: 10.1016/S0034-4257(02)00029-9.
-
Eckhardt D W, Verdin J P, Lyford G R.1990.Automated update of an irrigated lands GIS using SPOT HRV imagery. Photogrammetric Engineering and Remote Sensing, 56 (11): 1515–1522.
-
Elvidge C D, Yuan D, Weerackoon R D, Lunetta R S.1995.Relative radiometric normalization of Landsat Multispectral Scanner (MSS) data using an automatic scattergram-controlled regression. Photogrammetric Engineering & Remote Sensing, 61 (10): 1255–1260.
-
Freeman W T, Adelson E H.1991.The design and use of steerable filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13 (9): 891–906. DOI: 10.1109/34.93808.
-
Gong P, Wang J, Yu L, Zhao Y C, Zhao Y Y, Liang L, Niu Z G, Huang X M, Fu H H, Liu S, Li C C, Li X Y, Fu W, Liu C X, Xu Y, Wang X Y, Cheng Q, Hu L Y, Yao W B, Zhang H, Zhu P, Zhao Z Y, Zhang H Y, Zheng Y M, Ji L Y, Zhang Y W, Chen H, Yan A, Guo J H, Yu L, Wang L, Liu X J, Shi T T, Zhu M H, Chen Y L, Yang G W, Tang P, Xu B, Giri C, Clinton N, Zhu Z L, Chen J, Chen J.2013.Finer resolution observation and monitoring of global land cover:first mapping results with Landsat TM, ETM+data. International Journal of Remote Sensing, 34 (7): 2607–2654. DOI: 10.1080/01431161.2012.748992.
-
Hall F G, Strebel D E, Nickeson J E, Coetz S J.1991.Radiometric rectification:toward a common radiometric response among multidate, multisensor images. Remote Sensing of Environment, 35 (1): 11–27. DOI: 10.1016/0034-4257(91)90062-B.
-
Hansen M C, Potapov P V, Moore R, Hancher M, Turubanova S A, Tyukavina A, Thau D, Stehman S V, Goetz S J, Loveland T R, Kommareddy A, Egorov A, Chini L, Justice C O, Townshend J R G.2013.High-resolution global maps of 21st-century forest cover change. Science, 342 (6160): 850–853. DOI: 10.1126/science.1244693.
-
Hu C M, Tang P.2012.Automatic algorithm for relative radiometric normalization of data obtained from Landsat TM, HJ-1A/B charge-coupled device sensors. Journal of Applied Remote Sensing, 6 (1): 063509 DOI: 10.1117/1.JRS.6.063509.
-
Hu C M, Zhang W, Feng Z, Tang P.2014.Landsat TM/ETM+and HJ-1A/B CCD data automatic relative radiometric normalization and accuracy verification. Journal of Remote Sensing, 18 (2): 268–286. DOI: 10.11834/jrs.20143225. ( 胡昌苗, 张微, 冯峥, 唐娉. 2014. Landsat TM/ETM+与HJ-1A/B CCD数据自动相对辐射处理及精度验证. 遥感学报, 18 (2): 268–286. DOI: 10.11834/jrs.20143225. )
-
Huo L Z, Tang P.2014.A batch-mode active learning algorithm using region-partitioning diversity for SVM classifier. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (4): 1036–1046. DOI: 10.1109/JSTARS.2014.2302332.
-
Izadi M, Saeedi P.2012.Robust weighted graph transformation matching for rigid and Nonrigid image registration. IEEE Transactions on Image Processing, 21 (10): 4369–4382. DOI: 10.1109/TIP.2012.2208980.
-
Ke Y and Sukthankar R.2004.PCA-SIFT:a more distinctive representation for local image descriptors//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington, DC, USA:IEEE:Ⅱ-506-Ⅱ-513 [10.1109/CVPR.2004.1315206].
-
Kennedy R E, Cohen W B, Schroeder T A.2007.Trajectory-based change detection for automated characterization of forest disturbance dynamics. Remote Sensing of Environment, 110 (3): 370–386. DOI: 10.1016/j.rse.2007.03.010.
-
Kim S, Yoon K J and Kweon I S.2006.Object recognition using a generalized robust invariant feature and gestalt's law of proximity and similarity//Proceedings of the 2006 Conference on Computer Vision and Pattern Recognition Workshop (CVPRW'06).New York, NY, USA:IEEE:193 [DOI:10.1109/CVPRW.2006.146].
-
Koenderink J J, Van Doorn A J.1987.Representation of local geometry in the visual system. Biological Cybernetics, 55 (6): 367–375. DOI: 10.1007/BF00318371.
-
Lazebnik S, Schmid C and Ponce J.2004.Semi-local affine parts for object recognition//Proceedings of the British Machine Vision Conference.Kingston, United Kingdom:BMVA Press:779-788 [DOI:10.5244/C.18.98].
-
Lindeberg T. Scale-Space Theory in Computer Vision. US: Springer 1994 .
-
Lindeberg T.1998.Feature detection with automatic scale selection. International Journal of Computer Vision, 30 (2): 79–116. DOI: 10.1023/A:1008045108935.
-
Lindeberg T.2012.Scale invariant feature transform. Scholarpedia, 7 (5): 10491 DOI: 10.4249/scholarpedia.10491.
-
Lindeberg T.2013.Scale selection properties of generalized scale-space interest point detectors. Journal of Mathematical Imaging and Vision, 46 (2): 177–210. DOI: 10.1007/s10851-012-0378-3.
-
Lindeberg T.2015.Image matching using generalized scale-space interest points. Journal of Mathematical Imaging and Vision, 52 (1): 3–36. DOI: 10.1007/s10851-014-0541-0.
-
Lowe D G.1999.Object recognition from local scale-invariant features//Proceedings of the 7th IEEE International Conference on Computer Vision.Kerkyra:IEEE:1150-1157 [10.1109/ICCV.1999.790410].
-
Lowe D G.2004.Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 60 (2): 91–110. DOI: 10.1023/B:VISI.0000029664.99615.94.
-
Lucchese L, Doretto G, Cortelazzo G M.2002.A frequency domain technique for range data registration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24 (11): 1468–1484. DOI: 10.1109/TPAMI.2002.1046160.
-
Lucieer A, Robinson S and Turner D.2011.Unmanned Aerial Vehicle (UAV) Remote Sensing for Hyperspatial Terrain Mapping of Antarctic Moss Beds based on Structure from Motion (SfM) point clouds.Arko Lucieer
-
Mikolajczyk K, Schmid C.2005.A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27 (10): 1615–1630. DOI: 10.1109/TPAMI.2005.188.
-
Moravec H P.1981.Rover visual obstacle avoidance//Proceedings of the 7th International Joint Conference on Artificial Intelligence.San Francisco, CA, USA:Morgan Kaufmann Publishers Inc.:785-790
-
Nielsen A A, Conradsen K, Simpson J J.1998.Multivariate Alteration Detection (MAD) and MAF Postprocessing in Multispectral, Bitemporal image data:new approaches to change detection studies. Remote Sensing of Environment, 64 (1): 1–19. DOI: 10.1016/S0034-4257(97)00162-4.
-
Nielsen A A.2011.Kernel maximum autocorrelation factor and minimum noise fraction transformations. IEEE Transactions on Image Processing, 20 (3): 612–624. DOI: 10.1109/TIP.2010.2076296.
-
Rangarajan A, Chui H, Duncan J S.1999.Rigid point feature registration using mutual information. Medical Image Analysis, 3 (4): 425–440. DOI: 10.1016/S1361-8415(99)80034-6.
-
Reddy B S, Chatterji B N.1996.An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Transactions on Image Processing, 5 (8): 1266–1271. DOI: 10.1109/83.506761.
-
Reinhard E, Adhikhmin M, Gooch B, Shirley P.2001.Color transfer between images. IEEE Computer Graphics and Applications, 21 (5): 34–41. DOI: 10.1109/38.946629.
-
Rosenfeld A, Kak A C. Digital Picture Processing, Vol.I and Ⅱ. Orlando, FL: Academic Press 1982 .
-
Schaffalitzky F and Zisserman A.2002.Multi-view matching for unordered image sets, or ""How Do I Organize My Holiday Snaps?""//Proceedings of the 7th European Conference on Computer Vision.Copenhagen, Denmark:Springer:414-431 [10.1007/3-540-47969-4_28].
-
Schott J R, Selvaggio C, Volchok W J.1988.Radiometric scene normalization using pseudoinvariant features. Remote Sensing of Environment, 26 (1): DOI: 10.1016/0034-4257(88)90116-2.
-
Schroeder T A, Cohen W B, Song C H, Canty M J, Yang Z Q.2006.Radiometric correction of multi-temporal Landsat data for characterization of early successional forest patterns in western Oregon. Remote Sensing of Environment, 103 (1): 16–26. DOI: 10.1016/j.rse.2006.03.008.
-
Settles B. Active Learning Literature Survey. Madison: University of Wisconsin 2010 .
-
Shan X J, Tang P, Hu C M, Tang L, Zheng K.2014.Automatic geometric precise correction technology and system based on hierarchical image matching for HJ-1A/B CCD images. Journal of Remote Sensing, 18 (2): 254–266. DOI: 10.11834/jrs.20143220. ( 单小军, 唐娉, 胡昌苗, 唐亮, 郑柯. 2014. 图像分层匹配的HJ-1A/B CCD影像自动几何精校正技术与系统实现. 遥感学报, 18 (2): 254–266. DOI: 10.11834/jrs.20143220. )
-
Smith S M, Brady J M.1997.SUSAN-a new approach to low level image processing. International Journal of Computer Vision, 23 (1): 45–78. DOI: 10.1023/A:1007963824710.
-
Svedlow M, McGillem C D and Anuta P E.1976.Experimental examination of similarity measures and preprocessing methods used for image registration//Symposium on Machine Processing of Remotely Sensed Data.Indiana:Purdue University:4A-9-4A-17
-
Tang P, Zhang H W, Zhao Y C, Niu Z G, Zhong B, Hu C M, Shan X J.2014.Practice and thoughts of the automatic processing of multispectral images with 30 m spatial resolution on the global scale. Journal of Remote Sensing, 18 (2): 231–253. DOI: 10.11834/jrs.20143287. ( 唐娉, 张宏伟, 赵永超, 牛振国, 仲波, 胡昌苗, 单小军. 2014. 全球30 m分辨率多光谱影像数据自动化处理的实践与思考. 遥感学报, 18 (2): 231–253. DOI: 10.11834/jrs.20143287. )
-
Thévenaz P and Unser M.1998.An efficient mutual information optimizer for multiresolution image registration//Proceedings of the 1998 International Conference on Image Processing.Chicago, IL:IEEE:833-837 [10.1109/ICIP.1998.723645].
-
Toews M and Wells W.2009.SIFT-Rank:ordinal description for invariant feature correspondence//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Miami, FL:IEEEL 172-177 [10.1109/CVPR.2009.5206849].
-
Tong S and Koller D.2000.Support vector machine active learning with applications to text classification//Proceedings of the 17th International Conference on Machine Learning (ICML-00).Stanford, California:Morgan Kaufmann:287-295
-
Trajković M, Hedley M.1998.Fast corner detection. Image and Vision Computing, 16 (2): 75–87. DOI: 10.1016/S0262-8856(97)00056-5.
-
Tuia D, Ratle F, Pacifici F, Kanevski M F, Emery W J.2009.Active learning methods for remote sensing image classification. IEEE Transactions on Geoscience and Remote Sensing, 47 (7): 2218–2232. DOI: 10.1109/TGRS.2008.2010404.
-
Van Gool L, Moons T and Ungureanu D.1996.Affine/photometric invariants for planar intensity patterns//Proceedings of the F 4th European Conference on Computer Vision.Cambridge, UK:Springer:642-651 [10.1007/BFb0015574].
-
Viola P, Wells W M.1997.Alignment by maximization of mutual information. International Journal of Computer Vision, 24 (2): 137–154. DOI: 10.1023/A:1007958904918.
-
Wang B Y, Yu Y Z, Xu Y Q.2011.Example-based image color and tone style enhancement. ACM Transactions on Graphics (TOG), 30 (4): DOI: 10.1145/2010324.1964959.
-
Yarowsky D.1995.Unsupervised word sense disambiguation rivaling supervised methods//Proceedings of the 33rd Annual Meeting of the Association for Computational Linguistics.Stroudsburg, PA, USA:Association for Computational Linguistics:189-196 [10.3115/981658.981684].
-
Yu K, Jia L, Chen Y q, Xu W.2013.Deep Learning:Yesterday, Today, and Tomorrow. Journal of Computer Research and Development, 50 (9): 1799–1804. ( 余凯, 贾磊, 陈雨强, 徐伟. 2013. 深度学习的昨天、今天和明天. 计算机研究与发展, 50 (9): 1799–1804. )
-
Yu X M, Chen Y H.2007.Relative radiometric normalization of remotely sensed images based on improved automatic scattergram-controlled regression. Optical Technique, 33 (2): 185–188. ( 余晓敏, 陈云浩. 2007. 基于改进的自动散点控制回归算法的遥感影像相对辐射归一化. 光学技术, 33 (2): 185–188. )
-
Zhang J X, Ma R J.2000.Control Point Data Base for Graph and Imagery and its Application. Bulletin of Surveying And Mapping (1): 15–17. ( 张继贤, 马瑞金. 2000. 图形图像控制点库及应用. 测绘通报 (1): 15–17. )
-
Zhao Y Q, Shan X J, Tang P.2014.Spatial Consistency Analysis and Relative Geometric Correction of Low Spatial Resolution Multi-source Remote Sensing Data. Remote Sensing Technology and Application, 29 (1): 155–163. DOI: 10.11873/j.issn.1004-0323.2014.1.0155. ( 赵涌泉, 单小军, 唐娉. 2014. 低空间分辨率多源遥感数据的空间一致性分析和相对几何校正. 遥感技术与应用, 29 (1): 155–163. DOI: 10.11873/j.issn.1004-0323.2014.1.0155. )
-
Zhong B, Zhang Y H, Du T T, Yang A X, Lv W B, Liu Q H.2014.Cross-calibration of HJ-1/CCD over a desert site using Landsat ETM+imagery and ASTER GDEM product. IEEE Transactions on Geoscience and Remote Sensing, 52 (11): 7247–7263. DOI: 10.1109/TGRS.2014.2310233.