Print

出版日期: 2016-09-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20166050
2016 | Volumn20 | Number 5





                              上一篇|





下一篇
论文
高光谱图像稀疏信息处理综述与展望
expand article info 张良培1 , 李家艺1,2
1. 武汉大学 测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
2. 武汉大学 遥感信息工程学院, 湖北 武汉 430079
收稿日期: 2016-06-13; 修改日期: 2016-06-07; 优先数字出版日期: 2016-09-25
基金项目: 国家自然科学基金重点项目(编号： 41431175)
第一作者简介: 张良培(1962-), 男, 武汉大学教育部"长江学者"特聘教授, 研究方向为测绘、遥感图像处理、人工智能、模式识别等。E-mail:zlp62@whu.edu.cn
中图分类号: TP701
文献标识码: A
文章编号: 1007-4619(2016)05-1091-11

摘要

高光谱成像技术具有光谱连续、图谱合一，能够以较高的光谱诊断能力对地物目标进行精细化解译，可以大幅增强地物信息的提取能力。充分利用高光谱遥感图像丰富的空间、谱信息，进行观测目标地物的精细化解译，成为近年来遥感领域的研究热点和前沿领域，并在多个相关领域具有巨大的应用价值和广阔的发展前景。本文结合高光谱图像成像特点，对基于稀疏表示理论的高光谱图像处理与分析方法进行综述，概括了高光谱图像处理与分析主要研究，并对各个研究领域与方向进行分析和评价，最后对各研究领域发展提出建议和展望。

关键词

高光谱图像处理与分析 , 稀疏表示 , 高维信号处理 , 图像质量改善 , 影响分类

Development and prospect of sparse representation-based hyperspectral image processing and analysis
expand article info ZHANG Liangpei1 , LI Jiayi1,2
1.State Key Laboratory of Information and Engineering in Surveying, Mapping and Remote Sensing Wuhan University, Wuhan 430079, China
2.School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China

Abstract

Hyperspectral images, which span the visible to infrared spectrum with hundreds of contiguous and narrow spectral bands, are advantageous because of their subtle discriminative spectral characteristics. Owing to the fine spectral differences between various materials of interest, hyperspectral images support improved interpretation capabilities, and they perform important functions in various fields, such as the military, precision agriculture, and mineralogy. The sparsity of signals is a powerful and promising statistical signal modeling tool for hyperspectral image processing and analysis because signals can be compactly represented by only a few coefficients that carry the most important information in a certain basis or dictionary. A full diagram of Sparse Representation (SR) consists of sparse coding (regression) and dictionary learning. A brief review about this basic theory from the perspective of hyperspectral remote sensing is presented in the second section. With various forms of complex degradation and the demand for resolution enhancement considered, basic theories as well as recent studies in the area of hyperspectral image processing, including denoising, unmixing, super-resolution, and spectral-spatial image fusion in an SR manner, are presented in the third section. Dimensional reduction, classification, target detection, and anomaly detection, which are aimed at mining subtle diagnostic information on hyperspectral images in an SR manner, are also reviewed in the hyperspectral image analysis section. This review is followed by some suggestions and remarks on SR-based hyperspectral image processing and analysis. Processing literature considers denoising as the most fundamental task, single image super-resolution as problematic, and hyperspectral unmixing and spectral-spatial fusion as necessary subjects. In the hyperspectral analysis area, classification and detection are the most important tasks, and feature extraction/dimensional reduction works as a meaningful pre-processing step. The research on SR-based hyperspectral processing and analysis has recently attained some achievements. However, the obstacles mentioned in this paper still require further study. This review also presents several important remarks and outlines the future directions in this field. First, despite the increasing research on hyperspectral signal recovery and reconstruction, single image super-resolution and multi-resolution image fusion remain a problem area, mainly because of the limited availability of prior information within the remote sensing data and because of unstable sparse inverse optimization. Thus, the method for qualified over-completed dictionary design for specific hyperspectral image processing and delicate inverse optimization is an important study area. Second, the most important issue for hyperspectral image information extraction comes in the form of a discriminative dictionary. Most research ideas on hyperspectral target detection involve multiple sparse representation classification-based model simplification, whereas the anomaly detection method relies on the quality of the local ambient dictionary. Thus, the detection area should be studied further. In addition, reasonable approximated sparse coding combined with specific dictionary learning and some unique characteristics of hyperspectral images, such as manifold structure, multi-modality, and low rank property, should be regarded as useful tools for future research.

Key words

hyperspectral image processing and analysis , sparse representation , disposal of high dimension , improving the quality of image ,

1 引言

高光谱遥感技术是20世纪80年代以来综合对地观测的重要组成部分，也是国际对地观测技术竞争的制高点之一。作为研究热点和前沿领域，据统计，过去10年来国际权威期刊上关于高光谱遥感信息处理与应用以每年15%的速度增长。高光谱传感器在紫外、可见光、近红外和中红外等大量电磁波段获取近似连续的地物光谱曲线，将反映地物反射特性的光谱信息与反映地物空间位置关系的图像信息结合在一起，更为有效地对地物进行解译。然而，作为一种典型的超高维数据，高光谱信号处理面临如何从海量高维数据中挖掘出感兴趣地物诊断性信息的瓶颈问题，严重制约高光谱图像应用。

近几年来，稀疏表示作为一种新型的数据挖掘技术，利用海量高维数据的高冗余性与感兴趣信号的稀疏性，能够有效提取出高光谱地物信息(Chen等，2011b；Bioucas-Dias等，2012；Qian和Ye，2013；Zhao等，2011；Li等，2015b)。然而，早在20世纪70年代，信号处理领域已经出现了稀疏性的概念。当时诸如快速傅里叶变换、Karhunen-Loeve Transform(KLT)等方法均是基于线性变换的方法。直到20世纪90年代，基可变理论的引入使得稀疏表示往前迈进了一大步(Olshausen和Field，1997)。最近几年，稀疏表示SR(Sparse Representation)理论基于少数可压缩信号的线性预测包含足够的信息进行重建和处理(Candes和Tao, 2005, 2006)，因其不依赖传统Shannon Nyquist采样定律和高精度重建性能而迅速成为新型信号表达和图像处理方法，在信号压缩、图像质量改善、影像分类等领域得到广泛应用(Kulkarni等，2012；Li等，2014c；Lustig等，2007)。利用高光谱图谱合一的特性不仅能挖掘地物空间分布排列的稀疏性，谱间高相关性能够进一步助力地物稀疏信息挖掘，有其得天独厚的优势。考虑到由于传感器设计时空、谱高分辨率观测不能兼得，精细的光谱谱段更易受成像条件影响等问题，高光谱图像稀疏信息处理领域中存在大量技术难题有待攻关。近10年来，虽然基于稀疏表示技术的高光谱信号处理与应用取得了一定的研究进展，但系统的总结、分析与评价仍然相对欠缺。有鉴于此，本文首次系统阐述了基于稀疏表示理论的高光谱遥感图像信号恢复与重建、影像处理与分析，综述了国内外研究成果，依次进行分析和评价并提出建议和展望。

2 稀疏表示背景知识

稀疏表示理论认为，对于给定字典，每个信号都可以利用字典中的少数基元线性表达，如图 1所示。因此，如何设计一个过完备字典，并通过稀疏编码，获得每个信号的稀疏表示向量是稀疏表示的目的。稀疏表示中的字典和稀疏编码具有过完备性、自适应性和非局部选择性等特点。过完备性是指无需字典中所有基元即可实现任何信号的高保真重建。自适应性是指在过完备字典下的稀疏编码具有良好的信号匹配性。非局部选择性是指通过惩罚被激活字典基的个数保证与待表示信号相关的有限个字典原子被选中。


图 1 稀疏表示示意图
Fig. 1 Diagram of sparse representation

2.1 过完备字典

稀疏表示的关键问题是字典获取。现有字典大致可分为3类：预设字典、自适应字典和基于学习的字典。预设字典针对某些特定影像类型设计，如小波基(Du和Fowler，2007；Bozchalooi和Liang，2007)、轮廓波(Do和Vetterli，2005)等，较适用于程式化的卡通人物表示。自适应字典使用特定参数调控字典基元，其中较为典型的包括小波包(Sun和Chang，2002)和条带波(Le Pennec和Mallat，2005)。这两类字典变换速度快，但是表示过程的稀疏性与应用的泛化性能都具有明显局限(Elad和Bruckstein，2002)。基于学习的字典则通过学习样例集来保持与实际应用的高相关性(Kreutz-Delgado等，2003)，摆脱了前面两类字典从理论模型出发的构造方式，转而从待表示数据出发，寻求与待表示数据相关且完备的字典基元。该类字典灵活性大、表示性能好、但计算量大，需要根据具体的任务进行学习(Mairal等，2010)。在高光谱图像处理分析中，字典学习因具体任务设定可分为基于重建的字典学习和监督字典学习两类。基于重建的字典学习旨在找到高精度紧致表示所有训练样本的相互不相关的基元(Aharon等，2006)，监督字典学习在满足基于重建字典学习的目的基础上，要进一步挖掘字典基元组的判别特性(Mairal等，2009)。

2.2 稀疏编码

通过简洁的数学语言来建模，可以一窥稀疏编码的本质：

$ \min {\left\| {\boldsymbol \alpha} \right\|_0}\;\;\;\;\;{\rm{s}}.{\rm{t}}.\;\;{\boldsymbol x} = {\boldsymbol {D}} {\boldsymbol \alpha} $ (1)

式中，α为稀疏系数向量，D是过完备字典，X是重构信号，${\ell _0}$范数用来统计向量α中非零元的个数。考虑计算误差及噪声的影响，实际应用中常用二次罚函数进行等式逼近。经证明，式(1)是NP难问题(Elad和Bruckstein，2002)，其求解方式是稀疏表示理论的一大研究热点和难点。稀疏求解算法主要分为两种类型：贪婪法(Tropp，2004)和范数凸松弛法(Bruckstein等，2009)。

贪婪法首先确定解向量的支持集，然后直接利用最小二乘优化形式在支撑集上求解α。由于支持集是离散的，其计算方法也是离散的。正交匹配跟踪算法OMP(Orthogonal Matching Pursuit) (Tropp和Gilbert，2007)是贪婪算法中一种最为典型的算法，已经被广泛应用于高光谱稀疏表示分析中(Chen等，2011a；Zhang等，2015b)。此外，从算法精度、复杂度出发，相当多基于OMP的变体也得到广泛的研究，甚至有些算法在其他领域得到了新的应用和发展(Chen等，2011a；Rubinstein等，2008；Tropp等，2006)。

范数凸松弛法不关注支持集，而是把未知数$\boldsymbol \alpha \in {{\rm{R}}^h}$当作一个待求的向量，使用连续凸函数松弛罚函数${\left\| {\boldsymbol \alpha } \right\|_0}$，将原始非凸问题转化成凸优化问题进行求解。该类方法中的一种典型例子是迭代重加权最小二乘方法替换${\ell _0}$范数FOCUSS(FOCal Under-determined System Solver)方法(Gorodnitsky和Rao，1997)，将原问题转化为加权最小二乘的形式。另一种典型算法将非凸${\ell _0}$范数松弛为${\ell _1}$优化问题(Shaobing和Donoho，1994)，其中最小化收缩与选择算法LASSO(Least Absolute Shrinkage and Selection Operator)是目前较为常用的算法之一，其算法精度和效率较高，具有广泛的应用价值。更多相关研究参见Hastie等人(2007)、Tibshirani(2011)、Efron等人(2004)，以及Lee等人(2006)的相关文献。

3 高光谱遥感图像恢复与重建

空间分辨率是衡量遥感影像质量的一个重要指标，它反应了图像上能看到的地面最小目标尺寸，决定了实际应用中地面小目标的识别能力。然而，高光谱成像系统的光谱带宽很窄，图像成像过程中源自于成像系统内外各种不可避免的干扰更为严重，因而高光谱图像光谱分辨率的提高往往以空间分辨率的下降为代价。空间分辨率的不足和自然界地物分布的复杂多样性等问题，导致高光谱遥感图像中普遍存在混合像元(Bioucas-Dias等，2012，2013)。混合像元问题是传统像元级分类和面积量测精度难以达到实际应用要求的主要原因。鉴于此，基于稀疏表示的高光谱图像恢复与重建(Willett等，2014)主要从噪声去除，混合像元分解、单源影像空间超分辨率增强和多源信息融合等方面展开研究。

3.1 稀疏性驱动去噪

Aharon等人(2006)提出基于重建的K-SVD字典学习方法，其基本原理是迭代稀疏编码(利用OMP求解)与字典更新(利用奇异值分解)过程通过保持影像主要成分来抑制噪声(Elad和Aharon，2006)，在自然影像处理中得到广泛研究和应用(Mairal等，2007；Dong等，2013)。在高光谱图像去噪中，顾及影像空间域的结构相似性和光谱域的高冗余性，可以对稀疏性驱动的噪声抑制进一步研究。Qian和Ye(2013)将高光谱图像立方体展开成块，挖掘空间结构自相似性，能够同时建模高斯噪声和泊松噪声。Zhao和Yang(2015)利用稀疏表示建模影像空间域全局冗余/相关性和光谱域的局部冗余/相关性，同时挖掘无噪影像的低秩性(Zhang等，2014b)，保持了高光谱图像合适的信噪比。

然而，由于高光谱传感器成像机理的复杂性，传感器每个波段所对应的探元独立工作，不同波段代表不同信息，不仅传感器接收到的反射强度与影像噪声所分布的强度不尽相同，每个波段所受到的噪声影响因素都有可能不同。这就可能导致了不同波段上不同强度的噪声和不同类型的噪声等复杂问题的混叠。如何准确地建模噪声类型(Yue等，2014)，建立自适应稀疏表示去噪模型，关联高光谱图像谱间相似性结构，依旧是高光谱稀疏去噪待解决的难点热点问题。

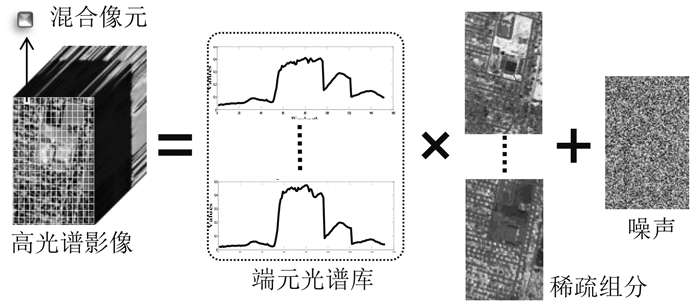
3.2 基于光谱库稀疏解混

由于高光谱遥感图像具有地物分布复杂、混合像元内部地物组成可变及地物同物异谱的特点，其本质上存在稀疏性，即端元光谱库中的端元个数一般远多于光谱波段数。因此，可以利用稀疏表示理论中的过完备字典思想构造出能够表征地物类别的过完备端元光谱库，从而借助该过完备的端元光谱库对高度混合的高光谱遥感图像进行有效表达。Iordache等人(2011a)提出了混合像元光谱稀疏分解(sparse unmixing)的理论与方法。如图 2所示，该方法首先构建纯净、完备的典型地物光谱库，以稀疏表示模型中的稀疏性限制实现端元光谱可变和混合像元内端元组成可变的有效约束，在丰度稀疏性、非负性与和为一性质驱动下，通过线性稀疏回归算法自动根据混合像元的光谱特征筛选最优端元子集，获得最终分解结果。


图 2 高光谱稀疏解混
Fig. 2 Diagram of hyperspectral sparse unmixing

由于有效地规避了纯净像元(Fu等，2015)缺失与端元估计(Xu等，2016)这两个高光谱混合像元分解的瓶颈问题，近几年基于稀疏表示的方法逐渐成为高光谱混合像元分解的热点研究方向(Bioucas-Dias等，2012)。但是，高光谱稀疏解混依旧存在以下问题：(1)过完备端元光谱库构造时的平台差异导致字典的可迁移性差。平台差异导致光谱库构造时无法避免大气辐射、地面高度、获取角度等不同成像环境带来的误差影响(Iordache等，2011a)，现有的观测手段或字典学习方式无法充分处理平台差异导致的误差影响(Fu等，2015)。(2)空间信息利用不足。虽然有学者提出了基于全变分正则化TV(Total Variation, Iordache等，2011b)的方法来促进同质区域光滑性，但此类空间一阶邻域方法会加剧空间过平滑现象。而空间结构自相似正则化(Zhong等，2014；Feng等，2015)虽然能利用空间高阶结构信息，但其高昂的计算代价制约了实际应用潜力。(3)端元光谱相似性过高造成稀疏求解不精确。针对此类问题虽然有学者利用协同稀疏表示模型优化求解过程(Iordache等，2014a)，但从逆问题求解模型优化的角度来看，上述过程并不能充分解决端元即字典基元相似性的问题。(4)端元同物异谱问题仍未完全解决。学者首先用子空间估计的方式从原始过完备光谱库中抽取多个潜在同物异谱端元(Iordache等，2014b)，提纯字典，提高计算效率，然而对于由场景差异、成像差异等造成的异谱问题仍然亟待研究。

3.3 单幅影像超分辨率重建

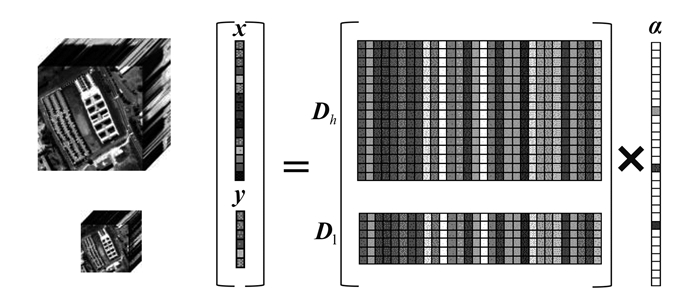
超分辨率重建分为多张影像重建和单幅影像重建，前者虽然发展较早，但由于需要单一地区同一时间多幅亚像素偏移的观测影像，性价比不高(Yuan等，2010)。相比之下，单幅影像超分辨率重建方法对物理要求较低，可以在任意已有传感器获得的影像上通过软件算法实现，逐渐成为影像超分辨率重建的主要研究方向(Tang等，2011；Yang等，2015)。其中，挖掘影像在跨空间尺度上的冗余性，使得基于稀疏表示的单幅影像超分辨率重建方法成为研究热点(Dong等，2011；Kim和Kwon，2010；Pan等，2013；Wu等，2016)。

近年来，基于稀疏学习的超分辨率重建方法按照字典构建方式可以分为基于外部数据字典训练和利用自身跨尺度相似性训练字典两种方式(图 3、图 4)。前者的优点是细节恢复能力强，缺点是需要外部训练数据且重建结果对于外部训练数据的质量和拟合程度有较大依赖(Yang等，2010，2012)，对于高光谱遥感图像而言，获取对传感器设计具有鲁棒性的高质量训练数据难度较大。利用自身数据训练字典的优点在于不依赖于任何外部数据，缺点是算法效果对影像自身自相似特征的显著程度比较依赖，且多尺度搜索时间代价比较大(Pan等，2013)。


图 3 基于耦合字典稀疏传递超分辨率重建
Fig. 3 Couple sparse representation based single image super-resolution


图 4 跨分辨率稀疏编码超分辨率重建
Fig. 4 Sparse representation based single image super-resolution by spatial relation mapping

按照学习的方式分类，单幅影像超分辨率重建又可以分为基于耦合字典隐式映射的方法和跨分辨率编码的方法。基于隐式映射的方法是从关联高低分辨率影像块投影到各自对应的字典上所得的稀疏表示系数之间是映射关系来实现影像超分辨率重构(Yang等，2012)。其研究重点主要在于高低分耦合字典的一一映射关系的强化。例如，有研究利用多特征描述耦合字典对方式加权映射关系(Wu等，2016)。将而基于直接映射的方式则是利用回归方法直接寻找低分辨率影像块到高分辨率影像块的映射函数(Zhao等，2011)。映射函数在基于给定的降至模型的基础上，通过图像先验信息挖掘来适应具体遥感场景地物分布，例如，有研究通过挖掘空间非局部先验约束稀疏逆问题求解，利用残差字典辅助高分字典稳定映射关系(Gou等，2014)。总之，在高光谱图像中，如何利用局部空间同质性约束映射关系以及如何利用光谱之间的冗余性来优化超分辨率重建过程，目前国内外研究还比较匮乏，具有较大的研究潜力和空间(Bioucas-Dias等，2013；Yang等，2015)。

3.4 空谱数据融合

空谱融合是将不同影像的空间和光谱信息结合从而得到同时具有高空间分辨率和高光谱分辨率影像的过程。空谱融合可以提高遥感影像空间分辨率、光谱分辨率，替代或者修补影像的缺陷；进而提升影像的解译能力与实际应用潜力，对军事侦察、生态环境评价、城市规划、地形图更新、地籍调查等具有重要应用价值。

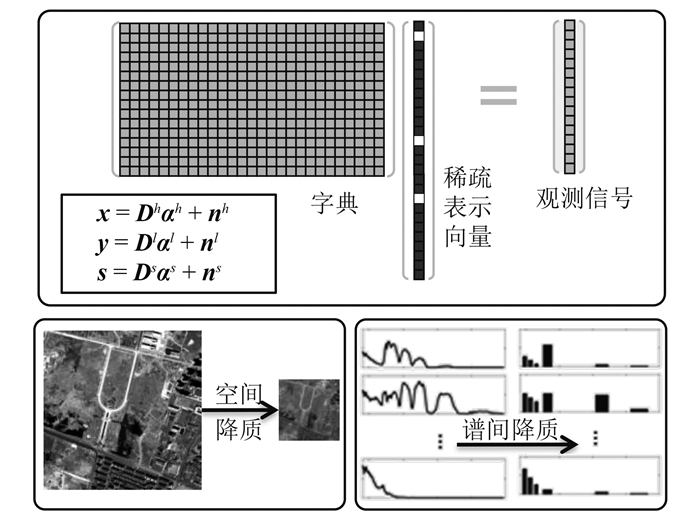
这类问题从单一平台搭载的高分辨率遥感影像全色增强发展而来，本文主要指的是全色/光谱影像和高光谱图像融合(Loncan等，2015；Yokoya等，2012)。受多源遥感数据分辨率差异过大、退化过程中信息损失严重以及光谱区间不一致等因素的影响，现有的融合方法均面临着重建影像的伪细节信息多的问题，限制了融合影像的进一步分析应用。从3.2节、3.3节中稀疏性驱动的混合像元分解和超分辨率重建的研究可以大胆预测，利用稀疏表示建立高光谱空谱数据融合将成为相当具有潜力的研究方向。

如图 5所示，这类方法将低空间分辨率高光谱图像和高空间分辨率影像分别视为高空间分辨率高光谱图像在空间维和光谱维降质模式下的结果，从而分别建立降至稀疏表示模型，关联降质过程中的映射关系，并添加先验约束，实现融合影像的复原(Wei等，2015)。在这类研究比较复杂，在考虑3.2节、3.3节应当需要注意的问题之外，对耦合稀疏逆问题求解精确、先验项建模合理性要求较高，对空/谱模式下耦合字典的构造与学习、隐式映射关联性待进一步深化研究，也是未来学科研究的难点所在。


图 5 空谱耦合稀疏融合
Fig. 5 Couple sparse representation for spectral-spatial image fusion

4 高光谱遥感图像分析

高光谱遥感图像所具有图谱合一性质，能够以较高的光谱诊断能力对地物目标进行精细分类与识别，大大增强了地物信息的提取能力。

4.1 谱稀疏驱动维度约减

高光谱图像信息量大，谱间相关性强，存在大量冗余信息。有研究表明，在不影响整体信息解译精度的前提下，高达90%的光谱波段是没有必要的(Chang，2007)。冗余信息的存在不仅会影响地物分类和探测的效果，同时也会增加数据处理的代价。因此，在地物解译之前，首先进行高光谱维度约减，减少冗余信息，提高计算效率，保留有价值的信息，具有实际应用意义。高光谱维数降低旨在保证解译性能的前提下利用尽可能少的特征，因此高光谱降维本质上也可以认为是一种稀疏学习过程。

一般来讲，降维算法研究分为两个方面：(1)特征选择，即直接从原始波段空间选择若干波段，约减之后的特征是原始高光谱特征的子集(Du等，2012)。该类方法能够有效地保持光谱波段的物理意义，但由于无法在有限的子集中灵活保持各波段的信息，目前国内外相关研究较少，主要集中在建模波段之间的相关性与稀疏性(Yuan等，2015a)。(2)特征提取，即原始高光谱特征通过一定的规则进行变换，在变换后特征中选择若干分量作为约减后特征(Zhang等，2014c)。利用高光谱局部波段相似性与稀疏主成分变换SPCA(Sparse Principle Component Analysis, Shen和Huang，2008)，有学者研究了组稀疏主成分变换(Khan等，2015)来保持原始光谱主要成分；利用稀疏表示构建图，应用稀疏子空间理论(Elhamifar和Vidal，2013；Soltanolkotabi等，2014；Yuan等，2015b)在高维空间中寻找保持信号本征结构所在低维子空间的稀疏保持投影算法SPP(Sparse Preser-vation Projection, Qiao等，2010)在高光谱图像降维中也得到发展，包括利用范数松弛(Ly等，2014)、半监督(Yan和Wang，2009)，监督信息嵌入(Hong和Mei，2015)等思想与SPP相结合。总的来讲，利用稀疏性驱动进行高光谱图像维数约减研究，已经成为业内的研究热点问题。

4.2 监督稀疏表示分类

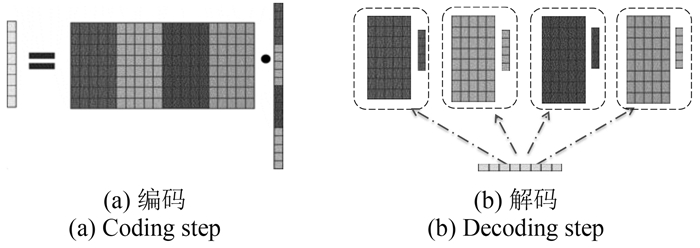
基于稀疏表示的高光谱图像分类器，其优越性主要表现在对当前待处理对象进行分类时，所有类别训练样本间的协同互助机制能够有效缓解高维度数据分析的小样本问题(Wright等，2009；Zhang等，2012)。稀疏表示学习包含编码和解码两个步骤。

如图 6所示，编码通过利用统一的过完备字典对待处理像素进行表示重构，能有效地解决过拟合问题。利用最优化算法获取表示系数，实现编码过程。解码过程与前述编码过程相对应，在各类别子字典张成的特征子空间中分别利用对应表示系数成分解码，对比各解码效果获取最终像素类别信息。依照训练样本的标记，前述的过完备字典能够灵活地分解为各类别的子字典，子字典在特征空间中张成的子空间能紧致重构该类别像素特征，而对其他类别特征的表示能力弱。


图 6 稀疏表示分类
Fig. 6 Diagram of sparse representation classification

然而，椒盐错分是像素级别的稀疏表示分类中不可避免的问题。为了缓解该类问题，国内外学者利用高光谱图像空间先验进行进一步深入研究。首先，在高光谱图像中通过邻域空间拉普拉斯算子与局部空间开窗扩展稀疏表示模型(Chen等，2011b)实现局部平滑(Li等，2014c)，利用非局部空间相关性(Zhang等，2014a)，结构形状先验(Fu等，2016)优化联合稀疏表示过程可以在一定程度上缓解过平滑现象。同时，顾及协同互助机制与稀疏性先验的研究(Li等，2014b)也成为研究热点。高光谱多模态多特征在类别判别层面的稀疏结构也逐渐成为研究热点(Li等，2014c，2015b；Zhang等，2015a)。此外，考虑到高光谱信号非线性可分性，核化算法也被进一步研究(Li等，2014a，2015a)。总之，虽然目前已经取得一定的成果，但是考虑到高光谱遥感图像同物异谱、异物同谱现象严重、地物分布复杂、空间尺度差异大、有标记样本少、噪声类型复杂多样等情况下，当前的影像分类研究仅能同时应对其中的部分问题，还难以自动化完成大面积地物识别的任务，高光谱图像稀疏表示分类研究依然是国际前沿热点问题。

4.3 目标稀疏驱动高光谱探测

高光谱图像光谱分辨率高，能够提供区分不同物质的诊断性光谱信息，结合精细光谱信息可提高对目标和背景进行定量分析的能力，因此高光谱目标检测技术在目标检测领域具有独特的优势。

按照感兴趣目标光谱信息使用层次分类，可以分为监督小目标分类和光谱异常检测。前者需要使用目标光谱信号的先验信息，常用的目标检测器假设高光谱数据服从多源正态分布，在地物类型较为复杂光谱混合现象严重的情况下，并不能很好地描述高光谱图像的统计特性。在基于稀疏表示的探测器中，可以把前述目标探测任务看做是二类分类问题，由二类稀疏表示分类问题演化为监督探测器(Chen等，2011c)，有效地提高了在复杂场景下的探测精度。在利用联合稀疏模型结合高光谱空间先验的情况下，探测器可以进一步抑制背景信息(Chen等，2011a；Huang等，2013)，获得空间平滑的探测结果。此外，也有学者考虑关联目标在遥感场景中稀疏存在的特性与统计假设来展开研究(Zhang等，2015b，2015c)，有效结合二者优势。

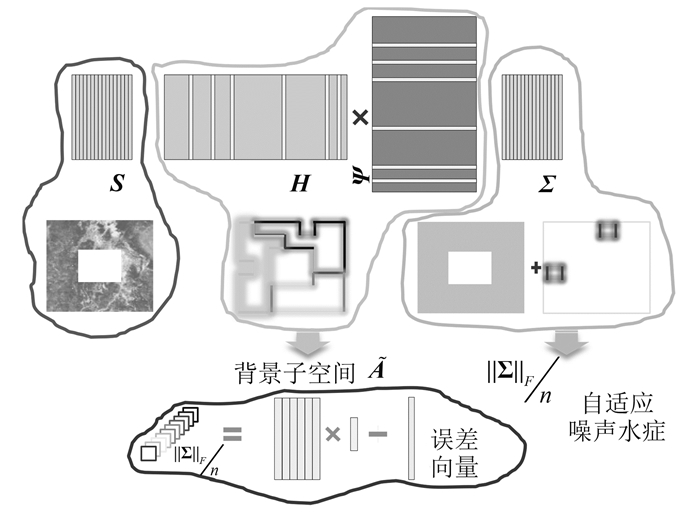
实际应用中由于缺少完备的光谱数据库，先验光谱信息的或缺使得目标字典获取变得非常困难。而异常探测算法不需要背景或者目标的先验光谱信息，具有较强的实用性(Matteoli等，2014)。由于可利用的先验信息较少，高光谱异常探测问题也是学科难点之一，特别在复杂地物分布，亚像元异常目标探测中亟待深入研究(Khazai等，2013)。如图 7所示，利用在全局构造候选字典基，在局部进行联合背景表示提纯背景字典，利用影像的低秩性和局部空间的相似性，基于稀疏驱动的异常探测能够在复杂的高光谱场景中灵活地抑制背景，同时自适应地估计局部干扰，实现异常目标甚至亚像元目标的检测(Li等，2015c)。


图 7 稀疏性驱动背景抑制的高光谱异常探测
Fig. 7 Joint sparsity driven background suppression for hyperspectral anomaly detection

5 结语

利用高光谱信号的稀疏特性，以及过完备字典将信号挖掘过程转化为基于优化计算的信号表示过程，本文对稀疏表示理论进行了描述，系统阐述了基于稀疏表示理论的高光谱遥感图像信号恢复与重建，影像处理与分析，综述了国内外研究成果，存在的公开问题及最新的相关理论。尽管目前高光谱信号处理基于稀疏表示的研究比较多，但笔者认为有以下几点内容可供读者参考：

(1)虽然目前基于信号恢复与重建的研究比较多，但是其中单幅影像超分辨率重建与空谱数据融合目前由于稀疏逆问题求解困难，可利用先验信息较少，成为研究难点。如何构造合适的过完备字典，钻研高精度的稀疏重建优化，实现信号的跨空/谱分辨率有效传递是值得考虑的研究角度。

(2)基于稀疏表示的高光谱分析研究主要问题即任务驱动的字典设计与学习。其中，目前的高光谱稀疏目标探测算法主要研究思路在于简化多类稀疏分类问题，而高光谱异常探测则依赖于局部字典、尚未实现模型的自动化学习。因此，相关领域也是值得进一步深入钻研的研究方向。

(3)在具体的研究方向与理论结合中，应注意合适的稀疏编码与字典学习优化算法的设计与应用；估计高光谱信号的流形结构、多态性与低秩性，联合高光谱信号先验性和稀疏性先验求解优化问题有望得到更好的结果。

参考文献(References)

  • Aharon M, Elad M, Bruckstein A.2006.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, 54 (11): 4311–4322. DOI: 10.1109/TSP.2006.881199.
  • Bioucas-Dias J M, Plaza A, Dobigeon N, Parente M, Du Q, Gader P, Chanussot J.2012.Hyperspectral unmixing overview:geometrical, statistical, and sparse regression-based approaches. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 5 (2): 354–379. DOI: 10.1109/JSTARS.2012.2194696.
  • Bioucas-Dias J M, Plaza A, Camps-Valls G, Scheunders P, Nasrabadi N M, Chanussot J.2013.Hyperspectral remote sensing data analysis and future challenges. IEEE Geoscience and Remote Sensing Magazine, 1 (2): 6–36. DOI: 10.1109/MGRS.2013.2244672.
  • Bozchalooi I S, Liang M.2007.A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection. Journal of Sound and Vibration, 308 (1/2): 246–267. DOI: 10.1016/j.jsv.2007.07.038.
  • Bruckstein A M, Donoho D L, Elad M.2009.From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Review, 51 (1): 34–81. DOI: 10.1137/060657704.
  • Candes E J, Tao T.2005.Decoding by linear programming. IEEE Transactions on Information Theory, 51 (12): 4203–4215. DOI: 10.1109/TIT.2005.858979.
  • Candes E J, Tao T.2006.Near-optimal signal recovery from random projections:Universal encoding strategies?. IEEE Transactions on Information Theory, 52 (12): 5406–5425. DOI: 10.1109/TIT.2006.885507.
  • Chang C-I. Hyperspectral Data Exploitation:Theory and Applications. New York: John Wiley & Sons 2007 .
  • Chen Y, Nasrabadi N M, Tran T D.2011a.Simultaneous joint sparsity model for target detection in hyperspectral imagery. IEEE Geoscience and Remote Sensing Letters, 8 (4): 676–680. DOI: 10.1109/LGRS.2010.2099640.
  • Chen Y, Nasrabadi N M, Tran T D.2011b.Hyperspectral image classification using dictionary-based sparse representation. IEEE Transactions on Geoscience and Remote Sensing, 49 (10): 3973–3985. DOI: 10.1109/TGRS.2011.2129595.
  • Chen Y, Nasrabadi N M, Tran T D.2011c.Sparse representation for target detection in hyperspectral imagery. IEEE Journal of Selected Topics in Signal Processing, 5 (3): 629–640. DOI: 10.1109/JSTSP.2011.2113170.
  • Do M N, Vetterli M.2005.The contourlet transform:an efficient directional multiresolution image representation. IEEE Transactions on Image Processing, 14 (12): 2091–2106. DOI: 10.1109/TIP.2005.859376.
  • Dong W S, Zhang L, Shi G M, Wu X L.2011.Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization. IEEE Transactions on Image Processing, 20 (7): 1838–1857. DOI: 10.1109/TIP.2011.2108306.
  • Dong W S, Shi G M, Li X.2013.Nonlocal image restoration with bilateral variance estimation:a low-rank approach. IEEE Transactions on Image Processing, 22 (2): 700–711. DOI: 10.1109/TIP.2012.2221729.
  • Du Q, Fowler J E.2007.Hyperspectral image compression using JPEG2000 and principal component analysis. IEEE Geoscience and Remote Sensing Letters, 4 (2): 201–205. DOI: 10.1109/LGRS.2006.888109.
  • Du Q, Bioucas-Dias J M and Plaza A.2012.Hyperspectral band selection using a collaborative sparse model//Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS).Munich, Germany:IEEE:3054-3057 [DOI:10.1109/IGARSS.2012.6350781].
  • Efron B, Hastie T, Johnstone I, Tibshirani R.2004.Least angle regression. The Annals of Statistics, 32 (2): 407–499. DOI: 10.1214/009053604000000067.
  • Elad M, Bruckstein A M.2002.A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Transactions on Information Theory, 48 (9): 2558–2567. DOI: 10.1109/TIT.2002.801410.
  • Elad M, Aharon M.2006.Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing, 15 (12): 3736–3745. DOI: 10.1109/TIP.2006.881969.
  • Elhamifar E, Vidal R.2013.Sparse subspace clustering:algorithm, theory, and applications. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35 (11): 2765–2781. DOI: 10.1109/TPAMI.2013.57.
  • Feng R Y, Zhong Y F, Zhang L P.2015.An improved nonlocal sparse unmixing algorithm for hyperspectral imagery. IEEE Geoscience and Remote Sensing Letters, 12 (4): 915–919. DOI: 10.1109/LGRS.2014.2367028.
  • Fu W, Li S T, Fang L Y, Kang X D, Benediktsson J A.2016.Hyperspectral image classification via shape-adaptive joint sparse representation. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 9 (2): 556–567. DOI: 10.1109/JSTARS.2015.2477364.
  • Fu X, Ma W K, Chan T H, Bioucas-Dias J M.2015.Self-dictionary sparse regression for hyperspectral unmixing:Greedy pursuit and pure pixel search are related. IEEE Journal of Selected Topics in Signal Processing, 9 (6): 1128–1141. DOI: 10.1109/JSTSP.2015.2410763.
  • Gorodnitsky I F, Rao B D.1997.Sparse signal reconstruction from limited data using FOCUSS:A re-weighted minimum norm algorithm. IEEE Transactions on Signal Processing, 45 (3): 600–616. DOI: 10.1109/78.558475.
  • Gou S P, Liu S Z, Yang S Y, Jiao L C.2014.Remote sensing image super-resolution reconstruction based on nonlocal pairwise dictionaries and double regularization. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (12): 4784–4792. DOI: 10.1109/JSTARS.2014.2328596.
  • Hastie T, Taylor J, Tibshirani R, Walther G.2007.Forward stagewise regression and the monotone lasso. Electronic Journal of Statistics, 1 : 1–29. DOI: 10.1214/07-EJS004.
  • Hong H, Mei Y.2015.Dimensionality reduction of hyperspectral images with sparse discriminant embedding. IEEE Transactions on Geoscience and Remote Sensing, 53 (9): 5160–5169. DOI: 10.1109/TGRS.2015.2418203.
  • Huang Z W, Shi Z W, Yang S.2013.Nonlocal similarity regularized sparsity model for hyperspectral target detection. IEEE Geoscience and Remote Sensing Letters, 10 (6): 1532–1536. DOI: 10.1109/LGRS.2013.2261455.
  • Iordache M D, Bioucas-Dias J M, Plaza A.2011a.Sparse unmixing of hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing, 49 (6): 2014–2039. DOI: 10.1109/TGRS.2010.2098413.
  • Iordache M D, Bioucas-Dias J M, Plaza A.2014a.Collaborative sparse regression for hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 52 (1): 341–354. DOI: 10.1109/TGRS.2013.2240001.
  • Iordache M D, Bioucas-Dias J M, Plaza A.2011b.Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 50 (11): 4484–4502. DOI: 10.1109/TGRS.2012.2191590.
  • Iordache M D, Bioucas-Dias J M, Plaza A, Somers B.2014b.MUSIC-CSR:hyperspectral unmixing via multiple signal classification and collaborative sparse regression. IEEE Transactions on Geoscience and Remote Sensing, 52 (7): 4364–4382. DOI: 10.1109/TGRS.2013.2281589.
  • Khan Z, Shafait F, Mian A.2015.Joint group sparse PCA for compressed hyperspectral imaging. IEEE Transactions on Image Processing, 24 (12): 4934–4942. DOI: 10.1109/TIP.2015.2472280.
  • Khazai S, Safari A, Mojaradi B, Homayouni S.2013.An approach for subpixel anomaly detection in hyperspectral images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (2): 769–778. DOI: 10.1109/JSTARS.2012.2210277.
  • Kim K I, Kwon Y.2010.Single-image super-resolution using sparse regression and natural image prior. IEEE Transactions on Pattern Analysis and Machine Intelligence, 32 (6): 1127–1133. DOI: 10.1109/TPAMI.2010.25.
  • Kreutz-Delgado K, Murray J F, Rao B D, Engan K, Lee T-W, Sejnowski T J.2003.Dictionary learning algorithms for sparse representation. Neural Computation, 15 (2): 349–396. DOI: 10.1162/089976603762552951.
  • Kulkarni N, Nagesh P, Gowda R, Li B X.2012.Understanding compressive sensing and sparse representation based super resolution. IEEE Transactions on Circuits and Systems for Video Technology, 22 (5): 778–789. DOI: 10.1109/TCSVT.2011.2180773.
  • Le Pennec E, Mallat S.2005.Bandelet image approximation and compression. Multiscale Modeling&Simulation, 4 (3): 992–1039. DOI: 10.1137/040619454.
  • Lee H, Battle A, Raina R and Ng A Y.2006.Efficient sparse coding algorithms//Advances in Neural Information Processing Systems 19.Vancouver:MIT Press:801-808
  • Li J Y, Zhang H Y, Zhang L P.2014a.Column-generation kernel nonlocal joint collaborative representation for hyperspectral image classification. ISPRS Journal of Photogrammetry and Remote Sensing, 94 : 25–36. DOI: 10.1016/j.isprsjprs.2014.04.014.
  • Li J Y, Zhang H Y, Huang Y C, Zhang L P.2014b.Hyperspectral image classification by nonlocal joint collaborative representation with a locally adaptive dictionary. IEEE Transactions on Geoscience and Remote Sensing, 52 (6): 3707–3719. DOI: 10.1109/TGRS.2013.2274875.
  • Li J Y, Zhang H Y, Zhang L P, Huang X, Zhang L F.2014c.Joint collaborative representation with multitask learning for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 52 (9): 5923–5936. DOI: 10.1109/TGRS.2013.2293732.
  • Li J Y, Zhang H Y, Zhang L P.2015a.A nonlinear multiple feature learning classifier for hyperspectral images with limited training samples. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (6): 2728–2738. DOI: 10.1109/JSTARS.2015.2400634.
  • Li J Y, Zhang H Y, Zhang L P.2015b.Efficient superpixel-level multitask joint sparse representation for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 53 (10): 5338–5351. DOI: 10.1109/TGRS.2015.2421638.
  • Li J Y, Zhang H Y, Zhang L P, Ma L.2015c.Hyperspectral anomaly detection by the use of background joint sparse representation. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (6): 2523–2533. DOI: 10.1109/JSTARS.2015.2437073.
  • Loncan L, de Almeida L B, Bioucas-Dias J M, Briottet X, Chanussot J, Dobigeon N, Fabre S, Liao W Z, Licciardi G A, Simões M, Tourneret J-Y, Veganzones M A, Vivone G, Wei Q, Yokoya N.2015.Hyperspectral pansharpening:a review. IEEE Geoscience and Remote Sensing Magazine, 3 (3): 27–46. DOI: 10.1109/MGRS.2015.2440094.
  • Lustig M, Donoho D, Pauly J M.2007.Sparse MRI:The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine, 58 (6): 1182–1195. DOI: 10.1002/mrm.21391.
  • Ly N H, Du Q, Fowler J E.2014.Collaborative graph-based discriminant analysis for hyperspectral imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (6): 2688–2696. DOI: 10.1109/JSTARS.2014.2315786.
  • Mairal J, Sapiro G and Elad M.2007.Learning Multiscale Sparse Representations for Image and Video Restoration (Preprint).Technical report, DTIC Document
  • Mairal J, Ponce J, Sapiro G, Zisserman A and Bach F R.2009.Supervised dictionary learning//Advances in Neural Information Processing Systems 22.Columbia:NIPS:1033-1040
  • Mairal J, Bach F, Ponce J.2010.Task-driven dictionary learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 34 (4): 791–804. DOI: 10.1109/TPAMI.2011.156.
  • Matteoli S, Diani M, Theiler J.2014.An overview of background modeling for detection of targets and anomalies in hyperspectral remotely sensed imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (6): 2317–2336. DOI: 10.1109/JSTARS.2014.2315772.
  • Olshausen B A, Field D J.1997.Sparse coding with an overcomplete basis set:a strategy employed by V1?. Vision Research, 37 (23): 3311–3325. DOI: 10.1016/S0042-6989(97)00169-7.
  • Pan Z X, Yu J, Huang H J, Hu S X, Zhang A W, Ma H B, Sun W D.2013.Super-resolution based on compressive sensing and structural self-similarity for remote sensing images. IEEE Transactions on Geoscience and Remote Sensing, 51 (9): 4864–4876. DOI: 10.1109/TGRS.2012.2230270.
  • Qian Y T, Ye M C.2013.Hyperspectral imagery restoration using nonlocal spectral-spatial structured sparse representation with noise estimation. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (2): 499–515. DOI: 10.1109/JSTARS.2012.2232904.
  • Qiao L S, Chen S C, Tan X Y.2010.Sparsity preserving projections with applications to face recognition. Pattern Recognition, 43 (1): 331–341. DOI: 10.1016/j.patcog.2009.05.005.
  • Rubinstein R, Zibulevsky M and Elad M.2008.Efficient Implementation of the K-SVD Algorithm Using Batch Orthogonal Matching Pursuit.CS Technion
  • Shaobing C, Donoho D.1994.Basis pursuit//Proceedings of 1994 Conference Record of the 28th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA:IEEE, 41 : 41–44.
  • Shen H P, Huang J Z.2008.Sparse principal component analysis via regularized low rank matrix approximation. Journal of Multivariate Analysis, 99 (6): 1015–1034. DOI: 10.1016/j.jmva.2007.06.007.
  • Soltanolkotabi M, Elhamifar E, Candès E J.2014.Robust subspace clustering. The Annals of Statistics, 42 (2): 669–699. DOI: 10.1214/13-AOS1199.
  • Sun Z, Chang C C.2002.Structural damage assessment based on wavelet packet transform. Journal of Structural Engineering, 128 (10): 1354–1361. DOI: 10.1061/(ASCE)0733-9445(2002)128:10(1354).
  • Tang Y, Yan P K, Yuan Y, Li X L.2011.Single-image super-resolution via local learning. International Journal of Machine Learning and Cybernetics, 2 (1): 15–23. DOI: 10.1007/s13042-011-0011-6.
  • Tibshirani R.2011.Regression shrinkage and selection via the lasso:a retrospective. Journal of the Royal Statistical Society:Series B (Statistical Methodology), 73 (3): 273–282. DOI: 10.1111/j.1467-9868.2011.00771.x.
  • Tropp J A.2004.Greed is good:Algorithmic results for sparse approximation. IEEE Transactions on Information Theory, 50 (10): 2231–2242. DOI: 10.1109/TIT.2004.834793.
  • Tropp J A, Gilbert A C, Strauss M J.2006.Algorithms for simultaneous sparse approximation. Part I:greedy pursuit.Signal Processing, 86 (3): 572–588. DOI: 10.1016/j.sigpro.2005.05.030.
  • Tropp J A, Gilbert A C.2007.Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, 53 (12): 4655–4666. DOI: 10.1109/TIT.2007.909108.
  • Wei Q, Bioucas-Dias J, Dobigeon N, Tourneret J-Y.2015.Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Transactions on Geoscience and Remote Sensing, 53 (7): 3658–3668. DOI: 10.1109/TGRS.2014.2381272.
  • Willett R, Duarte M, Davenport M, Baraniuk R.2014.Sparsity and structure in hyperspectral imaging:sensing, reconstruction, and target detection. IEEE Signal Processing Magazine, 31 (1): 116–126. DOI: 10.1109/MSP.2013.2279507.
  • Wright J, Yang A Y, Ganesh A, Sastry S S, Ma Y.2009.Robust face recognition via sparse representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31 (2): 210–227. DOI: 10.1109/TPAMI.2008.79.
  • Wu W, Yang X M, Liu K, Liu Y G, Yan B Y, Hua H.2016.A new framework for remote sensing image super-resolution:Sparse representation-based method by processing dictionaries with multi-type features. Journal of Systems Architecture, 64 : 63–75. DOI: 10.1016/j.sysarc.2015.11.005.
  • Xu M M, Zhang L P, Du B, Zhang L F.2016.An image-based endmember bundle extraction algorithm using reconstruction error for hyperspectral imagery. Neurocomputing, 173 : 397–405. DOI: 10.1016/j.neucom.2015.02.098.
  • Yan S C and Wang H.2009.Semi-supervised Learning by Sparse Representation.SDM:SIAM:792-801
  • Yang D Q, Li Z M, Xia Y T and Chen Z Z.2015.Remote sensing image super-resolution:challenges and approaches//Proceedings of 2015 IEEE International Conference on Digital Signal Processing (DSP).Singapore:IEEE:196-200 [DOI:10.1109/ICDSP.2015.7251858].
  • Yang J C, Wright J, Huang T S, Ma Y.2010.Image super-resolution via sparse representation. IEEE Transactions on Image Processing, 19 (11): 2861–2873. DOI: 10.1109/TIP.2010.2050625.
  • Yang J C, Wang Z W, Lin Z, Cohen S, Huang T.2012.Couple dictionary training for image super-resolution. IEEE Transactions on Image Processing, 21 (8): 3467–3478. DOI: 10.1109/TIP.2012.2192127.
  • Yokoya N, Yairi T, Iwasaki A.2012.Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Transactions on Geoscience and Remote Sensing, 50 (2): 528–537. DOI: 10.1109/TGRS.2011.2161320.
  • Yuan Q Q, Zhang L P, Shen H F, Li P X.2010.Adaptive multiple-frame image super-resolution based on U-curve. IEEE Transactions on Image Processing, 19 (12): 3157–3170. DOI: 10.1109/TIP.2010.2055571.
  • Yuan Y, Zhu G K, Wang Q.2015a.Hyperspectral band selection by multitask sparsity pursuit. IEEE Transactions on Geoscience and Remote Sensing, 53 (2): 631–644. DOI: 10.1109/TGRS.2014.2326655.
  • Yuan Y, Fu M, Lu X Q.2015b.Low-rank representation for 3D hyperspectral images analysis from map perspective. Signal Processing, 112 : 27–33. DOI: 10.1016/j.sigpro.2014.06.018.
  • Yue L W, Shen H F, Yuan Q Q, Zhang L P.2014.A locally adaptive L1-L2 norm for multi-frame super-resolution of images with mixed noise and outliers. Signal Processing, 105 : 156–174. DOI: 10.1016/j.sigpro.2014.04.031.
  • Zhang E L, Zhang X R, Liu H Y, Jiao L C.2015a.Fast multifeature joint sparse representation for hyperspectral image classification. IEEE Geoscience and Remote Sensing Letters, 12 (7): 1397–1401. DOI: 10.1109/LGRS.2015.2402971.
  • Zhang H Y, Li J Y, Huang Y C, Zhang L P.2014a.A nonlocal weighted joint sparse representation classification method for hyperspectral imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (6): 2056–2065. DOI: 10.1109/JSTARS.2013.2264720.
  • Zhang H Y, He W, Zhang L P, Shen H F, Yuan Q Q.2014b.Hyperspectral image restoration using low-rank matrix recovery. IEEE Transactions on Geoscience and Remote Sensing, 52 (8): 4729–4743. DOI: 10.1109/TGRS.2013.2284280.
  • Zhang L, Yang M, Feng X C, Ma Y and Zhang D.2012.Collaborative representation based classification for face recognition.Arxiv Preprint arXiv:1204.2358
  • Zhang L F, Zhang L P, Tao D C, Huang X.2014c.Sparse transfer manifold embedding for hyperspectral target detection. IEEE Transactions on Geoscience and Remote Sensing, 52 (2): 1030–1043. DOI: 10.1109/TGRS.2013.2246837.
  • Zhang Y X, Du B, Zhang L P.2015b.A sparse representation-based binary hypothesis model for target detection in hyperspectral images. IEEE Transactions on Geoscience and Remote Sensing, 53 (3): 1346–1354. DOI: 10.1109/TGRS.2014.2337883.
  • Zhang Y X, Zhang L P, Du B, Wang S G.2015c.A nonlinear sparse representation-based binary hypothesis model for hyperspectral target detection. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (6): 2513–2522. DOI: 10.1109/JSTARS.2014.2368173.
  • Zhao Y Q, Yang J X.2015.Hyperspectral image denoising via sparse representation and low-rank constraint. IEEE Transactions on Geoscience and Remote Sensing, 53 (1): 296–308. DOI: 10.1109/TGRS.2014.2321557.
  • Zhao Y Q, Yang J X, Zhang Q Y, Song L, Cheng Y M, Pan Q.2011.Hyperspectral imagery super-resolution by sparse representation and spectral regularization. EURASIP Journal on Advances in Signal Processing, 2011 : 87 DOI: 10.1186/1687-6180-2011-87.
  • Zhong Y F, Feng R Y, Zhang L P.2014.Non-local sparse unmixing for hyperspectral remote sensing imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (6): 1889–1909. DOI: 10.1109/JSTARS.2013.2280063.
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献