Print

出版日期: 2016-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20165143
2016 | Volumn20 | Number 4





                              上一篇|





下一篇
技术方法
加入地物倾角分析的LiDAR回波强度校正
expand article info 伊丕源1 , 满旺2 , 童鹏1 , 邱峻挺1 , 赵英俊1 , 张景发3
1. 核工业北京地质研究院遥感信息与图像分析技术国家级重点实验室, 北京 100029
2. 厦门理工学院空间信息技术研究所, 福建 厦门 361024
3. 中国地震局地壳应力研究所, 北京 100085
收稿日期: 2015-06-16; 修改日期: 2016-03-31; 优先数字出版日期: 2016-07-25
基金项目: 国家高技术研究发展计划（863计划）（编号：2012AA121304）；国防研究基金（编号：9140C72010112c72003）
第一作者简介: 伊丕源(1982-),男,博士研究生。研究方向为航空摄影测量、遥感图像处理、3维可视化技术等。E-mail:yipiyuan@163.com
中图分类号: TP721.2;P225.6
文献标识码: A
文章编号: 1007-4619(2016)04-0610-10

摘要

LiDAR回波强度数据的校正处理可以提升其在地物分类识别方面的利用价值。本文研究发现倾斜地物（如三角形、拱形房顶等）的自身倾角会改变激光反射角进而影响回波强度，而现有归一化校正模型缺乏对地物倾角的计算分析。随后结合LiDAR数据的采集方式和特点，以及倾斜地物的结构特征，提出了一种加入地物倾角计算的改进型归一化校正算法。首先，对激光点的回波强度值进行基于传输距离值的初步校正；然后，以平面距离值、高程、回波强度值差异为参考，判定激光点是否属于同一倾斜地物，若满足条件，则计算出激光点的趋势角，并依据制定的判定规则确定趋势角的正负；最后，将趋势角计算结果与扫描角数值结合计算出对应的反射角，并重新对回波强度值进行计算校正。实验表明，蓝铁皮材质的三角形、拱形房顶的回波强度值范围和均方差缩小，且采集的8种地物样本的回波强度均值的差异性与激光反射率测量结果基本一致，说明该算法能够有效识别具有一定面积且材质均一的倾斜人工地物并计算修正其自身倾角对回波强度带来的影响，从而进一步提高基于回波强度值的地物可分性。

关键词

机载激光雷达 , 回波强度 , 地物倾角 , 反射角 , 激光反射率 , 归一化校正

Calibration algorithm and object tilt angle analysis and calculation for LiDAR intensity data
expand article info YI Piyuan1 , MAN Wang2 , TONG Peng1 , QIU Junting1 , ZHAO Yingjun1 , ZHANG Jingfa3
1.National Key Lab. of Remote Sensing Information and Image Analysis Technique, Beijing Research Institute of Uranium Geology, Beijing 100029, China
2.School of Computer & Information Engineering, Xiamen University of Technology, Xiamen 361024, China
3.Institute of Crustal and Dynamics, China Earthquake Administration, Beijing 100085, China

Abstract

Calibration of Light Detection And Ranging (LiDAR) intensity data can improve classification reliability. The normalized algorithm based on laser transmission distance and scanning angle is the most common algorithm for LiDAR intensity data calibration. However, this study determined that the influence of the tilt angles of several round objects, such as triangular and arched roofs, on echo intensity can be hardly calibrated by the normalized algorithm.Therefore, an optimized algorithm that calculates the tilt angle and calibrates the corresponding influence on LiDAR intensity data was developed. Eight typical ground objects in the study area were selected and sampled. The laser reflectivity of the samples was measured with Lamada 950 and regarded as a reference to evaluate the intensity calibration results. The steps of the optimized algorithm are as follows:(1) calibrate the original intensity value based on laser transmission distance; (2) determine whether adjacent laser points belong to the same tilted object by comparing their plane distance, elevation, and intensity with cut-off values; (3) calculate the tilt angle when the adjacent laser points belong to the same tilted object; (4) propose a rule by analyzing the LiDAR data collection mode and features of tilted ground objects and use this rule to determine whether the tilt angle is negative or positive; (5) calculate the corresponding reflection angle by summing the tilt angle and absolution of the scanning angle; and (6) recalibrate the intensity based on the reflection angle and laser transmission distance to eliminate the influence of reflection angle. The differences in the mean intensity of ground objects calculated with the existing normalized algorithm are consistent with the laser reflection measurement results, except for the blue-and-white-painted iron from different roofs. By contrast, the differences in the mean intensity of all eight ground objects are in agreement with the laser reflection measurement results obtained by using the optimized algorithm. For instance, the range and mean-square deviation of the intensity of triangular and arched roofs with blue-painted iron are both reduced. A few unreliable high intensity values correspond to the laser points, such as the wall of buildings and street lamp. Although these points meet the cut-offs, they have a small plane distance value. Thus, the calculated tilt angles for these points are large, and the cosine values are small; this condition results in unreliable high intensity values. The optimized algorithm can identify the laser points of homogeneous ground objects with a certain area and the same material and calculate the corresponding tilt angles. The influence of tilt angle can be effectively eliminated after calibration based on the reflection angle obtained by summing the tilt and scanning angles. The optimized algorithm can therefore improve classification feasibility based on the intensity value. With regard to the few unreliable high intensity values, two possible solutions are proposed for further study. Given the reliable empirical cut-off values presented by numerous experiments, LiDAR data can be preliminarily classified prior to separate the laser points. The optimized algorithm can then be utilized to calibrate intensity.

Key words

airborne LiDAR , intensity , tilt angle , reflection angle , laser reflectivity , normalization calibration

1 引 言

机载激光雷达测量系统(LiDAR)是一种主动式对地观测系统，以激光扫描测距系统为传感器，集成全球定位系统、惯性导航等先进技术，能实时获取地形表面的3维空间信息，已经成为获取高时空分辨率的地球空间信息的一种重要技术手段。LiDAR数据除包含地物的3维坐标外，还记录回波强度、回波次数(序)、扫描角等信息。其中，回波强度值是经地物反射后返回的激光脉冲信号由接收器感应产生电压，经过放大处理和计算，转化为数字。目前大多数机载激光雷达设备具有4次回波记录能力，带有全波形记录仪的机载激光雷达系统也开始在市场上应用。传统LiDAR数据的滤波分类算法主要是利用激光点3维坐标信息(Li等，2008)，当前回波强度等信息的利用正在成为研究热点，越来越多的学者关注回波强度在地物信息提取中的应用研究(覃驭楚等，2011)。如在建筑物毁坏严重的震区，传统的依据激光点云3维坐标分类的方法效果较差，此时愈加凸显回波强度信息在地物分类方面的利用价值。理论上，每种物质对激光信号的反射特性是不一样的，地面介质表面的反射系数决定了激光回波能量的多少，根据这一特性，能够区分识别很多地物(Petzold和Axelsson，2000)。国外对激光雷达的研究起步较早，对激光雷达回波强度数据的处理和应用也开展了一定研究。Baltsavias(1999a)给出了激光后向散射强度的理论计算公式，部分学者对不同地物的激光反射特征进行分析，并评估了基于回波强度的地物分类可行性(Baltsavias，1999b；Song等，2002；Kaasalainen等，2005；Coren和Sterzai，2006)；德国Riegl公司还曾测试公布过部分地物对900 nm波长激光反射率(刘经南和张小红，2005)。也有学者通过布设标准地物样品，研究结合样品反射率测量值进行回波强度值校正(Vain等，2009；Kaasalainen等，2009)。这些研究表明激光脉冲回波信号强度主要与地物反射率、激光入射角、大气衰减、激光传输距离相关(Yoon等，2008)。目前，LiDAR 回波强度值校正处理方法主要包括：基于理论的辐射校正模型和归一化校正模型(Höfle和Pfeifer，2007)。其中，基于理论模型的辐射校正需要较多参数，具有一定实施难度；归一化校正方法通过将激光传输距离、大气衰减的影响平均化达到回波强度校正的目的，易于实现且结果具有参考意义，因此应用广泛。

以上两种方法都是假定地物为朗伯体且平坦，本文通过实验分析，发现对于很多倾斜地物而言(尤其是表面平整、材质均一的介质表面，如三角形、拱形房顶)，地物倾角对激光回波强度造成的影响不可忽略，而现有校正模型没有地物倾角的计算方法，无法解决此问题。随后重点针对地物趋势角的计算方法开展研究，并结合现有归一化校正方法，提出一种加入地物趋势角的回波强度校正算法。实践证明，对于城市人工地物的回波强度校正具有良好的效果。

需要指出的是，对于植被类地物(尤其是森林)而言，回波强度会受到叶面积、叶密度、叶倾角等多种因素影响，往往激光脉冲会产生多次回波，而归一化校正方法针对单次回波和首次回波激光点更为有效，尽管也有学者利用归一化方法处理回波强度用以辅助进行植被分类提取(Han等，2014)，但森林类地物更适合采用带有波形记录的LiDAR数据开展研究(Yao等，2012)，因此本文方法限定针对城市人工地物。

2 实验数据

实验数据基于ALTM Gemini机载激光雷达系统获得，设备与飞行实验方案的主要参数如表 1所示。实验区域位于石家庄机场，范围如图 1所示。图中两条红线为设计航线，采用运五飞机为搭载平台，飞行实验参数如表 1所示，激光脉冲频率100 kHz，飞行海拔高度1100 m，1号航线摆扫角度为±25°、摆扫频率35 Hz，2号航线摆扫角为±15°、摆扫频率50 Hz。

表 1 设备与飞行实验方案参数列表
Table 1 Parameter list of ALTM Gemini and flight plan

下载CSV 
参数 规格
设备 ALTM Gemini
激光波长 1064 nm
激光波束角 3 mrad
回波接收能力 4次
飞行航高(海拔高度) 1100 m
脉冲频率 100 kHz
摆扫频率 35 Hz(航带1)
50 Hz(航带2)
视场角 ±25°(航带1)
±15°(航带2)


图 1 实验区航线设计图
Fig. 1 Flightlines

3 经典校正方法

国外学者针对LiDAR回波强度值校正与利用开展了研究。LiDAR回波强度值校正处理方法主要分为两类：基于理论的辐射校正模型和归一化校正模型(Höfle和Pfeifer，2007)。

基于理论模型的辐射校正方法是基于雷达方程和激光传输理论，假定地面为朗伯体反射、大气条件已知(散射、透过率等)、激光发射功率恒定、接收功率与回波强度记录值线性相关，在满足以上条件下通过雷达方程计算公式进行回波强度值的校正(Yan等，2012)。

$ {{P}_{\text{r}}}=\frac{{{P}_{t}}{{D}_{r}}^{2}}{4\text{ }\!\! \pi \!\!\text{ }{{R}^{4}}{{\beta }_{t}}^{2}}{{\eta }_{\text{sys}}}{{\eta }_{\text{atm}}}\sigma $ (1)

式中，Pr代表激光接收器收到的信号，Dr为接收孔径，R为传感器与目标之间的距离，βt为激光波束宽度，ηsys为系统衰减系数，ηatm为大气衰减系数，σ为目标散射截面积。其中，σ的计算公式为：

$ \sigma =\frac{4\text{ }\!\!\pi\!\!\text{ }}{\Omega }\rho {{A}_{s}} $ (2)

式中，Ω为目标立体角，ρ为目标反射率，As为目标面积(对应于激光光斑面积)(Wagner等，2004)。由于需要较多参数，基于理论模型的辐射校正具有一定实施难度。

归一化校正模型，假定地面为朗伯体且平坦，记录的回波强度值与地面反射率呈比例关系，与飞行高度呈线性关系或者平方反比，然后通过计算对距离值变化引起的差异进行归一化处理，计算公式为：

$ {{I}_{\left(R \right){\rm{normalized}}}}=I \cdot{{R}^{2}}/{{R}_{S}}^{2} $ (3)

式中，I(R)normalized为标准化后的回波强度值，I为原始回波强度测量值，R是激光点与传感器之间距离值，Rs是参考距离值(Solberg等，2006；Donoghue等，2007)；

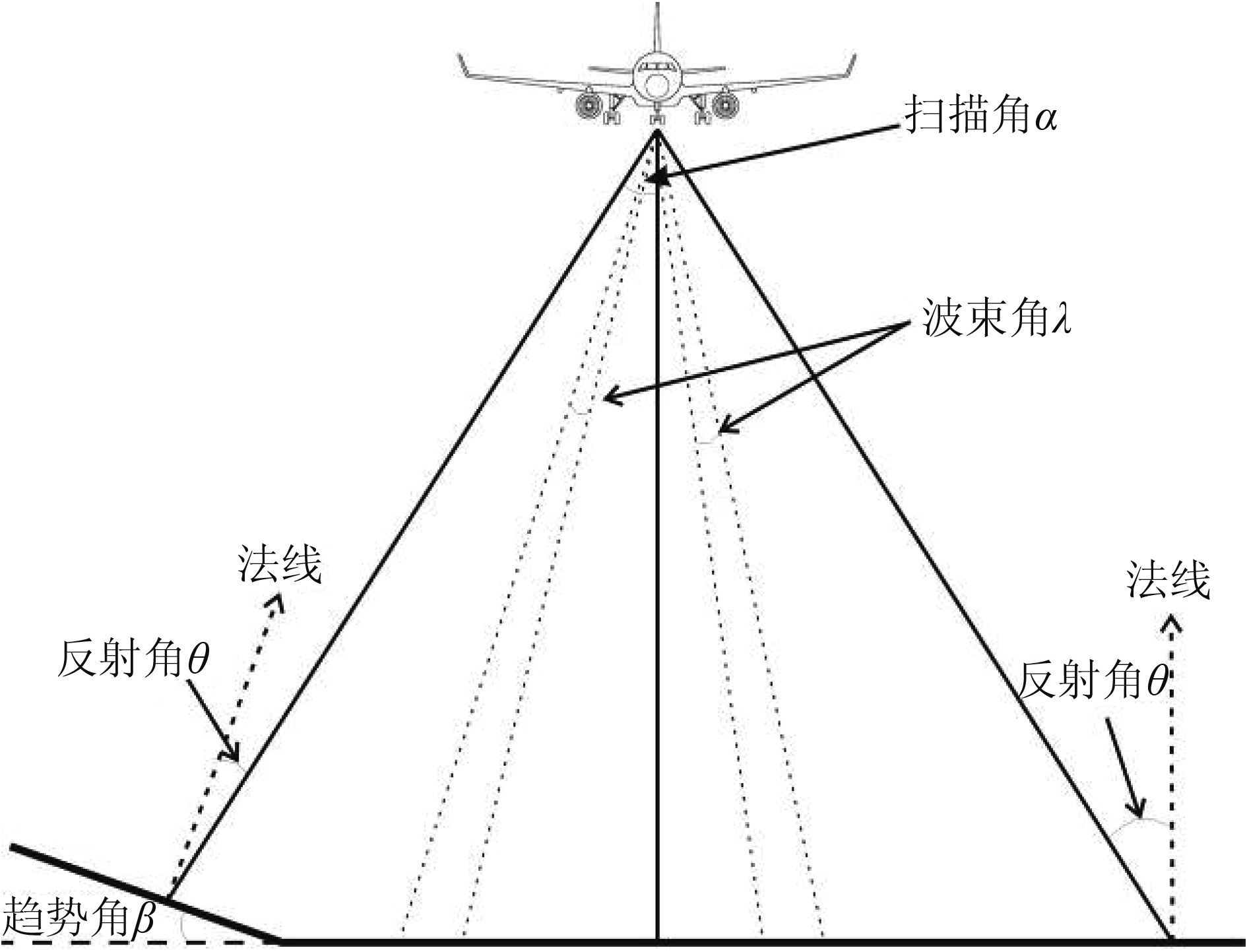
部分学者进一步考虑到激光入射角的影响，认为在假定地面为朗伯体的前提下，则其对激光的散射效应相同，即可近似认为地物对每一个激光脉冲光斑的散射相同，所以传感器接收的激光后向散射强度与入射角呈一定关系(Steinvall，2000)；如图 2所示反射角θ是激光光束与地面法线之间的夹角，在地面平坦时可认为反射角θ与激光扫描入射角α相等，但对于倾斜地物和崎岖山地，反射角θ应由扫描角α和摆扫方向上的地物趋势角β计算获得。在假定地面平坦的前提下，将式(3)改进为(Höfle和Pfeifer，2007；Burgess等，2011)：

$ {{I}_{\left(R \right){\rm{normalized}}}}=I \cdot {{R}^{2}}/({{R}_{S}}^{2} \cdot cos\alpha) $ (4)

因此，归一化校正模型忽略地物倾角对激光脉冲回波强度的影响，且通常只针对单次回波和首次回波激光点有效(Mesas-Carrascosa等，2012)。


图 2 机载LiDAR激光脉冲扫描及地物反射原理图
Fig. 2 Principle of LiDAR data acquisition

4 改进的归一化校正算法设计

本文结合LiDAR数据的采集方式和特点，以及倾斜地物的结构特征，设计提出了加入地物趋势角计算分析的归一化校正方法。

传统的地表坡度角计算方法是基于激光点云数据生成数字高程模型或数字地表模型，然后采用格网或不规则三角网的形式计算坡度、坡向(Chang，2006)。通过对地物结构特征和回波强度的统计分析，本文认为这些方法并不适用于激光点的趋势角计算。首先，只有在激光摆扫方向上的地物倾角才会产生影响，不必计算多个方向的坡向；其次，实际上只有激光光斑面积内的地物倾角才会对反射产生影响，不能只依据目标激光点与周边点的坐标差进行计算，如房屋边界点与地面点之间高差大，坡向角计算值也大，但该数值不是激光光斑对应的房顶顶部的趋势角度值；三是部分小型地物，如房顶太阳能板，若其在扫描方向上只产生单个激光点，只依据单个激光点难以准确判断太阳能板自身趋势角，且若不加以区别而误认为是房顶点进行趋势角计算也会造成错误，因此此类地物孤立点需要加以识别并忽略其趋势角计算；最后，趋势角的方向性十分重要，如图 3中所示，趋势角β1和β2对激光反射造成的影响不同，对反射角θ1而言：

$ {{\theta }_{1}}={{\alpha }_{1}}+{{\beta }_{1}}~ $ (5)

而反射角θ2为：

$ {{\theta }_{2}}={{\alpha }_{2}}-{{\beta }_{2}} $ (6)

因此不仅要计算趋势角β的数值，而且要结合地物结构特征判断其方向性，才能正确计算出反射角。


图 3 反射角计算原理示意图
Fig. 3 Relationship between the incidence angle of the beam and the scanningangle of the LiDAR sensor

综合以上分析，要依靠激光点实现地物趋势角计算，关键因素包括：确定激光扫描方向、地物边缘点判断、孤立点判断、反射角计算。

本文设计的包含地物趋势角计算的校正方法如下。

(1) 首先，对激光点的回波强度值进行基于传输距离值的校正，公式为：

$ {{I}_{\text{range-correct}}}={{I}_{\text{original}}}\cdot({{R}_{j}}^{2}{{R}_{\rm{A}}}^{2}) $ (7)

式中，Irange-correct为依据式(3)只进行距离校正后的回波强度值，Ioriginal为回波强度原始值，Rj为第j个激光点对应的传输距离，RA为平均传输距离。这一步骤的目的是首先将传输距离的影响进行归一化处理，以提高算法后续步骤中的回波强度差异判定的准确性。

(2) 设激光点Pj(j=1，…，n)，计算临近点的Pj-1和Pj+1与Pj点平面距离，如式(8)所示：

$ L = \sqrt {{{\left({{X_{\left({p{}_j} \right)}} - {X_{\left({p{}_j - 1} \right)}}} \right)}^2} + {{\left({{Y_{\left({p{}_j} \right)}} - {Y_{\left({p{}_j - 1} \right)}}} \right)}^2}} $ (8)

设定一个距离阈值，若距离值L小于设定阈值，则继续，若某一点的距离大于阈值，则放弃，若Pj临近点Pj-1和Pj+1都不满足阈值要求，则趋势角βj取值为0。

如前所述，只有在激光摆扫方向上的地物倾角才会产生影响，因此可以依据激光点的记录顺序选取Pj-1、Pj和Pj+13个点进行趋势角计算。

距离阈值的选取以激光点云的平均点密度(个/m2)为参考。由于飞行数据采集过程中多种因素影响，个别地方点密度分布不十分均匀，如果距离阈值取值等于平均点间距(1/平均点密度)，则可能出现漏判；若取值过大也不可，因为须要考虑到航带最边缘点以及水体等地物的影响，即位于航带两侧的最边缘点虽然存储顺序相连接，但空间距离远(航带宽度)，基本不属于同一地物，不可直接用于趋势角计算，另外理论上水体对1064 nm激光具有吸收作用，不产生回波信号，因此水域两侧存储顺序相连接的激光点也不可直接用于趋势角计算。因此，建议取值为平均激光点间隔距离值的3倍较为合适，具体可依据数据实际情况调整确定。

(3) 对满足(2)条件的激光点进行高程值分析，若Pj高程值同时大于Pj-1和Pj+1的高程值，则趋势角βj取值为0；否则，计算Pj与临近点Pj-1和Pj+1的高程差值小于设定阈值，则继续进行趋势角度计算，高差阈值的设置假定同一地物最大倾角为γ，则高差阈值为：

$ {{H}_{\rm{height}}}={{R}_{\rm{average}}}/{\rm tan}\left(90-\gamma\right) $ (9)

式中，Hheight代表高差阈值，Raverage为平均激光点间隔距离值，地物最大倾角γ的取值可依据测区的实际状况设置，一般建筑物最大倾角不超过60°；Pj-1和Pj+1中高程差值计算结果不满足阈值要求的激光点不参与下一步运算；若Pj-1和Pj+1中高程差值计算结果均不满足阈值要求，则趋势角βj取值为0。

高程值计算分析主要是进一步判断地物顶点及边缘点，如以房屋为例，若Pj高程值同时大于Pj-1和Pj+1，判定Pj为屋顶点；若Pj与Pj-1和Pj+1的高程差值大于设定阈值，则判定Pj为房屋边界点，也即Pj-1或Pj+1属于房屋下方地物的回波点。

(4) 进一步比较激光点Pj与Pj-1和Pj+1的回波强度值，若回波强度值的差值小于阈值，判定Pj-1和Pj+1(或仅有Pj-1或Pj+1)与Pj(j=1，…，n)属于同一地物的激光点，不满足阈值要求的激光点不参与下一步运算；若Pj-1和Pj+1两个激光点的回波强度差值计算结果均不满足阈值要求，则趋势角βj取值为0；回波强度差值阈值的选取以测区地物复杂程度为参考。

回波强度值经过初步校正后已具有一定参考意义，此处利用其判断去除孤立点。如实验区房顶安装的太阳能板，往往只产生一个回波强度较高的孤立点，因此可以通过回波强度值判定地物属性与房顶不同，并予以忽略。

(5) 依据Pj-1和Pj+1的高程、平面距离，由反三角函数计算Pj点的趋势角，如式(10)所示：

$ {\beta _j} = \arctan \frac{{\sqrt {{{\left({{Z_{\left({P{}_{j + 1}} \right)}} - {Z_{\left({P{}_{j - 1}} \right)}}} \right)}^2}} }}{{\sqrt {{{\left({{X_{\left({P{}_{j + 1}} \right)}} - {X_{\left({P{}_{j - 1}} \right)}}} \right)}^2} + {{\left({{Y_{\left({P{}_{j + 1}} \right)}} - {Y_{\left({P{}_{j - 1}} \right)}}} \right)}^2}} }} $ (10)

若经以上步骤判定后仅剩Pj-1(或Pj+1)，则趋势角度数值的计算公式为：

$ {\beta _j} = \arctan \frac{{\sqrt {{{\left({{Z_{\left({P{}_{j}} \right)}} - {Z_{\left({P{}_{j - 1}} \right)}}} \right)}^2}} }}{{\sqrt {{{\left({{X_{\left({P{}_j} \right)}} - {X_{\left({P{}_{j - 1}} \right)}}} \right)}^2} + {{\left({{Y_{\left({P{}_j} \right)}} - {Y_{\left({P{}_{j - 1}} \right)}}} \right)}^2}} }} $ (11)

趋势角数值计算完毕后，首先将激光点自身扫描角α取绝对值，然后依次比较Pj-1、Pj、Pj+1的扫描角与高程值变化，从而判定趋势角数值的正负，规则如下(其中，A代表扫描角度α的绝对值，Z代表高程)：

扫描角增大(Aj-1< Aj< Aj+1)，高程增加(Zj-1<Zj< Zj+1)，负值；

扫描角增大(Aj-1< Aj< Aj+1)，高程减小(Zj-1> Zj> Zj+1)，正值；

扫描角减小(Aj-1> Aj> Aj+1)，高程增加(Zj-1<Zj< Zj+1)，负值；

扫描角减小(Aj-1> Aj> Aj+1)，高程减小(Zj-1> Zj> Zj+1)，正值。

依据以上判定条件，赋予相应的正、负号。

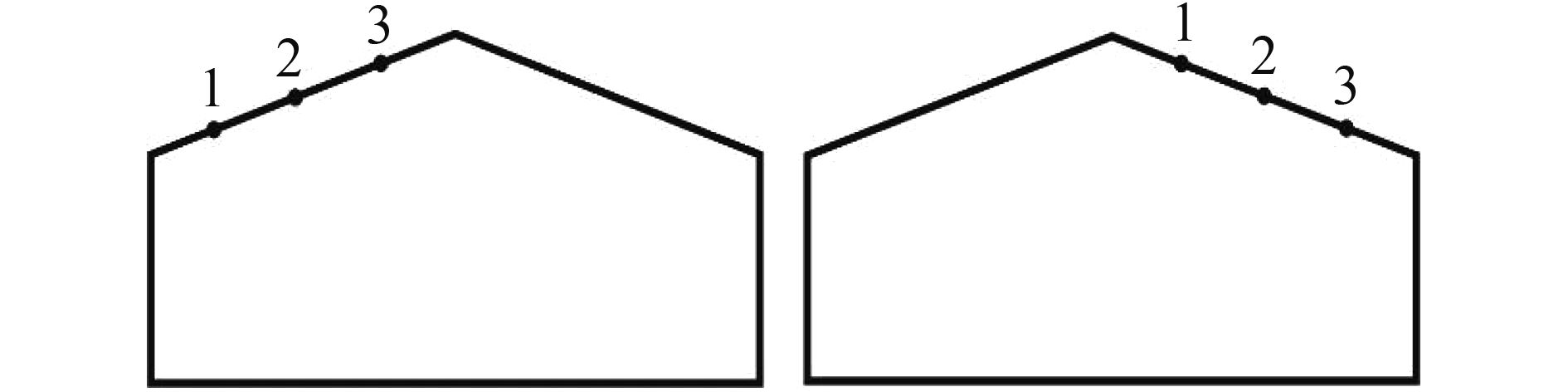
通常很多机载激光雷达设备采用以扫描器垂直中轴线为准(图 2、图 3)，将视场角左右区域的扫描角以正负号区别记录，因此先将其取绝对值，便于后续处理。选取其中的3个激光点1、2、3，并假设其位于倾斜房顶(图 4)，如果其扫描顺序为从1至3，扫描角度值依次增大，地物倾斜如图 3中所示包括两种情况，左图应减去趋势角，则为负，右图应加上趋势角，则为正；如果其扫描顺序为从3至1，扫描角度值依次增大，地物倾斜如图 4中所示包括两种情况，左图应加上趋势角，则为正，右图应减去趋势角，则为负。


图 4 倾斜地物激光点扫描分布示意图
Fig. 4 Schematic diagram of laser scanning points distribution for tilt ground objects

(6) 在步骤(1)校正结果的基础上，加入趋势角计算结果，重新对初始机载LiDAR数据进行回波强度值计算，公式为：

$ {{I}_{\text{cal}}}={{I}_{\text{range-correct}}}{\rm{cos}}({{\alpha }_{J}}+{{\beta }_{J}}) $ (12)

依据式(5)逐点计算并输出校正后的回波强度值。

以上方法可以基于ENVI LIDAR+IDL平台下编程实现。通过设置距离、高程差值、回波强度差异的阈值，采用if语句判定激光点是否符合条件，进一步比较扫描角、高程的数值大小，进行趋势角计算。存在的一个问题是由于ALTM Gemini设备记录的扫描角数值为整数，因此在高扫描频率下会出现数个激光点记录的扫描角数值相同的情况。本研究所用的数据即出现5个激光点扫描角数值相同的情况，对此程序设计中采用向下(或向上)循环判定的方法，即依据记录点号继续向下对比判定直至出现角度不等的情况，并依据比较结果判定扫描角度的变化趋势。

5 实验与分析

5.1 实验应用

分别采用归一化校正模型(见式(4))和改进的归一化校正算法进行回波强度值校正处理。采用改进型算法校正时，针对实验数据的基本情况，设置距离阈值为1 m、高程差值0.5 m、回波强度差值10。图 5是实验数据校正前后的对比。其中，图 5(a)是依据原始回波强度显示效果，图 5(b)和图 5(c)分别是采用经典归一化模型和本文改进型算法校正后的效果图。通过目视解译分析，航带两侧回波强度偏低(灰度偏暗)，由于1号线扫描角大于2号线，这一现象更明显。另外，飞机跑道材质较为均一，理论上其对应激光点的回波强度值接近，但在图 5(a)中两条航带重叠的跑道区域回波强度并不一致，这一点在校正后的激光点云数据中得到了较好的校正。


图 5 实验数据校正结果对比
Fig. 5 Comparison of calibration results with original data

5.2 对比分析

为进一步评价校正效果，对实验区的多种地物回波强度进行了统计，同时进行实地采样与激光反射率测量，对比分析回波强度数值的校正效果及影响因素。

对于同一测区相同飞行条件下获取的数据，经归一化校正后，可近似认为激光回波强度只同表面介质相关(张小红，2007)。因此采用Lamda950光度计对实验区地物样品进行了1064 nm波段激光反射率测量(冯国进等，2006)。本实验所测激光反射率指介质表面反射的能量与入射的能量的比值，即材料表面反射的辐射光通量与入射到材料表面的辐射光通量之比。理论上，物体的反射率是一定的，只与光源的波长有关(童庆禧等，2006)。因此，可以作为其参考，对回波强度数据进行对比分析。

选择8种地物样品，进行激光反射率测量及相应采样点地物的校正后回波强度值统计分析，结果如表 2所列。

表 2 地物样品反射率与回波强度值列表
Table 2 Laser reflectivity and intensity value of ground object samples

下载CSV 
样品名称 激光反射率 回波强度值范围
(经典方法)		 回波强度平均值
(经典方法)		 回波强度值范围
(改进型算法)		 回波强度平均值
(改进型算法)
蓝铁皮 0.311 18—86 51.9 27—58 43.6
白铁皮 0.442 22—63 44.9 28—55 48.9
枯草 0.505 49—78 52.8 49—78 52.8
灰色瓦片 0.313 23—39 35.4 23—39 35.4
柏油路面 0.188 16—28 27.8 16—28 27.8
水泥路面 0.263 28—39 33.8 28—39 33.8
塑胶跑道 0.229 26—36 30.9 26—36 30.9
假草皮 0.158 15—24 24.5 15—24 24.5

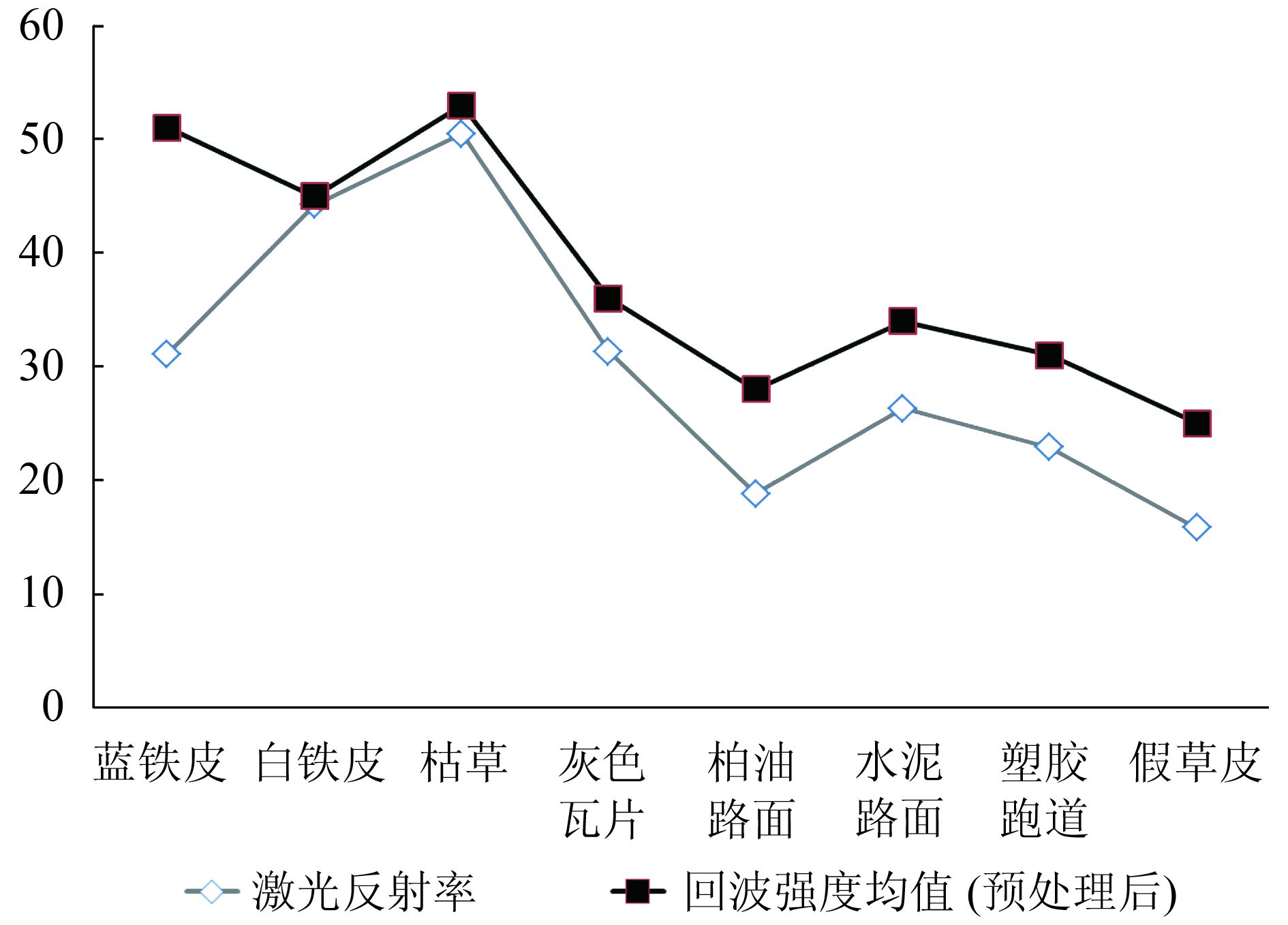
图 6是激光反射率测量值与经典方法校正后激光回波强度平均值的统计对比图。其中，蓝铁皮、白铁皮主要为部分房屋顶部材质，明显其回波强度值范围大，平均值与激光反射率也差异较大；枯草的回波强度值范围稍大，这主要与枯草地表面结构的粗糙有关；灰色瓦片(平房顶部)、柏油路面、水泥路面、塑胶跑道、假草皮(踩踏较平整)5种地物的回波强度范围较小且彼此之间的差异性与反射率测量结果基本一致。


图 6 激光反射率与回波强度均值(经典方法)对比
Fig. 6 Comparison of laser reflectivity and intensity value(calibrated by normalized algorithm)

图 7、图 8分别是蓝铁皮材质的三角形和拱形房顶的回波强度值分布图(依据灰度显示)。图中可见，经过经典方法的归一化校正后，材质相同的房顶两侧回波强度差异较明显，地物自身的趋势角的影响依然存在。


图 7 三角形房顶回波强度值(经典方法校正后)分布
Fig. 7 Intensity distribution character of triangular roof laser points(calibrated by normalized algorithm)


图 8 拱形房顶回波强度值(经典方法校正后)分布
Fig. 8 Intensity distribution character of arched roof laser points(calibrated by normalized algorithm)

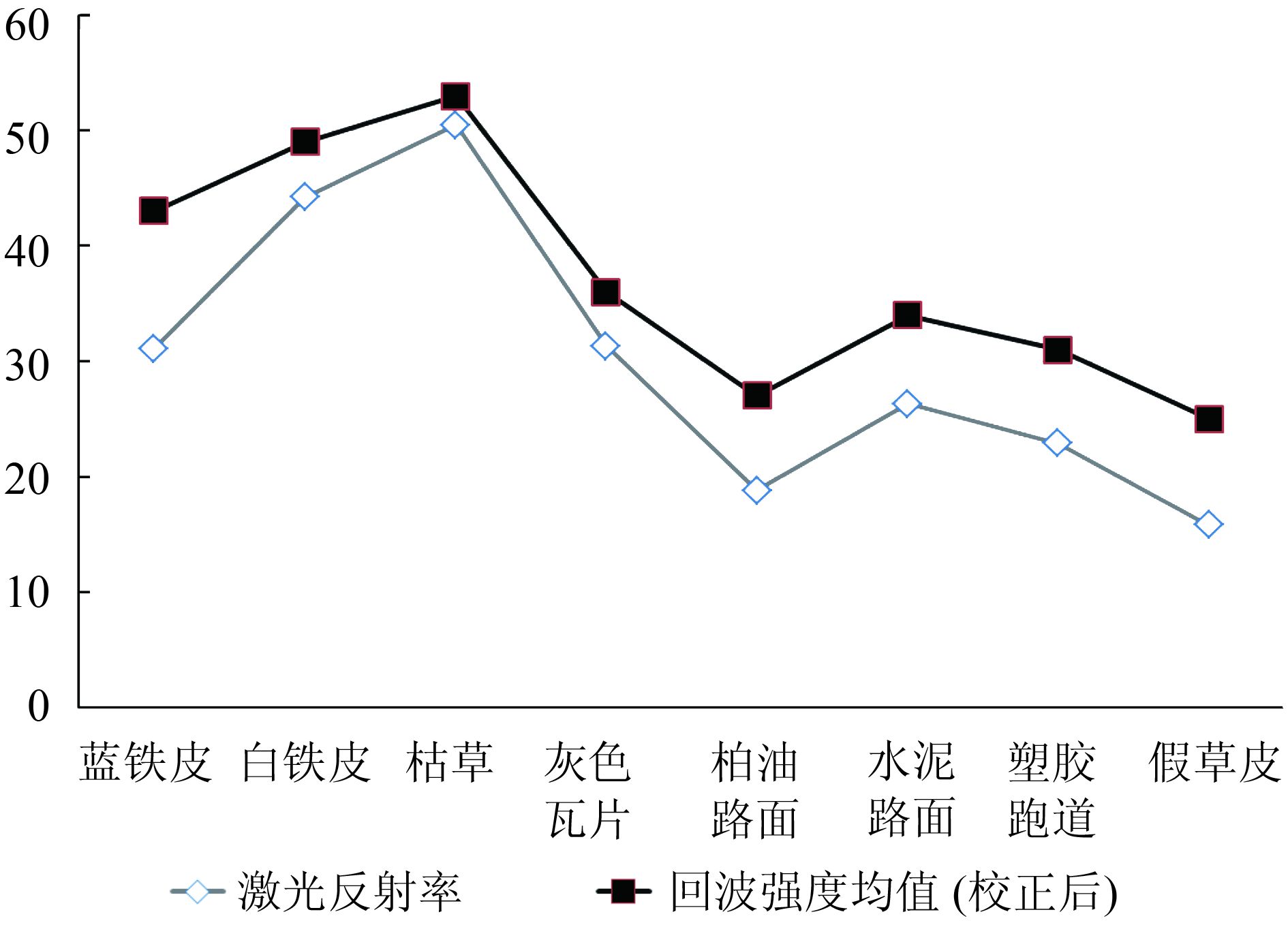
采用本文提出的改进型算法校正后的蓝铁皮回波强度值范围为27—58(平均值43.6)、白铁皮为28—55(平均值48.9)，枯草、灰瓦片、道路等地物不符合阈值判定条件，因此其未参与趋势角计算，回波强度值范围与经典方法校正后结果相同。对表 2中地物样品的激光反射率与改进算法校正后的回波强度进行对比统计，如图 9所示，地物之间回波强度差异与反射率基本一致，证明改进型算法能够有效去除地物自身趋势角的影响，校正后基于回波强度值的地物可分性进一步提升。


图 9 激光回波强度(加入趋势角计算校正后)与激光反射率对比
Fig. 9 Comparison of laser reflectivity and intensity value(calibrated by optimized algorithm)

图 10、图 11是采用改进型算法校正后的三角形、拱形房顶回波强度值显示效果。对比图 7、图 8其效果得到明显改善。进一步分别对三角形房顶82个激光点、拱形房顶3470个激光点的标准差如表 3所示。


图 10 三角形房顶回波强度值分布显示
Fig. 10 Intensity distribution character of triangular roof laser points(calibrated by optimized algorithm)


图 11 拱形房顶回波强度值分布显示
Fig. 11 Intensity distribution character of arched roof laser points(calibrated by optimized algorithm)

表 3 激光点回波强度值校正前后均方差统计
Table 3 Mean variance of intensity value

下载CSV 
三角形房顶 拱形房顶
初始值 6.709 7.047
经典算法校正后 8.283 6.051
改进型算法校正后 6.222 5.765

实验证明，经过趋势角度计算校正后，倾斜地物回波强度值的均方差更小，能够更好的反映出倾斜地物的介质属性，从而提高其分类识别的精确度。

针对表 3中的计算结果，结合材质分析，发现拱形房顶为较新的蓝铁皮材质，且表面较为平整，校正结果也较好；而三角形房顶的蓝铁皮较为陈旧，表面(尤其是房顶阳面)存在锈斑、褪色等现象，因此激光光斑面积内的介质属性不十分均一，获取的回波强度值存在一定偏差，因此采用经典算法校正后反而导致均方差数值略高。

另外，在对实验区 LiDAR数据的改进型算法校正结果检查中发现少量回波强度值异常高的激光点，主要为楼房侧面、路灯等地物的激光点。这部分激光点间的平面距离值很小，且高差符合阈值，因此所计算出的倾角数值很大，从造成cos(αJ+βJ)的数值极小，导致回波强度值极大。可以通过两个方法避免此类影响：一是合理设置判定阈值，并进一步设定一个最小阈值限定条件，如平面距离值或cos(αJ+βJ)必须大于一定数值；二是可依据传统方法对激光点云数据进行初步分类，将建筑物分类以后再进行校正处理。

6 结 论

结合LiDAR数据的获取方式和特点，以及倾斜地物的结构特征，提出了一种加入地物倾角计算分析的LiDAR回波强度归一化校正算法。

经过实验分析，主要结论如下：(1) 经典方法校正结果中，倾斜地物(蓝铁皮、白铁皮材质的房顶)回波强度与激光反射率数值的一致性不好，说明地物倾角的影响不可忽略；(2) 校正结果中，只有倾斜地物的回波强度值发生变化，而其他平坦地物的回波强度值与经典校正结果相同，说明依据改进型算法的判定规则，可以判定识别具有一定面积且材质均一的倾斜人工地物；(3) 利用本文提出的改进型算法校正后，蓝铁皮、白铁皮的激光回波强度值范围缩小，三角形、拱形房顶的回波强度值均方差更小，样本之间回波强度均值的差异性与激光反射率测量结果基本一致，说明改进型算法可以并有效地去除地物倾角的影响，从而提高了回波强度值对地物分类的利用价值。

本文提出的算法在实验中也存在不足之处：造成了少量的高异常回波强度值。主要为楼房侧面、路灯等地物的激光点，其符合实验设定的判定阈值，但倾角数值计算结果很大，从而导致校正后的回波强度值极大。今后工作中，应该通过更多的校正实验给出更加可靠地经验性阈值参数；另外，也可结合传统方法对激光点云数据进行初步分类处理，然后只针对倾斜地物的激光点云应用此方法，从而提高计算效率和准确率。

参考文献(References)

  • Baltsavias E P.1999a.Airborne laser scanning:basic relations and formulas. ISPRS Journal of Photogrammetry and remote Sensing, 54 (2/3) : 199–214 . [DOI:10.1016/S0924-2716(99)00015-5]
  • Baltsavias E P.1999b.A comparison between photogrammetry and laser scanning. ISPRS Journal of Photogrammetry and Remote Sensing, 54 (2/3) : 83–94 . [DOI:10.1016/S0924-2716(99)00014-3]
  • Burgess G, Shortis M R, Scott P.2011.Photographic assessment of retro reflective film properties. ISPRS Journal of Photogrammetric and Remote Sensing, 66 (5) : 743–750 . [DOI:10.1016/j.isprsjprs.2011.07.002]
  • Chang K T. Introduction to Geographic Information Systems. New York: McGraw-Hill Higher Education 2006 : 226 -231.
  • Coren F, Sterzai P.2006.Radiometric correction in laser scanning. International Journal of Remote Sensing, 27 (15) : 3097–3104 . [DOI:10.1080/01431160500217277]
  • Donoghue D N M, Watt P J, Cox N J, Wilson J.2007.Remote sensing of species mixtures in conifer plantations using Lidar height and intensity data. Remote Sensing of Environment, 110 (4) : 509–522 . [DOI:10.1016/j.rse.2007.02.032]
  • Feng G J, Wang Y, Zheng C D, Wu H P, Zhang Q X, Li P.2006.Research on measurement of FTIR specular reflection and transmission properties of Materials. China Metrology, (10) : 53–54 .
  • ( 冯国进, 王煜, 郑春第, 吴厚平, 张巧香, 李平. 2006. 材料的红外光谱透反射性能测量研究. 中国计量, (10) : 53–54. )
  • Han W Q, Zhao S H, Feng X Z, Chen L. Extraction of multilayer vegetation coverage using airborne LiDAR discrete points with intensity information in urban areas:acase study in Nanjing City, China. International Journal of Applied Earth Observation and Geoinformation. 2014 : 56 -64.
  • Höfle B, Pfeifer N. Correction of laser scanning intensity data:data and model-driven approaches. ISPRS Journal of Photogrammetry and Remote Sensing. 2007 : 415 -433.
  • Kaasalainen S, Ahokas E, Hyyppä J, Suomalainen J.2005.Study of surface brightness from backscattered laser intensity:calibration of laser data. IEEE Geoscience and Remote Sensing Letters, 2 (3) : 255–259 . [DOI:10.1109/LGRS.2005.850534]
  • Kaasalainen S, Hyyppa H, Kukko A, Litkey P, Ahokas E, Hyyppa J, Lehner H, Jaakkola A, Suomalainen J, Akujarvi A, Kaasalainen M, Pyysalo U.2009.Radiometric calibration of LIDAR intensity with commercially available reference targets. IEEE Transactions on Geoscience and Remote Sensing, 47 (2) : 588–598 . [DOI:10.1109/TGRS.2008.2003351]
  • Li Z L, Chen J, Baltsavias E.2008.Advances in Photogrammetry, Remote Sensing and Spatial Information Sciences:2008 ISPRS Congress Book. London:CRC Press Liu J N, Zhang X H. 2005.Classification of laser scanning altimetry data using laser intensity. Geomatics and Information Science of Wuhan University, 30 (3) : 189–193 .
  • ( 刘经南, 张小红. 2005. 利用激光强度信息分类激光扫描测高数据. 武汉大学学报·信息科学版), 30 (3) : 189–193. )
  • Mesas-Carrascosa F J, Castillejo-González I L, de la Orden M S, Porras A G F.2012.Combining LiDAR intensity with aerial camera data to discriminate agricultural land uses. Computers and Electronics in Agriculture, 84 : 36–46 . [DOI:10.1016/j.compag.2012.02.020]
  • Petzold B, Axelsson P.2000.Result of the OEEPE WG on Laser Data Acquisition. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 33 (B3) : 718–723 .
  • Qin Y C, Li B, Niu Z, Huang W J, Wang W J.2011.Stepwise decomposition and relative radiometric normalization for small footprint LiDAR waveform. Science China Earth Sciences, 54 (4) : 625–630 .
  • ( 覃驭楚, 李斌, 牛铮, 黄文江, 王长耀. 2011. 小光斑激光雷达全波形数据递进分解与相对辐射校正. 中国科学:地球科学, 41 (1) : 103–109. [DOI:10.1007/s11430-010-4120-y] )
  • Solberg S, Nansset E, Hanssen K H, Christiansen E.2006.Mapping defoliation during a severe insect attack on Scots pine using airborne laser scanning. Remote Sensing of Environment, 102 (3/4) : 364–376 . [DOI:10.1016/j.rse.2006.03.001]
  • Song J H, Han S H, Yu K, Kim Y I.2002.Assessing the possibility of land-cover classification using LIDAR intensity data//ISPRS Commission Ⅲ, Symposium 2002. Graz, Austria, 259 :
  • Steinvall O.2000.Effects of target shape and reflection on laser radar cross sections. Applied Optics, 39 (24) : 4381–4391 . [DOI:10.1364/AO.39.004381]
  • Tong Q X, Zhang B, Zheng L F. Hyperspectral Remote Sensing-Principle、Technology and Application. Beijing: High Education Press 2006 : 16 -18.
  • ( 童庆禧, 张兵, 郑兰芬. 2006. 高光谱遥感--原理、技术与应用. 北京: 高等教育出版社 : 16 -18. )
  • Vain A, Kaasalainen S, Hyyppä J, Ahokas E.2009.Calibration of laser scanning intensity data using brightness targets. The method developed by the Finnish geodetic institute. Geodesy and Cartography, 35 (3) : 77–81 . [DOI:10.3846/1392-1541.2009.35.77-81]
  • Wagner W, Ullrich A, Melzer T, Briese C, Kraus K.2004.From single-pulse to full-waveform airborne laser scanners:potential and practical challenges. International Archives of Photogrammetry and Remote Sensing, 35 : 201–206 .
  • Yan W Y, Shaker A, Habib A, Kersting A P.2012.Improving classification accuracy of airborne LiDAR intensity data by geometric calibration and radiometric correction. ISPRS Journal of Photogrammetry and Remote Sensing, 67 : 35–44 . [DOI:10.1016/j.isprsjprs.2011.10.005]
  • Yao W, Krzystek P, Heurich M.2012.Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sensing of Environment, 123 : 368–380 . [DOI:10.1016/j.rse.2012.03.027]
  • Yoon J S, Shin J I, Lee K S.2008.Land cover characteristics of airborne LiDAR intensity data:a case study. IEEE Geoscience and Remote Sensing Letters, 5 (4) : 801–805 . [DOI:10.1109/LGRS.2008.2000754]
  • Zhang X H. The Theory and Algorithms of Airborne Light Detection and Ranging Technology. Wuhan: Wuhan University Press 2007 : 118 -123.
  • ( 张小红. 2007. 机载激光雷达测量技术理论与方法. 武汉: 武汉大学出版社 : 118 -123. )