合成孔径雷达(SAR)是一种微波成像传感器，具有全天时、全天候、多波段、多极化等特点，在国民经济和国防建设中有广泛的应用，如反弹道导弹的防御系统、海洋监测系统、矿藏探测等(吴亮斌，2013)。

影响SAR图像自动目标识别(ATR)的关键因素包括特征提取及特征选择，以及分类器设计两方面(王寿彪等，2011)。目前SAR ATR采用的特征主要包括基于数学变换的特征、计算机视觉特征和电磁特征等。基于数学变换的特征有小波变换、主元分析、独立成分分析等。由于这类特征通常具有较高的目标识别率，一般可直接使用或对多个特征进行融合(Cui等，2013)。计算机视觉特征主要有纹理、姿态角、形状、分形维数、主导边界等(贺志国等，2008)；常见的电磁特征有散射中心、HRR剖面等。这两类特征能对应到成像场景中的目标，由于单个特征分类效果较差，一般通过使用多个特征组合以提高判别能力。对于一个SAR图像的多个特征而言，会存在特征集的冗余问题、过适应问题和实时显著特征的选取问题。特征选择是解决上述问题的有效手段之一。早期特征选择大部分来源于专家的经验，后来随着问题的深入和技术的发展，研究人员提出了一系列的特征选择算法。王培伟(2010)提出一种基于量子进化理论的特征选择方法，该方法结合了量子计算的并行性能力以及进化算法的寻优能力，在SAR图像分割方面取得了较好的效果。Maghsoudi等人(2012)提出一种封装式的特征选择方法来选择极化SAR特征，实验结果表明这种方法比基线分类器更适应于森林识别。Bhanu和Lin(2003)提取分形维数、方差、距离等SAR图像特征，提出了一种基于遗传算法(GA)的特征选择方法，对MSTAR实测数据取得了较好结果。在Bhanu和Lin(2003)基础上，高贵等人(2008)改进了遗传算法的适应度函数，增加指标漏报数，使得该适应度函数对于特征优劣的评价更全面。Amoon等人(2014)利用图像处理方法分割图像，然后提取Zernike矩作为候选特征，将粒子群算法(PSO)用于特征选择，能够较好地区分目标和杂波虚警，但由于目标受到噪声的影响，分割效果不是很好，且它的研究是在目标鉴别阶段，未在目标分类阶段进行进一步研究。

本文在上述研究基础上，首先提出了一种基于分形特征的方位角估计方法，然后基于未校正和校正后的图像提取Zernike矩、纹理特征等组成候选特征集合，最后基于混合智能优化算法实现了SAR图像分类的特征选择。采用MSTAR数据库对提出的特征提取和特征选择算法进行验证。

分形模型在一定尺度范围内可以很好地与自然物体的表面或者空间结构结构相吻合，而分形模型的这种规律性表达与人造目标的表面或者空间结构存在一定的差异性。根据分形特征的不同，提取自然背景中的人造目标来实现对人造目标的增强。多尺度分形特征(MFFK)是一个分形参数变化度量函数，MFFK可以理解为在ε_max的尺度范围内D维面积(K(x，y，ε))的变化程度，利用MFFK来实现突出人造目标与自然背景在分形特征上的差异(刘俊，2010)。

$ \sum\limits_{\varepsilon = 2}^{{\varepsilon _{\max }}} {{{\left[ {K\left({x，y，\varepsilon } \right)- \frac{1}{{{\varepsilon _{\max }} - 1}}\sum\limits_{\varepsilon = 2}^{{\varepsilon _{\max }}} {K\left({x，y，\varepsilon } \right)} } \right]}^2}} $      (1)

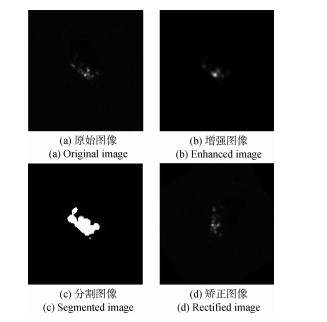
通过设置合适的最大尺度ε_max，对原始SAR图像中每个像素进行MFFK计算，并生成对应的MFFK图像，即可实现SAR图像中的目标增强，如图 1(b)所示。

点击放大

下载原图

图1 主站坦克T72的增强图像及矫正结果

Figure 1 Enhanced and rectified image for T72

目标方位角对SAR成像具有较大影响，同时目标方位角也是SAR目标的一个有效特征。设定阈值为5，对增强后图像进行分割得到二值化图像，如图 1(c)所示，然后利用Hu不变矩估计目标的方位角(Bradski，1998)，计算公式为

$ \theta = \frac{{{{\tan }^{ - 1}}\left({\frac{{2\left({\frac{{{M_{11}}}}{{{M_{00}}}} - {x_c}{y_c}} \right)}}{{\left({\frac{{{M_{20}}}}{{{M_{00}}}} - x_c^2} \right)- \left({\frac{{{M_{02}}}}{{{M_{00}}}} - y_c^2} \right)}}} \right)}}{2} $ (2)

式中，M₀₂、M₂₀、M₁₁为二阶矩，M₀₀为零阶矩，(x_c，y_c)表示图像的质心。图 1(d)显示了根据估计的方位角矫正后的图像。

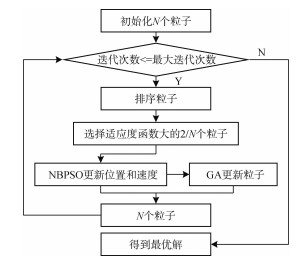
由于受相干斑噪声和目标阴影等的影响，使得估计得到的方位角会存在一定的误差，故本文基于未校正和校正后的图像分别提取Zernike矩、纹理特征等构成185维候选特征集合，分类器采用支持向量机(SVM)，采用一种融合遗传算法和改进二值粒子群的智能优化算法获得最优特征集合，算法流程图如图 2所示。下面将详细介绍特征集合构建及混合智能优化算法。

点击放大

下载原图

图2 基于混合智能优化算法的SAR图像特征选择流程图

Figure 2 Flow chart of feature selection for SAR image based on hybrid intelligent optimization algorithm

Zernike矩是一幅图像在一组Zernike多项式上的投影。Teague(1980)以复域Zernike多项式为基，得到了具有正交、旋转不变特性的Zernike矩。一幅离散图像I的n阶m重Zernike矩定义为

$ {Z_{n，m}} = \frac{{\left({n + 1} \right)}}{{\pi {{\left({N - 1} \right)}^2}}}\sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{N - 1} {I\left({x，y} \right){R_{n，m}}\left(\rho \right)} } {e^{jm\theta }} $ (3)

式中，n=0，1，2，…，0≤|m|≤n，且n－|m|为偶数。(ρ，θ)是在单位圆下的极坐标表现形式，R_n，m是径向多项式。Zernike矩有两个很重要的特点：(1)虽然Zernike矩依赖于目标的平移中心化，但幅值具有旋转不变性，即一幅图像在旋转之后幅值不发生变化，因此可以用Zernike矩的幅值提取SAR图像的形状特征；(2)R_n，m相互正交，可在忽略目标的形状情况下从感兴趣区域提取Zernike矩作为目标的幅值特征(Amoon等，2014)。当阶数n取值[2，10]时，分别基于原图像提取34维Zernike幅值特征和基于分形增强后的分割图像提取34维Zernike矩形状特征。

由于SAR图像的纹理特征也是常采用的分类特征，故本文通过灰度共生矩阵(Cluasi，2011)和Gabor滤波器(Cluasi，2011)两种方法提取纹理特征，灰度共生矩阵是用两个位置像素的联合概率密度来定义的，其不仅反映了影像亮度的分布特性，也反映了影像中具有同样亮度或相近亮度的像素之间的位置分布特性，将能量、熵、惯性矩、相关的均值和标准差作为8维纹理特征；Gabor滤波器具有很强的空间定位和方向选择性，通过一组Gabor小波获取SAR图像16维局部纹理特征。

利用分形特征得到的SAR分割图像提取1维方位角特征，基于原始SAR图像和矫正图像分别提取Zernike矩特征、纹理特征，联合构成185维候选特征集合。

GA和PSO是两种广泛采用的智能优化方法，其中GA具有广泛的空间搜索能力，但是进化时没有考虑个体自身的发展，算法收敛速度较慢；PSO具有实现容易、精度高、收敛快等优点，但容易陷入局部最优解(高卫峰和刘三阳，2011)。本文在吸收两类算法的优点基础上设计一种混合智能优化算法用于SAR图像特征选择。由于SAR图像特征选择问题属于离散优化问题，因此本文采用了一种改进的二进制粒子群算法(NBPSO)(Khanesar等，2007)，由于其在粒子更新过程中考虑了粒子前一时刻的状态，故能取得更好的优化效果。

在NBPSO中，粒子速度的更新公式为：

$ {v_{ij}} = \left\{ \begin{array}{l}v_{ij}^1\;\;\;\;若{x_{ij}} = 0\\v_{ij}^0\;\;\;\;若{x_{ij}} = 1\end{array} \right. $ (4)

式中，v¹_ij、v⁰_ij分别表示第i个粒子第j位的位置变为1或者0的概率。设P_ibst和P_gbest分别为第i个粒子的局部极值和所有粒子的全局最优值，当P_ibst或P_gbest为0时，v⁰_ij增加，v¹_ij减小；反之，当P_ibst或P_gbest为1时，v⁰_ij减小，v¹_ij增加，具体更新公式见Khanesar等人(2007)的文献。通过这种方式，粒子某一位变为1或变为0的方向能保持下去并用于粒子的更新。粒子位置的更新公式为：

$ {x_{ij}}\left({t + 1} \right)= \left\{ \begin{array}{l}{{\bar x}_{ij}}\left(t \right)\;\;\;若{r_{ij}} \le {v_{ij}}'\\{x_{ij}}\left(t \right)\;\;\;若{r_{ij}} > {v_{ij}}'\end{array} \right. $ (5)

式中，v′_ij(t)=sigv_ij(t)，_ij(t)表示x_ij(t)在二进制下的取反，r_ij是在[0，1]区间的随机数。

由于NBPSO容易陷入局部最优解，本文将GA的复制、交叉和变异操作运用到NBPSO中，得到更加优秀的下一代群体。采用的混合智能优化算法流程图如图 3所示。算法具体步骤如下：

点击放大

下载原图

图3 混合智能优化算法流程图

Figure 3 Flow chart of hybrid intelligent optimization algorithm

步骤1 初始化N个粒子的位置和速度；

步骤2 选择优秀粒子。根据N个粒子的适应度函数值排序，将适应度函数值高的N/2个粒子作为优秀粒子保留，另外N/2个粒子舍弃；

步骤3 粒子更新。首先采用NBPSO算法更新保留的N/2个粒子的位置和速度，然后对新粒子进行GA操作得到N/2个粒子，最后将两次得到的更新粒子组合成下一代N个粒子，这样就完成了整个粒子群的更新；

步骤4 判断是否达到最大迭代次数，若满足则停止迭代，否则继续进行步骤2、3。

粒子以及染色体编码和适应度函数设计是设计优化算法需解决的关键问题。本文编码方式采用二进制编码，1表示该特征被选中，0表示未被选中。适应度函数从目标识别率和识别时间两方面考虑，采用权重的方法获得的适应度函数如式(6)表示。

$ Fitness = a \times AC + b \times \left({1 - {L_0}/L} \right) $ (6)

式中，AC表示基于当前特征子集的识别率，L₀表示当前子集合的特征个数，L为特征总个数，权重系数a、b的取值分别为0.8、0.2。

采用MSTAR数据库验证本文提出的算法。MSTAR数据库中的SAR图像是通过采用HH极化、0.3 m×0.3 m分辨率、X波段的SAR传感器采集得到。本文采用了3种BMP2装甲车、1种BTR70装甲车、3种T72主战坦克共7种型号的地物目标，实验中采用训练集和测试集的种类和个数如表 1所示。图像的像素尺寸为128×128，目标方位角在0—360°之间变化，训练集和测试集的俯视角分别为17°、15°。某一方位角下的3类SAR目标图像如图 4所示。

表 1 MSTAR数据库概述
Table 1 Description of MSTAR database 下载CSV 

类型	型号	训练集	测试集
BMP2	SN_9563	233	195
	SN_9566	233	196
	SN_C21	233	196
BTR70	SN_C71	233	196
T72	SN_132	233	196
	SN_812	233	195
	SN_S7	232	191

点击放大

下载原图

图4 3类SAR目标图像

Figure 4 Images for three type of SAR objects

实验中采用交叉验证的方法训练分类模型，按照方位角把训练集分为4份，每一份覆盖0—360°方位角。对每一幅训练图像提取185维特征向量，分割SAR图像使用的阈值是5，以目标质心为中心裁剪61×61大小的图像，Gabor函数中波长设为1.5、高斯函数的两个参数都设为0.5。将185维候选特征集合采用混合智能优化算法的方法进行特征选择，初始种群用随机方法生成，参数如表 2所示。

表 2 混合智能优化算法参数
Table 2 Parameters of hybrid intelligent optimization algorithm 下载CSV 

	学习因子(两个)	惯性权重	交叉概率	变异概率	种群大小	最大迭代次数
参数取值	1	0.5	0.8	0.01	50	50

本文采用SVM作为分类器，惩罚因子C和参数γ由交叉验证和网格参数寻优方法训练得到，实验中取C=32，γ=2。PC参数为2.00 GB RAM、Pentium(R)/2.60 GHz，以MATLAB 2011a为实验环境。

此外，实现了基于GA(高贵等，2008)、NBPSO、GAPSO算法的特征选择，其中GA的初始交叉率为0.8，初始变异率ρ_m=0.01，在搜索过程中，若最优特征子集合的适应度函数值超过3代没有提高，那么以0.02的幅度按代增加变异率，一旦适应度增加，重置变异率为ρ_m=0.01；但是当变异率大于0.09 时，终止迭代寻优；NBPSO、GAPSO的参数与GANBPSO保持一致。表 3列出由4种特征选择算法得到的最优特征集合及特征数。

表 3 最优特征集合
Table 3 Optimal feature sets 下载CSV 

特征选择方法	最优特征集合	特征数
GA	1-3-5-7-8-9-10-11-13-16-20-22-23-25-26-27-30-33-35-37-40-42-44-46-55-62-65-67-68-69-75-77-78-79-83-84-85-86-89-90-92-93-95-98-99-101-102-104-109-111-121-123-127-128-130-132-137-142-146-150-154-157-160-164-167-170-173-174-175	68
NBPSO	1-5-6-7-12-13-16-17-19-20-21-25-37-38-39-43-46-52-55-59-60-61-62-63-64-65-73-77-78-84-92-93-98-99-102-105-107-110-111-116-117-118-119-120-122-123-124-127-129-134-137-138-139-140-143-144-145-149-150-151-152-154-155-156-160-169-170-171-172-177-178-182-184	73
GAPSO	3-4-7-9-15-16-17-19-21-23-24-25-26-28-31-34-37-40-41-45-46-52-57-59-62-64-65-66-67-70-77-80-82-84-87-88-94-96-103-105-106-110-113-115-121-126-132-135-140-143-152-154-161-163-164-165-169-170-171-176-177-179-180-181-182	65
GANBPSO	1-3-4-5-7-10-13-18-19-20-21-23-26-27-29-30-31-32-34-35-36-37-39-42-45-50-53-59-60-63-71-78-80-82-85-86-89-90-93-96-97-98-101-104-106-107-108-109-111-112-114-115-117-119-120-121-125-132-134-135-138-139-142-143-145-146-149-151-152-153-156-158-167-170-176-177-178-179-184	79

本文将最优特征集合在不同的实验条件下进行目标识别实验，测试样本均采用测试集中的所有样本，训练样本从训练集中抽取。表 4给出训练样本60个时的实验结果，分析5种特征集合的识别结果可知，4种优化方法得到的特征集合在识别率和识别时间上都优于采用全部特征的结果，识别时间缩减一半，其中GANBPSO的识别率是最高的；但是从识别时间来说NBPSO最快，这是因为特征提取时间和分类器模型复杂度决定识别时间，它们与特征个数和特征复杂度有关，特征个数少、特征复杂度低，那么特征提取时间短、分类器模型复杂度低，相应的识别时间也少。运用GANBPSO最优特征集合的平均识别率高于全部特征16.63%，每一类的识别率分别提升6.99%、38.26%、4.64%，第二类提升最多。GANBPSO与NBPSO、GA比较，平均识别率分别提高1.31%、6.30%，这是因为GA进化时没有考虑个体自身的发展、忽略了局部最优值，NBPSO容易陷入局部最优解。与GAPSO相比，GANBPSO最优集合的识别结果有了1.98%的提高，这说明GA与NBPSO方法结合相对于与普通的离散PSO结合能得到更好的优化解。识别率与识别时间是相互制约的，高识别率是SAR图像目标识别追求的最终目的，综合考虑，采用GANBPSO算法获得的最优特征集合的目标识别效果最好。

表 4 采用60个样本的目标识别结果
Table 4 Target recognition results using 60 samples 下载CSV 

特征集合	目标类别识别率			平均识别率	平均识别时间/s
	BMP2	BTR70	T72
全部特征	0.8143	0.4898	0.9141	0.7394	0.7732
GA算法	0.8416	0.7347	0.9519	0.8427	0.3485
NBPSO算法	0.8756	0.8520	0.9502	0.8926	0.3266
GAPSO算法	0.8825	0.8061	0.9691	0.8859	0.3286
本文算法	0.8842	0.8724	0.9605	0.9057	0.3621

表 5给出4个特征集合在训练样本分别采用训练集中所有图像条件下的实验结果。从识别率和识别时间两方面可以看出，基于4种方法的识别结果好于使用全部特征的结果，其中采用GANBPSO方法得到的最优特征集合的平均识别率高于全部特征3.47%，3类分别提升1.37%、6.63%、3.47%。与NBPSO、GA两种方法比较，基于GANBPSO特征选择后的识别结果最好。

表 5 采用全部样本的目标识别结果
Table 5 The target recognition results using all samples 下载CSV 

特征集合	目标类别识别率			平均识别率	平均识别时间/s
	BMP2	BTR70	T72
全部特征	0.9182	0.8776	0.9519	0.9159	1.6243
GA算法	0.9148	0.8673	0.9691	0.9171	0.5571
NBPSO算法	0.9319	0.8929	0.9708	0.9318	0.5803
GAPSO算法	0.9284	0.9133	0.9777	0.9398	0.5209
本文算法	0.9319	0.9439	0.9759	0.9506	0.5401

根据SVM的原理可知，训练样本数越多，目标特征分布的统计特性越明显，但由于噪声等影响，使得分类器复杂度也越高，从而使识别时间变慢。表 4中较表 5中对应的每一个特征集合的识别率都有一定的提升，识别时间也变长。综上所述，经本文算法优化后的特征集合能较好的识别目标，识别结果优于采用全部特征的结果，并提高了实时性。

本文提出了一种基于分形特征和图像矩的方位角估计方法，然后基于未校正和校正后的图像分别提取Zernike矩、Gabor小波系数和灰度共生矩阵构成候选特征集合，采用融合GA和NBPSO的优化算法进行特征选择。实验结果表明，采用优化后的特征集合进行目标分类，一方面提高了目标识别率，另一方面减少了算法的识别时间，具有一定的泛化能力。