|
|
|
收稿日期: 2015-06-10; 修订日期: 2015-09-09; 优先数字出版日期: 2015-09-16
基金项目: 教育部高等学校博士学科点专项科研基金资助(编号:20122121110007);国家自然科学基金面上项目(编号:41271435)
中图分类号: P237
文献标识码: A
文章编号: 1007-4619(2016)01-0103-11
|
摘要
为解决高分辨率遥感影像分割中,由光谱测度的空间复杂性、相同类型地物目标异质性增大带来的类属不确定性以及分割决策不确定性等引起的分割精度下降问题,提出一种融入空间关系的区间二型模糊模型高分辨率遥感影像监督分割方法。(1)建立高斯函数模型作为一型模糊模型,用来刻画像素类属的不确定性;(2)模糊化一型模糊模型中的均值或标准差,建立区间二型模糊模型,以强化类属的不确定表达和增加分割决策信息;(3)综合一型模糊模型及区间二型模糊模型的上、下隶属函数建模模糊决策模型;(4)融入邻域像素关系,使用待分像素及其邻域像素在模糊决策模型中的隶属度共同决定像素的类属。采用本文算法分别对真实高分辨遥感影像及合成影像进行分割,并对测试结果进行定性和定量分析。结果表明,本文算法可以得到更高的分割精度。
关键词
区间二型模糊模型; 不确定轨迹; 高分辨率; 遥感影像分割; 次隶属函数
1 引 言
高分辨率遥感数据能够更加清晰地呈现地物目标的细节信息,极大地消除了混合像元所引起的像素类属的不确定性,在地物目标的精准分割中表现出巨大的潜力与优势。然而,更加精细的空间尺度也使遥感影像中像素光谱测度的空间相关性变得更加复杂,如同一地物目标内像素光谱测度相似性减弱,不同地物目标间像素光谱测度相似性增强(Bruzzone和Carlin,2006),从而使相同类型地物表现出更多的异质性和空间破碎性。上述特征又从另一方面增加了像素类属的不确定性,同时由于高分辨率遥感影像覆盖地物的复杂性,缺乏真实地表覆盖信息,从而导致了分割决策的不确定性。上述两种不确定性,给高分辨率遥感影像分割带来新的问题与困难。
目前,模糊聚类方法(如一型模糊模型)是解决不确定数据聚类问题最为常用和有效的方法之一,其中融入像素相关性的模糊C均值FCM(Fuzzy C-Means)算法(Bezdek,1981),由于能够有效处理像素的空间相关性,具有充分刻画影像中存在的光谱测度的模糊性和不确定性等优良特征,应用最为广泛。该算法利用隶属度函数表征像素类属的不确定性,通过定义非相似性测度构建目标函数,并在构建目标函数的过程中定义邻域像素光谱测度的确定性函数建模邻域关系(Cai等,2007;Ahmed等,2002)或利用马尔可夫随机场(Markov R and om Field,MRF)建立邻域像素的相关性模型(Chatzis和Varvarigon,2008;刘思远等,2007),最后通过求解目标函数得到最佳模糊分割。虽然这些算法在一定程度上平滑了噪声,有效解决了由像素的空间相关性引起的像素类属的不确定性问题,进而提高了算法的分割精度,但却无法处理高分辨率影像中分割决策的不确定性对分割结果的影响。
应用二型模糊理论处理不确定性问题是近年出现的一种新方法。在二型模糊理论中,用主隶属函数和次隶函数表征二型模糊集合(Karnik和Mendel,2001),主隶属度集合中每个元素不再是单一确定的值,而是[0,1]之间的模糊集合。相对于一型模糊集合,二型模糊集合对不确定性描述更加精确,提供信息更加丰富,正确处理不确定信息的能力更强。目前已成功应用于模式识别(John等,2000;Liang和Mendel,2001),语音识别(Melin等,2006),数据挖掘(Mendel,2000)以及时间序列决策(Karnik等,1999)等领域。然而较高的计算代价限制了其应用性,在实际中最为常用的是区间二型模糊理论。该理论假定二型模糊集合中每个元素出现的概率相同,有效降低了计算的复杂度。目前,常用的区间二型模糊模型有基于MRF的二型模糊模型(Zeng等,2008),基于高斯混合模型的二型模糊模型(Zeng和Liu,2006;Ju和Liu,2012),基于FCM(Zhou和Liu,2010;Begum和Devi,2012)的二型模糊模型(T2FCM),基于遗传算法的二型模糊模型(Hidalgo等,2009)和基于神经网络的二型模糊模型(Sánchez和Melin等,2010)等。
将区间二型模糊模型降型为一型模糊模型(构建模糊分割决策模型)一直是二型模糊理论研究的重点,该模糊决策模型的质量直接影响识别的精度。Zeng和Xie(2008)通过定义模糊隐马尔科夫随机场计算得到区间型最佳状态序列,将该序列中各区间的重心序列作为最佳状态序列;在进行语音识别的过程中,Zeng和Liu(2006)首先扩展高斯混合模型得到区间二型模糊高斯混合模型,并将区间似然作为特征向量,建立广义线性模型作为决策模型,以提高识别精度;Begum和Devi(2012)将FCM目标函数中的模糊因子模糊化,计算得到区间型模糊隶属度矩阵和区间型模糊聚类中心,然后将该区间型模糊聚类中心的重心作为新的聚类中心,提高了分割精度。在反模糊化分割决策中,上述方法均依赖区间二型模糊模型上、下隶属函数,虽然在一定程度上提高了决策质量,却没有考虑到主隶属函数对于决策的重要影响。特别是在影像分割过程中没有考虑像素的空间相关性对分割精度的影响。
在影像分割中,为了合理建模高分辨率遥感影像中像素的光谱特征,有效处理像素类属的不确定性及分割决策的不确定性,提高分割精度,本文在二型模糊理论框架下,提出一种融入空间关系的高分辨遥感影像监督分割算法。该算法首先利用高斯函数对影像建立一型模糊模型,用来表征像素类属的不确定性;然后扩展一型模糊模型中的均值与标准差,构建区间二型模糊模型,用来改善一型模糊模型隶属度对类属不确定性的表达并为增强分割决策的准确性提供依据;再根据训练数据的主隶属度,上、下隶属度等信息对分割结果的影响程度构建模糊分割决策模型,得到刻画分割决策不确定性的隶属度;最后,由像素及其邻域像素的上述隶属度共同确定该像素的类属性,从而实现高分辨率遥感影像的最优分割。
2 算法描述
2.1 区间二型模糊集合
给定集合Z,∀z∈Z的二型模糊集合T2FS(Type-2 Fuzzy Set)记为$\tilde A$,用二型模糊隶属函数u$\tilde A$(z,u)表征,T2FS定义如下:
$ \begin{array}{*{20}{c}}{\tilde A = }\\{\left\{ {\left({\left({z,u} \right),{u_{\tilde A\left({z,u} \right)}}|\forall z \in Z,\forall u \in {J_z} \subseteq \left[ {0,1} \right]} \right)} \right\}}\end{array} $ (1)
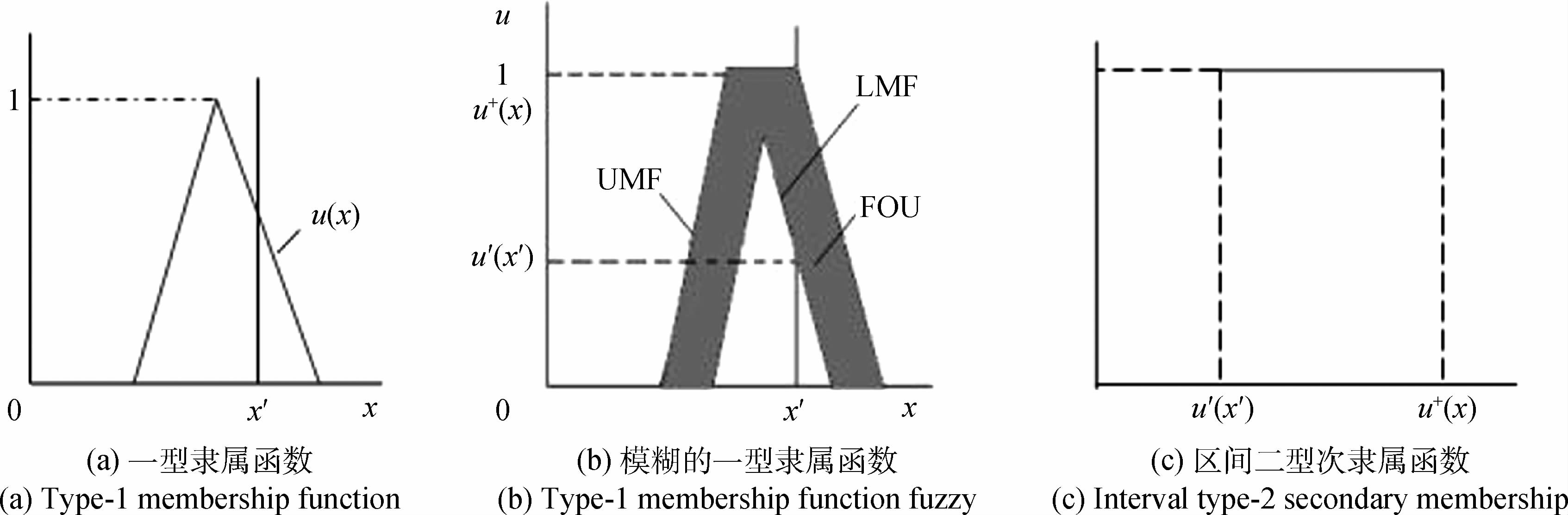
式中,u是z的一型隶属函数,Jz是u的区间取值。二型模糊隶属函数u$\tilde A$(z,u)是u的隶属函数,并且满足0≤u$\tilde A$(z,u)≤1。当u$\tilde A$(z,u)=1时,该二型模糊隶属函数称之为区间二型隶属函数ITMF(Interval Type-2 Membership Function),$\tilde A$称为区间二型模糊集合IT2FS(Interval Type-2 Fuzzy Set),ITMF上边界称为上隶属函数UMF(Upper Membership Function),下边界称为下隶属函数LMF(Lower Membership Function)。Jz的并集称为不确定轨迹(Footprint of Uncertainty,FOU)(Mendel和John,2002)。
图 1(a)为关于x的三角型隶属函数u(x)(一型隶属函数),其最大隶属度为1,在x′ 处的隶属度为u(x′);图 1(b)是向左向右移动u(x)得到的模糊化的一型模糊隶属函数,此时x的隶属函数为一区间型隶属函数,该区间即为x的FOU,如在x′处的隶属度为一区间取值[u-(x′),u+(x′)],u-(x′)为x′的下隶属度,u+(x′)为x′的上隶属度;图 1(c)表示对图 1(b)中FOU次隶属度取值u$\tilde A$(x,u)=1。此时图 1(b)即为ITMF。
2.2 模糊图像模型
(1)一型模糊模型
模糊方法中每个像素可以属于所有类别,并用模糊隶属度表示像素隶属于不同类别的程度。对于给定图像X={xj,j=1,…,n},j为像素索引,n为总像素数,xj为第j个像素光谱测度,建立如下模糊隶属度矩阵:
$ F = {\left[ {{F_{ji}}} \right]_{n \times m}} $ (2)
式中,m为类别,i=1,…,m为类别索引,Fji表示第j个像素属于第i类的隶属程度,满足约束条件0≤Fji≤1并且$\sum\limits_{j = 1}^n {{F_{ji}} = 1} $。 建立以下高斯函数模型作为一型模糊模型。
$ {F_{ji}} = {\beta _i} \times \frac{1}{{\sqrt {2\pi } {\sigma _i}}}\exp \left\{ { - \frac{{{{\left({{x_j} - {\mu _i}} \right)}^2}}}{{2\sigma _i^2}}} \right\} $ (3)
式中,系数0<βi≤1使Fji满足上述约束,μi、σi为第i类的均值和标准差。文中采用监督分割法按类别提取训练样本,最小二乘法对每一类训练样本进行直方图拟合建立上述一型模糊图像模型。
(2)具有不确定均值和标准差的区间二型模糊模型。
为了提高分割决策的准确性和增强像素类属的不确定性表达,扩展式(3)中的均值与标准差为一个区间,建立区间二型模糊图像模型。该模型中每个像素的隶属度为一个区间,并且区间内所有元素出现的概率相同。
具有不确定均值的区间二型模糊模型表达如下:
$ F{'_{ji}} = {\beta _i} \times \frac{1}{{\sqrt {2\pi } {\sigma _i}}}\exp \left\{ { - \frac{{{{\left({{x_j} - {\mu _{i1}}} \right)}^2}}}{{2\sigma _i^2}}} \right\} $ (4)
式中,F′ji∈[ Fji-,Fji+],μi1∈[μi-,μi+],μi-,μi+,Fji-,Fji+分别表示均值的上、下界和隶属度的上、下界。当μi1=μi-时F′ji=F′ji-,当μi1=μi+时F′ji=F′ji+ 。依据下式确定均值区间的上、下界:
$ \begin{array}{*{20}{c}}{\mu _i^ - = {\mu _i} - {\alpha _i} \times {\sigma _i}}\\{\mu _i^ + = {\mu _i} + {\alpha _i} \times {\sigma _i}\;\;\;{\alpha _i} \in \left[ {0,3} \right]}\end{array} $ (5)
式中,αi为调节因子,i=1,…,m,因为高斯分布中落在[μ-3σ,μ+3σ]之间的概率为99.7%,所以限制αi∈[0,3],来控制FOU的变化范围。
具有不确定均值的区间二型模糊模型的隶属度上界和下界计算如下:
$ F_{ji}^ + = \left\{ {\begin{array}{*{20}{c}} {F_{ji}^{, - }}&{{x_j}AAA\mu _i^ - }\\ 1&{\mu _i^ - \le {x_j} \le \mu _i^ + }\\ {F_{ji}^{, + }}&{{x_j} > \mu _i^ + } \end{array}} \right. $ (6)
$ F_{ji}^ - = \left\{ {\begin{array}{*{20}{c}} {F_{ji}^{, - }}&{{x_j} \le \frac{{\mu _i^ - + \mu _i^ + }}{2}}\\ {F_{ji}^{, + }}&{{x_j}AAA\frac{{\mu _i^ - + \mu _i^ + }}{2}} \end{array}} \right. $ (7)
具有不确定标准差的区间二型模糊模型为:
$ F{'_{ji}} = {\beta _i} \times \frac{1}{{\sqrt {2\pi } {\sigma _{i1}}}}\exp \left\{ { - \frac{{{{\left({{x_j} - {\mu _i}} \right)}^2}}}{{2\sigma _{i1}^2}}} \right\} $ (8)
式中,σi1∈[σi- ,σi+],σi-和σi+表示标准差的上、下界,依据下式确定:
$ \sigma _i^ - = \frac{{{\sigma _i}}}{{{c_i}}}\;\;\;\sigma _i^ + = {\sigma _i} \times {c_i}\;\;\;{c_i} \in \left[ {0.3,1} \right] $ (9)
式中,ci为调节因子,隶属度的上、下界依据下式计算:
$ F_{ji}^ + = {\beta _i} \times \frac{1}{{\sqrt {2\pi } \sigma _{ji}^ - }}\exp \left\{ { - \frac{{{{\left({{x_j} - {\mu _i}} \right)}^2}}}{{2\sigma _i^{ - 2}}}} \right\} $ (10)
$ F_{ji}^ - = {\beta _i} \times \frac{1}{{\sqrt {2\pi } \sigma _{ji}^ + }}\exp \left\{ { - \frac{{{{\left({{x_j} - {\mu _i}} \right)}^2}}}{{2\sigma _i^{ + 2}}}} \right\} $ (11)
2.3 模糊决策模型
灰度空间上,任意一点的一型模糊隶属度和区间二型模糊隶属函数的上、下隶属度对分割决策的影响程度与该点直方图频率值的相似性成正比,其相似性越大发挥的作用也越大;并且第j个像素属于i的类属程度不仅与上述3种隶属度有关,还与其邻域像素属于第i类的隶属程度有关,其邻域像素属于第i类的隶属度越大,第j个像素属于第i类的隶属程度就越高。根据以上原则建立融入空间关系的模糊决策模型:
$ F'{'_{ji}} = \frac{1}{{{N_j}}}\sum\limits_{k \in {N_j}} {\left({W_{ki}^ + F_{ki}^ + + {W_{ki}}{F_{ki}} + W_{ki}^ - F_{ki}^ - } \right)} $ (12)
式中,Nj=9为以第j个像素为中心的3×3窗口,k=1,…,9为窗口中像素索引。Fki 、Fki+和Fki-表示窗口中第k个像素属于第 i 类的主隶属度及上、下隶属度。0≤Wki≤1,0≤Wki+≤1,0≤Wki-≤1表示窗口内3种隶属度在模糊决策模型中的权重,并且满足约束条件Wki-+Wki+Wki+=1。文中用Euclidean距离定义各类别训练数据的3种隶属度与其对应直方图频率值的相似性程度,公式如下:
$ \begin{array}{*{20}{c}}{{A_{ki}} = \frac{1}{{{{\left({{y_{ki}} - {F_{ki}}} \right)}^2}}};}\\{A_{ki}^ + = \frac{1}{{{{\left({{y_{ki}} - F_{ki}^ + } \right)}^2}}};A_{ki}^ - = \frac{1}{{{{\left({{y_{ki}} - F_{ki}^ - } \right)}^2}}}}\end{array} $ (13)
式中,yki表示窗口内第k个像素在第i类直方图中的频率值。规则化式(13)得权重公式如下:
$ {W_{ki}} = \left\{ {\begin{array}{*{20}{c}}{\frac{{{A_{ki}}}}{{A_{ki}^ - + {A_{ki}} + A_{ki}^ + }}}&{{y_{ji}} \ne {F_{ji}}}\\1&{{y_{ji}} = {F_{ji}}}\end{array}} \right. $ (14)
$ W_{ji}^ - = \left\{ {\begin{array}{*{20}{c}}{\frac{{A_{ki}^ - }}{{A_{ki}^ - + {A_{ki}} + A_{ki}^ + }}}&{{y_{ji}} \ne F_{ji}^ - }\\1&{{y_{ji}} = F_{ji}^ - }\end{array}} \right. $ (15)
$ W_{ji}^ + = \left\{ {\begin{array}{*{20}{c}}{\frac{{A_{ki}^ + }}{{A_{ki}^ - + {A_{ki}} + A_{ki}^ + }}}&{{y_{ji}} \ne F_{ji}^ + }\\1&{{y_{ji}} = F_{ji}^ + }\end{array}} \right. $ (16)
由此可知,在不考虑邻域关系的情况下,当像素的某一隶属度值与对应的频率值相等时,该像素的类属仅由此隶属信息决定,其他隶属度不参与决策。依据式(14)—(16)对图像进行计算得到以下模糊隶属度矩阵:
$ {F^*} = {\left[ {F'{'_{ji}}} \right]_{n \times m}} $ (17)
为了得到明晰的分割结果,需要对模糊隶属度矩阵F*反模糊化,本文采用最大隶属度准则对图像进行区域划分:
$ {Z_j} = {\arg _i}\left\{ {\max \left\{ {F'{'_{ji}}} \right\}} \right\},\;\;\;i = 1,\cdots,m;j = 1,\cdots,n $ (18)
式中,Zj表示第j个像素的所属类别,并用Z={Z1,Z2,…,Zn}表示明晰分割结果。
3 实验结果与讨论
为了验证本文算法的可行性与有效性,分别对真实高分辨率影像与合成影像进行分割实验,并进行定性与定量评价。
3.1 高分辨率遥感影像
图 2(a)为1 m分辨率的IKONOS全色影像,灰度由浅到深包含土地、草坪和林区3种地物;图 2(e)和图 2(i)为0.5 m分辨率的World View-II全色影像,灰度由浅到深分别为房屋,地面和树林(图 2(e))以及道路、植被和水域(图 2(i))。图像尺寸均为256×256像素。
从图 2(a)的分割结果可以看出,相对于图 2(b)的最大似然分割方法,图 2(c)中由于区间二型模糊模型增强了对像素类属的不确定性表达,草坪的分割结果得到显著改善。林区灰度变化差异性较大,两种方法对林区的分割都存在较多的误分像素,而本文的分割方法(图 2(d))由于在二型模糊模型的基础上融入了像素的空间信息,分割结果中各类别区域内部几乎没有噪声,只在边界处存在极少的误分像素,保证了分割结果的可靠性与准确性。图 2(e)中由于3种地物同质区域内灰度变化较大,图 2(f)(g)两种方法都是基于像素本身的灰度特征进行分割,故3种地物中都存在不同程度的误分像素。图 2(h)中本文方法待分割的像素类属不但与自身特征相关,还受其周围像素类属影响,这种分割方法尤其适用于同质区域内灰度变化差异性较大的情况,故图 2(h)除了房屋中间的空隙的阴影遮挡被误分为树林,其他部分基本达到了正确分割。图 2(i)中,由于存在被树木遮挡的阴影,并且该阴影的灰度特征与水域更相近,故图 2(j)(k)中植被存在大量被分割成水域的误分像素。图 2(l)中使用本文方法植被中的误分像素与右上角水域中的误分像素大量减少,分割方法明显优于前两种方法。
3.2 合成影像
图 3为从盘锦地区World View-II全色影像中截取四类地物合成的256×256像素影像,包括Ⅰ农田、Ⅱ水域、Ⅲ居民地和Ⅳ林区。
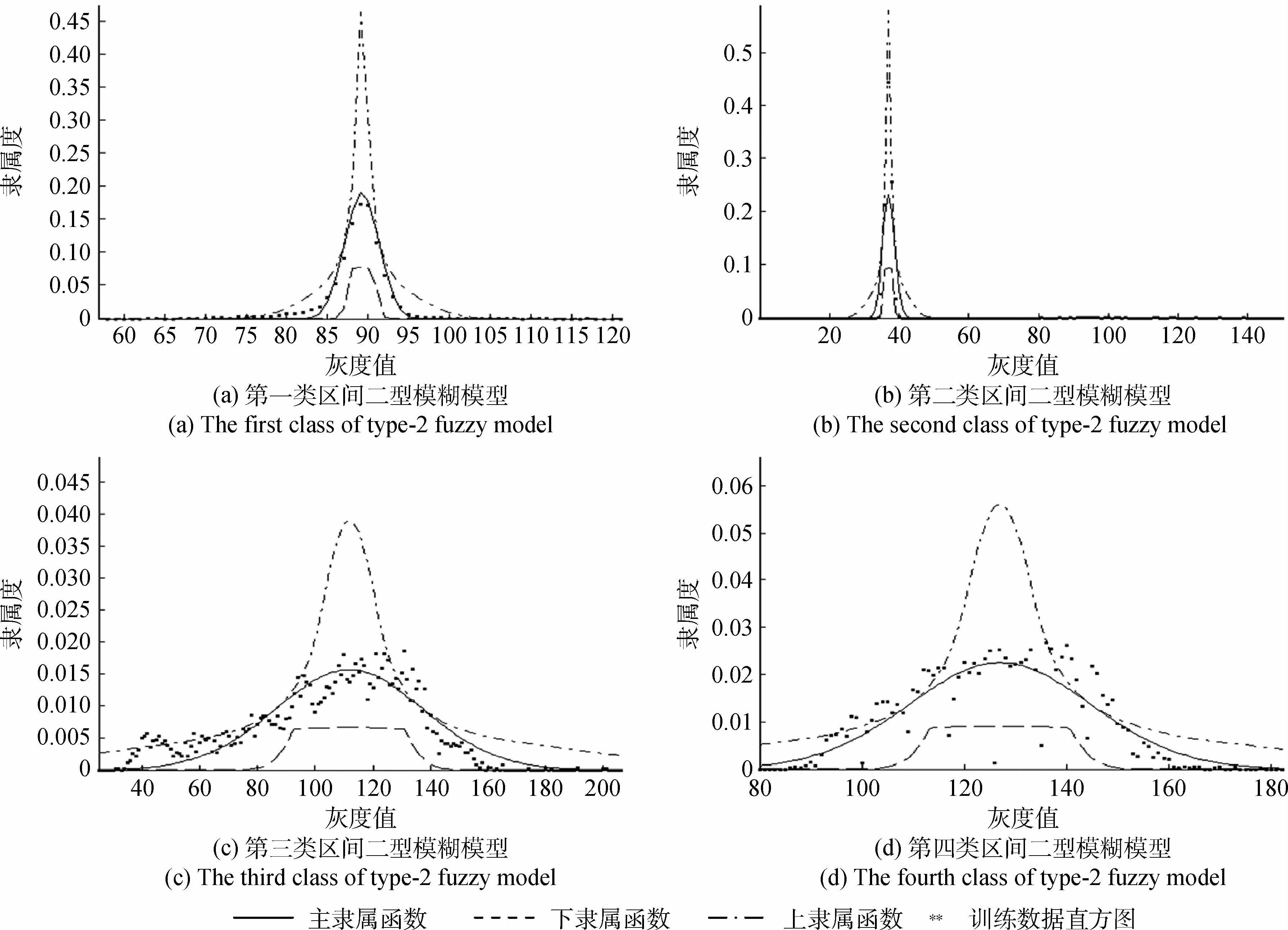
图 4是监督分割法按类别随机提取30%的训练样本并使用最小二乘法直方图拟合建立的高斯函数模型(一型模糊模型)。
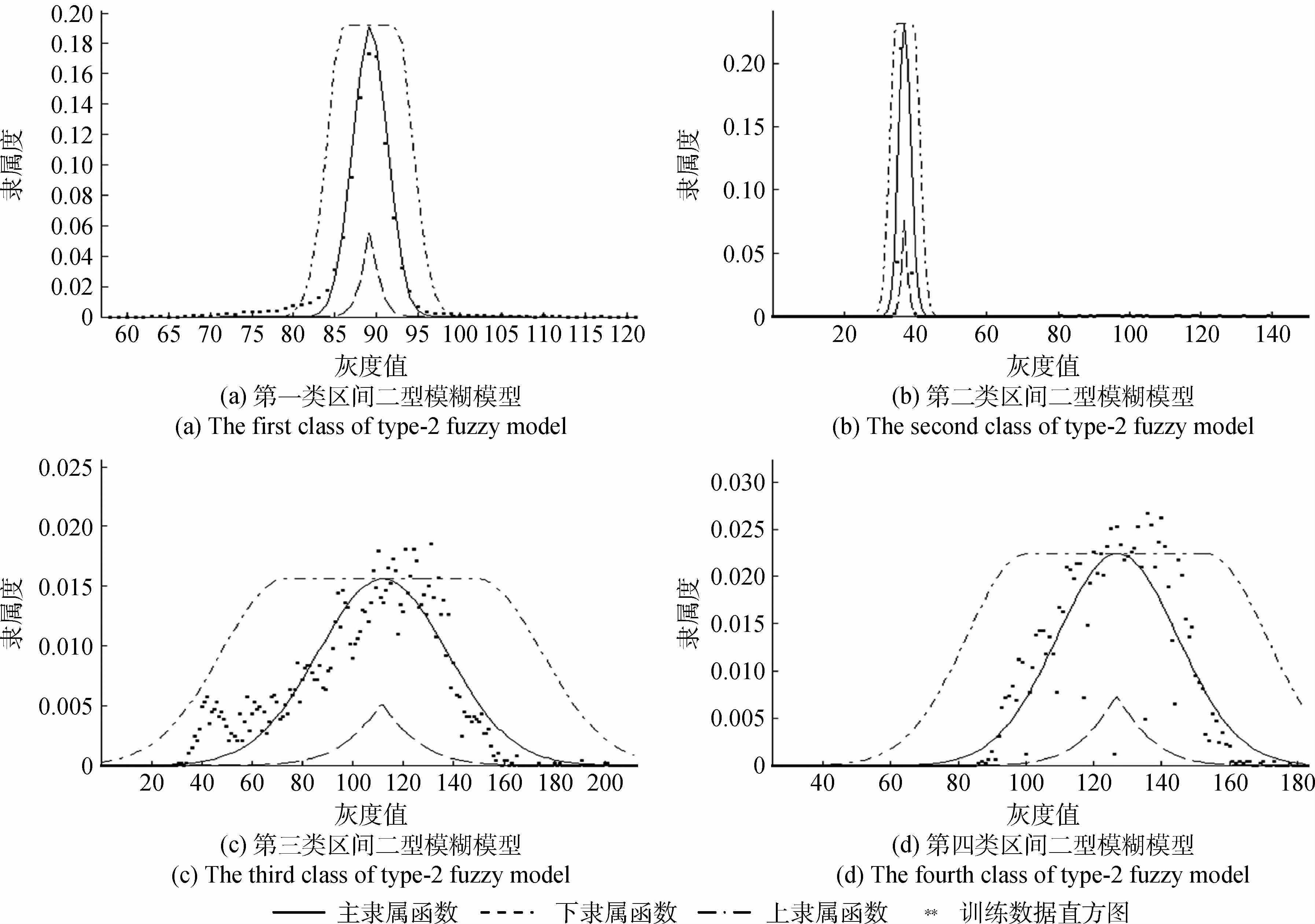
图 5表示调节因子c1=c2=c3=c4=0.4时的具有不确定标准差的区间二型模糊模型;图 6表示调节因子α1=α2=α3=α4=3时具有不确定均值的区间二型模糊模型。
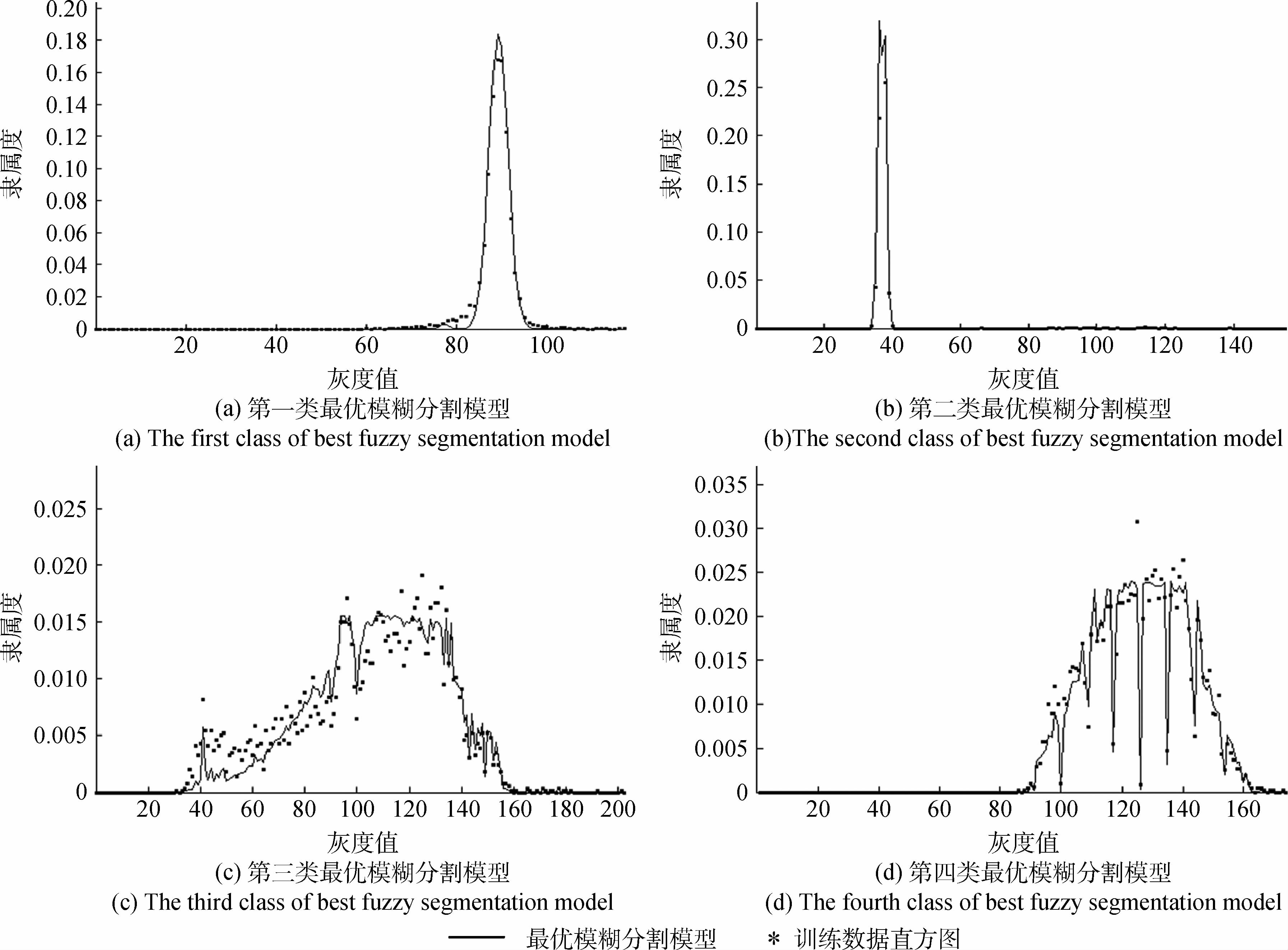
图 7表示调节因子c1=c2=c3=c4=0.4时,没有融入空间关系的具有不确定标准差的最优模糊分割决策模型;图 8表示调节因子α1=α2=α3=α4=3时,没有融入空间关系的具有不确定均值的最优模糊分割决策模型。
图 9(a)为原始影像,图 9(b)为最大似然分割结果,图 9(c)为通过调节不确定因子得到的基于不确定均值的最佳分割结果,此时α1=α2=α3=α4=3,图 9(d)为当α1=α2=α3=α4=3时,融入空间关系的区间二型模糊分割结果,图 9(e)为通过调节不确定因子得到的基于不确定标准差的最佳分割结果,此时c1=c2=c3=c4=0.4,图 9(f)为当c1=c2=c3=c4=0.4时,融入空间关系的区间二型模糊分割结果。
为了对本文方法进行定量评价,以合成影像的实际类别作为标准分别对上述分割结果求其混淆矩阵,计算用户精度、产品精度、总精度以及Kappa值(表 1),其中各项指标越大代表分割精度越高。
| 方法 | 精度指标 | 同质区域 | 调节因子 | |||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | |||
| 最大似然 | 用户精度 | 0.857 | 0.986 | 0.721 | 0.603 | |
| 产品精度 | 0.947 | 0.990 | 0.256 | 0.927 | ||
| 总精度=0.780;Kappa=0.707 | ||||||
| 区间二型 (标准差) | 用户精度 | 0.924 | 0.992 | 0.776 | 0.719 | c1=c2=c3=c4=0.4 |
| 产品精度 | 0.925 | 0.993 | 0.586 | 0.893 | ||
| 总精度=0.849;Kappa=0.800 | ||||||
| 邻域区间二型 (标准差) | 用户精度 | 0.980 | 0.992 | 0.988 | 0.971 | c1=c2=c3=c4=0.4 |
| 产品精度 | 0.995 | 0.999 | 0.953 | 0.985 | ||
| 总精度=0.983;Kappa=0.977 | ||||||
| 区间二型 (均值) | 用户精度 | 0.924 | 0.992 | 0.763 | 0.728 | α1=α2=α3=α4=3 |
| 产品精度 | 0.925 | 0.993 | 0.606 | 0.876 | ||
| 总精度=0.850;Kappa = 0.800 | ||||||
| 邻域区间二型 (均值) | 用户精度 | 0.980 | 0.992 | 0.987 | 0.971 | α1=α2=α3=α4=3 |
| 产品精度 | 0.995 | 0.998 | 0.953 | 0.984 | ||
| 总精度=0.983;Kappa=0.977 | ||||||
(1)图 3中,居民地和林区两种地物同质区域内灰度差异较大,几乎覆盖整个灰度区间,并且通过观察可以看出两类地物的灰度特征接近。图 4中第三类(居民地)和第四类(林区)两种地物的拟合模型存在相当大的重叠区域,这部分重叠区域存在的像素类属的不确定性显著,分割困难。
(2)图 5和图 6中大部分训练数据直方图被包围在区间二型模糊模型FOU内,相对于一型模糊模型区间二型模糊模型提供的信息更加丰富。图 7和图 8为没有融入空间关系最优模糊分割模型,该模型使用区间二型模糊模型的上、下隶属函数对拟合模型(一型模糊图像模型)进行全局约束,并以不规则形状拟合训练样本直方图。观察图 9(b)(c)和(e)可以看出,基于区间二型模糊模型的分割方法(c)和(e)对Ⅲ类居民地的分割结果得到很大程度上的改善。表 1中的最大似然分割方法居民地的用户精度为0.721,而产品精度仅为0.256,对于此类地物基于区间二型模糊模型的分割其用户精度为0.763和0.776,产品精度为0.606和0.586,总体精度提高7%。而对Ⅰ类中,农田的不同块交接处误分情况(被误分为居民地)无法处理,并且两种方法都不能对Ⅳ类林区实现很好的划分。
(3)图 9(d)和(f)为使用本文方法得到的分割结果,相对于以上两种方法,类别Ⅰ中,由于在二型模糊模型的基础上考虑了邻域像素的作用,Ⅰ类农田中只存在零星误分像素,Ⅱ类水域中的噪声被消除,Ⅲ类居民地和Ⅳ类林区的改善十分显著,对于居民地中存在的极少的其他像素,是因为居民区内会存在少量植被以及小块种植区,故有少量林区及农田像素存在,而房屋间的遮挡阴影灰度特征与水域显示,因此会出现被误分的零星水域像素。
(4)表 1中,使用最大似然分割其最低分割精度为0.256,总精度为0.780。使用基于区间二型模糊模型的分割,其最低分割精度为0.606和0.586,总精度为0.850,相对于最大似然精度有所提高。而本文方法由于融入邻域关系,最低分割精度为0.953,总精度达到0.983,分割精度提高显著,分割结果可靠。
4 结 论
本文提出一种融入空间关系的高分辨率遥感影像监督分割方法,以图像的一型模糊模型和区间二型模糊模型为基础,建立了模糊分割决策模型,并且融入空间关系使每个像素在模糊分割决策模型中的隶属度由窗口内像素共同确定,有效解决了高分辨率遥感影像中像素光谱测度的空间相关性带来的像素类属的不确定性问题,增强了分割决策的准确性。利用本文算法,最大似然分割方法以及没有融入空间关系的区间二型模糊模型分割方法对高分辨率真实影像和合成影像进行分割实验,并进行定性与定量对比分析验证了本文算法的可行性与有效性。本文方法考虑了邻域像素的空间相关性,克服了分割结果中的椒盐现象,对高分辨率遥感影像素灰度差异性较大的同质区域有较好的分割结果。然而,本文中使用高斯函数模型作为一型模糊模型,该模型对高分辨率遥感影像拟合能力有限,未来工作中将考虑使用高斯混合模型作为一型模糊模型,从而更精确地表达高分辨率遥感影像的细节特征,进一步提高影像的分割效果。
参考文献
Ahmed M N, Yamany S M, Mohamed N, Farag A A and Moriarty T. 2002. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data. IEEE Transactions on Medical Imaging, 21(3):193-199[DOI:10.1007/10704282_8] Begum S A and Devi O M. 2012. A Rough type-2 fuzzy clustering algorithm for MR image segmentation. International Journal of Computer Applications, 54(4):4-11[DOI:10.5120/8552-2114] Bezdek J C. 1981. Pattern Recognition with Fuzzy Objective Function Algorithms. New York:Plenum Press:79-88 Bruzzone L and Carlin L. 2006. A Multilevel context-based system for classification of very high spatial resolution images. IEEE Transactions on Geoscience and Remote Sensing, 44(9):2587-2600[DOI:10.1109/TGRS.2006.875360] Cai W L, Chen S C and Zhang D Q. 2007. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Pattern Recognition, 40(3):825-838[DOI:10.1016/j.patcog.2006.07.011] Chatzis S P and Varvarigon T A. 2008. A fuzzy clustering approach toward hidden Markov random field models for enhanced spatially constrained image segmentation. IEEE Transactions on Fuzzy Systems, 16(5):1351-1361[DOI:10./TFUZZ.2008.2005008] Hidalgo D, Castillo O and Melin P. 2009. Type-1 and type-2 fuzzy inference systems as integration methods in modular neural networks for multimodal biometry and its optimization with genetic algorithms. Information Sciences, 179(13):2123-2145[DOI:10.1016/j.ins.2008.07.013] John R I, Innocent P R and Barnes M R. 2000. Neuro-fuzzy clustering of radiographic tibia image data using type 2 fuzzy sets. Information Sciences, 125(1/4):65-82[DOI:10.1016/S0020-0255(00)00009-8] Ju Z J and Liu H H. 2012. Fuzzy gaussian mixture models. Pattern Recognition, 45(3):1146-1158[DOI:10.10.1016/j.patcog.2011.08.028] Karnik N N and Mendel J M. 2001. Centroid of a type-2 fuzzy set. Information Sciences, 132(1/4):195-220[DOI:10.1016/s0020-0255(01)00069-X] Karnik N N, Mendel J M and Liang Q L. 1999. Type-2 fuzzy logic systems. IEEE Transactions on Fuzzy Systems, 7(6):643-658[DOI:10.1109/91.811231] Liang Q L and Mendel J M. 2001. MPEG VBR video traffic modeling and classification using fuzzy technique. IEEE Transactions on Fuzzy Systems, 9(1):183-193[DOI:10.1109/91.917124] Liu S Y, Li X F, Wu H G and Li Z M. 2007. Research of fast image segmentation based on Markov spatial constraint and fuzzy C-means clustering. Application Research of Computers, 24(8):220-223 (刘思远, 李晓峰, 吴宏刚, 李在铭. 2007. FCM与马氏空间约束条件下的快速图像分割技术研究. 计算机应用研究, 24(8):220-223)[DOI:10.3969/j.issn.1001-3695.2007.08.071] Melin P, Urías J, Solano D, Soto M, Lopez M and Castillo O. 2006. Voice recognition with neural networks, type-2 fuzzy logic and genetic algorithms. Engineering Letters, 13(2):108-116 Mendel J M. 2000. Uncertain Rule-Based Fuzzy Logic Systems:Introduction and New Directions. New York:Prentice Hall Inc. Mendel J M and John R I B. 2002. Type-2 fuzzy sets made simple. IEEE Transactions on Fuzzy Systems, 10(2):117-127[DOI:10.1109/91.995115] Sánchez D and Melin P. 2010. Modular neural network with fuzzy integration and its optimization using genetic algorithms for human recognition based on iris, ear and voice biometrics//Studies in Computational Intelligence. Berlin Heidelberg:Springer:85-102[DOI:10.1007/978-3-642-15111-8_6] Zeng J and Liu Z Q. 2006. Type-2 fuzzy hidden Markov models and their application to speech recognition. IEEE Transactions on Fuzzy Systems, 14(3):454-467[DOI:10.1109/TFUZZ.2006.876366] Zeng J, Xie L and Liu Z Q. 2008. Type-2 fuzzy Gaussian mixture models. Pattern Recognition, 41(12):3636-3643[DOI:10.1016/j.patcog.2008.06.006] Zhou W H and Liu W P. 2010. Image segmentation algorithm based on type-2 fuzzy clustering. Computer Engineering, 36(24):211-213, 216 (周晚辉, 刘文萍. 2010. 基于Type-2模糊聚类的图像分割算法. 计算机工程, 36(24):211-213, 216) Segmentation of high-resolution remote sensing images with type-2 fuzzy model based on spatial relationship1. School of Mining Industry and Technology, Liaoning Technical University, Huludao 125105, China;2. School of Geomatics, Liaoning Technical University, Fuxin, 123000, ChinaAbstract
Image segmentation is a significant step in image processing. High-resolution remote sensing images can clearly characterize landscape information and eliminate the membership uncertainty caused by mixed pixels. It has considerable advantages and potential in precise segmentation. Nonetheless, the spatial complexity caused by spectral measurement and the enhanced differences among pixels in the same object may reduce segmentation result accuracy. Thus, this study establishes an interval type-2 fuzzy model for detected images. Interval type-2 fuzzy theory considers the main and the secondary membership functions; the latter is represented by the label "membership 1" to express the uncertainty of pixel membership and of a segmentation decision. The aforementioned problem is solved effectively with the proposed method. The drop type problem in type-2 fuzzy theory is another focus of research in this field; a fuzzy decision model is established by reducing the type-2 fuzzy model to a type-1 model. The fuzzy decision model directly influences segmentation accuracy, and recent studies are all based on the upper and lower membership functions. These models can improve decision quality to some extent; however, they do not consider the main membership function. This neglect may significantly influence decision results, particularly when the influence of neighborhood pixels cannot be incorporated into the supervised image segmentation algorithm. To overcome these shortcomings, we proposed high-resolution remote sensing image segmentation by introducing a spatial relationship into the interval type-2 fuzzy model. The proposed algorithm considers the influences of the upper, lower, and the main membership functions in establishing the fuzzy decision model.First, a type-1 fuzzy model is built with the Gauss function to characterize the uncertainty of pixel membership. Then, we extend the mean and variance of this model to construct the type-2 fuzzy model, which improves the expression of the membership function in the type-1 fuzzy model and serves as the knowledge basis to enhance segmentation decision accuracy. A segmentation decision model is then established based on the information derived from the upper, lower, and main membership functions of the trained data. Finally, the membership of a pixel is decided by the membership functions of both the pixel itself and its neighbors to optimize the segmentation of high-resolution remote sensing images.We compare this method with maximum likelihood segmentation and an interval type-2 fuzzy model segmentation without a spatial relationship via high-resolution real images. Qualitative and quantitative analysis findings indicate that the method applied in this study generates high segmentation accuracy.This study proposes a supervised image segmentation method based on an interval type-2 fuzzy model with a spatial relationship. This method improves the uncertainty expression of pixel membership, solves the problems caused by complicated spatial relevance, and enhances the accuracy of the segmentation strategy. Furthermore, the experiments show that this method is effective and feasible. In the future, the Gauss mixture model will be used as a type-1 fuzzy model to potentially improve the accurate characterization of landscape features.
Key words
interval type-2 fuzzy model; trajectory of uncertainty; high resolution; remote sensing image segmentation; secondary membership function