|
|
|
收稿日期: 2015-05-13; 修订日期: 2015-09-20; 优先数字出版日期: 2015-09-27
基金项目: 国家自然科学基金(编号:41501096,41371394,41401051); 重庆市基础与前沿计划项目(编号:cstc2014jcyjA00017,cstc2015jcyjA00007)
中图分类号: TP702
文献标识码: A
文章编号: 1007-4619(2016)01-0138-11
|
摘要
目的 大量城市建筑使得高分影像中含有许多阴影区。这些阴影区在土地利用分类、植被绿度调查等遥感应用中会较大地影响结果精度,降低数据使用效率并增加研究成本。基于同一地物阴影区与临近非阴影区反射率相等这一辐射特征关系,通过建立辐射传输方程,发展了一种新的城市高分遥感影像阴影校正方法RERB (Reflectance Equality Relationship Based Method)。利用RERB对不同城市(北京和荷兰Enschede)不同高分多光谱影像(GeoEye-1 和QuickBird)进行阴影校正,并对比分析其与被广泛采用的均值方差变换法MVT(Mean and Variance Transformation)的校正结果,通过定性和定量精度评价发现:(1)RERB能很好地将城市阴影区影像视觉特征(颜色、纹理、色调等)信息恢复到与非阴影区同一水平上;(2)RERB恢复后的阴影区具有丰富的细节信息且在视觉上与临近非阴影区具有良好的一致性;(3)RERB恢复后的城市柏油路面和水泥路面阴影区辐射信息具有较低的误差,可见光-近红外波段的平均误差分别为7%和9%。同时RERB能较好地恢复城市阴影区植被波谱特征信息。
关键词
辐射传输; 阴影去除; 阴影恢复; 建筑阴影; 大气校正; 辐射恢复; 光谱特征
1 引 言
高空间分辨率遥感影像(高分影像)以其精细的地物分辨能力,在资源环境遥感中发挥着重要作用。城市作为人类聚集区,其土地资源、生态环境与人类生活息息相关。利用高分影像进行城市资源环境监测是城市资源环境规划、保护与管理的重要手段和数据源(Myint等,2011;陈基伟和程之牧,2004)。然而,由于城区建筑阴影的广泛存在,城市高分影像中常常存在大量阴影,这严重制约了高分遥感数据的高效利用(Dare,2005)。
城市阴影在遥感影像上表现为低值区,并掩盖了阴影区地物本身辐射特性。当利用高分影像进行城市土地利用分类、资源调查时,这些低值区将极大地降低结果精度,因而降低数据使用效率(Zhan等,2005)。同时,城市高分影像获取成本通常较高,较低数据利用效率势必增加数据使用成本(陈锬,2014)。此外,由于城市阴影是固定的建筑等地物对太阳直接辐射遮挡产生的,而太阳方位角和高度角的变化规律也是固定的,这可能使得一些阴影区域在不同时期的遥感影像上一直存在,从而形成城市遥感监测的永久盲区(王卫国,2008)。因而,开展城市阴影校正(去除)并恢复阴影区有效地表辐射信息是城市遥感数据预处理的重要内容(Zhou等,2009)。
目前,国内外已开展了大量有关阴影校正算法方面的研究(Chen等,2007;Dare,2005;Jin等,2013;Richter和Müller,2005;Zhou等,2014),其中经典方法有直方图匹配法(Histogram Matching),伽玛(γ)校正(Gamma Correction)以及均值方差变换法MVT(Mean and Variance Transformation)(Shahtahmassebi等,2013)等。直方图匹配法是利用阴影区与临近非阴影区存在的相同地物进行直方图匹配,而后将该匹配参数应用于整个阴影区,从而实现阴影校正(Dare,2005;Sarab and i等,2004)。伽玛校正采用单一的γ因子用于整个阴影区,忽略了不同的阴影区背景地物的差异性特征(Nakajima等,2002)。均值方差变换法(MVT)则假设阴影区和非阴影区存在线性关系,通过提取各自区域的统计变量(均值与方差)构建该线性关系,从而实现阴影区校正(Chen等,2007;Zhan等,2005)。相关研究表明,MVT法以其较高的校正精度和操作简单方便的特点,相对于其他阴影校正方法具有明显的优越性,被广泛使用(Chen等,2007;Yamazaki等,2009;Liu和Yamazaki,2012)。
综观这些阴影校正方法,其核心都利用了阴影区内被记录的微弱辐射信号,并在此基础上利用阴影区和非阴影区之间的某种特殊统计特征关系实现阴影校正的(Shahtahmassebi等,2013)。事实上,阴影区与非阴影区除了存在这些统计特征关系之外,还广泛存在另一种物理特征关系:即在朗伯体表面假设下,同一地物在阴影区及其临近非阴影区具有相同的反射率(Pedrotti和Pedrotti,1993)。目前,这种关系在已有阴影校正方法体系中尚未被充分发掘(wen等,2015)。本研究将以此关系为基本出发点,发展一种基于辐射传输过程的城市高分遥感影像阴影区辐射校正方法。
2 方 法
2.1 基本原理
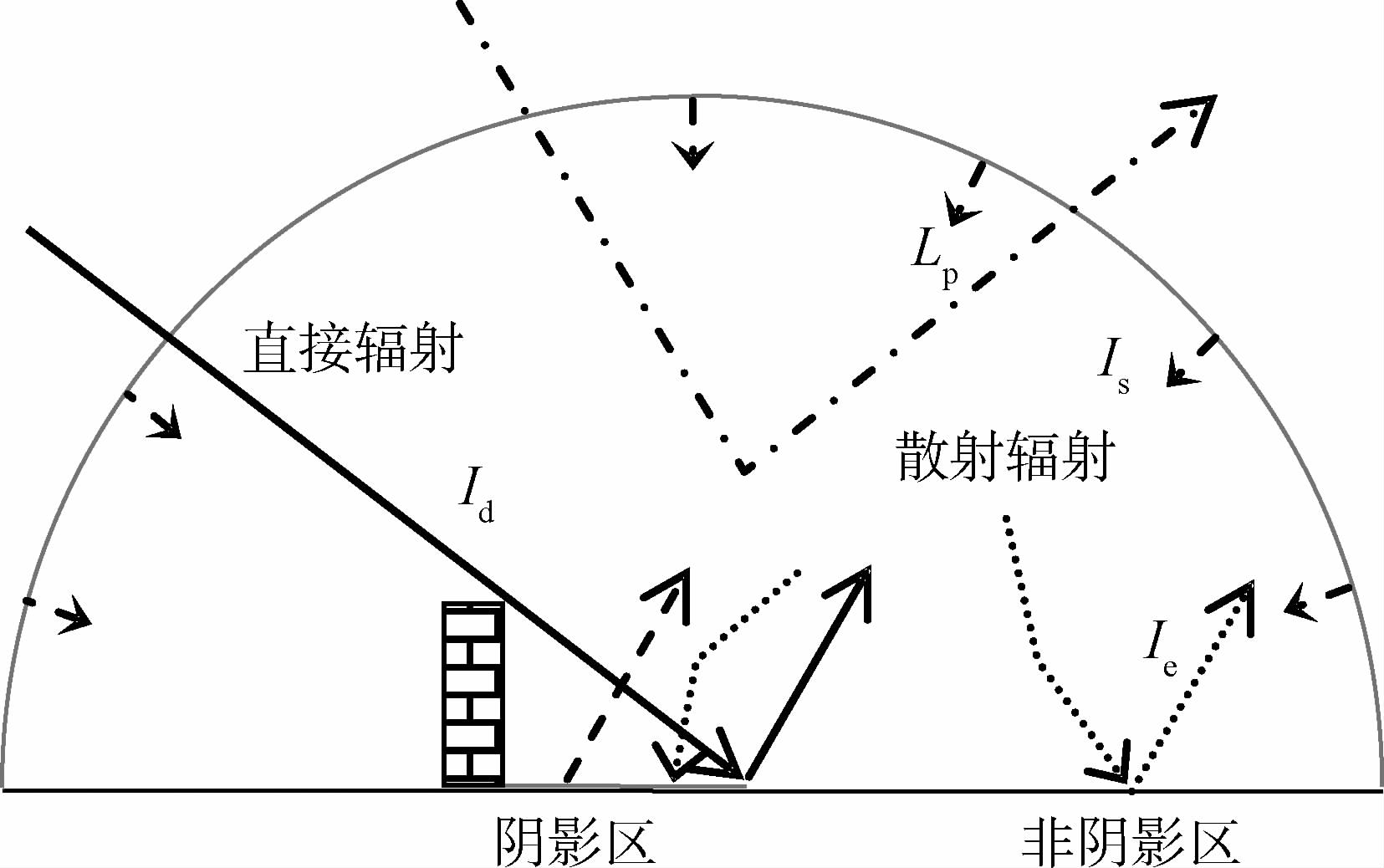
由于大气的散射作用,太阳辐射在经过大气层达到地表的过程中分为直接辐射(Id)和散射辐射两部分(图 1)。直接辐射在受到地表附近不透明物体(如建筑)阻挡时,形成阴影区。散射辐射可进一步分为向上和向下传输部分,其中向上传输部分沿传感器观测方向的叫做路径程辐射(Ip),向下传输达到地表的部分叫做大气向下散射辐射(Is)。同时,达到地表的各种辐射又将受到进一步各种复杂环境反射,一部分回馈给地表,这部分统称为环境反射辐射(Ie)。因此对于阴影区,到达区内的辐射主要为Is和Ie;而对于非阴影区,到达区内的辐射除了Is和Ie外,还有最主要的直接辐射Id(图 1)。这些辐射到达地表后,被进一步反射,并再次通过大气层被传感器接收。
利用遥感数据中记录的辐射信号反演地表真实反射率是定量遥感应用过程中的重要前提,这个过程也被地表反射率定标,而大气校正是其中的重要内容。该过程可通过式(1)表示(Liang等,2001):
${\rho _{sun}} = \frac{{\pi \left( {{L_{sun}} - {L_P}} \right)}}{{{T_V}\left( {{I_d} + {I_s} + {I_e}} \right)}} = \frac{{\pi \left( {{L_{sun}} - {L_P}} \right)}}{{{T_V}{I_{sun}}}}$ (1)
式中,ρsun表示非阴影区地表反射率,Lsun表示非阴影区表观辐亮度,Ip表示大气程辐射,Tv表示沿卫星观测方向大气辐射透过率,Isun表示达到非阴影区地表总辐射,即Id+Is+Ie。
同理,对于阴影地表(无直接辐射Id到达)反射率定标而言,亦可借鉴式(1)基本原理,即:
${\rho _{shw}} = \frac{{\pi \left( {{L_{shw}} - {L_P}} \right)}}{{{T_V}\left( {{I_s} + {I_e}} \right)}} = \frac{{\pi \left( {{L_{shw}} - {L_P}} \right)}}{{{T_V}{I_{shw}}}}$ (2)
式中,ρshw表示阴影区地表反射率,Lshw表示阴影区表观辐亮度,Ishw表示达到阴影区地表总辐射,即Is+Ie。
若阴影区和临近非阴影区内同时包含某种相同地物,如城市绿化草坪、城市路面等(表示为“*”),则在朗伯体地表假设下,该地物(*)在阴影区内的反射率与其在临近非阴影区的反射率相等(即$\rho _{_{shw}}^*$=$\rho _{_{sun}}^*$),据此可得到方程组式(3)。
$\left\{ \begin{array}{l} \rho _{shw}^* = \frac{{\pi \left( {L_{shw}^* - {L_P}} \right)}}{{{T_V}{I_{shw}}}}\\ \rho _{sun}^*\frac{{\pi \left( {L_{sun}^* - {L_P}} \right)}}{{{T_V}{I_{sun}}}}\\ \rho _{shw}^* = \rho _{sun}^* \end{array} \right.$ (3)
式中,$\rho _{_{sun}}^*$和${L_{_{sun}}^*}$分别表示地物(*)在非阴影区像元的地表反射率和表观辐射亮度,$\rho _{_{shw}}^*$和${L_{_{shw}}^*}$分别表示该地物在阴影区像元的地表反射率和表观辐射亮度。通过对式(3)进一步整理可得:
$\frac{1}{{{I_{shw}}}} = \frac{{L_{sun}^* - {L_P}}}{{{I_{sun}}\left( {L_{shw}^* - {L_P}} \right)}}$ (4)
将式(4)代入式(2)即得到:
${\rho _{shw}} = \frac{{\pi fc\left({{L_{shw}} - {L_P}} \right)}}{{{T_V}{I_{sun}}}}$ (5)
式中,fc表示为:
${f_c} = \frac{{L_{sun}^* - {L_P}}}{{L_{shw}^* - {L_P}}}$ (6)
由此,可通过式(5)和式(6)反演得到阴影区地表反射率,实现阴影校正。尽管如此,这种直接恢复阴影区地表反射率的阴影校正策略仍存在不足:需要的未知参数较多,包含fc、Ip、Tv及Isun。这些参数中,Ip、Tv及Isun亦是大气校正过程需要的主要参数,往往很难精确估计。虽然通过辐射传输软件包如6S可以模拟计算,但是这种模拟方法需要更多其他同步获取参数,不利用推广使用。为此,本研究将尝试在只利用影像自身信息的情况下,实现阴影校正。我们采用的策略是:首先在尽量较少未知参数的前提下,将阴影校正后的变量变为表观辐射亮度,即可达到阴影校正的目的。
对式(5)进一步变形得到:
${I_{sun}}{\rho _{shw}}{T_v} = \pi fc\left({{L_{shw}} - {L_P}} \right)= L_{shw}^{hyp}$ (7)
式(7)的左边部分表示了如下虚拟过程:非阴影区直射辐射(Isun)达到阴影区,并被阴影区地表反射(ρshw),经过大气(Tv)被传感器接收($L_{shw}^{hyp}$)。众所周知,阴影区在现实中是不可能有直射辐射(光)到达的;若有,则证明阴影区已不存在,即阴影被校正(去除)。因此,这里的$L_{shw}^{hyp}$应理解为传感器接收到来自校正后的阴影区的辐射值。同时,传感器端接收的总辐射(即表观辐亮度),还应包括大气程辐射(Ip)部分:
$L_{shw}^{rst} = \pi fc\left({{L_{shw}} - {L_P}} \right)+ {L_P}$ (8)
式中,$L_{shw}^{cor}$表示阴影区校正后的表观辐亮度。
采用式(6)与式(8)实现阴影校正,阴影校正结果变量为表观辐亮度,校正过程中未知变量只有Ip与fc。由于该方法是建立在阴影区与非阴影区同一地物反射率相等这一基本假设上的,我们用RERB(Reflectance Equality Relationship Based)表示该方法。
2.2 RERB阴影校正过程
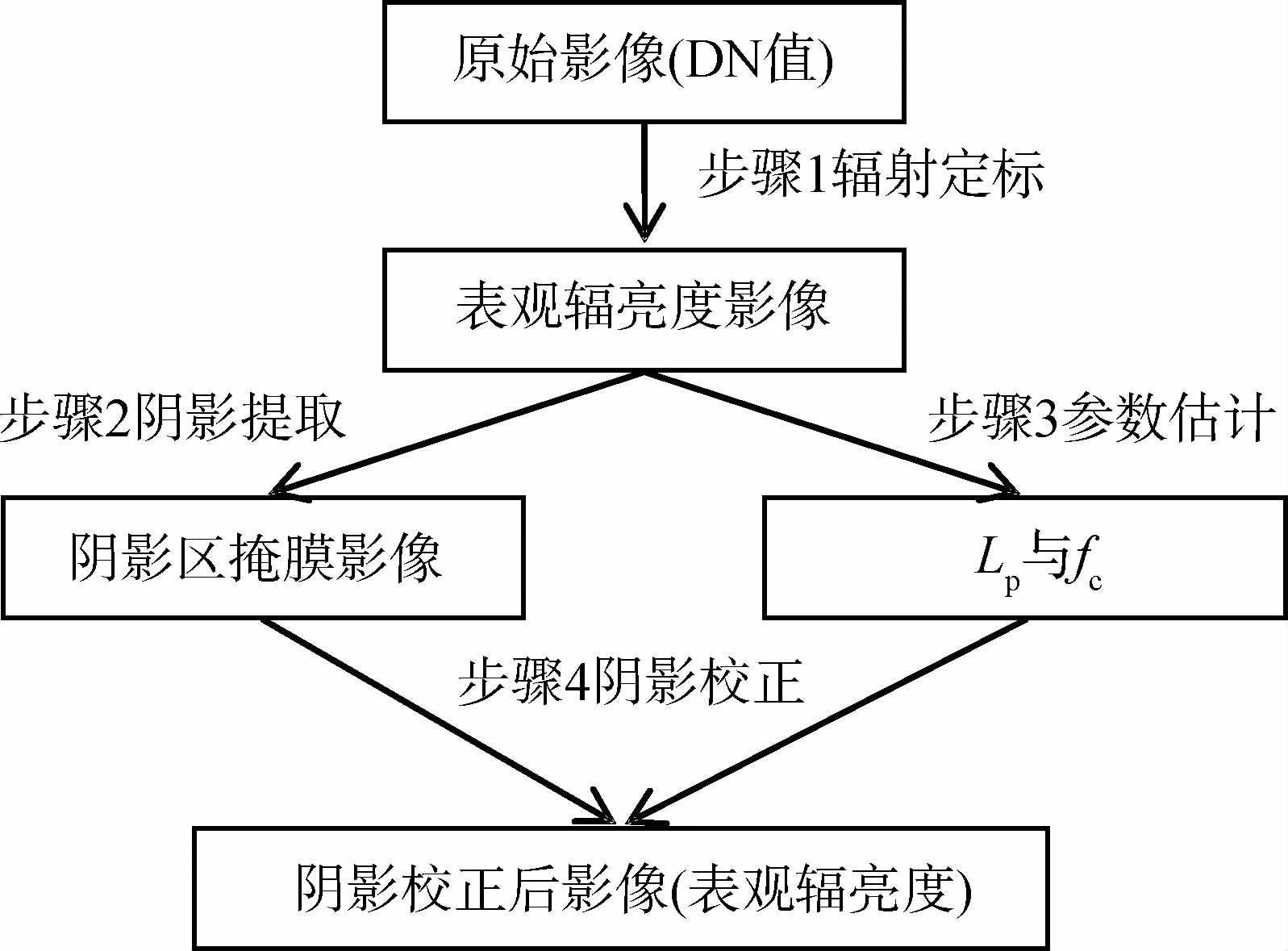
RERB阴影校正过程如图 2所示,具体处理过程分为4步。
步骤1 辐射定标
若原始影像像元值为DN值,则需要进行辐射定标,结果变量为表观辐亮度。辐射定标参数可通过影像元数据或头文件中获得。由于绝大多数常见影像类型辐射定标参数都已被预先集成在专业遥感图像处理软件如ENVI 5.0TM中,因此可直接利用这些专业软件辐射定标功能完成该过程。
步骤2 阴影提取
此步骤的目的是提取影像中的阴影区域,为后续阴影校正提供空间掩膜信息。目前已有大量的阴影提取算法(Arévalo等,2008;Makarau等,2011;Shahtahmassebi等,2013),其中直方图阈值法是最简单并被广泛使用的方法(Adeline等,2013)。本文中,首先利用直方图阈值法提取阴影区,后利用人工目视解译方法,对该阴影提取结果作进一步修正。
步骤3 参数估计
RERB采用式(6)与式(8)完成阴影校正过程,其中的两个重要未知参数分别为Ip与fc。Ip也是大气校正的重要参数,可通过多种方法获得。例如基于辐射传输模型的6S模拟法(Vermote等,2006)、直方图法和IDOS法(IDark-Object Subtraction)(Chavez,1988)。直方图法操作简单且能取得相对较好的估计精度,本文采用该法估算各个多光谱波段的Ip。fc采用式(6)计算得到,其中的关键步骤是选择阴影区与其邻近非阴影区具有反射率一致地物(如城市绿地草坪、学校操场、均一道路等),并分别提取各自的表观辐亮度ρ*shw与ρ*sun(Wen等,2015)。虽然这种方式较直接,但仍存在如下不足:一是需要人工选择地物,因此相对费时费力,且对使用人员遥感解译经验和对研究区的了解有较高要求,存在较多主观因素;二是相对于已经存在的阴影校正方法如MVT,该方法自动化程度较差。为此,本文将对选择阴影区与其邻近非阴影区具有反射率一致地物这一限定条件泛化,即假定研究区内所有阴影区的地物平均反射率与这些阴影区临近非阴影区域(如一定缓冲区范围内)的平均反射率相等,由此可利用各自平均表观辐射亮度计算分别代替$\rho _{_{shw}}^*$与$\rho _{_{sun}}^*$,计算fc。这种方式的优点整个过程可通过软件自动计算完成,无需人工参与即可得到fc。
步骤4 RERB阴影校正
利用式(8),在阴影区掩膜的支持下,利用步骤3获取的未知参数Ip与fc,实现阴影区辐射校正,最终结果变量同非阴影区一致,都为表观辐亮度。
2.3 精度评价
为了科学评价RERB阴影校正效果,还采用了目前被广泛使用的MVT方法来进行阴影校正,并对比分析这两种方法校正后结果。本文选择MVT法作比较研究的原因在于:(1)相对于其他方法(如直方图匹配法和伽马校正法),MVT法已在很多研究中证明了其简答、易操作、较高精度的特性,具有较好的实际应用效果(Chen等,2007;Yamazaki等,2009;Liu和Yamazaki,2012)。(2)本文RERB法与MVT法的建立前提存在一些相似之处:都是利用阴影区的微弱辐射信号,并通过与非阴影区辐射值建立关系进行阴影校正的。MVT方法的核心方程(Chen等,2007)如下:
$L_{shw}^{MVT} = \frac{{{S_{sun}}\left( {{L_{shw}} - {M_{shw}}} \right)}}{{{S_{shw}}}} + {M_{sun}}$ (9)
式中$L_{shw}^{MVT}$表示利用MVT方法校正后的表观辐亮度,Sshw于Ssun分别表示影像中所有阴影区和非阴影区的像元标准差,Mshw与Msun分别表示影像中所有阴影区和非阴影区的像元平均值,Lshw表示阴影区像元值。
影像色彩、纹理、色调、对比度等常见影像视觉特征可作为阴影校正结果定性评价的重要指标,若阴影校正效果较好,则阴影区的这些影像视觉特征应与临近非阴影区具有较好的一致性,反之亦然。如前所述,阴影区与邻近非阴影区同一地物应具有相同的反射率,因此阴影校正后该同一地物在阴影区的像元值应与临近非阴影区该地物像元值在统计意义上相同。基于此,本文采用相对均方根误差rRMSE(relative Root-Mean-Square Error)来定量评价某种地物下的阴影校正精度。
$rRMSE = \sqrt {\sum\limits_{I = 1}^N {{{\left({L_{shw}^i - {L_{ref}}} \right)}^2}} } {\rm{ \times }}100{\rm{\% }}$ (10)
式中,N表示从阴影校正后的阴影区某一种地物中随机选择的像元个数,${L_{shw}^i}$表示选择的阴影像元中第i个像元值,Lref表示该种地物在非阴影区的像元平均值,用于作为阴影校正后阴影区该种地物的参考值。
3 实验数据
本文使用GeoEye-1和QuickBird高分辨率多光谱影像用于阴影校正实验数据。GeoEye1影像覆盖了部分北京城区(图 3(a)),影像获取日期为2009年6月23日,数据格式为GeoTIFF,数据处理级别为St and ard Geometrically Corrected,像元为DN值。该影像多光谱波段分别为:红光(Red,450 nm—510 nm)、绿光(Green,510 nm—580 nm)、蓝光(Blue,655 nm—690 nm)及近红外(Near-infrared(NIR),780 nm—920 nm)波段,空间分辨率为2 m。QuickBird影像采集范围位于荷兰Enschede(图 3(c)),影像获取日期为2006年9月21日,数据格式为GeoTIFF,数据处理级别为St and ard Geometrically Corrected,像元为DN值。该影像多光谱波段分别为:红光(Red,450 nm—520 nm)、绿光(Green,520 nm—600 nm)、蓝光(Blue,630 nm—690 nm)及近红外(Near-infrared(NIR),760 nm—900 nm)波段,空间分辨率为2.44 m。
按照2.2节中的阴影校正步骤,分别对GeoEye-1和QuickBird多光谱影像进行辐射定标、阴影提取(包括邻近阴影区缓冲区建立(图 3(b)和图 3(d))、Ip及fc计算(见表 1),最终根据式(6)和式(8)实现阴影校正。
| 波段 | GeoEye-1多光谱影像 | QuickBird多光谱影像 | ||
| Lp | fc | Lp | fc | |
| 蓝 | 12.84 | 2.16 | 30.24 | 3.27 |
| 绿 | 7.63 | 3.29 | 18.23 | 4.17 |
| 红 | 2.24 | 3.68 | 8.85 | 6.11 |
| 近红外 | 1.83 | 4.98 | 3.80 | 6.17 |
4 结果与讨论
4.1 视觉评价
如图 4(a)(d)所示,原始影像含有大量的城市建筑阴影,且绝大多数阴影区内以城市道路为主,兼具少量绿化带。经过RERB和MVT阴影校正后,阴影区像元值得到了很好补偿(图 4(b)、图 4(c)、图 4(e)和图 4(f)),在图像亮度上基本与非阴影区达到同一水平。通过对校正影像局部细节观察,发现相对于MVT阴影校正结果,RERB校正后阴影区域内色彩、纹理等影像特征与非阴影区更具具一致性(图 5(b)和图 5(c)、图 5(e)和图 5(f)中的A区和B区)。同时,还可以观察到相对于MVT,RERB校正后阴影细节更清晰丰富、且与非阴影区过渡更加平滑自然。
4.2 精度定量评价
从GeoEye-1影像中选取两种典型阴影覆盖地物:柏油路面及绿化带,从QuickBird影像中选取两种典型阴影覆盖地物:水泥路面及绿化草坪,通过计算各自阴影校正后的rRMSE,定量评价RERB阴影校正精度(表 2)。
Table 2 rRMSE values per band in urban shadow areas before and after applying the RERB and MVT restorations 下载CSV
| /% | ||||||||||||
| 波段 | 柏油路面(GeoEye-1) | 绿化带(GeoEye-1) | 水泥路面(QuickBird) | 绿化草坪(QuickBird) | ||||||||
| 校正前 | RERB | MVT | 校正前 | RERB | MVT | 校正前 | RERB | MVT | 校正前 | RERB | MVT | |
| 蓝 | 31 | 4 | 14 | 5 | 43* | 22# | 35 | 5 | 10 | 17 | 6 | 15 |
| 绿 | 43 | 4 | 17 | 19 | 47* | 30# | 52 | 9* | 7 | 31 | 8 | 17 |
| 红 | 61 | 9 | 22 | 21 | 107* | 72# | 71 | 12 | 21 | 46 | 23 | 27 |
| 近红外 | 67 | 12 | 18 | 72 | 12 | 22 | 76 | 8 | 39 | 75 | 24 | 25 |
| 平均值 | 50 | 7 | 18 | 2 | 52 | 37 | 59 | 9 | 19 | 42 | 15 | 21 |
| 标准差 | 17 | 4 | 3 | 30 | 40 | 24 | 19 | 3 | 14 | 25 | 10* | 6 |
| 注:“*”表示该RERB校正后的rRMSE大于校正前的rRMSE,“#”表示该MVT校正后的rRMSE大于校正前的rRMSE。 | ||||||||||||
对于GeoEye-1中的柏油路面,RERB阴影校正后误差(rRMSE)范围为4%—12%(平均误差为7%);而MVT阴影校正后误差范围为14%—22%(平均误差为18%)。对于绿化带,RERB阴影校正后最小误差为12%(近红外波段),最大误差为107(红光波段),平均误差高达52%;相对而言,MVT表现更好,阴影校正后误差范围为22%—72%(平均误差为37%)。发现RERB阴影校正具有如下特征:(1)对于柏油路面(城市阴影区最主要地物)的阴影区校正,校正精度较高;而对于绿化带而言,其校正精度有限,特别是在红光波段(表 2);(2)RERB校正误差总体随着波长增加而增加。虽然对于QuickBird影像的校正结果也表现出了与GeoEye-1中相似的特征,但其总体精度都较高,且都优于MVT校正结果。
除了从单个波段评价阴影校正精度外,也从多波段光谱曲线的角度评价RERB法对光谱特征的恢复效果(图 6)。
总体而言,相对于MVT校正结果,RERB校正结果各波段辐射亮度值与参考辐射亮度更加接近(图 6(b)除外),曲线形状与参考曲线形状更为相似(图 6),很好地保持了阴影区地物的固有光谱性质。而对于绿化植被而言,尽管RERB和MVT校正后波段值与参考值相差较大,但各波段波谱特征曲线仍得到了较好的保持,这一结果对于以波谱曲线形状特征或波段指数(如NDVI)参与的影像分类研究非常重要,因而从这个意义上说,RERB对于城市阴影区绿化植被分类具有较好的应用潜力。
4.3 误差分析
4.3.1 误差分析
RERB的最基本假设是阴影区与临近非阴影区存在相同地物,且该地物反射率相等。满足这一假设的前提是该同一地物具有朗伯体表面,即该地物各方向反射率相等。自然状态下,绝对的朗伯体是不存在的,因此将同一地物当作朗伯体将给阴影校正结果带来误差。为了使这一基本假设带来的误差尽可能小,要求在选择同一地物时尽量选择表面粗糙均质的地物(例如水泥道路、沙地),这些地物在天顶观测角较小的情况下可近似为朗伯体地表(Lee和Kaufman,1986)。本文采用了另一种方案来减小人为选取同一地物时的不确定性以及朗伯体假设的不确定性:假设阴影区各种地物平均反射率与周围非阴影区地物平均反射率相等。这种方式的优点是较少了人工选择地物的主观不确定性因素且可实现阴影校正关键参数fc的自动计算。同时由于城市区域各种地物表面材质种类相对较少(如主要为水泥或沥青材质,少量的草坪、树木等),而地物反射率有其表面材质决定,这种特性为阴影区的平均反射率与临近非阴影区的平均反射率一致性假设提供了一定的合理性。另外,由于城市地物高低起伏不定,可在整体上可形成相当于漫反射综合体的一种城市地表,因而也可减少朗伯体假设带来的不确定性。
RERB的另一个基本假设是辐射进入研究区各像元的大气向下散射辐射与环境散射辐射之和(Is+Ie)相等,这一假设也是基于影像自身信息的大气校正方法如Dark-Object Subtraction(DOS),IDOS的重要前提,因而被广泛采用。然而,现实世界中此Is与Ie变量是空间位置的函数。例如,城市区域不同建筑密度、建筑高度将对Ie产生较大的空间异质性。因此,该假设也将对RERB校正精度带来一定不确定性。
4.3.2 阴影区地物本身辐射特性
在表 1中,发现RERB校正误差总体随着波长增加而增加,且对绿化植被红光波段的误差达到了107%。事实上,大气对太阳辐射的散射作用随波长增加而迅速减小,而这种散射辐射也是阴影区辐射能量的主要来源。由于阴影区本身辐射能量小,达到传感器的信号十分微弱,这无疑将给阴影区真实辐射信号记录带来了更多不确定性,并随着波长增长,这种不确定性也将增加。对于阴影区植被而言,红光作为较长的波段区间,本身到达地表的散射辐射较低,加之植被在该波段具有的低反射率特性,使得传感器探测到的值更加微弱,从而增加了该波段阴影校正的不确定性,降低了校正精度。
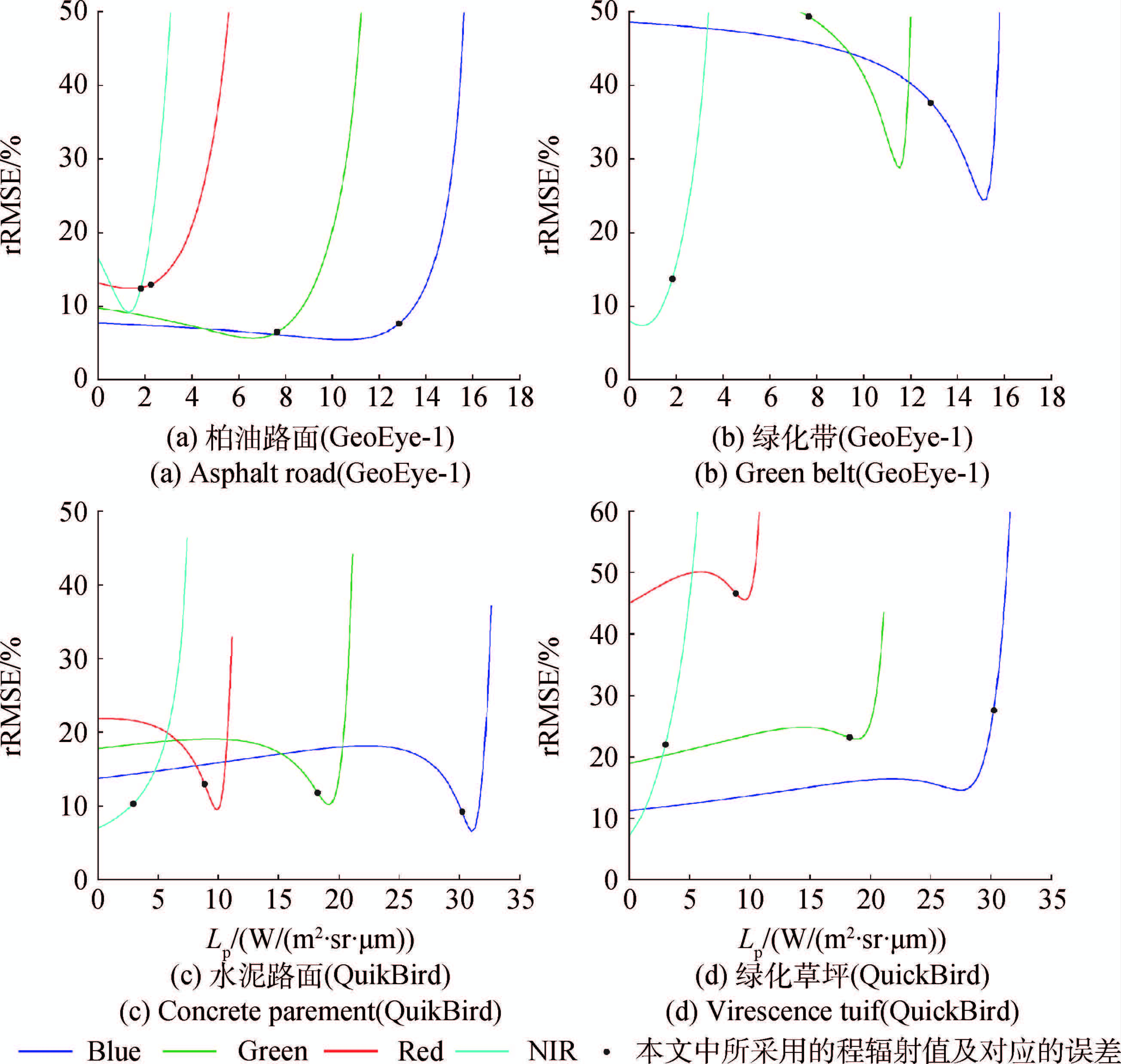
4.3.3 程辐射(Ip)误差
RERB的核心方程式(6)与式(8)都涉及路径程辐射Ip,其对于阴影校正精度将产生重要影响(图 7)。对于绝大多数波段而言,阴影区的校正精度随着Ip的增加而呈现“V”型变化格局,且在达到最低点OPR(Optimum Path Radiance,即rRMSE最小时的Ip)前,其rRMSE相对较低且下降速率较慢;当Ip超过OPR时,rRMSE呈现快速增加趋势。基于这样的认识,认为在估计Ip时,过低估计将比过高估计给阴影校正精度带来的风险小。
4.3.4 缓冲区距离对校正精度的影响
RERB采用阴影区与临近非阴影区反射率相等这一假设,获取阴影校正因子fc。本文通过确定阴影区周围一定范围的向外缓冲区内的平均反射率与阴影区的平均反射率相等来实现这一假设。由于向外缓冲区距离(这里以像元数)将直接影响缓冲区的范围,继而影响区内的平均辐射亮度(Lsun*),并通过式(6)影响fc及最终校正精度。图 8显示了不同缓冲区距离下,fc和几种主要阴影地物的校正精度(rRMSE)的变化。
可以发现,无论是GeoEye-1还是QuickBird影像,各主要阴影地物的各波段校正精度随着缓冲区距离的增加而逐渐减小(GeoEye-1中绿化带除外,如图 8(b)所示),且当缓冲区距离大于5个像元时(对于GeoEye-1为10 m,对于QuickBird为12.2 m)逐渐趋于平稳。而对于fc值而言,其变化趋势与精度变化趋势相反。这表明利用本文中RERB进行阴影校正时,合适的缓冲区距离应大于5个像元。本文中采用是Python语言,利用SciPy中的卷积函数实现不同大小缓冲区的建立(读者可直接联系通讯作者获得本文中的所有阴影校正程序脚本),由于卷积核越大,计算耗时越长,因而选取了5个像元的缓冲区距离计算fc并进行阴影校正。
5 结论
针对广泛存在的城市阴影给高分城市遥感应用带来的挑战,本研究借鉴已有阴影校正研究成果并充分利用阴影区微弱辐射信号,在辐射传输过程的支持下,以城市阴影中存在的阴影区地物及其临近阴影区可能存在的反射率一致性特性,发展了一种基于新的阴影校正方法(RERB)。通过对比应用RERB与成熟的基于统计特征的MVT方法在不同城市(北京及Enschede)、不同遥感数据类型(GeoEye-1和QuickBird)下阴影校正效果,研究发现:(1)RERB对城市阴影区各种地物辐射信号有较好的恢复效果,校正后阴影区地物细节丰富,且最低平均校正误差低至7%(GeoEye-1中柏油路面)。(2)RERB对阴影区各种地物的波谱特性都具有较好的恢复能力,这对于以波谱信息或植被指数参与的影像分类研究非常重要,将极大地提高阴影区数据使用效率。
本文除了利用RERB(式(6)和式(8))恢复阴影区表观辐亮度外,也讨论直接利用式(5)与式(6)直接校正阴影区地物反射率的方法策略。尽管该策略涉及参数较多(fc、Ip、Tv及Isun),但当有足够辅助数据支撑时,可以借助先进的大气校正算法精确获得Ip、Tv及Isun,并在此基础上实现阴影区反射率直接校正,仍然不失为一种选择。相关研究可在这些研究条件具备的情况下作进一步实验论证。
参考文献
-
Adeline K R M, Chen M, Briottet X, Pang S K and Paparoditis N. 2013. Shadow detection in very high spatial resolution aerial images:A comparative study. ISPRS Journal of Photogrammetry and Remote Sensing, 80:21-38[DOI:10.1016/j.isprsjprs.2013.02.003]
-
Arévalo V, González J and Ambrosio G. 2008. Shadow detection in colour high-resolution satellite images. International Journal of Remote Sensing, 29(7):1945-1963[DOI:10.1080/01431160701395302]
-
Chavez P S. 1988. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sensing of Environment, 24(3):459-479[DOI:10.1016/0034-4257(88)90019-3]
-
Chen J W and Cheng Z M. 2004. Urban remote sensing technology playing an important role in government decision-making——as an example of Shanghai. Science of Surveying and Mapping, 29(3):61-64 (陈基伟, 程之牧. 2004. 城市遥感技术在特大型城市政府决策中的重要作用——以上海市为例. 测绘科学, 29(3):61-64)
-
Chen T. 2014. Processing of Building Shadows in High-Spatial Resolution Image. Chengdu:Southwest Jiaotong University (陈锬. 2014. 高空间分辨率遥感影像中建筑物阴影的处理研究. 成都:西南交通大学)
-
Chen Y, Wen D, Jing L and Shi P. 2007. Shadow information recovery in urban areas from very high resolution satellite imagery. International Journal of Remote Sensing, 28(15):3249-3254[DOI:10.1080/01431160600954621]
-
Dare P M. 2005. Shadow analysis in high-resolution satellite imagery of urban areas. Photogrammetric Engineering and Remote Sensing, 71(2):169-177[DOI:10.14358/PERS.71.2.169]
-
Jin S M, Homer C, Yang L M, Xian G, Fry J, Danielson P and Townsend P A. 2013. Automated cloud and shadow detection and filling using two-date Landsat imagery in the USA. International Journal of Remote Sensing, 34(5):1540-1560[DOI:10.1080/01431161.2012.720045]
-
Lee T Y and Kaufman Y J. 1986. Non-lambertian effects on remote sensing of surface reflectance and vegetation index. IEEE Transactions on Geoscience and Remote Sensing, GE-24(5):699-708[DOI:10.1109/tgrs.1986.289617]
-
Liang S L, Fang H L and Chen M Z. 2001. Atmospheric correction of landsat ETM+ land surface imagery. I. Methods. IEEE Transactions on Geoscience and Remote Sensing, 39(11):2490-2498[DOI:10.1109/36.964986]
-
Liu W and Yamazaki F. 2012. Object-based shadow extraction and correction of high-resolution optical satellite images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 5(4):1296-302[DOI:10.1109/Jstars.2012.2189558]
-
Makarau A, Richter R, Muller R and Reinartz P. 2011. Adaptive shadow detection using a blackbody radiator model. IEEE Transactions on Geoscience and Remote Sensing, 49(6):2049-2059[DOI:10.1109/Tgrs.2010.2096515]
-
Myint S W, Gober P, Brazel A, Grossman-Clarke S and Weng Q H. 2011. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sensing of Environment, 115(5):1145-1161[DOI:10.1016/j.rse.2010.12.017]
-
Pedrotti F L and Pedrotti L S. 1993. Introduction to Optics (2nd edition). New Jersey:Prentice Hall.
-
Richter R and Müller A. 2005. De-shadowing of satellite/airborne imagery. International Journal of Remote Sensing, 26(15):3137-3148[DOI:10.1080/01431160500114664]
-
Sarabandi P, Yamazaki F, Matsuoka M and Kiremidjian A. 2004. Shadow detection and radiometric restoration in satellite high resolution images//Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Ancorage Alaska, USA:IEEE:3744-3747[DOI:10.1109/IGARSS.2004.1369936]
-
Shahtahmassebi A, Yang N, Wang K, Moore N and Shen Z Q. 2013. Review of shadow detection and de-shadowing methods in remote sensing. Chinese Geographical Science, 23(4):403-420[DOI:10.1007/s11769-013-0613-x]
-
Vermote E, Tanré D, Deuzé J L, Herman M, Morcrette J J and Kotchenova S Y. 2006. Second simulation of a satellite signal in the solar spectrum-vector (6SV). 6S User Guide Version 3
-
Wang W G. 2008. Study of Shadow Processing's Method in High-Spatial Resolution RS Image. Xi'an:Xian University of Science and Technology (王卫国. 2008. 高空间分辨率遥感影像阴影处理方法研究. 西安:西安科技大学)
-
Wen Z F, Shao G F, Mirrzaa Z A, Chen J L, Lü M Q and Wu S J. 2015. Restoration of shadows in multispectral imagery using surface reflectance relationships with nearby similar areas. International Journal of Remote Sensing, 36(16):4195-212[DOI:10.1080/01431161.2015.1079343]
-
Zhou W Q, Huang G L, Troy A and Cadenasso M L. 2009. Object-based land cover classification of shaded areas in high spatial resolution imagery of urban areas:a comparison study. Remote Sensing of Environment, 113(8):1769-1777[DOI:10.1016/j.rse.2009.04.007]
-
Zhou Y, Chen J, Guo Q H, Cao R Y and Zhu X L. 2014. Restoration of information obscured by mountainous shadows through landsat TM/ETM+ images without the use of dem data:a new method. IEEE Transactions on Geoscience and Remote Sensing, 52(1):313-328[DOI:10.1109/tgrs.2013.2239651]
Abstract
The presence of urban shadows in optical satellite images with high spatial resolution limits the application of remote sensing technology in urban areas. These shadows can misrepresent image information, thereby generating potential errors in the derivation of surface parameters such as surface reflectance and reflectance-based indices. Thus, these shadows must be corrected and their radiance information restored to improve the effectiveness of remote sensing images. Many shadow correction methods have been developed according to the complex statistical relationships between shadowed and sunlit areas because the former maintains weak spectral radiance information. In addition, another physical relationship has often been detected between shadowed and sunlit areas, namely, the reflectance equality relationship (RER). This relationship can be regarded as the reflectance of the fact that similar-type features can be identical in both a shadowed area and its nearby sunlit area under the Lambertian surface condition. RER is generally independent of shadow detection processing; nonetheless, this relationship has not been fully considered in the development of shadow restoration algorithms. In this study, an RER-based (RERB) method were derived to correct the shadowed areas in optical multispectral satellite imageries of urban areas according to the principles of radiance transfer processes.This approach reduces the number of parameters; thus, it can lower the risk of errors propagated by the uncertainties of additional parameters. The new RERB method is tested via GeoEye-1 and QuickBird multispectral imageries with high spatial resolution in two different urban areas (Beijing and Enschede) that exhibit many urban building shadows. As per a comparison of this method with the widely used mean and variance transformation method, the former can restore the colors, texture, tone, and brightness of the shadowed areas in the image to a visually satisfactory level. Quantitative analysis results suggest that the RERB method can help restore the reflectance of shadowed asphalt roads accurately, with a mean error of 7%. This method can also be used to effectively restore the spectral shape information on shadowed features; this information is particularly important when the RERB method is applied to restore multispectral imagery for classifying an image based on spectral information and band indices. Another RERB shadow correction strategy that restores shadow surface reflectance instead of apparent radiance is discussed as well; nonetheless, this strategy requires further study because much auxiliary data is needed.
Key words
radiance processing; shadow removal; shadow restoration; building shadow; atmospheric correction; radiance restoration; spectral features