|
收稿日期: 2015-05-13; 修改日期: 2015-11-10;
优先数字出版日期: 2016-05-25
基金项目: 国家自然科学基金(编号:41174001);湖南省教育厅科研一般项目(编号:15C0020);长沙理工大学公路养护技术国家工程实验室开放基金资助项目(编号:kfj150105);湖南省杰出青年基金(编号:14JJ1021);湖南省大学生研究性学习和创新性实验计划项目
第一作者简介:
邢学敏(1983-),女,博士,讲师,从事雷达干涉测量学在矿区变形监测中的理论和应用研究。E-mail:28008642@qq.com
中图分类号: P227
文献标识码: A
文章编号: 1007-4619(2016)03-0491-11
|
摘要
针对永久散射体差分干涉测量(PSInSAR)算法流程,发展了基于周期函数模型的空间维解缠方法,并将其应用于矿区时间序列地表变形反演。通过在研究区域内安装人工角反射器(CR),将CR点上计算所得的周期模型参数分量作为整个网络的约束,通过空间约束平差以实现空间维解缠。选取了河南省境内白沙水库附近的煤矿密集区为主要研究区域,采用周期函数模型对矿区线性及非线性形变分量进行模拟,反演了2007年2月-2010年2月的时间序列形变场,并采用研究区域内的水准实测数据作为外部验证数据。实验结果表明:白沙水库周围区域存在着较为明显的沉降,在煤矿分布区域内累积最大沉降量超过了10 cm。沉降区域内以线性沉降趋势为主,非线性沉降较为缓慢,仅在水库的西南方向较为明显。应用已有的水准点实测形变值对实验结果进行验证分析,结果表明该方法精度可达约±2.1 mm,证实了本文采用的方法在矿区地表时序形变反演中的可行性和可靠性,对预防过度采矿导致的矿区塌陷具重要现实意义。
关键词
永久散射体 , 人工角反射器 , 约束平差 , 矿区沉降 , 形变监测
Abstract
Due to the frequent mining activity and increasing mine geological disasters in our country, the long term dynamical monitoring and analysis of the mining area are of great importance to prevent the potential geological damage in mining area. The Permanent Scatterer Interferometric Synthetic Aperture Radar (PSInSAR), a newly developed ground deformation monitoring technique, which may not be influenced greatly by the spatial and temporal deccorelation, has been widely applied in study on regional displacement, including the deformation of urban area, terrain area and mining area. During the step of spatial unwrapping in PSInSAR algorithm, stable points or external known GPS points are necessary. The procedure of selecting the reference stable points is obviously uncertain and the external GPS data is difficult to obtain. Due to the shortcomings of traditional spatial unwrapping in PSInSAR algorithm, a new method of spatial unwrapping based on periodic function is developed. Since Corner Reflector (CR) point can be installed easily, which can be applied in the area without external constrained data (such as GPS data) and avoid the uncertainty of choosing reference point in the PS parametric adjustment network, the subsidence rates calculated on CR points are used as constraints for PS network while the spatial unwrapping is performed using the parametric adjustment method. With the improved method, the PSInSAR is applied in the inversion of time series ground deformation in mining area. With 14 ALOS PALSAR images from February 2007 to February 2010, the deformation inversion experiment is carried out. The colliery dense distribution area, around Baisha reservoir in Henan province, is chosen as the study area in the experiment. 6546 PS points except CR points are detected during the experiments. The linear velocities calculated out through traditional spatial unwrapping method are compared to that of the developed method. The algorithm achieves the integration of CR data and PSInSAR algorithm for the first time. The authors succeed to inverse the time series of subsidence from February in 2007 to February in 2010, using the periodic function to simulate the linear and nonlinear components of the deformation. The results show that there appears obviously time series subsidence around the reservoir, with the max value over 10 cm in the colliery distribution area, due to mining activities. The subsidence mainly performs to be linear subsidence. The nonlinear subsidence only appears to be a little obvious in the northeast of the reservoir. In order to validate the result of the experiment, deformation monitoring with leveling was also carried out in the area. With comparison to the deformation result of leveling, the accuracy of ± 2.1mm is calculated. It can be concluded from the good accordance that the method has the following advantages:(1) CR point can be installed easily, hence we can choose the study area freely, which can be applied in the area without external constrained data (such as GPS data); (2) CR Point can be taken as constraining data for the spatial unwrapping of PS network and increase the redundancy number of parametric adjustment model which can make the solutions more stable; (3) Corner reflectors have high reflectivity which can be identified easily on the SAR image, thus the inaccuracy within the step of coordinate transformation can be avoided and the accuracy of the solutions can be improved. (4) It can avoid the uncertainty of choosing reference point in the PS parametric adjustment network.
Key words
permanent scatters , Corner Reflector (CR) , constraint adjustment , mining subsidence , deformation monitoring
1 引 言
矿区塌陷事故近几年发生频繁,已经严重威胁到国民经济的发展及人民的财产安全,对矿区沉降的监测工作已经刻不容缓(朱建军,2011)。永久散射体雷达差分干涉测量技术(PSInSAR)是近年来发展起来的一项用于地表沉降监测的新技术,该技术是差分干涉测量(DInSAR)技术的延伸,由于其不受时间和空间失相关的影响,使得其适用范围和精度明显高于DInSAR,近几年被广泛地应用于地表沉降的监测(Ferretti,2000;Hooper 2012)。该技术通过对长时间序列影像中均保持稳定的点(PS点)进行相位分析以实现形变分量的提取(Ferretti,2001)。
空间维解缠是PSInSAR技术的重要环节,陈强(2007)提出可通过对PS基线网络进行间接平差的方法实现空间维解缠,应用区域内GPS控制点作为起算数据进行约束平差(陈强,2009;Chen,2010)。但由于GPS控制点分布的区域局限性,实验区域内很可能缺乏可用的外部GPS数据。为避免选取稳定参考点的不确定性和研究区域内缺少可用外部GPS数据的问题,邢学敏(2011)曾发展了一种基于线性速率模型的空间维解缠算法,该算法通过在研究区域内安装人工角反射器(CR)以达到对整个PS网进行约束的目的,由于CR点较强的后向散射系数使其在SAR图像上呈现亮点,方便识别,其安装的灵活性使其尤其适用于矿区,公路,高铁,风场等特殊区域的变形监测,当区域内无足够天然PS点时,可作为PS技术的补充(Xia,2002; Xia,2004)。
本文在原线性速率模型基础上,发展了基于周期函数模型的空间维解缠方法,在测试矿区内完整的实现了线性及非线性形变分量的模拟,并在此模型基础上应用附CR点约束的空间维解缠方法,实现了测试矿区的时间序列沉降场反演。
2 PSInSAR技术基本原理与处理流程
2.1 基线网络布设与形变模型建立
在研究区域内完成PS点提取和CR点目标识别工作后,需要布设PS网络。布网依据Delaunay布网原则,将相邻PS点连接成一条PS基线,并确保网内每一个CR点都与PS点连接。对网络中任意一条PS基线,将这两点的相位值作差,可建立如下模型(Liu,2009;Liu,2010):
| $ \begin{array}{l} \Delta \phi _{i,j}^m = - 2 \cdot \pi \cdot \Delta k_{i,j}^m + \displaystyle\frac{{4\pi {B_m}}}{{\lambda {R_p}\sin \theta }}\Delta \delta H_{i,j}^{} + \\ \displaystyle\frac{{4 \cdot \pi }}{\lambda }\Delta S_{i,j}^m + \Delta w_{i,j}^m \end{array} $ | (1) |
式中,m表示干涉对序号,i和j对应PS点序号,$\Delta \phi _{i,j}^m = \phi _i^m - \phi _j^m$
,$\Delta k_{i,j}^m = k_i^m - k_j^m$
分别表示任意PS基线相位增量和整周模糊度增量;$\Delta \delta H_{i,j}^{} = \delta H_i^{} - \delta H_j^{}$
表示高程改正数增量;$\Delta S_{i,j}^m$
为沿斜距向的形变增量,RP为PS点与卫星位置间距离,θ为雷达入射角;$\Delta w_{i,j}^m$
则是相位残差,包括了大气延迟、噪声等因素引起的误差,
| $ \begin{aligned} \Delta S_{i,j}^m = & S_i^m - S_j^m = \\[4pt] & \Delta v_{i,j}^m{T^m} + \Delta A_{i,j}^m\cos(2\pi \frac{1}{{\tilde T}}({T^m}))+ \\[2pt] & \Delta B_{i,j}^m\sin(2\pi \frac{1}{{\tilde T}}({T^m})) \end{aligned} $ | (2) |
式中,A,B称为周期速率;$\Delta {v_{i,j}} \!=\! {v_i} \!-\! {v_j}$,$\Delta {A_{i,j}} \!=\! {A_i} \!-\! {A_j}$$\Delta {B_{i,j}} = {B_i} \!- \!{B_j}$,分别表示相邻两PS点的线性速率增量,余弦速率增量和正弦速率增量(Kampes,2004); Tm为干涉对m的时间基线;$\tilde T$ 为周期参数,取365天。
式(1)(2)中未知参数为$\Delta k_{i,j}^m$,$\Delta \delta H_{i,j}^{}$ ,及形变参数增量$\Delta {v_{i,j}}$,$\Delta {A_{i,j}}$,$\Delta {B_{i,j}}$ ,可应用LAMDBA算法对缠绕的差分干涉相位进行时间维相位解缠(Xia,2004; Kampes,2005),求解出相邻两PS点间的形变未知参数增量和高程改正值增量$\Delta \delta H_{i,j}^{}$ 。但此时得出的只是相邻点上的相对形变未知参数和高程改正结果,需要在空间维解缠环节中获取每个PS点上的形变参数和高程改正值。
2.2 基于周期函数模型的空间维解缠方法
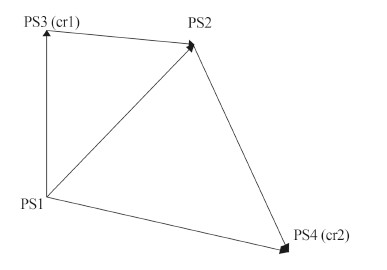
空间维解缠即为将形变参数增量值看作观测值,求解对应PS点上形变参数的过程。以线性形变速率V为例,可将$\Delta {v_{i,j}}$视为观测值,vi,vj为未知参数,依据间接平差法求解出最终未知参数的最优估值。但是利用这种算法需要有必要起算数据,否则基线网络间接平差网求解时,法方程为秩亏(张后苏,1995)。假设部分PS基线网络分布如图 1所示,可建立如下的间接平差观测模型:
| $ \begin{equation} \left\{ \begin{array}{l} \Delta {v_{12}} = {v_2} - {v_1}\\ \Delta {v_{13}} = {v_{\rm{cr}1}} - {v_1}\\ \Delta {v_{14}} = {v_{\rm{cr}2}} - {v_1}\\ \Delta {v_{32}} = {v_2} - {v_{\rm{cr}1}}\\ \Delta {v_{24}} = {v_{\rm{cr}2}} - {v_2} \end{array} \right. \end{equation} $ | (3) |
式中,vcr为CR点上的形变速率值将其作为必要起算数据其余各分量意义及求解方法可参看文献(邢学敏,2011),最终待求形变速率值可由下式求得:
| $ \begin{equation} V = {({{C}^{\rm{ T}}}{PC})^{ - 1}}{{C}^{\rm{ T}}}{PL} \end{equation} $ | (4) |
式中,V为待求PS点(PS1,PS2)的线性速率,C为式(3)右侧的系数阵,L为观测值向量与式(3)常数向量之差,P为权阵,可依据下式模型确定:
| $ \begin{equation} { P} = \left[ {\begin{array}{*{20}{c}} {{\gamma _1}}& {}& {}& {}\\ {}& {{\gamma _2}}& {}& {}\\ {}& {} & \ddots & {}\\ {}& {} & {}& {{\gamma _N}} \end{array}} \right] \end{equation} $ | (5) |
式中,N表示基线网络中基线边的数目,为基线网络中任一条基线边的时序相关系数均值:
| $ \begin{equation} \gamma = \frac{1}{n}\sum\limits_{i = 1}^n {(\cos(\Delta {w_i}})+ j\sin(\Delta {w_i})) \end{equation} $ | (6) |
同样的方法可用于求解周期速率A,B。将求解出的各形变参数解代入式(2),可得出任一PS点上累积变形结果:
| $ \begin{equation} \begin{array}{l} S_i^m = v_i^m{T^m} + A_i^m\cos(2\pi \displaystyle\frac{1}{{\tilde T}}({T^m}))+ \\[4pt] \quad \quad B_i^m\sin(2\pi \displaystyle\frac{1}{{\tilde T}}({T^m})) \end{array} \end{equation} $ | (7) |
由上式即可反演出研究区域内所有PS点的时间序列变形结果。
2.3 PSInSAR技术操作流程
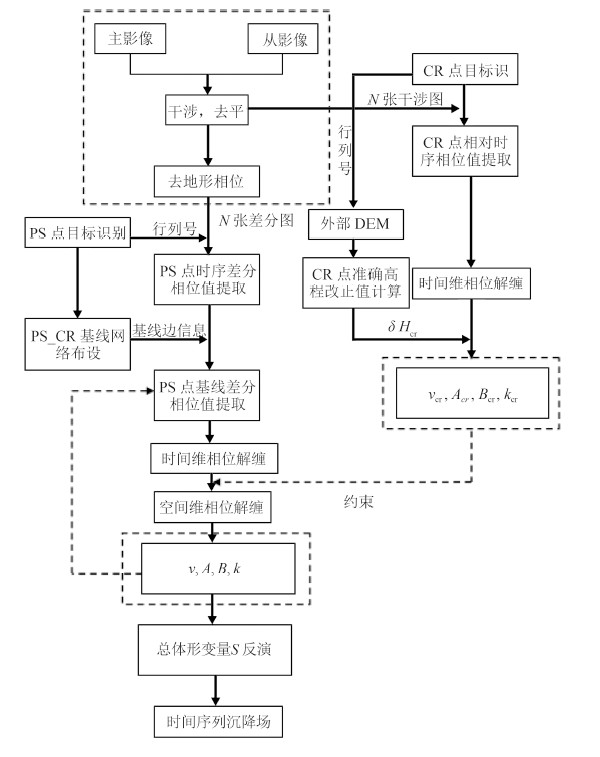
由上述讨论,将PSInSAR算法操作流程图表示在图 2中,首先对影像进行前期干涉处理,去除地形及平地相位后,可生成对应的差分干涉图。于此同时,分别提取干涉图(含地形相位)上各CR点的相位信息,建立式(2)周期函数模型,应用LAMDBA法进行相位解缠,求解出各CR点上的形变参数值vcr,Acr,Bcr,kcr,同时依据CR点上安装的GPS接收机测得的实际高程值可计算出每个CR点上的高程改正值Hcr。将上述CR点上各参数值分别作为空间维解缠网络的约束数据。完成上述前期工作后,进行PS点的提取。在此,综合考虑相干系数,振幅离差指数及强度信息,通过设定阈值可在主影像上选取一定数目的PS候选点,并储存相应PS点位置信息。处理中,可人为将PS点与CR点位置信息分别存储。由于PS点中存在部分虚假点,需要人为将其叠加在Google地图上进行比对,删除伪PS点。应用Delaunay三角网原则对选取出来的PS点与CR点共同布网,并根据邻接矩阵模型存储各基线边的信息,信息包括基线边上对应两PS点的位置信息。布网时为将大气延迟相位的影响减至最低,将基线边控制在1000 m内。
根据2.2节中介绍的方法,对基线网中所有基线边分别建立如式(3)的模型。模型中未知参数为Hij,vij,Aij,Bij,kij。为进一步分离缠绕相位,采用LAMDBA法进行时间维相位解缠,在原式基础上补充虚拟观测方程,解决方程观测个数不足的问题。通过求解,可得出高程改正值增量δHij,及形变参数增量值vij,Aij,Bij,以此作为空间维解缠的观测值。将预先求解得出的CR点上的形变参数及高程改正数作为间接平差形变速率网的约束数据,依据最小二乘原则,建立类似于式(4)的法方程,可求解出PS网中各PS点上的形变速率值v,周期参数A,B及高程改正值H,再将其分别代入式(8)中,即可获取得研究区域各PS点的时序形变结果。
3 实验数据与处理方法
3.1 实验数据
河南省是矿业发展大省,矿产资源分布密集,白沙水库位于禹州市西北与登封市的交界处,发源于少室山的颍河,自登封群山之中经白沙横贯禹州全境。白沙水库周围地区矿产资源分布较为密集,很多煤矿开展着持续地矿产资源开采,由于其周围地下暗河和蓄水丰富,土壤湿松,如果过量的开采矿产资源,不实施严格的监控,极易引发地表塌陷,严重时很可能触及地下蓄水层,使河床水通过采空区涌入井下,引发透水事故,造成人员伤亡。在2003年—2004年,登封市部分煤矿发生过严重透水事故,在2007年—2008年,河南郏县等地区煤矿又发生多起煤矿透水事故,人员伤亡和财产损失非常严重。为实现对矿区沉降的实时监测,尽可能的避免矿区事故的发生,及时预防安全隐患,本文选取白沙水库周边约100 km2范围为研究区域(如图 3所示),对其进行时序沉降场反演。由于距离城区较远,区域内居民区多以村落为主,区域南部地形以山体为主,且山体上植被覆盖稀少,多为裸露山体,而平坦地区多为河流及植被覆盖区。
实验中沿研究区域内高速公路安装了12个人工角反射器,对应在灰度影像上的分布位置、各组角反射器选取的参考点及实地安装图均表示在图 4中。实验数据采参数详见表 1。实验中选取09年8月9日的影像为主影像,采用JPL/NASA的3"空间分辨率外部地形数据用于去除地形相位,共生成13个差分干涉组合,差分干涉图见图 5。
表 1 SAR影像参数列表
Table 1 Basic parameters of SAR images used in the experiment
| 编号 | 日期 | 时间间隔/d | 垂直基线/m |
| 1 | 2007-02-01 | -920 | -335 |
| 2 | 2007-06-19 | -782 | -1000 |
| 3 | 2007-08-04 | -736 | -1489 |
| 4 | 2007-09-19 | -690 | -1282 |
| 5 | 2007-12-20 | -598 | -1774 |
| 6 | 2008-02-04 | -552 | -2483 |
| 7 | 2008-05-06 | -460 | -3022 |
| 8 | 2008-06-21 | -414 | -972 |
| 9 | 2008-12-22 | -230 | 1113 |
| 10 | 2009-08-09 | 0 | 0 |
| 11 | 2009-09-24 | 46 | 533 |
| 12 | 2009-11-09 | 92 | 773 |
| 13 | 2009-12-25 | 138 | 1082 |
| 14 | 2010-02-09 | 184 | 1079 |
3.2 处理方法
首先需对各CR点的相位进行建模分析。提取出各组CR点相对于参考CR点的干涉相位差,并应用CR点上高程信息计算地形相位分量$\Delta \varphi _{\rm{topo}}^{i,j}$,根据式(1)建立模型,最终求得CR的形变参数值(线性速率vcr,余弦参数Acr,正弦参数Bcr)。根据CR点的地理坐标,可提取出其在外部DEM上的高程信息,结合CR点上卫星接收机测得的高程值,即可计算出各CR点上的高程改正值。
在进行PS点选取时,采用相干系数,振幅离差指数及振幅信息,选取在时序相干系数高于0.5的点为候选点,设置振幅离差指数阈值为0.4进行二次筛选,最后采用振幅阈值法剔除残留在水体中的点。依据图 2的算法流程对这些候选PS点与CR点共同依据Delaunay三角网原则布网,并根据邻接矩阵模型识别出各基线边,存储基线边上相应PS点的位置信息,对PS点与CR点构建的网络建立基线边相位差的函数模型,依次进行时间维相位解缠,PS基线网络空间约束平差,最终求解出各候选PS点上形变参数值及高程改正值。
利用求解出的形变参数值计算出所有候选PS点的相位残差$w_{i,j}^m$,删除残差值大于0.8的PS点后,重复前面的步骤,直到所有PS候选点的相位残差值均小于1。最终在研究区域内提取出除CR点外共6546个PS点。在进行空间维解缠时,建立如式(3)所示的间接平差模型,根据式(6)依次计算所有PS网基线边的时序相关系数均值。为提高求解精度,删除
4 实验结果分析与验证
4.1 实验结果
为清晰显示沉降区域位置,以外部地形图为底图,将沉降速率场表示在地图坐标系下,如图 6 所示,其中三角形标示CR点位置。由图 6可见,在一年时间间隔内,研究区域内已经表现出了明显的沉降,特别是白沙水库周围的煤矿密集区域,沉降速率大部分超过了1.5 cm/a(颜色为红色)。分布在白山水库东南方向的方山镇二矿处已有一明显的沉降漏斗,其年沉降速率约5 cm/a,其附近的西下庄振杰煤矿,兴华二煤矿沉降速率也超过了4cm/a。研究区域的东北部地区由于煤矿分布较为稀疏,沉降不明显,人工角反射器分布的高速公路总体沉降分布在毫米级,但在朝阳沟煤矿和告城煤矿的分布区域依然可见明显的沉降漏斗,其沉降速率可达3 cm/a。由图可见研究区域的周期速率不起主导作用,其总体分布为毫米级,仅在研究区域的西南角位置周期速率相对明显,累积周期速率参数超过了1 cm/a。所得的研究结果证实了研究区域内的沉降以线性沉降速率为主,线性速率几乎占据了沉降总量的80%(详见4.2节)。
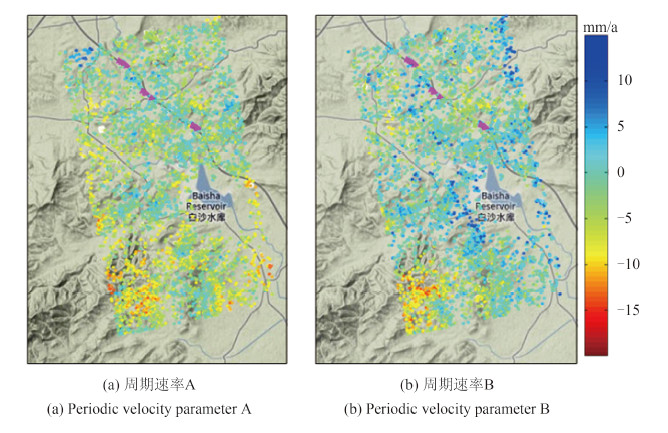
图 7为通过本文的实验获取的周期速率参数。为突出本文基于周期函数模型的空间维解缠方法的优势,同时对研究区域内进行了传统PSInSAR算法实验,传统算法实验中采用线性速率模型,空间维解缠环节不考虑CR点信息,选取一假设稳定点作为参考点以实现(参考点位置见图 8(a)中)。将传统PSInSAR算法与基于周期函数模型的空间维解缠法获取的线性速率场进行对比(图 8)。图 8(a)为应用传统算法所得的线性速率场。从图中对比可明显看出,两种算法所得的沉降趋势总体保持一致,但传统算法结果散乱程度较大,突变点较多,同时在研究区域的东北角处出现明显的抬升区(蓝色);而本文算法所得的沉降速率场区域连续性较好,突变点较少,只有极小区域有微量抬升,可能是由于大气延迟相位和噪声相位的影响所致。
4.2 实验结果分析验证
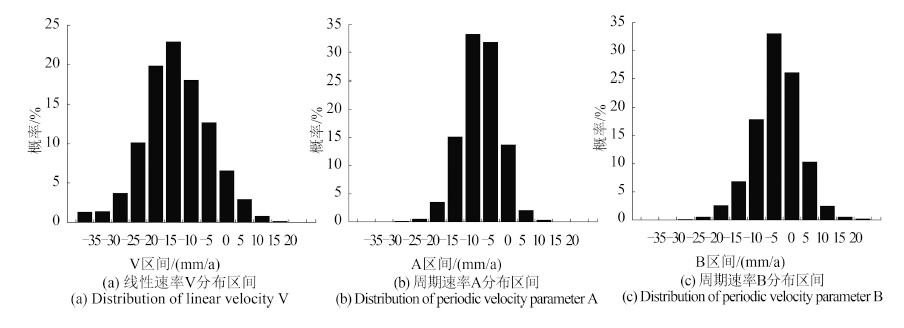
为分析研究区域内PS点的沉降参数值分布情况,本文对所得结果进行了量化统计,如图 9所示。沿斜距向的线性沉降速率v整体分布在-20—5 mm/a,表明研究区域内整体趋势以线性沉降为主,其沉降的明显程度不容忽视,由于白沙水库周围自然地理环境影响及煤矿分布的密集性决定了这一沉降特征。实际计算过程中,通过对相邻两PS点相位作差以消除大气相位影响,同时通过滤波方式消除影像的噪声,但这两种处理方法并不能完全消除大气延迟相位及噪声影响,存在少量的残余相位,因此实验结果中会出现少量抬升区(在图 7中可发现少量PS点的速率值分布在5—20 mm/a)。而周期速率A和B数值总体分布在-15—5 mm/a,其数值大小明显小于线性沉降速率数值,表明该研究区域内存在缓慢地非线性沉降,该趋势并不起主导作用,沉降趋势总体为线性沉降。
根据式(7)可以反演出研究区域内的时间序列沉降场,如图 10所示,图中起始时间为2007年2月。从2007年2月至2010年2月约3年的时间内,研究区域内发生了大面积的明显沉降。沉降趋势以线性沉降为主,特别是白沙水库周边地区沉降明显。图 10中a区和b区分别为方山镇二矿和朝阳沟煤矿所在位置,在图 10中可明显看出其沉降漏斗的发育情况。从2007年12月20日起沉降漏斗已经开始发育。
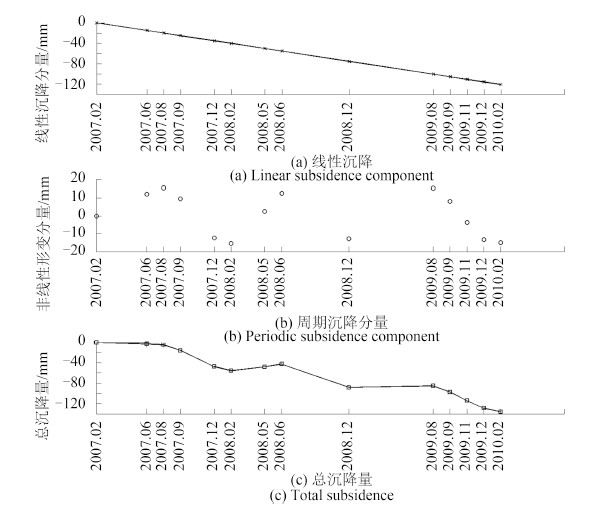
将分布在a区的PS点PS-1进行分析,将在13个时间段的沉降量表示在图 11中。从图 11中可以看出,该点从2007年2月起到2010年2月累积线性沉降量达12 cm,非线性沉降分量表现出明显的周期性。非线性沉降分量在2007年8月,2008年6月和2009年8月,2010年8月份别出现最大抬升值,而在2008年2月,2008年12月和2010年2月出现最大沉降值,表明该区域内的非线性沉降在冬季内表现最为明显。由文献(Kampes,2004)可知,非线性形变数值与温度的波动存在正比关系,因而在夏季温度出现正峰值时,非线性沉降分量达最大抬升值,相反在冬季气温达最低时,非线性形变分量达最低值,也就是沉降量达到最大。由于夏季降雨量较大,因而由于雨水的回灌导致区域地表发生隆起,非周期沉降量达抬升最大值。由于非线性沉降量的贡献导致该点的整体沉降量在近三年的时间内累积达到15 cm。非线性沉降分量占沉降总量的约20%左右,而线性沉降分量占约80%。由于在2008年6月,2008年12月和2009年8月非线性沉降量分别出现了抬升最大值和沉降最大值,因而总体沉降结果中半年内(2008年6月—2008年12月)的累积沉降总量略大于8个月(2008年12月—2009年8月)的累积沉降总量。正是由于非线性沉降量的贡献会出现这种在短时间内的沉降总量大于长时间累积沉降总量的结果。
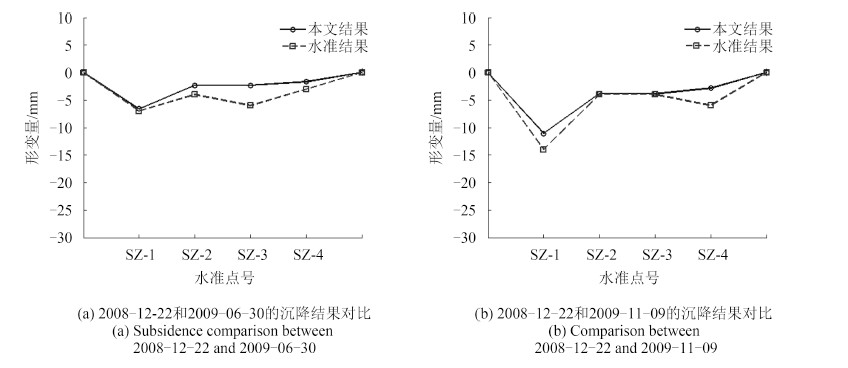
为验证结果合理性,还对研究区域开展了四期水准测量变形观测。水准点分布在图 10中星号所示位置。图 12为这四个水准点上的沉降量与PS点沉降量结果。在2008-12-22—2009-06-30期间,PS点沉降量均值与水准点位置沉降量间误差均分布在3 mm范围内。而在2008-12-22—2009-11-09期间,误差最大值为5 mm。PS点测量结果与各水准点的差异均方误差为±2.1 mm。
5 结 论
本文应用PSInSAR技术对河南境内白沙水库周围的煤矿分布密集区域进行了沉降监测,实现了矿区时序沉降场的反演。在实验过程中,选取周期函数模型对研究区域的线性与非线性形变量进行模拟,发展了一种基于周期函数模型的空间维解缠方法。该方法应用CRInSAR技术对CR点干涉相位进行分析,求得其准确的形变参数值和高程改正值,将其作为PS基线网络空间维解缠的约束,进而实现PS基线网络的空间维解缠。这一方法利用CR点安装的灵活性,不仅弥补了矿区内无可用外部数据的缺陷,且可避免人为选取参考点的不确定性。
应用该方法对白沙水库周围的煤矿进行了时序形变场反演,获取了该区域最终总体时序形变场,结果表明白沙水库周围区域存在着较为明显的沉降,在煤矿分布区域内累积最大沉降量超过了10 cm。沉降区域内以线性沉降趋势为主,非线性沉降较为缓慢,仅在水库的西南方向较为明显。选取分布于方山镇二矿区内的一个PS点进行分析可知,线性沉降量贡献约为总体沉降量的80%,应用已有的水准点实测形变值对实验结果进行验证分析,结果表明该方法精度可达约±2.1 mm。由于白沙水库周围地下蓄水层丰富,土质较为湿松,出现地表塌陷和矿区开采透水的机率高于普通煤矿分布区,因此本文方法对这一特殊地质环境的沉降监测更具重要意义。但由于在实验过程中没有进行大气相位的改正,会存在一部分大气延迟相位残留误差,导致结果中出现少量抬升区域,在后期研究中本文将会针对大气残余相位的去除开展进一步的研究工作。
参考文献(References)
-
Chen Q, Liu G X, Ding X L.2010.Tight integration of GPS observations and persistent scatterer InSAR for detectiong vertical ground motion in Hong Kong. International Journal of Applied Earth Observation and Geoinformation, 12 (6) : 477–486 . [DOI:10.1016/j.jag.2010.05.002]
-
Chen Q, Ding X L, Liu G X.2007.Radar differential interferometry based on permanent scatterers and its application to detecting regional ground subsidence. Chinese Journal of Geophysics, 50 (3) : 737–743 . [DOI:10.3321/j.issn:0001-5733.2007.03.012] ( 陈强, 刘国祥, 丁晓利, 李永树. 2007. 永久散射体雷达差分干涉应用于区域地表沉降探测. 地球物理学报, 50 (3) : 737–743. [DOI:10.3321/j.issn:0001-5733.2007.03.012] )
-
Chen Q, Ding X L, Liu G X.2009.Baseline recognition and parameter estimation of persistent-scatterer network in radar interferometry. Chinese Journal of Geophysics, 52 (9) : 2229–2236 . [DOI:10.3969/j.issn.0001-5733.2009.09.006] ( 陈强, 丁晓利, 刘国祥. 2009. 雷达干涉PS网络的基线识别与解算方法. 地球物理学报, 52 (9) : 2229–2236. [DOI:10.3969/j.issn.0001-5733.2009.09.006] )
-
Ferretti A, Prati C, Rocca F.2000.Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing, 38 (5) : 2202–2212 . [DOI:10.1109/36.868878]
-
Ferretti A, Prati C, Rocca F.2001.Permanent scatterers in SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing, 39 (1) : 8–20 . [DOI:10.1109/IGARSS.1999.772008]
-
Hooper A, Bekaert D, Spaans K, Arıkan M.2012.Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics., 514-517 : 1–13 . [DOI:10.21029/22004GL021737]
-
Kampes B M, Hanssen R F.2004.Ambiguity resolution for permanent scatterer interferometry. IEEE Transactions on Geoscience and Remote Sensing, 42 (11) : 2446–2453 . [DOI:10.1109/TGRS.2004.835222]
-
Kampes B M. Displacement Parameter Estimation using Permanent Scatterer Interferometry. Netherlands: Delft University of Technology 2005 : 2102 -2112.
-
Liu G X, Luo X J, Chen Q, Huang D F, Ding X L.2008.Detecting Land Subsidence in Shanghai by PS-Neworking SAR Interferometry. Klybeckstrasse:Sensors, 8 (8) : 4725–4741 . [DOI:10.3390/s8084725]
-
Liu G X, Sean M. B, Ding X L, Chen Q, Luo X J.2009.Estimating spatiotemporal ground deformation with improved persistent-Scatterer Radar Interferometry. IEEE Transactions on Geoscience and Remote Sensing, 47 (9) : 3209–3219 . [DOI:10.1109/TGRS.2009.2028797]
-
Xing X M, Ding X L, ZHU J J, Wang C C, Ding W, Yang Y F, Wang Y X.2011.Detecting the regional linear subsidence based on CRInSAR and PSInSAR integration. Chinese Journal of Geophysics, 54 (5) : 1193–1204 . [DOI:10.3969/j.issn.0001-5733.2011.05.008] ( 邢学敏, 丁晓利, 朱建军, 汪长城, 丁伟, 杨亚夫, 王永哲. 2011. CRInSAR与PSInSAR联合探测区域线性沉降研究. 地球物理学报, 54 (5) : 1193–1204. [DOI:10.3969/j.issn.0001-5733.2011.05.008] )
-
Xing X M. 2011. Study on Monitoring the Time Series Ground Deformation in Mining Area Based on CRInSAR and PSInSAR Integration[Ph.D.thesis].Changsha:Central South University
-
Xia Y, Kaufmann H. and Guo X F. 2002. Differential SAR Interferometry Using Corner Reflectors//IEEE 2002 International Geoscience and Remote Sensing Symposium, Washington, USA:IEEE computer society, 1243-1246.[DOI:10.1109/IGARSS.2002.1025902]
-
Xia Y, Kaufmann H, Guo X F.2004.Landslide monitoring in the Three Gorges area using D-InSAR and corner reflectors. Photogrammetric Engineering and Remote Sensing, 70 (10) : 1167–1172 .
-
Zhu J J, Xing X M, Hu J, Li Z W.2011.Monitoring of ground surface deformation in mining area with InSAR technique. Changsha:The Chinese Journal of Nonferrous Metals, 21 (10) : 2564–2574 . ( 朱建军, 邢学敏, 胡俊, 李志伟. 2011. 利用InSAR技术监测矿区地表形变. 有色金属学报, 21 (10) : 2564–2574. )
-
Zhang H S. Error Theory and Surveying Adjustment Basis. Chang Sha: Central South University Press 1995 : 41 -45. ( 张后苏. 1995. 误差理论与测量平差基础. 长沙: 中南工业大学出版社 : 41 -45. )