|
|
|
收稿日期: 2015-05-04; 修订日期: 2015-09-16;
优先数字出版日期: 2015-09-23
基金项目: 中国科学院遥感与数字地球研究所"一三五"重点培育方向
中图分类号: TP75
文献标识码: A
文章编号: 1007-4619(2016)01-0053-09
|
摘要
矿物的混合多属于致密型混合,在可见光-短波红外波段的混合呈现非线性特征,同时由于矿物混合的复杂性以及图像中完全纯净的像元可能不存在等原因,使得从图像上提取端元具有较大不确定性。本文根据矿物单次散射反照率的线性可加性,提出一种基于矿物单次散射反照率光谱库的稀疏解混算法,利用Hapke模型将矿物反射率转换成矿物单次散射反照率,构建矿物单次散射反照率光谱库,以半监督的方式通过稀疏回归的方法从光谱库中寻找最优端元组合,并估算混合像元中各端元的丰度。利用RELAB矿物混合光谱库进行算法验证,结果表明,丰度反演的平均绝对误差为3.12%;将本文方法应用于美国内华达州铜矿区的AVIRIS高光谱图像数据,所得丰度图与美国地质勘探局USGS矿物识别结果具有较好的一致性。本文算法不需要从图像提取端元,并且考虑到了矿物的非线性混合特征,能够得到较高的反演精度,在近地行星和卫星表面岩矿成分的探测等领域具有较好的应用前景。
关键词
光谱解混; Hapke模型; 稀疏回归; 光谱库; 单次散射反照率
1 引 言
致密型混合的矿物不仅广泛存在于地球上,同时也是其他星球表面的重要组成部分,定量反演致密型混合矿物的组分对于人类了解地球及进行深空探测具有重要的意义。在高光谱图像中,由于空间分辨率不足使得混合像元普遍存在,增加了地物识别的难度,光谱解混及亚像元技术是目前遥感领域解决混合像元问题的热点与难点(Keshava和Mustard,2002)。根据混合特性和机理不同,光谱混合可分为致密型混合、聚合型和整合型混合3种形式。致密型地物由于各个组分紧密混合在一起,为非线性混合。聚合型和整合型地物在忽略各组分之间的边界效应的前提下可看成线性混合。线性解混模型假设高光谱图像中每个像元光谱是各端元以所占面积比例为权重的线性组合(Quintano等,2012),由于其明确的物理意义和计算简单的特点使线性解混模型广泛应用到了光谱解混中(Hu等,1999)。线性光谱解混主要分为端元提取和丰度反演(张兵和高连如,2011)。但是,由于矿物光谱混合特性与机理复杂,从原始图像上提取的端元具有较大的不确定性。Iordache等人(2010)提出利用光谱库代替端元以一种半监督的方式进行光谱解混,从一个大规模光谱库中寻找端元子集来最优模拟混合光谱,并估算各端元的丰度,其中光谱库可以通过地面测量等方式获得。随后其加入空间信息对算法进行了改进(Iordache等,2012);Tang等人(2015)以加入先验知识的方式对稀疏解混的算法也进行了改进,但是它们仍属于线性光谱解混的范畴。矿物在的可见光—短波红外波段混合多属于非线性混合(Nascimento和Bioucas-Dias,2010),直接利用线性稀疏解混算法受到很大限制。
许多非线性光谱解混模型经验证与线性模型相比精度有很大提高(Heylen等,2014)。Hapke模型是最常用的非线性矿物解混模型之一,对于致密型混合矿物来说,组成混合物的粒子通常会出现复杂的光学反应,Hapke模型很好地描述了矿物的混合效应(Hapke等,1993;Hapke,1981)。Hapke模型经过实验室验证并且在深空探测中获得了杰出的成果(Lemelin等,2013;Yan等,2010),矿物单次散射反照率的混合呈现较强的线性特征,而通过Hapke 理论可以得到矿物的单次散射反照率,这就使得将非线性解混模型转换到线性空间进行求解成为可能(Nascimento和Bioucas-Dias,2010)。Liu和Yao(2012)基于简化的Hapke模型,结合单形体体积法对实验室测量的混合矿物光谱进行光谱解混,提高了丰度反演的精度;Heylen和Gader(2014)基于线性解混模型和Hapke模型构建了矿物的非线性解混模型,利用实验室混合光谱对模型进行了验证,并对实际图像数据进行了应用,但是算法的精度依赖于端元的提取算法。因此,本文提出一种基于矿物单次散射反照率光谱库的稀疏解混算法。通过Hapke模型构建矿物的单次散射反照率光谱库,单次散射反照率的混合呈现较强的线性特征,可以基于光谱库利用稀疏解混算法反演混合矿物各组分,省去了从遥感图像上提取端元的步骤,避免了图像提取端元的误差。
2 数据及预处理
2.1 算法验证数据及预处理
选用RELAB光谱库中的实验室模拟混合矿物光谱以及高光谱图像数据进行算法验证。所用实验室模拟数据包括石英、明矾石、橄榄石、古铜辉石及钙长石等矿物粉末按照不同比例混合而成的混合矿物光谱,包含421个波段,波谱范围为0.4—2.5 μm,入射天顶角为30°,观测角为0°。
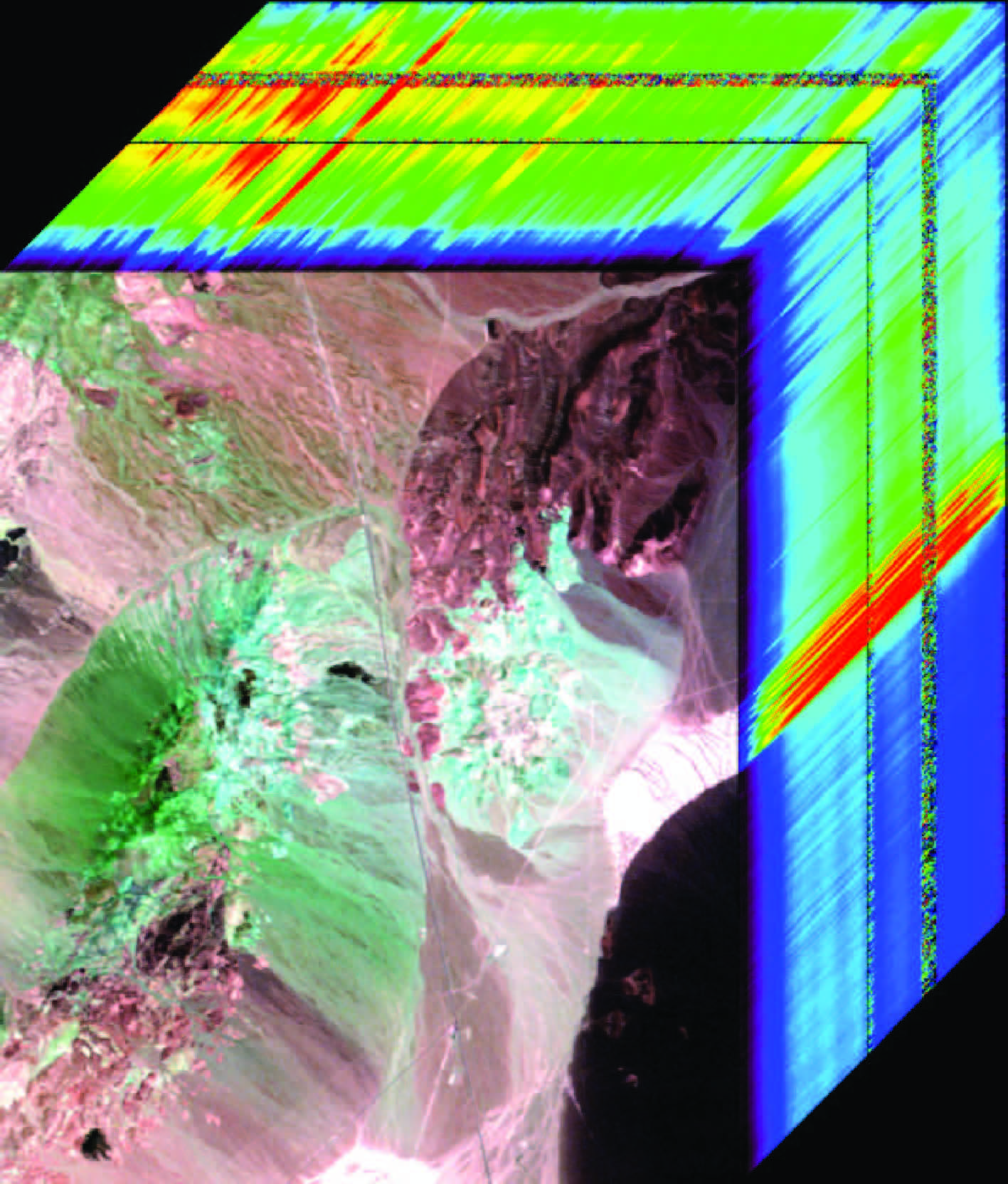
高光谱图像数据为美国内华达州铜矿区1995年的AVIRIS高光谱图像,该地区只有少数植被覆盖,大部分为矿物蚀变带,是进行遥感地质研究的典型样区。图像包含光谱范围0.4—2.5 μm的224个波段,大小为614×750像元(图 1)。其中,测量时的辐射入射角为10°,可以从元数据中计算获得;观测时一般认为相机垂直照射,辐射出射角为0°(Heylen和Gader,2014)。由于水吸收及低信噪比等原因需去除坏波段(波段1—波段2,波段105—波段115,波段150—波段170及波段223—波段224),最终剩余188个波段。
2.2 光谱库数据及预处理
美国地质调查局USGS光谱库中有881条矿物光谱,本文选择光谱范围为0.4—2.5 μm的342条光谱来构建解混光谱库,光谱库中包含不同类别的矿物。解混光谱库中光谱均由Beckman 5270光谱仪测得,利用Beckman 5270光谱仪测量时的辐射入射角设定为0°,辐射出射角设定为30°(Warell和Davidsson,2010)。将光谱库的反射率重采样到与AVIRIS高光谱图像数据的光谱范围和波长位置一致,光谱重采样采用距离加权算法,原理如下:
$R = a{R_l} + b{R_r}$ (1)
式中,a=y/(x+y),b=1-a。R为需要重建反射率,Rl和Rr分别为R左边和右边距离最近的反射率值,x和y分别为左右反射率中心波长距离R中心波长的波长距离。
3 原理与方法
算法核心包括矿物单次散射反照率光谱库的构建和稀疏解混模型构建及求解。首先构建矿物的反射率光谱库,利用Hapke模型将矿物反射率转换成单次散射反照率,同时也将高光谱图像的反射率转换成单次散射反照率;然后利用单次散射反照率光谱库基于稀疏解混模型得到矿物的丰度。采用实验室模拟混合矿物光谱和高光谱图像数据同时对反演结果进行评价,全面的评价算法的有效性。算法流程图如图 2所示。
3.1 单次散射反照率计算方法
基于辐射传输方程,Hapke等首次推导出混合矿物的反射率与介质光学和物理参数之间的关系(Hapke,1981),当半无限介质的颗粒大小大于波长λ时,双向反射率是单次散射反照率SSA的函数(Hapke,2005):
$\begin{gathered} r\left({{\mu _0},\mu,g} \right)= \frac{\omega }{{4\pi }}\frac{{{\mu _0}}}{{{\mu _0} + \mu }} \cdot \hfill \\ \left\{ {\left[ {1 + B\left(g \right)} \right]P\left(g \right)+ H\left({\omega,{\mu _0}} \right)H\left({\omega,\mu } \right)- 1} \right\} \hfill \\ \end{gathered}$ (2)
式中,μ0=cos(i),μ=cos(e),i和e分别是辐射入射角和出射角,g表示相位角,ω表示矿物的单次散射反照率,B(g)是后向散射系数,P(g)是介质的归一化相位函数,描述入射光在某方向上反射的概率,H(ω,μ)为各向同性散射函数。
对于致密型混合矿物来说,入射光在到达传感器前通常会与组成混合物的粒子发生多次作用,每次作用光子可能会在随机方向被吸收或散射,入射光被粒子散射的部分与粒子消光部分(粒子吸收部分和散射部分之和)的比值定义为单次散射反照率ω(SSA):
$\omega = \frac{S}{E} = \frac{S}{{S + A}}$ (3)
式中,S是介质的散射系数,E是消光系数,A为吸收系数。ω为0—1,当介质吸收所有的入射光时,ω=0,当介质散射所有的光时,ω=1,ω(λ)随着波长的变化而变化,可以用来描述微小尺度下光子与单个粒子间的相互作用。致密型混合矿物的反射率并不是组成混合矿物各端元反射率的线性混合,但是它们的单次散射反照率基本属于线性混合(Hapke,1981):
$\omega = \sum\limits_{m = 1}^M {{a_m}{\omega _m}}$ (4)
式中,am表示混合矿物各组分的丰度,ωm为混合矿物各组分的单次散射反照率。
为求得各组分的丰度,需要计算混合矿物及其各组分的单次散射反照率,但是式(2)比较复杂,需要较多输入参数,直接求解相对困难。Hapke对其进行了简化,作出如下假设:相位角g足够大时,可忽略后向散射的影响,此时B(g)=0;粒子的单次散射各向同性,相位函数P(g)=1。则矿物的反射率为:
$r\left({{\mu _0},\mu,\omega } \right)= \omega \frac{{H\left({\omega,{\mu _0}} \right)H\left({\omega,\mu } \right)}}{{H\left({1,{\mu _0}} \right)H\left({1,\mu } \right)}}$ (5)
H函数的近似表达为:
$H\left(\mu \right)= \frac{{1 + 2\mu }}{{1 + 2\mu \sqrt {1 - \omega } }}$ (6)
矿物反射率的表达式转换为:
$r\left({{\mu _0},\mu,\omega } \right)= \frac{\omega }{{\left({1 + 2\mu \sqrt {1 - \omega } } \right)\left({1 + 2{\mu _0}\sqrt {1 - \omega } } \right)}}$ (7)
如果矿物的反射率已知,则可根据式(8)得到矿物的单次散射反照率:
$\begin{gathered} \sqrt {1 - \omega } = \hfill \\ \frac{{{{\left[ {{{\left({{\mu _0} + \mu } \right)}^2}{r^2} + \left({1 + 4{\mu _0}\mu \cdot r} \right)\left({1 - r} \right)} \right]}^{\frac{1}{2}}} - \left({{\mu _0} + \mu } \right)r}}{{1 + 4{\mu _0}\mu \cdot r}} \hfill \\ \end{gathered}$ (8)
3.2 线性稀疏解混原理
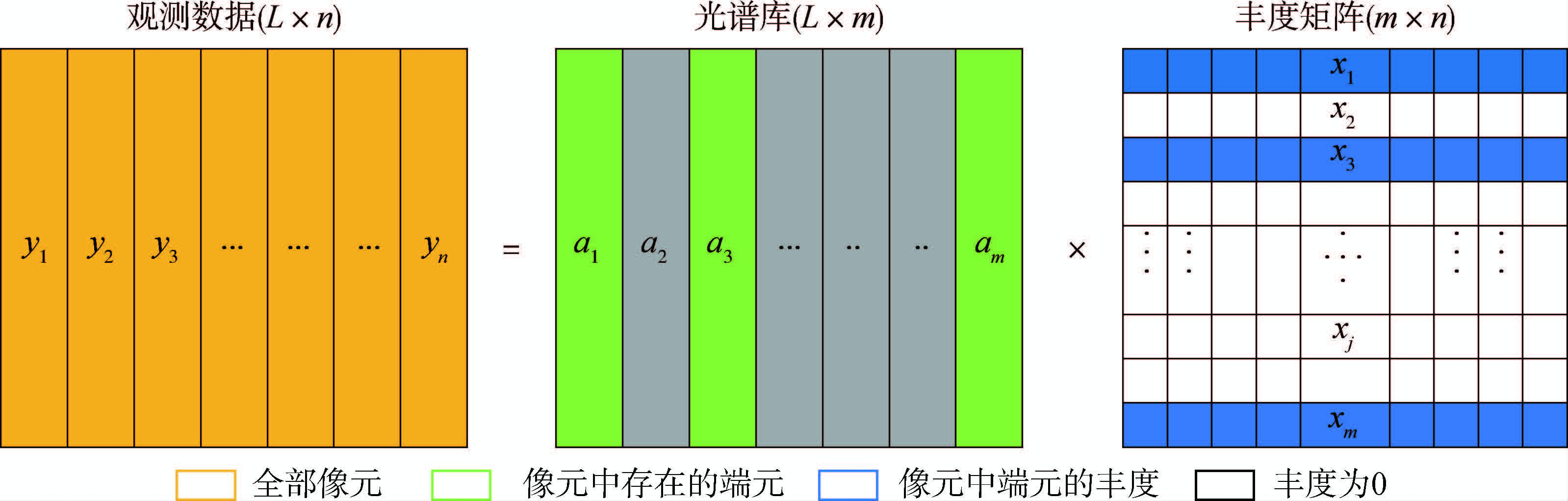
由于直接从高光谱遥感图像中提取端元面临很大挑战,因此解混可通过半监督的方式解决,利用光谱库的纯净光谱进行解混,光谱库作为先验知识使稀疏解混的算法不依赖于端元提取算法。由于一个混合像元中实际存在的端元数量往往远小于光谱库所有光谱的总数量,因此光谱解混问题实际上是一个基于稀疏正则化矩阵的高效稀疏回归问题,通过设定正则化参数对线性解混模型进行稀疏约束,得到光谱库中存在于像元内的端元及其对应的丰度,原理如图 3所示(Iordache等,2014)。
线性解混模型假设每个像元的光谱是由像元内各端元的线性组合,可表达为:
$Y = \sum\limits_{i = 1}^N {{a_i}{x_i} + n} = AX + n$ (9)
式中,对于稀疏解混来说,Y∈RL×N表示观测光谱,A表示光谱库,X是光谱库中各矿物在像元内的丰度比例,n代表误差项。由于图像像元内端元的数量远小于光谱库中光谱的数量,因此X是稀疏的。则稀疏回归的问题可以写成(Iordache等,2011):
$\begin{gathered} \mathop {\min }\limits_x {\left\| x \right\|_0}约束条件为 \hfill \\ {\left\| {Y - AX} \right\|_2} \leqslant \delta,x \geqslant 0,\sum\limits_{k = 1}^m {{x_k} = 1} \hfill \\ \end{gathered} $ (10)
式中,${\left\| x \right\|_0}$表示X中非零的个数,σ≥0是由于噪声和模型误差导致的容错度,${\left\| * \right\|_2}$表示l2范数,xk为光谱库中第k个矿物在像元中的丰度,m为光谱库中光谱个数。由于l0范数离散且非凸,使得式(8)求解困难,因此,用l1范数来近似代替l0范数,则稀疏解混的最优化问题变成:
$\begin{gathered} \mathop {\min }\limits_x {\left\| x \right\|_1}约束条件为 \hfill \\ {\left\| {Y - AX} \right\|_2} \leqslant \delta,x \geqslant 0,\sum\limits_{k = 1}^m {{x_k} = 1} \hfill \\ \end{gathered}$ (11)
经过稀疏约束后,在每个像元中,光谱库各矿物光谱对应的丰度值大部分为零,只有少数的矿物光谱对应的丰度值大于零。则像元中存在的矿物端元及其丰度可同时求出,即丰度值大于零的矿物为像元中存在的端元,所得丰度值为该矿物在像元中所占的比例。
3.3 基于矿物单次散射反照率光谱库的稀疏解混算法
在0.4—2.5 μm矿物混合光谱一般为组分反射率光谱的非线性混合,线性的解混模型使得矿物的丰度反演存在较大误差,Hapke模型考虑到矿物多次散射作用及角度对反射率的影响,较好地描述了矿物的非线性混合过程。稀疏解混算法利用预知的光谱库内的纯净端元光谱进行解混,使得光谱解混的精度不依赖于端元提取算法,减小了从图像中提取端元的不确定性对光谱解混精度的影响。本文结合Hapke模型和稀疏解混模型进行矿物的识别及丰度反演,所构建光谱解混模型为:
$\begin{gathered} \mathop {\min }\limits_x {\left\| x \right\|_1}约束条件为 \hfill \\ {\left\| {Y\left(\omega \right)- A\left(\omega \right)X} \right\|_2} \leqslant \delta,x \geqslant 0,\sum\limits_{k = 1}^m {{x_k} = 1} \hfill \\ \end{gathered}$ (12)
式中,Y(ω)表示图像的单次散射反照率,A(ω)代表矿物单次散射反照率光谱库,单次散射反照率可由式(8)获得。应用此模型时应尽量保证单次散射反照率光谱库足够完备,包含研究区高光谱图像可能存在的端元。
为求解以上稀疏解混问题,本文采用Iordache等人(2011)基于ADMM(Alternating Direction Method of Multipliers)(Eckstein和Bertsekas1992)发展的变量分裂和增广拉格朗日的稀疏解混算法(SUnSAL),该方法求解速度相对较快(宋义刚等,2013)。
4 实验与结果分析
4.1 实验室模拟数据验证
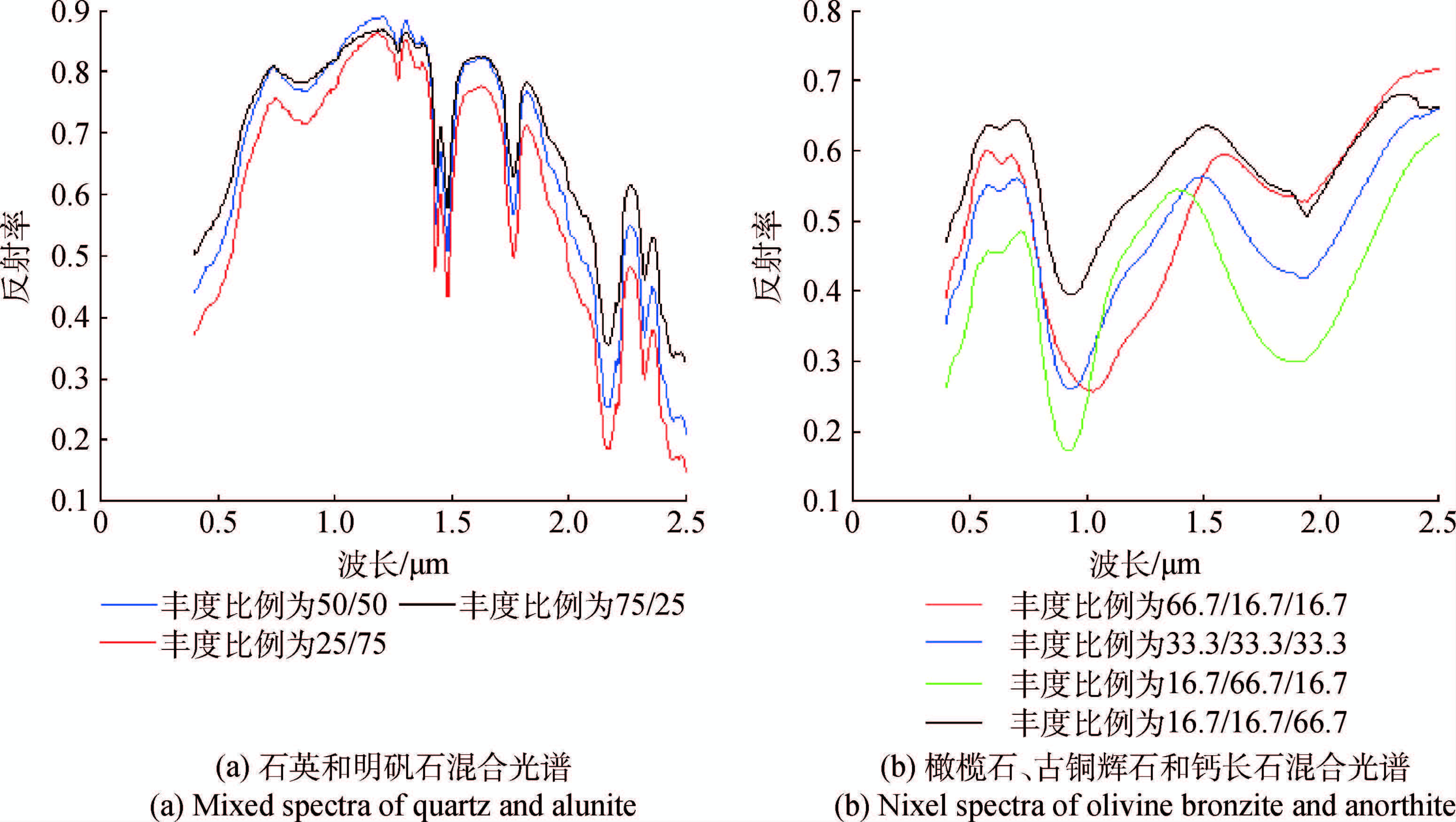
选用的RELAB光谱库中混合矿物样本名称分别为XT-CMP-002,XT-CMP-003,XT-CMP-004,XT-CMP-033,XT-CMP-034,XT-CMP-035和XT-CMP-036,每个样本都已知其组分所占的丰度比例,混合矿物的光谱如图 4所示。
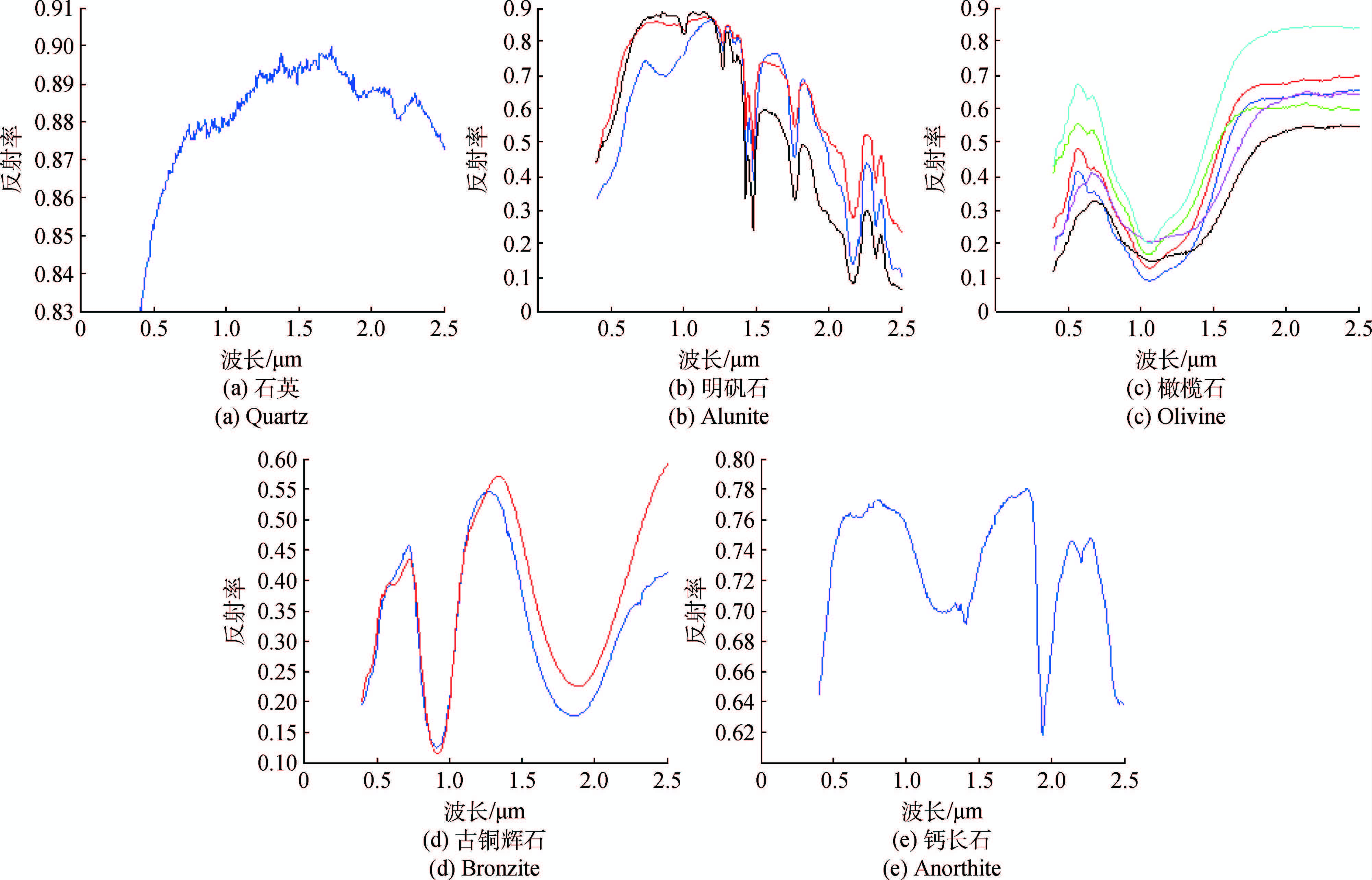
首先将反射率光谱库重采样到RELAB混合光谱的中心波长,然后将反射率光谱库转换成单次散射反照率光谱库,设定最小光谱角为2.5°去除相近的端元光谱,最终的单次散射反照率光谱库剩余矿物样本光谱112条,矿物种类77种。光谱库中石英、明矾石、橄榄石、古铜辉石和钙长石5类矿物中各类含有典型光谱1—6条,5类矿物的光谱库中端元光谱如图 5所示。
表 1列出了各混合矿物样本的光谱解混结果。从表 1反演的结果可以看出,线性解混模型的结果误差较大,并不能有效地从光谱库中识别出组成混合矿物的正确矿物端元。本文方法较线性稀疏解混算法在矿物识别和丰度定量反演方面都有很大的提高。
| 样本名称 | 矿物比例/% | SR/% | (Hapke+SR)/% |
| XT-CMP-002 | 75/25(石英/明矾石) | 0.98/79.99 | 69.76/27.77 |
| XT-CMP-003 | 50/50(石英/明矾石) | 0/86.30 | 49.10/50.04 |
| XT-CMP-004 | 25/75(石英/明矾石) | 0/96.14 | 24.59/74.40 |
| XT-CMP-033 | 66.7/16.7/16.7(橄榄石/古铜辉石/钙长石) | 62.57/32.41/0 | 61.66/15.00/18.56 |
| XT-CMP-034 | 16.7/66.7/16.7(橄榄石/古铜辉石/钙长石) | 16.09/80.13/0 | 13.94/63.63/21.75 |
| XT-CMP-035 | 16.7/16.7/66.7(橄榄石/古铜辉石/钙长石) | 47.75/18.85/0 | 13.02/12.62/73.31 |
| XT-CMP-036 | 33.3/33.3/33.3(橄榄石/古铜辉石/钙长石) | 39.21/51.75/0 | 27.11/28.82/37.91 |
| 注:SR代表直接利用线性稀疏回归的解混算法得到的结果,Hapke+SR代表本文方法得到的结果。 | |||
利用绝对误差、反演丰度与真实丰度线性拟合的相关系数两个指标来评价反演效果,矿物的反演含量与真实含量基本呈线性关系(闫柏琨等,2012),绝对误差是矿物反演丰度与真实丰度的差值。本文方法能够准确地识别混合矿物中的矿物端元,丰度反演绝对误差最大为6.61%,最小可达到0.4%,大部分结果小于5%。表 2显示了5种矿物丰度反演的绝对误差、线性拟合相关系数。5种矿物绝对误差、线性拟合相关系数的均值分别为3.12%和0.9977。由此可以看出,本文方法得到的矿物丰度与真实丰度相差不大,且基本呈现线性关系,有效提高了矿物丰度反演的精度。
| 石英 | 明矾石 | 橄榄石 | 古铜辉石 | 钙长石 | |
| 误差/% | 2.18 | 1.14 | 4.42 | 3.33 | 4.53 |
| 相关系数 r | 0.9976 | 0.9993 | 0.9970 | 0.9972 | 0.9973 |
4.2 高光谱图像数据验证
将光谱库中矿物反射率转换成单次散射反照率,构建单次散射反照率光谱库,为保证光谱库中尽量包括图像中所有存在的地物,本文利用所有342条光谱构成的单次散射反照率光谱库对内华达州铜矿区进行光谱解混,光谱库中矿物种类共178种。虽然直接利用342条光谱会使光谱库具有相对较高的相关性,对解的稀疏性会产生一定影响,但光谱库中光谱个数远大于一个混合像元内实际存在的端元个数,使得丰度解具有较高的稀疏性,可以在一定程度上减轻光谱库高相关性的影响。
由于没有实际的矿物丰度图作为验证,将本文结果与USGS矿物分布图(图 6)进行比较来说明结果的有效性.其中,USGS矿物分布图是基于USGS光谱库利用Tricorder算法得到的分类图(Clark等,2003)。
图 7显示了内华达铜矿区主要的6种矿物的丰度图及USGS分布图,可以看出,由本文方法得到的矿物丰度图与其相应的USGS识别结果基本一致,尤其是在丰度的高值部分。其中,明矾石、方解石、高岭石的丰度图与USGS分布图的一致性最好,云母、玉髓、地开石次之,可以从定性的角度说明基于矿物单次散射反照率光谱库的稀疏解混算法对真实高光谱图像数据光谱解混的有效性。需要指出的是,利用本文的光谱解混方法得到的丰度图与USGS分布图存在一定程度上的差异,这是因为利用Tricorder算法得到的分布图是分类图,认为高光谱图像中混合像元是纯净像元,把像元类别归为最能代表该像元的矿物端元类别,而光谱解混算法相当于亚像元级的分类,混合像元的丰度代表了矿物在像元中所占的比例,丰度高值区与识别结果的一致性表明本研究丰度反演结果的可靠性。
5 结论
根据矿物单次散射反照率的线性可加性,有针对性地提出一种基于矿物单次散射反照率光谱库的稀疏解混算法。利用Hapke模型将矿物反射率转换为矿物单次散射反照率,使得将非线性解混模型转换到线性空间进行求解成为可能;稀疏解混算法利用预知的光谱库内的纯净光谱进行解混,使得光谱解混的精度不依赖于端元的提取算法,减小了从图像中提取端元的不确定性对光谱解混精度的影响。基于Hapke模型构建的矿物单次散射反照率光谱库进行稀疏解混,有望提高高光谱遥感图像反演矿物丰度的可靠性。
通过对实验室模拟矿物混合光谱和AVIRIS高光谱图像数据的验证表明,本文算法有较高的反演精度。基于RELAB光谱库中已知矿物丰度比例的实验室混和光谱验证表明,丰度反演的平均绝对误差为3.12%;利用美国内华达州铜矿区AVIRIS图像验证表明,丰度反演结果高值区与USGS的识别结果具有较好一致性,明矾石、方解石、高岭石一致性最好,云母、玉髓、地开石次之,说明了本文方法光谱解混的有效性。对近地行星和卫星表面岩矿成分的探测是目前国际的研究热点之一,而星体表面岩矿混合复杂,端元具有很大的不确定性,本文的方法不需要从图像提取端元,而且考虑到了矿物的非线性混合特征,有望得到较高的反演精度,在深空探测中具有较好的应用前景。
Hapke模型在利用反射率推算单次散射反照率时对后向散射系数和相位函数进行了假设,实际的高光谱数据不一定完全满足它的简化条件,直接利用简化的Hapke模型推算每种矿物的单次散射反照率会存在一定误差。因此,根据矿物自身的物理参数(复折射系数、颗粒直径等)准确计算其单次散射反照率,并与Hapke简化模型进行比较,将是下一步研究的重点。
参考文献
-
Nascimento J M P and Bioucas-Dias J M. 2010. Unmixing hyperspectral intimate mixtures//Proc. SPIE 7830, Image and Signal Processing for Remote Sensing XVI. Toulouse, France:SPIE[DOI:10.1117/12.865118]
-
Clark R N, Swayze G A, Livo K E, Kokaly R F, Sutley S J, Dalton J B, McDougal R R and Gent C A. 2003. Imaging spectroscopy:earth and planetary remote sensing with the USGS Tetracorder and expert systems.Journal of Geophysical Research, 108(E12):5131 [DOI:10.1029/2002JE001847]
-
Eckstein J and Bertsekas D P. 1992. On the douglas-rachford splitting method and the proximal point algorithm for maximal monotone operators. Mathematical Programming, 55(1/3):293-318[DOI:10.1007/BF01581204]
-
Heylen R and Gader P. 2014. Nonlinear spectral unmixing with a linear mixture of intimate mixtures model. IEEE Geoscience and Remote Sensing Letters, 11(7):1195-1199[DOI:10.1109/LGRS.2013.2288921]
-
Hapke B. 1981. Bidirectional reflectance spectroscopy 1. Theory.Journal of Geophysical Research, 86(B4):3039-3054 [DOI:10.1029/JB086iB04p03039]
-
Hapke B. 2005. Theory of Reflectance and Emittance Spectroscopy. Cambridge, U.K.:Cambridge Univ.Press.
-
Hapke B W, Nelson R M and Smythe W D. 1993. The opposition effect of the moon:the contribution of coherent backscatter. Science, 260(5107):509-511[DOI:10.1126/science.260.5107.509]
-
Heylen R, Parente M and Gader P. 2014. A review of nonlinear hyperspectral unmixing methods. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7(6):1844-1868[DOI:10.1109/JSTARS.2014.2320576]
-
Hu Y H, Lee H B and Scarpace F L. 1999. Optimal linear spectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 37(1):639-644[DOI:10.1109/36.739139]
-
Iordache M D, Bioucas-Dias J M and Plaza A. 2011. Sparse unmixing of hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing, 49(6):2014-2039[DOI:10.1109/TGRS.2010.2098413]
-
Iordache M D, Bioucas-Dias J M and Plaza A. 2012. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 50(11):4484-4502[DOI:10.1109/TGRS.2012.2191590]
-
Iordache M D, Bioucas-Dias J M and Plaza A. 2014. Collaborative sparse regression for hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 52(1):341-354[DOI:10.1109/TGRS.2013.2240001]
-
Iordache M D, Plaza A and Bioucas-Dias J. 2010. On the use of spectral libraries to perform sparse unmixing of hyperspectral data//2010 2nd Workshop on Hyperspectral Image and Signal Processing:Evolution in Remote Sensing (WHISPERS). WHISPERS. Reykjavik:IEEE:1-4[DOI:10.1109/WHISPERS.2010.5594888]
-
Keshava N and Mustard J F. 2002. Spectral unmixing. IEEE Signal Processing Magazine, 19(1):44-57[DOI:10.1109/79.974727]
-
Lemelin M, Morisset C E, Germain M, Hipkin V, Go?ta K and Lucey P G. 2013. Ilmenite mapping of the lunar regolith over Mare Australe and Mare Ingenii regions:an optimized multisource approach based on Hapke radiative transfer theory.Journal of Geophysical Research:Planets, 118(12):2582-2593 [DOI:10.1002/2013JE004392]
-
Liu J and Yao G Q. 2012. Nonlinear decomposition of high spectral mixture pixel based on approximate hapke model and single physical volume method//2012 International Conference on Computer Science & Service System (CSSS). Nanjing:IEEE:393-396[DOI:10.1109/CSSS.2012.105]
-
Quintano C, Fernández-Manso A, Shimabukuro Y E and Pereira G. 2012. Spectral unmixing. International Journal of Remote Sensing, 33(17):5307-5340[DOI:10.1080/01431161.2012.661095]
-
Song Y G, Wu Z B, Wei Z H, Sun L and Liu J J. 2013. Survey of sparsity constrained hyperspectral unmixing. Journal of Nanjing University of Science and Technology, 37(4):486-492 (宋义刚, 吴泽彬, 韦志辉, 孙乐, 刘建军. 2013.稀疏性高光谱解混方法研究.南京理工大学学报, 37(4):486-492)
-
Tang W, Shi Z W, Wu Y and Zhang C S. 2015. Sparse unmixing of hyperspectral data using spectral a priori information. IEEE Transactions on Geoscience and Remote Sensing, 53(2):770-783[DOI:10.1109/TGRS.2014.2328336]
-
Warell J and Davidsson B J R. 2010. A Hapke model implementation for compositional analysis of VNIR spectra of Mercury. Icarus, 209(1):164-178[DOI:10.1016/j.icarus.2009.11.037]
-
Yan B K, Wang R S, Gan F P and Wang Z C. 2010. Minerals mapping of the lunar surface with Clementine UVVIS/NIR data based on spectra unmixing method and Hapke model. Icarus, 208(1):11-19[DOI:10.1016/j.icarus.2010.01.030]
-
Yan B K, Li J Z, Gan F P, Yang S M and Wang R S. 2012. A spectral unmixing method of estimating main minerals abundance of lunar soils. Spectroscopy and Spectral Analysis, 32(12):3335-3340 (闫柏琨, 李建忠, 甘甫平, 杨苏明, 王润生. 2012. 一种月壤主要矿物组分含量反演的光谱解混方法. 光谱学与光谱分析, 32(12):3335-3340)[DOI:10.3964/j.issn.1000-0593(2012)12-3335-06]
-
Zhang B and Gao L R. 2011. Hyperspectral Image Classification and Target Detection. Beijing:Science Press:102-117 (张兵, 高连如. 2011. 高光谱图像分类与目标探测. 北京:科学出版社:102-117)
Abstract
Mineral mixtures are intimate mixtures have been extensively generated both on Earth and on other planets. The scatter of the particles that comprise mineral mixtures typically initiates complex optical interactions that are not interpreted by a linear mixing model. Moreover, the extraction of endmember signatures from the original data may be difficult given complex mineral mixtures and the lack of completely pure spectral signatures in the scene. Thus, we propose a sparse unmixing algorithm based on the spectral library of a Single Scattering Albedo (SSA) to decompose intimate mixtures.The sparse unmixing method aims to determine the optimal subset of endmembers from a spectral library and to estimate its fractional abundances in each pixel. The data from the spectral library are considered prior information; thus, sparse unmixing does not rely on endmember extraction algorithms. The Hapke model can describe intimate mixing effects effectively, and SSA can be obtained based on the theory behind this model. The SSA of the component particles is a linear mixture; therefore, linear unmixing techniques can be applied in the SSA space instead of in the reflectance space. The data processing procedure in this study mainly consists of three steps:(1) Building the spectral library of reflectance and then resampling the library spectrum to wavelength range and position; (2) Converting the reflectance to SSA and constructing a SSA spectral library; (3) Sparse unmixing.The laboratory spectra of the mineral mixtures and of the AVIRIS Cuprite data set are used to verify our method. We can identify the endmembers of mixtures accurately given laboratory data, and the mean absolute retrieval error of abundance is 3.12%. The qualitative analysis of AVIRIS hyperspectral data indicates that the abundance maps derived with our method are consistent with the Tricorder maps of United States Geological Survey (USGS), particularly in places where abundance is high; nonetheless, the abundance maps determined with our method still do not confirm to Tricorder maps to some extent. The classification maps of hyperspectral data consider each pixel to be pure, and each pixel is classified as the class of the representative endmember in the pixel. By contrast, unmixing classifies the scene at subpixel level, and the abundances represent the proportion of endmembers in a pixel. Experiment results show that our method can identify endmembers from the spectral library accurately, and can also estimate abundance well. The Hapke model can simply be used to minimize errors by calculating SSA directly. In our future work, we will calculate SSA exactly based on physical mineral parameters.
Key words
spectral unmixing; Hapke model; sparse regression; spectral library; single scattering albedo