|
|
|
收稿日期: 2015-04-07; 修订日期: 2015-07-06; 优先数字出版日期: 2015-07-13
基金项目: 国家自然科学基金(编号:41271362,60962003); 广西自然科学基金(编号:2014GXNSFAA118302); 广西研究生创新项目(编号:YCSZ2014138); 广西自动检测技术与仪器重点实验室基金(编号:YQ15108); 桂林电子科技大学创新团队资助
中图分类号: P237
文献标识码: A
文章编号: 1007-4619(2016)01-0080-14
|
摘要
以摄影测量共线方程为严格配准模型,提出了一种引入针孔成像模拟过程的单张航空影像LiDAR点云配准迭代方法,共分为3个阶段:第一,利用航空影像内参数及初始外方位元素对LiDAR点云针孔模拟成像,生成与航空影像空间分辨率、几何形变相接近且具有相同幅面大小的透视影像-LiDAR深度影像;第二,以梯度互信息作为影像相似性测度依据,实施影像金字塔、分块处理策略实现LiDAR深度影像与航空影像几何变换参数快速估计,进而依据估计参数及LiDAR深度影像、激光脚点投影关系建立LiDAR点云航空影像概略相关;第三,以LiDAR点云影像概略相关下的近似同名像点为观测值,以像点梯度互信息为权重,实施摄影测量空间后方交会计算获得优化的影像外方位元素,生成新的LiDAR深度影像并重复上述过程,直至满足给定的迭代计算条件,实现单张航空影像与LiDAR点云数据的自动空间配准。实验表明,本文方法配准精度达亚像素级且自动化程度高。
关键词
影像地理配准;LiDAR;针孔成像模拟;梯度互信息
1 引 言
近年来,机载LiDAR(Light Detection and Ranging)数据与光学航空影像联合处理得到了对地观测领域的广泛重视,涉及“真”正射影像生成(钟成,2011)、城市3维可视化(吴军等,2006)、人工建筑提取(Rottensteiner和Jansa,2002)等广泛应用。由于在成像机理、量测特性(同一地物或目标的灰度、几何性质)及坐标参考框架存在较大差异,LiDAR 数据(称为“点云”)与光学航空影像的融合无论在精度还是自动化程度方面均面临较大困难,其中空间配准就是亟待解决的问题之一,成为当前的研究热点(钟成等,2009;张永军等,2012;马洪超等,2012;Zheng等,2013)。
光学影像与LiDAR数据配准是一个2维连续影像与3维离散点云间的复杂配准问题,广泛吸收来自图像处理、计算机视觉、摄影测量等相关领域的优秀成果,现有LiDAR点云与光学影像配准方法可概略分为两类:基于原始激光脚点的直接配准和基于复杂特征提取的间接配准。选取少量激光脚点作为控制点,基于摄影测量空间后方交会原理解算出的待配准影像外方位元素精度有限,多作为优化计算的初值(吴军等,2006)。针对激光点云和影像中获取的控制点信息存在选点误差、仪器误差问题,(王晏民和胡春梅,2012)
基于共线方程,给出了一种改进丹麦法选权迭代降权方法对初始参数进行精确配准,适合任意摄影角度影像,但激光脚点及其同名像点的自动相关问题并没有得到解决,仍需手动选取控制点。目前直接配准的基本思路是从重叠影像中匹配生成3维点集,将LiDAR数据和光学影像间的配准转化为两个3维点云间的配准(张帆等,2008),其代表方法是以欧氏距离为相似性测度的最邻近迭代ICP(Iterative Closest Point)(Zhao等,2005),难点在于两种点云在分辨率、尺度以及空间分布特性上的差异,如LiDAR点云不能准确记录易于影像匹配成功的、集中在灰度突变处的地物边界位置信息,两者之间没有真正意义上的同名点,相关的改进研究包括以影像点到LiDAR点云局部平面法向距离作为相似性测度(Zheng等,2013)、建立K-D树加速最邻近点查找效率(邓非,2006)等等,由于ICP算法易收敛到局部最小,必须提供较好的初值且应避免引入影像特征提取、匹配误差。从LiDAR点云和影像中获得高精度、分布合理的同名特征是实施间接配准的前提,相比于直接配准,间接配准方法总体上具有较好的灵活性与配准效果,但依赖于特征提取精度以及与同名影像特征相关的自动化程度,或基于建筑物矩形屋顶“质心”(Mitishita等,2008),或基于“点云”中3维直线段(Habib等,2005;马洪超等,2012),或基于垂直直线段相交得到的建筑角点(张永军等,2012),或基于建筑角点构建的水平三角形(钟成等,2009),或基于点、线相似不变性(张良等,2014)等高层次特征来建立变换模型并进行参数估计,由于在配准基元特征表达、高精度定位,尤其是配准基元相似性测度、自动相关问题方面并未得到有效解决,间接配准方法应用效率、精度以及鲁棒性受到不同程度制约。
LiDAR数据具有物方信息密集的特点,当局部配准基元特征提取、相关计算由于语义结构线索缺乏存在困难时,可充分发挥其整体物方信息密集优势来提高配准精度、效率,从这一角度出发,本文以摄影测量共线方程为严格配准模型,提出了一种针孔成像模拟下的单张航空影像与LiDAR点云迭代配准新方法,基本思想是直接从恢复全体激光脚点的摄影光束着手,以LiDAR点云针孔模拟成像生成的、与航空影像空间分辨率、几何形变相接近且具有相同幅面大小的灰度影像(LiDAR深度影像)为桥梁,通过与配准参数持续优化改进相联系的影像梯度互信息迭代计算过程,逐步获得使LiDAR点云之投影误差总体最小的最优空间配准参数,实现两者高效、高精度配准。
2 LiDAR点云像方迭代配准框架
本文配准满足以下前提条件:(1)配准区域为表面不连续性明显的城市区域;(2)LiDAR点云仅包含X,Y,Z空间坐标信息;(3)航空影像为中心投影的可见光影像,其摄影相机内方位元素已知并消除了影像光学畸变,影像具有低精度的POS信息(外方位元素初值),配准目标是将中心投影的航空影像纳入到LiDAR点云所在的空间坐标框架,并以摄影测量共线方程(张祖勋和张剑清,2002)来严格描述两者间的2D-3D配准几何模型:
$ \left\{ \begin{array}{l}x - {x_0} = \\\;\;\;\; - f\frac{{{a_1}\left({X - {X_s}} \right)+ {b_1}\left({Y - {Y_s}} \right)+ {c_1}\left({Z - {Z_s}} \right)}}{{{a_3}\left({X - {X_s}} \right)+ {b_3}\left({Y - {Y_s}} \right)+ {c_3}\left({Z - {Z_s}} \right)}}\\y - {y_0} = \\\;\;\;\;\; - f\frac{{{a_2}\left({X - {X_s}} \right)+ {b_2}\left({Y - {Y_s}} \right)+ {c_2}\left({Z - {Z_s}} \right)}}{{{a_3}\left({X - {X_s}} \right)+ {b_3}\left({Y - {Y_s}} \right)+ {c_3}\left({Z - {Z_s}} \right)}}\end{array} \right. $ (1)
式中,{ai,bi}为影像旋转矩阵元素,(Xs,Ys,Zs)为影像摄站中心,f为相机有效焦距,(x0,y0)为像主点坐标,(x,y),(X,Y,Z)为对应的像点、空间点。
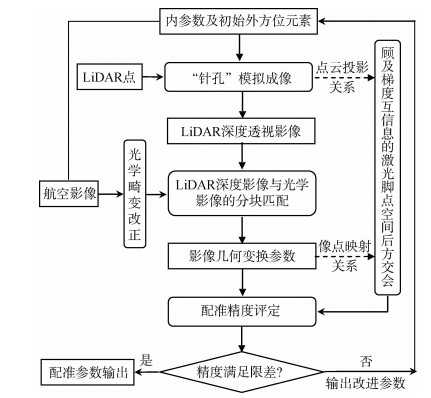
LiDAR点云是地表面的离散采样形式,摄影测量空间后方交会理论上适用于LiDAR点云与航空影像间的空间配准参数计算,困难在于如何从量测特性存在根本差异的两种数据集中获得高精度控制点对。注意到以下事实:(1)LiDAR激光脚点提供了传统空间后方交会计算所不具备的、极其密集的地面控制信息,这种物方控制信息密集优势可在一定程度上弥补控制点定位精度欠缺的影响;(2)LiDAR激光脚点在航空影像上的同名像素客观存在,这些像素虽因自身或局部邻域信息不显著而难以为影像特征提取算子成功检测,但总体上因数量众多而体现出有意义的统计特性,如信息熵。基于上述认识,本文以LiDAR点云与航空影像像素整体相关为突破口,设计了一套如图 1所示的单像LiDAR点云迭代配准框架,主要涉及3个方面。
(1)LiDAR点云针孔模拟成像,该方面目的在于解决因分辨率、尺度显著差异以及较大透视几何形变导致的LiDAR 点云航空影像配准难题,基本思想是在计算机OpenGL环境下,利用航空影像内参数及初始外方位元素对LiDAR 点云重构的数字表面模型DSM进行透视投影、遮挡分析以及插值处理,渲染生成与航空影像几何特性相接近的灰度影像-LiDAR深度影像,为后续LiDAR激光脚点像方相关计算奠定基础。由于OpenGL 3维渲染采用线性透视模型,这里需对航空影像进行非线性的光学畸变改正预处理。
(2)LiDAR深度影像与光学影像的分块匹配,该方面目的在于建立LiDAR深度影像与航空影像间的几何映射关系,进而以该映射关系为连接桥梁自动实现LiDAR深度影像与航空影像同名像点的整体概略相关,基本思想是以待配准影像分块区域的梯度互信息最大化为依据,估计两者的局部2维刚体变换参数。由于LiDAR点云与其透视影像间投影关系已知,则可借助影像变换参数建立LiDAR激光脚点与航空影像像点映射关系。
(3)顾及梯度互信息的激光脚点空间后方交会及配准精度评定,即以像素梯度互信息为权重,利用全体LiDAR激光脚点及其同名像点进行摄影测量空间后方交会计算得到优化的影像外方位元素,并以新外方位元素为基础重复上述步骤(1)—(3),直至LiDAR深度影像与航空影像几何变换参数值趋于零或全体LiDAR激光脚点空间后方交会计算满足精度条件,实现航空影像与LiDAR点云高精度配准。
3 LiDAR点云针孔模拟成像
本文利用计算机图形学程序库OpenGL模拟航空影像瞬时摄影姿态对LiDAR点云进行“针孔”成像,即根据OpenGL成像式(2),利用模型矩阵M对LiDAR点云进行旋转、平移及缩放,再经投影矩阵P的透视投影变换以及视口矩阵V的仿射变换获得模拟影像坐标(x,y)(李颖和薛海斌,2002):
$ {\left[ {x\;\;\;y\;\;\;1} \right]^T} = V \cdot P \cdot M \cdot {\left[ {X\;\;\;Y\;\;\;Z\;\;\;1} \right]^T} $ (2)
可以证明,OpenGL成像过程可用摄影测量方法进行定量控制(苏国中等,2006),关键在于设置与摄影测量影像方位元素(配准参数)相联系的投影矩阵P、视口矩阵V和模型矩阵>M。OpenGL视锥体与摄影测量相机内部参数相联系,定义了场景的观察视线、视角以及范围。对于焦距为f,像主点坐标为(x0,y0),影像幅面大小为(w,h)的摄影相机,与该相机等效的OpenGL投影矩阵P可设置为
$ P = \left[ {\begin{array}{*{20}{c}}{\frac{{2f}}{w}}&0&{\frac{{ - 2{x_0}}}{w}}&0\\0&{\frac{{2f}}{w}}&{\frac{{ - 2{y_0}}}{h}}&0\\0&0&{ - \frac{{S + 1}}{{S - 1}}}&{ - \frac{{2f}}{{S - 1}}}\\0&0&{ - 1}&0\end{array}} \right] $ (3)
式中,S为大的比例常数,它与f的乘积定义了OpenGL视锥体最远裁减面。
模型矩阵M与摄影测量相机外部参数相联系,用于将OpenGL 3维场景从模型(物方)坐标空间变换到视点(眼睛)坐标空间,该变换过程等价于摄影测量像空间坐标系到像空间辅助坐标系的转换(张祖勋和张剑清,2002),即有:
$ M = \left[ {\begin{array}{*{20}{c}}{{a_1}}&{{b_1}}&{{c_1}}&{ - {a_1}{X_s}}&{ - {b_1}{Y_s}}&{ - {c_1}{Z_s}}\\{{a_2}}&{{b_2}}&{{c_1}}&{ - {a_2}{X_s}}&{ - {b_2}Y}&{ - {c_2}{Z_s}}\\{{a_3}}&{{b_3}}&{{c_3}}&{ - {a_3}{X_s}}&{ - {b_3}Y}&{ - {c_3}{Z_s}}\\0&0&0&{}&1&{}\end{array}} \right] $ (4)
将式(3)、(4)代入式(2)可得:
| $ \left[ {\begin{array}{*{20}{c}}x\\y\\1\end{array}} \right] = v\left[ \begin{array}{l}\frac{2}{w}\left\{ {f\left[ {\left({{a_1}\left({X - {X_s}} \right)+ {b_1}\left({Y - {Y_s}} \right)+ {c_{\rm{1}}}\left({Z - {Z_s}} \right)- {x_0}\left[ {{a_3}\left({X - {X_s}} \right)+ {b_3}\left({Y - {Y_s}} \right)+ {c_3}\left({Z - {Z_s}} \right)} \right]} \right)} \right]} \right\}\\\frac{2}{h}\left\{ {f\left[ {\left({{a_2}\left({X - {X_s}} \right)+ {b_2}\left({Y - {Y_s}} \right)+ {c_2}\left({Z - {Z_s}} \right)- {y_0}\left[ {{a_3}\left({X - {X_s}} \right)+ {b_3}\left({Y - {Y_s}} \right)+ {c_3}\left({Z - {Z_s}} \right)} \right]} \right)} \right]} \right\}\\\;\;\;\;\;\;\;\;\; - {a_3}X\frac{{S + 1}}{{S - 1}} - {b_3}Y\frac{{S + 1}}{{S - 1}} - {c_3}Z\frac{{S + 1}}{{S - 1}} + \frac{{S + 1}}{{S - 1}}\left({{a_3}{X_s} + {b_3}{Y_s} + {c_3}{Z_s}} \right)- \frac{{2f}}{{S - 1}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {a_3}\left({X - {X_s}} \right)- {b_3}\left({Y - {Y_s}} \right)- {c_3}\left({Z - {Z_s}} \right)\end{array} \right] $ | (5) |
对比式(1)、(5)可知,当设置视口矩阵 $ v = \left[ {\begin{array}{*{20}{c}}{\frac{w}{2}}&0&0&0\\0&{\frac{h}{2}}&0&0\\0&0&0&1\end{array}} \right] $时,式(1)、(2)像点计算结果一致,表明LiDAR点云针孔模拟成像严格符合本文的LiDAR 点云航空影像配准模型-摄影测量共线方程。考虑到LiDAR点云是离散的且可能存在局部“孔洞”,本文LiDAR点云针孔模拟成像过程为:
(1)LiDAR点云构网,即以点云空间坐标(X,Y)为依据生成2维Delaunay三角网(Shewchuk,2002),建立目标场景的3维表面模型DSM,以满足OpenGL光线跟踪、遮挡判断等透视投影计算需要;
(2)设置OpenGL虚拟相机,即根据待配准影像初始空间参数及式(3)—(5)生成投影矩阵P、视口矩阵V和模型矩阵M,并调用相应OpenGL函数(李颖和薛海斌,2002):glMatrixMode(),glLoadMatrixf(),glViewport()等,导入相应矩阵完成OpenGL虚拟相机设置。
(3)OpenGL影像渲染生成与输出。值得注意是,虽然LiDAR点云构网建立的DSM存在不正确插值导致的局部误差,但由于后续点云空间后方交会计算仅依赖于实际的LiDAR激光脚点(解释见4.2节),整体配准精度受DSM误差的影响并不大,这一事实在后续配准试验中得到了有效验证。
4 LiDAR深度影像与光学影像分块匹配
针孔模拟成像下的LiDAR深度影像与待配准航空影像透视几何变形相接近,可通过简单几何变换来近似建立两者的像素映射关系,即两者相关计算可转化为影像几何变换参数的最优估计:
$ \begin{array}{l}Ma\mathop x\limits_p Similsrity\left({LI\left({x,y} \right),AI\left({x',y'} \right)} \right):\\\left({x',y'} \right)= \left({G_x^P\left({x,y} \right),G_y^P\left({x,y} \right)} \right)\end{array} $ (6)
式中,LI,AI分别表示LiDAR深度影像、航空影像;Similarity()为影像相关测度函数,两影像严格空间配准时该函数取最大值,表明影像整体相关性最好;GPx(x,y),GPy(x,y)表示LiDAR深度影像与航空影像间的坐标几何变换,P为变换参数。
4.1 梯度互信息迭代计算
LiDAR深度影像和光学航空影像存在像素灰度非线性畸变,对于这种异源影像目前较为有效的相关测度依据是计算其互信息(Mutual Information)(Viola和Wells,1997;邓非,2006),由于忽略影像空间位置信息,互信息计算对影像几何畸变敏感,主要适合于存在平移影像或影像间仅有微小的旋转、尺度变化。LiDAR深度影像与航空影像局部存在复杂的、非线性几何畸变,该几何畸变源于:(1)用于LiDAR “针孔”模拟成像的影像初始空间参数不准确;(2)LiDAR点云缺乏光学影像对地物几何形状的精确表达,如目标边界;(3)离散点云重构连续DSM的插值误差。为降低上述几何畸变影响,这里对传统的影像灰度互信息计算作如下改进。
(1)与影像空间参数持续改进过程相联系的互信息迭代计算。若忽略几何畸变(2)和(3),影像空间参数越趋于理想值,互信息计算结果受影像几何畸变影响的程度就越小。这就意味着,只要LiDAR深度影像与航空影像互信息最大化计算建立的LiDAR 激光脚点影像相关关系约束,能对影像初始空间参数进行部分程度的优化改进,就可利用优化参数模拟生成与航空影像更接近的LiDAR深度影像,进而获得新的、更为可靠的互信息计算结果,显然,这一与影像空间参数持续优化改进相联系的迭代计算过程将能逐步减少影像几何畸变对互信息最大化计算的干扰,确保LiDAR激光脚点影像相关的整体最优与渐进实现。
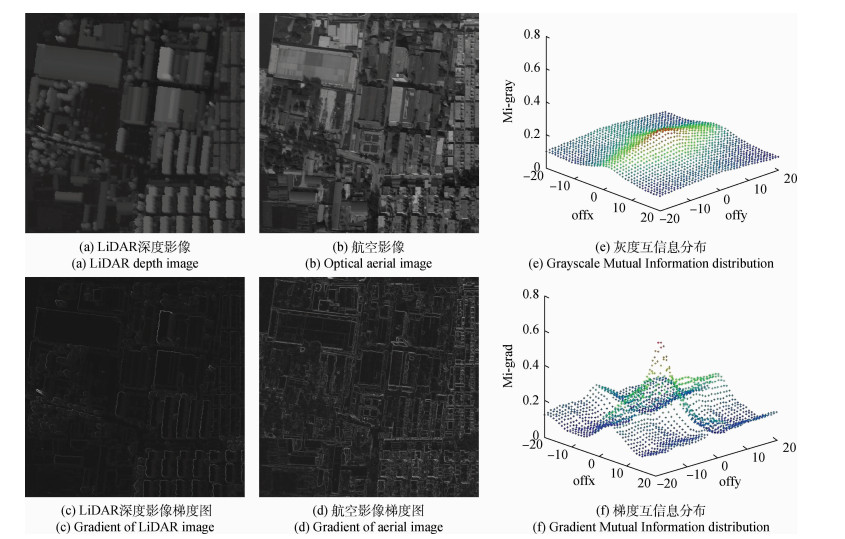
(2)互信息统计仅限于灰度变化显著的“有效”像素,并以梯度互信息计算取代灰度互信息计算。本质上,互信息影像配准是按信息量“大小”进行匹配,这里考虑以下两个事实:第一,灰度变化显著的像素位置,如边缘、边界等,是影像信息集中的地方;第二,影像上几何特性稳定的特征通常位于灰度变化显著位置。这就意味着,通过将互信息统计对象限于灰度变化显著的“有效”像素,可排除大部分受几何畸变干扰大的像素,另一方面,以梯度互信息计算取代灰度互信息计算,等价于将信息量“大小”与灰度变化的快慢程度相联系,对于按信息量大小来匹配不同灰度变化的“有效”像素也更为合理,图 2 给出了两幅配准图像的灰度互信息、梯度互信息统计对比示意,其中:图 2(a),2(b)为已配准好的局部LiDAR深度影像、航空影像;图 2(c),2(d)为相应的梯度(幅值)影像;图 2(e),2(f)为两影像沿行、列平移不同距离分别得到的灰度互信息、梯度互信息分布统计,可以看出,较之于灰度互信息,梯度互信息计算可获得更为“显著”的峰值,有利于提高影像互信息配准的可靠性。
梯度互信息计算需遍历可能的影像几何变换参数取值,顾及几何变换复杂性及互信息最大化计算效率,这里选用简单2维刚体变换作为影像几何变换模型,即假定航空影像由LiDAR深度影像依次经旋转、平移而得到:
$ \begin{array}{l}x' = \left({x\cos \theta + y\sin \theta } \right)- {T_x}\\y' = \left({y\cos \theta - x\sin \theta } \right)- {T_y}\end{array} $
式中,P=(Tx,Ty,θ)为平移、旋转参数,几何变换坐标原点位于影像中心。
对于有限的、离散2维刚体变换参数空间{P},尽管选用模型仅有3个自由度参数,但其平移参数与航空影像幅面大小相关,当影像幅面大时,仍将产生极高的计算代价;另一方面,简单的、全局2D刚体变换并不能精确描述存在局部、非线性几何畸变的透视变换,影像幅面越大,场景越复杂,两者误差就越大,影响迭代计算的收敛以及梯度互信息计算的可靠性,这里通过影像金字塔、分块联合处理来解决上述问题。
(1)几何变换误差控制方面,基于“分而治之”的思想,对影像进行分块,独立估计各分块影像的2维刚体变换参数,这等价于用多个、局部2维刚体变换的联合取代全局2维刚体变换,一方面可有效减小与透视变换的逼近误差,另一方面,尺寸小的分快影像可缩小其几何变换平移参数搜索范围,也有利于减少参数离散空间的总体规模。
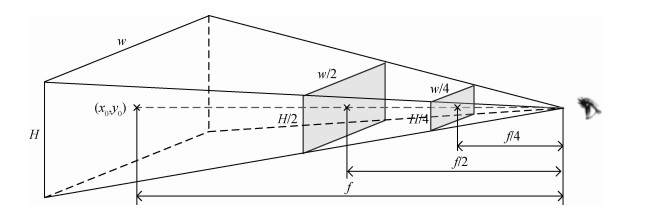
(2)互信息最大化计算效率方面,通过实施具有增大窗口“拉入”范围的影像金字塔处理(张祖勋和张剑清,2002)大规模减少几何变换参数离散空间搜索范围。需要注意的是,LiDAR深度影像金字塔的建立必须顾及与激光脚点的精确投影关系,以保证后续LiDAR点云影像映射的可靠性,由OpenGL “针孔”成像过程可知,保持相机外部参数不变,仅需对相机内部参数进行相应倍数缩放就可生成不同尺度的LiDAR深度影像,这就意味着,空间后方交会结果可沿金字塔层“传递”,为影像空间参数渐近优化提供了保障,图 3给出了倍数为2的LiDAR 深度影像金字塔建立过程示意,其中:W,H表示LiDAR深度影像(金字塔底层)幅面大小,(x0,y0),f分别为相机焦距、像主点坐标。
4.2 配准精度评定与迭代计算终止
由LiDAR深度影像与航空影像互信息配准建立的单个激光脚点影像映射或多或少存在误差(近似同名像点),但就点云整体而言,优于初始相机外部参数给出的映射关系,更趋于“理想”摄影条件,因而可对初始相机参数进行优化改进。将式(1)按泰勒级数展开并取一次项,可得误差方程式(7)。
$ v = AX - L:P $ (7)
$ \begin{array}{l}A = \left[ {\begin{array}{*{20}{c}}{\frac{{\partial f}}{{\partial {X_s}}}}&{\frac{{\partial f}}{{\partial {Y_s}}}}&{\frac{{\partial f}}{{\partial {Z_S}}}}&{\frac{{\partial f}}{{\partial \phi }}}&{\frac{{\partial f}}{{\partial \omega }}}&{\frac{{\partial f}}{{\partial \kappa }}}\\{\frac{{\partial f}}{{\partial {X_S}}}}&{\frac{{\partial f}}{{\partial {Y_S}}}}&{\frac{{\partial f}}{{\partial {Z_S}}}}&{\frac{{\partial f}}{{\partial \phi }}}&{\frac{{\partial f}}{{\partial \phi }}}&{\frac{{\partial f}}{{\partial \kappa }}}\end{array}} \right]\\X = {\left[ {d{X_s}\;\;\;d{Y_s}\;\;\;d{Z_s}\;\;\;d\phi \;\;\;\;d\omega \;\;\;d\kappa } \right]^T}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;L = \left({\begin{array}{*{20}{c}}{{L_1}}\\{{L_2}}\end{array}} \right)= \\\left[ {\begin{array}{*{20}{c}}{x - {x_0} + f\frac{{{a_1}\left({X - {X_S}} \right)+ {b_1}\left({Y - {Y_S}} \right)+ {c_1}\left({Z - {Z_S}} \right)}}{{{a_3}\left({X - {X_S}} \right)+ {b_3}\left({Y - {Y_S}} \right)+ {c_3}\left({Z - {Z_S}} \right)}}}\\{y - {y_0} + f\frac{{{a_2}\left({X - {X_S}} \right)+ {b_2}\left({Y - {Y_S}} \right)+ {c_2}\left({Z - {Z_S}} \right)}}{{{a_3}\left({X - {X_S}} \right)+ {b_3}\left({Y - {Y_S}} \right)+ {c_3}\left({Z - {Z_S}} \right)}}}\end{array}} \right]\end{array} $
式中,(X,Y,Z)为LiDAR激光脚点空间坐标,(x,y)为近似同名像点坐标,P为对应的观测值权阵,由像点梯度互信息大小给出,其余参数定义同式(1)。
对落在LiDAR深度影像上且未被遮挡的激光脚点,以其近似同名像点为观测值,可根据式(7)逐点建立方程,并以生成LiDAR深度影像的相机外部参数为初值进行最小二乘求解,其参数估计结果及单位权方差分别为:
$ \begin{array}{l}\hat X = {\left({{A^T}PA} \right)^{ - 1}}{A^T}PL,\\\hat \sigma _0^2 = \frac{{{V^T}PV}}{{n - t}}\end{array} $
单位权方差 $ {{\hat \sigma }_0}$反映了全体激光脚点的投影误差,可作为LiDAR点云与航空影像空间配准精度评定依据。需要指出的是,传统摄影测量空间后方交会过程利用分布合理的少量高精度控制点对来影像外方位参数,并根据解算参数给出影像上任一像素的摄影光束,是一种“像方”摄影光束恢复方式;与之相对,本文LiDAR点云空间后方交会过程则直接从建立全体激光脚点的摄影光束着手,充分利用LiDAR数据物方信息密集优势,寻求使之投影误差总体最小的相机外部参数最优估计,可视为一种“物方”摄影光束恢复方式。
当LiDAR点云与航空影像实现理想空间配准时,应同时满足两个方面:一方面,LiDAR点云空间后方交会单位权方差达到最小;另一方面,LiDAR深度影像与航空影像间的梯度互信息达到最大且两者2维刚体变换模型参数为0,这里假定LiDAR点云能完整重构DSM且互信息统计能充分克服LiDAR 深度影像与航空影像间的非线性光谱差异。据此,本文金字塔影像梯度互信息迭代计算按以下方式给出终止条件:
(1)非0层金字塔影像迭代计算终止条件:1)点云空间后方交会单位权方差小于1个像素;或2)各分块影像2D刚体变换模型参数中:平移绝对值不大于1个像素,旋转角度绝对值不大于1度;或3)迭代计算次数大于10次。
(2)0层(原始)影像迭代计算终止条件:1)点云空间后方交会单位权方差小于0.5个像素;或2)各分块影像2维刚体变换模型参数中:平移绝对值不大于1个像素,旋转角度绝对值不大于0.5度;或3)迭代计算次数小于20,若迭代计算按3)条件终止,则LiDAR点云与航空影像空间配准结果取单位权方差最小者。这里原始影像迭代计算采用更为严格条件,目的在于确保获得高精度配准。
5 实验与结论
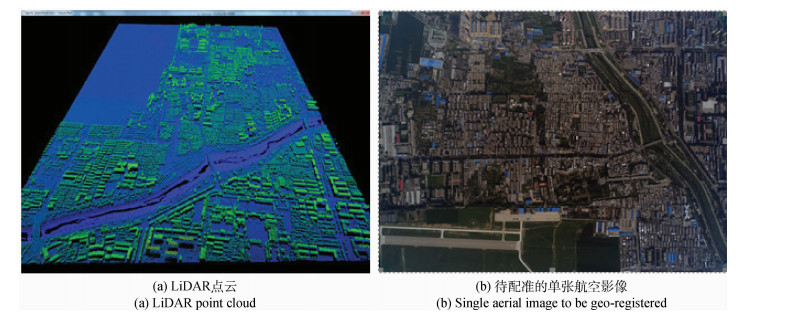
本文实验区域包含密集建筑、平坦飞机场、枯水河道及桥梁等各种地物,其中LiDAR“点云”数据垂直精度约15 cm,水平精度约25 cm,平均点间距约1.5 m;数字航空影像由Leica RCD105相机获取,像幅大小7216×5408像素,像素大小6.8 μm,空间分辨率约为0.5 m,相机于航拍前已严格标定,表 1列出了标定相机的内部参数及精度大小,影像初始配准参数由引入误差的飞行平台低精度导航参数提供并转换到摄影测量坐标参考系(表 2)。图 4给出了待配准的光学航空影像和LiDAR“点云”3维示意,其中航空影像已利用相机内部参数进行了光学畸变改正处理。
| 参数类型 | 主距f | 主点u0 | 主点v0 | 径向畸变K0 | 径向畸变K1 | 径向畸变K2 |
| 标定值 | 35.176 | -0.2870 | -0.1091 | 2.06482E-02 | -7.53494E-05 | 5.60491E-08 |
| 标定精度 | 0.002523598 | 0.0006 | 0.0007 | 6.43444E-05 | 4.23632E-08 | 5.2466E-11 |
Table 2 Statistic of registration results with different initial parameters as input 下载CSV
| 组数 | 结果 | 初始参数 | 配准参数 | 参数改正数 | m 0/像素 |
| 1 | X s/m | 261644.63 | 261616.88 | 27.75 | 0.55 |
| Y s/m | 4001373.43 | 4001354.01 | 19.42 | ||
| Z s/m | 1852.20 | 1864.37 | -12.17 | ||
| Phi/(°) | 4.9556 | 2.4075 | 2.5481 | ||
| Omega/(°) | -3.4287 | -0.5415 | -2.8872 | ||
| Kappa/(°) | 262.6740 | 267.7728 | -5.0988 | ||
| 2 | X s/m | 261614.95 | 261616.76 | -1.93 | 0.51 |
| Y s/m | 4001354.63 | 4001353.23 | 0.62 | ||
| Z s/m | 1865.13 | 1864.48 | 0.76 | ||
| Phi/(°) | 2.5234 | 2.4067 | 0.1159 | ||
| Omega/(°) | -0.4922 | -0.5109 | 0.0493 | ||
| Kappa/(°) | 267.6739 | 267.7716 | -0.0989 | ||
| 3 | X s/m | 261593.65 | 261615.13 | -21.48 | 0.56 |
| Y s/m | 4001332.48 | 4001353.22 | -20.74 | ||
| Z s/m | 1880.26 | 1864.12 | 16.14 | ||
| Phi/(°) | -0.5601 | 2.4580 | -3.0181 | ||
| Omega/(°) | 2.6480 | -0.5090 | 3.1570 | ||
| Kappa/(°) | 278.1199 | 267.7816 | 10.3383 | ||
| 4 | X s/m | 261589.56 | 261615.91 | -26.35 | 0.69 |
| Y s/m | 4001340.68 | 4001353.36 | -12.68 | ||
| Z s/m | 1875.77 | 1864.29 | 11.48 | ||
| Phi/(°) | -1.7452 | 2.4333 | -4.1785 | ||
| Omega/(°) | 3.5560 | -0.5165 | 4.0725 | ||
| Kappa/(°) | 280.8799 | 267.7779 | 13.1020 |
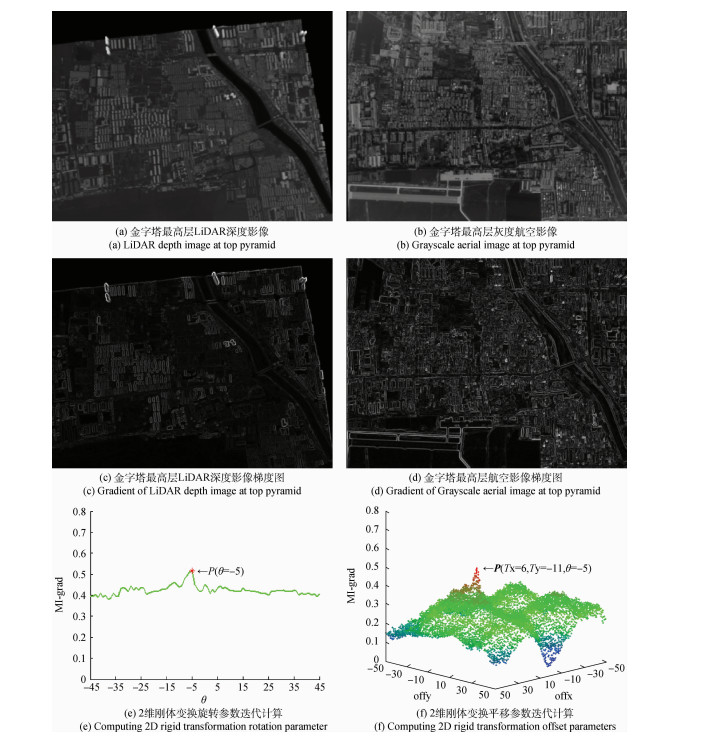
依据第2节给出的迭代配准框架及第四节提出的影像处理策略,首先在金字塔最高层进行LiDAR 深度影像与航空影像梯度互信息配准(图 5),图 5(a)、图 6(b)分别为下采样27倍数的金字塔最高层LiDAR深度影像、灰度航空影像示意,生成LiDAR 深度影像所需的OpenGL投影矩阵、视口矩阵和模型矩阵根据第3节中相应公式计算得到,其中模型矩阵计算采用表 2中影像初始外方位参数,投影矩阵、视口矩阵计算涉及的相机焦距、像主点坐标及影像幅面大小参数则需根据影像所在金字塔层数进行相应倍数缩放;LiDAR深度影像、灰度航空影像梯度(幅值)图利用Sober算子生成,见图 5(c)和图 5(d),取梯度图上大于平均梯度幅值的有效像素计算互信息(Hirschmüller,2008)并求其均值,进而通过比较搜索获得对应于最大梯度互信息的几何变换参数:P=(6,-11,-5),(图 5(e)、(f)),这里旋转角度范围限定为[-45°,+45°],沿坐标轴平移范围限定为[-50像素,+50像素];图 6 给出了新参数生成的LiDAR深度影像与原始航空影像(底层)叠加效果示意,对比图 5(a)、(b)可知,新LiDAR深度影像与航空影像整体形状更“接近”,两者已基本“套合”,(图 6(a)),但在局部区域如Ⅰ,Ⅱ,Ⅲ(图 6(b)),黄色箭头(LiDAR深度影像)与绿色箭头(航空影像)所指的同一地物的位置明显不一致,存在不同程度几何变形,将通过进一步的分块影像迭代配准来消除。
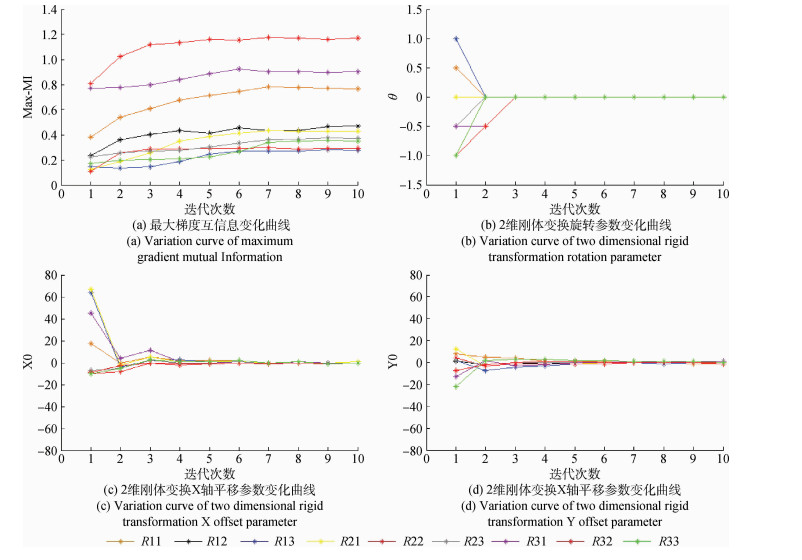
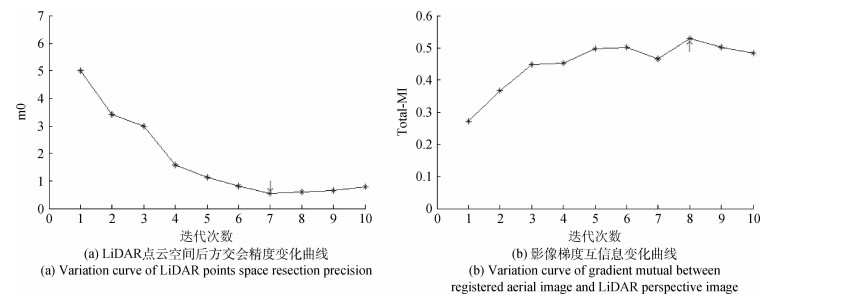
如图 6(a)格网所示,本文将待配准影像等分为9块区域:Rij(i,j=1,2,3),各分块影像独立进行梯度互信息配准以获得局部2D刚体变换参数估计,根据估计参数建立块内LiDAR点云影像映射关系,最后统一实施空间后方交会计算相机外部参数,并再次生成新的LiDAR深度影像重复上述过程,图 7给出了迭代配准过程中各分块影像最大梯度互信息及相应几何变换参数变化曲线,图 8则给出了LiDAR 点云空间后方交会精度变化以及新参数生成的LiDAR深度影像与航空影像梯度互信息变化曲线,迭代次数均为10次。由图 7、图 8中曲线变化可以看出,影像空间参数的不断修正使得重新生成的各分块LiDAR深度影像与航空影像相对几何畸变不断变小(几何变换旋转角度趋于0,平移距离小于1个像素),见图 7(b)—7(d),最大梯度互信息不断增大并达到迭代次数7后趋于稳定,见图 7(a);与此相对应的,LiDAR点云空间后方交会精度也随迭代次数不断提高,见图 8(a),迭代次数为7时精度达到最高,约为0.5个像素,交会参数生成的LiDAR深度影像与航空影像间的梯度互信息大小也与其参数精度高低变化总体相吻合(图 8(b)),梯度互信息最大值对应迭代次数(8)与最高参数精度对应迭代次数(7)不同的原因可能在于,重构DSM对地物几何形状精确表达的不足影响了LiDAR深度影像与航空影像间的完全“一致”性。本文LiDAR点云与航空影像空间配准参数以第7次空间后方交会结果为准(迭代终止),其估计参数及精度见表 2(黑体所示),图 9给出了该参数下的LiDAR点云与航空影像配准结果示意。
引入不同误差的初始外部参数,同时给出了同一影像另外3组配准结果(表 2),由表 2的配准参数、精度以及参数改正数大小可看出,本文方法迭代计算收敛结果稳定且具有较好的参数拉入范围,其中,初始外部参数沿坐标轴平移允许偏差平均可达20 m,俯仰、翻滚角度允许偏差最大可达4°,航向角允许偏差最大可达13°。对比Zheng等人(2013)给出的两种相机(Cannon EOS 5D Mark II和Nikon D300)获取影像配准参数的ICP算法投影误差统计RMSI:0.484像素,0.781像素,配准精度介于两者之间,但机载LiDAR点云密度、量测精度远低于该文献中的地面激光测距系统且不要求具备立体影像条件,显示出良好的适用性。通过以上的实验可以得出如下结论。
(1)通过“针孔”模拟成像以及影像梯度互信息迭代计算,可逐步建立LiDAR激光脚点和光学航空影像像点映射关系,成功解决了两种异源数据间的自动相关难题。
(2)直接从恢复全体激光脚点的摄影光束着手,充分LiDAR数据物方信息密集优势,借助于摄影测量空间后方交会计算获得投影误差总体最小的空间配准参数并给出可靠的精度评定。
(3)有效解决了单张航空影像与LiDAR数据的空间配准问题,自动化程度高且具有较高的配准精度,理论上适用于相机内参数已知的任意摄影角度航空影像。
6 结论
光学影像与激光点云数据在空间维数、分辨率、几何形变、特征表达等量测特性上的显著差异,使得两者空间配准的自动化程度、精度方面临诸多挑战。本文配准方法的特点在于巧妙回避了这两种异源数据的特征提取与自动相关难题,充分利用LiDAR点云数据物方信息密集优势以及“针孔”模拟成像下的互信息计算整体配准特点,实现了单航空影像与LiDAR点云的自动空间配准并达到约0.5像素配准精度,对于摄影测量单张影像测图、4D产品快速生成以及3维可视化处理已具备较高的实用价值。本文方法主要针对不连续性显著的城市场景,尝试以更具普遍意义、与LiDAR点云空间距离属性相接近的立体影像视差图互信息来取代单影像梯度互信息计算,对现有方法进行拓展、验证,以使其适用于不同类型的地理区域,将是下一步的研究方向。
参考文献
-
Deng F. 2006. Study on Registration and Objects Feature Extraction of LiDAR Data and Digital Images. Wuhan:Wuhan University (邓非. 2006. LiDAR数据与数字影像的配准和地物提取研究. 武汉:武汉大学)
-
Habib A, Ghanma M, Morgan M and Al-Ruzouq R. 2005. Photogrammetric and lidar data registration using linear features. Photogrammetric Engineering & Remote Sensing, 71(6):699-707[DOI:10.14358/pers.71.6.699]
-
Hirschmüller H. 2008. Stereo processing by semiglobal matching and mutual information. IEEE Transactions on Pattern Analysis and Machine Intelligence, 30(2):328-341[DOI:10.1109/TPAMI.2007.1166]
-
Li Y and Xue H B. 2002. OpenGL Function and Examples of Analysis Handbook. Beijing:National Defence Industry Press (李颖, 薛海斌. 2002. OpenGL函数与范例解析手册. 北京:国防工业出版社)
-
Ma H C, Yao C J and Wu J W. 2012. Registration of LiDAR point clouds and high resolution images based on linear features. Geomatics and Information Science of Wuhan University, 37(2):136-140 (马洪超, 姚春静, 邬建伟. 2012.利用线特征进行高分辨率影像与LiDAR点云的配准 武汉大学学报(信息科学版), 37(2):136-140) .
-
Mitishita E, Habib A, Centeno J, Machado A, Lay J and Wong C. 2008. Photogrammetric and LiDAR data integration using the centroid of a rectangular roof as a control point. The Photogrammetric Record, 23(121):19-35[DOI:10.1111/j.1477-9730.2008.00464.x]
-
Rottensteiner F and Jansa J. 2002. Automatic extraction of buildings from LIDAR data and aerial images. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 34(4):569-574
-
Shewchuk J R. 2002. Delaunay refinement algorithms for triangular mesh generation. Computational Geometry, 22(1/3):21-74[DOI:10.1016/s0925-7721(01)00047-5]
-
Su G Z, Zheng S Y, Zhang J Q and Zhang Z X. 2006. How to relate the OpenGL imaging process with exterior and interior parameters of photogrammetry. Journal of Image and Graphics, 11(4):540-544 (苏国中, 郑顺义, 张剑清, 张祖勋. 2006. OpenGL模拟摄影测量方法研究. 中国图象图形学报, 11(4):540-544)[DOI:10.11834/jig.20060489]
-
Viola P and Wells W M ⅡI. 1997. Alignment by maximization of mutual information. International Journal of Computer Vision, 24(2):137-154[DOI:10.1023/A:1007958904918]
-
Wang Y M and Hu C M. 2012. A robust registration method for terrestrial LiDAR point clouds and texture image. Acta Geodaetica et Cartographica Sinica, 41(2):266-272 (王晏民, 胡春梅. 2012.一种地面激光雷达点云与纹理影像稳健配准方法. 测绘学报, 41(2):266-272)
-
Wu J, Zhang Z X and Zhang J Q. 2006. 3D city modeling based on videogrammetry from helicopter. Journal of Image and Graphics, 11(8):1161-1170 (吴军, 张祖勋, 张剑清. 2006. 基于机载视频量测的3维城市建模. 中国图象图形学报, 11(8):1161-1170)[DOI:10.11834/jig.200608196]
-
Zhang F, Huang X F and Li D R. 2008. A review of registration of laser scanner data and optical image. Bulletin of Surveying and Mapping, (2):7-10 (张帆, 黄先锋, 李德仁. 2008.激光扫描与光学影像数据配准的研究进展 . 测绘通报, (2):7-10)
-
Zhang L, Ma H C, Gao G and Chen Z. 2014. Automatic registration of urban aerial images with airborne LiDAR points based on line-point similarity invariants. Acta Geodaetica et Cartographica Sinica, 43(4):372-379 (张良, 马洪超, 高广, 陈卓. 2014. 点、线相似不变性的城区航空影像与机载激光雷达点云自动配准. 测绘学报, 43(4):372-379)[DOI:10.13485/j.cnki.11-2089.2014.0056]
-
Zhang Y J, Xiong X D and Shen X. 2012. Automatic registration of urban aerial imagery with airborne LiDAR data. Journal of Remote Sensing, 16(3):579-595 (张永军, 熊小东, 沈翔. 2012. 城区机载LiDAR数据与航空影像的自动配准. 遥感学报, 16(3):579-595)[DOI:10.11834/jrs.20121082]
-
Zhang Z X and Zhang J Q. 2002. Digital Photogrammetry. Wuhan:Wuhan University Press (张祖勋, 张剑清. 2002.数字摄影测量学 . 武汉:武汉大学出版社)
-
Zhao W Y, Nister D and Hsu S. 2005. Alignment of continuous video onto 3D point clouds. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(8):1305-1318[DOI:10.1109/TPAMI.2005.152]
-
Zheng S Y, Huang R Y and Zhou Y. 2013. Registration of optical images with LiDAR data and its accuracy assessment. Photogrammetric Engineering and Remote Sensing, 79(8):731-741[DOI:10.14358/PERS.79.8.731]
-
Zhong C. 2011. High quality true orthoimage generation with LiDAR and RS image. Acta Geodaetica et Cartographica Sinica, 40(1):132 (钟成. 2011.集成LiDAR和遥感影像生成高质量真正射影像研究 . 测绘学报, 40(1):132)
-
Zhong C, Li H, Huang X F and Li D R. 2009. Automatic registration of LiDAR data and aerial image based on a 6-Tuples relaxation. Geomatics and Information Science of Wuhan University, 34(12):1426-1430 (钟成, 李卉, 黄先锋, 李德仁. 2009. 利用6元组松弛法自动配准LiDAR数据与航空影像. 武汉大学学报(信息科学版), 34(12):1426-1430)
Abstract
This paper presents our research on registering single aerial image to a LiDAR point cloud. Given its high spatial resolution, spatial positioning accuracy, and efficiency in capturing data of physical surfaces, LiDAR has been influenced by and has significantly changed photogrammetry. The fusion of LiDAR data with aerial images offers various applications, such as DOM generation, virtual reality, city modeling, and military training, because of the complementary nature of the information provided by the two systems. However, the two datasets should be geo-registered into a common coordinate frame prior to such integration, which proves to be quite challenging in terms of either automation or accuracy. Such a challenge may be partly caused by inefficiency in the feature measurement or detection stage. For example, the identification of point of interest or straight line feature is viable and reliable in optical images but is difficult to achieve in LiDAR point clouds because of its poor discontinuity measurements. To this end, an automatic geo-registration approach based on "pin-hole" imaging simulation and iterative gradient mutual information computation is proposed to align single aerial image to discrete LiDAR point clouds. The proposed approach takes photogrammetry collinear equation as strict mathematic mode and involves three stages. First, a virtual "pin-hole" imaging process restored from aerial image orientation parameters is established on urban LiDAR point clouds to generate simulated, gray, LiDAR-depth images. The generated LiDAR-depth images are geometrically similar to aerial images. Hence, difficulties in registration caused by distinct differences in spatial resolution, perspective distortion, and size between the two types of data sources can be greatly alleviated. Second, the geometric transform parameters between LiDAR depth images and aerial images are successfully estimated with the gradient mutual information as the similarity measurement. Moreover, the image pyramid partitioning strategy is implemented to accelerate the search for parameter space. In this stage, LiDAR laser feet points can be roughly mapped on aerial image pixels on the basis of the estimated geometric transform parameters and the known projection relations between LiDAR point clouds and their depth images. Third, the photogrammetry space resection algorithm is implemented using all the mapped aerial image pixels as observed values and their gradient mutual information as weight to improve image orientation parameters. The three stages are repeated until the given iterative calculation condition is met and the LiDAR point clouds are registered with single aerial image. Selected airborne LiDAR data and an aerial image with different initial parameter values are tested with the proposed approach. Approximately 0.5 pixel is obtained, indicating a higher registration precision compared with the ICP algorithm. (1) The "pin-hole" simulation imaging and iterative gradient mutual information calculation successfully resolve the difficult heterologous correspondence problem between LiDAR point clouds and optical aerial images; (2) The photogrammetry space resection algorithm can obtain registration parameters with minimum projection errors and reliable precision evaluation by maximizing the use of intensive space information from LiDAR data and recovering optical bundles of laser beams directly.
Key words
Image geo-registration;LiDAR;"pin-hole" imaging simulation;gradient mutual information