|
|
|
收稿日期: 2014-12-17; 修订日期: 2015-07-15;
优先数字出版日期: 2015-07-22
基金项目: 中国科学院遥感与数字地球研究所“一三五”规划培育计划(编号: Y3SG1500CX);国家高技术研究发展计划(863计划)(编号: 2013AA12A301)
第一作者简介: 赵理君(1986-), 男, 助理研究员, 现从事遥感图像分类, 高分辨率遥感图像场景理解研究。E-mail: zhaolj01@radi.ac.cn
通信作者简介: 唐娉(1968— ), 女, 研究员, 主要从事遥感图像处理、信息提取和数据挖掘技术研究。E-mail: tangping@radi.ac.cn
中图分类号: TP701
文献标识码: A
文章编号: 1007-4619(2016)02-0157-15
|
摘要
目前普遍采用的分类器通常都是针对单一或小量任务而设计的,在小数据量的处理中能取得比较满意的结果。但对于海量遥感数据的处理,其在处理时效和分类精度方面还有待研究。本文以遥感图像场景分类任务为例,着重对遥感数据分类问题中几种典型分类方法的适用性进行比较研究,包括K近邻(KNN)、随机森林(RF),支持向量机(SVM)和稀疏表达分类器(SRC)等。分别从参数敏感性,训练样本数据量,待分类样本数据量和样本特征维数对分类器性能的影响等几个方面进行比较分析。实验结果表明:(1)KNN, RF和L0-SRC方法相比RBF-SVM, Linear-SVM和L1-SRC,受参数影响的程度更弱;(2)待分类样本固定的情况下,随着训练样本数目的增加,SRC类型分类方法的分类性能最佳,SVM类型方法次之,然后是RF和KNN,在总体分类时间上呈现出L0-SRC > L1-SRC > RF > RBF-SVM/Linear-SVM > KNN/L0-SRC-Batch的趋势;(3)训练样本固定的情况下,所有分类方法的分类精度几乎都不受待分类样本数目变化的影响,RBF-SVM方法性能最佳,其次是L1-SRC,然后是Linear-SVM,最后是RF和L0-SRC/L0-SRC-Batch,在总体分类时间上,L1-SRC和L0-SRC相比其他分类方法最为耗时;(4)样本特征维数的变化不仅影响分类器的运行效率,同时也影响其分类精度,其中SRC和KNN分类器器无需较高的特征维数即可获得较好的分类结果,SVM对高维特征具有较强的包容性和学习能力,RF分类器对特征维数增加则表现得并不敏感,特征维数的增加并不能对其分类精度的提升带来更多的贡献。总的来说,在大数据量的遥感数据分类任务中,现有分类方法具有良好的适用性,但是对于分类器的选择应当基于各自的特点和优势,结合实际应用的特点进行权衡和选择,选择参数敏感性较小,分类总体时间消耗低但分类精度相对较高的分类方法。
关键词
遥感图像, 数据分类, 场景分类, 分类器, 适用性
Abstract
The classification of remote sensing data plays an important role in all stages of remote sensing data processing and analysis. With the increase in the volume of remote sensing data, new problems concerning remote sensing big data classification tasks arise. Currently, the commonly used classifiers are usually designed for simple tasks to provide satisfactory results. However, for the processing of large volumes of remote sensing data, the scalability of classification efficiency and precision should be further investigated. Therefore, this study emphasizes on the comparisons of the scalability of typical remote sensing data classification methods to achieve this goal. Method: This study takes remote sensing image scene classification as an example and selects four well-known classification methods for comparison, namely, K Nearest Neighbor (KNN), Random Forest (RF), Support Vector Machine (SVM), and Sparse Representation-based Classifier (SRC), to conduct scalability analysis. The comparisons are conducted in terms of parameter sensitivity, effect of training sample data volume on classifier performance, effect of testing sample data volume on classifier performance, and effect of feature dimension on classifier performance. Results: The experimental results are as below: (1) The classifiers of KNN, RF, and L0-SRC are less parameter-sensitive than the classifiers of RBF-SVM, Linear-SVM, and L1-SRC. (2) In cases where the samples to be classified are fixed, all the classifiers tend to increase with the increase in the number of training samples. The SRC-type classification methods have the highest accuracy, followed by the SVM-type classification methods, the RF, and the KNN classifiers. In terms of overall classification time, the results show that the methods can be ranked as below: L0-SRC > L1-SRC > RF > RBF-SVM/Linear-SVM > KNN/L0-SRC-Batch. (3) In cases where the training samples are fixed, the classification accuracies of all the classifiers are seldom affected by the number of samples to be classified, which may be due to the learning abilities of all the different classifiers. (4) The feature dimension affects the efficiency and accuracy of different classifiers, in which SRC and KNN can obtain satisfactory results without high feature dimensions. SVM is tolerant to high feature dimensions and has a good learning ability with such high feature dimensions. By contrast, RF is insensitive to the increase in feature dimensions, and higher feature dimensions do not contribute much to the improvement of classification performance. Under such circumstances, the RBF-SVM exhibits the best performance, followed by the L1-SRC classifier, the Linear–SVM classifier, and the RF and L0-SRC/L0-SRC-Batch classifiers. In terms of overall classification time, the classifiers of L1-SRC and L0-SRC are the most time-consuming, whereas the other classifiers have relatively higher efficiency. Conclusion: Different classification methods have different advantages and disadvantages. In the tasks of classifying a large volume of remote sensing data, the selection of classifiers should be balanced and based on their characteristics and practical applications. Generally, a classifier that is less parameter-sensitive and less time-consuming during classification and obtains more accurate classification results is preferable.
Key words
remote sensing image, data classification, scene classification, classifier, scalability
1 引 言
20世纪60年代以来,随着计算机科学和空间科学的进步,传感器技术、航天航空平台技术、数据通信技术得到飞速的发展。作为一种大范围综合性的对地观测手段,遥感技术在地球观测方面发挥着越来越重要的作用,并对人类社会发展的各个领域起着重大的促进作用。
近年来,星、机、地一体化的全球观测能力得到大幅度提升,遥感数据的获取途径极大丰富,每天都有数量庞大的不同分辨率的遥感信息从各种传感器上接收下来。相应地,所产生的遥感图像数据也急剧增长,人们所能获取到的遥感数据量达到了前所未有的水平,步入到遥感大数据的时代(孟圆,2013)。
面对日益增加、如此丰富的遥感数据,如何有效地进行数据挖掘与信息提取就显得尤为重要。在遥感数据处理和分析的整个过程中,遥感数据的分类是其中十分重要的环节。从早期基于像元的中低分辨率遥感图像分类,到后来面向对象的高分辨率遥感图像分类,再到现在基于场景内容的高分辨率遥感图像的理解分析和场景分类,有关遥感数据分类的各种方法层出不穷(Lu和Weng,2007; Friedl和Brodley,1997; Melgani和Bruzzone,2004; Stumpf和Kerle,2011; Chen等,2011; Zhao等,2014)。在这些分类方法中,分类器成为一项热门的研究内容(Li等,2014)。目前,普遍采用的分类器通常都是针对单一或小量任务,在小数据量的处理中能够取得比较满意的结果。但是,对于当前海量遥感数据的处理,处理时效和分类精度方面还有待研究。
因此,本文以此为出发点,着重对遥感数据分类问题中几种典型分类方法的适用性进行了比较分析研究。为了进行适用性分析,本文以遥感图像场景分类为例,选取了目前研究过程中所普遍采用和比较流行的几种分类方法,主要包括K-近邻KNN(Franco-Lopez等,2001),支持向量机SVM(Vapnik,1998),随机森林RF(Breiman,2001),稀疏表示SRC(Wright等,2009)。通过在不同数据量下的实验,对比分析了上述不同分类器的优缺点及其在海量遥感数据分类过程中的适用性。
2 分类方法
近几年来,在遥感数据分类的研究中,出现了许多有代表性的分类方法(Yang等,2003; Mountrakis等,2011; Pal,2005; Du等,2012; Song等,2014)。这些分类方法各具特点,早期研究多采用简单的分类器(Du等,2012),后来随着机器学习理论的不断发展,出现了各种新的分类器算法(Yang等,2003; Mountrakis等,2011; Pal,2005; Song等,2014),并在遥感数据分类任务中取得成功应用。目前,根据不同分类器的特点,可将分类方法大致归纳为以下几类:(1)基于简单相似性模型的方法,如KNN;(2)线性模型方法,如SVM、Logistic等;(3)非线性模型方法,如神经网络、决策树、随机森林等;(4)其他方法,如贝叶斯网络、基于稀疏表达思想的分类模型SRC。基于目前分类问题研究中各分类器算法的使用度和流行度,本文分别从各类方法中选取了其中的典型代表,即KNN,SVM,RF和SRC等。
2.1 KNN
KNN分类方法是所有分类算法中最简单的方法,它在理论上的研究已经十分成熟。该分类方法(王小美和张红利,2013)的基本思想是:找到一个样本在特征空间中的K个最相似或者最邻近的样本,如果这K个邻近样本中的大多数属于某一个类别,那么该样本就属于这个类别。在KNN算法中,所选择的邻近样本都是已经正确分类的训练样本。该方法在确定分类决策时只依据最邻近的一个或者几个样本的大多数类别来决定待分样本所属的类别。因此,KNN方法在类别决策时,只与极少量的相邻样本有关。
假设有N个训练样本,给定一个测试样本x,计算与之最相近的K个最近邻者,其中各类别所占个数为Ki,i = 1,2,$ \cdots $,c。定义判别函数为:
${g_i}(x)= {K_i}{\rm{,}}i = 1{\rm{,}}2{\rm{,}} \cdots {\rm{,}}c$ (1)
最终,测试样本x的类别判定可根据决策规则:
$ j = \arg \mathop {\max }\limits_i {g_i}(x)\text{,}i = 1\text{,}2\text{,} \cdots \text{,}c$ (2)
2.2 SVM
SVM是Vapnik等人在1995年提出的一种基于统计学习理论的机器学习算法(Vapnik,1999)。由于SVM是基于结构风险最小化准则的,因此其推广能力明显优于一些传统的学习方法,能够在分类问题中表现出很好的泛化能力,获得相对较高的分类精度。对于两类SVM而言,其分类基本原理是:通过寻找一个分类超平面来使得训练样本中的两类样本点能被分开,并且距离该平面尽可能地远。
给定训练集T = {(x1,y1),(x2,y2),$ \cdots $,(xl,yl)}∈(Rn × Y)l,其中训练数据xi∈Rn,其相应的类标号yi∈Y = {1,-1},i = 1,2,$ \cdots $,l。这样,求解最优分类超平面的问题可以归结为以下的二次规划问题:
$\begin{array}{l}\begin{array}{*{20}{c}}{\min }\\{w,b,\xi }\end{array}\frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^t {{\xi _i}} \\s.t.\;{y_i}\left({\left({w \cdot \Phi \left({{x_i}} \right)} \right)+ b} \right)\ge 1 - {\xi _i},i = 1,2 \ldots,l\\{\xi _i} \ge 0,i = 1,2,\ldots l\end{array}$ (3)
式中,Φ(·)是一个从输入空间Rn到特征空间F的映射,用于将训练数据x投影到一个高维空间中去;ξi是松弛系数,它允许出现错分的样本;C是惩罚参数,它控制着对错分样本的惩罚程度,w为分类面权重向量,b为偏置。最后,可以得到式(3)的对偶形式为
$\begin{array}{l}\mathop {\min }\limits_\alpha {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \frac{1}{2}\sum\limits_{i = 1}^1 {} \sum\limits_{j = 1}^l {{y_i}{y_j}} K({x_i}{\rm{,}}{x_j}){\alpha _i}{\alpha _j} - \sum\limits_{j = 1}^l {{\alpha _j}} \\{\rm{s}}.{\rm{t}}.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \sum\limits_{j = 1}^l {{y_i}{\alpha _j}} = 0{\mkern 1mu} \\0 \le {\alpha _i} \le C{\rm{,}}i = 1{\rm{,}}2{\rm{,}} \cdots {\rm{,}}l\end{array}$ (4)
式中,K(xi,xj)是核函数,可表示为K(xi,xj)= Φ(xi)·Φ(xj)。通过求解式(4),可以得到α* =(α1*,α2*,$ \cdots $,αl*)T,选取位于区间(0,C)中的α*的分量αj*,据此可计算出分类超平面函数为
$\begin{array}{l}\sum\limits_{j = 1}^l {{y_i}} \alpha _i^*K({x_i}{\rm{,}}x)+ {b^*} = 0\\{x^*} = {y_i} - \sum\limits_{j = 1}^l {{y_i}} \alpha _i^*K({x_i}{\rm{,}}{x_j})\end{array}$ (5)
最终的决策函数可以表示为
$f(x)= {\rm{sgn}}(\sum\limits_{j = 1}^l {{y_i}} \alpha _i^*K({x_i}{\rm{,}}x)+ b)$ (6)
上述SVM分类方法主要是用来解决二分类问题,对于多分类问题,通常可以采用一对一方法(OAO),一对多方法(OAA)等(Hsu和Lin,2002)。假设有k类样本,则一对一方法构造k(k - 1)/2个两类SVM分类器,每一个分类器用来区分两个类别,所有两类分类器采用投票法来进行决策;一对多方法则构造k个两类SVM分类器,每个两类分类器用来区分一个类和剩余的类,最后得到的决策结果是具有最大决策值的类获胜。
2.3 RF
RF是由Breiman(2001)提出的一种机器学习方法。它利用自助法(bootstrap)重抽样方法从原始样本中抽取多个样本,对每个自助样本集进行决策树建模,然后组合多棵决策树进行预测,通过投票得出最终预测结果。RF通过构造不同的训练集增加分类模型间的差异,从而提高组合分类模型的外推预测能力,具有较高的预测准确率,对异常值和噪声具有很好的容忍度,且不容易出现过拟合。
假设T为原始样本集合,首先从原始训练数据中生成k个自助样本集,每个自助样本集是每棵分类树的全部训练数据。然后,利用每个自助样本集构建单棵分类树,在树的每个节点处从M个特征中随机挑选m个特征(m<<M),按照节点不纯度最小的原则从这m个特征中选出一个特征进行分支生长,从而使这棵分类树进行充分生长,每个节点的不纯度达到最小。最后,根据生成的多个树分类器对新的数据进行预测,分类结果按照每个树分类器的投票多少而定。
2.4 SRC
SRC是近年来出现的一种新型的分类方法。该方法最早在人脸识别领域被提出(Wright等,2009),后被逐步用于其他分类领域。SRC认为同一类别的训练样本分布在同一子空间中,对于任意的测试样本y,可以通过训练样本集A的稀疏线性组合表示出来。
假设一组训练样本集包含样本总数为n,可以表示为
${ {A}} = [{ {A}_1}\text{,}{ {A}_2}\text{,}\cdots \text{,}{ {A}_c}] $ (7)
式中,c为类别数,且
$ {{A}_i} = [{{v}_{i,1}}\text{,}{{v}_{i,2}}\text{,}\cdots \text{,}{{v}_{i,{n_i}}}] \in {{\rm{R}}^{m \times {n_i}}}$ (8)
为第i类训练样本集,ni表示第i类样本的数目,m表示样本的特征维度,$ v_{i,n_i} $为Ai中的第ni个样本。那么,来自同一个类别的测试样本$ y = \in {{\rm{R}}^m} $可以用该类训练样本Ai的线性组合表示为
$ {{y}} = {{A}_i}{{x}_0} = {{\alpha} _{i\text{,}1}}{{v} _{i\text{,}1}} + {{\alpha} _{i\text{,}2}}{{v} _{i\text{,}2}} + \cdots + {{\alpha} _{i\text{,}{n_i}}}{{v} _{i\text{,}{n_i}}} $ (9)
式中,$\!\!{a_{i\text{,}\!\!j}} \in {\rm{{R}}} $为待求解的线性系数$\!\! j = 1\text{,}\!\!2\text{,}\!\!...\text{,}\!\!{n_i} $。
在分类的过程中,测试样本的类别通常是未知的,因此,式(9)可以改写为
$ {y} = {{A}}{{x}_0}$ (10)
${x_0} = {[0,\cdot \cdot \cdot,0,{\alpha _{i,1}},{\alpha _{i,{2_i}}} \cdot \cdot \cdot,{\alpha _{i,{n_i}}},0,\cdot \cdot \cdot,0]^{\rm{T}}} \in {{\rm{R}}^n} $ (11)
为了使得测试样本尽可能的用测试样本所在类的训练样本进行线性表示,所求得的系数向量x0包含的非零系数应该尽可能的少。对于x0的计算,通常可以通过最小化l0范数问题或最小化l1范数问题求解(Chen等,2011),这类问题的典型算法有正交匹配追踪算法(OMP)(Tropp和Gilbert,2007),基追踪去噪算法(BPDN)(Chen等,1998)等。通常情况下,所获取的数据中经常包含噪声,对于最小化l0范数问题,可通过如下优化问题求解:
$\begin{array}{l}\min \quad \parallel {x_{\rm{0}}}{\parallel _0}\\{\rm{s}}.{\rm{t}}.\quad {\mkern 1mu} {\mkern 1mu} \parallel y - A{x_{\rm{0}}}{\parallel _2} \le \varepsilon \end{array}$ (12)
式中,||•||0为l0范数,即非零元素个数;ε为误差限。
对于最小化l1范数问题,可通过如下优化问题求解:
3 实验结果与分析
3.1 实验环境
实验均在Matlab7.8.0软件平台下进行,操作系统为Windows 7(SP1),CPU为英特尔Xeon处理器E5-1620(3.60 GHz),内存为4 GB。本文所有的实验均未进行并行优化处理。
3.2 实验数据
为了研究不同的分类器在大数据量遥感数据分类任务中的适用性,本文以遥感图像场景分类为例,进行分类实验。所采用的数据集为公开的遥感土地利用及地物目标场景数据集(http://vision. ucmerced.edu/datasets)。该数据集所包含的图像均为高分辨率遥感图像,每幅图像大小为256 × 256,共有21个语义类别,即农田、飞机、棒球场、海滩、建筑物、丛林、高密度住宅区、森林、高速公路、高尔夫球场、港口、十字路口、低密度住宅区、移动家庭公园、立交桥、停车场、河流、跑道、稀疏住宅区、油罐仓库和网球场。数据集中每个类别包含100幅图像,共计2100幅图像。图 1给出了数据集的示例图像。
为了测试数据量对分类器性能的影响,本文对该数据集进行了扩充,对每一幅遥感图像分别进行了(90°,180°,270°)3个角度的旋转。最终,每个类别包含400幅图像,共计8400幅图像。需要指出的是,本文研究中,图像旋转的目的只是用于扩充样本数量,并不会影响不同分类器分类性能比较的公平性。这主要源于以下几方面的原因:(1)实验中,所有旋转前后的样本在样本集中都是充分混合的,所有图像均作为一般样本对待;(2)分类器分类性能仅取决于其对样本特征的学习能力,而其对于样本的旋转不变性,则从根源上取决于样本特征的表达方法,即如果特征表达不具有旋转不变性,那么无论使用哪种分类方法,其旋转前后该分类器的分类精度均会产生较大偏差;(3)在本文研究中,特征表达方法是统一的,且均不考虑特征表达的旋转不变性问题,因此,对于不同分类方法的比较具有公平性。
3.3 实验设置
3.3.1 特征提取
采用视觉词包(BOVW)特征提取方法(赵理君等,2014)计算图像的特征向量。BOVW特征是目前图像分析和图像分类领域中出现的一种新型,有效的中层特征表示方法,它首先提取图像中局部图像块的低层特征,然后利用K均值聚类算法对得到的低层特征进行量化,将每一个聚类中心视为视觉单词,构建视觉词典,最后统计并计算图像中所包含的视觉单词的频率直方图,以此作为表达图像内容的特征向量。
对图像采取16 × 16的格网划分,同时进行8个像元的窗口滑动,以此生成图像的局部图像块。采用的低层特征为具有良好不变性的Opponent Scale Invariant Feature Transform(OpponentSIFT)特征(van de Sande等,2009)。从数据集的每个类别里随机选取1/4的样本用于构建视觉词典。
3.3.2 分类器参数
对于不同的分类器,在分类模型的训练过程中需要设置不相同的参数。表 1列出了本文实验中所采用的各种分类器的待定参数。从表 1可以看出,大多数分类器都只需要选定一个参数值就可以构建分类模型,但对于RBF-SVM和RF分类器而言,通常需要同时设置两个参数,这在一定程度上增加了构建模型的复杂度,尤其是在参数值的选取方面,很大程度上降低了分类模型的构建效率。通常情况下,RF分类器尽管有两个参数需要设置,但是其中的mtry可以通过与特征变量数目相关的经验公式设定(Breiman,2001)。
表 1 分类器参数描述
Table 1 Descriptions of classifier parameters
| 分类器 | 参数个数 | 参数描述 | |
| KNN | 1 | 近邻数(K) | |
| SVM | Linear-SVM | 1 | 惩罚系数(C) |
| RBF-SVM | 2 | 惩罚系数C 核函数参数G |
|
| RF | 2 | 随机森林中树的个数ntree 树节点预选的变量个数mtry |
|
| SRC | L0-SRC | 1 | 误差限ε |
| L1-SRC | 1 | 误差限ε | |
3.3.3 性能评价
为了评价不同分类器的性能,本文分别采用总体精度,Kappa系数和运行时间来分析不同分类器方法的分类精度和分类时效。同时为了保证实验结果的可信度,每组实验均独立运行10次,最后计算10次运行结果的平均值。
3.4 实验结果
为了能够对各种分类器在遥感数据分类任务中的性能进行比较分析,将从参数敏感性、训练样本数据量、待分类样本数据量以及样本特征维数等方面分别对其分类效果进行研究。
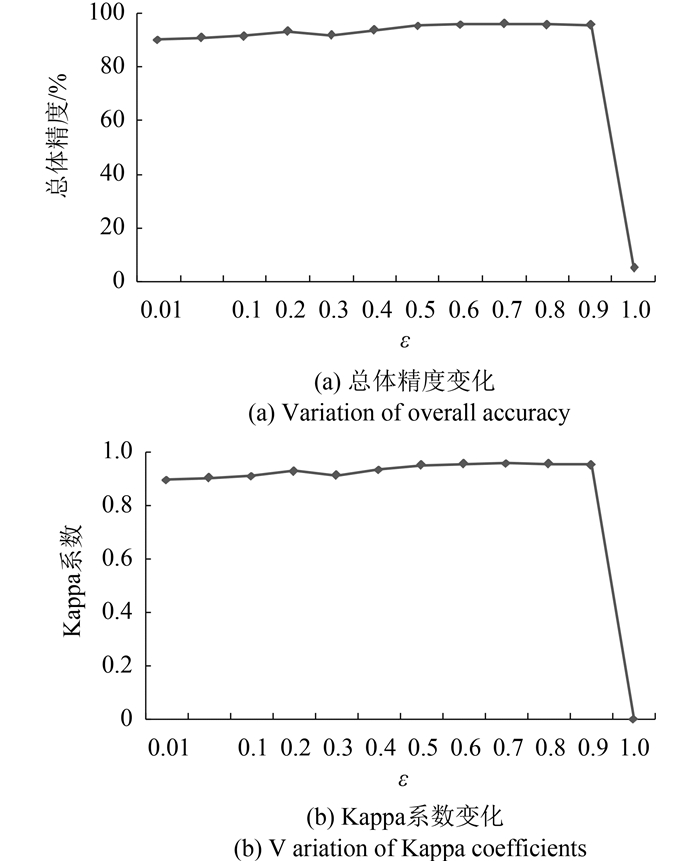
参数的选择是影响分类性能的一个重要因素。尤其是在海量遥感数据的分类任务中,一个对参数选择不敏感且分类精度较高的分类器,通常会成为分类任务优先考虑的方法。为了对不同的分类器进行参数敏感性分析,实验从样本集中随机选取了90%的样本用于训练,剩余10%的样本用于性能评价。训练样本和测试样本的比例为经验设定,将训练样本设定为较高比例的目的在于使不同分类器在训练过程中能够具有充足的训练样本量,从而对样本进行尽可能充分的学习。实验中,为了进行统一的比较,设置聚类中心数(视觉词典大小)为300,从而每幅图像均可表示为一个300维的特征向量。图 2—图 7给出了不同参数取值对于相应分类器分类性能的影响。
通过分析图 2—图 7,可以发现,对于所有分类方法来说,随着参数取值的变化,总体精度和Kappa系数的波动趋势大体保持一致。对于KNN分类器来说,K值过小会在一定程度上放大噪声数据的干扰,但由于实验数据中并没有包含噪声数据,因而较小的K值能够获得较好的分类结果,且随着K值的逐渐增大,分类器的分类性能也呈线性下滑态势。
对于Linear-SVM分类器来说,惩罚系数C的取值决定了分类模型对于错分情况的容忍程度,较大的C值通常都够提高分类器的分类性能,但同时也会降低分类模型的泛化性能。随着C值的不断增大,分类性能的提升空间也逐渐趋于饱和。对于RBF-SVM分类器来说,其分类模型的构建取决于两个参数,这在很大程度上提高了分类器选参的时间成本。
对于不同的参数组合,分类性能出现了较大的波动,这主要是因为其参数是在2维空间中选取的,分类性能同时受两个参数取值的影响和制约。通常情况下,对于这种情况下的参数选优可以通过网格选取的方法寻找最佳参数组合。实验主要是用于说明RBF-SVM分类方法的分类性能受参数选取的影响程度,因此,并没有考虑更精细的参数区间划分。对于RF分类器来说,由于其中的mtry可以通过经验公式直接计算得到,因此,实际上RF分类模型只有另一个参数决定,即随机森林中树的个数ntree。从实验结果中可以看出,随着参数ntree值的增大,在构建模型时的计算复杂度也不断增加,同时,RF分类模型的分类性能得到不断提升,尤其是在ntree < 500的情况下,分类性能的提升效果尤为明显,但随着ntree值的进一步增大,分类器的分类性能提升趋于平缓,甚至还出现了少量的下滑。对于L0-SRC分类器来说,其参数误差限的取值一般不易过大,较大的误差限会减少对误差的约束力,从而导致分类精度的降低。从实验结果可以看出,随着误差限取值的减小,分类性能呈现出先上升,后下降,最后趋于稳定的趋势。对于L1-SRC分类器来说,其分类性能的变化与参数误差限取值的关系与L0-SRC分类器相似。不同的是,当误差限取值增大时,L1-SRC分类器的分类性能出现了骤降现象。
表 2给出了各种分类方法受参数取值的影响程度,采用标准偏差来评价。对于每一种分类方法,标准偏差是基于所有参数取值情况下的分类结果计算出的,其中的每一次分类结果则是通过10次独立运行结果的平均值得到,而每一种方法在这10次运行结果中的标准偏差则大致相近,均在一定范围内(总体精度的偏差在1.0左右,Kappa系数的偏差在0.01左右)。从表 2可以看出,其中有3种分类器,即KNN,RF和L0-SRC,它们的总体精度和Kappa系数在不同的参数取值下具有较小的标准偏差,这说明这3种分类器的分类性能受参数取值的影响相对较小,对于参数的敏感性较弱。而另外的几种分类器,它们则对参数的取值具有较强的依赖性,分类性能受参数取值的影响也较大。
表 2 不同参数下分类器分类性能的标准偏差
Table 2 Standard deviations of performances for classifiers using different parameters
| 分类方法 | 总体精度偏差/% | Kappa系数偏差 |
| KNN | 2.04 | 0.02 |
| Linear-SVM | 27.06 | 0.28 |
| RBF-SVM | 34.68 | 0.36 |
| RF | 1.17 | 0.01 |
| L0-SRC | 7.09 | 0.07 |
| L1-SRC | 25.71 | 0.27 |
3.4.2 训练样本数据量对分类器性能的影响
随着遥感数据获取手段的多样化,遥感数据量得到不断扩充,这极大地丰富了遥感数据分类中训练样本集的多样性。在这种情况下,训练样本数据量对分类器性能的影响成为一项值得研究的问题。本节实验以此为目的,着重分析不同分类器的分类精度和分类效率与训练样本数据量的关系。
以下实验均在最佳参数选定的基础上进行。从8400幅图像的样本集中选取90%的样本构成训练样本集,剩余10%的样本构成待分类测试样本集。设置聚类中心数(视觉词典大小)为300,从而每幅图像均可表示为一个300维的特征向量。为了能够获得不同训练样本集数据量下,各分类器的分类效果,本文分别从训练样本集中随机抽选出不同比例(如10%,20%···)的样本进行分类器的训练测试实验。
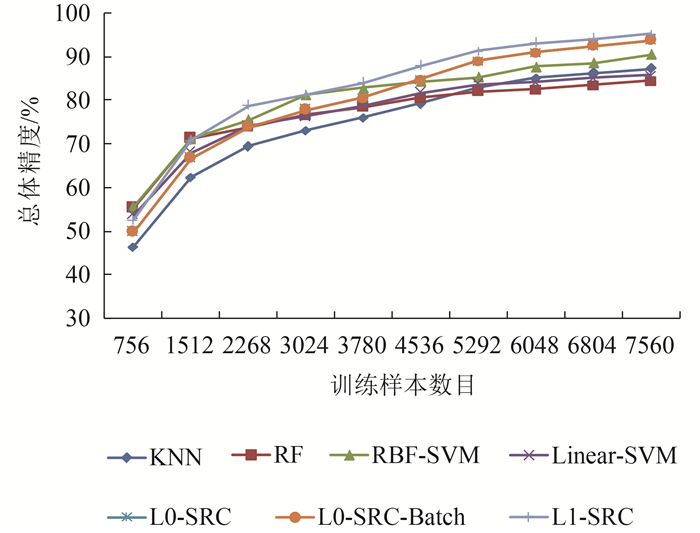
图 8和图 9给出了不同分类器方法在不同训练样本数目下的分类效果。其中,L0-SRC-Batch为L0-SRC分类器的批处理模式,即对所有待分类样本,通过一次性求解L0范数问题同时得到所有待分类样本的分类结果。从图 8和图 9可以看到,对于所有分类器方法来说,随着训练样本数目的增加,它们的分类总体精度和Kappa系数都呈现出不断上升趋势。在小样本量的情况下,KNN分类器的分类效果相对最差,其余几种分类器的分类性能基本相当。SVM作为一种针对小样本处理的分类方法,在小样本量的情况下并没有体现出绝对的优势,这可能与所选择样本的代表性有关系。当训练样本数据量不断增大的情况下,SRC类型的分类方法脱颖而出,分类效果上明显优于其他几种分类器方法。尽管RF适于处理大样本和高维数据,但其分类精度却随着样本数量的增大表现得相对较低。对于KNN分类器,其分类精度也高于RF,很大程度上可能与数据本身有关系,因为本文的实验数据中并没有考虑噪声数据,从而使得KNN分类器的优势充分发挥出来。具体来说,L1-SRC分类器精度最高,L0-SRC和L0-SRC-Batch分类结果相同,居第二位,然后分别是RBF-SVM分类器,Linear-SVM和KNN分类器,和RF分类器。不难发现,对于大数据量训练样本来说,SRC类型的分类方法能够取得相对更好的分类结果。
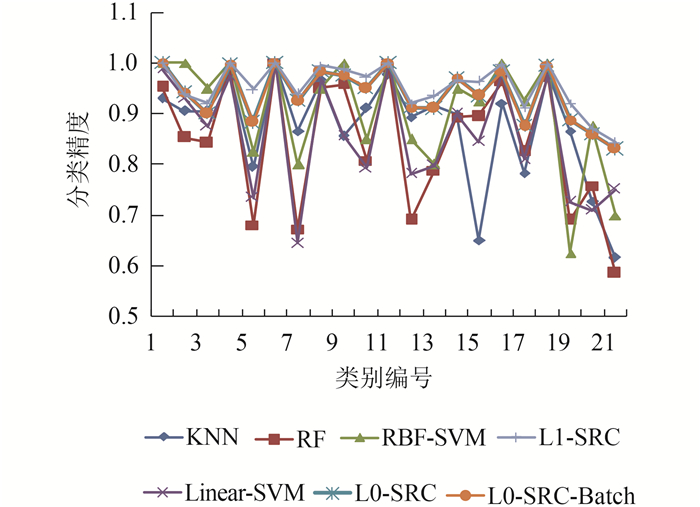
图 10给出了不同分类器针对各类别的分类精度,其中类别编号1—21分别对应实验数据中的21个语义类别,即农田、飞机、棒球场、海滩、建筑物、丛林、高密度住宅区、森林、高速公路、高尔夫球场、港口、十字路口、低密度住宅区、移动家庭公园、立交桥、停车场、河流、跑道、稀疏住宅区、油罐仓库和网球场。从图 10的分类结果可以看出,L1-SRC和L0-SRC分类器对不同类别的分类精度均能保持相对较高的水平,RBF-SVM分类器相对次之,其他分类器在对不同类别进行分类时呈现出较大程度的波动,即对部分类别分类精度较高,而对其他类别分类精度较低。
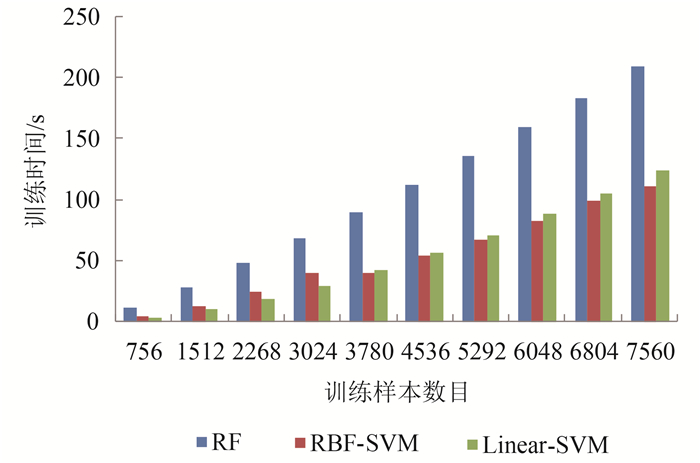
图 11—图 13给出了不同训练样本数目下,KNN、RF、SVM、及SRC几种分类方法在分类时效方面的变化趋势。从图 11可以看出,随着训练样本数目的增加,所有的分类器在时间消耗上都呈现逐步上升趋势。L0-SRC分类器的运行时间随训练样本数目的增加呈指数性增长,与之相比,L0-SRC-Batch则能够在保持分类精度不变的情况下,极大程度地减少运行时间,提高了分类的效率。在除L0-SRC之外的分类器中,所有的分类器随着训练样本数目的增加都呈现出线性的增长模式。其中,KNN分类器和L0-SRC-Batch分类器的运行时效受训练样本数目变化的影响最不明显。分类器RBF-SVM和Linear-SVM所消耗的分类时间大体相同,时效上仅次于KNN和L0-SRC-Batch分类器。分类器RF和L1-SRC成为相对最为耗时的分类方法,但是,在训练样本数目相对较少的情况下,RF分类器的分类时效仍然是高于L1-SRC的。总的来讲,在分类总体消耗时间上,L0-SRC > L1-SRC > RF > RBF-SVM/Linear-SVM > KNN/L0-SRC-Batch,分类器KNN和L0-SRC-Batch在时间消耗上受训练样本数目变化的影响最小。结合图 8和图 9,可以看出,在待分类样本数目一定的情况下,随着训练样本数目的增加,L0-SRC-Batch分类器在分类精度和分类时效上均体现出相对较大的优势。
为了进一步分析分类器在不同阶段的时效性,对分类消耗时间进行了细分,即训练时间和预测时间。由于KNN和SRC分类器的训练过程和预测过程均在同一阶段完成,因此这里只对其余的分类器在训练和预测两个阶段的运行时间效率进行了单独比较。由图 12和图 13可以看出,在训练阶段,3种分类器的时间消耗均随着训练样本数目的增加而增大,且RF分类器的时间消耗最大,明显高于SVM类型的分类方法。然而,在预测阶段,由于待分类样本的数目是固定不变的,RF分类器的时间消耗变得很小且基本不随训练样本数量的变化而变化,而两个SVM类型的分类方法则呈现出与训练样本数目正相关的增长趋势。这说明,这3种分类方法在训练阶段的时间消耗与训练样本数目的多少有直接关系;在预测阶段,RF分类器的时间消耗主要与待分类样本的数目有关,而RBF-SVM和Linear-SVM的时间消耗则在很大程度上仍与训练样本数目的多少有关。
3.4.3 待分类样本数据量对分类器性能的影响
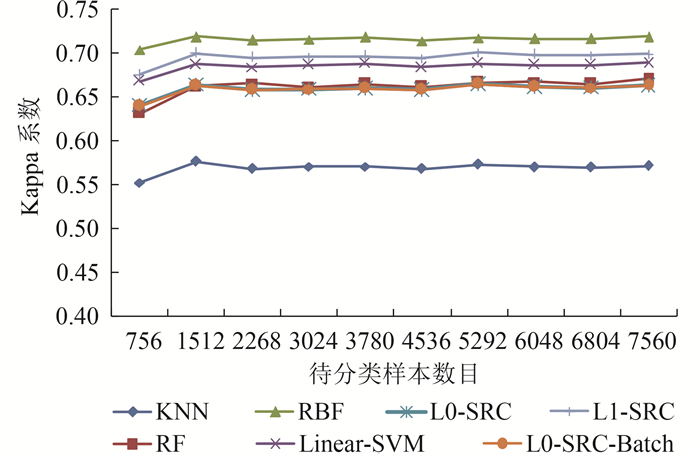
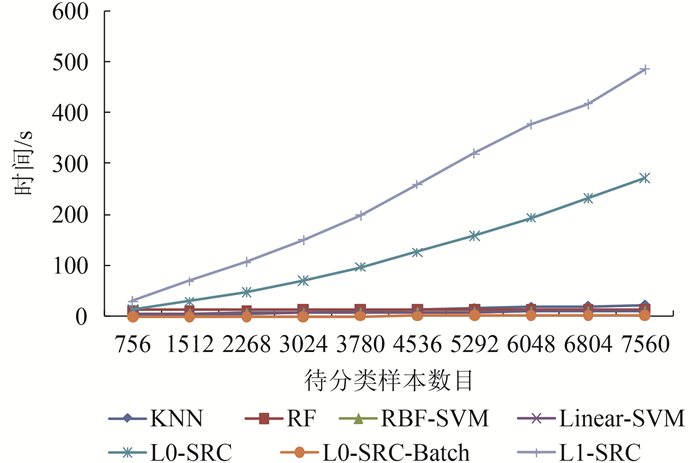
为了分析不同分类器的分类性能受待分类样本数据量的影响,从8400幅图像的样本集中随机选取了90%的样本构成待分类测试样本集,剩余10%的样本构成训练样本集。设置聚类中心数(视觉词典大小)为300,从而每幅图像均可表示为一个300维的特征向量。为了能够获得不同的待分类样本数据量,这里从实验数据集中选取了较高比例的样本数量作为待分类测试样本集,尽管实验中训练样本的相对数量较低,但是不同分类器所使用的训练样本均是一致的,另外,本组实验中所关心的是不同分类器受待分类样本数据量变化的影响程度,因此,无论训练样本是否充足,其代表性如何,在训练样本统一的情况下,对不同分类器性能的比较是公平的。本文分别从待分类测试样本集中随机抽选出了不同比例(如10%,20%,···)的样本。实验结果如图 14—图 18所示。
从图 14和图 15可以看到,对于所有分类器方法来说,随着待分类样本数目的增加,它们的分类总体精度和Kappa系数都基本维持在比较稳定的水平,并没有因为待分类样本数目的变化而发生显著变化。但是,不同分类器分类精度的高低却显而易见。在固定训练样本的情况下,KNN分类器的分类效果最差,说明其对训练样本的学习能力比较弱。而其余的几种分类器方法则保持着相对较高的分类水平。具体而言,RBF-SVM分类器分类效果最好,这也证实了其在样本学习能力方面的优势,其泛化性能较好。L1-SRC分类器分类效果次之,然后是Linear-SVM分类器。RF分类器和L0-SRC,L0-SRC-Batch分类器的分类效果相当,但总体差于RBF-SVM,L1-SRC和Linear-SVM。
从图 16可以看到,在训练样本数目固定,待分类样本数目不断增加的过程中,L1-SRC和L0-SRC分类器的总体时间消耗明显高于其他的分类方法,呈现出指数增长的趋势。这主要是因为它们需要对每一个待分类样本进行范数问题求解,而求解的过程是比较耗时的。其他的分类器,即KNN,RF,RBF-SVM,Linear-SVM和L0-SRC-Batch,在时间消耗上基本维持在一个相对较低的水平上,且因待分类样本数目而产生的变化幅度较小。
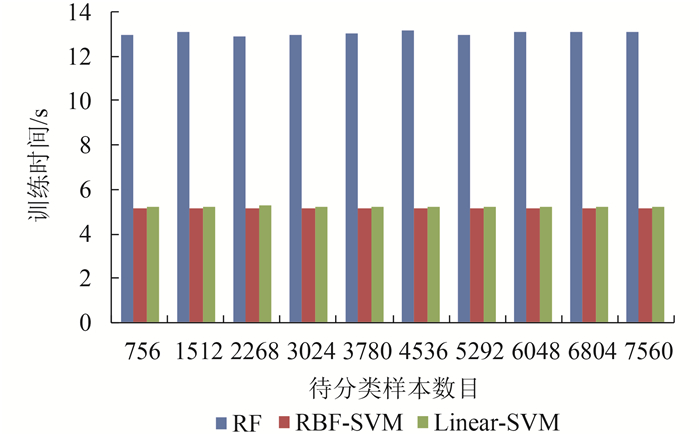
图 17和图 18给出了RF,RBF-SVM和Linear-SVM 这3种分类器在训练和测试过程中各自的时间消耗情况。从图 17和图 18中可以看出,在训练阶段,由于训练样本数目是固定的,3种分类器的时间消耗均与待分类样本无关,不随着待分类样本数目的增加而增大,而是保持在一个相对稳定的水平,但RF分类器的训练时间消耗最大,明显高于SVM类型的分类方法。在预测阶段,由于待分类样本的数目是不断增大的,3种分类方法的预测时间消耗也都呈现出逐步增大的趋势,但RF分类器的时间消耗明显低于SVM类型的分类方法。结合图 12和图 13可以看出,这3种分类方法在训练阶段的时间消耗主要与训练样本数目的多少有关;在预测阶段,RF分类器的时间消耗主要与待分类样本的数目有关,而RBF-SVM和Linear-SVM的时间消耗则同时与训练样本数目和待分类样本数目有关。另外,在训练阶段,RF分类耗时,而SVM类型的分类器相对省时;在测试阶段,刚好相反,RF分类器省时,而SVM类型的分类器相对费时。
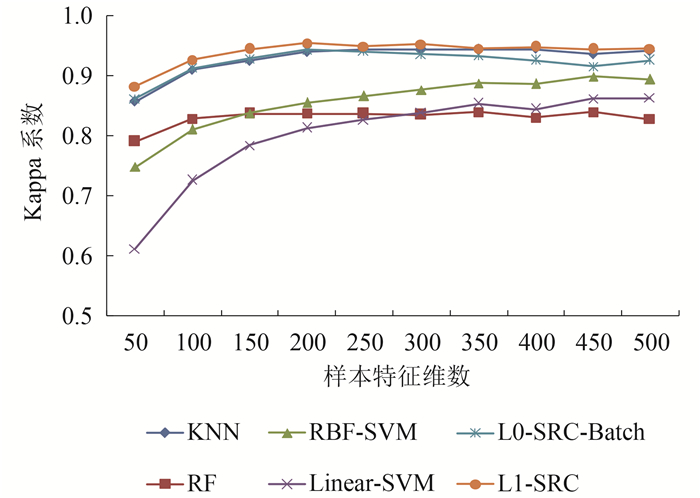
3.4.4 样本特征维数对分类器性能的影响
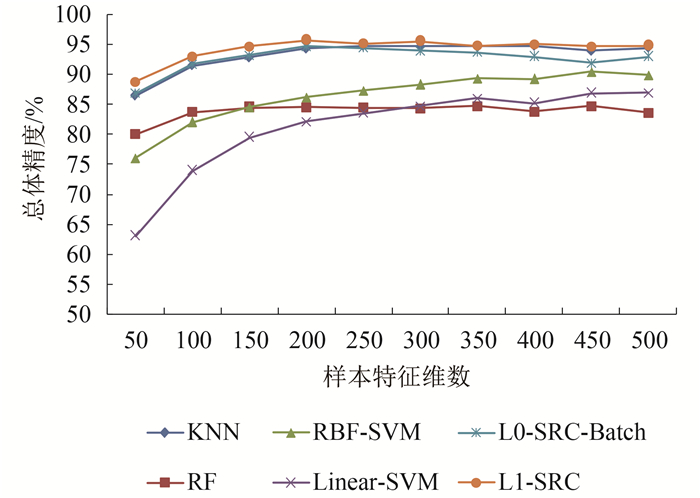
为了分析不同分类器方法受样本特征维数变化的影响程度,本节分别对不同特征维数下,不同分类器的学习性能进行了比较研究。这里,对实验数据集进行了9∶1的随机划分,得到90%的训练样本和10%的测试样本。实验中,特征维数与视觉词典的大小有关,为了比较研究不同特征维数对分类器分类性能的影响,分别设定样本特征维数为50,100,150,200,250,300,350,400,450和500。实验结果如图 19至图 21所示。
从图 19和图 20的实验结果可以看到,随着样本特征维数的不断增加,不同分类器在总体分类精度和Kappa系数上均呈现出了逐步上升的趋势。但是,这种上升趋势却因分类器类型的不同,表现为不同的增长程度和规律。其中,SRC类分类器和KNN分类器在最初使用低维特征阶段表现出一定的上升幅度,随后随着特征维数的增加,其分类总体精度和Kappa系数均趋于稳定,说明这两类分类器无需很高的特征维数即可取得较好的分类结果,而过高的特征维数并不会对分类结果的提升产生有效的积极影响;SVM类型分类器则随着特征维数的逐步增加,始终保持着上升的态势,说明SVM对高维特征具有较强的包容性和学习能力;RF分类器对特征维数增加则表现得并不敏感,始终保持在某一水平上下,这也反映了RF分类器在分类过程中,只有少数的特征变量对分类起着决定性的区分作用。
另一方面,从图 21的结果可以看到,在分类总体时间消耗上,L0-SRC-Batch分类器和KNN分类器随特征维数的增加涨幅并不显著,而其他几类分类器方法则随特征维数的增加呈现出明显的上升趋势。由此可见,样本特征的维数也是影响分类器分类效率的一项重要因素。
4 结 论
针对当前大数据量遥感数据处理中,典型遥感数据分类方法在处理时效和分类精度方面进行了比较分析研究。选了几种典型的分类器,KNN,RF,RBF-SVM,Linear-SVM,L0-SRC,L1-SRC,并分别在参数敏感性,训练样本数据量,待分类样本数据量和样本特征维数对分类器性能的影响等几个方面进行了详细的比较实验。
本文模拟了不同数据量分类的情况,对不同分类方法在分类精度和分类时效方面的适用性进行了实验。实验结果表明:KNN,RF和L0-SRC分类器的参数敏感性较小,而RBF-SVM,Linear-SVM和L1-SRC分类器的参数敏感性相对较大。在待分类样本固定的情况下,随着训练样本数据量不断增大,各分类器分类性能均呈现上升趋势,SRC类型的分类方法分类效果最佳,SVM类型的分类方法精度次之,RF和KNN分类器效果相对较差,分类总体消耗时间上,呈现出L0-SRC > L1-SRC > RF > RBF-SVM/Linear-SVM > KNN/L0-SRC-Batch的趋势。在训练样本固定的情况下,各分类器的分类效果基本不受待分类样本数据量变化的影响,主要依赖于各分类器对训练样本的学习能力,RBF-SVM分类器分类效果最好,L1-SRC分类器次之,然后是Linear-SVM分类器,紧接着是RF,L0-SRC/L0-SRC-Batch分类器,KNN分类器效果最差。在分类总体消耗时间上,L1-SRC和L0-SRC耗时最大,而其他的分类方法均耗时较小;样本特征维数的变化不仅影响着分类器的运行效率,同时也对其分类精度产生不同的影响,其中SRC和KNN分类器器无需较高的特征维数即可获得较好的分类结果,SVM对高维特征具有较强的包容性和学习能力,RF分类器对特征维数增加则表现得并不敏感,特征维数的增加并不能对其分类精度的提升带来更多的贡献。
总的来说,本文所研究的几种典型分类方法能够有效地用于不同数据量遥感数据分类任务中,在分类精度和分类时效方面均具有一定的适用性。但是在处理不同的遥感数据分类任务时,分类精度主要取决于分类器对训练样本的学习能力,训练样本数据量充分的情况下,能够发挥分类器的最大性能优势,但分类器在训练和预测阶段的时间消耗又成为挑选分类器时需要考虑的一个重要问题。因此,在大数据量的遥感数据分类任务中,对于分类器的选择应当基于各自的特点和优势,结合实际应用的特点进行权衡和选择,选择参数敏感性较小,分类总体时间消耗低但分类精度相对较高的分类方法,从而发挥其在大数据量遥感数据分类中的最佳性能。
本文研究的结论主要是基于小范围数据量上的变化进行的初步实验,下一步还需要针对大范围数据量上的变化进行进一步验证研究。
参考文献
-
Breiman L. 2001. Random forests. Machine Learning, 45(1):5-32[DOI:10.1023/A:1010933404324]
-
Chen S S B, Donoho D L and Saunders M A. 1998. Atomic decomposition by basis pursuit. SIAM Journal on Scientific Computing, 20(1):33-61[DOI:10.1137/S1064827596304010]
-
Chen Y, Nasrabadi N M and Tran T D. 2011. Hyperspectral image classification using dictionary-based sparse representation. IEEE Transactions on Geoscience and Remote Sensing, 49(10):3973-3985[DOI:10.1109/TGRS.2011.2129595]
-
Du P J, Xia J S, Zhang W, Tan K, Liu Y and Liu S C. 2012. Multiple classifier system for remote sensing image classification:a review. Sensors, 12(4):4764-4792[DOI:10.3390/s120404764]
-
Franco-Lopez H, Ek A R and Bauer M E. 2001. Estimation and mapping of forest stand density, volume, and cover type using the k-nearest neighbors method. Remote Sensing of Environment, 77(3):251-274[DOI:10.1016/S0034-4257(01)00209-7]
-
Friedl M A and Brodley C E. 1997. Decision tree classification of land cover from remotely sensed data. Remote Sensing of Environment, 61(3):399-409[DOI:10.1016/S0034-4257(97)00049-7]
-
Hsu C W and Lin C J. 2002. A comparison of methods for multiclass support vector machine. IEEE Transactions on Neural Networks, 13(2):415-425[DOI:10.1109/72.991427]
-
Li C C, Wang J, Wang L, Hu L Y and Gong P. 2014. Comparison of classification algorithms and training sample sizes in urban land classification with Landsat thematic mapper imagery. Remote Sensing, 6(2):964-983[DOI:10.3390/rs6020964]
-
Lu D and Weng Q. 2007. A survey of image classification methods and techniques for improving classification performance. International Journal of Remote Sensing, 28(5):823-870[DOI:10.1080/01431160600746456]
-
Melgani F and Bruzzone L. 2004. Classification of hyperspectral remote sensing images with support vector machines. IEEE Transactions on Geoscience and Remote Sensing, 42(8):1778-1790[DOI:10.1109/TGRS.2004.831865]
-
Meng Y. 2013. Test Strategy and System Optimization of Remote Sensing Big Data Processing System. Kaifeng:Henan University:1-2(孟圆. 2013. 遥感大数据处理系统测试策略与系统优化. 开封:河南大学:1-2)
-
Mountrakis G, Im J and Ogole C. 2011. Support vector machines in remote sensing:a review. ISPRS Journal of Photogrammetry and Remote Sensing, 66(3):247-259[DOI:10.1016/j.isprsjprs.2010. 11.001]
-
Pal M. 2005. Random forest classifier for remote sensing classification. International Journal of Remote Sensing, 26(1):217-222[DOI:10.1080/01431160412331269698]
-
Song B Q, Li J, Mura M D, Li P J, Plaza A, Bioucas-Dias J M, Benediktsson J A and Chanussot J. 2014. Remotely sensed image classification using sparse representations of morphological attribute profiles. IEEE Transactions on Geoscience and Remote Sensing, 52(8):5122-5136[DOI:10.1109/TGRS.2013.2286953]
-
Stumpf A and Kerle N. 2011. Object-oriented mapping of landslides using random forests. Remote Sensing of Environment, 115(10):2564-2577[DOI:10.1016/j.rse.2011.05.013]
-
Tropp J A and Gilbert A C. 2007. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, 53(12):4655-4666[DOI:10.1109/TIT. 2007.909108]
-
van de Sande K E A, Gevers T and Snoek C G M. 2009. Evaluating color descriptors for object and scene recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 32(9):1582-1596[DOI:10.1109/TPAMI.2009.154]
-
Vapnik V N. 1998. Statistical Learning Theory. New York:Wiley:1-768
-
Vapnik V N. 1999. The Nature of Statistical Learning Theory. New York:Springer-Verlag:1-333
-
Wang X M and Zhang H L. 2013. Hyperspectral remote sensing image classification using geodesic-based KNN. Journal of Shanxi Coal-Mining Administrators College, 26(4):135-137(王小美, 张红利. 2013. 基于测地距离的KNN高光谱遥感图像分类. 山西煤炭管理干部学院学报, 26(4):135-137)[DOI:10.3969/j.issn.1008-8881.2013.04.059]
-
Wright J, Yang A Y, Ganesh A, Sastry S S and Ma Y. 2009. Robust face recognition via sparse representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(2):210-227[DOI:10.1109/TPAMI.2008.79]
-
Yang C C, Prasher S O, Enright P, Madramootoo C, Burgess M, Goel P K and Callum I. 2003. Application of decision tree technology for image classification using remote sensing data. Agricultural Systems, 76(3):1101-1117[DOI:10.1016/S0308-521X(02)00051-3]
-
Zhao L J, Tang P and Huo L Z. 2014. A 2-D wavelet decomposition-based bag-of-visual-words model for land-use scene classification. International Journal of Remote Sensing, 35(6):2296-2310[DOI:10.1080/01431161.2014.890762]
-
Zhao L J, Tang P, Huo L Z and Zheng K. 2014. Review of the bag-of-visual-words models in image scene classification. Journal of Image and Graphics, 19(3):333-343(赵理君, 唐娉, 霍连志, 郑柯. 2014. 图像场景分类中视觉词包模型方法综述. 中国图象图形学报, 19(3):333-343)[DOI:10.11834/jig. 20140301]