0 引言
非线性双层规划 (nonlinear bilevel programming,NBLP) 是一类具有主从递阶关系的数学模型, 它是将优化问题作为约束条件的极值问题[1],并广泛用于经济规划、 管理、交通等工程实践领域[2]. NBLP问题通常是非凸不可微的, 文献$[3]$证明了即使搜索局部最优解,NBLP仍是NP难问题. 针对该问题传统的算法有$k$-best算法、分枝定界法、罚函数法等, 但仅对线性双层规划有效,对NBLP问题很难获得全局最优解. 由于智能优化算法对函数要求较低且具有较强的全局搜索能力被逐渐用于求解NBLP问题[4, 5, 6, 7, 8, 9]. 文献$[4]$首次利用遗传算法求解线性双层规划问题,随后出现基于神经网络[6]、禁忌搜索[7]、模糊理论[8]等求解双层规划的方法, 但都存在由于算法本身局限性而难以获得全局最优解的问题.
粒子群优化 (particle swarm optimization,PSO) 算法是一种基于社会群体行为的智能优化算法, 由Kennedy等人于1995年首次提出[10]. 由于PSO算法在易用性和时效性方面的突出表现, 使其在优化问题中取得巨大的成功,成为国内 外研究热点[11, 12]. 然而,基本PSO算法在进化后期常因为种群多样性丧失而陷入局部最优. 变邻域搜索[13, 14, 15, 16] (variable neighborhood search,VNS) 算法是一种求解优化问题的启发式算法, 由Hansen等于1997年首次提出[16], 其基本思想是系统地改变邻域结构 集来拓展搜索范围, 当在一种邻域结构下遇到局部最优时, 可以通过改变邻域结构的方法来继续搜索,在搜索过程中不断改善当前解的 目标函数值.
有鉴于此,本文将PSO算法的快速搜索能力和VNS算法的全局搜索能力合理结合,并嵌入审敛因子,提出求解NBLP问题的混合变邻域粒子群 (the particle swarm optimization with variable neighborhood search, PSO-VNS) 算法,该算法有效避免了上层函数为非凸不可微的NBLP问题容易陷入局部最优的问题. 最后,15个测试函数的仿真实验对比分析表明混合PSO-VNS算法的合理性和有效性. 1 NBLP问题描述
NBLP模型如式(1):
| $\left\{ {\begin{array}{l} {\displaystyle \mathop {\min\limits_xF(x,y)}},\\ {\displaystyle \mathop {mbox{s.t.} ~G(x,y)\leq 0}},$其中$y$求解$\\ {\displaystyle \mathop {\min\limits_yf(x,y)}},\\ {\displaystyle \mathop {mbox{s.t.} ~g(x,y)\leq 0}}\\ \end{array}} \right.$ | (1) |
对于NBLP模型给出如下基本概念[1]:
1)约束空间: $S=\{(x,y)\left| {G(x,y)\le 0,g(x,y)\le 0} \right.\}$;
2)对于固定的$x$,下层可行域为: $S(x)=\{y\left| {g(x,y)\le 0} \right.\}$;
3) $S$在上层决策空间的投影为: $S(X)=\{x\left| {\exists y,(x,y)\in S} \right.\}$;
4)对每个$x\in S(x)$,下层合理反映集为: $M(x)=\{y\left| {y\in \arg \min \{f(x,y),y\in S(x)\}} \right.\}$;
5)诱导域: $IR=\{(x,y)\left| {(x,y)\in S,y\in M(x)} \right.\}$.
本文对NBLP模型有如下假设:
1)为保证问题(1)有最优解,设$S$为非空紧集;
2)对每一个上层变量$x\in X$,下层存在唯一的最优解$y(x)$.
基于以上讨论,给出NBLP模型的可行解及最优解定义.
定义1 可行解. 若点$(x,y)\in IR$,则称$(x, y)$为NBLP模型的可行解.
定义2 最优解. 若点$(x^\ast ,y^\ast)$是NBLP模型的可行解, 且对任意$(x,y)\in IR$有$F(x^\ast ,y^\ast )\le F(x,y)$, 则称$(x^\ast ,y^\ast )$为NBLP模型的最优解.
对任意$x\in S(X)$,下层规划模型如式(2):
| ${\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}\left\{ {\begin{array}{l} \mathop {\min }\limits_y f(x,y),{\kern 1pt}{\kern 1pt}{\kern 1pt} \\ \mbox{s.t.}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}g(x,y)\le 0 \\ \end{array}} \right.{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}$ | (2) |
设$(\mathop x\limits^- ,\mathop y\limits^- )$为问题(1)的可行解,对于固定的$\mathop x\limits^- $,由最优性条件可知,下层规划问题等价于求解如下Kuhn-Tucker点问题,如式(3):
| ${\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}\left\{ {\begin{array}{l} \nabla _y f(\mathop x\limits^- ,\mathop y\limits^- )+\lambda ^{\rm T}\nabla _y g(\mathop x\limits^- ,\mathop y\limits^- )=0 \\ \lambda ^{\rm T}g(\mathop x\limits^- ,\mathop y\limits^- )=0 \\ \lambda \ge 0 \\ \end{array}} \right.{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}$ | (3) |
式(3)可等价变化为式(4):
| $\left\{ {\begin{array}{l} \mathop {\min }\limits_\lambda \| {\nabla _y f(\mathop x\limits^- ,\mathop y\limits^- )+\lambda ^{\rm T}\nabla _y g(\mathop x\limits^- ,\mathop y\limits^- )} \|^2+\| {\lambda ^{\rm T}g(\mathop x\limits^- ,\mathop y\limits^- )} \|^2 \\ \mbox{s.t.}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}\lambda \ge 0 \\ \end{array}} \right.{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}$ | (4) |
因此,若问题(1)存在可行解$(\mathop x\limits^- ,\mathop y\limits^- )$,则问题(4)存在最优解,且最优值为0. 换言之,可通过式(4)判定$(\mathop x\limits^- ,\mathop y\limits^- )$是否为NBLP的可行解,并定义$(\mathop x\limits^- ,\mathop y\limits^- )\in S$的可行性度量.
定义3 可行性度量. 令$w(x,y)=\min\limits_{\lambda \ge 0} \| {\nabla _y f(x,y)+} $${\lambda ^{\rm T}\nabla _y g(x,y)} \|^2+\| {\lambda ^{\rm T}g(x,y)} \|^2$,则$w(x,y)$为点($x$, $y$)是否为NBLP模型可行解的度量.
显然,$w(x,y)$越小,点$(x,y)$越接近可行域. $(x, y)$是NBLP模型的可行解当且仅当$w(x,y)=0$. 2 求解NBLP问题的混合PSO-VNS算法 2.1 PSO优化算法 2.1.1 基本PSO算法
基本PSO算法的粒子速度和位置更新公式如下:
| $\left\{ {\begin{array}{l} V_i (t+1)=\omega V_i (t)+c_1 \times rand()\times (P_i -X_i (t))+c_2 \times rand()\times (P_g -X_i (t)) \\ X_i (t+1)=X_i (t)+V_i(t+1) \\ \end{array}} \right.$ | (5) |
| $\omega =\omega _{\rm ini} -\frac{(\omega _{\rm ini} -\omega _{\rm end} )}{t_{\max } }\times t{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}(t=1,2,\cdots,t_{\max } )$ | (6) |
PSO优化算法在运行过程中, 粒子群会迅速靠拢当前的群体最优位置, 若该最优位置不是全局最优,算法将很难收敛到全局最优而出现 "早熟收敛"现象. 为克服基本PSO算法在运算后期由于种群多样性的快速丧失而造成的算法 "早熟收敛"问题,对$t$代种群中的粒子加入审敛因子. 审敛因子包括聚类操作和聚合度计算两个方面:
1)聚类操作: 对第$t$代粒子群执行$c$均值聚类算法,产生$c$个聚簇, 计算各聚簇内每个粒子与聚类中心粒子的距离;
2)聚合度判断: 判断第$t$代粒子群的聚合度$s$是否趋近于1. 聚合度$s\in(0,1)$是反映种群多样性的测度,$s$越小种群活性越强; $s$越大则粒子的聚集程度越高; 当$s=1$时,粒子趋于同一性.
定义4 收敛中心. 设种群中某个粒子的位置为$X_i =(x_{i1} ,x_{i2},\cdots,x_{id} )$ $(i=1,2,\cdots,m)$,聚簇$c_{j}$ $(j=1,2,\cdots)$的收敛中心为:
| $X_{c_{j}}=(x_{c_{j},1},x_{c_{j},2},\cdots,x_{c_{j},d})=\bigg(\sum\limits_{i\in c_{j}}x_{i ,1}/m,\sum\limits_{i\in c_{j}}x_{i,2}/m,\cdots,\sum\limits_{i\in c_{j}}x_{i,d}/m\bigg)$ | (7) |
聚簇$c_{j}$内第$i$个粒子与收敛中心$X_{c_{j}}$的距离为:
| $d_{i,c_{j}} =\sqrt {((x_{i1} -x_{c_j ,1} )^2+(x_{i2} -x_{c_j ,2} )^2+\cdots+(x_{id} -x_{c_j ,d} )^2)}$ | (8) |
聚簇$c_{j}$内每个粒子与收敛中心的平均距离为:
| $d_{c_{j{\rm ave}}}=\bigg(\sum\limits_{i\in c_{j}}\sqrt {((x_{i1} -x_{c_j ,1} )^2+(x_{i2} -x_{c_j ,2} )^2+\cdots+(x_{id} -x_{c_j ,d} )^2)}\bigg)\bigg/n_{j}$ | (9) |
定义5 聚合度. 设$t$代中所有粒子的历史最优平均值$avgpi_t ={(\sum_{i=1}^N {F(plbest_i )} _t )}/N$; $t$代中所有粒子的平均值$avg_t ={(\sum_{i=1}^N {F(x_i )} _t )}/N$; 则第$t$代粒子群的聚合度为:
| $s=\min (avgpi_t ,avg_t )/\max (avgpi_t ,avg_t )$ | (10) |
基于收敛距离和聚合度对每个粒子进行判断,若$d_{i,c_{j}} VNS的基本思想是从一个可行解出发,
在求解过程中通过动态地改变邻域结构集来拓展搜索范围,
从而使搜索过程跳出局部最优向全局 最优靠近.
对于函数优化问题:
Drazic等[13]将$\rho (x,y)$定义为:
下面给出VNS算法的详细步骤:
Step 1 初始化. 给出初始解$x$,根据式 (11)
构造邻域结构集$N_{k}(x)(k=1,2,\cdots,k_{\max})$和终止条件$(k=k_{\max})$;
Step 2 随机搜索.
在$x$的第$k$个邻域中随机搜索产生$x_{l}(x_l \in N_k (x))$;
Step 3 局部搜索. 令随机搜索产生的解$x_{l}$作为初始解,
由First/Best策略搜索,获得局部最优解$x_{l}'$;
Step 4 更新. 若局部最优解$x_{l}'$优于当前最优解,
则令$x_l =x_{l}'$,并继续在当前邻域结构内搜索;否则,令$k=k+1$;
Step 5 重构. 通过改变$p$的取值,
选择性的变换邻域结构集$N_{k}(x)$的几何结构,
以得到更好的全局寻优效果.
Step 6 判断是否满足终止条件$k=k_{\max}$. 若满足,
输出全局最优解$x^{\ast}$,算法运行结束; 否则,转Step 2,继续迭代.
可以看出,VNS算法的几个关键环节:
邻域结构集构造、终止条件设定、随机搜索以及局部搜索,所含参数少,
原理简单,时效性强.
一方面邻域结构集的构造和随机搜索保证了解的多样性;
另一方面局部搜索则保证了算法的搜索能力.
Mladenovic[14]已经证明了VNS算法求解连续优化问题的可行性和优越性.
2.3 混合PSO-VNS算法
下面给出混合PSO-VNS算法的详细步骤:
输入 对粒子群进行随机初始化,设置种群规模$N$,
最大迭代次数$t_{\max}$,聚簇个数$c$,邻域结构集个数$k_{\max}$,
迭代计数器$b$,惯性权重$\omega_{\rm ini} $、$\omega _{\rm end} $,
学习因子$c_{1}= c_{2}$.
输出 全局最优$P_{g}$,$F(x,y)$,$f(x,y)$.
工作流程
Step 1 初始化粒子. 随机初始化粒子位置和粒子速度;
Step 2 计算每个粒子的适应度值. 求解式 (4),
若存在可行解,且目标函数为0,则将粒子加入可行解队列,
并令上层目标函数值为粒子的适应度值; 否则,将粒子加入不可行解队列,
$w(x,y)$为粒子的适应度值;
Step 3 聚类操作.
对第$t$代种群中的粒子执行$c$均值聚类算法,产生$c$个聚簇,根据式
(7) 计算每聚簇的收敛中心$Xc_j $,并由式 (8)、(9)
分别计算聚簇内第$i$个粒子与其收敛中心$Xc_j
$的距离$d_{i,c_{j}}$和聚簇内每个粒子与收敛中心的平均距离$d_{c_{j{\rm
ave}}} $;
Step 4 聚合度计算. 根据式 (10)
计算第$t$代中每个粒子的聚合度$s$;
Step 5 审敛判断. 对于粒子$x_{l}$,
若$d_{i,c_{j}} Step 7 根据式 (5) 对粒子的速度和位置进行更新;
Step 8 判断是否满足终止条件. 如果满足,转Step 9; 否则,
转Step 2,继续迭代;
Step 9
输出全局最优$P_{g}$、上层目标函数值$F(x,y)$、下层目标函数值$f(x,y)$,
算法运行结束.
可以看出,求解NBLP问题的混合PSO-VNS算法具有如下优点:
1)现有的求解非线性双层规划的算法大多是给定上层决策变量$x$,
并通过$x$求解下层决策变量$y$,
而本文算法中上层决策变量由PSO算法随机产生,
进而由VNS算法和PSO算法更新粒子;
2)当粒子为不可行解时,用可行度测量$w(x,y)$,作为粒子的适应度值,
迫使不可行粒子向可行粒子靠近;
3)在PSO优化过程中,通过增加审敛因子,判断粒子是否陷入
"早熟收敛'';
4)利用VNS算法的全局搜索能力对已陷入 "早熟收敛''
的粒子进行变邻域搜索,既增加了种群的多样性又避免了PSO算法容易
陷入局部最优的问题,从而最终得到全局最优解.
混合PSO-VNS算法的流程如图 1所示.
本文选取了15个广泛使用的测试问题进行测试 (文献[5]),
其中T8$\sim$T15是上层目标函数为非凸不可微的NBLP问题.
对每个测试函数 独立运行50次,记录以下数据:
1)在50次运行中,所得到的最优解$(x^{*},y^{*})$;
2)上层目标函数$F(x,y)$的最优值、最差值、均值、均方差;
3)下层目标函数$f(x,y)$的最优值、最差值、均值、均方差;
4)适应度函数的平均计算次数 (mean numbers of individuals,
MNI)、平均CPU运行时间 (CPU)
以及算法首次得到最好解时的平均代数($g_{\rm
mean}$)以测试算法收敛速度.
设置种群规模$N=45$,最大迭代次数$t_{\max}=100$,聚簇个数$c=4$,
邻域结构集个数为$k_{\max}=5$,迭代计数器 $b=0$,
惯性权重$\omega_{\rm ini}=0.9$,$\omega _{\rm end} =0.4$,
学习因子$c_{1}=c_{2}=2$.
图 2描绘了问题T01的上层目标函数$F(x,y)$的最优值及均值,
可以看出混合PSO-VNS算法在求解过程 中成功地跳出了局部最优点,
具有较好的全局收敛特性.
为进一步测试算法性能,
本文将混合PSO-VNS算法的测试结果与文献[9]提出的PSO-CST算法、文献[5]提出的NEA算法进行比较,
测试结果对比分析见表 1$\sim$4. 其中,
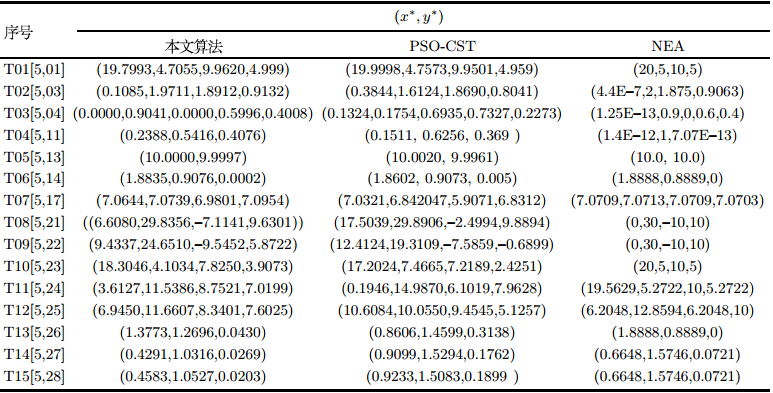
表 1为三种算法的最优解$(x^{*},y^{*})$;
表 2、表 3分别给出了上层目标函数$F(x,y)$及下层目标函数
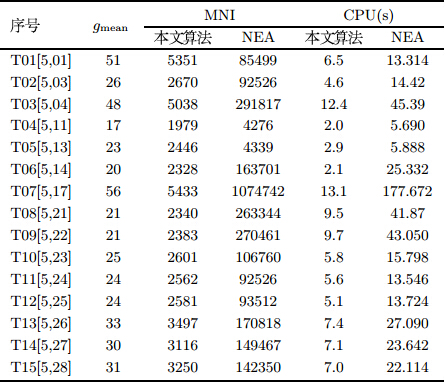
$f(x,y)$的最优值、最差值、均值和均方差; 表 4列出了平均代数$g_{\rm
mean}$、MNI以及平均CPU运行时间.
从表 1$\sim$3可以看出,对于问题T01$\sim$T07,
混合PSO-VNS算法对问题T02、T03、T05的计算结果优于文献中提供的数值,
表明原文献没有找到 相应问题的全局最优解. 而对于问题T06、T07,
从最优解的位置和上下两层目标函数最优值的差值来看,
已经很接近最优解. 对上层目标函数为非凸不可微的NBLP的问题
(T08$\sim$T15),问题T08、T09的上层目标函数值略差于NEA算法的结果,
但下层目标函数值却明显优于NEA算法. 对于其他问题,
混合PSO-VNS算法找到了与NEA算法接近或更优的解,
这说明混合PSO-VNS算法能有效求解含不可微函数的NBLP问题. 另外,
从表 2、表 3可以看出,15个测试问题的均方差都不超过$10^{-6}$数量级,
表明混合PSO-VNS算法是鲁棒的.
表 4给出了在50次运算中,混合PSO-VNS算法所需的平均代数$g_{\rm
mean}$,MNI以及平均CPU时间.不难看出,
与文献[5]所提出的NEA算法相比较,混合PSO-VNS算法所需要的$g_{\rm
mean}$、MNI以及平均CPU时间较少.
本文为解决NBLP问题容易陷入局部最优的问题,
结合PSO算法快速搜索以及VNS算法全局搜索的能力,
提出了求解NBLP问题的混合智能算法
--- PSO-VNS. 一方面通过审敛因子判断陷入局部最优的粒子; 另一方面利用VNS算法的全局搜索能力对已陷入"早熟收敛''的粒子
进行优化,既增加了种群的多样性又避免了算法陷入局部最优.
15个测试函数的仿真实验对比分析可以看出,混合PSO-VNS在求解NBLP问题
的寻优能力及收敛速度都有了显著提高,
不仅能够有效求解上层目标函数为非凸不可微的NBLP问题,
而且可以获得全局最优解,适合于处理工程应用中的NBLP问题. 不同参数
(如:邻域结构集的个数$k_{\max}$和聚合度$s$)
的取值对算法性能的影响是下一步亟待探究的问题.
邻域结构集$N_{k}(x)(k=1,2,\cdots,k_{\max})$定义为:
$global{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}\mathop {\min
}\limits_{x\in S} f(x),{\kern 1pt}{\kern 1pt}~~~~~~S\subset R^n,$
其中,$k_{\max}$为邻域结构集的个数; $\rho _k
$是邻域结构集的搜索半径,$\rho _k $随着$k$的增加单调递增,
故邻域结构按照由小到大排序: $\vert N_{1}(x)\vert \le \vert
N_{2}(x)\vert \le \cdots\le \vert N_{k\max}(x)\vert $.
$N_k (x)=\{y\in S\left| {\rho _{k-1} \le \rho (x,y)} \right.\le \rho _k \}$
(11)
其中,通常选取$p=1,2,\infty$,$p$的选取将决定邻域集的几何结构. 若当前几何结构无法获得全局最优解,则可通过改变$p$的值
以得到新的邻域结构集.
$\left\{ {\begin{array}{l}
{\displaystyle \mathop {\rho(x,y)=\bigg(\sum\limits_{i=1}^n |x_{i}-y_{i}|^{p}\bigg)^{1/p}},~~~~1\leq p<\infty }\\
{\displaystyle \mathop {\rho(x,y)=\max \limits_{1\le i\le n} |x_{i}-y_{i}|},~~~~~~~~~~~~~p=\infty} \\
\end{array}} \right.$
(12)
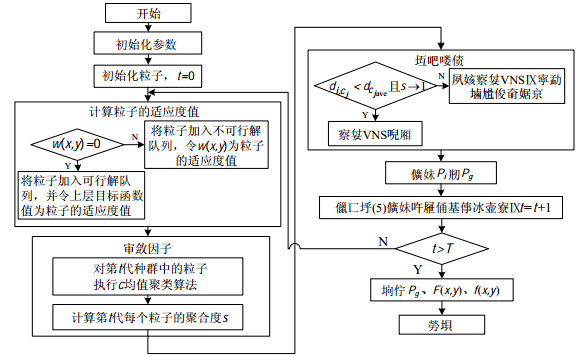
图 1 混合PSO-VNS算法流程图 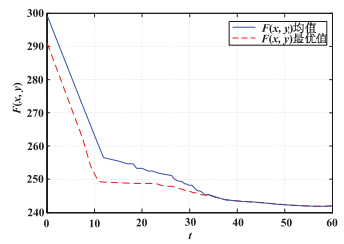
图 2 T01-$F(x,y)$的最优值及均值
| [1] | Bard J F. Practical bilevel optimization: Algorithm and applications[M]. The Netherlands: Kluwer Academic Publishers, 1998: 193-386. |
| [2] | 许项东, 程琳. 城市道路单行系统布局优化的双层规划模型和混合算法[J]. 系统工程理论与实践, 2009, 29(10): 180-187.Xu Xiangdong, Cheng Lin. Bilevel programming model and hybrid solution algorithm for the configuration of one-way streets[J]. Systems Engineering —— Theory & Practice, 2009, 29(10): 180-187. |
| [3] | Vicente L, Savard G, Judice J. Decent approaches for quadratic bilevel programming[J]. Journal of Optimization Theory and Applications, 1994, 81: 379-399. |
| [4] | Mathieu R. Genetic algorithm based approach to bilevel linear programming[J]. Operations Research, 1994, 28(1): 1-21. |
| [5] | Wang Y P, Jiao Y C, Li H. An evolutionary algorithm for solving nonlinear bilevel programming based on a new constraint-handing scheme[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C, 2005, 35(2): 221-232. |
| [6] | Yaakob S B, Watada J. Double-layered hybrid neural network approach for solving mixed integer quadratic bilevel problems[J]. Integrated Uncertainty Management and Applications, 2010, 68: 221-230. |
| [7] | Küςükaydin H, Aras N, Altinel I K. A hybrid tabu search heuristic for a bilevel competitive facility location model[J]. Hybrid Metaheuristics, 2010, 6373: 31-45. |
| [8] | Sakawa M, Katagiri H, Matsui T. Stackelberg solutions for fuzzy random two-level linear programming through probability maximization with possibility[J]. Fuzzy Sets and Systems, 2012, 188(1): 45-57. |
| [9] | Wan Z P, Wang G M, Sun B. A hybrid intelligent algorithm by combining particle swarm optimization with chaos searching technique for solving nonlinear bilevel programming problems[J]. Swarm and Evolutionary Computation, 2013, 8: 26-32. |
| [10] | Kennedy J, Eberhart R. Particle swarm optimization[C]// Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, Piscataway, 1995: 1942-1948. |
| [11] | 刘衍民, 隋常玲, 赵庆祯. 基于K-均值聚类的动态多种群粒子群算法及其应用[J]. 控制与决策, 2011, 26(7): 1019-1025.Liu Yanmin, Sui Changling, Zhao Qingzhen. Dynamic multi-swarm particle swarm optimizer based on K-means clustering and its application[J]. Control and Decision, 2011, 26(7): 1019-1025. |
| [12] | Marinakis Y, Iordanidou G R, Marinaki M. Particle swarm optimization for the vehicle routing problem with stochastic demands[J]. Applied Soft Computing, 2013, 13: 1693-1704. |
| [13] | Drazic M, Lavor C, Maculan N, et al. A continuous variable neighborhood search heuristic for finding the three-dimensional structure of a molecule[J]. European Journal of Operational Research, 2008, 185: 1265-1273. |
| [14] | Mladenovic N, Drazic M, Kovacevic-Vujcic V, et al. General variable neighborhood search for the continuous optimization[J]. European Journal of Operational Research, 2008, 191(3): 753-770. |
| [15] | Chen Y Y, Cheng C Y, Wang L C. A hybrid approach based on the variable neighborhood search and particle swarm optimization for parallel machine scheduling problems —— A case study for solar cell industry[J]. International Journal of Production Economics, 2013, 141: 66-78. |
| [16] | Hansen P, Mladenovic N. Variable neighborhood search[J]. Computers and Operations Research, 1997, 24(11): 1097-1100. |