2. 上海交通大学 中美物流研究院, 上海 200030
2. Sino-US Global Logistics Institute, Shanghai Jiaotong University, Shanghai 200030, China
0 引言
谣言是人类社会交往过程中形成的一种典型的社会现象, 它对人类的日常生活有着重大的影响[1]. 随着信息技术的发展和新型网络媒体的出现,谣言的影响日益增强. 当面临重大灾难事件时,比如最近发生的四川雅安地震, 我们可以通过微博等多种媒介快速传递灾情, 从而更好更快地采取救援措施. 这正是充分利用了社交网络传播速度快的特点, 但也有人利用社交网络或媒体的这种特点散播谣言, 造成群众恐慌甚至影响社会稳定. 因此, 如何更好地增加其正面影响并减少其负面影响成为了政府有关部门极为关心的问题, 学术界对谣言传播的研究也越来越多.
谣言传播的模型研究始于19 世纪60 年代,Daley等最早提出了DK 模型[2]. 在此模型中,人群被分为三类: 不知道谣言的人(无知者), 知道并传播谣言的人(传播者),知道但不传播谣言的人(免疫者). 随着对谣言传播的深入研究,Maki等在DK 模型的基础上提出了MT 模型[3],其中有一个假设: 当传播者与另一个传播者接触时, 只有该传播者转变为免疫者. 此后, 很多学者在这两种模型的基础上继续对谣言传播的规律进行研究[4, 5, 6]. 但是这两种模型没有考虑到网络的拓扑结构, 对大规模社会网络中的谣言传播并不适用, 因此之后陆续有学者展开了对网络拓扑结构的研究[7, 8, 9]. Zanette[10, 11] 在小世界网络中研究了谣言传播模型并发现了谣言传播存在的阈值. Moreno 等[12] 在无标度网络中研究了谣言传播的动力学机制.
在DK 和MT 模型中,传播者转变为免疫者只有一种途径, 即通过与其他传播者或免疫者的接触. 但在实际生活中, 传播者可能会自己忘记谣言或者因对其失去兴趣而不再传播, 从而转变为免疫者. Nekovee 等[13] 将遗忘机制加入到SIR(传播者- 无知者-免疫者) 模型中, 并通过建立平均场方程来分析谣言传播在不同网络中的阈值存在情况. 赵来军等[14, 15] 在基于遗忘率的基础上对谣言传播进行研究, 在社交网络LiveJournal 上的仿真得出了遗忘机制在谣言传播过程中起到重要作用的结论, 同时根据对遗忘记忆机制的研究提出一种新的SIHR 谣言传播模型. 王筱莉等[16] 在社会网络中研究了考虑怀疑机制的谣言传播模型, 根据怀疑机制理论把人群分为无知者、传谣者、反驳谣言者和移出者四类. Zhao 等[17] 在BBV 加权网络中研究了谣言传播的动态特征, 并给出了与点强度有关的谣言传播的平均场方程, 同时还推导出了与点强度有关的谣言传播的阈值.
以上各模型都对谣言传播的研究作出了重大贡献, 但这些模型均未将遗忘率作为变量来考虑. 在现实生活中, 人在得知谣言后, 其忘记该谣言或因失去兴趣而不再传播该谣言的可能性(即遗忘率) 并非固定不变,而会随着时间的推移而增大. 因此, 遗忘率是一个随时间变化的函数,而非常量. 随着对谣言研究的不断深入,遗忘率是随时间变化的函数也被考虑到了谣言传播模型中. Wei 和Gu 等人[18, 19] 在SI(知道信息-不知道信息) 模型中加入了遗忘机制和记忆机制,采用线 性和指数两种函数形式来描述遗忘记忆机制,并在BA 无标度网络中通过数值仿真方法来分析遗忘记忆机制 对信息传播的影响,得出遗忘记忆机制能导致谣言传播终止的结论. 但在此模型中,人群只被划分为两种 状态,即知道信息和不知道信息两种. Zhao 等人[20] 把人群划分为三种状态(无知者、传播者和免疫 者),在均匀网络中研究了考虑遗忘率变化的谣言传播模型, 但在其中没有考虑当传播者遇到其他传播者转变为免疫者的概率与当传播者遇到免疫者转变为免疫者的概率的差异性. 因此本文考虑传播者遇到其他传播者转变为免疫者的概率与传播者遇到免疫者转变为免疫者的 概率的差异性,在无标度网络中研究了遗忘率变化的谣言传播模型,并得到在无标度网络中谣言 传播模型的平均场方程,同时在社交网络人人网中数值模拟谣言传播过程来分析遗忘率参数对谣言传 播过程和最终规模的影响,并分别与遗忘率为常量、均匀网络环境下的谣言传播过程进行了对比分析. 1 遗忘率变化的谣言传播模型
随着复杂网络研究的不断深入,大量研究表明许多实际网络的度分布可以用幂律形式$P(k)\propto k^{-\xi}$ 来更好地描述. 由于这类网络的节点的度没有明显的特征长度, 故称为无标度网络. 度分布具有适当幂指数(通常为$2\leq\xi\leq3$) 的幂律形式的大多数无标度网络具有很强 的异质性,各节点间连接的不均匀性很大即 少数称为Hub 点的节点拥有大量的连接,而大部分节点所拥有的连接却很少. 也就是说,这些Hub 点对无标度网络的运行起着主导的作用. 在现实中,大部分社交网络如 Internet、WWW 等都具有无标度网络的特征. 特别是Fu 等人的研究[21] 表明人人网是一种度分布服从幂律分布,度系数$\xi=2.21$ 的无标度网络. 在无标度网络中研究谣言传播更符合实际情况, 所以本文在无标度网络中研究了遗忘率变化的谣言传播模型,并在人人网为案例的无标度网络中数值模拟了谣言传播的动态过程. 文中假设存在一个由$N$ 个人组成的无标度网络,顶点表示网络中的个体, 边表示个体之间的直接连接关系. 并将该网络视为无向网络$G=(V,E)$, 其中$V$ 为所有顶点的集合,$E$ 为所有边的集合.
谣言传播的具体过程如图 1 所示,网络中的人群被分为无知者$I$, 传播者$S$ 和免疫者$R$ 三类. 谣言传播的规则如下: 1. 当无知者与传播者接触时,无知者以$\lambda$ 的概率转化为传播者; 2. 当传播者与其他传播者接触时,该传播者以$\eta$ 的概率转化为免疫者; 3. 当传播者与免疫者接触时,该传播者以$\gamma$ 的概率转化为免疫者; 4. 传播者以$\delta(\tau)$ 的概率自己忘记谣言或因对其失去兴趣而不再传播,从而转变为免疫者. 其中,$\tau$ 表示该传播者从知道谣言到此时刻所经历的时间长度. 在各时刻开始,传播者首先遵循规则2、3 转化成免疫者,否则遵循规则4. 为区分这两种途径的先后顺序,更好地解释谣言传播过程, 引入了一种中间状态------传播者$S'$(见图 1). 传播者$S'$ 依旧属于传播者, 只是在该时刻内没有因遇到其他传播者或免疫者而转化为免疫者. 在每时刻末,此中间状态将不再存在,而是继续回到传播者$S$ 的状态或遵循规则4 转化成为免疫者$R$.
 |
| 图 1 遗忘率变化的谣言传播过程结构 |
此模型中,$I(t)$ 表示$t$ 时刻网络中的无知者密度,$S(t)$ 表示$t$ 时刻网络中的传播者密度,$R(t)$ 表示$t$ 时刻网络中的免疫者密度. 同时,$I_k(t)$ 表示$t$ 时刻网络中度为$k$ 的无知者密度,$S_k(t)$ 表示$t$ 时刻网络中度为$k$ 的传播者密度,$R_k(t)$ 表示$t$ 时刻网络中度为$k$ 的免疫者密度. 因此可得, $I(t)=\sum\limits_kI_k(t)P(k)$,$S(t)=\sum\limits_kS_k(t)P(k)$ 和$R(t)=\sum\limits_kR_k(t)P(k)$,其中$P(k)$ 表示网络中节点的度分布函数. 同时, 由于网络中只存在此三种状态的节点,因此三者的密度之和为1, 即满足$I(t)+S(t)+R(t)=1$ 和$S_k(t)+I_k(t)+R_k(t)=1$.
本文采用文献[17]中指数形式的遗忘率函数,具体如下:

本文所取的谣言传播时间节点$t$ 均为整数. 在$t$ 时刻, 网络中的传播者知道谣言的时间点并不相同,有的之前早已知道谣言, 有的才刚得知,亦即,$t$ 时刻网络中存在的传播者知道谣言的时间长短各不相同,从而使其在$t$ 时刻的遗忘率也不相同. 因此,需要根据不同的遗忘率对$t$ 时刻网络中的所有传播者进行分类. 本文中,用$t-\tau$ 表示一个传播者由无知者转化而来的时间点,$\tau$ 即代表传播者知道谣言的时长,其遗忘率为$\delta(\tau)$. $S_{k\tau}(t-i)$ 表示在$t-i$ 时刻,度为$k$ 的知道谣言后所经历的时长为$\tau$ 的传播者密度, 即此类传播者是在$t-\tau$ 时刻由无知者转化而来,其中$1\leq i\leq \tau$. 另外,$S_{k\tau}'(t-i)$ 表示在$t-i$ 时刻未遇到其他传播者和免疫者,或遇到却未转化为免疫者的度为$k$ 的知道谣言后所经历的时长为$\tau$ 的传播者密度. $S_{k\tau}(t)$ 表示因忘记谣言或失去兴趣而在$t$ 时刻转化为免疫者的度为$k$ 的传播者密度之和. 因此,$t$ 时刻网络中度为$k$ 的传播者具体分类如下: 1) $\tau=1$: 在$t-1$ 时刻转化而来的度为$k$ 的传播者. 其密度为:
| $S_{k1}(t-1)=I_k(t-2)-I_k(t-1)$ | (2) |
此类传播者遇到其它传播者或免疫者而在$t$ 时刻转化为免疫者的概率为$k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)$. 其中,$P(k'/k)$ 表示度为$k$ 的节点与度为$k'$ 的节点相连的条件概率, $\sum\limits_{k'}S_{k'}(t-1)P(k'/k)$ 表示度为$k$ 的节点在$t-1$ 时刻与传播者相连的概率. $\sum\limits_{k'}R_{k'}(t-1)P(k'/k)$ 表示度为$k$ 的节点在$t-1$ 时刻与免疫者相连的概率. 由此可知, 因此转化为免疫者的传播者密度为:
| $S_{k1}'(t-1)=S_{k1}(t-1)\cdot\bigg[k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg]$ | (3) |
这些传播者在$t$ 时刻因忘记谣言或失去兴趣而转化为免疫者的密度为:
| $S_{k1}(t)=S_{k1}'(t-1)\cdot\delta(1)$ | (4) |
因此可得:
| $S_{k1}(t)=[I_k(t-2)-I_k(t-1)]\cdot\bigg[k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg]\cdot\delta(1)$ | (5) |
2) $\tau=2$: 在$t-2$ 时刻转化而来的度为$k$ 的传播者密度为:
| $S_{k2}(t-2)=I_k(t-3)-I_k(t-2)$ | (6) |
此类传播者遇到其它传播者或免疫者而在$t-1$时刻转化为免疫者的概率为$k\eta\sum\limits_{k'}S_{k'}(t-2)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-2)P(k'/k)$. 由此可知,未因此转化为免疫者的传播者密度为:
| $S_{k2}'(t-2)=S_{k2}(t-2)\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-2)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-2)P(k'/k)\bigg)\bigg]$ | (7) |
这些传播者在$t-1$ 时刻不因遗忘机制转化为免疫者的密度为:
| $S_{k2}(t-1)=S_{k2}'(t-2)\cdot(1-\delta(1))$ | (8) |
同时,这些传播者不因遇到其它传播者或免疫者而在$t$ 时刻转化为免疫者的密度为:
| $S_{k2}'(t-1)=S_{k2}(t-1)\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg)\bigg]$ | (9) |
因此可得这些传播者在$t$ 时刻由于遗忘机制而转化为免疫者的密度变化为:
| $S_{k2}(t)=S_{k2}'(t-1)\cdot\delta(2)$ | (10) |
| $\begin{aligned} S_{k2}(t)= &[I_k(t-3)-I_k(t-2)]\cdot\bigg[1- \bigg(k\eta \sum\limits_{k'}S_{k'}(t-2)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-2)P(k'/k)\bigg)\bigg]\cdot(1-\delta(1)) \\ \\ &\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg)\bigg]\cdot\delta(2)\\ \end{aligned}$ | (11) |
3) 同理可得$\tau=3,4,\cdots,t-1$ 时度为$k$ 的传播者密度变化.
4) $\tau=t$: 初始时刻的度为$k$ 的传播者密度,即$S_k(0)$. 其由于遗忘机制在$t$ 时刻转化为免疫者的密度变化可由以下公式获得:
| $S_{kt}(0)=S_k(0)$ | (12) |
| $S_{kt}'(0)=S_{kt}(0)\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(0)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(0)P(k'/k)\bigg)\bigg]$ | (13) |
| $S_{kt}(1)=S_{kt}'(0)\cdot(1-\delta(1))$ | (14) |
| $S_{kt}'(1)=S_{kt}(1)\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(1)P(k'/k)\bigg)\bigg]$ | (15) |
| $S_{kt}(2)=S_{kt}'(1)\cdot(1-\delta(2))$ | (16) |
| $S_{kt}'(2)=S_{kt}(2)\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(2)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(2)P(k'/k)\bigg)\bigg]$ | (17) |
| $$\cdot\cdot\cdot$$ |
| $S_{kt}(t-1)=S_{kt}'(t-2)\cdot(1-\delta(t-1))$ | (18) |
| $S_{kt}'(t-1)=S_{kt}(t-1)\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg)\bigg]$ | (19) |
| $S_{kt}(t)=S_{kt}'(t-1)\cdot\delta(t)$ | (20) |
即:
| $\begin{aligned} S_{kt}(t)=&S_k(0)\cdot\bigg[1-\bigg(k\eta\sum\limits_{k'}S_{k'}(0)P(k'/k)+k\gamma\sum\limits_{k'}R_{k'}(0)P(k'/k) \bigg)\bigg](1-\delta(1))\\ &\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(1)P(k'/k)\bigg)\bigg]\\ &\cdot(1-\delta(2))\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(2)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(2)P(k'/k) \bigg)\bigg]\cdot\cdot\cdot(1-\delta(t-1))\\ &\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg)\bigg]\cdot\delta(t) \end{aligned}$ | (21) |
度为$k$ 的传播者由于遗忘机制在$t$ 时刻转化为免疫者的密度$S_{k\delta}(t)=\sum_{\tau=1}^{t}S_{k\tau}(t)$, 由以上各分类可知:
| $\begin{aligned} S_{k\delta}(t)=&\sum\limits_{\tau=2}^{t-1}\bigg\{[I_k(t-\tau-1)-I_k(t-\tau)]\prod\limits_{n=1}^{\tau}\bigg[1-\bigg(k\eta\sum\limits_{k'}S_{k'}(t-n)P(k'/k)\\ &+k\gamma \sum\limits_{k'}R_{k'}(t-n)P(k'/k)\bigg)\bigg]\cdot\prod\limits_{n=1}^{\tau-1}[1-\delta(n)]\cdot\delta(\tau)\bigg\}+[I_k(t-2)-I_k(t-1)]\\ &\cdot\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg)\bigg]\cdot\delta(1)\\ &+S_k(0)\cdot\prod\limits_{n=1}^{t}\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-n)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-n)P(k'/k)\bigg)\bigg]\cdot\prod\limits_{n=1}^{t-1}[1-\delta(n)]\cdot\delta(t) \end{aligned}$ | (22) |
因此可得无标度网络中的平均场方程如下:
| $\frac{\mathrm{d}I_k(t)}{\mathrm{d}t}=-\lambda kI_k(t)\sum\limits_{k'}S_{k'}(t)P(k'/k)$ | (23) |
| $\begin{aligned} &\frac{\mathrm{d}S_k(t)}{\mathrm{d}t}\\ =&\lambda kI_k(t)\sum\limits_{k'}S_{k'}(t)P(k'/k)-k\eta \sum\limits_{k'}S_{k'}(t)P(k'/k)-k\gamma \sum\limits_{k'}R_{k'}(t)P(k'/k)\\ &-\sum\limits_{\tau=2}^{t-1}\bigg\{[I_k(t-\tau-1)-I_k(t-\tau)] \prod\limits_{n=1}^{\tau}\bigg[1-\bigg(k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-1) P(k'/k)\bigg)\bigg]\\ &\cdot\prod\limits_{n=1}^{\tau-1}[1-\delta(n)]\cdot\delta(\tau)\bigg\}-[I_k(t-2)-I_k(t-1)] \bigg[1-\bigg(\eta \sum\limits_{k'}S_{k'}(t-1)+\gamma \sum\limits_{k'}R_{k'}(t-1)\bigg)kP(k'/k)\bigg]\cdot\delta(1)\\ &-S_k(0)\cdot\prod\limits_{n=1}^{t}\bigg[1-\bigg(\eta \sum\limits_{k'}S_{k'}(t-n)+\gamma \sum\limits_{k'}R_{k'}(t-n)\bigg)kP(k'/k)\bigg]\cdot\prod\limits_{n=1}^{t-1}[1-\delta(n)]\cdot\delta(t) \end{aligned}$ | (24) |
| $\begin{aligned} \frac{\mathrm{d}R(t)}{\mathrm{d}t}=&k\eta \sum\limits_{k'}S_{k'}(t)P(k'/k)+k\gamma\sum\limits_{k'}R_{k'}(t)P(k'/k) +\sum\limits_{\tau=2}^{t-1}\bigg\{[I_k(t-\tau-1)-I_k(t-\tau)]\\ &\cdot\prod\limits_{n=1}^{\tau}\bigg[1-k\eta \sum\limits_{k'}S_{k'}(t-n)P(k'/k)-k\gamma \sum\limits_{k'}R_{k'}(t-n)P(k'/k) \bigg]\\ &\cdot\prod\limits_{n=1}^{\tau-1}[1-\delta(n)]\cdot\delta(\tau)\bigg\}+[I_k(t-2)-I_k(t-1)]\\ &\cdot\bigg[1-k\eta \sum\limits_{k'}S_{k'}(t-1)P(k'/k)-k\gamma \sum\limits_{k'}R_{k'}(t-1)P(k'/k)\bigg]\cdot\delta(1)\\ &+S_k(0)\cdot\prod\limits_{n=1}^{t}\bigg[1-k\eta\sum\limits_{k'}S_{k'}(t-n)P(k'/k)+k\gamma \sum\limits_{k'}R_{k'}(t-n)P(k'/k)\bigg]\cdot\prod\limits_{n=1}^{t-1}[1-\delta(n)]\cdot\delta(t) \end{aligned}$ | (25) |
由于此平均场方程中的遗忘率为变量,公式复杂,很难求出其解析解. 因此,本文在以人人网为 案例的无标度网络上进行数值仿真来观察遗忘率函数的参数对谣言传播的影响. 2 数值仿真
人人网成立于2005 年,2011 年在美国纽交所上市, 是我国知名的为用户提供服务的SNS 社交网站. 其注册用户可通过发布状态、日志、相册、音乐视频与其它用户进行资源分享和互动交流. 网站中的注册用户可被视为网络节点, 用户与其好友间的关系可视为节点间的边. 根据Fu 等人的研究[21], 人人网是一种无标度网络,其度分布服从幂律分布,度系数$\xi=2.21$, 平均度$\langle k\rangle=18.74$. 根据人人网2006 年对外的公开资料, 人人网拥有真实注册用户超过2 亿,活跃人数超过3000 万. 只有网络中的活跃用户对谣言传播过程有影响, 因此本文中网络的总个体数选取后者,即$N=30,000,000$.
本文运用Matlab 软件在该社交网络中进行谣言传播过程的数值仿真. 假设在初始时刻,网络中只有一个传播者,其他均为无知者, 然后采用有限差分法求解平均场方程,得出各时刻传播者和免疫者的密度. 另外, 由于选取初始传播者的不同会对网络中传播者和免疫者的密度变化有影响, 为不失一般性,我们选取了30 次度不同的初始传播者, 并对所得结果取平均值.
首先,本文通过改变遗忘率函数的参数来研究传播者的密度变化; 其次, 本文将研究遗忘率函数的参数会如何影响网络中免疫者的数量; 再次, 本文对遗忘率为常量和变量时的谣言传播情况进行对比分析; 另外, 本文还对参数$\eta$ 和参数$\gamma$ 对谣言传播最终规模的影响进行对比分析; 最后, 本文将对比在无标度网络和均匀网络中的谣言传播过程, 研究网络结构对谣言传播的影响.
图 2 表示遗忘率函数的参数变化对网络中传播者密度变化的影响. 从图 2(a) 可看出,当其它参数不变时,$\beta$ 值越小,网络中传播者密度$S(t)$ 达到峰值所需的时间越长,峰值也越高. 同样地,如图 2(b),随$v$ 值的减小,网络中传播者密度$S(t)$ 达到峰值所需的时间增长, 峰值也增大. 这意味着,遗忘率越小,表示谣言的重要性越大, 人们对其兴趣越高,很难忘记谣言成为免疫者, 从而导致谣言传播的时间越久,谣言爆发时的规模也就越大. 从图 2 还可看出,刚开始时,网络中传播者密度$S(t)$ 的增长速度几乎相同. 这表明在谣言传播初期,遗忘率参数大小对谣言传播的影响很小, 直至达到一段时间后,其效果才开始呈现. 从第1节介绍遗忘率函数中得到$v-1$ 代表谣言对传播者而言的吸引程度和影响力,其值越大, 更容易忘记该谣言或失去兴趣而不再传播,而参数$\beta$ 可理解为遗忘率的变化速度,其值越大,遗忘率的变化速度越大, 谣言更容易被忘记或失去兴趣而停止传播,图 2 仿真结果与这些结论相一致. 在网络化时代,信息量剧增, 其中人们所关注的热点信息(谣言) 不断地涌现,使人们对热点信息(谣言) 关注也频繁转变. 而网络中不断出现的热点信息(谣言) 可促进遗忘率变化速度$\beta$ 的增大, 使得在相同条件下人们遗忘率增大. 而新热点不断出现和转变, 也会降低人们对老热点的关注度即相当于提高了$v$ 值,其值越大, 谣言的吸引力越小,个体对谣言产生的兴趣也越小即遗忘率越大. 所以根据图 2 中的结论可以得到政府有关部门可以利用热点信息(谣言) 的不断转变和涌现来增大参数$\beta$ 和$v$ 的值进而降低谣言传播的最终规模.
 |
| 图 2 当$\langle k\rangle=18.74$,$\lambda=0.5$, $\eta=\gamma=0.5$,(a) $v=1.1$ 和(b) $\beta=0.2$ 时, 传播者密度$S(t)$ 随时间$t$ 的变化图 |
本文用$Rs$ 表示谣言传播过程中免疫者密度$R(t)$ 的稳态值. 如图 3 所示, 随着$\beta$ 或$v$ 的增加,$Rs$ 会迅速减少,最后保持不变. 由此可知, $Rs$ 对$\beta$ 和$v$ 的取值很敏感,$\beta$ 和$v$ 的值越大,$Rs$ 越小. 原因如下: 当$\beta$ 增大时,传播者的遗忘速度增加, 更容易转化为免疫者,这将导致网络中谣言无法得到更有效地传播, 从而使最终免疫者的密度减少; 另外,随着$v$ 值的增加, 谣言的重要性减小, 也就意味着谣言更容易被传播者忘记或者失去兴趣而不再传播, 从而使网络中的传播者变少,进而导致免疫者的最终密度减少. 然而,遗忘率函数对谣言传播的影响是有限的. 从图 3(a) 可看出,其它参数固定时, 当$\beta$ 达到2.3 之后, 谣言传播过程中最终的免疫者密度将会稳定在0.445 左右, 而不再继续减小. 也就是说,对于既定的$\lambda$ 和$\alpha$, 遗忘机制的影响效果是有限的,谣言始终会在网络中得到传播.
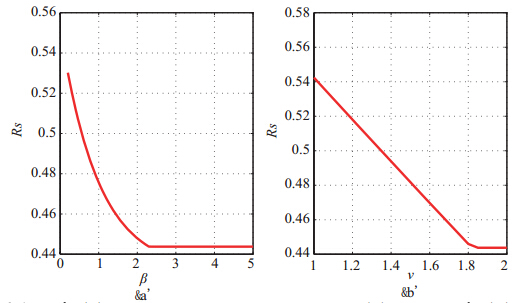 |
| 图 3 当$\langle k\rangle=18.74$,$\lambda=0.5$, $\eta=\gamma=0.5$,(a) $v=1.1$ 和(b) $\beta=0.2$ 时,$Rs$ 随$v$ 的变化图 |
其次, 本文将遗忘率为常数与遗忘率为变量两种情况下的谣言传播过程进行对比分析. 当$v=1.5$,$\beta=0.5$ 时,为使对比更有意义, 选取遗忘率函数的算术平均值 $[\int _0 ^{\frac{-{\rm ln}(v-1)}{\beta}} (v-{\rm e}^{-\beta\tau}) {\rm d}\tau)]/\frac{-{\rm ln}(v-1)}{\beta}=0.75$ 作为遗忘率常数. 由图 4 可知,与遗忘率为常数的情况相比,遗忘率为变量下的谣言传播峰值更低, 谣言传播达到稳态时网络中的免疫者密度也更小. 在谣言传播初期, 变量情况下的遗忘率比常量小,但对谣言传播的影响很小, 两种情况下的传播者密度变化相似. 经过一定时间后, 遗忘率函数的值越来越大,超过其算术平均值, 而此时遗忘率的效果也开始呈现出来, 从而使得其传播峰值比常量情况下的值小,这正好与图 2 相符合.
 |
| 图 4 当$\langle k\rangle=18.74$,$\lambda=0.5$, $\eta=\gamma=0.5$ 时,遗忘率为常量和变量两种情况下的$S(t)$ 和$R(t)$ 变化图 |
另外,本文还对比了参数$\eta$ 和$\gamma$ 在不同取值情况下对谣言传播过程的影响. 从图 5 可知, 当其他参数固定时,参数$\gamma$ 或$\eta$ 越大,免疫者密度$R(t)$ 达到稳定状态时的值越小,即当其他参数不变的情况下,增大参数$\gamma$ 或$\eta$ 的值,可以降低谣言传播的最终规模. 从图 5 还可以看出参数$\gamma$ 对谣言传播最终规模的影响更大, 即增大传播者遇到免疫者转变为免疫者的比率$\gamma$ 可以更有效地降低谣言传播的最终规模. 例如在社会网络中可以通过提升免疫者(如专家或学者) 的可信度或增大免疫者的影响力来提高参数$\gamma$ 的值, 降低谣言传播的最终规模.
 |
| 图 5 当$\langle k\rangle=18.74$,$\lambda=0.5$, $v=1.1$,$\beta=0.2$,(a) $\gamma=0.6$ 和(b) $\eta=0.2$ 时, 免疫者密度$R(t)$ 随时间\\ $t$ 的变化图 |
最后,本文基于Zhao 等人[20] 研究成果, 对比了在无标度网络与均匀网络两种网络结构中的谣言传播过程. 其中依旧选取人人网数据作为无标度网络,同时, 假设一个平均度和节点总数都与人人网相同的均匀网络, 以更好地分析网络结构对谣言传播的影响. 从图 6 可以看出, 在网络节点总数和平均度都相同的情况下, 谣言在无标度网络中传播得更快,达到峰值的时间越早, 谣言的最终传播规模也越小. 这是由无标度网络的拓扑结构所决定, 因为无标度网络中有一部分度很大的Hub 节点,与他们相连的个体很多, 这就导致这些Hub 节点很容易得知谣言并将谣言传播给其它无知者, 从而加速了谣言的传播过程. 同理,这些Hub 节点成为传播者或免疫者后, 也更容易使得与其相连的传播者变为免疫者,从而加速了谣言传播的终止, 使得谣言的最终规模更小.
 |
| 图 6 当$\lambda=0.5$,$\eta=\gamma=0.5$,$v=1.1$, $\beta=0.2$ 时,无标度网络和均匀网络中的$S(t)$ 和$R(t)$ 变化图 |
1) 在考虑传播者转化为免疫者不同途径差异和遗忘率变化的基础上, 建立了无标度网络中遗忘率变化的谣言传播模型, 并通过对此谣言传播过程的分析得到了对应的平均场方程.
2) 用有限差分法在社交网络人人网上对谣言传播过程进行了数值模拟. 结果表明: 遗忘率函数中的参数变化对谣言传播的规模有显著影响, 初始遗忘率的增大会导致谣言传播的最终规模减小, 遗忘速度的增大也会导致谣言的影响范围变小; 相同条件下, 当遗忘率为变量时,社交网络中谣言传播的最终规模更小.
3) 数值结果还表明: 传播者遇到免疫者转变为免疫者的比率$\gamma$ 对谣言传播的最终规模影响更大,即增大参数$\gamma$ 的值可以有效地降低谣言传播的最终规模; 网络结构对谣言的传播也有重要影响,与均匀网络相比, 谣言在无标度网络中传播速度更快,最终规模更小.
本文只在无标度网络中研究了考虑遗忘率变化的谣言传播模型, 在加权网络中考虑遗忘率变化的谣言传播模型将是进一步的研究方向.
| [1] | Bhavnani R, Findley M G, Kuklinski J H. Rumor dynamics in ethnic violence[J]. The Journal of Politics, 2009, 71: 876-892. |
| [2] | Daley D J, Kendall D G. Epidemics and rumours[J]. Nature, 1964, 204: 1118. |
| [3] | Maki D, Thomson M. Mathematical models and applications[M]. Prentice-Hall, Engle-wood Cliffs, 1973. |
| [4] | Lefevre C, Picard P. Distribution of the final extent of a rumor process[J]. Journal of Applied Probability, 1994, 31: 244-249. |
| [5] | Pittel B. On a Daley-Kendall model of random rumors[J]. Journal of Applied Probability, 1990, 27: 14-27. |
| [6] | Kawachi K, Seki M, Yoshida H, et al. A rumor transmission model with various contact interactions[J]. Journal of Theoretical Biology, 2008, 253(1): 55-60. |
| [7] | Sudbury A. The proportion of population never hearing a rumour[J]. Journal of Applied Probability, 1985, 22: 443-446. |
| [8] | Chierichetti F, Lattanzi S, Panconesi A. Rumor spreading in social networks[J]. Theoretical Computer Science, 2011, 412: 2602-2610. |
| [9] | Doerr B, Fouz M, Friedrich T. Social networks spread rumors in sublogarithmic time[J]. Electronic Notes in Discrete Mathematics, 2011, 38: 303-308. |
| [10] | Zanette D H. Critical behavior of propagation on small-world networks[J]. Physical Review E, 2001, 64(5): 050901. |
| [11] | Zanette D H. Dynamics of rumor propagation on small-world networks[J]. Physical Review E, 2002, 65(4): 041908. |
| [12] | Moreno Y, Nekovee M, Pacheco A. Dynamics of rumor spreading in complex networks[J]. Physical Review E, 2004, 69(6): 066130. |
| [13] | Nekovee M, Moreno Y, Bianconi G, et al. Theory of rumor spreading in complex social networks[J]. Physica A: Statistical Mechanics and its Applications, 2007, 374(1): 457-470. |
| [14] | Zhao L J, Wang Q, Cheng J J, et al. Rumor spreading model with consideration of forgetting mechanism: A case of online blogging Live Journal[J]. Physica A: Statistical Mechanics and its Applications, 2011, 390(13): 2619-2625. |
| [15] | Zhao L J, Wang J J, Chen Y C, et al. SIHR rumor spreading model in social networks[J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(7): 2444-2453. |
| [16] | 王筱莉, 赵来军. 社会网络中具有怀疑机制的谣言传播模型[J]. 上海理工大学学报, 2012, 34(5): 424-428. Wang Xiaoli, Zhao Laijun. Rumor spreading model with skepticism mechanism in social networks[J]. University of Shanghai for Science and Technology, 2012, 34(5): 424-428. |
| [17] | Zhao L J, Wang X L, Qiu X Y, et al. A model for the spread of rumors in Barrat-Barthelemy-Vespignani networks[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(21): 5542-5551. |
| [18] | Wei L, Jiao G, Xu C. Message spreading and forget-remember mechanism on a scale-free network[J]. Chinese Physics Letters, 2008, 25(6): 2303-2306. |
| [19] | Gu J, Li W, Cai X. The effect of the forget-remember mechanism on spreading[J]. The European Physical Journal B, 2008, 62(2): 247-255. |
| [20] | Zhao L J, Xie W L, Gao O H, et al. A rumor spreading model with variable forgetting rate[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(23): 6144-6154. |
| [21] | Fu F, Chen X J, Liu L H, et al. Social dilemmas in an online social network: The structure and evolution of cooperation[J]. Physics Letters A, 2007, 371(1): 58-64. |


