系统在运行过程中会承担多项任务,这些任务通常具有不同的起止时间,而且各任务对系统的结构和组成也会有所不同,这类系 统称为多阶段任务系统(phased mission system,PMS)[1, 2, 3]. 在航天、军事、医疗、机械制造等领域, 为满足系统的高任务可靠性要求,系统在执行多阶段任务的过程中不仅会设置设备备份,同时也会设置复杂 的任务执行方案备份,设备失效造成一种任务完成方式无法继续,并不意味着系统工作任务一定失败,系统可以通过切换 到其他可执行任务方案,保证系统继续完成相关任务. 对于这些领域的多阶段任务系统来说,如何合理地评估其可靠性水平以及制 定合理的任务执行方案以提高系统的任务可靠性具有重要意义.
很多文献[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]都对多阶段任务系统进行了研究,其可靠性建模与分析方 法大致可分为静态方法与动态方法. 静态方法主要有可靠性框图法[5, 11]和故障树法[12, 13],其优点是简洁直观,缺点是无法正确描述动态系统中各单元之间和阶段间的相关性; 动态方法主要 是基于Markov过程的分析方法,包括各阶段单独建模,[6, 8, 14]和建立统一模型[11, 15],其优点是能够处理动态可修系统,同时能够正确描述阶段内部件之间以及部件跨阶段的 依赖性. 而在上述多阶段任务系统的可靠性研究中,主要是对各阶段具有固定结构的系统进行建模. 实际系统运行过 程中,在各阶段任务执行之初可能会 投入不同数量设备,而设备的这种组合方案常常会在很大程度上决定任务的完成成功率. 文献[1]通过定义任务结构函数 来表示阶段任务成功与部件的关系,研究了在给定备件组合方案下的多阶段任务成功性评估模型, 但是其主要研究目的是确定固定组合方案下备件的携行量. 本文通过研究设备数量确定、组合方案不确定条件下,多阶段系统在各阶段初的设备投入策略,以提高多阶段系统的任务成功率.
1 问题描述及基本假设 1.1 问题描述本文研究的问题可描述为: 由$ N$类设备组成且各类设备数量分别为${\xi _i}(i = 1,2,\cdots,N)$的系统,执行$ K$项不同起止时间的任务,研究该类系统的任务可靠性问题及不同阶段初的设备投入策略问题. 其中,任务的执行标准为: 各项任务单独执行时对各类设备具有不同的数量要求,当多项任务同时执行时,可通过不同数量的设备组合方式同 时单独完成各项任务,也可通过1个第$ N$类设备的切换动作与某单独执行的任务同时完成. 在系统所有任务执行过程中,各类设备受工时费用的约束不可能参与全部过程.
1.2 基本假设为了便于系统的建模,对本文的多任务系统进行如下假设:
1) 记第$j$种设备的失效率为${\lambda _j}$,各设备失效相互独立,设备寿命服从指数分布;
2) 记第$j$种设备的修复率为${\mu _j}$,维修时间服从指数分布;
3) 系统任务失败定义为系统状态不能满足任务能力要求;
4) 系统中各类可执行任务的设备组合方式可瞬时完成;
5) 设备一旦在阶段初投入使用,其便开始作为工作元件或热备份元件消耗工时.
2 基于任务可靠性的多阶段系统设备投入策略优化模型 2.1 任务阶段划分记${M_k}$为要执行的第$k$项任务($k = 1,2,\cdots,K$),且第$k$项任务的起止时间为$[S{M_k},E{M_k}]$. 记集合${\bf{\Psi}}= \{ S{M_1},S{M_2}, \cdots ,S{M_K},E{M_1},E{M_2}, \cdots ,E{M_K}\} $,定义$\bf{\Psi'}$为集合${\bf{\Psi}} $按时间先后次序排列得到的一个新集合,且将集合中值相等的元素合并. 记${\bf{\Psi'}}(i)$为集合${\bf{\Psi'}}$中的第$i$个 元素,则有${\bf{\Psi'}}(1) < {\bf{\Psi'}}(2) < \cdots < {\bf{\Psi'}}(|{\bf{\Psi'}}|)$, $|{\bf{\Psi'}}|$为集合${\bf{\Psi'}}$元素的个数,则系统的任务阶段数为$M=|{\bf{\Psi'}}|-1$, 第$m$个任务阶段起止时间为$[{\bf{\Psi'}}(m),{\bf{\Psi'}}(m + 1)]$,故第$m$阶段的系统任务时长${t_m}={\bf{\Psi'}}(m + 1)-{\bf{\Psi'}}(m)$. 记${{\bf\vartheta}} _m$为第$m$个任务阶段需要承担的任务集合, $|{{\bf\vartheta }}_m|$为该集合的任务数量,第$l$项任务单独执行时对各设备的数量要求为$({\gamma _{l,1}}(m),{\gamma _{l,2}}(m),\cdots,{\gamma _{l,N}}(m))$. 例如,起止时间为$[0,300]$、$[100,200]$与$[200,400]$的三项任务,按上述方法${\bf{\Psi'}}=\{ 0,100,200,300,400\}$,可划分为4个阶段,且第2阶段包含1, 2两项任务、第三阶段包含1, 3两项任务,第一与第四阶段各包含一项任务.
2.2 系统状态空间系统由$N$类设备构成,各类设备的数量为${\xi _i}(i = 1,2,\cdots,N)$,总的设备数量为$\Im = \sum_{i = 1}^N {{\xi _i}} $. 每个设备分正常及故障两种状态,记时刻$t$系统的状态向量为: ${X(t)} = ({X_1}(t),{X_2}(t),\cdots ,{X_\Im }(t))$,则在一般Markov模型中,该类系统的微观状态空间共$\left| \Omega \right| = {2^\Im }$ 个状态. 记第$m$个任务阶段初可投入运行的第$k$类设备数量为${\ell _k}(m)$,根据问题及假设可知,初始阶段的系统状态可用该时刻各类元件可用数目组合$({\ell _1}(m),{\ell _2}(m),\cdots,{\ell _N}(m))$来描述,对于该任务阶段的$|{\vartheta _m}|$ 项任务,假设此阶段系统的可行运行结构集合为$\Phi $,其对应了系统在该阶段的正常运行状态集合${T_m}$,若$\Omega $ 为系统所有的可行运行结构,那么$\Omega - \Phi $即为系统在该阶段的不可行运行结构集合,对应于该阶段的吸收态集合$T_m^c$,满足以下条件的运行方式即为系统的可运行状态:
| \begin{equation} \label{eq1} {T_m} = \left\{ {\Phi \left| {{\ell _1}(m) \ge \sum\limits_{l = 1}^k {{\gamma _{l,1}}(m)} ,\cdots,{\ell _{N - 1}}(m) \ge \sum\limits_{l = 1}^k {{\gamma _{l,N - 1}}(m)} ,{\ell _N}(m) \ge \left| {{\vartheta _m}} \right| - k} \right.} \right\} \end{equation} | (1) |
第$m$个任务阶段系统状态变化构成的连续马尔可夫链的最小生成元矩阵为
| \begin{equation} \begin{bmatrix} {q_{0,0}^{(m)}} & {q_{0,1}^{(m)}} & \cdots & {q_{0,{Z_m}}^{(m)}} \cr {q_{1,0}^{(m)}} & {q_{1,1}^{(m)}} & \cdots & {q_{1,{Z_m}}^{(m)}} \cr \vdots & \vdots & \cdots & \vdots \cr {q_{{Z_m},1}^{(m)}} & {q_{{Z_m},2}^{(m)}} & \cdots & {q_{{Z_m},{Z_m}}^{(m)}} \cr \end{bmatrix} \end{equation} | (2) |
由上述分析不难得出,第$m$ 个任务阶段系统的最小生成元矩阵系数为

|
$p_{i,j}^{(m)}(t) = P\{ S(t) = j|S(0) = i\} $ 表示第$m$ 个任务阶段,系统从状态$i$ 经过一段长度为$t$ 的时间后转移到状态$j$ 的概率. 记
| \begin{equation} \begin{bmatrix} {p_{1,1}^{(m)}(t)} & {p_{1,2}^{(m)}(t)} & {\cdots} & {p_{1,{Z_m}}^{(m)}(t)} \cr {p_{2,1}^{(m)}(t)} & {p_{2,2}^{(m)}(t)} & {\cdots} & {p_{2,{Z_m}}^{(m)}(t)} \cr \vdots & \vdots & {\cdots} & \vdots \cr {p_{{Z_m},1}^{(m)}(t)} & {p_{{Z_m},2}^{(m)}(t)} & {\cdots} & {p_{{Z_m},{Z_m}}^{(m)}(t)} \cr \end{bmatrix} \end{equation} | (4) |
上式满足Kolmogorov后向方程:
| $\begin{equation} \label{eq2} {{\rm d} \over {{\rm d}t}}{{{P}}_m}\left( t \right) = {{{Q}}_m}{{{P}}_m}(t) \end{equation}$ | (5) |
所以, (5)式的解为
| ${{{P}}_m}(t) = \exp({{{Q}}_m}t)$ | (6) |
第$m$ 任务阶段初始状态概率分布向量与终状态概率分布向量分别为$p_{t0}^{(m)} = [p_{t0,1}^{(m)},p_{t0,2}^{(m)},\cdots,p_{t0,{z_m}}^{(m)}]$ 与$p_{tc}^{(m)} = [p_{tc,1}^{(m)},p_{tc,2}^{(m)},\cdots,p_{tc,{z_m}}^{(m)}]$,其中$p_{t0,i}^{(m)}$ 与$p_{tc,i}^{(m)}$ 分别为第$m$ 个任务阶段初始状态与结束状态为$i$ 的概率. 根据公式(6)的状态转移概率矩阵,有
| $ p_{tc}^{(m)} = p_{t0}^{(m)}\exp({{{Q}}_m}t)$ | (7) |
若第$m + 1$
任务阶段没有新设备投入也没有旧设备退出,那么该阶段系统的初始状态概率向量等于第$m$
阶段的终状态概率向量.
在系统执行各阶段任务的过程中,考虑到运行成本、系统该阶段的任务数量$|{\vartheta
_{m + 1}}|$
以及该阶段具体任务对不同设备的要求,各阶段初各类设备的数量会不同程度的增加或减少.
假设各类设备在第$m + 1$ 阶段初的变化数量为$(\Delta {\ell _1}(m +
1)$,$\Delta {\ell _2}(m + 1)$,$\cdots$,$\Delta {\ell _N}(m +
1))$,用$\varpi $ 表示第$m + 1$ 阶段初系统状态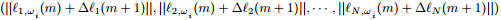 在该阶段状态空间${\Omega _{m + 1}}$ 中对应的编号,这里,
$\left\| x \right\|$ 表示非负函数($\left\| x \right\| = 0,x < 0$),
$\omega $ 表示第$m$ 阶段状态空间${\Omega _m}$
中满足条件的与${\Omega _{m + 1}}$ 中$\varpi $
对应的状态编号集合,由此,下一阶段的初始状态概率$p_{t0,\varpi }^{(m
+ 1)}$ 为
在该阶段状态空间${\Omega _{m + 1}}$ 中对应的编号,这里,
$\left\| x \right\|$ 表示非负函数($\left\| x \right\| = 0,x < 0$),
$\omega $ 表示第$m$ 阶段状态空间${\Omega _m}$
中满足条件的与${\Omega _{m + 1}}$ 中$\varpi $
对应的状态编号集合,由此,下一阶段的初始状态概率$p_{t0,\varpi }^{(m
+ 1)}$ 为
| $p_{t0,\varpi }^{(m + 1)} = \sum\limits_{{\omega _i} \in \omega } {p_{tc,{\omega _i}}^{(m)}}$ | (8) |
将系统开始执行多阶段任务时的初始状态概率向量$p_{t0}^{(1)}$ 代入公式(7)得出第1个任务阶段终状态概率向量$p_{tc}^{(1)}$,然后根据下一阶段新投入使用的设备的数量以及公式(8)得出 第2个任务阶段初始状态概率向量$p_{t0}^{(2)}$,将其代入公式(7)得出第2个任务阶段终状态概率向量$p_{tc}^{(2)}$,通过反 复迭代可以计算出系统任意阶段终状态概率分布,所以,系统第$m$ 个阶段的任务可靠度为
| $M{R^{(m)}} = \sum\limits_{i \in {T_m}} {p_{tc,i}^{(m)}}$ | (9) |
上节给出了系统任务可靠性计算方法,本节以系统任务可靠性为目标、设备投入使用的工时以及可用设备 数量作为约束条件,以各阶段投入使用的设备数量作为决策变量,构建设备投入策略优化模型.
目标函数是要求各阶段初投入设备数量策略集合$Str$ 下的系统任务可靠性最高
| $M{R_{^{\rm opt}}} = {\rm{ \{ }}\max M{R_{Str}}{\rm{| }}Str\}$ | (10) |
约束条件包括:
1)阶段初实际投入的设备数量要保障该阶段系统各种最基本工作模式要求,也即是设备的数量和种类要保证系统可以运行. 这里,$k$ 可为$[0,|{\vartheta _m}|]$ 区间中任意一个正整数,
| $\bigg\{ \ell {'_1}(m) \ge \sum\limits_{l = 1}^k {{\gamma _{l,1}}(m)} ,\cdots{\rm{ ,}}\ell {'_{N - 1}}(m) \ge \sum\limits_{l = 1}^k {{\gamma _{}}_{l,N - 1}(m)} ,\ell {'_N}(m) \ge \left| {{\vartheta _m}} \right| - k\bigg\} ^{Str},m = 1,2,\cdots ,M$ | (11) |
2)为减少系统的运行成本,假设系统的运行费用只由设备的投入运行产生,且设备的运行费用与运行时间成正比,记$W{H_j}$ 为第$j$ 种设备的可用工时.
| $\bigg\{ \sum\limits_{m = 1}^M {\ell {'_j}(m)} (\Psi '(m + 1) - \Psi '(m)) \le W{H_j}\bigg\} ^{Str},j = 1,2,\cdots,N$ | (12) |
遗传算法由于其整体搜索策略和内在的隐含并行性及优化时不依赖梯度信息的特点[16],在处理离散型随机变 量,非线性目标函数的优化问题时,能取得满意的结果,本文采用遗传算法对上述模型进行求解. 算法的基本流程为:
步骤 1 输入数据: 设备可靠性数据、设备数目与工时限制、任务数据及各任务的设备数量要求;
步骤 2 任务阶段划分,确定各阶段的任务数量及可执行任务组合方案;
步骤 3 设置遗传算法基本参数: 种群规模,最大迭代次数,变异概率与交叉概率等,并生成首个任务阶段的初始运行方案;
步骤 4 遗传算法对该阶段的设备投入策略进行交叉与变异操作,其目标是提高系统该阶段的任务可靠性;
步骤 5 确定该阶段末的最优组合方案与下个阶段设备数量要求之间的映射关系(式(8)),对可投入运行的设备数量组合方案进行遗传操作,并检验设备的工时限制要求是否满足;
步骤 6 重复步骤5直至系统的最后一个任务阶段;
步骤 7 计算系统最后一个阶段的可靠性指标,并确定系统在各阶段的设备投入方案.
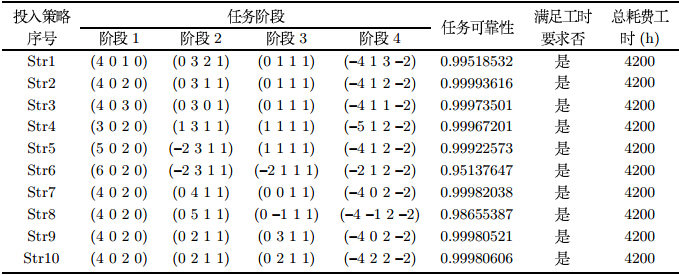
3 算例分析 3.1 系统数据算例由4类设备20个元件组成,各类设备的数量分别为5,6,7, 2个,且其可用工时分别为1200h,1200h,1500h与300h. 系统的初始状态所有设备均完好,4类设备的故障率分别为0.0005 h$^{-1}$、0.0003h$^{-1}$、0.0004 h$^{-1}$与0.0015h$^{-1}$,其平均修复时间分别为20h、15h、12h与10h. 系统用于完成4项不同要求的任务,各项任务对各类设备的数量要求见表 1,其中设备D是系统多任务情形时的切换设备.
根据本文的阶段划分方法,该系统执行的4项任务可划分为4个任务阶段,各阶段的起止时 间、阶段内的任务编号以及该阶段内任务可执行的基本条件见表 2.
遗传算法的种群规模设置为30,最大迭代次数为100,交叉概率为0.9, 变异率为0.05,可靠性计算与优化算法均采用Matlab r2010a编程实现. 满足工时限制条件的几个典型设备投入策略的评估结果见表 3.
由表 3 的结果可以看出,设备投入策略Str2是满足各类设备工时要求下系统四项任务可靠性最高的策略. 就本文算例的实际投入策略来看,第四类设备的最佳的投入策略应为在由2项任务构成的第二阶段以及由3项任务构成的第三阶段 初各投入1个作为多项任务的热备份,并受工时限制在第四阶段初退出使用. 而由于在第四阶段的两项任务中不 需要第一类设备,所以在前三阶段中投入使用的该类设备在第四阶段初应该全部退出使用. 这个分析结果与策略2的优化结果比较相符, 因此,为提高大规模问题的求解效率,在优化算法的设计中,应充分考虑问题本身隐含的初始条件. 图 1给出了该策略下各阶段任务可靠性的详细变化情况,各阶段末的任务可 靠性分别为0.99997341,0.99996004,0.99993921与0.99993616.
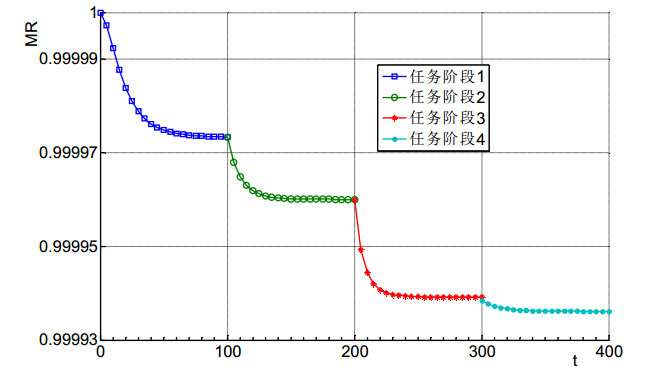 |
| 图 1 系统各阶段任务可靠性 |
由图 1可以看出,系统在给定任务时间内的可靠性并不是连续的,具体原因包括两个方面: 1)在各个阶段初不断有新设备投入使用或者在各个阶段末有旧设备退出使用,导致系统的运行结构有所改变; 2) 各阶段任务数量和种类有所变化,导致其对不同设备的数量要求不同,所以该阶段的可执行任务状态集合发生变化. 另外,还需要看到,系统的任务可靠性,并不能单纯地依靠某个阶段具有较高的可靠性. 这就要求系统在投入或退出设备 时要科学考量,适时适量地投入或退出不同种类的设备.
4 结论多阶段任务系统在执行各阶段任务的过程中不仅会设置设备备份,同时也会设置复杂的任务执行方案备份. 本 文建立了这类多阶段系统的Markov可靠性模型,并构建了以各阶段初的设备投入策略为决策变量,系统的任务可 靠性为优化目标,设备投入工时为约束条件的系统任务可靠性优化模型. 为该类系统的任务可靠性研究提供了理论方 法. 本文在建模时根据各项任务的执行要求,将各阶段的状态空间描述为各类设备的数量组合模式,在较大程度上压缩 了系统的状态空间,但也应该看到,实际系统执行的各项任务对各类设备的要求也许更为复杂,因此,其马尔可夫模型的 构建会更加困难. 另外,本文的设备投入策略优化模型中,约束条件只考虑了各类设备的工时要求,没有考虑更为复杂的 运行成本因素,例如维修、更换、切换费用等. 关于多阶段系统的设备投入策略优化模型有待更进一步的深入研究.
| [1] | 郭波,张涛,张泉,等. 备件组合方案下的多阶段任务成功性评估模型[J].系统工程理论与实践, 2005, 25(2): 94-100.Guo Bo, Zhang Tao, Zhang Quan, et al. Phased-mission availability assessment model for system given limited spares[J]. Systems Engineering —— Theory & Practice, 2005, 25(2): 94-100. |
| [2] | 余建,胡涛,杨春辉. 基于满意度的贮备多阶段任务系统可靠性优化[J]. 北京航空航天大学学报, 2011, 37(3): 374-378.Yu Jian, Hu Tao, Yang Chunhui. Reliability optimization of standby phased mission systems based on desirability function[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(3): 374-378. |
| [3] | 许双伟, 武小悦.高可靠多阶段任务系统可靠性仿真的高效方法[J]. 装备学院学报, 2012, 23(3): 69-74.Xu Shuangwei, Wu Xiaoyue. An efficient reliability simulation method for highly reliable phased mission system[J]. Journal of Academy of Equipment, 2012, 23(3): 69-74. |
| [4] | Burdick G R, Fussell J B, Rasmuson D M, et al. Phased mission analysis: A review of new developments and an application[J]. IEEE Transactions on Reliability, 1977, 26(1): 43-49. |
| [5] | Esary J D, Ziehms H. Reliability analysis of phased missions[C]// Proceedings of the Conference on Reliability and Fault Tree Analysis, Phildelphia, USA: SIAM, 1975: 213-236. |
| [6] | Alam M, Al-Saggaf U M. Quantitative reliability evaluation of repairable phased-mission systems using Markov approach[J]. IEEE Transactions on Reliability, 1986, 35(5): 498-503. |
| [7] | Alam M, Song M, Hester S L, et al. Reliability analysis of phased-mission systems: A practical approach[C]// Proceedings —— Annual Reliability and Maintainability Symposium, Newport Beach, CA, United States: Institute of Electrical and Electronics Engineers Inc, 2006: 551-558. |
| [8] | Kim K, Park K S. Phased-mission system reliability under Markov environment[J]. IEEE Transactions on Reliability, 1994, 43(2): 301-309. |
| [9] | Shrestha A, Xing L, Dai Y. Reliability analysis of multi-state phased-mission systems[C]// Reliability and Maintainability Symposium. Fort Worth, TX, United States: Institute of Electrical and Electronics Engineers Inc, 2009: 151-156. |
| [10] | Wang D, Trivedi K S. Reliability analysis of phased-mission system with independent component repairs[J]. IEEE Transactions on Reliability, 2007, 56(3): 540-551. |
| [11] | Dugan J B. Automated analysis of phased-mission reliability[J]. IEEE Transactions on Reliability, 1991, 40(1): 45-52. |
| [12] | Zang X, Sun H, Trivedi K S. A BDD-based algorithm for reliability analysis of phased-mission systems[J]. IEEE Transactions on Reliability, 1999, 48(1): 50-60. |
| [13] | Xing L, Dugan J B. Analysis of generalized phased-mission system reliability, performance, and sensitivity[J]. IEEE Transactions on Reliability, 2002, 51(2): 199-211. |
| [14] | Somani A K, Ritcey J A, Au S H L. Computationally-efficient phased-mission reliability analysis for systems with variable configurations[J]. IEEE Transactions on Reliability, 1992, 41(4): 504-511. |
| [15] | Boyd M A. Converting fault trees to Markov chains for reliability prediction[D]. Department of Computer Science, Duke University, 1986. |
| [16] | 王小平. 遗传算法:理论应用与软件实现[M]. 西安: 西安交通大学出版社, 2002. |