2. 西安工业大学 经济管理学院, 西安 710032;
3. 机械制造系统工程国家重点实验室, 西安 710049
2. School of Economics and Management, Xi'an Technological University, Xi'an 710032, China;
3. The State Key Lab for Manufacturing Systems Engineering, Xi'an 710049, China
0 引言
在快递揽件服务中,快递车辆从公司出发,沿途根据顾客的需求进行揽件服务,最后将所有揽件返回公 司寄出,快递车辆的目标是以尽可能小的成本服务所有的需求. 当快递车辆已知待收快件的位置和可以 接受服务的时间时,该情形可以用Homing TSP问题刻画. 但是,在实际快递揽件服务中,信息是不对 称的. 与一般TSP问题相比,这一服务过程具有三点特殊性: 第一,快递服务网络具有非对称性. 由于快 递车辆使用的城市交通网络存在单行道和禁行道路,因此两个需求点之间往返的距离不完全相同. 第二,顾 客需求具有在线性. 即快递车辆事先无法获知顾客发快递的需求将在何时,何处出现并且顾客需求是序贯到 来的. 因此,对于新出现的揽件服务需求,快递车辆只能根据当前已知的情形决定下一步行驶方向. 第三,快递车 辆在服务过程中具有一定预知信息. 即当收到顾客需要发快递的服务需求时,快递车辆不一定能立即服务该需 求,但是可以立即获知该需求的位置和可以被服务的时间. 尽管TSP问题的研究成果较多,但是同时考虑上述 三个特征时应该如何建模求解,目前尚未研究. 因此,本文提出非对称网络上的带有预知信息的在 线Homing ATSP问题(online homing asymmetric TSP with advanced information),进而设计在线算 法并分析算法的竞争性能,研究结论将为快递车辆的科学调度提供理论支持.
信息完全时,对于非对称网络上要求车辆返回原点, 并且以服务全部需求的总成本最小为目标的问题,可以用Homing ATSP 来描述. Frieze等最早在满足三角不等式的网络上设计了近似比为$O( {\rm log} n)$的近似算法,[1],后来学者对此 算法略有改进[2, 3], 但该问题是否存在常数近似比的算法仍是开放问题. 以上研究中的需求是事先已知的,未考 虑需求到来的不确定性. 对于需求到来事先无法预知的TSP问题,可以用在线方法进行分析. Ausiello等在2001年最早提 出Online TSP问题, 并且在一般网络上给出2-竞争比的算法,在直线上给出1.75- 竞争比的算法[4]. Lipmann将直 线上的结果改进到1.64, 达到直线上该问题的下界[5]. Blom等进一步将网络限制在非负半轴上,给出1.5-竞争比 的算法[6]. Jaillet等将单服务器情形扩展到$m$-服务器情形, 给出2$\rho$-竞争比的算法[7]. 随着研究的 深入, Jaillet等及Allulli等分别提出, 当在线服务器能够预知未来一段时间内需求到来的情况时,竞争算法的性能 将有所改进并且在对称网络上给出了相应的竞争算法,[8, 9]. 温新刚等研究了考虑预知信息时的在 线Nomadic TSP 问题[10] 及同时考虑预知信息和服务时间约束的在线TSP 问题[11]. 以上的在线TSP 问题的结果全部是在对称网络上 得到的, 仅有Ausiello等研究了非对称网络的情形并在一般网络上给出$\frac{{3 + \sqrt 5 }}{2}$-竞争比的 算法[12],但是未涉及预知信息. 综上, 同时考虑非对称网络和预知信息的在线TSP问题,目前在理论上 需要进一步探讨.
本文提出非对称网络上的带有预知信息的在线Homing ATSP问题. 这里的预知信息是指在需求可以接受服务的时 间(需求释放时间)之前的某一时刻(需求揭露时间), 在线车已经获知该需求的位置和释放时间. 如果需求揭露时 间与需求释放时间相同,则本问题就转化为一般的在线Homing ATSP问题, 因此,本文的研究更具有一般性. 本 文首先给出问题描述和基本定义, 然后在一个特殊网络上证明了该问题竞争比的下界, 进而在一般网络图上设计 了 SS-dd$(\alpha)$算法和 PAH-dd 算法, 分析了算法各自的竞争比,并给出一个算例说明算法在 现实中的可行性, 最后给出结论. 1 问题描述与基本定义
给定一个有向网络$M$,$d$为定义在$ M$上两点间的距离函数且满足$d: {M^2} \to \mathbb{R}_+$. $D = \{ d( \cdot ,\cdot )\} $为$M$ 的距离矩阵. $M$ 满足以下属性: (1) ${D^{\rm T}} ≠D$,即$ M$是非对称的; (2)对于所有的$x,y ∈M$,当且仅当$x=y$ 时, $d(x,y)=0$; (3)对于所有的$x,y,z ∈M$,满足不等式$d(x,y) \leqslant d(x,z) + d(z,y)$. 一系列待服务的需求位于$M$ 上, 将需求$i$ 表示为$(l_i,r_i,q_i)$,$i = 1,2,\cdots ,n$,其中$n$ 为需求的总数量. ${l_i} ∈M$ 为需求$i$ 的位置; ${r_i} \ge 0$ 表示需求$i$ 的释 放时间(release time), 只有到达释放时间的需求才可以接受服务; ${q_i} \ge 0$ 表示需求$i$ 的揭露时间(disclosure time),即被在线车所获知的时间,在此时刻, 在线车知道该需求$i$ 的位置$l_i$ 和可以接受服务的时间$r_i$. 将所有需求的集合记 为$N = \{ 1,2,\cdots ,n\} $,则对于$\forall i \in N$,有${r_i} \ge {q_i} \ge 0$,在本文中,假 设${q_i} = {({r_i} - a)^ + }$,即在线车有固定的预知信息,对于在线车来说, 需求是逐渐被揭露的且每一个需求所 需要的服务时间为0, 即经过该需求就视为服务完成. 0 时刻时,在线车位于起点$o$, 其目标是以尽可能小的成本服 务所有的需求并返回起点, 此处的成本为在线车花费的总服务时间.
用$C_{\rm online}^A$表示在线算法$A$服务$n$个需求的总成本, 用$C_{\rm opt}$表示相应的最优离线成本. 如果 对于任意的$n$, 存在常量$\rho$和$ \gamma$使得$C_{\rm online}^A \le \rho {C_{\rm opt}} + \gamma $,那么 则称策略$A$ 具有大小为$\rho$的竞争比[13]. 2 带有预知信息的在线Homing ATSP问题的下界
定理1 对于带有预知信息的在线ATSP问题,如果$\rho$为任一确定 性在线算法的竞争比,则$\rho \ge {c^*}$,其中,${c^*} = \left\{ {\begin{array}{*{20}{c}} {1 + \phi } \\ {\frac{1}{2} + \frac{{\sqrt {{{(a + 1)}^2} + 4} }}{{2(a + 1)}} + \frac{1}{{a + 1}}} \\ \end{array}} \right.\begin{array}{*{20}{c}} {} & {\begin{array}{*{20}{c}} {a = 0} \\ {a > 0} \\ \end{array}} \\ \end{array}$,$\phi = \frac{{1 + \sqrt 5 }}{2}$.
证明 给定任意$\varepsilon > 0$,构造图 1证明定理1,令$\phi $ 为黄金分割比. 在图 1 中有$7+4n$个节点, $n = 1 + \lceil {\frac{{\phi - 1}}{\varepsilon }} \rceil $,除了标记弧长为1 的弧以外,其他弧的长 度均为$\varepsilon$,如果有一条纵轴通过$o$点,这个图相对于该轴是对称的.
不失一般性,我们假定在1时刻之前,没有需求被揭露, 而在线车在该图的左边. 1 时刻时,$A$ 点揭露一个需求,由于具 有预知信息$a$,该需求在$1+a$ 时刻才被释放. 令$t$ 为在线车第一次到达$D$(或$E$)的时间,$T^*$ 为一特定时刻,我们按照 $t$与$T^*$的关系区分两种情形讨论:
情形1 当$t \ge {T^*}$时,离线对手不再揭露其他需求.
先考虑离线车的成本,令离线最优成本为$C_{\rm opt}$. 由于$A$点需求的释放时间为$1+a$,而离线车 从0时刻起就可以出发并于$1 + 2\varepsilon$ 到达$A$ 点,如果$a \le 2\varepsilon $, 则立即可以服 务$A$,服务完$A$的成本为$1 + 2\varepsilon$, 再加上返回起点$o$的时间,则有${C_{\rm opt}} \le 1 + 2\varepsilon + \varepsilon$; 反之,如果$a \ge 2\varepsilon $, 要等待到$1+a$才能服务$A$,则有${C_{\rm opt}} \le 1 + a + \varepsilon$. 因此,${C_{\rm opt}} \le \max \{ 1 + 2\varepsilon ,1 + a\} + \varepsilon$.
 |
| Figure 1">图 1 下界证明用图 |
对于在线车的成本,由于图 1的对称性,假设$t$时刻在线车刚好到达$E$ 点,则其到达$A$ 点的时间为$t + 1 + \varepsilon $. 此时,分两种情况讨论:
情形1.1 $t + 1 + \varepsilon \ge 1 + a$
此时,在线车可以直接服务$A$处需求后返回$o$点,总服务时间为${C_{\rm online}} \ge t + 1 + 2\varepsilon $. 因此,$\frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{t + 1 + 2\varepsilon }}{{\max \{ 1 + 2\varepsilon ,1 + a\} + \varepsilon }}$.
情形1.2 $t + 1 + \varepsilon \le 1 + a$
此情形下,当在线车到达$A$点时,$A$处需求尚未释放,在线车需要在$A$ 点等待到$1+a$ 才能服务$A$ 处需求, 则其服务完$A$处需求的成本为${C_{\rm online}} = 1 + a + \varepsilon \ge t + 1 + 2\varepsilon $,因此,$\frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{t + 1 + 2\varepsilon }}{{\max \{ 1 + 2\varepsilon ,1 + a\} + \varepsilon }}$.
由情形1的讨论,可得: $$\begin{cases} \frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{t + 1 + 2\varepsilon }}{{1 + 2\varepsilon + \varepsilon }} = t + 1 & a \le 2\varepsilon ,\varepsilon \to 0,\\ \frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{t + 1 + 2\varepsilon }}{{1 + a + \varepsilon }} = \frac{{t + 1}}{{1 + a}} & a \ge 2\varepsilon ,\varepsilon \to 0 . \\ \end{cases} $$
情形2 当$t \in [1,{T^*}]$ 时,由于图 1的对称性, 假设$t$时刻在线车刚好到达$E$点,此时,离线对手在$t$时刻于$B_i$ 处揭露一个需求,$i = \lceil {\frac{{t - 1}}{\varepsilon }} \rceil $.
情形2下,离线车先服务$B_i$再服务$A$. 对于离线车来说, 从0时刻出发到$B_i$最多需要$t + 2\varepsilon $,如果$a \le 2\varepsilon $,则可以立即服务$B_i$,其成本为$t + 2\varepsilon $; 反之,$B_i$ 处的需求还 未释放,离线车需要等待,则成本为$t + a$. 因此,离线车服务$B_i$处的需求的时间最多 为$\max \left\{ {t + 2\varepsilon ,t + a} \right\}$,然后到达$A$点后立即服务$A$ 点处的需 求并返回$o$点,因此,${C_{\rm opt}} \le \max \left\{ {t + 2\varepsilon ,t + a} \right\} + 2\varepsilon $.
在线车只能先通过$EC$ 服务$A$ 然后返回$o$后才能服务$B_i$. 而在线车到达$A$ 点的时间为$t + 1 + \varepsilon $. 此时,分两种情况讨论:
情形2.1 $t + 1 + \varepsilon \ge 1 + a$
此情形下,在线车可以直接服务$A$处需求,则其返回$o$点的时间为$t + 1 + 2\varepsilon $. 并且于$(t + 1 + 2\varepsilon ) + \varepsilon + 1 + \varepsilon \left\lceil {\frac{{t - 1}} {\varepsilon }} \right\rceil $ 到达$B_i$ 点. 由于$t + 1 + 3\varepsilon + 1 + \varepsilon \left\lceil {\frac{{t - 1}}{\varepsilon }} \right\rceil \ge (t + 1 + \varepsilon ) + (t + 2\varepsilon ) \ge 1 + a + t + 2\varepsilon $,因此,在线车可以立即服务$B_i$, 再考虑在线车返回$o$的时间,则${C_{\rm online}} \ge (t + 1 + \varepsilon ) + (t + 2\varepsilon ) + 2\varepsilon $. 因此,$\frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{(t + 1 + \varepsilon ) + (t + 2\varepsilon ) + 2\varepsilon }}{{\max \{ t + 2\varepsilon ,t + a\} + 2\varepsilon }}$.
情形2.2 $t + 1 + \varepsilon \le 1 + a$
此情形下,在线车服务$A$处需求的时间为$1+a$. 其到达$B_i$点的时间为$1 + a + 2\varepsilon + 1 + \varepsilon \left\lceil {\frac{{t - 1}}{\varepsilon }} \right\rceil \ge t + a + 1 + 2\varepsilon $, 由于$B_i$点需求的释放时间为$t+a$,在线车可以立即服务该需求,再考虑在线车返回$o$的时间,则${C_{\rm online}} \ge t + a + 1 + 4\varepsilon \ge t + (t + 1 + \varepsilon ) + 4\varepsilon $. 因此,$\frac{{{C_{\rm online}}}} {{{C_{\rm opt}}}} \ge \frac{{t + (t + 1 + \varepsilon ) + 4\varepsilon }}{{\max \{ t + 2\varepsilon ,t + a\} + 2\varepsilon }}$.
由情形2的讨论,可得: $$\begin{cases} \frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{(t + 1 + \varepsilon ) + (t + 2\varepsilon ) + 2\varepsilon }} {{t + 2\varepsilon + 2\varepsilon }} = \frac{{2t + 1}}{t} & {a \le 2\varepsilon ,\varepsilon \to 0} ,\\ \frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{t + (t + 1 + \varepsilon ) + 4\varepsilon }}{{t + a + 2\varepsilon }} = \frac{{2t + 1}}{{t + a}} & {a \ge 2\varepsilon ,\varepsilon \to 0}. \\ \end{cases}$$
综上,当$a \le 2\varepsilon $,$t = {T^*} = \phi $时,$\rho \ge \max \min \{ t + 1,2 + \frac{1}{t}\} = 1 + \phi $; 当$a \ge 2\varepsilon $ 时,令$x = \frac{{t + 1}}{{1 + a}}$,$y = \frac{{2t + 1}}{{t + a}}$,如果$\rho $为在线 Homing ATSP 问题任一确定性在线算法的竞争比,则$\rho \ge \max \min \{ x,y\} $, 当$x = y$时,可求 出${T^*} = t = \frac{{(a + 1) + \sqrt {{{(a + 1)}^2} + 4} }}{2}$,则$\rho \ge \frac{1}{2} + \frac{{\sqrt {{{(a + 1)}^2} + 4} }}{{2(a + 1)}} + \frac{1}{{a + 1}}$. 令${c^*} = \frac{1}{2} + \frac{{\sqrt {{{(a + 1)}^2} + 4} }}{{2(a + 1)}} + \frac{1}{{a + 1}}$. 得证.
由定理1可知,没有预知信息($a=0$)时的在线Homing ATSP问题是本文模型的一个特例,此时,达到在线Homing ATSP 问题的下界$1 + \phi $. 3 SS-dd$(\alpha)$算法及其竞争比
SS-dd$(\alpha)$算法} (smartstart with disclosure date) 在线车总是在原点等待一个 特定时刻出发服务所有已经被揭露但是尚未被服务的需求,具体步骤是:
a.定义$S$为截止到$t$时刻出现的所有已经被揭露但是尚未被服务的需求的集合.
b.在线车在起点$o$时的每一时刻$t$,通过算法$A$计算一条能服务$S$中所有未被服务需求的最优路径$T^*(t)$并记录 该路径的长度$|T^*(t)|$. 其中$A$为离线车所采用的不考虑揭露时间、并且服务当前所有尚未被服务需求的算法.
c.在线车在起点$o$等待一个时刻$t'$,当$t' \ge \alpha |{T^*}(t')|$时,在线车立即沿着当前的最 优路径$T^*(t')$服务$S$中的需求,在返回原点之前忽略所有新揭露的需求.
d.当在线车返回起点$o$后,保持静止并继续监视$|T^*(t)|$的值,等待下一次满足出发条件的时刻再继续 服务未被服务需求.
定理2 SS-dd$(\alpha)$算法的竞争比为$C$,其中,$C = (1 + \beta ) + \frac{{(1 - \beta ) + \sqrt {{{(1 - \beta )}^2} + 4(1 - \beta )} }}{2}$,$\beta = \frac{a}{{{C_{\rm opt}}}}$.
证明 令$t$为最后一个需求的揭露时间. 根据最后一个需求被揭露时在线车是否正在起点等待,分为两种情形讨论:
情形1 最后一个需求被揭露时,在线车正在起点等待.
情形1.1 当最后一个需求揭露时,在线车立即于$t$时刻出发.
根据 SS-dd$(\alpha)$算法,由算法$A$得到的最优路径是$T^*(t)$, 令在线车沿$T^*(t)$ 服 务所有需求的成本为$\mathcal{T}$, 则在线车的总成本为$C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} = t + \mathcal{T}$. 由于$\mathcal{T} \le a + |{T^*}(t)|$, $|{T^*}(t)| \le t/\alpha $,可得$C_{\rm online}^{{\rm SS\mbox{-} dd}(\alpha )} \le t + a + |{T^*}(t)| \le (1 + \frac{1}{\alpha })t + a$,而$t + a \le {C_{\rm opt}}$,因此, $C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} \le (1 + \frac{1}{\alpha })({C_{\rm opt}} - a) + a$,由此可知, $\frac{{C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )}}}{{{C_{\rm opt}}}} \le 1 + \frac{1}{\alpha } - \frac{a} {{\alpha {C_{\rm opt}}}}$. 令$\beta = \frac{a}{{{C_{\rm opt}}}}$,则$\frac{{C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )}}}{{{C_{\rm opt}}}} \le 1 + \frac{1}{\alpha } - \frac{\beta }{\alpha }$.
情形1.2 当最后一个需求揭露时, 在线车需要等到特定时刻再出发.
假设在线车等待至$t'(t' > t)$时刻出发. 由于$t$时刻后再没有揭露新的需求,因此由算法$A$得到的最 优路径仍然是$T^*(t)$. 此时,在线车的总成本为$C_{\rm online}^{{\rm SS\mbox{-} dd}(\alpha )} = t' + \mathcal{T}$,而$t' = \alpha |{T^*}(t)|$,$\mathcal{T} \le a + |{T^*}(t)|$,可得$C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} = t' + \mathcal{T} \le \alpha |{T^*}(t)| + a + |{T^*}(t)| = (1 + \alpha )|{T^*}(t)| + a$, 而$|{T^*}(t)| \le {C_{\rm opt}}$,因此,$C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} \le (1 + \alpha ){C_{\rm opt}} + a$, 由此可知,$\frac{{C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )}}}{{{C_{\rm opt}}}} \le 1 + \alpha + \frac{a}{{{C_{\rm opt}}}}$. 令$\beta = \frac{a}{{{C_{\rm opt}}}}$,则$\frac{{C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )}}}{{{C_{\rm opt}}}} \le 1 + \alpha + \beta $.
由情形1.1和情形1.2的分析可知,SS-dd$(\alpha )$算法在情形1下在线与离线成本之比不大于$1 + \alpha + \beta $.
情形2 最后一个需求被揭露时, 服务器尚在沿着路径${T^*}(t)$ 服务需求的途中.
情形2.1 在线车在完成路径${T^*}(t)$后, 需要在原点等到特定时刻再出发服务最后一个需求, 则与情形1.2的分析相同.
情形2.2 在线车在完成路径${T^*}(t)$后, 立即出发服务最后一个需求.
令$T'(t)$为在线车服务$t$时刻才揭露的需求的最优路径, 在线车沿$T'(t)$ 服务所有需求的成本为$\mathcal{T}'$. 由于 在线车在完成路径$T^*(t)$后立即从原点出发沿$T'(t)$ 服务已揭露的需求,其总成本为$C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} = t + \mathcal{T} + \mathcal{T}'$,而$\mathcal{T} \le a + |{T^*}(t)|$,$\mathcal{T}' \le a + |T'(t)|$,因此, $C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} \le t + |{T^*}(t)| + |T'(t)| + 2a$. 由算法知,$t \ge \alpha |{T^*}(t)|$, 则$t + |{T^*}(t)| \le (1 + \frac{1}{\alpha })t$.
在$t$时刻才揭露的需求中,考虑离线车的服务的第一个需求$({l_f}, {r_f},{q_f})$,令其与原点之间的距离 为$d(o,{l_f})$. 由于服务该需求的时间最少为$t+a$,则离线车从$l_f$ 处继续服务其他需求并返回原点的距离最 多为${C_{\rm opt}} - (t + a)$. 如果在线车采取路径$T'$ 服务$t$ 时刻揭露的需求: 首先从起点处选择最短路径到 达离线车服务的第一个需求$({l_f},{r_f}, {q_f})$并服务,之后采取与离线车一样的路径服务其余需求,则该路 径长度不大于$d(o,{l_f}) + {C_{\rm opt}} - (t + a)$. 显然$|T'(t)| \le d(o,{l_f}) + {C_{\rm opt}} - (t + a)$. 而$d(o,{l_f}) \le {C_{\rm opt}} - a$,因此,$C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} \le (1 + \frac{1}{\alpha })t + {C_{\rm opt}} - a + {C_{\rm opt}} - (t + a) + 2a$,化简得,$C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} \le \frac{1}{\alpha }t + 2{C_{\rm opt}}$,又因为$t + a \le {C_{\rm opt}}$,则 $C_{\rm online}^{{\rm SS\mbox{-}dd}(\alpha )} \le \frac{1}{\alpha } ({C_{\rm opt}} - a) + 2{C_{\rm opt}} = (2 + \frac{1}{\alpha }){C_{\rm opt}} - \frac{a}{\alpha }$. 令$\beta = \frac{a}{{{C_{\rm opt}}}}$,则SS-dd$(\alpha )$ 算法在情形2 下的在线与离线成本之比不大于$2 + \frac{1}{\alpha } - \frac{\beta }{\alpha }$.
综上,SS-dd$(\alpha )$算法的竞争比为$C = \min \max \{ 1 + \alpha + \beta ,2 + \frac{1}{\alpha } - \frac{\beta }{\alpha }\} $,令$1 + \alpha + \beta = 2 + \frac{1}{\alpha } - \frac{\beta }{\alpha }$,即当$\alpha = \frac{{(1 - \beta ) + \sqrt {{{(1 - \beta )}^2} + 4(1 - \beta )} }}{2}$ 时,求得SS-dd$(\alpha )$ 算法的竞争比为$C = (1 + \beta ) + \frac{{(1 - \beta ) + \sqrt {{{(1 - \beta )}^2} + 4(1 - \beta )} }}{2}$. 得证.
根据定理2可知,当没有预知信息时($a = 0$), SS-dd$(\alpha)$算法的竞争比为$1 + \phi $,并且随着预知信息越多, SS-dd$(\alpha)$算法的竞争性能越好. 4 Zealous算法 Zealous算法是指满足以下两个条件的算法: a.
如果有待服务的需求,采用Zealous算法的在线车不会在某处静止, 它总是最大速 度(单位速度)移动至需求点或起点; b. 存在待服务的需求时,只有在以下三种情况下,采用Zealous 算法的在线车才能改变移 动的方向: (1)出现了一个新的需求; (2) 在线车位于起点; (3) 在线车位于一个刚刚被服务完的需求处.
一般而言,Zealous算法的竞争比在最坏情形下要劣于非Zealous算法. Zealous 算法主要用于衡量服务器在移动过程中等待的重要性. 4.1 Zealous算法的下界
定理3 对于带有预知信息的在线ATSP问题,如果$\rho $为任一确定性Zealous 算法的竞争比,则$\rho \ge {c^*}$,${c^*} = \left\{ {\begin{array}{*{20}{c}} {\frac{3}{{1 + a}}\begin{array}{*{20}{c}} {} & {a \le 1 + 2\varepsilon } \\ \end{array}} \\ {\frac{{2 + a}}{{1 + a}}\begin{array}{*{20}{c}} {} & {a \ge 1 + 2\varepsilon } \\ \end{array}} \\ \end{array}} \right. $.
证明 使用图 1证明定理3. 假设在1时刻,在线车处于起点$o$, 此时离线对手在$A$点揭露一个需求. 如果 在线车通过边$EC$ 服务$A$ 点需求,则其到达$E$ 点的时间为$1 + \varepsilon $,此时, 离线对手立即在$B_0$处揭露一个需求.
先考虑离线车的成本. 离线车从0时刻出发,首先服务$B_0$点再服务$A$ 点. 当其于$1 + \varepsilon $ 到达$B_0$点时,需要 等待到$1 + \varepsilon +a$ 才能服务$B_0$ 点需求,因此, 离线车总的服务成本为${C_{\rm opt}} \le 1 + a + 3\varepsilon $.
由于在线车采用Zealous算法,当有需求存在时, 它总是以最大速度(单位速度)移动至需求点. 因此, 在线车会先服务$A$点再 服务$B_0$点. 其到达$A$点的时间为$2 + 2\varepsilon $,而$A$点处的需求在$1+a$ 时刻释放,如果$a \le 1 + 2\varepsilon $,则$A$ 点可以立即接受服务. 这种情形下,当在线车于$3 + 4\varepsilon $到达 $B_0$点时,也可以直接服务$B_0$点的需求. 因此, 总 的服务成本${C_{\rm online}} \ge 3 + 6\varepsilon $, 则$\frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{3 + 6\varepsilon }}{{1 + a + 3\varepsilon }}$,当$\varepsilon \to 0$时,$\frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{3}{{1 + a}}$. 反之,如果$a \ge 1 + 2\varepsilon $,则在线车到达$A$点后, 至少需要等待至$1+a$ 才能服务该需求,之后于$1 + a + 1 + 2\varepsilon $到 达$B_0$点时,可以直接服务$B_0$点需求,因此, 总的服务成本${C_{\rm online}} \ge 2 + a + 4\varepsilon $. 因此,$\frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{2 + a + 4\varepsilon }}{{1 + a + 3\varepsilon }}$, 当$\varepsilon \to 0$时,$\frac{{{C_{\rm online}}}}{{{C_{\rm opt}}}} \ge \frac{{2 + a}}{{1 + a}}$.
综上,Zealous算法的下界为: $$\left\{ {\begin{array}{*{20}{c}} {\frac{3}{{1 + a}}\begin{array}{*{20}{c}} {} & {a \le 1 + 2\varepsilon } ,\\ \end{array}} \\[3mm] {\frac{{2 + a}}{{1 + a}}\begin{array}{*{20}{c}} {} & {a \ge 1 + 2\varepsilon } . \\ \end{array}} \\ \end{array}} \right. $$ 4.2 PAH-dd 算法及其竞争比
PAH-dd 算法} (plan-at-home-discloure-dates) 在线车位于起点时, 根据是否存在已揭露但尚未被服务的需求来做出行动决策,具体是:
a. 当在线车位于起点,如果没有已揭露但尚未被服务的需求时,在线车在原点等待.
b. 当在线车位于起点,如果存在已揭露但尚未被服务的需求时,由算法$A$ 计算一条路径,在线车沿该路径服 务所有已揭露但还未被服务的需求,并且在未返回原点之前忽略所有新揭露的需求. 其中,算法$A$为只考虑释 放时间、不考虑揭露时间,并且服务所有当前未被服务需求的算法. 定理4 PAH-dd 法的竞争比是$3 - \beta $,其中$\beta = \frac{a}{{{C_{\rm opt}}}}$.
证明 令$t$为最后一个需求的揭露时间, 假设$t$时刻在线车正处于路径$T$上,令服务器沿$T^*(t)$ 服务所有需求的成本为$\mathcal{T}$. 如果在线车在$t'$ 时刻返回起点, 则$t' \le t + |T|$,并且在线车返回原点后会立即出发. 令$t'$时刻出发时的路径为$T'$,相应的成本为$\mathcal{T}'$,则$t' \le t + \mathcal{T} + \mathcal{T}'$. 由于$t \le {C_{\rm opt}} - a$,$\mathcal{T} \le {C_{\rm opt}}$,$\mathcal{T}' \le {C_{\rm opt}}$,因此,$t' \le 3{C_{\rm opt}} - a$. 则$\frac{{C_{\rm online}^{{\rm PAH\mbox{-}dd}}}}{{{C_{\rm opt}}}} \ge 3 - \frac{{a}}{{{C_{\rm opt}}}}$,令$\beta = \frac{a}{{{C_{\rm opt}}}}$,得证.
由定理4,当没有预知信息时($a=0$),PAH-dd 算法的竞争比为3,
并且随着预知信息越多,PAH-dd 算法的竞争性能越好.
5 算例分析} 一般网络上的TSP问题是NP-hard问题,
无法在多项式时间内求得精确解,因此,本文给出一个规模较小的 算例,
来说明上述在线算法的可行性. 某快递网络包括4个节点,
各点之间的行车时间如图 2中标出. $t=0$时刻时,快 递车处于起点$o$处,
网络上的各节点处均有可能产生快递揽件需求. 假设预知时间$a=2$,
如果需求按照下列次序 逐渐揭露: $t=4$时,$A$点揭露一个揽件需求;
$t=8$ 时,$B$点揭露一个揽件需求; $t=12$,$C$点揭露一个揽 件需求.
那么,快递车应如何选择路径,
使得服务所有需求并返回起点的总时间最小?
先分析离线情形. 如果快递车0时刻时即可获知所有的需求序列,
则可以选择从$t=0$ 时立即出发,沿路径$o-A-B-C-o$ 服务所有需求.
当快递车到达节点$A$,$B$,$C$ 时,恰好需求释放可以立即接受 服务.
这样,总的服务时间为$6+4+4+6=20$,并且可计算出$\beta = 0.1$,
$\alpha=1.5 $.
对于在线情形而言,需求是被逐渐揭露的,
快递车只能在已知信息下做出路径决策. 如表 1 所示,如果快 递车采取
SS-dd$(\alpha)$算法,则快递车将在起点不断监测服务完集合$S$
中所有需求的最优路径 长度,以决定出发时间.
最终快递车于$t'=30$出发,
沿路径$o-A-B-C-o$于$t=50$服务完所有需求返回起 点,因此竞争比为2.5
(优于理论值2.6). 如果快递车采取 PAH-dd 算法,则只要有需求存在,
快递车 就必须全速行驶对其服务. 经计算,
快递车将于$t=4$出发沿路径$o-A-o$ 服务$A$ 点需求,并于$t=20$再次
出发沿路径$o-A-B-C-o$服务$B$ 点和$C$ 点需求,总的完成时间为40,
因此,竞争比为2 (优于理论值2.9).
由算例可以得出,由于理论上的算法竞争比为最坏情形分析,而现实快递网络中揽件需求的出现次序不一
定是最坏情形,因此,本文给出的两个在线算法的实际执行效果明显优于理论结果.
6 结论
针对快递服务网络结构上的非对称性以及可提前获知服务需求位置和释放时间的特征,本文构建了带有预知
信息的在线Homing ATSP问题模型. 证明了该问题的竞争比下界,在一般网络图上给出 SS-dd$(\alpha)$算法
和 PAH-dd 算法(zealous算法),并证明了算法各自竞争比. 对比两个算法发现,服务器采取适时等待策略
比采取zealous策略更优. 当无预知信息时,模型就转化为一般的在线Homing ATSP 问题,因此本研究是在
线Homing ATSP问题的一般形式. 并且预知信息越多,在线算法的竞争性能越优. 本文考虑了服务器必须返
回原点的情形,对于允许服务器在服务完所有需求后可以在任意点停止的情形,未来可进一步研究.
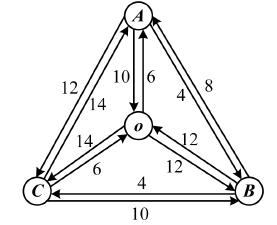
图 2 算例用图
| [1] | Frieze M, Galbiati G, Maffioli F. On the worst-case performance of some algorithms for the asymmetric traveling salesman problem[J]. Networks, 1982, 12(1): 23-39. |
| [2] | Bläser M. A new approximation algorithm for the asymmetric TSP with triangle inequality[C]// Proceedings of the 14th annual ACM-SIAM symposium on discrete algorithms. PA, USA: Society for Industrial and Applied Mathematics Philadelphia, 2003: 638-645. |
| [3] | Kaplan H, Lewenstein M, Shafrir N, et al. Approximation algorithms for asymmetric TSP by decomposing directed regular multigraphs[C]// Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science. Washington, DC, USA: IEEE Computer Society, 2003: 56. |
| [4] | Ausiello G, Feuerstein E, Leonardi S, et al. Algorithms for the on-line travelling salesman[J]. Algorithmica, 2001, 29(4): 560-581. |
| [5] | Lipmann M. The online traveling salesman problem on the line[D]. Amsterdam, Netherlands: University of Amsterdam, 1999. |
| [6] | Blom M, Krumke S O, De-Paepe W E, et al. The online-TSP against fair adversaries[J]. Informs Journal on Computing, 2001, 13(2): 138-148. |
| [7] | Jaillet P, Wagner M. Generalized online routing: New competitive ratios, resource augmentation and asymptotic analyses[J]. Operations Research, 2008, 56(3): 745-757. |
| [8] | Jaillet P, Wagner M. Online routing problems: Value of advanced information as improved competitive ratios[J]. Transportation Science, 2006, 40(2): 200-210. |
| [9] | Allulli L, Ausiello G, Bonifaci V, et al. On the power of lookahead in on-line server routing problems[J]. Theoretical Computer Science, 2008, 408(2): 116-128. |
| [10] | 温新刚,徐寅峰,丁黎黎. 基于预知信息的占线Nomadic TSP问题[J]. 系统工程理论与实践, 2013, 33(1): 1-7. Wen Xingang, Xu Yinfeng, Ding Lili. Online nomadic TSP based on the advanced information[J]. Systems Engineering —— Theory & Practice, 2013, 33(1): 1-7. |
| [11] | Wen X G, Xu Y F, Zhang H L. Online traveling salesman problem with deadline and advanced information[J]. Computers & Industrial Engineering, 2012, 63(4): 1048-1053. |
| [12] | Ausiello G, Bonifaci V, Laura L. The on-line asymmetric traveling salesman problem[J]. Journal of Discrete Algorithms, 2008, 6(2): 290-298. |
| [13] | Borodin A, El-Yaniv R. Online computation and competitive analysis[M]. Cambridge: Cambridge University Press, 1998. |



