0 引言
加工制造企业生产过程中机器故障、新工件到达、交货期调整等[1]内外部不确定性因素导致干扰事件时有发生,使得原始最优加工时间表不再最优甚至不再可行, 需要实时地制定新的加工时间表,在优化加工成本的同时, 最小化干扰事件带来的扰动, 这是"干扰管理''这一管理科学领域研究前沿所致力解决的问题[2] 生产调度干扰管理研究根据问题及事件特点建立干扰管理模型, 在考虑由经典调度目标度量的加工成本同时, 快速形成系统扰动最小的干扰应对方案. 干扰事件发生后如果只优化系统的原始成本目标, 会对已经付诸实施的准备工作造成广泛消极影响,降低客户满意度, 有效降低扰动已引起国内外学者的高度重视[3].
在生产调度研究领域中面临源自系统内部的机器中断[4, 5]及系统外部的新工件到达[6]等干扰事件, 已有学者从单机[6]、平行机[7]、并行机[8]、流水车间[9]、车间作业[10]等各个环境下进行研究, 分别考虑了初始最优加工时间表为基于指派规则如最短加工时间优先(shortest processing time rule,SPT)[11]、 加权折扣加工时间优先(weighted discounted shortest processing time rule,WDSPT)[12]等,以及基于数学规划[13, 14] 等干扰管理问题,具体研究内容可参见领域相关综述[2].
由Aytug等[2]综述可知, 目前生产调度干扰管理问题大部分都假设工件的加工时间为固定常数, 与工件在加工时间表中的位置无关. 然而, 加工制造业特别是钢铁冶炼行业普遍存在的一类现象是工件的实际加工时间和位置相关,实际加工时间为开始时间递增函数的现象称为恶化效应. 具有恶化效应的生产调度作为一类重要的现代排序问题, 得到学术界和工业界的广泛关注[15] 在恶化效应背景下, 面对干扰事件的影响,Zhao等[16] 指出单机环境下考虑恶化效应的加工成本最优方案是按照SPT规则, 设计动态规划算法优化了原目标和扰动目标的线性加权. Zhang等[17]研究单机环境恶化效应下考虑一致性参数的新工件到达问题, 以工件位置扰动或时间扰动为约束最小化总延误, 并给出多项式时间算法或动态规划算法. Zhao等[15]研究单机恶化效应下的新工件到达问题, 分别以两种不同的基于起始加工时间的线性递增函数代表工件实际加工时间, 研究扰动约束下的最小化完工时间和问题. Liu 等[18]研究同时考虑恶化效应和学习效应的新工件到达问题, 以最大位置扰动为约束优化最大完工时间以及以线性加权的方式同时优化最大位置扰动与最大完工时间.
由以上分析可以看出,尽管在具有恶化效应的生产调度干扰管理问题中, 已经有部分学者展开了相关研究,但是目前研究仍处于刚起步阶段, 有待于深入展开: 目前研究大多针对特定问题, 将原目标和扰动目标进行线性加权或者化目标为约束, 然后设计精确型算法进行求解. 这种思路对于问题结构具有较高要求, 方法缺乏一定的普适性. 此外,针对多目标干扰管理问题, 设计一次运行输出一系列有效解的算法在执行效率上要高于一次运行只输出一个有效解[19] 针对已有研究的不足,本文研究单机恶化效应下新工件到达问题, 充分重视系统扰动对生产过程的影响, 将加工成本与系统扰动作为问题的两个优化目标. 综合算法优势, 设计混合元启发式算法对上述难题进行优化求解, 得出可供决策者从加工成本和系统扰动进行权衡选择的多个干扰应对策略. 分析问题的Pareto最优解特性,以降低决策变量的规模和搜索范围, 提升问题求解效率及有效前沿质量.
本文的研究工作分析问题Pareto最优解特性, 并将其引入问题的求解过程以提高算法性能的思路, 可供复杂问题求解时借鉴; 设计的混合元启发式算法适用于求解其他领域多目标优化问题, 有助于改善有效前沿在与最优有效前沿的邻近性和多样性等方面的质量, 并为混合元启发式算法的发展提供改进思路和对比参照. 1 问题描述
某加工制造企业在具有恶化效应的单机不可中断环境下为最优化加工成本进行工件加工. 在生产调度干扰管理领域,制造商的生产成本通常是问题的初始目标, 它主要取决于加工制造过程中设备运转费用及人工费用, 这些是与工件的完工时间密切相关的, 因此使用所有工件的完工时间和对加工成本进行度量[20] 根据Zhao等[16]的研究, 此时初始最优加工时间表${{\rm{\pi}}^{\rm{*}}}$中所有工件(称"旧工件'')满足最短加工时间优先规则(shortest processing time rule,SPT)排序,且工件间无空闲时间. 由于加工环境不确定性,假定$\pi ^\ast$确定后, 旧工件加工前的0时刻到达一批新工件,不失一般性, 如果新工件晚于$0$时刻到达,那么将加工完的旧工件从问题移除; 将任何部分加工的旧工件继续加工完. 为有效应对干扰, 在最小化加工成本的同时,降低系统扰动对生产过程的影响, 需要对所有旧工件进行重调度,并将新工件插入到重调度的加工时间表.
令$J_O = \left\{ {J_1 ,J_2 ,\cdots ,J_{n_o } } \right\}$代表问题中$n_o $个旧工件,$J_N = \left\{ {J_{n_o + 1} ,J_{n_o + 2} ,\cdots ,J_{n_o + n_N } } \right\}$代表$n_N $个新工件,$J = J_O \cup J_N $,$n = n_O + n_N $,每个工件$J_j \in J$的正常加工时间为$p_j $,恶化效应下工件$J_j $的实际加工时间[15]为$p_j^A = p_j \left( {a + bt_j } \right)$,其中常数$a > 0$,恶化率$b > 0$,$t_j $为$J_j $的起始加工时间. 对工件$J_j \in J$的任意加工时间表$\sigma $, 令${\bar C_j}$表示工件$J_j \in J_O $在原始加工时间表中的完工时间; $t_j \left( \sigma \right)$表示工件$J_j \in J$在$\sigma $中的起始加工时间; $C_j \left( \sigma \right)$表示工件$J_j \in J$在$\sigma $中的完工时间; $T_j \left( \sigma \right)$表示工件$J_j \in J_O $在$\sigma$中相对于${\bar C_j}$的延迟; $\left[{J_j \left( \sigma \right)}\right]$表示工件$J_j \in J$ 在$\sigma$中的加工位置. 在不引起歧义的情况下,$t_j \left( \sigma \right)$,$C_j\left( \sigma \right)$,$T_j \left( \sigma \right)$和$\left[{J_j \left( \sigma \right)} \right]$可分别简记为$t_j $,$C_j $,$T_j $和$\left[{J_j }\right]$.
在初始加工时间表执行过程中,发生了多个新工件到达的干扰事件. 现实中常规干扰应对策略为保持初始加工时间表不变, 将新到达工件按照SPT序安排至队尾进行加工. 通过本文研究可以发现, 此时会产生较大加工成本. 然而干扰管理需要同时考虑加工成本和系统扰动, 在两者之间进行有效权衡,常规干扰应对策略有待改善.
下面给出本文干扰管理模型的初始目标和扰动目标. 初始目标为加工成本, 包括加工过程中设备运转费用及人工费用,通过工件完工时间和进行度量:
| \begin{equation} {f_1} = \sum {{C_j}\left( \sigma \right)} = \sum\limits_{j = 1}^{{n_O} + {n_N}} {\left( {p_j^A\left( \sigma \right) + {t_j}\left( \sigma \right)} \right)} \end{equation} | (1) |
系统扰动包括旧工件延迟完工导致的管理费用、违约费用、运输费用等与供应商和顾客扰动相关的协作费用以及客户满意度影响等, 与原始加工时间表偏差有关, 使用旧工件相对于初始完工时间的延迟$T_j\left( \sigma \right)$进行度量:
| \begin{equation} {f_2} = \sum {{T_j}\left( \sigma \right)} = \sum\limits_{j = 1}^{{n_O}} {\max\left\{ {{C_j}\left( \sigma \right) - {{\bar C}_j},0} \right\}} \end{equation} | (2) |
使用三参数表示法[20]$\left. {\rm{\alpha }} \right|\left. \beta \right|\gamma $,本文的问题可记为式(3). 文中以下部分将式(3)简称为问题 P.
| \begin{equation} \left. 1 \right|\left. {{p_j}\left( {a + b{t_j}} \right)} \right|\sum {{C_j}\left( \sigma \right)} ,\sum {{T_j}\left( \sigma \right)} \end{equation} | (3) |
针对加工时间固定初始最优化工件完工时间和的调度问题,受新工件到达影响用完工时间延迟度量扰动, 文献[6]已经证明该问题为NP难问题. 而本文在此基础上考虑加工时间具有恶化效应,问题难度不会比文献[6]中的问题更低. 因此对本文研究问题精确型算法无法在多项式时间内对其求解. 当问题规模较大时,元启发式算法成为有效求解手段. Pareto最优化调度问题的目标是寻找所有Pareto最优解,其中每个Pareto最优解对应一个Pareto最优加工时间表[21] 本部分将对问题的Pareto最优解特性进行分析,以期降低问题求解难度,为算法设计奠定基础. 引理1 对于问题$\left. 1 \right|\left. {p_j \left( {a + bt} \right)} \right|C_{\max} \left( \sigma \right)$,其中$C_{\max} \left( \sigma \right)$表示给定加工时间表的加工时间表长. 若加工时间表$\sigma $中$J = \left\{ {J_1 ,J_2 ,\cdots ,J_n } \right\}$的$J_1 $起始加工时间为$t$,那么$J_j \in J$的加工时间表长与工件加工顺序无关,并且
\[C_{\max} \left( \sigma \right) = t\mathop \prod \limits_{j = 1}^n \left( {1 + bp_j } \right) + \frac{a}{b}\left( {\mathop \prod \limits_{j = 1}^n \left( {1 + bp_j } \right) - 1} \right), \]
其中常数$a > 0$,恶化率$b > 0$,$p_j $为工件$J_j \in J$的正常加工时间.引理2 对于问题$\left. 1 \right|\left. {{p_j}\left( {a + bt} \right)} \right|\sum {{C_j}\left( \sigma \right)} $, 若加工时间表$\sigma $中$J = \left\{ {J_1 ,J_2 ,\cdots ,J_n } \right\}$的$J_1 $起始加工时间为$t$,那么$J_j \in J$按照$p_j $的非减顺序(SPT规则)排序可得到问题最优解,完工时间和为
\[\sum {{C_j}\left( \sigma \right)} = t\mathop \sum \limits_{j = 1}^n \mathop \prod \limits_{i = 1}^j \left( {1 + b{p_i}} \right) + \mathop \sum \limits_{j = 1}^n \frac{a}{b}\left( {\mathop \prod \limits_{i = 1}^j \left( {1 + b{p_i}} \right) - 1} \right).\]
由于SPT规则为问题$\left. 1 \right|\left. {{p_j}\left( {a + bt} \right)} \right|\sum {{C_j}\left( \sigma \right)} $ 提供最优解, 问题P的原始加工时间表$\pi ^\ast $中所有旧工件按SPT规则排序并标引,即$p_1\le p_2 \le \cdots \le p_{n_O } $,并且$\pi ^\ast $中旧工件之间无空闲时间. 类似地, 所有工件按照SPT规则排序加工,将得到问题P 的原目标最优加工时间表. 在引理1和引理2的基础上, 有如下定理及证明:
定理1 问题$\left. 1 \right|\left. {{p_j}\left( {a + b{t_j}} \right)} \right|\sum {{C_j}\left( \sigma \right)} ,\sum {{T_j}\left( \sigma \right)} $ 的Pareto最优加工时间表中, 所有旧工件$J_j \in J_O$ 按照SPT规则排序,所有新工件$J_j \in J_N $按照SPT规则排序,且所有工件$J_j \in J$间无空闲时间.
证明 首先考虑旧工件排序,假定$\sigma ^\ast $为问题的Pareto最优加工时间表,$J_i $为$\sigma ^\ast $中不满足SPT规则排序的第一个旧工件,$J_j $为$\sigma ^\ast $中先于$J_i $加工的最后一个旧工件,$J_j $起始加工时间$t_0 $, $\widetilde{J_1},\widetilde{J_2 },\cdots ,\widetilde{J_h }$为$\sigma ^\ast $中排序在$J_j $与$J_i $间的新工件,显然$i < j$, $p_i < p_j $,$C_i \left( {\pi ^\ast } \right) < C_j \left( {\pi ^\ast } \right)$,$C_j \left( {\sigma ^\ast } \right) = t_0 + p_j \left( {a + bt_0 } \right)$.
①交换$J_j $与$J_i $的位置构造新加工时间表$\tilde \sigma $,那么 ${C_i}\left( {\tilde \sigma } \right) = {t_0} + {p_i}\left( {a + b{t_0}} \right) < {C_j}\left( {{\sigma ^*}} \right)$, $\widetilde{J_1},\widetilde{J_2 },\cdots,\widetilde{J_h }$在$\tilde \sigma $中完工时间小于在$\sigma ^\ast $中完工时间. 又由引理1,$C_j \left( \tilde \sigma \right) = C_i \left( {\sigma ^\ast } \right)$. 于是交换位置后所有工件完工时间和变小.
②对于扰动目标,如果$T_i \left( \tilde \sigma \right) > 0$,那么当$T_j \left( {\sigma ^\ast } \right) > 0$时,$\left( {T_j \left( \tilde \sigma \right) + T_i \left( \tilde \sigma \right)} \right) - \left( {T_j \left( {\sigma ^\ast } \right) + T_i \left( {\sigma ^\ast } \right)} \right) = C_j \left( \tilde \sigma \right) - C_i \left( {\sigma ^\ast } \right) + C_i \left( \tilde \sigma \right) - C_j \left( {\sigma ^\ast } \right) < 0$; 当$T_j \left( {\sigma ^\ast } \right) = 0$时,$\left( {T_j \left( \tilde \sigma \right) + T_i \left( \tilde \sigma \right)} \right) - T_i \left( {\sigma ^\ast } \right) = C_j \left( \tilde \sigma \right) - C_j \left( {\pi ^\ast } \right) + C_i \left( \tilde \sigma \right) - C_i \left( {\sigma ^\ast } \right) < C_j \left( {\sigma ^\ast } \right) - C_j \left( {\pi ^\ast } \right) < 0$.
如果$T_i \left( \tilde \sigma \right) = 0$,那么$T_j \left( {\sigma ^\ast } \right) = 0$,当$T_i \left( {\sigma ^\ast } \right) > 0$,$T_j \left( \tilde \sigma \right) > 0$时,$T_j \left( \tilde \sigma \right) - T_i \left( {\sigma ^\ast } \right) = C_j \left( \tilde \sigma \right) - C_j \left( {\pi ^\ast } \right) - C_i \left( {\sigma ^\ast } \right) + C_i \left( {\pi ^\ast } \right) < 0$; 当$T_i \left( {\sigma ^\ast } \right) > 0$, $T_j \left( \tilde \sigma \right) = 0$时,$ - T_i \left( {\sigma ^\ast } \right) < 0$; 当$T_i \left( {\sigma ^\ast } \right) = 0$, $T_j \left( \tilde \sigma \right) = 0$时,旧工件的延迟没有变化.
于是交换位置后所有旧工件的延迟没有变大.
因此$\tilde \sigma $比$\sigma ^\ast $对于问题P更加稳定和优化. 继续将$\tilde \sigma $中不满足SPT规则排序的第一个旧工件与先于其加工的最后一个旧工件交换位置, 如此反复,直至所有旧工件全部满足SPT规则排序, 得到新工件位置给定情形下问题的Pareto 最优加工时间表.
对于新工件排序的分析过程与旧工件类似,不再赘述. 综合上述分析, $\tilde \sigma $中所有旧工件满足SPT序、所有新工件满足SPT序以及Pareto最优解特点表明所有工件间无空闲时间, 否则除去空闲以保持加工时间表可行和目标值最优.
定理2 问题$\left. 1 \right|\left. {{p_j}\left( {a + b{t_j}} \right)} \right|\sum {{C_j}\left( \sigma \right)} ,\sum {{T_j}\left( \sigma \right)} $ 的Pareto最有加工时间表 $\tilde \sigma $中,任意新工件$J_j $ 的排列位置$\left[{J_j \left( \tilde \sigma \right)} \right]$介于$\left[{J_j \left( {\sigma ^\ast } \right)} \right]$和$\left[{J_j \left( \tilde \pi \right)} \right]$之间,其中$\sigma ^\ast $为完工时间和最优加工时间表, $\tilde \pi $为将所有新工件以SPT序排列于$\pi ^\ast $中旧工件之后构造的加工时间表.
证明 由定理1,假定所有工件的正常加工时间满足$p_1 \le p_2
\le \cdots \le p_l \le p_{n_O + 1} \le p_{l + 1} \le \cdots \le
p_{n_O } \le p_{n_O + 2} \le \cdots \le p_{n_O + n_N } $.
问题描述中已知$\pi ^\ast $中所有旧工件满足SPT序,
将新工件以SPT序排列于$\pi ^\ast $中旧工件之后构造$\tilde \pi $,
即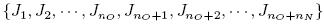 中所有工件以SPT规则排序,即
中所有工件以SPT规则排序,即 ,由引理2可知,$\sigma ^\ast
$为原目标最优加工时间表.
,由引理2可知,$\sigma ^\ast
$为原目标最优加工时间表.
若将$\tilde \pi $中$J_{n_O + 1} $前移一个位置构造加工时间表$\tilde \sigma $,由引理1可知$C_{n_O + 1} \left( \tilde \pi \right) = C_{n_O } \left( \tilde \sigma \right)$,又$p_{n_O + 1} \le p_{n_O } $,于是$C_{n_O + 1} \left( \tilde \sigma \right) \le C_{n_O } \left( \tilde \pi \right)$,$\sum {{C_j}\left( {\tilde \sigma } \right)} \le \sum {{C_j}\left( {\tilde \pi } \right)} $. 交换后原目标没有增加,但扰动目标增加. 当$p_{n_O + 1} < p_{n_O } $时,交换后原目标减少,扰动目标增加.
将$\tilde \pi $中$J_{n_O + 1} $继续前移至$p_l $之后任意位置时,对原目标和扰动目标影响同上.
将$\tilde \pi $中$J_{n_O + 1} $继续前移至$p_l $之前任意位置时,随移动进行,原目标没有减少,而扰动目标增加. 因此为使加工时间表最优,$J_{n_O + 1} $最多移至$\left[{J_{n_O + 1} \left( {\sigma ^\ast } \right)} \right]$位置.
由于$\tilde \pi $中所有新工件满足SPT序,由定理1,将$\tilde \pi $中$J_{n_O + 1} $后移将使目标值变差. 于是$J_{n_O + 1} $在Pareto最优加工时间表$\tilde \sigma $中的位置满足$\left[{J_{n_O + 1} \left( {\sigma ^\ast } \right)} \right] \le \left[{J_{n_O + 1} \left( \tilde \sigma \right)} \right] \le \left[{J_{n_O + 1} \left( \tilde \pi \right)} \right]$. 推证中发现, 当且仅当所有新工件加工时间均大于等于旧工件加工时间时,$\tilde \pi $ 为问题最优加工时间表.
定理3 问题$\left. 1 \right|\left. {{p_j}\left( {a + b{t_j}} \right)} \right|\sum {{C_j}\left( \sigma \right)} ,\sum {{T_j}\left( \sigma \right)} $ 的Pareto最优加工时间表$\tilde \sigma $中, 正常加工时间大于等于所有旧工件的新工件排序于所有旧工件之后, 正常加工时间小于等于所有新工件的旧工件排序于所有新工件之前.
证明 根据定理1及定理2, 在旧工件满足SPT序以及新工件满足SPT序的问题Pareto最优加工时间表$\tilde \sigma$中, 不存在新工件排序在正常加工时间小于等于它的旧工件之前的情形, 正常加工时间大于等于加工时间最长旧工件的新工件之后同样不存在旧工件, 于是定理得证.
因此,通过对问题Pareto最优解特性分析,和对$n_O + n_N
$个工件进行重调度相比,
只需确定$n_N-l$个满足SPT规则排序的新工件的不同加工位置.
问题的解空间由$(n_O + n_N )!$降低为$\left( {n_N - l}\right)!$,
并且解的质量在搜索过程中得以提高. 问题P最一般的解可以表示为$n_O + n_N$
个工件的加工次序置换(permutation). 在本文剩余部分中,
将首先设计基于置换的元启发式算法.
然后通过本节Pareto最优解特性分析,降低解空间的
搜索范围并提高解的质量,
最后通过随机生成数值算例验证本文设计算法的有效性和Pareto最优解特性对于算法的改进.
3 算法设计
问题P是多目标问题,
其两个优化目标之间存在相互制约关系,
加工成本的降低可能引起系统扰动的增加.
实际中无法同时使加工成本与系统扰动达到最优,
只能在两者之间进行协调权衡和折中处理. 求解问题P得出的Pareto有效前沿对应多个干扰应对策略,
决策者可以根据不同偏好选择使用. 鉴于问题P的内在复杂性,无法在多项式时间内求得Pareto 最优解.
元启发式算法不需要复杂的数学模型基础即可获得较为满意的Pareto有效解集,
成为解决生产调度问题简单有效的常用方法.
本文综合现有元启发式算法的优势,
设计混合元启发式算法对问题进行求解,
并引入Pareto最优解特性对算法做进一步改进.
3.1 元启发式算法比较分析
基于遗传算法求解多目标问题引起运筹学领域及计算机科学领域学者的广泛关注[23]
新的非支配排序遗传算法[24] (non-dominated sorting genetic
algorithm with elitist,
NSGA-II)作为目前公认最为有效的多目标优化算法之一[25],
采用新的非支配排序方法、精英选择策略及拥挤距离计算方法,
降低了算法的复杂度并能搜索到更优的有效前沿[24];
其隐形精英解保留策略明显改善算法的收敛性,
并避免丢失进化过程中取得的Pareto最优解.
但NSGA-II进化过程中宽松的较优个体选择压力可能造成大部分非支配个体处于第一前端这一非支配前沿,
容易使种群收敛于局部最优[25]
与此相对,归档式多目标模拟退火算法(archived multi objective
simulated annealing,AMOSA)是
Bandyopadhyay等[26]于2008年提出的一种多目标优化高效算法.
该算法利用爬山操作和支配关系对个体进行迭代改进,
在目标空间搜索过程中按照Metropolis准则以一定概率接受劣个体,
表现出搜索过程中的概率突跳能力. 伴随温度的不断下降,重复进行抽样.
这既可保持退火过程中较优个体选择的压力,
又可避免搜索过程陷入局部最优,
并使求解结果最终趋于问题的全局最优有效前沿.
利用AMOSA求解多目标优化问题,表现出优于NSGA-II
的全局寻优能力和效率[27]
为提供更好的优化能力,并改善有效前沿的质量,
算法混合的思想已成为提高算法优化性能的一个有效途径[28]
综合以上分析,若能将AMOSA在全局寻优方面的优势与NSGA-II
快速收敛到Pareto有效前沿的局部搜索能力和种群多样性方面的优势结合起来设计混合元启发式算法,
将有希望对问题P进行有效求解.
3.2 混合元启发式算法设计
本节将设计混合元启发式算法(hybrid meta-heuristics algorithm,
HMHA),综合NSGA-II和AMOSA各自优点,
利用NSGA-II的局部寻优能力进行有效前沿搜索;
利用AMOSA在退火过程中以一定概率接受劣解的特点,
在保持较优个体选择压力的同时,保证算法的全局寻优能力,
从而改进主流算法NSGA-II 的有效前沿质量.
HMHA种群进化过程中以向量$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over x} = \left\{ {{x_1},{x_2},{x_3},\cdots ,{x_{{n_O} +
{n_N}}}} \right\}$作为种群个体,采用基于$n_O +
n_N$个工件位置的整数编码方式,其中$x_i
$对应个体染色体的第$i$个基因,代表工件$J_i \in
J$在加工时间表中的位置,$1\le x_i \le n_O + n_N $,且当$i \ne
j$时,$x_i \ne x_j $,$i,j = 1,2,\cdots ,n_O + n_N $.
HMHA的流程图如图 1所示,具体实现步骤如下:
步骤1
初始化种群规模、循环迭代次数、档案文件尺寸、爬山操作次数、Markov链长、交叉概率$P_c$及变异概率$P_m $.
对算法的初始参数进行设置,包括进化过程中的种群规模$pop$;
作为非支配排序遗传代数及归档式多目标模拟退火过程外循环终止条件[29]的循环迭代次数$iterations$;
档案文件尺寸$HL$、$SL$;
初始化或更新档案文件时对群体执行爬山操作次数$climbUpNum$;
在同一温度下重复执行Metropolis过程的次数即Markov链长$markovChainLength$;
控制遗传进化过程的参数交叉概率$P_c$及变异概率$P_m $.
步骤2 根据问题描述生成初始种群.
根据问题P随机生成初始种群$P_0$. 种群个体对应$n$个工件的可能位置序列.
步骤3
随机产生一组状态,确定两两状态间的最大目标值差,并据此利用初始温度计算函数确定初温.
冷却进度表是控制模拟退火算法进程的一组参数,
是影响算法性能的重要因素.
这组参数包括初始温度、温度更新函数、终止条件和Markov 链长度.
合理选择冷却进度表是算法应用的关键. 实验表明,初温越大,
获得高质量有效前沿的概率越大,但要增加时间开销[30]
因此需要折中考虑优化质量和优化效率确定初始温度.
这里采用类似步骤2的方式随机产生问题P的一组状态,
计算两两状态间对应的目标向量距离理想点的最大距离差$\left| {\Delta
_{\max} } \right|$,并利用初始温度计算函数$T_0 = - \left|
{\Delta_{\max} } \right| / \ln p_r
$确定归档式多目标模拟退火过程的noindent 初始温度[30],其中$p_r$为初始接受概率.
若$p_r$取值接近1,
且随机产生的初始状态能在一定程度上表征整个状态空间,
退火过程将以几乎等同的概率接受任何状态,完全不受极小个体限制.
这里理想点$( {f_1^*(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } ),f_2^*(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } )} )$每个分量分别对应问题$1 | {{p_j}( {a + b{t_j}} )}
|{f_1}(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over
y} } )$和$1 |{p_j ( {a + bt_j } )} |f_2 (
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over
y} })$的最优解,其中 $f_1^ * (
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over
y} } ) = \min ( {{f_1}(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over
y} } )} )$,$f_2^*(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } ) = \min( {{f_2}(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } )} )$.
对于问题$( {\rm {\bf {\rm P}}} )$的有效前沿,$( {f_1^*(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } ),f_2^*(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } )} )$往往无法达到. $f_1^*(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } )$由对所有待处理工件进行SPT排序得到; $f_2^*(
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} } )$由保持初始加工时间表不变,
将新到达工件集按照SPT排序并安排到工件队尾排序得到.
令迭代变量$t = 0$. 退火过程当前温度$T_t = T_0 $.
步骤4 根据当前种群个体间的支配关系,进行有效前沿划分.
NSGA-II在多目标优化前提下,采取非支配排序方法保证种群的多样性和与最优有效前沿的邻近性. 非支配排序方法包括有效前沿的划分和适应度值的分配[24]
在有效前沿划分阶段,根据个体间的支配关系,种群$P_t $被划分为$K_t$个不同的非支配前端$F_1 $,$F_2 $,$ \cdots$,同一前端个体间不存在支配关系. 对于任意两个前端$F_i $和$F_j $,如果$i 步骤5 从考虑种群距离最优有效前沿的距离和保证种群多样性的角度为所有个体分配适应度值.
对有效前沿划分后,根据以下规则为所有个体分配适应度值.
(1)对于不同前端个体,如果$i < j$,给$F_i
$中的个体分配比$F_j$中个体更高的适应度值.
(2)对于同一前端个体,计算并使用其拥挤距离衡量个体所处区域的稀疏程度,为处于更稀疏区域的个体分配更高的适应度值.
规则(1)考虑种群距离最优有效前沿的距离,规则(2)保证种群的多样性.
步骤6 对当前种群进行选择、交叉、变异操作.
对种群$P_t
$进行非支配排序后执行锦标赛选择,确定用于遗传操作的父辈个体,以交叉概率$P_c$进行交叉操作,将互相配对的两个染色体按照两点交叉方式相互交换其部分基因; 以变异概率$P_m$进行变异操作,将个体染色体的某些基因替换为其他等位基因,得到子代种群$Q_t$,进而构造新群体$R_t = P_t^M \cup Q_t $.
步骤7 对$R_t $执行若干次爬山操作,并初始化或更新档案文件.
对新群体$R_t$中的每个个体执行若干次爬山操作,接受支配原始个体的新个体. 再将最多$HL$个非支配个体存储到档案文件中. 若非支配个体数量超出$HL$,使用聚类操作将其数量降至$HL$.
设定当前温度下,记录Metropolis过程执行次数的计数器$m =0$. 同时从档案文件中随机选择一个个体作为当前解$current-pt$.
步骤8 基于非时齐算法对档案文件个体执行Metropolis过程,在退火过程中以一定概率接受劣个体.
非时齐算法是指退火过程无需各温度下均达到平稳分布,但温度需按一定的概率下降的退火过程. 高温下可接受与当前状态能差较大的新状态,而低温时只能接受与当前状态能差较小的新状态,这与不同温度下热运动的影响完全一致. 在温度为0时,不能接受任意一个大于当前能量值的新状态,这就是Metropolis准则.
接受准则是影响模拟退火算法性能的又一重要因素. 本算法基于新个体与当前个体和档案文件中个体的支配状态分如下三种情形制定接受准则. 其中$\Delta
dom_{a,b} = \prod\nolimits_{i = 1,f_i \left( a \right) \ne f_i \left( b
\right)}^M {\left( {\left| {f_i \left( a \right) - f_i \left( b \right)}
\right| / R_i } \right)}
$表示个体$a$对个体$b$的支配量,$M$为个体的决策变量数,$R_i$为第$i$个决策表里变量的范围值[26] 扰动当前个体产生新个体$new - pt$.
(1)若当前个体支配新个体,则新个体替代当前个体的概率$P = \frac{1}{1
+ \exp( {\Delta dom_{avg} \times T_t } )}$,其中$\Delta dom_{avg}
= ( {( {\sum\nolimits_{i = 1}^k {\Delta dom_{i,new - pt} } \Delta
dom_{i,new - pt} } )\Delta dom_{current - pt,new - pt} } ) / ( {k
+ 1} )$,$k \ge 0$为档案文件中支配新个体的个体数量.
(2)若当前个体与新个体之间是非支配的,那么根据新个体与归档文件中个体的支配状态,分如下三种情形进行考虑.
①若归档文件有$k$ ($k \ge 1$)个个体支配新个体,
则新个体替代当前给他的概率$P = \frac{1}{1 + \exp\left( {\Delta
dom_{avg} \times T_t } \right)}$,其中$\Delta do{m_{avg}} = (
{\sum\nolimits_{i = 1}^k {\Delta do{m_{i,new - pt}}} } )/k$.
②若新个体与归档文件中个体是非支配的,则新个体替代当前个体的概率为1,并将新个体加入归档文件. 若此时归档文件个体数量超过$SL$,对归档文件中个体执行聚类操作将数量降至$HL$.
③若新个体支配归档文件中$k$ ($k \ge1$)个个体,
则新个体替代当前个体的概率为1,并将新个体加入归档文件,
同时从归档文件中移除被新个体支配的$k$ 个个体.
(3)若新个体支配当前个体,那么根据新个体与归档文件中个体的支配状态,分如下三种情形进行考虑.
①若新个体支配当前个体,且归档文件中有$k$ ($k \ge
1$)个个体支配新个体,其中$\Delta dom_{\min}
$代表新个体与归档文件中$k$个支配个体之间支配量差值的最小值.
归档文件中对应最小差值支配量的个体以概率$P= \frac{1}{1 +
\exp\left( { - \Delta dom_{\min} } \right)}$替代当前个体,
否则新个体以概率1替代当前个体.
②若新个体与归档文件中个体是非支配的除非当前个体位于归档文件中,
那么新个体以概率1替代当前个体,并将新个体加入归档文件.
若当前个体位于归档文件中,则将其移除.
若此时归档文件个体数量超过$SL$,
对归档文件中个体执行聚类操作将数量降至$HL$.
③若新个体支配归档文件中 $k$ ($k \ge 1$)个个体,
则新个体以概率1替代当前个体,并将新个体加入归档文件。
同时将归档文件中被新个体支配的$k$个解移除.
以上过程称为Metropolis过程. 在同一温度下,
重复执行Metropolis过程的次数称为Markov链长.
步骤1中已经对Markov链长进行设定以确定各温度下产生候选个体数目的内循环终止条件.
按照一定的退火方法逐渐降低控制温度,
重复Metropolis过程直至达到结束准则,就构成了模拟退火算法.
该算法能收敛到全局最优有效前沿或近似全局最优有效前沿.
步骤9 对档案文件进行种群多样性修补,形成新种群.
如果内循环终止条件成立,依据步骤6遗传进化得到的父子种群将当前档案文件进行种群多样性修补,
选择其中适应度值较好的个体形成种群$P_{t+ 1} $; 否则,重复执行步骤8.
步骤10 以温度更新函数更新控制温度
选用Kirkpatrick等提出的温度更新函数$T_{t + 1} = \lambda
T_t$进行控制温度的更新,其中$\lambda $是一个接近1 的常数,
取$\lambda =0.95^{[31]
步骤11 输出问题的有效前沿
如果外循环迭代终止条件成立,输出种群$P_{t + 1}
$对应的Pareto有效前沿; 否则,重复执行步骤4.
根据文献[24],NSGAII算法的复杂性取决于非支配排序过程,
该算法进行$I$次迭代的计算复杂性为$O({I\times M\times N^2} )$,
空间复杂性为$O( {N^2})$,其中$M$表示目标个数,$N$表示种群规模.
本文设计的HMHA算法是在NSGA-II算法基础上,融入AMOSA
算法中的爬山操作和Metropolis 过程. 根据文献[24, 26]及HMHA
算法优化步骤,
爬山操作并初始化或更新归档文件的计算复杂性为$O({M\times 4N^2})$,
空间复杂性为$O( {4N^2})$; 执行Metropolis过程的计算复杂性为$O(
{T\times N\times ({M + \mbox{log}( N )} )} )^{[26],
空间复杂性为$O({4N^2})$,
其中$T$表示执行Metropolis过程的Markov链长. 经过对比分析,
HMHA算法的复杂性同样取决于非支配排序过程. 因此,HMHA进行$I$
次迭代的计算复杂性为$O({I\times M\times N^2} )$,空间复杂性为$O(
{N^2} )$.
3.3 引入Pareto最优解特性的混合元启发式算法设计
为进一步提高求解性能,根据分析得出的问题Pareto最优解特性,
可将问题P降维至$\left( {n_N -
l}\right)!$规模进行处理,将该特性引入算法HMHA,
形成混合元启发式算法(hybrid meta-heuristics algorithm with optimal
solution feature,HMHA-OSF)对问题P进行求解,具体步骤如下:
步骤1 确定正常加工时间小于等于所有新工件的旧工件个数$k$,
以及正常加工时间大于等于所有旧工件的新工件个数$l$.
步骤2 确定正常加工时间小于某一旧工件的$n_N -
l$个新工件在加工成本最优加工时间表$\sigma ^\ast $
中的位置$\overrightarrow {min} = \left\{
{mi{n_1},mi{n_2},\cdots,mi{n_{{n_N} - l}}} \right\}$,
及其在加工时间表$\tilde \pi $ 中的位置 $\overrightarrow {max} =
\left\{ {ma{x_1},ma{x_2},\cdots,ma{x_{{n_N} - l}}} \right\}$,
其中$\tilde \pi $ 是将所有新工件以SPT序排列于$\pi ^\ast
$中旧工件之后构造的加工时间表.
步骤3$\sim$步骤13
HMHA-OSF算法剩余步骤与3.2节中HMHA算法的步骤1$\sim$步骤11相似,
种群进化过程中采用基于$n_N - l$个新工件位置的整数编码方式,
以向量$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}
\over y} = \left\{ {{y_1},{y_2},{y_3},\cdots ,{y_{{n_N} - l}}}
\right\}$作为种群个体,$y_i $对应个体染色体的第$i$个基因,
代表工件$J_{i + n_O } \in J_N $在加工时间表中的位置,$min_i \le
y_i \le max_i $,且当$i < j$时,$y_i < y_j $,$i,j = 1,2,\cdots
,n_N - l$. 具体求解步骤参见3.2节,这里不再赘述.
HMHA-OSF算法的优化过程与HMHA类似,
区别在于HMHA的种群个体基因数为$n_O + n_N $,
HMHA-OSF的种群个体基因数为$n_N$. 因此,
HMHA-OSF算法与HMHA具有相同的计算复杂性$O( {I\times M\times N^2}
)$和空间复杂性为$O( {N^2} )$.
引入Pareto最优解特性的HMHA-OSF算法在对问题求解过程中,
降低了决策变量的规模和搜索范围,将有效提高算法性能及求解质量.
4 仿真实验及结果分析
为了验证本文混合元启发式算法和问题Pareto最优特性对于求解干扰管理问题的有效性,
本部分设计随机数值实验并引入度量有效前沿收敛性和多样性的公认指标进行验证.
与现有研究类似[32],将 NSGA-II求解结果作为基本参照,
首先比较HMHA和NSGA-II的性能. 在此基础上,
分析引入问题Pareto最优解特性的HMHA-OSF相对于HMHA的改进.
4.1 参数设置
根据问题描述,设置旧工件数量$n_O $,新工件数量$n_N $.
所有工件正常加工时间$p_j $均以等概率随机取自$\left( {0,100}
\right]$,并按照定理3中$\tilde \pi $重新标引,即$J_j \in J$,$j =
1,2,\cdots ,n$,其中$j = n_O + 1,n_O + 2,\cdots ,n_O + n_N
$对应新工件. 恶化效应中常数$a = 1$,恶化率$b = 0.0001$.
为了检验不同情况下算法性能,令$n_O $和$n_N$分别满足不同规模,
针对4种情况分别进行30次实验,
对比分析NSGA-II、HMHA及HMHA-OSF算法的求解效果,
验证HMHA比NSGA-II在算法上的改进,
以及引入Pareto最优解特性的HMHA-OSF比HMHA在求解性能上的改进.
实验1$\sim$ 实验4的参数分别为$n_O = 30$,$n_N =10$; $n_O =50$,
$n_N =20$; $n_O =80$,$n_N =35$; $n_O = 130$,$n_N = 55$.
基于种群的优化算法,其种群规模对算法求解效果有很大影响[33] 本文针对每组实验参数,分别设定不同的种群规模$pop_{Lab1}= 100$,$pop_{Lab2} = 150$,
$pop_{Lab3} = 180$,$pop_{Lab4} =200$,以提高算法求解性能. NSGA-II和HMHA的初始种群由随机生成的可行加工时间表构成,HMHA-OSF的初始种群由随机生成的
满足Pareto 最优解特性的可行加工时间表构成. 使用MATLAB语言,在MATLAB R2012b 8.0.0.783版本环境下对三种算法进行编程运算和优化过程绘制.
为公平对比,每种算法的同类型参数设置均相同,
其中包括外循环迭代次数$iterations= 200$;
档案文件尺寸$HL$与种群规模相同,$SL = \beta \times HL$,$\beta \ge
2$; 爬山操作次数$climbUpNum = 3$; Markov链长$markovChainLength
=3$; 交叉概率$P_c = 0.9$,变异概率$P_m = 0.1$.
4.2 实验结果分析
在数值实验过程中,我们发现HMHA-OSF、HMHA和NSGA-II针对实验1$\sim
$实验4呈现出类似的结果.
为表达直观,本文给出实验2的30次实验中的一次典型求解过程.
通过引入度量有效前沿质量的性能指标,给出其余实验的指标统计值.
首先,对比HMHA比NSGA-II在算法层面的改进.
图 2给出HMHA与NSGA-II在求解过程中种群进化的对比情况,
其中星号与圆圈分别代表HMHA与NSGA-II的种群个体,
上三角表示实际中无法达到的理想点,由原目标和扰动目标的最优值构成.
为充分体现混合元启发式算法优势,
HMHA与NSGA-II基于相同初始种群进行搜索,如图 2(a)所示.
随着算法不断进化,
沿着原目标和扰动目标优化的方向在15代左右超越NSGA-II的种群,
如图 2(b) 和图 2(c)所示,
HMHA种群个体比NSGA-II更加快速地向理想点靠近.
从图 2(d)和图 2(e)可以看出,当HMHA
种群超越NSGA-II种群后始终保持稳定领先状态,直至算法结束,
最终种群对比如图 2(f)所示.
这说明本文所提出的HMHA比NSGA-II具有更快的收敛速度,
以及每代种群在与理想点的邻近性方面的优势.
接下来,
对比引入Pareto最优解特性的HMHA-OSF比HMHA在求解性能上的改进,
图 3给出HMHA-OSF与HMHA求解过程中与理想点距离收敛曲线,每种算法对应的上下两条曲线分别对应求解过程中每代种群的有效前沿距离理想点的平均距离与最优距离.
可直观看到,
两种算法求解过程中平均距离曲线和最优距离曲线均呈下降趋势,
HMHA-OSF的最优距离曲线与平均距离曲线的起始点明显接近横轴,
体现其初始种群即表现出与理想点的邻近; 同时,
两条距离曲线均先于HMHA平稳收敛,
且HMHA-OSF最优距离曲线的收敛位置更接近理想点,
体现HMHA-OSF能更加快速有效地对问题求解.
图 4给出两种算法进行200次迭代后,输出的有效前沿. 为便于观察,
将图 4中黑色框区域进行局部放大,得到右上角局部有效前沿对比效果,
横纵轴单位分别为$1\times 10^4$和$1\times10^5$. 可以直观发现,
HMHA-OSF的有效前沿在支配关系、个体数量及多样性方面均优于HMHA.
图中橘色正方形代表将所有工件按照SPT规则排序这一常用策略对应的目标值点,
此时原目标最小,但扰动目标较大;
橘色菱形代表将所有新工件以SPT序排列于原始加工时间表中旧工件之后这一常用策略对应的目标值点,
此时扰动目标为0,但原目标较大; 对比得出,
采用元启发式算法求解得出的干扰应对策略比常用干扰应对策略更加丰富和实用.
从图 4还可以看出,扰动目标随着原目标的减小而增大,
干扰应对过程中为了降低加工成本只能增大系统扰动,
原目标与扰动目标之间存在抵消关系.实际生产调度干扰管理过程中,
若仅考虑加工成本就可能产生较大的系统扰动,引发更多的扰动费用,
并对系统的服务水平带来消极影响,降低客户的满意度,
这也印证干扰管理的必要性.
决策者可以按照一定偏好从得到的Pareto有效前沿中权衡选择加工成本和系统扰动均理想的策略进行干扰事件应对.
其他实验的求解过程及分析结果与实验2类似,此处不再赘述.
为进一步量化证明引入Pareto最优解特性的HMHA-OSF的求解优势,
本文引入针对有效前沿的若干衡量算法搜索能力的指标[32],
基于实验1$\sim$ 实验4的30次求解结果,
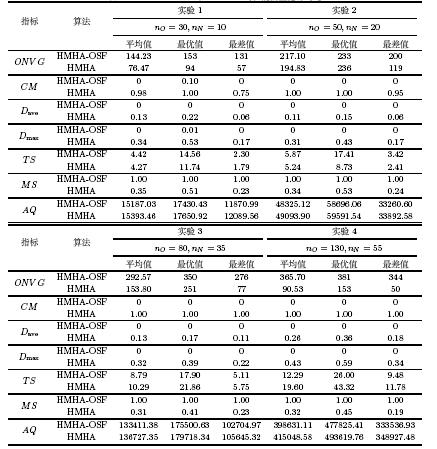
对比分析HMHA-OSF与HMHA的有效前沿质量,如表 1所示,
指标结果均来自30次实验结果的统计值,并通过四舍五入保留2位小数.
令$E$和$E'$分别表示HMHA-OSF和HMHA算法求得的有效前沿,
$R$表示最优有效前沿. 本研究中由于无法预知$R$,
因此混合$E$和$E'$中所有有效解共同构成$R$. 性能衡量指标[32]
中,$ONVG\left(E \right)$表示$E$中不同有效前沿的个数; $CM\left(
{E,E'}\right)$表示$E$被$E'$中有效前沿所支配的比例,
体现两个有效前沿间的支配关系,$E$
和$E'$之间可能存在互相均不支配的有效前沿,因此$CM\left({E,E'}
\right))$与$CM\left( E' \right)$之和不一定等于1; ${D_{\rm
ave}}\left( {E,R} \right)$和${D_{\max}}\left( {E,R}
\right)$分别表示$R$中每个可行解到$E$中所有可行解的最近距离的平均值和最大值,
值越小说明$E$ 与$R$的邻近性越好; $TS\left(E \right)$表示$E$
的均匀程度,值越小说明$E$ 的多样性越好;
$MS\left({E,R}\right)$表示$R$被$E$覆盖的程度,
值越大说明$E$覆盖$R$的程度越大; $AQ\left(
E\right)$表示$E$在与最优有效前沿邻近性以及可行解分布情况两方面的平均质量,
值越小$E$的平均质量越好.
分析实验2中算法性能衡量指标对比,可以得出如下结果:
1)对于$ONVG$和$CM$,HMHA-OSF的指标值均明显大于HMHA,
说明HMHA-OSF的有效前沿在数量上和质量上均优于HMHA. 2)对于$D_{\rm
ave} $和$D_{\max}$,HMHA-OSF的指标值均小于HMHA,
说明HMHA-OSF的有效前沿比HMHA更加接近最优有效前沿.
3)对于$TS$和$MS$,HMHA-OSF的$MS$指标值均大于HMHA,
说明HMHA-OSF的有效前沿对最优有效前沿的覆盖程度要优于HMHA,
且100\%覆盖最优有效前沿;而HMHA-OSF的$TS$指标值虽然大于HMHA,
但对应的$CM$、$D_{\rm ave}$和$D_{\max} $ 指标均优于HMHA,
说明HMHA-OSF的有效前沿更加接近于最优有效前沿. 4)对于$AQ$,
HMHA-OSF的指标值均小于HMHA,
说明HMHA-OSF的有效前沿在与最优有效前沿邻近性以及可行解分布的平均质量方面优于HMHA.
综合上述分析,HMHA-OSF的有效前沿在与最优有效前沿的邻近性、分布均匀情况、对最优有效前沿的覆盖程度及可行解数量等方面均优于HMHA. 分析其他实验均可得出同样的结论. 因此,HMHA-OSF比HMHA对问题P的求解结果更好,体现问题Pareto最优解特性能指导算法进行快速有效的求解.
根据第3节算法设计部分对HMHA和HMHA-OSF算法的计算复杂性和空间复杂性分析结果,
以及文献[24]中给出的NSGAII算法复杂性分析结果可知,
本文设计的HMHA和HMHA-OSF算法在求解出优于NSGA-II的有效前沿过程中,
花费的计算资源和存储资源与NSGA-II处于同一数量级,
不会对计算设备造成额外负担.
通过上述数值实验分析,可以得出如下管理启示:
①具有恶化效应的单机不可中断生产调度过程中,当新工件到达时,
最简单的处理方式是将新工件排列于已有加工时间表中旧工件后边进行加工,
此时不会产生系统扰动,但加工成本通常较高,
因此需要调整已有加工时间表; ②为降低加工成本,
可以将所有工件按照SPT规则排序加工,此时加工成本最低,
但系统扰动可能较大;
③应对新工件到达事件的理想加工时间表中新旧工件分别具有一定的SPT规则特性,
可以作为制定简单应对策略的理论指导.
5 结论
(1)本文以加工制造企业在恶化效应下的生产调度为背景,研究单机环境下的新工件到达干扰管理问题,在恶化效应普遍存在于生产加工过程这一客观情境下,考虑优化加工成本的同时,充分注重系统扰动对生产调度过程的影响,避免延迟造成较多的扰动费用及客户满意度影响,使决策者可以在加工成本与系统扰动间权衡选择,使理论研究更加符合生产实际. 决策者可以根据问题求解得出的有效前沿,在加工成本和系统扰动之间权衡选择,提出有效的干扰应对策略,从而充分降低企业的加工成本和系统扰动,全面提升企业经济效益和管理水平.
(2)本文结合已有元启发式算法NSGA-II和AMOSA的各自优势,
设计混合元启发式算法HMHA对本文的干扰管理问题求解,并在此基础上,
引入分析得出的问题Pareto最优解特性构造HMHA-OSF算法.
通过设计随机生成数值实验,
结合度量有效前沿收敛性和多样性的公认指标结果分析,验证了HMHA比
NSGA-II在求解该类问题时具有更好的收敛能力和有效前沿质量,
以及引入Pareto最优解特性的HMHA-OSF比HMHA在算法性能上的进一步改进,
体现设计的HMHA比已有主流算法更加快速高质量的求解问题,
以及分析得出的问题Pareto最优解特性的科学合理性及其在指导算法进行快速有效求解时发挥的重要作用.
(3)本文设计的混合元启发式算法能快速有效求解问题,
进一步证明了算法混合的思想是提高算法优化性能的一个有效途径;该混合元启发式算法可以供相关领域多目标优化问题求解时使用或作为算法设计的参照;该算法的混合策略及设计思路可以作为设计其他混合元启发式算法的策略借鉴和技术参考,
并有助于推动元启发式算法领域的发展。
(4)本文通过对问题的Pareto最优解特性进行分析,进而将其引入算法设计过程以有效提升算法性能这一问题求解思路,不同于已有研究中使用元启发式算法直接对问题进行求解的方式,表现出快速高效的问题求解能力,这一求解问题的新思路可以为其他干扰管理问题的求解提供参照.
具有恶化效应的新工件到达事件广泛存在于加工制造等领域,除了采用重调度的方式有效地应对干扰外,仍需进一步研究能够增强企业柔性的干扰应对手段,如通过分配资源对工件加工时间压缩,或者以一定费用拒绝加工部分工件等方式应对扰动,成为接下来将要开展的研究工作.
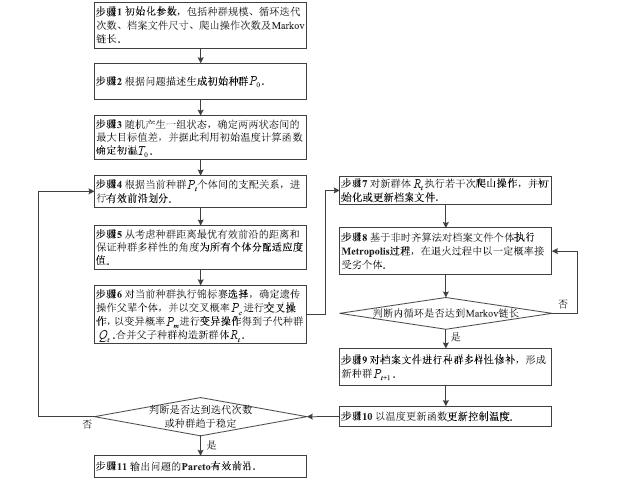
图 1 HMHA的流程图 
图 2 HMHA与NSGA-II求解过程中种群对比图 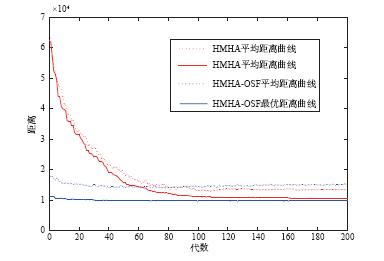
图 3 HMHA-OSF和HMHA求解过程中与理想点距离收敛曲线 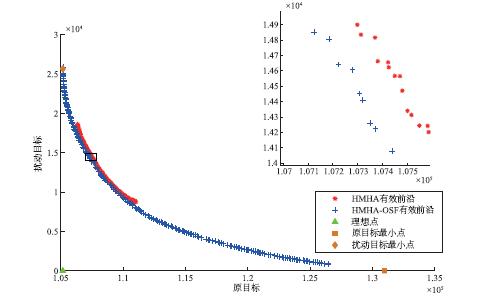
图 4 HMHA-OSF与HMHA的有效前沿对比
| [1] | Cowling P, Johansson M. Using real time information for effective dynamic scheduling[J]. European Journal of Operational Research, 2002, 139(2): 230-244. |
| [2] | Aytug H, Lawley M A, McKay K, et al. Executing production schedules in the face of uncertainties: A review and some future directions[J]. European Journal of Operational Research, 2005, 161(1): 86-110. |
| [3] | 胡祥培, 张漪, 丁秋雷, 等. 干扰管理模型及其算法的研究进展[J]. 系统工程理论与实践, 2008, 28(10): 40-46.Hu Xiangpei, Zhang Yi, Ding Qiulei, et al. Review on disruption management model and its algorithm[J]. Systems Engineering —— Theory & Practice, 2008, 28(10): 40-46. |
| [4] | 唐恒永, 唐春晖, 赵传立. 突发事件应急管理中的中断-继续随机排序模型[J]. 系统工程理论与实践, 2010, 30(4): 751-757.Tang Hengyong, Tang Chunhui, Zhao Chuanli. A preemptive-resume stochastic scheduling model with disruption[J]. Systems Engineering —— Theory & Practice, 2010, 30(4): 751-757. |
| [5] | 李巧云, 王冰, 王晓明. 随机机器故障下单机预测调度方法[J]. 系统工程理论与实践, 2011, 31(12): 2387-2393.Li Qiaoyun, Wang Bing, Wang Xiaoming. Predictable scheduling approach for single machine subject to random machine breakdown[J]. Systems Engineering —— Theory & Practice, 2011, 31(12): 2387-2393. |
| [6] | Hall N G, Potts C N. Rescheduling for new orders[J]. Operations Research, 2004, 52(3): 440-453. |
| [7] | Lee C Y, Leung J, Yu G. Two machine scheduling under disruptions with transportation considerations[J]. Journal of Scheduling, 2006, 9(1): 35-48. |
| [8] | Ozlen M, Azizoglu M. Rescheduling unrelated parallel machines with total flow time and total disruption cost criteria[J]. Journal of the Operational Research Society, 2011, 62(1): 152-164. |
| [9] | Katragjini K, Vallada E, Ruiz R. Flow shop rescheduling under different types of disruption[J]. International Journal of Production Research, 2013, 51(3): 780-797. |
| [10] | He W, Sun D H. Scheduling flexible job shop problem subject to machine breakdown with route changing and right-shift strategies[J]. International Journal of Advanced Manufacturing Technology, 2013, 66(1-4): 501-514. |
| [11] | Qi X T, Bard J F, Yu G. Disruption management for machine scheduling: The case of SPT schedules[J]. International Journal of Production Economics, 2006, 103(1): 166-184. |
| [12] | Liu F, Wang J J, Yang D L. Solving single machine scheduling under disruption with discounted costs by quantum-inspired hybrid heuristics[J]. Journal of Manufacturing Systems, 2013, 32(4): 715-723. |
| [13] | Akturk M S, Atamturk A, Gurel S. Parallel machine match-up scheduling with manufacturing cost considerations[J]. Journal of Scheduling, 2010, 13(1): 95-110. |
| [14] | 刘锋, 王征, 王建军, 等. 加工能力受扰的可控排序干扰管理[J]. 系统管理学报, 2013, 22(4): 505-512.Liu Feng, Wang Zheng, Wang Jianjun, et al. Disruption management in scheduling with controllable and disrupted processing capability[J]. Journal of Systems & Management, 2013, 22(4): 505-512. |
| [15] | Zhao C L, Tang H Y. Rescheduling problems with deteriorating jobs under disruptions[J]. Applied Mathematical Modelling, 2010, 34(1): 238-243. |
| [16] | Zhao C L, Zhang Q L, Tang H Y. Scheduling problems under linear deterioration[J]. Acta Automatica Sinica, 2003, 29(4): 531-535. |
| [17] | Zhang X G, Wang Y. Rescheduling problems with agreeable job parameters to minimize the tardiness costs under deterioration and disruption[J]. Mathematical Problems in Engineering, 2013: 1-7. |
| [18] | Liu L, Zhou H. Single-machine rescheduling with deterioration and learning effects against the maximum sequence disruption[J]. International Journal of Systems Science, 2014. doi:10.1080/00207721.2013.876519. |
| [19] | Xiong J, Xing L N, Chen Y W. Robust scheduling for multi-objective flexible job-shop problems with random machine breakdowns[J]. International Journal of Production Economics, 2013, 141(1): 112-126. |
| [20] | Pinedo M L. Scheduling: Theory, algorithms, and systems[M]. 3rd ed. New York: Springer, 2008: 50-54. |
| [21] | Zhao Q L, Yuan J J. Pareto optimization of rescheduling with release dates to minimize makespan and total sequence disruption[J]. Journal of Scheduling, 2013, 16(3): 253-260. |
| [22] | Kononov A, Gawiejnowicz S. NP-hard cases in scheduling deteriorating jobs on dedicated machines[J]. Journal of the Operational Research Society, 2001, 52(6): 708-717. |
| [23] | Siinivas N, Deb K. Multiobjective optimization using nondominated sorting in genetic algorithms[J]. Evolutionary Computation, 1994, 2(3): 221-248. |
| [24] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
| [25] | 张超勇, 董星, 王晓娟, 等.基于改进非支配排序遗传算法的多目标柔性作业车间调度[J]. 机械工程学报, 2010, 46(11): 156-164.Zhang Chaoyong, Dong Xing, Wang Xiaojuan, et al. Improved NSGA-II for the multi-objective flexible job-shop scheduling problem[J]. Journal of Mechanical Engineering, 2010, 46(11): 156-164. |
| [26] | Bandyopadhyay S, Saha S, Maulik U, et al. A simulated annealing-based multiobjective optimization algorithm: AMOSA[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(3): 269-283. |
| [27] | Sengupta S, Bandyopadhyay S. De Novo design of potential RecA inhibitors using multiobjective optimization[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2012, 9(4): 1139-1154. |
| [28] | Wang K, Choi S H, Qin H, et al. A cluster-based scheduling model using SPT and SA for dynamic hybrid flow shop problems[J]. International Journal of Advanced Manufacturing Technology, 2013, 67(9-12): 2243-2257. |
| [29] | 王凌. 智能优化算法及其应用[M]. 北京: 清华大学出版社, 2001.Wang Ling. Intelligent optimization algorithm and its application[M]. Beijing: Tsinghua University Press, 2001. |
| [30] | Suman B, Kumar P. A survey of simulated annealing as a tool for single and multiobjective optimization[J]. Journal of the Operational Research Society, 2006, 57(10): 1143-1160. |
| [31] | Kirkpatrick S, Gelatt C D J, Vecchi M P. Optimization by simulated annealing[J]. Science, 1983, 220(4598): 671-680. |
| [32] | Li B, Wang L. A hybrid quantum-inspired genetic algorithm for multiobjective flow shop scheduling[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part B —— Cybernetics, 2007, 37(3): 576-591. |
| [33] | Vidal T, Crainic T G, Gendreau M, et al. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems[J]. Operations Research, 2012, 60(3): 611-624. |