0 引言
在金融市场中,以往占统治地位的是有效市场假说EMH. 20世纪90年代初,Peters[1, 2]根据Hurst创造的重标极差分析法,提出分形时间序列的概念,先后出版了两本专著,他提出的分形市场假说FMH极大程度地挑战了EMH的统治地位.他认为,信息依其投资者的投资起点而被评价.因为不同的投资起点对信息的估价是不同的,信息的传播也是参差不齐的.价格不可能每一次都反映所有可适合的信息,而只反映对投资起点重要的信息.这与EMH的基本假设产生了冲突,而Peters在随后的实证研究中证实了FMH,得到了令人满意的结果.
近年来,国内外的学者也都利用分形理论对各国股市进行了实证研究.崔鑫等[3]就资本市场非线性理论研究给出了综述与展望.王新宇等[4]利用分形理论验证了中国证券市场的非线性特征.宿成建等[5]利用分形理论分别计算了上证A股,深证A股及B股的Hurst指数.都国雄等[6]利用多重分形分析的三种方法分析了不同时间标度对多重分形特性的影响.魏宇等[7]建立了基于多标度分形谱两个主要参数的上海证券市场风险测度指标,弥补了传统风险测度指标在非有效市场条件下的不足.周炜星[8]深入细致地研究了上证指数高频数据,发现上证指数本身并不具有多重分形特性. Grech[9]等人对波兰本国的股票市场进行了研究,发现了一些股市运行与市场Hurst指数之间的关系. Serletis[10]等人利用DMA方法为基础重新计算了美国三大股指的Hurst指数,得到了Hurst指数小于0.5,即美国股市存在均值回复现象的结论. Lee[11]研究了韩国股票市场,发现收益率序列呈现出分形特征. Onali[12]利用分形理论考察了欧洲的八个股票市场的有效性,发现它们分别处在各个成熟阶段的理论依据.苑莹[13]等人对中国股市进行了研究,发现沪深两市均具有长记忆性特征.
复杂网络理论近些年也逐渐成为研究金融市场复杂性的热点理论,它最初起源于社会学领域,它以个体作为节点,以个体间的某种定性定量关系作为节点的边,利用图论理论及各种统计方法定性或定量地考察群体的宏观性质和个体间的关系特性[14, 15, 16].金融市场作为一个典型的复杂系统,非常适合利用复杂网络理论来进行研究,近些年利用复杂网络进行的研究,都试图给出金融市场在各维度各层面的运行规律.Namaki等[17]利用阈值法建立复杂网络,研究了伊朗的股票市场,发现所构建网络在一定情况下具有无标度特性.Tabak等[18]研究了巴西股票市场,建立了网络的最小生成树,发现股票按照板块聚类,金融,能源及原材料等板块在网络中的位置最为重要.Galazka[19]研究了波兰股票市场,构建了有权的复杂网络和最小生成树,发现网络具有无标度特性.李英等[20]在复杂网络理论环境下对少数者博弈模型进行了金融市场的仿真研究.蔡世民等[21]对金融市场的网格结构进行了实证研究.
从目前国内外的已有研究成果来看,分形理论和复杂网络理论同为研究金融市场复杂性的重要理论工具,一直以来却没有相关的研究把这两种理论方法结合起来.究其原因,本文认为:一方面,分形理论在金融市场的研究一直专注于金融市场的时间序列分析,更多的研究金融市场在时间维度方面的特性,而并没有在分形几何学[22]的方面有所发展;另一方面,复杂网络理论却由于其社会学研究的传统,使得近些年实证研究的主要进展都集中于静态网络,也就是一个固定的空间概念下的性质研究.这就使得这两种理论在时间和空间这两个维度上分别对金融市场复杂性展开了研究,而却很难相互结合.
本文研究遵循的逻辑思考是:金融市场复杂网络的空间特性并非不存在分形特征.首先将研究金融市场复杂性的分形理论从时间维度回到空间维度,在统一的空间维度下进行研究,寻找静态的中国股市复杂网络的分形几何学特性.同样,金融市场复杂网络也并非不存在时间序列的特性.通过建立中国股市的动态复杂网络,将原来静态的网络变成一组动态网络族,而其参数的变化自然形成了一个时间序列,这就将复杂网络从静态空间维度转化为动态的时间维度,也就可以利用分形时间序列的理论进行研究.本文将从这两方面展开探索.
本文第1节对中国股市复杂网络的空间分形特征进行研究,第2节对中国股市复杂网络的时间分形特征进行研究,最后得出结论. 1 中国股市复杂网络的空间分形特征 1.1 网络的构建及聚集系数
本节利用传统的阈值法构建一个静态的复杂网络,具体方法如下:
利用$P_{i}(t)$表示股票$i$在时期$t$的收盘点位.
| $R_i (t)=\ln (P_i (t)/P_i (t-1))$ | (1) |
式(2)为股票$i$和股票$j$对数收益率的相关系数$C_{ij}$,即
| $C_{ij}=\frac{E(R_{i}R_{j})-E(R_{i})E(R_{j})}{\sqrt{Var(R_{i})Var(R_{j})} }$ | (2) |
令每支股票为网络的节点,对任意节点$i$和节点$j$,如果股票$i$和股票$j$的对数收益率的相关系数$C_{ij}$($C_{ij}\in [-1, 1]$)大于或者等于所指定的阈值$\theta (\theta \in [-1, 1]$),就认为节点$i$和节点$j$之间有无向无权的边相连.边集\textbf{\textit{W}}定义如下:
| $\begin{equation} W=\left\{ \begin{array}{ll} w_{ij} =1,& i\ne j\ \mbox{and}\ c_{ij} \ge \theta \\ w_{ij} =0,& i\ne j\ \mbox{and}\ c_{ij} <\theta \\ w_{ij} =0,& i=j \\ \end{array} \right. \end{equation}$ | (3) |
这样便构建了一个复杂网络,其中节点是每只股票,边的状态是由阈值\textit{$\theta$}控制,随着阈值\textit{$\theta $}的 变化,网络的状态也是变化的. 聚集系数$C$用来描述网络中节点的聚集情况.假设节点$i$通过$k_{i}$条边与其他$k_{i}$个节点相连接,在这$k_{i}$个节点之间最多可能有$k_{i}$($k_{i}-1)/2$条边,而这$k_{i}$个节点之间实际存在的边数$E_{i}$和总的可能的边数$k_{i}$($k_{i}-1)/2$之比就定义为节点$i$的聚集系数$C_{i}$,即
| $\begin{eqnarray} C_i =2E_i /[k_i (k_i -1)] \end{eqnarray}$ | (4) |
聚集系数是复杂网络理论中考察网络小世界效应的重要参数,它反映了网络的紧密程度.在本文以下的研究中并不使用小世界效应中的另一个重要参数平均路径长度,因为计算平均路径长度需要网络的连通性作为前提,而在下面的实证研究中很难保证这一前提,而聚集系数已可较好地展现网络中的分形特征. 1.2 空间分形特征
传统分形理论中分形几何学的概念表现为客观对象整体和部分的自相似性,而体现这一自相似性的数学表达一般就是分形维数.实际中测定分形维数的方法有很多,例如利用观察尺度,测度关系,相关函数等等.在这里,本文使用一种类似于通过改变观察尺度的方法来找到节点数目$N$和聚集系数$C$之间的关系.
在建立好的复杂网络中,首先随机选择5个节点以及它们之间的边作为一个子网络,计算这一子网络的聚集系数,重复随机选择100次,得到100个子网络的聚集系数,取其均值作为5个节点子网络的聚集系数.然后再随机选择10个节点,15个节点等等,重复上面的步骤,得到相应的聚集系数,节点数逐渐增多直至整个网络.这样我们就得到了两个相对应的数组,节点数目$N$,和相应的聚集系数$C$.
利用这样的方法,本文将节点数目$N$视作观察整个网络的尺度,将聚集系数$C$视作在相应观察尺度下网络的参数.依据传统分形理论,参数$C$与观察尺度$N$应有如下关系:
| $\begin{eqnarray} C(N)\propto N^{-D} \end{eqnarray}$ | (5) |
如果实证研究中的聚集系数$C$和节点数目$N$,这二者之间存在类似于式(5)的函数关系,则可以认为随着观察尺度$N$的变化,网络的局部参数和整体参数之间存在某种关系,这与Mandelbrot提出的分形定义"一个分形是一个对象,它的部分以某种方式与整体相关"是相符合的.这样就可以认定所建立的复杂网络在这种度量方法下具有空间分形特征. 1.3 实证研究
本节使用中国上海证券市场2011年4月27日至2011年10月21日共120个交易日910只A股的前复权收盘价作为基本数据,总数据量共计10万余条,用1.1节的方法构建复杂网络.
在构建网络时,阈值作为控制边存在的参数变量,其实际的意义在于股票间收益率走势的相关程度,也可以认为是价格走势的相关程度.而股票的对数收益率相关系数大于给定阈值则认为股票间在给定的参数水平下走势基本一致.这里讨论的是各个股票对数收益率的相关度.如果当某支股票的对数收益率与其它股票的对数收益率的相关系数为负时,即说明该股票的走势跟其它股票不一致,这与相关系数小于某一阈值时所反映的情况是相同的.都说明在一定数量概念的水平下,股票间走势的不同.这时,可以认为该股票与其它股票在构建网络时无边相连.从图 1给出的所有股票对数收益率相关系数的概率分布可以看出,股票对数收益率相关系数为负数的概率较小,所以并不会影响本文后面的分析结果.
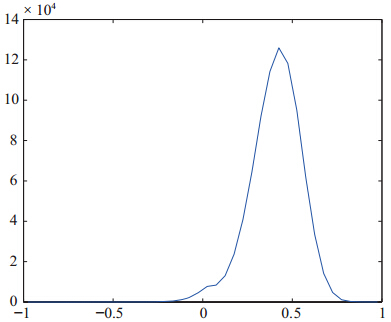 |
| 图 1 网络相关系数概率分布 |
相关系数的均值为0.4061,这里分别选取阈值$\theta$为股票收益率相关系数的均值,1.5倍均值和2倍均值构建三个网络,再利用1.2节所述的方法分别计算子网络的节点数目$N$和聚集系数$C$,共计算五万四千多个子网络,得到散点图 2.
 |
| 图 2 网络的节点数目与聚集系数散点图 |
利用指数函数拟合图 2中的散点,分别可以得到1倍均值网络,1.5倍均值网络,2倍均值网络的节点数目$N$与聚集系数$C$的指数函数拟合图,如图 3所示.
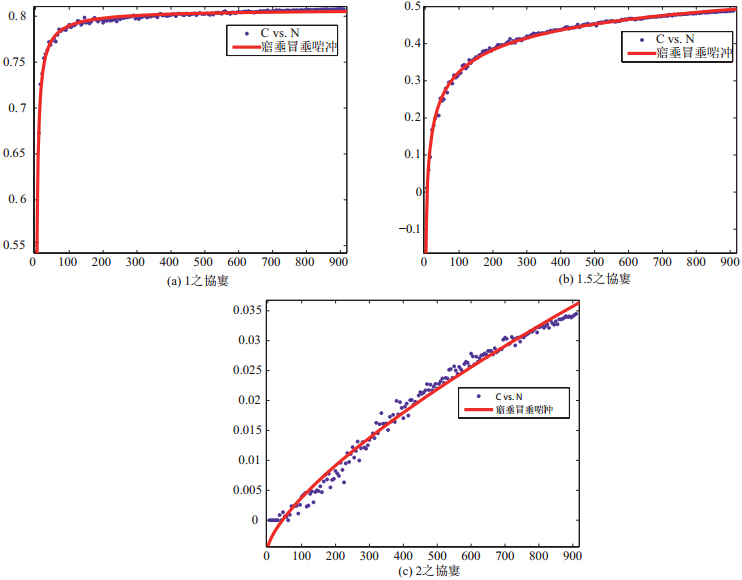 |
| 图 3 网络的节点数目与聚集系数指数函数拟合图 |
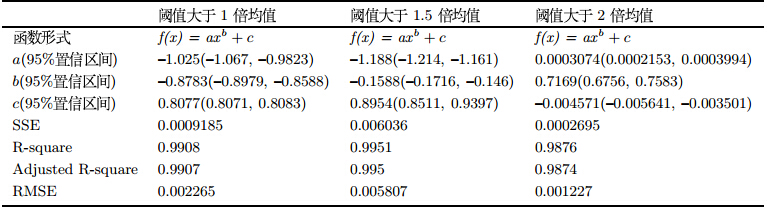
具体拟合结果如表 1所示.
由表 1所示,网络的节点数目$N$和聚集系数$C$可以有以下函数关系:
| $\begin{eqnarray} C(N)=aN^b+c \end{eqnarray}$ | (6) |
依据表 1的数据,1倍均值网络的节点数目$N$和聚集系数$C$的函数关系为:
| $\begin{eqnarray} C(N)=-1.025N^{-0.8783}+0.8077 \end{eqnarray}$ | (7) |
同式(5)比较,除去常数项外,聚集系数$C$与节点数目$N$完全满足传统理论中的分形公式的形式,其中分形维数$D=-b$,为0.8783.
同样地,在1.5倍均值网络和2倍均值网络中,节点数目$N$和聚集系数$C$的函数关系分别为式(8)和式(9)所示.
| $\begin{eqnarray} C(N)=-1.188N^{-0.1588}+0.8954 \end{eqnarray}$ | (8) |
| $\begin{eqnarray} C(N)=0.0003074N^{0.7169}-0.004571 \end{eqnarray}$ | (9) |
从拟合的效果来看,各项指标均非常良好,可以认定在这种方法下,聚集系数$C$与节点数目$N$存在上述的函数关系.
在传统分形理论中,分形维数往往解释为自由度的限制,分形几何学中的分形维数往往是大于拓扑维数的,也就是对象体现出更加精细的内部结构.在本节的静态网络研究中,随着节点数目的增加,子网络范围的扩大,事实上是更加精细地对网络本身进行观察,虽然参数$N$是增加的,但这与传统分形几何学观测尺度的减小在针对对象观察的实际意义上是一致的.那么此时的分形维数又意味着什么呢?在建立的静态网络中,聚集系数体现的是整体网络的紧密程度,也就是股票之间的整体关联性,随着阈值的提高,相同节点数目子网络的聚集系数的绝对值是递减的.这表明在阈值提高的过程中,整体网络反映的股票关系逐渐减少,整体的紧密程度下降.但是与此同时,高阈值下所展现的网络恰恰是相关性较强的股票之间的联系.此时网络中存在的边都体现了较强的股票相互关系,由此形成的网络是一个整体联系较弱而存量边联系较强的网络.而此时的分形维数反映了这一存量边的相互制约,所以随着阈值的增加,分形维数逐渐降低,也就是自由度的降低.反映在网络中,就是节点相关性的增强.也就是说,在较高的相关程度下,存在相互联系的股票之间的局部整体相关性,要强于在较低的相关程度下存在相互联系的股票之间的局部整体相关性.
在实际市场中,这一性质可以应用于投资组合的设计中,注意到在1倍和1.5倍均值的网络中,当节点数目达到一定程度后,聚集系数的增长就十分的有限,也就是说,在这一相关程度水平上,构建投资组合只需要一定的品种数量就可以达到涵盖整体市场相关性的水平.以"1倍均值"为例,图 2(a)和图 3(a)中可以看出,当股票数量增加到100左右时,网络聚集系数基本已经达到非常大的水平.那么可以认为,持有100只左右的股票组合就已经可以涵盖市场上的非系统性波动.对于机构投资者来讲,其重仓股大致多于10只,而对于较大型的基金公司,由于其资金体量和人员数量的优势,持仓中涵盖百只股票的情况也是较为常见的.
而随着阈值的增加,涵盖整体市场相关性的水平的投资组合品种数量也相应增加.这是因为随着阈值的增加,股票相关性增强,保留在网络中的边反映的是较强的股票联系,而这种联系往往分布在不同的股票类别中,也就是在整体网络中的多个小团簇.那么,要涵盖整体市场相关性的话,就需要更多的涵盖这些团簇,也就增加了投资组合的品种数量.
上述分析表明,随着阈值的增加,分形维数逐渐降低,这表明此时股票的相关性在增强,但这种相关性指的是局部股票团簇的整体相关性,而网络的整体相关性对应于聚集系数的绝对值.投资组合的设计也是依赖于这一网络聚集系数的绝对值.这与传统结论确无差别,这一部分的主要创新在于利用分形理论分析复杂网络理论的参数,进而得到相应的结论.也就是说尝试从不同的角度给出这一结论. 2 中国股市复杂网络的时间分形特征 2.1 网络的构建及聚集系数时间序列
本节仍然利用1.1节所述的阈值法建立复杂网络,选取聚集系数$C$来考察网络的性质.
选取中国上海股票市场自1990年12月19日至2011年10月21日去除摘牌的所有股票的前复权收盘价格作为基本数据, 总数据量达到四百多万条.
具体构建网络的方法如下:
1)从1990年12月19日起选取15天的数据构建一个网络.
2)将时间窗口后移一天,得到第二个网络.
3)再把时间窗口后移一天,直至最后,得到一小族共5083个网络.
4)选取阈值分别为0.4,0.5,0.6,0.7,进行上述步骤,共得到4小族网络.这4小族网络共同组成了1大族网络.
5)将时间窗口分别设为30天,60天,120天重复上述步骤,分别得到3大族网络,12小族网络.其中30天大族网络共4小族,每 小族网络个数为5068;60天大族网络共4小族,每个数网络个数为5038;120天大族网络共4小族,每小族网络个数为4078.
6)共得到4大族,16小族共77068个网络,分别计算聚集系数.可以得到4组,16个基本时间序列.
7)类似于计算收益率时间序列,用$P_{i}(t)$表示时间序列$i$在时期$t$的数值,$R_{i}(t)=\ln(P_{i}(t)/P_{i}(t-1))$定义为时间序列$i$从第($t-1$)期到第$t$期的对数变化率,从而得到16个用于下文计算的变化时间序列.
由于聚集系数表示网络的紧密程度,在任一静态网络中它代表着股票间的收益率关系集合.而随着时间的推移,股票收益率的整体关系由于投资者的买卖行为而发生变化.而得到的时间序列的实际意义在于反映了由于投资者交易而引起的股票收益率的整体关系的变化量,也就是一种群体交易整体性的变化量. 2.2 经典R/S分析
Hurst提出了R/S分析方法,采用统计量$H$来识别系统性的非随机特征,即Hurst指数,其计算的具体步骤如下:
1)定义长度为$N$的收益序列{\{}$R_{t}${\}},并将它分割为长度为$n$的$A$个连续子区间.将每一子区间标为$I_{a}$,$a=1,2,\cdots,A$.于是$I_{a}$中每一点可以表示为$R_{k,a}$,$k=1,2,\cdots,n$; $a=1,2,\cdots,A$.
2)对每一长度为$n$的子区间$I_{a}$,计算其均值为:
| $e_a =\frac{1}{n}\sum\limits_{k=1}^n {R_{k,a} }$ | (10) |
对单个子区间计算其累积均值离差$X_{k,a}$:
| $X_{k,a} =\sum\limits_{i=1}^k {(R_{i,a} -e_a )} ,k=1,2,\cdots,n$ | (11) |
3) 由式(11)可知,单个子区间累积均值离差序列{\{}$X_{1,a},X_{2,a},\cdots,X_{n,a}${\}}之和为零.定义单个子区间的极差为:
| $R_{I_{a}}=\max(X_{k,a})-\min(X_{k,a}),k=1,2,\cdots,n$ | (12) |
4)计算每一子区间的标准差$S_{Ia}$,并用它对极差进行重标度/标准化($R_{Ia}/S_{Ia}$):
| $S_{I_a } =\sqrt {\frac{1}{n}\sum\limits_{k=1}^n {(E_{k,a} -e_a )^2} }$ | (13) |
5)因此,对划分长度$n$,可以计算$A$个子区间平均的重标度极差:
| $(R/S)_n =\frac{1}{A}\sum\limits_{a=1}^A {(R_{I_a } /S_{I_a } )}$ | (14) |
6)对不同的划分长度(即不同的时间尺度)$n$重复以上计算过程,可得到多个平均重标度极差值.$\log(R/S)$与$\log(n)$存在线性关系:
| $\log(R/S)_{n}=a+H\log(n)$ | (15) |
7)对$n$和$R/S$进行双对数回归,其斜率就是长程相关的参数,即Hurst指数$H$.因此,可以通过普通最小二乘法得出序列的长程相关参数$H$.
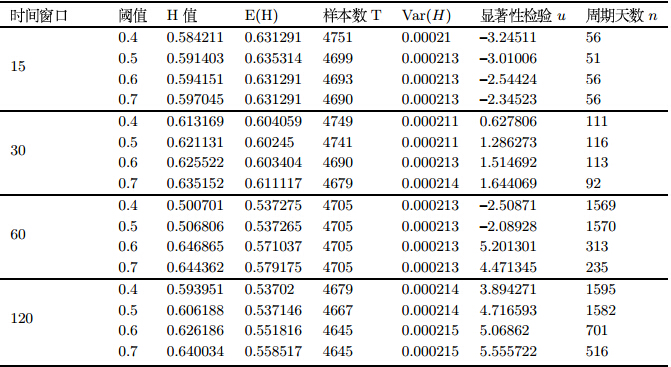
Hurst指数能够区分出分形时间序列,并能够进一步判定该序列是持久性序列还是反持久性序列:当$H=0.5$时,该过程是一个独立同分布过程;当$0.5 本节首先展示2.1节得到的16个时间序列的基本统计量,如表 2所示.
从表 2可以看出,大部分时间序列呈现右偏,且峰度大于3,表现出尖峰厚尾现象.JB统计量说明时间序列属于非正态分布.
利用R/S分析方法对2.1节得到的16个时间序列进行分析.结果如图 4(只展示部分图片结果)和表 3所示.
其中显著性检验利用公式(16),
从表 3可以看出,16个时间序列的$H$值均大于0.5,但从显著性检验的结果来看,表中最后6个时间序列通过了$Z_{0.05}=1.96$的显著性检验.
2.4 结果分析及讨论
从表 3的结果来看,可以得到以下结论:
1)本节分析的16个时间序列的$H$值均大于0.5,其中通过显著性检验的时间序列有6个,这说明所研究时间序列具有长记忆性和持久性.由2.1节所述,时间序列的实际意义是一种群体交易整体性的变化量,那么这一长记忆性和持久性就可以解释为交易者的群体心理惯性.在实际的市场中,各类投资者虽然交易的时限和频度不同,但是他们都具有自身的某种交易习惯,而且这种交易习惯并不会轻易改变.那么,由交易者引起的市场价格的变化也会形成某种"习惯"且不会轻易改变.因此,由此产生的时间序列就展现出这种长记忆性和持久性,这些性质事实上是交易者群体行为惯性的体现.
2)通过显著性检验的时间序列共有6个,其中60天组有2个,120天组有4个,而其余并未通过检验.这说明这6个时间序列所展示的长记忆性和持久性是值得信赖的,而其余的时间序列的长记忆性和持久性有待进一步确认.考虑到时间序列的实际意义,长时间窗口组别时间序列所包含的交易者群体行为惯性应该较短时间窗口组别的时间序列更为稳定和完整的.这与实际市场中的情况应该是一致的,单个投资者在较长时间形成的交易习惯一般上要比短时间形成的交易习惯更为持久和稳定,而整个市场投资者的群体习惯则更是如此.另外,长时间窗口包含的交易日较多,期间发生的事件和其它因素也较为充分,本身也具备一定的抗扰和去噪的特性.这也使得最终的分析结果更为良好.
3)从$H$值的具体数值来看,大致呈现出随着时间窗口和阈值的增加而增加的规律.也就是说随着时间窗口和阈值的递增,时间序列呈现出的长记忆性和持久性越明显.$H$值随着时间窗口的递增而递增的解释与本小节第二点的结论解释相类似,这里就不再重复了.而$H$值随着阈值的递增而递增则说明了这样的情况.在网络中,高阈值表示的是股票网络整体联系度的增强,那么此时的$H$值较高则说明整体联系度较强的股票网络背后的交易者群体行为惯性也较强.在实际市场中,关联度较高的股票往往是同一板块或是有其它某种共同特征的股票,而相较于低阈值时的情况,投资这些关联度较高股票的投资者的投资范围往往更为集中,对所投资股票的研究程度也较高,所以形成的投资习惯也更难改变,这就使得产生的交易者群体行为惯性更强.
4)从周期天数$n$的数值来看,呈现出随着时间窗口的增加而增长的规律,说明在实际市场中,较长时间窗口下形成的交易者群体行为惯性的循环周期更长,这也应该是得益于长时间窗口形成的交易习惯较为稳定.但在60天和120天组别中,随着阈值的增加,$n$的数值呈下降趋势.这说明在实际市场中,投资关联度较高股票的投资者产生的交易者群体行为惯性的循环周期更短.这是由于在市场中,中国股市的不成熟使得市场股票往往随着宏观及产业政策的变化而出现大面积轮动的现象.这就使得关联度较高的股票种类较低阈值的情况而更不稳定.那么,随着宏观及产业政策的变化,投资于某些关联度较高股票的投资者的投资习惯也会随着股票走势的大面积轮动发生变化,其周期天数必然变小.而在低阈值时,由于此时网络涵盖股票数量较多,受到政策面影响时网络变化不会很大,所以产生的交易者群体行为惯性的持续周期更长.
值得进一步说明的是,
$H$值高低表示的是在循环周期内区别于传统的随机游动的趋势性的强度,具体到本节,说明的是投资者在投资关联度较高股票时的交易者群体行为惯性的趋势性的强度,也就是说交易者群体在一定时间内保持这种交易习惯的可能性更大.而循环周期$n$则说明这种趋势性的周期长度,也就是交易者群体保持这种交易习惯的周期.在文献[3]中计算的股票数据中,也存在$H$值和周期天数$n$不一致的现象,但这并不矛盾.
传统分形分析也得到了股市的对记忆性和长程相关性,但是本文与传统方法的研究对象有所不同.传统方法的对象主要是股票指数,而本文是针对复杂网络的宏观参数进行分析,所不同的是,指数事实上是反映了市场股票价格的某种加权平均值,而本文的复杂网络参数是利用了网络的视角得到的整体市场统计特性.相比较而言,以往的分析对象相对简单,而本文的分析方法更贴近市场产生的本源动力,也就是交易者的行为集合.
3 结论
本文从空间和时间两个角度分析中国股市复杂网络的分形特征.在空间角度上,通过建立三个静态网络,利用类似于改变观测尺度的方法计算网络的分形维数.在时间角度上,通过建立中国股市复杂网络聚集系数的时间序列,利用R/S分析方法得出时间序列的分形特征.具体结论如下:
1)按照本文所述的方法,中国股市复杂网络存在空间分形特征,且其分形维数随着网络阈值的增大而减小.这说明,在较高的相关程度下存在相互联系的股票之间的整体相关性较强.
2)在实际市场中,构建投资组合只需要一定的品种数量就可以达到涵盖整体市场相关性的水平.
3)中国股市复杂网络聚集系数时间序列具有长记忆性和持久性,且在长时间窗口下这一性质更值得信赖.从$H$值的具体数值来看,大致呈现出随着时间窗口和阈值的增加而增加的规律.从周期天数$n$的数值来看,呈现出随着时间窗口的增加而增长,随着阈值的增加而下降的规律.
4)在实际市场中,长时间窗口和高联系度股票产生的交易者群体行为惯性更强,长时间窗口和低联系度股票产生的交易者群体行为惯性的持续周期更长.
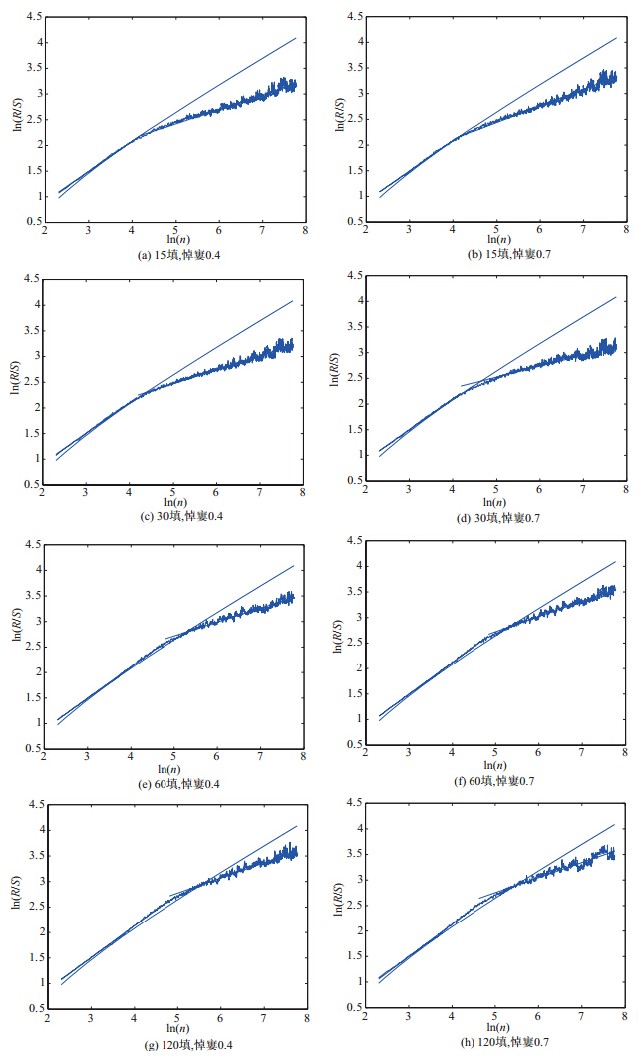
图 4 R/S分析结果
$u=\frac{H-E(H)}{\sqrt {Var(H)} }\sim N(0,1)$
(16)
| [1] | Peters E E. Chaos and order in the capital market[M]. New York: Wiley, 1991: 127-128. |
| [2] | Peters E E. Fractal market analysis[M]. New York: Wiley, 1994: 38-47. |
| [3] | 崔鑫,邵芸,王宗军. 资本市场非线性理论研究综述与展望[J]. 管理科学学报, 2004, 7(3): 75-85. Cui Xin, Shao Yun, Wang Zongjun. On non-linearity in capital market: Summary and prospect[J]. Journal of Management Sciences in China, 2004, 7(3): 75-85. |
| [4] | 王新宇,宋学峰,吴瑞明. 中国证券市场的分形分析[J]. 管理科学学报, 2004, 7(5): 67-74. Wang Xinyu, Song Xuefeng, Wu Ruiming. Fractal analysis of China stock markets[J]. Journal of Management Sciences in China, 2004, 7(5): 67-74. |
| [5] | 宿成建,缪晓波,刘星. 中国证券市场的非线性特征与分形维分析[J]. 系统工程理论与实践, 2005, 25(5): 68-73. Su Chengjian, Miao Xiaobo, Liu Xing. Nonlinear characteristics and fractal dimension analysis of Chinese stock markets[J]. Systems Engineering —— Theory & Practice, 2005, 25(5): 68-73. |
| [6] | 都国雄,宁宣熙. 上海证券市场的多重分形特性分析[J]. 系统工程理论与实践, 2007, 27(10): 40-47.Du Guoxiong, Ning Xuanxi. Multifractal analysis on Shanghai stock market[J]. Systems Engineering —— Theory & Practice, 2007, 27(10): 40-47. |
| [7] | 魏宇,黄登仕. 基于多标度分形理论的金融风险测度指标研究[J]. 管理科学学报, 2005, 8(4): 50-59. Wei Yu, Huang Dengshi. Study on financial risk measure based on multifractal theory[J]. Journal of Management Sciences in China, 2005, 8(4): 50-59. |
| [8] | 周炜星. 上证指数高频数据的多重分形错觉[J]. 管理科学学报, 2010, 13(3): 81-86. Zhou Weixing. Illusionary multifractality in high-frequency data of Shanghai stock exchange composite index[J]. Journal of Management Sciences in China, 2010, 13(3): 81-86. |
| [9] | Grech D, Pamula G. The local Hurst exponent of the financial time series in the vicinity of crashes on the Polish stock exchange market[J]. Physica A, 2008, 387(18): 4299-4308. |
| [10] | Serletis A. Mean reversion in the US stock market[J]. Chaos, Solitons and Fractals, 2009, 40(18): 2007-2015. |
| [11] | Lee C Y. Characteristics of the volatility in the Korea composite stock price index[J]. Physica A, 2009, 388(18): 3837-3850. |
| [12] | Onali E, Goddard J. Are European equity markets efficient? New evidence from fractal analysis[J]. Physica A, 2011, 20(18): 59-67. |
| [13] | 苑莹,庄新田. 中国股票市场的长记忆性与市场发展状态[J]. 数理统计与管理, 2008, 27(1): 156-163.Yuan Ying, Zhuang Xintian. Long memory and state of market development in Chinese stock markets[J]. Application of Statistics and Management, 2008, 27(1): 156-163. |
| [14] | Albert R, Barabási A L. Statistical mechanics of complex networks[J]. Reviews of Modern Physics, 2002, 74(1): 47-97. |
| [15] | Newman M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(3): 167-256. |
| [16] | 刘涛,陈忠,陈晓荣. 复杂网络理论及其应用研究概述[J]. 系统工程, 2005, 23(6): 1-7. Liu Tao, Chen Zhong, Chen Xiaorong. A brief review of complex networks and its application[J]. Systems Engineering, 2005, 23(6): 1-7. |
| [17] | Namaki A, Shirazi A H, Raei R, et al. Network analysis of a financial market based on genuine correlation and threshold method[J]. Physica A, 2011, 390(1): 3835-3841. |
| [18] | Tabak M B, Serra R T, Cajueiro O D. Topological properties of stock market networks: The case of Brazil[J]. Physica A, 2010, 389(2): 3240-3249. |
| [19] | Galazka M. Characteristics of the Polish stock market correlations[J]. International Review of Financial Analysis, 2011, 20(1): 1-5. |
| [20] | 李英,曹宏铎,邢浩克. 基于复杂网络少数者博弈模型的金融市场仿真研究[J]. 系统工程理论及实践, 2012, 32(9): 1882-1890.Li Ying, Cao Hongduo, Xing Haoke. Modeling and simulation of complex finance network based on minority game[J]. Systems Engineering —— Theory & Practice, 2012, 32(9): 1882-1890. |
| [21] | 蔡世民,洪磊,傅忠谦,等.基于复杂网络的金融市场网络结构实证研究[J].复杂系统与复杂性科学, 2011, 8(3): 29-33. Cai Shimin, Hong Lei, Fu Zhongqian, et al. Empirical study on network structure of financial market based on complex network theory[J]. Complex Systems and Complexity Science, 2011, 8(3): 29-33. |
| [22] | Mandelbrot B B. How long is the coast of Britain? Statistical self-similarity and fractal dimension[J]. Science, 1967, 156(3775): 636-638. |