2. 重庆科技学院石油与天然气工程学院, 重庆 沙坪坝 401331;
3. 中国石油川庆钻探工程有限公司钻采工程技术研究院, 四川 广汉 618300
2. School of Petroleum and Natural Gas Engineering, Chongqing University Of Science & Technology, Shapingba, Chongqing 401331, China;
3. Drilling & Production Engineering Research Institute, CNPC Chuanqing Drilling Engineering Co. Ltd., Guanghan, Sichuan 618300, China
随着石油天然气勘探开发工作的不断深入,环 空带压问题越来越突出。据有关统计资料,美国外 大陆架区域大部分油气井存在环空带压现象,统计 的8 122 口井中存在11 498 个环空带压套管段,且 50% 发生在生产套管和油管之间的环形空间。水泥 环的密封完整性是影响环空带压的关键因素之一, 水泥环密封失效将导致层间气窜、环空带压和套管 损坏等问题,对于高含硫气井还可能诱发严重的人 员伤亡、环境污染和经济损失。因此,保持水泥环 完整性对降低井口环空带压、提高井筒安全性、延 长开采寿命具有重要意义。
高温高压井主要是指储层温度大于150 ℃、地 层压力梯度大于18 kPa/m 或井口压力大于70 MPa 的井,且通常为深井、超深井[1]。由于特殊的高温 高压井筒环境,使得高温高压井井筒完整性管理 越来越受到国内外油田专家和学者的重视[2-6]。在 试压、压裂酸化(井口加背压,提高油管柱力学可靠 性)以及正常生产过程中,受作业载荷、油管或封隔 器泄漏等因素影响,水泥环失效将加剧环空带压, 带来潜在安全隐患。为此,在现有井筒水泥环力学 模型基础上[7-17],建立考虑温度效应的套管水泥 环地层耦合力学模型,研究水泥环的失效准则,讨 论考虑井筒温度效应时环空带压对水泥环密封性能 的影响,以期确定更合理的最大允许井口环空带压 值,并提升高温高压气井环空带压管理水平。
1 水泥环力学模型水泥浆凝固后,套管、水泥环和地层可视为一 个复合圆柱体。由于套管、水泥环和地层的物性参 数差异较大,套管内压、地层压力(外压)作用和复 合圆柱体温度的变化时,在套管与水泥环之间的胶 结面及水泥环和地层之间的胶结面会产生接触压 力或拉应力。考虑两界面完全胶结,则可根据界面 处的位移连续条件计算水泥环界面接触压力,最终 计算出水泥环径向和切向的应力场。水泥环力学模 型基本假设:套管无几何缺陷、水泥环结构完整,水 泥环第一、第二胶结面胶结良好,3 者均视为厚壁圆 柱体;套管、水泥环、地层岩石都为均质各向同性材 料,且水泥环无残余内应力;将复合圆柱体受力简 化为平面应变问题,其受力示意图见图 1。
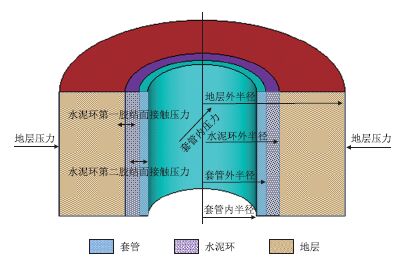 |
| 图1 套管-水泥环-地层岩石复合圆柱体模型受力示意图 Fig. 1 Pressure contrast of different development ways |
考虑温度效应时,圆柱体切向应变为
| ${{\varepsilon }_{\theta }}\text{=}\frac{1}{E}\left[ {{\sigma }_{\theta }}-v\left( {{\sigma }_{z}}+{{\sigma }_{r}} \right) \right]+\alpha \Delta T$ | (1) |
式中:εθ -切向应变,无因次;
E-弹性模量,MPa;
σr,σθ,σz 径向应力、切向应力和轴向应力, MPa;
ν-材料泊松比,无因次;
α-材料线膨胀系数,℃−1;
ΔT 温度变化值,℃。
圆柱体轴向应变为
| ${{\varepsilon }_{z}}\text{=}\frac{1}{E}\left[ {{\sigma }_{z}}-v\left( {{\sigma }_{\theta }}+{{\sigma }_{r}} \right) \right]+\alpha \Delta T$ | (2) |
式中:εz 轴向应变,无因次。
根据复合圆柱体平面应变假设,满足εz ≈ 0,由 式(2),可得
| ${{\sigma }_{z}}=v\left( {{\sigma }_{\theta }}+{{\sigma }_{r}} \right)+\alpha E\Delta T$ | (3) |
将式(3)代入式(1)中可得
| ${{\varepsilon }_{\theta }}=\frac{1}{E}\left[ \left( 1-{{v}^{2}} \right){{\sigma }_{\theta }}-\left( v-{{v}^{2}} \right){{\sigma }_{r}}+\left( 1-v \right)\alpha E\Delta T \right]$ | (4) |
从而得到圆柱体的径向变形量为
| ${{\delta }_{r}}=\frac{r}{E}\left[ \left( 1-{{v}^{2}} \right){{\sigma }_{\theta }}-\left( v+{{v}^{2}} \right){{\sigma }_{r}}+\left( 1-v \right)\alpha E\Delta T \right]$ | (5) |
式中:δr-圆柱体的径向变形量,mm;
r-圆柱体的半径,mm。
对于套管,受内压力(pi)、外挤压力(pc1)作用, 由拉梅公式可得套管径向应力分布
| ${{\sigma }_{\text{rs}}}=\frac{{{p}_{\text{i}}}{{a}^{2}}-{{p}_{\text{c}1}}{{b}^{2}}}{{{b}^{2}}-{{a}^{2}}}-\frac{\left( {{p}_{\text{i}}}-{{p}_{\text{c}1}} \right){{a}^{2}}{{b}^{2}}}{{{b}^{2}}-{{a}^{2}}}\frac{1}{{{r}^{2}}}$ | (6) |
式中:σrs-套管径向应力,MPa;
pi-套管内压力,MPa;
pc1-套管外挤压力(水泥环第一胶结面接触压 力),MPa;
a-套管内半径,mm;
b-套管外半径(水泥环内半径),mm。
套管切向应力分布
| ${{\sigma }_{\theta \text{s}}}=\frac{{{p}_{\text{i}}}{{a}^{2}}-{{p}_{\text{c}1}}{{b}^{2}}}{{{b}^{2}}-{{a}^{2}}}+\frac{\left( {{p}_{\text{i}}}-{{p}_{\text{c}1}} \right){{a}^{2}}{{b}^{2}}}{{{b}^{2}}-{{a}^{2}}}\frac{1}{{{r}^{2}}}$ | (7) |
式中:σθs-套管径向应力,MPa。
根据假设,套管中∂(ΔT)/∂r = 0,则由式(5)~ 式(7)可得套管外壁(r = b)处径向变形量为
| $\begin{align} & {{\delta }_{\text{rso}}}=\frac{b}{{{E}_{\text{s}}}}\left( 1-v_{\text{s}}^{2} \right)\left[ \frac{2{{a}^{2}}{{p}_{\text{i}}}-{{p}_{\text{c}1}}\left( {{a}^{2}}+{{b}^{2}} \right)}{{{b}^{2}}-{{a}^{2}}} \right]+ \\ & \frac{b}{{{E}_{\text{s}}}}\left( {{v}_{\text{s}}}+v_{\text{s}}^{2} \right){{p}_{\text{c}1}}+b\left( 1-{{v}_{\text{s}}} \right){{\alpha }_{\text{s}}}\Delta T \\ \end{align}$ | (8) |
式中:δrso-套管外壁径向变形量,mm;
Es-套管弹性模量,MPa;
νs—套管泊松比,无因次;
αs-套管线膨胀系数,℃−1。
对于水泥环,其内外壁分别受接触压力pc1、pc2 作用,水泥环中径向应力为
| ${{\sigma }_{\text{rc}}}=\frac{{{p}_{\text{c}1}}{{b}^{2}}-{{p}_{\text{c}2}}{{c}^{2}}}{{{c}^{2}}-{{b}^{2}}}-\frac{\left( {{p}_{\text{c}1}}-{{p}_{\text{c}2}} \right){{b}^{2}}{{c}^{2}}}{{{c}^{2}}-{{b}^{2}}}\frac{1}{{{r}^{2}}}$ | (9) |
式中:σrc-水泥环径向应力,MPa;
pc2-水泥环第二胶结面接触压力,MPa;
c-水泥环外半径,mm。
水泥环切向应力为
| ${{\sigma }_{\theta \text{c}}}=\frac{{{p}_{\text{c}1}}{{b}^{2}}-{{p}_{\text{c}2}}{{c}^{2}}}{{{c}^{2}}-{{b}^{2}}}+\frac{\left( {{p}_{\text{c}1}}-{{p}_{\text{c}2}} \right){{b}^{2}}{{c}^{2}}}{{{c}^{2}}-{{b}^{2}}}\frac{1}{{{r}^{2}}}$ | (10) |
式中:σθc -水泥环切向应力,MPa。
根据假设,水泥环中∂(ΔT)/∂r = 0,则由式(5)、 式(9)、式(10)可得水泥环内壁(r = b)处径向变形量为
| $\begin{align} & {{\delta }_{\text{rci}}}=\frac{b}{{{E}_{\text{c}}}}\left( 1-v_{\text{c}}^{2} \right)\left[ \frac{{{p}_{\text{c}1}}\left( {{b}^{2}}+{{c}^{2}} \right)-2{{c}^{2}}{{p}_{\text{c}2}}}{{{c}^{2}}-{{b}^{2}}} \right]+ \\ & \frac{b}{{{E}_{\text{c}}}}\left( {{v}_{\text{c}}}+v_{\text{c}}^{2} \right){{p}_{\text{c}1}}+b\left( 1-{{v}_{\text{c}}} \right){{\alpha }_{\text{c}}}\Delta T \\ \end{align}$ | (11) |
式中:δrci-水泥环内壁径向变形量,mm;
Ec-水泥环弹性模量,MPa;
νc-水泥环泊松比,无因次;
αc-水泥环线膨胀系数,℃−1。
由套管外壁和水泥环内壁连续条件可知, 式(8)和式(11)中两个径向变形量应该相等,有
| $\begin{align} & A{{p}_{\text{i}}}+B{{p}_{\text{c}1}}+C{{p}_{\text{c}2}}={{E}_{\text{c}}}{{E}_{\text{s}}}\Delta T \\ & \left[ \left( 1-{{v}_{\text{c}}} \right){{\alpha }_{\text{c}}}-\left( 1-{{v}_{\text{s}}} \right){{\alpha }_{\text{s}}} \right] \\ \end{align}$ | (12) |
其中:
$\begin{align} & A=\frac{2{{a}^{2}}}{{{b}^{2}}-{{a}^{2}}}{{E}_{\text{c}}}\left( 1-v_{\text{s}}^{2} \right);C=\frac{2{{c}^{2}}}{{{c}^{2}}-{{b}^{2}}}{{E}_{\text{s}}}\left( 1-v_{\text{c}}^{2} \right); \\ & B=\frac{2{{b}^{2}}v_{\text{s}}^{2}+\left( {{b}^{2}}-{{a}^{2}} \right){{v}_{\text{s}}}-\left( {{b}^{2}}+{{a}^{2}} \right)}{{{b}^{2}}-{{a}^{2}}}{{E}_{\text{c}}}- \\ & \frac{\left( {{b}^{2}}+{{c}^{2}} \right)-2{{b}^{2}}v_{\text{c}}^{2}+\left( {{c}^{2}}-{{b}^{2}} \right){{v}_{\text{s}}}}{{{c}^{2}}-{{b}^{2}}}{{E}_{\text{s}}} \\ \end{align}$。
由(5)、式(9)、式(10)也可得到水泥环第二胶结面 r=c处的径向变形量为
| $\begin{align} & {{\delta }_{\text{rco}}}=\frac{c}{{{E}_{\text{c}}}}\left( 1-v_{\text{c}}^{2} \right)\left[ \frac{2{{b}^{2}}{{p}_{\text{c}1}}-{{p}_{\text{c}2}}\left( {{b}^{2}}+{{c}^{2}} \right)}{{{c}^{2}}-{{b}^{2}}} \right]+ \\ & \frac{c}{{{E}_{\text{c}}}}\left( {{v}_{\text{c}}}+v_{\text{c}}^{2} \right){{p}_{\text{c}2}}+c\left( 1-{{v}_{\text{c}}} \right){{\alpha }_{\text{c}}}{{E}_{\text{c}}}\Delta T \\ \end{align}$ | (13) |
式中:δrco-水泥环外壁径向变形量,mm。
对于地层岩石,其内外壁分别受接触压力pc2 和地层压力pf 作用,地层岩石中径向和切向应力分 别为
| ${{\sigma }_{\text{rf}}}=\frac{{{p}_{\text{c}2}}{{c}^{2}}-{{p}_{\text{f}}}{{d}^{2}}}{{{d}^{2}}-{{c}^{2}}}-\frac{\left( {{p}_{\text{c}2}}-{{p}_{\text{f}}} \right){{b}^{2}}{{c}^{2}}}{{{d}^{2}}-{{c}^{2}}}\frac{1}{{{r}^{2}}}$ | (14) |
| ${{\sigma }_{\theta \text{f}}}=\frac{{{p}_{\text{c}2}}{{c}^{2}}-{{p}_{\text{f}}}{{d}^{2}}}{{{d}^{2}}-{{c}^{2}}}+\frac{\left( {{p}_{\text{c}2}}-{{p}_{\text{f}}} \right){{c}^{2}}{{d}^{2}}}{{{d}^{2}}-{{c}^{2}}}\frac{1}{{{r}^{2}}}$ | (15) |
式中:σrf-地层径向应力,MPa;
pf-地层压力,MPa;
d-地层外半径,mm;
σθf-地层切向应力,MPa
根据假设,地层中∂(ΔT)/∂r = 0,则由式(5)、 式(14)、式(15)水泥环第二胶结面(r = c)处径向变 形量为
| $\begin{align} & {{\sigma }_{\text{rfi}}}=\frac{c}{{{E}_{\text{f}}}}\left( 1-v_{\text{f}}^{2} \right)\left[ \frac{{{p}_{\text{c}2}}\left( {{c}^{2}}+{{d}^{2}} \right)-2{{d}^{2}}{{p}_{\text{f}}}}{{{d}^{2}}-{{c}^{2}}} \right]+ \\ & \frac{c}{{{E}_{\text{f}}}}\left( {{v}_{\text{f}}}+v_{\text{f}}^{2} \right){{p}_{\text{c}2}}+c\left( 1-{{v}_{\text{f}}} \right){{\alpha }_{\text{f}}}\Delta T \\ \end{align}$ | (16) |
式中:δrfi--水泥环第二胶结面径向变形量,mm;
Ef--地层岩石弹性模量,MPa;
αf--地层岩石线膨胀系数,℃−1;
νf--地层岩石泊松比,无因次。
由水泥环外壁和地层岩石内壁连续条件可得 式(13)和式(16)中两个变形量也应该相等,从而有
| $\begin{align} & U{{p}_{\text{c}1}}+V{{p}_{\text{c}2}}+W{{p}_{\text{f}}}={{E}_{\text{c}}}{{E}_{\text{f}}}\Delta T \\ & \left[ \left( 1-{{v}_{\text{f}}} \right){{\alpha }_{\text{f}}}-\left( 1-{{v}_{\text{c}}} \right){{\alpha }_{\text{c}}} \right] \\ \end{align}$ | (17) |
其中:$\begin{align} & U=\frac{2{{b}^{2}}}{{{c}^{2}}-{{b}^{2}}}{{E}_{\text{f}}}\left( 1-v_{\text{c}}^{2} \right);W=\frac{2{{b}^{2}}}{{{d}^{2}}-{{c}^{2}}}{{E}_{\text{c}}}\left( 1-v_{\text{f}}^{2} \right); \\ & V=\frac{2{{c}^{2}}v_{\text{c}}^{2}+\left( {{c}^{2}}-{{b}^{2}} \right){{v}_{\text{c}}}-\left( {{c}^{2}}+{{b}^{2}} \right)}{{{c}^{2}}-{{b}^{2}}}{{E}_{\text{f}}}- \\ & \frac{\left( {{d}^{2}}+{{c}^{2}} \right)-2{{c}^{2}}v_{\text{f}}^{2}+\left( {{d}^{2}}-{{c}^{2}} \right){{v}_{\text{f}}}}{{{d}^{2}}-{{c}^{2}}}E \\ \end{align}$。
联立式(13)、式(17)可得水泥环内外壁接触压 力pc1 和pc2。从而,由式(9)、式(10)可求得水泥环 在任意半径r 处的径向应力和切向应力。
2 水泥环失效准则水泥环失效主要有胶结面受拉失效和水泥环本 体受压失效,水泥环在拉应力和压应力共同作用下 也会发生剪切失效。水泥环受纯拉伸载荷时,可采 用最大主应力准则来判断失效,但水泥环的失效有 时主要受压缩载荷而非拉伸载荷控制,这时可采用 莫尔库仑准则来预测不同应力状态下水泥环的失 效,脆性材料摩尔-库仑失效准则见表 1。
| 表1 脆性材料摩尔-库仑失效准则表 Table 1 Recovery ratio amplification of different development ways |
对于高温高压井,由于作业试压、压裂酸 化(需环空加压)等井下工况会使环空带压升高, 同时,受温度、压力变化使环空流体膨胀以及 由于油气从地层经水泥隔离层和环空液柱向 上窜流也会引起环空压力的升高。为了讨论环 空带压、温度变化对水泥环应力和失效的影响, 假设:(1)ϕ215.90 mm井眼下入ϕ177.80 mm(壁厚 10.36 mm)P110 套管;(2)水泥环厚度为21.34 mm; (3)P110 套管弹性模量为200 GPa、泊松比为0.23、 线膨胀系数为1.50×10−5 ℃−1;(4)水泥环弹性 模量为5.6 GPa、泊松比为0.18、线膨胀系数为 1.05×10−5 ℃−1、抗拉强度为4.2 MPa、抗压强度为 41.0 MPa;(5)地层岩石弹性模量为17 GPa、泊松比 为0.20、线膨胀系数为1.05×10−5 ℃−1。
3.2 结果分析 3.2.1 环空带压对水泥环应力的影响为了讨论环空压力、井筒温度对水泥环密封失 效的影响,计算了环空带压0~50.00 MPa、开采过程 井筒温度升高0~50 ℃等工况下水泥环径向应力和 切向应力的变化情况。不考虑井筒温度变化时,不 同环空带压下水泥环中径向应力和切向应力分布 情况如图 2、图 3 所示。可以看出:水泥环沿径向 受压,沿切向受拉,且最大压应力和拉应力均出现 在第一胶结面,表明水泥环将最先在此处失效。当 环空带压为50.00 MPa,水泥环与套管界面处最大 径向压应力为12.74 MPa,表明水泥环不会发生压 缩失效;但当环空带压为45.00 MPa 时,水泥环与 套管界面处切向拉应力已达4.28 MPa,该值已超过 水泥环的抗拉强度4.20 MPa,此时水泥环将出现微 裂纹。
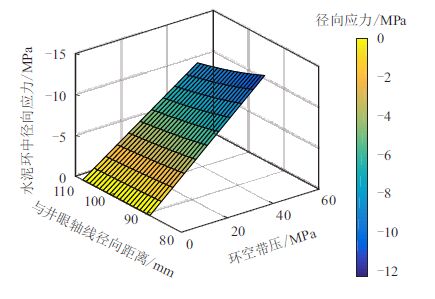 |
| 图2 不同环空带压下水泥环中径向应力(ΔT = 0 ℃) Fig. 2 Radial stress within cement sheath under different SCP value(ΔT = 0 ℃) |
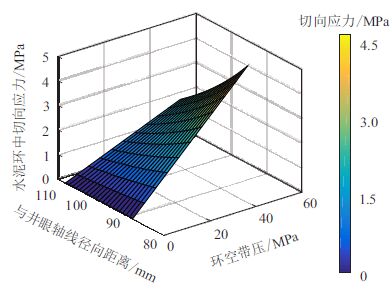 |
| 图3 不同环空带压下水泥环中切向应力(ΔT = 0 ℃) Fig. 3 Tangential stress within cement sheath under different SCP value(ΔT = 0 ℃) |
不同环空带压及温度变化下水泥环第一、第 二胶结面径向应力分布情况如图 4、5 所示。可以 看出:水泥环沿径向受压,且最大压应力出现在水 泥环与套管界面,表明水泥环将最先在此处失效; 环空带压越大、温度变化越大,水泥环胶结面径向 压应力越大。当环空带压为50.00 MPa、温度变化50 ℃时,水泥环与套管界面处最大径向压应力为 14.08 MPa,表明水泥环不会发生压缩失效。
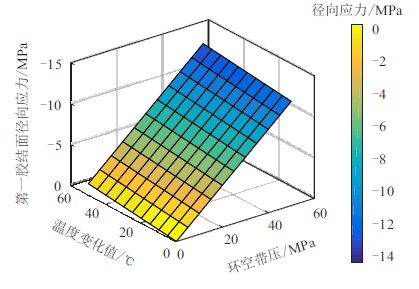 |
| 图4 不同环空带压及不同温度变化下第一胶结面径向应力 Fig. 4 Radial stress of the first cemented surface under different SCP value and temperature |
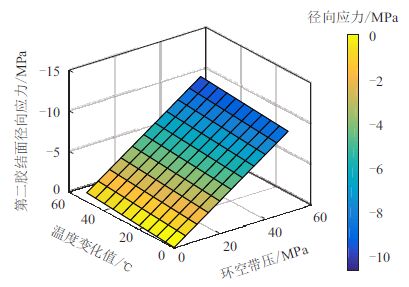 |
| 图5 不同环空带压及不同温度变化下第二胶结面径向应力 Fig. 5 Radial stress of the second cemented surface under different SCP value and temperature |
不同环空带压及不同温度变化下水泥环第一、 第二胶结面切向应力分布情况如图 6、7 所示。
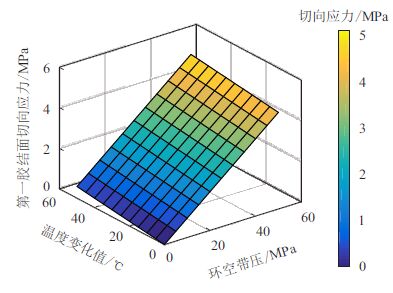 |
| 图6 不同环空带压及不同温度变化下第一胶结面切向应力 Fig. 6 Tangential stress of the first cemented surface with different SCP value and temperature |
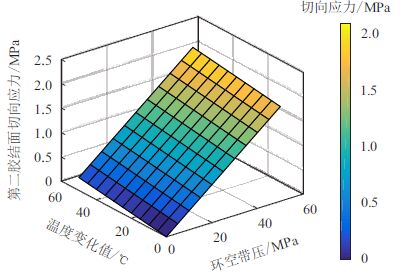 |
| 图7 不同环空带压及不同温度变化下第二胶结面切向应力 Fig. 7 Tangential stress of the second cemented surface with different SCP value and temperature |
可以看出:水泥环沿切向受拉,且最大拉应力 均出现在水泥环与套管界面,表明水泥环将最先在 此处失效;环空带压越大、温度变化越大,水泥环胶 结面切向拉应力越大。当环空带压为40.00 MPa、 温度变化35 ℃时,水泥环与套管界面处切向拉应 力已达4.21 MPa,该值已超过水泥环的抗拉强度 4.20 MPa,此时水泥环将开始被拉坏。
3.2.2 环空带压对水泥环失效的影响在环空带压作用下,水泥环将最先在套管与水 泥环界面处发生失效,为分析高温高压井环空带 压对水泥环失效的影响,根据表 1 中水泥环失效准 则,计算了井筒温度变化值为0~50 ℃、环空带压 为0~50.00 MPa 时自由套管段底部水泥环安全系 数(图 8,图中粉色平面的安全系数等于1.0)。
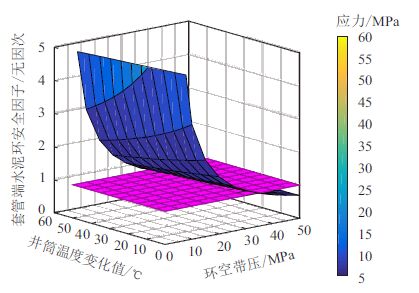 |
| 图8 自由套管段底部水泥环安全系数 Fig. 8 Safety factors of cement sheath at the free casing bottom |
可以看出:环空带压越大,自由套管段底部水 泥环安全系数越低,且温度效应对安全系数的影响 较小。环空带压小于35.00 MPa 时,井筒温度变化 对水泥环安全系数影响较明显,随井筒温度升高, 水泥环安全系数减小;当环空带压大于35.00 MPa 时,井筒温度变化对水泥环安全系数影响很小,但 总体上井筒温度升高时水泥环更易失效。对具体一口井,可根据井身结构(地层水泥环套管)参数建 立水泥环安全系数图版,然后根据井筒温度场、环 空带压值判断水泥环是否会失效,并以此确定合理 的最大允许环空带压值,这对提高高温高压气井环 空压力管理水平,保证井筒安全、延长气井开采寿 命具有重要指导意义。
4 结语(1)环空带压使水泥环中产生的切向拉应力是 水泥环失效的主要因素。井筒温度升高会产生切向 拉应力和径向压应力,此切向拉应力会加剧水泥环 密封失效风险。
(2)高温高压井环空带压工况下,自由套管段 底部水泥环一般最先失效,应将此处失效作为水泥 环失效的薄弱点。
(3)环空带压越大,自由套管段底部水泥环安 全系数越低,且温度效应对安全系数的影响较小。
(4)根据井身结构(地层水泥环套管)参数, 建立水泥环安全系数图版,然后根据井筒温度场、 环空带压值判断水泥环是否会失效,可为确定合理 的最大允许环空带压值提供依据。
| [1] | TAOUTAOU S, BONNECAZE A L, DONDALE A T, et al. Ensuring well integrity in HP/HT wells:Brunei case study[C]. SPE 136884, 2010. |
| [2] |
储胜利, 樊建春, 张来斌, 等. 套管段井筒完整性风险评价方法研究[J].
石油机械, 2009, 37 (6) : 1 –4.
CHU Shengli, FAN Jianchun, ZHANG Laibin, et al. Research on the risk assessment method for wellbore integrity in casing section[J]. China Petroleum Machinery, 2009, 37 (6) : 1 –4. |
| [3] |
张智, 周延军, 付建红, 等. 含硫气井的井筒完整性设计方法[J].
天然气工业, 2010, 30 (3) : 67 –69.
ZHANG Zhi, ZHOU Yanjun, FU Jianhong, et al. A method of well integrity design for sour gas wells[J]. Natural Gas Industry, 2010, 30 (3) : 67 –69. |
| [4] |
车争安, 张智, 施太和, 等. 高温高压含硫气井环空流体热膨胀带压机理[J].
天然气工业, 2010, 30 (2) : 88 –90.
CHE Zheng'an, ZHANG Zhi, SHI Taihe, et al. Mechanism of annular fluid thermal expansion pressure in HTHP sour gas wells[J]. Natural Gas Industry, 2010, 30 (2) : 88 –90. |
| [5] |
胡顺渠, 陈琛, 史雪枝, 等. 川西高温高压气井井筒完整性优化设计及应用[J].
海洋石油, 2011, 31 (2) : 82 –85.
HU Shunqu, CHEN Chen, SHI Xuezhi, et al. Optimal design of well integrity and its application in HPHT gas well in western region of Sichuan[J]. Offshore Oil, 2011, 31 (2) : 82 –85. |
| [6] |
刘健, 郭小阳, 李早元. 储气库固井水泥石关键力学参数测试方法研究[J].
西南石油大学学报(自然科学版), 2013, 35 (6) : 115 –120.
LIU Jian, GUO Xiaoyang, LI Zaoyuan. Study of the test method of key mechanical parameters of set cement in the gas storage well[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2013, 35 (6) : 115 –120. |
| [7] | GOODWIN K J, CROOK R J. Cement sheath stress failure[J]. SPE Drilling Engineering, 1992, 7 (4) : 291 –296. DOI:10.2118/20453-PA |
| [8] | BAUMGARTE C,THIERCELIN M,KLAUS D. Case studies of expanding cement to prevent microannular formation[C]. SPE 56535, 1999. |
| [9] | BOSMA M, RAVI K, VAN DRIEL W, et al. Design approach to sealant selection for the life of the well[C]. SPE 56536, 1999. |
| [10] | MUELLER D T, GOBONCAN V, DILLENBECK R L, et al. Characterizing casing-cement-formation interactions under stress conditions:impact on long-term zonal isolation[C]. SPE 90450, 2004. |
| [11] | LAIDLER A, TAOUTAOU S, JOHNSON C R, et al. A risk analysis approach using stress analysis models to design for cement sheath integrity in a multilateral well[C]. SPE 11059, 2007. |
| [12] | SAINT-MARC J, GARNIER A, BOIS A P. Initial state of stress:the key to achieving long-term cement-sheath integrity[C]. SPE 116651, 2008. |
| [13] |
王耀锋, 李军强, 杨小辉. 套管-水泥环-地层系统应力分布规律研究[J].
石油钻探技术, 2008, 36 (5) : 7 –10.
WANG Yaofeng, LI Junqiang, YANG Xiaohui. Stress distribution in casing-cement-stratum[J]. Petroleum Drilling Techniques, 2008, 36 (5) : 7 –10. |
| [14] | LI Y, LIU S, WANG Z, et al. Analysis of cement sheath coupling effects of temperature and pressure in nonuniform in-situ stress field[C]. SPE 131878, 2010. |
| [15] |
李伟超, 齐桃, 管虹翔, 等. 海上稠油热采井井筒温度场模型研究及应用[J].
西南石油大学学报(自然科学版), 2012, 34 (3) : 105 –110.
LI Weichao, QI Tao, GUAN Hongxiang, et al. Research and application of wellbore temperature field models for thermal recovery well in offshoreheavy oilfield[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (3) : 105 –110. |
| [16] | HAIDER M G, SANJAYAN J, RANJITH P G. Modeling of a well-bore composite cylinder system for cement sheath stress analysis in geological sequestration of CO2[C]//The 46th US Rock Mechanics/Geomechanics Symposium, American Rock Mechanics Association, 2012. |
| [17] |
张智, 黄熠, 李炎军, 等. 考虑腐蚀的环空带压井生产套管安全评价[J].
西南石油大学学报(自然科学版), 2014, 36 (2) : 171 –177.
ZHANG Zhi, HUANG Yi, LI Yanjun, et al. Safety evaluation of production casing considering corrosion in gas well with sustained casing pressure[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36 (2) : 171 –177. |
 2016, Vol. 38
2016, Vol. 38


