Phy-LInformers approach toward structural seismic response prediction
-
摘要: 为了准确评估建筑结构在地震作用下的动力特性和延性性能并促进韧性城乡的建设，本文提出了一种名为Phy-LInformers的深度学习框架，该框架综合运用了长短期记忆网络（long short-term memory，LSTM）、Transformer类模型Informer以及物理先验知识，以实现对建筑结构非线性地震响应的精确预测。该框架的核心思想是结合Informer的编码（Encoder）和解码（Decoder）结构，在Decoder部分引入了LSTM以预测建筑物先前的历史状态信息。同时，通过将现有的物理知识（例如预测变量之间的状态依赖关系和运动控制方程等）编码到损失函数中，对Phy-LInformers进行指导并约束其学习空间，同时提高有限训练数据下深度学习模型的预测性能。随后，通过2个模拟数据算例验证所提框架的性能。结果表明，所提出的Phy-LInformers是一种鲁棒性良好、预测性能优秀的非线性地震响应预测方法，即使在训练样本非常少（例如仅有10条）的情况下依然能准确预测结构在地震作用下的动力响应。这一特性使得Phy-LInformers在工程实践中具有可行性，并且在建筑结构抗震性能评价领域展现出良好的应用前景。Abstract: In order to accurately assess the dynamic and ductile properties of building structures under seismic action and to promote the construction of resilient cities and towns, in this study, we introduce a novel deep learning framework denoted as Phy-LInformers, which integrates long short-term memory (LSTM), Transformer-based model Informer, and prior physical knowledge to achieve precise prediction of nonlinear seismic responses in building structures. The central concept of Phy-LInformers lies in fusing the Encoder and Decoder architectures of Informer, while integrating LSTM within the Decoder component to forecast preceding historical states of the building. Meanwhile, the learning space of the Phy-LInformers’ training process is instructed and constrained by encoding existing physical knowledge (e.g., state dependencies between predictor variables and motion control equations, etc.) into the loss function. And at the same time, the prediction performance of the deep learning model is improved with limited training data. Subsequently, the satisfactory performance of the proposed framework is successfully demonstrated through two illustrative examples. The results demonstrate that the proposed Phy-LInformers is a nonlinear seismic response prediction method with better robustness and superior prediction performance, which can still accurately predict the dynamic response of a structure under seismic excitation even with very few training samples (e.g., only 10 samples). This feature makes Phy-LInformers feasible for engineering practice and shows promising application prospects in the field of seismic performance evaluation of building structures.
-
地震是造成人类生产、生活损失巨大的自然灾害之一，地震可能导致建筑物产生严重的结构损伤、变形甚至倒塌，给人民的生命财产安全带来巨大威胁，同时也对社会稳定产生消极影响。据统计，自 1900 年以来，全球平均每年会发生 6.0 级以上地震 133 次，7.0 级以上地震 20 次，8.0 级以上地震 1 次[1] 。结构系统的动态响应预测一直是设计和评估单个建筑物以及基础设施和大型城市区域可靠性分析的重要工具。地震中约 95% 的人员伤亡是由建筑物（结构）倒塌造成的[2]，准确评估建筑结构在地震作用下的动力特性和延性性能，是一个具有高度理论和应用价值的持久课题。除此之外，震后短时间内对区域建筑结构开展高效的地震损伤评估，可协助政府制定抗震救灾方案[3]，因此，建筑结构的地震响应分析与预测是结构工程以及工程抗震防灾的重要课题，也是进行地震风险评估和建设韧性城乡的基础工作。
学者们在研究建筑结构在强震下的动力响应时采用了不同的方法，主要分为物理驱动和数据驱动2类。物理驱动方法，如容量谱法（capacity spectrum method，CSM）[4]和时程分析法（time history analysis，THA）[5]，通过对结构力学的基础模型进行建模来估计结构响应。容量谱法通过考虑关键的地面振动特征如基本周期的谱加速度简化结构模型，是一种简单而有效的方法。基于有限元法的时程分析是最常用、最精确的方法，适用于具有已知物理特性（如质量、刚度和阻尼矩阵）的结构，但对结构的非线性组件需要精确地分析模型。然而，在实际情况中，数值模型所需的参数可能不可观测或者很难给出精确的模拟，因此根据数值模型精确计算结构地震响应是一项具有挑战性的工作。此外，在实际工程中，基于数值模型的时程分析计算量大、效率低，难以在震后短时间内为应急响应提供支持。
以大数据、人工智能等基础技术为核心的替代方法能够弥补建筑结构计算方法的诸多缺陷[6]。人工智能一直以来都是科学和技术领域中最有用和最具前景的工具之一，特别是机器学习已显示出学习和预测大型和嘈杂数据集中的非线性行为和趋势的巨大潜力。随着机器学习建模方法的发展，基于数据驱动模型的地震响应预测方法逐渐受到关注。郑史雄等[7]归纳总结了人工智能技术在地震动分析预测、桥梁地震响应预测和模式识别及快速评估方面的应用。许多研究利用了考虑地震、土壤和结构特性等的若干手工选择参数，采用了（artificial neural network，ANN） [8-10]、极限梯度增强（extreme gradient boosting，XGBoost）[9]、自适应增强（adaptive boosting，Adaboost）[11]、卷积神经网络（convolutional neural network，CNN）[12-13]、多层感知机（multilayer perceptron，MLP）[14]、长短期记忆网络（long short-term memory，LSTM）[15]、支持向量机（support vector machine，SVM）[16]和随机森林（random forest，RF）[17]等机器学习算法，用于预测地震激励下建筑物的层间位移比、峰值位移或峰值加速度等指标。Chou等[18]也使用SVM算法进行了类似的研究，预测了钢筋混凝土深梁的抗剪强度；Morfidis等[19]提出了一种基于MLP的临界角估计方法；李金珂[20]提出一种数据驱动的基于层间位移角谱和深度卷积神经网络的震后建筑结构最大层间位移角预测方法；施静[21]用贝叶斯优化算法对 CatBoost 模型进行改进，构建了BO-CatBoost 模型对最大震级进行预测研究；禹海涛等[22]提出一种基于人工神经网络ANN的圆形隧道地震响应预测方法，以基岩地震动峰值、隧道埋深等为基本输入参数，对圆形隧道在不同地震动作用下的衬砌受力和变形(包括弯矩、轴力、剪力、直径变化率等结构关键响应指标)进行预测。然而，这些研究中涉及人为介入特征选择，可能引入主观偏见，影响模型的性能。
建筑结构的破坏通常是损伤逐渐积累的结果，而地震则是导致结构损伤累积的一个主要因素。因此，对于全面分析结构行为，准确预测完整的地震响应时程显得至关重要。在前述研究中，大多数侧重于预测单一响应指标（如峰值位移），而未能全面预测每个时刻的完整时间序列响应。通过预测完整的地震响应时程，能够更全面、深入地理解结构的动态响应特性，从而为结构的性能评估和改进提供更有力的支持。在当前研究趋势中，许多学者倾向于使用基于时间的深度神经网络方法，以更全面、准确地模拟结构地震响应。例如，Zhang等[23]提出了2种基于LSTM网络的数据驱动方案，用于结构地震响应时程建模；Oh等[24]提出了一种基于CNN的方法，用于预测建筑结构的地震响应，该方法中，CNN的输入层是测量的地震加速度响应时程，输出是对应的位移响应时程；Torky等[25]利用混合深度学习技术进行结构非线性多分量地震反应预测，使用混合卷积–LSTM (ConvLSTM)网络捕捉建筑物地基和上部结构的加速度时间序列之间的映射关系；Zamani等[26]利用改进的多状态相关参数模型估计方法，预测了地震作用下楼层的加速度时程。已有研究表明，多种深度学习技术和架构被成功应用于完整时序的地震响应预测中。
然而，训练可靠的深度学习模型需要大量且包含丰富输入输出关系的数据。此外，"黑盒"模型对输入数据标记的质量高度依赖，可能导致模型在可用数据集（如训练和验证数据集）之外的数据上准确性和泛化性较差。物理知识引导的深度学习（physics-informed dachine learning，PIDL）是一种新兴的范式，旨在将基于数据的深度学习模型与基于物理的模型融合，以充分利用机器学习的数据发现能力，并同时保留有价值的物理/领域知识[27-28]。物理知识驱动的深度学习算法在土木工程领域的应用不断增加，学者们对相关研究进行了总结[29-30]。Yu等[31]开发了一种物理引导的机器学习方法，将循环神经网络和多层感知器与结构动力学方程相结合，以预测结构的动态响应；Eshkevari等[32]设计了一个基于物理的递归神经网络模型，该模型能够估计线性和非线性多自由度系统的地震响应，其递归块的结构受到微分方程求解算法（Newmark-β方法）的启发；Guo[33]将深度神经网络(deep neural network，DNN)与经典数值积分方法相结合，并采用混合积分时间步方法进行结构非线性地震反应预测；受龙格–库塔(Runge-Kutta，RK)数值算法的启发，Wang等[34]提出了一种Runge-Kutta递归神经网络（Runge-Kutta recurrent neural network，RKRNN）用于地震响应预测；Zhang等[35-36]提出结合物理定律约束的CNN和LSTM体系结构PhyCNN和PhyLSTM2以预测结构地震响应时程。
在PIDL领域，针对结构地震响应预测已经取得了显著的进展。然而，目前的跨学科研究往往忽略了与结构先前状态相关的关键信息。建筑物对当前地震激励的响应与其在之前震动下的状态密切相关。现有研究主要集中在建模建筑物在地震激励下对应时刻的响应，例如基于LSTM的地震响应预测。LSTM的遗忘门机制强调了对短期依赖的捕捉，并保持了对长期依赖的记忆能力，类似于逐步积分法，这也是LSTM在地震响应预测中表现优异的原因。然而，这些研究未考虑建筑物在先前震动下的状态。
为解决上述问题，本文提出了一种结合物理知识的Phy-LInformers网络，用于地震激励下建筑物的响应预测。Phy-LInformers网络框架综合运用了LSTM、Transformer[37]类模型Informer[38]以及物理先验知识，以实现对建筑结构非线性地震响应的精确预测。首先，地震激励通过Encoder编码，得到其高维特征向量；然后，先前时刻的地震激励序列送入LSTM进行时间和空间映射，通过LSTM的遗忘门机制捕捉先前时刻地震动的特征，预测出建筑物先前时刻的响应状态信息；随后，建筑物的先前状态信息联合当前地震动的高维特征向量共同输入到解码器进行解码，得到建筑物的响应；同时，本文通过将运动控制方程和响应之间的依赖关系等先验知识加入损失函数，对Phy-LInformers的训练过程进行指导并约束其学习空间，以使预测的响应结果更符合物理约束，同时减小深度学习模型对训练数据的需求。
Phy-LInformers的主要创新之处在于引入在自然语言处理等领域表现出色的Transformer类模型Informer，并结合LSTM捕捉先前时刻地震动的特征，纳入建筑物先前时刻的响应状态信息，为模型训练和预测提供更丰富的信息；同时利用物理先验知识设计损失函数，指导模型学习并降低对训练数据量的依赖。这一创新为PIDL领域的地震响应预测提供了新的研究思路，为AI在科学研究中的应用做出了积极的实践。
本文的方法具有以下显著特点：1）预测过程结合了建筑物的先前状态；2）在有限训练数据下表现出色的能力，有效解决数据稀疏性的挑战；3）将先验知识编码到损失函数，引导模型学习物理规律，提升预测结果的物理合理性。
1. 基于Informer和物理知识的地震响应预测模型
1.1 问题定义
本文的研究目标是开发一种端到端的深度学习框架，该框架能结合物理知识和结构的先前状态，准确预测非线性地震反应。为了更好地说明问题，本文考虑一个建筑结构，并假设该结构在地震激励下的响应符合非线性运动方程（equations of motion，EOM）为
$$ \boldsymbol{M}\ddot{\boldsymbol{x}}+\boldsymbol{C}\dot{\boldsymbol{x}}+\lambda \boldsymbol{K}\boldsymbol{x}+\left(1-\lambda \right)\boldsymbol{K}\boldsymbol{r}=\mathrm{ }-{\boldsymbol{M}}{\boldsymbol{\varGamma}} {\boldsymbol{a}}_{\boldsymbol{g}} $$ (1) 式中
$ ：\boldsymbol{M} $ 为质量矩阵；$ \boldsymbol{C} $ 为阻尼矩阵；$ \boldsymbol{K} $ 为刚度矩阵；$ \boldsymbol{x} $ 、$ \dot{\boldsymbol{x}} $ 和$ \ddot{\boldsymbol{x}} $ 为到地面的相对位移、速度和加速度矢量；$ \boldsymbol{r} $ 为辅助的非观测迟滞参数（或称为迟滞位移）；$ \lambda \in \left(0\right.,\left.1\right] $ 是屈服后刚度与屈服前(弹性)刚度的比值；$ {\boldsymbol{a}}_{\boldsymbol{g}} $ 为地震动的加速度；${\boldsymbol{ \varGamma}} $ 为力分布向量；$ \boldsymbol{C}\dot{\boldsymbol{x}}+\lambda \boldsymbol{K}\boldsymbol{x}+\left(1-\lambda \right)\boldsymbol{K}r $ 为总非线性恢复力，记为$ \boldsymbol{h} $ 。基于质量矩阵$ \boldsymbol{M} $ 对式（1）进行归一化，EOM方程可以改写为更一般的形式：$$ \ddot{\boldsymbol{x}}+\boldsymbol{g}=\mathrm{ }-{\boldsymbol{\varGamma}} {\boldsymbol{a}}_{\boldsymbol{g}} $$ (2) 式中：
$\boldsymbol{g}\left({t}\right)={\boldsymbol{M}}^{-1}\boldsymbol{h}\left({t}\right)$ 为质量归一化恢复力，$ \boldsymbol{g}\left({t}\right)= \boldsymbol{\psi }\left(\boldsymbol{S}\left({t}\right)\right) $ ，$ \boldsymbol{\psi } $ 为未知潜函数。$ \boldsymbol{S} $ 为状态空间(state space，SS)变量，它包括位移$ \boldsymbol{x} $ 、速度$ \dot{\boldsymbol{x}} $ 和滞回参数$ \boldsymbol{r} $ ，即$ \boldsymbol{S}={\left({\boldsymbol{Z}}_{1},{\boldsymbol{Z}}_{2},{\boldsymbol{Z}}_{3}\right)}^{\mathrm{T}}={\left(\boldsymbol{x},\dot{\boldsymbol{x}},\boldsymbol{r}\right)}^{\mathrm{T}} $ ，完整的结构响应状态空间变量记为$ \boldsymbol{Z}={\left({\boldsymbol{Z}}_{1},{\boldsymbol{Z}}_{2},{\boldsymbol{Z}}_{3},{\boldsymbol{Z}}_{4}\right)}^{\mathrm{T}}={\left(\boldsymbol{x},\dot{\boldsymbol{x}},\boldsymbol{r},\ddot{\boldsymbol{x}}\right)}^{\mathrm{T}} $ ，即$ \boldsymbol{S}\in \boldsymbol{Z} $ 。基于物理学建立数学上接近的非线性降阶模型是非常困难的，尤其是当非线性是隐式、复杂且高阶时。本文旨在开发一种深度学习代理模型，实现从地震激励到建筑结构地震响应的高效而精确的映射，例如
$ {\boldsymbol{a}}_{\boldsymbol{g}}\xrightarrow{{\mathrm{深}\mathrm{度}\mathrm{学}\mathrm{习}\mathrm{代}\mathrm{理}\mathrm{模}\mathrm{型}}}\boldsymbol{Z} $ 。深度学习代理模型的本质是把地震动$ {\boldsymbol{a}}_{\boldsymbol{g}} $ 映射到结构响应$ \boldsymbol{x} ，\; \dot{\boldsymbol{x}} $ 和$ \ddot{\boldsymbol{x}} $ 和$ \boldsymbol{r} $ 。1.2 Phy-LInformers模型
由于地震波的非线性和时序性以及建筑结构本身的特殊性，地震激励到建筑响应的映射模型具有强烈的非线性和复杂性。考虑到建筑物的地震响应随时间不断变化，纳入建筑物先前的状态可为训练预测映射模型提供宝贵的信息。此外，在监督学习框架内建立可靠的深度学习模型需要大量的标签数据，但在大多数工程场景中却难以满足这一需求。针对地震响应预测领域中现有方法忽略建筑结构先前状态的问题，同时考虑到该领域获取大规模标记数据困难的情况，本文提出了一种创新的物理信息嵌入的深度学习预测框架Phy-LInformers，该模型通过LSTM网络捕捉先前时刻地震动的特征，预测出建筑物先前时刻的响应状态信息。随后，利用Informer网络的编码器–解码器结构将建筑结构的先前状态信息纳入模型，并依据运动控制方程和响应之间的依赖关系设计损失函数，以使预测的响应结果更为符合物理约束，同时，缓解深度学习模型对训练数据的依赖。
1.2.1 整体架构
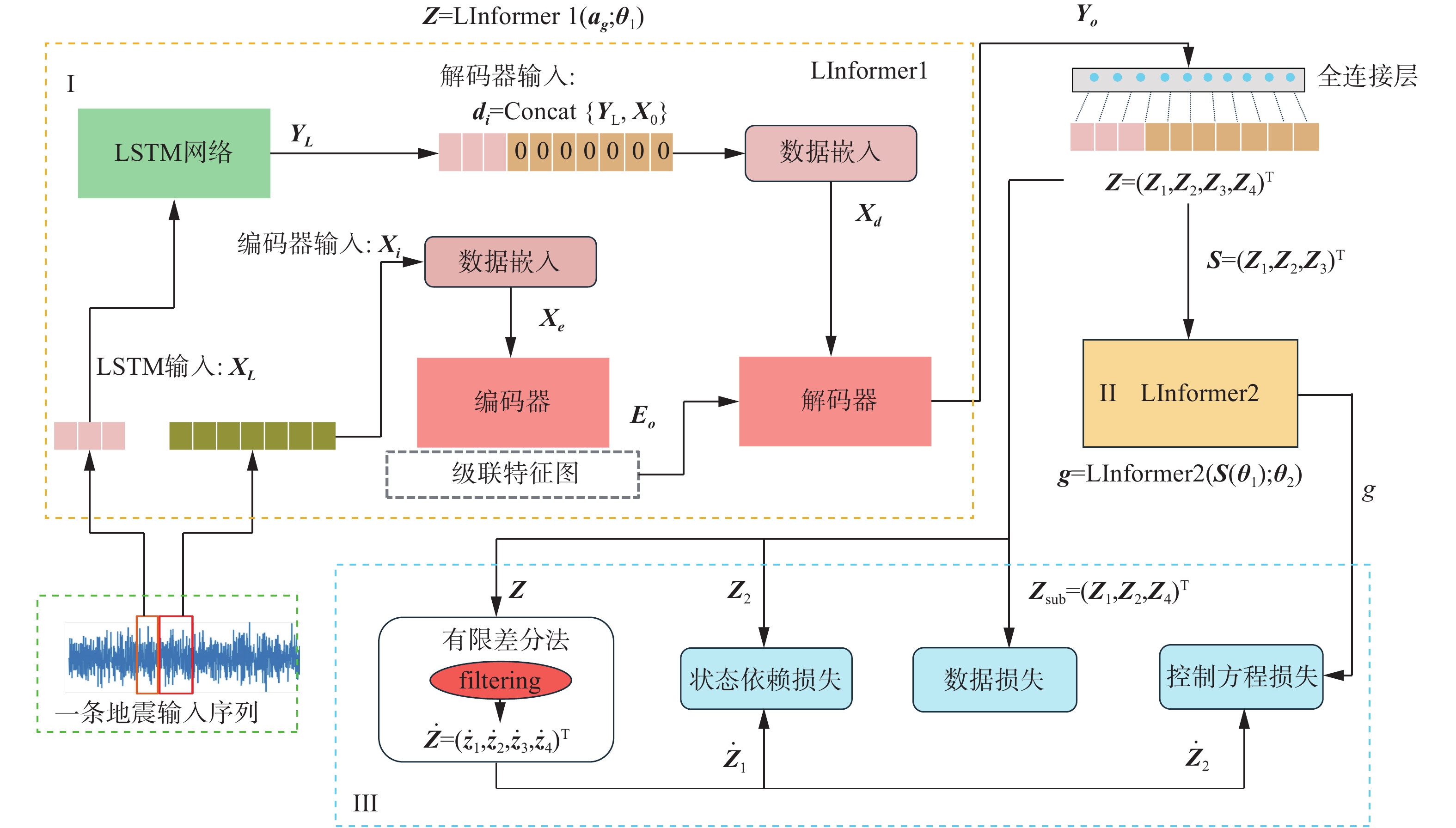
Phy-LInformers整体架构如图1所示。此框架由2个堆叠的LInformer网络块组成（见图1的黄色框），用于非线性结构系统的元建模。
图 1 Phy-LInformers总体架构Fig. 1 Overall architecture of Phy-LInformers
下载:
全尺寸图片
LInformer1和LInformer2是2个结构类似但输入输出不同的神经网络。LInformer1模块用来建立地面运动
$ {\boldsymbol{a}}_{\boldsymbol{g}} $ 到响应$\boldsymbol{Z}={\left(\boldsymbol{x},\dot{\boldsymbol{x}},\boldsymbol{r},\ddot{\boldsymbol{x}}\right)}^{\rm{T}}$ 的非线性映射。LInformer2引入物理定律（见式（1）），将响应$ \boldsymbol{Z} $ 的子集$\boldsymbol{S}={\left(\boldsymbol{x},\dot{\boldsymbol{x}},\boldsymbol{r}\right)}^{\rm{T}}$ 映射到质量归一化的恢复力$ \boldsymbol{g} $ 。2个堆叠的LInformer网络块通过损失函数将可用的物理信息（例如控制方程、状态依赖关系）编码到网络架构中，从而有效缓解了深度学习模型对数据的依赖并增强了模型的可解释性。在预测过程中，地震激励通过LInformer的编码器进行编码，得到其高维特征向量；然后，先前时刻的地震激励序列送入LSTM网络进行时间和空间映射，通过LSTM网络的遗忘门机制捕捉先前时刻地震动的特征，预测出建筑物先前时刻的响应状态信息；随后，建筑物的先前状态信息联合当前地震动的高维特征向量共同输入到解码器进行解码，得到建筑物的响应。
1.2.2 LInformer网络
在结构地震响应预测中，需要根据地震动序列映射得到结构在地震激励下的响应序列。为了有效地解决这一问题，本章设计了LInformer网络，LInformer以Informer作为总体框架，并引入LSTM网络以捕捉先前的响应状态信息。Informer作为总体框架，可以有效建模序列到序列的映射问题，并且其Probsparse-Attention机制可提高自注意力机制的计算效率。此外，Informer的编码器–解码器结构（Encoder-Decoder）可用于引入先前时刻的响应状态信息。LSTM的遗忘门机制强调了对短期依赖的捕捉，并保持了对长期依赖的记忆能力，类似于逐步积分法，这也是LSTM在地震响应预测中表现优异的原因。因此本章选择LSTM以捕捉结构的先前时刻响应状态信息。LSTM和Informer网络的融合最终形成了“LInformer”模块，充分结合了这2种网络的优势。
LInformer网络包括地震波编码器模块、结构先前状态预测模块和震动响应解码器模块。接下来详细介绍LInformer的3个模块。
1）地震波编码器模块
将输入的地震波数据
$ \boldsymbol{X}=\left({x}_{1},{x}_{2},\cdot \cdot \cdot ,{x}_{n}\right)\in {\bf{R}}^{n\times {d}_{I}} $ 和对应输出的建筑物响应数据进行等长切片，$ n $ 代表一条地震波的长度，$ {d}_{I} $ 表示输入的维度，在本文中设置为1。取切片后的地震波加速度序列$ {\boldsymbol{X}}_{\boldsymbol{i}}=\left({x}_{t},{x}_{t+1}, \cdots ,{x}_{t+{L}_{q}-1}\right)\in {\bf{R}}^{{L}_{q}\times {d}_{I}}(t\geqslant 1\mathrm{且}t+{L}_{q}-1\leqslant n) $ 作为LInformer网络地震波编码器的输入，其中$ {L}_{q} $ 是切片样本的序列长度。数据输入编码器之前会经过数据嵌入块，包括特征编码、位置编码以及时间戳编码3个部分，最终得到包含局部和全局信息的输入向量${\boldsymbol{X}}_{{e}}$ ，计算公式为$$ {\boldsymbol{X}}_{{e}}={f}_{\mathrm{D}\mathrm{E}}\left({\boldsymbol{X}}_{{i}}\right)\in {\bf{R}}^{{L}_{q}\times {d}_{m}} $$ 式中：
$ {f}_{\mathrm{D}\mathrm{E}} $ 为数据嵌入块；$ {d}_{m} $ 为模型的维度，默认值为512。LInformer的Encoder模块用于对输入向量$ {\boldsymbol{X}}_{{e}} $ 进行编码，编码器采用了Probsparse-Attention机制，有效降低了计算复杂度。采用多头注意力机制生成不同的稀疏的“查询–键对”（query-key pairs），从而避免了严重的信息丢失。最后通过Encoder得到输入地震序列的高维特征表示$ {\boldsymbol{E}}_{{o}} $ ，捕捉到了重要的地震数据模式和特征，计算公式为$$ {\boldsymbol{E}}_{{o}}={f}_{\mathrm{E}\mathrm{N}}{(\boldsymbol{X}}_{{e}})\in {\bf{R}}^{{L}_{q}\times {d}_{m}} $$ 2）震动响应解码器模块
震动响应解码器模块的输入由2部分组成，具体表示为
$$ {\boldsymbol{d}}_{\boldsymbol{i}}={\mathrm{Concat}}({\boldsymbol{Y}}_{\boldsymbol{L}},{\boldsymbol{X}}_{0})\in {\bf{R}}^{{(L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}+{L}_{\mathrm{p}\mathrm{r}\mathrm{e}})\times {d}_{o}} $$ 式中：
${\boldsymbol{Y}}_{{L}}\in {\bf{R}}^{{L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}\times {d}_{o}}$ 是LSTM预测的建筑物先前时刻的响应，作为对目标响应序列预测的辅助引导；$ {\boldsymbol{X}}_{0}\in {\bf{R}}^{{L}_{\mathrm{p}\mathrm{r}\mathrm{e}}\times {d}_{o}} $ 是目标响应序列的占位符(填充为0)；$ {L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}} $ 和$ {L}_{\mathrm{p}\mathrm{r}\mathrm{e}} $ 分别为引导序列和预测目标序列的长度；$ {d}_{o} $ 为Informer网络输出的特征数。和Encoder类似，数据输入Decoder前也会经过Data Embedding块。Decoder解码器部分的Probsparse-Attention自注意计算中应用了掩码多头注意力，将掩码的点积设置为$-\mathrm{\infty } $ ，防止模型获得未来信息。Decoder结合LSTM给出的先前时刻响应的状态信息，学习响应序列和地震激励的高维特征向量之间的映射关系，最后经过一个全连接层获得最终的响应$ \boldsymbol{Z} $ ：$$ {\boldsymbol{X}}_{{d}}={f}_{\mathrm{D}\mathrm{E}}\left({\boldsymbol{d}}_{{i}}\right)\in {\bf{R}}^{{(L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}+{L}_{\mathrm{p}\mathrm{r}\mathrm{e}})\times {d}_{m}} $$ $$ {\boldsymbol{Y}}_{{o}}={f}_{\mathrm{d}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}}\left({\boldsymbol{X}}_{{d}}\right)\in {\bf{R}}^{{(L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}+{L}_{\mathrm{p}\mathrm{r}\mathrm{e}})\times {d}_{m}} $$ $$ \boldsymbol{Z}={f}_{\mathrm{F}\mathrm{C}}\left({\boldsymbol{Y}}_{{o}}\right)\in {\bf{R}}^{{(L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}+{L}_{\mathrm{p}\mathrm{r}\mathrm{e}})\times {d}_{o}} $$ 3）结构先前状态预测模块
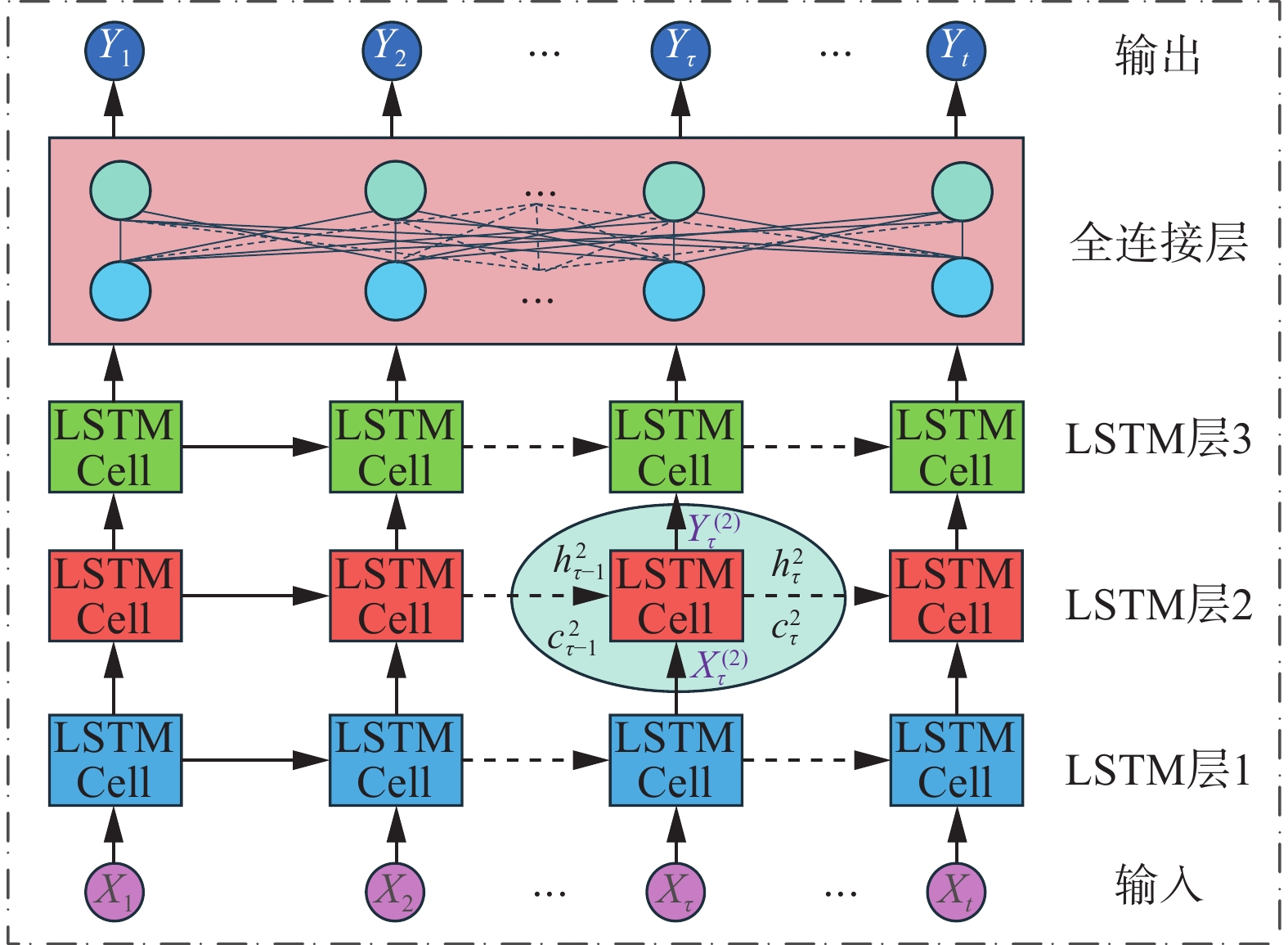
结构先前状态预测模块(如图1框1中绿色块所示)将输入序列
${\boldsymbol{X}}_{{L}}=\left({x}_{t-{L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}},{x}_{t-{L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}+1},\cdots , {x}_{t-2}, {x}_{t-1}\right)\in {\bf{R}}^{{L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}\times {d}_{I}}$ 与引导序列${\boldsymbol{Y}}_{{L}}$ 之间的关系进行建模。它将${\boldsymbol{X}}_{{L}}$ 在时间和空间维度上进行映射，以生成所需的输出序列${\boldsymbol{Y}}_{{L}}$ ：$$ {\boldsymbol{Y}}_{{L}}={f}_{\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}}\left({\boldsymbol{X}}_{{L}}\right)\in {\bf{R}}^{{L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}\times {d}_{O}} $$ 随后，
${\boldsymbol{Y}}_{{L}}$ 集成到Decoder输入中，为模型提供补充信息。结构先前状态预测模块的详细结构如图2所示，包括1个输入层、3个LSTM层、1个全连接层和1个输出层。在本研究中，3个LSTM层内的单元数量和FC层内的节点数量都配置为100。
图 2 LSTM网络的详细结构Fig. 2 Details of LSTM network下载:
全尺寸图片
1.2.3 物理知识嵌入的学习过程
损失函数由初始数据损失和2个物理定律（运动控制方程和响应之间的依赖关系）控制的物理损失共3个部分组成，用于模型的训练和优化。
本文首先将结构响应组合到一组状态空间变量
$ \boldsymbol{Z}={\left({\boldsymbol{Z}}_{1},{\boldsymbol{Z}}_{2},{\boldsymbol{Z}}_{3},{\boldsymbol{Z}}_{4}\right)}^{\mathrm{T}}={\left(\boldsymbol{x},\dot{\boldsymbol{x}},\boldsymbol{r},\ddot{\boldsymbol{x}}\right)}^{\mathrm{T}} $ ，每个状态空间变量都有相同数量的$ {L}_{\mathrm{p}\mathrm{r}\mathrm{e}} $ 个样本点。LInformer1网络建立从地震动$ {\boldsymbol{a}}_{{g}} $ 到响应$ \boldsymbol{Z} $ 的非线性映射，表示为$$ \boldsymbol{Z}=\mathrm{L}\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}1({\boldsymbol{a}}_{{g}};{\boldsymbol{\theta }}_{1}) $$ 式中
$ {\boldsymbol{\theta }}_{1} $ 为$ \mathrm{L}\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}1 $ 网络的可训练权值和偏差。利用测量到的数据$ {(\boldsymbol{x},\dot{\boldsymbol{x}},\ddot{\boldsymbol{x}})}^{\mathrm{T}} $ ，本文可以得到模型的数据损失，其表达式为$$ \begin{gathered} {J}_{d}\left({\theta }_{1}\right)= \frac{1}{L_{\rm{pre}}} \displaystyle\sum_{i=1}^{L_{\rm{pre}}} \left({\big|\big|{{Z}_{1}}^{i}\left({\boldsymbol{\theta }}_{1}\right)-{x}^{i}\big|\big|}_{2}^{2}+\big|\big|{{Z}_{2}}^{i}\left({\boldsymbol{\theta }}_{1}\right)-\right.\\ \left.{\dot{x}}^{i}\big|\big|_{2}^{2}+{\big|\big|{{Z}_{4}}^{i}\left({\boldsymbol{\theta }}_{1}\right)-{\ddot{x}}^{i}\big|\big|}_{2}^{2}\right) \end{gathered}$$ 通过有限差分法对状态空间变量
$ \boldsymbol{Z} $ 求导得到$ \dot{\boldsymbol{Z}}={(\dot{{\boldsymbol{Z}}_{1}},\dot{{\boldsymbol{Z}}_{2}},\dot{{\boldsymbol{Z}}_{3},}{\dot{\boldsymbol{Z}}}_{4})}^{\mathrm{T}}={(\dot{\boldsymbol{x}},\ddot{\boldsymbol{x}},\dot{\boldsymbol{r}},{\boldsymbol{x}}^{\left(3\right)})}^{\mathrm{T}} $ 。基于状态空间变量相等条件，构造“状态依赖损失”。$$ {J}_{e}\left({\theta }_{1}\right)=\frac{1}{{L}_{\mathrm{p}\mathrm{r}\mathrm{e}}}\sum _{i=1}^{{L}_{\mathrm{p}\mathrm{r}\mathrm{e}}}\left({\big|\big|{{\dot{Z}}_{1}}^{i}\left({\boldsymbol{\theta }}_{1}\right)-{{Z}_{2}}^{i}\left({\boldsymbol{\theta }}_{1}\right)\big|\big|}_{2}^{2}\right) $$ LInformer2网络将响应
$ \boldsymbol{Z} $ 的子集$ \left(\boldsymbol{S}\right) $ 映射到质量归一化的恢复力$ \boldsymbol{g} $ ，表示为$$ \boldsymbol{g}=\mathrm{ }\mathrm{L}\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}2\left(\boldsymbol{S}\left({\boldsymbol{\theta }}_{1}\right);{\boldsymbol{\theta }}_{2}\right) $$ 式中
$ {\boldsymbol{\theta }}_{2} $ 为$ \mathrm{I}\mathrm{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{r}2 $ 网络的可训练权值和偏差。结合由运动控制方程得到的式（2），本文构造“控制方程损失”为$$ {J}_{g}\left({\theta }_{1},{\theta }_{2}\right)=\frac{1}{{L}_{{\mathrm{pre}}}}\sum _{i=1}^{{L}_{{\mathrm{pre}}}}\left({\big|\big|{{\dot{Z}}_{2}}^{i}\left({\theta }_{1}\right)+{g}^{i}\left({\theta }_{1},{\theta }_{2}\right)+\varGamma {a}_{g}\big|\big|}_{2}^{2}\right) $$ 将3部分损失结合起来，形成了本文提出的网络的总损失，通过Adam算法解决以下优化问题来训练该网络。
$$ \left\{{\hat{\theta }}_{1},{\hat{\theta }}_{2}\right\}=_{\left\{{\theta }_{1},{\theta }_{2}\right\}}^{{\mathrm{arg\;min}}}\left\{\alpha {J}_{d}\left({\theta }_{1}\right)+\beta {J}_{e}\left({\theta }_{1}\right)+\gamma {J}_{g}\left({\theta }_{1},{\theta }_{2}\right)\right\} $$ 式中
$ \alpha $ 、$ \beta $ 和$ \gamma $ 为定义的权重系数收敛控制参数，反比于每个损失项的大小。本文的目的是优化网络参数，使网络能够在满足物理约束的情况下给出精确的响应预测结果。2. 数值验证与结果分析
本文通过2个数值示例（Data_Num[35]、 Data_BoucWen[36]）验证了所提出的Phy-LInformers网络的性能。此外，在单变量设置下，还做了附加的消融实验和参数敏感性实验，以研究不同参数设置对网络性能的影响。
2.1 实验设置和评价指标
在训练阶段，本文使用了Python环境和PyTorch深度学习框架。训练和仿真过程在一台服务器上进行，该服务器配备了16核32线程的Intel(R) Xeon(R) Gold
6135 CPU @ 3.40 GHz和4块NVIDIA Tesla V100S_PCIe _32 GB显卡。在训练阶段中，对一些实验的超参数进行了设置，这些超参数及其描述如表1所示。其中，学习率是一个重要的超参数，它随着训练的进行逐渐减小，以便模型进行更小的更新，从而有可能更好地收敛到最优解。学习率的变化公式为
表 1 实验参数设置Table 1 Experimental parameter settings参数 描述 默认值 batch_size 每次处理的样本数 8 learning_rate 初始学习率 0.0001 d_model 模型维度 512 d_ff 全连接层的维度 2048 head 注意力头的数量 8 Epoch 训练轮数 20 drop_out 隐藏结点丢弃率 0.05 e_layers Encoder层数 2 d_layers Decoder层数 1 $$ {L}_{r}={L}_{r}\left({\frac{1}{2}}^{({E}_{p}-1)}\right) $$ 本文使用不同长度的滑动窗口切片来处理数据集，滑动步幅为1，切片的预处理可以将数据分解为多个较小的样本，从而降低数据的维度，使模型更容易处理和训练，也有助于了解不同切片长度对模型性能的影响，并确定最佳的切片长度。
此外，由于不同的初始化参数会导致模型的训练结果存在一定的差异，为了保证文中实验结果的可复现性，需要保证每一次训练的初始化参数都不变，因此本文在训练过程中设置固定的随机种子，使得每次运行程序时生成的随机数序列相同。本文将随机种子值固定为
2023 。同时，在训练深度学习模型过程中，设置了早停策略以防止过拟合，具体来说，在每次训练迭代后，监测模型在验证集上的损失函数。如果连续3个训练回合验证集上的损失函数都没有下降且训练轮数还未到达默认值，则触发早停条件停止训练，节省计算资源。
为了评估模型在预测地震激励下建筑结构响应方面的有效性，本文采用了6个不同的指标。其中包括响应时程曲线预测图、相关系数概率分布图2个直观分析评价指标和误差在不同置信区间内的置信水平（confidence level, CL）、均方误差（mean squared error，MSE）、平均绝对误差（mean absolute error，MAE）、均方根误差（root mean squ-ared error，RMSE）这4个量化评估指标。为了计算这些指标，本文假设
$ {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}} $ 代表真实的结构响应，$ {y}^{\mathrm{p}\mathrm{r}\mathrm{e}} $ 代表预测的响应。相关系数的概率分布图表示在测试集所有样本中得到某一相关系数预测结果的概率，较为全面地反映了预测模型在整体趋势上的预测效果，计算方法为
$$ {P}_{{r}}=\frac{1}{N}\mathrm{N}\mathrm{u}\mathrm{m}\left(\mathfrak{R}\right({y}_{i}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}},{y}_{i}^{\mathrm{p}\mathrm{r}\mathrm{e}}\left)\right),\quad i=\mathrm{1,2},\cdots,N $$ 式中：
$ \mathfrak{R}({y}_{i}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}},{y}_{i}^{\mathrm{p}\mathrm{r}\mathrm{e}}) $ 为计算测试集第i个样本真值序列和预测值序列的相关系数，N为测试集的样本数量。假设$ \mathfrak{R}({y}_{i}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}},{y}_{i}^{\mathrm{p}\mathrm{r}\mathrm{e}}) $ 结果为r$ \in [-\mathrm{1,1}] $ ,$ \mathrm{N}\mathrm{u}\mathrm{m}(\cdot ) $ 函数用来统计相关系数为$ r $ 的样本数量，${P}_{{r}}$ 代表相关系数为$ r $ 的样本所占的概率，该指标反映了响应序列在趋势上的预测效果。相关系数越接近1且占的概率越高，说明模型预测序列趋势的效果越好。同时，为了衡量单个样本中每个时间点拟真实值与预测值的误差，在对其误差进行归一化处理之后，将各个样本对应的归一化误差进行平均，最终得到预测结果的样本归一化误差概率密度分布。并且，为了对样本中对应时间点的预测值与真实值的相对误差大小进行统计，对归一化误差置信区间为[−10%，10%]和[−5%，5%]时的置信水平进行求解。CL反映了整个数据集样本的整体预测精度。归一化误差分布的概率密度函数 （probability density function，PDF） 定义为
$$ {\pi }_{i}=\mathrm{PDF}\left(\frac{{y}_{i}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}-{y}_{i}^{\mathrm{p}\mathrm{r}\mathrm{e}}}{{\max}(\left|{y}_{i}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}\right|)}\right) $$ 求解得到的归一化误差置信区间为[−10%,10%]时的置信水平为 88.76%，可以简单理解为，在模型对线性数据集测试集中每一条样本的预测中，样本中有 88.76% 的时间点将会落在[−10%,10%]的误差范围之内。
还有用于评估回归模型性能的3个常见指标，MSE(EMS)、MAE(EMA)和RMSE(ERMS)的定义如下：
$$ E_{{\mathrm{MS}}}=\frac{1}{N}\sum _{i=1}^{N}{\left({y}_{i}^{{\mathrm{true}}}-{y}_{i}^{{\mathrm{pre}}}\right)}^{2} $$ $$ E_{{\mathrm{MA}}}=\frac{1}{N}\sum _{i=1}^{N}\left|{y}_{i}^{{\mathrm{true}}}-{y}_{i}^{{\mathrm{pre}}}\right| $$ $$ E_{\mathrm{RMS}}=\sqrt{{E_{{\mathrm{MS}}}}} $$ 2.2 数值验证实验1：Data_Num
本研究采用了公开的Data_Num合成数据集作为实验数据来源。文献[35]提供了数据集生成的具体步骤和参数设置，读者可以更深入地了解Data_Num的生成过程和背景信息。
Data_Num合成数据集包含100个样本，该数据集通过数值模拟模拟了单自由度非线性系统在PEER强震动数据集中选定地震记录激励下的响应。每次模拟执行时间为50 s，采样频率为20 Hz，因此每个记录包含
1001 个数据点。每个记录都包括位移、速度和加速度3个响应序列。本文从中选择了10条具有地震输入和相应结构响应的数据，作为已知数据集用于训练和验证（分割比为0.8/0.2），剩余的数据集则作为未知数据集，用于测试训练后模型的预测性能。选择相对较小的训练集比例旨在模拟实际工程应用中常见的数据量短缺问题。
为了说明本文所提方法Phy-LInformers的性能，本文将该方法与同样是物理引导的PhyCNN模型进行了比较。此外，PhyCNN作为基线模型在公开数据集Data_Num上达到SOTA(state of the art)水平。
PhyCNN模型由多个卷积层、全连接层以及基于图的张量微分器和物理约束组成，PhyCNN能够以数据驱动的方式准确地预测建筑物的地震响应，此模型性能优于传统的非物理引导神经网络模型（比如CNN）。
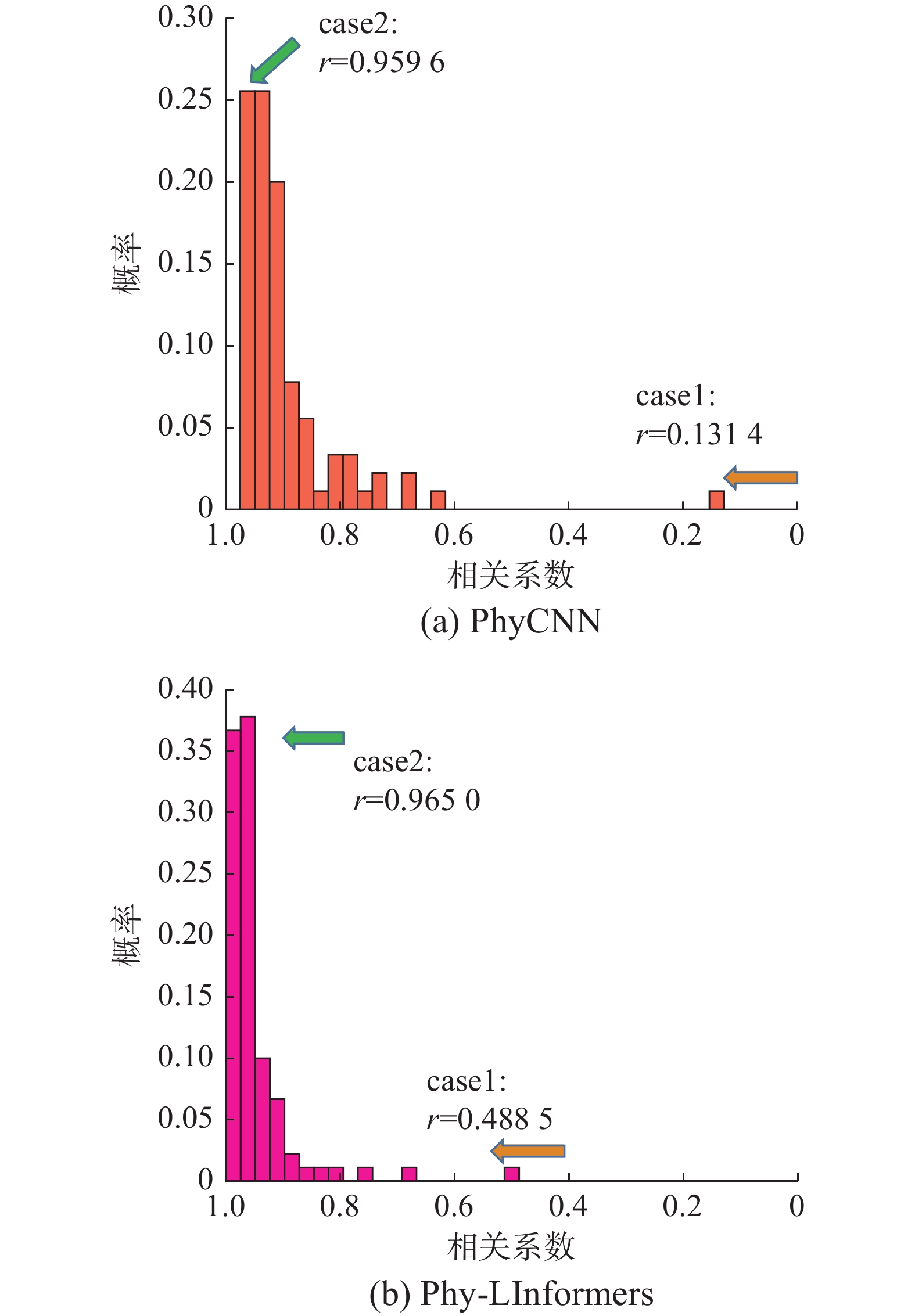
图3和图4对SOTA模型PhyCNN和Phy-LInformers在Data_Num数据集上的预测性能进行了可视化比较。图3总结了在90个测试数据集上预测的速度维度时间历程的回归分析结果。“case1”和“case2”分别代表相关系数的最小值和最高百分比区间内所有相关系数的平均值。可见，Phy-LInformers在速度预测精度方面的相关系数（用r表示）显著提高，在最差情况下达到
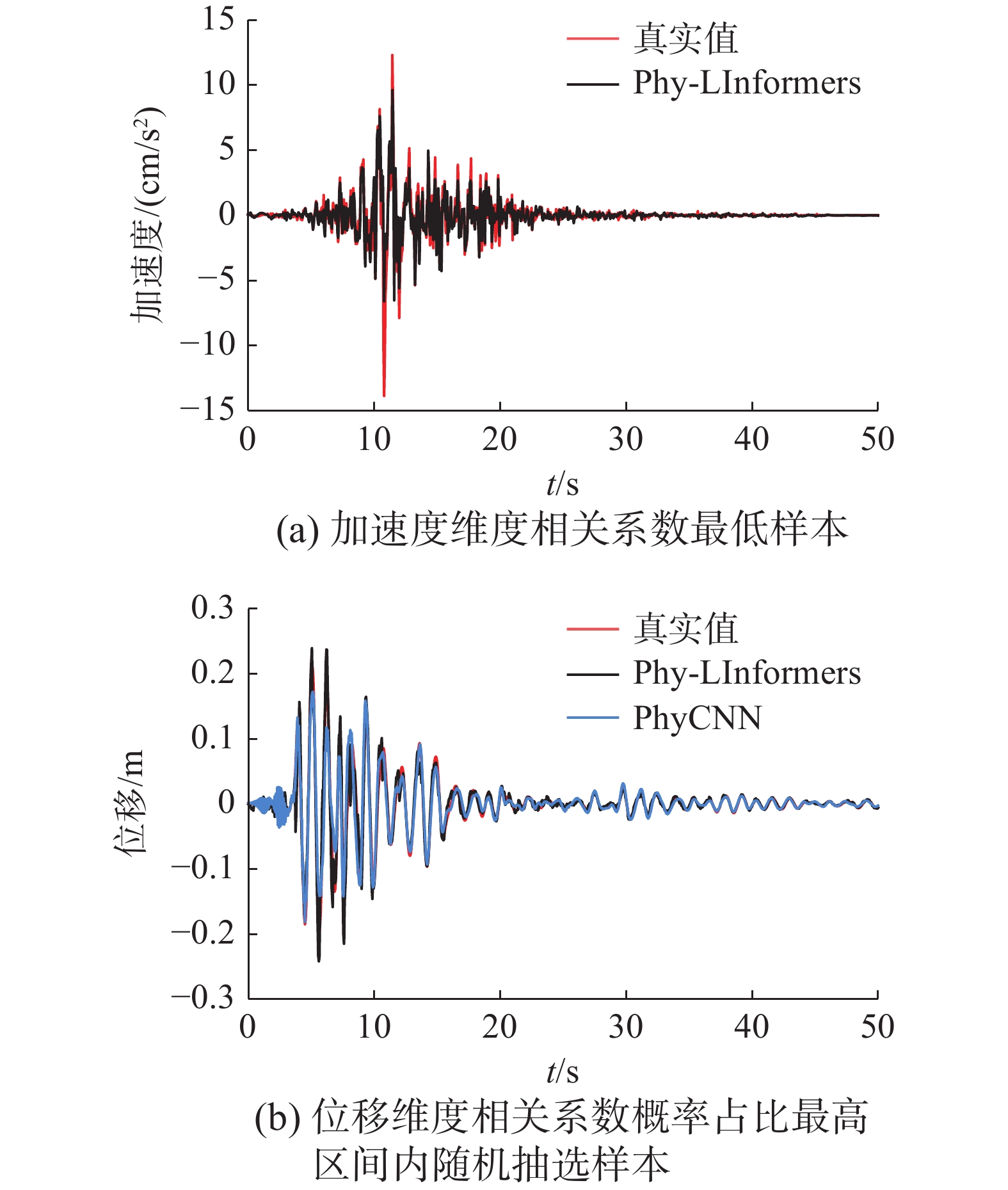
0.4885 ，而PhyCNN的最低相关系数为0.1314 。进一步的分析表明，在速度维度上，Phy-LInformers的相关系数主要集中在0.94~1.00，而PhyCNN的相关系数则集中在0.93~0.96，表明Phy-LInformers的预测更为准确。
图 3 Data_Num数据集速度维度的回归分析结果Fig. 3 Regression analysis results of the speed dimension of the Data_Num dataset下载:
全尺寸图片
Phy-LInformers的另一显著特点是其对加速度状态的精确预测，而基线PhyCNN则不具备这种能力。图4（a）给出了Phy-LInformers在加速度维度的相关系数最低样本的预测响应时程曲线，明显可见，Phy-LInformers即使在最差情况，其预测结果也与真实值表现出较高的一致性。图4（b）给出随机选择位移维度相关系数概率占比最高区间内的一条测试样本的时程响应预测情况。在相关系数较高的情况下，相对于PhyCNN方法，Phy-LInformers的预测与真实值更贴合，尤其在峰值的预测方面有明显的提升，彰显了其在时程预测准确性方面相对于PhyCNN方法的显著优势。
为了全面评估所提出方法的有效性，本文在表2和表3中总结了2种方法的定量指标结果。结果清晰地展示了Phy-LInformers在地震响应预测方面的优异性能。较低的MSE和RMSE值以及较小的MAE值表明Phy-LInformers相比于PhyCNN能够更准确地预测建筑物的地震响应。此外，对于归一化误差置信区间在[−10%，10%]的置信水平，Phy-LInformers在位移响应预测维度相较于基线方法分别有11%的显著提升。当置信区间收敛至[−5%，+5%]，在位移和速度维度，置信水平分别提升了24.8%和34.7%，进一步验证了Phy-LInformers预测效果的稳定性和可靠性。此外，Phy-LInformers方法还实现了对扩展的加速度维度的高精度预测。上述结果在预测长度为3和标签长度为3的条件下获得。
表 2 Data_Num数据集的MSE、MAE、RMSE结果Table 2 MSE, MAE, RMSE results of the Data_Num网络 MSE MAE RMSE $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyCNN 0.0011 0.0284 — 0.0143 0.0697 — 0.0326 0.1685 — Phy-LInformers 0.0006 0.0110 0.5720 0.0123 0.0383 0.3201 0.0248 0.1049 0.7563 表 3 Data_Num数据集不同置信区间的CL结果Table 3 Confidence level with different confidence intervals of the Data_Num% 网络 置信区间10% 置信区间5% $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyCNN 84.98 93.07 — 52.81 63.62 — Phy-LInformers 94.33 99.73 100 65.93 85.68 100 
图 4 Data_Num数据集2个维度的时程响应预测曲线Fig. 4 Time history response curves for the two dimensions of the Data_Num dataset下载:
全尺寸图片
无论是最差情况（case1）还是普遍情况(case2)，本文方法在所有维度均能提供更精确的预测。从直观分析到量化评估，Phy-LInformers的表现都优于SOTA方法，有效证明了本文所提方法的性能。从上述的结果中，本文可以得出结论，Phy-LInformers 能有效地结合结构动力学知识和先前的状态，从非常有限的数据中（只有10条训练样本）学习和识别遵循给定规则的隐藏模式，从而提供令人满意的预测结果，验证了Phy-LInformers作为一个地震响应预测框架的有效性和潜力。
2.3 数值验证实验2：Data_BoucWen
为了评估Phy-LInformers在各种建筑结构上的性能，本文使用了公开数据集Data_BoucWen（100条样本）来评估其在复杂滞后建模方面的能力。对不同震级下的随机带限白噪声地震动激励下的单自由度非线性系统进行了数值模拟。每个模拟过程持续30 s，采样频率设置为50 Hz，每个记录有
1501 个数据点。Data_BoucWen数据集的生成细节在文献[36]中进行了详细描述。该数据集的划分方式与数值验证实验1相同。在此案例中，本文使用Data_BoucWen数据集对提出的Phy-Informers网络以及在该数据集上可获得的表现最优的PhyLSTM2网络进行了复杂滞回建模的性能测试和比较。
PhyLSTM2网络将物理知识(例如物理定律、科学原理)整合到深度长短期记忆网络中。对于动力结构，考虑了运动方程的物理定律和滞回本构关系来构造物理损失。已有研究证明，PhyLSTM2的模型性能优于传统的非物理引导神经网络模型（比如LSTM）。
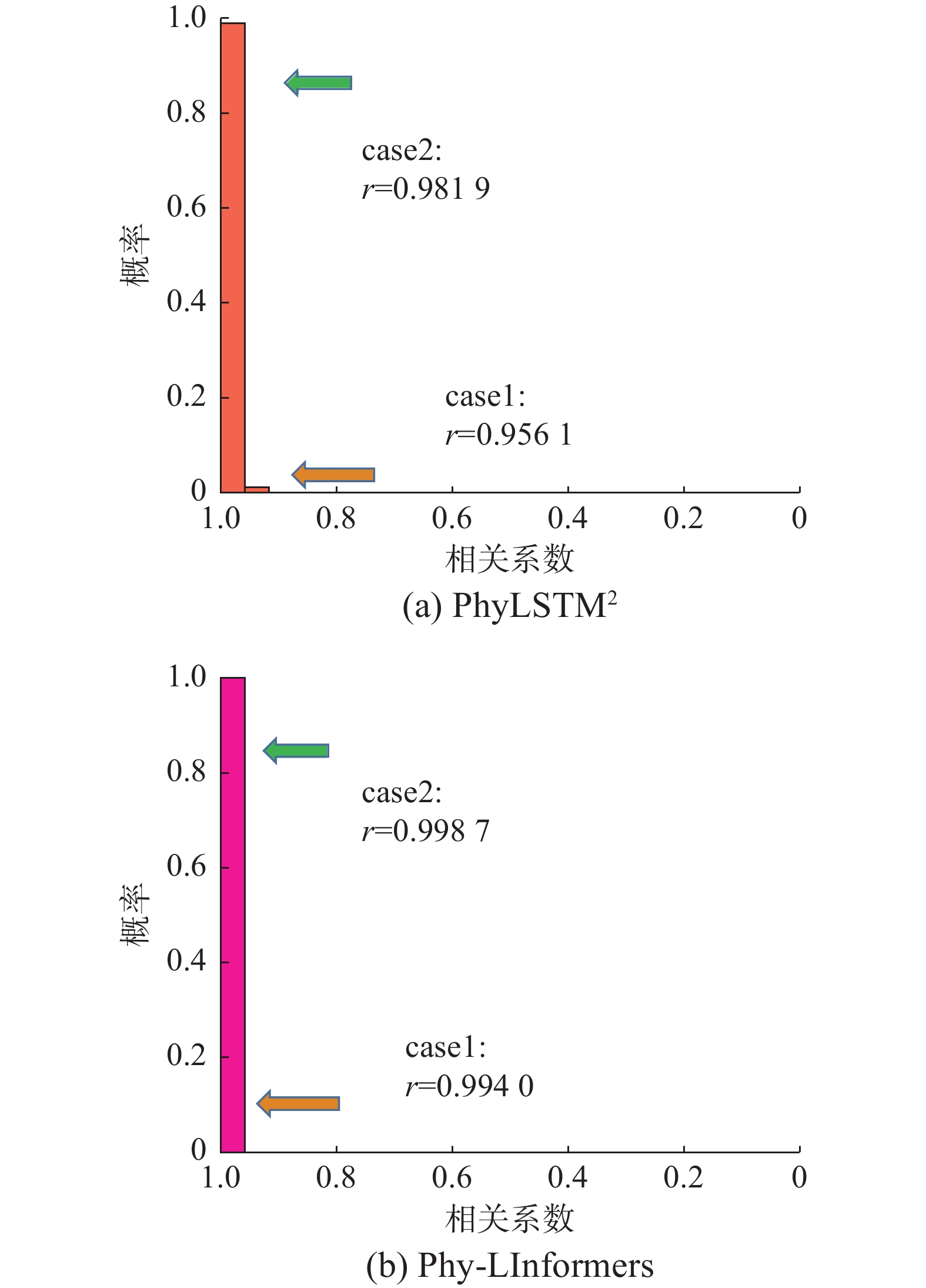
图5中的回归分析结果直观地给出了2种方法在Data_BoucWen数据集速度维度的预测表现。它们在速度和加速度维度上取得了显著优异的结果，2种方法的相关系数均集中在0.95以上，但Phy-LInformers的均值略高于基线方法，表明了更为精准的预测性能。
图 5 Data_BoucWen数据集上速度维度的回归分析结果Fig. 5 Regression analysis results of the speed dimension of the Data_BoucWen dataset下载:
全尺寸图片
表4和表5总结了在Data_BoucWen数据集上的量化分析结果。在速度维度，2种方法均表现出更好的预测准确性。尽管如此，Phy-LInformers仍然提供了更准确的预测，在量化指标上表现更优秀，具有更低的预测误差MSE和更高的预测精度CL。具体而言，PhyLSTM2对应于10%置信区间的CL值为93.92%，而Phy-LInformers的CL值为100%，差距显著。当置信区间收敛时，Phy-LInformers依然能够保持高精度的预测（CL为99.94%），而PhyLSTM2的CL则下降了30%，有力证明了本文方法的优越性。在加速度维度方面，2种方法的CL值即使在5%置信区间，也均在99%以上，Phy-LInformers的量化结果略优于PhyLSTM2。
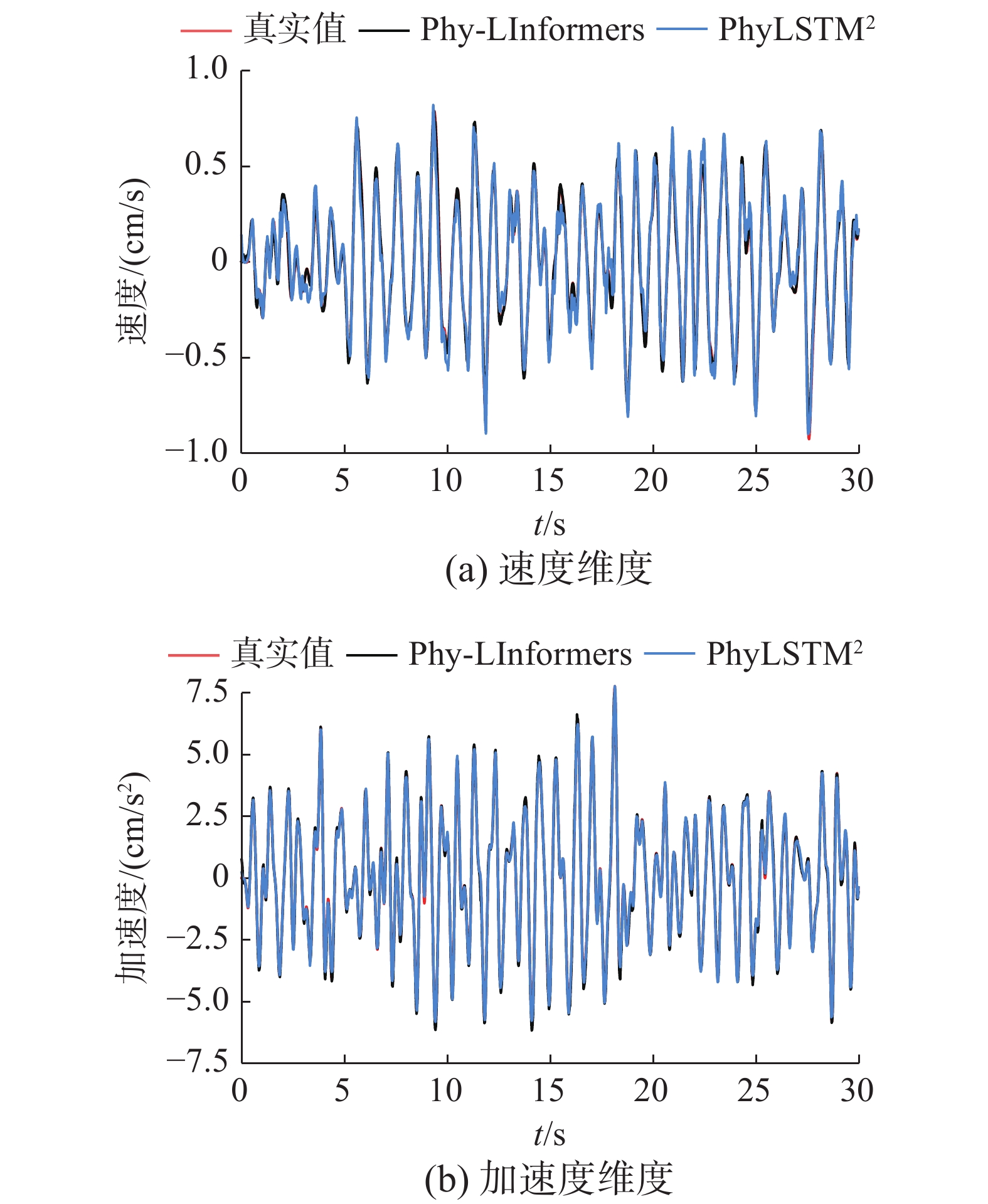
表 4 Data_BoucWen数据集的MSE、MAE、RMSE结果Table 4 MSE, MAE, RMSE results of the Data_BoucWen网络 MSE MAE RMSE $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyLSTM2 0.0062 0.0037 0.0173 0.0566 0.0452 0.0985 0.0785 0.0611 0.1314 Phy-LInformers 0.0071 0.0003 0.0128 0.0631 0.0115 0.0800 0.0845 0.0168 0.1131 表 5 Data_BoucWen数据集不同置信区间的CL结果Table 5 Confidence level (prediction accuracy) with different confidence intervals for the Data_BoucWen% 网络 置信区间10% 置信区间5% $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyLSTM2 40.27 93.92 100 20.83 65.15 99.89 Phy-LInformers 37.18 100 100 19.06 99.94 99.99 图6给出了基于Data_BoucWen数据集的速度和加速度维度的时程预测曲线，遵循了与Data_Num数据集相同的样本选择规则。针对速度和加速度维度的时程预测图中，2种方法的预测曲线与地面真实值密切吻合。为了更加清晰地对比2种方法的预测结果，本文将选出的相关系数更高的速度和加速度样例进行局部放大，仅展示10~20 s的响应时程，其结果如图7。PhyLSTM2在速度维度的幅值预测会出现一定程度的偏差且在幅值附近的预测曲线出现小锯齿，其预测效果相对不理想，而Phy-LInformers在幅值附近的预测相比PhyLSTM2有明显的优势，和真值表现出超高的一致性，显示出更加稳定和准确的预测性能。在加速度维度，2种方法的预测曲线和真值几乎完全吻合，表现出优秀的预测性能。
图 6 Data_BoucWen数据集2个维度的时程响应预测曲线Fig. 6 Time history response curves for the two dimensions of the Data_BoucWen dataset下载:
全尺寸图片
总之，从整体来看，Phy-LInformers表现出了更稳健的预测性能。值得一提的是，在本文的实验中，没有使用额外的50条样本数据来指导基于物理约束的模型训练，本文所使用的训练数据比基线更少，这进一步证实了本文将Informer和先验状态以及物理知识结合的框架的优越性。
图 7 速度、加速度局部放大Fig. 7 Local magnification display of velocity and acceleration下载:
全尺寸图片
3. 消融实验和参数敏感性实验
在单变量设置下，本文对2个数据集进行了附加的消融实验，以研究物理约束对网络性能的影响。同时，本文比对了预测长度、引导长度和batch_size这3个参数在不同参数设置下模型性能的对比，以更全面地展示模型性能。
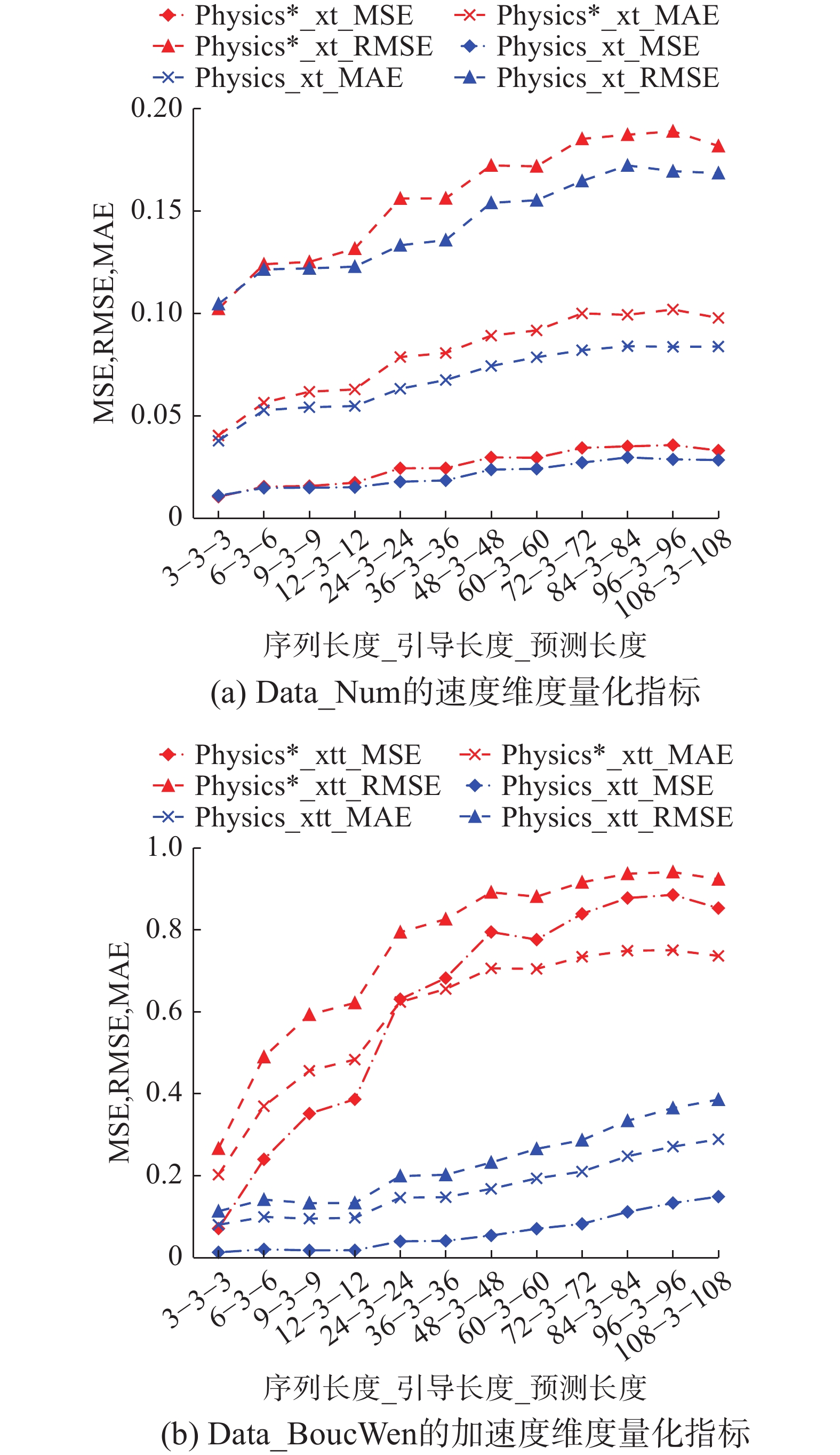
表6和表7汇总了2个数据集上消融实验的结果。在绝大多数情况下，引入物理约束的网络都表现出更高的预测精度，特别是在预测长度增加时，Phy-LInformers在速度和加速度维度的预测精度仍能保持在90%以上，而没有物理知识的网络的预测精度在2个数据集上大幅下降。图8（a）和图8（b）分别给出了模型在不同预测长度下在Data_Num数据集速度维度和Data_BoucWen数据集加速度维度的量化分析结果。其中，红色线代表未引入物理约束的，蓝色则代表Phy-LInformers的预测结果。在图8的2个子图中，蓝色线一直处于红色线下方，且在图8（b）中的差距表现更加明显。本文认为，物理损失可以被视为先验知识的引入，它可以对模型进行指导并约束其学习空间。加入的物理约束（位移和速度的关系、控制方程损失）将物理定律编码到损失函数中，在寻找最优解方面发挥着重要作用，使模型明确地倾向于收敛到符合基础物理约束的解决方案。因此，融合了物理知识的Phy-LInformers提供了更精确的预测。
表 6 Data_Num数据集的消融实验CL结果Table 6 Confidence level results of ablation experiments on Data_Num$ {L}_{\mathrm{s}\mathrm{e}\mathrm{q}} $ $ {L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}} $ $ x $_置信区间±10%/$ x $_置信区间±5% $ \dot{x} $_置信区间±10%/$ \dot{x} $_置信区间±5% $ \ddot{x} $_置信区间±10%/$ \ddot{x} $_置信区间±5% Phy-
LInformersLInformer Phy-
LInformersLInformer Phy-
LInformersLInformer 3 1 90.63/59.81 88.77/57.28 99.58/84.79 99.49/83.88 99.95/91.71 99.94/91.42 2 91.99/61.85 88.75/57.25 99.60/84.98 99.55/84.41 99.97/92.66 99.95/91.93 3 94.33/65.93 92.00/61.86 99.73/85.68 99.67/85.57 100.0/100.0 99.98/94.09 6 94.22/65.72 92.64/62.90 99.37/82.84 99.60/84.98 99.97/93.00 99.98/93.97 6 1 94.56/66.39 90.45/59.54 98.84/79.32 98.20/76.31 99.98/93.66 99.95/91.98 3 96.63/71.17 92.16/62.11 98.84/79.30 98.65/78.33 99.98/93.90 99.97/92.64 6 97.36/73.31 93.68/64.71 98.99/80.18 98.85/79.37 99.96/92.50 99.93/92.39 9 97.14/72.61 92.56/62.77 98.83/79.23 98.65/79.35 99.94/91.52 99.92/91.28 9 1 96.30/70.29 90.46/59.56 98.49/77.56 97.21/72.84 99.97/93.06 99.95/91.98 3 97.64/74.23 94.73/66.74 98.80/79.08 98.58/77.99 99.97/92.97 99.97/91.86 6 97.67/74.32 92.69/62.98 98.68/78.45 98.3476.90 99.95/91.75 99.95/91.95 12 95.32/67.98 90.93/60.23 97.90/75.14 97.60/74.10 99.82/88.20 99.81/87.87 36 1 93.32/64.06 83.78/51.54 97.21/72.84 94.05/65.40 99.04/80.45 98.53/77.73 3 94.38/66.19 85.93/53.96 97.59/74.47 95.02/67.30 99.18/81.50 98.72/78.86 6 95.22/67.77 86.76/54.82 97.72/74.50 95.92/69.37 99.17/81.29 98.93/79.80 18 89.42/58.13 80.64/48.43 94.27/65.81 91.50/61.09 98.41/77.19 97.56/73.94 39 79.30/47.19 73.15/41.99 87.09/55.21 84.99/52.83 96.13/69.88 95.56/68.52 108 1 83.97/51.73 77.62/45.70 90.39/59.46 87.28/55.43 96.35/70.42 95.73/68.91 3 86.94/54.94 81.55/49.18 93.09/63.76 90.80/60.10 97.00/72.13 96.84/71.50 6 87.72/55.96 82.24/49.98 92.96/63.44 91.93/61.74 97.54/73.90 97.35/73.28 54 79.45/47.33 74.17/42.81 86.79/54.05 86.09/54.85 94.74/66.74 94.67/66.61 111 74.07/42.73 73.79/42.50 85.10/50.24 80.50/52.94 93.49/62.13 92.17/61.36 表 7 Data_BoucWen数据集的消融实验CL结果Table 7 Confidence level results of ablation experiments on Data_BoucWen$ {L}_{\mathrm{s}\mathrm{e}\mathrm{q}} $ $ {L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}} $ $ x $_置信区间±10%/$ x $_置信区间±5% $ \dot{x} $_置信区间±10%/$ \dot{x} $_置信区间±5% $ \ddot{x} $_置信区间±10%/$ \ddot{x} $_置信区间±5% Phy-
LInformersLInformer Phy-
LInformersLInformer Phy-
LInformersLInformer 3 1 37.15/19.04 37.08/19.02 100.0/99.90 100.0/97.60 100.0/99.94 99.27/82.00 2 37.16/10.04 37.12/19.03 100.00/99.89 99.98/94.07 100.0/99.99 99.94/91.39 3 37.18/19.06 37.13/19.03 100.0/99.94 99.99/94.92 100.0/99.99 99.88/89.50 6 37.26/19.10 37.20/19.08 100.0/99.98 99.97/96.89 100.0/99.99 99.70/86.21 6 1 37.17/19.06 36.84/18.95 100.0/99.73 99.81/87.92 100.0/99.83 92.39/62.48 3 37.24/19.09 37.05/18.99 100.0/99.56 98.43/77.28 100.0/99.79 92.15/62.11 6 37.31/19.13 37.13/19.03 100.0/99.81 99.12/80.96 100.0/99.80 91.23/60.68 9 37.37/19.16 37.05/18.99 100.0/99.67 99.00/80.22 100.0/99.80 89.69/58.50 9 1 37.24/19.10 36.70/18.87 100.0/98.84 95.99/69.52 100.0/99.68 85.70/53.61 3 37.28/19.11 36.96/18.94 100.0/98.99 92.82/63.19 100.0/99.88 85.42/53.29 6 37.35/19.15 37.08/19.01 100.0/99.44 93.95/65.21 100.0/99.86 84.72/52.53 12 37.47/19.22 36.77/18.91 99.73/86.61 73.57/42.33 100.0/98.02 82.54/50.28 36 1 37.30/19.13 36.01/18.49 99.54/84.31 69.62/39.68 99.99/94.47 70.56/39.99 3 37.41/19.19 36.05/18.51 99.91/90.54 70.13/39.28 100.0/96.71 70.30/39.80 6 37.41/19.19 35.81/18.39 99.65/85.56 68.23/38.26 99.99/95.31 69.80/39.42 18 36.87/18.96 35.16/18.04 90.08/59.02 61.52/33.61 97.17/72.72 66.34/36.91 39 36.40/18.71 34.36/17.60 63.18/34.72 51.48/27.29 69.38/39.11 55.20/29.56 108 1 33.66/17.22 35.39/18.16 86.49/54.51 58.92/31.91 94.37/66.00 62.43/34.22 3 37.19/19.05 35.69/18.33 91.44/61.02 62.20/34.07 97.46/73.63 64.90/35.96 6 37.41/10.19 35.45/18.19 93.62/64.60 62.68/34.39 98.31/76.77 64.89/35.89 54 36.47/18.74 34.25/17.54 58.77/31.81 50.42/26.66 64.88/35.89 53.29/28.39 111 36.10/18.55 34.85/17.87 56.10/30.12 48.38/25.45 61.33/33.49 50.40/26.65 
图 8 预测长度的参数敏感性Fig. 8 Parameter sensitivity of prediction length下载:
全尺寸图片
随着预测长度的增加，表6和表7的结果显示3个维度的预测精度呈现下降趋势，特别是在置信度为±5%时，模型的预测精度下降愈发显著。图8中的MSE、MAE和RMSE值随着预测长度的增加也呈现出明显的上升趋势。这些现象可能由多重原因引起：首先，过长的输入输出序列可能增加模型的计算复杂性，降低其学习能力；其次，输入输出序列的增加可能导致特征之间的关联性变得更加复杂，使得模型更难以提取有用的信息；此外，过长的输入序列还可能引入冗余或无关的信息，干扰模型对关键特征的捕捉和理解能力，从而影响模型的预测结果。
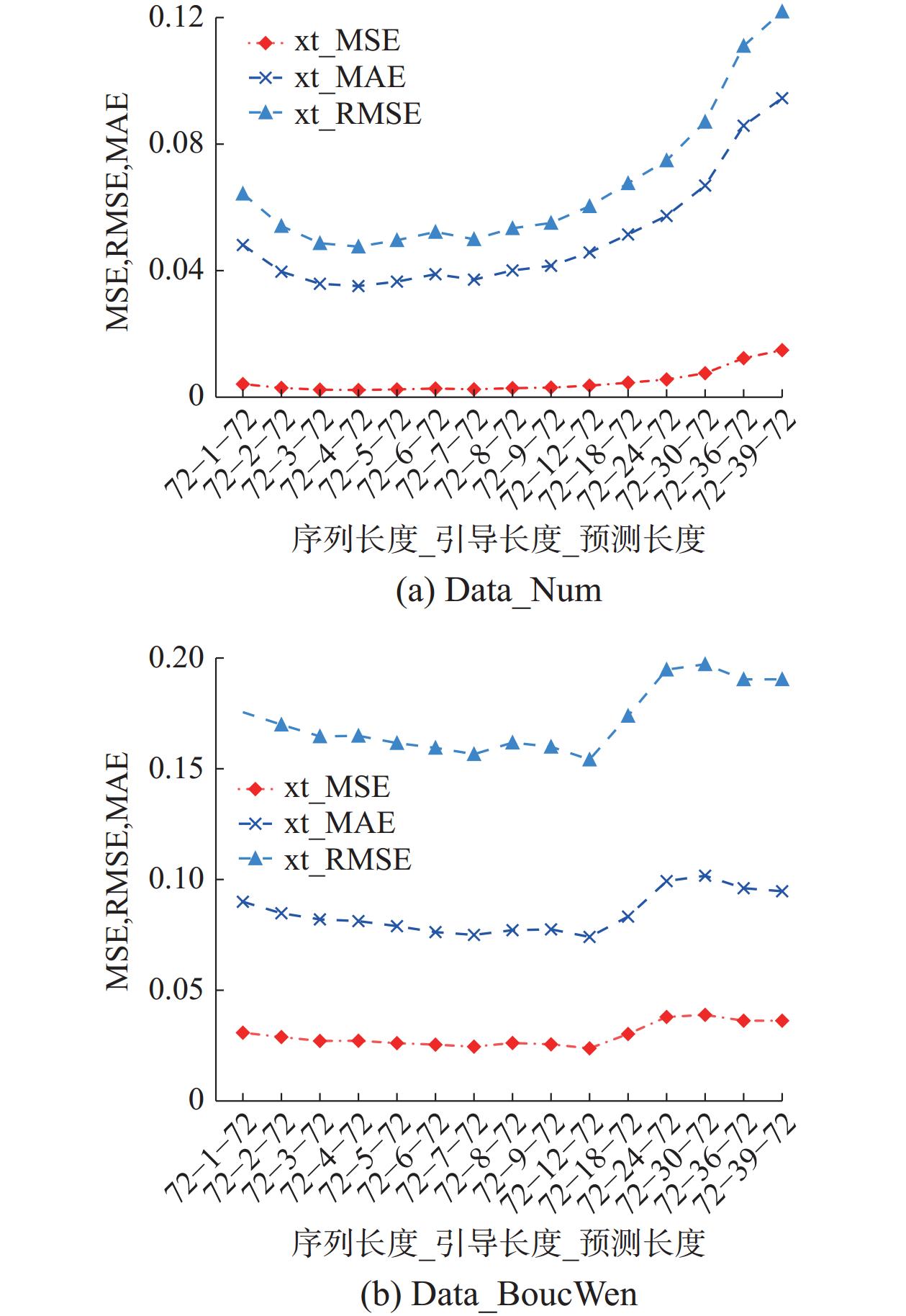
图9以2个数据集的速度维度为例，对引导长度进行了敏感性分析。经过分析，可以发现适度的引导长度在一定范围内有助于提升模型性能。类似于活动语义识别中的Hawkes过程，已发生的历史事件对未来事件发生具有“激励”作用，其中历史事件发生的时间越早，对当前时刻的影响越小，而距当前时刻越近的历史事件产生的影响越大。在预测模型中，适当的引导长度有助于更好地捕捉历史事件的影响，并利用这些信息进行预测。但当引导长度过长时，模型可能会受到冗余信息的干扰，降低了其预测的准确性。
图 9 引导长度的参数敏感性Fig. 9 Parameter sensitivity of lable length下载:
全尺寸图片
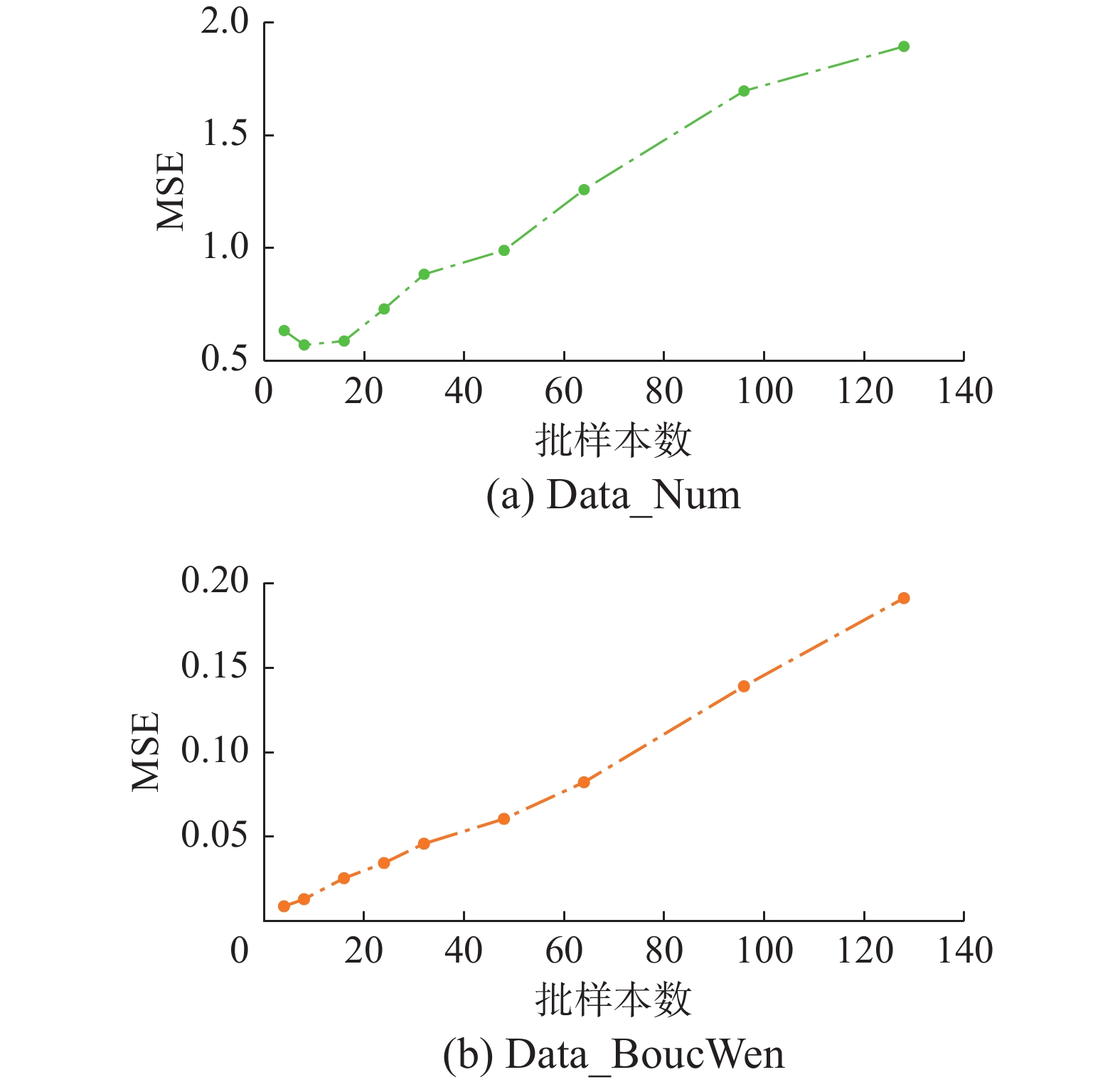
图10则给出了不同batch_size参数下，Phy-LInformers模型在2个公开数据集加速度维度的预测性能。图10中，随着batch_size的增大，预测的MSE不断增加，本文认为出现此现象的原因与训练数据的大小有关。训练集相对较小，选择较大的 batch_size 可能会导致模型对训练集过拟合，从而影响了模型的泛化能力。
图 10 batch_size的参数敏感性Fig. 10 Parameter sensitivity of batch_size下载:
全尺寸图片
此外，由于预处理时对地震动数据进行了切片操作，可能会导致训练集中的样本分布不均匀，较大的 batch_size 可能会导致梯度估计的不准确性，从而影响模型的训练效果。通过对不同batch_size的实验对比，本文最终选择了将batch_size设置为8。这个选择旨在在训练效率和训练精度之间取得平衡，以确保模型在训练过程中能够充分利用计算资源，同时保持对训练数据的有效学习和表现能力。
4. 结束语
本文提出结合先进时间序列预测框架Informer、结构先前状态、物理知识的Phy-LInformers体系结构来开发数据驱动的代理模型，用于建模/预测建筑结构的地震反应。通过2个数值算例和消融实验验证了所提方法的有效性。1）研究结果表明，Phy-LInformers模型相比于SOTA方法表现出了更强的预测能力；2）将物理定律和运动平衡方程编码到损失函数中，对模型的训练学习过程进行指导，使模型明确地倾向于预测更符合基础物理的解；3）物理信息和建筑结构先前状态的结合可以有效地降低深度学习模型对训练数据的依赖。这一优点增加了其在其他类似工程实践应用中的可行性；4）提出的Phy-LInformers在仅有10个训练样本的情况下依然能够提供可靠的预测，充分展示了其在地震响应预测方面的强大能力；5）预测建筑物先前震后状态的LSTM还可以替换为CNN等预测网络，具有很强的灵活性。经过训练的模型可以进一步作为发展建筑物脆弱性评估的基础，用于深入评估建筑结构的损伤状况，以便权衡拆除重建和维护使用之间的决策。
在未来的工作中，将考虑将物理先验知识、时域和频域的特征结合起来进行建筑物的响应预测，以进一步提升预测精度。此外，考虑到不同建筑的固有属性对于模型的泛化能力至关重要，将努力提高模型的泛化性，使其能够自适应地预测不同类型建筑的地震响应，这也是地震响应预测课题中存在的重大挑战。
-
图 1 Phy-LInformers总体架构
Fig. 1 Overall architecture of Phy-LInformers
下载:
全尺寸图片
图 2 LSTM网络的详细结构
Fig. 2 Details of LSTM network
下载:
全尺寸图片
图 3 Data_Num数据集速度维度的回归分析结果
Fig. 3 Regression analysis results of the speed dimension of the Data_Num dataset
下载:
全尺寸图片
图 4 Data_Num数据集2个维度的时程响应预测曲线
Fig. 4 Time history response curves for the two dimensions of the Data_Num dataset
下载:
全尺寸图片
图 5 Data_BoucWen数据集上速度维度的回归分析结果
Fig. 5 Regression analysis results of the speed dimension of the Data_BoucWen dataset
下载:
全尺寸图片
图 6 Data_BoucWen数据集2个维度的时程响应预测曲线
Fig. 6 Time history response curves for the two dimensions of the Data_BoucWen dataset
下载:
全尺寸图片
图 7 速度、加速度局部放大
Fig. 7 Local magnification display of velocity and acceleration
下载:
全尺寸图片
图 8 预测长度的参数敏感性
Fig. 8 Parameter sensitivity of prediction length
下载:
全尺寸图片
图 9 引导长度的参数敏感性
Fig. 9 Parameter sensitivity of lable length
下载:
全尺寸图片
图 10 batch_size的参数敏感性
Fig. 10 Parameter sensitivity of batch_size
下载:
全尺寸图片
表 1 实验参数设置
Table 1 Experimental parameter settings
参数 描述 默认值 batch_size 每次处理的样本数 8 learning_rate 初始学习率 0.0001 d_model 模型维度 512 d_ff 全连接层的维度 2048 head 注意力头的数量 8 Epoch 训练轮数 20 drop_out 隐藏结点丢弃率 0.05 e_layers Encoder层数 2 d_layers Decoder层数 1 表 2 Data_Num数据集的MSE、MAE、RMSE结果
Table 2 MSE, MAE, RMSE results of the Data_Num
网络 MSE MAE RMSE $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyCNN 0.0011 0.0284 — 0.0143 0.0697 — 0.0326 0.1685 — Phy-LInformers 0.0006 0.0110 0.5720 0.0123 0.0383 0.3201 0.0248 0.1049 0.7563 表 3 Data_Num数据集不同置信区间的CL结果
Table 3 Confidence level with different confidence intervals of the Data_Num
% 网络 置信区间10% 置信区间5% $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyCNN 84.98 93.07 — 52.81 63.62 — Phy-LInformers 94.33 99.73 100 65.93 85.68 100 表 4 Data_BoucWen数据集的MSE、MAE、RMSE结果
Table 4 MSE, MAE, RMSE results of the Data_BoucWen
网络 MSE MAE RMSE $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyLSTM2 0.0062 0.0037 0.0173 0.0566 0.0452 0.0985 0.0785 0.0611 0.1314 Phy-LInformers 0.0071 0.0003 0.0128 0.0631 0.0115 0.0800 0.0845 0.0168 0.1131 表 5 Data_BoucWen数据集不同置信区间的CL结果
Table 5 Confidence level (prediction accuracy) with different confidence intervals for the Data_BoucWen
% 网络 置信区间10% 置信区间5% $ x $ $ \dot{x} $ $ \ddot{x} $ $ x $ $ \dot{x} $ $ \ddot{x} $ PhyLSTM2 40.27 93.92 100 20.83 65.15 99.89 Phy-LInformers 37.18 100 100 19.06 99.94 99.99 表 6 Data_Num数据集的消融实验CL结果
Table 6 Confidence level results of ablation experiments on Data_Num
$ {L}_{\mathrm{s}\mathrm{e}\mathrm{q}} $ $ {L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}} $ $ x $_置信区间±10%/$ x $_置信区间±5% $ \dot{x} $_置信区间±10%/$ \dot{x} $_置信区间±5% $ \ddot{x} $_置信区间±10%/$ \ddot{x} $_置信区间±5% Phy-
LInformersLInformer Phy-
LInformersLInformer Phy-
LInformersLInformer 3 1 90.63/59.81 88.77/57.28 99.58/84.79 99.49/83.88 99.95/91.71 99.94/91.42 2 91.99/61.85 88.75/57.25 99.60/84.98 99.55/84.41 99.97/92.66 99.95/91.93 3 94.33/65.93 92.00/61.86 99.73/85.68 99.67/85.57 100.0/100.0 99.98/94.09 6 94.22/65.72 92.64/62.90 99.37/82.84 99.60/84.98 99.97/93.00 99.98/93.97 6 1 94.56/66.39 90.45/59.54 98.84/79.32 98.20/76.31 99.98/93.66 99.95/91.98 3 96.63/71.17 92.16/62.11 98.84/79.30 98.65/78.33 99.98/93.90 99.97/92.64 6 97.36/73.31 93.68/64.71 98.99/80.18 98.85/79.37 99.96/92.50 99.93/92.39 9 97.14/72.61 92.56/62.77 98.83/79.23 98.65/79.35 99.94/91.52 99.92/91.28 9 1 96.30/70.29 90.46/59.56 98.49/77.56 97.21/72.84 99.97/93.06 99.95/91.98 3 97.64/74.23 94.73/66.74 98.80/79.08 98.58/77.99 99.97/92.97 99.97/91.86 6 97.67/74.32 92.69/62.98 98.68/78.45 98.3476.90 99.95/91.75 99.95/91.95 12 95.32/67.98 90.93/60.23 97.90/75.14 97.60/74.10 99.82/88.20 99.81/87.87 36 1 93.32/64.06 83.78/51.54 97.21/72.84 94.05/65.40 99.04/80.45 98.53/77.73 3 94.38/66.19 85.93/53.96 97.59/74.47 95.02/67.30 99.18/81.50 98.72/78.86 6 95.22/67.77 86.76/54.82 97.72/74.50 95.92/69.37 99.17/81.29 98.93/79.80 18 89.42/58.13 80.64/48.43 94.27/65.81 91.50/61.09 98.41/77.19 97.56/73.94 39 79.30/47.19 73.15/41.99 87.09/55.21 84.99/52.83 96.13/69.88 95.56/68.52 108 1 83.97/51.73 77.62/45.70 90.39/59.46 87.28/55.43 96.35/70.42 95.73/68.91 3 86.94/54.94 81.55/49.18 93.09/63.76 90.80/60.10 97.00/72.13 96.84/71.50 6 87.72/55.96 82.24/49.98 92.96/63.44 91.93/61.74 97.54/73.90 97.35/73.28 54 79.45/47.33 74.17/42.81 86.79/54.05 86.09/54.85 94.74/66.74 94.67/66.61 111 74.07/42.73 73.79/42.50 85.10/50.24 80.50/52.94 93.49/62.13 92.17/61.36 表 7 Data_BoucWen数据集的消融实验CL结果
Table 7 Confidence level results of ablation experiments on Data_BoucWen
$ {L}_{\mathrm{s}\mathrm{e}\mathrm{q}} $ $ {L}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}} $ $ x $_置信区间±10%/$ x $_置信区间±5% $ \dot{x} $_置信区间±10%/$ \dot{x} $_置信区间±5% $ \ddot{x} $_置信区间±10%/$ \ddot{x} $_置信区间±5% Phy-
LInformersLInformer Phy-
LInformersLInformer Phy-
LInformersLInformer 3 1 37.15/19.04 37.08/19.02 100.0/99.90 100.0/97.60 100.0/99.94 99.27/82.00 2 37.16/10.04 37.12/19.03 100.00/99.89 99.98/94.07 100.0/99.99 99.94/91.39 3 37.18/19.06 37.13/19.03 100.0/99.94 99.99/94.92 100.0/99.99 99.88/89.50 6 37.26/19.10 37.20/19.08 100.0/99.98 99.97/96.89 100.0/99.99 99.70/86.21 6 1 37.17/19.06 36.84/18.95 100.0/99.73 99.81/87.92 100.0/99.83 92.39/62.48 3 37.24/19.09 37.05/18.99 100.0/99.56 98.43/77.28 100.0/99.79 92.15/62.11 6 37.31/19.13 37.13/19.03 100.0/99.81 99.12/80.96 100.0/99.80 91.23/60.68 9 37.37/19.16 37.05/18.99 100.0/99.67 99.00/80.22 100.0/99.80 89.69/58.50 9 1 37.24/19.10 36.70/18.87 100.0/98.84 95.99/69.52 100.0/99.68 85.70/53.61 3 37.28/19.11 36.96/18.94 100.0/98.99 92.82/63.19 100.0/99.88 85.42/53.29 6 37.35/19.15 37.08/19.01 100.0/99.44 93.95/65.21 100.0/99.86 84.72/52.53 12 37.47/19.22 36.77/18.91 99.73/86.61 73.57/42.33 100.0/98.02 82.54/50.28 36 1 37.30/19.13 36.01/18.49 99.54/84.31 69.62/39.68 99.99/94.47 70.56/39.99 3 37.41/19.19 36.05/18.51 99.91/90.54 70.13/39.28 100.0/96.71 70.30/39.80 6 37.41/19.19 35.81/18.39 99.65/85.56 68.23/38.26 99.99/95.31 69.80/39.42 18 36.87/18.96 35.16/18.04 90.08/59.02 61.52/33.61 97.17/72.72 66.34/36.91 39 36.40/18.71 34.36/17.60 63.18/34.72 51.48/27.29 69.38/39.11 55.20/29.56 108 1 33.66/17.22 35.39/18.16 86.49/54.51 58.92/31.91 94.37/66.00 62.43/34.22 3 37.19/19.05 35.69/18.33 91.44/61.02 62.20/34.07 97.46/73.63 64.90/35.96 6 37.41/10.19 35.45/18.19 93.62/64.60 62.68/34.39 98.31/76.77 64.89/35.89 54 36.47/18.74 34.25/17.54 58.77/31.81 50.42/26.66 64.88/35.89 53.29/28.39 111 36.10/18.55 34.85/17.87 56.10/30.12 48.38/25.45 61.33/33.49 50.40/26.65 -
[1] 史翔宇. 基于机器学习回归算法的地震预测研究及其在中国地震科学实验场的应用[D]. 北京: 中国地震局地震预测研究所, 2021. SHI Xiangyu. Research on earthquake prediction based on machine learning regression algorithm and its application in China seismic experimental site[D]. Beijing: Institute of Earthquake Forecasting of the China Earthquake Administration, 2021. [2] 孙柏涛, 张桂欣. 中国大陆建筑物地震灾害风险分布研究[J]. 土木工程学报, 2017, 50(9): 1−7. SUN Baitao, ZHANG Guixin. Study on seismic disaster risk distribution of buildings in mainland China[J]. China civil engineering journal, 2017, 50(9): 1−7. [3] 邓家屯. 基于机器学习的区域RC框架结构地震响应与构件损伤预测[D]. 广州: 华南理工大学, 2022. DENG Jiatun. Seismic response and component damage prediction of regional RC frame structures based on machine learning[D]. Guangzhou: South China University of Technology, 2022. [4] 商昊江, 祁皑. 高层隔震结构减震机理探讨[J]. 振动与冲击, 2012, 31(4): 8−12,17. doi: 10.3969/j.issn.1000-3835.2012.04.002 SHANG Haojiang, QI Ai. Isolation mechanism of high-rise isolation structrue[J]. Journal of vibration and shock, 2012, 31(4): 8−12,17. doi: 10.3969/j.issn.1000-3835.2012.04.002 [5] 武芳文, 赵雷. 大跨度斜拉桥地震响应非线性时程分析[J]. 世界地震工程, 2009, 25(4): 18−24. WU Fangwen, ZHAO Lei. Nonlinear time-history analysis of seismic response of a long-span cab le-stayed bridge[J]. World earthquake engineering, 2009, 25(4): 18−24. [6] 汪鑫. 基于优化神经网络的多层钢筋混凝土结构地震响应预测[D]. 哈尔滨: 哈尔滨工业大学, 2020. WANG Xin. Prediction of seismic response of multi-story reinforced concrete structures based on optimized neural network[D]. Harbin: Harbin institute of Technology, 2020. [7] 郑史雄, 雷川鹤, 贾宏宇, 等. 人工智能技术在桥梁抗震领域的应用综述[J]. 地震工程与工程振动, 2023, 43(4): 1−13. ZHENG Shixiong, LEI Chuanhe, JIA Hongyu, et al. Application overview of artificial intelligence technology in bridge seismic field[J]. Earthquake engineering and engineering dynamics, 2023, 43(4): 1−13. [8] DE LAUTOUR O R, OMENZETTER P. Prediction of seismic-induced structural damage using artificial neural networks[J]. Engineering structures, 2009, 31(2): 600−606. doi: 10.1016/j.engstruct.2008.11.010 [9] NGUYEN H D, DAO N D, SHIN M. Prediction of seismic drift responses of planar steel moment frames using artificial neural network and extreme gradient boosting[J]. Engineering structures, 2021, 242: 112518. doi: 10.1016/j.engstruct.2021.112518 [10] 赵煜东, 许卫晓, 于德湖, 等. 基于人工神经网络的RC框架结构地震响应预测方法[J]. 地震研究, 2024, 47(1): 123−134. ZHAO Yudong, XU Weixiao, YU Dehu, et al. Response prediction method of the RC frame structure based on the artificial neural network[J]. Journal of seismological research, 2024, 47(1): 123−134. [11] HWANG S H, MANGALATHU S, SHIN J, et al. Machine learning-based approaches for seismic demand and collapse of ductile reinforced concrete building frames[J]. Journal of building engineering, 2021, 34: 101905. doi: 10.1016/j.jobe.2020.101905 [12] 牛志辉, 陈波, 卜春尧. 基于卷积神经网络的速度大脉冲识别方法研究[J]. 震灾防御技术, 2021, 16(3): 485−491. doi: 10.11899/zzfy20210307 NIU Zhihui, CHEN Bo, BU Chunyao. Identification of pulse-like strong ground motions based on convolution neural network[J]. Technology for earthquake disaster prevention, 2021, 16(3): 485−491. doi: 10.11899/zzfy20210307 [13] WEN Weiping, ZHANG Chenyu, ZHAI Changhai. Rapid seismic response prediction of RC frames based on deep learning and limited building information[J]. Engineering structures, 2022, 267: 114638. doi: 10.1016/j.engstruct.2022.114638 [14] OH B K, GLISIC B, PARK S W, et al. Neural network-based seismic response prediction model for building structures using artificial earthquakes[J]. Journal of sound and vibration, 2020, 468: 115109. doi: 10.1016/j.jsv.2019.115109 [15] XU Y, LU X, CETINER B, et al. Real-time regional seismic damage assessment framework based on long short-term memory neural network[J]. Computer-aided civil and infrastructure engineering, 2021, 36(4): 504−521. doi: 10.1111/mice.12628 [16] LIN KY, LIN TK, LIN Y. Real-time seismic structural response prediction system based on support vector machine[J]. Earthquakes and structures, 2020, 18(2): 163−170. [17] ZHANG Xiaoyu, CHEN Jia, WU Yang, et al. Predicting the maximum seismic response of the soil-pile-superstructure system using random forests[J]. Journal of earthquake engineering, 2022, 26(15): 8120−8141. doi: 10.1080/13632469.2021.1988766 [18] CHOU J S, NGO N T, PHAM A D. Shear strength prediction in reinforced concrete deep beams using nature-inspired metaheuristic support vector regression[J]. Journal of computing in civil engineering, 2016, 30(1): 04015002. doi: 10.1061/(ASCE)CP.1943-5487.0000466 [19] MORFIDIS K, KOSTINAKIS K. Rapid prediction of seismic incident angle’s influence on the damage level of RC buildings using artificial neural networks[J]. Applied sciences, 2022, 12(3): 1055. doi: 10.3390/app12031055 [20] 李金珂. 基于低成本层间位移监测的建筑结构地震安全评定方法[D]. 大连: 大连理工大学, 2021. LI Jinke. Seismic safety assessment method of building structures based on low-cost inter-story displacement monitoring methods[D]. Dalian: Dalian University of Technology, 2021. [21] 施静. BO-CatBoost在西部地区地震预测中的应用[D]. 桂林: 广西师范大学, 2023. SHI Jing. Application of BO-CatBoost to earthquake prediction in western China[D]. Guilin: Guangxi Normal University, 2023. [22] 禹海涛, 朱晨阳. 基于BP神经网络的圆形隧道地震响应预测方法及参数分析[J]. 隧道与地下工程灾害防治, 2023, 5(3): 19−26. YU Haitao, ZHU Chenyang. A BP neural network-based prediction method for seismic response of circular tunnel linings and parameter analysis[J]. Hazard control in tunneling and underground engineering, 2023, 5(3): 19−26. [23] ZHANG Ruiyang, CHEN Zhao, CHEN Su, et al. Deep long short-term memory networks for nonlinear structural seismic response prediction[J]. Computers & structures, 2019, 220: 55−68. [24] OH B K, PARK Y, PARK H S. Seismic response prediction method for building structures using convolutional neural network[J]. Structural control and health monitoring, 2020, 27(5): e2519. [25] TORKY A A, OHNO S. Deep learning techniques for predicting nonlinear multi-component seismic responses of structural buildings[J]. Computers & structures, 2021, 252: 106570. [26] ZAMANI A A, ETEDALI S. Seismic response prediction of open-and closed-loop structural control systems using a multi-state-dependent parameter estimation approach[J]. International journal of computational methods, 2022, 19(5): 2250006. doi: 10.1142/S0219876222500062 [27] MENG Chuizheng, SEO S, CAO D, et al. When physics meets machine learning: a survey of physics-informed machine learning[EB/OL]. (2022−03−31) [2023−03−07]. https://arxiv.org/abs/2203.16797. [28] HAO Zhongkai, LIU Songming, ZHANG Yichi, et al. Physics-informed machine learning: a survey on problems, methods and applications[EB/OL]. (2022−11−15)[2023−03−07]. https://arxiv.org/abs/2211.08064. [29] KARNIADAKIS G E, KEVREKIDIS I G, LU L, et al. Physics-informed machine learning[J]. Nature reviews physics, 2021, 3: 422−440 doi: 10.1038/s42254-021-00314-5 [30] WILLARD J, JIA X, XU S, et al. Integrating physics-based modeling with machine learning: a survey[EB/OL]. (2020−3−10)[2022−03−14]. https://arxiv.org/abs/2003.04919v1. [31] YU Yang, YAO Houpu, LIU Yongming. Structural dynamics simulation using a novel physics-guided machine learning method[J]. Engineering applications of artificial intelligence, 2020, 96: 103947. doi: 10.1016/j.engappai.2020.103947 [32] ESHKEVARI S S, TAKA M, PAKZAD S N, et al. DynNet: physics-based neural architecture design for nonlinear structural response modeling and prediction[J]. Engineering structures, 2021, 229: 111582. doi: 10.1016/j.engstruct.2020.111582 [33] GUO Jia. Combination of physics-based and data-driven modeling for structural seismic response prediction[C]// The 66th Japan National Congress for Theoretical and Applied Mechanics. Tokyo: National Committee for IUTAM, 2022: 131. [34] WANG T, LI H, NOORI M, et al. Seismic response prediction of structures based on Runge-Kutta recurrent neural network with prior knowledge[J]. Engineering structures, 2023, 279: 115576. doi: 10.1016/j.engstruct.2022.115576 [35] ZHANG Ruiyang, LIU Yang, SUN Hao. Physics-guided convolutional neural network (PhyCNN) for data-driven seismic response modeling[J]. Engineering structures, 2020, 215: 110704. doi: 10.1016/j.engstruct.2020.110704 [36] ZHANG Ruiyang, LIU Yang, SUN Hao. Physics-informed multi-LSTM networks for metamodeling of nonlinear structures[J]. Computer methods in applied mechanics and engineering, 2020, 369: 113226. doi: 10.1016/j.cma.2020.113226 [37] VASWANJ A, SHAZEER N, PARMAR N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30. [38] ZHOU Haoyi, ZHANG Shanghang, PENG Jieqi, et al. Informer: beyond efficient transformer for long sequence time-series forecasting[C]//Proceedings of AAAI. Vancouver: AAAI. 2021.
