Neural radiance field optimization based on Fourier frequency domain truncation
-
摘要: 神经辐射场(neural radiance fields, NeRF)作为一种通用的场景表达方法，可以更好地理解三维世界的同时创造出更加逼真的感官体验。然而在实际应用中，输入图像较少导致重建效果不佳是一个常见的问题。为此，本文提出了基于傅里叶频域截断的神经辐射场(sparse views neural radiance fields, Sv-NeRF)，通过在频域空间对输入频率进行截断并应用正则化策略来控制高频信号的输入来优化NeRF的位置编码机制，有效地降低了高频噪声，保留了关键的细节信息以提升渲染的质量和稳定性。该方法提升了模型对场景的理解能力，相较于现有方法在渲染质量、细节保留能力上均有显著提升，尤其适用于稀疏输入视角的场景重建工作。Abstract: Neural radiance field (NeRF), as a general method of scene expression, can better understand the three-dimensional (3D) world and create a more realistic sensory experience. However, in practical application, it is a common problem that less input images lead to poor reconstruction effect. Thus, a sparse-view neural radiance field (Sv-NeRF) is proposed in this study based on Fourier frequency domain truncation. The position coding mechanism of NeRF is optimized by truncating the input frequency in the frequency domain space and applying a regularization strategy to control the input of high-frequency signals. This method effectively reduces high-frequency noise and retains key details to improve the quality and stability of rendering. Compared with other methods, the proposed method improves the ability of the model to understand the scene significantly, and improves the rendering quality and detail preservation ability. It is especially suitable for scene reconstruction from the sparse input perspective.
-
基于图像的视图合成技术是计算机图形学和计算机视觉领域共同研究的一个重要问题。传统计算机图形学方法通常涉及正向渲染过程，其中需要显式提供场景内的光照和材质等参数，以生成目标视图。传统视图合成方法通过多视图的拼接来实现效果，但受到了目标场景的限制，从而影响到方法的可扩展性[1]。基于图像的视图合成技术借助不同视角下拍摄的图像作为输入，通过显式或隐式的方式来表达图像中三维场景的几何、材质和光照等属性，从而合成新视角下的视图。随着可微分神经渲染技术的进步，目前流行的神经辐射场(neural radiance fields, NeRF)技术使用多层感知机(multilayer perceptron, MLP)来映射视角与三维场景参数间的关系，而后通过体渲染技术生成最终视图[2]。NeRF同时也存在如训练速度慢、泛化性能差、模型精细程度难以保证等缺点，因此，研究人员在提升算法模型性能和渲染效果方面进行了大量的探索。Barron等[3]对标准NeRF进行改进，提出了Mip-NeRF，该方法更适合处理宽基线(即视角变化较大)情况，从而更高效地渲染相对复杂的场景。Mip-NeRF采用了一种多尺度表示方法，它在体渲染过程中考虑了光线的锥形(cone-shaped)路径，而非传统NeRF中的直线路径，使其更好地应对模糊图像以及差异分辨率的情况。但其多尺度渲染和锥形光线表示的方法相比于传统NeRF大幅增加了计算复杂度，同时对输入图像规模有较高的要求。NVIDIA研究团队提出的Instant-NGP(instant neural graphics primitives)[4]使用多尺度哈希表来表示神经网络权重，模型能够快速访问和更新神经网络参数，大大加速了神经网络的训练和推理过程，但在渲染细节部分并未取得较好的效果。
NeRF及其相关的的方法依赖于大量的视角信息来生成清晰的新视角，这样在相对稀疏的视角信息情况下进行有效的三维重建是一个很大的挑战，例如考古遗址的重建[5]、远程探索(如深海或太空任务)以及历史建筑的数字化[6]，都难以获取充足的视角数据，而在实际拍摄和数据采集过程中，减少输入图像数量可以显著节约时间和算力资源，使重建过程更加高效，因此在稀疏输入前提下，如何对NeRF及其相关模型进行优化成为了一个非常关键的研究问题。Yu等[7]提出了PixelNeRF，在相对稀疏的视角约束下，该方法使用一个深度神经网络来预测场景的体素表示，然后利用神经辐射场技术渲染出不同视角下的图像来达到高效渲染的目的，虽然不需要显式的深度信息或更多的视角，但会损失较多的场景细节。Chen等[8]提出MVSNeRF(multi-view stereo neural radiance fields)，结合了多视角立体视觉(multi-view stereo, MVS)和NeRF相关优势，可以从一组稀疏图像输入中重建出高质量三维场景，但需要大量的计算资源以及高质量的图像输入。
基于以上内容，本文为解决NeRF在稀疏输入条件下渲染效果不佳的问题，提出了一种基于FFT (fast Fourier transform)的频率截断的稀疏视角神经辐射场(sparse views neural radiance fields, Sv-NeRF)，主要贡献如下：
1)分析了稀疏视角条件下的神经辐射场渲染效果不佳的原因，分别对保留了不同频率信息的图像数据进行渲染，验证了高频信号对模型的负面影响，并将傅里叶级数与NeRF中位置编码模块进行关联，提出了一种基于FFT的频域选择性控制策略神经辐射场模型框架，对稀疏视角下的神经辐射场进行改进优化。
2)提出FFT的频率截断策略基础上，通过调整频率变化的同时应用正则化策略来控制高频信号的输入，从而优化NeRF渲染模型的位置编码机制，减少了模型仅获取有限视角信息情况下的过拟合现象，提高了渲染的质量和稳定性。通过动态地、精细地调节输入数据的频率成分，在训练初期有效地降低了高频噪声，在模型进行几何结构渲染的同时保留了关键的细节信息。提升了模型对场景的理解能力，同时还增强了从新视角进行图像渲染时的一致性和真实感。
3)在多个数据集上进行了该方法的有效验证，证实了所提方法的有效性，在3个评价指标：峰值信噪比 (peak signal-to-noise ratio, PSNR)[9]、结构相似性(structural similarity, SSIM)[10]、学习感知图像块相似度(learned perceptual image patch similarity, LPIPS)[11]上均有明显提升，且在渲染质量、细节保留以及抗过拟合能力上均有显著进步，尤其适用于稀疏视角情况下的神经渲染场景。
1. 相关工作
1.1 神经辐射场技术
神经辐射场技术在2020年被提出，并迅速成为计算机视觉和图形处理领域的一个热门话题，该技术已被广泛用于虚拟现实、增强现实等领域，可以生成逼真的三维场景和高质量的图像，成为计算机视觉和深度学习领域的研究热点之一。
NeRF作为一种新三维重建技术拥有广泛的应用范围。比如，它可以应用于建筑和工程领域，创建三维模型来辅助设计、展示和规划；在电影和游戏制作中，它能构建虚拟的场景和人物，实现逼真的视觉效果和交互体验；对于机器人技术，它可以用于模拟和控制机器人的行为，还可以用于优化工厂的生产流程。在最近的工作中，NeRF不仅能在虚拟现实和增强现实中生成全新的视角，增加观感的丰富性；还能在电影和游戏中提供新的视角或视角序列，提升观众的沉浸体验；英伟达公司使用该技术用于推动自动驾驶技术的进展，通过生成不同视角的图像序列，可以增强汽车的感知与判断力；在监控和安全领域，它能够提供从多个角度或位置的新视角图像，优化监控效果和提高识别准确性。
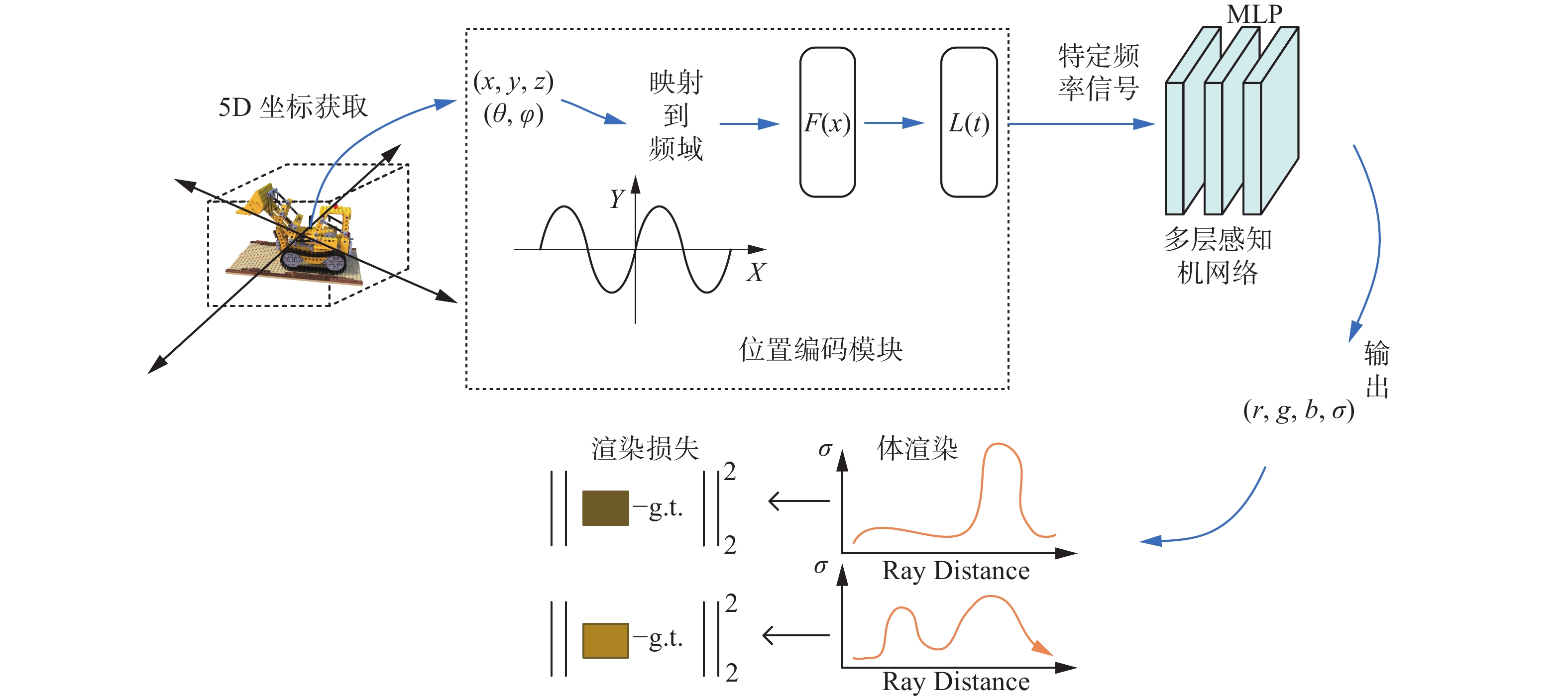
NeRF将体绘制与多层感知机MLP相结合，对神经场(neural fields)进行参数化，并添加了位置编码来拟合高频细节，通过输入大量的场景图像作为监督信息，首次实现了从任意场景的二维图像中合成具有照片级真实感的结果。其优势在于没有使用传统的离散化的网格或体素表示场景，其连续的函数表示可以在获得高质量渲染效果的同时生成任意的场景视角。整体的渲染流程如图1所示。
图 1 NeRF渲染流程Fig. 1 NeRF rendering process
下载:
全尺寸图片
首先，通过COLMAP软件获取图像5维信息(空间位置和视角方向)，再将数据通过位置编码映射到高维空间，然后将这些信息输入到多层感知机网络中，生成颜色和体密度信息；其次，使用体渲染技术将这些值合成为图像；最后，通过最小化合成图像和真实观察图像之间的残差来优化场景表示。该算法使用全连接(非卷积)深度网络来表示场景，其输入是单个连续5D坐标(空间位置
$(x,y,{\textit{z}})$ 和视角方向$ \left( {\theta ,\phi } \right) $ ，其输出是该空间位置的体密度与颜色$ c = \left\{ {r,g,b} \right\} $ 。为了实现这个表示，NeRF使用2个MLP网络，将输入的5维坐标映射为相应的体密度和颜色信息，在网络中，NeRF将方向表示为3D笛卡尔单位向量$ {\boldsymbol{d}} $ 。通过优化网络的权重，用 MLP网络$ {F_\theta }\left( {x,{\boldsymbol{d}}} \right) \to \left( {c\left( {r,g,b} \right),\sigma } \right) $ 来近似表示这个连续的5维场景。具体实现方面，MLP网络$ {F_\theta } $ 首先使用8个全连接层来处理输入的3D坐标x，并输出$ \sigma $ 和一个256维特征向量，然后将该特征向量与相机光线的视角方向连接起来，通过额外的全连接层来输出与视角相关的RGB颜色。体密度
$ \sigma (x) $ 可以解释为光线在位置$ x $ 处终止的微小粒子的微分概率。相机光线$ r\left( t \right) = o + t{\boldsymbol{d}} $ 在近界限$ {t_n} $ 和远界限$ {t_f} $ 范围内的期望颜色$ C\left( r \right) $ 公式为$$ C(r)=\int_{t_{n}}^{t_{f}} T(t) \sigma(r(t)) c(r(t), {\boldsymbol{d}}) \mathrm{d} t, $$ 式中
$ T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(r(s)) {\mathrm{d}} s\right) $ ，表示从$ {t_n} $ 到$ t $ 的射线累积透射率，即射线从$ {t_n} $ 到$ t $ 没有与其他粒子碰撞的概率。为了渲染连续神经辐射场的视图，模型需要估计通过每个所需虚拟相机像素的相机射线的积分$ C\left( r \right) $ ，为了对这个连续积分进行估计，使用了数值积分的方法。通常，确定性积分通常用于渲染离散化的体素网格，而MLP只会在一组固定的离散位置进行查询，这便限制了模型的表示分辨率，因此模型采用了分层采样的方法，将$ \left[ {{t_n},{t_f}} \right] $ 划分为N个均匀间隔的区间，并在每个区间内均匀随机抽取一个样本：$$ {t_i} \sim U\left[ {{t_n} + \frac{{i - 1}}{N}({t_f} - {t_n}),{t_n} + \frac{i}{N}({t_f} - {t_n})} \right] $$ (1) NeRF使用离散样本集进行积分估计，但通过分层采样，使得模型能够表示连续的场景，从而在优化过程中实现在连续位置上的评估。NeRF利用这些样本按照体渲染相关文献[12]提到的积分规则(如Max)来估计
$ C\left( r \right) $ ：$$ \hat{C}(r)={\displaystyle \sum _{i=1}^{N}{T}_{i}\left(1-\mathrm{exp}\left(-{\sigma }_{i}{\delta }_{i}\right)\right){c}_{i}} $$ (2) 其中，
$$ {T}_{i}=\mathrm{exp}\left(-{\displaystyle\sum _{j=1}^{i-1}{\sigma }_{j}{\delta }_{j}}\right) $$ 式中：
$ {\delta _i} = {t_i} + 1 $ ，$ {t_i} $ 是相邻样本之间的距离。从一组$ \left( {{c_i},{\sigma _i}} \right) $ 值计算$ \hat C (r) $ 的函数是可微的，并且可以简化为使用$ \alpha $ 值进行传统的Alpha合成，其中$ {\alpha _i} = \left( {1 - \exp \left( { - {\sigma _i}{\delta _i}} \right)} \right) $ 。NeRF使用了一种新的渲染策略，提高了渲染效率并解决分辨率限制，即同时优化2个网络，分别是“粗糙”网络和“细致”网络。首先，使用分层采样方法，在一组
$ {N_c} $ 个位置上进行采样，并根据式(1)、(2)使用“粗糙”网络进行评估，根据“粗糙”网络的输出，对每条射线上的点进行更加智能的采样。将式(2)中$ \hat C (r) $ 重新表示为沿射线采样的所有颜色$ {c_i} $ 的加权求和，这样的处理方式降低了重复率，同时提高了渲染效率和分辨率，使NeRF能够更准确地表示连续场景，公式表示为$$ \hat C (r) = \sum _{i = 1}^{{\text{Nc}}} {{W_i}{C_I},{W_i} = {T_i}\left( {1 - \exp \left( { - {\sigma _i}{\delta _i}} \right)} \right)} $$ NeRF使用逆变换采样方法采样第2组包含
$ {N_f} $ 个位置的样本，然后使用第1组样本和第2组样本的并集来评估网络。通过式(2)和使用所有$ {N_c} + {N_f} $ 个样本，计算射线的最终渲染颜色。NeRF直接将采样值用作整个积分域的非均匀离散化，而非独立概率估计方式，这降低了重复率都同时提高了采样的效率和精确性，使其能够更好地表示连续场景。NeRF使用一个独立的神经连续体表示网络去优化每个场景，为此需要捕获RGB图像数据集、相机视角和内参参数以及场景边界，对于合成的图像数据集，模型直接使用真实的相机视角、内参和边界；对于实拍的图像数据，NeRF将使用COLMAP结构估计这些参数。在每次优化迭代中，从数据集的所有像素中随机采样一个相机射线批次，然后根据层次化采样方法，从粗糙网络中查询
$ {N_c} $ 个样本，并从精细网络中查询$ {N_c} + {N_f} $ 个样本。接下来，渲染每条射线的颜色，包括粗糙渲染和精细渲染。在损失函数方面考虑了粗糙和精细渲染的渲染像素颜色与真实像素颜色之间的总平方误差，通过最小化这个误差$ L $ ，能够优化网络的参数，使渲染结果更接近真实图像：$$ L = \sum\limits_{r \in {\boldsymbol{R}}} {\left[ {\left\| {{{\hat C }_c}\left( r \right) - C\left( r \right)} \right\|_2^2 + \left\| {{{\hat C }_f}\left( r \right) - C\left( r \right)} \right\|_2^2} \right]} $$ 式中：
$ {\boldsymbol{R}} $ 代表每个批次中的射线集合，$ C\left( r \right) $ 表示射线$ r $ 的真实颜色，$ {\hat C _c}(r) $ 表示粗糙体积预测颜色，$ {\hat C _f}\left( r \right) $ 表示精细体积预测颜色。尽管最终渲染结果来自$ {\hat C _f}\left( r \right) $ ，但NeRF仍然最小化$ {\hat C _c}(r) $ 的损失，以使粗糙网络中的权重分布能够在精细网络中合理地分配样本。1.2 稀疏输入条件下的场景渲染
NeRF作为一种新兴的三维重建技术，在生成高度逼真的三维场景方面取得了出色的效果[13]。然而，大多数现有的方法都依赖于从多个视角获得的丰富数据，在现实世界的许多场景中，获取这种大量的视角数据依然是一个棘手的问题[14]。因此稀疏输入条件下的神经辐射场渲染具有更为重要的实际应用价值，这包括如何在有限的数据支持下高效地学习场景的几何和光照信息，以及如何优化神经网络结构和训练过程以提高效率和准确性，这些研究挑战有助于提高神经辐射场技术在图像数据有限情况下的适用性和鲁棒性。
许多研究都试图通过利用额外的信息来解决具有挑战性的稀疏视角下的神经辐射场渲染问题。例如，Niemeyer等[15]提出了基于几何和外观的正则化RegNeRF，这种正则化处理能够从未观察到的视角渲染图像块，提高了从稀疏输入合成视图的性能表现，RegNeRF针对稀疏输入情境下常见的问题，如估计场景几何结构时的误差和训练初期的偏差行为，提出了解决方案，比如通过在训练过程中调节光线采样空间，从而有效地减少这些问题，虽然RegNeRF对单一场景的优化表现出色，但对于模型而言，获取必要的预训练数据可能会增加大量工作量。Zhang等[16]通过引入神经反射表面(neural reflectance surfaces)、感知正则化，提出NeRS这种有效改善稀疏输入条件下三维重建效果的方法，NeRS能够用神经网络建模物体形状，对封闭表面进行建模，并且保证该表面与球形拓扑结构同构，从而确保重建结果完全密闭。另外，NeRS可以根据稀疏的图片推测出物体的3D形状，可利用日常采集数据(非实验室数据)对物体进行三维重建，提高了神经辐射场在日常研究中的可用性，但同时NeRS在区分某些情况下的图像时存在困难且渲染精细程度有限。Roessle等[17]提出通过结合稀疏视图深度先验信息进行渲染，该方法旨在从远少于常规所需的图像数量(仅18～36张图像)中合成整个房间的新视角。它利用从运动结构预处理步骤中获得的稀疏深度数据，将这些稀疏点转换为密集深度图和不确定性估计，用以指导NeRF的优化。但是该方法也存在一系列局限性，例如渲染时间依旧很长、视角依赖效应有限、深度先验网络对数据集规模需求较大等。
1.3 基于频率采样的位置编码
频域控制是一种通过在频域对信号进行调整和截断的技术手段，通过对输入信号进行频率成分调节，影响模型的学习和泛化[18]。这种方法在信号处理领域已经有了广泛的应用，而在深度学习中，它正逐渐显现出其强大的潜力，特别是在图像处理[19]、音频分析[20]和三维重建[21]等领域。
采样频率是NeRF模型中的关键参数[22]，直接影响渲染结果的精度和计算效率，适当调整采样频率对平衡模型性能和计算成本至关重要，较高的采样频率可以更准确地捕捉场景的微观结构和细节，提高图像的视觉质量[23]。然而，这也带来了更多的计算负担，相反，较低的采样频率可以减少计算负担，但会因此导致失真和模糊，尤其是在复杂场景中[24]。所以，在NeRF中，选择适当的采样频率是一个重要的因素，需要考虑场景复杂性、硬件性能和任务需求。优化采样频率并让模型在保持渲染质量的同时提高计算效率、降低数据需求量，是研究中的关键挑战。以往的研究中，高频成分通常对应于信号的快速变化部分，如图像的边缘或音频的尖锐声音，而低频成分则代表更平滑或更一致的部分[25]。通过控制频域成分，可以对模型施加正则化，从而提高其泛化能力，如抑制过高频率成分可以帮助模型避免过拟合噪声或无关细节[26]。在不同的深度学习应用中，频域控制被用来提高模型的泛化能力。通过限制或调整输入信号的高频成分，可以减少模型对训练数据中的噪声或无关细节的依赖。由此本文提出一种神经辐射场中输入频域控制策略，使NeRF在稀疏视角输入情况下过拟合大幅度减轻、渲染精度较原有模型有了一定提高。
2. 基于频域控制的神经辐射场
2.1 位置编码
在神经网络中，直接将位置和视角作为网络的输入会使渲染分辨率降低，原始的输入坐标对于神经网络来说可能过于“平滑”，难以捕捉到高频细节。使用位置编码的方式将可以有效地解决这个问题，位置编码通常将输入信号映射为正余弦相位来实现，基本思想是通过位置编码将输入坐标(如空间位置和视角方向)映射到一个高维空间，以便捕捉到更细微的空间变化。给定一个输入位置信息
$ x $ ，其位置编码$ \gamma \left( x \right) $ 可以表示为一系列正弦和余弦函数值：$$ \begin{gathered} {\gamma _L}\left( x \right) = \left[ {\sin \left( {{2^0}{\text{π}} x} \right),\cos \left( {{2^0}{\text{π}} x} \right)} \right.,\sin \left( {{2^1}{\text{π}} x} \right),\cos \left( {{2^1}{\text{π}} x} \right), \cdots {\text{,}}\\ \left. \sin \left( {{2^{L - 1}}{\text{π}} x} \right),\cos \left( {{2^{L - 1}}{\text{π}} x} \right) \right] \\ \end{gathered} $$ 式中
$ L $ 是位置编码的层数，决定了编码的频率范围，较高的层数能够捕捉到更高频的信息。位置编码使神经网络能够更敏感地响应输入空间中的微小变化，从而在重建场景时更精确地表示细节。这也带来了一个问题，即过高频率的信息可能导致模型学习到噪声等不必要的细节，且在稀疏视角条件下影响尤为明显，高频输入会加剧过拟合问题，高频率的映射会导致高频组分更快地收敛，这种快速收敛会阻止NeRF探索低频信息，从而使结果倾向于不希望得到的高频伪像。本文在位置编码模块中引入了一种频域选择性控制策略，提出了Sv-NeRF，解决了以上问题，网络结构可见图2，对高频信号进行动态选择，改善模型性能，频域控制允许模型专注于更有意义的频率范围，从而能够在稀疏视角的条件下成功渲染更平滑、自然的模型，同时保持细节的清晰度。
图 2 Sv-NeRF整体网络结构Fig. 2 Network structure of Sv-NeRF下载:
全尺寸图片
2.2 频域选择性控制策略
稀疏视角下的神经辐射场渲染中最常见的失败原因是模型过拟合，NeRF在没有明确的3D几何结构信息时，通过一组2D图像学习3D场景的表示，其中3D几何结构是通过优化其在2D投影视图中的外观来隐式学习的[27]。然而，只给定稀疏输入视图时，容易过拟合这些2D图像，而不能以多视角一致的方式解释3D几何结构。从这样的模型合成新视角会导致失败。如图3所示，在稀疏视角情况下，使用传统NeRF进行模型渲染很难成功，基本无法构建出模型原有几何结构，模型细节信息也非常模糊。
图 3 稀疏视角输入情况下的神经辐射场渲染Fig. 3 NeRF with limited viewpoint inputs下载:
全尺寸图片
Tancik等[28]的研究显示，稀疏视角的神经辐射场渲染中的过拟合问题可能因高频输入加剧，更高频率的映射可以使高频组件更快收敛。然而，这种利用高频信息导致的过快收敛阻碍了模型探索低频信息，并产生高频伪影，在只有稀疏图像可供学习几何一致性的情况下，对噪声的敏感性会更高。
以往的图形学研究表明，在频率域中，图像的低频成分代表了图像的整体趋势(如渐变、大区域的亮度变化)，而高频成分则代表了图像的细节和纹理(如边缘、细节特征)[29]。图4所示是将图像经过傅里叶变换并手动控制输入频率由低到高的结果，最后给出了经过低通滤波、高通滤波后的变换结果，可以看到在过滤掉大部分高频信号后，图像虽然变模糊了但是整体结构依旧完整，而在仅保留高频信号时，图像仅剩一些边缘细节，整体结构难以保存。
图 4 不同比例高频信号输入条件下的图像Fig. 4 Images under different ratios of high-frequency signal input conditions下载:
全尺寸图片
而在NeRF模型中，高频信号可以帮助模型捕捉场景的精细结构，如光照变化、阴影和物体表面的细节；低频信号通常代表图像中的整体布局和形状，对于NeRF模型来说，低频信息有助于模型学习场景的全局一致性和几何基础结构，在训练早期，优先使用低频信号可以让模型先建立起对场景的基本理解，构建模型几何结构，避免被阴影、边缘变化、物体表面细节等高频信号干扰，导致模型过拟合[30]。傅里叶变换是一种将时域信号转换到频域的数学工具，它能够揭示信号的频率成分，实现对输入信息的频域截断，控制和调节高低频信号的输入。本文基于此思路，结合了傅里叶变换思想，将傅里叶变换应用到模型的位置编码模块中，傅里叶级数的公式为
$$ f\left( t \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\sin \left( {n\omega t} \right) + {b_n}\cos \left( {n\omega t} \right)} \right)} $$ 位置编码和傅里叶变换都使用正弦和余弦函数。位置编码通过一系列正弦和余弦函数将输入的数据映射到一个高维空间，而傅里叶变换则是使用正弦和余弦函数来分解信号为不同频率的成分，受此启发本文将傅里叶变换思想结合到NeRF模型当中，对稀疏视角情况下神经辐射场渲染不佳的情况进行优化。
在NeRF这类3D场景重建和渲染技术中，傅里叶变换可以起到重要作用，尤其是在控制输入信号的频率内容方面。通过傅里叶变换，可以仅将特定频率范围的信号输入到模型中，这可以帮助模型在训练初期集中于学习场景的基本几何和大尺度结构，从而避免在稀疏视角的情况下过拟合噪声或高频细节，随着训练的进行，可以逐步放宽这一限制，允许模型学习更多的高频细节，从而逐渐增加渲染图像的清晰度和细节。在上文式(1)中已经阐明了NeRF模型中位置编码的一般形式，将傅里叶变换与位置编码结合，模型在对坐标进行位置编码时，能够将输入信息映射到高维并通过傅里叶变换及掩码动态调整这些信息的频率成分，选择性控制频域信息。首先，定义位置编码函数
$F\left( {x,t} \right)$ ：$$ F\left( {x,t} \right) = \left[ {\sin \left( {{2^k}{\text{π}} x} \right),\cos \left( {{2^k}{\text{π}} x} \right)} \right]_{k = 0}^{\max \left( {1,L\left( t \right) - 1} \right)} $$ 式中
$ k $ 代表了正弦和余弦函数的频率级数。位置编码通常涵盖一系列不同的频率，不同的$ k $ 值对应着输入数据的不同频率成分。$L(t)$ 代表了在当前训练迭代$ t $ 时使用的频率层数，是一个随训练进度逐渐增加的值。在$F\left( {x,t} \right)$ 函数中，$L(t)$ 大于1的情况下，$ k $ 的范围是0～$L(t) - 1$ ，这样可以保证至少有一对基础频率$ k = 0 $ 存在，并且随着训练的进行，增加更多的高频项。如果$L(t) = 1$ ，那么$ k $ 的取值只有一个，即$ k $ ，这样$F\left( {x,t} \right)$ 仅包含基础频率项。随着$ t $ 的增长，$ k $ 的上限将随$L(t)$ 增加而增加。接下来，设计一个频域掩码来实现选择性的允许特定频率信号通过：$$ L\left( t \right) = \left\{ \begin{gathered} {\text{1}},\qquad \qquad \qquad \qquad \;\;\;\; \, t \leqslant T/4 \\ \left\lfloor {{L_{\max }} \cdot \left( {4t/T - 1} \right)} \right\rfloor , \qquad\; T{\text{/4 < }}t{\text{ }} \leqslant T/2{\text{ }} \\ {L_{\max }}, \qquad \qquad \qquad \qquad t{\text{ > }}T{\text{/2}} \\ \end{gathered} \right. $$ (3) 式中：
$ {L_{\max }} $ 是最大频率层数，用于确定位置编码的最高频率范围；$ t $ 代表了当前训练迭代次数；$ T $ 代表了总训练迭代次数，用于控制频率层数的增加速度。$F\left( {x,t} \right)$ 函数是根据当前训练迭代$ t $ 计算的动态频率截断的位置编码。这个公式的原理是：在训练初期，即当训练迭代次数$ t $ 不超过总迭代次数的1/4时，$L(t)$ 保持为0，即模型仅使用最低频率层，这有助于模型首先捕捉场景的粗略几何结构；当$ t $ 超过$ {T \mathord{\left/ {\vphantom {T 4}} \right. } 4} $ 但不超过$ {T \mathord{\left/ {\vphantom {T 2}} \right. } 2} $ 时，$L(t)$ 线性增加，直到$ {L_{\max }} $ ，随着训练的进行，模型开始接触到更高频率的信息，这允许模型逐渐学习和捕捉更加细致的细节和纹理；当$ t $ 超过$ {T \mathord{\left/ {\vphantom {T 2}} \right. } 2} $ 时，$L(t)$ 保持在$ {L_{\max }} $ ，即模型使用所有可用的频率层。通这种方法可以帮助NeRF模型在训练过程中优先学习低频信息，在模型训练初期，通过抑制高频成分，有助于模型先学习场景的基本结构和大尺度特征，随着训练的进行，可以逐渐增加对高频信息的敏感度，使模型能够捕捉到更多细节，进而抑制高频噪声，同时保留了在训练后期可能需要的高频细节。该方法允许更平滑的过渡，更细粒度的控制，有助于在数据稀疏或噪声较多的场景下防止模型过拟合，提高渲染质量。2.3 损失函数
本文提出了一种频域选择性控制模块，通过定义位置编码函数
$F\left( {x,t} \right)$ 以及一个时间依赖的频域掩码$L(t)$ ，动态地控制输入信息的频率成分来改善稀疏输入条件下神经辐射场渲染结果不佳的问题，其核心是允许模型在训练的不同阶段对不同频率层级的信号敏感，为此定义损失函数：$$ {L_{{\mathrm{total}}}}\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {L\left( t \right) \cdot } {\left\| {{{\hat C }_i}\left( t \right) - {C_i}} \right\|^2} $$ 式中：
$L(t)$ 代表了在当前训练迭代$ t $ 时使用的频率层数，在本式中是根据当前训练阶段对应的频域掩码函数(详见式(3))。$ N $ 是样本总数，$ {\hat C _i}\left( t \right) $ 是模型在时间$ t $ 对第$ i $ 个样本的预测颜色，$ {C_i} $ 是第$ i $ 个样本的真实颜色。3. 实验结果与分析
3.1 数据集与实验环境
实验所用数据集来自Blender Synthetic和DTU数据库。Blender Synthetic数据库是使用Blender 软件制作的，该数据集包括各种类型的场景、对象、光照条件和视角，它的主要优势是可以精确控制生成图像中的每一个元素，这种高度的控制能力对于理解算法的性能和限制很有帮助，局限性在于合成图像无法完全捕捉到真是世界中的复杂内容，仅使用合成数据不能保证算法的泛化能力。DTU数据库是一个广泛用于计算机视觉领域的多视图立体数据库，由丹麦技术大学研究团队制作，其中包含了一系列在严格控制的实验室环境中拍摄的图像，涵盖了各种不同的物体和场景，每个场景的图像从多个不同角度拍摄，保证了图像质量和一致性。本文通过使用不同来源的图像数据集(合成数据、实拍数据)，充分验证了本文方法的优越性和泛化能力。训练所使用的硬件平台GPU为NVIDIA GeForce RTX 3090，CPU为Intel Core i7-13700 k，软件平台CUDA版本为11.3，PyTorch版本为1.12.1。
3.2 评价指标
为合理评价模型性能，本文使用了峰值信噪比(PSNR)、结构相似性(SSIM)、学习感知图像块相似度(LPIPS)作为评价指标。
PSNR用于衡量图像质量，它通过比较原始图像与重建图像之间的峰值信噪比来评估它们之间的相似度。计算方法是，首先计算原始图像与重建图像之间的均方误差(mean squared error, MSE)，然后将MSE转换为PSNR值：
$$ P_{\text{SNR}}=10\cdot\mathrm{lg}\left(\frac{M_{\text{AX}}^2}{M_{\text{SE}}}\right) $$ 式中
$ {M_{{\text{AX}}}} $ 是图像像素值的最大可能取值(通常为255，表示8位图像)。PSNR值越高，表示重建图像与原始图像之间的相似度越高，图像质量越好。SSIM是一种用于衡量图像结构相似性的指标，它不仅考虑亮度信息，还考虑对比度和结构信息。SSIM值在0到1之间，越接近1表示重建图像与原始图像结构和质量越相似。SSIM的计算基于滑动窗口实现，即每次计算均从图片上取一个尺寸为
$ N \times N $ 的窗口，基于窗口计算SSIM指标，遍历整张图像后再将所有窗口的数值取平均值，作为整张图像的SSIM指标。假设$ x $ 表示第1张图像窗口中的数据，$ y $ 表示第2张图像窗口中的数据，其中图像的结构相似性由3部分构成：亮度$ l $ 、对比度$ c $ 、结构$ s $ 。则SSIM的计算公式为$$ {\text{SSIM}}\left( {x,y} \right) = \frac{{\left( {2{\mu _x}{\mu _y} + {c_1}} \right)\left( {2{\sigma _{xy}} + {c_2}} \right)}}{{\left( {\mu _x^2 + \mu _y^2 + {c_2}} \right)\left( {\sigma _x^2 + \sigma _y^2 + {c_2}} \right)}} $$ 式中：
$ {\mu _x} $ 和$ {\mu _y} $ 依次表示$ x $ 和$ y $ 的均值，$ {\sigma _x} $ 和$ {\sigma _y} $ 依次表示$ x $ 和$ y $ 的方差，$ {\sigma _{xy}} $ 表示$ x $ 和$ y $ 之间的协方差，$ {c_1} = {\left( {{k_1}L} \right)^2} $ 、$ {c_2} = {\left( {{k_2}L} \right)^2} $ 以及$ {c_3} = {{{c_2}} \mathord{\left/ {\vphantom {{{c_2}} 2}} \right. } 2} $ 表示3个常数，$ {k_1} $ 和$ {k_2} $ 依次默认为0.01和0.03，$ L $ 表示图像像素值的范围。LPIPS是一种基于深度学习的图像相似性指标，在图像质量评估领域具有广泛的应用。LPIPS使用预训练的深度网络接收输入的图像，并在不同的深度层提取特征，通过计算特征之间的距离，评估图像之间的相似度。LPIPS更接近人类感知，并且能够更好地应用于真实场景中，可以解决一些传统指标无法处理的问题，例如图像失真类型的多样性和小尺度变化的敏感性，因为它考虑了图像的感知特征，而不仅仅是像素级别的差异，在实验中，该指标越低表示2张图像越相似，反之则差异越大。
3.3 对比实验与结果分析
为了更好地对比改进后模型的优势，实验将和原始NeRF[2]、mipNeRF[3]、pixelNeRF[7]、MVSNeRF[8]、RegNeRF[15]、SparseNeRF[31]等几种主流神经辐射场进行比对，在同类问题研究中，一般使用2～10张图像模拟稀疏输入条件，本文设置了多组不同图像输入条件的对比试验以体现稀疏视角信息输入下的各模型渲染情况。
为了对比改进后的NeRF和相关方法的性能差异，使用相同的实验设置在3个不同类型的场景中进行了对比实验，对本文方法和其他方法进行100 000次训练迭代至损失函数收敛后，实验结果见图5、表1～2。
图 5 Sv-NeRF与其他方法渲染效果对比结果Fig. 5 Comparison of rendering effects between Sv-NeRF and other methods下载:
全尺寸图片
表 1 在仅输入6张照片情况下的实验结果对比Table 1 Comparison of experimental results when only 6 photos are input方法 输入设置 PSNR↑ SSIM↑ LPIPS↓ 场景1 场景2 场景3 场景1 场景2 场景3 场景1 场景2 场景3 NeRF 6-views 7.83 8.37 6.10 0.535 0.527 0.603 0.372 0.442 0.519 mipNeRF 6-views 15.88 16.32 15.19 0.657 0.642 0.581 0.391 0.365 0.372 pixelNeRF 6-views 20.24 19.32 19.58 0.810 0.753 0.792 0.293 0.374 0.289 MVSNeRF 6-views 18.73 17.99 19.72 0.772 0.695 0.845 0.192 0.264 0.243 RegNeRF 6-views 20.44 20.85 20.19 0.648 0.702 0.682 0.232 0.196 0.202 SparseNeRF 6-views 20.10 21.38 20.97 0.718 0.684 0.698 0.219 0.210 0.193 Sv-NeRF 6-views 21.37 21.59 21.18 0.814 0.734 0.769 0.183 0.201 0.197 表 2 在场景2下输入3、6、9张照片情况下的结果对比Table 2 Comparison of the results when 3, 6 and 9 photos are input in scene 2方法 PSNR↑ SSIM↑ LPIPS↓ 3-views 6-views 9-views 3-views 6-views 9-views 3-views 6-views 9-views NeRF 5.83 8.37 11.56 0.215 0.527 0.674 0.731 0.442 0.368 mipNeRF 8.66 16.32 19.31 0.531 0.642 0.749 0.451 0.365 0.172 pixelNeRF 16.95 19.32 20.73 0.652 0.753 0.788 0.433 0.374 0.258 MVSNeRF 15.02 17.99 21.05 0.602 0.695 0.791 0.326 0.264 0.218 RegNeRF 17.31 20.85 23.17 0.660 0.702 0.853 0.271 0.196 0.103 SparseNeRF 18.85 21.38 23.63 0.624 0.684 0.768 0.257 0.231 0.093 Sv-NeRF 19.11 21.59 24.35 0.632 0.734 0.871 0.252 0.201 0.059 如图5所示，对合成结果从视觉效果方面进行分析，在仅输入6张图像的稀疏视角情况下，Sv-NeRF能够获得更加接近真实物体的渲染效果，虽然在模型边缘、细节处存在一定的模糊情况，但是通过频率控制策略后的模型能够在极端情况下清晰地重建模型整体结构，避免了重建失败的情况。结果中可以看到原始NeRF和mipNeRF在此类极端情况下难以得到渲染清晰的结果。如表1～2所示，以 NeRF 作为基准，“↑”表示该项指标越高越好，“↓”表示该项指标越低越好。从评价指标方面分析：
1) 结果表明本文使用的频域频率控制策略方法有效地提升了网络性能，NeRF的PSNR、SSIM、LPIPS指标均表现不佳，这表明在图像重建时存在较多的失真和噪声，低PSNR通常意味着重建的图像与原始图像在像素级别上的差异较大，SSIM指标较低则说明在该实验中重建后的结构与原图相比有较大差异，LPIPS较高说明从感知质量的角度来看重建图像与原图差距较大。分析结果，NeRF在仅输入6张图像时无法渲染出精细的模型，图像出现明显的伪影，模型无法被识别，高频信息过早地输入造成了这一现象。
2) mipNeRF相较于NeRF有改善，归因于其在处理几何和视角不连续性方面的优化；针对稀疏视角优化的pixelNeRF的PSNR值更高，显示出更好的重建质量，因为其使用一个深度神经网络来预测场景的体素表示，在稀疏输入条件下补充视角信息；MVSNeRF的表现类似pixelNeRF，但在个别数据例如SSIM中显示出劣势，这表明其在特定情境下不如pixelNeRF稳定；RegNeRF与SparseNeRF的表现较好，但本文方法较两者仍体现出优势。
3)Sv-NeRF的PSNR值相较于其他6种算法最高，从渲染结果上也可以看出虽然有轻微的细节损失，但是整体结构渲染体现出明显优势，在像素级别上重建图像与原始图像相似。SSIM指标略大于其他方法，说明重建结果在结构、亮度、对比度方面与原图保持高度一致。LPIPS指标显著优于其他方法，重建结果在边缘、纹理、形状方面与原图像高度一致，说明本文方法虽然在训练初期截断了高频信号的输入，但随着训练的进行逐渐增加高频信息，模型能够在利用低频信号构建几何结构的同时保留高频细节信息，证明了本文方法在还原图像时保持了更高的质量和准确性，与原图的差异最小。
另外，为了证明选取6张图像进行试验的合理性，额外添加了选取3、9张图像的对比实验，验证了不同程度稀疏条件下多种方法的性能。由表2结果可知，本文方法在不同程度稀疏输入条件下均能取得较好结果，相较于其他方法，本文方法在PSNR、SSIM、LPIPS 3项评价指标上均有不同程度的优势，并且本组实验避免了单一输入条件对实验结果的影响。
综上所述，本文提出的频域控制策略相比其他模型，更大程度地缓解了NeRF在稀疏视角信息输入时过拟合的问题，同时提高了渲染性能，符合轻量化模型的需求，有利于进行迁移和应用。
3.4 消融实验
为了评估高频信号对稀疏视角条件下的NeRF模型渲染的影响，以及本文策略的优越性，设置2组消融实验。
1)首先使用NeRF领域最常见的NeRF _ synthetic场景，从该场景的数据集中选取6张图片进行预处理，设置6组对照组。对图像依次进行傅里叶变换并截断不同比例频率信息：保留全部低频信号，分别只保留10%、30%、50%、70%、90%和100%的高频信号，然后使用NeRF进行渲染。实验结果如图6所示。由实验结果可以观察到，在输入全部图像低频信号、仅输入10%高频信号的情况下，模型能够正确重建，PSNR指标也能达到18.38，显示模型渲染较为成功，但是细节部分较为模糊。随着高频信号输入比例的增加，PSNR指标快速下降，在输入高频信号超过30%后，指标均低于10，肉眼基本不可见完整的模型，在不过滤高频信号时，PSNR指标为最低的7.69，输出的渲染结果为一片非常模糊的影子，渲染失败。
图 6 不同高频信号输入比例渲染结果Fig. 6 Rendering results of different high-frequency signal input ratios下载:
全尺寸图片
2)如图7所示，使用本文的Sv-NeRF，输入6张照片进行渲染，可以观察到对模型的渲染能够获得较好的结果，再选取5个不同场景的图像进行渲染，评价指标方面全面优于仅输入10%高频信号时的数值。可以观察到以上6组实验结果均表现优异，能够在仅有6张照片的情况下渲染出清晰的模型，同时也能有较好的评价指标数值。由此可见，对位置编码模块添加的频域选择性控制策略是可行有效的，实验结果体现出了本方法对稀疏输入条件下神经辐射场渲染的优化，在训练初期控制高频信号的输入，让模型构建粗糙的几何结构，又能够随着训练的进行逐渐增加高频信号的输入，增加模型高频细节信息，使得模型能够拥有较为丰富的细节，模型整体更加精细。
图 7 在多个场景应用Sv-NeRF方法的渲染结果Fig. 7 Rendering results of Sv-NeRF method in multiple scenes下载:
全尺寸图片
4. 结束语
本文提出了一种新的NeRF优化方法，通过对频域中的输入信号进行截断并应用动态选择策略，有效地解决了在稀疏输入条件下的三维场景渲染挑战问题。本方法不仅减少了在训练初期高频信号对模型的干扰，还能做到保留重要的场景细节，提升了渲染结果的质量。模型中添加的频域选择性控制模块能够动态地调节输入的信息频率，通过在多个场景数据集上的实验验证，证明了Sv-NeRF在PSNR、SSIM、LPIPS评价指标上相较于现有技术的显著提升，展示了高质量的渲染效果。另外，在一些实际场景中可使用本文提出的方法进行三维场景重建，例如：地理文化遗产数字化工作中，许多地点难以获取充分的视角数据，Sv-NeRF可以利用有限的图像数据，有效重建出遗址的三维模型，对于保护和研究工作有着重要作用；在一些极端的勘探工作中，例如深海或太空探索项目，获取大量高质量视角数据难度较大，本文的频域选择性控制策略能够帮助科研人员从有限的图像数据中重建出更为准确的三维场景，辅助科学研究。尽管本文方法在处理稀疏输入条件下的神经辐射场渲染工作时能够获得更好的结果，但它仍存在一些局限性，主要包括以下3点：1)数据质量依赖性，若输入图像噪声较大或包含大量的遮挡，则会影响重建的准确性和细节的保留；2)引入傅里叶变换和频域选择性控制策略模块增加了模型的计算负担，在处理大规模场景时，需要更多的计算资源和时间，这在实际应用时会导致方法局限性；3)本文通过动态控制高频信号输入减少模型过拟合，但这也可能导致牺牲高频细节，如场景中的微小纹理和光影变化。本文工作主要集中在位置编码模块进行优化改进以达到优化结果，未来工作将进一步优化本文方法，探索神经辐射场在多种非理想场景下的渲染效果增强，如处理非均衡光照、图像质量退化等条件下的渲染问题，进一步提升神经辐射场技术在稀疏输入条件下的重建性能和应用范围。
-
图 1 NeRF渲染流程
Fig. 1 NeRF rendering process
下载:
全尺寸图片
图 2 Sv-NeRF整体网络结构
Fig. 2 Network structure of Sv-NeRF
下载:
全尺寸图片
图 3 稀疏视角输入情况下的神经辐射场渲染
Fig. 3 NeRF with limited viewpoint inputs
下载:
全尺寸图片
图 4 不同比例高频信号输入条件下的图像
Fig. 4 Images under different ratios of high-frequency signal input conditions
下载:
全尺寸图片
图 5 Sv-NeRF与其他方法渲染效果对比结果
Fig. 5 Comparison of rendering effects between Sv-NeRF and other methods
下载:
全尺寸图片
图 6 不同高频信号输入比例渲染结果
Fig. 6 Rendering results of different high-frequency signal input ratios
下载:
全尺寸图片
图 7 在多个场景应用Sv-NeRF方法的渲染结果
Fig. 7 Rendering results of Sv-NeRF method in multiple scenes
下载:
全尺寸图片
表 1 在仅输入6张照片情况下的实验结果对比
Table 1 Comparison of experimental results when only 6 photos are input
方法 输入设置 PSNR↑ SSIM↑ LPIPS↓ 场景1 场景2 场景3 场景1 场景2 场景3 场景1 场景2 场景3 NeRF 6-views 7.83 8.37 6.10 0.535 0.527 0.603 0.372 0.442 0.519 mipNeRF 6-views 15.88 16.32 15.19 0.657 0.642 0.581 0.391 0.365 0.372 pixelNeRF 6-views 20.24 19.32 19.58 0.810 0.753 0.792 0.293 0.374 0.289 MVSNeRF 6-views 18.73 17.99 19.72 0.772 0.695 0.845 0.192 0.264 0.243 RegNeRF 6-views 20.44 20.85 20.19 0.648 0.702 0.682 0.232 0.196 0.202 SparseNeRF 6-views 20.10 21.38 20.97 0.718 0.684 0.698 0.219 0.210 0.193 Sv-NeRF 6-views 21.37 21.59 21.18 0.814 0.734 0.769 0.183 0.201 0.197 表 2 在场景2下输入3、6、9张照片情况下的结果对比
Table 2 Comparison of the results when 3, 6 and 9 photos are input in scene 2
方法 PSNR↑ SSIM↑ LPIPS↓ 3-views 6-views 9-views 3-views 6-views 9-views 3-views 6-views 9-views NeRF 5.83 8.37 11.56 0.215 0.527 0.674 0.731 0.442 0.368 mipNeRF 8.66 16.32 19.31 0.531 0.642 0.749 0.451 0.365 0.172 pixelNeRF 16.95 19.32 20.73 0.652 0.753 0.788 0.433 0.374 0.258 MVSNeRF 15.02 17.99 21.05 0.602 0.695 0.791 0.326 0.264 0.218 RegNeRF 17.31 20.85 23.17 0.660 0.702 0.853 0.271 0.196 0.103 SparseNeRF 18.85 21.38 23.63 0.624 0.684 0.768 0.257 0.231 0.093 Sv-NeRF 19.11 21.59 24.35 0.632 0.734 0.871 0.252 0.201 0.059 -
[1] 李静, 杨宜民, 蔡述庭. 多视图的三维景物中平表面重建[J]. 智能系统学报, 2014, 9(4): 454−460. doi: 10.3969/j.issn.1673-4785.201309029 LI Jing, YANG Yimin, CAI Shuting. 3-D scene plane reconstruction based on multiple views[J]. CAAI transactions on intelligent systems, 2014, 9(4): 454−460. doi: 10.3969/j.issn.1673-4785.201309029 [2] MILDENHALL B, SRINIVASAN P P, TANCIK M, et al. NeRF: representing scenes as neural radiance fields for view synthesis[J]. Communications of the ACM, 2021, 65(1): 99−106. [3] BARRON J T, MILDENHALL B, TANCIK M, et al. Mip-NeRF: a multiscale representation for anti-aliasing neural radiance fields[C]//2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 5835−5844. [4] MÜLLER T, EVANS A, SCHIED C, et al. Instant neural graphics primitives with a multiresolution hash encoding[J]. ACM transactions on graphics, 2022, 41(4): 1−15. [5] 陈国龙. 郑州双槐树遗址景观演化复原与三维建模[D]. 北京: 中国科学院大学(中国科学院空天信息创新研究院), 2022. CHEN Guolong. Landscape evolution restoration and 3D modeling of Shuanghuaishu site in Zhengzhou[D]. Beijing: Aerospace Information Research Institute, Chinese Academy of Sciences, 2022. [6] 罗畅. 基于GIS与BIM技术的历史建筑数字孪生管理系统研究[J]. 房地产世界, 2023(21): 82−84. LUO Chang. Research on digital twin management system of historical buildings based on GIS and BIM technology[J]. Real estate world, 2023(21): 82−84. [7] YU A, YE V, TANCIK M, et al. PixelNeRF: neural radiance fields from one or few images[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 4576−4585. [8] CHEN Anpei, XU Zexiang, ZHAO Fuqiang, et al. MVSNeRF: fast generalizable radiance field reconstruction from multi-view stereo[C]//2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 14104−14113. [9] TANCHENKO A. Visual-PSNR measure of image quality[J]. Journal of visual communication and image representation, 2014, 25(5): 874−878. doi: 10.1016/j.jvcir.2014.01.008 [10] HORÉ A, ZIOU D. Image quality metrics: PSNR vs. SSIM[C]//2010 20th International Conference on Pattern Recognition. Istanbul: IEEE, 2010: 2366−2369. [11] KETTUNEN M, HÄRKÖNEN E, LEHTINEN J. E-LPIPS: robust perceptual image similarity via random transformation ensembles[EB/OL]. (2019−06−10)[2024−01−29]. https://arxiv.org/abs/1906.03973. [12] DENG Kangle, LIU A, ZHU Junyan, et al. Depth-supervised NeRF: fewer views and faster training for free[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 12872−12881. [13] 范腾, 杨浩, 尹稳, 等. 基于神经辐射场的多尺度视图合成研究[J]. 图学学报, 2023, 44(6): 1140−1148. FAN Teng, YANG Hao, YIN Wen, et al. Multi-scale view synthesis based on neural radiance field[J]. Journal of graphics, 2023, 44(6): 1140−1148. [14] 付前程. 基于神经隐式学习的多视图三维重建算法研究[D]. 武汉: 华中科技大学, 2023. FU Qiancheng. Research on multi-view 3D reconstruction algorithm based on neural implicit learning[D]. Wuhan: Huazhong University of Science and Technology, 2023. [15] NIEMEYER M, BARRON J T, MILDENHALL B, et al. RegNeRF: regularizing neural radiance fields for view synthesis from sparse inputs[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 5470−5480. [16] ZHANG J, YANG Gengshan, TULSIANI S, et al. NeRS: neural reflectance surfaces for sparse-view 3D reconstruction in the wild[J]. Advances in neural information processing systems., 2021(34): 29835−29847. [17] ROESSLE B, BARRON J T, MILDENHALL B, et al. Dense depth priors for neural radiance fields from sparse input views[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 12882−12891. [18] GOODWIN M M, AVENDANO C. Frequency-domain algorithms for audio signal enhancement based on transient modification[J]. AES: journal of the audio engineering society, 2006, 54(9): 827−840. [19] 王玉文, 胡顺波. 数字图像处理形态学的空域与频域实现[J]. 电脑知识与技术, 2022, 18(18): 74−76. doi: 10.3969/j.issn.1009-3044.2022.18.dnzsyjs-itrzyksb202218027 WANG Yuwen, HU Shunbo. Spatial and frequency domain realization of digital image processing morphology[J]. Computer knowledge and technology, 2022, 18(18): 74−76. doi: 10.3969/j.issn.1009-3044.2022.18.dnzsyjs-itrzyksb202218027 [20] 陈树丽, 张学帅, 张鹏远, 等. 静音掩蔽和频域分段的音频指纹检索算法[J]. 声学学报, 2022, 47(4): 531−540. CHEN Shuli, ZHANG Xueshuai, ZHANG Pengyuan, et al. Audio fingerprint retrieval method using anti-fingerprint and frequency domain segmentation[J]. Acta acustica, 2022, 47(4): 531−540. [21] SHEN Weichao, JIA Yunde, WU Yuwei. 3D shape reconstruction from images in the frequency domain[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 4466−4474. [22] ĆIRIĆ D, PERIĆ Z, NIKOLIĆ J, et al. Audio signal mapping into spectrogram-based images for deep learning applications[C]//2021 20th International Symposium INFOTEH-JAHORINA. East Sarajevo: IEEE, 2021: 1−6. [23] SHARAN R V, MOIR T J. Subband time-frequency image texture features for robust audio surveillance[J]. IEEE transactions on information forensics and security, 2015, 10(12): 2605−2615. doi: 10.1109/TIFS.2015.2469254 [24] ZHANG Ruiqi, SONG Peng, LIU Baohua, et al. Low-frequency swell noise suppression based on U-Net[J]. Applied geophysics, 2020, 17(3): 419−431. doi: 10.1007/s11770-020-0825-7 [25] DUCHÊNE S, RIANT C, CHAURASIA G, et al. Multiview intrinsic images of outdoors scenes with an application to relighting[J]. ACM transactions on graphics, 2015, 34(5): 1−16. [26] LIANG Zexiao, TAN Guoliang, SUN Chen, et al. An effective clustering algorithm for the low-quality image of integrated circuits via high-frequency texture components extraction[J]. Electronics, 2022, 11(4): 572. doi: 10.3390/electronics11040572 [27] SONG Liangchen, LI Zhong, GONG Xuan, et al. Harnessing low-frequency neural fields for few-shot view synthesis[EB/OL]. (2023−03−15)[2024−01−29]. https://arxiv.org/abs/2303.08370. [28] TANCIK M, SRINIVASAN P P, MILDENHALL B, et al. Fourier features let networks learn high frequency functions in low dimensional domains[C]//Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: ACM, 2020, 33: 7537−7547. [29] SHENG Zehua, LIU Xiongwei, CAO Siyuan, et al. Frequency-domain deep guided image denoising[J]. IEEE transactions on multimedia, 2022, 25: 6767−6781. [30] PREWITT J M S. Object enhancement and extraction[J]. Picture processing and psychopictorics, 1970, 10(1): 15−19. [31] WANG Guangcong, CHEN Zhaoxi, LOY C C, et al. SparseNeRF: distilling depth ranking for few-shot novel view synthesis[C]//2023 IEEE/CVF International Conference on Computer Vision. Paris: IEEE, 2023: 9031−9042.
