Multiscale knowledge-guided local enhancement method for few-shot fine-grained image classification
-
摘要: 小样本细粒度图像分类任务中,由于支持样本与查询样本之间缺少局部关联性,导致图像关键可区分区域不易精确定位。针对这一问题,提出了多尺度知识引导局部增强的小样本细粒度图像分类方法,采用图像金字塔向下降低采样率获得多个不同分辨率的子图作为输入图像,融合多尺度特征,丰富了样本信息,利用知识引导模块捕获支持样本和查询样本之间的语义相关性,增强了支持样本重要区域的特征表示,对支持样本和查询样本的嵌入特征图进行克罗内克积操作,生成的空间相关图,更精确地定位样本特征之间的位置对应关系,突出了辨别性区域。实验结果表明该方法在小样本细粒度图像分类任务中表现出较好的分类性能。Abstract: In few-shot fine-grained image classification tasks, the absence of local correlation between support and query samples causes difficulty in precisely identifying discriminative regions in images. To solve this problem, this study proposes a multiscale knowledge-guided local enhancement method for few-shot fine-grained image classification. Multiple sub-images with different resolutions are obtained as input images by reducing the sampling rate downward using the image pyramid and by integrating multi-scale features to enrich the sample information. A knowledge-guided module is employed to capture semantic correlations between support and query samples, which enhances the feature representation of important regions in support samples. Kronecker product operations are performed on the embedded feature maps of support and query samples to generate spatial correlation maps. This way enables more accurate localization of the positional correspondence between sample features and highlights the discriminative area. Experimental results confirm the robust classification performance of the method in the classification task of few-shot fine-grained images.
-
深度神经网络(deep neural networks, DNN)[1-4]在计算机视觉方面的成功很大程度上依赖于大量的人工标记的低噪声的训练数据。但是在许多特定的场景中,比如对不同种类的鸟类、狗、汽车进行细粒度图像分类[5]时,能够用于训练的数据较少。细粒度图像分类的目的是准确区分属于同一类别的不同子类别,例如鸟类的物理结构特征非常相似,“黑喙杜鹃”和“黄喙杜鹃”都属于杜鹃鸟类,外形、羽毛颜色十分相似,因鸟喙的颜色不同而被分类为杜鹃鸟类的子类别,由于这些子类存在细微的类间差异和显著的类内差异[6-7],这种任务通常很难获得大量的丰富标记的训练样本,而减轻DNN过度依赖标签丰富的训练数据的一种解决办法就是小样本学习(few-shot learning, FSL) [8-10],其目的是从基类中挖掘可转移的元知识,使DNN能够利用这些知识,在仅有少量训练数据的情况下,轻松识别出新的类。
现有的小样本细粒度图像分类方法,特别是基于度量学习的方法,如匹配网络(matching network)[11]、原型网络(prototypical network)[12]等,这些方法通常包括2个阶段:特征提取器和用于分类的度量模块。特征提取器提取支持样本和查询样本的特征表示,然后度量模块依赖预定义的距离度量函数(如余弦相似性或欧几里得距离)得出嵌入样本之间的相似性。仅依赖于固定的度量函数计算图像之间的相似度往往导致识别不准确。因此,关系网络(relation network)[13]被提出,基于可学习的度量而不是固定度量来学习可传递的嵌入。该方法包括2个卷积神经网络模块:一个模块学习图像表示,而另一个模块学习这些表示之间的关系。
关系网络在比较特征时仅依赖单一尺度的特征进行比较,这可能会由于对象的尺度变化而导致泛化能力较差,当特征尺度较小时,特征图分辨率比较低,单个像素的感受野比较大,感受野重叠区域增加,此时的像素点代表的信息是一个区域的信息,语义信息相对比较丰富,更具有全局性,但全局特征容易受环境干扰,如光照、遮挡、噪声等因素的影响;而特征尺度较大时,特征图分辨率比较高,单个像素的感受野比较小,感受野重叠区域也较小,可以捕获更多细粒度信息和纹理信息,比如边缘、棱角信息等,特征更具体、细致和具有局部性。融合更细节的局部信息,特征间相关度小,可以减少噪声特征的影响,融合多个尺度的样本进行特征提取,结合全局信息和局部信息可以避免特征信息的单一性。
细粒度图像具有类间差异小、类内差异大的特点,定位更具辨别性局部区域是区分不同子类别的关键[14],以往的研究大多集中在生成足够数量的支持样本,这些方法依赖于复杂的模型和额外的数据,并且由于不同查询样本中的查询对象可能在视图、形状、照明等方面不同,与查询样本相关的支持样本中的可区分区域可能非常不同,因此学习支持样本和查询之间的语义相关性,获取有用的辨别“知识”以及增强支持样本中的判别区域以产生校准的类中心对于生成适于查询的决策边界是至关重要的。为了解决这个问题,可以通过捕获支持样本与查询样本之间的语义相关性,从查询样本中学习与支持样本具有强相关的局部区域作为一组“知识”,将这组“知识”与支持样本结合生成针对每个查询样本的唯一的新的支持样本,以此增强支持样本中的局部重要判别区域,引导网络学习更关键可区分部位的特征,对细粒度图像作出更准确地分类。
本文受到已有方法的启发,提出了一种新的小样本细粒度学习方法,称为多尺度知识引导局部增强的小样本细粒度图像分类方法(multi-scale knowledge-guided region enhancementmethod for few-shot fine-grained image classification, MKGRE)。MKGRE是一种端到端可训练的方法,遵循提出的周期性训练机制,融合多个尺度特征,捕捉样本对之间语义相关性较强的关键区域, 避免不重要因素和噪声因素的干扰。与关系网络相比,提出的方法能够进行更有效的相似度学习和更好的特征比较。本文的主要贡献总结如下:
1) 本文提出了一种基于多尺度知识引导局部增强的小样本细粒度图像分类方法,通过知识引导模块捕获支持和查询样本之间的语义相关性,以及增强支持表示的判别区域,在少量训练样本下定位和整合细粒度图像中差异细微的重要判别区域。
2) 为了在比较特征时将关系网络扩展到位置感知,本文引入了一个克罗内克积模块,该模块集成了比较的特征图之间的位置相关性,能够有效地学习任意位置对象的深度关系。
3) 为了处理对象的尺度变化,本文扩展了框架,以整合多尺度特征,实现更强大和更准确的表示学习。本文在4个广泛使用的小样本细粒度图像分类数据集(MiniImagenet、CUB-200-2011、Stanford Dogs、Stanford Cars)上进行对比和消融实验,证明本文提出的方法具有更好的实验效果。
1. 相关工作
1.1 小样本学习
小样本学习是指从少量的样本中学习特征训练模型,将训练好的模型用于识别新的类。在本节中,本文主要从基于数据增强方法和基于度量学习的方法来回顾小样本细粒度图像学习的相关工作。训练样本的缺乏是训练偏差和过拟合的重要原因之一,数据增强是增加训练样本数量的一种传统而有效的方法,基于数据增强的方法旨在利用生成器网络从有限的训练数据中创建新的样例,或者利用外部信息来支持小样本学习任务。一些增强操作,如翻转、裁剪、平移和添加噪声,已经被广泛应用于计算机视觉研究。然而这些朴素的增强方法已不足以提高小样本学习模型的泛化能力。Hariharan等[15]认为,某些类内变异模式可以跨类推广,于是将基类的变异模式转移到新类中,以“变幻”出额外的例子。基于度量学习的方法使用一组嵌入函数来学习信息丰富的相似性度量,目的是找到合适的测量方式来量化查询图像和给定支持图像之间的关系。例如,Siamese Network[16]依赖于孪生卷积网络,该网络学习对输入之间的相似性进行排序。为了解决特征关注以前见过的类的对象而忽略新类的对象的问题,Hou等[17]提出了一个交叉注意网络,该网络对每个类和查询特征之间的语义相关性进行建模。考虑到可学习深度局部描述符的重要性,Li等[18]引入了深度最近邻神经网络(deep nearest neighbor neural networks, DN4),该网络用基于图像到类度量的局部描述符替换了图像级特征。DN4遵循单向的“从查询到支持”范式,通过为查询特征找到最接近的支持特征来实现分类。Wu等[19]提出了位置感知关系网络(position aware relation networks, PARN)通过使用可变形的特征提取器提取更有效的特征,并引入双重相关注意机制来处理关系网络在比较不同空间位置的物体时失效的问题。针对关系网络对比较对象的空间位置较敏感的问题,Abdelaziz等[20]提出克罗克内积关系网络,将特征映射与多尺度特征之间的克罗内克积运算生成的位置空间相关映射相结合,将关系网络扩展到位置感知。
1.2 细粒度图像分类
细粒度图像分类是近年来一个热门的研究课题,由于细粒度子类别的类别内方差大,类别间方差小,因此比一般的目标对象识别更具挑战性。在早期的研究中,一些传统的方法(如HPM[21])被提出在训练和推理阶段利用先验信息或手工制作的特征来定位判别部分,但这种方法严重依赖于手工标注,因此性能和泛化效果不理想。深度细粒度分类方法可以大致分为2类:基于区域特征的方法和基于全局特征的方法。Zhang等[22]首先将R-CNN与几何先验结合成细粒度分类器,并使用对象检测来定位局部区域。为了易于部署,Zhang等[23]提供了一个细粒度的图像分类系统,它只对训练图像的标签进行分类。Song等[24]设计的方法不仅可以捕获有差异的部分,还可以使用文本描述中的知识进行交互式对齐。相比之下,基于全局特征的方法从整个图像中提取特征,而无需明确定位目标对象。与之前的工作相比,本文在一个更具挑战性的小样本学习环境中研究细粒度分类任务,称为小样本细粒度图像分类(few-shot fine-grain vision classification, FS-FGVC),其中有限的标记样本被提供给模型以识别新的细粒度类别。
1.3 小样本细粒度图像分类
小样本细粒度图像分类的目的是在给定少量的标记样本情况下,对一个通用类别区分其差异更细微的新的子类。近些年来,深度学习技术发展迅速,在细粒度图像分类和识别等方面取得了突出的成果[25-26]。Wei等[27]首先定义了FS-FGR任务的设置,该模型使用双线性编码器来捕获细微的图像特征。Ruan等[28]提出空间注意力比较网络,支持集和查询集的多尺度特征被逐个像素地动态地赋予不同的权重,基于选择性比较将支持集的特征与查询集的特征进行融合。Xu等[29]提出双重注意力网络(dual attention network, Dual Att-Net),该网络将硬注意力和软注意力2个分支结合,显式地建模细粒度对象部分的关键关系,而且还可以隐式地捕捉细微的细粒度细节。Munjal等[30]提出一种查询引导网络适用于细粒度分类和人物搜索任务,包含查询引导的siamese-squeese-and-excitation子网,该子网在所有网络层中重新加权查询和库特征,一个查询引导的区域建议子网用于查询特定的本地化,以及一个查询引导的相似性子网用于度量学习。解耀华等[31]采用可变形卷积融合多粒度特征来定位不同粒度的辨别性局部区域。LRPABN(low-rank pairwise alignment bilinear network)[32]通过引入成对双线性池化算子,利用特征对齐来学习合适的度量空间。MattML(multi-attention meta learning)[33]作为一种基于元学习的方法,引入了任务嵌入网络,通过注意机制自动学习任务指定的初始化,达到了最先进的性能。原有的方法通常使用一组类中心生成的共享决策边界对每个查询样本进行分类。然而,原有方法忽略了由于支持样本数量有限而引入的不准确决策边界和不相关特征对模型效果的影响。在这项工作中,本文扩展了基于度量学习的方法,引入了知识引导模块(knowledge-guided module, KGM)来学习查询样本上与支持样本最相关的重要判别区域,并为每个查询样本创建生成具有判别性新支持样本,受文献[34]的启发,为了处理关系网对空间位置的敏感性,MKGRE还引入了克罗内克积模块(kronecker-product module, KPM),该模块创建空间位置相关图,以捕获比较对象的特征图的每个空间位置的重要性。此外,MKGRE集成了多尺度特征,提供了更多的多尺度信息,解决了目标对象的尺度不匹配问题。
2. 本文方法
2.1 问题定义
标准的基于度量的小样本学习分类过程一般有2个阶段:元训练和元测试。在元训练阶段,通常提供包含基类和每个类中足够的标记样本的基础数据集
${{\boldsymbol{D}}_{{\text{train}}}}$ 。用${{\boldsymbol{D}}_{{\text{val}}}}$ 验证集验证训练好的模型之后,在元测试阶段,新的数据集${{\boldsymbol{D}}_{{\text{test}}}}$ 包含新的类,其中每个类仅具有少量的标记样本。小样本学习的目的是对新数据集进行分类。小样本细粒度问题通常被形式化为“N-way K-shot”任务,并采用情景训练机制,每个情景设置包含支持集
${\boldsymbol{S}} = \{ ({{\boldsymbol{s}}_{1,1}},{{\boldsymbol{c}}_1}),({{\boldsymbol{s}}_{1,2}},{{\boldsymbol{c}}_2}), \cdots ,({{\boldsymbol{s}}_{1,{K_{\boldsymbol{S}}}}},{{\boldsymbol{c}}_N})\} $ 和查询集$ {\boldsymbol{Q}} = \{ {{\boldsymbol{q}}_{1,1}},{{\boldsymbol{q}}_{1,2}}, \cdots ,{{\boldsymbol{q}}_{1,{K_{\boldsymbol{Q}}}}},{{\boldsymbol{q}}_{2,{K_{\boldsymbol{Q}}}}}, \cdots ,{{\boldsymbol{q}}_{N,{K_{\boldsymbol{Q}}}}}\} $ 也可简单地表示为${\boldsymbol{Q}} = \{ {{\boldsymbol{q}}_m}|m = 1,2, \cdots ,M\} ,M = N{K_{\boldsymbol{Q}}}$ ,样本通常包含N个类别,每个类别都有${K_{\boldsymbol{S}}}$ 个带标签的支持样本和${K_{\boldsymbol{Q}}}$ 个不带标签的查询样本。2.2 网络结构
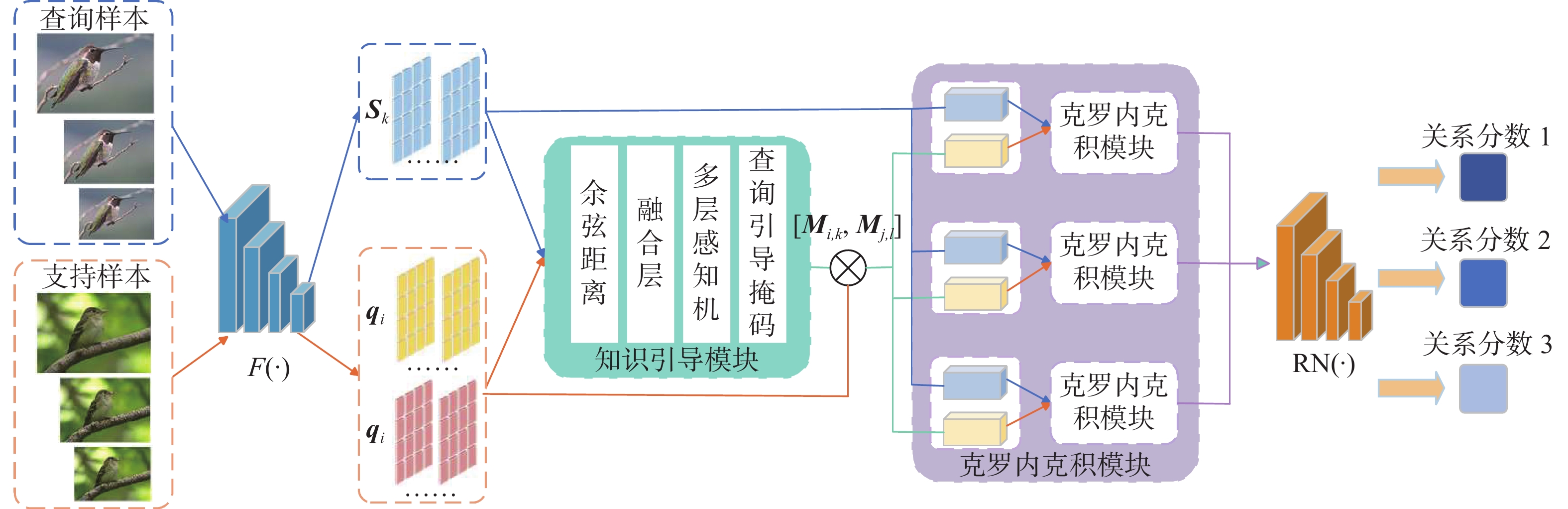
这一节将介绍本文提出的多尺度知识引导局部增强网络模型(emulti-scale knowledge-guided region enhancement method, MKGRE)。图像金字塔是一种以多分辨率来解释图像的有效但概念简单的结构,将一张图像不断地降低采样率产生多个不同的分辨率子图作为模型的输入图像,每个分辨率子图都保留了原始图像的目标对象,粒度相对密集的采样可以看到更多的细节,粒度更稀疏的采样可以看到整体趋势,目的是为了获取更强大的特征表示。如图1所示,MKGRE框架主要由4部分组成:1)多尺度特征提取模块(feature extraction module, FEM),本文采用图像金字塔将一张图像不断地降低采样率产生多个不同的分辨率大小的子图,使用Conv-64F[35]作为特征提取网络,Conv-64F将查询样本和支持样本的多尺度图像嵌入到特征空间中,输出卷积结果;2)知识引导模块(knowledge-guided module, KGM),获得特征提取器输出的卷积特征图,学习捕捉支持样本与查询样本空间中的丰富的语义相关性,多层感知机将样本间的语义关联映射到一组掩码,掩码代表一对样本中不同区域的内在关联程度,对于每个查询样本,KGM生成支持样本对应的唯一查询引导掩码,并作用于相应的支持表示,引导网络更多地关注相关的信息区域;3)克罗内克积模块(kronecker-product module, KPM),对特征图之间进行两两特征间的内积运算,生成空间相关图,以确定特征图之间的位置对应关系;4)关系网络(relation network, RN),最后将克罗内克积模块得到的这些空间相关图与它们对应的特征图拼接在一起,输入到关系网络模块中计算支持样本与查询样本之间的关系得分,以多尺度方式捕捉样本特征之间的位置相似性,更准确地定位细粒度图像关键可区分性区域。
2.3 知识引导模块
小样本学习模型通常仅使用少量支持样本进行训练,这往往会在这几个样本上过度拟合并形成有偏差的类中心。如图2所示,由于查询样本中不同的查询对象在视图、形状、光照等方面可能存在差异,支持样本中与每个查询样本相关的判别部分可能存在较大差异。捕获支持样本和查询样本的语义相关性可以极大地帮助网络生成校准的类中心,并生成适于查询的决策边界。本文引入KGM,KGM将来自查询集和支持集的一对样本作为输入,并学习捕获空间中丰富的语义相关性。然后,多层感知器将语义相关性映射到一个掩码簇,该掩码簇表示一对样本中不同区域的固有相关度。对于每个查询样本,KGM生成对应于支持样本的唯一多聚类掩码,称为查询知识引导掩码。查询知识引导的掩码被应用于相应的支持表示,允许网络更加关注相关的信息区域,并生成用于对查询样本进行分类的具有特定知识引导的支持样本。KGM将查询样本表示和支持样本表示作为输入,并学习为每个查询样本
${{\boldsymbol{q}}_m} \in \{ {{\boldsymbol{q}}_1}, {{\boldsymbol{q}}_2}, \cdots ,{{\boldsymbol{q}}_M}\} $ 生成由查询样本引导的支持样本特征表示。在训练过程中,支持样本$\{ {\boldsymbol{s}}_{n,k}^{(i)}\} $ $, n \in \{ 1, 2, \cdots ,N\} , k \in \{ 1, 2, \cdots ,{K_{\boldsymbol{S}}}\} , i \in \{ 1,2,3\}$ 和查询样本$\{ {\boldsymbol{q}}_m^{(i)}\} ,i \in \{ 1,2,3\} $ 通过图像金字塔向下降低采样率产生3个不同的分辨率子图作为输入图像,被输入到具有可训练参数$\theta $ 的特征提取器${{{F}}_\theta }$ 来获得其特征表示$ \{ {{{F}}_\theta }\left({\boldsymbol{s}}_{n,k}^{(i)}\right)\} \in {{\bf{R}}^{C \times HW}} $ 和$\{ {{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})\} \in {{\bf{R}}^{C \times HW}}$ ,其中C、H、W分别表示特征图的通道数、高度和宽度。然后特征表示进一步被传递到KGM,KGM学习查询−支持之间的成对语义相关性生成查询引导的支持特征表示,每个查询样本对应特定的新的支持表示,然后通过对每个类别的支持表示进行平均,细化后的支持特征形成校准的类中心以此来推断查询样本的类别。KGM的目的是生成查询样本引导掩码,首先,对于输入的查询样本特征
${{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})$ ,支持样本特征${{{F}}_\theta }\left({\boldsymbol{s}}_{n,k}^{(i)}\right)$ 输入到模块中用余弦距离计算支持特征和查询特征之间语义相关图,可以定义为$$ {\boldsymbol{D}}_{m,n,k}^{(i)} = {\left( {\frac{{{{{F}}_\theta }\left({\boldsymbol{s}}_{n,k}^{(i)}\right)}}{{{{\left\| {{{{F}}_\theta }\left({\boldsymbol{s}}_{n,k}^{(i)}\right)} \right\|}_2}}}} \right)^{\text{T}}}\left( {\frac{{{{{F}}_\theta }\big({\boldsymbol{q}}{}_m^{(i)}\big)}}{{{{\left\| {{{{F}}_\theta }\big({\boldsymbol{q}}{}_m^{(i)}\big)} \right\|}_2}}}} \right) $$ 式中:
${\boldsymbol{D}}_{m,n,k}^{(i)} \in {{\bf{R}}^{WH \times WH}}$ ,${\boldsymbol{D}}_{m,n,k}^{(i)}$ 表示余弦距离的集合,$ \boldsymbol{D}_{m,n,k}^{(i)}=\left\{d_1,d_2,\cdots,d_{WH}\right\} $ ,$ {d_i} \in {{\bf{R}}^{WH}} $ 表示支持样本的局部区域特征与查询样本的每个局部区域特征之间的相关性。然后使用融合层对局部支持区域与整个查询嵌入样本之间的相关性进行建模。融合层将语义相关图
$ {\boldsymbol{D}}_{m,n,k}^{(i)} $ 作为输入,并应用最大池化操作融合每个局部关联$ {d_i} $ ,可以得到最终输出的$ \widehat {\boldsymbol{D}}_{m,n,k}^{(i)} $ :$$ \widehat {\boldsymbol{D}}_{m,n,k}^{(i)} = \{{\text{MaxPool}}({d_1}), {\text{MaxPool}}({d_2}), \cdots ,{\text{MaxPool}}({d_{WH}})\} $$ 最后,将得到融合后的语义相关图传送到包含一个隐藏层的多层感知器,由此产生查询知识引导掩码
${\boldsymbol{M}}_{m,n,k}^{(i)} \in {{\bf{R}}^{WH}}$ :$$ {\boldsymbol{M}}_{m,n,k}^{(i)} = {\text{MLP}}\left(\widehat {\boldsymbol{D}}_{m,n,k}^{(i)}\right) = \sigma \left(\frac{1}{\tau }{{\boldsymbol{W}}_1}\left({{\boldsymbol{W}}_0}\left(\widehat {\boldsymbol{D}}_{m,n,k}^{(i)}\right)\right)\right) $$ 式中:
$ \sigma (\cdot) $ 表示Sigmoid函数,$\tau $ 是温度系数,${{\boldsymbol{W}}_0} \in {{\bf{R}}^{C \times C/r}}$ 和${{\boldsymbol{W}}_1} \in {{\bf{R}}^{C \times r/C}}$ 为权重值,$C$ 表示特征图中的通道数,$r$ 是衰减率,在实验中设置$r = \sqrt C $ ,${{\boldsymbol{W}}_0}$ 后面是BN(batch normalization)层和ReLU函数。对于查询嵌入样本
${{{F}}_\theta }\left({\boldsymbol{q}}_m^{(i)}\right)$ ,通过知识引导模块获得新的支持样本特征表示${\boldsymbol{U}}_{m,n,k}^{(i)}$ :$$ {\boldsymbol{U}}_{m,n,k}^{(i)} = {\boldsymbol{M}}_{m,n,k}^{(i)} * {{{F}}_\theta }\left({\boldsymbol{s}}_{n,k}^{(i)}\right) $$ 式中*表示掩码与每个通道的特征执行逐元素乘法运算。
2.4 克罗内克积关系网络模块
2.4.1 克罗内克积模块
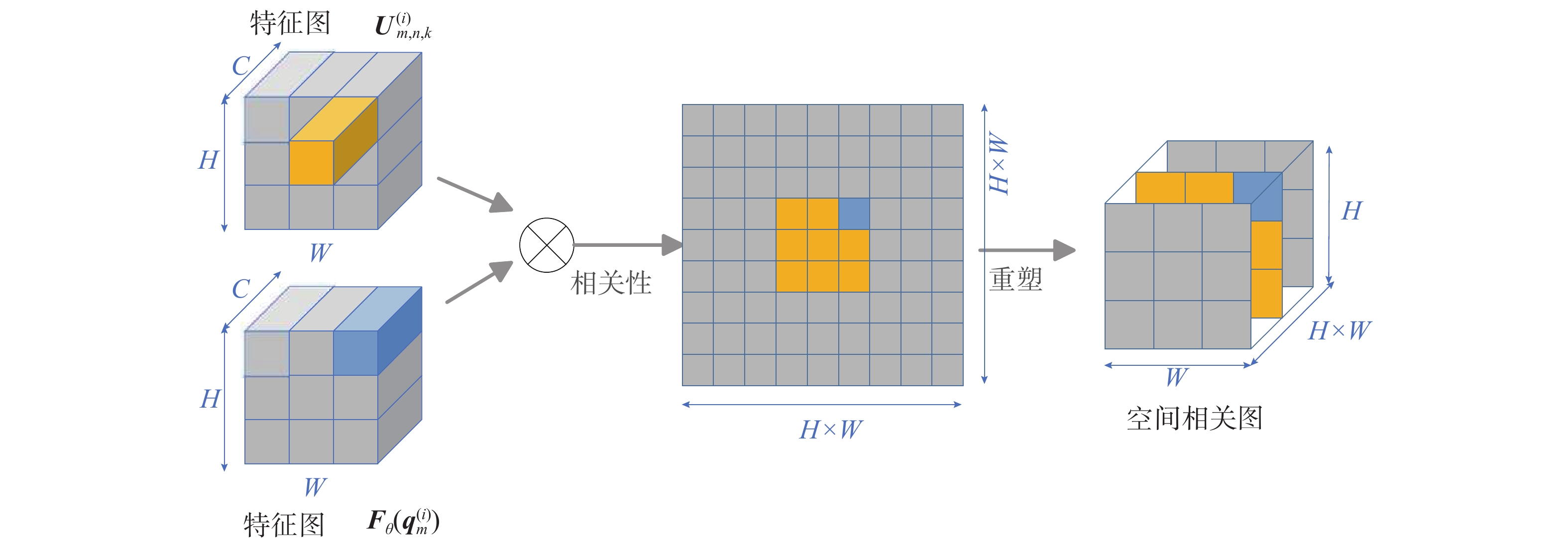
简单的矩阵内积是矩阵中2个分量的乘积之和,结果为一个标量,而克罗内克积是2个任意大小的矩阵间的运算,一般的2个矩阵乘积可相乘的条件为前面矩阵的列数必须等于后面矩阵的行数,否则就无法进行乘积运算的限制,而克罗内克积没有这个条件,使得特征矩阵之间的运算变得更简单、高效。因此克罗内克积关系网络模块能从嵌入的2个特征表示中捕捉任何空间位置的双重重要性,学习来自相同尺度的支持−查询样本特征图对之间的关系。该模块通过2个操作实现:首先,对特征映射进行求克罗内克积操作,生成空间相关映射图。然后,在减少空间大小后,将生成的空间相关图与输入的特征表示相连接,传递通过关系网络以学习最终的关系得分。具体地,本文将特征提取器生成的多尺度查询样本特征
${{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})$ 和经过知识引导模块生成的新的多尺度支持样本特征${\boldsymbol{U}}_{m,n,k}^{(i)}$ 输入到克罗内克积模块,如图3所示,相同尺度的支持样本特征${\boldsymbol{U}}_{m,n,k}^{(i)}$ 和查询样本特征${{{F}}_\theta }\left({\boldsymbol{q}}_m^{(i)}\right)$ 通过分别计算来每对样本${\boldsymbol{s}}_{n,k}^{(i)}$ 和${\boldsymbol{q}}_m^{(i)}$ 位置之间的内积来表示位置空间相关图:$$ {{\boldsymbol{\beta}} _{\left({\boldsymbol{U}}_{m,n,k}^{(i)},{F_\theta }({\boldsymbol{q}}_m^{(i)})\right)}} = {\boldsymbol{U}}_{m,n,k}^{(i)} \otimes {{{F}}_\theta }({\boldsymbol{q}}_m^{(i)}) $$ 式中
${\boldsymbol{\beta}} \in {{\bf{R}}^{HW \times HW}}$ 。在实验中,每个H×W的子矩阵的克罗内克积都可以被看作是来自
${\boldsymbol{U}}_{m,n,k}^{(i)}$ 的1×C×1×1滤波器与来自${{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})$ 的1×C×H×W特征映射之间的卷积运算,对于一个有效的克罗内克积运算,将${\boldsymbol{U}}_{m,n,k}^{(i)}$ 的维数置换成H×C×1×1,然后将其作为卷积权重与${{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})$ 进行卷积。为了将所获得的位置空间相关图与输入特征相结合,在其最后一个维度上进行逐元素最大化操作来减少空间大小,得到最大化位置空间相关图$ {\boldsymbol{\beta}} $ ,其中$\widehat {\boldsymbol{\beta}} \in {{\bf{R}}^{HW \times HW}}$ 计算公式为$$ {\widehat {\boldsymbol{\beta}} _{\left({\boldsymbol{U}}_{m,n,k}^{(i)},{F_\theta }(q_m^{(i)})\right)}} = {\text{Max}}\left({{\boldsymbol{\beta}} _{\left({\boldsymbol{U}}_{m,n,k}^{(i)},{F_\theta }({\boldsymbol{q}}_m^{(i)})\right)}}\right) $$ 随后,
$\widehat {\boldsymbol{\beta}} $ 被扩展为具有与输入特征图相同的维度,即$\widehat {\boldsymbol{\beta}} \in {{\bf{R}}^{H \times W}}$ ,其整合了关于${\boldsymbol{U}}_{m,n,k}^{(i)}$ 和${{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})$ 的空间位置的更多信息,最后,将${\boldsymbol{U}}_{m,n,k}^{(i)}$ 和${{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})$ 通过共享的1×1卷积层之后获得的4个特征结合起来,可得最终的特征图:$$ \begin{gathered} \widehat {{\boldsymbol{\beta}} '} = {\widehat {\boldsymbol{\beta}} _{\left({\boldsymbol{U}}_{m,n,k}^{(i)},{F_\theta }({\boldsymbol{q}}_m^{(i)})\right)}}\\ \widehat {{\boldsymbol{\beta}} ''} = {\widehat {\boldsymbol{\beta}} _{\left({F_\theta }({\boldsymbol{q}}_m^{(i)}),{\boldsymbol{U}}_{m,n,k}^{(i)}\right)}} \end{gathered} $$ $$ {{\boldsymbol{G}}_{{\boldsymbol{U}}_{m,n,k}^{(i)},{{{F}}_\theta }({\boldsymbol{q}}_m^{(i)})}} = {\text{Concat}}\left({\boldsymbol{U}}_{m,n,k}^{(i)},\widehat {{\boldsymbol{\beta}} '},\widehat {{\boldsymbol{\beta}} ''},{{{F}}_\theta }\left({\boldsymbol{q}}_m^{(i)}\right)\right) $$ 2.4.2 关系网络模块
如图4(a) 所示,查询样本落在正确类的分布区域,分类正确,而查询样本落在混淆类的分布区域,导致识别不准确,因此仅依赖于固定的度量函数可能不是衡量图像表示相似性的最佳方式;如图4(b) 所示,关系网络基于可学习的度量计算来自同一尺度的支持−查询样本对特征图之间的相似性或关系得分,能够更灵活的处理复杂的非线性关系。将克罗内克积模块生成的特征图通过关系网络RN学习支持−查询样本之间的关系得分,对于N-way K-shot分类任务,关系得分可以表示为
$$ {{\boldsymbol{R}}_{i,j}} = {\mathrm{RN}}\left({{\boldsymbol{G}}_{{\boldsymbol{U}}_{m,n,k}^{(i)},{F_\theta }({\boldsymbol{q}}_m^{(i)})}};\Re \right) $$ 式中:
$ i=1,2,\cdots,N\times K_{\boldsymbol{S}};j=1,2,\cdots,N\times K_{\boldsymbol{q}} $ ;$\Re $ 表示关系网络RN的网络参数,最后生成的$N \times {K_{\boldsymbol{S}}}$ 个关系得分表示为不同尺度下的来自支持集的支持样本和来自查询集的查询样本之间的相似性。根据相似性分数分类得出查询样本的预测样本标签
$\hat y$ ,本文在每个不同尺度特征图上采用最小化均方误差(mean square error, MSE)作为损失函数,计算预测样本标签$ {{\hat y_i}}$ 与真实样本标签${y_j}$ 之间的损失:$$ {L_{{\text{MSE}}}} = \mathop {\arg \min }\limits_{F,\Re } {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\left({{\bf{R}}_{i,j}} - \delta \left( {{ {\hat y}_i}} - {y_j}\right)\right) ^2} }} $$ 式中
$\delta (0) = 1$ (否则为0)。3. 实验结果与分析
3.1 实验设计
为了验证本文提出的方法在小样本细粒度图像分类任务中的有效性,分别在4个广泛应用的小样本细粒度领域的数据集上进行相关实验,如表1所示,这些数据集分别是MiniImageNet[11]、CUB_200_2011[36]、Stanford Cars[37]、Stanford Dogs[38]。本文的所有实验过程不使用额外的数据,模型设置300 000个情景训练,在5-way 1-shot和5-way 5-shot设置下,均采用Conv-64F作为特征提取器,在训练过程中对查询样本运用随机裁剪、随机水平翻转进行数据增强,输入样本图像大小设置成3个不同尺度,大小分别是84像素×84像素、64像素×64像素和48像素×48像素,采用Adam优化器从头开始训练模型,学习率初始化为0.001。在测试阶段,通过600个随机生成的情景来计算测试样本平均分类准确率。
表 1 数据集信息表Table 1 Datasets information数据集名称 类别
总数训练集
类别数验证集
类别数测试集
类别数MiniImageNet 100 64 16 20 CUB_200_2011 200 130 20 50 Stanford Cars 196 130 17 49 Stanford Dogs 120 70 20 30 本文用分类准确率
$ A\mathrm{_{cc}} $ 作为小样本细粒度图像分类人物的实验评估方法:$$ A_{\mathrm{cc}}=M_X/M $$ 式中:M是测试集的图片数量,
${M_X}$ 表示测试集图片中分类正确的图片数量。3.2 对比实验及分析
为了评估MKGRE在小样本细粒度图像分类任务中的有效性,本文分别在MiniImageNet、CUB_200_2011、Stanford Cars、Stanford Dogs数据集上将其与其他最先进的方法比较。
3.2.1 MiniImageNet小样本数据集实验结果
本文方法在MiniImageNet数据集上进行实验,实验结果如表2所示,从表中可以观察到,在5-way 1-shot任务场景中,分别比传统基于度量学习的模型MatchNet、ProtoNet、RelationNet的分类准确率提高了约14百分点、8百分点和7百分点,所有方法中,MsKPRN具有较高的准确率,该方法首先将支持样本和查询样本图像划分成3个不同尺度大小嵌入网络,然后进行克罗内克积操作,计算出样本之间的位置相关图,通过关系网络得出查询样本与所有支持样本的相关系数,利用多损失函数优化整个网络,实现分类。这种方法只考虑了查询样本与支持样本特征之间的位置关系,忽略了特征之间所包含的语义相关性,因此本文提出采用知识引导模块捕捉查询样本与每个支持样本之间的语义信息,增强支持样本的重要区域特征表示,1-shot场景下最后分类准确率相较于MsKPRN提高了约0.7百分点。在5-way 5-shot任务场景中MKGRE也取得了较好的分类效果,但是没有1-shot场景的效果显著,主要是由于本文方法的目的是在较少的训练样本下实现细微差异的图像分类,即训练图片越少,本文方法提升分类性能效果相对越好。
表 2 MiniImageNet数据集分类结果Table 2 Classification results of MiniImageNet dataset% 方法 MiniImageNet 1-shot 5-shot MatchNet[11] 43.56±0.84 55.31±0.73 ProtoNet[12] 49.42±0.78 68.20±0.66 RelationNet[13] 50.44±0.82 65.32±0.70 GNN[39] 50.33±0.36 66.41±0.63 DN4[18] 51.24±0.74 71.02±0.64 MSDN[40] 52.59±0.81 68.51±0.69 RPMN[41] 53.35±0.78 69.35±0.59 RCN[42] 53.47±0.84 71.63±0.70 MsKPRN[20] 56.07±0.84 71.56±0.66 MKGRE(本文) 57.78±0.94 72.08±0.63 3.2.2 细粒度图像数据集实验结果
本文提出的方法在CUB_200_2011、Stanford Cars、Stanford Dogs 3个细粒度图像数据集上进行实验并与其他方法进行比较,实验结果如表3所示,使用Conv-4为特征提取器,结果表明在5-way 1-shot和5-shot实验中MKGRE在细粒度数据集上获得的分类性能要优于基于度量学习的方法,细粒度数据集因其图像“类内差异大,类间差异小”的特点,所以要比普通数据集更具有挑战性。RCN利用余弦相似性来为支持样本和查询样本对之间的比较区域分配权重。MsKPRN仅使用一个克罗内克积模块来检测支持样本和查询样本之间的重要共同区域位置,忽略了样本对之间的语义相关性。与之不同的是本文的MKGRE先通过知识引导模块捕捉支持样本和查询样本之间的语义相关性,增强支持样本中与查询样本相关的重要区域表示,再通过克罗内克积操作获得特征图之间的位置相关性,结合语义信息和位置信息定位差异细微的细粒度图像的关键可区分区域。在CUB_200_2011数据集上的1-shot和5-shot实验中比RCN方法性能分别提升了约5百分点和1.6百分点,相较于MsKPRN方法准确率分别提升了约2百分点和0.7百分点。在Stanford Cars数据集上的1-shot实验中比MsKPRN方法准确率提升了约2百分点。
表 3 细粒度图像数据集分类结果Table 3 Classification results of fine-grained image datasets% 方法 CUB_200_2011 Stanford Cars Stanford Dogs 1-shot 5-shot 1-shot 5-shot 1-shot 5-shot MatchNets[11] 45.30±1.03 59.50±1.01 34.80±0.99 44.70±1.03 35.80±0.99 47.50±1.08 ProtoNets[12] 37.36±1.00 45.28±1.03 40.90±1.01 52.93±1.03 37.80±0.99 48.19±1.03 RelationNets[13] 53.11±1.01 67.45±0.79 47.67±0.47 60.59±0.40 43.33±0.42 55.23±0.41 GNN[39] 51.83±0.98 63.69±0.94 55.85±0.97 71.25±0.89 46.98±0.98 62.27±0.95 DN4[18] 53.15±0.84 81.90±0.60 61.51±0.44 89.60±0.44 45.73±0.73 66.33±0.66 LRPABN[25] 63.63±0.77 76.06±0.58 60.28±0.76 73.29±0.58 45.72±0.75 60.94±0.76 RCN[42] 66.48±0.88 82.04±0.58 — — 54.29±0.96 72.65±0.66 MattML[33] 66.29±0.56 80.34±0.30 66.11±0.54 82.80±0.28 54.84±0.53 71.34±0.38 MsKPRN[20] 69.49±0.95 82.94±0.65 76.64±0.84 89.88±0.46 57.05±0.91 75.85±0.68 MKGRE(本文) 71.72±0.90 83.91±0.58 78.51±0.84 90.00±0.45 58.63±0.98 75.53±0.66 这些改进反映了用多尺度特征代替单尺度特征和捕捉图像之间的语义信息和位置信息来定位重要辨别性区域对小样本细粒度图像分类性能提升有积极的作用。
3.3 消融实验
本文在CUB_200_2011数据集上进行了一些消融实验,来探究在不同尺度大小的输入图像上采用知识引导模块和克罗内克积模块对小样本细粒度图像分类任务的有效性。不同尺度特征信息对模型分类准确率的消融实验结果如表4所示。
表 4 消融实验结果Table 4 Ablation results% 尺度大小 CUB_200_2011 84×84 64×64 48×48 5-way 1-shot 5-way 5-shot √ 71.38±0.92 83.13±0.62 √ √ 71.72±0.90 83.91±0.58 √ √ √ 71.00±0.97 82.90±0.63 只在单一尺度下进行图像特征提取所提取的特征信息比较单一,导致在小样本细粒度分类任务中的性能较弱。在84像素×84像素和64像素×64像素的2个尺度下提取图像特征比在单一尺度下得到的分类准确率高约0.4百分点,比3个尺度特征分类准确率高约0.7百分点。这是因为在训练样本较少的情况下提取的有用的特征信息较少,多尺度特征提取可以解决单尺度无法充分提取特征信息的问题,实现高分辨率特征与低分辨率特征之间信息互补。加上更小的48像素×48像素大小图像的特征信息分类性能反而下降,由于特征图太小导致感受野过大,忽略了要提取的特征区域,使所要区分的物体成为背景噪声,从而影响分类效果。综上,通过提取多个不同尺度的图像特征信息,再利用知识引导模块对支持样本局部增强和克罗内克积模块生成位置相关图,对提高小样本细粒度图像分类任务有显著意义。
为了验证知识引导模块和克罗内克积模块对对于网络学习特征能力的影响,以CUB_200_2011数据集的5-way 1-shot任务场景为例,在关系网络RN的基础上,对每一个模块进行消融实验。实验结果见表5。
表 5 模块消融实验结果Table 5 Experimental results of module ablation% 模块 骨干网络 准确率 RN Conv-64F 53.11±1.01 RN+KGM Conv-64F 68.03±0.01 RN+KPM Conv-64F 69.48±0.95 RN+KGM+KPM Conv-64F 71.72±0.90 以结合RN模块的Conv-64F作为骨干网络,分别测试KGM和KPM的有效性。通过分析表5中的数据可以得知,结合了KGM的关系网络的准确率比单独使用关系网络提高了15百分点,虽然此时网络学到了相关性强的细微特征,但是区域特征的位置关系对于细粒度图像分类任务来说也是相对重要的,同时结合KGM和KPM的关系网络比单独使用这2个模块的分类效果更好,分类准确率达到了71.72%,由此可以看出关联性强的细节特征还要辅以两两对应的位置关系才能发挥更好的作用。
为了进一步证明提出的MKGRE网络学习的特征更具有局部区分性,对CUB_200_2011数据集图像进行可视化,热力图红色区域表示特征响应较高的地方,图5分别进行了RN、MsKPRN以及本文的MKGRE 3种不同方法对应的网络提取特征的热力图可视化,从图中可以看出MKGRE方法响应较高的部分主要集中在鸟头、鸟翼等关键局部区域,说明鸟的头部和鸟翼部分对分类结果的贡献最大,本文通过从查询样本中学习与支持样本具有强相关的局部区域作为一组“知识”,增强支持样本中的局部重要判别区域,引导网络学习更关键可区分部位的特征,同时用克罗内克积模块获取位置关系信息,对小样本细粒度图像分类任务是有效的。可视化结果从侧面也说明了在细粒度图像上分类效果不佳的主要原因是因为样本外观相对固定,提取的特征可区分性不大造成的,因此,证明了增强对关键可辨性区域特征的提取对该任务的必要性。
4. 结束语
本文面向小样本细粒度图像分类任务,提出了一种多尺度知识引导局部增强的方法,该网络融合多个尺度的特征图提取更丰富的样本信息解决样本单一的问题,引入知识引导模块通过捕获支持和查询样本之间的语义相关性,以及增强支持样本表示的判别区域,允许网络更加关注相关的辨别性区域和采用克罗内克积模块来捕获比较样本之间的空间位置关系。大量的实验表明,所提出的方法在小样本细粒度基准数据集上比传统的基于度量学习的方法有更大的提升。未来的工作将致力于通过去除更多的背景噪声,结合全局与局部特征信息捕获对象间更细微的差异来提升小样本细粒度图像分类方法的性能。
-
表 1 数据集信息表
Table 1 Datasets information
数据集名称 类别
总数训练集
类别数验证集
类别数测试集
类别数MiniImageNet 100 64 16 20 CUB_200_2011 200 130 20 50 Stanford Cars 196 130 17 49 Stanford Dogs 120 70 20 30 表 2 MiniImageNet数据集分类结果
Table 2 Classification results of MiniImageNet dataset
% 方法 MiniImageNet 1-shot 5-shot MatchNet[11] 43.56±0.84 55.31±0.73 ProtoNet[12] 49.42±0.78 68.20±0.66 RelationNet[13] 50.44±0.82 65.32±0.70 GNN[39] 50.33±0.36 66.41±0.63 DN4[18] 51.24±0.74 71.02±0.64 MSDN[40] 52.59±0.81 68.51±0.69 RPMN[41] 53.35±0.78 69.35±0.59 RCN[42] 53.47±0.84 71.63±0.70 MsKPRN[20] 56.07±0.84 71.56±0.66 MKGRE(本文) 57.78±0.94 72.08±0.63 表 3 细粒度图像数据集分类结果
Table 3 Classification results of fine-grained image datasets
% 方法 CUB_200_2011 Stanford Cars Stanford Dogs 1-shot 5-shot 1-shot 5-shot 1-shot 5-shot MatchNets[11] 45.30±1.03 59.50±1.01 34.80±0.99 44.70±1.03 35.80±0.99 47.50±1.08 ProtoNets[12] 37.36±1.00 45.28±1.03 40.90±1.01 52.93±1.03 37.80±0.99 48.19±1.03 RelationNets[13] 53.11±1.01 67.45±0.79 47.67±0.47 60.59±0.40 43.33±0.42 55.23±0.41 GNN[39] 51.83±0.98 63.69±0.94 55.85±0.97 71.25±0.89 46.98±0.98 62.27±0.95 DN4[18] 53.15±0.84 81.90±0.60 61.51±0.44 89.60±0.44 45.73±0.73 66.33±0.66 LRPABN[25] 63.63±0.77 76.06±0.58 60.28±0.76 73.29±0.58 45.72±0.75 60.94±0.76 RCN[42] 66.48±0.88 82.04±0.58 — — 54.29±0.96 72.65±0.66 MattML[33] 66.29±0.56 80.34±0.30 66.11±0.54 82.80±0.28 54.84±0.53 71.34±0.38 MsKPRN[20] 69.49±0.95 82.94±0.65 76.64±0.84 89.88±0.46 57.05±0.91 75.85±0.68 MKGRE(本文) 71.72±0.90 83.91±0.58 78.51±0.84 90.00±0.45 58.63±0.98 75.53±0.66 表 4 消融实验结果
Table 4 Ablation results
% 尺度大小 CUB_200_2011 84×84 64×64 48×48 5-way 1-shot 5-way 5-shot √ 71.38±0.92 83.13±0.62 √ √ 71.72±0.90 83.91±0.58 √ √ √ 71.00±0.97 82.90±0.63 表 5 模块消融实验结果
Table 5 Experimental results of module ablation
% 模块 骨干网络 准确率 RN Conv-64F 53.11±1.01 RN+KGM Conv-64F 68.03±0.01 RN+KPM Conv-64F 69.48±0.95 RN+KGM+KPM Conv-64F 71.72±0.90 -
[1] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770−778. [2] 葛轶洲, 刘恒, 王言, 等. 小样本困境下的深度学习图像识别综述[J]. 软件学报, 2022, 33(1): 193−210. GE Yizhou, LIU Heng, WANG Yan, et al. Survey on deep learning image recognition in dilemma of small samples[J]. Journal of software, 2022, 33(1): 193−210. [3] WEN Qi, LI Shuang, HAN Bingfeng, et al. ZiGAN: fine-grained Chinese calligraphy font generation via a few-shot style transfer approach[C]//Proceedings of the 29th ACM International Conference on Multimedia. Virtual Event: ACM, 2021: 621−629. [4] ZHANG Bo, CHEN Tao, WANG Bin, et al. Joint distribution alignment via adversarial learning for domain adaptive object detection[J]. IEEE transactions on multimedia, 2022, 24: 4102−4112. doi: 10.1109/TMM.2021.3114550 [5] 杨祺, 孙俊. 融合多粒度特征的细粒度图像分类网络[J]. 小型微型计算机系统, 2023, 44(4): 818−824. YANG Qi, SUN Jun. Multi-granularity feature fusion network for fine-grained visual classification[J]. Journal of Chinese computer systems, 2023, 44(4): 818−824. [6] HE Ju, CHEN Jieneng, LIU Shuai, et al. TransFG: a transformer architecture for fine-grained recognition[C]//Proceedings of the AAAI conference on artificial intelligence. Vancouver: AAAI, 2022: 852−860. [7] 许可凡. 基于注意力机制的细粒度图像分类技术的研究与应用[D]. 北京: 北京邮电大学, 2023. XU Kefan. Research and application of fine-grained image classification technology based on attention mechanism[D]. Beijing: Beijing University of Posts and Telecommunications, 2023. [8] 苗培昊. 基于度量学习的小样本细粒度图像识别研究[D]. 徐州: 中国矿业大学, 2022. MIAO Peihao. Research on small sample fine-grained image recognition based on metric learning[D]. Xuzhou: China University of Mining and Technology, 2022. [9] 周凯锐, 刘鑫, 景丽萍, 等. 概念驱动的小样本判别特征学习方法[J]. 智能系统学报, 2023, 18(1): 162−172. doi: 10.11992/tis.202203061 ZHOU Kairui, LIU Xin, JING Liping, et al. Concept-driven discriminative feature learning for few-shot learning[J]. CAAI transactions on intelligent systems, 2023, 18(1): 162−172. doi: 10.11992/tis.202203061 [10] YANG Shuo, LIU Lu, XU Min. Free lunch for few-shot learning: distribution calibration[EB/OL]. (2021−01−16)[2023−09−01]. https://arxiv.org/abs/2101.06395. [11] VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching networks for one shot learning[J]. Advances in neural information processing systems, 2016: 3637−3645. [12] SNELL J, SWERSKY K, ZEMEL R. Prototypical networks for few-shot learning[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: ACM. 2017: 4080−4090. [13] SUNG F, YANG Yongxin, ZHANG Li, et al. Learning to compare: relation network for few-shot learning[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 1199−1208. [14] LEE S, MOON W, HEO J P. Task discrepancy maximization for fine-grained few-shot classification[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 5321−5330. [15] HARIHARAN B, GIRSHICK R. Low-shot visual recognition by shrinking and hallucinating features[C]//2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 3037−3046. [16] KOCH G, ZEMEL R, SALAKHUTDINOV R. Siamese neural networks for one-shot image recognition[C]//Proceedings of the 32 nd International Conference on Machine Learning-Volume 37. Lille: JMLR, 2015: 1−8. [17] HOU Ruibing, CHANG Hong, MA Bingpeng, et al. Cross attention network for few-shot classification[EB/OL]. (2019−10−17)[2023−09−01]. https://arxiv.org/abs/1910.07677. [18] LI Wenbin, WANG Lei, XU Jinglin, et al. Revisiting local descriptor based image-to-class measure for few-shot learning[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 7253−7260. [19] WU Ziyang, LI Yuwei, GUO Lihua, et al. PARN: position-aware relation networks for few-shot learning[C]//2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 6658−6666. [20] ABDELAZIZ M, ZHANG Zuping. Multi-scale kronecker-product relation networks for few-shot learning[J]. Multimedia tools and applications, 2022, 81(5): 6703−6722. doi: 10.1007/s11042-021-11735-w [21] XIE Lingxi, TIAN Qi, HONG Richang, et al. Hierarchical part matching for fine-grained visual categorization[C]//2013 IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 1641−1648. [22] ZHANG Ning, DONAHUE J, GIRSHICK R, et al. Part-based R-CNNs for fine-grained category detection[C]//European Conference on Computer Vision. Cham: Springer, 2014: 834−849. [23] ZHANG Yu, WEI Xiushen, WU Jianxin, et al. Weakly supervised fine-grained categorization with part-based image representation[J]. IEEE transactions on image processing, 2016, 25(4): 1713−1725. doi: 10.1109/TIP.2016.2531289 [24] SONG Kaitao, WEI Xiushen, SHU Xiangbo, et al. Bi-modal progressive mask attention for fine-grained recognition[J]. IEEE transactions on image processing, 2020, 29: 7006−7018. doi: 10.1109/TIP.2020.2996736 [25] TANG Hao, YUAN Chengcheng, LI Zechao, et al. Learning attention-guided pyramidal features for few-shot fine-grained recognition[J]. Pattern recognition, 2022, 130: 108792. doi: 10.1016/j.patcog.2022.108792 [26] WU Jijie, CHANG Dongliang, SAIN A, et al. Bi-directional feature reconstruction network for fine-grained few-shot image classification[C]//Proceedings of the AAAI conference on artificial intelligence. Washington: AAAI, 2023: 2821−2829. [27] WEI Xiushen, WANG Peng, LIU Lingqiao, et al. Piecewise classifier mappings: learning fine-grained learners for novel categories with few examples[J]. IEEE transactions on image processing, 2019, 28(12): 6116−6125. doi: 10.1109/TIP.2019.2924811 [28] RUAN Xiaoqian, LIN Guosheng, LONG Cheng, et al. Few-shot fine-grained classification with Spatial Attentive Comparison[J]. Knowledge-based systems, 2021, 218: 106840. doi: 10.1016/j.knosys.2021.106840 [29] XU Shulin, ZHANG Faen, WEI Xiushen, et al. Dual attention networks for few-shot fine-grained recognition[J]. Proceedings of the AAAI conference on artificial intelligence, 2022, 36(3): 2911−2919. doi: 10.1609/aaai.v36i3.20196 [30] MUNJAL B, FLABOREA A, AMIN S, et al. Query-guided networks for few-shot fine-grained classification and person search[J]. Pattern recognition, 2023, 133: 109049. doi: 10.1016/j.patcog.2022.109049 [31] 解耀华, 章为川, 任劼, 等. 基于自适应特征融合的小样本细粒度图像分类[J]. 计算机工程与应用, 2023, 59(3): 184−192. doi: 10.3778/j.issn.1002-8331.2204-0201 XIE Yaohua, ZHANG Weichuan, REN Jie, et al. Adaptive feature fusion embedding network for few shot fine-grained image classification[J]. Computer engineering and applications, 2023, 59(3): 184−192. doi: 10.3778/j.issn.1002-8331.2204-0201 [32] HUANG Huaxi, ZHANG Junjie, ZHANG Jian, et al. Low-rank pairwise alignment bilinear network for few-shot fine-grained image classification[J]. IEEE transactions on multimedia, 2020, 23: 1666−1680. [33] ZHU Yaohui, LIU Chenlong, JIANG Shuqiang. Multi-attention meta learning for few-shot fine-grained image recognition[C]//Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. Yokohama: ACM, 2020: 1090−1096. [34] SHEN Yantao, XIAO Tong, LI Hongsheng, et al. End-to-end deep kronecker-product matching for person re-identification[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 6886−6895. [35] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278−2324. doi: 10.1109/5.726791 [36] WAH C, BRANSON S, WELINDER P, et al. The Caltech-UCSD birds-200-2011 dataset[R]. California: California Institute of Technology, 2011. [37] KRAUSE J, STARK M, JIA Deng, et al. 3D object representations for fine-grained categorization[C]//2013 IEEE International Conference on Computer Vision Workshops. Sydney: IEEE, 2013: 554−561. [38] DENG Jia, DONG Wei, SOCHER R, et al. ImageNet: a large-scale hierarchical image database[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009: 248−255. [39] GARCIA V, BRUNA J. Few-shot learning with graph neural networks[EB/OL]. (2017−11−10)[2023−09−01]. https://arxiv.org/abs/1711.04043. [40] WANG Xiaoru, MA Bing, YU Zhihong, et al. Multi-scale decision network with feature fusion and weighting for few-shot learning[J]. IEEE access, 2020, 8: 92172−92181. [41] XUE Zhiyu, XIE Zhenshan, XING Zheng, et al. Relative position and map networks in few-shot learning for image classification[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Seattle: IEEE, 2020: 4032−4036. [42] XUE Z, DUAN Lixin, LI Wen, et al. Region comparison network for interpretable few-shot image classification[EB/OL]. (2020−09−08)[2023−09−01]. https://arxiv.org/abs/2009.03558.









 下载:
下载: