Numerical reasoning method for graph neural networks and numerically induced regularization
-
摘要: 数值推理是机器阅读理解的一项关键能力,而数值推理任务中的数据类型多样,数值之间潜在的运算关系对数值推理任务有着更高的要求。为了进一步提升数值推理能力,一方面继承图神经网络方法并探索新的图结构,采用异构图神经网络结构进行数值推理,另一方面在预训练语言模型中引入数值诱导正则化方法,增强模型的数值理解能力。在DROP数据集上实验的结果表明,2种方法得到76.5%的精准匹配率,与基线模型对比以及对方法的消融实验表明,上述2种方法能够提升机器的数值推理能力。Abstract: Numerical reasoning is a crucial capability in machine reading comprehension. However, the varying data types in this task introduce complexity. As a result, the identification of potential numerical arithmetic relationships has high requirements in this task. Two approaches are considered to improve numerical reasoning ability. First, the graph neural network method is incorporated to explore a heterogeneous graph-based neural network structure designed for numerical reasoning. Second, numerical-induced regularization is introduced into the pre-trained language model to enhance its numerical comprehension ability. Experimental results on the DROP dataset indicate that the two methods obtain an exact match rate of 76.5%. Furthermore, the comparison with the baseline model and the ablation experiments of the methods show that the two methods mentioned above can enhance the numerical reasoning ability of the machine.
-
随着自然语言处理的发展,机器阅读理解已经突破了人类水平,更复杂的推理机器阅读理解任务也随之出现,比如数值推理机器阅读理解[1]。该任务是考察模型是否能够理解自然语言和数值的关系,根据与问题相关的信息进行数值运算,最后得到给定问题的答案。该任务不仅涵盖一般机器阅读理解需要解决的问题,而且需要模型对数学语言具有较强的敏感性,还需要掌握基础的数值运算能力。此任务在现实世界中同样有各种不同的应用场景,所以对数值推理阅读理解探索与突破有助于将自然语言处理扩展到众多数学领域,促进教育、金融、统计等行业的发展。在大数据时代下,人类需要从蕴含数字的庞大文本中得到想要的信息是极为困难的,这里机器阅读理解可以辅助人类去理解庞大的文档,人类只需要去询问想要知道的问题即可。
目前数值推理任务的研究方法主要有3种,第1种是基于语义解析的方法,比如神经符号阅读器(neural symbolic reader, NeRd)[2] 是一个由阅读器和程序设计器组成的生成模型,操作驱动离散推理架构(operation-pivoted discrete reasoning framework, OPERA)[3]模型将推理步骤总结为一组操作。它们都是将自然语言映射成逻辑形式,然后执行得出答案,所以在可解释性上有优势,但受到轻微的干扰就会导致错误,模型构建也较为复杂。
第2种是基于预训练阶段的神经网络的端到端方法,自动生成数据的BERT(automatic data generation BERT, GenBERT)[4]、基于数值语境的BERT(numerical-contextual BERT, NC-BERT)[5]、基于结构化查询语言的程序执行器(program executors of structured query language, POET-SQL)[6]等模型使用的是该方法,通过大量数值数据对语言模型进行数值方面的预训练从而得到具有数值理解能力的语言模型,其缺点是过度依赖预训练语料集和下游任务的契合度。
第3种是基于微调阶段的神经网络的端到端方法。多类型-多跨度网络(multi-type multi-span network, MTMSN)[7]、数值感知图神经网络(numerically-aware graph neural network, NumNet)[8] 、基于问题的有向图注意力网络(question directed graph attention network, QDGAT)[9]等模型使用此方法,该方法使用没有数值理解能力的语言模型得到词嵌入,然后通过具体的方法对数据集进行微调训练,得到拥有数值推理能力的模型。该方法容易达到较好的效果,但可解释性较差,方法选择也是难点之一。
该任务中推理的复杂性,数值运算的多样性,导致任务在推理上还不够完善,本文将使用异构图神经网络[10]对推理过程进行加强,图结构对数值有着天然的敏感性,便于将数值理解能力注入模型中,此外通过数值类型构建的异构图能够增强模型的数值推理能力。又因为该任务的主流模型都是采用没有推理能力的语言模型进行微调,直接运用这类没有推理能力的语言模型会影响模型的整体性能,为了能让模型在微调前就有一定的数值理解能力,同时在微调后又能获得数值推理能力,本文构建了基于图结构与数值诱导正则化的数值推理模型(numerical reasoning model base on graph structure and numerical induced egularization, G-NIR)。该模型首先采用数值诱导正则化将数值理解能力注入预训练语言模型中,其次使用异构图神经网络进行数值推理工作,最后根据图推理结果进行预测从而得出答案。
本文的主要贡献包括3个方面:
1) 本文主要设计了一个基于图神经网络和数值诱导正则化的神经网络,首先使用命名实体识别对数值类型进行判别,再通过该类型构建基于数值推理的异构图神经网络,调整图神经网络参数以提升其性能;
2) 本文通过语言模型增加新的损失函数,利用数值诱导正则化提升预训练语言模型的数值理解能力;
3) 通过在公开的数值推理数据集DROP上进行验证,证明本文设计的模型具有很好的性能,能够取得最佳的效果。
1. 相关工作
数值推理任务是机器阅读理解任务中的特殊任务,它需要模型根据给定的文章,找到与问题关键字相关的数值,通过推理的方式得出正确的答案。
1.1 数值推理
自数值推理任务出现,研究者们先是使用传统神经网络模型,如使用单词表示的全局向量(global vectors for word representation, GloVe)词嵌入方法的数值感知问答网络(numerically-aware question answer network, NAQANet)[11]和在GloVe基础上加入启发式运算的NumNet[8],但效果不佳。预训练语言模型逐渐应用在自然语言处理的各类任务上,同样也促进着数值推理任务的研究,极大地提升了模型在数值推理任务中的效果。即便如此,仅使用预训练语言模型一方面远不足以解决数值推理问题,另一方面难以应对多种答案类型的判断,本文通过筛选出数值符号并得到其含义,再利用其构建图结构,进而通过图神经网络进行数值推理工作。
1.2 预训练语言模型
数值推理也属于自然语言处理任务,任务中涵盖大量自然语言,所以一方面可以直接通过预训练好的语言模型得到任务的上下文表示,另一方面也可以根据不同任务的数据生成相应的语料进行预训练,得到更适合某一任务的语言模型。2018年,基于变换器的双向编码器(bidirectional encoder representation from transformers, BERT)[12]的提出,让自然语言处理上升到了一个新的高度。2019年,Liu等[13]在BERT基础上进行改进并提出了稳健优化的 BERT 预训练方法 (robustly optimized BERT pretraining approach, RoBERTa),让其与下游任务更加匹配。RoBERTa采用动态掩码,可以在有效的语料集上发挥更大的作用。RoBERTa采用了更大的批量大小,能够找到更准确的梯度下降方向,提高预训练语言模型的语言理解能力。RoBERTa因良好的性能被广泛应用,本文所使用的预训练语言模型即RoBERTa。
1.3 图神经网络
在本任务中,图神经网络主要用在推理模块。图结构与数学语言同属于一种严谨的体系,两者相似且契合,所以在数学符号推理或逻辑符号推理等问题上有着得天独厚的优势。
早在2008年,图神经网络概念就由Scarselli等[14]提出。图卷积神经网络[15-16]将图结构的信息处理方式融入到卷积神经网络之中,但因为该网络使用全样本数据,导致其收敛过慢,难以扩展成大规模网络。Hamilton等[17]提出了图采样聚合方法(graph sample and aggregate, GraphSAGE),该方法利用节点的信息和边信息,从节点的局部邻居采样并聚合邻居节点和该节点的边信息,获取到节点新的的图词嵌入。另外,该方法对于节点分类和链接预测问题也有很不错的表现。Velickovic等[18]提出了图注意力网络,该网络使用注意力掩码层解决了图卷积网络模型的部分问题,使得该网络更适用于解决归纳学习问题和转导学习问题。2020年,Hu等[19]提出了异构图神经网络,该方法利用异构图的多关系网络来构建包含大量信息的图,通过对各关系进行消息传递和消息聚合来参数化权重矩阵。2022年,谢小杰等[20]提出的图卷积异质网络有效对节点分类,降低网络结构的复杂度,提高训练速度。同年任嘉睿等[21]提出元图卷积异质网络嵌入学习算法,该算法降低图嵌入维数,减少训练计算的时间的同时也拥有更好的性能。
2. 基于异构图的数值推理方法
为了解决机器对数值理解能力不足的问题,本文设计了G-NIR模型。这一小节将介绍基于异构图的数值推理机器阅读理解方法。G-NIR模型结构如图1所示,模型主要由3部分组成,第1是特征提取模块,第2是异构图神经网络模块,第3是答案预测模块。
2.1 特征提取模块
模型的输入是由Q与P 2部分组成,因为本文使用的预训练语言模型为RoBERTa,所以先利用RoBERTa提供的分词方法对Q和P进行数据分词,Q与P的语义表示向量为Q'和P'。则有公式Q', P' = RoBERTa(Q, P)[7]。实验得到预训练语言模型输出的语义表示向量中的数字,随后对RoBERTa的分词形式进行数据预处理。
异构图神经网络模块需要通过数值类型来构建异构图,因此在数据预处理过程中,需要提前对数据集中的数字作命名实体识别,得到数值类型以便后续图的构建。命名实体识别工具使用的是斯坦福大学提供的共同核心自然语言处理 (common core natural language processing, CoreNLP)[22],获得数值类型有多种方案,方案1是单纯地将数词后一位单词的类型作为该数值的类型;方案2是考虑到数词后可能跟随无效类型的单词,所以判断数词后几位单词,将最接近数词的有效类型作为该数值的类型;方案3是规定数值类型为一个集合,其包括数字、百分数、日期等类型,首先给数词赋初始值为数字类型,然后根据前后单词判断该数词是否为其他类型,如果是则修改数值类型。在实验过程中发现,方案1得到的数值类型过于单一,导致数值类型的可用性差;而方案2所获取的数值类型并不会提升模型的性能,原因可能是英语语言的灵活性,语言构成复杂,通过复杂且硬性的规则获取的数值类型相对杂乱,并不能很好地反映该数词;最终实验选用方案3获得数值类型。得到数值类型后,将数值类型处理后与数据预处理结果封装在一起,随后将封装的数据作为预训练语言模型的输入,得到每个序列的语义表示向量。
使用带有数值类型的语义表示向量构建异构图神经网络,在图神经网络模块,数值的语义表示向量根据数值大小和数值类型的不同进行变化,模型通过训练最终获得新的数值语义表示向量,然后修正原有语义表示向量。最后将修正后的语义表示向量作为答案预测模块的输入,通过该模块,模型将输出最终的答案。
2.2 异构图神经网络模块
异构图模块主要解决模型缺乏数值推理能力的问题。具体来说,该模块将文章和问题中的数值以及数值之间的关系构建一个有向图,通过构建的图结构进行推理。它的输入是数据预处理时得到的数值类型等索引信息以及预训练语言模型输出的语义表示向量,输出则是修正后的数值语义表示向量。异构图是以数字的语义表示向量为节点,以任意两节点的映射关系为边来构建。本文使用3种不同的映射关系来连接2个节点,其一是数值类型映射关系,它将相同数值类型的节点连接,辅助模型找到相同数值类型进行计算,提升模型的性能。其二和其三是大小映射关系,通过这2种关系,将数值理解能力注入模型中。由于数值推理需要对数值的大小有一定的敏感度,所以本文的异构图使用对应上述3种映射关系的3条有向边来加强图推理工作,第1条边的特征是数字节点的数值类型,从任意一条数字节点出发,与该节点拥有相同数值类型的节点建立一条类型边。第2条边的特征是数字节点的大于关系,从一条数字节点出发,与任意一个数值小于该节点的边建立一条大于边。第3条边的特征是数字节点的小于关系,从一条数字节点出发,与任意一个数值大于该节点的边建立一条小于边。
接下来将用DROP数据集中的1个例子来说明图的构建,例子如表1所示。
表 1 数值推理数据集DROP的例子Table 1 Examples of numerical reasoning datasets DROP文章 问题 答案 1942年发行的第1期包括1、5、10和50分以及1、5和10比索的面值。1944年推出了100比索纸币,不久后因通货膨胀又推出了500比索纸币。1945年,日本发行了1 000比索纸币。 问题1:1942年有多少种不同面额的分? 4 问题2:在第1次发行1、5、10和50分硬币几年后,日本人发行了1 000比索纸币? 3 问题3:最大的比索是在1944年还是1945年印制的? 1945 问题4:1942年最大的分面值是多少? 50 表1是数据集中一篇文章及其4个问答对,表中问题1是计数问题,答案“4”通过对“1、5、10、50”计数得到。问题2是年份的加减问题,答案3是通过计算“1945-1942”得到。问题3不仅是比较问题,问题中还隐含着最值问题,模型需要找到“1944年”和“1945年”对应的比索纸币“500”、“1 000”,通过对比大小得知答案是纸币面额更大的“1945”。问题4是最值问题,答案“50”是从“1、5、10、50”中选择最大的值得到。
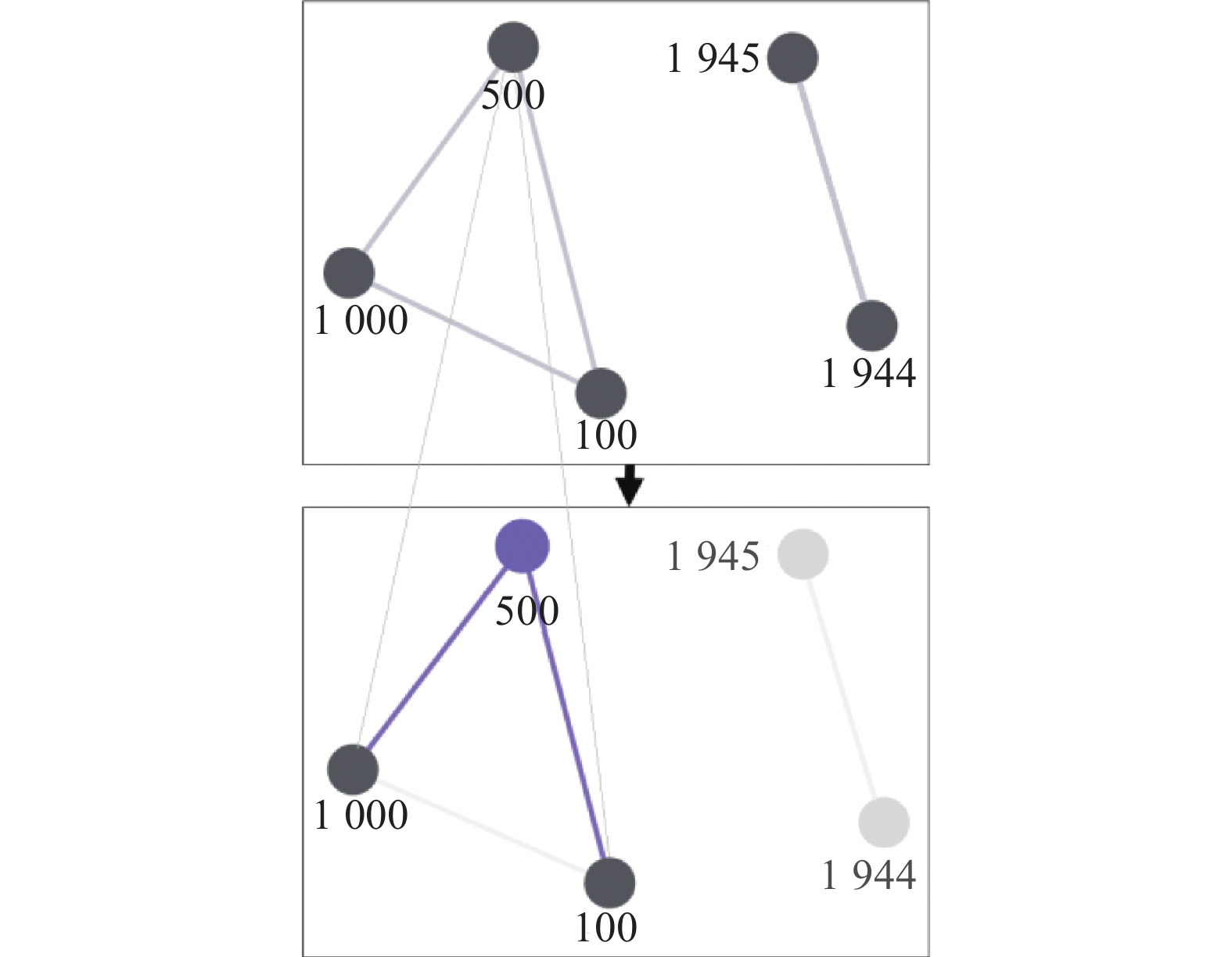
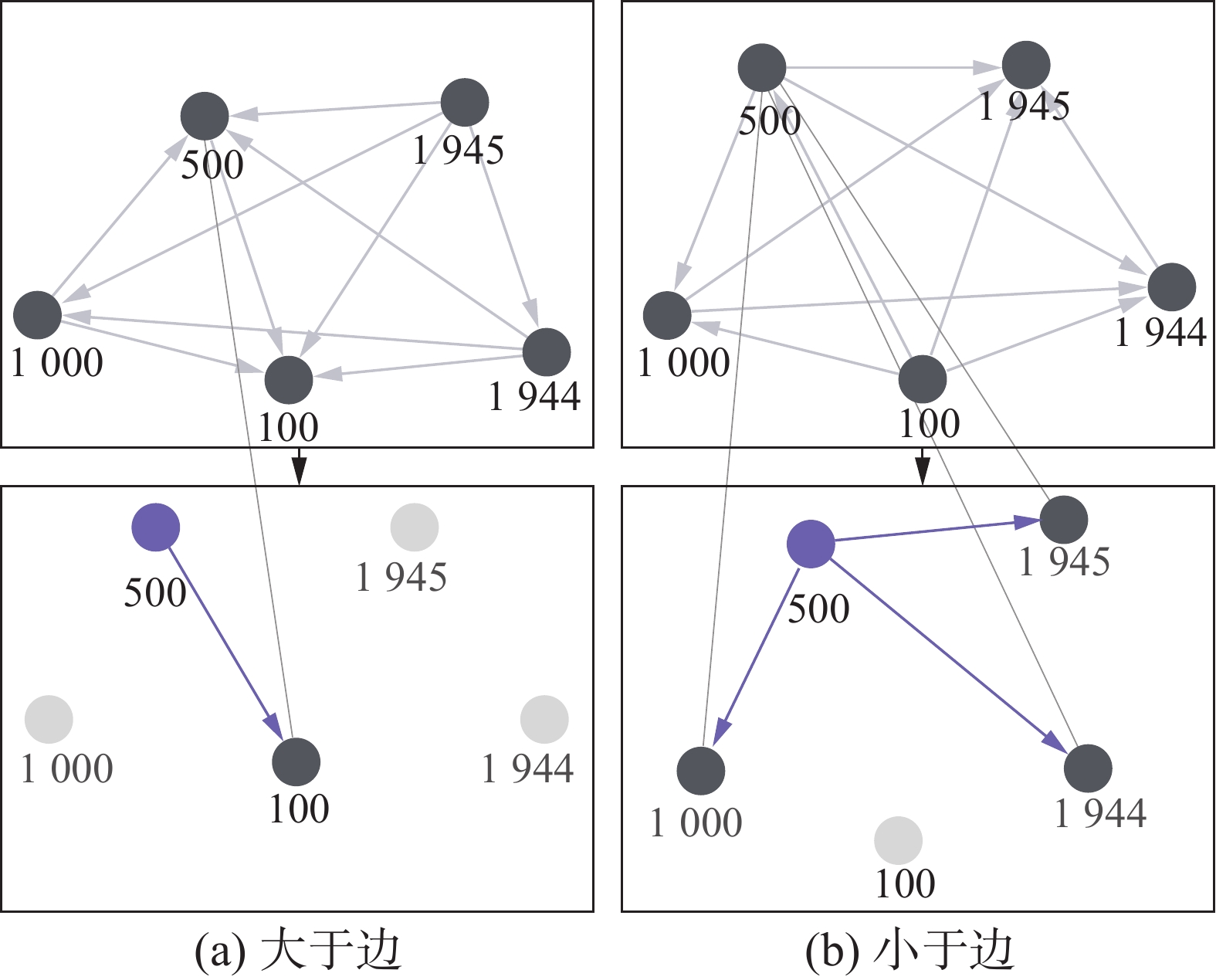
图2和图3使用表1例子中的5个数字来构建3种边,数字分别是纸币面额“100”、“500”、“1 000”和年份“1944”、“1945”。图2上半部分中“100”、“500”和“1 000”是相同类型的数字节点,它们两两相连,“1944”和“1945”同理。下半部分中是“500”数字节点的消息传递过程,过程中该数字节点将会与其所有相同类型的数字节点进行消息传递。图3中,左边两图给出了图神经网络中的大于边,右边两图给出了小于边。图中消息传递则都以数值为“500”的节点为例。从图中可以看到,任意一个节点都有一条大于边和小于边与其他节点关联,在消息传递过程中,2条边相辅相成,完成1个节点的全部联系。
针对上述不同的3种边,本文设计了2种图神经网络结构进行处理。类型边使用GraphSAGE,大于边和小于边使用图卷积神经网络。之所以设计大于边和小于边2种网络结构,是因为以下几点:首先,无论构建大于边还是构建小于边,边所提供的信息是不完全的[23],所以需要用2种边来给图提供完全的信息。其次,无向边并不能区别两节点数值大小关系,然而构建图卷积神经网络的目的是让模型学习数值的大小关系,所以使用有向边作为图结构的大于边和小于边同样也是必要的。因此,通过异构图卷积(heterogeneous graph convolution, HeteroGraphConv)将上述3种边作为子模块进行更新,并将特征写入节点,通过求均值的方法将相同节点的信息进行聚合。
本文使用图卷积神经网络对大于边和小于边进行处理,将数字的大小关系注入模型中。图卷积神经网络首先遍历所有数值节点,分别对当前节点的大于边和小于边的邻居节点进行消息传递与消息聚合。为了增强聚合效果,本文采用“两两握手”原则,任意2个节点都建立1条大于边和1条小于边,让聚合效果最大化。
图卷积神经网络消息传递和聚合的具体公式为
$$ {\boldsymbol{h}}_i^{(l + 1)} = \sigma \left({{\boldsymbol{b}}^{(l)}} + \sum\limits_{j \in \mathcal{N}(i)} {\frac{1}{{{c_{ji}}}}} {\boldsymbol{h}}_j^{(l)}{{\boldsymbol{W}}^{(l)}}\right) $$ 式中:σ(·)表示激活函数,集合
$\mathcal{N}(i) $ 表示i节点的所有邻居,cji表示j节点与其所有邻居的度数、i节点与其所有邻居的度数两者的平方根之积,公式表示为$$ {c_{ji}} = \sqrt {|\mathcal{N}(j)|} \sqrt {|\mathcal{N}(i)|} $$ 本文使用GraphSAGE对类型边进行处理,目的是让模型更好地理解各数字在上下文中的意义。通过聚合相同类型数值节点的特征,然后更新同类型节点,使模型能够辨别各数字在上下文中的含义,根据问题所述可以快速找到对应的数值进行计算。
GraphSAGE的构造公式为
$$ {\boldsymbol{h}}_{\mathcal{N}(i)}^{(l + 1)} = {{\mathrm{aggregate}}} (\{ {{\boldsymbol{e}}_{ji}}{\boldsymbol{h}}_j^l,\forall j \in \mathcal{N}(i)\} ) $$ (1) $$ {\boldsymbol{h}}_i^{(l + 1)} = \sigma \left( {{\boldsymbol{W}} \cdot {\text{concat}}({\boldsymbol{h}}_i^l,{\boldsymbol{h}}_{\mathcal{N}(i)}^{l + 1})} \right) $$ (2) $$ {\boldsymbol{h}}_i^{(l + 1)} = {{\mathrm{norm}}} ({\boldsymbol{h}}_i^{(l + 1)}) $$ (3) 式中eji是j指向i的边,并且保证eji与hlj满足矩阵的广播机制。式(1)表示对目标节点i的邻居进行随机采样,用激活函数对采样后的节点进行处理,然后统一放入集合
$\mathcal{N}(i) $ 中,$\mathcal{N}(i) $ 表示目标节点i的采样邻居节点。式(2)通过聚合函数集合式(1)获得的采样邻居节点的信息,得到目标节点i的预测值。通过式(3)进行正则化处理,得到图神经网络输出的节点向量。最后该模块的输出是更新后的所有节点向量。2.3 答案预测模块
由于该任务的数据集拥有多种答案类型(比如数值、日期、文章片段),根据DROP数据集建议的方法以及NumNet模型[8],本文采用4种答案类型的方法。
模块首先用异构图神经网络模型输出的向量更新预训练语言模型的后4层的数值向量,然后将更新后的这4层权重矩阵命名为M0、M1、M2、M3。这4种答案类型分别为文章片段(passage span)、问题片段(question span)、计数(count)和数值表达式(arithmetic expression)。
2.3.1 文章片段
答案在文章中的开始索引和结束索引的概率公式表示分别为
$$ {p^{{\text{p\_start}}}} = {\text{softmax}}({\text{FFN}}([{{\boldsymbol{M}}_0};{{\boldsymbol{M}}_1}]) $$ $$ {p^{{\text{p\_end}}}} = {\text{softmax}}({\text{FFN}}([{{\boldsymbol{M}}_0};{{\boldsymbol{M}}_2}]) $$ 式中FFN表示2层激活函数为ReLU的前馈网络。模型根据公式中不同层的权重矩阵进行训练,M0表示最后1层矩阵,M1和M2分别表示倒数第2层和倒数第3层矩阵。
2.3.2 问题片段
由于存在答案出现在问题中,而不是出现在文章中的情况,因此有了该答案类型,问题开始索引和结束索引的概率计算公式为
$$ {p^{{\text{q\_start}}}} = {\text{softmax}}({\text{FFN}}([{\boldsymbol{Q}};\exp |{\boldsymbol{Q}}| \otimes {\boldsymbol{h}}]) $$ $$ {p^{{\text{q\_end}}}} = {\text{softmax}}({\text{FFN}}([{\boldsymbol{Q}};\exp |{\boldsymbol{Q}}| \otimes {\boldsymbol{h}}]) $$ 因为即便答案只出现在问题中,也要理解文章的含义,所以需要对文章的语义表示h进行处理。带有标识的外积符号(
$ \exp |{\boldsymbol{Q}}| \otimes $ )表示对h每个单词都进行计算。2.3.3 计数
对文章中多次出现的实体进行计数,计数的范围是0~9。因为计数是简单的任务,所以公式表达也很简单:
$$ {p^{{\text{count}}}} = {\text{softmax}}({\text{FFN}}({\boldsymbol{h}})) $$ 2.3.4 数值表达式
数值表达式的计算公式为
$$ p_i^{{\text{sign}}} = {\text{softmax}}({\text{FFN}}({\boldsymbol{h}}_i^N)) $$ 式中:
$ {\boldsymbol{h}}_i^N $ 表示第i个数值的语义表示向量,而$ p_i^{{\text{sign}}} $ 表示第i个数值的算术表达式符号的概率。符号有3种:正、负和零,答案需要将标记为正的数字相加,再减去标记为负的数字,标记为零表示该数字与答案无关。上述公式中的FFN是结构相同参数独立的前馈网络。本文通过最大化所有正确可能的边际概率来训练模型,其损失函数为
$$ {L_{{\text{ans}}}} = - \log \sum\limits_t {P({\boldsymbol{t}})P({\boldsymbol{r}}|{\boldsymbol{t}})} $$ 式中t和r分别表示答案类型和模型输出的结果。
3. 损失函数
语言模型未在数值方面专门作预训练,会导致模型缺乏数值计算的能力,造成其在图神经网络中进行推理训练时对数值不敏感,使数值推理注入效果不佳。为了让预训练语言模型输出的语义表示向量在推理训练前就具备理解数字的能力,本文通过调整预训练语言模型的输出,使模型输出更能体现数值的向量,进而增加模型对于数字的理解能力,本文采用了数值诱导正则化损失(deterministic independentof-corpus embeddings loss, DICE-loss)[24-25]进行训练。
DICE-loss通常被使用在医学图像任务中,旨在应对语义分割中正负样本强烈不平衡的场景,DICE-loss是一个区域性相关的损失值,一个像素与其邻近的像素相关,故使用该损失值可减少正负样本不平衡的情况。而将DICE-loss引入到数值理解中是由于数值之间的大小关系与图像中相邻的像素类似,都存在某种相关性。任意2个数字的语义向量的关系和其数值的关系存在不平衡问题,所以利用与图像同样的原理减少语义向量和数值间不平衡的情况。数值诱导正则化的具体做法是,先从文章中随机选取2个数字a和b,再从预训练语言模型中获得数字的隐层输出向量va和vb。然后计算数字a与数字b的标量距离,以及va和vb向量的余弦距离,得到它们最终的差值,公式为
$$ {L}_{\text{num}}=\left\| 2\frac{|a-b|}{\left|a\right|+\left|b\right|}-{d}_{\text{cos}}({{\boldsymbol{v}}}_{a},{{\boldsymbol{v}}}_{b})\right\|_{2} $$ 上述公式作为一种有效的正则化器,可以约束数字之间的相对大小关系,从而调整模型输出,训练出更具数学理解能力的模型。所以最终损失函数为
$$ L = L_{\text{ans}} + L_{\text{num}} $$ 4. 实验结果与分析
本小节主要从数据集、评估标准、实验设置、实验结果和消融实验5个方面来介绍实验过程。
4.1 数据集
实验使用的数据集是DROP[11],它是由AI2实验室发布的机器阅读理解数据集,主要考察模型对数值运算的处理能力,如今在数值推理任务中被广泛使用。该数据集共有6 735篇文章和96 567个问答对,训练集、验证集和测试集按8∶1∶1的比例划分,其中需要进行数值推理的问题占60%以上。如表1所示,每篇文章对应若干个问答对,文章平均长度200词,问题平均长度11词,答案由多种类型组成,包括数值类型、日期类型、单跨度答案、多跨度答案,其中数值类型答案最多,占比61.94%。
4.2 评估标准
实验的评价指标采用机器阅读理解通用的标准进行评价,分别为精确匹配(exact match, EM)指标以及F1值。EM表示模型的精确度,需要模型预测的答案与真实答案完全一致。F1值表示预测答案与真实答案重叠度,即便预测的答案与真实答案不一致,但可能也有所相关,该评判标准相比EM条件有所放宽。它是精确率与召回率的调和平均值。
4.3 实验设置
本实验使用的基准为NumNet+,实验中的图神经网络推理步数为3。优化器使用Adam优化器,以参数β1=0.8,β2=0.999,ε=10−7来最小化目标函数。学习率设置为5×10−4,L2权重衰退λ设置为10−7,梯度裁剪的最大值为5。模型训练使用的batch size为16,epoch设置为5。
实验使用的Python版本为3.8,PyTorch版本为1.12.0,CUDA版本为11.3,GPU使用的是内存为24 GB的NVIDIA GeForce GTX 3090。
4.4 实验结果
表2给出了本文模型和其他方法在DROP数据集的实验结果,NumNet+和G-NIR是本文主要对比的2个模型。
NAQANet是DROP数据集原文提出的模型,作为该数据集的基础模型。NumNet模型在原有模型的基础上增加了图神经网络进行推理,性能上有一定的提升。NumNet+模型则是在NumNet上使用预训练语言模型进行词嵌入,可以看到在使用了预训练语言模型后性能又有所提升。GenBERT模型利用生成数据对语言模型进行预训练,从而使模型拥有数值理解能力,性能在NumNet之上。MTMSN模型在使用预训练语言模型的基础上,又对算术表达式作了重新排序,让模型能够更准确地找到需要计算的数值,从而提升其准确率。
从表中可以明显地看到,G-NIR在一定程度上优于上述方法,在测试集上取得了EM指标76.5%和F1值80.36%的结果,这证明本文的方法是可行有效的。
同时,在相同实验参数设置中,NumNet+每个批次耗费时间5 h,收敛较慢。G-NIR每个批次运行时间为4 h,能更快地收敛,可以节省20%的时间。根据代码可知NumNet+模型在图神经网络更新中遍历了全部节点,而本文在实验中使用的GraphSAGE图神经网络不作全节点更新,只更新批次用到的邻居节点,其大大降低算法的时间复杂度,有效节省训练时间。但由于本文使用的异构图需要用到包括数值及其数值类型在内的大量信息,空间复杂度要比NumNet+模型高。
总的来说,G-NIR在实验性能上比基线模型较好,且有着更短的训练时间。
4.5 消融实验
表3给出了消融实验结果,其中w/o DICE-loss是使用异构图神经网络进行推理而去掉数值诱导正则化方法的模型,w/o heterogeneous graphs是使用数值诱导正则化但没有使用异构图方法的模型。
表 3 消融实验Table 3 Ablation experiment% Model EM F1值 G-NIR_5 74.18 78.27 w/o DICE-loss 73.33 77.27 w/o heterogeneous graphs 73.09 76.87 NumNet+_5 72.36 76.10 如表3所示,首先本文移除数值诱导正则化的损失项DICE-loss,可以看到实验结果性能有明显下降,说明该损失项是有助于模型提升对数值的理解能力的。一方面可以看出移除该损失项的性能优于NumNet+_5,另一方面也说明了异构图在模块中的有效性。其次实验针对G-NIR_5移除掉异构图神经网络,将其换回NumNet+_5模型的图神经网络,得到的结果要弱于G-NIR_5,说明异构图对于该任务是有效的,并且对比NumNet+_5的结果可以看出,去掉异构图但是保留DICE-loss损失项对于原模型来说也是有提升的。
5. 案例分析
本节给出了2个例子来分析模型的数值推理结果,如表4所示。表4通过2个例子比较了NumNet+和G-NIR 2个模型的不同预测结果。第1个例子询问“韩国移民男性比妇女儿童多多少?”,NumNet+模型的结果是通过总人数减去妇女儿童的人数得到的,实际上就是男性移民的人数,与问题不符。而G-NIR模型明确地知道需要使用男性移民数量减去妇女儿童移民的数量,最终得到了正确的结果。第2个例子是关于年份的计算,NumNet+模型使用了错误的年份作减法导致答案错误,而G-NIR通过在图神经网络中引入数值类型,能够比较精准地找到相应的年份作计算。通过表中的2个例子G-NIR得出正确答案而NumNet+得出错误答案,验证了G-NIR模型的有效性。
表 4 NumNet+和G-NIR模型在DROP上的预测Table 4 The predictions from the NumNet+ and G-NIR are illustrated问题和答案 文章 NumNet+ G-NIR 问题:韩国移民中男性比女性儿童多多少?
答案:5711905年,1 003名韩国移民,包括802名男子和231名妇女儿童,乘坐伊尔福德号船从仁川切姆浦港出发,前往墨西哥瓦哈卡州的萨利纳克鲁兹。 1 003−231=802 802−231=571 × √ × √ √ √ 问题:从阿方索六世的基督教军队夺回瓜达拉哈拉到拉斯纳瓦斯德托洛萨战役已经过去了多少年?
答案:127从1085年基督教军队夺回瓜达拉哈拉到1212年的拉斯纳瓦斯德托洛萨战役爆发,这座城市持续遭受战火的蹂躏。好在1133年,城市居民从阿方索七世那里获得了燃料。 1 133−1 085=48 1 212−1 085=127 × √ × √ √ √ 6. 结束语
对于数值推理型的机器阅读理解任务,本文采用2种方法进行改进以提升其性能。第1种是应用异构图神经网络,利用数值的类型对数值进行分门别类的处理,使改进后的模型相比原有模型有了更好的数值理解能力。第2种是引入了数值诱导正则化,它利用数值之间的特性,可以对没有数值理解能力的预训练语言模型进行数值理解能力提升。当前预训练语言模型多为通用型,相对地就没有数值理解能力。所以本文引用数值诱导正则化到预训练语言模型里,显性地增加其数值理解能力,然后再进行针对DROP数据集的微调,实验结果证明,本文提出的模型相比之前从零开始训练数值理解能力来说,能让模型更快更好地学习到数值理解能力。
未来需要做的工作有2点:
1) 探索其他更适合本任务的图神经网络,并选择合适的消息传递方式以应对该任务,以提升图神经网络对模型数值推理的效果。
2) 将本文的方法扩展到其他数值推理数据集上,进一步提高模型的泛化能力。
-
表 1 数值推理数据集DROP的例子
Table 1 Examples of numerical reasoning datasets DROP
文章 问题 答案 1942年发行的第1期包括1、5、10和50分以及1、5和10比索的面值。1944年推出了100比索纸币,不久后因通货膨胀又推出了500比索纸币。1945年,日本发行了1 000比索纸币。 问题1:1942年有多少种不同面额的分? 4 问题2:在第1次发行1、5、10和50分硬币几年后,日本人发行了1 000比索纸币? 3 问题3:最大的比索是在1944年还是1945年印制的? 1945 问题4:1942年最大的分面值是多少? 50 表 2 在DROP数据集的实验结果
Table 2 Experimental results on DROP dataset
% 表 3 消融实验
Table 3 Ablation experiment
% Model EM F1值 G-NIR_5 74.18 78.27 w/o DICE-loss 73.33 77.27 w/o heterogeneous graphs 73.09 76.87 NumNet+_5 72.36 76.10 表 4 NumNet+和G-NIR模型在DROP上的预测
Table 4 The predictions from the NumNet+ and G-NIR are illustrated
问题和答案 文章 NumNet+ G-NIR 问题:韩国移民中男性比女性儿童多多少?
答案:5711905年,1 003名韩国移民,包括802名男子和231名妇女儿童,乘坐伊尔福德号船从仁川切姆浦港出发,前往墨西哥瓦哈卡州的萨利纳克鲁兹。 1 003−231=802 802−231=571 × √ × √ √ √ 问题:从阿方索六世的基督教军队夺回瓜达拉哈拉到拉斯纳瓦斯德托洛萨战役已经过去了多少年?
答案:127从1085年基督教军队夺回瓜达拉哈拉到1212年的拉斯纳瓦斯德托洛萨战役爆发,这座城市持续遭受战火的蹂躏。好在1133年,城市居民从阿方索七世那里获得了燃料。 1 133−1 085=48 1 212−1 085=127 × √ × √ √ √ -
[1] 杜永萍, 赵以梁, 阎婧雅, 等. 基于深度学习的机器阅读理解研究综述[J]. 智能系统学报, 2022, 17(6): 1074−1083. doi: 10.11992/tis.202107024 DU Yongping, ZHAO Yiliang, YAN Jingya, et al. Survey of machine reading comprehension based on deep learning[J]. CAAI transactions on intelligent systems, 2022, 17(6): 1074−1083. doi: 10.11992/tis.202107024 [2] CHEN Xinyun, LIANG Chen, YU Wei Adams, et al. Neural symbolic reader: scalable integration of distributed and symbolic representations for reading comprehen-sion[C]//2020 International Conference on Learning Representations. Addis Ababa: ICLR, 2020: 1–16. [3] ZHOU Yongwei, BAO Junwei, DUAN Chaoqun, et al. OPERA: operation-pivoted discrete reasoning over text[C]//Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. Seattle: ACL, 2022: 1655–1666. [4] GEVA M, GUPTA A, BERANT J. Injecting numerical reasoning skills into language models[C]//Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. Online: ACL, 2020: 946–958. [5] KIM J, KANG Junmo, KIM K M, et al. Exploiting numerical-contextual knowledge to improve numerical reasoning in question answering[C]//Findings of the Association for Computational Linguistics. Seattle: ACL, 2022: 1811–1821. [6] PI Xinyu, LIU Qian, CHEN Bei, et al. Reasoning like program executors[C]//Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing. Abu Dhabi: ACL, 2022: 761–779. [7] HU Minghao, PENG Yuxing, HUANG Zhen, et al. A multi-type multi-span network for reading comprehension that requires discrete reasoning[C]//Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing. Hong Kong: ACL, 2019: 1596–1606. [8] RAN Qiu, LIN Yankai, LI Peng, et al. NumNet: machine reading comprehension with numerical reasoning[C]//Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing. Hong Kong: ACL, 2019: 2474–2484. [9] CHEN Kunlong, XU Weidi, CHENG Xingyi, et al. Question directed graph attention network for numerical reasoning over text[C]//Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing. Online: ACL, 2020: 6759–6768. [10] 孟祥福, 温晶, 李子函, 等. 多重注意力指导下的异构图嵌入方法[J]. 智能系统学报, 2023, 18(4): 688−698. MENG Xiangfu, WEN Jing, LI Zihan, et al. Heterogeneous graph embedding method guided by the multi-attention mechanism[J]. CAAI transactions on intelligent systems, 2023, 18(4): 688−698. [11] DUA D, WANG Yizhong, DASIGI P, et al. DROP: a reading comprehension benchmark requiring discrete reasoning over paragraphs[C]//Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics. Minneapolis: NAACL, 2019: 2368–2378. [12] DEVLIN J, CHANG Mingwei, LEE K, et al. BERT: pre-training of deep bidirectional transformers for language understanding[C]//Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics. Minneapolis: NAACL, 2019: 4171–4186. [13] LIU Zhuang, LIN Wayne, SHI Ya, et al. A robustly optimized bert pre-training approach with post-training [C]//Proceedings of the 20th Chinese National Conference on Computational Linguistics. Huhhot: CCL, 2021: 1218–1227. [14] SCARSELLI F, GORI M, TSOI A C, et al. The graph neural network model[J]. IEEE transactions on neural networks, 2009, 20(1): 61−80. doi: 10.1109/TNN.2008.2005605 [15] KIPF T, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. (2016−09−09)[2023−08−31]. https://arxiv.org/abs/1609.02907. [16] 吴国栋, 查志康, 涂立静, 等. 图神经网络推荐研究进展[J]. 智能系统学报, 2020, 15(1): 14−24. doi: 10.11992/tis.201908034 WU Guodong, ZHA Zhikang, TU Lijing, et al. Research advances in graph neural network recommendation[J]. CAAI transactions on intelligent systems, 2020, 15(1): 14−24. doi: 10.11992/tis.201908034 [17] HAMILTON W, YING R, LESKOVEC L. Inductive representation learning on large graphs[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: NIPS, 2017: 1025–1035. [18] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[EB/OL]. (2017−10−30)[2023−08−31]. https://arxiv.org/abs/1710.10903. [19] HU Ziniu, DONG Yuxiao, WANG Kuansan, et al. Heterogeneous graph transformer[C]//Proceedings of The Web Conference 2020. Taipei: ACM, 2020: 2704–2710. [20] 谢小杰, 梁英, 王梓森, 等. 基于图卷积的异质网络节点分类方法[J]. 计算机研究与发展, 2022, 59(7): 1470−1485. doi: 10.7544/issn1000-1239.20210124 XIE Xiaojie, LIANG Ying, WANG Zisen, et al. Heterogeneous network node classification method based on graph convolution[J]. Journal of computer research and development, 2022, 59(7): 1470−1485. doi: 10.7544/issn1000-1239.20210124 [21] 任嘉睿, 张海燕, 朱梦涵, 等. 基于元图卷积的异质网络嵌入学习算法[J]. 计算机研究与发展, 2022, 59(8): 1683−1693. doi: 10.7544/issn1000-1239.20220063 REN Jiarui, ZHANG Haiyan, ZHU Menghan, et al. Embedding learning algorithm for heterogeneous network based on meta-graph convolution[J]. Journal of computer research and development, 2022, 59(8): 1683−1693. doi: 10.7544/issn1000-1239.20220063 [22] MANNING C, SURDEANU M, BAUER J, et al. The stanford CoreNLP natural language processing toolkit[C]//Proceedings of 52nd Annual Meeting of the Association for Computational Linguistics: System Demonstrations. Baltimore: ACL, 2014: 55–60. [23] XU Runxin, LIU Tianyu, LI Lei et al. Document-level event extraction via heterogeneous graph-based interac- tion model with a tracker[C]//Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing. Online: ACL, 2021: 3533−3546. [24] THAWANI A, RUJARA J, LLIEVSKI F, et al. Representing numbers in NLP: a survey and a vision[C]//Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. Online: ACL, 2021: 644−656. [25] SUNDARARAMAN D, SI Shijing, SUBRAMANIAN V, et al. Methods for numeracy-preserving word embeddings[C]//Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing. Online: ACL, 2020: 4742–4753.


 下载:
下载: