随着中国资本市场的发展，股票投资逐渐进入大众视野。股票投资的相关研究对于个人和投资机构而言，可以通过预测分析协助投资者作出更加理性的决策，获得可观的投资回报；对于国家和社会而言，可以通过探寻证券市场风险波动的内在机理，为政府监管部门的政策制定提供智能决策辅助，防患化解重大金融风险。因此，对股票市场进行预测分析具有重要的现实意义。

早期的股票预测方法主要基于历史股价序列，通过传统统计学方法构建自回归模型。然而，这类方法对于高度非线性、非平稳的金融数据等拟合能力较差，比如常见的差分整合自回归移动平均(auto-regressive integrated moving average, ARIMA) 模型在小规模的可平稳化处理的时间序列预测任务中表现优异，但是模型超参数的确定需要人工参与，并且得出的预测结果往往滞后于实际的价格变动，大大限制了模型在实际场景中的应用^[1]。随着大数据，人工智能等技术的不断发展，基于机器学习的预测方法受到了广泛的研究和关注^[2-3]。

近年来，随着计算机算力的进一步提升以及可用于训练学习的数据爆发式增长，深度学习技术可以利用多层人工神经网络实现任意非线性函数的逼近，其在图像处理、语音识别、自然语言处理等领域的性能逐渐超越了传统的机器学习方法。例如Hoseinzade等^[4]提出了一种基于卷积神经网络的模型，提取信号不同尺度上的抽象特征，丰富了信号的特征表示，实验结果表明，深度学习方法优于浅层方法。Zhang等^[5]提出了基于状态频率内存(state frequency memory, SFM)的方法，将长短期记忆网络(long short-term memory, LSTM)存储单元的隐藏状态分解为多个频率分量，以发现多频交易模式。Ding等^[6]提出的融合多尺度高斯先验的Transformer^[7]模型在股票趋势预测中取得了显著的结果。

但是上述股票预测方法仅考虑单一的股票时间序列，忽视了股票之间复杂的关系。研究表明，金融市场时间序列概念背后的空间维度，即股票间关系信息，在很大程度上会影响模型预测的准确性^[8]。鉴于金融市场数据信息的非欧几里得特性，研究人员引入了图神经网络方法来学习实体间的分布表示。图神经网络 (graph neural network, GNN) ^[9-10]是建模实体间关系最常见模型之一，它采用邻接矩阵来表示实体之间成对相关性，并用于分析未来趋势。在股票预测建模中，图中的顶点和边分别表示股票及其关系，通过顶点表示学习来捕获每对股票之间的关系。例如，Chen等^[11]根据市场投资事件构建了公司实体关系图，并通过图卷积神经网络整合公司股票间关系信息，获得了更准确的预测结果。Feng等^[12]收集行业关系元数据和公司股权信息构建静态关系图，并通过LSTM来学习序列特征，然后将学习到的序列特征输入到图卷积注意力网络对股票进行排名预测，提高了模型预测效果。

然而，在真实市场中，股票之间的关系往往比成对关系更复杂，而普通图结构只能描述两点之间的关系，无法对高阶关系进行建模。例如“行业内联动”现象：同一行业内的相关个股受到同一外部事件冲击时，股价变化具有同一的趋势^[13]。“行业间联动”现象：在供应链中，上游公司的经营调整会对相关下游公司造成影响，在股价上也会表现出对应的变化趋势。这些协同关系自然地将股票作为集体联系在一起，而不是成对关系。GNN不足以对股票之间的这种协同关系进行建模。作为图的扩展，超图具有比图更强的关系建模能力^[14]。超图引入关联矩阵来表示这种协同关系，顶点和超边分别是关联矩阵的行索引和列索引。在超图中，超边可以连接属于同一组内的多支股票，表明它们具有共同的内在属性。同时，一支股票可以连接到多个超边，这意味着它具有多个特征。超图模型已经在许多领域取得了进展，包括物体识别^[15]、交通预测^[16]和推荐系统^[17]等。在股票预测方面，Sawhney等^[18]使用超图学习来捕获股票间的复杂关系。Cui等^[19]提出了超图注意力网络用于股票趋势预测。Li等^[20]提出了一种基于超图的股票投资组合强化学习方法，通过嵌入超图注意力模块来显式建模股票之间的高阶关系从而优化投资选择。

目前基于图或超图神经网络模型的股票预测方法已经取得了不错的效果，但是仍存在2个待解决的问题：1) 现有图方法仅对股票进行成对关系的建模，忽略了股票间的高阶协同关系。2) 现有图或超图的方法仅通过预定义信息给出了股票之间的静态关系，而未对股票随时间变化的动态关系进行建模。为了解决上述问题，本文提出了一种基于动态超图卷积神经网络的股票趋势预测框架。在该框架中，首先基于改进的Transformer模型编码股票时序信息，增强模型对股票的短期趋势感知能力。然后，通过构建静态超图和动态超图将股票间协同关系信息引入到时序建模中。最后，预测层融合静态超图和动态超图的信息进行趋势预测。

1.   相关理论

1.1   超图建模

在使用超图$ \mathcal{G} = ({\boldsymbol{V}},{\boldsymbol{E}},{\boldsymbol{W}}) $建模时，单支股票由超图中的顶点$ v $表示，且$ v \in {\boldsymbol{V}} $，股票间的多元关系由超边$e$表示。超边集中的每条超边$e \in {\boldsymbol{E}}$都被赋予一个正的权重${{\boldsymbol{W}}_{ee}}$，初始时权重都为1，表示每条超边权重相同，$ {\boldsymbol{W}} = {\boldsymbol{I}} \in {{\bf{R}}^{\left| {\boldsymbol{V}} \right| \times \left| {\boldsymbol{E}} \right|}} $。文献[21]已经证明，当且仅当每条超边连接2个顶点时，超图退化为普通图。

1.2   超图关联矩阵

超图中的关联矩阵揭示了顶点和超边之间的关系，对于一个没有孤立点的无向超图的关联矩阵$ {\boldsymbol{H}} \in {{\bf{R}}^{\left| {\boldsymbol{V}} \right| \times \left| {\boldsymbol{E}} \right|}} $，其定义为

对于超图中一个顶点，其度被定义为与该顶点相关联的所有超边权重之和：

超边的度被定义为

式中$ {\boldsymbol{D}} \in {{\bf{R}}^{\left| {\boldsymbol{V}} \right| \times \left| {\boldsymbol{V}} \right|}} $和$ {\boldsymbol{B}} \in {{\bf{R}}^{\left| {\boldsymbol{E}} \right| \times \left| {\boldsymbol{E}} \right|}} $都是对角矩阵。

2.   模型框架

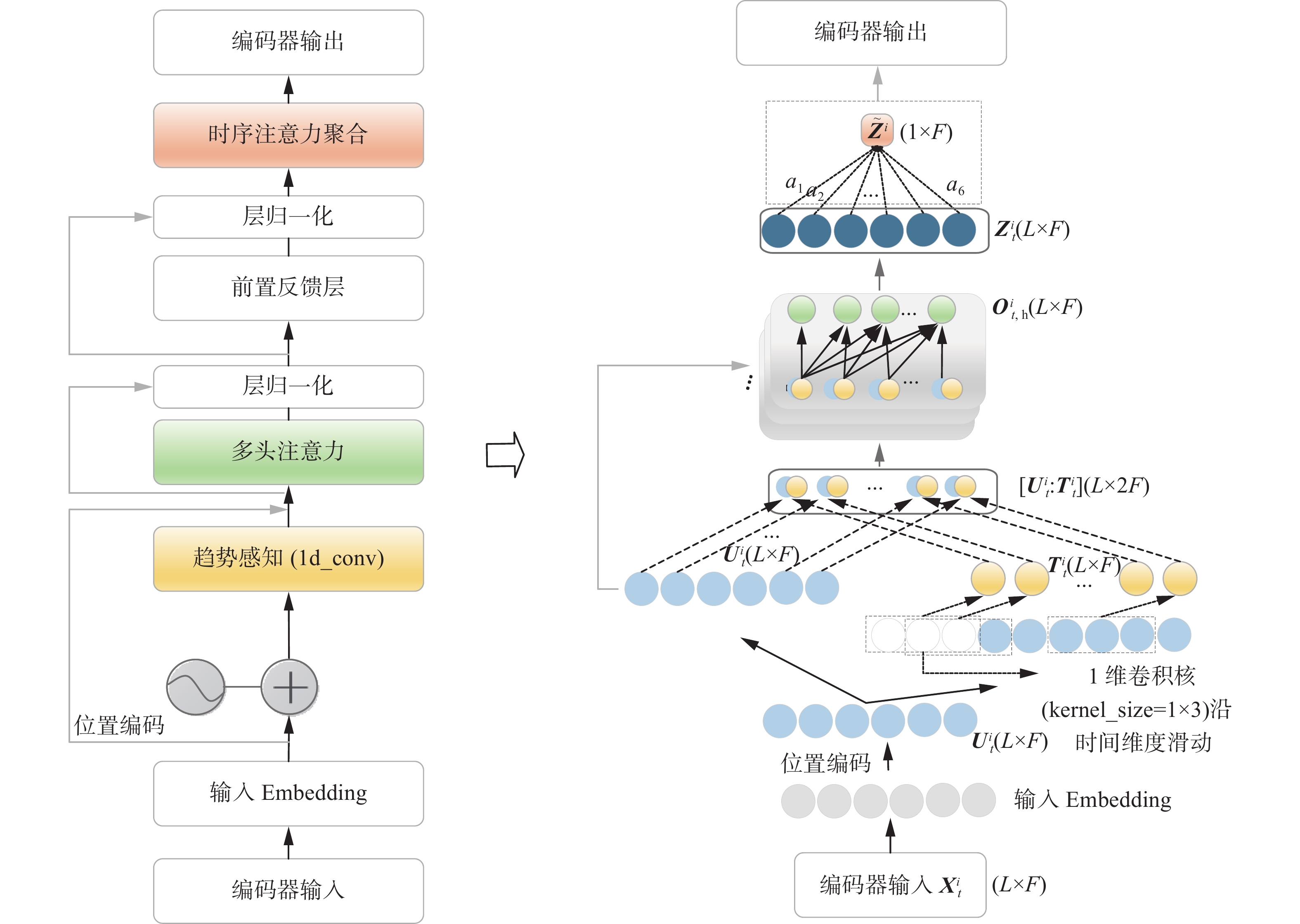
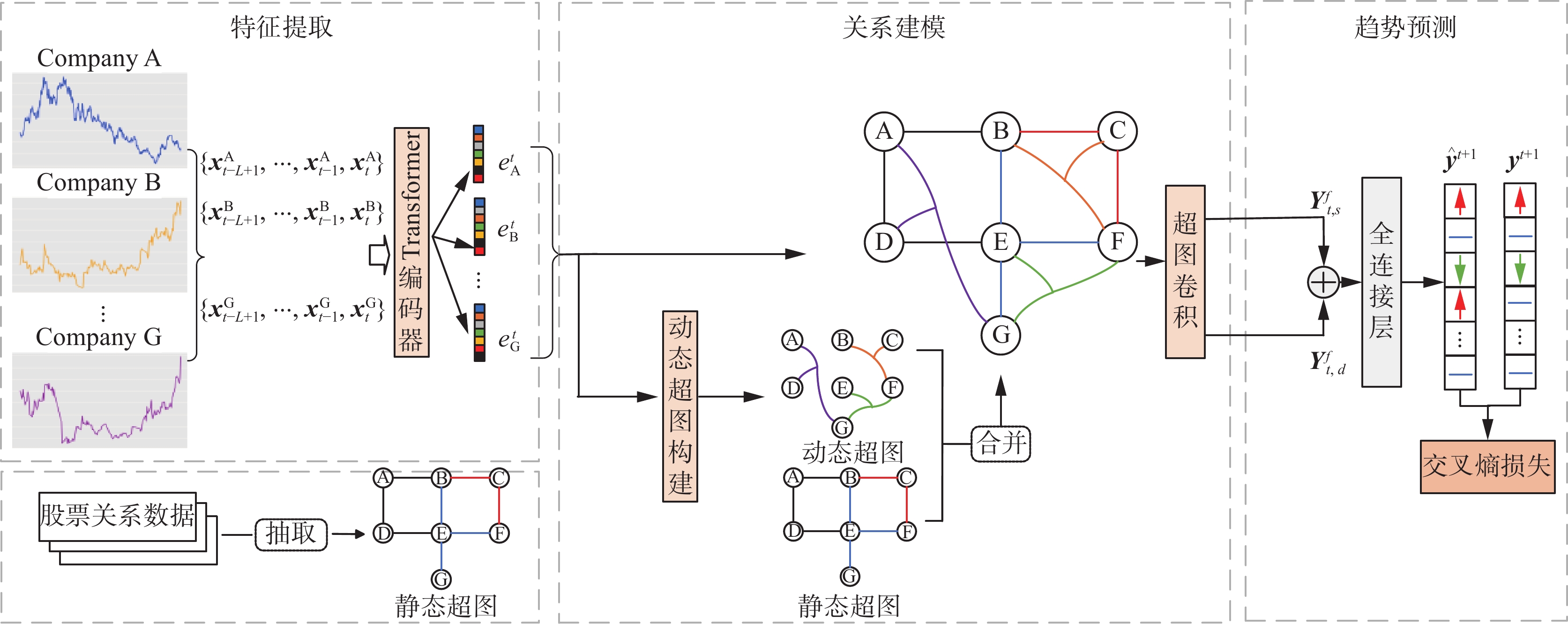
本文提出了一种改进Transformer和动态超图卷积神经网络的框架，用于端到端的股票趋势预测。该框架包括时序特征提取、关系建模和趋势预测3个部分，如图1所示。

图  1  基于改进Transformer和动态超图卷积神经网络的整体框架

Fig.  1  Overall framework based on improved Transformer and dynamic hypergraph convolutional neural network

下载: 全尺寸图片

2.1   问题描述

给定含有N支股票的股票集$ {\boldsymbol{S}} = \{ {s_1},{s_2}, \cdots ,{s_N}\} $，在t时收集每支股票过去L天交易记录$ {{\boldsymbol X}_t} \in {{\bf{R}}^{N \times L \times F}} $。对于$ {\boldsymbol X}_t^{{s_i}} = \{ [{\boldsymbol{x}}_{t - L + 1}^{{s_i}}, \cdots ,{\boldsymbol{x}}_{t - 1}^{{s_i}},{\boldsymbol{x}}_t^{{s_i}}],{s_i} \in {\boldsymbol{S}}\} \in {{\bf{R}}^{L \times F}} $，其中$ {\boldsymbol{x}}_t^{{s_i}} \in {{\bf{R}}^F} $是股票$ {s_i} $在第t个交易日时的价格属性集合，例如开盘价、收盘价等，F是原始特征的数量。

股票趋势预测是一个典型的分类预测任务，给定历史交易记录$ {\boldsymbol X} \in {{\bf{R}}^{N \times L \times F}} $和由行业关系构造的静态超图$ {\mathcal{G}_{ s}} $，模型旨在学习一个函数$f({\boldsymbol{X}},{\mathcal{G}_{ s}},{\boldsymbol{\varTheta}} )$，${\boldsymbol{\varTheta}} $是模型参数，函数$f( \cdot )$将$ {\boldsymbol X} $映射为第 t+1个交易日的涨跌预测概率分布。

2.2   时序特征提取

股票的历史价格记录在预测其未来趋势方面起着关键作用^[22]。本文设计了一种只有编码器结构的Transformer变体从每支股票的时间序列价格数据中捕获其时间动态特征。

Transformer编码器通过多头自注意力机制对序列的长期依赖关系进行建模取得较好效果，但由于标准的自注意力机制的计算过程是基于点对点进行查询(query)−键(key)匹配，这可能存在2个问题：1)标准的自注意力计算可能受局部噪声点影响，导致学习到的特征嵌入掺杂了噪声点的信息。2)股票时间序列往往存在周期性趋势，而点对点的计算无法感知短期的周期性趋势。如图2所示，实线框标注出宁德时代(300750.SZ，简称CATL)公司股票在一段时间内出现相似的波动，这对于未来的股票趋势预测具有重要的意义。

图  2  宁德时代股票价格周期性波动规律示例

Fig.  2  Example description of the periodic fluctuation pattern of CATL’s stock price

下载: 全尺寸图片

为解决上述问题，本文通过设计趋势感知模块来增强Transformer模型对于短期趋势的感知能力。具体来说，在日期t时N支股票过去L天的历史交易记录$ {{\boldsymbol X}_t} \in {{\bf{R}}^{N \times L \times F}} $经过位置编码后得到$ {{\boldsymbol{U}}_t} \in {{\bf{R}}^{N \times L \times {F_{\mathrm{P}}}}} $，将其作为多头注意力模块的输入。为便于说明，以多头注意力处理某支股票i为例，股票i经位置编码后的输入特征为$ {\boldsymbol{U}}_t^i \in {{\bf{R}}^{L \times {F_{\mathrm{P}}}}} $，首先将$ {\boldsymbol{U}}_t^i $变换成R个不同的值(value)矩阵$ {\boldsymbol{V}}_{t,r}^i = U_t^iW_r^v $，其中$ {\boldsymbol{W}}_r^v \in {{\bf{R}}^{{F_{\mathrm{P}}} \times {F_{\mathrm{P}}}}} $表示可学习的参数矩阵，$r \in \{ 1,2, \cdots ,R\} $表示多头注意力中的头索引。为了使输出的短期趋势特征和状态特征$ {\boldsymbol{U}}_t^i $窗口长度对齐，如图3所示，在卷积操作之前进行填充操作，然后使用大小为1×c一维卷积核沿时序维度提取短期趋势特征，得到短期趋势特征$ {{\boldsymbol{T}}_t} \in {{\bf{R}}^{L \times {F_{\mathrm{P}}}}} $，公式表示为

图  3  改进的Transformer编码器整体结构

Fig.  3  Overall structure of improved Transformer encoder

下载: 全尺寸图片

式中：短期趋势特征$ {\boldsymbol{T}}_t^i $表示当前股票价格特征$ {\boldsymbol{U}}_t^i $的前c日股价趋势，将二者拼接起来$ [{\boldsymbol{U}}_t^i:{\boldsymbol{T}}_t^i] $，经过线性变化$ {\boldsymbol{W}}_r^q $和$ {\boldsymbol{W}}_r^k $得到R个不同的Query矩阵和Key矩阵，公式表示为

式中$ {\boldsymbol{W}}_r^q $和$ {\boldsymbol{W}}_r^k \in {{\bf{R}}^{2{F_{\mathrm{P}}} \times 2{F_{\mathrm{P}}}}} $。最后由$ {\boldsymbol{Q}}_{t,r}^i,{\boldsymbol{K}}_{t,r}^i \in {{\bf{R}}^{L \times 2{F_{\mathrm{P}}}}} $和$ {\boldsymbol{V}}_{t,r}^i \in {{\bf{R}}^{L \times {F_{\mathrm{P}}}}} $计算多头注意力得到输出$ {\boldsymbol{O}}_{t,r}^i $：

式中$ {\boldsymbol{M}} \in {{\bf{R}}^{L \times L}} $是非零元素都为1的下三角掩码矩阵。最后平均池化所有头输出得到$ {\boldsymbol{Z}}_t^i \in {{\bf{R}}^{L \times {F_{\mathrm{P}}}}} $：

同理N支股票实体最终的编码输出是$ {{\boldsymbol{Z}}_t} \in {{\bf{R}}^{N \times L \times {F_{\mathrm{P}}}}} $。

由于股票存在日历效应^[19]，即过去不同时刻的价格信息对预测股票未来趋势的重要性不同，为此把多头注意力的模块输出作为时序注意力聚合模块的输入，有选择地强调过去交易日的关键状态。具体而言，某个交易日的状态重要性是通过其与Query向量进行相似度衡量得出的，选择最近一个交易日的状态作为Query向量，则时间注意力权重$ {\alpha _t} $定义为

以股票i为例，特征为$ {{\boldsymbol{z}}^i} = {{\boldsymbol{Z}}_t}[i,:,:] $，股票i第L天状态特征为$ {\boldsymbol{z}}_L^i = {{\boldsymbol{z}}^i}[L - 1,:] $，式中${\mathrm{sim}}({\boldsymbol{z}}_t^i,{\boldsymbol{z}}_L^i)$为相关度评分函数，用于衡量在时间t状态特征$ {\boldsymbol{z}}_t^i \in {{\bf{R}}^{{F_{\mathrm{P}}}}} $与Query向量$ {\boldsymbol{z}}_L^i \in {{\bf{R}}^{{F_{\mathrm{P}}}}} $相关程度，定义为

最后，对线性变换后状态特征$ {{\boldsymbol{P}}_v}{\boldsymbol{z}}_t^i $进行加权聚合，得到新的状态特征$ {{\tilde{\boldsymbol{z}}^i}}$，表示股票i在时间窗口大小为L的全局时间动态特征：

上述${{\boldsymbol{P}}_q}$、${{\boldsymbol{P}}_k}$和${{\boldsymbol{P}}_v}$是需要学习的参数矩阵，同理可得N支股票经过时序注意力聚合模块输出$ {{\tilde{\boldsymbol{Z}}_t}} \in {{\bf{R}}^{N \times {F_{\mathrm{P}}}}}$。

2.3   超图构建

上述时序建模将不同股票视为相互独立的个体，然而，股票之间存在着密切关系，并且关系密切的股票集合更容易出现一定的波动规律。因此，本节通过构建超图来挖掘股票间成组的协同关系。

2.3.1   静态超图构建

属于同一行业的股票往往会受到相同外部事件的影响，它们的价格往往会呈现相似的趋势。使用一条超边$e \in {\boldsymbol{E}}$，连接同一个行业的所有股票，这样由不同行业构成的多条超边形成超边集，即静态超图。

2.3.2   动态超图构建

动态超图用来捕获公司间动态变化的关联关系。为便于说明定义如下符号：${\boldsymbol{p}}(e)$表示某条超边$e$所拥有的顶点组成的集合，${\boldsymbol{a}}(v)$表示顶点$v$所加入的超边组成的集合，分别表示为

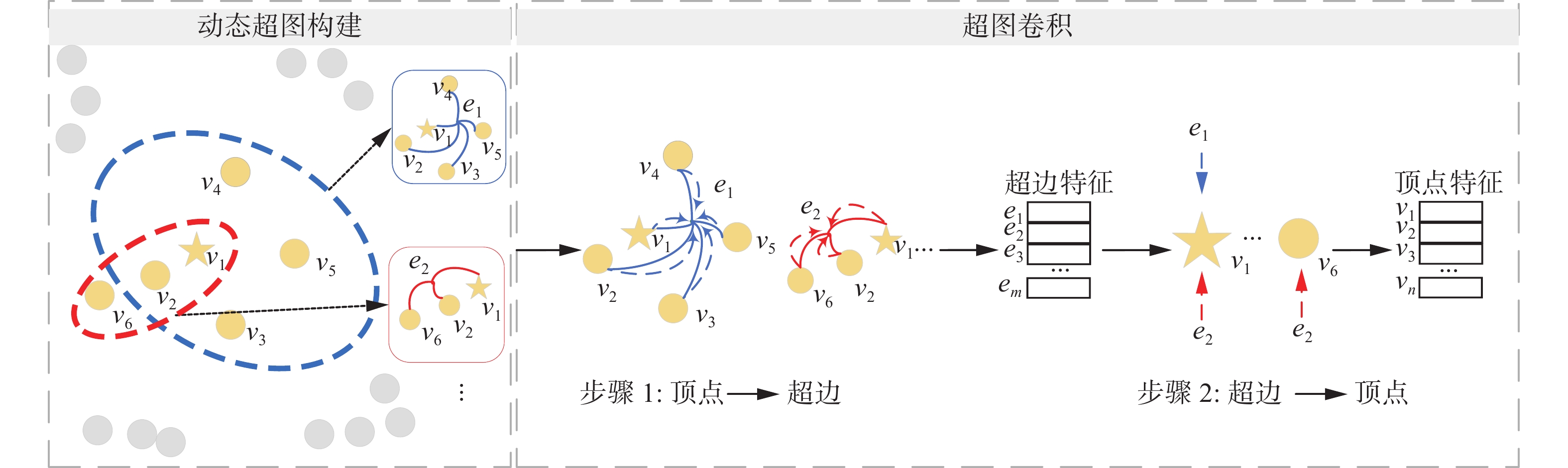
式中：${n_e}$和${m_v}$分别表示超边$e$中的顶点个数和包含顶点$v$的超边数目。

由图4可知，对于顶点${v_2}$~${v_5}$而言，它们的最近点是${v_1}$(图中的星状顶点)，这5个点构成一条超边(蓝色虚线框)。同理对于${v_6}$和${v_1}$，它们的最近点是${v_2}$，这3个点构成一条超边(红色虚线框)。

图  4  动态超图构建和超图卷积

Fig.  4  Dynamic hypergraph construction and hypergraph convolution

下载: 全尺寸图片

本文通过以下步骤创建动态超图：

1) 使用改进的Transformer编码后的时序信息$ {{\tilde{\boldsymbol{Z}}_t}} \in {{\bf{R}}^{N \times {F_{\mathrm{P}}}}}$作为动态超图构建模块的输入，对于每条超边$e$，将其特征初始化为每个顶点$v$的嵌入表示，即初始化时有N条超边；

2) 每个顶点寻找离自身最近的一条超边，排除使用自身特征初始化的超边；

3) 每个顶点加入离自己最近的那条超边，同时删除没有包含任何顶点的超边，各条超边加入其特征初始化所使用的顶点。

在每个时间步都执行上述流程，当股票特征嵌入随着网络的加深而不断演化时，超边集也在动态调整。

2.4   超图卷积

基于空间域图理论的超图卷积将超图学习视为存在相邻关系的相关顶点之间的信息交换^[21]。超图空间域卷积通过一个闭环的消息传递循环机制将时序信息$ {\boldsymbol{X}}_t^{(l)} $更新为新特征$ {\boldsymbol{X}}_t^{(l + 1)} $，超图卷积的初始输入$ {\boldsymbol{X}}_t^{(0)} = {{ \tilde{\boldsymbol{Z}}_t}} $$ \in {{\bf{R}}^{L \times {F_{\mathrm{P}}}}} $。闭环的消息传递循环机制涉及2个阶段定向的消息流传播，通过矩阵形式描述如下：

第1阶段，$ {\boldsymbol{U}}_t^{(l)} = {\boldsymbol{W}}{{\boldsymbol{B}}^{ - 1}}{{\boldsymbol{H}}^{\mathrm{T}}}{\boldsymbol{X}}_t^{(l)} $表示每个顶点特征$ {\boldsymbol{X}}_t^{(l)} \in {{\bf{R}}^{N \times {F_{\mathrm{P}}}}} $汇聚为超边特征$ {\boldsymbol{U}}_t^{(l)} \in {{\bf{R}}^{\left| {\boldsymbol{E}} \right| \times {F_{\mathrm{p}}}}} $。

第2阶段，$ {\boldsymbol{X}}_t^{(l + 1)} = \sigma ({{\boldsymbol{D}}^{ - 1}}{\boldsymbol{HU}}_t^{(l)}{\boldsymbol{\varTheta}} ) $表示每个顶点通过汇聚超边特征进行特征更新，$ \sigma ( \cdot ) $表示激活函数。

超图卷积的完整更新规则为

式中：$ {\boldsymbol{\varTheta}} $是一个可学习的参数矩阵，LeakyReLU是修正线性单元激活函数，D、B、H和W已在上文第1节相关理论中定义。

2.5   融合注意力机制的超图卷积

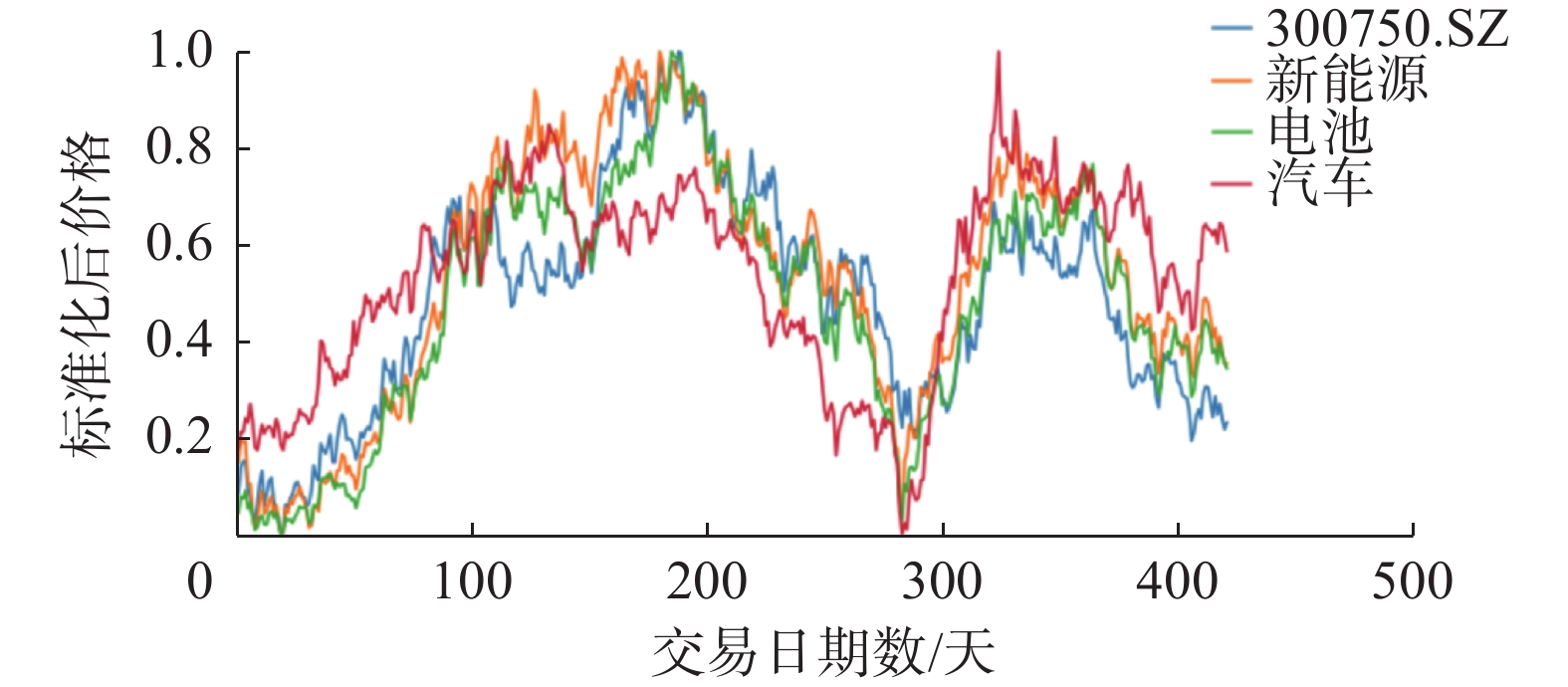
仅通过关联矩阵的元素0或1来决定股票直接隶属哪个分组缺乏合理性，即便可以确定隶属哪个分组，但其隶属度是动态变化的。如图5所示，根据股票机构的分类标准，股票300750.SZ属于电池(BK1033)和新能源(399808.SZ)板块，但其股价波动规律不仅与电池和新能源板块相似，还与汽车(BK1029)板块相似。

图  5  宁德时代股票价格波动与相关行业价格波动规律示例

Fig.  5  Example description of the fluctuation pattern of CATL’s stock price and related sectors

下载: 全尺寸图片

本节引入融合注意力机制的超图卷积，通过隶属度来详细、合理地描述股票之间随时间演化的关系。首先对关联矩阵H嵌入注意力机制^[23]，通过超边−顶点注意力机制来自适应地学习同一超边内不同顶点的重要性。给定某个顶点${v_i} \in {\boldsymbol{V}}$及其所加入的某条超边${e_j} \in {\boldsymbol{E}}$，使用顶点${\nu _i}$的时序特征$ {{\tilde{\boldsymbol{z}}^i}} $以及超边${e_j}$的特征$ {{\boldsymbol{m}}^j} $来计算一个注意力系数$ {H_{ij}} $，该系数表示顶点${\nu _i}$对于超边${e_j}$的重要程度。

超边${e_j}$的特征$ {{\boldsymbol{m}}^j} $通过以下步骤计算。首先计算超边平均特征$ {\boldsymbol{c}} $，它是由超边${e_j}$包含的顶点嵌入平均池化和非线性变换得到：

式中$ {{\boldsymbol{W}}_c} $是可学习的参数矩阵。基于超边平均特征$ {\boldsymbol{c}} $，可以计算该条超边内每个顶点的注意力权重。对于超边包含的每个顶点，计算每个顶点特征和超边平均特征$ {\boldsymbol{c}} $之间的余弦相似度，顶点越相似于超边平均特征$ {\boldsymbol{c}} $获得的权重越高。最后，超边${e_j}$特征是其包含的顶点嵌入加权和$ \boldsymbol{m}^j $：

其余各条超边的特征计算同理。最后由顶点特征$ {{\tilde{\boldsymbol{z}}^i}} $和超边特征$ {{\boldsymbol{m}}^j} $得到：

式中：$ \sigma ( \cdot ) $为修正线性单元激活函数，$ {\boldsymbol{P}} $是可学习参数矩阵。$ {\mathcal{N}_i} $表示顶点${\nu _i}$的邻居集，它可以通过上文定义的超图关联矩阵来获取。$ {\mathrm{sim}}( \cdot ) $是相似性计算函数，$ {\mathrm{sim}}({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) = {{\boldsymbol{r}}^{\mathrm{T}}}[{{\boldsymbol{x}}_i}\parallel {{\boldsymbol{x}}_j}] $，r是可学习的权重向量，$ [ \cdot \parallel \cdot ] $表示2个向量拼接。此时关联矩阵的元素是介于0到1的连续值，不再是离散值。本节使用$ {\boldsymbol{H}}_{}^{{\mathrm{att}}} $替换超图卷积更新公式中的H。

静态超图卷积和动态超图卷积采用相同的卷积方式，二者唯一区别在于关联矩阵H不同。2种不同类型关联矩阵应用超图卷积后输出$ {\boldsymbol{X}}_{t,s}^{(l + 1)} $和$ {\boldsymbol{X}}_{t,d}^{(l + 1)} $，经过线性变换和LeakyReLU函数得到2种股票趋势表征，分别是静态趋势表征$ {{\boldsymbol{Y}}_{t,s}} $和动态趋势表征$ {{\boldsymbol{Y}}_{t,d}} $，公式表示为

2.6   趋势预测层

将2种不同的股票表征$ {{\boldsymbol{Y}}_{t,s}} $和$ {{\boldsymbol{Y}}_{t,d}} $相加得到$ {{\boldsymbol{Y}}_t} = {{\boldsymbol{Y}}_{t,s}} + {{\boldsymbol{Y}}_{t,d}} $，并将$ {{\boldsymbol{Y}}_t} $输入全连接层得到预测概率分布：

采用交叉熵损失函数作为优化目标：

式中：$ \hat {\boldsymbol{y}}_i^{t + 1} $是股票${s_i}$在接下来的t +1交易日中预测概率分布，选择概率最大的作为预测的趋势方向；$ {\boldsymbol{y}}_i^{t + 1} $是表示股票${s_i}$真实趋势方向的独热向量；$ {\boldsymbol{y}}_{i,b}^{t + 1} $和$ \hat {\boldsymbol{y}}_{i,b}^{t + 1} $分别是$ {\boldsymbol{y}}_i^{t + 1} $和$ \hat {\boldsymbol{y}}_i^{t + 1} $中第b个元素。根据股票收盘价的涨跌幅得到标签，将涨幅不小于0.55%的标记为“上涨”，跌幅不小于0.50%的标记为“下跌”，其余为“持平”。

3.   实验及结果分析

3.1   数据集

采用中国A股股票数据集和美股股票数据集来评估本文模型在不同市场下的鲁棒性。

A股数据集　收集了2013年1月4日—2019年12月31日期间A股市场中的2 433支股票，通过保留交易日超过98%的股票，最终筛选得到758支股票^[19]。收集的2种类型数据，包括股票历史价格数据和行业关系数据。

1) 股票历史价格数据：收集758支股票的历史价格数据，对于突发事件造成的数据缺失使用前一日的数据填充。股票历史价格数据涉及6个基本价格特征 (开盘价、最高价、最低价、收盘价、成交量和交易额) 和4个技术指标特征(5、10、20和30日移动平均线)。最后这些数据经过标准化处理后得到10维特征作为模型的输入。

2) 行业关系数据：按照申万行业划分标准对所有股票进行分组，分为104个行业类别。

美股数据集　收集了2013年1月2日—2017年8月12日期间1 026只纳斯达克交易所(NASDAQ)股票和1 737只纽约证券交易所(NYSE)股票 ^[12]。对于这些股票，同样收集2种类型数据：股票历史价格数据和行业关系数据。

3.2   训练设置

本文模型基于PyTorch框架实现，并使用网格搜索来确定最佳超参数。为了保证实验结果的公平性，首先将每个交易日的股票价格数据嵌入到16维空间中，然后输入到不同的方法中。模型使用Adam 优化器进行训练，初始学习率设置为0.003，dropout 设置为 0.4，最大epoch 设置为 600。对于改进的Transformer在集合{16, 32, 64}内搜索特征嵌入维度大小，在区间(2, 8)内搜索一维卷积核大小，在集合{16, 32, 64}内搜索超图神经网络特征嵌入维度大小。所有超参数使用验证集进行了优化，在时间窗口大小为25，一维卷积核大小为6，Transformer网络和超图神经网络的特征嵌入维度大小为32时，模型取得最佳效果。

实验环境为：Windows10操作系统、AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz、Nvidia GeForce GTX 3060 GPU。

3.3   评价指标及基准模型

选取分类任务中广泛使用的4个评价指标：准确率(accuracy)、精确率(precision)、召回率(recall)和调和平均值(F1-score)。

3.4   实验结果与分析

为了验证模型的性能，本文将其与一些现有的模型进行了比较。基准模型包括: LSTM、DARNN^[24]、SFM^[5]、GCN^[11]、TGC^[12]、HATS^[25]、STHGCN^[18]、HGTAN^[19]。

DARNN^[24]：该方法是LSTM的扩展，采用双重注意力机制，在每个时间步自适应地提取相关输入特征，并在所有时间步内选择相关的编码器隐藏状态。

SFM^[5]：该方法是LSTM的扩展，将LSTM存储单元的隐藏状态分解为多个频率分量，以发现多频交易模式。

GCN^[11]：该方法是基于图的方法，使用LSTM对股票的历史价格数据进行编码，然后将结果输入到GCN中，以根据股票之间的关系进行学习。

TGC^[12]：该方法是基于图的方法，在LSTM基础上，通过设计时间图卷积模块，根据股票之间的关系进行学习并生成股票的关系嵌入。

HATS^[25]：该方法是基于图的方法，设计了一种分层图注意力网络，该网络有选择地聚合不同类型的关系数据来学习股票表征。

STHGCN^[18]：该方法是基于超图的方法，通过股票的行业归属关系预定义静态超图，并引入门控时间卷积来捕获股票价格特征中的时间依赖关系。

HGTAN^[19]：该方法是基于超图的方法，通过股票的行业归属关系和主动型基金持股关系预定义静态超图，并引入三重注意力机制来引导信息流在超图上传播。

实验结果如表1所示。

由对比实验结果可以得出以下结论：

1) 考虑股票间关系的方法如GCN、TGC、HATS、STHGCN、HGTAN和DHGCN在多个指标上优于LSTM、DARNN和SFM，说明融合关系信息可以提高模型预测精度。

2) HGTAN和DHGCN都是基于超图的模型，二者预测结果都优于基于图的模型，这也说明超图具有捕获股票间高阶协同关系的能力。

3) DHGCN的性能超越了其他基准模型，它在Recall和 F1-score指标上分别超过次优模型3.8%和0.6%。此外，DHGCN模型的实验结果优于同是基于超图的模型(STHGCN 和HGTAN)，这可能归因于DHGCN采用的是数据驱动的方式自动构建动态超图，而后者则需要先验信息进行预先定义。

表2给出了不同方法在美股数据集上的预测性能。可以看到，DHGCN在多个评估指标中取得最好或持平结果，尤其是在NYSE数据集上，4项指标分别优于次好模型(HGTAN)1.26%、5.70%、1.53%和13.63%。此外本文还注意到通过引入股票间的关系信息，基于图或超图的模型性能都得到了显著提高，这一结果与A股数据集上的结果一致。

3.5   模型消融实验

1) Transformer：基于标准的多头注意力机制编码时序信息用于趋势预测。

2) I-Transformer (improved-Transformer)：在1) 基础上改进多头注意力机制和增添时序注意力聚合模块用于趋势预测。

3) I-Transformer+static：在2) 基础上融合静态关系信息用于趋势预测。

4) I-Transformer+dynamic：在2)基础上融合动态关系信息用于趋势预测。

5) I-Transformer+static+dynamic(DHGCN)：在2) 基础上融合静态和动态关系信息用于趋势预测。

表3给出了不同DHGCN变体的性能。可以看到，改进的Transformer模型(I-Transformer)在4项指标上均高于Transformer，这表明感知股票历史时段相类似的价格波动规律对于股票趋势预测是有效的。未考虑实体间关系信息的模型(Transformer和I-Transformer)预测性能低于其他考虑了股票间实体关系信息的模型，说明捕捉股票之间的关系信息是有价值的。此外，融合静态和动态关系信息的模型(DHGCN)比仅考虑静态关系信息的模型(Transformer+static)或仅考虑动态关系信息的模型(Transformer+dynamic)表现更好。这也证明了静态关系和动态关系都是重要的，二者缺一不可。DHGCN取得了最好的预测效果，证实了融合不同模块信息能够增强特征嵌入表示趋势的能力。

3.6   模型超参数分析

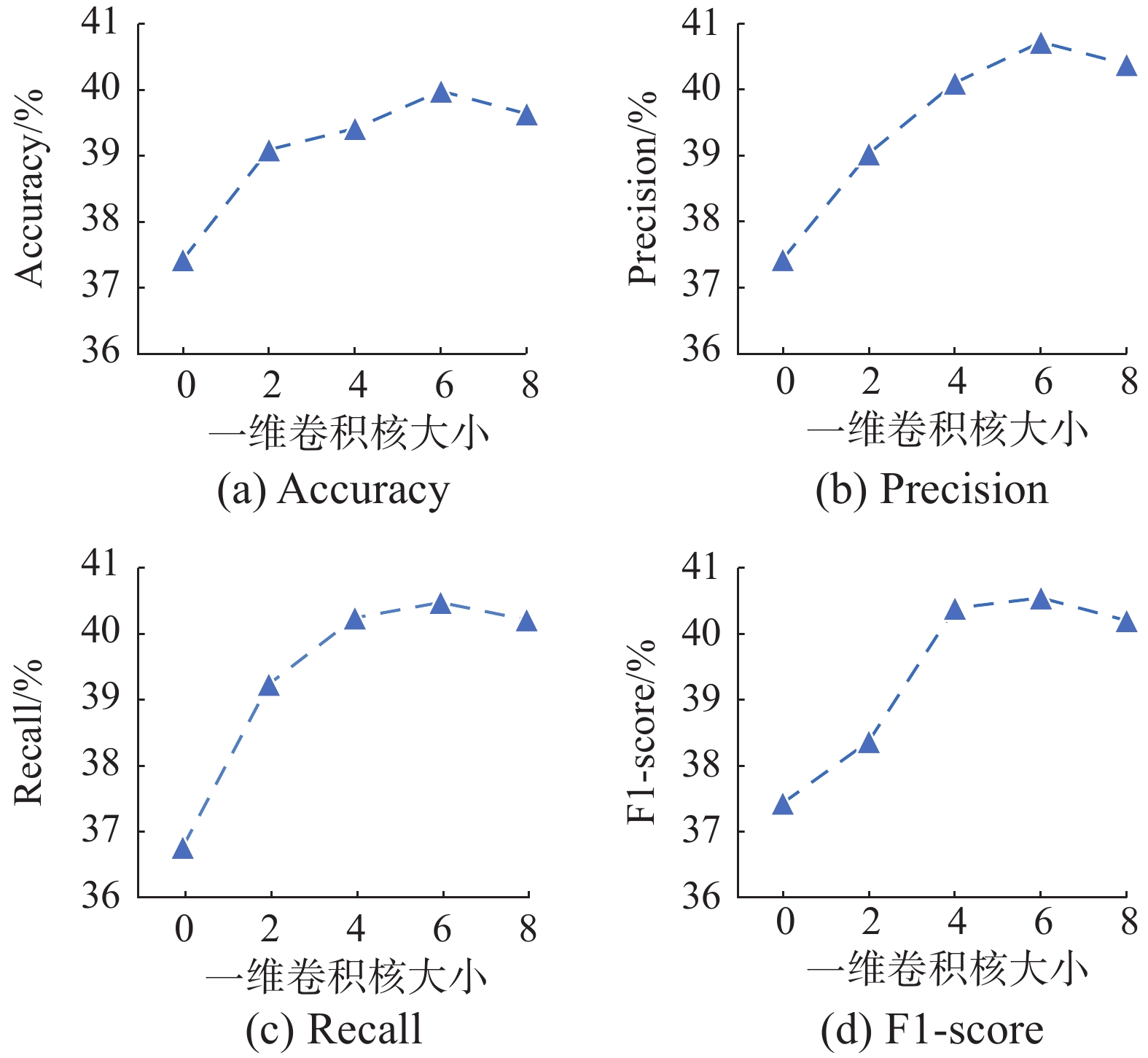
本文通过调整一维卷积核大小c来了解DHGCN在4项指标上的表现，使用3.2节中提到的默认设置来固定其他超参数。

图6(a)~(d)给出了改变一维卷积核大小c，结果呈现出先升后降的趋势。在c=6时获得了最好的结果。当c过小时，模型无法学习当前和历史时段是否存在类似波动规律，尤其是当c=0时，改进的Transformer网络退化为标准的Transformer网络；当c过大时，模型提取到的趋势特征包含了多种短期趋势，造成模型对特征识别的混淆。

图  6  改进的Transformer网络中一维卷积核大小对模型整体性能的影响

Fig.  6  Impact of one-dimensional convolutional kernel size of the improved Transformer network on the overall performance

下载: 全尺寸图片

4.   结束语

本文提出了一种基于改进的Transformer和动态超图卷积神经网络的股票趋势预测框架DHGCN。首先使用改进后Transformer编码序列的时间维度信息，然后通过静−动态超图和超图卷积建模序列的空间维度信息，将不同序列关系信息引入到时序建模中，最后趋势预测层融合静−动态信息用于股票趋势预测。对比实验结果表明，在A股数据集和美股数据集上，本文模型的预测性能都有明显的优势。此外本文还对模型进行了消融实验，验证了所提模型各个组件的有效性。在未来工作中，将探索融合多源信息，如在线金融新闻和社交媒体信息等用于股票综合预测。