Research on graph contrastive learning method based on ternary mutual information
-
摘要: 最近，图对比学习成为一种成功的无监督图表示学习方法，大多数方法都基于最大化互信息原则，通过数据增强来得到两个视图，并最大化两个视图的互信息。然而，两个视图的互信息可能包含不利于下游任务的信息。为了克服这些缺陷，提出基于三元互信息的图对比学习框架。该框架首先对输入图进行随机数据增强来生成两个视图，使用权重共享的编码器获得两个节点表示矩阵，随后使用共享权重解码器解码两个视图的节点表示。通过对比损失函数分别计算视图之间和视图与原图之间的损失，以最大化视图之间和视图与原图之间的互信息。实验结果表明，该方法在节点分类准确性方面的表现优于基线方法，甚至超过部分监督学习方法，验证了框架的有效性。Abstract: Recently, graph contrastive learning has emerged as a successful method for unsupervised graph representation learning. Most existing methods are based on the principle of maximizing mutual information by obtaining two views through data augmentation and maximizing their mutual information. However, the mutual information of these two views may include information that is not beneficial for downstream tasks. To overcome these shortcomings, we propose a graph contrastive learning framework based on ternary mutual information. The framework first performs stochastic data augmentation on the input graph to generate two views. A weight-shared encoder is then used to obtain two node representation matrices. Subsequently, a shared weight decoder decodes the node representations of the two views. The loss between views, and between views and the original graph, is calculated separately using a contrast loss function. This approach maximizes the mutual information between the views, as well as between views and the original graph. The experimental results show that the method outperforms the baseline method in terms of node classification accuracy. Moreover, it even outperforms some supervised machine learning methods, verifying the effectiveness of the framework.
-
近年来，图神经网络(graph neural network, GNN)已经广泛应用于推荐系统、交通预测和生物科学等领域[1-2]。传统神经网络因为图数据不具有固定的网络拓扑结构，所以无法直接处理图结构数据。为了解决这个问题，图神经网络引入了聚合函数。通过聚合邻居节点的特征信息来结合图的结构信息，以获得更好的表示。图神经网络在图表示学习中的使用受到了广泛的关注，其目的是通过保留原有图的网络拓扑结构和节点特征，将图中节点高维稀疏向量表示转为低维稠密向量表示，以便下游任务用简单的算法进行处理。然而，现有的大多数GNN模型都是依赖于标签的监督学习[3-5]。在现实世界中，在图数据中获取标签信息代价是昂贵的，因此寻求一种有效的无监督学习方法非常重要。最近，基于最大化互信息原则的对比学习已经在许多领域取得了成功[6]，例如计算机视觉[7-9]和自然语言处理[10-11]。这些对比学习方法不依赖标签信息，而是通过对比正样本对和负样本对来最大化目标样本及其表示的互信息，从而学习到更好的表示。
在其他领域对比学习成功经验的启发下，当前图神经网络领域中最先进的无监督图表示学习方法大多采用对比学习的方式[12]。这些方法的基本原理是在向量空间中，通过拉近相关表示、推开不相关表示的方式来约束互信息的下界，从而最大化互信息，以此获得更好的表示。例如，MVGRL(contrastive multi-view representation learning on graphs)[13]和GRACE(deep graph contrastive representation learning)[14]方法，通过数据增强生成两个视图（即对原图进行数据增强过后得到的新图）来学习节点表示，拉近两个图中相同节点的表示，推远其他节点的表示。然而，这类方法学习的表示只考虑到了两个视图间的互信息，而未考虑到原图中的信息。通过数据增强生成的两个视图可能在数据增强过程中丢失了部分重要信息，因此两个视图之间的互信息可能包含了原图之外的信息，这部分信息是对下游任务无益的。
为了解决上述问题，本文提出了一个新的无监督图对比学习框架，称为基于三元互信息的图对比学习框架(graph contrastive learning based on ternary mutual information, GCLTMI)。在GCLTMI中，首先通过对输入数据进行随机数据增强来生成两个相关的视图，使用一个编码器编码两个视图的表示，然后使用对比损失来训练模型，以最大化这两个视图中节点表示的一致性。除此以外，本文还使用一个解码器解码两个视图的表示，以便对比两个视图的表示和原图的特征，从而最大化两个视图中节点表示中关于原图的信息。本文的主要贡献是：
1）提出一种无监督图对比学习方法GCLTMI，与以前的方法相比，该方法考虑到了原图的信息，使其学习到的表示能够更好地应用于下游任务。
2）在常用的线性评估协议下，通过对5个公共基准数据集的综合实证研究，在节点分类方面比较了14种比较方法，验证了该方法的有效性。
1. 相关工作
1.1 对比学习
近年来，无监督学习方法因在计算机视觉等领域的出色表现而受到了广泛关注[15-16]。而对比学习则是其中最具代表性的无监督学习方法之一。对比学习通过对比正负样本来学习判别表示，通常通过最大化输入和学习表示之间的互信息来实现这一目标。一种常见的对比学习方法是 CPC (contrastive predictive coding)[17]，将序列数据中目标样本的上下文的样本作为正样本，将随机采样的样本作为负样本，对比正负样本对的局部特征，以预测序列数据中未来的局部特征。而DIM (deep infomax)[18]结合全局特征，对比了目标样本的全局特征和其他正负样本的局部特征，进一步提升了效果。SimCLR (a simple framework for contrastive learning of visual representations)[19]将互信息最大化原理扩展到多个视图，通过数据增强生成多个视图，并最大化数据增强生成的视图之间的互信息，为后续对比学习工作构建起了一个通用的对比学习框架。随着对比学习的兴起，同时也存在着一些问题。为了获得更好的效果，需要增加负样本的样本量，这会导致显存不足的问题。为了解决这个问题，MoCo (momentum contrast for unsupervised visual representation learning)[8]通过使用字典队列来存储和采集负样本，以及利用动量更新技术来更新非对称编码器的参数，促进无监督对比学习。BYOL (bootstrap your own latent: a new approach to self-supervised learning)[20]则在MoCo的基础上进一步简化结构，取消了负采样操作，而是使用非对称网络结构，分为在线网络和目标网络，用在线网络去预测目标网络的表示，隐式地实现正负对比，其中目标网络不执行梯度回传，而是通过动量更新操作更新权重。此外，Barlow Twins方法[21]从一个全新的角度看待对比学习为什么能起作用，其不采用常用的对比损失函数，而是在特征维度上计算两个视图的互相关矩阵，并迫使互相关矩阵接近于单位矩阵，以此来学习表示并最小化冗余。由于其是在特征维度上计算的，因此计算量远小于其他对比学习方法，为对比学习提供了新思路。
1.2 无监督图表示学习
许多传统的无监督图表示学习方法本质上也遵循对比范式[22-23]。在过去的研究中，无监督图表示学习主要集中在基于随机游走的局部对比模式上，这种模式的前提假设是相邻的节点具有相似的表示。例如，在DeepWalk[22]和Node2Vec[23]中处于相同随机游走路径上的节点被认为是正样本，而其他节点被认为是负样本。然而，这些基于随机游走的方法被证明在理论上是在执行隐性矩阵分解[24]，其缺陷在于过度强调编码的邻近性结构信息。
随着图神经网络的兴起，基于图神经网络的图表示学习方法[25]逐渐开始取代传统图表示学习方法。由于对比学习在计算机视觉等领域的成功，受到DIM的启发，DGI(deep graph infomax)[12]将对比学习扩展到图领域中，通过对比图的局部表示和全局表示来学习节点的表示，并在节点分类基准上获得了良好的性能。GMI(graph representation learning via graphical mutual information maximization)[26]将传统的互信息计算思想从向量空间推广到图域，并从节点特征和拓扑结构两方面对互信息进行度量。此外，一些方法将数据增强技术引入图表示学习中，通过创建图的两个视图来学习节点表示。例如，GRACE[14]和GCA (graph contrastive learning with adaptive augmentation)[27]通过不同数据增强策略来创建两个视图，并拉近同一节点在不同视图中的表示，同时推开其他节点的表示。而MVGRL[13]通过节点扩散的方法生成多个视图，并对比一个视图节点表示与另一个视图的图表示来学习节点级和图级表示。此外，一些研究将在计算机视觉邻域取得成功的对比学习方法引入到图领域中。例如BGRL (large scale representation learning on graphs via bootstrapping)[28]将BYOL的方法扩展到图邻域，引入了非对称网络结构，并使用两种编码器网络（在线网络和目标网络）来对比在线网络和目标网络输出的表示，此外它依赖梯度停止和动量更新技术来防止平凡解。G-BT (a self-supervised representation learning framework for graphs)[29]则是将Barlow Twins方法[21]应用于图领域中，简化了网络结构和计算复杂度，为图对比学习提供了新思路。最后，COSTA (covariance preserved feature augmentation for graph contrastive learning)[30]创新性地在特征空间里进行数据增强，并在对比学习中应用这些增强数据来学习表示。
然而，这些方法只考虑到数据增强后两个视图的互信息，没有考虑到原图的信息。与以往的工作不同，本文通过最大化两个视图和原图之间的三元互信息，提高了模型的有效性。
2. 基于三元互信息图对比学习
传统的图对比学习方法通常采用对称结构进行多视图对比。其目的是使不同视图之间的互信息最大化。设随机变量X、Y间互信息I(X, Y)的表达式为
$$ {I} \left( {X, Y} \right) = \sum\limits_{y \in Y} {\sum\limits_{x \in X} {{p} \left( {x, y} \right){\text{log}}\left( {\frac{{{p} \left( {x,y} \right)}}{{{p} \left( x \right){p} \left( y \right)}}} \right)} } $$ 式中：p(x, y)是X和Y的联合概率分布函数，p(x)和p(y)分别是X和Y的边缘概率分布函数。对比学习的目的是学习到节点表示，并保留表示两个视图之间共享的信息。根据信息论中的数据处理不等式，定义马尔可夫转移过程A→B→C的互信息不等式为
$$ {I} \left( {A, A} \right) \geqslant {I} \left( {A, B} \right) \geqslant {I} \left( {A, C} \right) $$ (1) 将神经网络视为一条马尔可夫链，常见的图对比学习方法可以看作马尔可夫过程：
$$ {\boldsymbol{X}}\xrightarrow{{{f} \left( \cdot \right)}}{\boldsymbol{H}}\xrightarrow{{{h} \left( \cdot \right)}}{\boldsymbol{Z}} $$ 式中：f(∙)为GNN编码器，h(∙)为一个简单的多层感知器（multi layer perception, MLP）。可以得到相应的互信息不等式：
$$ {I} \left( {{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) \geqslant {I} \left( {{{\boldsymbol{X}}_1},{{\boldsymbol{Z}}_2}} \right) \geqslant {I} \left( {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}} \right) $$ 式中：X1、X2为输入图经过数据增强的视图，Z1、Z2为数据增强后的两个视图经过编码器和MLP生成的表示。图对比学习的优化目标是最大化I(Z1, Z2)，使其尽可能接近I(X1, X2)。期望最终原图
$ \mathcal{G} $ 经过编码器后获得用于下游任务的节点表示H，尽可能地包含X1和X2的共享信息，常规图对比学习最大化互信息示意如图1(a)所示。其中E(∙)为信息熵，E(∙|∙)为条件熵。
图 1 常规图对比学习最大化互信息与GCLTMI最大化互信息示意Fig. 1 Schematic diagram of conventional graph contrastive learning maximizing mutual information and GCLTMI maximizing mutual information
下载:
全尺寸图片
2.1 三元互信息图对比学习
传统图对比学习最大化Z1、Z2之间的互信息，并不一定能得到最有益于下游任务的信息。通过数据增强生成的视图可能会损失原图里有益于下游任务的信息，这样学到的表示不利于下游任务的学习。数据增强方法在一定程度上能增加模型的泛化能力，但同时也可能会改变原始数据的特征或结构，导致一些有用的信息在增强后的数据中不可用或被削弱，这样可能会丢失一些对模型预测有用的关键信息，从而降低模型的性能。例如，采用随机丢弃边和节点特征掩盖的方式进行数据增强，可能会导致一些节点成为孤立节点，无法从邻居节点获取信息，或者导致节点关键特征的丢失，使得模型难以学到有用的信息。因此，本文在两个视图的基础上引入了原图特征X的信息，GCLTMI最大化互信息示意如图1(b)所示，并将三元互信息I(X, X1, X2)作为最重要的信息。三元互信息I(X, X1, X2)定义为
$$ \begin{gathered} {I} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) = {K} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) + {I} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1}} \right) + \\ {I} \left( {{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) + {I} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_2}} \right) \\ \end{gathered} $$ 式中K(X, X1, X2)定义为
$$ \begin{gathered} {K} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) = {E} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) + {E} \left( {\boldsymbol{X}} \right) + \\ {E} \left( {{{\boldsymbol{X}}_1}} \right) + {E} \left( {{{\boldsymbol{X}}_2}} \right) \\ \end{gathered} $$ 式中：E(∙)为信息熵，E(∙,∙,∙)为联合信息熵。
同样把神经网络视为一条马尔可夫链，本文所提出的框架可以看作为
$$ {\boldsymbol{X}}\xrightarrow{{{f} \left( \cdot \right)}}{\boldsymbol{H}}\xrightarrow{{{h} \left( \cdot \right)}}{\boldsymbol{Z}}\xrightarrow{{{d} \left( \cdot \right)}}{\boldsymbol{D}} $$ 式中：f(∙)为GNN编码器，h(∙)为非线性映射的映射头，d(∙)为解码器，具体细节见2.3节。根据式(1)可以得到相应的数据处理不等式：
$$ \begin{gathered} {I} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) = {K} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) + {I} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1}} \right) + \\ {I} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_2}} \right) + {I} \left( {{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) \geqslant {K} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) + {I} \left( {{\boldsymbol{X}},{{\boldsymbol{Z}}_1}} \right) + \\ {I} \left( {{\boldsymbol{X}},{{\boldsymbol{Z}}_2}} \right) + {I} \left( {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}} \right) \geqslant {K} \left( {{\boldsymbol{X}},{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}} \right) + {I} \left( {{\boldsymbol{X}},{{\boldsymbol{D}}_1}} \right) + \\ {I} \left( {{\boldsymbol{X}},{{\boldsymbol{D}}_2}} \right) + {I} \left( {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}} \right) \\ \end{gathered} $$ 期望最终用于下游任务的节点表示尽可能包含I(X, X1, X2)中的信息，则要最大化I(Z1, Z2)、I(X, D1)和I(X, D2)，使得[K(X, X1, X2)+I(X, D1)+I(X, D2)+I(Z1, Z2)]尽可能接近I(X, X1, X2)。则最终的优化目标为
$$ {\text{max}}\left[ {{I} \left( {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}} \right) + {I} \left( {{\boldsymbol{X}},{{\boldsymbol{D}}_1}} \right) + {I} \left( {{\boldsymbol{X}},{{\boldsymbol{D}}_2}} \right)} \right] $$ 2.2 算法框架
本文所提出的GCLTMI的优化目标是最大化不同视图和原图的三元互信息，其算法步骤如下：
1）整体流程是在每次迭代时，输入原图
$ \mathcal{G} $ 并进行数据增强以生成两个视图$ \mathcal{G} _1 $ 、$ \mathcal{G} _2 $ 。2）使用共享权重的GNN编码器f(∙,∙)得到下游任务需要的特征表示H1、H2，通过共享权重的映射头h(∙)将它们非线性变化映射到指定特征空间表示Z1、Z2。
3）使用共享权重的解码器解码得到D1、D2。
4）计算Z1、Z2视图之间的对比损失，再分别计算D1、D2与原图的特征矩阵X的对比损失。
5）通过最小化损失更新参数，完成一轮训练迭代，并返回步骤1）。
6）在训练结束后，将原图
$ \mathcal{G} $ 输入到训练好的GNN编码器f(∙,∙)中得到结果表示H。本文的框架总体如图2所示。
图 2 基于三元互信息的图对比学习框架Fig. 2 Graph contrastive learning framework based on ternary mutual information下载:
全尺寸图片
在图2中，设
$\mathcal{G}=( \mathcal{V}, \mathcal{E}) $ 表示图，其中$\mathcal{V} $ ={v1, v2, ···, vN}为节点集，N为节点数；$\mathcal{E} $ ={e1, e2, ···, eM}为边集，M为边数。X∈RN×F是节点特征矩阵，F是特征维度。A∈{0,1}N×N是邻接矩阵，若(vi, vj)∈$\mathcal{E} $ ，则Aij=1，否则Aij=0。2.3 实现
2.3.1 数据增强
数据增强生成视图是图对比学习方法重要组成部分。在框架每次迭代中，通过随机数据增强生成视图，本文选择了边丢弃和节点特征掩盖两种增强方式生成
$\mathcal{G}_1 $ 和$\mathcal{G}_2 $ 两个视图。在边丢弃的情况下，生成一个掩码矩阵M∈{0,1}N×N，在Aij=1的情况下从伯努利分布Mij~$\mathcal{B} $ (1−pE)中采样，其他情况Mij=0，pE为边丢弃的概率。由此产生的邻接矩阵A计算为$$ {\boldsymbol{A}} = {\boldsymbol{A}} \odot {\boldsymbol{M}} $$ 式中
$ \odot $ 为哈达玛积。在节点特征掩盖时，使用类似的方案从伯努利分布$ \mathcal{B} $ (1−pF)中采样，生成掩盖向量m∈{0,1}F，pF为节点特征掩盖的概率。此时节点特征X为$$ {\boldsymbol{X}} = \left[ {{{\boldsymbol{x}}_1} \odot {\boldsymbol{m}}{\text{; }}{{\boldsymbol{x}}_2} \odot {\boldsymbol{m}}{\text{; }} \cdots {\text{; }}{{\boldsymbol{x}}_N} \odot {\boldsymbol{m}}} \right] $$ 式中：[;]是连接操作，xi为X的行向量。
2.3.2 编码器
本文的目标是学习一个GNN编码器f(X, A)∈RN×F'，它接收图的特征X和邻接矩阵A作为输入，产生低维的节点表示，即F'
$ \ll $ F。H=f(X, A)为节点表示矩阵，其中矩阵的行向量hi是节点vi的表示，这些表示用于网络结构分析的下游任务。编码器f(∙,∙)使用GCN[4]编码器，其表达式为$$ {{\boldsymbol{H}}^{\left( {l + 1} \right)}} = {f} \left( {{{\boldsymbol{H}}^{\left( l \right)}},{\boldsymbol{A}}} \right) = \sigma \left( {{{{{\hat {\boldsymbol{D}}}}}^{ - \frac{1}{2}}}{{\hat {\boldsymbol{A}}}}{{{{\hat {\boldsymbol{D}}}}}^{ - \frac{1}{2}}}{{\boldsymbol{H}}^{\left( l \right)}}{\boldsymbol{W}}_f^{\left( l \right)}} \right) $$ 式中：l表示层数；H(0)=X；σ(∙)为非线性激活函数；
${\boldsymbol{W}}_f^{\left( l \right)}$ 为编码器的第l层权重；${{\hat {\boldsymbol{A}}}} = {{{\boldsymbol{A}} + {\boldsymbol{I}}}}$ ，其中I是单位矩阵；${{\hat {\boldsymbol{D}}}}$ 为${{\hat {\boldsymbol{A}}}}$ 的节点度矩阵； H=H(L)，L为总层数。两个视图
$ \mathcal{G}_1 $ 和$\mathcal{G}_2 $ 通过同一个编码器f，分别产生两个对应的节点表示矩阵H1和H2。在具体实验中，本文的编码器通常只由两层或三层GCN组成。2.3.3 映射头
一个简单的MLP h(∙)，将经过编码器f得到两个节点表示矩阵H1和H2进行非线性变换映射到指定的特征空间得到Z1、Z2。映射头h(∙)为
$$ {{\boldsymbol{Z}}^{\left( {l + 1} \right)}} = {h} \left( {{{\boldsymbol{Z}}^{\left( l \right)}}} \right) = \sigma \left( {{{\boldsymbol{Z}}^{\left( l \right)}}{\boldsymbol{W}}_h^{\left( l \right)}} \right) $$ 式中：l表示层数；Z(0)=H；
${\boldsymbol{W}}_h^{\left( l \right)}$ 为映射头的第l层权重；Z=Z(L)，L为总层数。目的是将节点表示非线性映射到应用对比损失的空间，方便计算对比损失，同时避免在训练时计算对比损失丢掉一些重要的特征。2.3.4 解码器
解码器是本文所提出的框架与常规的多视图对比学习方法不同之处，解码器d(∙)的输出为
$$ {\boldsymbol{D}} = \sigma \left( {{\boldsymbol{Z}}{{\boldsymbol{W}}_d}} \right) $$ 式中Wd为解码器的权重。本文的解码器只使用了一层全连接层和激活函数来实现。将映射头得到的Z1、Z2解码并映射到原图特征X相同维度得到D1、D2，用于计算视图与原图的对比损失。
2.3.5 损失函数
本文选择常用的infoNCE[17]作为损失函数。不失一般性，infoNCE损失函数定义为
$$ {\mathcal{L}_{{\text{infoNCE}}}} = - \mathop {\rm{E}}\limits_X \left[ {{\text{log}}\frac{{{f} \left( {c,{x_i}} \right)}}{{\displaystyle\sum\limits_{{x_j} \in X} {{f} \left( {c,{x_j}} \right)} }}} \right] $$ 式中：X={x1, x2, ···, xN}是一组样本，f(∙,∙)是计算相似性分数函数，c为目标样本，(c, xi)为正样本对，(c, xj)为负样本对。
根据CPC[17]的工作的证明，c和xi之间的互信息满足：
$$ I\left( {c,{x_i}} \right) \geqslant {\text{log}}\left( N \right) - {\mathcal{L}_{{\text{infoNCE}}}}\left( {c,{x_i}} \right) $$ (2) 式中：N为样本数量，是一个常数，最小化infoNCE损失函数就是最大化互信息的下限。具体到本方法中，一个视图的节点表示ui作为目标样本，与另一个视图对应的节点表示vi作为正样本对，同时ui分别与另一个视图里所有节点的表示{v1, v2, ···, vN}构成N个负样本对，则本文采用的infoNCE损失函数定义为
$$ \mathcal{L}\left( {{\boldsymbol{U}},{\boldsymbol{V}}} \right) = - \frac{1}{N}\sum\limits_{i = 1}^N {{\text{log}}\frac{{{\text{exp}}\left( {\sigma \left( {{{\boldsymbol{u}}_i},{{\boldsymbol{v}}_i}} \right)/\tau } \right)}}{{\displaystyle\sum\limits_{k = 1}^N {{\text{exp}}\left( {\sigma \left( {{{\boldsymbol{u}}_i},{{\boldsymbol{v}}_k}} \right)/\tau } \right)} }}} $$ (3) 式中：
$ {{\boldsymbol{u}}_i} $ ∈U；$ {{\boldsymbol{v}}_i} $ 、$ {{\boldsymbol{v}}_k} $ ∈V；σ(∙,∙)为余弦相似性；τ为超参数温度系数，控制模型对负样本的区分度。本文的最终优化目标为最大化[I(X, D1)+ I(X, D2)+I(Z1, Z2)]，可以分为两部分，即最大化视图间的互信息I(Z1, Z2)和最大化视图与原图间的互信息[I(X, D1)+ I(X, D2)]。根据式(2)那么视图间的损失
${\mathcal{L}_{{\text{view}}}} $ 可以定义为$$ {\mathcal{L}_{{\text{view}}}} = {{\left( {\mathcal{L}\left( {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}} \right) + \mathcal{L}\left( {{{\boldsymbol{Z}}_2},{{\boldsymbol{Z}}_1}} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\mathcal{L}\left( {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}} \right) + \mathcal{L}\left( {{{\boldsymbol{Z}}_2},{{\boldsymbol{Z}}_1}} \right)} \right)} 2}} \right. } 2} $$ 经过解码器解码的视图表示与原图特征X的损失
${\mathcal{L}_{{\text{decoder}}}} $ 定义为$$ {\mathcal{L}_{{\text{decoder}}}} = {{\left( {\mathcal{L}\left( {{\boldsymbol{X}},{{\boldsymbol{D}}_1}} \right) + \mathcal{L}\left( {{\boldsymbol{X}},{{\boldsymbol{D}}_2}} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\mathcal{L}\left( {{\boldsymbol{X}},{{\boldsymbol{D}}_1}} \right) + \mathcal{L}\left( {{\boldsymbol{X}},{{\boldsymbol{D}}_2}} \right)} \right)} 2}} \right. } 2} $$ 最终的总体损失ℓ为
$$ \ell = \left( {1 - \lambda } \right){\mathcal{L}_{{\text{view}}}} + \lambda {\mathcal{L}_{{\text{decoder}}}} $$ 式中λ是一个取值范围为0到1的超参数，控制两部分损失线性组合比例。本文计算损失的流程为：先计算Z1、Z2图视图间的损失
${\mathcal{L}_{{\text{view}}}} $ ，然后再分别计算D1、D2与X之间的损失${\mathcal{L}_{{\text{decoder}}}} $ ，将这两部分损失线性组合后作为模型整体损失。2.4 算法伪代码
综上所述，最终GCLTMI算法的整个流程伪代码如算法 1所示。
算法 1 GCLTMI算法流程
输入 迭代次数T，图的特征矩阵X，图的邻接矩阵A，随机数据增强函数ℸ，神经网络f、h和d，根据式(3)的损失函数
$\mathcal{L} $ ，线性组合比例λ。输出 用于下游任务的节点表示H
1）for i=1 to T do
2）X1, A1←ℸ(X, A)
3）X2, A2←ℸ(X, A)
4）H1←f(X1, A1)
5）H2←f(X2, A2)
6）Z1←h(X1, A1)
7）Z2←h(X2, A2)
8）
${\mathcal{L}_{{\text{view}}}} $ ←(${\mathcal{L}} $ (Z1, Z2)+${\mathcal{L}} $ (Z2, Z1))/29）D1←d(X1, A1)
10）D2←d(X2, A2)
11）
${\mathcal{L}_{{\text{decoder}}}} $ ←(${\mathcal{L}} $ (X, D1)+${\mathcal{L}} $ (X, D2))/212）ℓ←(1−λ)
${\mathcal{L}_{{\text{view}}}} $ +λ${\mathcal{L}_{{\text{decoder}}}} $ 13）更新网络 f、 h 和 d 以最小化 ℓ
14）end for
15）return H←f(X, A)
3. 实验设置
实验使用广泛使用的基准数据集来评估模型的性能，测试任务为网络中节点分类。本节将概述所使用的数据集、实验环境细节以及对结果的讨论。代码基于Pytorch和 Pytorch-Geometric库实现，在一个24 GB显存的NVIDIA TESLA P40 GPU上执行所有实验。
3.1 数据集
为了评估本文的方法，在以前的工作[12,27]中采用了5个常用的基准数据集。表1中介绍数据集的基本统计信息。
表 1 实验中使用的数据集的信息Table 1 Information on the dataset used in the experiment数据集 节点数 边数 特征数 分类数 Cora 2 708 5 429 1 433 7 CiteSeer 3 327 4 732 3 703 6 PubMed 19 717 44 338 500 3 Amazon-Computers 13 752 245 861 767 10 Amazon-Photo 7 650 119 081 745 8 接下来将为每个数据集提供简短的表述，包括基本的统计信息和节点分类下游任务的数据集划分：
Cora、CiteSeer、PubMed: 这些是最常见的引文网络数据集，其中节点表示论文，边表示引用。所有节点都根据论文的主题进行标记。数据集划分采用公共划分，未做任何修改。在这些数据集的划分中，每个类别20个节点作为训练集，500个节点作为验证集，1 000个节点作为测试集，其余节点无标签。
Amazon-Computers、Amazon-Photo: 这两个数据集都是基于亚马逊的共同购买数据。节点表示产品，边表示它们被一起购买的频率。每个产品都根据评论进行描述。由于这些数据集没有可用的公共划分，所以按照训练集/验证集/测试集10%/10%/80%的比例随机划分。
3.2 评估方案
所有实验都采用与之前的工作[25-27]中相同的评估方案。首先，每个模型在只具有结构信息和节点特征的整个图上进行无监督方式的训练。然后，将原图输入经过训练后的编码器得到结果表示。最后，使用在前一步中得到的结果表示训练一个L2正则化线性分类器。线性分类器为
$$ {\boldsymbol{Y}} = {\boldsymbol{WX}} + {\boldsymbol{b}} $$ 式中：X表示模型训练好的结果表示，W表示权重矩阵，b表示偏置，Y表示最终输出结果。在所有实验中，使用不同的随机种子重复实验5次，并报告所有算法的平均结果及相应的标准差。GCLTMI所有参数都通过网格搜索得到，具体超参数设置见表2，并使用Adam优化器[31]进行优化。激活函数采用ELU[32]。为所有数据集分别设置[0.001, 0.01]范围内的初始学习率和[0.0,
0.0001 ]范围内的权重衰减。表 2 不同数据集的超参数设置Table 2 Hyperparameter settings for different datasets数据集 pE, 1 pE, 2 pF, 1 pF, 2 λ τ Cora 0.4 0.4 0.3 0.3 0.6 0.8 CiteSeer 0.8 0.8 0.7 0.7 0.5 1.0 PubMed 0.2 0.4 0.3 0.2 0.5 0.9 Amazon-Computers 0.3 0.5 0.2 0.2 0.5 0.5 Amazon-Photo 0.3 0.3 0.3 0.3 0.4 0.4 3.3 基线方法
为了比较GCLTMI与以往的工作，本文选择了1个传统算法DeepWalk，2个半监督学习算法GCN[4]和GAT[5]以及11个无监督学习算法GAE[33]、VGAE[33]、DGI[12]、GMI[26]、GRACE[14]、MVGRL[13]、GCA[27]、BGRL[28]、G-BT[29]、COSTA[30]、SUGRL[34]。原始特征被直接用于节点分类任务。对于所有基线方法，本文报告了它们基于官方实现的性能，从原始文件中使用默认的超参数。
4. 结果与分析
4.1 实验结果
本文方法在5个真实图数据集上与基线方法在节点分类进行了对比。结果如表3所示，表中数据为节点分类结果的准确率和标准差，其中加黑的结果为最好表现。GCLTMI算法在分类准确率方面与基线方法相比表现出具有竞争力的性能，在大多数数据集上超越了基线算法。
表 3 所有方法在5个数据集上节点分类的准确率和标准差Table 3 Accuracy and standard deviation of node classification for all methods on five datasets% 方法 输入数据 Cora CiteSeer PubMed Amazon-Photo Amazon-Computers Raw Feature X 47.0±0.4 49.3±0.3 69.1±0.2 78.5±0.2 73.8±0.1 DeepWalk A 67.2±0.2 43.2±0.4 65.3±0.5 89.4±0.1 85.3±0.1 GCN A, X, Y 81.5±0.2 70.3±0.4 79.0±0.5 91.6±0.3 84.5±0.3 GAT A, X, Y 83.0±0.2 72.5±0.3 79.0±0.5 91.8±0.1 85.7±0.1 GAE A, X 74.9±0.4 65.6±0.5 74.2±0.3 91.0±0.1 85.1±0.4 VGAE A, X 76.3±0.2 66.8±0.2 75.8±0.4 91.5±0.2 85.8±0.3 DGI A, X 82.3±0.5 71.5±0.4 79.4±0.3 91.3±0.2 87.8±0.3 GMI A, X 83.0±0.2 72.4±0.2 79.9±0.4 90.6±0.2 82.2±0.4 GRACE A, X 83.1±0.2 72.1±0.1 79.6±0.5 91.9±0.3 86.8±0.2 MVGRL A, X 82.9±0.3 72.6±0.4 80.1±0.7 91.7±0.1 86.9±0.1 GCA A, X 81.8±0.2 71.9±0.9 81.0±0.3 92.4±0.4 87.7±0.1 BGRL A, X 82.7±0.4 71.3±0.8 80.3±0.9 91.6±0.5 87.4±0.4 G-BT A, X 82.6±0.5 72.0±0.3 80.5±0.2 92.6±0.6 87.9±0.4 COSTA A, X 83.3±0.3 72.0±0.3 81.2±0.2 92.6±0.5 88.3±0.1 SUGRL A, X 83.4±0.5 73.0±0.4 81.9±0.3 93.3±0.4 88.8±0.2 GCLTMI A, X 84.0±0.4 73.1±0.3 82.8±0.4 94.3±0.5 88.9±0.6 在表3中，与基准对比方法DGI相比，GCLTMI在5个数据集上平均准确率分别提高了1.7、1.6、3.4、3.0、1.1百分点，和最佳对比方法SUGRL相比，本文提出的方法平均提高了0.54百分点。具体而言，GCLTMI在这几个数据集上均优于多视图对比学习方法(COSTA、GRACE、MVGRL、GCA等)。同时，与在学习过程中使用标签信息的半监督方法(GCN和GAT)相比，GCLTMI也取得了优异的性能。与GAT相比，本文提出的方法平均提高了2.22百分点。此外，大多数对比学习模型都优于基于重建误差的模型（即DeepWalk、GAE、VGAE），这反映了对比学习的优势，基于重建误差的模型不太适合节点级别的任务。
总之，在节点分类任务上与现有的最先进的方法相比，GCLTMI展现了优越的性能，验证了本文提出框架的有效性。
4.2 消融实验
本节将验证GCLTMI的各个组成部分的有效性。在其他结构和参数不变的情况下，依次取消映射头和解码器这两部分结构来验证有效性。值得注意的是，取消解码器，模型就不能最大化视图和原图的互信息，只能最大化视图之间的互信息，即退化成普通的多视图对比学习方法。
不同结构对框架性能的影响如表4所示，在没有映射头和解码器，模型仅有编码器的情况下也有一定的性能，映射头和解码器都可以改善模型的性能，结合映射头和解码器进一步提高了模型的性能，与仅使用编码器的情况相比，在5个数据集上分别获得了6.8、2.3、2.7、9.6、5.3百分点的提升。在CiteSeer数据集上取消映射头的模型效果比取消解码器的模型效果还要好。需要注意的是，CiteSeer数据集存在部分节点度数为0的节点，这些节点干扰了图神经网络的性能表现，而取消映射头的模型因为还保留着解码器，仅依靠最大化视图与原图的互信息也能取得不错的效果，验证了本文方法的有效性。
表 4 不同结构对框架性能的影响Table 4 Impact of different structures on framework performance% 结构 数据集 映射头 编码器 Cora CiteSeer PubMed Amazon-Computers Amazon-Photo × × 77.2 70.8 80.1 79.3 89.0 √ × 82.7 72.1 82.5 85.1 93.8 × √ 81.5 72.6 80.7 85.9 90.4 √ √ 84.0 73.1 82.8 88.9 94.3 4.3 参数λ分析
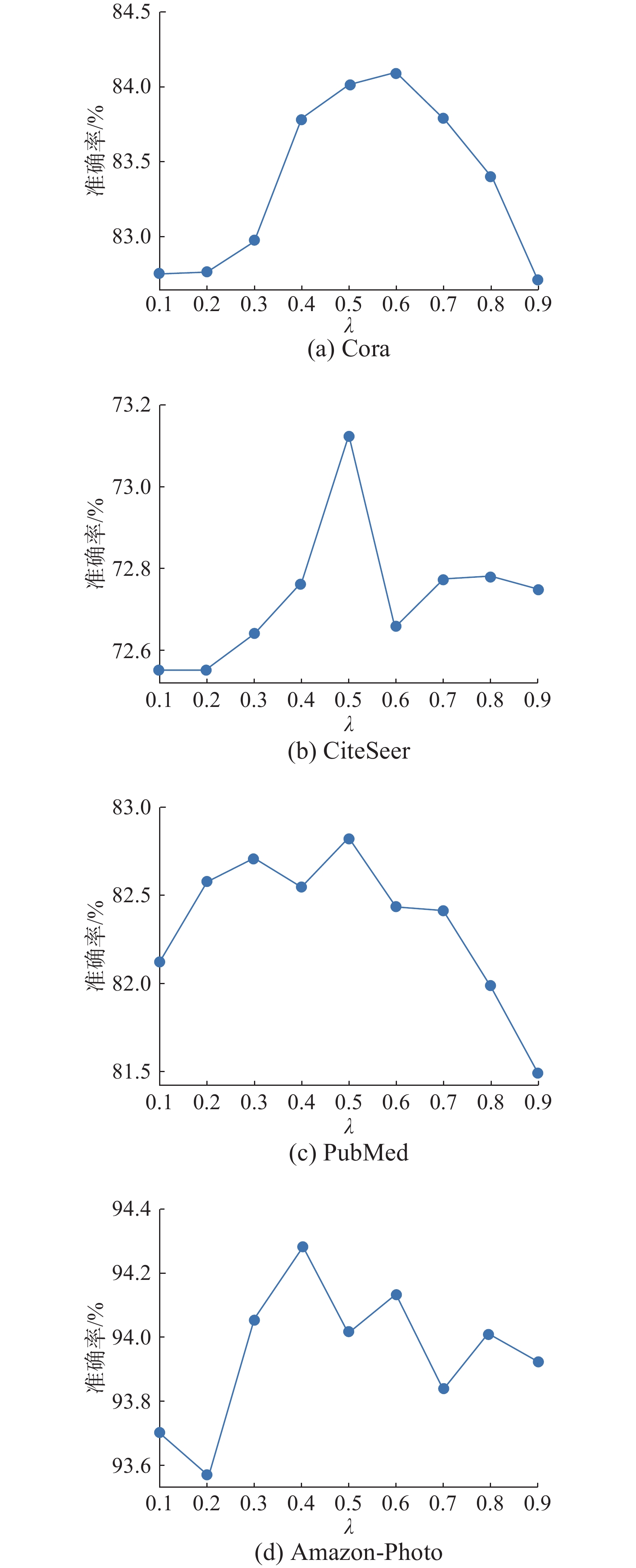
本节主要对GCLTMI框架的超参数λ进行分析，将λ的值设置在0.1～0.9，在Cora、CiteSeer、PubMed、Amazon-Photo这4个数据集上进行节点分类实验。根据图3给出的实验结果可知：λ越小模型越关注视图之间的互信息，越接近于常规的多视图对比学习模型；λ越大，模型越关注视图与原图之间的互信息。从整体来看，随着λ增大，模型分类准确率也随之增大。当λ为0.5左右时，模型分类准确率达到最大，说明视图之间的互信息和视图与原图之间的互信息都很重要，进一步验证了模型的有效性。
图 3 不同数据集上超参数λ对节点分类准确率的影响Fig. 3 Impact of hyperparameter λ on node classification accuracy on different datasets下载:
全尺寸图片
4.4 参数τ分析
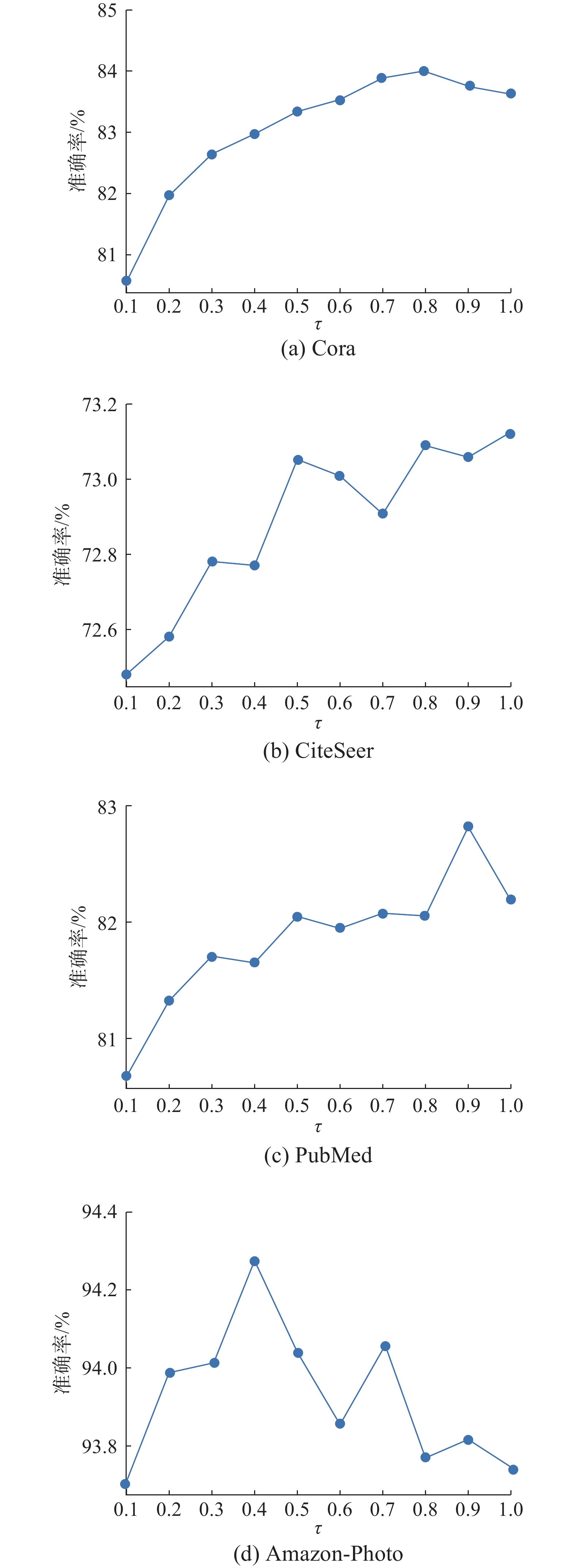
在对Cora、CiteSeer、PubMed、Amazon-Photo 4个数据集进行节点分类实验中，将τ的值设置在0.1~1，结果如图4中所示。从整体来看，随着温度系数τ值的增加，节点分类准确率也随之上升。当τ到达一定值的时候，节点分类准确率达到最高，然后随着τ的增加而下降。τ越小，模型越关注那些困难的负样本；τ越大，则模型不再特别关注那些困难的负样本。τ为1的时候，infoNCE损失函数退化为交叉熵损失函数。合适的温度系数τ设置可以帮助模型更好地学习这些困难的负样本，从而提高模型的性能。由于不同数据集的特点和性质可能不同，例如数据集大小、样本分布的不平衡性、样本噪声程度、任务的复杂性等，因此需要针对每个数据集选择适合的温度系数τ。
图 4 不同数据集上超参数τ对节点分类准确率的影响Fig. 4 Impact of hyperparameter τ on node classification accuracy on different datasets下载:
全尺寸图片
4.5 参数pE和pF对信息丢失的改善分析
为了验证本文方法可以改善传统数据增强生成的两个视图可能会丢失重要信息这一缺陷，本节使用了常规的多视图对比学习模型与GCLTMI进行对比实验。实验中，边丢弃概率pE和节点特征掩盖概率pF设置在0.1~0.9，将两个视图的pE和pF的值设置为相等，在Cora和CiteSeer数据集上进行节点分类实验，常规的多视图对比学习模型不设置解码器，其他结构与GCLTMI保持一致，与GCLTMI相比缺少最大化三元互信息。最终实验结果如图5所示，常规的多视图对比学习模型的分类结果如图5(a)、(c)所示，从图中可以看出，当参数pF不太大时，节点分类的准确率相对稳定。但如果参数pF过大，原图将被严重破坏，信息将会严重丢失。例如pF为0.9时，原图的节点特征基本被掩盖，从而导致生成的视图有大量没有足够信息的节点。在这种情况下，GNN编码器很难从节点邻域中学习到有用的信息，这将导致难以优化对比目标，严重影响性能。而参数pE对模型的影响相对于pF来说较小，模型主要依靠于节点特征进行学习。因此，常规的多视图对比学习模型对参数pE不敏感。
图 5 Cora、CiteSeer数据集上pE和pF对节点分类准确率的影响Fig. 5 Impact of pE and pF on node classification accuracy on Cora and CiteSeer datasets下载:
全尺寸图片
GCLTMI的节点分类结果如图5(b)、(d)所示，从图中可以看出，当参数较小时，节点分类的准确率相对稳定。这表明本文所提出的模型对这些参数不敏感，证明了对超参数扰动的鲁棒性。GCLTMI模型相对于常规的多视图模型有着全面的提升。当pF为0.9，pE过小的时候模型性能不佳。这是因为此时视图与原图的差异不够大，模型学习到很多冗余的信息。当pE较大时，视图与原图的差异较大，最大化视图与原图之间的互信息能有效地提升模型的性能，使模型仍然能够学习到有用的信息，保持较高的性能。
综上所述，当参数过大时，数据增强生成的视图丢弃了过多的边或节点特征，即丢失了过多的信息，其中可能包含有益于下游任务的重要信息。常规的多视图对比学习模型很难学习到有用的信息，导致性能下降。然而，本文提出的方法，由于引入了原图的信息，使得模型在视图丢失了过多的信息的情况下，仍然能够学习到有用的信息，验证了本文所提出方法的有效性。
5. 结束语
本文提出了一种全新的基于三元互信息的图对比学习框架。该框架通过最大化数据增强生成的两个视图与原图的三元互信息来学习表示。具体而言，该框架首先利用数据增强和编码器得到两个视图的节点表示矩阵，随后使用对比损失函数计算视图间的损失，最后经过解码器解码后计算视图和原图之间的损失，从而最大化三元互信息。本文在真实世界的不同的数据集上进行了全面的实验。实验结果表明，本文提出的GCLTMI方法均取得较好的结果，甚至超过了一些监督学习方法，证明了本文研究框架的有效性。
本文所提出的框架仅关注图的节点，在未来工作中，计划将框架迁移至其他任务上，使其能够处理边级或图级的任务。
-
图 1 常规图对比学习最大化互信息与GCLTMI最大化互信息示意
Fig. 1 Schematic diagram of conventional graph contrastive learning maximizing mutual information and GCLTMI maximizing mutual information
下载:
全尺寸图片
图 2 基于三元互信息的图对比学习框架
Fig. 2 Graph contrastive learning framework based on ternary mutual information
下载:
全尺寸图片
图 3 不同数据集上超参数λ对节点分类准确率的影响
Fig. 3 Impact of hyperparameter λ on node classification accuracy on different datasets
下载:
全尺寸图片
图 4 不同数据集上超参数τ对节点分类准确率的影响
Fig. 4 Impact of hyperparameter τ on node classification accuracy on different datasets
下载:
全尺寸图片
图 5 Cora、CiteSeer数据集上pE和pF对节点分类准确率的影响
Fig. 5 Impact of pE and pF on node classification accuracy on Cora and CiteSeer datasets
下载:
全尺寸图片
表 1 实验中使用的数据集的信息
Table 1 Information on the dataset used in the experiment
数据集 节点数 边数 特征数 分类数 Cora 2 708 5 429 1 433 7 CiteSeer 3 327 4 732 3 703 6 PubMed 19 717 44 338 500 3 Amazon-Computers 13 752 245 861 767 10 Amazon-Photo 7 650 119 081 745 8 表 2 不同数据集的超参数设置
Table 2 Hyperparameter settings for different datasets
数据集 pE, 1 pE, 2 pF, 1 pF, 2 λ τ Cora 0.4 0.4 0.3 0.3 0.6 0.8 CiteSeer 0.8 0.8 0.7 0.7 0.5 1.0 PubMed 0.2 0.4 0.3 0.2 0.5 0.9 Amazon-Computers 0.3 0.5 0.2 0.2 0.5 0.5 Amazon-Photo 0.3 0.3 0.3 0.3 0.4 0.4 表 3 所有方法在5个数据集上节点分类的准确率和标准差
Table 3 Accuracy and standard deviation of node classification for all methods on five datasets
% 方法 输入数据 Cora CiteSeer PubMed Amazon-Photo Amazon-Computers Raw Feature X 47.0±0.4 49.3±0.3 69.1±0.2 78.5±0.2 73.8±0.1 DeepWalk A 67.2±0.2 43.2±0.4 65.3±0.5 89.4±0.1 85.3±0.1 GCN A, X, Y 81.5±0.2 70.3±0.4 79.0±0.5 91.6±0.3 84.5±0.3 GAT A, X, Y 83.0±0.2 72.5±0.3 79.0±0.5 91.8±0.1 85.7±0.1 GAE A, X 74.9±0.4 65.6±0.5 74.2±0.3 91.0±0.1 85.1±0.4 VGAE A, X 76.3±0.2 66.8±0.2 75.8±0.4 91.5±0.2 85.8±0.3 DGI A, X 82.3±0.5 71.5±0.4 79.4±0.3 91.3±0.2 87.8±0.3 GMI A, X 83.0±0.2 72.4±0.2 79.9±0.4 90.6±0.2 82.2±0.4 GRACE A, X 83.1±0.2 72.1±0.1 79.6±0.5 91.9±0.3 86.8±0.2 MVGRL A, X 82.9±0.3 72.6±0.4 80.1±0.7 91.7±0.1 86.9±0.1 GCA A, X 81.8±0.2 71.9±0.9 81.0±0.3 92.4±0.4 87.7±0.1 BGRL A, X 82.7±0.4 71.3±0.8 80.3±0.9 91.6±0.5 87.4±0.4 G-BT A, X 82.6±0.5 72.0±0.3 80.5±0.2 92.6±0.6 87.9±0.4 COSTA A, X 83.3±0.3 72.0±0.3 81.2±0.2 92.6±0.5 88.3±0.1 SUGRL A, X 83.4±0.5 73.0±0.4 81.9±0.3 93.3±0.4 88.8±0.2 GCLTMI A, X 84.0±0.4 73.1±0.3 82.8±0.4 94.3±0.5 88.9±0.6 表 4 不同结构对框架性能的影响
Table 4 Impact of different structures on framework performance
% 结构 数据集 映射头 编码器 Cora CiteSeer PubMed Amazon-Computers Amazon-Photo × × 77.2 70.8 80.1 79.3 89.0 √ × 82.7 72.1 82.5 85.1 93.8 × √ 81.5 72.6 80.7 85.9 90.4 √ √ 84.0 73.1 82.8 88.9 94.3 -
[1] CAI Biao, ZHU Xinping, QIN Yangxin. Parameters optimization of hybrid strategy recommendation based on particle swarm algorithm[J]. Expert systems with applications, 2021, 168: 114388. doi: 10.1016/j.eswa.2020.114388 [2] CAI Biao, YANG Xiaowang, HUANG Yusheng, et al. A triangular personalized recommendation algorithm for improving diversity[J]. Discrete dynamics in nature and society, 2018, 2018: 3162068. [3] HU Fenyu, ZHU Yanqiao, WU Shu, et al. Hierarchical graph convolutional networks for semi-supervised node classification[C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. Macao: International Joint Conferences on Artificial Intelligence Organization, 2019: 4532–4539. [4] KIPF T, WELLING M. Semi-supervised classification with graph convolutional networks[C]//Proceedings of the 5th International Conference on Learning Representations. Toulon: ICLR, 2017: 1–14. [5] VELIKOVI P, CUCURULL G, CASANOVA A, et al. Graph attention networks[C]// Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018: 1–12. [6] LINSKER R. Self-organization in a perceptual network[J]. Computer, 1988, 21(3): 105–117. doi: 10.1109/2.36 [7] BACHMAN P, HJELM R D, BUCNWALTERuchwalter W. Learning representations by maximizing mutual information across views[C]//Proceedings of the 33rd International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2019: 15535–15545. [8] HE Kaiming, FAN Haoqi, WU Yuxin, et al. Momentum contrast for unsupervised visual representation learning[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 9726–9735. [9] TIAN Yonglong, KRISHNAN D, ISOLA P. Contrastive multiview coding[C]//European Conference on Computer Vision. Cham: Springer, 2020: 776–794. [10] COLLOBERT R, WESTON J. A unified architecture for natural language processing: deep neural networks with multitask learning[C]//Proceedings of the 25th International Conference on Machine Learning-ICML ’08. Helsinki: ACM, 2008: 160–167. [11] MNIH A, KAVUKCUOGLU K. Learning word embeddings efficiently with noise-contrastive estimation[C]// Proceedings of the 26th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2013: 2265–2273. [12] VELIKOVI P, FEDUS W, HAMILTON W L, et al. Deep graph infomax[C]//Proceedings of the 7th International Conference on Learning Representations. New Orleans: ICLR, 2018: 1–17. [13] HASSANI K, KHASAHMADI A H. Contrastive multi-view representation learning on graphs[C]//Proceedings of the 37th International Conference on Machine Learning. New York: Association for Computing Machinery, 2020: 4116–4126. [14] ZHU Yanqiao, XU Yichen, YU Feng, et al. Deep graph contrastive representation learning[EB/OL]. (2020–06–07)[2023–08–03]. http://arxiv.org/abs/2006.04131. [15] SONG Jingkuan, ZHANG Hanwang, LI Xiangpeng, et al. Self-supervised video hashing with hierarchical binary auto-encoder[J]. IEEE transactions on image processing: a publication of the IEEE signal processing society, 2018, 27(7): 3210–3221. doi: 10.1109/TIP.2018.2814344 [16] XU Xing, LU Huimin, SONG Jingkuan, et al. Ternary adversarial networks with self-supervision for zero-shot cross-modal retrieval[J]. IEEE transactions on cybernetics, 2020, 50(6): 2400–2413. doi: 10.1109/TCYB.2019.2928180 [17] VAN DEN OORD A, LI Yazhe, VINYALS O. Representation learning with contrastive predictive coding[EB/OL]. (2018–07–10) [2023–08–03]. http://arxiv.org/abs/1807.03748. [18] HJELM R D, FEDOROV A, LAVOIE-MARCHILDON S, et al. Learning deep representations by mutual information estimation and maximization[EB/OL]. (2018–08–20)[2023–08–03]. http://arxiv.org/abs/1808.06670. [19] CHEN Ting, KORNBLITH S, NOROUZI M, et al. A simple framework for contrastive learning of visual representations[C]//Proceedings of the 37th International Conference on Machine Learning. New York: ACM, 2020: 1597–1607. [20] GRILL J B, STRUB F, ALTCHÉ F, et al. Bootstrap your own latent: A new approach to self-supervised learning[C]//Proceedings of the 34th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2020: 21271–21284. [21] ZBONTAR J, JING L, MISRA I, et al. Barlow Twins: self-supervised learning via redundancy reduction[C]//Proceedings of the 38th International Conference on Machine Learning. New York: Association for Computing Machinery, 2021: 1231012320. [22] PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014: 701–710. [23] GROVER A, LESKOVEC J. Node2Vec: scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016: 855–864. [24] QIU Jiezhong, DONG Yuxiao, MA Hao, et al. Network embedding as matrix factorization: unifying deepwalk, line, pte, and node2vec[C]//Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining. New York: Association for Computing Machinery, 2018: 459–467. [25] HAMILTON W L, YING R, LESKOVC J. Inductive representation learning on large graphs[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2017: 1025–1035. [26] PENG Zhen, HUANG Wenbing, LUO Minnan, et al. Graph representation learning via graphical mutual information maximization[C]//Proceedings of The Web Conference 2020. New York: Association for Computing Machinery, 2020: 259–270. [27] ZHU Yanqiao, XU Yichen, YU Feng, et al. Graph contrastive learning with adaptive augmentation[C]//Proceedings of the Web Conference 2021. New York: Association for Computing Machinery, 2021: 2069–2080. [28] THAKOOR S, TALLEC C, AZAR M G, et al. Large-scale representation learning on graphs via bootstrapping[EB/OL]. (2021–02–12)[2023–08–03]. http://arxiv.org/abs/2102.06514. [29] BIELAK P, KAJDANOWICZ T, CHAWLA N V. Graph barlow twins: a self-supervised representation learning framework for graphs[EB/OL]. (2021–06–04)[2023–08–03]. https://arxiv.org/abs/2106.02466. [30] ZHANG Yifei, ZHU Hao, SONG Zixing, et al. COSTA: covariance-preserving feature augmentation for graph contrastive learning[C]//Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2022: 2524–2534. [31] KINGMA D, BA J. Adam: a method for stochastic optimization[C]//Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015: 1–15. [32] CLEVERT D A, UNTERTHINER T, HOCHREITER S. Fast and accurate deep network learning by exponential linear units (ELUs)[C]//Proceedings of the 4th International Conference on Learning Representations. San Juan: ICLR, 2016: 1–14. [33] KIPF T N, WELLING M. Variational graph auto-encoders[C]//Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: Association for Computing Machinery, 2021: 2827–2831. [34] MO Yujie, PENG Liang, XU Jie, et al. Simple unsupervised graph representation learning[C]//Proceedings of the 36th AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2022, 36(7): 7797–7805.
