Vein recognition algorithm combining K-nearest neighbor and graph iterative based on deep learning
-
摘要: 深度学习在计算机视觉中具有强大的特征表达能力，近年来广泛应用于静脉特征的提取与识别。通常，基于深度学习的静脉识别模型在训练阶段，每次仅输入1幅图像及其对应的标签，学习图像与标签之间的映射关系，然而，这种每次只处理单幅图像的方法，难以捕捉不同类别多幅静脉图像之间的关系。为了解决该问题，提出一种基于深度学习的K近邻图迭代静脉识别算法。用较优的深度学习模型提取掌静脉图像特征；利用K近邻算法通过特征距离在训练集中选出最近的K幅图像及其标签，通过这些特征向量生成标签传播矩阵和标签矩阵；利用图迭代算法预测待分类图像的标签，完成分类。在香港理工大学和同济大学提供的掌静脉数据集上进行实验，最高识别精度分别为99.67%和92.72%。Abstract: In recent years, deep learning has been widely applied in the extraction and recognition of vein features due to its excellent performance in computer vision. Usually, vein recognition models based on deep learning learn the mapping between a single input image and its label. This approach barely captures the connections between multiple vein images from different categories. To solve this problem, this study introduces a deep learning-based K-nearest neighbor iterative vein recognition algorithm. First, the algorithm extracts features from palm vein images by using advanced deep learning models. Then, it calculates the distances between an image to be classified and training images by using the K-nearest neighbor algorithm, which determines the K most similar images and their labels. A label propagation matrix and a label matrix are created from these feature vectors. Finally, a graph iteration algorithm is used to predict the classifications. Tests are conducted on palm vein datasets provided by Hong Kong Polytechnic University and Tongji University. Recognition accuracies of 99.67% and 92.72% are obtained for the two datasets, respectively.
-
随着互联网技术的广泛应用，用户对信息安全越来越重视。传统的身份识别技术，如密码、智能卡、钥匙存在身份信息易丢失、易盗用、易伪造等问题。而生物特征识别技术[1]能够有效地解决上述问题，并被广泛应用。生物特征识别技术是指利用计算机技术将人体固有的身体特征和行为特征进行取样，转化为数字信息进行身份认证。常用的生物特征识别技术分为外部生物特征和内部生物特征。外部生物特征包括指纹、人脸和手势等。外部生物特征比内部生物特征更明显，但更容易受到外部因素干扰。如指纹位于皮肤表面，当有伤口、污渍时会影响识别率；提取脸部特征时，光照变化、姿势、亮度、遮挡等因素，会对人脸识别率产生影响[2]；手势需要特别记忆，而且很容易泄露。内部生物特征主要是静脉特征，因静脉位于皮肤下层，日光下不易观察、不易受到外界因素干扰，同时具有非接触性和良好的稳定性，并且具有活体检测和难以复制伪造的优势，是目前最为安全的生物特征识别技术之一[3]。因此，静脉识别技术受到了广泛的关注。
静脉识别技术的研究可以追溯到2000年，日本医学研究员Kono等[4]首次将静脉图像用于身份验证。一般情况下，在可见光下静脉特征很难采集，然而掌静脉中的血红蛋白相对于皮肤、肌肉等其他生理组织对近红外光的吸收率更高，当采用波长为950 nm左右的红外光照射手掌时，会呈现出黑白分明的图像，因此可用相机获得清晰的静脉血管纹路图像[5]。目前，研究者已经提出了大量的静脉识别算法，它们可以分为2类：基于传统方法的静脉识别和基于深度学习的静脉识别。在基于传统方法的静脉识别算法研究方面，Qin等[6]提出通过在不同的样本上运行区域算子，利用横截面轮廓的连续性和对称性，提高静脉特征的鲁棒性；Song等[7]通过平均曲率方法，将静脉图像视为几何形状，并找到具有负平均曲率的谷状结构，能够有效地提取静脉纹理；Miura等[8]提出利用静脉图像横截面轮廓中局部最大曲率的方法，能够有效地提取纹理的中心线。Gabor滤波在静脉识别方面的应用有：Qiu等[9]在提取静脉纹路上采用了Gabor滤波的多方位方法，使得静脉图像的边缘更加清晰和连续；杨如民等[10]对静脉图像使用Hessian矩阵的特征值进行图像增强，随后采用了Gabor滤波提取静脉特征。局部二进制模式(local binary patterns, LBP)在静脉识别方面的应用有：Lee等[11]提取静脉图像的重点区域，进行仿射变换对齐图像后使用LBP获取静脉信息；Gu等[12]提出了一种使用迁移学习将LBP的特征与ResNet-50(residual networks-50)框架相融合的方法。然而传统的静脉识别方法是假设静脉图像服从某一分布，并基于该分布建立特征提取模型，所以这些方法只有在特定的情形下才能提高识别效率，泛化能力差。近年来基于深度学习的算法在计算机视觉方面取得了很好的特征表达性能。为了解决传统方法泛化性问题，研究人员将深度学习方法引入到了静脉识别任务中，例如：Qin等[13]利用卷积神经网络(convolutional neural networks, CNN)进行静脉模式分割，然后设计了一个全卷积神经网络来迭代恢复缺失的静脉特征；胡娜等[14]利用旋转不变模式的LBP算子与双向二维主成分分析(bilateral two-dimensional principal component analysis, B2DPCA)技术的手指静脉识别方法；Hou等[15]提出了一种提取类间和类内特征的网络模型。为了从低质量图像中提取辨别特征，提出了一种联合注意力模块注意力机制，以聚集特征图的空间和通道维度的信息，用于静脉识别；Yang等[16]提出了一种基于生成对抗网络的新方法，即手指静脉对抗生成网络(finger vein generative adversarial networks, FV-GAN)，FV-GAN从手指静脉图像和模式图的联合分布中学习，针对样本异常值的静脉识别问题具有更强的鲁棒性；Wang等[17]提出了金字塔视觉变换器，该方法在静脉图像的密集区上进行训练以获得高输出分辨率，能够有效地提取静脉特征，从而提高静脉识别精度。
深度学习方法有良好的特征表达能力，并能有效提取鲁棒的静脉特征。然而，现有的模型在训练过程中，每次只输入1个训练样本或者测试样本，所以这些模型很难学习到多个样本之间相关的信息，而这些信息往往有助于静脉特征的分类。为了解决这些问题，文献[18]提出一种基于K近邻的自然语言模型。在分类过程中，利用深度神经网络语言模型提取每个训练样本和测试样本的特征。然后，计算测试样本特征向量和训练样本特征向量之间的距离，得到测试样本的K个近邻的训练样本。通过聚合K个训练样本的标签得到测试集的预测标签。最后，将其与语言模型的预测概率进行结合得到测试样本的最终预测标签。
当前的深度学习分类方法旨在学习样本和标记之间的变换模型，而本文方法在标签预测过程中利用测试样本和所有训练样本的距离信息。换句话说，原始深度模型输入待测试静脉图像和标签，以学习图像和真实标签之间的映射。通过训练后，模型能够“记住”每一个样本的类别，即“记忆学习”。然而，该方法在学习过程中没有充分利用输入图像与训练图像特征之间的关系，而是单纯地“记住”每幅图像的标签知识，使得分类精度不高。本文将K+1幅训练静脉图像的特征向量构成的特征矩阵与对应真实标签构成的标签矩阵一块输入到模型中，预测待测试图像的标签。在测试过程中将1幅测试图像和K幅训练图像同时输入到模型中预测测试图像的标签，所以模型不需要“记忆”所有训练图像的信息，只需要判断测试图像与K幅图像关系，预测分类结果，降低了学习的难度。因此，将现有深度学习模型的“记忆学习”变成了新的“抄写学习”，提高模型的分类精度。
由此，本文提出一种新的“抄写学习”的静脉识别算法，即K近邻图迭代算法。该方法通过图迭代的思想充分利用样本之间的相关矩阵，对训练集合中数据的标签进行多次传播，实现对测试样本标签的预测，有效提高了静脉图像的分类精度。
1. 本文方法
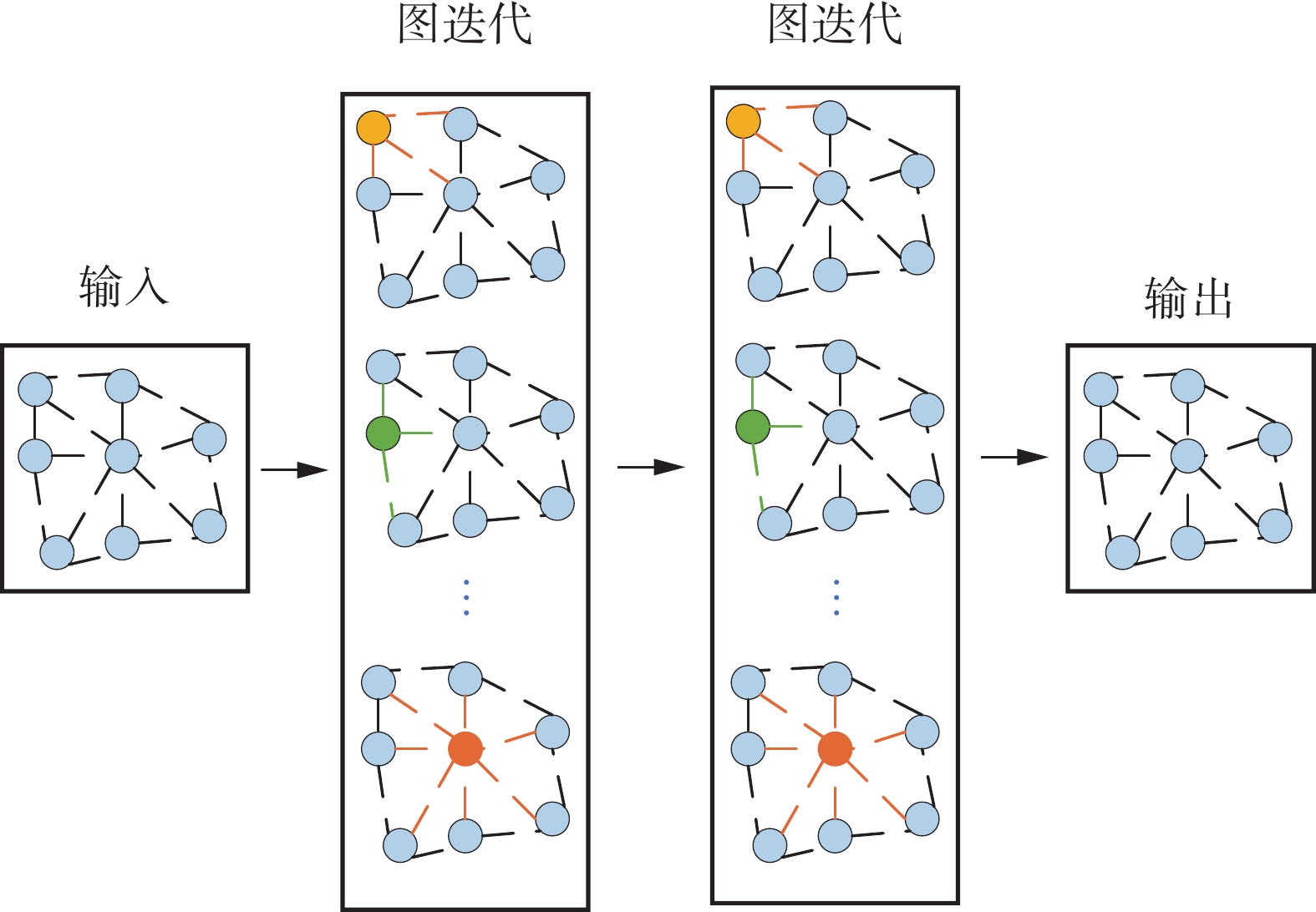
由于静脉图像的纹理特征维度较高，包含大量冗余信息，为了更好地提取静脉特征，首先需要将静脉图像从高维特征空间映射到低维特征空间。然后，通过计算待分类静脉图像的特征向量与数据集中其余静脉图像特征向量之间的距离，获得K幅最邻近的静脉图像。接着，利用图迭代算法学习特征向量之间的相关信息，最终实现对待分类样本标签的预测。本文算法总体流程如图1所示。
图 1 本文算法总体流程Fig. 1 Framework of our approach
下载:
全尺寸图片
1.1 编码器
由于原始静脉图像的维度较高，不利于后续KNN的聚类，因此本文利用基于深度学习的模型如：ResNet-50[19]、掌静脉卷积神经网络识别网络 (plam vein convolutional neural networks, PV-CNN)[20]和手指静脉识别与对抗欺骗网络(finger-vein recognition and antispoofing network, FVRAS-Net)[21]，来提取待分类图像和训练图像的鲁棒特征。设
$ [\boldsymbol{x}_1\ \boldsymbol{x}_2\ \cdots\ \boldsymbol{x}_s] $ 对应标签$ [y_1\ y_2\ \cdots\ y_s] $ 是数据集中C个类的样本。特别地，$ {{\boldsymbol{x}}_0} $ 和$ {{{y}}_0} $ 分别表示待分类静脉图像及其标签。特征提取模型表示为$ {\phi _{\boldsymbol{W}}}(\cdot) $ ，其中W是可训练权重。则分类静脉图像和训练集中的静脉图像的提取特征向量$ [\boldsymbol{z}_0\ \boldsymbol{z}_1\ \cdots\ \boldsymbol{z}_d] $ 公式为$$ {{\boldsymbol{z}}_i} = {\phi _{\boldsymbol{W}}}({{\boldsymbol{x}}_i}),i = \{ 1,2, \cdots ,s\} $$ (1) 式中
$ {\phi _{\boldsymbol{W}}}( \cdot ) $ 是一个特征提取器，能够将静脉图像从高维特征空间映射到低维特征空间，使映射后的特征向量具有良好的可分性。当数据集中静脉图像完成特征提取后，将所有图像的特征向量组成集合的形式。1.2 KNN算法
直接将待分类图像与训练集中所有样本输入图迭代模型中来预测标签，不仅计算量大，而且得到的关系矩阵非常稀疏，导致标签的预测精度低。因此在图迭代前，利用K-最近邻(K-nearest neighbors, KNN)算法确定K幅图像，并将这些图像与待分类图像输入到图迭代模型中进行训练或测试。
因此，本文提出了一种简单有效的方法，即利用KNN[22]算法得到待分类图像的K幅近邻图像，并利用它们的特征向量建立稠密的关系矩阵实现标签预测。首先利用式(1)中编码器提取待分类静脉图像
$ {{\boldsymbol{x}}_0} $ 和所有训练图像的特征得到它们的特征向量$ [\boldsymbol{z}_0\ \boldsymbol{z}_1\ \cdots\ \boldsymbol{z}_d] $ ，其中$ \boldsymbol{z}_m=\left[\boldsymbol{z}_{m1}\ \boldsymbol{z}_{m2}\ \cdots\ \boldsymbol{z}_{md}\right]^{\text{T}} $ 和$ \boldsymbol{z}_n=\left[\boldsymbol{z}_{n1}\ \boldsymbol{z}_{n2}\ \cdots\ \boldsymbol{z}_{nd}\right]^{\text{T}} $ 分别表示第m幅图像与第n幅图像的特征向量。计算第m幅图像与第n幅图像的曼哈顿距离$L({{\boldsymbol{z}}_m},{{\boldsymbol{z}}_n})$ ，公式为$$ L({{\boldsymbol{z}}_m},{{\boldsymbol{z}}_n}) = \sum\limits_{k = 1}^d | {{\boldsymbol{z}}_{mi}} - {{\boldsymbol{z}}_{ni}}| $$ 式中
$L$ 表示曼哈顿距离，$L$ 越小，表明静脉图像越相似。最后，利用得到距离确定与待分类图像最近的K个样本和对应标签，并建立集合$ \boldsymbol{\varOmega} $ ，公式为$$ {\boldsymbol{\varOmega }} = \left[ {\left( {{\boldsymbol{z}}_1^\prime ,{{{y}}_1}} \right),\left( {{\boldsymbol{z}}_2^\prime ,{{{y}}_2}} \right), \cdots ,\left( {{\boldsymbol{z}}_k^\prime ,{{{y}}_k}} \right)} \right] $$ (2) KNN算法简单、易实现，相比传统的模型只能单独学习每个样本的特征，很难综合学习不同样本之间的关系，通过KNN算法能够得到待分类图像的K幅近邻图像因此利用图迭代算法能够综合学习到不同样本之间的相关信息。
1.3 图迭代
利用KNN算法可以得到待分类样本的K幅近邻静脉图像及其标签，并建立标签矩阵。在此基础上，利用图迭代(graph iterative, GI)算法计算待分类样本及其K幅近邻图像之间的相似度矩阵，然后通过相似度矩阵对标签信息进行多次传播，实现对待分类静脉图像标签的预测，达到分类目的。图迭代算法的流程如图2所示。
图 2 图迭代流程Fig. 2 Framework of graph iterative下载:
全尺寸图片
首先通过得到的待分类样本与K幅近邻样本的One-Hot[23]标签，建立标签矩阵
${{\boldsymbol{H}}^{(k + 1) \times C}}$ ，其中C为类别数。然后，计算K+1(1幅待分类样本+K幅近邻样本)幅样本之间的相似度，建立相似度矩阵${\boldsymbol{A}} = {\left[ {{a_{mn}}} \right]^{(k + 1) \times (k + 1)}}$ 矩阵。2个特征向量${{\boldsymbol{z}}_m}$ 和$ {{\boldsymbol{z}}_n} $ 的相似度的计算公式为$$ a_{m n}= \begin{cases}\exp \left(-\left\|{\boldsymbol{z}}_m-{\boldsymbol{z}}_n\right\|^2 / 2\right), & m \neq n \\ 1, & m=n\end{cases} $$ (3) 利用相似度矩阵A计算迭代传播矩阵D，公式为
$$ {\boldsymbol{D}} = {{{{\boldsymbol{\varLambda}}}} ^{^{ - 1/2}}}A {{\boldsymbol{\varLambda}} ^{^{ - 1/2}}} $$ 式中
${\boldsymbol{\varLambda}} = {[{b_{mn}}]^{(k + 1) \times (k + 1)}}$ 为对角矩阵相应元素构成，由相似度矩阵A得到：$ {b_{mm}} = \displaystyle\sum\limits_{n = 1}^{k + 1} {{a_{mn}}} $ 。已知数据集共有C个类别，在训练集中的每张静脉图像的标签用One-Hot表示。利用标签矩阵
$ {{\boldsymbol{H}}^{(k + 1) \times {{C}}}} $ 初始化的标签传播矩阵${{\boldsymbol{H}}^0}$ ，即${{\boldsymbol{H}}^0}{ { = }}{{\boldsymbol{H}}^{(k + 1) \times C}}$ 。结合相似度矩阵和初始标签矩阵，对标签矩阵进行更新，即标签传播，公式为$$ {{\boldsymbol{H}}^t} = \mu {\boldsymbol{D}}{{\boldsymbol{H}}^{t - 1}} + (1 - \mu ){{\boldsymbol{H}}^0} $$ (4) 式中
$\mu \in (0,1)$ 是超参数，决定了初始化标签传播矩阵${{\boldsymbol{H}}^0}$ 对最终待分类图像标签的影响程度。通过式(4)的迭代预测待分类图像标签。当t=1时${{\boldsymbol{H}}^{t - 1}} = {{\boldsymbol{H}}^0}$ ，因此通过式(4)可以将初始化标签传播矩阵${{\boldsymbol{H}}^0}$ ，公式为$$ {{\boldsymbol{H}}^t} = {(\mu {\boldsymbol{D}})^t}{{\boldsymbol{H}}^0} + (1 - \mu )\sum\limits_{n = 0}^{t - 1} ( \mu {\boldsymbol{D}}{)^t}{{\boldsymbol{H}}^0} $$ (5) 标签传播矩阵可以对角化为
${\boldsymbol{H}} = {{\boldsymbol{Q}}^{\mathrm{T}}}{\boldsymbol{\varLambda}} {\boldsymbol{Q}}$ ，Q是正交矩阵。${\boldsymbol{\varLambda}} = {{\mathrm{diag}}} [{\lambda _1},{\lambda _2}, \cdots ,{\lambda _{k + 1}}]$ 是包含H特征值的对角矩阵。其中在$ \mu \in(0,1) $ 的设置下，式(5)的第1项由极限的定义得到，公式为$$ \begin{gathered} \mathop {\lim }\limits_{t \to \infty } {\left( {\mu {\boldsymbol{D}}} \right)^t}{{\boldsymbol{H}}^0} = \mathop {\lim }\limits_{t \to \infty } {\mu ^t}{\left( {{{\boldsymbol{Q}}^{\text{T}}}{\boldsymbol{\varLambda}} {\boldsymbol{Q}}} \right)^t}{{\boldsymbol{H}}^0} = \mathop {\lim }\limits_{t \to \infty } {\mu ^t}{{\boldsymbol{Q}}^{\text{T}}}{\boldsymbol{\varLambda}} { ^t}{\boldsymbol{Q}}{{\boldsymbol{H}}^0} {{ = 0}} \end{gathered} $$ (6) 式(5)中的第2项由极限的定义可以推导为
$\mathop {\lim }\limits_{t \to \infty } \displaystyle\sum\limits_{i = 0}^{t - 1} ( \mu {\boldsymbol{D}}{)^t} = {({\boldsymbol{E}} - \mu {\boldsymbol{D}})^{ - 1}}$ ，证明如下：$$ \begin{gathered} \left( {{\boldsymbol{E}} - \mu {\boldsymbol{D}}} \right)\mathop {\lim }\limits_{t \to \infty } \sum\limits_{i = 0}^{t - 1} {{{\left( {\mu {\boldsymbol{D}}} \right)}^i}} = \mathop {\lim }\limits_{t \to \infty } \left( {{\boldsymbol{E}} - \mu {\boldsymbol{D}}} \right) \\ \sum\limits_{i = 0}^{t - 1} {{{\left( {\mu {\boldsymbol{D}}} \right)}^i}} = \mathop {\lim }\limits_{t \to \infty } ({\boldsymbol{E}} - {(\mu {\boldsymbol{D}})^t}) {{ = }}{\boldsymbol{E}} \\ \end{gathered} $$ (7) 因此经过计算式(5)中第2项的极限，由式(7)计算后得到等价于公式为
$$ \mathop {\lim }\limits_{t \to \infty } (1 - \mu )\sum\limits_{t \to 0}^{t - 1} ( \mu {\boldsymbol{D}}{)^i}{{\boldsymbol{H}}^0} = (1 - \mu ){({\boldsymbol{E}} - \mu {\boldsymbol{D}})^{ - 1}}{{\boldsymbol{H}}^0} $$ 结合式(6)和式(7)的计算，可以得到当t趋于无穷大时，式(3)的标签传播过程将会收敛到
${{\boldsymbol{H}}^*}$ ，公式为$$ {{\boldsymbol{H}}^*} = (1 - \mu ){({\boldsymbol{E}} - \mu {\boldsymbol{D}})^{ - 1}}{{\boldsymbol{H}}^0} $$ (8) 因此，上述过程通过KNN算法选取待分类静脉图像的K幅近邻图像，然后由初始化标签传播矩阵
${{\boldsymbol{H}}^0}$ 和迭代传播矩阵D简化为式(8)，证明了图迭代算法可以有效聚合不同图像的标记信息，并最终收敛到$ {{\boldsymbol{H}}^*} $ ，从而实现对待分类图像标签的预测，达到分类目的。1.4 K近邻图迭代算法步骤
K近邻图迭代算法的具体步骤为：
1) 首先待分类静脉图像与训练集静脉图像通过编码器后分别得到待分类静脉图像特征向量和训练集特征向量集合。
2) 待分类静脉图像特征向量通过曼哈顿距离依次与训练集中的特征向量进行比较，从训练集中选取K幅近邻静脉图像的特征向量及相对应的标签，构成了特征向量矩阵及标签矩阵。
3)然后根据得到的特征向量及对应的标签，将迭代传播矩阵和标签传播矩阵经过图迭代算法，充分学习特征向量之间的关系。最后实现待分类静脉图像的预测。
本文算法无需训练过程，只要能将训练集和测试集中所有的图像，经过现有的静脉编码器得到相应的特征向量集合和训练集中图像标签集合，便于后续的测试过程的使用能够实现预测标签。
测试过程中，充分利用静脉图像特征向量之间的距离信息，将待分类静脉图像由曼哈顿距离在训练集中得到K幅近邻图像，待分类静脉图像与K幅近邻图像的特征矩阵和标签矩阵，构成的迭代传播矩阵和标签传播矩阵经图迭代算法得到待分类图像标签。
2. 实验结果分析
2.1 实验环境及数据集
为了验证本文K近邻图迭代静脉识别算法的有效性，分别在香港理工大学[20]和同济大学[24]提供的掌静脉数据集上进行验证。实验中，所有算法通过PyTorch深度学习平台实现，并在高性能计算机上进行算法性能验证。该计算机的硬件包括i7-7700K处理器、16 GB RAM和NVIDIA GTX 1080Ti显卡。
数据集A 香港理工大学掌静脉数据集，由250名志愿者提供的左手和右手掌静脉图像组成。样本数据分2次采集，间隔时间约为9天。每次从每个手掌上采集6幅静脉图像，2个采集阶段在每个手掌共采集了12幅静脉图像。最终，250人共提供了6 000 (250×2×6×2)幅掌静脉图像。每幅掌静脉图像的分辨率为200像素×200像素，灰度级为256。数据集A中部分图像如图3所示。
图 3 数据集A中的掌静脉图像Fig. 3 Palm vein image in dataset A下载:
全尺寸图片
数据集B 同济大学掌静脉数据集，由300名志愿者提供的左手和右手掌静脉图像组成。样本数据分2次采集，每次从每个手掌上采集10幅静脉图像，2次的时间间隔约为60天。因此，每个手掌在2次采集中共提供了20幅静脉图像。用这种方式，300人可以提供12 000(300×2×10×2)幅掌静脉图像。每幅掌静脉图像的分辨率为128像素×128像素，灰度级为256。数据集B中部分图像如图4所示。
图 4 数据集B中的掌静脉图像Fig. 4 Palm vein image in dataset B下载:
全尺寸图片
2.2 实验样本设置
在采集数据集A和数据集B中的掌静脉图像时，充分考虑了光照、温度、角度等因素的影响。使得获得的静脉图像更具有多样性。为了模拟实际应用，研究者们分别在不同时间段内对静脉图像进行采集，本文将第1次采集的静脉图像作为训练图像，第2次采集的静脉图像作为测试图像，并且得到训练集和测试集。在算法性能测试时，本文固定测试集样本个数。为了测试不同训练样本下算法的识别性能，本文将训练集分成多个子集。例如，在数据集A中，由于每个采集阶段各采集了
3000 幅图像，训练集和测试集分别包含了3000 幅图像。然后，从训练集每个手掌的6幅训练图像中随机选取3、4、5、6张分别作为训练样本，因此得到4个子训练集A3、A4、A5、A6。相似地，根据2个采集阶段，可以将数据集B拆分成训练集和测试集，各包含6000 幅图像。对于训练集中每个手掌10幅图像，随机选取2、4、6、8、10幅图像训练分类器，得到5个子训练集，分别表示为B2、B4、B6、B8、B10。为了测试算法性能，分别在子训练集上对模型进行训练，然后记录其在测试集上的识别结果。为了有效评估本文算法的性能，本文利用现有的深度学习模型如ResNet-50、PV-CNN和FVRAS-Net来提取静脉图像的特征，然后利用KNN计算K幅近邻图像，最后利用图迭代方法进行标签聚合，实现分类。另外，在对比实验中，本文也比较了当前先进的静脉识别算法如Lightweight[25]和SE-Net[26]的识别性能。
2.3 超参数的选择
本文算法中超参数K值和
$\mu $ 值选择的主要依据为，根据式(2)，超参数K值太小会减少信息的交换，反之K值太大会导致过度平滑。在式(4)中，超参数$\mu $ 的取值能够在迭代传播矩阵和标签传播矩阵对信息交换产生影响，$\mu $ 取值太小会接近于初始状态，$\mu $ 取值太大影响信息在传播矩阵之间的交流。根据文献[18]提出的一种基于K近邻的自然语言模型中K值的选择方法，本文确定参数K=15。在数据集A和数据集B中，每个类的样本最多为10张，因此在K>10情况下可以有效学习不同类别的关系，计算得到的待分类静脉图像得标签更有效。
当参数K=15时，不同的
$\mu $ 值也会对测试精度产生影响。在式(4)中$\mu $ 取值太小会导致标签过度依赖于初始状态${{\boldsymbol{H}}^0}$ ，待分类图像学习不到和其他类别的关系。相反地，$\mu $ 取值太大会强化和其他标签之间的关系，弱化了该类的标记信息。为了能够充分学习类别之间的关系，同时保持该类的类别信息不被弱化，参考文献[18]的参数设置，本文选择超参数$\mu $ =0.7。2.4 各种识别算法的性能比较
为了测试本文方法的有效性，本文分别利用现有的3种深度学习的方法ResNet-50、PV-CNN、FVRAS-Net提取静脉特征，然后结合本文的标签增强算法学习样本之间的关系，实现图像分类。在实验中，它们分别表示为ResNet-50+KNN+GI、PV-CNN+KNN+GI、FVRAS-Net+KNN+GI。本文也比较了目前先进的深度静脉识别算法Lightweight和SE-Net的识别结果。各种方法在2个静脉数据集上的识别结果如表1～2所示。
表 1 各种方法在数据集A中的识别精度Table 1 Accuracy of various approaches in dataset A% 训练子集 A3 A4 A5 A6 ResNet-50+KNN+GI 96.20 98.57 99.34 99.54 PV-CNN+KNN+GI 99.14 99.60 99.60 99.67 FVRAS-Net+KNN+GI 97.40 99.04 99.44 99.54 Lightweight 94.34 96.72 98.08 99.16 SE-Net 95.04 97.54 98.30 99.43 表 2 各种方法在数据集B中的识别精度Table 2 Accuracy of various approaches in dataset B% 训练子集 B2 B4 B6 B8 B10 ResNet-50+KNN+GI 55.47 68.69 76.24 79.02 85.23 PV-CNN+KNN+GI 70.57 86.04 91.79 92.72 89.34 FVRAS-Net+KNN+GI 62.65 77.05 83.37 84.84 87.64 Lightweight 44.95 63.67 70.90 75.07 77.62 SE-Net 41.10 64.49 71.44 75.37 78.21 本文方法在训练阶段输入待分类图像和多幅训练图像，模型能够学习到图像之间的关系，有助于分类。相似地，在测试阶段，需要同时输入待分类图像和各个类的训练图像，模型能够自动地计算待分类图像与其他类别图像关系，实现高精度分类。正如引言部分所述，现有深度学习模型主要集中在“记住”每幅图像的类别，测试时利用记忆知识进行分类。然而，本文的方法采用“抄写”方式存储了训练类别信息，测试时只需要将待测试图像和训练图像进行比较，实现图像的分类。
从表1和表2的实验结果可以看出，本文提出的方法在不同训练样本下的识别精度均高于现有2种识别方法Lightweight和SE-Net。例如，本文方法在数据集A中，每个类的训练样本为6时，其最高识别率达到99.67%。在数据集B中，每个类的训练样本为8时，其最高识别率达到92.72%，明显优于现有方法。主要原因在于现有的深度学习方法每次独立输入1幅图像进行训练，很难学习到不同样本或类别之间的关系。
从表1和表2可以看出，随着每个类训练图像的增加，所有方法的识别精度越来越高。这主要由于训练样本的增加，使得各个深度学习模型训练更加充分，同时增加训练样本使得模型能够学习到样本的多样性信息。总体上，各种方法在数据集A上的实验结果优于数据集B上的实验结果。例如，所有方法在数据集A上的最低识别精度高于94%，而在数据集B上的最高识别精度为92.72%。造成该实验结果的主要原因可能是数据集A中的图像包含的变化较少，分布较为相似，而数据集B中图像对比较低，同一类别图像的差异较大。2个数据集的建立过程也可以支撑该结论，如数据集A中图像的2个采集阶段时间间隔约为9天，而数据集B中2个阶段的时间间隔约60天。一般来说间隔较长时间采集的图像之间的差异更大，因此对于数据集B中静脉图像识别难度更具有挑战性。
2.5 消融实验
为了验证本文方法的KNN和GI模块的识别性能，本文在2个数据集上进行了消融实验。首先本文验证了原始的3个分类器ResNet-50、PV-CNN、FVRAS-Net的性能。然后，利用3种分类器作为特征提取器，并结合KNN来提取待测样本与训练样本的相关信息，并进行分类。为了便于描述，将该方法表示为“原始分类器+KNN”。另外，本文将3种分类作为特征提取器，结合KNN计算近邻样本，在此基础上，利用图迭代来学习样本的相关信息，实现分类。该方法表示为“原始分类器+KNN+GI”，即为本文的方法。所有方法在2个数据集上的实验结果如表3和表4所示。
表 3 在数据集A中消融实验Table 3 Ablation experiment in dataset A% 分类方法 原始分类器 原始分类器+
KNN原始分类器+
KNN+GIResNet-50 99.47 99.54 99.54 PV-CNN 99.63 99.40 99.67 FVRAS-Net 98.70 98.24 99.54 表 4 在数据集B中消融实验Table 4 Ablation experiment in dataset B% 分类方法 原始分类器 原始分类器+
KNN原始分类器+
KNN+GIResNet-50 82.10 81.65 85.23 PV-CNN 86.27 85.95 89.34 FVRAS-Net 78.83 83.75 89.64 从数据集A和数据集B中的实验结果可以看出“原始分类器+KNN”的方法实优于原始3个分类器的性能。换句话说，利用KNN计算样本关系可以提高分类器的识别精度。另外，相比于KNN，基于图迭代模型的识别方法可以学习样本之间的相关性，提高识别精度。因此，“原始分类器+KNN+GI”方法的识别精度总体上高于“原始分类器+KNN”的方法，尤其是在数据集B上，前者比后者的平均识别率高约4百分点。
3. 结束语
本文提出了一种基于K近邻图迭代静脉识别算法，它包括特征提取模块、KNN算法和图迭代算法3个部分。首先利用现有的深度学习方法提取静脉图像特征，然后利用KNN算法计算测试图像的近邻图像，最后通过图迭代方法学习样本之间的关系。相比于现有的基于深度学习的静脉识别方法，该方法能够学习待分类样本与每个类训练样本之间的关系，提高静脉识别系统的识别精度。在2个公共的掌静脉数据集上对本文算法的性能进行测试。实验结果表明，本文的方法优于现有的基于深度学习的静脉识别算法，能够有效捕捉图像之间的关系，提高静脉识别系统的性能。然而，本文使用的图迭代算法依赖专门的算法设计和公式定义，不够灵活。希望在未来静脉识别的过程中能够设计出一种自主学习特征向量关系的算法，进一步提高静脉识别系统的性能。
-
图 1 本文算法总体流程
Fig. 1 Framework of our approach
下载:
全尺寸图片
图 2 图迭代流程
Fig. 2 Framework of graph iterative
下载:
全尺寸图片
图 3 数据集A中的掌静脉图像
Fig. 3 Palm vein image in dataset A
下载:
全尺寸图片
图 4 数据集B中的掌静脉图像
Fig. 4 Palm vein image in dataset B
下载:
全尺寸图片
表 1 各种方法在数据集A中的识别精度
Table 1 Accuracy of various approaches in dataset A
% 训练子集 A3 A4 A5 A6 ResNet-50+KNN+GI 96.20 98.57 99.34 99.54 PV-CNN+KNN+GI 99.14 99.60 99.60 99.67 FVRAS-Net+KNN+GI 97.40 99.04 99.44 99.54 Lightweight 94.34 96.72 98.08 99.16 SE-Net 95.04 97.54 98.30 99.43 表 2 各种方法在数据集B中的识别精度
Table 2 Accuracy of various approaches in dataset B
% 训练子集 B2 B4 B6 B8 B10 ResNet-50+KNN+GI 55.47 68.69 76.24 79.02 85.23 PV-CNN+KNN+GI 70.57 86.04 91.79 92.72 89.34 FVRAS-Net+KNN+GI 62.65 77.05 83.37 84.84 87.64 Lightweight 44.95 63.67 70.90 75.07 77.62 SE-Net 41.10 64.49 71.44 75.37 78.21 表 3 在数据集A中消融实验
Table 3 Ablation experiment in dataset A
% 分类方法 原始分类器 原始分类器+
KNN原始分类器+
KNN+GIResNet-50 99.47 99.54 99.54 PV-CNN 99.63 99.40 99.67 FVRAS-Net 98.70 98.24 99.54 表 4 在数据集B中消融实验
Table 4 Ablation experiment in dataset B
% 分类方法 原始分类器 原始分类器+
KNN原始分类器+
KNN+GIResNet-50 82.10 81.65 85.23 PV-CNN 86.27 85.95 89.34 FVRAS-Net 78.83 83.75 89.64 -
[1] 谭振林, 刘子良, 黄蔼权, 等. 掌静脉识别的深度学习方法综述[J]. 计算机工程与应用, 2024, 60(6): 55−67. doi: 10.3778/j.issn.1002-8331.2306-0168 TAN Zhenlin, LIU Ziliang, HUANG Aiquan, et al. Review of deep learning methods for palm vein recognition[J]. Computer engineering and applications, 2024, 60(6): 55−67. doi: 10.3778/j.issn.1002-8331.2306-0168 [2] 赵程, 马彦波, 景荣, 等. 基于面部识别和掌静脉识别的AFC支付技术研究[J]. 智能城市, 2023, 9(5): 13−17. ZHAO Cheng, MA Yanbo, JING Rong, et al. Research on AFC payment technology based on facial recognition and palmar vein recognition[J]. Intelligent city, 2023, 9(5): 13−17. [3] WU Zhendong, TIAN Longwei, LI Ping, et al. Generating stable biometric keys for flexible cloud computing authentication using finger vein[J]. Information sciences, 2018, 433: 431−447. [4] KONO M. A new method for the identification of individuals by using of vein pattern matching of a finger[C]//Proc Fifth Symposium on Pattern Measurement. Yamaguchi: CiNii, 2000: 9−12. [5] 刘伟业, 鲁慧民, 李玉鹏, 等. 指静脉识别技术研究综述[J]. 计算机科学, 2022, 49(S1): 1−11. doi: 10.11896/jsjkx.210400056 LIU Weiye, LU Huimin, LI Yupeng, et al. Survey on finger vein recognition research[J]. Computer science, 2022, 49(S1): 1−11. doi: 10.11896/jsjkx.210400056 [6] QIN Huafeng, LAN Qin, YU Chengbo. Region growth–based feature extraction method for finger-vein recognition[J]. Optical engineering, 2011, 50(5): 057208. doi: 10.1117/1.3572129 [7] SONG W, KIM T, KIM H C, et al. A finger-vein verification system using mean curvature[J]. Pattern recognition letters, 2011, 32(11): 1541−1547. doi: 10.1016/j.patrec.2011.04.021 [8] MIURA N, NAGASAKA A, MIYATAKE T. Extraction of finger-vein patterns using maximum curvature points in image profiles[J]. IEICE - transactions on information and systems, 2007, E90-D(8): 1185−1194. [9] QIU Xinwei, KANG Wenxiong, TIAN Senping, et al. Finger vein presentation attack detection using total variation decomposition[J]. IEEE transactions on information forensics and security, 2018, 13(2): 465−477. doi: 10.1109/TIFS.2017.2756598 [10] 杨如民, 许琳英, 余成波. 基于Hessian矩阵和Gabor滤波的手指静脉特征提取[J]. 兵器装备工程学报, 2019, 40(3): 103−107, 111. YANG Rumin, XU Linying, YU Chengbo. Finger vein feature extraction based on Hessian matrix and Gabor filtering[J]. Journal of ordnance equipment engineering, 2019, 40(3): 103−107, 111. [11] LEE E C, LEE H C, PARK K R. Finger vein recognition using minutia-based alignment and local binary pattern-based feature extraction[J]. International journal of imaging systems and technology, 2009, 19(3): 179−186. doi: 10.1002/ima.20193 [12] GU Gaojie, BAI Peirui, LI Hui, et al. Dorsal hand vein recognition based on transfer learning with fusion of LBP feature[C]//Biometric Recognition. Cham: Springer, 2021: 221−230. [13] QIN Huafeng, EL YACOUBI M A, LIN Jihai, et al. An iterative deep neural network for hand-vein verification[J]. IEEE access, 2019, 7: 34823−34837. doi: 10.1109/ACCESS.2019.2901335 [14] 胡娜, 马慧, 湛涛. 融合LBP纹理特征与B2DPCA技术的手指静脉识别方法[J]. 智能系统学报, 2019, 14(3): 533−540. doi: 10.11992/tis.201801014 HU Na, MA Hui, ZHAN Tao. Finger vein recognition method combining LBP texture feature and B2DPCA technology[J]. CAAI transactions on intelligent systems, 2019, 14(3): 533−540. doi: 10.11992/tis.201801014 [15] HOU Borui, YAN Ruqiang. ArcVein-arccosine center loss for finger vein verification[J]. IEEE transactions on instrumentation and measurement, 2021, 70: 5007411. [16] YANG Wenming, HUI Changqing, CHEN Zhiquan, et al. FV-GAN: finger vein representation using generative adversarial networks[J]. IEEE transactions on information forensics and security, 2019, 14(9): 2512−2524. doi: 10.1109/TIFS.2019.2902819 [17] WANG Wenhai, XIE Enze, LI Xiang, et al. Pyramid vision transformer: a versatile backbone for dense prediction without convolutions[C]//2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 548−558. [18] KHANDELWAL U, LEVY O, JURAFSKY D, et al. Generalization through memorization: nearest neighbor language models[EB/OL]. (2019−11−01)[2023−07−12]. https://arxiv.org/abs/1911.00172. [19] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770−778. [20] QIN Huafeng, EL-YACOUBI M A, LI Yantao, et al. Multi-scale and multi-direction GAN for CNN-based single palm-vein identification[J]. IEEE transactions on information forensics and security, 2021, 16: 2652−2666. doi: 10.1109/TIFS.2021.3059340 [21] YANG Weili, LUO Wei, KANG Wenxiong, et al. FVRAS-net: an embedded finger-vein recognition and AntiSpoofing system using a unified CNN[J]. IEEE transactions on instrumentation and measurement, 2020, 69(11): 8690−8701. doi: 10.1109/TIM.2020.3001410 [22] 袁臣虎, 刘铁根, 李秀艳. 基于kNN-SVM的手背静脉虹膜和指纹融合身份识别[J]. 光电工程, 2013, 40(4): 101−105. YUAN Chenhu, LIU Tiegen, LI Xiuyan. Identification algorithm for fusion of hand vein iris and fingerprint based on kNN-SVM[J]. Opto-electronic engineering, 2013, 40(4): 101−105. [23] 刘辉玲, 陶洁, 邱磊. 基于Python的One-hot编码的实现[J]. 武汉船舶职业技术学院学报, 2021, 20(3): 136−139. LIU Huiling, TAO Jie, QIU Lei. Implementation of one-hot encoding based on python[J]. Journal of Wuhan Institute of Shipbuilding Technology, 2021, 20(3): 136−139. [24] ZHANG Lin, CHENG Zaixi, SHEN Ying, et al. Palmprint and palmvein recognition based on DCNN and a new large-scale contactless palmvein dataset[J]. Symmetry, 2018, 10(4): 78. doi: 10.3390/sym10040078 [25] SHEN Jiaquan, LIU Ningzhong, XU Chenglu, et al. Finger vein recognition algorithm based on lightweight deep convolutional neural network[J]. IEEE transactions on instrumentation and measurement, 2022, 71: 1−13. [26] HU Jie, SHEN Li, SUN Gang. Squeeze-and-excitation networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 7132–7141.
