Community search schemata and their classification systems based on attribute graphs
-
摘要: 当前在属性图中的社区搜索方法较多、类型繁杂，没有系统的分类方式，约束了社区搜索的应用。为明确属性图社区搜索的类别，对属性图社区搜索分类方法进行研究。首先，首次提出属性图社区搜索模式的概念，深入分析属性图社区搜索模式之间存在的联系，提出属性图社区搜索模式的等价、从属、交叉、全异4种关系；其次，以搜索模式的输入图属性、输出图拓扑结构和各属性图社区搜索模式的实际意义为基础，构建两层分类体系，第1层是由输入属性图相同的模式集合构成的集族，这里的输入属性图包括时序、空间、关键字、权值、空属性图，第2层是由输出图拓扑结构及实际意义定位到的每一个具体的属性图社区搜索模式；然后，针对第2层中每一种模式，给出对应社区搜索算法的对比分析结果；最后，对所有属性图社区搜索模式的特性集中分析。总体而言，属性图社区搜索模式不仅为理解和分析复杂网络结构提供有力工具，也为解决实际问题提供新的视角和方法。Abstract: At present, there are many community search methods in the attribute graph, and there is no systematic classification method, which restricts the application of community search. In order to clarify the category of community search in attribute graph, the classification method of attribute community search is studied. Firstly, the concept of attribute community search schema is proposed to analyze the relationship between attribute community search schemata in depth, proposing four relationships of community search mode of attribute graph: equivalence, affiliation, intersected and exclusion. Secondly, a two-layer classification system is constructed based on the input graph attributes of the search mode, the topology of the output graph and the practical significance of the search mode of each attribute community. The first layer is a family of sets composed of the same set of schemata in the input attribute graph. The input attribute graph here includes sequence, space, keyword, weight, and empty attribute graph. The second layer is each specific community search schema located by the topology and practical meaning of the output graph. Then, the comparative analysis result of corresponding community search algorithm is given for each schema in the second layer. Finally, the characteristics of all the community search modes of attribute graphs are analyzed centrally. Overall, the attribute graph community search pattern not only provides a powerful tool for understanding and analyzing complex network structures, but also provides a new perspective and method for solving practical problems.
-
Keywords:
- graph theory /
- attributed graph /
- community search /
- schema /
- cohesiveness /
- topology /
- relation /
- community search algorithm
-
图作为有效描述大数据的数据结构，扮演着越来越重要的角色。现实世界中的许多数据及其关系都可以用属性图描述，进而通过属性图上的研究来解决基于大数据的实际问题。例如蛋白质网络分析[1]、社交网络分析[2]、知识图谱分析[3]等。社区搜索问题由Sozio等[4]于2010年提出，是近年来的图计算领域的热门研究课题。社区搜索问题的输入为图，输出为满足一定内聚性的连通子图（即社区）。研究者们从不同角度、层次对社区搜索问题进行了研究。早期社区搜索问题主要关注结构内聚性，近年来随着在应用领域的深入，属性内聚性也成为关注点之一。社区的结构内聚性是以不同的拓扑结构来约束的，经典的子图拓扑结构按照其出现顺序，可分为k-ECC、k-clique、k-core和k-truss。属性图中的社区搜索研究关注的属性包括空属性以及节点的关键字、位置、时序、权值和边的权值属性等。
当前对社区搜索的研究，集中在提出并解决具有不同输入图属性与输出图结构组合的新的社区搜索问题，或完善现有社区搜索问题的解决方法，从而集中了大量类型繁杂的的社区搜索问题。而这些社区搜索问题之间隐含的联系及可能存在的关系并没有引起重视。本文总结了社区搜索的3大要素：输入初始图的属性、输出子图的拓扑结构及各社区搜索问题具体实际意义，将各类具有共性的社区搜索问题定义成属性图社区搜索模式，并分析归纳了这些模式之间的4种关系：等价、从属、交叉、全异。这种定义及分类能够快速定位到所需要的最合适的社区搜索模式。除此之外，这些属性图社区搜索模式种类繁多且没有系统的分类方式，极大程度地限制了社区搜索的应用。本文提出了属性图社区搜索模式的两层分类体系。第1层基于各模式输入图的属性，将所有属性图社区搜索模式分为6个集族；第2层按照返回社区拓扑结构及具体实际意义，从这些集族拆分出具体的属性图社区搜索模式。
本文第1节分别定义了社区搜索模式及属性图社区搜索模式，并根据4种拓扑结构定义了各属性图社区搜索模式之间的关系；第2节提出了对属性图社区搜索模式的两层分类体系，并对分别对空属性与时序、空间、关键字、权值社区搜索模式进行了具体定义及归纳，分析了现阶段属于各模式的算法，并对个模式之间的关系分析后系统表述；第3节对非空属性图社区搜索模式对比分析，直观展示各模式的重点特征，可根据需求快速选择合适的社区搜索模式，给出该使用案例并在真实数据集中运行；第4节对社区搜索模式的发展提出自己的建议，为后来研究者的深入研究提出几种的思路。
1. 属性图社区搜索模式及其关系
本节形式化定义了各种属性图并根据社区搜索的3大要素（输入初始图的属性、输出子图的拓扑结构、各社区搜索问题的实际意义）将各类具有共性的社区搜索问题定义成属性图社区搜索模式，并定义了这些模式之间的4种关系。
定义1 属性图：一个属性图是G=(V，E，Σ，L)，其中V为点集，E为边集，(Σ=C)∨(Σ=K)∨(Σ=W)，C为二维坐标集，K为关键字集，W为权值集，L为顶点或边对应的函数。
社区搜索模式中所用到的输入属性图可分为空属性图、时序属性图、位置属性图、关键字属性图和权值属性图。
定义2 空属性图
当一个属性图GO=(V，E，Σ，L)中Σ为空集且∀e∈E是一个二元组(u,v)时，称G为简单图或空属性图。
定义3 时序属性图
时序属性图GT=(V，E，Σ，L)是一个包含点集V、边集E的图，∀e∈E是一个三元组(u,v,t)。其中u,v∈V，t是u和v交互的时间点。
定义4 位置属性图
位置属性图GC=(V，E，Σ，L)是一个包含点集V、边集E的图，Σ=C，C中元素为二维坐标系(vx,vy)，∀v∈V与Σ中元素通过函数L一一对应。
定义5 关键字属性图
关键字属性图GK=(V，E，Σ，L)是一个包含点集V、边集E的图，Σ=K，K为关键字集，∀v∈V与Σ中元素通过函数L一一对应。
定义6 权值属性图
权值属性图GW=(V，E，Σ，L)是一个包含点集V、边集E的图，Σ=W，W为权值集。∀v∈V与Σ中元素Wv通过函数L一一对应时，称该权值属性图为点权属性图；当∀e∈E与Σ中元素We通过函数L一一对应时，称该权值属性图为边权属性图。
定义7 社区搜索[4]
给定一个无向图G(V，E)、一个查询节点集Q⊆V、一个优度函数f，需要找到一个G的诱导子图H(VH，EH)，满足如下性质：1)VH包含Q；2)H是连通的；3)所有的可行解中f(H)值满足给定约束条件。
社区搜索模式（community search schema，CSS）是一类社区搜索的集合。
定义8 属性图社区搜索
给定一个属性图G=(V，E，Σ，L)，这里的属性图可为定义2~6中的空属性图、时序属性图、位置属性图、关键字属性图或权值属性图，一个查询节点集Q⊆V，一个属性评分函数f，需要找到一个G的诱导子图H(VH，EH，ΣH，LH)，满足如下性质：1)VH包含Q；2) H是连通的，且满足一定拓扑结构；3)所有的可行解中f(H)值最大或最小。
属性图社区搜索模式（attribute community search schema，ACSS）是一类属性图社区搜索问题的集合，表示为
$S{\text{ = \{ }}q{\text{|}}\forall {\text{v}} \in S{\text{\} }}$ 为同一类属性图社区搜索问题${\text{\} }}$ 。由于属性图可以分为空属性图、时序属性图、位置属性图、关键字属性图、权值属性图，所以属性图社区搜索模式可分为空属性图社区搜索模式、时序属性图社区搜索模式、位置属性图社区搜索模式、关键字属性图社区搜索模式和权值属性图社区搜索模式。
社区搜索的输出社区需要满足一定的结构内聚性，社区的结构内聚性是以不同的拓扑结构来约束的，下面是4种常见拓扑结构。
定义9 k-core
k-core是一个给定图G的最大子图H，满足∀v∈V，degH(v)。
定义10 k-truss
k-truss是一个给定图G的最大子图，且满足∀e∈EH，sup(e,H)≥k−2。
定义11 k-clique
给定图G的最大子图H(VH，EH)，且满足任意的vi,vj∈VH之间都有一条边。
定义12 边连通度
对于一个给定图G=(V，E)，在去掉任意k−1条边后，所得的子图仍然连通，但去掉k条边后不连通，则称k为图G的边连通度，记为λ(G)。
定义13 k-ECC
k-ECC是一个满足边连通度为k的G的子图H。
由定义9、10、11、13可知[5]：
1）k-clique一定是k-truss的子图；
2）k-truss的连通子图一定是特定k-ECC的子图；
3）k-truss一定是(k−1)-core的子图；
4) k-ECC一定是k-core的子图。
所以，上述4种结构的内聚度大致为：k-core≤k-ECC≤k-truss≤k-clique。
属性图社区搜索模式最重要的3点要素为输入初始图的属性、输出社区的拓扑结构和各社区搜索问题的具体实际意义。下文根据前2种要素为社区搜索模式（下称“模式”）提出4种社区搜索模式关系（下称“关系”），包括等价、从属、交叉、全异。
定义14 等价关系
若模式A与模式B中所有问题的输入初始图的属性、输出社区的拓扑结构都相同，则称模式A与模式B具有等价关系，那么在无特殊情况下，模式A、B中的算法都可以解决模式A和B中的问题，如2.3.1节中模式19与模式21。
定义15 从属关系
若模式A与B中所有问题的输入初始图的属性相同，且模式A与模式B中所有问题对应返回社区的拓扑结构分别为k-clique和k-truss、k-clique和k-core、k-truss和k-core或k-ECC和k-core时，则称模式B从属于模式A。无特殊情况下，模式B所返回的社区为模式A的可行解，如2.3.2节中模式25与模式31。
定义16 交叉关系
若模式A与模式B中所有问题的输入初始图的属性相同，输出社区的拓扑结构之间对应关系不属于定义15中提到的4种关系，则称模式A与模式B具有交叉关系。无特殊情况下，模式A所返回的社区与模式B所返回的社区存在一定的关联，如2.3.2节中模式22与模式24。
定义17 全异关系
若模式A与模式B中所有问题的输入初始图的属性不同，则称模式A与模式B全异。
2. 两层分类体系
属性图社区搜索模式的3要素为初始输入属性图的属性、输出子图的拓扑结构以及各属性图社区搜索问题的实际意义，本节根据这3要素提出了属性图社区搜索模式的两层分类体系。依据定义2~6，本文将输入属性图的属性作为第1层分类依据将各属性图社区搜索模式分成输入图属性为时序、位置、关键字、点权、边权和空属性的集族。以输出子图的拓扑结构及属性图社区搜索模式的实际意义作为第2层分类依据，将第1层分出的6个集族再次具体分为各类具体的属性图社区搜索模式,具体见定义18、25、29、31、34。
如图1所示，所有属性图社区搜索模式在第1层中被划分为6个集族，其中权值属性图社区搜索模式按照输入属性图的权值为顶点的权值或是边的权值可进一步细分为点权以及边权属性图中的社区搜索模式。第2层中除空属性图社区搜索模式外的4类属性图搜索模式按照返回社区的拓扑结构及模式的实际意义将其分为各个具体的社区搜索模式；由于空属性图社区搜索模式大多不存在实际意义，按照返回社区的拓扑结构分为各个具体的社区搜索模式。
图 1 两层分类体系Fig. 1 Two-tier classification system
下载:
全尺寸图片
2.1 空属性图社区搜索模式
早期的社区搜索问题研究很少考虑在实际中的应用，初始输入图多为简单图。本节基于这些简单图上的社区搜索问题提出了空属性图社区搜索模式，并按照返回社区拓扑结构的不同将其划分。
定义18 空属性图社区搜索模式
给定一个空属性图GO=(V，E，Σ，L)、一个查询节点集Q⊆V、一个属性评分函数f，需要找到一个G的诱导子图H(VH，EH，ΣH，LH)，满足如下性质：1) VH包含Q；2)H是连通的，且满足一定拓扑结构；3) 所有的可行解中f(H)值最大。
2.1.1 基于k-core的空属性图社区搜索模式
模式1 规模无限制的社区搜索[4]（size unbounded community search, SBCS）模式
给定一个空属性图GO=(V，E，Σ，L)、一个查询节点集Q⊆V、一个优度函数f，返回一个GO的子图H(VH,EH)，满足以下性质：1) Q⊆VH；2) H是连通的；3)在所有可行解Hi中H具有最大的最小度。
SBCS模式包含全局搜索算法、局部搜索算法以及基于ShellStruct索引结构和CoreStruct索引结果的搜索算法[6]共3种算法。SBCS模式应用在大型图上返回的结果往往不太理想
模式2 规模有限制的社区搜索[4]（size bounded community search, SUCS）模式
给定1个空属性图GO=(V，E，Σ，L)，1个查询节点集Q⊆V，2个整数d、k，1个优度函数f，返回1个GO的子图H(VH,EH)，满足性质：1) Q⊆VH；2) H是连通的；3)DQ(H)≤d[4]；4)|VH|≤k；5) 所有的可行解中，H的得分f(H)最大。
该社区搜索模式包括GREEDYDIST和GREEDYFAST共2种启发式算法[4]。类似的，Cui等[7]提出了具有阈值约束的社区搜索问题。
模式3 条件社区搜索（condition community search, CCS）模式[8]
给定连通图G=(V，E)和节点集V′⊂V，寻找至少一个满足如下条件的节点集H：1) H⊂V；2) G[H]是连通的，G[H]表示H的诱导子图；3) H满足定义在V′上的用户给定搜索条件F；4) H满足用户给定的社区定义C。
对于一个条件社区搜索模式，如果有且仅有一组节点变量的取值能满足它的搜索条件F，则称其为单项条件社区搜索（single condition community search，SCCS）。为了解决SCCS模式，Zhu等[8]给出了“社区搜索+过滤”方法，即用查询节点进行社区搜索、用禁止节点进行过滤以及基于标签传播给点加权的方法。
定义19 (k,l)-core
给定1个有向图G=(V，E)，2个非负数k、l。(k,l)-core是一个满足入度小于给定k值、出度大于给定k值的G的最大子图。
模式4 有向图中社区搜索（community search on directed graphs, CSD）模式[9]
给定1个有向空属性图GO=(V，E，Σ，L)和2个非负整数k、l以及1个查询节点q，返回1个连通子图GQ⊆GO，GQ是1个(k,l)-core。
文献[9]中利用 (k,l)-cores的嵌套特性，给出了3种方法可以优化时间及空间复杂度。
2.1.2 基于k-truss的空属性图社区搜索模式
定义20 三角连通
在图G=(V，E)中给定2个三角形△1、△2。如果2个三角形有一条公共边，则称这2个三角形为邻接的。对∀e1,e2∈E，如果e1、e2属于同一个三角形或通过若干个邻接的三角形可以相互到达，则称e1、e2是三角连通的。
定义21 Degree-Support
给定图G一个子图H(VH，EH)、一个非负数α，则边e(u,v)∈EH的Degree-Support定义为degsupH(e)=max{supH(e)+2,α∙○H(e)}。
定义22 k-core-truss
给定图G、一个非负参数α、一个整数k≥2、一个k-core-truss H是G的极大子图，且对于H中每条边e，都满足degsupH(e)≥k。
Liu等[10]研究了在有向图中的社区搜索模式并提出了D-truss拓扑结构，并在该结构的基础上提出了D-truss社区搜索模式。
定义23 D-truss
给定一个有向图G、2个整数kc、kf满足csupH(e)≥kc且fsupH(e)≥kf的G的极大子图H为D-truss，也叫做(kc,kf)-truss。
本节根据以上拓扑结构将在空属性图中基于k-truss的社区搜索模式分为三角连通truss社区搜索模式、基于k-truss-core的社区搜索模式[11]和基于D-truss的社区搜索模式[10]。
模式5 三角连通truss社区搜索（triangle-connected truss community, TTC）模式[11]
给定一个空属性图GO=(V，E，Σ，L)、一个查询节点q⊆V、一个整数k≥2，返回所有满足下面条件的子图H⊆GO：1) 结构内聚性，H包含查询节点q，且∀e∈EH，sup(e,H)≥(k-2)；2) 三角连通性，∀e1,e2∈EH，都是三角连通的；3) 极大子图，H是满足上述2条性质的极大子图。
TTC搜索模式包含在线搜索算法、基于k-truss索引的算法和一种基于TCP-index的搜索算法[12]以及基于EquiTruss-index[13]的搜索算法。
模式6 最密集社区（closest truss community, CTC）搜索模式[14]
给定一个图G和一个查询节点集Q，返回一个子图H⊆G，满足：1) H包含Q和一个拥有最大k值的连通的k-truss；2) H是满足性质1且具有最小直径（图中任意2点间距离的最大值）的G的子图。
CTC模式中性质1要求社区中包含查询节点集Q中的所有元素，性质2规定图直径来约束社区中所有节点的接近程度，有效地避免了搭便车（free rider）效应。
模式7 D-truss社区搜索模式
给定一个有向图G=(VG，EG)和2个整数kc、kf，一个查询节点集Q⊆VG。D-truss社区搜索旨在找到一个弱连通子图H⊆G满足：1)Q⊆V(H)；2) H是一个D-truss; 3) diam(H)是满足上述2条性质的子图Hi中最小的。
D-truss社区搜索模式对应全局搜索算法、局部搜索算法以及基于D-truss索引的算法共3种算法[11]。
2.1.3 基于k-clique的空属性图社区搜索模式
模式8 多样化Top-k clique搜索（diversified top-k Clique, DTKC）模式[15]
给定空属性图GO=(V，E，Σ，L)、一个整数k。DTKC搜索模式旨在找到一个集合H满足：1)∀C∈H是一个极大团；2)|H|<k；3)|cov(D)|是最大的。
极大团枚举问题为DTKC搜索模式提供2个基础的解决方案：EnumAll和EnumSub。该模式还对应EnumKBasic[15]、TOPKLS[16]2个算法。
定义24 k-clique分量
以C表示一个k-clique中的连通分量，那么一个k-clique分量就是C中所有k-clique内节点的集合。
模式9 最密集clique过滤社区搜索（densest clique percolation community, DCPC）模式
给定一个空属性图GO=(V，E，Σ，L)和一系列的查询节点Q⊆V，需要找到包含Q中所有节点的具有最大k值的k-clique分量。
DCPC的一种解决方案是用k-clique分量检测算法[17]来检查是否存在k-clique分量。为了有效地支持在线DCPC搜索，Yuan等[18]先后提出了团邻接树、有序邻接树2种树结构，并由此提出了基于DCPC-index的搜索算法，能够更加快速地查询KCPC。
2.1.4 基于k-ECC的空属性图社区搜索模式
模式10 Steiner 最大连通子图（steiner maximum connected component，SMCC）搜索模式[19]
给定一个空属性图GO=(V，E，Σ，L)、一组查询节点Q⊆V，返回GO的子图H(VH,EH)满足以下性质：1) VH包含q；2) 在所有满足k-ECC结构的Hi中，H的边连通度λ(H)是最大的；3) 不存在其他子图H′满足上述性质且有H⊆H′。
模式 11 最小SMCC搜索模式[20]
给定一个空属性图GO=(V，E，Σ，L)、一组查询节点Q⊆V，返回GO的子图H(VH,EH)，H是一个SMCC且在所有满足条件的Hi中|VH|最小。
模式12 极小 SMCC搜索模式[20]
给定一个空属性图GO=(V，E，Σ，L)、一组查询节点Q⊆V，H′(V′，E′) ，H′是一个SMCC，要求在图GO中没有其他H′′是一个SMCC，且满足H′′⊂H′。
如表1，本文对不同子图的内聚性、使用次数、典型在线搜索算法时间复杂度进行了对比。通过对近年来社区搜索方向的30多种模式分析可以发现，学者们对于最终返回社区的子图结构的选择有着一致的偏向性。学者们更倾向于选择k-core结构进行社区搜索研究。在表1中：n为节点数量，m为边数量，s为极大团个数，T为枚举极大团的时间，h、l为常数界。
表 1 不同拓扑结构对比Table 1 Comparison of different topology结构 内聚性 使用度 在线搜索算法时间复杂度 k-core ▲ ▲▲▲▲ O(n) k-truss ▲▲▲ ▲▲ O(m1.5) k-clique ▲▲▲▲ ▲▲ O(lognsT) k-ECC ▲▲ ▲ O(hlm) 注：▲数目越多代表该度量越高。 2.2 时序、位置属性图社区搜索模式
时间、空间属性是图数据中常见的属性，具有这样属性的属性图被称为时序属性图和位置属性图。
2.2.1 时序属性图中的社区搜索模式
时序属性图即边具有时间间隔的属性图。
定义25 时序属性图社区搜索模式
给定一个时序属性图GT=(V，E，Σ，L)、一个查询节点集Q⊆V、一个属性评分函数f，需要找到一个G的诱导子图H(VH，EH，ΣH，LH)，满足性质：1)VH包含Q；2)H是连通的，且满足一定拓扑结构；3)所有的可行解中f(H)值最大。
2.2.1.1 持续社区搜索模式
为了体现时序属性图上的社区的动态性，Li等[21]提出了极大(θ,k)-persistent-core间隔，并在此基础上定义了(θ,τ)-persistent-core结构。
定义26 (θ,τ)-persistent-core结构
给定一个时序属性图G和参数θ、τ、k，一个(θ,τ)-persistent-core是一个G的诱导时序子图C(VC,EC)，满足：1) F(θ,k,C)≥τ[21]；2)不存在诱导时间子图H′包含H且满足性质1)。
模式13 持续社区搜索（persistent community search，PC）模式
给定一个时序属性图GT和参数θ、τ、k。搜索出G中极大(θ,τ)-persistent-core。
Li等[21]给出一种剪枝搜索算法，通过将时序属性图的整个时间跨度分解成多个子区间，每个子区间都有很多可剪枝的节点。
2.2.1.2 最小化低效率值社区搜索模式[22]
模式14 最小化低效率值时序社区搜索模式
给定一个时序属性图GT=(V，E，Σ，L)、一个参数α∈[0,1]、一个查询节点集Q⊆V，旨在找到一个最小低效率时序子图。
该模式的核心概念为时序网络低效率值[23]。Ruchansky等[22]通过图形变换、时序连接、最小化低效率时序子图 [23]共3个步骤解决了该问题。
2.2.2 位置属性图社区搜索模式
位置属性图即将地理位置信息作为节点属性的图，如地理社交网络等。
定义27 位置属性图社区搜索模式
给定一个位置属性图GC=(V，E，Σ，L)、一个查询节点集Q⊆V、一个属性评分函数f，需要找到一个G的诱导子图H(VH，EH，ΣH，LH)，满足如下性质：1) VH包含Q；2) H是连通的，且满足一定拓扑结构；3) 所有可行解中f(H)值最大。
2.2.2.1 限定子图位置的社区搜索模式
模式15 限定子图地理位置的社区搜索模式
给定一个位置属性图GC=(V，E，Σ，L)、一个查询节点q∈V、一个空间约束Λ，返回一个子图Gq⊆GC，满足以下条件：1) 连通性，Gq中包含q且是连通的；2) 结构内聚性，Gq满足一定的拓扑结构；3) 空间内聚性，Gq满足空间内聚约束Λ。
对于不同模式，性质2) 结构内聚性和性质3)空间内聚性可能是不同的。SAC搜索模式、RB k-core搜索模式、地理社交社区查询（geo-social group queries，GSGQs）模式都属于限定子图地理位置的社区搜索模式，相同之处在于使用同样的拓扑结构k-core作为结构内聚性约束；不同之处在于所用的约束空间内聚性的条件不同。
1）SAC搜索模式所采用的空间约束Λ要求返回社区的最小覆盖圆（minimal cover circle，MCC）[24]的半径最小。 Guo等[24]根据密克定理开发出的2种近似算法一定程度上提高了搜索效率。
2）RB k-core搜索模式所采用的空间约束Λ也是MCC但其半径需要小于一个给定值r，且需要再加入一条极大性约束：不存在其他的子图G′q满足上述性质且有Gq⊆G′q。Wang等[25]为该模式提供了 TriV、 BinV和RotC共3种算法。
3）GSGQs模式中，Zhu等[26]所使用的空间约束Λ包括3种： 1) Λ是用于包含Gq的空间矩形； 2) Λ是以q为中心的圆；3) Λ是满足约束2）的圆，且Gq恰好包含k+1个节点。Zhu等[26]提出了social-aware r-trees索引，基于该索引开发了高效的算法来解决具有不同空间约束的GSGQs。
对限定子图位置的社区搜索所用到的3个模式的解决算法的时间复杂度总结如表2。表2中：n为节点数量，m为边数量，
${\varepsilon _F}$ 为给定参数，k为最小度。表 2 限定子图位置的3种社区搜索模式对比Table 2 Comparison of three community search models that limit the location of subgraphs模式 空间限制 算法 时间复杂度 SAC[24,27-28] MCC Exact O(m∙n3) AppInc O(mn) AppFast $O\left( m \cdot {\text{min} }\left\{ n{\text{,log} }\dfrac{ {\text{1} } }{ { {\varepsilon _F} } }\right\}\right){\varepsilon _F}{\text{ > 0} }$
$O{\text{(}}mn{\text{),}}{\varepsilon _F}{\text{ = 0}}$AppAcc $O\left(\dfrac{m}{ {\varepsilon _{{F} }^{\text{2} } } } \cdot {\text{min } }\left\{n{\text{,log} }\dfrac{ {\text{1} } }{ { {\varepsilon _F} } }\right\}\right)$ Exact+ $O\left(\dfrac{m}{ {\varepsilon _F^{\text{2} } } } \cdot {\text{min } }\left\{n{\text{,log} }\dfrac{ {\text{1} } }{ { {\varepsilon _F} } } \right\}+ m{\left| { {F_{\text{1} } } } \right|^{\text{2} } }\right)$ RB k-core[25] 半径固定的圆 TriV $O{\text{(}}{n^3} \cdot {\text{(}}m{\text{ + }}n{\text{))}}$ BinV $O{\text{(}}{n^2} \cdot {\text{(}}m{\text{ + }}n{\text{))}}$ RotC $O{\text{(}}{n^2} \cdot {\text{(log}}n{\text{ + }}m'{\text{))}}$ GSGQs[26] 矩形，中心固定的圆 CBR $O{\text{(}}m \cdot {\text{log}}n{\text{)}}$ GSGQrange $O{\text{(}}m{\text{ + }}n{\text{)}}$ GSGQrkNN $O{\text{(}}n \cdot {\text{(}}m{\text{ + }}n{\text{))}}$ GSGQkNN $O{\text{(C} }_k^{n{\text{–1} } }\left(m{\text{ + } }n\right)$ 2.2.2.2 共位社区搜索模式
共位社区是一个具有高空间内聚度的连通图。
定义28 共位社区 [27]
给定一个位置属性图GC=(V，E，Σ，L)，共位社区是一个子图J⊆GC，且满足：1) 连通性，J是连通的；2) 结构内聚性，子图J满足一定的内聚性结构；3) 空间内聚性，J中所有节点在空间上相临近。
模式16 最佳共位社区[28]（best co-located community, BCC）搜索模式
给定一个位置属性图GC = (V，E，Σ，L)、一个关键字属性集T、一个正整数k、一个直径D，BCC搜索模式旨在找到一个子图Gk满足如下性质：1) 结构内聚性为k-core；2) 节点的位置可以被直径为D的圆包围；3) 质量Q(Gk)在满足前面2个条件中是最大的。
BCC搜索模式包含2种基线算法BSL1、BSL2以及基于索引AC-tree算法共3种算法。
模式17 最具结构内聚性的共位社区（most cohesive co-located community，MC3）搜索模式[29]
给定一个位置属性图GC = (V，E，Σ，L)、一个关键字属性集T、直径D，MC3搜索模式旨在找到一个子图Gk满足：1) Gk是一个k-core；2) Gk中节点位置可以被一个直径为D的圆包围；3) 在所有满足上述2个条件的可行解中，Gk是一个具有最大k值的k-core。
MC3搜索模式包含一种基线算法以及一种基于四叉树索引DkQ-tree的搜索算法[29]。
模式18 (k,d)-MCCs搜索模式
给定一个位置属性图GC = (V，E，Σ，L)、一个正整数k和参数d，返回一个共位社区H(VH，EH)，满足：1) H是一个k-truss；2) H中任意2点之间的空间距离不大于d；3) 不存在其他的共位社区H′满足上述条件且有|V(H′)|＞|V(H)|。
(k,d)-MCCs搜索模式包含一个基线算法、一个近似算法[29]以及一个基于四叉树的索引算法。
2.2.2.3 位置属性搜索模式关系
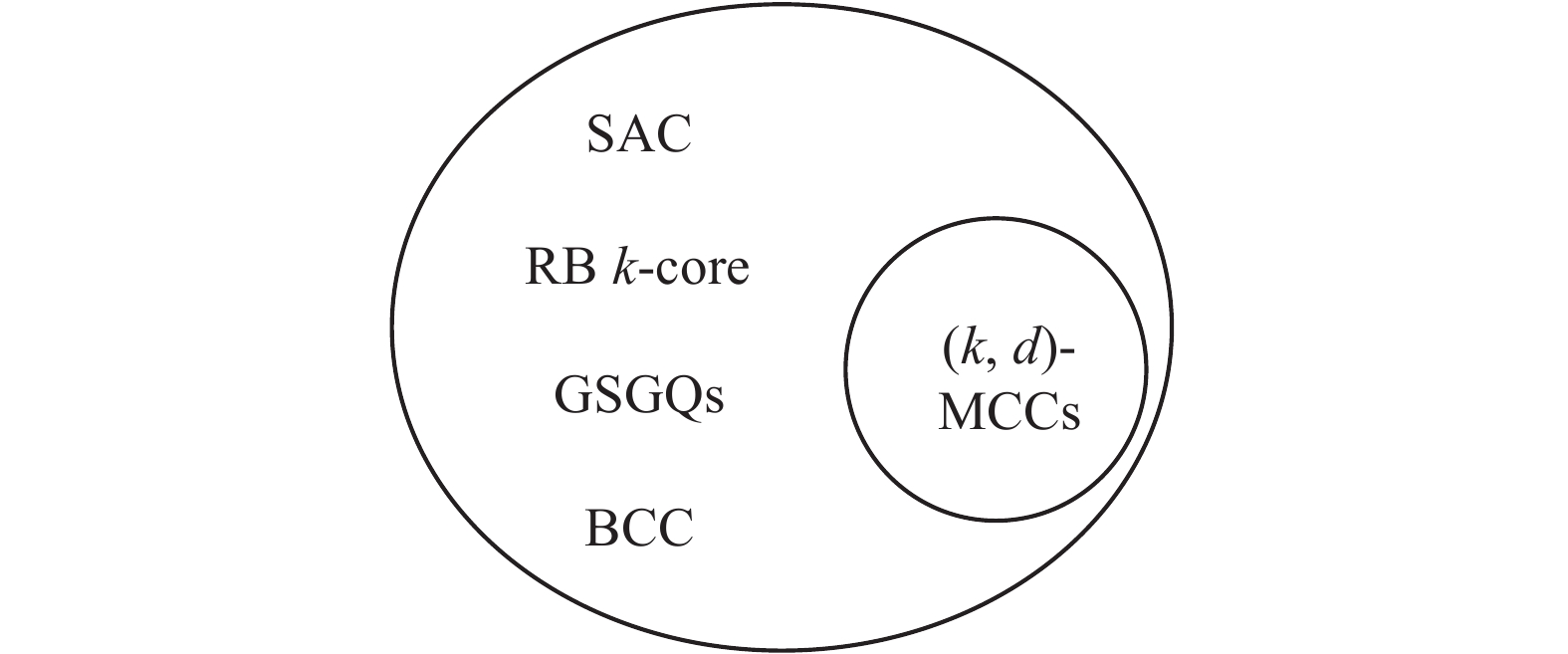
由定义14~17可得，本节介绍的几种位置属性图中的搜索模式(k,d)-MCCs搜索模式从属于RB k-core、SAC、BCC、GSGQs模式，其中RB k-core、SAC、BCC、GSGQs模式相互等价。其关系表示如图2。
图 2 位置属性CS模式关系Fig. 2 Relationship between some location_based CS schema下载:
全尺寸图片
共位社区搜索的3种典型模式的异同点总结如表3所示。
2.3 关键字、权值属性图社区搜索模式
具有关键字、权值属性的属性图分别被称为关键字属性图和权值属性图，许多社区搜索问题的提出建立在这2种属性图中。
2.3.1 关键字属性图社区搜索模式
关键字属性图，即将关键字作为节点属性的图，研究关键字属性图中的社区搜索模式可以直观地找到在复杂网络中具有共性的社区。
定义29 关键字属性图社区搜索模式
给定一个关键字属性图GK=(V，E，Σ，L)、一个查询节点集Q⊆V、一个属性评分函数f，需要找到一个G的诱导子图H(VH，EH，ΣH，LH)，满足如下性质：1) VH包含Q；2)H是连通的，且满足一定拓扑结构；3) 所有的可行解中f(H)值最大。
2.3.1.1 传统的关键字属性图社区搜索模式
传统的关键字属性图上的社区搜索模式可以概括为给定一个关键字属性图、一个查询节点集、一个查询属性集和一个与关键字相关的属性评分函数，返回一个或多个满足一定拓扑结构的子图。
模式19 属性社区查询（attribute community query, ACQ）模式[30]
给定一个关键字属性图GK=(V，E，Σ，L)、一个正整数k、一个查询节点q∈V以及一个查询属性集S⊆W(q)，ACQ模式需要返回一个元素为GK的子图Gq所构成的的集合S。∀Gq∈H，需要满足：1) 连通性，Gq是连通的且包含查询节点q；2) 结构内聚性，Gq是一个k-core；3) 关键字内聚性，S与Gq中所有元素共有的所有关键字属性的集合L(Gq,S)中的元素是最多的。
最简单处理ACQ模式的算法为枚举法，Fang等[30]还提出了一个基于索引CL-tree的搜索算法，其空间和时间复杂度几乎达到了初始图的线性水平。
模式20 属性驱动的truss社区（attribute-driven truss community, ATC）搜索模式[31]
给定一个关键字属性图GK=(V，E，Σ，L)、一个包含查询节点Vq和目标关键字Wq的查询集Q=(Vq,Wq)以及2个常数k和d，返回一个社区H满足：1) H是包含Vq的(k,d)-truss；2) 满足上一条性质的子图中，H的属性得分f(H,Wq)最大[31]。
ATC搜索模式包含一种全局搜索算法以及一种基于索引的算法，Huang等[31]提出了另一种基于ATindex的搜索算法，可以快速识别出一个好的候选答案。
2.3.1.2 极小覆盖r-clique社区搜索模式
定义30 覆盖r-clique
一个覆盖r-clique C是给定图G中具有所有查询关键字的节点的集合，其中任意一对关键字节点之间的最短距离不大于r。
定义31 极小覆盖r-clique(minimal covered r-clique, MCCr)[32-33]
当满足不存在其他的r-clique C′⊆C，则称C为G的极小覆盖r-clique。
极小覆盖r-clique社区搜索模式[32]目标为在给定图G中找到具有目标关键字的极小覆盖r-clique社区。
该模式包含Bron-Kerbosch关键字搜索（Bron-Kerbosch-based keyword search，BKS）算法，该算法添加预处理，并构建递归树，来提高广度优先算法（breadth first search，BFS）效率；以及一种改进了递归树后提出的BKSR算法， 进一步提高了搜索效率。提出BKSRM算法，当迭代次数为T时，时间复杂度减小到了
$\dfrac{{O{\text{(|}}{C_{{\text{max}}}}{{\text{|}}^{l{\text{ + 1}}}}{\text{)}}}}{T}$ 。2.3.1.3 属性多样化的社区搜索模式
基于关键字属性的社区搜索模式往往以寻找节点关键字相似的社区为目标，另有属性多样化社区搜索模式目标在于找到具有尽量多不同属性的社区。如在一场高校举办的联谊会上，举办者可能希望更多所在不同学院的学生相互联谊。
模式21 属性多样化社区搜索模式（attribute diversified community search, ADCS）[33]
给定关键字属性图GK=(V，E，Σ，L)，返回子图H具有性质：1) H满足k-core结构；2) H的平均边多样性在所有满足条件1）中的社区中是最大的。
ADCS问题目前有基线枚举算法、advADC共2种解决方法，与前者相比，添加了额外的循环，以更小的成本修建k-core，使得迭代的次数大大减小。
大部分属性图社区搜索模式都会对不同属性构建不一样的属性评分函数。属性评分函数在社区搜索问题中应用极广，例如2.3.1.1节中f(H,Wq)[31]以及f=|(Gq,S)|，它可以将搜索需求公式化，以函数的计算结果反映返回社区与需求的契合程度。但是，大多数社区搜索问题的属性评分函数难以全方位考虑到所有影响因素。Wang等[34]在评分函数f(H,Wq)的基础上提出了新的属性评分函数
${\text{AttriScore(}}H{\text{,}}{W_q}{\text{) = }}{|{W_q}|}\sqrt[ ]{{\mathop \prod \limits_{w \in {W_q}} {\text{score(}}H{\text{,}}w{\text{)}}}}$ ，它满足了Wang等[34]提出的构造属性评分函数的4个准则：1) 与查询属性相关的节点越多的社区得分更高；2) 覆盖更多查询属性的节点所在社区得分更高；3) 如果有一个节点只覆盖很少量的属性，其所在的社区的得分函数应该更低；4) 规模更大的社区与规模较小的社区，前者的得分应该更高。Liu等[35]为了将单一属性下的社区搜索延伸到多属性，提出一种属性评分函数
${\text{ma}}{{\text{x}}_{u{\text{,}}v \in {V_G}}} {\text{score(}}u{\text{,}}v{\text{)}}$ [35]，旨在衡量包含多属性图中的社区搜索所返回的社区的优劣。2.3.1.4 关键字属性图社区搜索模式关系
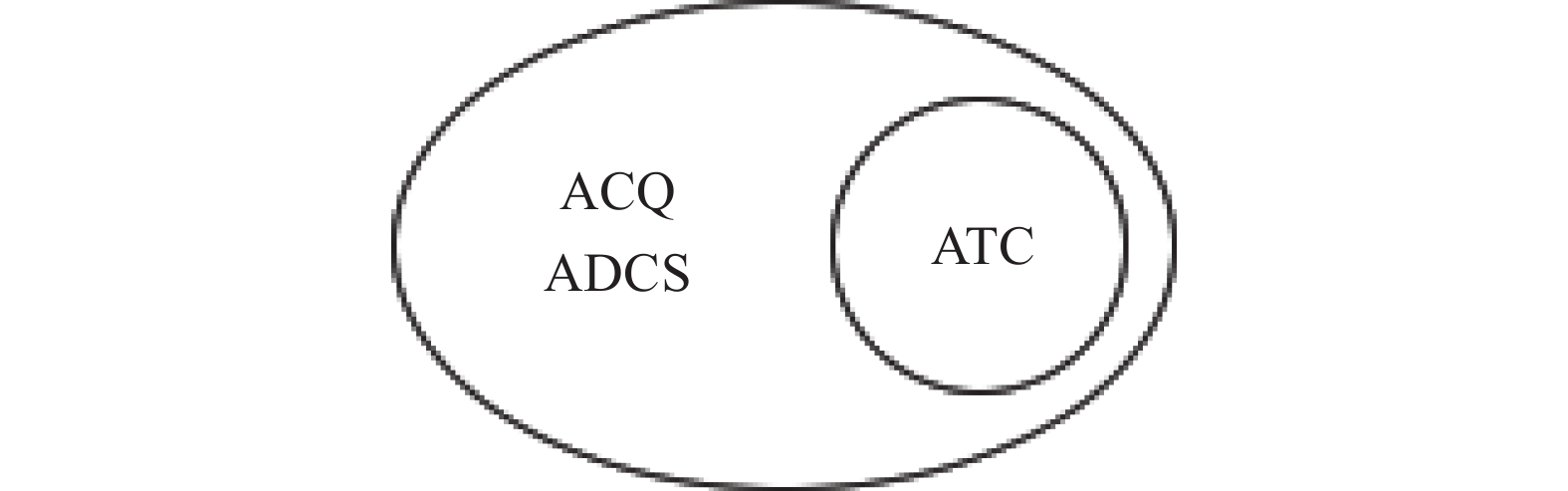
2.3.1.1节定义的几种模式下的问题中，ATC搜索问题与ADCS及ACQ问题的输入初始图属性都是关键字属性图，输出社区的拓扑结构分别为k-truss、k-core及k-clique。则根据定义14~17，ACQ模式与ADCS模式相互等价且ATC模式从属于ACQ与ADCS模式。其关系表示如图3，读者在选择相应搜索模式时，应考虑其从属关系，选择详细或简略的搜索模式。
图 3 关键字属性CS模式关系Fig. 3 Relationship between some keyword based CS schema下载:
全尺寸图片
2.3.2 权值属性社区搜索模式
权值属性图即以权值为属性的图结构。
定义32 权值属性图社区搜索模式
给定一个权值属性图GW=(V，E，Σ，L)、一个查询节点集Q⊆V、一个属性评分函数f，需要找到一个G的诱导子图H(VH，EH，ΣH，LH)，满足如下性质：1)Q⊆VH；2)H是连通的，且满足一定拓扑结构；3) 所有的可行解中f(H)值最大。
这里的权值可以为节点的权值或是边的权值。下文将以节点权值为属性的图称为点权属性图，边的权值为属性的图称为边权属性图。权值在不同的模式中也可以称为重要性、影响力等。
2.3.2.1 点权属性社区搜索模式
点权属性图是一个无向图G=(V，E)，其中每个节点v∈V，都对应一个权值
${w_v}$ ，代表着节点v的重要性。假设将所有权重组成向量W=(w1,w2,···,wn)，且满足降（增）序排列，需要满足：对于任意2个节点${v_i}$ 和${v_j}$ ，如果$i \ne j$ ，那么${w_i} \ne {w_j}$ [36]。每个点至多对应一个权值的属性图称为一维点权属性图，对应一个以上权值的属性图称为多维点权属性图[37]，多维点权属性图是一个多值图
$G{\text{(}}V{\text{,}}E{\text{,}}X{\text{)}}$ ，其中V、E分别代表节点集和边集，X是$d$ 维向量组成的一个集合。在多值图$G{\text{(}}V{\text{,}}E{\text{,}}X{\text{)}}$ 中，每个节点$v \in V$ 与${{d}}$ 维向量Xv=${\text{(}}x_{\text{1}}^v{\text{,}} x_{\text{2}}^v, \cdots {\text{,}}x_d^v{\text{)}}$ 相对应。点权属性社区搜索模式可细分为以下3类模式:
1）一维点权属性图中的社区搜索模式
一维点权属性图G中，图权值W(G)即图G中所有节点权值的最小值，基于图权值定义了k-influential社区、非包含k-influential社区[38-39] 2类社区。
定义33 k-influential社区[36]
给定一个点权属性图GW=(V，E，Σ，L)、一个整数k，则k-influential社区
${H^k}{\text{ = (}}V_H^k{\text{,}}E_H^k{\text{)}}$ 为${G_W}$ 的一个诱导子图，满足：1) 连通性，${H^k}$ 是连通的；2) 内聚性，${H^k}$ 中每个节点的度数至少是$k$ ；3) 极大性，没有其他诱导子图$ \bar H $ 在满足性质1)、性质2)和$ \bar H $ 包含${H^k}$ 的前提下，有$f{\text{(}}{H^k}{\text{) = }}f{\text{(}}\bar H{\text{)}}$ ，这里的$f{\text{(}}H{\text{) }}= {{\text{min}}_{u \in {V_H}}}{\text{\{ }}{w_u}{\text{\} }}$ 。模式22 top-k-influential社区搜索模式
给定一个点权属性图
${G_W}=(V，E，\Sigma，L)$ 、一个整数${{k}}$ ，找到$f$ 的大小为top-k的k-influential社区。定义34 非包含k-influential社区
非包含k-influential社区
${H^k}$ 是一个k-influential社区且${H^{{k}}}$ 不能包含一个${\bar H^k}$ 满足$ f{\text{(}}{\bar H^k}{\text{) = }}f{\text{(}}{H^k}{\text{)}} $ 。模式23 top-k非包含k-influential社区搜索模式
给定一个点权属性图
${G_W}=(V，E，\Sigma，L)$ 、一个整数$k$ ，找到权值最高的top-k个非包含k-influential社区。Li等[36]给出了一种在线搜索算法，Chen等[40]提出一种反向搜索算法，将没有希望成为结果社区的搜索分支提前终止。Li等[36]还给出了一种基于权值社区保存索引（influential-community preserved index，ICP-index）的搜索算法，一定程度上提高了搜索效率。
2）多维点权属性图上的社区搜索模式
多维点权属性图中，所有的节点
$v \in V$ ，$x_i^v$ 形成了一个严格的顺序。即对于任意$u \ne v$ ，$x_i^v \ne x_i^u$ 。若多维点权属性图$G$ 的所有诱导子图$H{\text{，}}{H_{\text{1}}}{\text{,}}{H_{\text{2}}}{\text{,}}\cdots{\text{,}} {H_n}$ ，${H_i} \prec H$ 对$ \forall i\in \text{[1}，n\text{]} $ 成立，称$H$ 为skyline社区[37]。模式24 Skyline社区搜索模式[37]
给定一个多值图
$G{\text{(}}V{\text{，}}E{\text{，}}X{\text{)}}$ 和一个整数$k$ ，该模式旨在找到一个Skyline 社区，它是$G$ 的一个诱导子图$H{\text{ = (}}{V_H}{\text{,}}{E_H}{\text{,}}{X_H}{\text{)}}$ ，满足：①$H$ 是一个连通的k-core；② 不存在$G$ 的子图$H'$ 是连通的k-core且有$H \prec H'$ ；③ 极大性：对任意${\text{1}} \leqslant i \leqslant d$ ，不存在$G$ 的子图$H'$ 满足上述条件且有${f_{\text{i}}}{\text{(}}H{\text{) = }}{f_{\text{i}}}{\text{(}}H'{\text{)}}$ ，$f{\text{(}}H{\text{) }}= {{\text{min}}_{v \in {V_H}}}{\text{\{ }}x_i^v{\text{\} }}$ 。对于该模式，Li等[37]开发了名为Skyline Com-m2D的高效算法，它的时间复杂度是
$O{\text{(}}s{\text{(}}m{\text{ + }}n{\text{))}}$ ，这里的$s$ 指的是所找到的skyline社区的数量。为了能够更好地处理高维的情况，Li等提出了一种空间划分算法来有效地寻找Skyline社区。3）点权属性社区搜索模式关系
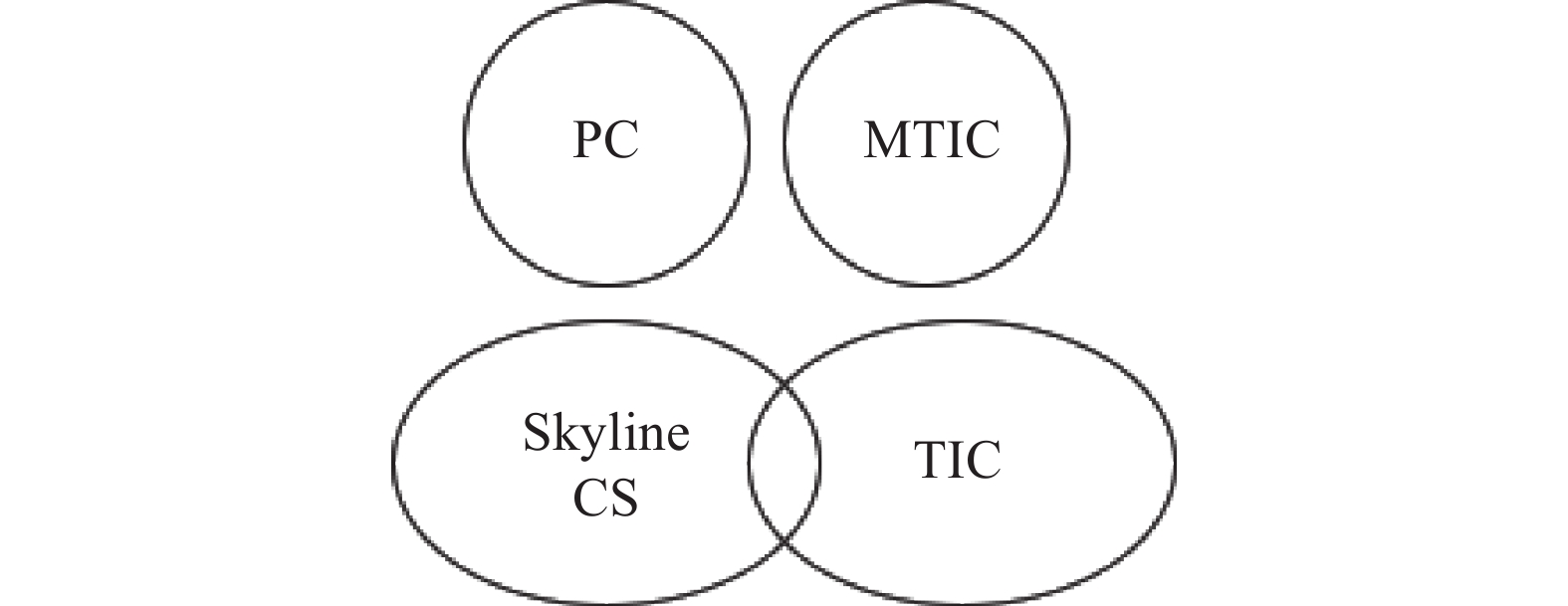
由定义14~17可得，本小节介绍的几种点权属性图中的搜索模式中，Skyline CS模式与TIC搜索模式具有相交的关系，且二者与PC、MTIC搜索模式之间不相关，其关系表示如图4。
图 4 点权属性CS模式关系Fig. 4 Relationship between some node weighted based CS schema下载:
全尺寸图片
2.3.2.2 边权属性社区搜索模式
根据定义6，边权属性图是一个权值属性图
${G_W}=(V，E，\Sigma，L)$ ，其中每个节点$e \in E$ ，都对应一个权值${w_e}$ ，可以表示边$e$ 的权重、构成该边的节点之间的紧密程度、传播概率等。本节将边权属性图分为了常规边权属性图、二部边权属性图和不确定图。1） 常规边权属性图中的社区搜索模式
为了适合在常规边权属性图上社区搜索，以下拓扑结构被提出：加权truss[41]、pk-clique[42]、kr-clique[2]、pkd-truss[43]、紧密core组[44]。
定义35 加权truss社区（weighted truss community, WTC）
给定一个边权属性图
${G_W}=(V，E，\Sigma，L)$ 和一个正整数$k$ ，WTC是${G_W}$ 的一个诱导子图$H$ ，具有以下性质：①$\forall {e_{\text{1}}}{\text{,}}{e_{\text{2}}} \in E{\text{(}}H{\text{)}}$ ，满足${e_{\text{1}}}{\text{,}}{e_{\text{2}}}$ 在H中是三角连通的；②$H$ 是一个k-truss；③$H$ 是满足上述性质的极大子图，即在${G_W}$ 中不存在其他$H \subset \bar H$ ，且这2个子图的权值相等。模式25 WTC搜索模式
给定一个边权属性图
${G_W}=(V，E，\Sigma，L)$ 、一个正整数$k$ ，找出权值大小为top-k的WTC。为了提高搜索效率，Zheng等[41]设计了一个索引结构KEP-index，基于KEP-index，WTC search可以在线性时间内完成。
定义36 pk-clique
给定图G、参数p和k，pk-clique Cpk(Vpk,Epk)是G的一个诱导子图且满足以下性质：① Cpk是一个完全图；② Cpk中任意2个节点可以通过一条MIP相连，其路径权值大于p，且Cpk中至少要有k个节点；③ Cpk是G的所有满足上述条件的pk-clique中节点最多的。
模式26 Top-k影响力社区搜索模式[42]
给定一个边权属性图
${G_W}=(V，E，\Sigma，L)$ 、一个正整数$k$ ，找到对查询节点$s$ 影响最大的top-k个pk-clique。定义37 kr-clique
给定图
$G$ 和2个整数$k$ 、$r$ ，kr-clique$H$ 满足如下条件：①$H$ 是$G$ 的诱导子图；②$H$ 至少有$k$ 个节点；③$H$ 中任一对节点可以在$r$ 次跳跃内到达彼此。模式27 最具影响力的社区搜索模式（most influential community search，MICS）
给定一个边权属性图
${G_W}=(V，E，\Sigma，L)$ 、整数$k$ 、$r$ 以及一个常数$t$ ，返回一个kr-clique$H$ ，在所有满足要求的kr-clique中$H$ 的得分score(H)最高。该模式包括一种基线算法，Li等[2]提出了一种树形索引C-Tree，基于C-Tree并使用DFS的算法SO和SO+，可以显著地提高搜索最大kr-clique的速度。鉴于DFS的特性，Li等[2]又开发出了一种算法，能够以更稳定的速度搜索到kr-clique。
定义 38 pkd-truss社区
该社区是一个(k,d)-truss[43]，且满足任意节点到给定节点之间的最大路径影响值不小于p。
Xie等[43]以pkd-truss结构为基础提出了pkd-truss社区搜索模式。
模式28 pkd-truss社区搜索模式
给定一个边权属性图
${G_W}=(V，E，\Sigma，L)$ 、一个查询节点集(Vq，Wq)、参数$p{\text{、}}k{\text{、}}d$ ，该模式目标是找到一个pkd-truss社区$H$ ，其得分最高。定义39 紧密core组
给定边权属性图
$G$ 、一个查询节点集、一个参数$k$ ，一个紧密core组社区是$G$ 的子图$H$ 满足下面条件：①$H$ 包含查询节点集中的所有元素；②$H$ 是一个连通的k-core；③$H$ 是满足上述2条件中图权值最小的，这里的图权值定义为图中所有边权之和。模式29 紧密core组搜索（intimate-core group search，LEKS）模式[44]
给定边权属性图
${G_W}=(V,E,\Sigma,L)$ 、一个查询节点集$Q$ 、一个参数$k$ ，目标在于找到$G$ 的子图$H$ 满足：①$H$ 包含查询节点集中的所有元素；②$H$ 是一个连通的k-core；③$H$ 是满足上述2条件中图权值最小的。 对于LEKS模式，Sun等[44]给出了2种在线搜索算法ICG-S和ICG-M，并提出了一种基于k-core索引的搜索算法提高了搜索效率。2）二部边权属性图中的社区搜索模式
由于二部图的特殊性，在二部边权属性图上基于传统拓扑结构的社区搜索模式相对较少。有很多由传统拓扑结构衍生出来的新结构被设计出来应用在二部图中，如(α，β)-core[45]、bitruss[46]、biclique[47]。
将二部边权属性图G的2个互不相交的点集分别记为上层（upper layer）
$U{\text{(}}G{\text{)}}$ 和下层（lower layer）$L{\text{(}}G{\text{)}}$ ，则首先给出(α，β)-core的定义：定义40 (α，β)-core
图G的(α，β)-core Rα，β满足Rα，β：①
$ {\text{de}}{{\text{g}}_{U{\text{(}}G{\text{)}}}}{\text{(}}u{\text{)}} \geqslant a $ ，${\text{de}}{{\text{g}}_{L{\text{(}}G{\text{)}}}}{\text{(}}u{\text{)}} \geqslant \beta $ ；② 不存在其他的子图H满足性质①且有${R_{\alpha ,\beta }} \subseteq H$ 。模式30 重要(α，β)社区(significant (α, β)-community, SC)搜索模式[45]
给定一个二部边权属性图G，找到一个具有最大边权的(α，β)-core子图。
针对该模式，Liu等[45]先提出了基于索引
$I_{bs}^\partial $ 的搜索算法和基于$I_{bs}^\beta $ 的搜索算法，又提出了一种基于退化有界索引${I_\delta }$ 的搜索算法，有效地解决了当二部图中部分节点度数过高导致的搜索效率过低的问题。3）不确定图上的属性图社区搜索模式
大部分的社区搜索问题都在确定图上被提出，即假定各个节点之间的关系是固定的。这种假设忽略了节点之间的不确定性。因此，在不确定图[48-50]中研究社区搜索模式是很有必要的。
定义41 (k, η)-influential社区
给定一个不确定图G、参数k、
$\eta $ ，(k, η)-influential社区是G的最大子图，H满足：① H是连通的；②$ \forall v \in H $ ，$v$ 至少有k个邻居的概率不小于$\eta $ ；③不存在其他$G$ 的诱导子图$H'$ 满足上面2个条件且有$f{\text{(}}H'{\text{)}} = f{\text{(}}H{\text{)}}$ ，这里$f{\text{(}}H{\text{) = mi}}{{\text{n}}_{v \in {V_H}}}{\text{\{ }}w{\text{(}}v{\text{)\} }}$ [49]。模式31 (k, η)-influential社区搜索模式
给定一个不确定图G，一个查询节点q，参数k、
$\eta $ ，找到一个(k, η)-influential社区。为了解决(k, η)-influential社区搜索问题，Luo等[49]提出了在线搜索算法、基于ICU-index的搜索以及基于FICU-index的算法共3种搜索算法。
定义42 (k, θ)-community
给定一个不确定图G，查询节点q，2个参数k、
$\theta $ 。其中$k \geqslant {\text{2}}$ ，且$k$ 为正整数，${\text{0 < }}\theta {\text{ < 1}}$ 。(k,θ)-community$H$ 是$G$ 的一个连通子图，且满足：①$q \in H$ ；②$\forall v \in H$ ，$v$ 有至少有$k$ 个邻居；③$\forall e \in H$ ，e存在的概率不小于$\theta $ ；4) 在所有满足上面条件的${H_i}$ 中，$H$ 包含最多的顶点。模式32 (k,θ)-community搜索模式
给定一个不确定图G，查询节点q，2个参数k、θ，找到一个(k,θ)-community[50]。
为了解决(k,θ)-community搜索问题，Miao等[50]首先提出了GSP、NCP共2种剪枝策略，并提出CD-index以高效完成剪枝过程，一定程度上缩小了候选集的规模。进而提出了一种惰性分层抽样算法，在保证精度的前提下加快了搜索速度。
4）边权属性图社区搜索模式关系
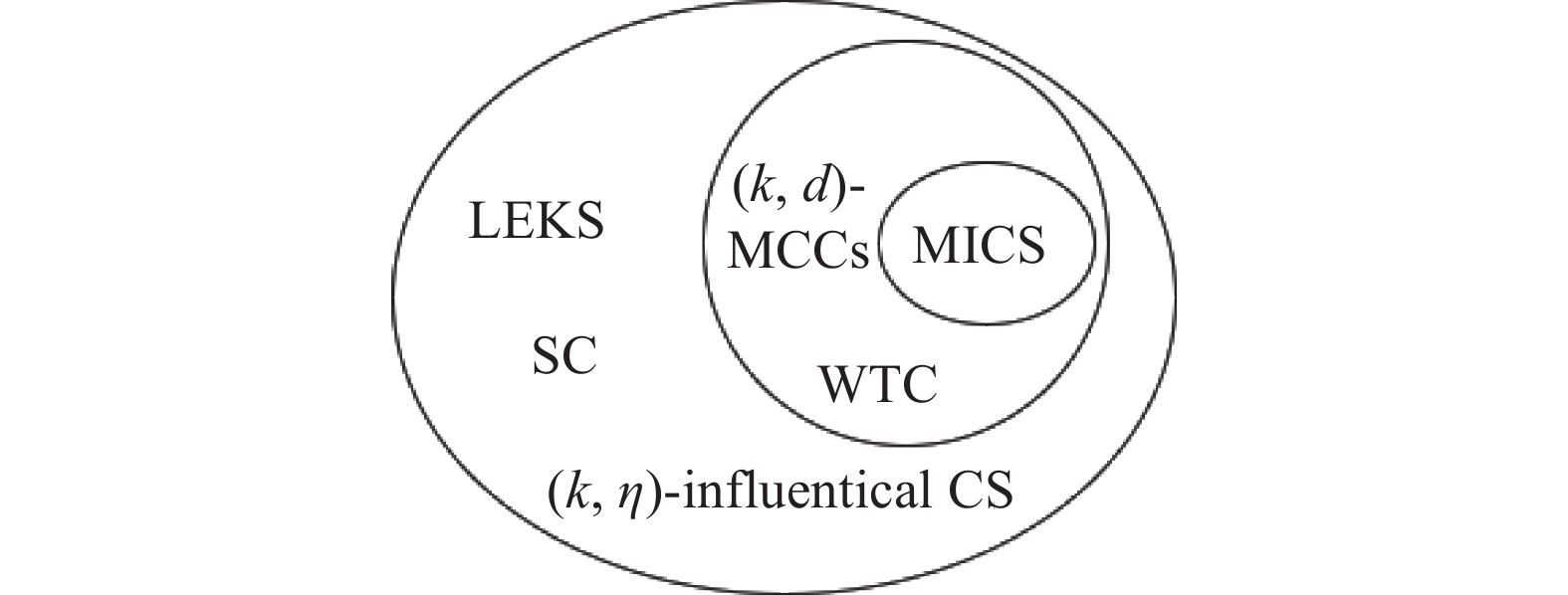
由定义14~17可得，本小节介绍的几种边权属性图中的搜索模式中：MICS模式从属于(k,d)-MCCs和WTC模式；(k,d)-MCCs和WTC模式相互等价且从属于LEKS、SC、(k,η)-influential CS搜索模式，且这3种模式相互等价。其关系表示如图5所示。
图 5 边权属性CS模式关系Fig. 5 Relationship between edge weighted_based CS schema下载:
全尺寸图片
权值（点权、边权）作为不仅是图模式中最常见的属性，在各类研究[51-54]中都经常用到。社区搜索在权值属性图中的研究相较于其他属性也更多。如表4对权值属性图中的社区搜索的一些经典模式以及其算法时间复杂度进行了对比。但是在解决实际问题中，不同模式在解决不同社区搜索问题时有着独特的优势，并不一定以时间复杂度作为最主要的参考依据。表4中，n为顶点数量，m为边数量，s为skyline社区的数量，ρ为AWG的荫度，r为迭代次数。
表 4 几种权值属性图社区搜索模式对比Table 4 Comparison of several community search models in weighted graphs模式 算法 时间复杂度 TIC Union-Find $O{\text{(}}n{\text{ + }}m \cdot {\text{log}}n{\text{)}}$ CountIC $O{\text{(}}m{\text{ + }}n{\text{)}}$ EnumtIC $O{\text{(}}m{\text{ + }}n{\text{)}}$ TnIC NC1 $O{\text{(}}m{\text{)}}$ NC2 $O{\text{(}}m{\text{)}}$ Skyline CS Comm2D $O{\text{(}}s{\text{(}}m{\text{ + }}n{\text{))}}$ WTC 基于KEP-index $O{\text{(}}{m^{{\text{1}}{\text{.5}}}}{\text{ + }}{k_{{\text{max}}}} \cdot n{\text{)}}$ MCP $O\left( {{{\text{3}}^{n/3}}} \right)$ pkd-truss CS IACSM $O{\text{(}}{n^{\text{2}}}{\text{ + }}\rho m{\text{ + }}rn \cdot {\text{|AttriLis}}{{\text{t}}_q}{\text{|)}}$ SC Basic:$I_{bs}^\alpha $ $O{\text{(}}{\partial _{{\text{max}}}} \cdot m{\text{)}}$ Basic:$I_{bs}^\beta $ $O{\text{(}}{\beta _{{\text{max}}}} \cdot m{\text{)}}$ 3. 属性图社区搜索模式分析与检索
由于存在过多的属性社区搜索模式，研究者难以根据需求快速选择其中最合适的。本节分析各种模式的输入属性图属性、输出社区的拓扑结构、是否用到属性评分函数以及现存的算法种类，得出表5。学者们可根据需求，依据表5快速得到适合的属性社区搜索模式。
表 5 模式对比Table 5 Schemas comparison模式 属性函数 输入属性 算法 输出 局部 全局 基于索引 19 √ 关键字 × × √ k-core 20 √ 关键字 √ √ √ k-truss 21 √ 关键字 √ × √ k-core 15 √ 位置 √ √ √ k-core 16 √ 位置 √ × √ k-core 17 × 位置 × √ √ k-core 18 × 位置 × √ √ k-truss 13 × 时序 × √ × k-core 14 √ 时序 × √ × k-clique 22 √ 权值 × √ √ k-core 24 √ 权值 × √ × k-core 25 × 权值 × √ √ k-truss 26 × 权值 × √ √ k-clique 27 √ 权值 × √ √ k-clique 28 √ 权值 √ × × k-truss 29 × 权值 × √ √ k-core 30 × 权值 × √ × k-core 31 √ 权值 × √ √ k-core 3.1 属性图社区搜索模式特性分析
本节将非空属性图中的社区搜索进行对比分析。表5描述了每一种模式的输入属性图的类别、输出的拓扑结构类别、使用属性函数与否、该类模式中的现有算法。如在ACQ模式中，其输入是一张关键字属性图，该模式包括了一种基于索引的算法，最终输出一张满足拓扑结构为k-core的子图，并使用了属性评分函数来约束子图的优劣。
3.2 属性图社区搜索模式检索
当明确了已知问题的前置条件后，本文可以帮助研究者在众多的社区搜索问题中准确定位到需要的解决方法，具体实现方法如下例。
图6(a)数据来源于DBLP网络[55]，共计
9824681 条数据，本文为了清晰地呈现数据，截取了2000 条数据构建了权值属性图。其中节点表示学者，标签表示学者的姓名（为了展现清晰，标签未标注），边表示相邻学者之间有过合著论文的关系，边权表示合著论文的篇数。将图6(a)为初始图输入，给定查询节点q代表作者如Francesco Pa-lmirei，要求尽快搜索到结构紧密且与查询节点所代表的作者之间产生合著关系尽可能多的社区，若要求返回子图为k-core结构。
图 6 社区搜索示例Fig. 6 Example of community search下载:
全尺寸图片
1）根据要求，在表5中选定条件分别为“权值”、“k-core”，则返回满足条件的社区搜索模式为LEKS模式、SC搜索模式或(k,η)-influential CS模式。
2）为了追求更快的搜索速度，排除不具有基于索引算法的SC搜索模式。再定位到模式29及模式30，由于(k,η)-influential CS模式更适用于二部图中的社区搜索，故选定LEKS模式解决该问题。
3）选定LEKS模式并选用该模式的ICG-S算法，给定参数k=5，最终返回社区如图6(b)，社区满足包含查询结点Francesco Palmirei的5-core社区中图权值最大的。
LEKS模式中要求返回社区的图权值最小，本例中更改LEKS模式中条件3）为返回社区H是满足上述2条件中图权值最大的。在DBLP网络中进行社区搜索可以迅速找到与目标作者合著最多的作者所在的社区，帮助学者迅速、准确地找到相关方向论文。
4. 结束语
综上所述，随着图查询研究的逐步深入，社区搜索作为图查询研究中极其重要的一环，已被广泛应用于诸多实际应用中，具有重要的理论和实践意义。本文首先从社区搜索问题的要素入手，定义了属性图中各种社区搜索模式及其之间的关系；其次分析了各种属性图社区搜索模式并对相关算法进行对比分析，进一步提出了属性图社区搜索模式的检索方式，能够以简单、在线的方式找到满足用户需求的社区搜索模式。
本文在前人总结的社区搜索问题的基础上提出了属性图中的社区搜索模式，并提出了两层分类体系，以帮助研究者更准确地定位所需的算法。这种全新的模式为社区搜索领域的研究者提供了一个更具体和系统的框架，通过提供这种模式总结和分类方法，为研究者提供了一个全面的概念视角，并将他们从烦杂的综述中解放出来，能够更快速地找到和应用适合需求的算法，提高了社区搜索领域的研究效率和准确性。
-
图 1 两层分类体系
Fig. 1 Two-tier classification system
下载:
全尺寸图片
图 2 位置属性CS模式关系
Fig. 2 Relationship between some location_based CS schema
下载:
全尺寸图片
图 3 关键字属性CS模式关系
Fig. 3 Relationship between some keyword based CS schema
下载:
全尺寸图片
图 4 点权属性CS模式关系
Fig. 4 Relationship between some node weighted based CS schema
下载:
全尺寸图片
图 5 边权属性CS模式关系
Fig. 5 Relationship between edge weighted_based CS schema
下载:
全尺寸图片
图 6 社区搜索示例
Fig. 6 Example of community search
下载:
全尺寸图片
表 1 不同拓扑结构对比
Table 1 Comparison of different topology
结构 内聚性 使用度 在线搜索算法时间复杂度 k-core ▲ ▲▲▲▲ O(n) k-truss ▲▲▲ ▲▲ O(m1.5) k-clique ▲▲▲▲ ▲▲ O(lognsT) k-ECC ▲▲ ▲ O(hlm) 注：▲数目越多代表该度量越高。 表 2 限定子图位置的3种社区搜索模式对比
Table 2 Comparison of three community search models that limit the location of subgraphs
模式 空间限制 算法 时间复杂度 SAC[24,27-28] MCC Exact O(m∙n3) AppInc O(mn) AppFast $O\left( m \cdot {\text{min} }\left\{ n{\text{,log} }\dfrac{ {\text{1} } }{ { {\varepsilon _F} } }\right\}\right){\varepsilon _F}{\text{ > 0} }$
$O{\text{(}}mn{\text{),}}{\varepsilon _F}{\text{ = 0}}$AppAcc $O\left(\dfrac{m}{ {\varepsilon _{{F} }^{\text{2} } } } \cdot {\text{min } }\left\{n{\text{,log} }\dfrac{ {\text{1} } }{ { {\varepsilon _F} } }\right\}\right)$ Exact+ $O\left(\dfrac{m}{ {\varepsilon _F^{\text{2} } } } \cdot {\text{min } }\left\{n{\text{,log} }\dfrac{ {\text{1} } }{ { {\varepsilon _F} } } \right\}+ m{\left| { {F_{\text{1} } } } \right|^{\text{2} } }\right)$ RB k-core[25] 半径固定的圆 TriV $O{\text{(}}{n^3} \cdot {\text{(}}m{\text{ + }}n{\text{))}}$ BinV $O{\text{(}}{n^2} \cdot {\text{(}}m{\text{ + }}n{\text{))}}$ RotC $O{\text{(}}{n^2} \cdot {\text{(log}}n{\text{ + }}m'{\text{))}}$ GSGQs[26] 矩形，中心固定的圆 CBR $O{\text{(}}m \cdot {\text{log}}n{\text{)}}$ GSGQrange $O{\text{(}}m{\text{ + }}n{\text{)}}$ GSGQrkNN $O{\text{(}}n \cdot {\text{(}}m{\text{ + }}n{\text{))}}$ GSGQkNN $O{\text{(C} }_k^{n{\text{–1} } }\left(m{\text{ + } }n\right)$ 表 3 共位社区搜索的3种典型模式对比
Table 3 Comparison of three typical co-located community search models
表 4 几种权值属性图社区搜索模式对比
Table 4 Comparison of several community search models in weighted graphs
模式 算法 时间复杂度 TIC Union-Find $O{\text{(}}n{\text{ + }}m \cdot {\text{log}}n{\text{)}}$ CountIC $O{\text{(}}m{\text{ + }}n{\text{)}}$ EnumtIC $O{\text{(}}m{\text{ + }}n{\text{)}}$ TnIC NC1 $O{\text{(}}m{\text{)}}$ NC2 $O{\text{(}}m{\text{)}}$ Skyline CS Comm2D $O{\text{(}}s{\text{(}}m{\text{ + }}n{\text{))}}$ WTC 基于KEP-index $O{\text{(}}{m^{{\text{1}}{\text{.5}}}}{\text{ + }}{k_{{\text{max}}}} \cdot n{\text{)}}$ MCP $O\left( {{{\text{3}}^{n/3}}} \right)$ pkd-truss CS IACSM $O{\text{(}}{n^{\text{2}}}{\text{ + }}\rho m{\text{ + }}rn \cdot {\text{|AttriLis}}{{\text{t}}_q}{\text{|)}}$ SC Basic:$I_{bs}^\alpha $ $O{\text{(}}{\partial _{{\text{max}}}} \cdot m{\text{)}}$ Basic:$I_{bs}^\beta $ $O{\text{(}}{\beta _{{\text{max}}}} \cdot m{\text{)}}$ 表 5 模式对比
Table 5 Schemas comparison
模式 属性函数 输入属性 算法 输出 局部 全局 基于索引 19 √ 关键字 × × √ k-core 20 √ 关键字 √ √ √ k-truss 21 √ 关键字 √ × √ k-core 15 √ 位置 √ √ √ k-core 16 √ 位置 √ × √ k-core 17 × 位置 × √ √ k-core 18 × 位置 × √ √ k-truss 13 × 时序 × √ × k-core 14 √ 时序 × √ × k-clique 22 √ 权值 × √ √ k-core 24 √ 权值 × √ × k-core 25 × 权值 × √ √ k-truss 26 × 权值 × √ √ k-clique 27 √ 权值 × √ √ k-clique 28 √ 权值 √ × × k-truss 29 × 权值 × √ √ k-core 30 × 权值 × √ × k-core 31 √ 权值 × √ √ k-core -
[1] LI Xiaoli, WU Min, KWOH Chee-keong, et al. Computational approaches for detecting protein complexes from protein interaction networks: a survey[J]. BMC geno-mics., 2010, 11(1): 1–19. doi: 10.1186/1471-2164-11-1 [2] LI Jiaxin, WANG Xinjue, DENG Ke, et al. Most influential community search over large social networks[C]//2017 IEEE 33rd International Conference on Data Engineering. San Diego: IEEE, 2017: 871−882. [3] CAI Liwei, WANG Yang. KBGAN: adversarial learning for knowledge graph embeddings[C]//Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. New Orleans: NAACL, 2018: 1470−1480. [4] SOZIO Mauro, GIONIS Aristides. The community search problem and how to plan a successful cocktail party[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data mining. Washington DC: KDD, 2010: 939−948. [5] FANG Yixiang, HUANG Xin, QIN Lin, et al. A survey of community search over big graphs[J]. The VLDB journal, 2020, 29(1): 353–392. doi: 10.1007/s00778-019-00556-x [6] BARBIERI N, BONCHI F, GALIMBERTI E, et al. Efficient and effective community search[J]. Data mining and knowledge discovery, 2015, 29(5): 1406–1433. doi: 10.1007/s10618-015-0422-1 [7] CUI Wanyun, XIAO Yanghua, Wang Haixun, et al. Local search of communities in large graphs[C]//Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. Snowbird: MOD, 2014: 991−1002. [8] ZHU Junchao, WANG Chaokun. Approaches to community search under complex conditions[J]. Journal of software, 2019, 30(3): 552–572. [9] FANG Yixiang, WANG Zhihong, CHENG Reynold, et al. Effective and efficient community search over large directed graphs[J]. IEEE transactions on knowledge and data engineering, 2019, 31(11): 2093–2107. doi: 10.1109/TKDE.2018.2872982 [10] LIU Qing, ZHAO Minjun, HUANG Xin, et al. Truss-based community search over large directed graphs[C]// Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data. New York: MOD, 2020: 2183−2197. [11] LI Zhenjun, LU Yunting, ZHANG Weipeng, et al. Discovering hierarchical subgraphs of k-core-truss[J]. Data science and engineering, 2018, 3(2): 136–149. doi: 10.1007/s41019-018-0068-2 [12] HUANF Xin, CHENG Hong, QIN Lin, et al. Querying k-truss community in large and dynamic graphs[C]//Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. Snowbird: SIGMOD, 2014: 1311−1322. [13] AKBAS Esra, ZHAO Peixiang. Truss-based community search: a truss-equivalence based indexing approach[J]. Proceedings of the VLDB endowment, 2017, 10(11): 1298–1309. doi: 10.14778/3137628.3137640 [14] HUANG Xin, LAKSHMANAN L V S, YU J X, et al. . Approximate closest community search in networks[EB/OL]. (2015-03-22)[2023-03-25]. https://arxiv.org/abs/1505.05956.pdf. [15] YUAN Long, QIN Lu, LIN Xuemin, et al. Diversified top-k clique search[J]. The VLDB journal, 2016, 25(2): 171–196. doi: 10.1007/s00778-015-0408-z [16] WU Jun, LI Chumin, JIANG Lu, et al. Local search for diversified Top-k clique search problem[J]. Computers & operations research, 2020, 116: 104867. [17] PALLA G, DERÉNYI I, FARKAS I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(7043): 814–818. doi: 10.1038/nature03607 [18] YUAN Long, QIN Lu, ZHANG Wenjie, et al. Index-based densest clique percolation community search in networks[J]. IEEE transactions on knowledge and data engineering, 2017, 30(5): 922–935. [19] HU Jiafeng, WU Xiaowei, CHENG R, et al. On minimal steiner maximum-connected subgraph queries[J]. IEEE transactions on knowledge and data engineering, 2017, 29(11): 2455–2469. doi: 10.1109/TKDE.2017.2730873 [20] CHANG Lijun, LIN Xuemin, QIN Lu, et al. Index-based optimal algorithms for computing steiner components with maximum connectivity[C]//Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data. Melbourne: MOD, 2015: 459−474. [21] LI Ronghua, SU Jiao, QIN Lu, et al. Persistent community search in temporal networks[C]//2018 IEEE 34th International Conference on Data Engineering. Paris: IEEE, 2018: 797−808. [22] RUCHANSKY N, BONCHI F, GARCÍA-SORIANO D, et al. To be connected, or not to be connected: that is the minimum inefficiency subgraph problem[C]//Proceedings of the 2017 ACM on Conference on Information and Knowledge Management. New York: CIKM, 2017: 879−888. [23] TSALOUCHIDOU I, BONCHI F, BAEZA-YATES R. Adaptive community search in dynamic networks[C]//2020 IEEE International Conference on Big Data. Atlanta: IEEE, 2020: 987−995. [24] GUO Tao, CAO Xin, CONG Gao. Efficient algorithms for answering the m-closest keywords query[C]//Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data. New York: MOD, 2015: 405−418. [25] WANG Kai, CAO Xin, LIN Xuemin, et al. Efficient computing of radius-bounded k-cores[C]//2018 IEEE 34th International Conference on Data Engineering. Paris: IEEE, 2018: 233−244. [26] ZHU Qijun, HU Haibo, XU Cheng, et al. Geo-social group queries with minimum acquaintance constraints[J]. The VLDB journal, 2017, 26(5): 709–727. doi: 10.1007/s00778-017-0473-6 [27] CHEN Lu, LIU Chengfei, ZHOU Rui, et al. Maximum co-located community search in large scale social networks[J]. Proceedings of the VLDB endowment, 2018, 11(10): 1233–1246. doi: 10.14778/3231751.3231755 [28] LUO Jiehuan, CAO Xin, XIE Xike, et al. Best Co-located community search in attributed networks[C]//Proceedings of the 28th ACM International Conference on Information and Knowledge Management. New York: CIKM, 2019: 2453−2456. [29] LUO Jiehuan, CAO Xin, QU Qiang, et al. Efficient search of the most cohesive Co-located community in attributed networks[C]//International Conference on Database Systems for Advanced Applications. Chiang Mai: Springer, 2019: 398−415. [30] FANG Yixiang, CHENG R, LUO Siqiang, et al. Effective community search for large attributed graphs[J]. Proceedings of the VLDB endowment, 2016, 9(12): 1233–1244. doi: 10.14778/2994509.2994538 [31] HUANG Xin, LAKSHMANAN L V S. Attribute-driven community search[J]. Proceedings of the VLDB endowment, 2017, 10(9): 949–960. doi: 10.14778/3099622.3099626 [32] GHANBARPOUR A, NIKNAFS K, NADERI H. Efficient keyword search over graph-structured data based on minimal covered r-cliques[J]. Frontiers of information technology & electronic engineering, 2020, 21(3): 448–464. [33] CHOWDHARY A A, LIU Chengfei, CHEN Lu, et al. Finding attribute diversified communities in complex networks[C]//International Conference on Database Systems for Advanced Applications. Jeju: Springer, 2020: 19−35. [34] WANG Chunnan, WANG Hongzhi, CHEN Hanxiao, et al. Attributed community search based on effective scoring function and elastic greedy method[J]. Information sciences, 2021, 562: 78–93. doi: 10.1016/j.ins.2021.01.013 [35] LIU Qing, ZHU Yifan, ZHAO Minjun, et al. VAC: vertex-centric attributed community search[C]//2020 IEEE 36th International Conference on Data Engineering. Dallas: IEEE, 2020. [36] LI Ronghua, QIN Lu, YU Jeffreyxu, et al. Influential community search in large networks[J]. Proceedings of the VLDB endowment, 2015, 8(5): 509–520. doi: 10.14778/2735479.2735484 [37] LI Ronghua, QIN Lu, YE Fanghua, et al. Skyline community search in multi-valued networks[C]//Proceedings of the 2018 International Conference on Management of Data. Houston: MOD, 2018: 457−472. [38] LUO Wensheng, ZHOU Xu, YANG Jianye, et al. Efficient approaches to Top-R influential community search[J]. IEEE internet of things journal, 2020, 8(16): 12650–12657. [39] BI Fei, CHANG Lijun, LIN Xuemin, et al. An optimal and progressive approach to online search of top-k influential communities[J]. Proceedings of the VLDB endowment, 2018, 11(9): 1056–1068. doi: 10.14778/3213880.3213881 [40] CHEN Shu, WEI Ran, POPOVA D, et al. Efficient computation of importancebased communities in web-scale networks using a single machine[C]//ACM International. Indianapolis: ACM, 2016. [41] ZHENG Zibin, YE Fanghua, LI Ronghua, et al. Finding weighted K-truss communities in large networks[J]. Information sciences, 2017, 417: 344–360. doi: 10.1016/j.ins.2017.07.012 [42] XU Jiao, FU Xiaoyi, WU Yiming, et al. Personalized top-n influential community search over large social networks[J]. World wide web, 2020, 23(3): 2153–2184. doi: 10.1007/s11280-020-00788-w [43] XIE Xiaoqin, SONG Mingjie, LIU Chiming, et al. Effective influential community search on attributed graph[J]. Neurocomputing, 2021, 444: 111–125. doi: 10.1016/j.neucom.2020.08.088 [44] SUN Longxu, HUANG Xin, LI Ronghua, et al. Fast algorithms for intimate-core group search in weighted graphs[C]//International Conference on Web Information Systems Engineering. Hong Kong: Springer, 2020: 728−744. [45] LIU Boge, YUAN Long, LIN Xuemin, et al. Efficient (α, β)-core computation: an index-based approach[C]//The World Wide Web Conference. San Francisco: ACM, 2019: 1130−1141. [46] WANG Kai, LIN Xuemin, QIN Lu, et al. Efficient bitruss decomposition for large-scale bipartite graphs[C]//2020 IEEE 36th International Conference on Data Engineering. Dallas: IEEE, 2020: 661−672. [47] ZHANG Yun, PHILLIPS C A, ROGERS G L, et al. On finding bicliques in bipartite graphs: a novel algorithm and its application to the integration of diverse biological data types[J]. BMC bioinformatics, 2014, 15(1): 1–18. doi: 10.1186/1471-2105-15-1 [48] ZHANG Wenqiang, ZHONG Yingli, YANG Yan. Community search in spatial uncertain network[J]. Journal of physics conference series, 2021, 1952(4): 042112. [49] LUO Wensheng, ZHOU Xu, LI Kenli, et al. Efficient influential community search in large uncertain graphs[J]. IEEE transactions on knowledge and data engineering, 2021, 35(4): 3779–3793. [50] MIAO Xiaoye, LIU Yue, GAO Yunjun, et al. Reliable community search on uncertain graphs[C]//2022 IEEE 38th International Conference on Data Engineering. Kuala Lumpur: IEEE, 2022. [51] 王旭东,韩晓磊,邹功鑫,等. 基于权值的新能源集控电量均衡CSMA/CA改进算法[J]. 微型电脑应用, 2024, 40(5): 227–230. WANG Xudong, HAN Xiaolei, ZOU Gongxin, et al. Improved CSMA/CA algorithm of new energy centralized control power balance based on weight[J]. Microcomputer applications, 2024, 40(5): 227–230. [52] 梁正平,刘程,王志强,等. 基于存档和权值扩展的大规模多目标优化算法[J]. 计算机学报, 2022, 45(5): 951–972. LIANG Zhengping, LIU Cheng, WANG Zhiqiang, et al. Large-scale multi-objective optimization algorithm based on archive and weight extension[J]. Chinese journal of computers, 2022, 45(5): 951–972. [53] 毛华, 刘祎超. 基于权值最大圈的概念格构造算法[J]. 智能系统学报, 2016, 11(4): 519–525. MAO Hua, LIU Yichao. An algorithm for concept lattice construction based on maximum cycles of weight values[J]. CAAI transactions on intelligent systems, 2016, 11(4): 519–525. [54] 陈侃松,李豪科,阮玉龙,等. 基于局部邻居节点和链路权值的改进AODV路由协议[J]. 软件学报, 2021, 32(4): 1186–1200. CHEN Kansong, LI Haoke, RUAN Yulong, et al. Improved AODV routing protocol based on local neighbor nodes and link weights[J]. Journal of software, 2021, 32(4): 1186–1200. [55] 王余蓝. 基于图形数据库的DBLP数据存储[J]. 计算机技术与发展, 2013, 23(8): 18–20, 26. WANG Yulan. DBLP data storage based on graphics database[J]. Computer technology and development, 2013, 23(8): 18–20, 26.
