基于动态阈值和差异性检验的自训练算法

吕佳,  邱鸿波,  肖锋

downloadPDF
吕佳, 邱鸿波, 肖锋. 基于动态阈值和差异性检验的自训练算法 [J]. 智能系统学报, 2024, 19(4): 839-852. doi: 10.11992/tis.202306047
引用本文: 吕佳, 邱鸿波, 肖锋. 基于动态阈值和差异性检验的自训练算法 [J]. 智能系统学报, 2024, 19(4): 839-852. doi: 10.11992/tis.202306047
shu
LYU Jia, QIU Hongbo, XIAO Feng. Self-training algorithm based on dynamic threshold and difference test [J]. CAAI Transactions on Intelligent Systems, 2024, 19(4): 839-852. doi: 10.11992/tis.202306047
Citation: LYU Jia, QIU Hongbo, XIAO Feng. Self-training algorithm based on dynamic threshold and difference test [J]. CAAI Transactions on Intelligent Systems, 2024, 19(4): 839-852. doi: 10.11992/tis.202306047
shu

基于动态阈值和差异性检验的自训练算法

doi: 10.11992/tis.202306047
  • 1.

    重庆师范大学 计算机与信息科学学院, 重庆 401331;

  • 2.

    重庆市数字农业服务工程技术研究中心, 重庆 401331

基金项目: 国家自然科学基金重大项目（11991024）；重庆市教委“成渝地区双城经济圈建设”科技创新项目（KJCX2020024）；重庆市高校创新研究群体资助项目（CXQT20015）.
详细信息
    作者简介:

    吕佳，教授，博士，主要研究方向为机器学习、数据挖掘。主持或参与国家级、省部级科研项目共20项，发表学术论文70余篇。E-mail：lvjia@cqnu.edu.cn;

    邱鸿波，硕士研究生，主要研究方向为机器学习、凸优化算法、噪声标签学习算法。E-mail：2021110516007@cqnu.edu.cn;

    肖锋，硕士研究生，主要研究方向为机器学习、数据挖掘、数据流算法。E-mail：2021210516083@cqnu.edu.cn.

    通讯作者:

    吕佳. E-mail：lvjia@cqnu.edu.cn.

  • 中图分类号: TP181

Self-training algorithm based on dynamic threshold and difference test

  • 1.

    College of Computer and Information Sciences, Chongqing Normal University, Chongqing 401331, China;

  • 2.

    Chongqing Digital Agriculture Service Engineering Technology Research Center, Chongqing 401331, China

    摘要
  • 摘要: 针对自训练算法在迭代训练分类器的过程中存在难以有效选取高置信度样本以及误标记样本错误累积的问题，本文提出了基于动态阈值和差异性检验的自训练算法。引入样本的局部离群因子，据此剔除有标签样本中的离群点以及分类标注无标签样本，依据标注分批次处理无标签样本，以使模型更易选取到高置信度的无标签样本；根据新增伪标签样本的数量和对比隶属度的变化，设计一种动态隶属度阈值函数，提升高置信度样本的质量；定义密集距离度量样本间的差异性，分别计算伪标签样本与同类和不同类样本之间的密集距离之和，从而找出不确定度高的伪标签样本，并将此类样本并入下轮训练的无标签样本集中，缓解误标记样本错误累积的问题。实验结果表明，该算法在12个UCI基准数据集上均取得理想效果。

     

    Abstract: In the process of iterative training of the classifier by a self-training algorithm, it is difficult to effectively select high-confidence samples and there exists mislabeled samples error accumulation. To address the above issues, this paper proposes a self-training algorithm based on dynamic threshold and difference test. The local outlier factor of the sample is introduced to remove the outliers from the labeled samples, classify and label the unlabeled samples. The unlabeled samples are subsequently fed into the model in batches based on the assigned mark, allowing the model to more easily select high-confidence unlabeled samples. Further, a dynamic membership threshold function is designed based on the changes in the number of newly added pseudo-labeled samples and the contrast membership. This function aims to improve the quality of high-confidence samples. Finally, the dense distance is defined to measure the difference between samples. The sum of dense distances between pseudo-labeled samples and samples of the same class and different classes is calculated separately to find the pseudo-labeled samples with high uncertainty, and incorporate these samples into the unlabeled samples set of the next round of training, which alleviates error accumulation of mislabeled samples. The experimental results demonstrate effectiveness of this algorithm on 12 benchmark UCI datasets.

     

    • HTML全文

  • 有监督学习依赖大量有标签样本才能训练出有效的分类器，但在自然语言处理[1]、医疗诊断图片分类[2]和文本分类[3]等实际应用场景中，获取有标签样本往往代价高昂，而获取无标签样本相对容易。在此背景下，半监督学习(semi-supervised learning，SSL)[4]因其能在少量有标签样本的监督下，利用大量无标签样本信息从而学习出性能较优的模型，得到了学者们的广泛关注。SSL研究中常用的算法[5-6]有基于一致性正则化(consistency regularization，CR)[7-8]算法、基于标签传播算法(label propagation algorithm，LPA)[9-10]以及自训练(self-training，ST)[11-13]算法等。CR是对样本做一定的扰动希望模型预测一致，不依赖于伪标签，可以有效减少错误累积，但需要额外的计算开销，且对数据分布的假设要求较高。LPA通过在图上传播已标记节点的标签来对无标记节点进行标签预测，能充分利用数据间的关系信息，但对图的构建和选择敏感。ST算法首先使用少量有标签样本训练初始分类器，随后利用分类器从无标签样本中选取高置信度样本并赋予伪标签来扩充有标签样本集，再用扩充后的有标签样本集训练分类器，重复此过程直至满足迭代训练的终止条件。ST算法简单高效且适用性广，但ST算法仍面临如何有效选取高置信度样本和缓解错误累积的挑战[14]。

    为了解决分类器难以有效地选取高置信度样本的问题。Wang等[15]提出自适应阈值的半监督学习，根据模型学习状态自适应调整置信度阈值，引入自适应类公平正则化惩罚，更有效地选取高置信度样本。Park等[16]提出一种自训练的知识蒸馏框架用于胸部X光片诊断，采用知识蒸馏的方法将教师模型的知识传递给学生模型，能更有效选取高置信度样本，提高模型性能。基于知识蒸馏的ST算法在训练方式、知识传递方式不同于其他ST算法，需要引入额外的计算开销，且受限于教师模型的稳定性，可能会导致错误的知识传递，从而降低学生模型的性能。Gan等[17]提出在自训练迭代过程中嵌入半监督模糊C均值聚类算法(self-training semi-supervised fuzzy C-means algorithm，STSFCM)，将类簇隶属度大于设定阈值的样本作为高置信度样本，使用模糊C均值聚类算法发现数据的空间结构，可以更快地找到高置信度样本，但在非凸数据集上效果不佳。Wu等[18]提出一种密度峰值自训练算法(self-training semi-supervised classification based on density peaks of data，STDP)，使用密度峰值聚类来发现样本的空间结构，并对无标签样本进行标记，依据标记分批次输入模型，使得模型更易于选取高置信度样本，但未考虑误标记样本累积的问题。

    针对训练过程中误标记样本累积的问题，Zou等[19]提出一种置信度正则化的自训练框架，利用软标签和模型平滑的思想，降低错误伪标签对模型的影响。Mukherjee等[20]提出一种基于不确定性感知的少量有标签的文本分类自训练算法，采用贝叶斯不一致主动学习找出不确定性高的伪标签样本，避免错误累积。Wei等[21]提出基于密度峰值与割边权重统计的自训练算法(self-training method with density peaks and cut edge weight statistic，STDPCEWS)，使用割边权重作为样本的统计量进行假设检验，选出未被正确标记的样本，有效地找到错误标记样本。吕佳等[22]提出结合密度峰值和改进的自然邻居的自训练算法(self-training method based on density peaks and improved natural neighbor，STDPINN)，使用加权自然邻居噪声过滤器找出高不确定性的标记样本，由人工赋予标签，能为错误标记样本赋予正确标签。Li等[23]提出基于密度峰值的全局自适应多局部噪声过滤器的自训练算法(self-training algorithm based on density peaks combining globally adaptive multi-local noise filter，STDPMLM)，采用全局自适应多局部噪声滤波器找到误标记样本，充分考虑每个类簇中空间分布的影响，能有效找出错误标记样本。然而上述的ST算法仍难以有效应对以下问题： 1)初始训练样本中存在离群点，导致分类器预测能力降低。初始分类器性能较弱，难以选取到高置信度样本。2)隶属度阈值大多依赖于手工选取，而过高阈值导致选取过少的伪标签样本，忽略了大量置信度低于阈值但分类正确的样本。反之，过低阈值导致模型容易选取分类错误的伪标签样本，误导分类器学习。现有的动态阈值方法均采用深度学习技术，导致较高的计算量负担。3)当有标签样本位于低密度区域时，其附近的无标签样本容易被误分类，使得模型分类边界往高密度区域移动，造成样本的错误分类。

    为了解决上述问题，本文提出基于动态阈值和差异性检验的自训练算法(self-training algorithm based on dynamic threshold and difference test，STDTDT)。STDTDT算法具体创新如下：

    1)利用局部离群因子剔除有标签样本中的离群点以及分类标注无标签样本，依据标注分批次处理无标签样本，使分类器能选取到高置信度的无标签样本。

    2)设计一个动态隶属度阈值的分段函数，提高分类器选取高置信度样本的质量，同时避免阈值过高导致选取样本数量过少。

    3)提出一种伪标签差异性检验方法，使得分类边界尽可能位于低密度区域，缓解了伪标签错误传播造成的错误累积。

    1.   自训练算法的理论基础

    1.1   ST算法

    ST算法通过从无标签样本中选取高置信度的样本并赋予伪标签来扩充有标签样本集。其算法的伪代码如下：

    输入　L、U；

    输出　H。

    1) 利用L训练H；

    2) While U不为空 do

    3) 使用H从U中选则高置信度样本S；

    4) H赋予S伪标签，使用S扩充L；

    5) 删除U中的S；

    6) 利用扩充后的L训练H；

    7) End while

    1.2   全局密度和局部密度

    全局密度反映的是样本在整体样本的密度信息，而局部密度反映的是样本与邻近样本的相对密度信息。计算全局密度和局部密度的步骤如下：

    1) 计算样本xi与样本xj之间的距离：

    $$ d({x_i},{x_j}) = \;||{x_i} - {x_j}|{|_2} $$

    2) 找到样本xi的Nk(xi)，Nk(xi)集合中不包括样本xi，其中，|Nk(xi)| = K。

    3) 计算样本xi的全局密度g(xi)：

    $$ g{_k}({x_i}) = 1\left/\left(\sum\limits_{{x_j} \in {N_k}({x_i})} {||{x_i} - {x_j}|{|_2}} /|{N_k}({x_i})|\right) \right.$$

    4) 计算样本xi的局部密度l(xi)：

    $$ l_{k}（{x}_{i}）=(|{N}_{k}({x}_{i})|\cdot g_{k}({x}_{i}))\left/{\displaystyle \sum _{{x}_{j}\in {N}_{k}({x}_{i})}g_{k}({x}_{j})} \right.$$

    局部密度越大，样本的密集程度越高。

    1.3   对比隶属度

    隶属度表示样本属于模糊集合的程度，隶属度越大，代表属于此类集合的程度越高。

    隶属度定义为

    $$ {P_{ij}} = \frac{{P({C_j}|{x_i};\phi )}}{{\displaystyle\sum\limits_{s = 1}^c {P({C_s}|{x_i};\phi )} }}\left(\displaystyle\sum\limits_{s = 1}^c {P({C_s}|{x_i};\phi ) = 1} \right) $$

    式中：i$ \in ${1,2,…,m}，j$ \in ${1,2,…,c}，P(Cj|xi;$\phi $)为样本xi属于类别Ck(k=1,2,…,c)的概率，$\phi $为隶属度函数，m是为无标签样本总数，c为样本类别个数。当c较大时，存在样本xi分属于每个类别的隶属度都较小，相互间差值范围较小，难以有效选取高置信度样本。由此，受对比思想启发，提出对比隶属度为

    $$ {N_{{{ij}}}} = {\text{max(}}P{\text{(}}{C_j}{\text{|}}{x_i}{\text{;}}\; \phi {\text{))}}/{\text{max(}}P{\text{(}}{C_{j'}}{\text{|}}{x_i}{\text{;}}\; \phi {\text{)}}) $$

    式中$j' \in \{ 1,2,\cdots ,c|j' \ne j\}$，对比隶属度值越大，样本归属于此类集合程度越高。本文将对比隶属度大于隶属度阈值的无标签样本称为高置信度样本。

    2.   本文算法的结构与伪代码

    2.1   样本的剔除与划分

    由于ST算法中有标签样本可能存在离群点，其附近的点容易被误标记[24-25]，导致伪标签错误传播，造成错误累积，从而降低分类器性能。局部离群因子算法[26]的鲁棒性强和适用性广，因此通过计算局部离群因子来检测样本中的离群点。为了解决局部离群因子算法计算成本较高的问题，本文使用样本局部密度的倒数作为局部离群因子，样本xi的局部离群因子$ \tau $(xi)为

    $$ \tau ({x_i}) = 1/l{_k}({x_i}) $$

    局部离群因子的值越大，样本离群程度越高，离群程度越高的有标签样本越容易产生误标记样本。剔除有标签样本中局部离群因子较大的样本，将有助于提高有标签样本质量。

    由于ST算法中初始有标签样本数量较少，训练的初始分类器性能较弱，导致挑选高置信度样本困难[27]。因此，依据局部离群因子对无标签样本进行分类标注，根据标注顺序分批次输入训练模型。依据局部离群因子把无标签样本划分为3类：

    1) 高密度区域的密集样本，局部离群因子在(0:1]的点，密集样本的全局密度大于周边样本的平均全局密度。

    2) 低密度区域的边界样本，局部离群因子在(1:$ \tau $avg+3]的点，边界样本的全局密度小于周边样本的平均全局密度。其中，$ \tau $avg是训练样本的局部离群因子的平均值。

    3) 边缘区域的离群样本，局部离群因子在($ \tau $avg+3:$\infty $]的点，离群样本的全局密度远小于周边样本的平均全局密度。

    通过剔除边缘区域的离群样本，提高无标签样本的质量。根据局部离群因子的值对无标签样本从小到大依次标注，依据标注大小分批次输入模型，优先输入易于分类的高密度区域的密集样本，后输入低密度区域的边界样本，使得分类器能选取高置信度的无标签样本。

    2.2   动态隶属度阈值函数

    ST算法设置固定值作为隶属度阈值，算法无法有效区分高置信度样本[28-29]。然而，已有的动态阈值方法会引起较大的计算负担。因此，本文设计一种简易且高效的动态隶属度阈值函数，该阈值应随着分类器性能的提升而逐渐增大。分类器性能与新增的有标签样本数量和质量有关，有标签样本数量越多、质量越好则分类器性能越强[30-31]。此外考虑到隶属度阈值过高会导致选取高置信度样本过少的问题，通过设计分段函数来进一步调整阈值，在选取高置信度样本数量为0时，降低阈值。综上，设计动态隶属度阈值函数的过程如下：

    1) 计算第i次迭代与第i−1次迭代中有标签样本增加的数量之比：

    $$ {r_i} = N{_i}/N{_{ i- 1}} $$

    式中Ni为训练过程中第i次迭代增加的有标签样本数量。ri值越大，代表分类器第i次迭代相比第i−1次迭代选取的高置信度样本更多，分类器性能更强。

    2) 计算分类器第i次迭代选取的高置信度样本的对比隶属度的平均值与第i−1次选取的高置信度样本的对比隶属度的平均值之比：

    $$ {t_i} = {P_i}/{P_{i - 1}} $$

    式中Pi为分类器第i次迭代选取的高置信度样本的对比隶属度的平均值，平均值越大代表选取的高置信度样本质量越好。ti值越大，代表分类器第i次选取的高置信度样本比第i−1次选取的高置信度样本的质量越好。

    3) 计算第i次迭代与第i−1次迭代中选取高置信度样本数量、对比隶属度的平均值和有标签样本数量的比值：

    $$ {R_i} = {r_i} \cdot {t_i} \cdot \left(\sum\limits_{j = 1}^i {{N_j}} \left/\sum\limits_{j = 1}^{i - 1} {{N_j}} \right) \right.$$

    Ri值越大代表第i次迭代比第i−1次迭代时分类器性能更强。

    4) 设计动态隶属度阈值分段函数T。

    当i $ \leqslant $ 2时：

    $$ T_i=T_0 $$

    当i > 2且第i−1次迭代分类器选取的高置信度样本不为零时：

    $$ T_i=\max\left\{ T_{i-1}\cdot \log_2\left( R_{i-1}+1\right) , T_0 \right\} $$

    当i > 2且第i−1次迭代分类器选取的高置信度样本为零时：

    $$ T_i=\max\left\{ T_{i-1}\cdot \log_2\left( R_{i-1}+1\right)-1 , T_0 \right\} $$

    通过设置动态隶属度阈值函数，致使Ti的值不低于T0，避免由于阈值过低使得分类器选取到较多错误的伪标签样本，从而提高选取高置信度样本的质量。同时，通过设计分段函数，当出现阈值过高导致分类器无法选取高置信度样本，降低max函数中$T_{i-1}\cdot \log_2\left( R_{i-1}+1\right) $的值，避免阈值过高导致选取高置信度样本过少的问题。

    2.3   伪标签差异性检验

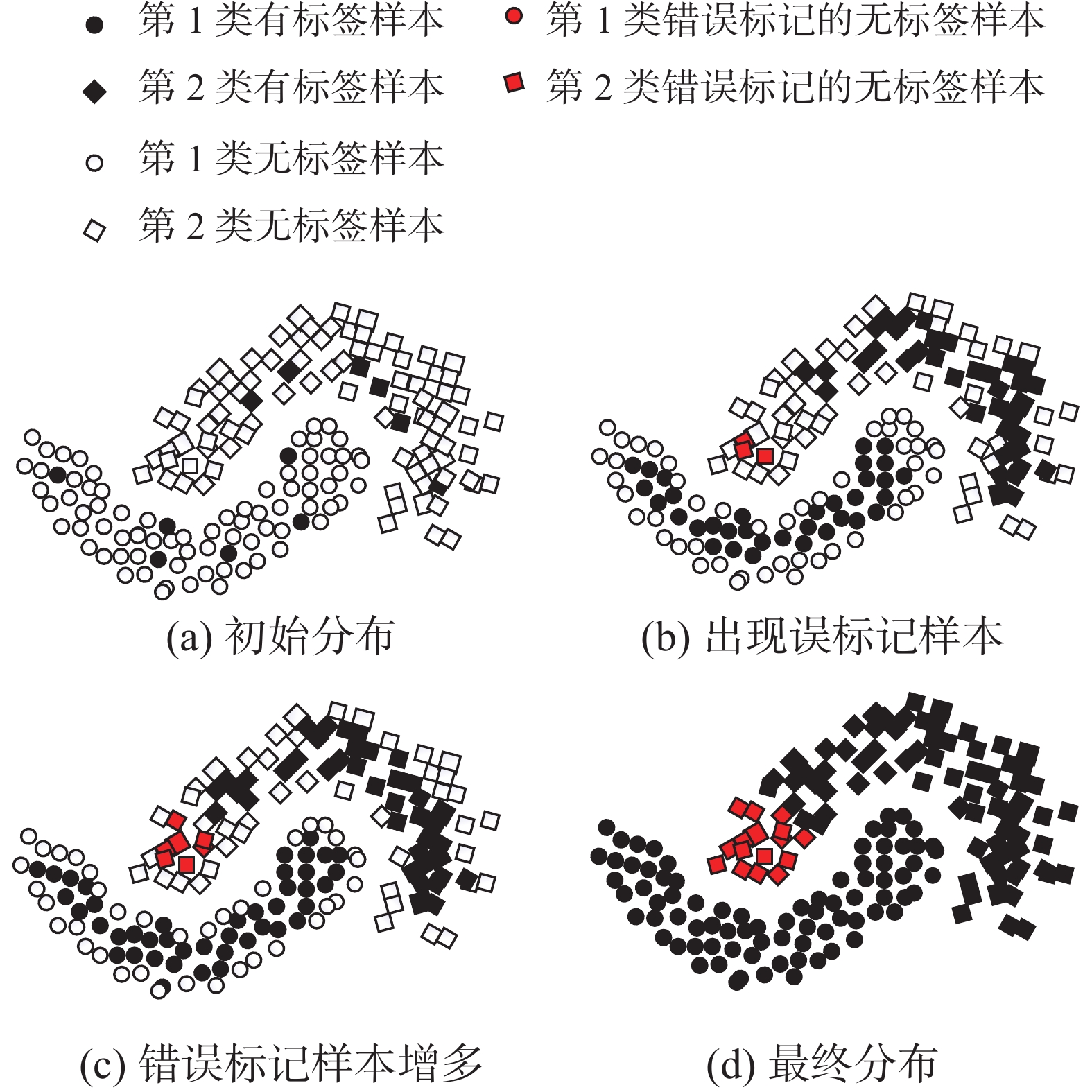
    在STDTDT算法中无标签样本是依据局部离群因子从小到大分批次输入模型。优先输入无标签样本中的密集样本，密集样本依据最近的k个有标签样本判断其类别，然而这种方法可能会导致密集样本被误标记，导致伪标签错误传播，最终使得分类边界位于高密度区域。如图1(a)所示，部分高密度区域的第2类无标签样本更靠近低密度区域的第1类的有标签样本。随着模型迭代训练，部分高密度区域的第2类无标签样本被误标记，形成错误的伪标签样本，如图1(b)中红色样本所示。随着模型迭代次数增加，红色样本使得附近更多无标签样本被误标记，导致误标记样本的错误累积，如图1(c)所示。随着模型训练完成，误标记样本的错误累积使得分类边界穿过高密度区域，如图1(d)所示。

    图  1  样本误标记示意
    Fig.  1  Diagram of samples mislabeling
    下载: 全尺寸图片

    针对上述问题，受到插值一致性[32]与无标签样本是不平等[33]启发，本文提出了一种伪标签差异性检验的方法。插值一致性鼓励样本之间的插值样本在预测上保持一致，使得分类边界位于到低密度区域。分类边界位于低密度区域，可以促使分类边界尽可能往低密度区域移动，避免分类边界往高密度区域移动。而分类边界的移动易受伪标签样本的影响，伪标签样本基于最近的k个有标签样本判断其类别。本文使用局部离群因子划分高密度区域和低密度区域。假设与伪标签样本最近且同类别的k个有标签样本的平均局部离群因子大于最近且不同类别的k个有标签样本的平均局部离群因子，伪标签样本将推动分类边界往高密度区域移动。同时为避免分类边界需要穿过高密度区域到达低密度区域，将推动分类边界往高密度区域移动的伪标签样本剔除类别，放入下轮迭代的无标签样本中。因此，伪标签差异性检验的具体过程如下：

    1) 定义（密集距离）样本xi、xj之间的密集距离为

    $$ {v_{ij}} = {\tau _i}{\tau _j}||{x_i} - {x_j}|{|_2} $$

    式中$ \tau $i、$ \tau $j分别是样本xi、xj的局部离群因子。

    2)分别计算伪标签样本${x'_i}$与NL(${x'_i}$)、NU(${x'_i}$)中样本的密集距离之和：

    $$ {V_L}({x'_i}) = \sum\limits_{{x_p} \in {N_L}({x_i}^\prime )} {{v_{ip}}} $$
    $$ {V_U}({x'_i}) = \sum\limits_{{x_q} \in {N_U}({x_i}^\prime )} {{v_{iq}}} $$

    式中：NL(${x'_i}$)是与${x'_i}$相距最近且同类别的K个样本集合，NU(${x'_i}$)是与${x'_i}$相距最近且不同类别的K个样本集合。

    3) 计算伪标签样本${x'_i}$的不确定度：

    $$ P({x'_i}) = L{V_k}({x'_i})/U{V_k}({x'_i}) $$

    式中P(${x'_i}$)越大代表伪标签样本${x'_i}$的不确定度越高，越容易被误标记。

    4) 选出不确定度大于1的伪标签样本，剔除类别，并入下轮迭代的无标签样本中。其中，当伪标签样本${x'_i}$的不确定度大于1时，NL(${x'_i}$)中样本的平均局部离群因子大于NU(${x'_i}$)中样本的平均局部离群因子。

    伪标签样本${x'_i}$的VL(${x'_i}$)、VU(${x'_i}$)为

    $$ {V_L}({x'_i}) = {\tau _i}\sum\limits_{{x_p} \in {N_L}({x_i}^\prime )} {{\tau _p}||{{x'}_i} - {x_p}|{|_2}} $$
    $$ {V_U}({x'_i}) = {\tau _i}\sum\limits_{{x_q} \in {N_U}({x_i}^\prime )} {{\tau _q}||{{x'}_i} - {x_q}|{|_2}} $$

    由于伪标签样本${x'_i}$与NL(${x'_i}$)中的样本具有相同的类别可得：

    $$ \sum\limits_{{x_p} \in {N_L}({x_i}^\prime )} {||{{x'}_i} - {x_p}|{|_2}} \;\; < \sum\limits_{{x_q} \in {N_U}({x_i}^\prime )} {||{{x'}_i} - {x_q}|{|_2}} $$ (1)

    由于${x'_i}$不确定度大于1，所以VL(${x_1}^\prime $)大于VU(${x'_i}$)可得：

    $$ \sum\limits_{{x_p} \in {N_L}({x_i}^\prime )} {{\tau _p}||{{x'}_i} - {x_p}|{|_2}} \;\; > \sum\limits_{{x_q} \in {N_U}({x_i}^\prime )} {{\tau _q}||{{x'}_i} - {x_q}|{|_2}} $$ (2)

    由拉格朗日中值定理，对于函数f(x)，一定存在一个或多个点c$ \in $[a,b]，得到：

    $$ \int_a^b {f(x)} {\rm{d}}x = f(c) \cdot (b - a) $$

    式中：f(c)为f(x)在区间[a,b]上的均值，若a=min($ \tau $p)， b=max($ \tau $p)，xp$ \in $NL(${x'_i}$)，当K取值较大时，存在xc$ \in $NL(${x'_i}$)满足：

    $$ \sum\limits_{{x_p} \in {N_L}({x_i}^\prime )} {{\tau _p}||{{x'}_i} - {x_p}|{|_2}} \approx {\tau _c}\sum\limits_{{x_p} \in {N_L}({x_i}^\prime )} {||{{x'}_i} - {x_p}|{|_2}} $$

    同理可得存在xd $ \in $ NU(${x'_i}$)满足：

    $$ \sum\limits_{{x_q} \in {N_U}({x_i}^\prime )} {{\tau _q}||{{x'}_i} - {x_q}|{|_2}} \approx {\tau _d}\sum\limits_{{x_q} \in {N_U}({x_i}^\prime )} {||{{x'}_i} - {x_q}|{|_2}} $$

    由式(1)、(2)可得：

    $$ {\tau _c} > {\tau _d} $$

    由于$ \tau $c、$ \tau $d分别代表NL(${x'_i}$)、NU(${x'_i}$)中样本的平均局部离群因子，VL(${x'_i}$)值比VU(${x'_i}$)越大，NU(${x'_i}$)中的样本更可能位于低密度区域，伪标签样本${x'_i}$的类别就越可能出现图1所示情况，越容易被误标记，并造成误标记样本的错误累积。

    2.4   STDTDT算法

    STDTDT算法的伪代码如下：

    输入　L、U；

    输出　H。

    1) 计算L与U的局部离群因子，并依照局部离群剔除掉L和U中的离群点，后对U进行分类标注；

    2) 利用L训练H；

    3) While U$ \ne \varnothing $或U连续3次相同 do

    4) 从U中取标注最小前m/10个样本存入$U'$；

    5) 使用H从$U'$中选出高置信度样本S，并赋予其伪标签，使用动态阈值函数更新阈值；

    6) S进行伪标签差异性检验，找出不确定度大于1的高置信度样本$S'$；

    7) $L \leftarrow L + S - S'$，$ U \leftarrow U - S + S' $，$U' \leftarrow S'$;

    8) 用扩充后的L训练H；

    9) End while

    3.   实验结果与分析

    3.1   实验设置和数据集描述

    为了验证本文算法的有效性，在12个基准数据集上进行实验，实验中配置环境如下：本文的实验平台均为windows 10专业版，CPU为AMD Ryzen 7 5700 GB，显存为32 GB。12个数据集均来源于公开的UCI数据库，数据集的详细信息如表1所示。数据集Breast_Cancer_Wisconsin、Wine_Quality_Red、Pima_Indians_Diabetes、Qualitative_Bankruptcy、Indian_Liver_Patient_Dataset在表格中分别简写为Breast、Wine_Q_R、Pima、Qualitative、Indian_L_P。选取9个相关的ST算法进行对比，分别为编辑自训练算法(self-training with editing, SETRED)[34]、编辑多标签自训练算法(multi-label self-training method with editing, MLSTE)[35]、结合密度峰值与最近邻居噪声过滤器的自训练算法(self-training method with density peaks and edied nearest neighbor, STDPENN)[36]、结合密度峰值与全近邻噪声过滤器的自训练算法(self-training method with density peaks and all knn, STDPAKNN)[36]、STSFCM[19]、STDP[20]、STDPC-EWS[21]、STDPINN[22]、STDPMLM[23]。各个算法的参数设置如表2所示，STDP[10]已经详细讨论参数Pa的设定。

    表  1  UCI数据集描述
    Table  1  Description of UCI datasets
    数据集数量类别数维度
    Breast69929
    Gauss502000250
    Liver34526
    Gauss50X2000250
    Ecoil33678
    German1000224
    Pima76828
    Qualitative25026
    Segmentation2310719
    Indian_L_P583210
    Vehicle846418
    Wine_Q_R1599611
    表  2  参数设置描述
    Table  2  Description of the parameter setting
    算法参数
    SETREDk=10
    MLSTE$\theta $=0.1
    STFCM${\varepsilon _1} = 1/c$
    STDPPa=2，k=3
    STDPENNPa=2，k=3
    STDPAKNNPa=2，k=3
    STDPCEWSPa=2，$\theta $=0.1
    STDPINNPa=2
    STDPMLMPa=2，r=k×c
    STDTDTK=15，k=3，T0=4

    3.2   对比实验

    为了验证STDT算法的性能，本文选取12个数据集进行实验。同时为了减少实验误差，本文在每个数据集上采用十折交叉验证。在训练过程中，从训练样本集中随机选取10%作为有标签样本集，在每个数据集上运行50次，以计算各算法在测试集的分类准确率及伪标签样本集准确率的平均值和标准差。模型在测试集上的实验结果如表3与表4所示，模型在伪标签样本集上的实验结果如表5与表6所示。

    表  3  不同算法在测试集上分类准确率
    Table  3  Classification accuracy of different algorithms on the test sets %
    算法BreastGauss50LiverGauss50XEcoilGerman
    SETRED96.25±2.1679.47±4.1757.67±7.9387.49±2.6281.79±6.6069.24±4.10
    MLSTE73.49±10.9890.54±1.7855.67±8.1191.15±2.0781.92±5.5766.32±4.59
    STFCM96.50±1.9889.02±1.9958.31±7.9789.13±1.8581.14±6.2068.98±4.24
    STDP95.73±2.2287.92±2.0759.93±9.3389.09±1.7881.49±6.6867.8±3.51
    STDPENN96.76±1.8989.52±1.8060.11±8.4390.19±2.0680.00±6.5769.18±4.29
    STDPAKNN96.56±1.8588.45±2.1059.75±8.2890.52±2.1780.42±7.3568.86±4.15
    STDPCEWS96.16±2.2287.82±2.2159.92±8.8089.18±1.9081.84±5.8167.8±3.67
    STDPINN95.39±2.5688.81±3.3859.79±3.9890.78±2.5280.79±8.4365.26±5.35
    STDPMLM96.30±2.1089.61±2.1962.49±7.3090.44±1.9684.12±6.0667.04±4.78
    STDTDT97.01±1.8391.02±1.6264.53±8.2691.38±1.8985.02±5.7069.54±4.18
    注：加黑代表最优结果，下同。
    表  4  不同算法在测试集上分类准确率
    Table  4  Classification accuracy of different algorithms on the test sets %
    算法PimaQualitativeSegmentationIndian_L_PVehicleWine_Q_R
    SETRED67.58±6.1175.60±9.6380.28±2.6865.90±5.9647.97±4.5947.07±3.74
    MLSTE66.81±5.4170.72±9.1576.09±2.7845.95±8.2244.81±5.6425.63±4.81
    STFCM66.23±5.3473.12±8.8183.54±2.0666.52±4.6550.62±4.9946.59±3.49
    STDP62.84±7.3774.00±10.0384.17±2.4068.16±5.1850.47±5.0746.55±3.62
    STDPENN63.02±5.8270.64±11.6982.68±2.3468.12±5.8549.37±5.9047.68±3.54
    STDPAKNN65.44±5.7670.48±11.9082.96±2.6468.57±6.5747.98±5.9747.11±3.21
    STDPCEWS62.45±7.1974.96±9.7983.97±2.3467.09±5.4250.54±5.1946.72±3.61
    STDPINN64.82±6.2572.64±10.5784.45±2.6169.73±6.1144.05±6.0347.17±4.09
    STDPMLM71.12±5.0277.76±3.5387.28±1.7666.24±5.4860.83±4.5043.58±3.96
    STDTDT73.55±5.8178.88±8.3288.43±2.2471.59±5.4761.87±5.6850.46±4.06
    表  5  不同算法中伪标签的准确率
    Table  5  Accuracy of different algorithms on the pseudo-label sample sets %
    算法BreastGauss50LiverGauss50XEcoilGerman
    SETRED93.63±0.7977.64±1.9957.63±2.9586.93±1.1879.37±1.7368.24±1.07
    MLSTE62.38±8.0296.04±0.2147.99±1.7694.70±0.2387.73±1.6767.85±0.98
    STFCM91.18±0.7788.33±0.4861.46±2.9991.15±0.5381.02±1.6969.07±0.94
    STDP90.44±1.0787.51±0.8461.45±3.1489.64±0.8084.68±2.2068.27±1.31
    STDPENN92.03±0.6091.58±0.6061.87±4.4693.65±0.4983.30±2.3169.82±0.85
    STDPAKNN92.45±0.6291.72±1.0961.60±4.0594.14±0.6786.82±1.8770.75±0.75
    STDPCEWS93.60±1.4087.43±1.0160.86±3.8789.84±0.8784.25±2.4268.42±1.51
    STDPINN90.46±1.8992.25±16.4160.37±4.7891.75±1.2079.65±3.4869.83±8.03
    STDPMLM90.44±0.7591.80±0.7166.25±2.3194.14±0.5185.86±1.8072.38±1.50
    STDTDT93.69±1.2496.89±0.3768.18±2.5197.56±0.5388.42±1.3973.35±1.05
    表  6  不同算法中伪标签准确率
    Table  6  Accuracy of different algorithms on the pseudo-label sample sets %
    算法PimaQualitativeSegmentationIndian_L_PVehicleWine_Q_R
    SETRED65.65±2.4853.61±5.4477.75±1.1465.52±1.7347.82±1.6753.07±1.86
    MLSTE65.96±1.3040.53±5.2178.41±2.2854.09±1.6645.67±2.080.89±0.60
    STFCM66.56±2.4849.96±3.8081.59±0.7165.66±1.2151.05±1.4951.79±1.07
    STDP61.92±3.9454.48±5.9482.98±1.2667.30±1.6149.87±2.2052.07±1.60
    STDPENN63.10±4.3044.70±7.7483.61±1.1868.51±1.6849.41±2.4654.48±1.39
    STDPAKNN68.24±3.5945.57±7.7186.91±1.0768.94±1.4952.38±2.8255.37±1.36
    STDPCEWS61.68±4.2655.55±5.6982.85±1.4266.79±2.0449.93±1.8652.50±1.60
    STDPINN68.59±4.4062.25±6.4184.54±2.8963.77±5.5248.90±4.9254.61±5.02
    STDPMLM74.95±1.3970.35±3.1485.52±1.3967.97±1.9659.10±1.8350.15±1.28
    STDTDT76.67±1.8774.23±7.6590.17±0.9172.01±0.8260.52±3.3757.79±1.21

    根据表3与表4可知，STDTDT算法在12个UCI数据集上测试集的分类准确率均高于对比算法。在Wine_Quality_Red、Indian_Liver_Patient_Dataset、Pima_Indians_Diabetes、Liver上分别比第2名提高了2.78%、1.86%、2.43%、2.04%。由于上述数据集的样本数量较少，属于同一类别的样本数量较少，同时维度较低，所以局部密度反映的空间信息越准确[37-38]，差异性检验的效果越强，虽然Wine_Quality_Red数据集的样本数量较多，但同一类别的数量较少，局部密度也能相对准确地反映样本的空间信息。

    根据表5与表6可得，在12个数据集上，STDTDT算法伪标签样本的准确率均优于对比的ST算法。在Pima_Indians_Diabetes、Gauss50、Gauss 50X、Segmentation数据集上，选取伪标签样本的准确率分别比第2名提高了2.43%、4.64%、2.86%、3.26%。STDTDT算法选取的伪标签样本的准确率高，相对应的STDTDT算法选取的伪标签样本集的质量优于对比算法选取的伪标签样本集。由于STDTDT算法考虑有标签样本在训练样本中分布对模型的影响，使用伪标签差异性检验的方法，降低位于低密度区域的边界样本产生的误标记样本数量，同时使用动态阈值，提高选取高置信度样本的质量，所以本文算法性能优于对比算法。

    3.3   有标签样本比例对分类器性能的影响

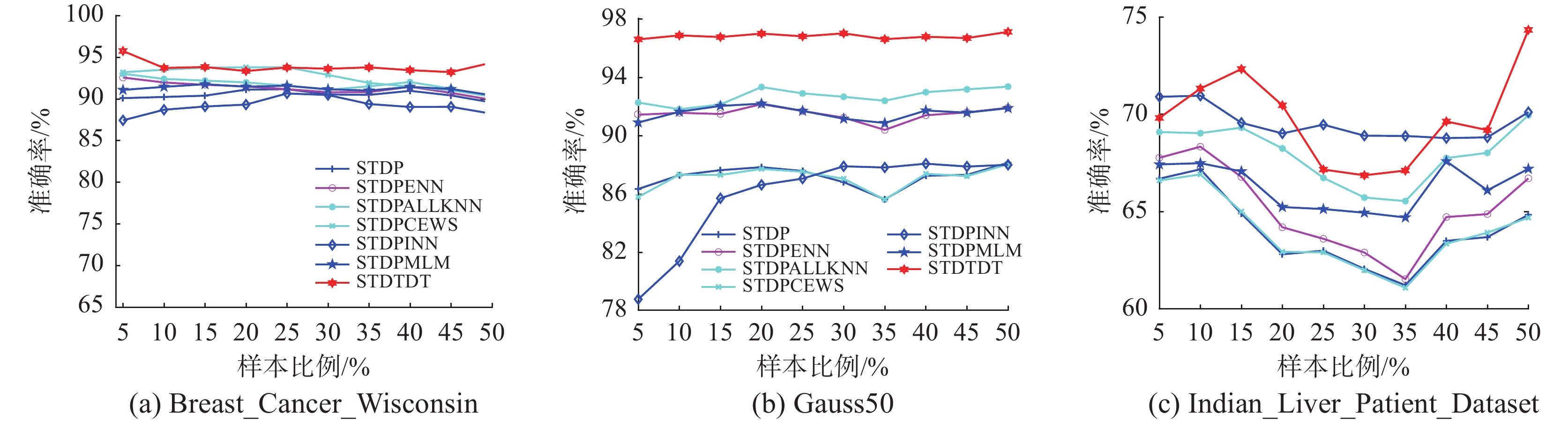
    为了验证有标签样本占训练样本的比例对STDTDT性能的影响，本文选取STDP、STDPENN、STDPAKNN、STDPCEWS、STDPINN、STDPML-M算法进行对比实验，选取比例为5%~50%的初始有标签样本进行实验。实验结果如图2所示，在12个数据集上分别给出不同比例下这些算法中测试集的分类准确率。

    图  2  不同有标签比例与分类准确率的关系曲线
    Fig.  2  Graph of the relationship between different label proportions and classification accuracy
    下载: 全尺寸图片

    由图2可见在Liver、Gauss50X、Ecoil、Pi-ma_Indians_Diabetes、Qualitative_Bankruptcy、Segmentation、Vehicle、Wine_Quality_Red数据集上，随着有标签样本占训练样本比例的增加，测试集的分类准确率明显上升。在Breast_Cancer_Wisc-onsin、Gauss50、Indian_Liver_Patient_Dataset数据集上，当有标签样本比例小于10%时，随着有标签比例增加，测试集的分类准确率明显增加，当有标签样本比例大于15%时，随着有标签比例增加，测试集的分类准确率先下降后上升，当有标签比例大于40%时，所有算法均取得相近的分类准确率。在Breast_Cancer_Wisconsin、Gauss50、Indian_Liver_ Patient_Dataset数据集上，有标签比例的增加，反而会降低分类器性能，可能由于数据维度较高，ST算法出现距离聚集等问题，模型效果不佳，后续通过学习曲线对比实验进一步探究。在12个数据集上，STDTDT算法性能大部分情况都优于对比算法，这是因为STDTDT算法使用动态阈值和伪标签差异性检验，阈值随着分类器性能变化而改变，使得分类器能更有效地区分高置信度样本。此外，伪标签差异性检验能有效找到被误标记的样本，把误标记样本重新变为无标签样本，放入下轮训练的无标签样本中，从而降低误标记样本数量，提高伪标签样本的质量。

    3.4   学习曲线对比实验

    为了进一步探究在Breast_Cancer_Wisconsin、Gauss50、Indian_Liver_Patient_Dataset数据集上出现的随着有标签样本比例增加，导致分类器性能下降的原因。本文选取STDP、STDPENN、STDPAKNN、STDPCEWS、STDPINN、STDPML-M、STDTDT算法，选取比例为5%~50%的初始有标签样本进行实验。在3个数据集上分别给出不同比例下不同算法选取的伪标签样本集的准确率，实验结果如图3所示。使用主成分分析[39]分别将Breast_Cancer_Wisconsin、Gauss50、Indian_Liver_ Patient_Dataset数据集由原来9、50、10维分别降为5、25、5维。在降维后的3个数据集上分别给出不同比例下算法在测试集上的分类准确率，实验结果如图4所示。通过主成分分析对数据集进行可视化分析，实验结果如图5所示。

    图  3  不同有标签比例与伪标签样本集准确率的关系曲线
    Fig.  3  Graph of the relationship between different label proportions and pseudo-labeled sample sets accuracy
    下载: 全尺寸图片
    图  4  降维数据集上有标签比例与分类准确率的关系曲线
    Fig.  4  Graph of the relationship between label proportions and classification accuracy on the reduced-dimension datasets
    下载: 全尺寸图片

    如图3所示，随着有标签样本比例增加，分类器在Indian_Liver_Patient_Dataset数据集上伪标签样本集的准确率波动较大，呈现先下降后上升的趋势，模型在训练数据与测试数据上的表现趋势相同，并未出现过拟合现象。

    如图4所示，在降维前和降维后的数据集上，随着有标签样本比例的不断增加，分类器性能在降维后的Gauss50、Breast_Cancer_Wisconsin数据集上相对稳定，性能不断增强。降维前的Gauss50、Breast_Cancer_Wisconsin数据集上出现随着有标签比例增加，分类器性能先下降后上升是受维度的影响。在Gauss50数据集上，随着有标签样本比例增加，分类器性能反而降低是由于数据维度较高导致。在Breast_Cancer_Wisconsin数据集上，由于样本数量较少，难以捕获数据的复杂性，降维后的数据复杂性降低，使得模型更容易发现数据的空间结构。

    如图5所示，Indian_Liver_Patient_Dataset与Breast_Cancer_Wisconsin、Gauss50数据集中有两种类别，图5中黑色和红色分别代表一种类别。相比与Indian_Liver_Patient_Dataset数据集，Gauss50和Breast_Cancer_Wisconsin数据集的样本更符合半监督平滑假设和聚类假设，相邻点之间存在相对平滑的标签变化。Breast_Cancer_Wisconsin、Gauss50、Indian_Liver_Patient_Dataset数据集的类别不平衡比率分别为1.9、1、2.5。Indian_Liver_Patient_Dataset相比Breast_Cancer_Wisconsin数据集类别更不平衡。

    图  5  数据集可视化
    Fig.  5  Visualization of the datasets
    下载: 全尺寸图片

    Indian_Liver_Patient_Dataset数据集出现随着有标签样本比例的增加分类器性能下降的原因，可能由于类别不平衡、非典型数据分布导致，受本算法的局限性，未来将进一步研究和拓展本项工作[40-43]。

    3.5   消融实验

    为了分别验证STDTDT算法采用局部离群因子剔除部分有标签样本、动态阈值选取高置信度样本、差异性检验缓解错误累积的有效性，本文对STDTDT算法和不剔除部分有标签样本的STDTDT1、使用固定阈值的STDTDT2、不使用差异性检验的STDTDT3算法进行了消融实验。实验中设置与对比实验相同，实验参数如表3所示，在各数据集上运行50次，计算测试集的平均分类准确率，实验结果如表7所示。

    表  7  STDTDT算法的消融实验
    Table  7  Ablation experiment of STDTDT algorithm %
    数据集STDTDT1STDTDT2STDTDT3STDTDT
    Breast97.11±2.5097.02±2.2397.13±2.2797.11±2.50
    Gauss5091.28±1.9990.99±1.8191.05±1.8191.28±1.99
    Liver63.69±7.7558.63±8.1658.40±7.8663.69±7.75
    Gauss50X90.82±2.1890.48±2.1990.62±2.0190.82±2.18
    Ecoil85.07±6.6381.21±6.7980.85±6.7285.19±6.54
    German69.14±4.6469.05±4.9568.48±4.9669.14±4.64
    Pima73.63±4.3870.38±3.9970.30±3.7673.68±4.29
    Qualitative78.17±2.2077.28±2.6777.52±2.3778.41±2.21
    Segmentation90.75±1.9888.33±2.4387.88±2.4190.86±1.94
    Indian_L_P71.51±5.7871.15±5.9471.39±6.0171.51±5.78
    Vehicle60.72±4.5759.33±4.4358.15±4.6660.89±4.56
    Wine_Q_R50.91±3.4148.65±3.4348.89±3.5150.91±3.41

    由表7可知，使用局部离群因子剔除部分有标签样本，在Ecoil、Pima_Indians_Diabetes、Segmentation、Vehicle数据集上均有小幅度提升。由于数据集中存在低质量的有标签样本，此类样本的离群程度较高，容易误导模型学习错误的分类边界[30]，从而降低分类器的性能。在其他数据集上STDTDT算法与STDTDT1算法结果相同，由于有标签样本中离群点的数量为零，导致算法在测试集上的分类结果相同。使用固定阈值替代动态阈值，在12个数据集上模型性能均小于STDTDT算法。由于动态阈值使得阈值随着分类器性能增强而不断增长，阈值的增长能提高选取的高置信度样本的质量，同时为防止由于阈值过高导致的选取高置信度样本数量过少，在每次选取高置信度样本为零时降低阈值。STDTDT3算法在12个数据集上算法结果均小于STDTDT算法。由于差异性检验能检测部分误标记样本，减少错误累积。

    3.6   超参数实验

    验证计算局部离群因子的近邻个数K与动态阈值函数中参数T对于实验影响，实验中选取有标签样本、无标签样本、测试样本比例与对比实验相同。其中，K$ \in $[2,20]，T$ \in $[1,10]，K和T$ \in $N+，实验结果如图6所示。选取STDTDT算法在12个数据集上的最优效果，如表8所示。

    图  6  不同参数在不同数据集上的分类准确率
    Fig.  6  Classification accuracy of different parameters on different datasets
    下载: 全尺寸图片

    由图6所示，在Gauss50、Gauss50X、Ecoil、Indian_Liver_Patient_Dataset、Wine_Quality_Red、Pima_Indians_Diabetes、German数据集上，当K的取值小于5时，STDTDT算法在测试集上的分类准确率较低。这是因为近邻个数不合适，导致不能准确反映样本的局部密度，以及后续差异性检验效果不佳。由表8可知，最优参数下的STDTDT算法在Segmentation、German、Wine_Quality_Red数据集上提高了1.97%、3.01%、8.13%。因为在数据集样本数量较多时，随着K的增大，局部密度能更准确反映空间信息，使用局部密度的伪标签差异性检验的效果更优，模型的性能更好。Segmentation、Wine_Quality_Red提高T0值，提高动态阈值函数的最低阈值，使得分类器选取的高置信度样本的质量更好，模型性能更优。

    表  8  STDTDT算法测试集的最高分类准确率
    Table  8  Highest classification accuracy of the test datasets in STDTDT algorithm
    数据集KT0准确率/%
    Breast4497.54
    Gauss507591.87
    Liver71065.53
    Gauss50X9492.98
    Ecoil16186.14
    German18672.55
    Pima4674.35
    Qualitative2679.20
    Segmentation12290.40
    Indian_L_P17973.47
    Vehicle10261.96
    Wine_Q_R10658.59

    4.   结束语

    针对ST算法存在的问题，本文提出了一种基于动态阈值与差异性检验的自训练算法。该算法首先利用样本与周边样本的密集情况，剔除有标签样本中的离群点，依据局部离群因子对无标签样本进行分类标注后分批次处理，使得分类器更易于选取高置信度样本。其次依据样本的变化设计动态隶属度阈值函数，以提高选取的高置信度样本的质量。最后，使用伪标签差异性检验的方法，使得分类边界尽可能在低密度区域，解决误标记样本累积的问题。在12个UCI数据集上的对比实验表明，STDTDT算法在测试集和伪标签样本集上的分类性能优于对比算法，验证算法有效性。

    然而，本文算法仍存在以下不足： 1)样本维度较高时，容易形成距离聚集的问题； 2)簇间密度差异较大时，使用局部离群因子无法准确衡量样本是否位于高密度区域。因此，后续将进一步研究在维度较高且复杂的数据集上如何更有效解决错误累积问题，同时减少大量无标签样本引起的计算复杂度，在后续工作中找到更准确地衡量样本是否位于高密度区域的方法。

  • 图  1   样本误标记示意

    Fig.  1   Diagram of samples mislabeling

    下载: 全尺寸图片

    图  2   不同有标签比例与分类准确率的关系曲线

    Fig.  2   Graph of the relationship between different label proportions and classification accuracy

    下载: 全尺寸图片

    图  3   不同有标签比例与伪标签样本集准确率的关系曲线

    Fig.  3   Graph of the relationship between different label proportions and pseudo-labeled sample sets accuracy

    下载: 全尺寸图片

    图  4   降维数据集上有标签比例与分类准确率的关系曲线

    Fig.  4   Graph of the relationship between label proportions and classification accuracy on the reduced-dimension datasets

    下载: 全尺寸图片

    图  5   数据集可视化

    Fig.  5   Visualization of the datasets

    下载: 全尺寸图片

    图  6   不同参数在不同数据集上的分类准确率

    Fig.  6   Classification accuracy of different parameters on different datasets

    下载: 全尺寸图片

    表  1   UCI数据集描述

    Table  1   Description of UCI datasets

    数据集数量类别数维度
    Breast69929
    Gauss502000250
    Liver34526
    Gauss50X2000250
    Ecoil33678
    German1000224
    Pima76828
    Qualitative25026
    Segmentation2310719
    Indian_L_P583210
    Vehicle846418
    Wine_Q_R1599611

    表  2   参数设置描述

    Table  2   Description of the parameter setting

    算法参数
    SETREDk=10
    MLSTE$\theta $=0.1
    STFCM${\varepsilon _1} = 1/c$
    STDPPa=2，k=3
    STDPENNPa=2，k=3
    STDPAKNNPa=2，k=3
    STDPCEWSPa=2，$\theta $=0.1
    STDPINNPa=2
    STDPMLMPa=2，r=k×c
    STDTDTK=15，k=3，T0=4

    表  3   不同算法在测试集上分类准确率

    Table  3   Classification accuracy of different algorithms on the test sets %

    算法BreastGauss50LiverGauss50XEcoilGerman
    SETRED96.25±2.1679.47±4.1757.67±7.9387.49±2.6281.79±6.6069.24±4.10
    MLSTE73.49±10.9890.54±1.7855.67±8.1191.15±2.0781.92±5.5766.32±4.59
    STFCM96.50±1.9889.02±1.9958.31±7.9789.13±1.8581.14±6.2068.98±4.24
    STDP95.73±2.2287.92±2.0759.93±9.3389.09±1.7881.49±6.6867.8±3.51
    STDPENN96.76±1.8989.52±1.8060.11±8.4390.19±2.0680.00±6.5769.18±4.29
    STDPAKNN96.56±1.8588.45±2.1059.75±8.2890.52±2.1780.42±7.3568.86±4.15
    STDPCEWS96.16±2.2287.82±2.2159.92±8.8089.18±1.9081.84±5.8167.8±3.67
    STDPINN95.39±2.5688.81±3.3859.79±3.9890.78±2.5280.79±8.4365.26±5.35
    STDPMLM96.30±2.1089.61±2.1962.49±7.3090.44±1.9684.12±6.0667.04±4.78
    STDTDT97.01±1.8391.02±1.6264.53±8.2691.38±1.8985.02±5.7069.54±4.18
    注：加黑代表最优结果，下同。

    表  4   不同算法在测试集上分类准确率

    Table  4   Classification accuracy of different algorithms on the test sets %

    算法PimaQualitativeSegmentationIndian_L_PVehicleWine_Q_R
    SETRED67.58±6.1175.60±9.6380.28±2.6865.90±5.9647.97±4.5947.07±3.74
    MLSTE66.81±5.4170.72±9.1576.09±2.7845.95±8.2244.81±5.6425.63±4.81
    STFCM66.23±5.3473.12±8.8183.54±2.0666.52±4.6550.62±4.9946.59±3.49
    STDP62.84±7.3774.00±10.0384.17±2.4068.16±5.1850.47±5.0746.55±3.62
    STDPENN63.02±5.8270.64±11.6982.68±2.3468.12±5.8549.37±5.9047.68±3.54
    STDPAKNN65.44±5.7670.48±11.9082.96±2.6468.57±6.5747.98±5.9747.11±3.21
    STDPCEWS62.45±7.1974.96±9.7983.97±2.3467.09±5.4250.54±5.1946.72±3.61
    STDPINN64.82±6.2572.64±10.5784.45±2.6169.73±6.1144.05±6.0347.17±4.09
    STDPMLM71.12±5.0277.76±3.5387.28±1.7666.24±5.4860.83±4.5043.58±3.96
    STDTDT73.55±5.8178.88±8.3288.43±2.2471.59±5.4761.87±5.6850.46±4.06

    表  5   不同算法中伪标签的准确率

    Table  5   Accuracy of different algorithms on the pseudo-label sample sets %

    算法BreastGauss50LiverGauss50XEcoilGerman
    SETRED93.63±0.7977.64±1.9957.63±2.9586.93±1.1879.37±1.7368.24±1.07
    MLSTE62.38±8.0296.04±0.2147.99±1.7694.70±0.2387.73±1.6767.85±0.98
    STFCM91.18±0.7788.33±0.4861.46±2.9991.15±0.5381.02±1.6969.07±0.94
    STDP90.44±1.0787.51±0.8461.45±3.1489.64±0.8084.68±2.2068.27±1.31
    STDPENN92.03±0.6091.58±0.6061.87±4.4693.65±0.4983.30±2.3169.82±0.85
    STDPAKNN92.45±0.6291.72±1.0961.60±4.0594.14±0.6786.82±1.8770.75±0.75
    STDPCEWS93.60±1.4087.43±1.0160.86±3.8789.84±0.8784.25±2.4268.42±1.51
    STDPINN90.46±1.8992.25±16.4160.37±4.7891.75±1.2079.65±3.4869.83±8.03
    STDPMLM90.44±0.7591.80±0.7166.25±2.3194.14±0.5185.86±1.8072.38±1.50
    STDTDT93.69±1.2496.89±0.3768.18±2.5197.56±0.5388.42±1.3973.35±1.05

    表  6   不同算法中伪标签准确率

    Table  6   Accuracy of different algorithms on the pseudo-label sample sets %

    算法PimaQualitativeSegmentationIndian_L_PVehicleWine_Q_R
    SETRED65.65±2.4853.61±5.4477.75±1.1465.52±1.7347.82±1.6753.07±1.86
    MLSTE65.96±1.3040.53±5.2178.41±2.2854.09±1.6645.67±2.080.89±0.60
    STFCM66.56±2.4849.96±3.8081.59±0.7165.66±1.2151.05±1.4951.79±1.07
    STDP61.92±3.9454.48±5.9482.98±1.2667.30±1.6149.87±2.2052.07±1.60
    STDPENN63.10±4.3044.70±7.7483.61±1.1868.51±1.6849.41±2.4654.48±1.39
    STDPAKNN68.24±3.5945.57±7.7186.91±1.0768.94±1.4952.38±2.8255.37±1.36
    STDPCEWS61.68±4.2655.55±5.6982.85±1.4266.79±2.0449.93±1.8652.50±1.60
    STDPINN68.59±4.4062.25±6.4184.54±2.8963.77±5.5248.90±4.9254.61±5.02
    STDPMLM74.95±1.3970.35±3.1485.52±1.3967.97±1.9659.10±1.8350.15±1.28
    STDTDT76.67±1.8774.23±7.6590.17±0.9172.01±0.8260.52±3.3757.79±1.21

    表  7   STDTDT算法的消融实验

    Table  7   Ablation experiment of STDTDT algorithm %

    数据集STDTDT1STDTDT2STDTDT3STDTDT
    Breast97.11±2.5097.02±2.2397.13±2.2797.11±2.50
    Gauss5091.28±1.9990.99±1.8191.05±1.8191.28±1.99
    Liver63.69±7.7558.63±8.1658.40±7.8663.69±7.75
    Gauss50X90.82±2.1890.48±2.1990.62±2.0190.82±2.18
    Ecoil85.07±6.6381.21±6.7980.85±6.7285.19±6.54
    German69.14±4.6469.05±4.9568.48±4.9669.14±4.64
    Pima73.63±4.3870.38±3.9970.30±3.7673.68±4.29
    Qualitative78.17±2.2077.28±2.6777.52±2.3778.41±2.21
    Segmentation90.75±1.9888.33±2.4387.88±2.4190.86±1.94
    Indian_L_P71.51±5.7871.15±5.9471.39±6.0171.51±5.78
    Vehicle60.72±4.5759.33±4.4358.15±4.6660.89±4.56
    Wine_Q_R50.91±3.4148.65±3.4348.89±3.5150.91±3.41

    表  8   STDTDT算法测试集的最高分类准确率

    Table  8   Highest classification accuracy of the test datasets in STDTDT algorithm

    数据集KT0准确率/%
    Breast4497.54
    Gauss507591.87
    Liver71065.53
    Gauss50X9492.98
    Ecoil16186.14
    German18672.55
    Pima4674.35
    Qualitative2679.20
    Segmentation12290.40
    Indian_L_P17973.47
    Vehicle10261.96
    Wine_Q_R10658.59
    • 参考文献(43)
  • [1] LAI C I, CHUANG Y S, LEE H Y, et al. Semi-supervised spoken language understanding via self-supervised speech and language model pretraining[C]//ICASSP 2021−2021 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2021: 7468−7472.
    [2] LIU Quande, YU Lequan, LUO Luyang, et al. Semi-supervised medical image classification with relation-driven self-ensembling model[J]. IEEE transactions on medical imaging, 2020, 39(11): 3429–3440. doi: 10.1109/TMI.2020.2995518
    [3] LI Changchun, LI Ximing, OUYANG Jihong. Semi-supervised text classification with balanced deep representation distributions[C]//Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing. Stroudsburg: Association for Computational Linguistics, 2021: 5044–5053.
    [4] VAN ENGELEN J E, HOOS H H. A survey on semi-supervised learning[J]. Machine learning, 2020, 109(2): 373–440. doi: 10.1007/s10994-019-05855-6
    [5] YANG Xiangli, SONG Zixing, KING I, et al. A survey on deep semi-supervised learning[J]. IEEE transactions on knowledge and data engineering, 2023, 35(9): 8934–8954. doi: 10.1109/TKDE.2022.3220219
    [6] DUARTE J M, BERTON L. A review of semi-supervised learning for text classification[J]. Artificial intelligence review, 2023, 56(9): 9401–9469. doi: 10.1007/s10462-023-10393-8
    [7] SOHN K, BERTHELOT D, LI Chunliang, et al. FixMatch: simplifying semi-supervised learning with consistency and confidence[EB/OL]. (2020-01-21)[2023-03-25]. https://arxiv.org/abs/2001.07685.pdf.
    [8] KIM J, MIN Y, KIM D, et al. ConMatch: semi-supervised learning with confidence-guided consistency regularization[C]//European Conference on Computer Vision. Cham: Springer, 2022: 674−690.
    [9] ZHANG Zhiwu, JING Xiaoyuan, WANG Tiejian. Label propagation based semi-supervised learning for software defect prediction[J]. Automated software engineering, 2017, 24(1): 47–69. doi: 10.1007/s10515-016-0194-x
    [10] ISCEN A, TOLIAS G, AVRITHIS Y, et al. Label propagation for deep semi-supervised learning[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2019: 5070−5079.
    [11] ZHAO Zhen, ZHOU Luping, WANG Lei, et al. LaSSL: label-guided self-training for semi-supervised learning[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2022, 36(8): 9208–9216. doi: 10.1609/aaai.v36i8.20907
    [12] XU Qiantong, BAEVSKI A, LIKHOMANENKO T, et al. Self-training and pre-training are complementary for speech recognition[C]//ICASSP 2021−2021 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2021: 3030−3034.
    [13] 程康明, 熊伟丽. 一种自训练框架下的三优选半监督回归算法[J]. 智能系统学报, 2020, 15(3): 568–577. doi: 10.11992/tis.201905033

    CHENG Kangming, XIONG Weili. Three-optimal semi-supervised regression algorithm under self-training framework[J]. CAAI transactions on intelligent systems, 2020, 15(3): 568–577. doi: 10.11992/tis.201905033
    [14] CHEN Baixu, JIANG Junguang, WANG Ximei, et al. Debiased Self-Training for Semi-Supervised Learning[C]//Proceedings of the Annual Conference on Neural Information Processing Systems. Red Hook: Curran Associates, 2022: 92−100.
    [15] WANG Yidong, CHEN Hao, HENG Qiang, et al. FreeMatch: self-adaptive thresholding for semi-supervised learning[EB/OL]. (2022-05-15)[2023-05-12].https://arxiv.org/abs/2205.07246.
    [16] PARK S, KIM G, OH Y, et al. Self-evolving vision transformer for chest X-ray diagnosis through knowledge distillation[J]. Nature communications, 2022, 13: 3848. doi: 10.1038/s41467-022-31514-x
    [17] GAN Haitao, SANG Nong, HUANG Rui, et al. Using clustering analysis to improve semi-supervised classification[J]. Neurocomputing, 2013, 101: 290–298. doi: 10.1016/j.neucom.2012.08.020
    [18] WU Di, SHANG Mingsheng, LUO Xin, et al. Self-training semi-supervised classification based on density peaks of data[J]. Neurocomputing, 2018, 275: 180–191. doi: 10.1016/j.neucom.2017.05.072
    [19] ZOU Yang, YU Zhiding, LIU Xiaofeng, et al. Confidence regularized self-training[C]//2019 IEEE/CVF International Conference on Computer Vision. Piscataway: IEEE, 2019: 5982−5991.
    [20] MUKHERJEE S, AWADALLAH A H. Uncertainty-aware self-training for text classification with few labels[EB/OL]. (2020-06-27)[2023-05-12].https://arxiv.org/abs/2006.15315.
    [21] WEI Danni, YANG Youlong, QIU Haiquan. Improving self-training with density peaks of data and cut edge weight statistic[J]. Soft computing, 2020, 24(20): 15595–15610. doi: 10.1007/s00500-020-04887-8
    [22] 吕佳, 刘强, 李帅军. 结合密度峰值和改进自然邻居的自训练算法[J]. 南京大学学报(自然科学版), 2022, 58(5): 805–815.

    LYU Jia, LIU Qiang, LI Shuaijun. Self-training method based on density peaks and improved natural neighbor[J]. Journal of Nanjing university (natural science edition), 2022, 58(5): 805–815.
    [23] LI Shuaijun, LYU Jia. Self-training algorithm based on density peaks combining globally adaptive multi-local noise filter[J]. Intelligent data analysis, 2023, 27(2): 323–343. doi: 10.3233/IDA-226575
    [24] CHEN Hao, TAO Ran, FAN Yue, et al. SoftMatch: addressing the quantity-quality trade-off in semi-supervised learning[EB/OL]. (2023-01-26)[2023-05-12].https://arxiv.org/abs/2301.10921.
    [25] OUYANG Boya, SONG Yu, LI Yuhai, et al. EBOD: an ensemble-based outlier detection algorithm for noisy datasets[J]. Knowledge-based systems, 2021, 231: 107400. doi: 10.1016/j.knosys.2021.107400
    [26] BREUNIG M M, KRIEGEL H P, NG R T, et al. LOF: identifying density-based local outliers[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2000: 93−104.
    [27] GUO Lanzhe, ZHANG Zhenyu, JIANG Yuan, et al. Safe deep semi-supervised learning for unseen-class unlabeled data[C]//Proceedings of the 37th International Conference on Machine Learning. New York: ACM, 2020: 3897−3906.
    [28] XU Yi, SHANG Lei, YE Jinxing, et al. Dash: semi-supervised learning with dynamic thresholding[EB/OL]. (2021-09-01)[2023-05-12].https://arxiv.org/abs/2109.00650.
    [29] GUO Lanzhe, LI Yufeng. Class-imbalanced semi-supervised learning with adaptive thresholding[C]//Proceedings of International Conference on Machine Learning. New York: ACM, 2022: 8082−8094.
    [30] YAO Huifeng, HU Xiaowei, LI Xiaomeng. Enhancing pseudo label quality for semi-supervised domain-generalized medical image segmentation[EB/OL]. (2022-01-21)[2023-05-12].https://arxiv.org/abs/2201.08657.
    [31] 刘学文, 王继奎, 杨正国, 等. 密度峰值隶属度优化的半监督Self-Training算法[J]. 计算机科学与探索, 2022, 16(9): 2078–2088. doi: 10.3778/j.issn.1673-9418.2102018

    LIU Xuewen, WANG Jikui, YANG Zhengguo, et al. Semi-supervised self-training algorithm for density peak membership optimization[J]. Journal of frontiers of computer science and technology, 2022, 16(9): 2078–2088. doi: 10.3778/j.issn.1673-9418.2102018
    [32] VERMA V, KAWAGUCHI K, LAMB A, et al. Interpolation consistency training for semi-supervised learning[J]. Neural networks, 2022, 145: 90–106.
    [33] REN Zhongzheng, YEH R A, SCHWING A G. Not all unlabeled data are equal: learning to weight data in semi-supervised learning[EB/OL]. (2020-07-02)[2023-05-16].https://arxiv.org/abs/2007.01293.
    [34] LI Ming, ZHOU Zhihua. SETRED: self-training with editing[C]//Proceedings of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. New York: ACM, 2005: 611−621.
    [35] WEI Zhihua, WANG Hanli, ZHAO Rui. Semi-supervised multi-label image classification based on nearest neighbor editing[J]. Neurocomputing, 2013, 119: 462–468.
    [36] LI Junnan, ZHU Qingsheng, WU Quanwang. A self-training method based on density peaks and an extended parameter-free local noise filter for k nearest neighbor[J]. Knowledge-based systems, 2019, 184: 104895.
    [37] HOULE M E, KRIEGEL H P, KRÖGER P, et al. NII Technical Reports[R]. [S.l.: s.n.], 2009: 1−29.
    [38] ZIMEK A, SCHUBERT E, KRIEGEL H P. A survey on unsupervised outlier detection in high-dimensional numerical data[J]. Statistical analysis and data mining: the ASA data science journal, 2012, 5(5): 363–387.
    [39] 许子微, 陈秀宏. 自步稀疏最优均值主成分分析[J]. 智能系统学报, 2021, 16(3): 416–424.

    XU Ziwei, CHEN Xiuhong. Sparse optimal mean principal component analysis based on self-paced learning[J]. CAAI transactions on intelligent systems, 2021, 16(3): 416–424.
    [40] 陆宇,赵凌云,白斌雯,等. 基于改进的半监督聚类的不平衡分类算法[J]. 计算机应用, 2022, 42(12): 3750–3755.

    LU Yu, ZHAO Lingyun, BAI Binwen, et al. Imbalanced classification algorithm based on improved semi-supervised clustering[J]. Applied science and technology, 2022, 42(12): 3750–3755.
    [41] 陈波,朱英韬. 基于噪声估计的钢材表面图像增强与缺陷检测[J]. 应用科技, 2023, 50(3): 116–121.

    CHEN Bo, ZHU Yingtao. Image enhancement and defect detection of steel surface based on noise estimation[J]. Applied science and technology, 2023, 50(3): 116–121.
    [42] 高玉森,朱昌明,岳闻. 一种改进的增强组合特征判别性的典型相关分析[J]. 应用科技, 2022, 49(2): 119–126.

    GAO Yusen, ZHU Changming, YUE Wen. An improved canonical correlation analysis to enhance the discriminability of combined features[J]. Applied science and technology, 2022, 49(2): 119–126.
    [43] 王立国, 马骏宇, 李阳. 联合多种空间信息的高光谱半监督分类方法[J]. 哈尔滨工程大学学报, 2021, 42(2): 280–285.

    WANG Liguo, MA Junyu, LI Yang. Hyperspectral semi-supervised classification algorithm considering multiple spatial information[J]. Journal of Harbin Engineering University, 2021, 42(2): 280–285.
WeChat 点击查看大图
图(6)  /  表(8)
出版历程
  • 收稿日期:  2023-06-26
  • 网络出版日期:  2023-11-24

目录

    /

    返回文章
    返回