Review of the research of granular fuzzy rule-based modeling
-
摘要: 本文旨在梳理粒度模糊规则模型中的主要研究及构建方法，并且进行系统分析与总结。粒计算是一种能模拟人类思维方式和求解复杂问题的新兴理论体系，以此为基础的粒度模型为复杂非线性系统的描述和问题求解探索了新的方向。粒度模糊规则模型将信息粒融入现有的模糊规则建模方法中，进行粒度级别的系统建模，以实现更高层次的数据分析与推理。本文简要介绍模糊聚类和模糊规则模型的基础知识；归纳了信息粒的构建方法，并讨论了相应的评估方法；总结了典型的粒度模糊规则模型的设计架构和优化方法。Abstract: The purpose of this paper is to explore the main research and construction method for granular fuzzy rule model, and make a systematic analysis and summary of it. Granular computing is an emerging theoretical system that simulates patterns of human thinking and solves complex problems, and the granular model based on it explores a new direction for the description and problem solving of complex nonlinear system. Among which the granular fuzzy rule-based model incorporates information granule into existing fuzzy rule-based modeling methods to achieve granular-level system modeling for data analysis and inference at a higher level. This paper first briefly introduces the basics of fuzzy clustering and fuzzy rule-based models, next summarizes the construction method of information granules and discusses corresponding evaluation methods. Further, the design architecture and optimization method are summarized.
-
人类处理问题的一个显著优势是根据问题的特性在不同抽象程度中进行分析思考[1-3]。随着人工智能技术的不断发展，当前智能系统的研究重点关注认知机理的理解、分析和模拟[4]，着重分析人类的认知和信息处理方法，包括人类的学习、分析、推理和决策能力等。粒计算(granular computing, GrC)能够模拟人类思考过程，从抽象角度对问题进行分析推理，并反映人类思考和处理信息的过程。作为计算智能中一种新型信息处理范式，粒计算的研究涵盖了基于不同粒度解决复杂问题的理论、方法、技术和工具，属于人工智能认知机理研究的领域。1996年，文献[5]首次提出粒计算这一概念，一直沿用至今。1997年，Zadeh[5]在模糊集和模糊系统的基础上，首次创新性地提出了信息粒度化(information granulation)的概念[6]。文章中讨论了不同领域中信息粒的不同表现形式，并将模糊逻辑与其他处理不精确性和不确定性的方法区分开来。1985年，Hobbs[7]发表名为“粒度(granularity)”的论文，围绕信息粒的分解与合并方法进行讨论。自此，一些研究人员[8-10]先后围绕信息粒的结构分析、信息表征以及模型框架等问题进行探索，国内外围绕粒计算的研究迅速发展。粗糙集理论的引入[11]为不精确、不完备的问题提供了理论方法。1988年，Lin[8]构建了基于邻域系统的粒度模型。1996年，“词计算”理论[12]的提出，为基于模糊理论的推理模型奠定基础。Yao[13]围绕信息粒的构造和计算等基本问题进行分析讨论。王国胤等[14-15]针对不完备信息系统，对于信息粒的规则表示和分解算法进行应用研究。基于商空间理论的模型[16-17]的提出，从多粒度的角度为数据挖掘提供了新的计算方法和工具。随着粒计算理论[18-20]的不断发展，与其他机器学习方法相结合的研究不断涌现。
在粒度神经网络的概念[21]提出之前，模糊集与神经网络的协同研究已经不断发展。Song等[22]围绕粒度神经网络的架构、类别和应用进行系统地总结。同时，一些学者开展了粒度神经网络在分类问题[23]和推荐系统[24]等领域中的应用研究。粒度认知图[25]是基于图学习的粒度模型的代表。其目标是利用概念集和彼此之间的因果关系表示问题，已经被广泛应用于时间序列分析[26]、自然语言处理[27]等领域中。在决策问题研究中，粒计算也受到了学界的广泛关注，Qin等[28]对粒计算在决策中的应用进行了系统概述。一些学者利用云模型[29-30]、三支决策模型[31]、数据驱动的粒度神经网络模型[32]，以及新型的粒度模型[33]在基于信息粒度优化分配的覆盖特异性度量、多粒度语言决策等领域开展了相关研究。Pedrycz[34]全面总结信息粒的构建和计算方法，详细归纳粒计算思想下的数据分析方法。在2022年中国人工智能系列白皮书《粒计算与知识发现》中，将粒计算研究分为基于粒的表征[35-36]、度量[37]、计算[38]和决策[28]4个方面，全面介绍了粒计算框架下理论方法的发展现状，同时归纳了粒计算在生物医疗、智能控制等领域的应用，讨论分析粒计算的后续研究方向。
粒度模型主要围绕模糊集[38-39]、粗糙集[40-41]、商空间[16-17]和云模型[42-43]等理论分析问题。这些粒度模型都在抽象层次以信息粒作为最小单位构建一个通用框架，根据它们对应研究目标的不同，可以将其分为两大类[18,24]：将不确定性计算作为研究目标的模糊集理论模型[18]和以多粒度计算为目标的粗糙集理论模型[40]、商空间理论模型[19]和与模型理论模型[20]等3种模型。Zadeh[5,12]在模糊集理论的基础上定义信息粒的概念，并基于模糊集合论构造以词为定义域的推理及计算方法，该方法与人类思维方式更为接近。在此基础上，Pedrycz等[26,44]设计模糊信息粒构建理论框架，进一步发展基于模糊集的粒计算模型。模糊集理论模型通过隶属度值描述不确定问题，后续研究不断扩展基于隶属度函数计算的理论方法，如区间模糊集[27,45] 和二型模糊集[46]等。粗糙集理论是由Pawlak[11]提出用于解决集合边界不确定问题的方法，该理论通过近似空间刻画了目标概念的不确定性，并探究知识空间中粒的表示、转换和相互依存等主要问题。大量研究[20,47]对基于粗糙集的粒计算模型进行了优化，并结合实际问题构建了模糊粗糙集[47]、多粒度粗糙集[45,48] 等模型。结合人类从不同粒度空间分析问题这一现象，张钹等[49]结合商级理论，构建了商空间理论模型。商空间理论模型可以由包括问题论域、论域属性和拓扑结构的三元组表示，并利用“保真原理”和“保假原理”进行模型推理。商空间理论模型通过对商空间之间的关系、综合、分析和推理进行研究，从而求解复杂问题。张玲等[50]进一步将模糊集思想引入了商空间理论，为商空间理论后续发展提供了有力理论支撑。在概率论的基础上，李德毅[51]提出云模型理论，该理论模型面向语言值中的随机性、模糊性、关联性等问题进行探究，从而能够实现定性定量转换的认知模型。相关学者围绕云模型[43]进行扩展，王国胤等[52]对云模型与粒计算的交叉研究进行分析，并进行了系统的总结。
不同理论体系所构建的粒度模型存在区别，但之间也相互关联[16,48]。同时，尽管粒度模型构建的方法不同，粒计算的本质都是数据信息的粒化、计算和推理。在模糊集理论模型中，基于模糊方法的粒度规则模型在数据挖掘的基础上，增强了模型的鲁棒性和可解释性[53]。由于其高效且实用性强的特点和优势，近年来吸引了越来越多的关注和研究。在围绕信息粒构建和以此为基础的粒度模糊规则模型构建的研究中，以加拿大的Witold [34,46,54]、Oscar等[55-56]为代表的研究团队开展了大量研究。相关论文相继在IEEE Transactions on Cybernetics、IEEE Transactions on Fuzzy Systems、IEEE Transactions on Systems, Man, and Cybernetics: Systems、Pattern Recognition、Information Sciences、Knowledge-Based Systems和Applied Soft Computing等高水平期刊上发表。然而，在国内从事该方向的研究人员相对较少，在中文文献中，也缺乏系统地总结粒度模糊规则模型构建方法的研究成果。因此，本文聚焦近年来粒度模糊规则模型的构建方法，归纳总结了当前领域中关键问题和重要成果，为相关研究人员在该领域的进一步研究提供参考。
1. 粒度模糊规则模型预备知识
在粒度模糊规则模型中，聚类方法和模糊规则模型分别是信息粒化和近似推理的基础，因此本节围绕这两部分进行简要介绍。
1.1 模糊聚类
聚类方法[57]是近年机器学习与数据挖掘的研究热点之一。它通过某种相似性度量划分数据，使得簇内样本差异尽可能小同时簇间样本差异尽可能大，从而挖掘数据隐藏的结构信息。聚类的实现依赖数据本身属性信息，无需标签信息，是一种有效的无监督数据分析方法。模糊聚类算法[57-58]可以构造能够描述模糊边界的隶属度函数，是一种软聚类方法，能够以模糊相似度描述数据的结构和关系方面发挥重要作用。其中，模糊C均值(fuzzy C means, FCM)算法[59-60]是一种常用的数据挖掘方法。
具体而言，FCM通过最小化目标函数
$J$ ，不断迭代优化[60]产生聚类中心集合$v = \left[ {{v_1},{v_2}, \cdots ,{v_c}} \right]$ 和对应的隶属度矩阵${{\boldsymbol{U}}_{ki}}$ 。目标函数表示为$$ J =\sum_{i = 1}^c \sum_{k = 1}^N u_{ki}^m|\left| {{x_k} - {v_i}} \right||_2^2 $$ 式中：
$m\left( {m > 1} \right)$ 为模糊化系数；$c$ 为聚类中簇的个数；${u_{ki}}$ 为隶属度矩阵中的元素，表示数据${x_k}$ 对第$i$ 个聚类中心的隶属度值；$\left\| {{x_{{k}}} - {v_{{i}}}} \right\|_2$ 为数据${x_{{k}}}$ 和聚类中心${v_{{i}}}$ 之间的欧氏距离。隶属度函数和聚类中心表示为$$ {u_{ki}} = \frac{1}{{\displaystyle\sum_{j = 1}^c {{\left( {\frac{{\left\| {{x_k} - {v_i}} \right\|_2^2}}{{\left\| {{x_k} - {v_j}} \right\|_2^2}}} \right)}^{\frac{2}{{m - 1}}}}}} $$ $$ {v_i} = \frac{{\displaystyle\sum_{k = 1}^N u_{ki}^m{x_k}}}{{\displaystyle\sum_{k = 1}^N u_{ki}^m}} $$ 一旦满足终止条件（如设置最大迭代次数）便停止迭代。由于聚类过程中的参数（聚类中心的个数
$c$ 和模糊系数$m$ ）对于聚类的性能具有很大影响，相关的优化算法[61-62]不断提出以应对不同问题的需求。FCM的本质特征是将相似的对象组合，整个过程以数据为驱动而无需先验知识，最终聚合的簇能够实现对数据的抽象表示。因此FCM是一种形成粒结构的有效工具。在一些研究中，将FCM产生的聚类中心称作原型。
1.2 模糊规则模型
规则模型能够捕获输入和输出空间之间的关联关系，将复杂问题合理划分为一系列子问题，实现对复杂信息的局部处理。基于“IF-THEN”(如果…，则…)规则的模型由于其鲁棒性和可解释性，能够实现复杂非线性系统的建模[37,63]。通过不同的算法和优化方法，基于规则的模型可以多种形式构建。由于模糊建模能够发现和挖掘隐藏的数据信息，实现以人为中心的知识表征，因此模糊规则系统已成为模糊规则生成的常用框架。在众多模糊规则模型的扩展方法中，高木关野(takagi-sugeno, TS) 模糊规则模型[64]将复杂非线性系统分解为多个局部模型，建模过程简洁且具有可解释性，是一种经典的模糊规则模型架构。
给定一组输入−输出空间的数据样本
$\left[ {{\boldsymbol{x}},{\boldsymbol{y}}} \right]$ ，其中${\boldsymbol{x}} = \left[ {{x_1}\;\;{x_2}\;\; \cdots \;\;{x_n}} \right]$ ，TS模糊模型的规则描述为$$ {\text{If }}x{\text{ is }}{U_i}\left( x \right),{\text{ Then }}{f_i}\left( x \right) = {a_{i0}} + {a_{i1}}{x_{i1}} + {a_{i2}}{x_{i1}}+ \cdots + {a_{in}}{x_{in}} $$ 式中：
$i=1,2,\cdots ； c$ 为规则的总数；${\boldsymbol{a}} = \left[ {a_{i0}}\;\;{a_{i1}}\;\; \cdots \;\; {a_{in}} \right]^{\rm{T}}$ 为输入变量的参数向量；${U_i}\left( x \right)$ 为在$n$ 维输入空间${{\bf{R}}^n}$ 中的隶属度函数，常被看作一种信息粒。在当前的许多研究中采用FCM构建信息粒，并基于该信息粒建立模糊规则模型。规则中结论部分${f_i}\left( {\boldsymbol{x}} \right)$ 的形式多样，一般采用线性函数表征。一些研究[65]在线性函数${f_i}\left( {\boldsymbol{x}} \right)$ 中引入信息粒，可以表示为$$ {f_i}\left( {\boldsymbol{x}} \right) = {{\boldsymbol{w}}_i} + {\boldsymbol{a}}_i^{\rm{T}} \left( {{\boldsymbol{x}} - {{\boldsymbol{v}}_i}} \right) $$ 式中：
${{\boldsymbol{w}}_i}$ 和${{\boldsymbol{v}}_i}$ 分别对应于输出空间和输入空间的原型，参数向量$a$ 通过最小二乘法实现。采用FCM方法，满足
$\displaystyle\sum_{i = 1}^c {U_i}=1$ 的约束，通过加权聚合机制得到输出$\hat y$ 为$$ \hat y = \displaystyle\sum_{i = 1}^c {U_i}{f_i}\left( {\boldsymbol{x}} \right) $$ 在数值TS模糊模型的设计中，引入了模糊集的思想，通过构建信息粒从原始数据空间中挖掘有效信息，进而实现可解释的规则推理。值得注意的是，从大量数据中选择合理的有效信息这一思想，与近些年来发展的原型学习（prototype learning）十分相近。原型学习[65-67]旨在从样本空间中寻求包含数据信息的原型，有利于减少冗余信息、发掘数据结构，是当前机器学习的研究重点之一。
2. 信息粒的构建方法
信息粒是知识表示和学习的关键组件。同时，根据问题复杂性的不同，信息粒的大小（包含信息量的具体程度）也会不同。过细的信息粒（单个元素）无法从抽象层次上表述问题，过粗的信息粒中信息量过于宽泛，无法学习有效信息。因此，信息粒度决定了问题的抽象程度，对于问题的描述和解决至关重要[35,37]。显然，信息粒的学习和表征由问题驱动，不存在通用的信息粒度满足所有问题。在这一部分围绕信息粒的主要形式和粒化与解粒化机制两部分分析信息粒的构建。
2.1 信息粒的主要形式
在粒计算中，信息粒有多种形式，其中包括：
1)集合（区间）[68-71]：集合并非通过枚举法选择其中的元素，而是通过二分法在区间[0,1]中的特征函数描述抽象概念。简单来说，信息粒中存在的元素必须是唯一确定的，即元素可以在区间信息粒中或元素不在区间信息粒中，但不允许两种情况同时发生。则在论域X中，映射函数
${{\varPhi }}$ 表示为$$ {{\varPhi }}\left( x \right) = 1,x \in {{\varPhi }}\text{；}{{\varPhi }}\left( x \right) = 0,x \notin {{\varPhi }} $$ 2)模糊集[47,54]：由数据空间中的元素映射到区间[0,1]的隶属度函数实现抽象程度的描述，避免二分法严格划分的要求。隶属度函数
${{{\varPhi }}_A}$ 表示元素$x$ 对于模糊集${{A}}$ 的隶属程度：${{{\varPhi }}_A}:x \to \left[ {0,1} \right], x \to {{{\varPhi }}_A}\left( x \right)$ ，${{{\varPhi }}_A}$ 越大，说明元素属于集合的程度越高。显然，区间集合是模糊集的一种特殊情况。3)粗糙集[47,72-73]：在难以区分的元素关系中，利用近似空间中的近似算子（上近似集和下近似集）描述抽象程度。粗糙集基于分类的思想，根据现有知识将数据划分。上近似集包括明确可分的元素，下近似包括存在不确定性的元素的最小集合，实现不确定性的数据表征。
4)阴影集[74-76]：根据某些阈值将元素分为完全属于某一类，完全不属于某一类和无法确定。与模糊集有些相似，由于不确定性，无法为阴影元素分配明确的隶属关系，因此使用[0,1]区间中的值进行表征。阴影集的构建是通过原始空间
$x$ 到空间$\{ 0,\left[ {0,1} \right]$ ,1}的映射实现的。除上述的几种理论外，还有公理模糊集[77]、概率集[78-79]等。
2.2 粒化与解粒化
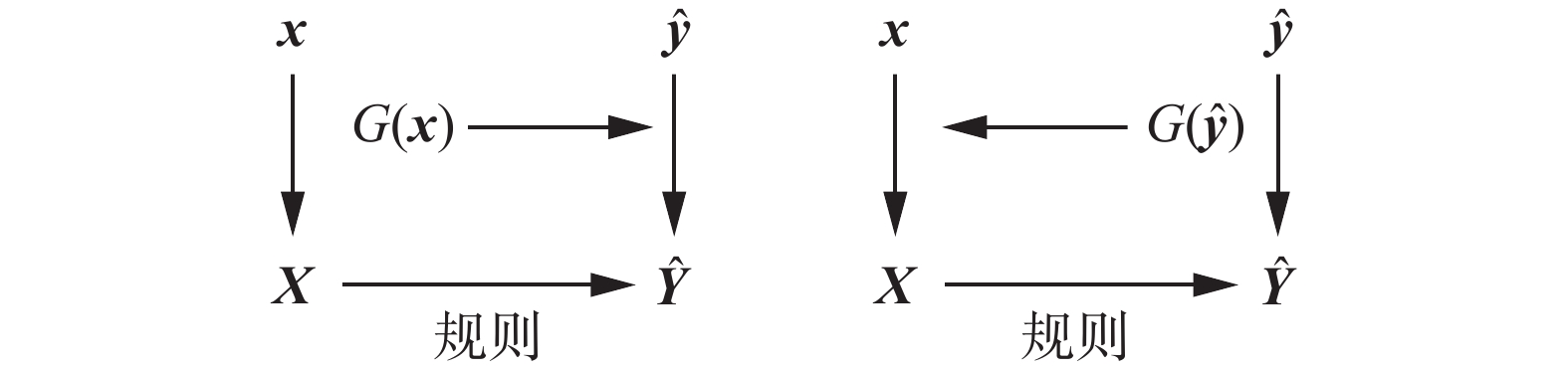
信号处理问题中存在编码与解码过程[80-81]，深度学习方法存在编码解码机制，这都是信息提取和重建的过程。粒化与解粒化(granulation and degranulation)的过程类似，目的都是提取信息中的关键特征[35]。人类凭借经验知识将某些接近或相似的元素聚合为实体集合，并以一种合理的抽象层次进行感知、分析和推理，推理的结果用以分析每个具体实体。该过程中的集合便是信息粒，将相似特征的实体聚合的过程为粒化机制，解粒化是在已构建信息粒的基础上，实现原始数据的重建。理想情况下，信息粒可以映射到原始数据空间[82]。在这一部分，本文主要围绕基于模糊集的粒化与解粒化机制进行分析。
假设有一个数据集合
$x = \left\{ {{x_1},{x_2}, \cdots ,{x_N}} \right\}$ ，其中，$ {x}_{i}位于n维度输入空间{{\bf{R}}}^{n} $ 。粒化（编码）是指信息粒集合${A_i}$ 表征原始数据集合$x$ 的过程，其中$i = 1, 2, \cdots ,c$ 。可以将其视为从原始数据空间到定义在[0,1]区间的模糊集空间的映射：$G:x \to {\left[ {0,1} \right]^c}$ 。而解粒化（解码）在粒化（模糊集）的基础上，通过某些评价指标实现原始数据的重建$\hat x$ 。解粒化的目标可以表示为${G^{ - 1}}\left( {G\left( x \right)} \right) = x$ ，但在实际情况中，重建数据集$\hat x \approx x$ ，其中$\hat x = {G^{ - 1}}\left( {G\left( x \right)} \right)$ 。映射${G^{ - 1}}$ 实现抽象程度高的空间到抽象程度低的空间的详细表征，因此这个过程并不是唯一的。对于简单的一维输入空间，三角模糊函数能够实现重构误差为零的粒化−解粒化机制[82]。但对于多变量数据而言，其他构建函数的方法更为有效。由于实用性和高效的优势，FCM成为构建模糊函数的一种常用方法。在粒化过程中，基于FCM构造的原型和隶属度矩阵描述原始数据结构，解粒化的过程与聚类的逆问题类似，在已知的原型和隶属度矩阵的基础上，重建原始数据。一般而言，解粒化通过重建性能指标（重建数据和原始数据之间的重建误差）指导该过程，重建误差越小，表明粒化机制越好。此外，一些研究也将聚类性能（如分类精度）指标作为重建误差衡量粒化的性能。
Pedrycz在文献[35]中首次基于FCM讨论与分析粒化−解粒化机制的原理，提出重建误差：
$P = \dfrac{1}{N}\displaystyle\sum_{k = 1}^N {\left| {\left| {\hat x - {x_k}} \right|} \right|^2}$ ，并分析模糊系数对于重建机制的影响。为了提高重建的质量，Hu等[83]引入原型增强机制，基于多种群体优化算法实现分区矩阵的优化。Zhang等[36]关注重构误差的监督机制对于聚类性能的影响，将聚类原型和重构数据的对偶表达式引入FCM从而实现算法增强。Graves等[84]引入核函数思想，比较原型位于不同特征空间的情况，对数据的分类精度和重建误差进行了综合研究。针对原型优化的监督机制的研究[37,85-86]不断发展，有助于增强算法的实用性。Izakian等[87]考虑到时空数据的特殊性，通过增广距离函数赋予聚类算法更大的灵活性。同时分析重建误差和预测误差评价指标指导数据重建的过程，成功将模型应用于时序数据分析。进一步，Izakian等[88]将粒化−解粒化的思想引入时序数据异常检测问题的研究，在设计框架中，采用粒化机制揭示时序数据的潜在结构信息，并将重建误差作为异常检测的评价指标，指导和学习异常数据的形状信息。模糊聚类产生的数值型表示方法不能完全表征数据本质，超立方体的信息粒结构作为一种替代的增强方案，可以应对更高层次的数据分析。如Galaviz等[89]以FCM得到的原型为核心，构造一种超矩形信息粒（超盒），并提出2种约束策略避免信息粒的重叠。Zhu等[90]围绕数值原型进行分配合理的信息粒度，通过参与粒化−解粒化机制实现信息粒的增强。在合理粒度准则的基础上，Zhang[91]在粒化过程中产生信息粒并利用解粒化机制指导信息粒的优化，从而应对非理想条件下的源检测问题。
除此之外，基于矢量量化概念的数据重建[92]，围绕不确定性原则实现的二型模糊集[93-94]等方法的粒化−解粒化机制都对于信息粒的构建具有重要意义。基于FCM的粒化−解粒化机制的分类与相关研究如表1所示。
3. 粒度模糊规则模型的构建
本节通过不同的粒化策略对粒度模糊规则模型的构建进行系统地分析，首先阐述模糊规则模型的整体框架，其次结合现有的理论方法分析不同策略的粒度模型。
3.1 粒度模糊规则模型的基本框架
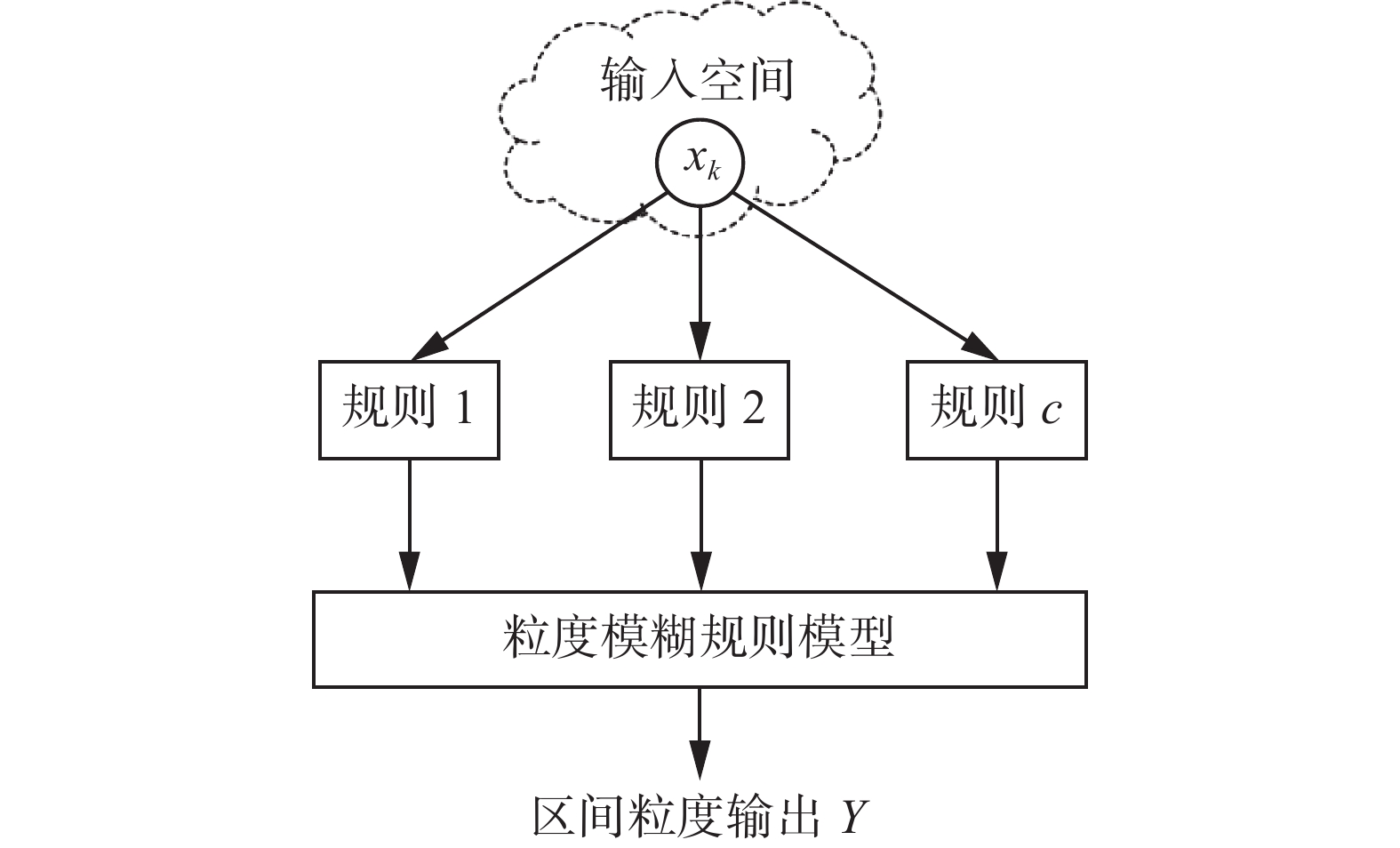
现有研究已经围绕模糊规则模型的设计和分析进行了大量的探索与实践，但数值结构的模型很难与目标输出的模型完全一致。为了应对这一问题，引入粒计算的思想，构建抽象程度的粒度模型，以弥补模型与目标模型之间的差异。模型的框架设计如图1所示。
图 1 粒度模糊规则模型的基本框架Fig. 1 Basic framework of granular fuzzy rule-based model
下载:
全尺寸图片
在粒度模糊规则模型框架中，对于输入空间
$x$ ，通过对c个模糊规则进行聚合实现粒度输出。基于TS模糊规则，其粒度模型结构设计为$$ {\text{Rule }}{\text{:}}{\text{ }}{\text{If }}x{\text{ is }}G\left( {{A_i}\left( x \right)} \right),{\text{ Then }}Y = {F_i}\left( x \right) $$ 规则可以表现出不同的语义。为了说明基于规则的建模的本质，采用基于聚类的粒化机制。利用聚类算法构建信息粒，实现输入空间数据与区间信息粒的映射
$G\left( {{A_i}\left( x \right)} \right)$ 的关联，从而通过规则聚合的方式实现粒度输出：$$ \hat Y = \displaystyle\sum_{i = 1}^p G\left( {{A_i}\left( x \right)} \right){F_i}\left( x \right) $$ 3.2 粒化策略设计方法
本节分析了2类粒化策略设计方法，并对当前相关的研究进行讨论，如表2所示。
3.2.1 数值型模糊规则模型的粒化策略
在合理的粒度分配策略指导下，数值模型扩展为粒度模糊规则模型。数值型模糊规则模型的粒化策略可以分为基于参数的粒化机制、基于输入空间的粒化机制和基于输入输出空间的协同粒化机制3种。
1)基于参数的粒化机制。
Pedrycz[54]从模糊规则模型出发，讨论粒度模型隐含的基本原理和关键结构，并从粒度参数空间分析粒度模型的基础设计过程。围绕规则参数构建粒度扩展范式，并用符号
$G\left( \cdot \right)$ 描述。随后，Pedrycz[34]在数值原型的基础上，引入抽象程度（信息粒度）增强数据关系的描述，利用合理的粒度原则量化信息粒的质量，构建由数据到数值原型到粒度原型的范式。Hu[95]借助数值模糊模型的设计，将粒度概念引入规则中的参数，创新性地提出3种参数空间的粒化策略：局部线性函数的参数($a$ )；规则中的原型($V$ )；将参数($a$ )和原型($V$ )结合，通过合理的粒度分配策略，将3种参数空间扩展为粒度形式，实现由数值空间到粒度空间的转化。值得一提的是，基于FCM算法构建的模糊集通常定义于$n$ 维空间中，在粒化过程中，将原型视为空间${{\bf{R}}^n}$ 中的元素并将其投影到各个维度的坐标上以便计算。通过对原型分配不同程度的信息粒度，将其构造为一个超矩形，从而模糊集以更为抽象的方式(区间)揭示输入数据空间中的结构。尽管FCM是描述模糊集的有效工具，但由于其算法本身的限制影响聚类的有效性。从这个角度出发，Zhu[96]利用特征加权的聚类算法构造用于条件部分的模糊集，以降低重构误差。通过对原型的粒度分配，构建更为有效的粒度模糊模型。同样，Hanyu[62]从聚类算法的改进入手，使其与规则结论部分中非线性映射的方向性保持一致，通过引入阈值区分规则，从而构建基于区间信息粒的粒度模型。围绕参数空间的3种粒化策略中，基于原型的策略使用最为广泛。在当前研究不断改进的基础上，所构建的粒度模糊模型也被用来解决不同复杂环境下的问题。Pedrycz[97]介绍了一种分布式模糊建模方法。在建模过程中采用增广FCM算法确定粒度参数，引入合理粒度原则指导粒度模糊模型的形成。Li[98]针对大规模多变量数据，将模糊规则与数据缩减和降维方法相结合，通过将原型扩展为区间信息粒形式，构建可解释的粒度模糊规则框架。该机制以数值向量的参数为中心，设计结构可以表示为
$$ \begin{array}{c} {{\boldsymbol{y}} = {f_i}\left( {{\boldsymbol{x}},{\boldsymbol{a}},\left[ {{\boldsymbol{v}},{\boldsymbol{w}}} \right]} \right) \to Y}{ = {f_i}\left( {{\boldsymbol{x}},G\left( {\boldsymbol{a}} \right),G\left( {\left[ {{\boldsymbol{w}},{\boldsymbol{v}}} \right]} \right)} \right)}= \\ { {F_i}\left( {{\boldsymbol{x}},{\boldsymbol{A}},\left[ {{\boldsymbol{V}},{\boldsymbol{W}}} \right]} \right)} \end{array} $$ 式中：G(·)为对数值参数向量应用某种粒度分配策略，从而生成相对应的粒度表征（如A是参数
$a$ 的区间粒度表示）。2)基于输入空间的粒化机制。
粒度输入空间往往是围绕输入数据构建的。一般而言，建模的过程是寻找输入属性到输出空间的映射关系，粒度输入空间对于模型起着至关重要的作用。不同的输入变量对模型的输出表现出不同的敏感性，基于输入空间的粒化机制将这一表现通过信息粒度的设置进行描述。针对这一点，Hu[99]围绕输入空间提出了一种合理的粒度分配策略并进行全局敏感度分析。Song[100]提出了一种层次性粒度分配策略以实现输入空间的粒度构建。在现实环境下数据存在不确定性（如信息缺失、高噪声等），导致后续的特征学习与规则推理存在误差。位于输入空间的信息粒以抽象层次捕获信息的同时，在一定程度上避免数据不确定性的影响。针对这一问题，一些研究围绕粒度输入空间构建模型。Zhong[101]依赖合理的粒度分配策略，构建将估算的缺失属性表示为信息粒的方法，并提出粒度量化指标指导该过程。针对粒度输入空间中信息粒中心学习的这一问题，Hu[102]引入基于概率信息粒度策略的FCM算法进行聚类。由于原型是通过聚类和监督学习方法生成和优化，其包含的数据特征和输出空间信息能够近似表示缺失属性。基于此，通过信息粒度的分配，将输入空间的估算值扩展为区间信息粒；尽管完整属性表示为区间形式，但左右边界相等，易于区分。从而利用模糊规则进一步构建粒度模糊模型。
该机制以数值输入向量为中心，设计结构可以表示为
$$ \begin{array}{c} {{\boldsymbol{y}} = {f_i}\left( {{\boldsymbol{x}},{\boldsymbol{a}},\left[ {{\boldsymbol{v}},{\boldsymbol{w}}} \right]} \right) \to Y}{ = {f_i}\left( {G\left( {\boldsymbol{x}} \right),{\boldsymbol{a}},\left[ {{\boldsymbol{v}},{\boldsymbol{w}}} \right]} \right)}= \\ { {F_i}\left( {{\boldsymbol{X}},{\boldsymbol{a}},\left[ {{\boldsymbol{v}},{\boldsymbol{w}}} \right]} \right)} \end{array} $$ 式中：
$G\left( {\boldsymbol{x}} \right)$ 为对数值输入应用粒度分配策略，生成输入信息粒${\boldsymbol{X}}$ 。3)基于输入输出空间的协同粒化机制。
上述信息粒构建策略中存在特定模式，即通过粒度参数实现输入到输出映射，得到区间形式的粒度输出。与基于规则参数的粒度分配策略不同，Li[103]从规则聚合的过程入手，考虑到加权数据在一定程度上表示输出空间的信息，借助合理的粒度分配策略构建区间信息粒，同时利用权重实现信息粒大小的缩放。构建的粒度模型无需提前进行数值计算，简化了模型构建和推导过程。为了避免基于模糊规则的回归模型产生的误差，Zhu[104]构建误差模型对回归模型的数值输出进行指导，两者聚合实现区间输出信息粒的构建。考虑到输入输出空间相关联的特性，Shen[105]使用改进FCM算法提升原型表征性能，并从输出空间出发，引入知识引导机制指导信息输入空间学习。Zhang[106]针对分布式环境中的数据特点，将数值模型视为分布式框架的局部表征，以数值误差均方根误差（root mean square error, RMSE）作为局部权重参数，在聚合过程中引入合理的粒度分配策略实现区间粒度输出。
基于输入输出空间的协同粒化机制的设计结构如图2所示。
$G\left( {\boldsymbol{x}} \right)$ 和$G\left( {\hat {\boldsymbol{y}}} \right)$ 分别对应输入空间和输出空间的粒化策略。
图 2 基于输入输出空间的协同粒化机制结构Fig. 2 Diagram of collaborative granulation mechanism based on input-output space下载:
全尺寸图片
3.2.2 粒度模糊规则模型直接构建策略
比起从数值结构扩展到粒度结构的两阶段过程，一个更简单的设计思想是如何直接构建信息粒反映原始数值数据的主要特征，实现粒度输入和输出空间的直接映射。
Lu[107]在研究中探讨了超盒的几何结构，强调了信息粒以超盒（多维区间）的形式出现对于揭示多维变量的本质和内在关系的重要性。并以此为基础，在输入输出空间直接构建信息粒，利用规则实现两者之间的联系建立粒度模型。Reyes-Galaviz[89]按照一定原则将输出数据划分为区间信息粒，由于输入数据与每个区间的输出数据密切相关，基于改进FCM围绕数据构造超盒粒。同时利用2种约束策略对其进行优化。Lu[108]在文献[107]的基础上，通过优化算法实现输入空间原型的优化，以此增强输出区间信息粒和原型信息之间的关联结构，进一步，在文献[109]中讨论3种不同的输出区间划分方法，从而指导具有置信度的输入超盒粒，围绕超参数实现粒度模糊模型的优化。
4. 粒度模糊规则模型的评估
粒度模型的性能依赖于合理的粒度分配策略，因此本节首先讨论常用的2种粒度分配策略方法，其次总结常用的性能评估指标。
4.1 粒度分配策略设计方法
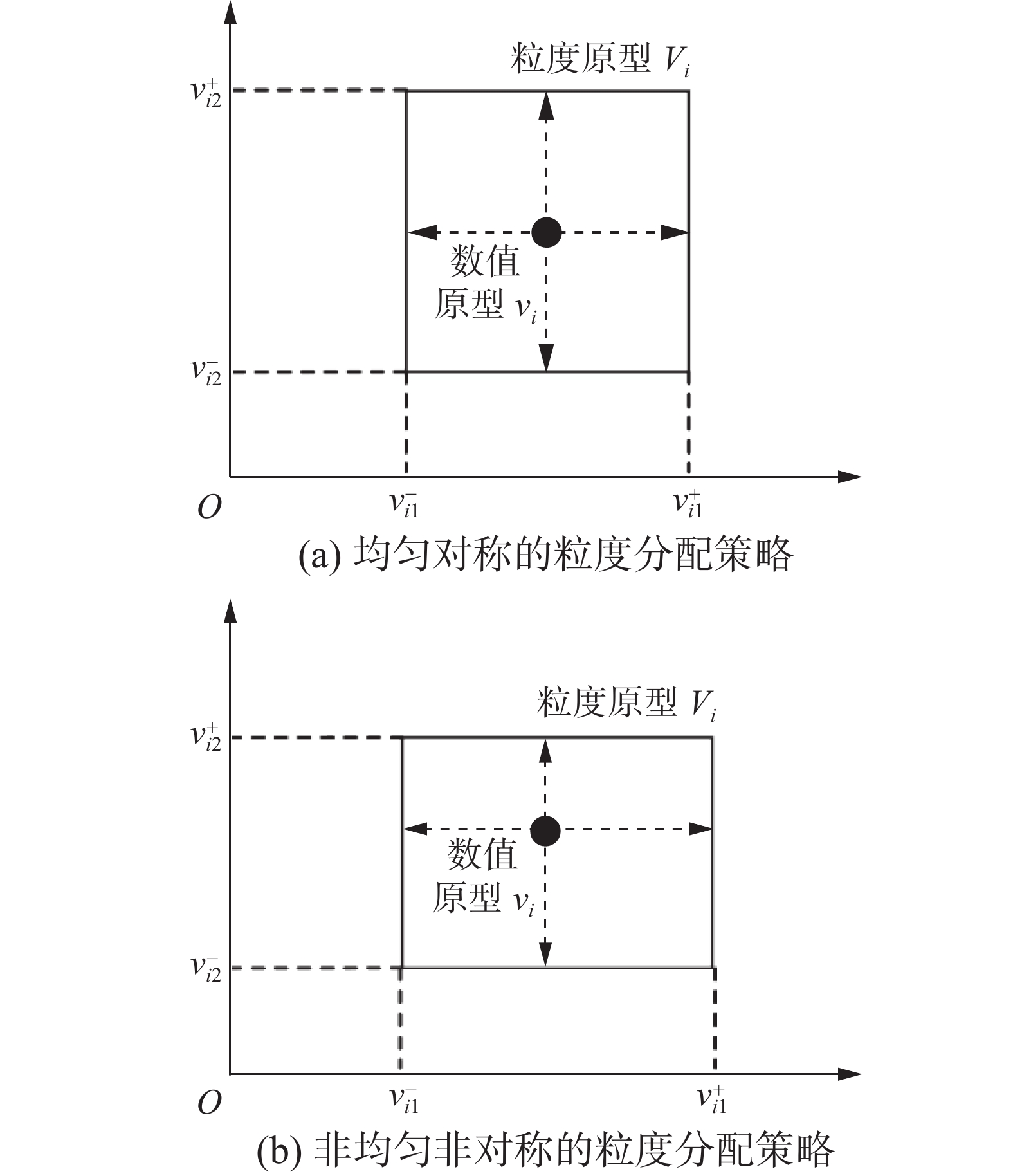
在基于数值模型的粒化策略中，通过合理的粒度分配策略构建粒度结构。当初始化的随机信息粒度
${{\varepsilon }}$ 分配给某个参数时，每个参数被赋予不同的抽象程度。信息粒度的值越高，信息粒的灵活性就越大，但信息粒度${{\varepsilon }}$ 受到单位区间的约束。如何给数值参数的每个特征分配合理的信息粒度，使得所构建的粒度模型具有更高的覆盖率和特异性是一个核心问题。对于给定的信息粒度${{\varepsilon }}$ ，粒度分配策略一般有2种形式： 1)均匀对称的粒度分配策略； 2)非均匀非对称的粒度分配策略[110]。在这一部分，本文以数值原型的粒度扩展为例，对于2种分配策略进行分析。均匀对称的粒度分配策略通过对数值原型分配相同的信息粒度构建区间信息粒：
$$ {{\boldsymbol{v}}_i} \to {{\boldsymbol{V}}_i}\left( {{\varepsilon _0}{R}_i^x,{\varepsilon _0}{R}_i^x, \cdots ,{\varepsilon _0}{R}_i^x} \right) $$ 式中
${R}_i^x = {x_{{\rm{max}}}} - {x_{{\rm{min}}}}$ 。$$ \begin{array}{*{20}{c}} {}&{w_i^ - = {\rm{min}}\left( {{w_i} - {\varepsilon _0}{R}_i^y,{w_i} + {\varepsilon _0}{R}_i^y} \right)} \\ {}&{w_i^ + = {\rm{max}}\left( {{w_i} - {\varepsilon _0}{R}_i^y,{w_i} + {\varepsilon _0}{R}_i^y} \right)} \end{array} $$ 式中
${\varepsilon }_{0}=\dfrac{\varepsilon }{2c\left(n+1\right)}且{R}_{i}^{y}={y}_{{\rm{max}}}-{y}_{{\rm{min}}}$ 。如图3(a)所示，针对不同的数据特征，均匀对称分配策略赋予数值原型同样的抽象程度，计算复杂度相对较低。这一方法虽然简单但是没有考虑到不同特征的信息量不同这一问题，限制了信息粒对于数据的表征能力。
图 3 2种不同的粒度分配策略Fig. 3 Two different allocation strategies of information granularity下载:
全尺寸图片
非均匀非对称的粒度分配策略认为数值原型中不同特征的每个区间长度是不相等的：
$$ \begin{array}{*{20}{c}} {}&{{v_i} \to {V_i}\left( {\varepsilon _{i1}^ - {R}_i^x,\varepsilon _{i1}^ + {R}_i^x, \cdots ,\varepsilon _{in}^ - {R}_i^x,\varepsilon _{in}^ + {R}_i^x} \right)} \end{array} $$ $$ \begin{array}{*{20}{c}} {w_i^ - = {\rm{min}}\left( {{w_i} - \varepsilon _i^{w - }{R}_i^y,{w_i} + \varepsilon _i^{w + }{R}_i^y} \right),} \\ {w_i^ + = {\rm{max}}\left( {{w_i} - \varepsilon _i^{w - }{R}_i^y{w_i} + \varepsilon _i^{w + }{R}_i^y} \right)} \end{array} $$ 其中，变量
${{\varepsilon }}_{ij}^{v - },{{\varepsilon }}_{ij}^{v + },{{\varepsilon }}_{ij}^{w - }$ 和${{\varepsilon }}_{ij}^{w + }$ 满足如下条件：$$ 0 \leqslant \varepsilon _{ij}^{v - },\varepsilon _{ij}^{v + },\varepsilon _{ij}^{w - },\varepsilon _{ij}^{w + } \leqslant 1 $$ $$ \displaystyle\sum_{i = 1}^c \left( {\displaystyle\sum_{j = 1}^n {{\varepsilon }}_{ij}^{v - } + \displaystyle\sum_{j = 1}^n {{\varepsilon }}_{ij}^{v + } + {{\varepsilon }}_i^{w - } + {{\varepsilon }}_i^{w + }} \right) = \varepsilon $$ 如图3(b)所示，对于二维数值原型，非均匀非对称的粒度分配策略针对不同特征空间分配了不同程度的信息粒度，构造了矩形的信息粒。当维度逐渐增加时，信息粒会呈现出不规则的超立方体。其他参数的粒度分配策略采用同样的思想实现信息粒构建。
4.2 粒度模糊规则模型的评估方法
理想的信息粒应该包含尽可能多的数据信息，同时需要信息描述得尽可能具体。针对这2个需求，现有的研究工作[111-112]常用2种评价指标对于信息粒的性能进行评估。以区间信息粒
${{{\boldsymbol{\varOmega}} }} = \left[ {{\omega _1},{\omega _2}} \right]$ 为例进行介绍。覆盖率(coverage)[82,112]表示了信息粒包含数据的多少，可以表示为
$$ Q_c\left({\boldsymbol{\varOmega}}\right) = \frac{1}{N}{\rm{card}}\left\{{x}_{k}\right|{x}_{k}\in {\boldsymbol{\varOmega}}\} $$ 式中：
${\rm{card}}\left\{ . \right\}$ 为区间${\boldsymbol{\varOmega}}$ 包含元素的个数，$N$ 为数据样本数目。特异性(specificity)[34,54]量化信息粒包含数据信息的具体程度，如图4所示，即保证区间长度尽可能的小。简而言之，
$Q_s \left( {\boldsymbol{\varOmega}} \right)$ 应该表示为区间长度的单调递减函数：$Q_s \left( {\boldsymbol{\varOmega}} \right) = g\left( {{\rm{length}}\left( {\boldsymbol{\varOmega}}\right)} \right)$ 。当区间长度为0时，信息粒退化为数值形式，如图5所示。此时信息粒专注于细节描述而忽略了高层次的信息表征，$Q_s = 1$ 且$Q_c = 0$ ；当区间长度与论域长度相同时（如图6所示），信息粒可以覆盖所有数据，$Q_c = 1$ ，但由于信息粒过于宽泛，$Q_s = 0$ ，对于数据分析没有很大帮助。很多研究[54,96]中采用了不同的特异性计算公式，常用的形式计算为
图 4 特异性示意图：区间信息粒${\boldsymbol{\varOmega}}$ Fig. 4 Diagram of specificity: interval information granule${\boldsymbol{\varOmega}} $ 下载:
全尺寸图片
图 5 特异性示意图：区间长度为0的信息粒${\boldsymbol{\varOmega}} $ Fig. 5 Diagram of specificity: information granule${\boldsymbol{\varOmega}} $ with interval length of 0下载:
全尺寸图片
图 6 特异性示意图：区间长度最大时的信息粒${\boldsymbol{\varOmega}} $ Fig. 6 Diagram of specificity: information granule${\boldsymbol{\varOmega}} $ with the largest interval length下载:
全尺寸图片
$$ Q_s \left( {{{\boldsymbol{\varOmega}} }} \right) = 1 - \frac{{\left| {{\omega _2} - {\omega _1}} \right|}}R $$ 式中R为区间所在论域的长度。
结合上述信息粒度分配策略，进一步讨论粒度模糊规则模型的性能评估指标。给定粒度模糊规则模型的区间输出
${Y_k} = \left[ {Y_k^ - \;\; Y_k^ + } \right]$ 与实际输出${y_k}$ ，覆盖性可以表示为$$ Q_c = \frac{1}{N}\displaystyle\sum_{k = 1}^N {\rm{incl}}\left( {{y_k},{Y_k}} \right) $$ 式中
${\rm{incl}}\left( {{y_k},{Y_k}} \right)$ 为区间输出${Y_k}$ 包含数据样本${y_k}$ 的数目。同样，考虑利用区间输出的长度量化特异性：$$ Q_s = {{\rm{e}}^{ - \frac{1}{N}\sum\limits_{K = 1}^N \left| {Y_k^+ - Y_k^ - } \right|}} $$ 显然，覆盖率和特异性是相互矛盾的，特异性的增加会降低覆盖率，覆盖率较高时特异性会降低。为了综合评估所构建的区间粒度模糊模型，采用2个指标的乘积[69]量化粒度模糊规则模型的整体性能为
$$ Q = Q_c \times Q_s^\beta $$ (1) 式中：参数
$\,\beta \in \left[ {0,1} \right]$ 表示特异性指标的重要程度，通过调整$\,\beta$ 可以实现不同问题对于2个指标的不同要求。从式(1)可以看出，由性能指标
$Q$ 表述的区间粒度模糊模型的性能直接取决于信息粒度$\varepsilon $ 的值。因此，可以使用以信息粒度$\varepsilon$ 为变量的曲线下面积(area under curve, AUC)衡量粒度模型的性能[82]：$$ L = \mathop \int \nolimits_0^1 Q\left( {\varepsilon} \right){\rm{d}}{\varepsilon} $$ 5. 粒度模糊规则模型的优化
针对不同的复杂问题，不同抽象程度的信息粒会影响模型的性能，因此大部分研究[109,113]围绕面向问题和数据的非均匀非对称策略进行。尽管非均匀非对称策略能够差异化表征不同维度信息，但无法直接确定信息粒度
${{\varepsilon }}$ 的取值。如第4节所述，区间输出可以用性能指标Q来量化。因此，粒度分配问题可以表示目标函数为Q，且存在约束的信息粒度${{\varepsilon }}$ 的优化。传统的数学优化方法在求解这一问题时存在困难，因此，现有的研究主要是借助群体智能优化技术实现粒度分配策略的优化。群体智能优化技术通过模拟动物的群体行为，利用彼此间交互与合作的方式实现全局问题的优化。在群体智能优化算法中，粒子群优化算法(particle swarm optimization, PSO)、遗传算法(genetic algorithm, GA)和差分进化算法(differential evolution, DE)被广泛应用于各种复杂问题的求解。PSO的种群大小对求解时间的影响较小，同时搜索空间的连续性较好，在计算过程中无需解的排序，实现较为简单。因此，大量研究[110,113]考虑利用PSO实现粒度模型的优化。基于数值模型的构建的粒度策略，将性能指标Q作为PSO的目标函数[101,103,108,111]，实现合理的粒度分配以构建高效的粒度模型。此外，在直接构建的粒度模糊模型中，如超盒信息粒[89,107]，尽管粒度分配策略有所不同，同样借助了PSO来优化模型。考虑到输出的特异性和覆盖率对于不同信息粒的复杂依赖性，一些研究[99]提出了改进的粒子群优化算法。GA通过交叉变异等特定方式生成新的种群，计算过程中需要排序，参数设置相对简单。DE与GA相似，将变异作为搜索机制，算法稳定性优于PSO，因此在粒度模型构建过程中也常常采用GA和DE作为优化手段[96,112,114]。一些研究[110,114]还采用了多种优化方法并对于不同的优化技术下的模型性能进行分析。此外，部分研究从优化的目标函数出发，将优化过程构造为多目标问题[115]进行求解。
6. 结束语
粒计算作为认知智能的新型范式，能够模仿人类利用已有知识进行高层级的逻辑推理，对于人工智能的研究具有重要意义。粒度模糊规则模型由于其简洁性、鲁棒性和可解释性等特点，成为计算智能研究的一大热点。本文着眼于粒度模糊规则模型，梳理了不同设计方法的粒度模型，探讨了信息粒的构建方法，归纳了粒度模糊规则模型的设计框架和评估优化方法。由于国内对于粒度模糊规则模型的研究缺少系统总结，本文的主要目的是系统归纳粒度模糊模型研究，对于不同粒度构建方法及其代表性研究工作的基本机制、方法和特点进行总结分析，从而促进粒度模糊规则模型的研究，以及粒计算的理论、技术和应用的广泛发展。
-
图 1 粒度模糊规则模型的基本框架
Fig. 1 Basic framework of granular fuzzy rule-based model
下载:
全尺寸图片
图 2 基于输入输出空间的协同粒化机制结构
Fig. 2 Diagram of collaborative granulation mechanism based on input-output space
下载:
全尺寸图片
图 3 2种不同的粒度分配策略
Fig. 3 Two different allocation strategies of information granularity
下载:
全尺寸图片
图 4 特异性示意图：区间信息粒
${\boldsymbol{\varOmega}}$ Fig. 4 Diagram of specificity: interval information granule
${\boldsymbol{\varOmega}} $ 下载:
全尺寸图片
图 5 特异性示意图：区间长度为0的信息粒
${\boldsymbol{\varOmega}} $ Fig. 5 Diagram of specificity: information granule
${\boldsymbol{\varOmega}} $ with interval length of 0下载:
全尺寸图片
图 6 特异性示意图：区间长度最大时的信息粒
${\boldsymbol{\varOmega}} $ Fig. 6 Diagram of specificity: information granule
${\boldsymbol{\varOmega}} $ with the largest interval length下载:
全尺寸图片
表 1 基于FCM的粒化−解粒化机制的分类与相关研究
Table 1 Classification and studies of granulation-degranulation Mechanism based on FCM
-
[1] 苗夺谦, 张清华, 钱宇华, 等. 从人类智能到机器实现模型: 粒计算理论与方法[J]. 智能系统学报, 2016, 11(6): 743–757. MIAO Duoqian, ZHANG Qinghua, QIAN Yuhua, et al. From human intelligence to machine implementation model: theories and applications based on granular computing[J]. CAAI transactions on intelligent systems, 2016, 11(6): 743–757. [2] NORI H, JENKINS S, KOCH P, et al. Interpretml: a unified framework for machine learning interpretability[J]. (2019−09−19)[2023−06−15]. https://arxiv.org/abs/1909.09223v1.pdf. [3] 焦李成. 类脑感知与认知的挑战与思考[J]. 智能系统学报, 2022, 17(1): 213–216. JIAO Licheng. Challenges and reflections on brain-like perception and cognition[J]. CAAI transactions on intelligent systems, 2022, 17(1): 213–216. [4] WANG Guoyin, YANG Jie, XU Ji. Granular computing: from granularity optimization to multi-granularity joint problem solving[J]. Granular computing, 2017, 2(3): 105–120. doi: 10.1007/s41066-016-0032-3 [5] ZADEH L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy sets and systems, 1997, 90(2): 111–127. doi: 10.1016/S0165-0114(97)00077-8 [6] YAO Y. Perspectives of granular computing[C]//2005 IEEE International Conference on Granular Computing. Piscataway: IEEE, 2005: 85−90. [7] HOBBS J R. Granularity[M]. Amsterdam: Elsevier, 1990: 542−545. [8] LIN T Y. Neighborhood systems and relational databases[C]//Proceedings of the 1988 ACM sixteenth annual conference on Computer science. New York: ACM, 1988: 725. [9] LIN T Y. Granular computing: fuzzy logic and rough sets[M]. Heidelberg: Physica-Verlag HD, 1999: 183−200. [10] YAO Yiyu. A partition model of granular computing[M. Heidelberg: Springer Berlin Heidelberg, 2004: 232−253. [11] PAWLAK Z. Rough set theory and its applications to data analysis[J]. Cybernetics and systems, 1998, 29(7): 661–688. doi: 10.1080/019697298125470 [12] ZADEH L A. Fuzzy logic = computing with words[J]. IEEE transactions on fuzzy systems, 1996, 4(2): 103–111. doi: 10.1109/91.493904 [13] YAO Y Y. Granular computing: basic issues and possible solutions[J]. Proceedings of the joint conference on information sciences, 2000, 5(1): 186–189. [14] WANG Guoyin, HU Feng, HUANG Hai, et al. A granular computing model based on tolerance relation[J]. The journal of China universities of posts and telecommunications, 2005, 12(3): 86–90. [15] 胡峰, 黄海, 王国胤, 等. 不完备信息系统的粒计算方法[J]. 小型微型计算机系统, 2005, 26(8): 1335–1339. doi: 10.3969/j.issn.1000-1220.2005.08.012 HU Feng, HUANG Hai, WANG Guoyin, et al. Granular computing in incomplete information systems[J]. Mini-micro systems, 2005, 26(8): 1335–1339. doi: 10.3969/j.issn.1000-1220.2005.08.012 [16] 张铃, 张钹. 模糊相容商空间与模糊子集[J]. 中国科学:信息科学, 2011, 41(1): 1–11. ZHANG Ling, ZHANG Bo. Fuzzy tolerance quotient spaces and fuzzy subsets[J]. Scientia sinica (informationis), 2011, 41(1): 1–11. [17] ZHANG Yanping, ZHANG Ling, WU Tao. Description method of different granularity world−Business Space Law[J]. Chinese journal of computers, 2004, 27(3): 328–333. [18] 王国胤, 张清华, 马希骜, 等. 知识不确定性问题的粒计算模型[J]. 软件学报, 2011, 22(4): 676–694. doi: 10.3724/SP.J.1001.2011.03954 WANG Guoyin, ZHANG Qinghua, MA Xiao, et al. Granular computing models for knowledge uncertainty[J]. Journal of software, 2011, 22(4): 676–694. doi: 10.3724/SP.J.1001.2011.03954 [19] 李道国, 苗夺谦, 张红云. 粒度计算的理论、模型与方法[J]. 复旦学报(自然科学版), 2004, 43(5): 837–841. LI Daoguo, MIAO Duoqian, ZHANG Hongyun. The theory models and approaches of granular computing[J]. Journal of Fudan University, 2004, 43(5): 837–841. [20] 苗夺谦, 胡声丹. 基于粒计算的不确定性分析[J]. 西北大学学报(自然科学版), 2019, 49(4): 487–495. MIAO Duoqian, HU Shengdan. Uncertainty analysis based on granular computing[J]. Journal of Northwest University (natural science edition), 2019, 49(4): 487–495. [21] LEITE D, COSTA P, GOMIDE F. Evolving granular neural networks from fuzzy data streams[J]. Neural networks, 2013, 38: 1–16. doi: 10.1016/j.neunet.2012.10.006 [22] SONG Mingli, WANG Yongbin. A study of granular computing in the agenda of growth of artificial neural networks[J]. Granular computing, 2016, 1(4): 247–257. doi: 10.1007/s41066-016-0020-7 [23] 罗建豪, 吴建鑫. 基于深度卷积特征的细粒度图像分类研究综述[J]. 自动化学报, 2017, 43(8): 1306–1318. LUO Jianhao, WU Jianxin. A survey on fine-grained image categorization using deep convolutional features[J]. Acta automatica sinica, 2017, 43(8): 1306–1318. [24] 任俊伟, 曾诚, 肖丝雨, 等. 基于会话的多粒度图神经网络推荐模型[J]. 计算机应用, 2021, 41(11): 3164–3170. doi: 10.11772/j.issn.1001-9081.2021010060 REN Junwei, ZENG Cheng, XIAO Siyu, et al. Session-based recommendation model of multi-granular graph neural network[J]. Journal of computer applications, 2021, 41(11): 3164–3170. doi: 10.11772/j.issn.1001-9081.2021010060 [25] PEDRYCZ W, HOMENDA W. From fuzzy cognitive maps to granular cognitive maps[J]. IEEE transactions on fuzzy systems, 2014, 22(4): 859–869. doi: 10.1109/TFUZZ.2013.2277730 [26] WANG Yihan, YU Fusheng, HOMENDA W, et al. The trend-fuzzy-granulation-based adaptive fuzzy cognitive map for long-term time series forecasting[J]. IEEE transactions on fuzzy systems, 2022, 30(12): 5166–5180. doi: 10.1109/TFUZZ.2022.3169624 [27] FALCON R, NÁPOLES G, BELLO R, et al. Granular cognitive maps: a review[J]. Granular computing, 2019, 4(3): 451–467. doi: 10.1007/s41066-018-0104-7 [28] QIN Jindong, MARTÍNEZ L, PEDRYCZ W, et al. An overview of granular computing in decision-making: extensions, applications, and challenges[J]. Information fusion, 2023, 98: 101833. doi: 10.1016/j.inffus.2023.101833 [29] LIU Keyu, YANG Xibei, FUJITA H, et al. An efficient selector for multi-granularity attribute reduction[J]. Information sciences, 2019, 505: 457–472. doi: 10.1016/j.ins.2019.07.051 [30] YANG Xin, LI Tianrui, LIU Dun, et al. A temporal-spatial composite sequential approach of three-way granular computing[J]. Information sciences, 2019, 486: 171–189. doi: 10.1016/j.ins.2019.02.048 [31] LIU Dun, YANG Xin, LI Tianrui. Three-way decisions: beyond rough sets and granular computing[J]. International journal of machine learning and cybernetics, 2020, 11(5): 989–1002. doi: 10.1007/s13042-020-01095-6 [32] SONG Mingli, LI Yan, PEDRYCZ W. Time series prediction with granular neural networks[J]. Neurocomputing, 2023, 546: 126328. doi: 10.1016/j.neucom.2023.126328 [33] PEDRYCZ W, BARGIELA A. An optimization of allocation of information granularity in the interpretation of data structures: toward granular fuzzy clustering[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2012, 42(3): 582–590. doi: 10.1109/TSMCB.2011.2170067 [34] PEDRYCZ W. Granular computing for data analytics: a manifesto of human-centric computing[J]. CAA journal of automatica sinica, 2018, 5(6): 1025–1034. doi: 10.1109/JAS.2018.7511213 [35] PEDRYCZ W, VALENTE DE OLIVEIRA J. A development of fuzzy encoding and decoding through fuzzy clustering[J]. IEEE transactions on instrumentation and measurement, 2008, 57(4): 829–837. doi: 10.1109/TIM.2007.913809 [36] ZHANG Liyong, ZHONG Wanxie, ZHONG Chongquan, et al. Fuzzy C-Means clustering based on dual expression between cluster prototypes and reconstructed data[J]. International journal of approximate reasoning, 2017, 90: 389–410. doi: 10.1016/j.ijar.2017.08.008 [37] ZHU Xiubin, PEDRYCZ W, LI Zhiwu. Fuzzy clustering with nonlinearly transformed data[J]. Applied soft computing, 2017, 61: 364–376. doi: 10.1016/j.asoc.2017.07.026 [38] PEDRYCZ A, HIROTA K, PEDRYCZ W, et al. Granular representation and granular computing with fuzzy sets[J]. Fuzzy sets and systems, 2012, 203: 17–32. doi: 10.1016/j.fss.2012.03.009 [39] WANG Hai, XU Zeshui, PEDRYCZ W. An overview on the roles of fuzzy set techniques in big data processing: trends, challenges and opportunities[J]. Knowledge-based systems, 2017, 118: 15–30. doi: 10.1016/j.knosys.2016.11.008 [40] WANG Guoyin. Extension of rough set under incomplete information systems[C]//2002 IEEE World Congress on Computational Intelligence. 2002 IEEE International Conference on Fuzzy Systems. FUZZ-IEEE'02. Proceedings (Cat. No. 02CH37291). Piscataway: IEEE, 2002: 1098−1103. [41] 韩祯祥, 张琦, 文福拴. 粗糙集理论及其应用综述[J]. 控制理论与应用, 1999, 16(2): 153–157. HAN Zhenxiang, ZHANG Qi, WEN Fushuan. A survey on rough set theory and its application[J]. Control theory & applications, 1999, 16(2): 153–157. [42] LI Deyi, LIU Changyu, GAN Wenyan. A new cognitive model: cloud model[J]. International journal of intelligent systems, 2009, 24(3): 357–375. doi: 10.1002/int.20340 [43] WANG Guoyin, XU Changlin, LI Deyi. Generic normal cloud model[J]. Information sciences, 2014, 280: 1–15. doi: 10.1016/j.ins.2014.04.051 [44] An A, Stefanowski J, Ramanna S, et al. Rough sets, fuzzy sets, data mining and granular computing[C]//Proceedings of RSFDGrC2007, LNAI4482, Berlin:Springer-Verlag, 2007:. [45] DESCHRIJVER G. Arithmetic operators in interval-valued fuzzy set theory[J]. Information sciences, 2007, 177(14): 2906–2924. doi: 10.1016/j.ins.2007.02.003 [46] CASTILLO O, MELIN P, KACPRZYK J, et al. Type-2 fuzzy logic: theory and applications[C]//2007 IEEE International Conference on Granular Computing (GRC 2007). Piscataway: IEEE, 2007: 145−145. [47] JI W, PANG Y, JIA X, et al. Fuzzy rough sets and fuzzy rough neural networks for feature selection: a review[J]. Wiley interdisciplinary reviews:data mining and knowledge discovery, 2021, 11(3): e1402. doi: 10.1002/widm.1402 [48] XU W, WANG Q, ZHANG X. Multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space[J]. International journal of fuzzy systems, 2011, 13(4). [49] 张钹, 张铃. 问题求解理论及应用[M]. 北京: 清华大学出版社, 1990. ZHANG Bai, ZHANG Ling. Theory and application of problem sSolving [M]. Beijing: Tsinghua University Press, 1990. (in Chinese) [50] 张铃, 张钹. 模糊商空间理论(模糊粒度计算方法)[J]. 软件学报, 2003, 14(4): 770–776. ZHANG Ling, ZHANG Bo. Theory of fuzzy quotient space (methods of fuzzy granular computing)[J]. Journal of software, 2003, 14(4): 770–776. [51] 李德毅, 刘常昱, 杜鹢, 等. 不确定性人工智能[J]. 软件学报, 2004, 15(11): 1583–1594. LI Deyi, LIU Changyu, DU Yi, et al. Artificial intelligence with uncertainty[J]. Journal of software, 2004, 15(11): 1583–1594. [52] 王国胤, 云模型与粒计算[M]. 北京: 科学出版社, 2012. WANG Guoyin. Cloud model and particle computing[M]. Beijing: Science Press, 2012. [53] MAGDALENA L. Fuzzy rule-based systems[M]. Heidelberg: Springer Berlin Heidelberg, 2015: 203−218. [54] PEDRYCZ W. From fuzzy models to granular fuzzy models[J]. International journal of computational intelligence systems, 2016, 9(suppl 1): 35. [55] CASILLAS J, CORDON O, DEL JESUS M J, et al. Genetic tuning of fuzzy rule deep structures preserving interpretability and its interaction with fuzzy rule set reduction[J]. IEEE transactions on fuzzy systems, 2005, 13(1): 13–29. doi: 10.1109/TFUZZ.2004.839670 [56] CORDÓN O. A historical review of evolutionary learning methods for Mamdani-type fuzzy rule-based systems: designing interpretable genetic fuzzy systems[J]. International journal of approximate reasoning, 2011, 52(6): 894–913. doi: 10.1016/j.ijar.2011.03.004 [57] XU R, WUNSCHII D. Survey of clustering algorithms[J]. IEEE transactions on neural networks, 2005, 16(3): 645–678. doi: 10.1109/TNN.2005.845141 [58] BARALDI A, BLONDA P. A survey of fuzzy clustering algorithms for pattern recognition. I[J]. IEEE transactions on systems, man and cybernetics, part B (cybernetics), 1999, 29(6): 778–785. doi: 10.1109/3477.809032 [59] BEZDEK J C, EHRLICH R, FULL W. FCM: the fuzzy c-means clustering algorithm[J]. Computers & geosciences, 1984, 10(2/3): 191–203. [60] SUGANYA R, SHANTHI R. Fuzzy c-means algorithm-a review[J]. International journal of scientific and research publications, 2012, 2(11): 1. [61] DING Yi, FU Xian. Kernel-based fuzzy c-means clustering algorithm based on genetic algorithm[J]. Neurocomputing, 2016, 188: 233–238. doi: 10.1016/j.neucom.2015.01.106 [62] HANYU E, CUI Ye, PEDRYCZ W, et al. Enhancements of rule-based models through refinements of Fuzzy C-Means[J]. Knowledge-based systems, 2019, 170: 43–60. doi: 10.1016/j.knosys.2019.01.027 [63] Zhao F, Li G, Guo H, et al. Rule-based models via the axiomatic fuzzy set clustering and their granular aggregation[J]. Applied Soft Computing, 2022, 130: 109692. doi: 10.1016/j.asoc.2022.109692 [64] ANGELOV P P, FILEV D P. An approach to online identification of Takagi-Sugeno fuzzy models[J]. IEEE transactions on systems, man, and cybernetics part B, cybernetics:a publication of the IEEE systems, man, and cybernetics society, 2004, 34(1): 484–498. doi: 10.1109/TSMCB.2003.817053 [65] HU Xingchen, PEDRYCZ W, WANG Xianmin. From fuzzy rule-based models to their granular generalizations[J]. Knowledge-based systems, 2017, 124: 133–143. doi: 10.1016/j.knosys.2017.03.007 [66] ZHANG X, ZHU Z, ZHAO Y, et al. Self-supervised deep low-rank asignment model for prototype selection[C]//IJCAI. 2018: 3141−3147. [67] Wang S, Mao W, Wei P, et al. Knowledge structure driven prototype learning and verification for fact checking[J]. Knowledge-Based Systems, 2022, 238: 107910. doi: 10.1016/j.knosys.2021.107910 [68] LIN Shuai, LIU Chen, ZHOU Pan, et al. Prototypical graph contrastive learning[J]. IEEE transactions on neural networks and learning systems, 2021, 35(2): 2747–2758. [69] CHEN Min, MIAO Duoqian. Interval set clustering[J]. Expert systems with applications, 2011, 38(4): 2923–2932. doi: 10.1016/j.eswa.2010.06.052 [70] MOORE R E, KEARFOTT R B, CLOUD M J. Introduction to interval analysis[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2009. [71] ALEFELD G, HERZBERGER J. Introduction to interval computation[M]. Herzberger: Academic press, 2012. [72] ZHANG Qinghua, XIE Qin, WANG Guoyin. A survey on rough set theory and its applications[J]. CAAI transactions on intelligence technology, 2016, 1(4): 323–333. doi: 10.1016/j.trit.2016.11.001 [73] CAO Bin, ZHAO Jianwei, LV Zhihan, et al. Multiobjective evolution of fuzzy rough neural network via distributed parallelism for stock prediction[J]. IEEE transactions on fuzzy systems, 2020, 28(5): 939–952. doi: 10.1109/TFUZZ.2020.2972207 [74] YANG Jilin, YAO Yiyu. A three-way decision based construction of shadowed sets from atanassov intuitionistic fuzzy sets[J]. Information sciences, 2021, 577: 1–21. doi: 10.1016/j.ins.2021.06.065 [75] ZHANG Qinghua, CHEN Yuhong, YANG Jie, et al. Fuzzy entropy: a more comprehensible perspective for interval shadowed sets of fuzzy sets[J]. IEEE transactions on fuzzy systems, 2020, 28(11): 3008–3022. doi: 10.1109/TFUZZ.2019.2947224 [76] BOSE A, MALI K. Gradual representation of shadowed set for clustering gene expression data[J]. Applied soft computing, 2019, 83: 105614. doi: 10.1016/j.asoc.2019.105614 [77] LIU Xiaodong, PEDRYCZ W, CHAI Tianyou, et al. The development of fuzzy rough sets with the use of structures and algebras of axiomatic fuzzy sets[J]. IEEE transactions on knowledge and data engineering, 2009, 21(3): 443–462. doi: 10.1109/TKDE.2008.147 [78] HIROTA K. Concepts of probabilistic sets[J]. Fuzzy sets and systems, 1981, 5(1): 31–46. doi: 10.1016/0165-0114(81)90032-4 [79] FUJITA H, GAETA A, LOIA V, et al. Hypotheses analysis and assessment in counterterrorism activities: a method based on OWA and fuzzy probabilistic rough sets[J]. IEEE transactions on fuzzy systems, 2020, 28(5): 831–845. doi: 10.1109/TFUZZ.2019.2955047 [80] SUN Junzi. The 1090 megahertz riddle: a guide to decoding mode S and ADS-B signals[M]. Delft: TU Delft OPEN, 2021. [81] NACHMANI E, MARCIANO E, LUGOSCH L, et al. Deep learning methods for improved decoding of linear codes[J]. IEEE journal of selected topics in signal processing, 2018, 12(1): 119–131. doi: 10.1109/JSTSP.2017.2788405 [82] PEDRYCZ W. An introduction to computing with fuzzy sets[J]. IEEE ASSP magazine, 2021: 190. [83] HU Xingchen, PEDRYCZ W, WU Guohua, et al. Data reconstruction with information granules: an augmented method of fuzzy clustering[J]. Applied soft computing, 2017, 55: 523–532. doi: 10.1016/j.asoc.2017.02.014 [84] GRAVES D, PEDRYCZ W. Kernel-based fuzzy clustering and fuzzy clustering: a comparative experimental study[J]. Fuzzy sets and systems, 2010, 161(4): 522–543. doi: 10.1016/j.fss.2009.10.021 [85] REYES-GALAVIZ O F, PEDRYCZ W. Enhancement of the classification and reconstruction performance of fuzzy C-means with refinements of prototypes[J]. Fuzzy sets and systems, 2017, 318: 80–99. doi: 10.1016/j.fss.2016.07.002 [86] XU Kaijie, PEDRYCZ W, LI Zhiwu, et al. Optimizing the prototypes with a novel data weighting algorithm for enhancing the classification performance of fuzzy clustering[J]. Fuzzy Sets and Systems, 2021, 413: 29–41. [87] IZAKIAN H, PEDRYCZ W, JAMAL I. Clustering spatiotemporal data: an augmented fuzzy C-means[J]. IEEE transactions on fuzzy systems, 2013, 21(5): 855–868. doi: 10.1109/TFUZZ.2012.2233479 [88] IZAKIAN H, PEDRYCZ W. Anomaly detection in time series data using a fuzzy c-means clustering[C]//2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS). Piscataway IEEE, 2013: 1513−1518. [89] REYES-GALAVIZ O F, PEDRYCZ W. Granular fuzzy modeling with evolving hyperboxes in multi-dimensional space of numerical data[J]. Neurocomputing, 2015, 168: 240–253. doi: 10.1016/j.neucom.2015.05.102 [90] ZHU Xiubin, PEDRYCZ W, LI Zhiwu. Granular representation of data: a design of families of ϵ-information granules[J]. IEEE transactions on fuzzy systems, 2018, 26(4): 2107–2119. doi: 10.1109/TFUZZ.2017.2763122 [91] ZHANG Rui, XU Kaijie, ZHU Shengqi, et al. Modeling of number of sources detection under nonideal conditions based on fuzzy information granulation[J]. IEEE transactions on aerospace and electronic systems, 2022: 1−10. [92] PEDRYCZ W, HIROTA K. Fuzzy vector quantization with the particle swarm optimization: a study in fuzzy granulation-degranulation information processing[J]. Signal processing, 2007, 87(9): 2061–2074. doi: 10.1016/j.sigpro.2007.02.001 [93] LINDA O, MANIC M. General type-2 fuzzy C-means algorithm for uncertain fuzzy clustering[J]. IEEE transactions on fuzzy systems, 2012, 20(5): 883–897. doi: 10.1109/TFUZZ.2012.2187453 [94] ROH S B, OH S K, PEDRYCZ W, et al. Design methodology for radial basis function neural networks classifier based on locally linear reconstruction and conditional fuzzy C-means clustering[J]. International journal of approximate reasoning, 2019(106): 228–243. [95] HU Xingchen, PEDRYCZ W, WANG Xianmin. Granular fuzzy rule-based models: a study in a comprehensive evaluation and construction of fuzzy models[J]. IEEE transactions on fuzzy systems, 2017, 25(5): 1342–1355. doi: 10.1109/TFUZZ.2016.2612300 [96] ZHU Xiubin, PEDRYCZ W, LI Zhiwu. A design of granular takagi–sugeno fuzzy model through the synergy of fuzzy subspace clustering and optimal allocation of information granularity[J]. IEEE transactions on fuzzy systems, 2018, 26(5): 2499–2509. doi: 10.1109/TFUZZ.2018.2813314 [97] PEDRYCZ W, AL-HMOUZ R, BALAMASH A S, et al. Designing granular fuzzy models: a hierarchical approach to fuzzy modeling[J]. Knowledge-based systems, 2015, 76: 42–52. doi: 10.1016/j.knosys.2014.11.025 [98] LI Yan, HU Xingchen, PEDRYCZ W, et al. Multivariable fuzzy rule-based models and their granular generalization: a visual interpretable framework[J]. Applied soft computing, 2023, 134: 109958. doi: 10.1016/j.asoc.2022.109958 [99] HU Xingchen, PEDRYCZ W, WANG Xianmin. Optimal allocation of information granularity in system modeling through the maximization of information specificity: a development of granular input space[J]. Applied soft computing, 2016, 42: 410–422. doi: 10.1016/j.asoc.2016.02.001 [100] SONG Mingli, JING Yukai. Granular neural networks: the development of granular input spaces and parameters spaces through a hierarchical allocation of information granularity[J]. Information sciences, 2020, 517: 148–166. doi: 10.1016/j.ins.2019.12.081 [101] ZHONG Chunfu, PEDRYCZ W, WANG Dan, et al. Granular data imputation: a framework of Granular Computing[J]. Applied soft computing, 2016, 46: 307–316. doi: 10.1016/j.asoc.2016.05.006 [102] HU Xingchen, PEDRYCZ W, WU Keyu, et al. Information Granule-based classifier: a development of granular imputation of missing data[J]. Knowledge-based systems, 2021, 214: 106737. doi: 10.1016/j.knosys.2020.106737 [103] LI Menghang, WANG Degang, SONG Wenyan. A design of direct granular model based on takagi-sugeno fuzzy model[C]//2020 7th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS). Piscataway IEEE, 2020: 457−462. [104] ZHU Xiubin, PEDRYCZ W, LI Zhiwu. A granular approach to interval output estimation for rule-based fuzzy models[J]. IEEE transactions on cybernetics, 2022, 52(7): 7029–7038. doi: 10.1109/TCYB.2020.3025668 [105] SHEN Yinghua, PEDRYCZ W, JING Xuyang, et al. Identification of fuzzy rule-based models with output space knowledge guidance[J]. IEEE transactions on fuzzy systems, 2021, 29(11): 3504–3518. doi: 10.1109/TFUZZ.2020.3024804 [106] ZHANG Bowen, PEDRYCZ W, FAYEK A R, et al. Granular aggregation of fuzzy rule-based models in distributed data environment[J]. IEEE transactions on fuzzy systems, 2021, 29(5): 1297–1310. doi: 10.1109/TFUZZ.2020.2973956 [107] LU Wei, SHAN Dan, PEDRYCZ W, et al. Granular fuzzy modeling for multidimensional numeric data: a layered approach based on hyperbox[J]. IEEE transactions on fuzzy systems, 2019, 27(4): 775–789. doi: 10.1109/TFUZZ.2018.2870050 [108] LU Wei, PEDRYCZ W, YANG Jianhua, et al. Granular fuzzy modeling guided through the synergy of granulating output space and clustering input subspaces[J]. IEEE transactions on cybernetics, 2021, 51(5): 2625–2638. doi: 10.1109/TCYB.2019.2909037 [109] LU Wei, MA Cong, PEDRYCZ W, et al. Design of granular model: a method driven by hyper-box iteration granulation[J]. IEEE transactions on cybernetics, 2023, 53(5): 2899–2913. doi: 10.1109/TCYB.2021.3124235 [110] SONG Mingli, WANG Yongbin. Human centricity and information granularity in the agenda of theories and applications of soft computing[J]. Applied soft computing, 2015, 27: 610–613. doi: 10.1016/j.asoc.2014.04.040 [111] LU Wei, ZHANG Liyong, PEDRYCZ W, et al. The granular extension of Sugeno-type fuzzy models based on optimal allocation of information granularity and its application to forecasting of time series[J]. Applied soft computing, 2016, 42: 38–52. doi: 10.1016/j.asoc.2016.01.021 [112] ZUO Hua, ZHANG Guangquan, PEDRYCZ W, et al. Granular fuzzy regression domain adaptation in takagi–sugeno fuzzy models[J]. IEEE transactions on fuzzy systems, 2018, 26(2): 847–858. doi: 10.1109/TFUZZ.2017.2694801 [113] SONG Mingli, LIU Yapeng. A development framework of granular prototypes with an allocation of information granularity[J]. Information sciences, 2021, 573: 154–170. doi: 10.1016/j.ins.2021.06.001 [114] ZHU Xiubin, PEDRYCZ W, LI Zhiwu. A development of hierarchically structured granular models realized through allocation of information granularity[J]. IEEE transactions on fuzzy systems, 2021, 29(12): 3845–3858. doi: 10.1109/TFUZZ.2020.3028939 [115] 柳春华, 刘宏兵. 基于多目标优化的超盒粒计算分类算法[J]. 信阳师范学院学报(自然科学版), 2014, 27(1): 127–130. LIU Chunhua, LIU Hongbing. The hyperbox granular computing classification algorithm based on multi-objective optimization[J]. Journal of Xinyang Normal University (natural science edition), 2014, 27(1): 127–130.
