Research on TOPSIS decision-making method based on multi-granularity hesitant fuzzy linguistic term sets
-
摘要: 为了解决在实际决策时，由于知识背景不同决策者采用不同粒度语言术语集来表达而导致决策结果不准确的问题，本文提出了一种基于多粒度犹豫模糊语言术语集的逼近理想解排序（technique for order preference by similarity to ideal solution, TOPSIS）决策方法。首先选用各术语集中的最大粒度作为标准粒度，通过转换算法将每个决策者的语言术语集转换到同一标准粒度下进行集结，得出相应的隶属度语言术语集；然后结合TOPSIS方法，计算每个备选方案与正、负理想点距离，以相对贴近度的大小排序实现最优方案的选择；最后，通过一个实例，验证该方法的可行性和优越性。本文所提方法可应用于最优方案的选择问题中，提升决策结果准确度。Abstract: In order to solve the problem that decision makers adopt different granularity linguistic term sets for expression and thus lead to inaccurate decision results due to different knowledge backgrounds in practical decision making, this paper proposes a technique for order preference by similarity to ideal solution(TOPSIS) decision-making method based on multi-granularity hesitant fuzzy linguistic term sets. Firstly, the maximum granularity of each term set is selected as the standard granularity, and the linguistic term set of each decision maker is converted to the same standard granularity for clustering through the conversion algorithm, which results in corresponding subordination linguistic term set; Then, combining with TOPSIS, the distance between each alternative and the positive and negative ideal points is calculated, and the selection of the optimal solution is realized by the ordering of the magnitude of relative closeness; Finally, the feasibility and superiority of the method are verified by an example. The method proposed in this paper can be applied to the problem of choosing the optimal solution to improve the accuracy of decision-making results.
-
多属性决策是决策者根据多个属性对若干方案进行评价后排序并择优的过程，很多现实世界中的管理决策问题，如飞机健康监测、图像识别和铁路智能等领域都可以从多属性决策的视角进行考虑[1-6]。但多属性决策问题存在着一定的不确定性，导致决策者难以用精确的数值描述评价对象，于是便会选择用语言术语来表达信息。传统语言决策问题中，只考虑决策者使用单个语言术语表示，而面对高度复杂的决策问题时，决策者很有可能会在一些语言术语之间犹豫，无法给出唯一的准确评价值，为此Rodriguez等[6]提出犹豫模糊语言术语集（hesitant fuzzy linguistic term sets, HFLTSs）的概念，它允许决策者使用多个连续的语言术语来表达他们的评价。这类决策被归为语言类多属性决策问题，使用的语言表述方式在捕捉日常决策中的评价信息方面更具贴切性，受到学者广泛关注[7-9]。
近些年，学者们对犹豫模糊集进行了大量的研究。例如，为了描述犹豫模糊集之间的接近程度，Xu等[10]定义了犹豫模糊集之间的距离测度和相似测度，并将它们应用于多属性决策中。为了描述犹豫模糊集之间的相关性，许叶军等[11]提出了多粒度语言术语集的转化准则，并且定义了相应的转换函数及其性质，以实现多粒度语言术语集的统一化。实际上，单个数值通常不能准确地表示评价信息，区间评价信息往往更贴近现实情形。因此，Chen等[12]提出了区间值犹豫模糊集，它的隶属度是由多个属于[0,1]的区间组成的。同样，基于区间值犹豫模糊集，Wei等[13]提出了区间值犹豫模糊集之间的距离测度和相似性测度，并给出了它们的相关性质。由于犹豫模糊集的隶属度是由多个数值组成的，存在一定的不确定性。为了刻画这种不确定性，Li等[14]提出犹豫模糊集的犹豫度，并且在犹豫度的基础上定义了犹豫模糊集之间的距离测度和相似性测度。
自犹豫模糊集的犹豫度提出以来，引起了专家学者的广泛关注，许多学者对犹豫模糊语言集进行了进一步拓展研究。例如，Liao等[15]定义了犹豫模糊语言集间的距离和相似性测度，并将它们应用于实际决策中。Rodríguez等[16]优化大规模群体决策下凝聚力驱动，定义犹豫模糊语言共识达成过程。Liu等[17]扩展犹豫模糊语言集的Type-2模糊包络，将复杂的语言信息应用到犹豫模糊语言术语集中来减少偏好聚合过程中的信息丢失，并将其应用至多属性决策问题中。Ali等[18]提出对偶犹豫模糊语言术语集的向量相似度，并将其应用于实际问题中。
然而在面对实际的多属性决策问题时，由于自身专业知识、个人偏好等因素的影响，在决策过程中决策者通常更偏向于对评价对象采用语言术语集进行定性描述，此时多粒度犹豫模糊语言又为多属性决策问题提供了一条新的思路。Meng等[19]基于逼近理想解排序（technique for order preference by similarity to ideal solution, TOPSIS）法提出了一种处理多粒度犹豫模糊语言群决策问题的方法；Wu等[20]提出2个基于犹豫模糊语言的多属性决策模型，考虑犹豫模糊语言术语集具有额外可能性分布，能代表更广泛的语言。Jin等[21]定义两对邻域犹豫模糊关系，构造相应的犹豫模糊覆盖粗糙集，并提出一种基于犹豫模糊邻域的改进TOPSIS决策方法。陈秀明等[22]基于熵权提出了多粒度犹豫模糊语言VIKOR群推荐方法；于文玉等[23]基于指派模型提出了权重信息不完全的多粒度犹豫模糊语言的群决策方法；Zhao等[24]通过扩展有序加权平均算子，在基于多粒度犹豫模糊语言术语集的相对投影模型上，提出了基于相似度的多粒度犹豫诱导加权平均算子来集结专家的意见。在熵测度方面，Wang等[25]提出了多粒度概率语言术语集的扩展交叉熵测度；Zhang等[26]将多粒度犹豫模糊语言转换为语言分布评估，通过统一语言分布评估来解决双向匹配决策问题，并以绿色建筑匹配证明该方法的特点；Zhang等[27]提出全集赋值法，即将概率总和与1的差值分配给当前语言变量所属的语言术语集；Li等[28]采用语言术语的语义来实现语言术语间的相互转换，把这种方法的思想应用于处理多粒度犹豫模糊语言信息，有益于解决更多实际问题。
在实际决策问题中，当决策者使用不同粒度的犹豫模糊语言术语集来评价时，会出现决策信息的不匹配性以及决策结果的不准确性的问题。本文的研究动机为通过构建多粒度犹豫模糊语言术语集的TOPSIS决策方法，将各决策者给出的不同粒度的语言术语集转换到同一粒度下进行集结，得到同一粒度下的隶属度语言术语集，计算相应权重之后得出所有备选方案的决策矩阵，结合TOPSIS方法对方案进行优劣排序从而选择最优方案，来帮助决策者做出更准确的决策。实例的结果也验证了提出方法的可行性和准确性。
1. 基础知识与理论背景
多属性决策是指根据各方案的指标属性值，采用某种集成融合的方法，将属性值转化为方案的综合评价值，以此获得方案的排序结果，选择出最优方案。在决策时，决策者会使用语言术语来表示他们的评估信息，并且会在一些语言术语之间犹豫而无法给出唯一的评价值。下面简单介绍相关概念。
1.1 多属性决策
定义1 在一个多属性决策问题中，设
$ A = \left\{ {{A_1},{A_2}, \cdots, {A_m}} \right\} $ 是由$ m $ 个方案组成的方案集，$ C = \left\{ {{C_1},{C_2}, \cdots, {C_n}} \right\} $ 是由$ n $ 个属性组成的属性集，其对应的权重向量为${\boldsymbol{\omega}} = {\left[ {{\omega _1}\;\;{\omega _2}\;\; \cdots \;\; {\omega _n}} \right]^{{\rm{T}}}}, {\omega _j} \in [0,1],$ $ \displaystyle\sum\limits_{j = 1}^n {{\omega _j}} = 1 $ 。方案$ {A_j} $ 在属性$ {C_j} $ 下的属性值可以用一个直觉模糊数表示，其中隶属度$ {\mu _{ij}} $ 和非隶属度$ {\nu _{ij}} $ 分别表示方案$ {A_j} $ 对属性$ {C_j} $ 的满足程度和不满足程度，决策专家可以通过以上信息对方案进行决策。1.2 犹豫模糊语言术语集
在模糊集的基础上，Rodriguez等[6]提出了由多个语言变量组合形式来评价的犹豫模糊语言术语集（hesitant fuzzy linguistic term sets, HFLTSs）。
定义2 设
$ X = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\} $ 是一个固定集合，$ S = \left\{ {{s_\varepsilon } = \varepsilon = - \tau , \cdots ,\tau } \right\} $ 是语言集，则$ X $ 上的犹豫模糊语言集$ {H_s} $ 可以定义为$$ {H_s} = \left\{ {\left\langle {{x_i},{h_s}\left( {{x_i}} \right)} \right\rangle |{x_i} \in X} \right\} $$ 式中
$ {h_s}\left( {{x_i}} \right) = \left\{ {{s_l}|} \right. $ $ {s_l} \in S,l = 1,2, \cdots, L\left. {\left( {{h_s}\left( {{x_i}} \right)} \right)} \right\} $ 表示$ {x_i} \in X $ 所有可能的隶属度。当$ X $ 只含有一个元素$ x $ 时，称$ {h_s}\left( x \right) $ 为犹豫模糊语言术，简记为$ {h_s} $ 。1.3 多粒度语言术语集
在实际决策问题中，不同决策者所使用的“不确定性的粒度”（语言术语集的基数）有可能不同，针对此问题，Herrera-Viedma等[7]提出了多粒度语言术语集。
定义3 语言术语集是一个含有奇基数离散元素的集合，定义为
$$ Y = \{ {g_\alpha }{\text{|}}\alpha = -{{ m}}, \cdots,0,\cdots,m,\quad m \in {N^ + }\} $$ 式中：
$ {g_\alpha } $ 为第$ \alpha $ 个语言术语，$ {N^ + } $ 为正整数，语言术语集的粒度（基数）是$ 2m + 1 $ 。多粒度语言术语集是具有不同粒度级别的语言术语集的组合，即$$ Y_n^{{\text{t}}(n)} = \{ g_{_\alpha }^{t(n)}{\text{|}}\alpha= - {\text{ }}{{{m}}_n}, \cdots,0, \cdots,\left. {{m_n}} \right\},\;\;\;\left( {n = 1,2} \right.,\cdots ,N) $$ 式中：
$ Y_n^{{\text{t}}(n)} $ 为第$ n $ 个语言术语集，$ t(n) = 2{m_n} + 1 $ 为粒度，$ N $ 为语言术语集的个数。2. 多粒度犹豫模糊语言TOPSIS方法
2.1 多粒度犹豫模糊语言信息的转换
Chen等[29]为了将多粒度语言信息进行集结，提出了一种多粒度语言信息的转换方法，从而实现多个粒度间的相互转换。
$S{\text{ = }}\left\{ {{s_0},{s_1},\cdots,{s_g}} \right\},{s_i}\left( {0 \leqslant i \leqslant g} \right)$ 的语义长度为$ \left[ {\dfrac{i}{{g + 1}},\dfrac{{i + 1}}{{g + 1}}} \right]，S $ 中的各部分均匀覆盖在$ \left[ {0,1} \right] $ ，且相互之间没有重叠，同时称${S^{g_T}} = \left\{ {s_0^{{g_T}},s_1^{{g_T}}, \cdots ,s_{{g_T}}^{{g_T}}} \right\}$ 为其隶属度语言术语集。定义4 设
$ {S^{{g_i}}} = \left\{ {s_0^{{g_i}},s_1^{{g_i}}, \cdots ,s_{{g_i}}^{{g_i}}} \right\} $ 和${S^{g_T}} = \left\{ s_0^{{g_T}}, s_1^{{g_T}}, \cdots , s_{{g_T}}^{{g_T}} \right\}$ 是2个语言术语集，其中$ {g_i} \ne {g_T}, $ 从$ {S^{{g_i}}} $ 转换到$ {S^{{g_T}}} $ 的隶属度语言术语集的函数如下：$$ {\tau }_{{s}^{{g}_{{}_{i}}}{s}^{{g}_{{}_{T}}}}^{，}\left({s}_{j}^{{g}_{i}}\right)=\left\{\left({s}_{k}^{{g}_{{}_{T}}},{\mu }_{jk}\left(x\right)\right)\right\},\forall {s}_{j}^{{g}_{i}}\in {S}^{{g}_{i}} $$ $$ {\mu }_{jk}\left(x\right)=\left\{\begin{aligned} & 1,\quad {k}_{\mathrm{min}}＜k＜{k}_{\mathrm{max}}\\ &\left(\dfrac{k+1}{{g}_{T}+1}-\dfrac{j}{{g}_{i}+1}\right)\left({g}_{T}+1\right),\quad k={k}_{\mathrm{min}}\\ &\left(\dfrac{j+1}{{g}_{j}+1}-\dfrac{k}{{g}_{T}+1}\right)\left({g}_{T}+1\right),\quad k={k}_{\mathrm{max}}\\ &\dfrac{{g}_{T}+1}{{g}_{i}+1},\quad k={k}_{\mathrm{min}}={k}_{\mathrm{max}}\\ & 0,\quad 其他\end{aligned} \right.$$ 式中：
$ {k_{\min }} $ 和$ {k_{\max }} $ 的取值是$ {s^{{g_T}}} $ 和$ s_j^{{g_i}} $ 语义相交部分的首位和末位语言术语的下标，定义为$$ \begin{gathered} \dfrac{{{k_{\min }}}}{{{g_T} + 1}} \leqslant \dfrac{j}{{{g_i} + 1}} \leqslant \dfrac{{{k_{\min }} + 1}}{{{g_T} + 1}},\quad j = 0,1, \cdots,{g_i} \\ \dfrac{{{k_{\max }}}}{{{g_T} + 1}} \leqslant \dfrac{{j + 1}}{{{g_i} + 1}} \leqslant \dfrac{{{k_{\max }} + 1}}{{{g_T} + 1}},\quad j = 0,1, \cdots,{g_i} \\ \end{gathered} $$ 但上述方法只适用于决策者只用一个术语进行评价时的转换，而当决策者在几个术语之间犹豫不决时，则会产生多粒度犹豫模糊语言术语集的转换。
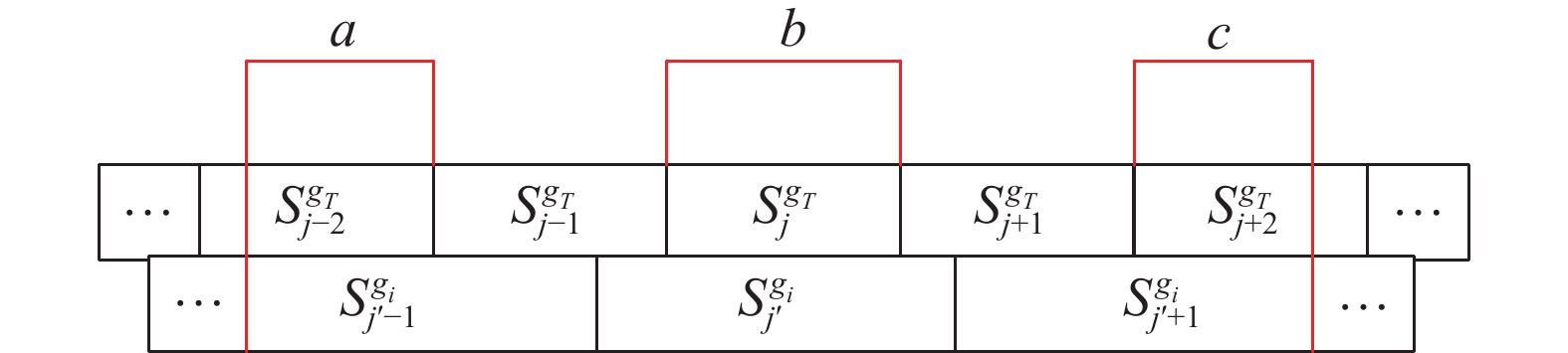
图1是将
$ {S^{{g_i}}} $ 中某个犹豫模糊语言术语集$ \left\{ {s_{{j^{'}} - 1}^{{g_i}},s_{j'}^{{g_i}},s_{{j^{'}} + 1}^{{g_i}}} \right\} $ 转换为目标语言术语集$ {S^{{g_T}}} $ 中的语言信息的基本思想。其中设$ s_{{j^{'}} - 1}^{{g_i}} $ 覆盖$ s_{j - 2}^{{g_i}} $ 的长度为$ a $ ，$ s_{{j^{'}} + 1}^{{g_i}} $ 覆盖$ s_{j + 2}^{{g_i}} $ 的长度为$ b $ ，$ {S^{{g_T}}} $ 的语义长度为$ c $ 。故$ s_{j - 2}^{{g_T}}、s_{j - {\text{1}}}^{{g_T}}、s_j^{{g_T}}、$ $s_{j{\text{ + 1}}}^{{g_T}}、 s_{j{\text{ + }}2}^{{g_T}}$ 的隶属度为$ \dfrac{a}{c}、1、1、1、\dfrac{b}{c} $ ，$ {S^{{g_i}}} $ 则可以转换为$ {S^{{g_T}}} $ 中的相应的隶属度语言术语集$ \left\{ {\left( {s_{j - 2}^{{g_T}},\dfrac{a}{c}} \right)} \right.,\left( {s_{j - 1}^{{g_T}},1} \right), $ $ \left. {\left( {s_j^{{g_T}},1} \right),\left( {s_{j + 1}^{{g_T}},1} \right),\left( {s_{j + 2}^{{g_T}},\dfrac{b}{c}} \right)} \right\} $ 。
图 1 多粒度HFLTSs转换Fig. 1 Multi-grained HFLTs conversion
下载:
全尺寸图片
定义5 设
$ {S^{{g_i}}} = \left\{ {s_0^{{g_i}},s_1^{{g_i}}, \cdots ,s_{{g_i}}^{{g_i}}} \right\} $ 和${S^{g_T}} = \left\{ s_0^{{g_T}},s_1^{{g_T}}, \cdots , s_{{g_T}}^{{g_T}} \right\}$ 为2个不同粒度的语言术语集，$ {S^{{g_i}}} $ 上犹豫模糊语言术语集为$$ {H^{{S^{{g_i}}}}} = \left\{ {\left\{ {s_p^{{g_i}},s_{p + 1}^{{g_i}}, \cdots ,s_{p + q}^{{g_i}}} \right\}\bigg|\forall s_{p + q}^{{g_i}} \in {S^{{g_i}}}} \right\} $$ 其转换函数为
$$ \begin{gathered}{\tau }_{{H}^{{S}^{{g}_{{}_{i}}}{S}^{{g}_{{}_{T}}}}}\left(\left\{{s}_{p}^{{g}_{i}},{s}_{p+1}^{{g}_{i}},\cdots ,{s}_{p+q}^{{g}_{i}}\right\}\right)=\\ \left\{\left({s}_{k}^{{g}_{{}_{T}}},{\mu }_{\left\{{s}_{p}^{{g}_{i}},{s}_{p+1}^{{g}_{i}},\cdots ,{s}_{p+q}^{{g}_{i}}\right\}}{}_{,k\left(x\right)}\right)\bigg|,\quad k\in \left\{0,1,\cdots ,{g}_{T}\right\}\right\},\\ \forall \left\{{s}_{p}^{{g}_{i}},{s}_{p+1}^{{g}_{i}},\cdots ,{s}_{p+q}^{{g}_{i}}\right\}\in {H}^{{S}^{{g}_{{}_{i}}}}。\end{gathered} $$ $$ {\mu }_{\left\{{s}_{p}^{{g}_{{}_{i}}},\cdots ,{s}_{p+q}^{{g}_{{}_{i}}}\right\}},k\left(x\right)= \left\{\begin{aligned} &\text{1}\text{，} \quad {k}_{\mathrm{min}}< k < {k}_{\mathrm{max}}\\ &\left(\dfrac{k+1}{{g}_{T}+1}-\dfrac{p}{{g}_{i}+1}\right)\left({g}_{T}+1\right), \quad k={k}_{\mathrm{min}}\\ &\left(\dfrac{p+q+1}{{g}_{i}+1}-\dfrac{k}{{g}_{T}+1}\right)\left({g}_{T}+1\right), \quad k={k}_{\mathrm{max}}\\ & \dfrac{\left(q+1\right)\left({g}_{T}+1\right)}{{g}_{i}+1}, \quad k={k}_{\mathrm{min}}={k}_{\mathrm{max}}\\ &\text{0}\text{，} \quad 其他\end{aligned} \right.$$ (1) 与多粒度语言信息转化类似，
$ {k_{\min }} $ 和$ {k_{\max }} $ 的取值是$ {S^{{g_T}}} $ 与${{\rm{HFLTS}}}\left\{ {s_p^{{g_i}}, s_{p+1}^{{g_i}},\cdots ,s_{p + q}^{{g_i}}} \right\}$ 语义相交部分的首位和末位语言术语的下标，定义为$$ \begin{gathered} \dfrac{{{k_{\min }}}}{{{g_T} + 1}} \leqslant \dfrac{p}{{{g_i} + 1}} \leqslant \dfrac{{{k_{\min }} + 1}}{{{g_T} + 1}} \\ \dfrac{{{k_{\max }}}}{{{g_T} + 1}} \leqslant \dfrac{{p + q + 1}}{{{g_i} + 1}} \leqslant \dfrac{{{k_{\max }} + 1}}{{{g_T} + 1}} \end{gathered} $$ 为方便决策过程，定义隶属度语言术语集加权平均算子。
定义6[30] 设
${\textit{z}} = \{ {{{\textit{z}}_1},{{\textit{z}}_2}, \cdots,{{\textit{z}}_n}} \}，{{\textit{z}}_i} = \{ {( {{s_0},} }$ ${p_0^i} ), ( {s_1}, p_1^i ), \cdots, ( {{s_{{g_T}}},p_{{g_T}}^i} ) \},$ 其对应权向量为$\omega = ( {\omega _1},{\omega _2},\boldsymbol{L}, {\omega _n} )^{{\rm{T}}}$ ，式中$ \displaystyle\sum\limits_{j = 1}^n {{\omega _j} = 1} ,{\omega _j} \geqslant 0, $ $ \left\{ {{{\textit{z}}_1},{{\textit{z}}_2}, \cdots,{{\textit{z}}_n}} \right\} $ 的加权平均算子为$$ W{_\omega }\left( {{{\textit{z}}_1},{{\textit{z}}_2}, \cdots,{{\textit{z}}_n}} \right) = \left\{ {\left( {{s_t}, {{\bar p_t}} } \right)|t = 0,1,2, \cdots ,{g_T}} \right\} {{\bar p_t}} = \displaystyle\sum\limits_{i = 1}^n {{w_i}p_t^i} $$ (2) 第
$ k $ 个决策者的决策矩阵转换为相应的隶属度语言集的过程为$$ \begin{aligned} &{\boldsymbol{X}^k} = {\left( {x_{ij}^k} \right)_{n \times m}} = \left[ {\begin{array}{*{20}{c}} {x_{11}^k}&{x_{12}^k}& \cdots &{x_{1m}^k} \\ {x_{21}^k}&{x_{22}^k}& \cdots &{x_{2m}^k} \\ \vdots & \vdots & \ddots & \vdots \\ {x_{n1}^k}&{x_{n2}^k}& \ldots &{x_{nm}^k} \end{array}} \right],\quad k \in K \\ &\qquad\quad {\textit{z}}_{ij}^k = \left\{ {\left( {s_t^{{g_T}},p_{i,j,t}^k} \right)|t = 0,1, \cdots ,{g_T}} \right\} \end{aligned}$$ $$ {\boldsymbol{Z}^k} = {\left( {{\textit{z}}_{ij}^k} \right)_{n \times m}} = \left[ {\begin{array}{*{20}{c}} {{\textit{z}}_{11}^k}&{{\textit{z}}_{12}^k}& \cdots &{{\textit{z}}_{1m}^k} \\ {{\textit{z}}_{21}^k}&{{\textit{z}}_{22}^k}& \cdots &{{\textit{z}}_{2m}^k} \\ \vdots & \vdots & \ddots & \vdots \\ {{\textit{z}}_{n1}^k}&{{\textit{z}}_{n2}^k}& \ldots &{{\textit{z}}_{nm}^k} \end{array}} \right],\quad k \in K $$ 2.2 基于多粒度犹豫模糊语言术语集的TOPSIS决策方法
本节所提出的核心模型，首先采用上文提出的犹豫模糊语言术语集转化为隶属度语言术语集的方法将每个决策者的信息进行统一；然后将所得隶属度语言术语集集结成各方案的综合评价；最后结合TOPSIS方法得出决策结果。具体步骤如下：
1）根据式(1)，将各决策者原始不同粒度下的的犹豫模糊语言集转换为同一粒度下的语言术语集（规定选择粒度大的语言术语集作为标准）。
设
$ {S^{{g_T}}} = \left\{ {s_0^{{g_T}},s_1^{{g_T}}, \cdots ,s_{{g_T}}^{{g_T}}} \right\}, $ 将$ x_{ij}^k $ 转换为$$ {\textit{z}}_{ij}^k = \left\{ {\left( {s_t^{{g_T}},p_{ij,t}^k} \right)|t = 0,1,2, \cdots, {g_T}} \right\},i \in I, j \in J, k\in K。 $$ 转换后每个决策者的决策矩阵为
$$ {{\boldsymbol{Z}}^k} = {\left( {{\textit{z}}_{ij}^k} \right)_{n \times m}} = \left[ {\begin{array}{*{20}{c}} {{\textit{z}}_{11}^k}&{{\textit{z}}_{12}^k}& \cdots &{{\textit{z}}_{1m}^k} \\ {{\textit{z}}_{21}^k}&{{\textit{z}}_{22}^k}& \cdots &{{\textit{z}}_{2m}^k} \\ \vdots & \vdots & \ddots & \vdots \\ {{\textit{z}}_{n1}^k}&{{\textit{z}}_{n2}^k}& \cdots &{{\textit{z}}_{nm}^k} \end{array}} \right],k \in K $$ 2）假设每个决策者的权重为
$\boldsymbol {\lambda} = [ 0.3\;\;0.4\;\; 0.3 ]^{{\rm{T}}}$ ，由式(2)，得到$ \overline Z = {\left( {{{\overline {\textit{z}} }_{ij}}} \right)_{n \times m}}, $ ${\overline {\textit{z}} _{ij}} = W{_\lambda }\left( {{Z^1},{Z^2}, \cdots ,{Z^q}} \right)$ ，从而得出决策者综合评价矩阵。3）假设属性的权重为
$\boldsymbol{\omega} = \left[ {0.5,} \right.{\left. {0.3\;\;0.2} \right]^{\rm{T}}}$ ，由式(2)得${\overline{{\textit{z}}}}_{i}=W_{\omega }({\overline{{\textit{z}}}}_{{i}_{1}}，$ $ \left. {{{\overline {\textit{z}} }_{{i_2}}}, \cdots ,{{\overline {\textit{z}} }_{{i_m}}}} \right) $ ，从而得出所有备选方案的综合评价矩阵。4）根据群体决策矩阵确定正理想解
$ Z_s^ + $ 、负理想解$ Z_s^ - $ 。5）分别计算每个备选方案与正理想解和负理想解的距离。
$$\begin{aligned} &D_i^ + = \sqrt {\displaystyle\sum\limits_{j = 1}^n {{{\left( {{Z_{ij}} - Z_s^ + } \right)}^2}} } ,\;\;i = 1,2, \cdots ,m;\;\;j = 1,2, \cdots ,n \\ &D_i^ - = \sqrt {\displaystyle\sum\limits_{j = 1}^n {{{\left( {{Z_{ij}} - Z_s^ - } \right)}^2}} } ,\;\;i = 1,2, \cdots ,m;\;\;j = 1,2, \cdots ,n \end{aligned}$$ 6）最后计算每个备选方案的贴近度系数。
$ R{_i} = \dfrac{{D_i^ - }}{{D_i^ - + D_i^ + }},i = 1,2, \cdots ,m $ 7）根据
$ R{_i} $ 的大小将所有备选方案进行排序，$ R{_i}\left( {i = 1,2, \cdots ,m} \right) $ 越大，方案越佳。3. 案例分析
本文采用文献[23,31-32]中的例子来对所提的决策方法进行说明。
某医院现有
$ {A_1} $ 焚烧处理、$ {A_2} $ 填埋处理、$ {A_3} $ 蒸汽灭菌、$ {A_4} $ 微波处理、$ {A_5} $ 电化技术处理5个医疗废物处理技术可供选择。为选择最佳的医疗废物处理技术，该医院邀请了3组不同领域的专家进行决策分析，3组专家分别包括该医院的专家$ {d_{\text{1}}} $ 、相关研究机构专家$ {d_2} $ 和废物处理方面的技术专家$ {d_3} $ ，3组专家的权重向量为$ {\boldsymbol{\lambda}} = {\left[ {0.3\;\;0.4\;\;0.3} \right]^{{\rm{T}}}} $ 。同时和以下3个准则一起进行了讨论：$ {U_1} $ 成本、$ {U_2} $ 环保和$ {U_3} $ 技术可靠性，3个准则的权重分别为${\boldsymbol{\omega}} = \left[0.5\;\;0.3\;\;0.2\right]^{\text{T}}。$ 经过讨论，每组专家均使用犹豫模糊语言术语集对A1~A5这5种处理技术进行了语言评价，给出的模糊评价信息如表1和表2所示。
表 1 d1和d2使用的7粒度语言术语集Table 1 7-granularity linguistic term set used in d1 and d2粒度 0 1 2 3 4 5 6 评价信息 非常差 差 有点差 一般 有点好 好 非常好 表 2 d3使用的5粒度语言术语集Table 2 5-granularity linguistic term set used in d3粒度 0 1 2 3 4 评价信息 差 有点差 一般 有点好 好 $ {d_1} $ 和$ {d_{\text{2}}} $ 使用7粒度的语言术语集${S^7} = \left\{ s_0^7, s_1^7, \cdots , s_6^7 \right\}$ ，$ {d_{\text{3}}} $ 使用5粒度的语言术语集$ {S^5} = \left\{ {s_0^5,s_1^5, \cdots ,s_4^5} \right\} $ ，他们给出的犹豫模糊语言决策矩阵分别为$$\begin{aligned} {{\boldsymbol{X}}^1} = \left[ {\begin{array}{*{20}{c}} {\left\{ {s_4^7,s_5^7} \right\}}&{\left\{ {s_3^7} \right\}}&{\left\{ {s_4^7} \right\}} \\ {\left\{ {s_2^7} \right\}}&{\left\{ {s_5^7,s_6^7} \right\}}&{\left\{ {s_3^7} \right\}} \\ {\left\{ {s_1^7} \right\}}&{\left\{ {s_5^7} \right\}}&{\left\{ {s_3^7,s_4^7} \right\}} \\ {\left\{ {s_5^7,s_6^6} \right\}}&{\left\{ {s_4^7} \right\}}&{\left\{ {s_3^7} \right\}} \\ {\left\{ {s_3^7} \right\}}&{\left\{ {s_1^7} \right\}}&{\left\{ {s_5^7,s_6^7} \right\}} \end{array}} \right]\\ {{\boldsymbol{X}}^2} = \left[ {\begin{array}{*{20}{c}} {\left\{ {s_5^7} \right\}}&{\left\{ {s_2^7} \right\}}&{\left\{ {s_3^7,s_4^7} \right\}} \\ {\left\{ {s_3^7,s_4^7} \right\}}&{\left\{ {s_4^7,s_5^7} \right\}}&{\left\{ {s_2^7} \right\}} \\ {\left\{ {s_2^7} \right\}}&{\left\{ {s_3^7,s_4^7} \right\}}&{\left\{ {s_3^7,s_4^7} \right\}} \\ {\left\{ {s_5^7} \right\}}&{\left\{ {s_5^7,s_6^7} \right\}}&{\left\{ {s_3^7} \right\}} \\ {\left\{ {s_3^7} \right\}}&{\left\{ {s_2^7} \right\}}&{\left\{ {s_5^7} \right\}} \end{array}} \right] \\ {{\boldsymbol{X}}^3} = \left[ {\begin{array}{*{20}{c}} {\left\{ {s_4^5} \right\}}&{\left\{ {s_2^5} \right\}}&{\left\{ {s_2^5,s_3^5} \right\}} \\ {\left\{ {s_2^5} \right\}}&{\left\{ {s_4^5} \right\}}&{\left\{ {s_2^5} \right\}} \\ {\left\{ {s_3^5,s_4^5} \right\}}&{\left\{ {s_3^5} \right\}}&{\left\{ {s_2^5,s_3^5} \right\}} \\ {\left\{ {s_3^5,s_4^5} \right\}}&{\left\{ {s_3^5} \right\}}&{\left\{ {s_2^5} \right\}} \\ {\left\{ {s_2^5} \right\}}&{\left\{ {s_0^5,s_1^5} \right\}}&{\left\{ {s_4^5} \right\}} \end{array}} \right] \end{aligned} $$ 1）根据式(1)，将3个专家原始不同粒度下的的犹豫模糊语言集都转换为
$ {S^6} $ 下的隶属度犹豫模糊语言术语集${{\boldsymbol{Z}}^1}、{{\boldsymbol{Z}}^2}、{{\boldsymbol{Z}}^3}$ ：$$ \begin{gathered} {{\boldsymbol{Z}}^1} = \\ \left[ {\begin{array}{*{20}{c}} {\left( {0,0,0,0,1,1,0} \right)}&{\left( {0,0,0,1,0,0,0} \right)}&{\left( {0,0,0,0,1,0,0} \right)} \\ {\left( {0,0,1,0,0,0,0} \right)}&{\left( {0,0,0,0,0,1,1} \right)}&{\left( {0,0,0,1,0,0,0} \right)} \\ {\left( {0,1,0,0,0,0,0} \right)}&{\left( {0,0,0,0,0,1,0} \right)}&{\left( {0,0,0,1,1,0,0} \right)} \\ {\left( {0,0,0,0,0,1,1} \right)}&{\left( {0,0,0,0,1,0,0} \right)}&{\left( {0,0,0,1,0,0,0} \right)} \\ {\left( {0,0,0,1,0,0,0} \right)}&{\left( {0,1,0,0,0,0,0} \right)}&{\left( {0,0,0,0,0,1,1} \right)} \end{array}} \right] \\ \end{gathered} $$ $$ \begin{gathered} {{\boldsymbol{Z}}^2} = \\ \left[ {\begin{array}{*{20}{c}} {\left( {0,0,0,0,0,1,0} \right)}&{\left( {0,0,1,0,0,0,0} \right)}&{\left( {0,0,0,1,1,0,0} \right)} \\ {\left( {0,0,0,1,1,0,0} \right)}&{\left( {0,0,0,0,1,1,0} \right)}&{\left( {0,0,1,0,0,0,0} \right)} \\ {\left( {0,0,1,0,0,0,0} \right)}&{\left( {0,0,0,1,1,0,0} \right)}&{\left( {0,0,0,1,1,0,0} \right)} \\ {\left( {0,0,0,0,0,1,0} \right)}&{\left( {0,0,0,0,0,1,1} \right)}&{\left( {0,0,1,0,0,0,0} \right)} \\ {\left( {0,0,0,1,0,0,0} \right)}&{\left( {0,0,1,0,0,0,0} \right)}&{\left( {0,0,0,0,0,1,0} \right)} \end{array}} \right] \\ \end{gathered} $$ $$ \begin{gathered} {{\boldsymbol{Z}}^3} = \left[ {a{\text{ }}b{\text{ }}c} \right] \\ {\boldsymbol{a}} = \left[ {\begin{array}{*{20}{c}} {\left( {0,0,0,0,0,0.4,1} \right)} \\ {\left( {0,0,0.2,1,0.2,0,0} \right)} \\ {\left( {0,0,0.2,1,0.2,0,0} \right)} \\ {\left( {0,0,0,0,0.8,1,1} \right)} \\ {\left( {0,0,0.2,1,0.2,0,0} \right)} \end{array}} \right] \\ \end{gathered} $$ $$ {\boldsymbol{b}} = \left[ {\begin{array}{*{20}{c}} {\left( {0,0,0.2,1,0.2,0,0} \right)} \\ {\left( {0,0,0,0,0,0.4,1} \right)} \\ {\left( {0,0,0,0,0.8,0.6,0} \right)} \\ {\left( {0,0,0,0,0.8,0.6,0} \right)} \\ {\left( {1,1,0.8,0,0,0,0} \right)} \end{array}} \right] $$ $$ {\boldsymbol{c}} = \left[ {\begin{array}{*{20}{c}} {\left( {0,0,0.2,1,1,0.6,0} \right)} \\ {\left( {0,0,0.2,1,0.2,0,0} \right)} \\ {\left( {0,0,0.2,1,1,0.6,0} \right)} \\ {\left( {0,0,0.2,1,0.2,0,0} \right)} \\ {\left( {0,0,0,0,0,0.4,1} \right)} \end{array}} \right] $$ 2）由
$\boldsymbol {\lambda} = {\left [{ 0.3 \;\ 0.4 \;\ 0.3}\right] ^{{\rm{T}}}}$ 及式(2)，可以得到3个专家的综合评价，具体为$$ \begin{gathered} \overline {\boldsymbol{Z}} = \left[ {\boldsymbol A{\text{ }}\boldsymbol B{\text{ }}\boldsymbol{ C}} \right] \\ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\left( {0,0,0,0,0.3,0.82,0.3} \right)} \\ {\left( {0,0,0.36,0.7,0.46,0,0} \right)} \\ {\left( {0,0.3,0.46,0.3,0.06,0,0} \right)} \\ {\left( {0,0,0,0,0.24,1,0.6} \right)} \\ {\left( {0,0,0.06,1,0.06,0,0} \right)} \end{array}} \right] \\ {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\left( {0,0,0.46,0.6,0.06,0,1} \right)} \\ {\left( {0,0,0,0,0.4,0.82,0.6} \right)} \\ {\left( {0,0,0,0.4,0.64,0.48,0} \right)} \\ {\left( {0,0,0,0,0.54,0.58,0.4} \right)} \\ {\left( {0.3,0.6,0.64,0,0,0,0} \right)} \end{array}} \right] \end{gathered} $$ $$ {\boldsymbol{C}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\left( {0,0,0.06,0.7,1,0.18,0} \right)} \\ {\left( {0,0,0.46,0.6,0.06,0,0} \right)} \\ {\left( {0,0,0.06,1,1,0.18,0} \right)} \\ {\left( {0,0,0.46,0.6,0.06,0,0} \right)} \\ {\left( {0,0,0,0,0,0.82,0.6} \right)} \end{array}} \right] $$ 3）由
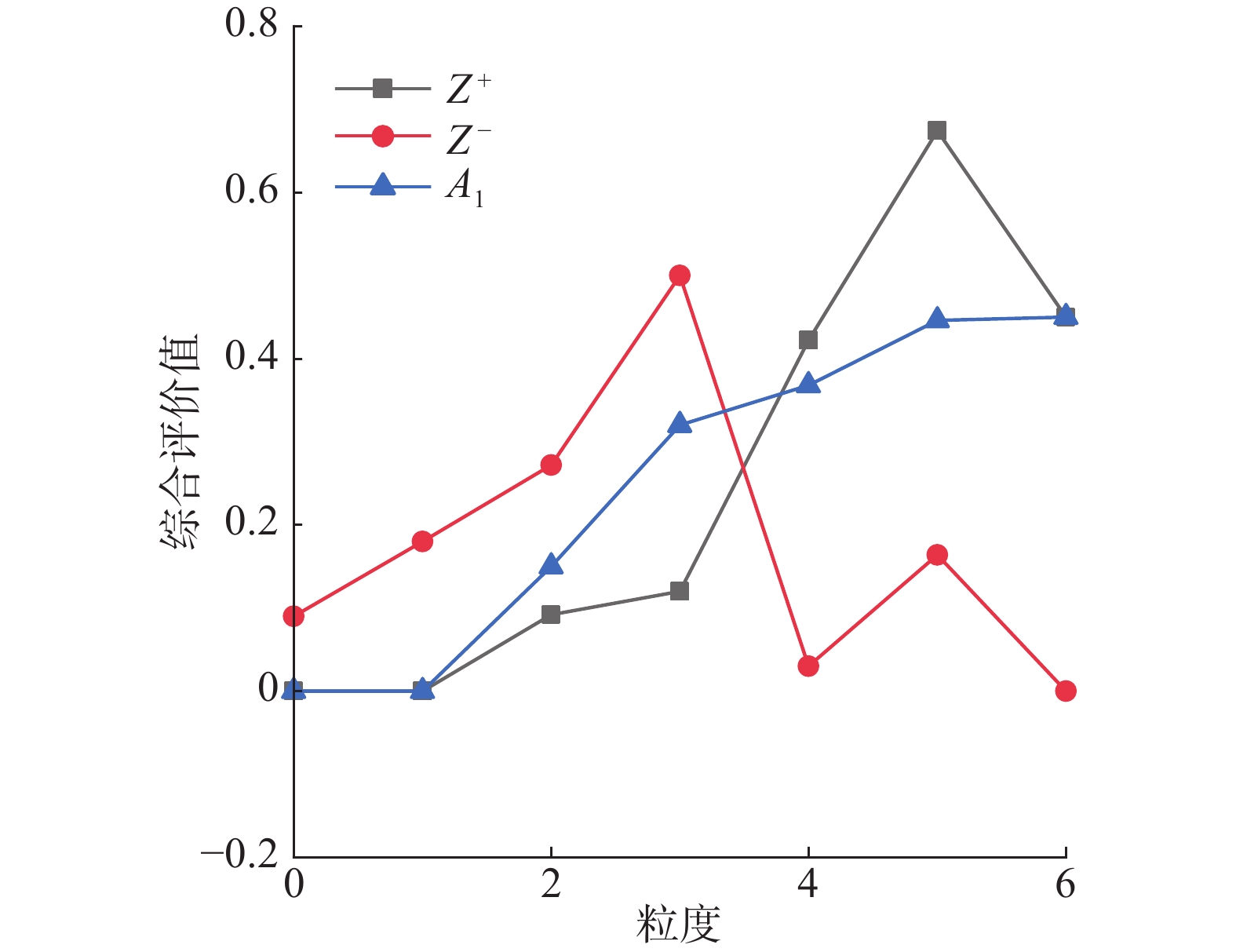
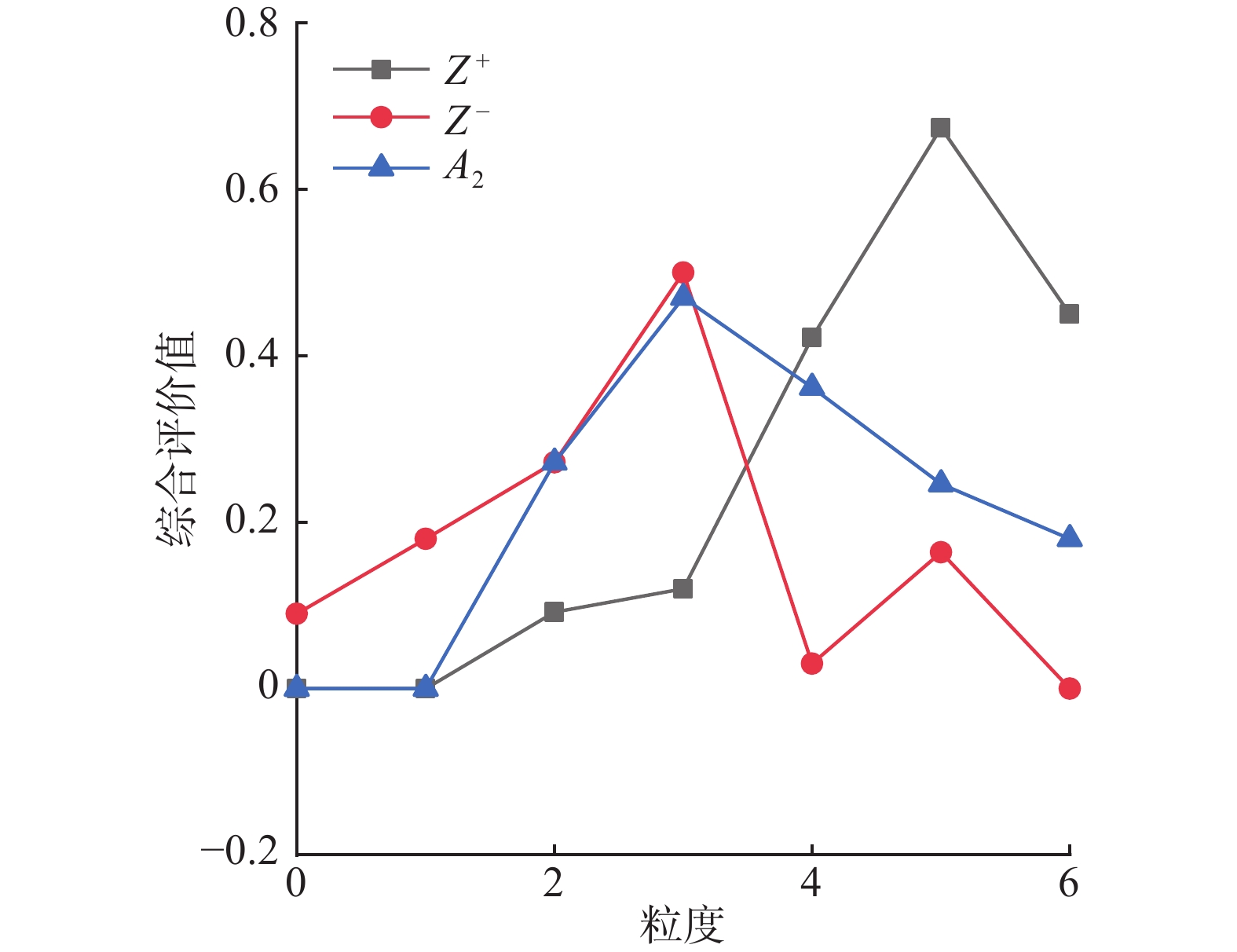
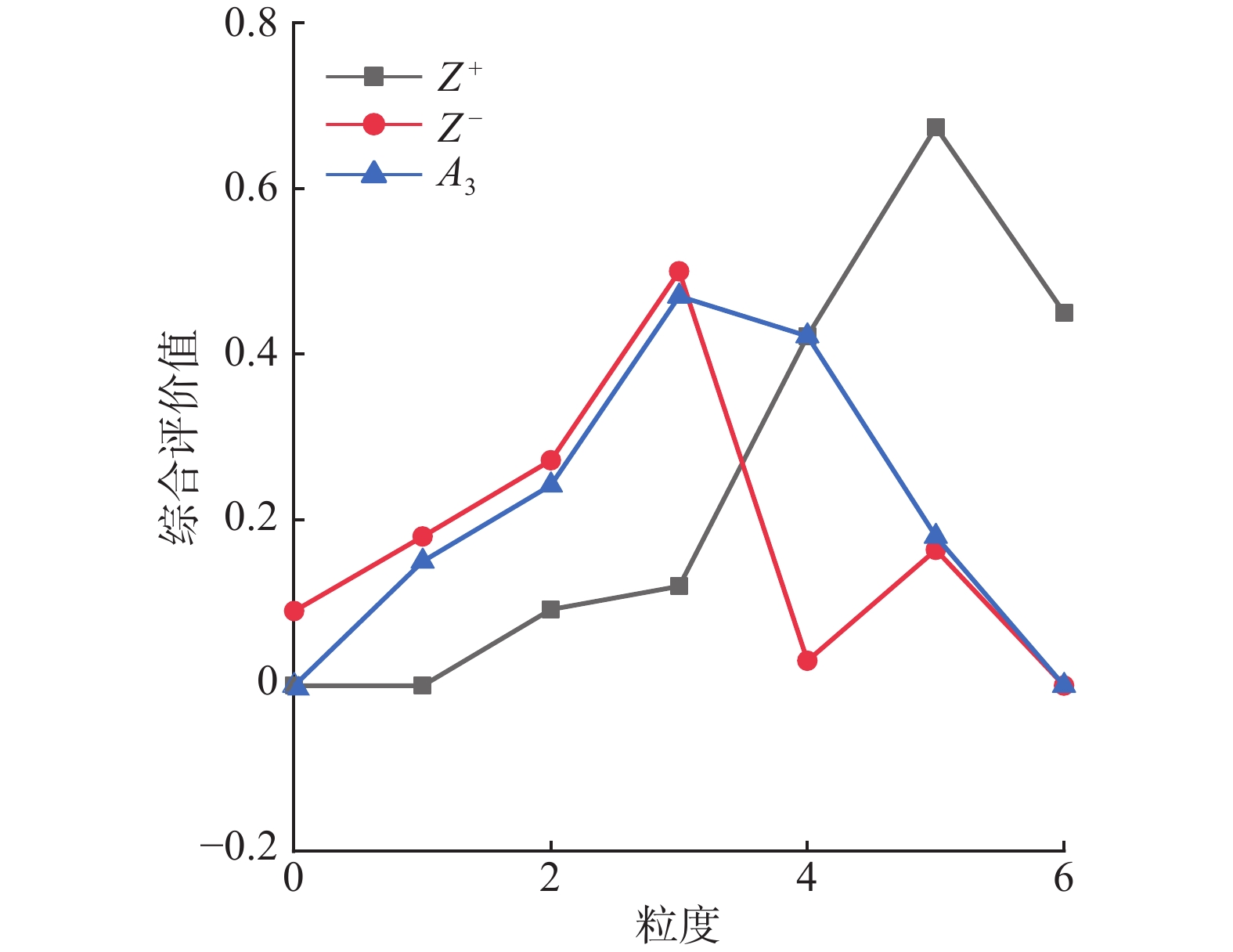
$ \boldsymbol{\omega} = {\left[ {0.5\;\;0.3\;\;0.2} \right]^{{\rm{T}}}} $ 及式(2)，可以得到5个技术方案的综合评价：$$ {{\bar{ \textit{z}}_1}} = \left( {0,0,0.15,0.32,0.368,0.446,0.45} \right) $$ $$ {{\bar{\textit{z}}_2}} = \left( {0,0,0.272,0.47,0.362,0.246,0.18} \right) $$ $$ {{\bar{\textit{z}}_3}} = \left( {0,0.15,0.242,0.47,0.422,0.18,0} \right) $$ $$ {{\bar{\textit{z}}_4}} = \left( {0,0,0.092,0.12,0.294,0.674,0.42} \right) $$ $$ {{\bar{\textit{z}}_5}} = \left( {0.09,0.18,0.222,0.5,0.03,0.164,0.12} \right) $$ 从而得到7粒度语言术语集下的综合评价矩阵：
$$ {{\overline{\boldsymbol{Z}}_s}} = \left[ {\begin{array}{*{20}{c}} 0&0&{0.15}&{0.32}&{0.368}&{0.446}&{0.45} \\ 0&0&{0.272}&{0.47}&{0.362}&{0.246}&{0.18} \\ 0&{0.15}&{0.242}&{0.47}&{0.422}&{0.18{\text{0}}}&0 \\ 0&0&{0.092}&{0.12}&{0.294}&{0.674}&{0.42} \\ {0.09}&{0.18}&{0.222}&{0.5{\text{0}}}&{0.03}&{0.164}&{0.12} \end{array}} \right] $$ 4）确定决策矩阵的正、负理想解（低粒度代表专家对该方案不满意，故选用最小值作为正理想点，最大值作为负理想点；高粒度则代表专家对该方案满意，故选用最大值作为正理想点，最小值作为负理想点）。
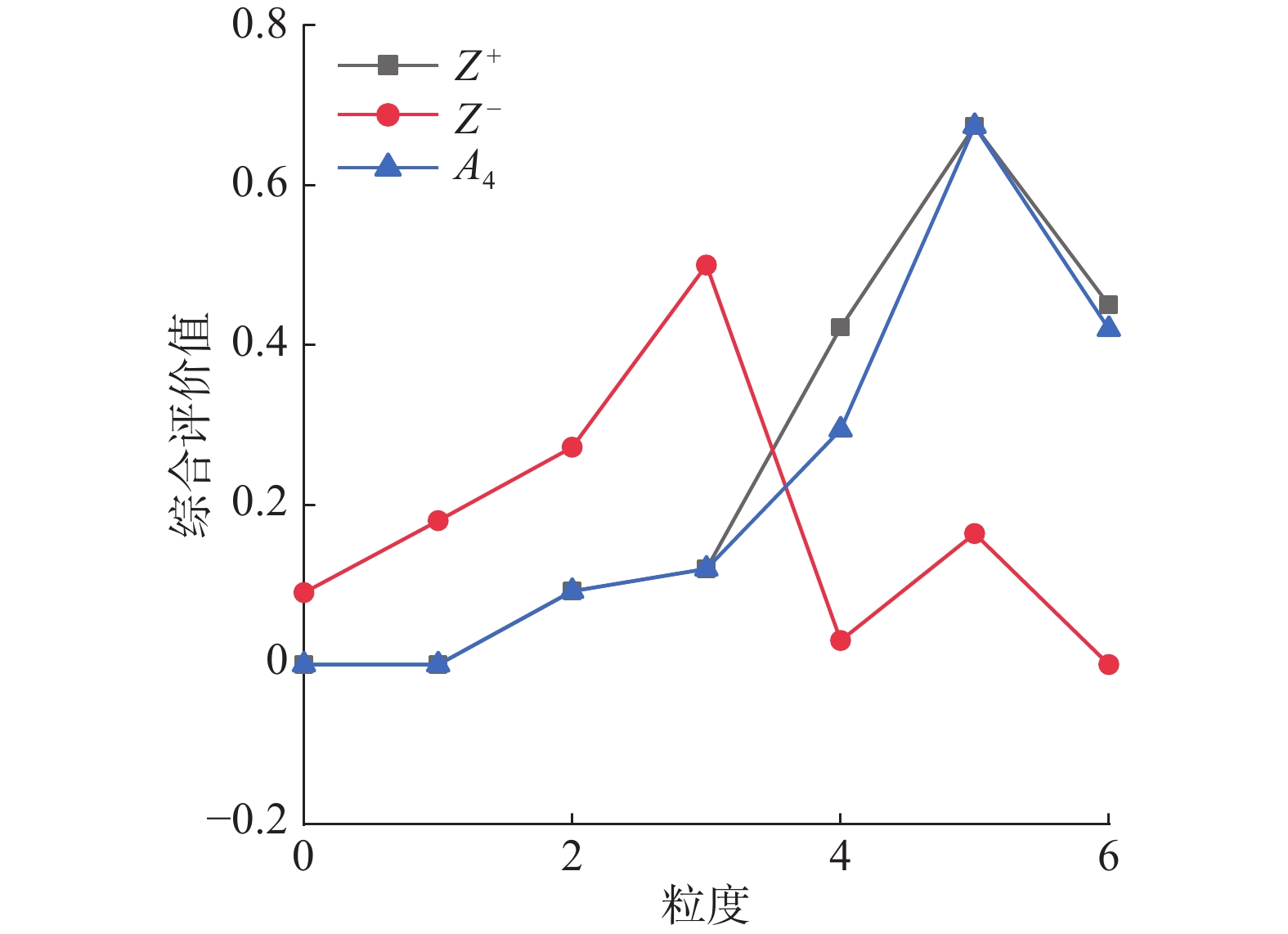
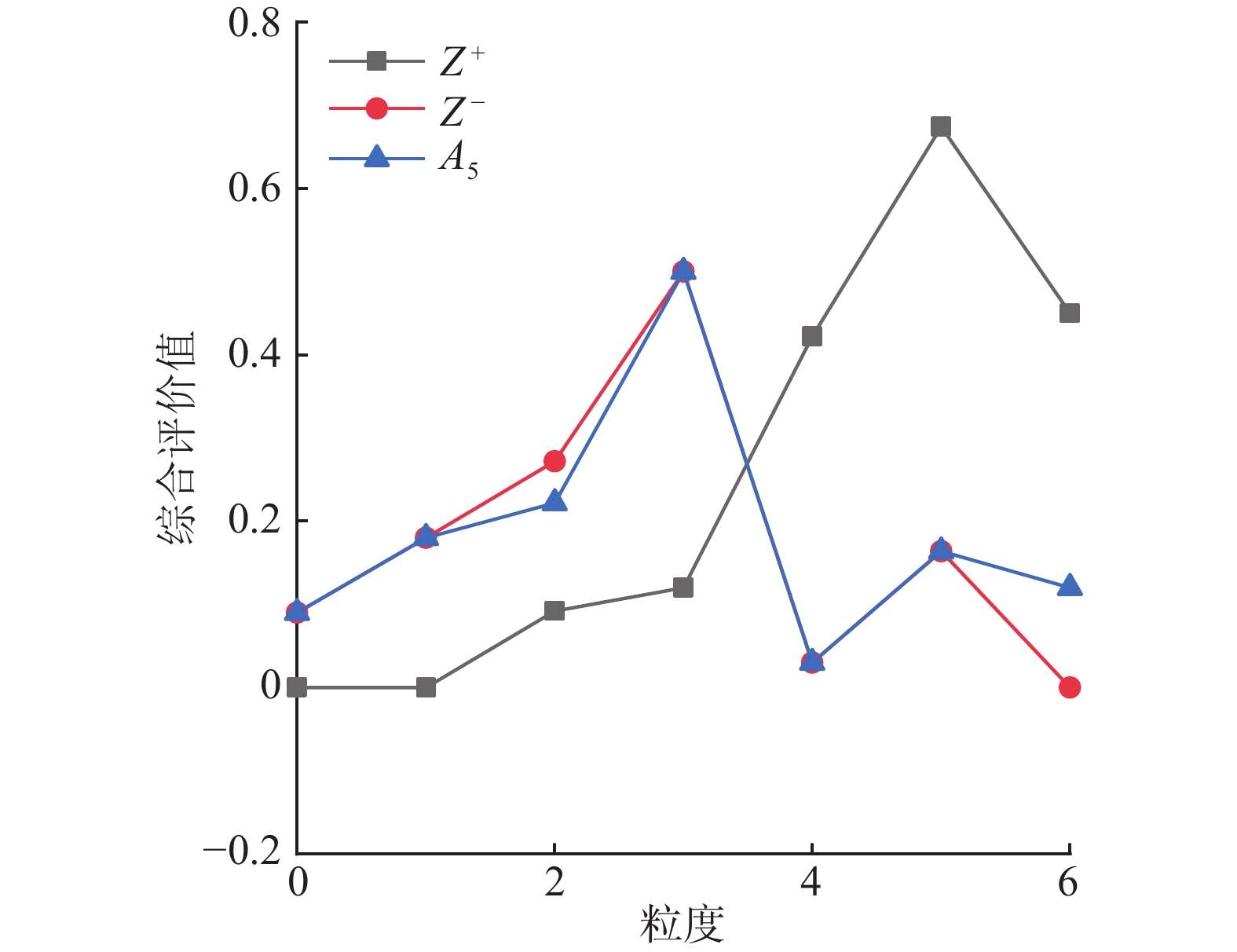
$$\begin{aligned} & {Z}_{s}^{\text+}=\left\{\text{0}，\text{0}，\text{0}\text{.092}，\text{0}\text{.12}，\text{0}\text{.422}，\text{0}\text{.674}，\text{0}\text{.45}\right\}\\ & Z_s^{\text{ - }} = \left\{ {{\text{0}}{\text{.09}}，{\text{0}}{\text{.18}}，{\text{0}}{\text{.272}}，{\text{0}}{\text{.5}}，{\text{0}}{\text{.03}}，{\text{0}}{\text{.164}}，{\text{0}}} \right\} \end{aligned} $$ 在综合考虑专家和属性准则的权重后，所得出的每个方案综合评价值与该决策矩阵正、负理想解之间的关系如图2~6所示。
图 2 A1与正负理想解关系Fig. 2 Relationship between A1 and positive and negative ideal solutions下载:
全尺寸图片
图 3 A2与正负理想解关系Fig. 3 Relationship between A2 and positive and negative ideal solutions下载:
全尺寸图片
图 4 A3与正负理想解关系Fig. 4 Relationship between A3 and positive and negative ideal solutions下载:
全尺寸图片
图 5 A4与正负理想解关系Fig. 5 Relationship between A4 and positive and negative ideal solutions下载:
全尺寸图片
图 6 A5与正负理想解关系Fig. 6 Relationship between A5 and positive and negative ideal solutions下载:
全尺寸图片
当专家评价信息在高粒度下值越大时，证明专家对此方案越满意，可以看出在同等粒度评价信息下，
$ {A_4} $ 在高粒度下最接近正理想解，$ {A_5} $ 在低粒度下最接近负理想解。5）分别计算每个技术方案与正理想解以及负理想解的距离：
$$ D_{\text{1}}^ + = \sqrt {0.{\text{098}}} {\text{ = }}0.{\text{314}},D_{\text{1}}^ - = \sqrt {0.{\text{484}}} {\text{ = }}0.{\text{696}} $$ $$\begin{aligned} & D_{\text{2}}^ + {\text{ = }}\sqrt {0.{\text{292}}} {\text{ = }}0.{\text{54}},D_{\text{2}}^ - {\text{ = }}\sqrt {0.{\text{191}}} {\text{ = }}0.{\text{437}}\\ & D_{\text{3}}^ + {\text{ = }}\sqrt {0.{\text{614}}} {\text{ = }}0.{\text{784}},D_{\text{3}}^ - {\text{ = }}\sqrt {0.{\text{165}}} {\text{ = }}0.{\text{406}}\\ & D_4^ + = \sqrt {0.{\text{017}}} {\text{ = }}0.{\text{131}},D_4^ - = \sqrt {0.{\text{724}}} {\text{ = }}0.{\text{801}} \\ & D_5^ + = \sqrt {0.{\text{725}}} {\text{ = }}0.{\text{851}},D_5^ - = \sqrt {0.{\text{017}}} {\text{ = }}0.{\text{131}} \end{aligned}$$ 6）计算每个技术方案的贴近度系数
$ R{_i} $ ：$$ R{_1} = \dfrac{{D_1^ - }}{{D_1^ - + D_1^ + }} = \dfrac{{0.{\text{696}}}}{{{\text{1}}{\text{.01}}}}{\text{ = }}0.{\text{689}} $$ $$ R{_2} = \dfrac{{D_2^ - }}{{D_2^ - + D_2^ + }} = \dfrac{{0.{\text{437}}}}{{{\text{0}}{\text{.977}}}}{\text{ = }}0.{\text{447}} $$ $$ R{_3} = \dfrac{{D_3^ - }}{{D_3^ - + D_3^ + }} = \dfrac{{0.{\text{406}}}}{{1.{\text{19}}}}{\text{ = }}0.{\text{341}} $$ $$ R{_4} = \dfrac{{D_4^ - }}{{D_4^ - + D_4^ + }} = \dfrac{{0.{\text{801}}}}{{{\text{0}}{\text{.932}}}}{\text{ = }}0.{\text{859}} $$ $$ R{_5} = \dfrac{{D_5^ - }}{{D_5^ - + D_5^ + }} = \dfrac{{0.{\text{131}}}}{{{\text{0}}{\text{.982}}}}{\text{ = }}0.{\text{133}} $$ 根据
$ R{_i} $ 的大小对5个技术方案进行降序排序，可得备选方案之间的优先级排序为$ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_{\text{3}}} > {A_{\text{5}}} $ ，故$ {A_4} $ 为最佳方案，且与文献[23,31-32]的结果对比如表3所示。表 3 结果比较Table 3 Comparison of results方 法 排序结果 最优方案 文献[23]方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_5} > {A_3} $ A4 文献[31]方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_5} > {A_3} $ A4 文献[32]方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_{\text{3}}} > {A_{\text{5}}} $ A4 本文方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_{\text{3}}} > {A_{\text{5}}} $ A4 由表3可知，本文提出方法所决策出的最佳方案结果与其他方法一致，说明了此方法的可行性和准确性。对于排序结果的不同，原因在于本文提出的方法和文献[30]的方法同时考虑了专家权重与属性权重对决策结果的影响，而文献[23]和文献[31]的方法只考虑了专家权重或只考虑了属性权重。
4. 结束语
基于多粒度犹豫模糊语言术语集的多属性决策方法具有十分重要的应用背景，但目前相关研究较少。本文在已有研究基础上，将多粒度犹豫模糊语言术语集转换为同一粒度下的隶属度语言术语集，通过引用TOPSIS方法将所有备选方案进行优劣排序，最终向决策者给出最佳方案。案例表明模型为解决多粒度犹豫模糊多属性决策问题提供了另一种新思路。在未来的研究中，将继续开展基于多粒度犹豫模糊语言术语集的相关决策问题。
-
图 1 多粒度HFLTSs转换
Fig. 1 Multi-grained HFLTs conversion
下载:
全尺寸图片
图 2 A1与正负理想解关系
Fig. 2 Relationship between A1 and positive and negative ideal solutions
下载:
全尺寸图片
图 3 A2与正负理想解关系
Fig. 3 Relationship between A2 and positive and negative ideal solutions
下载:
全尺寸图片
图 4 A3与正负理想解关系
Fig. 4 Relationship between A3 and positive and negative ideal solutions
下载:
全尺寸图片
图 5 A4与正负理想解关系
Fig. 5 Relationship between A4 and positive and negative ideal solutions
下载:
全尺寸图片
图 6 A5与正负理想解关系
Fig. 6 Relationship between A5 and positive and negative ideal solutions
下载:
全尺寸图片
表 1 d1和d2使用的7粒度语言术语集
Table 1 7-granularity linguistic term set used in d1 and d2
粒度 0 1 2 3 4 5 6 评价信息 非常差 差 有点差 一般 有点好 好 非常好 表 2 d3使用的5粒度语言术语集
Table 2 5-granularity linguistic term set used in d3
粒度 0 1 2 3 4 评价信息 差 有点差 一般 有点好 好 表 3 结果比较
Table 3 Comparison of results
方 法 排序结果 最优方案 文献[23]方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_5} > {A_3} $ A4 文献[31]方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_5} > {A_3} $ A4 文献[32]方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_{\text{3}}} > {A_{\text{5}}} $ A4 本文方法 $ {A_4} > {A_{\text{1}}} > {A_{\text{2}}} > {A_{\text{3}}} > {A_{\text{5}}} $ A4 -
[1] 陈华鹏, 鹿守山, 雷晓燕, 等. 数字孪生研究进展及在铁路智能运维中的应用[J]. 华东交通大学学报, 2021, 38(4): 27–44. CHEN Huapeng, LU Shoushan, LEI Xianyan, et al. Progress of digital twin research and its application in railroad intelligent operation and maintenance[J]. Journal of East China Jiaotong University, 2021, 38(4): 27–44. [2] 李杰, 孟凡熙, 张子辰, 等. 基于融合神经网络的发动机排气温度裕度预测[J]. 华东交通大学学报, 2022, 39(6): 90–97. LI Jie, MENG Fanxi, ZHANG Zichen, et al. Engine exhaust temperature margin prediction based on fusion neural network[J]. Journal of East China Jiaotong University, 2022, 39(6): 90–97. [3] SUN Hong, YANG Zhen, CAI Qiang, et al. An extended exp-TODIM method for multiple attribute decision making based on the Z-Wasserstein distance[J]. Expert systems with applications, 2023, 214: 119114. doi: 10.1016/j.eswa.2022.119114 [4] 张泓, 范自柱, 石林瑞, 等. 一种基于多尺度特征融合的人头计数检测方法研究[J]. 华东交通大学学报, 2021, 38(2): 115–121. ZHANG Hong, FAN Zizhu, SHI Linrui, et al. Research on a head counting detection method based on multi-scale feature fusion[J]. Journal of East China Jiaotong University, 2021, 38(2): 115–121. [5] 王茜玉.基于多粒度概率语言信息的多属性决策方法及应用研究[D]. 济南: 山东财经大学, 2022. WANG Xiyu. Research on multi-attribute decision-making method and application based on multi-granularity probabilistic linguistic information[D]. Jinan: Shandong University of Finance and Economics, 2022. [6] RODRIGUEZ R M, MARTINEZ L, HERRERA F. Hesitant fuzzy linguistic term sets for decision making[J]. IEEE transactions on fuzzy systems, 2011, 20(1): 109–119. [7] HERRERA-VIEDMA E, PALOMARES I, LI C C, et al. Revisiting fuzzy and linguistic decision making: Scenarios and challenges for making wiser decisions in a better way[J]. IEEE transactions on systems, man, and cybernetics:systems, 2020, 51(1): 191–208. [8] JIN Feifei, GUO Shuyan, CAI Yuhang, et al. 2-tuple linguistic decision-making with consistency adjustment strategy and data envelopment analysis[J]. Engineering applications of artificial intelligence, 2023, 118: 105671. doi: 10.1016/j.engappai.2022.105671 [9] XUE Siyu, YANG Yang, DENG Xinyang. A novel probabilistic linguistic decision-making model based on discrete evidence fusion and attribute weight optimization[J]. Engineering applications of artificial intelligence, 2023, 125: 106706. doi: 10.1016/j.engappai.2023.106706 [10] XU Zeshui, XIA Meimei. Distance and similarity measures for hesitant fuzzy sets[J]. Information sciences, 2011, 181(11): 2128–2138. doi: 10.1016/j.ins.2011.01.028 [11] 许叶军, 达庆利. 基于不同粒度语言判断矩阵的多属性群决策方法[J]. 管理工程学报, 2009(2): 69–73. doi: 10.3969/j.issn.1004-6062.2009.02.013 XU Yejun, DA Qingli. A multi-attribute group decision- making method based on different granularity linguistic judgment matrices[J]. Journal of management engineering, 2009(2): 69–73. doi: 10.3969/j.issn.1004-6062.2009.02.013 [12] CHEN Na, XU Zeshui. Interval-valued hesitant preference relations and their applications to group decision making[J]. Knowledge-based systems, 2013, 37: 528–540. doi: 10.1016/j.knosys.2012.09.009 [13] WEI Guiwu, LIN Rui, WANG Hongjun. Distance and similarity measures for hesitant interval-valued fuzzy sets[J]. Journal of intelligent & fuzzy systems, 2014, 27(1): 19–36. [14] LI Deqing, ZENG Wenyi, LI Junhong. New distance and similarity measures on hesitant fuzzy sets and their applications in multiple criteria decision making[J]. Engineering applications of artificial intelligence, 2015, 40: 11–16. doi: 10.1016/j.engappai.2014.12.012 [15] LIAO Huchang, XU Zeshui, ZENG XiaoJun. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making[J]. Information sciences, 2014, 271: 125–142. doi: 10.1016/j.ins.2014.02.125 [16] RODRÍGUEZ R M, LABELLA A, SESMA-SARA M, et al. A cohesion-driven consensus reaching process for large scale group decision making under a hesitant fuzzy linguistic term sets environment[J]. Computers & industrial engineering, 2021, 155: 107158. [17] LIU Y, RODRÍGUEZ R M, QIN J, et al. Type-2 fuzzy envelope of extended hesitant fuzzy linguistic term set: application to multi-criteria group decision making[J]. Computers & industrial engineering, 2022, 169: 108208. [18] ALI J, AL-KENANI A N. Vector similarity measures of dual hesitant fuzzy linguistic term sets and their applications[J]. Symmetry, 2023, 15(2): 471. doi: 10.3390/sym15020471 [19] MENG Fanyong, CHEN Xiaohong. A hesitant fuzzy linguistic multi-granularity decision making model based on distance measures[J]. Journal of intelligent & fuzzy systems, 2015, 28(4): 1519–1531. [20] WU Zhibin, XU Jiuping, JIANG Xianglan, et al. Two MAGDM models based on hesitant fuzzy linguistic term sets with possibility distributions: VIKOR and TOPSIS[J]. Information sciences, 2019, 473: 101–120. doi: 10.1016/j.ins.2018.09.038 [21] JIN Chenxia, MI Jusheng, LI Fachao, et al. An improved TOPSIS method for multi-criteria decision making based on hesitant fuzzy β neighborhood[J]. Artificial intelligence review, 2023: 1−39. [22] 陈秀明, 刘业政. 基于熵权的多粒度犹豫模糊语言VIKOR群推荐方法[J]. 控制与决策, 2018, 33(1): 111−118. CHEN Xiuming, LIU Yezheng. Multi-granular hesitant fuzzy linguistic term sets and their application in group recommendation based on entropy measure and VIKOR method [J] Control and decision, 2018, 33 (1): 111−118. [23] 于文玉, 仲秋雁, 张震. 权重信息不完全的多粒度犹豫模糊语言群决策[J]. 系统工程理论与实践, 2018, 38(3): 777−785. YU Wenyu, ZHONG Qiuyan, ZHANG Zhen. Multi- grained hesitation fuzzy linguistic group decision making with incomplete weight information[J]. System engineering theory and practice, 2018, 38 (3): 777−785. [24] ZHAO Mengke, WU Jian, CAO Mingshuo, et al. A dematel and consensus based MCGDM approach for with multi-granularity hesitant fuzzy linguistic term set[J]. Journal of intelligent & fuzzy systems, 2020, 38(4): 5215–5229. [25] WANG Juxiang. A MAGDM algorithm with multi-granular probabilistic linguistic information[J]. Symmetry, 2019, 11(2): 127. doi: 10.3390/sym11020127 [26] ZHANG Zhen, GAO Junliang, GAO Yuan, et al. Two-sided matching decision making with multi-granular hesitant fuzzy linguistic term sets and incomplete criteria weight information[J]. Expert systems with applications, 2021, 168: 114311. doi: 10.1016/j.eswa.2020.114311 [27] ZHANG Xiaolu, LIAO Huchang, XU Bin, et al. A probabilistic linguistic-based deviation method for multi-expert qualitative decision making with aspirations[J]. Applied soft computing, 2020, 93: 106362. doi: 10.1016/j.asoc.2020.106362 [28] LI Congcong, GAO Yuan, DONG Yucheng. Managing ignorance elements and personalized individual semantics under incomplete linguistic distribution context in group decision making[J]. Group decision and negotiation, 2021, 30(1): 97–118. doi: 10.1007/s10726-020-09708-9 [29] CHEN Z, BEN-ARIEH D. On the fusion of multi-granularity linguistic label sets in group decision making[J]. Computers & industrial engineering, 2006, 51(3): 526–541. [30] FACCHINETTI G, RICCI R G, MUZZIOLI S. Note on ranking fuzzy triangular numbers[J]. International journal of intelligent systems, 1998, 13(7): 613–622. doi: 10.1002/(SICI)1098-111X(199807)13:7<613::AID-INT2>3.0.CO;2-N [31] WEI Cuiping, LIAO Huchang. A multigranularity linguistic group decision-making method based on hesitant 2-tuple sets[J]. International journal of intelligent systems, 2016, 31(6): 612–634. doi: 10.1002/int.21798 [32] 陈余杰, 朱兰萍, 魏翠萍. 多粒度犹豫模糊语言信息融合方法及其在群决策中的应用[J]. 系统科学与数学, 2022, 42(2): 355. doi: 10.12341/jssms21047 Chen Yujie, Zhu Lanping, Wei Cuiping. A fusion method of multi-granular hesitant fuzzy linguistic information and its application in group decision making[J]. Systems science and mathematics, 2022, 42(2): 355. doi: 10.12341/jssms21047
