恶意代码又称为恶意软件，是对各种敌对和入侵软件的概括性术语，指故意编制、具有一定破坏性的、对计算机或网络系统产生威胁的计算机代码或软件。恶意代码随着计算机技术的蓬勃发展而不断发展，呈现出数量增长快、形式变化多等特点，这对恶意代码的分析和防御工作带来了更大的挑战。

现有的恶意代码检测方法可分为静态分析方法和动态分析方法2类。静态分析方法主要是在没有实际运行的情况下对恶意代码的静态特征加以分析，而动态恶意软件分析方法是在受控环境中系统地运行，使用工具来提取其动态特征进行分析。这2种检测方式都在一定程度上缓解了恶意代码检测所面临的压力。深度学习和人工智能的快速发展，向恶意代码分析技术提供了新的方向^[1]。大量基于深度学习的恶意代码检测模型不断被提出^[2-3]，然而现有的基于深度学习的检测模型通常将检测问题视为分类问题，采用二支决策的方式进行分类^[4]，将样本分为良性类和恶意类。这意味着，无论分类器学习到的信息是否充分，都会对待分类的样本做出一个确定的决策。而在实际恶意代码检测问题中，由于在做出良性或恶意决定时的基本信息有限，一些样本不能被立即判断或很容易被错误分类，因此，需要在收集更多的可用信息后，再次对这些样本进行确定性决策。

序贯三支决策^[5]是一种可以更好地处理此类问题的动态三支决策^[6]思想。它在传统二支决策的基础上引入了更加符合人类认知的延迟决策选项。通过构建多粒层结构，从最粗粒度层级到最细粒度层级进行一系列的多阶段三支决策，在决策时允许决策者对信息不充分的对象进行延迟处理。然而，序贯三支决策方法也存在一些问题。在传统的概率粗糙集三支决策模型^[7]中，三支决策阈值通常是根据给定的代价函数矩阵来确定，这需要合适的先验知识或专家预先设定损失函数，具有一定的主观随意性，这在一定程度上阻碍了概率粗糙集三支决策模型的实际应用。

为解决上述问题，本文提出了一种基于高维多目标序贯三支决策的恶意代码检测模型（maliciouscode detection model based on many-objective sequential three-way decision， MO-STWD）。序贯三支决策用于构建更适合真实数据环境的恶意代码检测模型。利用高维多目标优化算法获得最优阈值对及参数，可以避免先验知识或专家设定的主观随意性，有效地平衡综合分类性能、决策效率及决策风险损失。本文的主要研究贡献如下：

1) 针对现有检测模型面临信息不足导致的盲目决策问题，将序贯三支决策引入恶意代码检测领域，提出一种序贯三支实时恶意代码检测模型。

2) 为了综合考虑恶意代码检测模型的综合分类性能、决策效率以及决策风险损失，构建了一种高维多目标序贯三支决策模型。

1.   恶意代码检测与三支决策模型

随着计算机技术的迅速发展，机器学习和人工智能近年来逐渐在人脸识别^[8]、推荐系统^[9-10]等多个领域掀起研究热潮。深度学习因其具有从海量数据中学习数据特征的能力，适合处理高维、复杂的恶意代码样本。因此，许多研究者将深度学习方法应用于恶意代码检测领域。Kuo等^[11]将 Android 应用包文件解压缩为 classes.dex 文件，然后利用训练卷积神经网络模型判断输入的 classes.dex 文件是否为恶意代码。Cui等^[12]利用蝙蝠算法降低不平衡数据对恶意代码检测的影响，通过卷积神经网络对图像数据集进行训练，以达到更好的分类效果。Wang等^[13]基于 DenseNet网络良好的图像分类性能和恶意软件家族在图像上的视觉相似性，将恶意软件转换后的灰度图像输入到模型中，结合DenseNet 网络和注意力机制进行恶意软件家族分类。Almahmoud等^[14]构建了一个用于恶意软件检测的递归神经网络分类模型，通过静态分析提取了4种不同类型的静态特征，利用递归神经网络模型对恶意软件进行分类。Cui等^[15]构建了多目标受限玻尔兹曼机模型，利用评价指标衡量数据分类效果，引入策略池提高数据融合性能，同时为了减轻数据不平衡带来的问题，他们还使用多目标优化算法来处理不平衡的恶意软件家族。然而这些方法都是基于现有的信息进行分类决策，忽略了信息不足带来的影响。

三支决策模型在经典二支决策的理论基础上加入了更加符合人类思维的延迟决策选项，从而使整个决策过程更加完善合理。序贯三支决策是在三支决策基础上的重要延伸和扩展，它将三支决策视为一个中间过程。鉴于序贯三支决策模型更适合实际应用场景，近年来，序贯三支决策模型在很多领域得到了应用。Ye等^[16]考虑到多级推荐信息特征和推荐结果的可解释性，构建了一种基于序贯三支决策的可解释推荐模型。在垃圾邮件过滤领域，袁国鑫等^[17]对无法判断类别的邮件进行延迟决策, 在获得更多信息后再做出最终决策。武慧琼等^[18]提出了一种基于三支决策的花卉图像分类方法, 有效地提高了花卉图像的分类精度。Dai等^[19]在图像识别领域引入了序贯三支决策思想, 以解决传统支持向量机图像特征提取不完全的问题。孙勇等^[20]为了解决目标检测领域中代价不平衡和信息不完全的问题, 设计了一种基于多粒度序贯三支决策和代价敏感学习的目标检测方法。

2.   卷积神经网络与智能优化算法

本文所提方法主要基于卷积神经网络、序贯三支决策和高维多目标优化算法,下面就相关概念和基本知识予以介绍。

2.1   卷积神经网络

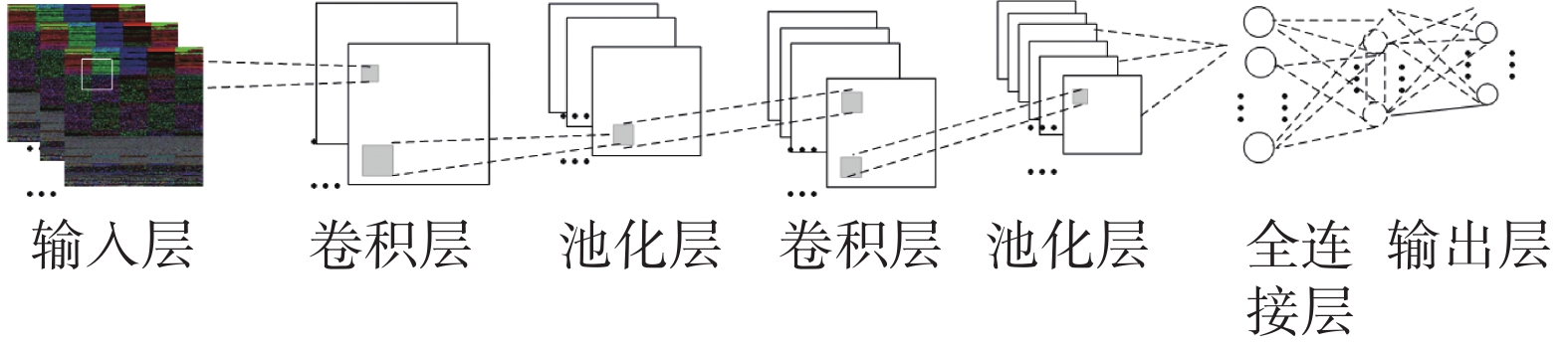
受人类视觉神经系统的启发，卷积神经网络广泛应用于图像分类、语义检索和目标检测等领域。它通过对输入图像进行卷积、激活和池化等操作来提取重要的特征信息。因此，本文模型中使用卷积神经网络来进行特征提取和多粒度特征集的构造。在实验中，卷积神经网络的损失函数选用分类交叉熵损失，输入图像大小为128×128×3，批处理个数设置为64，训练次数设置为30，学习率设置为0.001，卷积神经网络结构如图1所示。

图  1  卷积神经网络结构

Fig.  1  Structure of convolutional neural network

下载: 全尺寸图片

2.2   序贯三支决策

在研究粗糙集模型时，Yao等^[6]提出了三支决策理论。该理论以决策粗糙集理论和贝叶斯定理为核心，其中决策粗糙集理论通过状态集和决策集展开。

给定状态集Ω={X, $\neg $X}，决策集D={D_P, D_B, D_N}，其中D_P、D_B、D_N分别表示将状态集中的样本划分入，执行不同的决策行为可能会产生不同的风险代价。风险代价函数如表1所示，表1中λ_PP、λ_BP、λ_NP分别表示当前样本x属于状态X时，执行D_P、D_B、 D_N操作时的损失；λ_PN、λ_BN、 λ_NN分别表示当前样本x属于状态X时，执行D_P、 D_B、 D_N操作时的损失。其中D代表正域POS(x)，B代表边界域BND(x)，N代表负域NEG(x)。假设0≤λ_PP≤λ_BP≤λ_NP，0≤λ_NN≤λ_BN≤λ_PN，根据文献[21]的计算方式，可以得到：

式中：$ 0 < \beta < \gamma < \alpha < 1 $。令P(X|[x])表示样本x被分为状态X的概率，可以得到如下3条规则：

1)如果P(X|[x]) ≥ α, x∈POS(x)；

2)如果β<P(X|[x)<α, x∈BNN(x)；

3)如果P(X|[x]) ≤ β, x∈NEG(x)。

序贯三支决策结合粒计算，将三支决策视为中间过程，构建具有不同粒度特征的多粒度层次空间。假设论域$ U $由$ n $层粒度构成，即$ \{{g}_{1},{g}_{2}, \cdots ,{g}_{n}\} $，在每个粒层$ {g}_{i} $($ 1\leqslant i\leqslant n-1 $)上，存在样本x被分为状态X的概率$ {P}^{i}\left(X\right|\left[x\right]] $ ($ 1\leqslant i\leqslant n-1 $)及该粒层相应的阈值对$ ({\alpha }_{i},{\beta }_{i})(1\leqslant i\leqslant n-1) $，根据三支决策的划分规则可将待分类样本集划分为$ {\rm{PO}}{{\rm{S}}}^{i}\left(x\right) $、$ {\rm{BN}}{{\rm{D}}}^{i}\left(x\right) $和$ {\rm{NE}}{{\rm{G}}}^{i}\left(x\right)，(1\leqslant i\leqslant n-1) $。对于处于$ {\rm{BN}}{{\rm{D}}}^{i}\left(x\right) $中的样本，在更细粒度将被重新评估，得到更精确的分类。随着粒度层的增加，边界域将越来越小。当在第$ n $粒度需要终止该序贯过程时，可采取二支决策的方案，通过$ {\gamma }_{n} $将所有待分类样本分入$ {\rm{PO}}{{\rm{S}}}^{n}\left(x\right) $和$ {\rm{BN}}{{\rm{D}}}^{n}\left(x\right) $中。

2.3   NSGA-III算法

高维多目标优化问题由$ n(n > 3) $个目标函数和相关约束条件组成。其中需要被优化的目标通常具有一定的冲突或者没有直接的关联，需要决策者根据实际应用需求从候选解集中选择所需要的解。高维多目标优化问题定义为

式中：$ {f}_{m}\left(x\right) $为第$ m $个目标函数；$x=\left({x}_{1},{x}_{2},\cdots ,{x}_{i}\right)， {x}_{i}$为第i个决策变量；${h}_{i}\left(x\right)\geqslant 0$ ，$i=1, 2,\cdots ,r$定义了不等式约束；$ {g}_{j}\left(x\right)=0 $，$j=1, 2,\cdots ,t$表示等式约束。

常见的多目标优化算法(如 NSGA-II^[22])在面对目标函数大于3个时，由于维数增多选择压力下降，不能很好地平衡多样性和收敛性。针对这一问题，Deb等^[23]提出了基于参考点和非支配排序的高维多目标进化算法(many-objective optimization algorithm using reference-point-based nondominated sorting approach, NSGA-III)。NSGA-III算法以基于快速非支配排序的多目标优化算法(multi-objective optimization algorithm using nondominated sorting-based approach, NSGA-II)的框架为基础，使用参考点策略代替了NSGA-II算法中的拥挤度排序策略，以解决在高维空间中非支配解集分布不均匀的问题。非支配排序策略和参考点策略是NSGA-III算法的核心。算法通过非支配排序策略按照个体之间的支配关系对种群进行分层，将种群中收敛性较好的解选择出来，而参考点策略通过计算种群中个体与参考点、理想点连接构成的参考向量之间的距离来保持算法的多样性。

3.   序贯三支决策恶意代码检测模型

为了提高恶意代码检测性能，避免因信息不充分而导致的误报漏报，本文提出了基于序贯三支决策的恶意代码检测模型。在此基础上，构建了高维多目标序贯三支决策模型，并采用NSGA-III算法对该模型进行求解，可以同时优化模型的综合检测性能、决策风险代价和决策效率，从而获得恶意代码检测过程中的最优模型。

3.1   序贯三支决策恶意代码检测模型基础框架

鉴于序贯三支决策能够动态地处理不确定性决策问题，本文提出了序贯三支决策恶意代码检测模型。该模型的详细框架如图2所示，主要由2部分组成：采用卷积神经网络(convolutional neural network, CNN)模型来构建多粒度特征集并估计待分类样本条件概率；在决策时采用序贯三支决策理论对待分类样本做出决策。

图  2  恶意代码检测模型框架

Fig.  2  Diagram of malicious code detection model

下载: 全尺寸图片

基于序贯三支决策的恶意代码检测模型的具体步骤如下：

使用现有的标记样本集训练初始CNN模型，将所有待分类样本输入到CNN模型与SoftMax函数中，评估每个应用行为属于正域的条件概率值P(X|[x])。

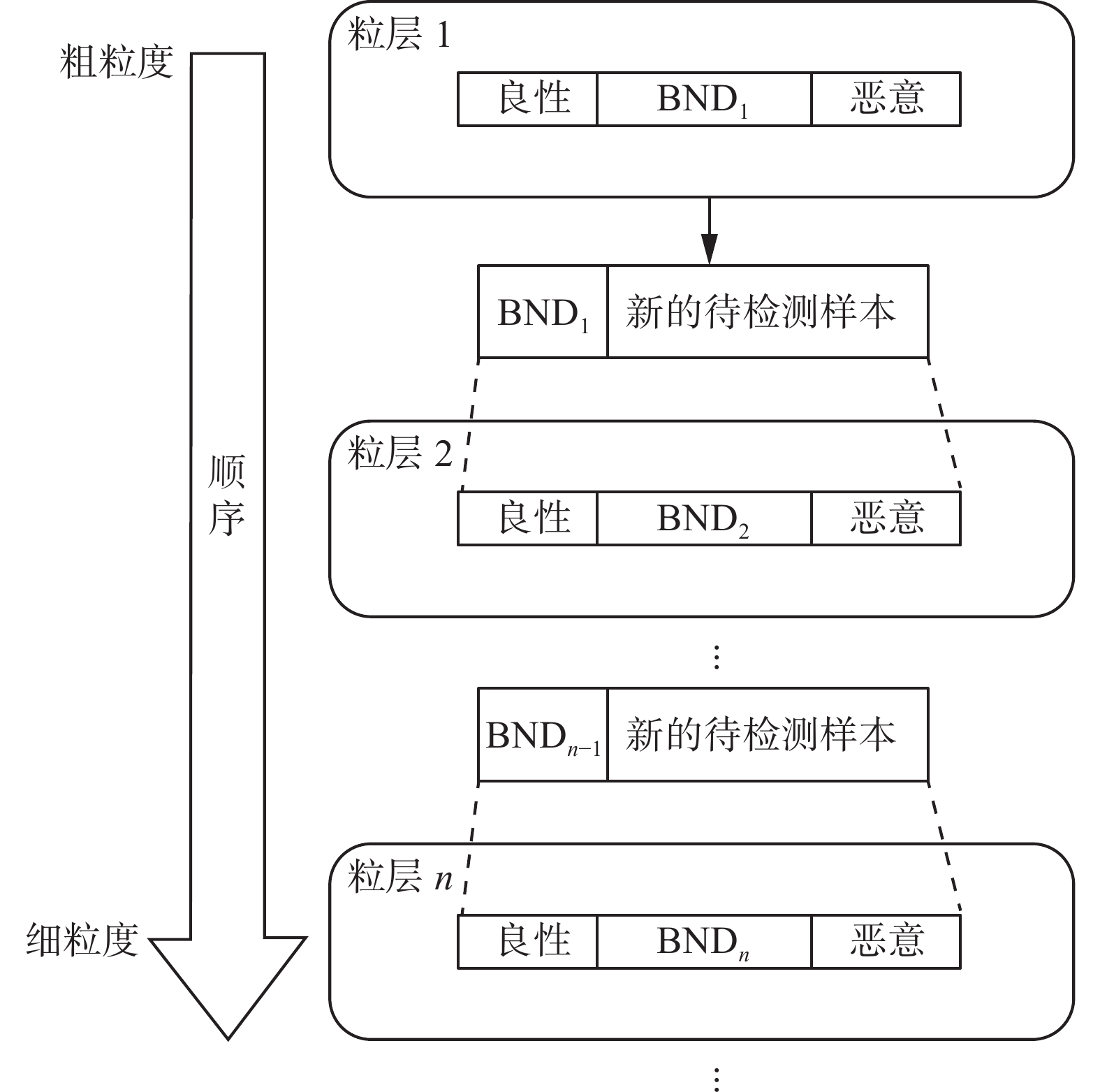
随后，将P(X|[x])与当前粒层的阈值对$ ({\alpha }_{i},{\beta }_{i}) $进行比较，根据三支决策规则，将所有样本划分到相应的正域$ {\rm{PO}}{{\rm{S}}}^{i}\left(x\right) $、边界域$ {\rm{BN}}{{\rm{D}}}^{i}\left(x\right) $和负域$ {\rm{NE}}{{\rm{G}}}^{i}\left(x\right) $中。由于三支决策独特的延迟决策理论，边界域$ {\rm{BN}}{{\rm{D}}}^{i}\left(x\right) $中的样本需要在最初的判定条件中不断地加入新的信息来进行下一步决策，所以CNN模型在每次分类完成之后会把已经划分入正域$ {\rm{PO}}{{\rm{S}}}^{i}\left(x\right) $ 和负域$ {\rm{NE}}{{\rm{G}}}^{i}\left(x\right) $中的样本作为新的训练集进行训练，得到下一粒度的决策模型。在每一粒度层，将上一粒度的边界域样本及当前粒度的待分类样本合并构成新的待检测样本集，并依据三支决策规则对其进行分类决策。循环上述步骤即形成了一个序贯三支决策恶意代码检测模型的过程。序贯三支决策多粒度决策过程具体如图3所示。

图  3  序贯三支决策多粒度决策过程

Fig.  3  Sequential three-way multi-granularity decision

下载: 全尺寸图片

3.2   高维多目标模型

在恶意代码检测的实际应用场景中，序贯三支决策模型为用户提供了求解信息不充分、不确定问题的一个新的方向。为了能在提升检测模型的综合分类性能的同时，尽可能地提升决策效率、降低决策风险代价，在上述模型的基础上，构建了高维多目标序贯三支决策模型。

3.2.1   目标函数

检测模型的综合分类性能可通过分类问题中常见的评价指标来衡量，本文利用这些评价指标作为目标函数，多个评价标准可以从各个方面衡量检测模型的综合分类性能。因此，综合分类性能可通过召回率(true positive rate,TPR)和假阳性率(false positive rate, FPR) 2个目标来衡量。

目标 1：最大化TPR。TPR表示在实际为正的样本中被预测为正样本的比例，其定义为

式中：$ {{\rm{POS}}}_{\left(\alpha ,\beta \right)}\left(x\right) $和$ {{\rm{NEG}}}_{\left(\alpha ,\beta \right)}\left(x\right) $分别为划分到正域和负域中的样本，$ X $为实际为正的样本，$\left|{{\rm{POS}}}_{\left(\alpha ,\beta \right)}\left(x\right)\cap X \right|$为实际为正被预测为正的样本数量，$ \left|{{\rm{NEG}}}_{\left(\alpha ,\beta \right)}\left(x\right)\cap X\right| $为实际为正被预测为负的样本数量。

目标 2：最小化FPR。FPR表示在实际为负的样本中被预测为正样本的比例，其定义为

式中：$ \neg X\mathrm{为} $实际为负的样本，$\left|{{\rm{POS}}}_{\left(\alpha ,\beta \right)}\left(x\right)\cap \neg X \right|$为实际为负被预测为正的样本数量，$\left|{{\rm{NEG}}}_{\left(\alpha ,\beta \right)}\left(x\right)\cap \neg X\right|$为实际为负被预测为负的样本数量。

目标 3：最大化决策效率。在恶意代码检测模型的序贯过程中，模型的检测效率是通过承诺率(commitment rate, CMR)来度量的。承诺率是指在当前三支决策下，在当前所有检测的样本中被划分到确定性域的比例，其计算公式为

承诺率越大，意味着被划分到正域和负域的样本数量越多，其边界域不确定性越低，表明决策效率越高。

目标 4：最小化风险代价。使用三支决策进行分类时，每种决策行为都应该承担相应的风险代价， 其风险代价函数如表1所示。假设样本$ X $属于正域的条件概率为$ {p}_{i} $，则将样本$ X $划分到3个域的风险代价可定义为

假设将样本正确分类所需承担的风险代价为0， 即${\lambda }_{{\rm{PP}}}={\lambda }_{{\rm{NN}}}=0$。则所有待分类样本做出决策时需要承担的风险代价总和为

依据式(1)~(3)，可将$ {\lambda }_{{\rm{PN}}}、{\lambda }_{{\rm{NP}}}、{\lambda }_{{\rm{BP}}}\mathrm{和}{\lambda }_{{\rm{BN}}} $与$ \alpha 、\beta 、\gamma $之间的关系反推出，将其代入式(8)可得：

综上所述，本文构建的高维多目标模型为

3.2.2   决策变量

在序贯三支决策恶意代码检测模型中，卷积神经网络的超参数选择及三支决策阈值对的变化是影响模型性能的关键参数。因此，本文将卷积神经网络的超参数及三支决策阈值$ \alpha \mathrm{、}\beta \mathrm{、}\gamma $作为优化上述目标的决策变量。决策变量的设计为

式中：$ {p}_{1}\mathrm{、}{p}_{2}\mathrm{、}{p}_{3} $分别为卷积神经网络的超参数：学习率$l_r$、dropout参数以及优化器的类型。

3.2.3   模型求解

本文采用NSGA-III算法对所提出的高维多目标模型进行求解。NSGA-III求解步骤如下：

1)初始化包含N个个体的种群$ {P}_{t}=\{{I}_{1},{I}_{2}, \cdots ,{I}_{N}\} $，并令算法代数t = 0；

2)根据种群中的个体生成不同的卷积神经网络训练构建多粒度特征集，并进行三支决策；

3)根据式(10)，计算种群中每个个体的召回率、假阳性率、承诺率以及决策风险代价；

4)生成理想点，并通过交叉变异操作生成N个子代个体组成的$ {Q}_{t}=\{{Q}_{1},{Q}_{2}, \cdots ,{Q}_{N}\} $，将父代与子代组合生成大小为2N的新种群${{P}}_{t}'={P}_{t}\cup {Q}_{t}$；

5)按照非支配排序策略和参考点策略，在新种群${P}_{t}'$中选取N个优秀的个体组成新的父代种群$ {P}_{t+1} $，并令算法代数$ t=t+1 $；

6)判断是否满足最大迭代次数，满足则算法结束，不满足则返回2)。

4.   MO-STWD模型实验分析

4.1   实验设计

实验环境为Intel core Xeon® E5-2620CPU (2.10 GHz)、Nvidia GeForce RTX 2080Ti GPU、128 GB RAM、windows 10操作系统，软件平台使用pycharm和Matlab2019b。其中恶意代码模型基本框架在pycharm环境下基于keras框架下完成，高维多目标优化算法及其对比算法在Matlab2019b版本下优化算法平台(evolutionary multi-objective optimization platform，PlatEMO)上进行。为了证明本文所提模型的有效性，本文在2个数据集上进行了实验。第1个数据集是由Kaggle平台提供的，简称Kaggle数据集。该数据集中包含12 015张图像，其中恶意软件图像6 006张、良性软件图像6 009张。第2个数据集采用公开的工业物联网数据集Leopard Mobile，共包含14 733个恶意软件样本和2 486个良性样本。为了模拟实际恶意代码检测的动态过程，本文将测试集随机分成5个部分来模拟时间动态过程，并在第5个粒度进行二支决策，以便与其他模型进行比较。卷积神经网络及优化算法相关参数设置如表2所示。

4.2   评价指标

恶意代码检测通常被视为二分类问题。因此，可以采用分类问题中常见的评价指标对模型进行评价。本文使用准确率(accuracy)、精确率(precision)、召回率(recall, TPR)和假阳性率(false positive rate, FPR)以对模型提供全面的评估。评价指标计算方式为

式中：T_P和F_P分别表示正确和错误地被分类为恶意的样本数量，T_N和F_N表示被正确地和错误地归类为良性的样本数量。

4.3   实验结果与分析

4.3.1   三支决策分类器与传统二支决策分类器的性能对比

为了验证基于序贯三支决策的恶意代码检测模型的有效性，本节在保证使用同样的卷积神经网络进行特征提取的情况下，将序贯三支决策分类器与传统的二支决策分类器进行比较。实验使用支持向量机(support vector machine, SVM)、Softmax分类器和K-最近邻(K-nearest neighbor, KNN)与序贯三支决策分类器进行对比试验。在Kaggle数据集上的实验结果见表3。

表3中展示了卷积神经网络与不同分类器结合后, 在准确率、精确率、TPR和FPR上的分类结果.表3中可以看出, 本文提出的基于高维多目标序贯三支决策的恶意代码检测模型（malicious code detection model based on many-objective sequential three-way decision，MO-STWD）在卷积神经网络下的准确率达到98.06%， 精确率和TPR指标均超过97%, 而 FPR为2.61%，与其他分类模型相比, 该模型在大多数指标上都表现出更好的结果。对于第1个指标Accuracy, 三支决策分类器比SoftMax分类器高出0.0492, 与SVM和KNN相比, 该指标分别高出0.0137和0.0354。在FPR中, 其他分类模型的指标值分别比三支决策分类模型高0.1063、0.0209和0.0510。此外, 对于Precision, 本文方法也表现出最好的结果。但在Recall中, 虽然没有达到最大值0.9947, 也仅低于最大值0.0060。这些数据表明, 序贯三支决策分类模型在综合性能上要优于其他分类模型。在引入延迟决策后, 避免了一些不确定样本被错误分类的风险, 提升了整体模型的检测性能。因此, 基于序贯三支决策的恶意代码检测方法优于传统的基于二支决策的方法。

4.3.2   不同算法在求解高维多目标序贯三支决策模型上的对比

在该实验中，使用不同的优化算法，分别为NSGA-III、参考向量引导多目标优化进化算法（reference vector guided evolutionary algorithm, RVEA）^[24]、基于网格的多目标优化进化算(grid-based evolutionary algorithm, GrEA) ^[25]和基于指标的约束多目标进化算(indicator-based constrained multi-objective evolutionary algorithms, HyPE)^[26]，对本文构建的高维多目标序贯三支决策模型在Kaggle数据集上进行求解，以验证NSGA-III算法的可取性。其中对比优化算法对应的参数是默认设置的。为了直观地比较具有相同目标函数的每种算法的性能，在表4中给出了在不定义终点的情况下，各个算法第5个粒度时在TPR、FPR、CMR和Risk上的结果比较。不同优化算法的每个目标值是所有个体的平均值。从表4中可以看出，NSGA-III算法在FPR和Risk上取得了最优，分别为2.19%和91.8024。在召回率(TPR)上，HyPE 算法的结果更好。GrEA算法在承诺率(CMR)上的结果较好。从求解目标上来看，与其他算法相比，NSGA-III算法在该模型的优化性能有更好的效果。

为了比较整体模型检测性能，本文以5个粒度为例，并在最后一个粒度中使用二支决策进行分类，这与之前的实验类似。

表5给出了使用各种算法优化高维多目标模型的准确度、精确度、TPR和FPR的分类结果。显然，从表5中可以看出，对于精确率而言，NSGA-III比最低值高出0.42%。对于准确率而言，NSGA-III与HyPE算法均取得最优。对于Recall而言，NSGA-III的性能不是最优的，但也仅比最优的HyPE低0.5%。但对于FPR而言。NSGA-III算法的结果是最优的。从整体上来看，NSGA-III算法在该模型的求解性能较为突出，因此，本文采用NSGA-III算法对高维多目标序贯三支决策模型进行求解。

4.3.3   不同恶意代码检测模型的对比

为了进一步衡量基于高维多目标序贯三支决策的恶意代码检测模型的性能，将本文模型与其他恶意软件检测模型在Kaggle数据集上进行了比较实验。该实验选取的对比模型包括基于蝙蝠优化算法的动态采样模型 (dynamic resampling method based on the bat algorithm, DRBA）^[12]，多目标CNN^[27]，及多目标受限玻尔兹曼机（restricted boltzmann machine, RBM）模型^[15]。这些模型都是基于二支决策的检测模型，通过深度学习模型从恶意代码图像中提取特征，直接对样本进行二支分类决策。

表6给出了在实验环境不变的情况下，本文模型和其他恶意代码检测模型的对比结果。可以看出，本文提出的检测方法在4个评价指标上都表现出最好的结果。与其他恶意代码检测模型相比，本文所提模型的Accuracy值提升了0.0183~0.0310，假阳性率降低了0.0125~0.0380。本文模型相较于其他模型在综合性能上表现更好的优势在于该模型将延迟决策引入，将基于当前信息无法分类的样本先划入边界域中，避免因特征不足或数据不充分而导致样本被错误分类的风险；使用卷积神经网络进行特征提取，结合动态检测过程构建多粒度特征空间，将边界域中的样本在更细粒度的特征空间中进行分类，可提升模型的准确率。

为了验证本文所提模型的泛化性，将Kaggle数据集替换成Leopard Mobile数据集，表7给出了在保持实验环境不变的情况下，本文模型与其他模型的对比结果。从表7中可以看出，本文所提的基于高维多目标序贯三支决策的恶意代码检测模型在准确率、精确率及假阳性率方面优于其他3个对比模型。这表明本文模型适用于不同的恶意代码数据集，具有一定的泛化性。

5.   结束语

本文综合考虑了恶意代码检测问题的分类性能、决策效率及决策风险损失，提出了一种基于高维多目标序贯三支决策的恶意代码检测模型。该模型结合了卷积神经网络和序贯三支决策的特点对恶意代码样本进行分类检测，此外，本文在两个真实数据集上对模型进行了测试，数值结果表明，本文所提的方法不仅能够提升恶意代码的检测性能和决策效率，而且还能控制模型的决策风险代价。在未来的工作中，可以对高维多目标模型进行改进，并探寻更优的算法进行求解，进一步降低模型的复杂度，提升恶意代码检测性能。