现实世界中，各种基础设施网络（如能源、交通、通信等）甚至社会关系网络（如经济、舆论等）之间，相互依存、协同工作的情况非常之普遍。这样的存有相互依赖关系的网络可以称之为相依网络，网络之间的相互依赖关系，一方面提高了网络整体的运转效率，另一方面也增强了网络的脆弱性^[1]。当某一网络产生故障，故障将通过网路间的相依关系传播到另一网络，同时，另一网络的故障也将传回，进一步加速整个相依网络的瘫痪^[2-4]。这些基础设施网络或社会关系网络一旦发生故障瘫痪（如2003 年意大利发生的因电力系统和通信网相继故障而导致的大停电^[5]，2019年委内瑞拉国内电网半个月内经历３次高强度攻击，导致超过90%的州大停电^[6]），势必会给社会经济活动和民生造成极其重要的影响。因此，如何提高相依网络鲁棒性，有效地应对和控制故障传播，避免相依网络发生结构性破碎,以及在相依网络发生结构性破碎后如何快速有效地进行网络修复，成为复杂网络研究领域的重要问题^[7]。

根据复杂网络理论，在网络出现故障前实行防御措施，通过对节点进行重要性排序^[8-13]，鉴定出关键节点进行预先保护，是一种避免网络发生结构性破碎的有效手段。如根据节点度数、介数^[8]、佩奇排名值(Pagerank) ^[9]在相依网络中的相依边及相连边数^[10]或依存强度^[11]。然而，网络故障出现前的防御研究与故障的传播是互不干涉的一个静态过程。对于时刻处于变化中的真实网络，仅仅只是静态的防御并不足够，及时有效的修复措施是必要的。在单一网络中，Chi 等^[14]提出了一种随机重连的鲁棒性增强修复策略。Hu等^[15]针对复杂网络中的3种攻击类型提出了3种分析策略，并分析了这些策略在不同攻击下的修复效果。文献[16]提出了一种带有应急修复机理并引入节点过载故障概率的网络级联故障模型。Tang等^[17]为研究复杂网络在遭遇随机故障或蓄意攻击时的鲁棒性，构建了故障节点概率传播模式下的级联失效模型，并设计了概率修复和阶段修复2种故障节点修复策略，级联失效模型中节点故障概率随故障次数增加而逐渐降低。文献[18]提出一种基于系统弹性的结构评价方法，根据节点重要度评价，识别出系统关键节点，应用弹性损失三角形，进行多种故障情况下区域轨道交通网络的最优恢复策略研究。也有学者研究了单一网络中的连边故障失效及针对网络连边的修复^[19-22]。近来，有研究人员把单一网络中相关理论推广移植到多层网络，结合多层网络层内异构性、层间耦合等因素^[23-25]开展了多层网络的修复性研究。赵善男^[26]提出了一种基于网络节点特征的故障修复策略，以北京市公共汽车−轨道交通网络为例，验证分析了该修复策略的可行性。根据初始攻击比例的不同，相依网络发生级联失效后处于完全崩溃状态或不完全崩溃状态，文献[27]针对这2种网络状态建立了相应的模型，提出了相应的择优修复策略。文献[28]分析了相依网络在修复过程中的级联故障，提出了一个修复鲁棒性指数，用于评估相依网络对修复过程中的级联故障的修复能力，采用基于网络中心性知识的6种策略来找到重要节点，通过保护重要节点以增强相依网络在修复中的鲁棒性。为实现在相依网络出现故障时及时响应，且在故障蔓延的同时修复失效节点及失效边，将损失降到最小。文献[29]提出了一种基于一对一点耦合相依网络的级联失效过程与修复过程动态交替的修复模型。

在该模型中，通过定义共同边界节点，即与相对应的网络中的极大连通片的拓扑距离都为1的耦合失效节点对，在每一轮修复过程中，对共同边界节点进行随机修复。文献[30]在此基础上做进一步研究，根据边界节点与极大连通片内外节点的原有链接对共同节点进行择优修复。

以上这些关于相依网络级联失效修复的研究成果大多是针对节点相依网络，即网络间的节点具有依赖关系。然而，由于现实中许多网络功能体现在连边上，相互依赖关系体现在网络连边相互依赖而不是节点相互依赖。如公司之间的资金交易网络与供应链网络，当公司之间的资金来往被阻断时，它们之间的商品供应链关系势必将受到损害，这种资金交易及供应链关系的破坏将进一步威胁到其他相关公司之间的金融联系，最终可能导致整个系统的级联故障。对于这类边耦合相依网络，文献[31-36]以不同的方法构建了此类网络的级联失效理论分析模型，但关于此种边耦合网络模型的修复研究尚待开展。因此，本文借鉴文献[29]中的点耦合相依网络动态修复模型，通过定义出共同边界连边，构建出边耦合相依网络中的动态修复模型，对共同边界连边进行择优修复，寻找最优修复策略，使得边耦合相依网络在随机故障及蓄意攻击下能够快速有效地得到修复。从网络发生级联失效进入稳态时极大连通片的规模，及进入稳态所需要的迭代步数2方面来评估修复效果。

1.   边耦合相依网络修复模型

在文献[29]的修复模型中，通过定义共同边界节点，开创性地提出了一种适用于相依网络的动态修复模型。该模型中点耦合相依网络的级联失效过程与修复过程动态交替，在每一轮修复过程中，对共同边界节点进行修复。而在Gao等^[31]提出的边耦合相依网络中，因为网络间的依赖关系存在于2个网络的连边之间，所以并不存在共同边界节点。为构建适用于边耦合相依网络的动态修复模型（下文简称修复模型），本文定义了共同边界连边（mutual boundary edges）。

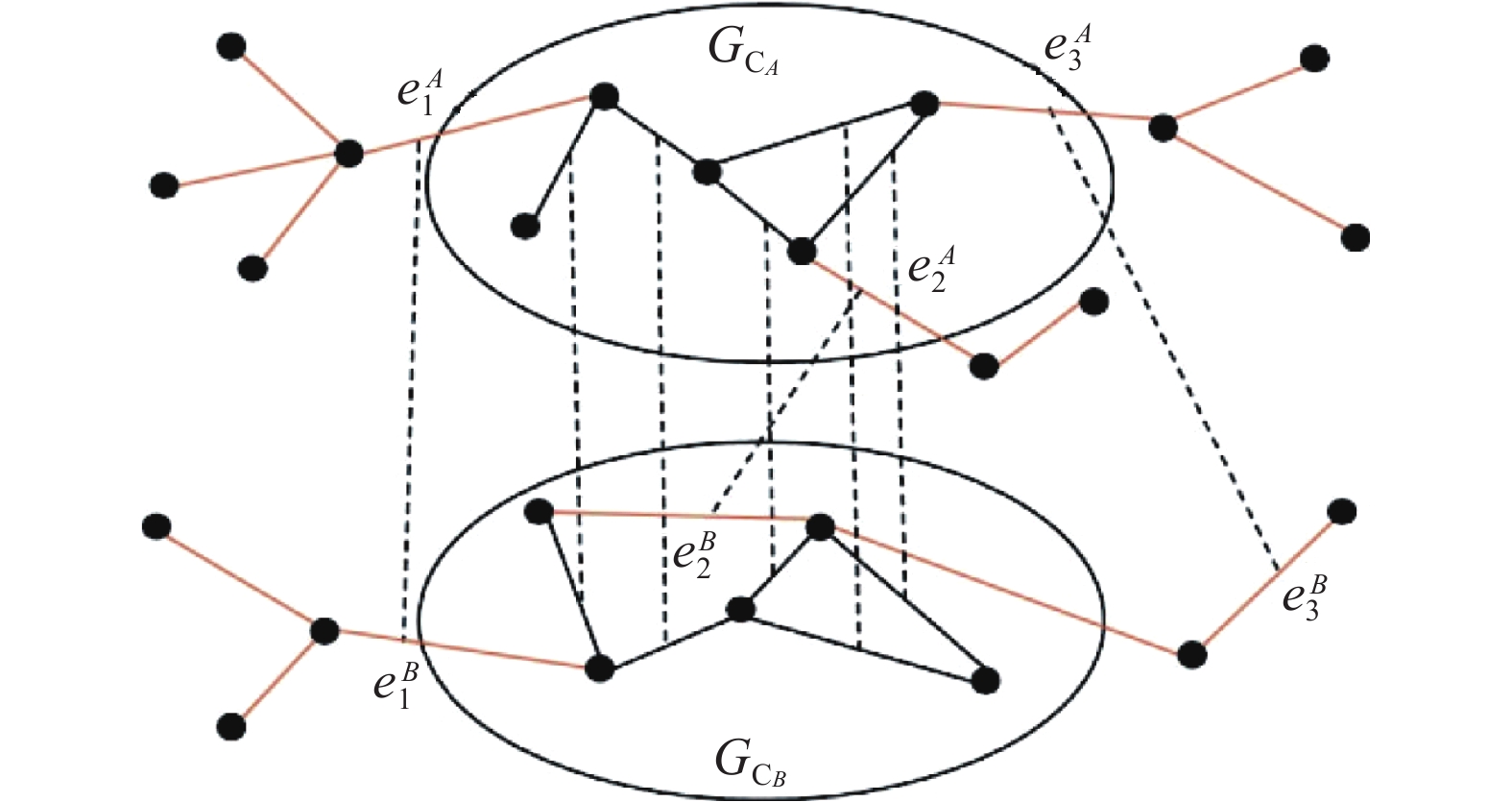
共同边界连边是指在网络A（网络B）中一条失效连边$e_i^A$$\left( e_j^B \right)$连接着一个失效节点${a_i}$（${b_j}$）与网络A（B）中极大连通片(giant component of internet A/B, ${G_A}$/${G_B}$)，并且在网络B（网络A）与其耦合的失效连边$e_j^B$$\left( e_i^A \right) $同样连接着极大连通片${G_B}$(${G_A}$)，那么就称这一对耦合连边为共同边界连边，如图1。在修复模型中，只有共同边界连边才能作为待修复候选目标。这样的定义具有现实性和合理性：1)现实世界中，当基础设施网络发生故障时，受时空等物理条件的限制，通常都是优先抢修正常区域周边的设施单位，由近到远逐步修复；2）如果候选修复目标不是共同边界连边，那么就很有可能因其对应的耦合连边并不连接着脱离极大连通片而反复失效，导致这样的修复行为没有实际意义。

图  1  边耦合相依网络的共同边界连边

Fig.  1  Mutual boundary edges of edge-coupled interdependent networks

下载: 全尺寸图片

图1中，连边$e_3^A$对应的耦合连边$e_3^B$并不连接着$ G_{C_B} $，所以耦合连边$\left( e_3^A,e_3^B \right) $并不是共同边界连边，$\left( e_1^A,e_1^B \right) $与$\left( e_2^A,e_2^B \right)$才是。节点之间的虚线代表失效连边，连边之间的双向箭头表示连边之间存在耦合关系。

修复模型可分为初始阶段、级联失效阶段和修复阶段3个阶段。在初始阶段，随机选择或特意选择网络A中$ 1 - p $比例的边使其失效，模拟真实网络中的随机攻击及蓄意攻击。根据文献[31]中的相依网络模型，节点脱离极大连通片即失效，节点相连边也随之失效。修复模型具体逻辑流程如下：

1）网络A遭遇初始故障，网络中$ 1 - p $比例的连边失效，脱离$G_{C_A}$的节点及其相连边失效；

2）由于网络A中连边$e_i^A$失效导致网络B中与之有耦合关系的连边$e_i^B$失效，另外由此造成的部分节点脱离$G_{C_B}$失效，其相连边一并失效；

3）修复机制介入，筛选出共同边界连边，对共同边界连边进行选择性修复：

4）网络A中正常连边$e_j^A$的耦合连边$e_j^B$失效，则$e_j^A$失效，脱离$G_{C_A}$的节点及其相连边失效；

5）重复步骤2)~4)，直到整个相依网络达到稳定状态，不再有新的节点与连边失效，修复模型流程终止。

2.   边耦合相依网络修复策略

对共同边界连边的择优筛选方法有经典的随机修复策略（randomly repair strategy，RR），及根据连边基础属性介数的择优筛选策略（selective repair strategy based on edge betweenness，SREB），对介数值大的共同边界连边进行修复。

针对边耦合相依网络，判断连接边的重要性还可以依据连边冗余度^[31]，连边冗余度是连边两端节点除去连边本身的其他连边数之和，能够衡量连边失效之后节点不易失效的能力，并且连边冗余度大的连边有着更大的概率连接着那些度大的节点，因此本文提出以共同边界连边的复合冗余度值（compound excessive degree，CED）作为共同边界连边择优指标的复合冗余度择优修复（selective repair strategy based on compound excessive degree，SRCED），复合冗余度为共同边界连边中2条连边的连边冗余度之和。SRCED方法步骤如下：

1)在网络未遭受故障或攻击时，计算相依网络中各耦合连边CED值；

2）第n次迭代时，在修复阶段筛选出相依网络中所有共同边界连边；

3）对共同边界连边的CED值进行降序排序，筛选出前 λ的共同边界连边进行修复。

另外受CED的概念启发，本文进一步提出一种改进的复合冗余度择优修复方法（Improved selective repair strategy based on compound excessive degree，ISRCED），ISRCED方法步骤如下：

1）第n次迭代时，在修复阶段筛选出相依网络中所有共同边界连边；

2）计算共同边界连边$ \left(e_m^A,e_m^B\right) $，$ m = 1,2, \cdots $；在初始未故障网络中的CED值$ {K_0} $：

式中$ K_p^i $与$ K_q^i $为网络 i中连边$ e_m^i $两边端点p和q的度值；

3）计算共同边界连边$ \left(e_m^A,e_m^B\right) $在第n次迭代中现存网络中的CED值$ {K_1} $：

式中：$ \overline {e_m^A} $与$ \overline {e_m^B} $是共同边界连边在现存网络中的连${b_j}$边冗余度，$ \overline {K_p^i} $与$ \overline {K_q^i} $为现存网络 i 中连边$ e_m^i $两边端点p、q的度值；

4）计算共同边界连边ISRCED重要性指标$ {I_m} $，$ {I_m} $值越大，意味着共同边界连边两端节点连接着更多的失效节点，后续迭代中有更多共同边界连边出现：

5）根据重要性指标$ {I_m} $，对共同边界连边进行降序排列，选择前λ的共同边界连边进行修复。

3.   修复策略仿真结果与分析

本文对上述4种可能的修复策略进行仿真分析，目的是为边耦合相依网络的修复找到最佳最有效的策略。以下为修复策略评价指标和方法：

1）观察网络中极大联通片中的存活节点比例（giant component，GC）及相依网络迭代至稳定状态的迭代步数（number of iteration steps，NOI）随相依网路初始故障下存留连边比例p的变化情况曲线，不同曲线中在同一横坐标时的GC值的大小体现着相依网络使用不同修复策略的鲁棒性，GC值越大鲁棒性越好；同一横坐标时的迭代步数越少，意味着实施该修复策略下网络进入稳态越快。

2）比较不同修复策略下相依网络极大连通片曲线纵坐标GC值从0变为非零值的阈值点$ {P_c} $，$ {P_c} $值越小，相依网络鲁棒性越好，这意味着相依网络能够承受更大程度的初始故障攻击。

3）使用修复鲁棒系数（recover robustness，$ {R_{{\rm{rc}}}} $）^[28]来衡量实施不同修复策略下网络鲁棒性。$ {R_{{\rm{rc}}}} $计算公式为

式中：${P_R}$修复区间为选中的故障攻击下存活连边比例 p 的区间，${f_{{\rm{rc}}}}(p)$为相依网络稳态时，网络存活节点比例。修复鲁棒系数${R_{{\rm{rc}}}}$以数值的方式，衡量着不同修复策略在某一修复区间的鲁棒性。

为简化分析比较各种策略的有效性，本文就现实中具有代表性的ER（Erdős-Rényi）随机网络和SF（Scale-Free）无标度网络构建同构相依网络，进行级联失效动态修复仿真。参照文献[31]的取值和方法，构建ER-ER相依网络、SF-SF相依网络，网络中子网络节点规模为10000，网络总规模N=20000，ER网络节点平均度为$\left\langle k \right\rangle =5$，SF网络$ {K_{\min }} = 2 $，$ {K_{\max }} = 70 $，γ=2.8。在R语言仿真平台上根据以上数据，对构建的相依网络进行随机故障以及蓄意攻击下的仿真模拟，以下数据均为100次独立重复仿真实验的平均值。

3.1   随机故障下的修复

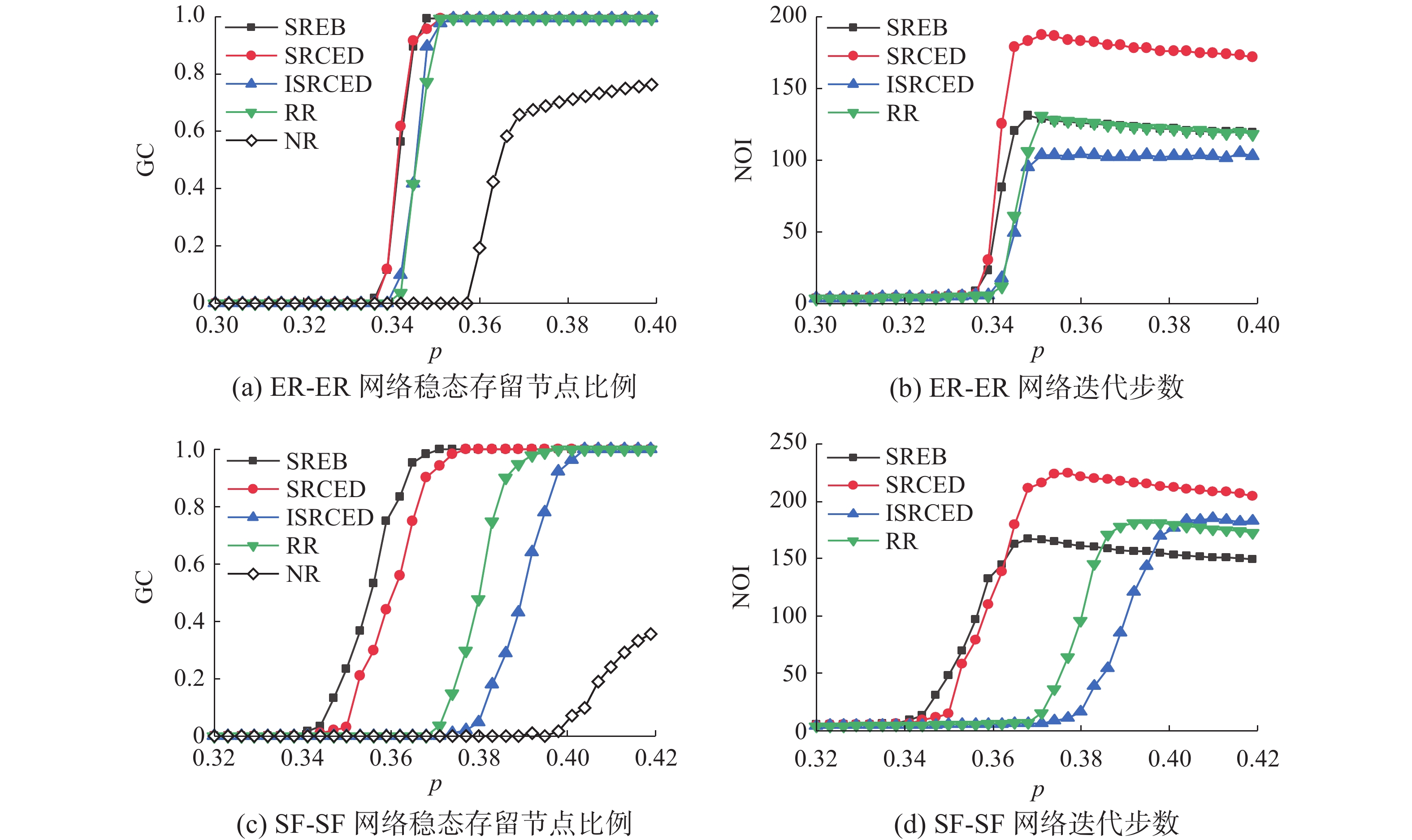
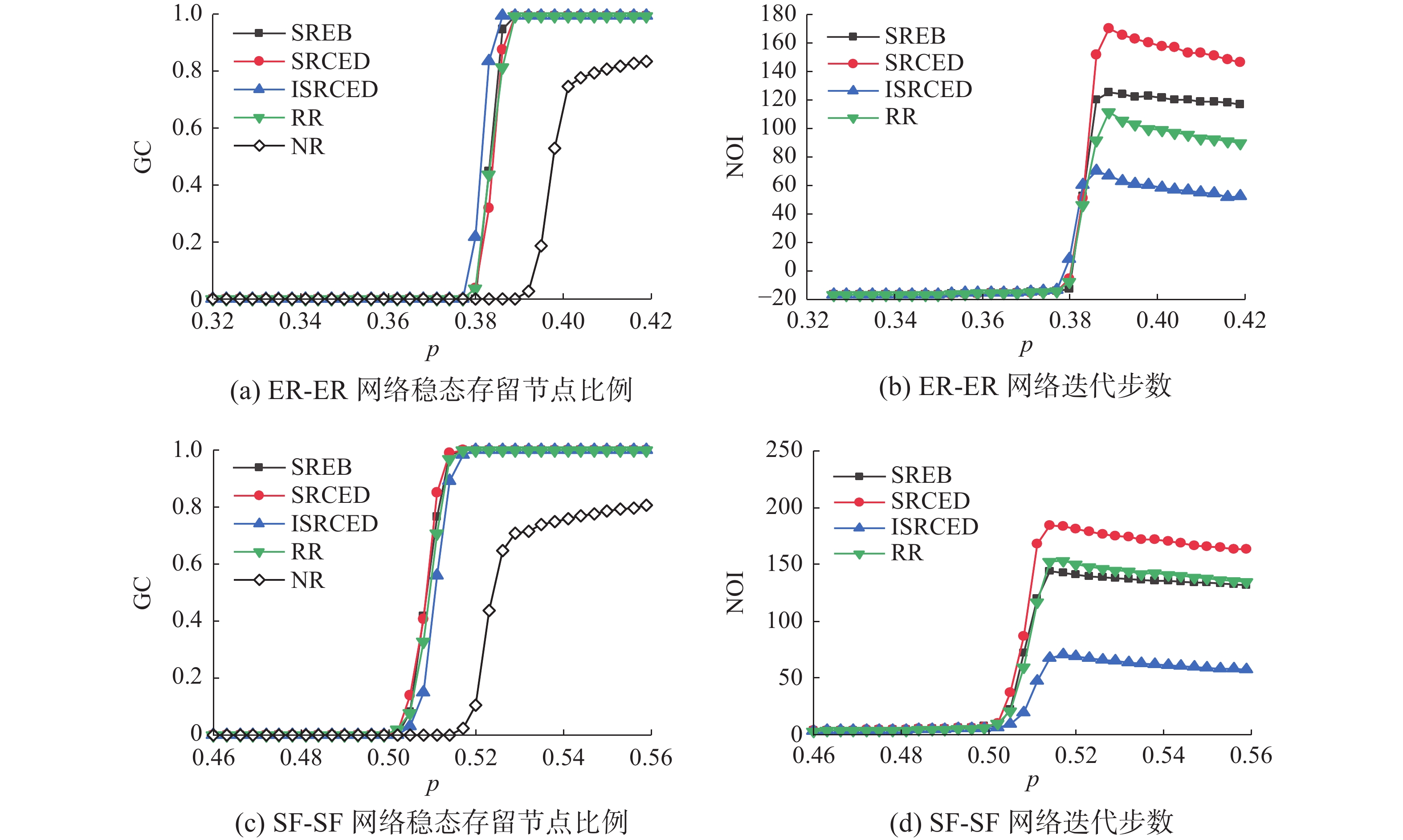
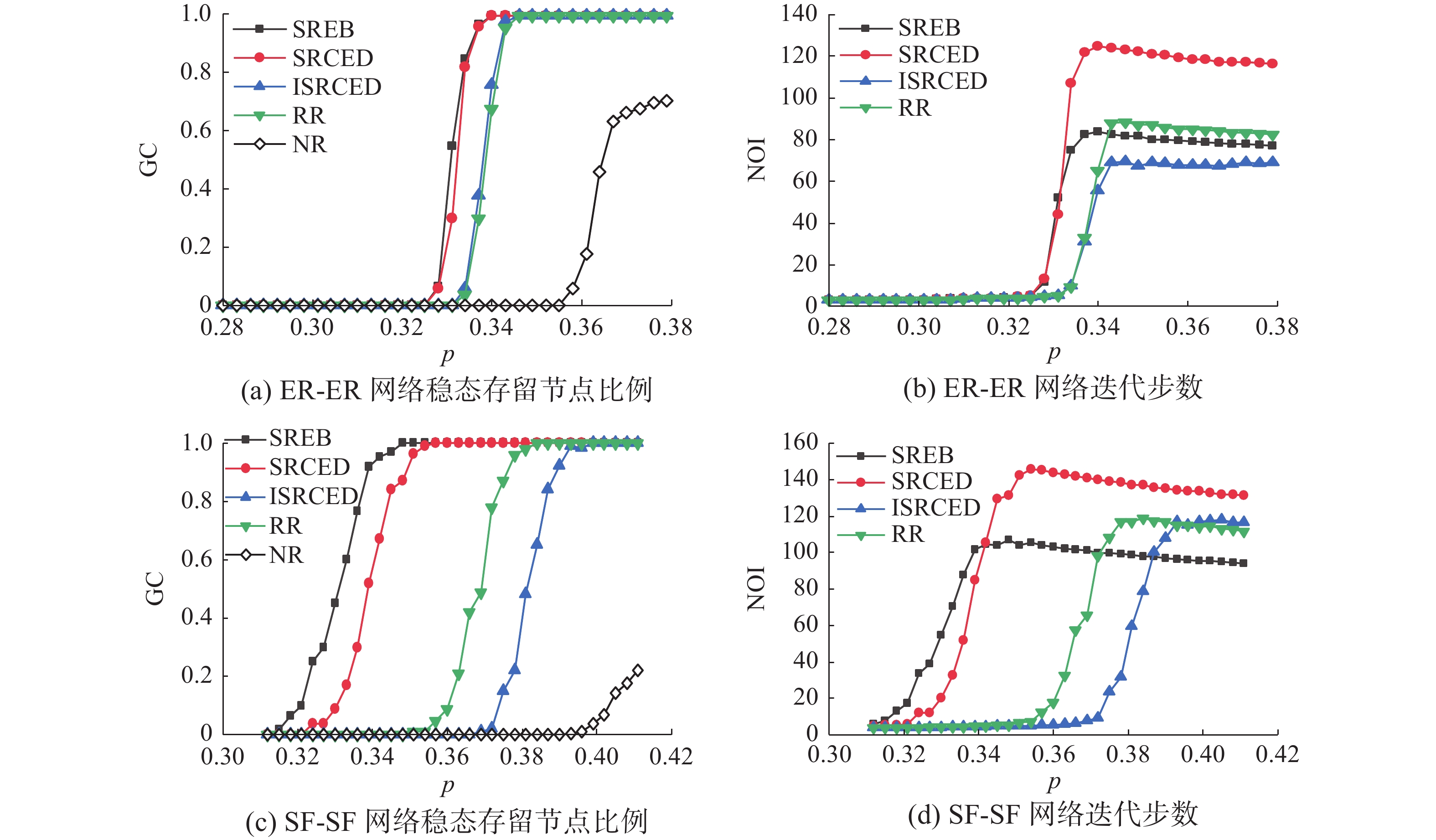
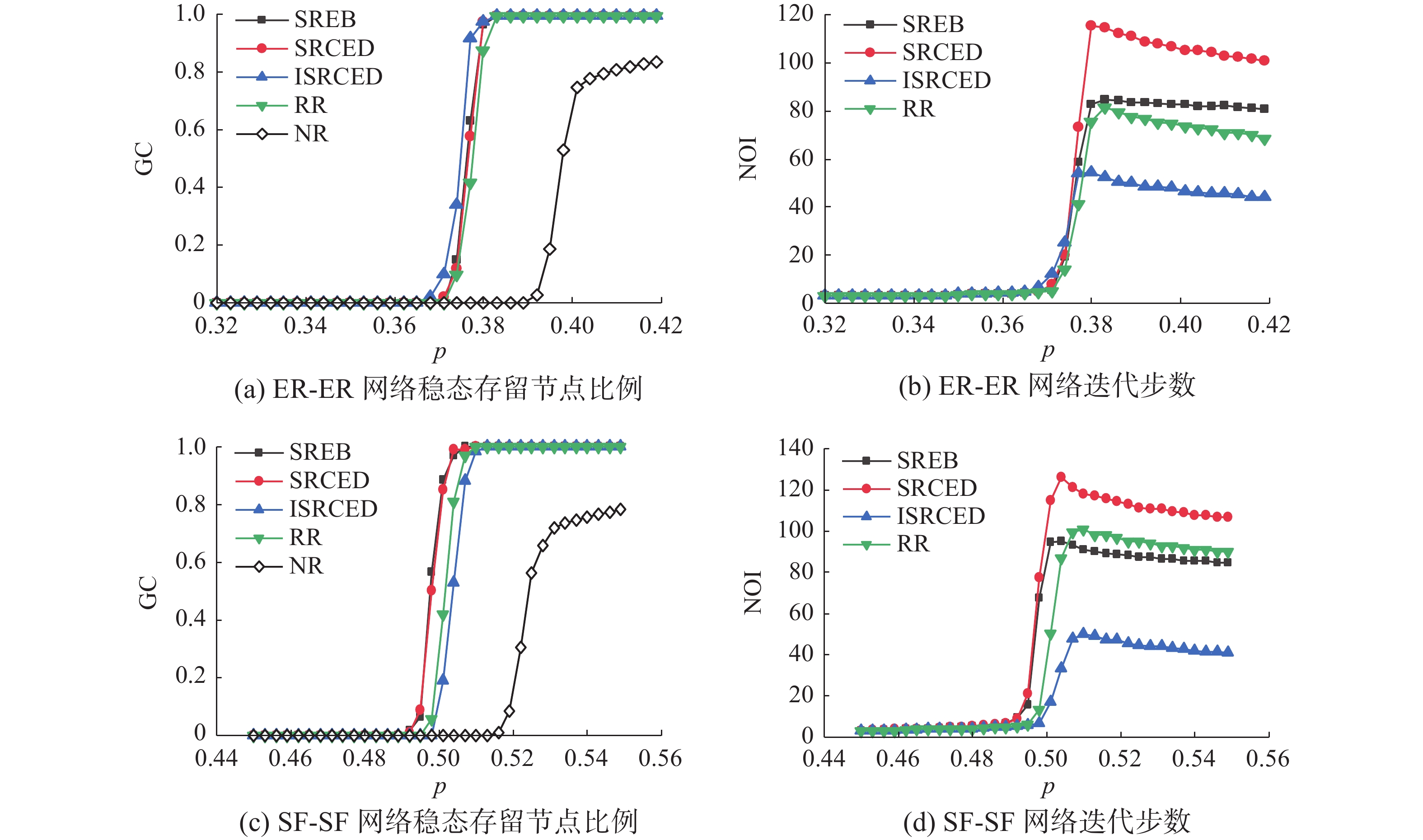
图2表示共同边界连边修复比例λ=3%时，ER-ER相依网络以及SF-SF相依网络在遭受故障攻击后，网络中极大连通片中的存活节点比例GC及相依网络迭代至稳定状态的迭代步数（number of iteration steps, NOI）随相依网路初始故障下存留连边比例p的变化情况。图2中空白菱形为对应存留连边比例p下相依网络不修复（no repair, NR）时的极大连通片规模曲线。以图2（a）ER-ER网络上随机修复策略(RR)曲线为例，可将相依网络修复分为3个阶段，分别为不可修复阶段（网络崩毁，稳态下节点存活比例少于0.1%，曲线GC值接近0）、完全修复阶段（稳态下节点存活比例大于99%，曲线GC值接近1），及部分修复阶段（稳态下节点存活比例介于不可修复阶段和完全阶段之间）。观察图2(a)可见，相比于其他策略，实施SREB、SRCED策略下的相依网络在同一阈值点$ {p_c} = 0.339 $，分别以$ {p_{0.339}} = 0.116 $、$ {p_{0.339}} = 0.119 $的节点存活比例更早进入部分修复阶段，表明这2种修复策略下的相依网络鲁棒性优于其他策略。图2(c)为不同修复策略下ER-ER相依网络级联失效迭代至稳定状态的迭代步数情况，可以看到在各修复策略的完全修复阶段，ISRCED修复策略所需的迭代步数远少于其他策略。随着共同边界连边修复比例的增大，如图3(a)、图3(c)、图4(a)、图4(c)所示，SREB、SRCED修复策略的阈值点$ {p_c} $依然相同且小于其他策略，保持着鲁棒性良好的优势，能够在更大的连边初始故障比例下起效，并且因为修复比例的增加鲁棒性优势有进一步的提升，但是在部分修复阶段，比较表1、表2中各策略下网络的修复鲁棒系数$ {R_{{\rm{rc}}}} $可以证明，SREB修复策略相较于SRCED修复策略能够更多的修复回失效节点。而当修复比例较小时，ISRCED修复策略在进入完全修复阶段时所需的迭代步数少于其他各策略，如图2(c)、图3(c)；当修复比例较大时，SREB修复策略在进入完全修复阶段时所需的迭代步数，其曲线开始与ISRCED修复策略的迭代步数曲线重叠，具有相同的迭代步数优势，如图4(c)。这意味着在修复比例较大时，在ER-ER相依网络中，可以直接使用SREB修复策略作为全局最优修复策略。

图  2  随机故障下λ=3%时，不同修复策略下相依网络稳态时极大连通片规模及迭代步数曲线

Fig.  2  When λ=3% under random faults, the curves of the giant component size and the number of iteration steps in the steady state of the interdependent networks under different recover strategies

下载: 全尺寸图片

图  3  随机故障下λ=5%时，不同修复策略下相依网络稳态时极大连通片规模及迭代步数曲线

Fig.  3  When λ=5% under random faults, the curves of the giant component size and the number of iteration steps in the steady state of the interdependent networks under different recover strategies

下载: 全尺寸图片

图  4  随机故障下λ=20%时，不同修复策略下相依网络稳态时极大连通片规模及迭代步数曲线

Fig.  4  When λ=20% under random faults, the curves of the giant component size and the number of iteration steps in the steady state of the interdependent networks under different recover strategies

下载: 全尺寸图片

表  1  随机故障下ER-ER相依网络不同修复比例下不同修复策略下网络的${R_{{\rm{rc}}}}$值（∆p=0.003）

Table  1  The $ {R_{{\rm{rc}}}} $ value of the network under different recover strategies under different recover ratios of ER-ER interdependent networks under random faults (∆p=0.003)

修复比例及修复区间	SREB	SRCED	ISRCED	RR
λ=3% ${P_R}$=[0.33,0.36]	0.596	0.598	0.488	0.472
λ=5% ${P_R}$=[0.32,0.35]	0.581	0.544	0.377	0.359
λ=20% ${P_R}$=[0.29,0.32]	0.643	0.634	0.386	0.372

表  2  随机故障下SF-SF相依网络不同修复比例下不同修复策略下网络的$ {R_{{\rm{rc}}}} $值（∆p=0.003）

Table  2  The $ {R_{{\rm{rc}}}} $ value of the network under different recover strategies under different recover ratios of SF-SF interdependent networks under random faults (∆p=0.003)

修复比例及修复区间	SREB	SRCED	ISRCED	RR
λ=3% ${P_R}$=[0.34,0.40]	0.754	0.673	0.199	0.354
λ=5% ${P_R}$=[0.31,0.40]	0.754	0.661	0.202	0.351
λ=20% ${P_R}$=[0.25,0.35]	0.812	0.729	0.118	0.419

对以上的结论可以做如下的解释：在网络连边初始故障比例较大时，从图2(a)、图3(a)、图4(a)中网络不修复曲线可以看到网络结构与功能遭受到彻底的破坏，当网络连边初始存留比例p<0.36时，稳态下相依网络中节点比例接近0，近乎没有节点存留。从级联失效过程出发，网络的崩溃并不是瞬时的，有一个迭代的过程，迭代过程中因为随机故障的随机性质，度值大的节点总是能够有更大的几率连接到网络极大连通片从而存活下来，而那些因为随机故障而脱离极大连通片的节点也为度值大而更容易有连边成为共同边界连边，同时也因为节点度值大，其连边相较于其他度值小的节点的连边，一般拥有着更大的介数值以及CED值，这使得这些介数值以及CED值大的连边更容易成为SREB、SRCED修复策略的择优目标。通过将度值大的失效节点重新连回极大联通片，这种对节点及其连边直接有效的筛选使得SREB、SRCED修复策略能够相比其他策略更早地起效。当相依网络所遭受的连边初始故障比例不那么大时，就进入到了ISRCED的优势阶段，从ISRCED重要性指标$ {I_m} $考虑，可以知道ISRCED修复策略所筛选出的连边在每一轮迭代时的现有网络中总是连接着那些拥有更多失效连边的节点，他使得ISRCED修复策略能够在下一轮迭代时拥有更多的候选共同边界连边，在相同的修复比例下修复回更多的节点，以更少的迭代步数使网络进入稳态。

图2(b)与图2(d)分别为共同边界连边修复比例λ=3%时的SF-SF相依网络在遭受不同比例的初始连边故障攻击后，经由不同修复策略，网络进入稳态时的极大连通片规模以及所需迭代步数。图2(b)中曲线可以看出，在SF-SF相依网络中，随机故障下SREB修复策略能够在更大的连边初始故障比例下更早的生效，使相依网络拥有更小的阈值点，鲁棒性更好。并且因为SF-SF网络中大部分节点只拥有少量的连边，而网络中占少数的Hub节点拥有着极高的度值，Hub节点其连边天然的就具有高的介数值，这使得SREB修复策略在SF-SF网络中相比在ER-ER网络中表现出更强的修复鲁棒性，与其他修复策略在阈值点比较上差别更明显。类似的，在修复比例为λ=5%（图3（b）、（d））、及λ=20%（图4（b）、（d））时，SREB策略同样的具有修复鲁棒性好的优势。不过不同于在ER-ER网络中，ISRCED修复策略在完全修复阶段并不具有迭代步数少的优势了，这是因为SF-SF网络中Hub节点占据的比例很小，大部分连边所连接的是度数小的节点，使用ISRCED修复策略对共同边界连边进行筛选，在修复完少部分的连接着Hub节点的共同边界连边后，这种筛选方法在接下来的迭代过程中作用并不明显，进入网络稳态所需的迭代步数甚至多于RR修复策略。SREB修复策略成为在完全修复阶段进入网络稳态所需迭代步数最少的策略，这表明随机故障下的SF-SF相依网络中，SREB修复策略为全局最优修复策略，不论修复比例的大小。

3.2   蓄意攻击下的修复

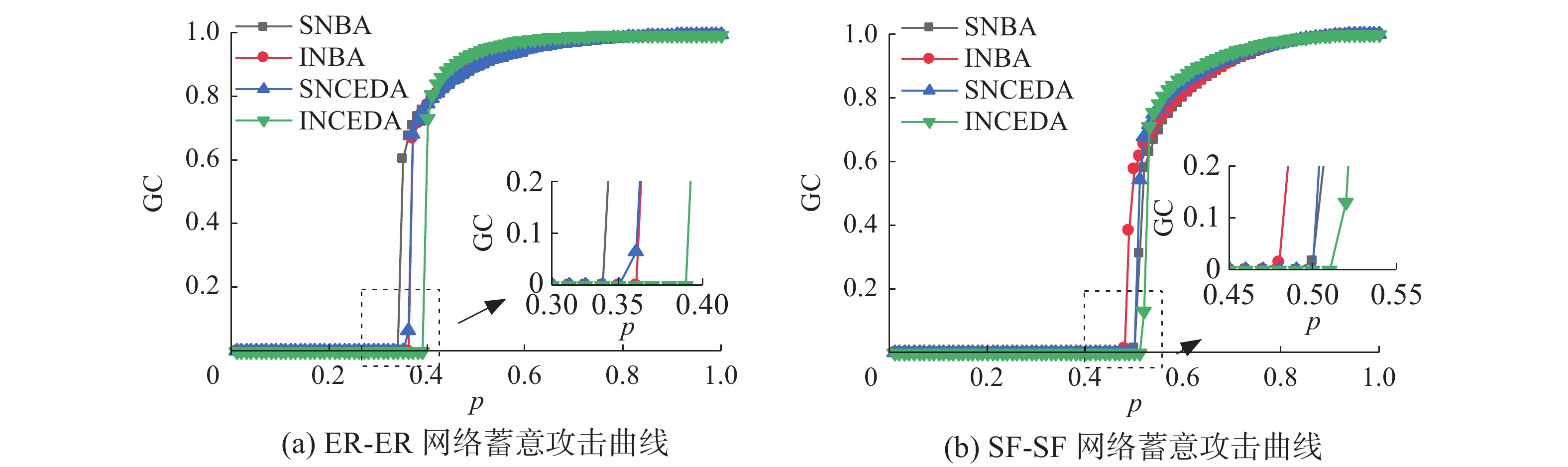
复杂网络的发生级联失效时，随机故障从来不是唯一的风险，被敌方蓄意攻击也是一种情况。图5为ER-ER相依网络与SF-SF相依网络，在4种蓄意攻击方法下存活节点比例的情况。

图  5  不同攻击方法下相依网络稳态时极大连通片规模随初始攻击比例p的变化

Fig.  5  Changes in the size of the giant component with the initial attack ratio p in the steady state of the interdependent networks under different attack methods

下载: 全尺寸图片

4种蓄意攻击方法为考虑单一网络的连边介数攻击（single network betweenness attack, SNBA)以及连边CED值攻击(single network CED attack, SNCEDA），考虑相依网络2个子网络的连边介数攻击（interdependent network betweenness attack, INBA）和连边CED值攻击(interdependent network CED attack, INCEDA)。

图5可以看到，ER-ER相依网络中在初始攻击比例较小，初始存留连边比例p较大时，SNBA、INBA以及INCEDA攻击方法曲线高度重合，在攻击效果是效果上优于INCEDA攻击方法，能够较为有效的破坏网络导致更多失效节点的出现。而在初始存留连边比例 p 较小时，如p<0.4时，INCEDA攻击手段展现出了优于其他3种攻击方法的攻击效果，在网络相变阈值点上大于其他节点，相同攻击比例下INCEDA攻击方法使得网络更早的崩溃。SF-SF相依网络中 p 较大时以SNBA攻击方法效果最优，p较小时以INCEDA攻击方法效果最优。本文选择使得相依网络级联失效相变点最大的攻击方法，即ER-ER、SF-SF相依网络攻击方法都为INCEDA攻击方法。

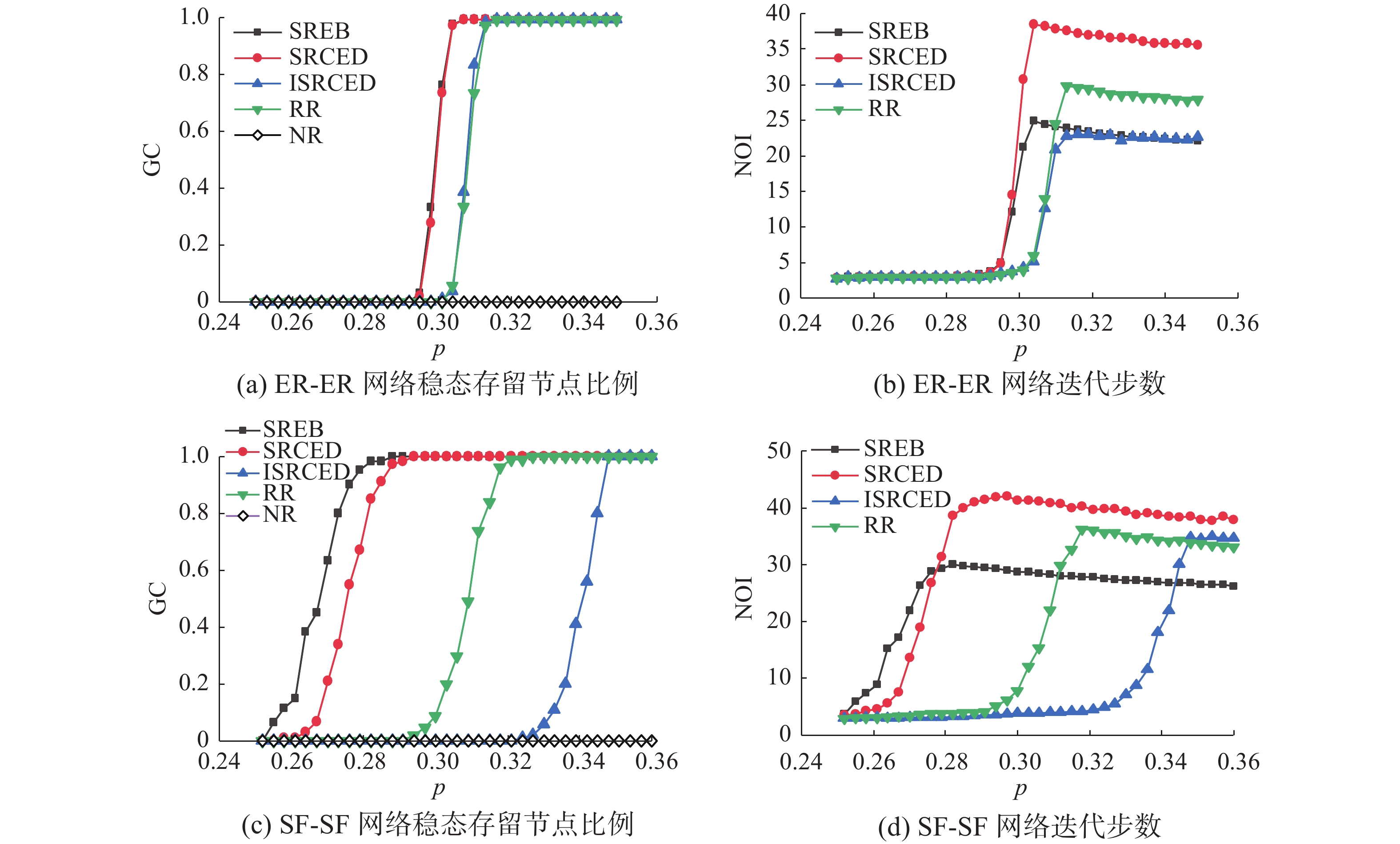
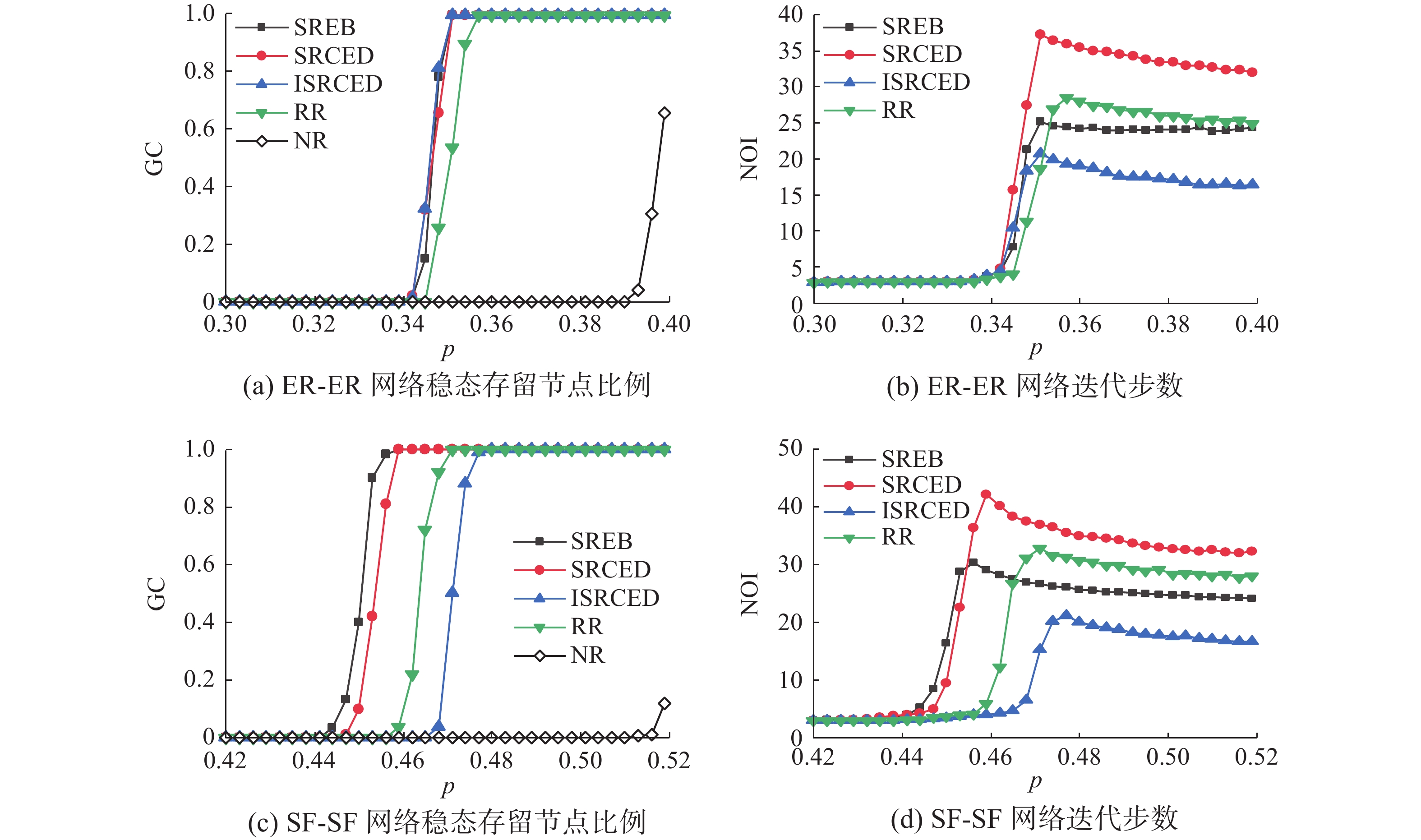
观察图6(a)、图6(c)和图7(a)、图7(c)可以看出，在ER-ER相依网络遭受到蓄意攻击时，在共同边界连边修复比例较小的情况下，相较于其他修复策略，实施ISRCED修复策略的相依网络在稳态下的存活节点比例以及所需迭代步数上都具有一定的优势。如图8(a)所示，在共同边界连边修复比例 λ=20% 时， SRCED、ISRCED以及SREB修复策略的曲线，在图像上存有密切贴合之处，且拥有着同样的网络阈值点，以及在同样的p值下进入完全修复阶段，但是通过比较表3中不同修复比例下实施各修复策略的网络的$ {R_{{\rm{rc}}}} $值能证明，部分修复阶段ISRCED修复策略下的网络在稳态下的存活节点比例更大，其在迭代步数上的显著优势可以通过直接观察图6~8得知，在蓄意攻击下的ER-ER网络中，可以直接使用ISRCED修复策略作为全局修复策略。当SF-SF相依网络遭受蓄意攻击当修复比例较小时，见图6(b)，各修复策略的GC值曲线难以通过直接观察分出高低，但是借助修复鲁棒系数（见表4）可以看到，SRCED修复策略下网络的$ {R_{{\rm{rc}}}} $值在修复比例 λ=3% 时高于其他策略，但随着修复比例的提升，SREB修复策略的$ {R_{{\rm{rc}}}} $值大于其他策略，在图7(b)、图8(b)中也能看出。实施ISRCED修复策略的网络在鲁棒性上甚至弱于RR随机修复策略，拥有着更大的阈值点，但是如同在ER-ER相依网络中，其在完全修复阶段使网络进入稳态所需的迭代步数远远少于其他策略，这一点在不同修复比例下均成立，见图6(d)、图7(d)、图8(d)。

图  6  蓄意攻击下λ=3%时，不同修复策略下相依网络稳态时极大连通片规模及迭代步数曲线

Fig.  6  When λ=3% under deliberate attack, the curves of the giant component size and the number of iteration steps in the steady state of the interdependent networks under different recover strategies

下载: 全尺寸图片

图  7  蓄意攻击下λ=5%时，不同修复策略下相依网络稳态时极大连通片规模及迭代步数曲线

Fig.  7  When λ=5% under deliberate attack, the curves of the giant component size and the number of iteration steps in the steady state of the interdependent networks under different recover strategies

下载: 全尺寸图片

图  8  蓄意攻击下λ=20%时，不同修复策略下相依网络稳态时极大连通片规模及迭代步数曲线

Fig.  8  When λ=20% under deliberate attack, the curves of the giant component size and the number of iteration steps in the steady state of the interdependent networks under different recover strategies

下载: 全尺寸图片

表  3  蓄意攻击下ER-ER相依网络不同修复比例下不同修复策略下网络的${R_{{\rm{rc}}}}$值（∆p=0.003）

Table  3  The $ {R_{{\rm{rc}}}} $ value of the network under different recover strategies under different recover ratios of ER-ER interdependent networks under deliberate attacks (∆p=0.003)

修复比例及修复区间	SREB	SRCED	ISRCED	RR
λ=3% ${P_R}$=[0.37,0.39]	0.341	0.318	0.434	0.326
λ=5% ${P_R}$=[0.36,0.39]	0.429	0.424	0.484	0.397
λ=20% ${P_R}$=[0.34,0.36]	0.718	0.722	0.736	0.605

表  4  蓄意攻击下SF-SF相依网络不同修复比例下不同修复策略下网络的$ {R_{{\rm{rc}}}} $值（∆p=0.003）

Table  4  The $ {R_{{\rm{rc}}}} $ value of the network under different recover strategies under different recover ratios of SF-SF interdependent networks under deliberate attacks (∆p=0.003)

修复比例及修复区间	SREB	SRCED	ISRCED	RR
λ=3% ${P_R}$=[0.50,0.52]	0.531	0.550	0.451	0.513
λ=5% ${P_R}$=[0.49,0.51]	0.563	0.554	0.323	0.407
λ=20% ${P_R}$=[0.44,0.48]	0.746	0.667	0.244	0.421

4.   结束语

本文构建出在边耦合相依网络中的动态修复模型，提出共同边界连边的概念，对不同耦合连边策略进行分析比较，分别对随机故障下和蓄意攻击下的网络寻找最优修复策略。通过对R网络以及SF无标度网络构建的ER-ER、SF-SF边耦合相依网络进行级联失效修复仿真研究，在随机故障下，无论是ER-ER网络还是SF-SF网络中，SREB修复策略都能够在更大的连边初始故障比例下修复网络至存活节点比例超过99%，修复比例越大这种优势越明显，然而各修复策略进入完全修复阶段时，使网络进入稳态所需的迭代步数来说，在ER-ER网络中是IDSRCED修复策略最少，在SF-SF网络中为SREB修复策略所需步数最少；在蓄意攻击下，ER-ER网络中ISRCED能够在部分修复阶段使网络进入稳态时拥有更高的节点存活比例，同时在完全修复阶段所需的迭代步数远远少于其他修复策略，SF-SF网络中，SREB修复策略下的网络相比其他修复策略有着更小的阈值点，能够承受更大的初始连边失效比例，而在ISRCED的完全修复阶段，其所需的迭代步数仍然远少于其他策略。

本文通过对共同边界连边进行择优修复，寻找边耦合相依网络在随机故障以及蓄意攻击下的最优修复策略。该项研究工作对于现实生活中相依网络遭受到故障攻击时的应急决策及修复措施具有一定的科学指导意义。