Knowledge representation and extraction method of partially-known fuzzy semiconcepts
-
摘要: 为了使“区间”形式加以表述的不确定信息的提取具有侧重性,需提取出对象(属性)集对应的属性(对象)区间集。本文在模糊形式背景中,通过引入2个阈值,将单边区间集与经典半概念结合,提取出属性(对象)集对应的对象(属性)区间集,从而提出区间集外延–集合内涵(集合外延–区间集内涵)(interval set extent-set intent(set extent-interval set intent),ISE-SI(SE-ISI))型单边区间集模糊半概念。全体ISE-SI(SE-ISI)型单边区间集模糊半概念构成格,并给出基于格搜寻全体ISE-SI(SE-ISI)型单边区间集模糊半概念的算法。通过与已有成果对比,显示出这2种知识表示形式的多方优势。本文所得结果在知识表示及提取方法上具有适用范围广、实际应用强等优点。Abstract: To ensure that the extraction of uncertain information expressed in the form of "intervals" is focused, it is necessary to extract the corresponding attribute (object) interval set for the object (attribute) set. By introducing two thresholds from the fuzzy context, the unilateral interval set is combined with the classical semiconcept to extract the corresponding object (attribute) interval set for the attribute(object) set, and thereby the interval set extent-set intent(set extent-interval set intent)(ISE-SI (SE-ISI)) type partially-known fuzzy semiconcept is proposed. All ISE-SI (SE-ISI) type partially-known fuzzy semiconcepts form a lattice, and the algorithm based on lattice search for all ISE-SI (SE-ISI) type partially-known fuzzy semiconcepts is given. The multiple advantages of these two knowledge representation forms are demonstrated by comparing them with existing achievements. The results obtained in this paper have the advantages of broad applicability and strong practical application in knowledge representation and extraction methods.
-
Wille[1]于1982年提出了形式概念分析(formal concept analysis, FCA)理论。以形式背景为研究基础,包含了对象集和属性集,还有定义在对象集和属性集上的二元关系。FCA在知识提取[2-6]和信息挖掘[7-11]等方面具有重要应用。由于许多实际背景蕴含的知识存在不确定性以及模糊性,导致对象和属性之间不能简单地用二元关系来描述。因此,不完备形式背景[12-14]和模糊形式背景[12,15-16]等其他背景得以产生,以更真实且直观的方式反映出对象和属性之间的关系。
对于知识的定性表示,Yao[17]利用粗糙集上下近似的思想[18-19],提出了用于描述不确定信息的区间集理论。因此,区间集与FCA相结合得以产生区间集概念格[20]。由于经典的形式概念(Wille[1]提出的概念)是一种特殊的区间集概念(一种外延和内涵都用区间集形式加以表述的概念),而反之不成立。所以区间集概念一经提出,便得到了广泛的关注。目前,已取得不少研究成果。例如,Ma等[21]将区间集理论应用到面向对象概念格中,提出面向对象区间集概念格;郭庆春等[22]引入区间集协调集,给出对偶区间集概念格上区间集协调集的一系列判定定理,进而讨论了利用区间集协调集获取区间集属性约简的方法;马建敏等[23]将区间集思想引入决策形式背景,研究决策形式背景上的区间集概念格及其属性约简。
区间集概念可根据其外延和内涵的表述形式分为4类[24-25]:1) 外延和内涵都为集合形式;2) 外延为区间集形式,内涵为集合形式;3) 外延为集合形式,内涵为区间集形式;4) 外延和内涵都为区间集形式。
对1)中的形式,Wille等研究人员已研究的十分透彻。在已有的区间集概念成果中,讨论较多的只是“双边”形式,即形式4)。对于实践中常用的2种“单边”形式2)和3),分别称为区间集外延–集合内涵(interval set extent-set intent,ISE-SI)型单边区间集概念和集合外延–区间集内涵(set extent-interval set intent,SE-ISI)型单边区间集概念。这2种单边区间集概念通过固定外延或内涵的某一边为集合,来挖掘出对应另一边区间集所蕴含的不确定信息,这其实就是单边区间的思想,同时也符合人类的思维方式。比如,对于ISE-SI型单边区间集概念来说,它的内涵是集合形式,而外延是区间集形式,这是由于在知识提取的过程中,通过挖掘出属性被哪些对象一定拥有和可能拥有所产生的。从而能够有效地提取出该类型的概念中关于属性所对应的不确定信息,并将不确定信息以区间集形式表述在该概念的外延中,使不确定信息的提取更加具有针对性和侧重点。
然而,从已有成果和以上的分析中可以看出,目前存在的主要问题如下:
1) 从单边区间集概念的定义可知,需要考虑对象集中所有对象共同拥有的属性和属性集中所有属性被哪些对象所共同拥有的这种“双向”问题,但面对实际问题中仅需考虑对象集中所有对象共同拥有的属性,或属性集中所有属性被哪些对象所共同拥有的这两种“单向”问题时,却无能为力。
2) 目前关于单边区间集概念的成果[24-26]大多都在不完备形式背景下展开,对于完备形式背景下的研究却寥寥无几。
为了解决以上问题,本文的主要贡献如下:
1) 在对单边区间集概念的研究中,本文将融合FCA中半概念的“单向”思维[27-30],结合成单边区间集半概念,从而可考虑“单向”问题。
2) 完备形式背景分为经典形式背景和模糊形式背景,而实践中的数据总会受到一些因素的影响,使得大部分情况常常不满足布尔型数据的要求。模糊形式背景通过建立隶属度函数,实现对经典形式背景的拓展,从而能够包容更多的数据。因此,通过对模糊形式背景展开对单边区间集半概念的讨论,在经典形式背景下会同样适用。
本文将结合FCA中经典半概念和单边区间的思想[24],在模糊形式背景下利用算子和任意给定的2个不同的阈值构造出对象集或属性集对应的区间,挖掘出它们各自蕴含的不确定信息,分别构造出2种知识表示形式,从而提供了一种有效的模糊形式背景下的知识提取方法。
1. 预备知识
定义1[17] 设
$U$ 为一个非空有限论域,对$ {X_l} \subseteq {X_u} \subseteq U $ ,$[{X_l},{X_u}] = \{ X \in {{P}}(U)|{X_l} \subseteq X \subseteq {X_u}\}$ ,称$[{X_l},{X_u}]$ 为定义在$U$ 上的区间集。其中,${{P}}(U)$ 表示$U$ 的幂集,${{{P_I}}}(U)$ 表示定义在$U$ 上区间集全体。对于区间集
$[{X}_{l},{X}_{u}],[{Y}_{l},{Y}_{u}]\in {{P_I}}(U)$ ,定义它们的一些运算法则如下:$$ [{X_l},{X_u}]\widetilde \cap [{Y_l},{Y_u}] = [{X_l} \cap {X_u},{Y_l} \cap {Y_u}] $$ $$ [{X_l},{X_u}]\widetilde \cup [{Y_l},{Y_u}] = [{X_l} \cup {X_u},{Y_l} \cup {Y_u}] $$ $$ [{X}_{l},{X}_{u}]=[{Y}_{l},{Y}_{u}]\iff {X}_{l}={X}_{u}且{Y}_{l}={Y}_{u} $$ $$ [{X}_{l},{X}_{u}]\tilde{\subseteq }[{Y}_{l},{Y}_{u}]\iff {X}_{l}\subseteq {Y}_{l}且{X}_{u}\subseteq {Y}_{u} $$ 定义2[1-2] 设
$L$ 是一个非空集合,$\forall x,y,{\textit{z}} \in L$ ,称定义在$L$ 上的二元关系$ \leqslant $ 是一个偏序关系,如果它满足下面的3条性质:1) 自反性:
$ x \leqslant x $ ;2) 反对称性:
$x \leqslant y$ 和$y \leqslant x\Rightarrow x=y$ ;3) 传递性:
$x\leqslant y$ 且$y \leqslant {\textit{z}}\Rightarrow x \leqslant {\textit{z}}$ 。集合
$L$ 和偏序关系$ \leqslant $ 构成一个偏序集$ (L, \leqslant ) $ 。$\forall x,y \in L$ ,$x$ 和$y$ 的下确界$x \wedge y$ 和上确界$x \vee y$ 都存在,这时偏序集$ (L, \leqslant ) $ 构成格。定义3[27-28] 称
$(G,M,I)$ 为一个形式背景,若$G$ 和$M$ 是2个非空有限集合,分别称为对象集和属性集,I为G和M之间的一个二元关系,$ I \subseteq G \times M $ 。对于对象$x \in G$ ,属性$a \in M$ ,当$(x,a) \in I$ 时就表示对象x拥有属性a。在对象子集
$X \in {{P}}(G)$ 与属性子集$A \in {{P}}(M)$ 上定义一对对偶算子如下:$$ {X^ * } = \{ a|a \in M,\forall x \in X,xIa\} $$ $$ {A^ * } = \{ x|x \in G,\forall a \in A,xIa\} $$ 若序对
$(X,A)$ 满足或$X = {A^ * }$ ,则称$(X,A)$ 为一个经典半概念,简称半概念。其中,只满足${X^ * } = A$ 的半概念也称为$ \cap $ –半概念;只满足$X = {A^ * }$ 的半概念也称为$ \cup $ –半概念。令${(G,M,I)_ \cap }$ 和${(G,M,I)_ \cup }$ 分别为$ \cap $ –半概念和$ \cup $ –半概念的全体。定义4[15] 称
$(G,M,\widetilde I)$ 为一个模糊形式背景,若$G$ 和$M$ 是2个非空有限集合,分别称为对象集和属性集,$\widetilde I$ 为定义在$ G \times M \to [0,1] $ 上的一个模糊关系。对任意二元对$(x,a) \in G \times M$ ,$\widetilde I(x,a)$ 为对象$x$ 关于属性$a$ 的隶属度,表示$x$ 拥有$a$ 的程度。显然有
$0 \leqslant \widetilde I(x,a) \leqslant 1$ ,在一个模糊形式背景$(G,M,\widetilde I)$ 中,给定一个阈值$\varepsilon $ ,则定义一对模糊算子$^{{ * _\varepsilon }}:{{P}}(G) \to {{P}}(M)$ 和$^{{ * _\varepsilon }}:{{P}}(M) \to {{P}}(G)$ 如下(对$\forall X \in $ ${{P}}(G)$ 和$ \forall A \in {{P}}(M) $ ):$$ {X^{{ * _\varepsilon }}} = \{ a|a \in M,\forall x \in X,\widetilde I(x,a) \geqslant \varepsilon \} $$ $$ {A^{{ * _\varepsilon }}} = \{ x|x \in G,\forall a \in A,\widetilde I(x,a) \geqslant \varepsilon \} $$ 若序对
$(X,A)$ 满足${X^{{ * _\varepsilon }}} = A$ 且${A^{{ * _\varepsilon }}} = X$ ,则称$(X,$ $A)$ 为一个模糊概念。令${(G,M,\widetilde I)_{{\text{FC}}}}$ 为全体模糊概念。由于实际问题背景的有限性,所以本文的所有讨论均为有限。
下面通过一个实验案例对区间集、半概念和模糊概念进行解释。
例1 某护林员培训机构对5名护林员在三大林区学习实践过程中的表现进行评价,主要依据的是护林员在这些林区的工作时长、熟悉程度等,然后用
$[0,1]$ 的某个数来量化评价,得到如表1的评价表。表 1 评价统计表Table 1 Evaluation statistics护林员 东北林区 西南林区 东南林区 陈某 0.76 0.58 0.24 刘某 0.45 0.70 0.16 张某 0.13 0.87 0.74 王某 0.92 0.22 0.45 李某 0.08 0.95 0.80 设
$({G_1},{M_1},\widetilde {{I_1}})$ 是一个模糊形式背景,令对象集${G_1} = \{ {x_1},{x_2},{x_3},{x_4},{x_5}\} $ ,其中${x_1}为$ 陈某,${x_2}为$ 刘某,${x_3}为$ 张某,${x_4}为$ 王某,${x_5}为$ 李某;令属性集$ {M_1} = $ $ \{ {a_1},{a_2}, $ $ {a_3}\} $ ,其中${a_1}为$ 东北林区,${a_2}为$ 西南林区,${a_3}为$ 东南林区;模糊关系$\widetilde {{I_1}}$ 如表1所示,比如$ \widetilde {{I_1}}({x_1},{a_3})=$ $ 0.24 $ 表明护林员陈某对于东南林区的隶属度为0.24(当某护林员对某林区的隶属度越接近于1时就表明该护林员在该林区上的评价越高,越可能胜任到该林区执行护林任务;相反评价越低,越不可能胜任)。表2为表1所示评价统计表的数学表达。表 2 相应的数学表达Table 2 Corresponding mathematical expression${G_1}$ ${a_1}$ ${a_2}$ ${a_3}$ ${x_1}$ 0.76 0.58 0.24 ${x_2}$ 0.45 0.70 0.16 ${x_3}$ 0.13 0.87 0.74 ${x_4}$ 0.92 0.22 0.45 ${x_5}$ 0.08 0.95 0.80 为了方便表达,集合
$\{ {x_1},{x_2},{x_3},{x_4}\} $ 可表示为$ {x_1} $ $ {x_2}{x_3}{x_4} $ ,其他集合也同样表达为此方式。1) 由于
${x_1} \subseteq {x_1}{x_4} \subseteq {G_1}$ ,根据定义1可知,$[{x_1}, {x_1}{x_4}$ 构成一个区间集。对于另一个区间集$[{x_1}, {x_1}{x_3}]$ ,有$[{x_1},{x_1}{x_4}]\widetilde \cap [{x_1},{x_1}{x_3}] = [{x_1} \cap {x_1},{x_1}{x_4} \cap {x_1}{x_3}] = [{x_1}, {x_1}]$ 。同理,可对运算法则$\widetilde \cup $ 、=和$\widetilde \subseteq $ 进行类似解释。2) 由于半概念只适用于经典形式背景,从而在
$ ({G_1},{M_1},\widetilde {{I_1}}) $ 中不妨设阈值$\beta = 0.70$ ,将$({G_1},{M_1},\widetilde {{I_1}})$ 转换成如表3所示的经典形式背景$({G_1},{M_1},{I_1})$ 。表 3 1个经典形式背景$({G_1},{M_1},{I_1})$ Table 3 A classical formal context$({G_1},{M_1},{I_1})$ ${G_1}$ ${a_1}$ ${a_2}$ ${a_3}$ ${x_1}$ 1 0 0 ${x_2}$ 0 1 0 ${x_3}$ 0 1 1 ${x_4}$ 1 0 0 ${x_5}$ 0 1 1 根据定义3可知,若
$X = {x_4}$ ,则${X^ * } = {a_1}$ ,从而$({x_4},$ ${a_1})$ 是一个$ \cap $ –半概念;同理,若$A = {a_1}$ ,则${A^ * } = {x_1}{x_4}$ ,从而$({x_1}{x_4},{a_1})$ 是一个$ \cup $ –半概念。3) 由于模糊概念只涉及一个阈值,不妨设阈值
$\beta = 0.70$ ,从而由定义4知,若$X = {x_1}{x_4}$ ,$A = {a_1}$ ,由于${\{ {x_1}{x_4}\} ^ * } = {a_1}$ 且${x_1}{x_4} = {\{ {a_1}\} ^ * }$ ,从而$({x_1}{x_4},{a_1})$ 是一个模糊概念。2. ISE-SI型单边区间集模糊半概念
为了简便,将本文所讨论的ISE-SI型单边区间集模糊半概念简称为ISE-SI模糊半概念。
本节首先构建ISE-SI模糊半概念算子,并挖掘出这些算子满足的一些性质;然后利用这些算子得到ISE-SI模糊半概念的定义;接着发现全体ISE-SI模糊半概念的格结构;最后在此基础上给出了获取全体ISE-SI模糊半概念的算法。
2.1 ISE-SI模糊半概念的算子及定义
定义5 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,定义一对算子$^{\underline * }:{{P}}(M) \to {{P}}(G)$ 和$^{\overline * }:{{P}}(M) \to {{P}}(G)$ (对$ \forall A \in {{P}}(M) $ ):$$ {A^{\underline * }} = \{ x \in G|\forall a \in A,\widetilde I(x,a) \geqslant \beta \} $$ (1) $$ {A^{\overline * }} = \{ x \in G|\forall a \in A,\widetilde I(x,a) \geqslant \alpha \} $$ (2) ${A^{\underline * }}$ 中的对象$x$ 对应$A$ 中所有属性的隶属度都不小于$\beta $ ,可以说对象$x$ 一定拥有$A$ 中所有属性;而${A^{\overline * }}$ 中的对象$x$ 对应$A$ 中所有属性的隶属度都不小于$\alpha $ ,可以说对象$x$ 可能拥有$A$ 中所有属性。下面,借助算子
$^{\underline * }$ 和$^{\overline * }$ 给出ISE-SI模糊半概念算子的定义。定义6 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,定义ISE-SI模糊半概念算子$^ \triangleleft :{{P}}(M) \to {{P_I}}(G))$ (对$\forall A \in {{P}}(M)$ ):$$ {A^ \triangleleft } = [{A^{\underline * }},{A^{\overline * }}] $$ 通过比较定义5中的式(1)、(2)可得
${A^{\underline * }} \subseteq {A^{\overline * }}$ 成立。故,${A^{\underline * }}$ 和${A^{\overline * }}$ 可构成属于${{P_I}}(G)$ 的区间集$[{A^{\underline * }},{A^{\overline * }}]$ 。下面,挖掘算子
${\underline * }$ ,${\overline * }$ 和$ \triangleleft $ 满足的一些性质。定理1 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,对$\forall A,B \in {{P}}($ $ M) $ ,有下列结论成立:1)
$A \subseteq B \Rightarrow {A^{\underline * }} \supseteq {B^{\underline * }},{A^{\overline * }} \supseteq {B^{\overline * }},{A^ \triangleleft }\widetilde \supseteq {B^ \triangleleft }$ 。2)
${(A \cup B)^{\underline * }} = {A^{\underline * }} \cap {B^{\underline * }}$ ,${(A \cup B)^{\overline * }} = {A^{\overline * }} \cap {B^{\overline * }}$ ,${(A \cup B)^ \triangleleft } = {A^ \triangleleft }\widetilde \cap {B^ \triangleleft }$ 。3)
${(A \cap B)^{\underline * }} \supseteq {A^{\underline * }} \cup {B^{\underline * }}$ ,${(A \cap B)^{\overline * }} \supseteq {A^{\overline * }} \cup {B^{\overline * }}$ ,${(A \cap B)^ \triangleleft } \supseteq {A^ \triangleleft }\widetilde \cup {B^ \triangleleft }$ 。证明 结论1)的证明如下:
如果
$ x \in {B^{\underline * }} $ ,也就是对于所有的$ a \in B $ 都成立$ \widetilde I(x,a) \geqslant \alpha $ ,而$A \subseteq B$ 就使得所有的$ a \in A $ 也都成立$ \widetilde I(x,a) \geqslant \alpha $ 。因此,$ x \in {A^{\underline * }} $ 。从而有${A^{\underline * }} \supseteq {B^{\underline * }}$ 。同理可证明${A^{\overline * }} \supseteq {B^{\overline * }},{A^ \triangleleft }\widetilde \supseteq {B^ \triangleleft }$ 。结论2)的证明如下:
$x \in {(A \cup B)^{\underline * }} \Leftrightarrow $ 对于所有的$ a \in A \cup B $ 都成立$\widetilde I(x, a) \geqslant \alpha \Leftrightarrow$ 对于所有的$ a \in A $ 都成立$ \widetilde I(x,a) \geqslant \alpha $ 且对于所有的$ a \in B $ 也都成立$ \widetilde I(x,a) \geqslant \alpha \Leftrightarrow $ $x \in {A^{\underline * }}$ 且$x \in {B^{\underline * }} \Leftrightarrow $ $x \in {A^{\underline * }} \cap {B^{\underline * }}$ 。同理可证明$ {(A \cup B)^{\overline * }} = $ $ {A^{\overline * }} \cap {B^{\overline * }} $ ,${(A \cup B)^ \triangleleft } = {A^ \triangleleft }\widetilde \cap {B^ \triangleleft }$ 。结论3)的证明如下:
如果
$x \in {A^{\underline * }} \cup {B^{\underline * }}$ ,那么$x \in {A^{\underline * }}$ 或$x \in {B^{\underline * }}$ 。由于$ A\cap B\subseteq A、A\cap B\subseteq B $ ,通过结论1)可知,${(A \cap B)^{\underline * }} \supseteq $ ${A^{\underline * }}$ 且${(A \cap B)^{\underline * }} \supseteq {B^{\underline * }}$ 。因此,$x \in {(A \cap B)^{\underline * }}$ 。从而有$(A \cap $ $B{)^{\underline * }} \supseteq {A^{\underline * }} \cup {B^{\underline * }}$ 。利用定义5和6,结合Yao[17]的区间集理论,给出ISE-SI模糊半概念的定义。
定义7 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ 。若$A \in {{P}}(M)$ ,$[{X_l},{X_u}] \in {P_I}(G)$ ,则称序对$([{X_l},{X_u}],A)$ 为一个ISE-SI模糊半概念当且仅当${A^ \triangleleft } = [{A^{\underline * }},{A^{\overline * }}] = [{X_l},{X_u}]$ 。称
$[{X_l},{X_u}]$ 为ISE-SI模糊半概念$([{X_l},{X_u}],A)$ 的外延,$A$ 为ISE-SI模糊半概念$([{X_l},{X_u}],A)$ 的内涵。令${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 为ISE-SI模糊半概念的全体。下面,通过一个实验案例解释算子
$^{\underline * }$ ,$^{\overline * }$ 和$^ \triangleleft $ 以及ISE-SI模糊半概念。例2(续例1) 在例1所示模糊形式背景
$({G_1},{M_1},$ $\widetilde {{I_1}})$ 中,设阈值$\alpha = 0.40$ ,$\beta = 0.70$ 。当属性子集$A = {a_1}$ 时,${A^{\underline * }} = {x_1}{x_4}$ 。这表明对于东北林区来说,一定能胜任此林区的任务有陈某和王某;而${A^{\overline * }} = {x_1}{x_2}{x_4}$ 则表明对于东北林区来说,可能能胜任此林区任务的有陈某、刘某和王某。即,${A^ \triangleleft } = [{x_1}{x_4},{x_1}{x_2}{x_4}]$ 。故,根据定义7,$([{x_1}{x_4},{x_1}{x_2}{x_4}],{a_1})$ 是一个ISE-SI模糊半概念。2.2 ISE-SI模糊半概念的格结构
定义8 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,设${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 为此背景所有ISE-SI模糊半概念。定义二元关系“$ \leqslant $ ”如下(对$ \forall ([{X_l},{X_u}],A),([{Y_l},{Y_u}],B) $ $ \in {(G,M,\widetilde I)_{{\text{ISE-SI}}}} $ ):$$ ([{X}_{l},{X}_{u}],A) \leqslant ([{Y}_{l},{Y}_{u}],B)\iff A\subseteq B且[{X}_{l},{X}_{u}]\tilde{\supseteq }[{Y}_{l},{Y}_{u}] $$ 当
$ ([{X}_{l},{X}_{u}],A) \leqslant ([{Y}_{l},{Y}_{u}],B) $ 时,称$ ([{X_l},{X_u}],A) $ 为$ ([{Y_l},{Y_u}],B) $ 的子半概念,称$ ([{Y_l},{Y_u}],B) $ 为$ ([{X_l},{X_u}],A) $ 的母半概念。定理2 在一模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且$0 \leqslant \alpha < \beta \leqslant 1$ ,“$ \leqslant $ ”为定义8给出的二元关系,则$ ({(G,M,\tilde{I})}_{\text{ISE-SI}}, \leqslant ) $ 构成一个偏序集。证明 由偏序集的定义可知,需证明“
$ \leqslant $ ”满足自反性、反对称性与传递性。任取$ ([{X_l},{X_u}],A), $ $ ([{Y_l},{Y_u}],B),([{Z_l},{Z_u}],C) \in {(G,M,\widetilde I)_{{\text{ISE-SI}}}} $ 。1) 证明“
$ \leqslant $ ”满足自反性。由于
$ A\subseteq A且[{X}_{l},{X}_{u}]\tilde{\supseteq }[{X}_{l},{X}_{u}] $ ,从而根据定义8有$ ([{X}_{l},{X}_{u}],A) \leqslant ([{X}_{l},{X}_{u}],A) $ 。2) 证明“
$ \leqslant $ ”满足反对称性。设
$ ([{X}_{l},{X}_{u}],A) \leqslant ([{Y}_{l},{Y}_{u}],B) $ 且$ ([{Y}_{l},{Y}_{u}],B) \leqslant $ $ ([{X_l}, {X_u}],A) $ ,根据定义8有$ A \subseteq B $ 且$ A \supseteq B $ ,$ [{X_l},{X_u}] $ $ \widetilde \supseteq [{Y_l},{Y_u}] $ 且$ [{X_l},{X_u}]\widetilde \subseteq [{Y_l},{Y_u}] $ ,有$ A = B $ 和$ [{X_l},{X_u}] = $ $ [{Y_l},{Y_u}] $ ,从而$ ([{X_l},{X_u}],A) = ([{Y_l},{Y_u}],B) $ 。3) 证明“
$ \leqslant $ ”满足传递性。设
$ ([{X}_{l},{X}_{u}],A) \leqslant ([{Y}_{l},{Y}_{u}],B) $ 且$ ([{Y}_{l},{Y}_{u}],B) \leqslant $ $([{Z_l}, {Z_u}], C)$ ,根据定义8有$ A \subseteq B $ 且$ B \subseteq C $ ,$[{X_l},{X_u}]\widetilde \supseteq [{Y_l},{Y_u}]$ 且$ [{Y_l},{Y_u}]\widetilde \supseteq [{Z_l},{Z_u}] $ ,有$ A \subseteq C $ 和$ [{X_l},{X_u}]\widetilde \supseteq [{Z_l},{Z_u}] $ ,从而$ ([{X}_{l},{X}_{u}],A) \leqslant ([{Z}_{l},{Z}_{u}],C) $ 。定理3 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ 。偏序集$((G,M,$ $ \tilde{I}{)}_{\text{ISE-SI}}, \leqslant ) $ 构成一个格。其中,上确界“$ \vee $ ”和下确界“$ \wedge $ ”分别定义为(对任意的$([{X_l},{X_u}],A), ([{Y_l},{Y_u}],$ $ B) \in {(G,M,\widetilde I)_{{\text{ISE-SI}}}} $ )$$ ([{X_l},{X_u}],A) \vee ([{Y_l},{Y_u}],B) = ({(A \cup B)^ \triangleleft },A \cup B) $$ (3) $$ ([{X_l},{X_u}],A) \wedge ([{Y_l},{Y_u}],B) = ({(A \cap B)^ \triangleleft },A \cap B) $$ (4) 证明 由于
$(G,M,\widetilde I)$ 的有限性,所以依据格论[1]可知,仅需证明定理3中式(3)、(4)的一个成立。下面,以式(3)为例进行相关证明。1) 证明
$({(A \cup B)^ \triangleleft },A \cup B) \in {(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 。由定义7可知,
$({(A \cup B)^ \triangleleft },A \cup B)$ 是一个ISE-SI模糊半概念。2) 证明
$({(A \cup B)^ \triangleleft },A \cup B)$ 是$([{X_l},{X_u}],A)$ 和$([{Y_l},{Y_u}], B)$ 的上界。由
$A \subseteq A \cup B$ 且$[{X_l},{X_u}] = {A^ \triangleleft }\widetilde \supseteq {(A \cup B)^ \triangleleft }$ ,根据定义8有$ ([{X}_{l},{X}_{u}],A) \leqslant ({(A\cup B)}^{⊲},A\cup B) $ 。同理也有$ ([{Y}_{l},{Y}_{u}],B) \leqslant ({(A\cup B)}^{⊲},A\cup B) $ 。因此,$({(A \cup B)^ \triangleleft },A \cup $ $B)$ 是$([{X_l},{X_u}],A)$ 和$([{Y_l},{Y_u}],B)$ 的上界。3) 证明
$({(A \cup B)^ \triangleleft },A \cup B)$ 是$([{X_l},{X_u}],A)$ 和$([{Y_l},{Y_u}], B)$ 的上确界。设
$ ([{Z_l},{Z_u}],C) $ 是$([{X_l},{X_u}],A)$ 和$([{Y_l},{Y_u}],B)$ 的一个上界。根据定义8有$A \subseteq C$ 且$B \subseteq C$ ,$[{X_l},{X_u}]\widetilde \supseteq [{Z_l},{Z_u}]$ 且$[{Y_l},{Y_u}]\widetilde \supseteq [{Z_l},{Z_u}]$ ,有$A \cup B \subseteq C$ 和$[{X_l},{X_u}]\widetilde \cap [{Y_l},{Y_u}] = {A^ \triangleleft }\widetilde \cap {B^ \triangleleft } = {(A \cup B)^ \triangleleft }\widetilde \supseteq [{Z_l},{Z_u}] =$ ${C^ \triangleleft }$ 。因此,$ ({(A \cup B)^ \triangleleft },A \cup B) $ 是$([{X_l},{X_u}], A)$ 和$ ([{Y_l}, $ $ {Y_u}],B) $ 的上确界。综上所述,
$ ({(G,M,\tilde{I})}_{\text{ISE-SI}}, \leqslant ) $ 构成一个格,称之为ISE-SI模糊半概念格,从而也构成完备格。2.3 ISE-SI模糊半概念的构造算法
设
$(G,M,\widetilde I)$ 为一个模糊形式背景,下面给出寻找全体ISE-SI模糊半概念${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 的算法。算法1 构造
${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 输入 一个模糊形式背景
$(G,M,\widetilde I)$ ,2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ;输出 所有ISE-SI模糊半概念
${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 。1) Set
${(G,M,\widetilde I)_{{\text{ISE-SI}}}} = \varnothing$ ;2) for each
$A \in {{P}}(M)$ do3)
${X_l} = {A^{\underline * }}$ 且${X_u} = {A^{\overline * }}$ ;4)
${(G,M,\widetilde I)_{{\text{ISE-SI}}}} = {(G,M,\widetilde I)_{{\text{ISE-SI}}}} \cup ([{X_l},$ $ {X_u}],A) $ ;5) end for
6) Return
${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 。定理3保证了算法1的正确性。
算法1的复杂度分析:
1) 算法的步骤1)中,将集合
${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 设为空集,这个过程的时间复杂度为$ O(1) $ 。2) 对
${{P}}(M)$ 中的每一个集合$A$ 进行算法步骤2)~5)的操作:利用定义5中的算子${\underline * }$ 和${\overline * }$ ,将${A^{\underline * }}$ 的值赋给集合${X_l}$ ,${A^{\overline * }}$ 的值赋给集合${X_u}$ *,把得到的ISE-SI模糊半概念$([{X_l},{X_u}],A)$ 放到集合${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 中,这个过程的时间复杂度为$ O({2^{|M|}}) $ 。其中,$ |M| $ 为模糊形式背景$(G,M,\widetilde I)$ 中属性集$ M $ 中包含属性的个数。3) 当每一个
$A$ 进行完复杂度分析2)中的操作后,所得集合${(G,M,\widetilde I)_{{\text{ISE-SI}}}}$ 便包含了模糊形式背景$K$ 下外延为$[{X_l},{X_u}]$ 内涵为$A$ 的所有ISE-SI模糊半概念,这个过程的时间复杂度为$ O(1) $ 。通过上面的分析可知,算法1的时间复杂度为
$ O(1 + {2^{|M|}} + 1) = O({2^{|M|}}) $ 。下面,通过一个实验案例对算法1来具体说明。
例3(续例1) 在例1所示的模糊形式背景
$({G_1},$ ${M_1},\widetilde {{I_1}})$ 中,阈值$\alpha = 0.40$ ,$\beta = 0.70$ 。下面,将具体实验过程和结果进行展现。首先,按照算法1的步骤1),可以得到初始值
${({G_1},{M_1},\widetilde {{I_1}})_{{\text{ISE-SI}}}} = \varnothing$ 。其次,按照算法1中步骤2)~5)的循环语句,例如可得到
$A = {a_2}{a_3} \in {{P}}({M_1})$ 、${X_l} = {A^{\underline * }} = {x_3}{x_5}$ 、$ {X_u} = $ ${A^{\overline * }} = {x_3}{x_5}$ ,则有$ ([{x_3}{x_5},{x_3}{x_5}],{a_2}{a_3}) \in {({G_1},{M_1},\widetilde {{I_1}})_{{\text{ISE-SI}}}} $ 。再有,对于
${{P}}({M_1})$ 中的其余取值情况,可依照上面的其次部分的循环过程进行实现。最后,按照算法1的步骤6),返回
$ ({G_1},{M_1}, $ $ \widetilde {{I_1}}{)_{{\text{ISE-SI}}}} $ 的值。表 4 相关实验结果Table 4 Related experimental results$A$ ${A^{\underline * }}$ ${A^{ * }}$ $[{A^{\underline * }},{A^{ * }}]$ $\varnothing $ ${G_1}$ ${G_1}$ $[{G_1},{G_1}]$ ${a_1}$ ${x_1}{x_4}$ ${x_1}{x_2}{x_4}$ $[{x_1}{x_4},{x_1}{x_2}{x_4}]$ ${a_2}$ ${x_2}{x_3}{x_5}$ ${x_1}{x_2}{x_3}{x_5}$ $[{x_2}{x_3}{x_5},{x_1}{x_2}{x_3}{x_5}]$ ${a_3}$ ${x_3}{x_5}$ ${x_3}{x_4}{x_5}$ $[{x_3}{x_5},{x_3}{x_4}{x_5}]$ ${a_1}{a_2}$ $\varnothing $ ${x_1}{x_2}$ $[\varnothing ,{x_1}{x_2}]$ ${a_1}{a_3}$ $\varnothing $ ${x_4}$ $[\varnothing ,{x_4}]$ ${a_2}{a_3}$ ${x_3}{x_5}$ ${x_3}{x_5}$ $[{x_3}{x_5},{x_3}{x_5}]$ ${M_1}$ $\varnothing $ $\varnothing $ $[\varnothing ,\varnothing ]$ 因
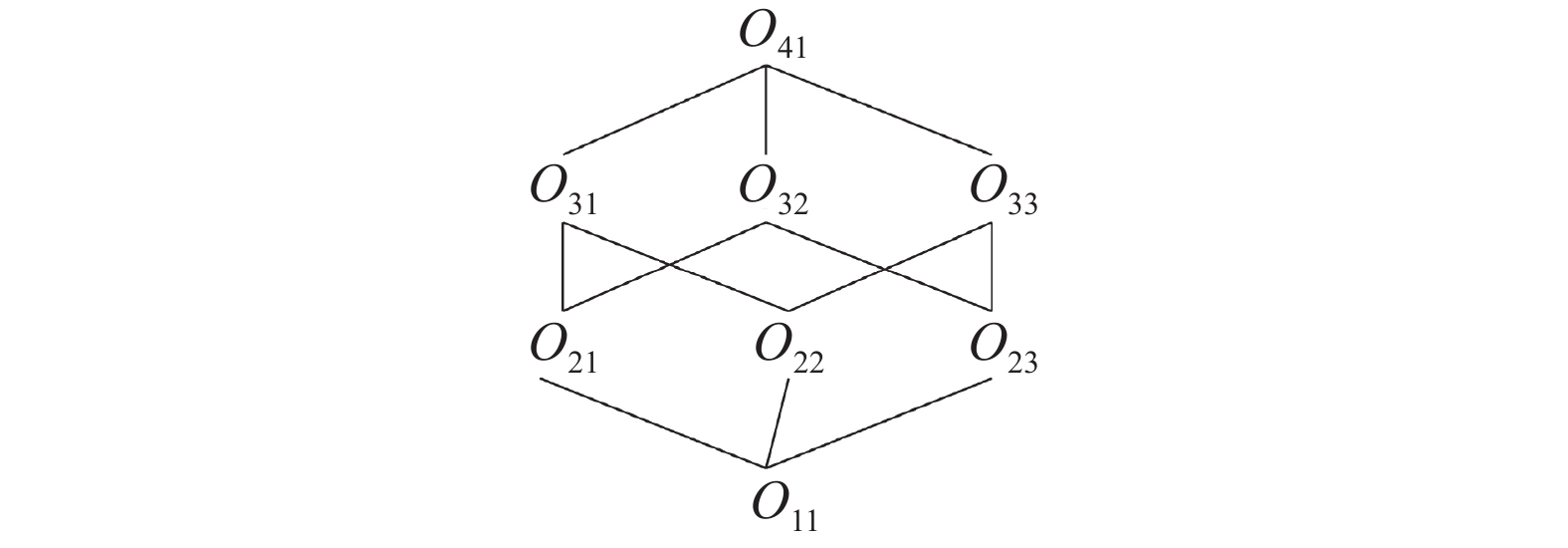
$ |{M_1}| = 3 $ ,构造例1中的所有ISE-SI模糊半概念的算法时间复杂度为$O({2^3})$ 。为了方便表示,在表5中把所有ISE-SI模糊半概念都给出了各自对应的标号。根据定理3,图1所示为
$({G_1},{M_1},\widetilde {{I_1}})$ 下的ISE-SI模糊半概念格。表 5 ISE-SI模糊半概念Table 5 ISE-SI fuzzy semiconcepts标号 ISE-SI模糊半概念 标号 ISE-SI模糊半概念 ${O_{11}}$ $ ([{G_1},{G_1}],\varnothing ) $ ${O_{31}}$ $([\varnothing ,{x_1}{x_2}],{a_1}{a_2})$ ${O_{21}}$ $ ([{x_1}{x_4},{x_1}{x_2}{x_4}],{a_1}) $ ${O_{32}}$ $([\varnothing ,{x_4}],{a_1}{a_3})$ ${O_{22}}$ $ ([{x_2}{x_3}{x_5},{x_1}{x_2}{x_3}{x_5}],{a_2}) $ ${O_{33}}$ $([{x_3}{x_5},{x_3}{x_5}],{a_2}{a_3})$ ${O_{23}}$ $([{x_3}{x_5},{x_3}{x_4}{x_5}],{a_3})$ ${O_{41}}$ $([\varnothing ,\varnothing ],{M_1})$ 3. SE-ISI型单边区间集模糊半概念
为了简便起见,将本文所讨论的SE-ISI型单边区间集模糊半概念简称为SE-ISI模糊半概念。
ISE-SI模糊半概念的外延为区间集形式,内涵为集合形式。因此,依据第2节中ISE-SI模糊半概念的相关定义和结论,可以对偶地给出SE-ISI模糊半概念的相关定义和结论。
定义9 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,定义一对算子$^{\underline * }:{{P}}(G) \to {{P}}(M)$ 和$^{\overline * }:{{P}}(G) \to {{P}}(M)$ (对$\forall X \in {{P}}(G)$ )。$$ {X^{\underline * }} = \{ a \in M|\forall x \in X,\widetilde I(x,a) \geqslant \beta \} $$ (5) $$ {X^{\overline * }} = \{ a \in M|\forall x \in X,\widetilde I(x,a) \geqslant \alpha \} $$ (6) 可以看到,
${X^{\underline * }}$ 中的属性$a$ 对应$X$ 中所有对象的隶属度都不小于$\beta $ ,这可以认为属性$a$ 一定被$X$ 中所有对象所拥有;而${X^{\overline * }}$ 中的属性$a$ 对应$X$ 中所有对象的隶属度都不小于$\alpha $ ,这可以认为属性$a$ 可能被$X$ 中所有对象所拥有。定义10 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,定义SE-ISI模糊半概念算子$^ \triangleright :{{P}}(G) \to {{{P_I}}}(M)$ (对$\forall X \in {{P}}(G)$ )。$$ {X^ \triangleright } = [{X^{\underline * }},{X^{\overline * }}] $$ 通过比较定义9中的式(5)、(6),
${X^{\underline * }} \subseteq {X^{\overline * }}$ 成立。故,${X^{\underline * }}$ 和${X^{\overline * }}$ 可构成属于${{P_I}}(M)$ 的区间集$[{X^{\underline * }},{X^{\overline * }}]$ 。定理4 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ 。对$ \forall X,Y \in $ ${{P}}(G)$ ,有下列结论成立:4)
$X \subseteq Y \Rightarrow {X^{\underline * }} \supseteq {Y^{\underline * }},{X^{\overline * }} \supseteq {Y^{\overline * }},{X^ \triangleleft }\widetilde \supseteq {Y^ \triangleleft }$ 。5)
${(X \cup Y)^{\underline * }} = {X^{\underline * }} \cap {Y^{\underline * }}$ ,$ {(X \cup Y)^{\overline * }} = {X^{\overline * }} \cap {Y^{\overline * }} $ ,${(X \cup Y)^ \triangleleft } = {X^ \triangleleft }\widetilde \cap {Y^ \triangleleft }$ 。6)
${(X \cap Y)^{\underline * }} \supseteq {X^{\underline * }} \cup {Y^{\underline * }}$ ,${(X \cap Y)^{\overline * }} \supseteq {X^{\overline * }} \cup {Y^{\overline * }}$ ,${(X \cap Y)^ \triangleleft } \supseteq {X^ \triangleleft }\widetilde \cup {Y^ \triangleleft }$ 。除了上面定理提到的结论外,还可以结合定义5和6中的算子给出下面的结论。
定理5 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,对$\forall A,B \in $ ${{P}}(M)$ 与$\forall X,Y \in {{P}}(G)$ ,有下列结论成立:7)
$A \subseteq {({A^{\underline * }})^{\underline * }}$ ,$A \subseteq {({A^{\overline * }})^{\overline * }}$ ,$X \subseteq {({X^{\underline * }})^{\underline * }}$ ,$X \subseteq {({X^{\underline * }})^{\underline * }}$ 。8)
${A^{\underline * }} = {({({A^{\underline * }})^{\underline * }})^{\underline * }}$ ,${A^{\overline * }} = {({({A^{\overline * }})^{\overline * }})^{\overline * }}$ ,${X^{\underline * }} = {({({X^{\underline * }})^{\underline * }})^{\underline * }}$ ,${X^{\overline * }} = {({({X^{\overline * }})^{\overline * }})^{\overline * }}$ 。9)
$A \subseteq {X^{\underline * }} \Leftrightarrow X \subseteq {A^{\underline * }}$ ,$A \subseteq {X^{\overline * }} \Leftrightarrow X \subseteq {A^{\overline * }}$ 。证明 结论7)的证明如下:
如果
$a \in A$ ,那么对于所有的$x \in {A^{\underline * }}$ 都成立$\widetilde I(x,a) \geqslant \alpha $ ,从而有$a \in {({A^{\underline * }})^{\underline * }}$ 。因此,$A \subseteq {({A^{\underline * }})^{\underline * }}$ 。同理可证明$A \subseteq {({A^{\overline * }})^{\overline * }}$ 、$X \subseteq {({X^{\underline * }})^{\underline * }}$ 、$X \subseteq {({X^{\underline * }})^{\underline * }}$ 。结论8)的证明如下:
由结论7)可知,
${A^{\underline * }} \subseteq {({({A^{\underline * }})^{\underline * }})^{\underline * }}$ ,其次由1)可知,${A^{\underline * }} \supseteq {({({A^{\underline * }})^{\underline * }})^{\underline * }}$ 。因此,${A^{\underline * }} = {({({A^{\underline * }})^{\underline * }})^{\underline * }}$ 。同理可证明${A^{\overline * }} = {({({A^{\overline * }})^{\overline * }})^{\overline * }}$ 、${X^{\underline * }} = {({({X^{\underline * }})^{\underline * }})^{\underline * }}$ 、${X^{\overline * }} = {({({X^{\overline * }})^{\overline * }})^{\overline * }}$ 。结论9)的证明如下:
$( \Rightarrow )$ :因为$A \subseteq {X^{\underline * }}$ ,由结论1)可知,${A^{\underline * }} \supseteq {({X^{\underline * }})^{\underline * }}$ ;又由结论7)可知,${({X^{\underline * }})^{\underline * }} \supseteq X$ 。因此,$X \subseteq {A^{\underline * }}$ 。$( \Leftarrow )$ 同理可证。同理可证明$A \subseteq {X^{\overline * }} \Leftrightarrow X \subseteq {A^{\overline * }}$ 。定义11 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,对$\forall X \in {{P}}(G)$ ,$\forall [{A_l},{A_u}] \in {{{P_I}}}(M)$ ,称序对$(X,[{A_l},{A_u}])$ 为一个SE-ISI模糊半概念当且仅当${X^ \triangleright } = [{X^{\underline * }},{X^{\overline * }}] = [{A_l},{A_u}]$ 。称
$X$ 和$[{A_l},{A_u}]$ 分别为SE-ISI模糊半概念$ (X, $ $ [{A_l},{A_u}]) $ 的外延和内涵。定义12 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,设$(G,M,$ $\widetilde I{)_{{\text{SE-ISI}}}}$ 为此背景下所有SE-ISI模糊半概念的集合。定义二元关系“$ \leqslant $ ”如下(对$ \forall (X,[{A_l},{A_u}]),(Y,[{B_l}, $ $ {B_u}]) \in {(G,M,\widetilde I)_{{\text{SE-ISI}}}} $ ):$$(X,[{A}_{l},{A}_{u}]) \leqslant (Y,[{B}_{l},{B}_{u}])\iff X\subseteq Y且[{B}_{l},{B}_{u}]\tilde{\supseteq }[{A}_{l},{A}_{u}] $$ 当
$ (X,[{A}_{l},{A}_{u}]) \leqslant (Y,[{B}_{l},{B}_{u}]) $ 时,称$ (X,[{A_l},{A_u}]) $ 为$ (Y,[{B_l},{B_u}]) $ 的子半概念,称$ (Y,[{B_l},{B_u}]) $ 为$ (X,[{A_l}, $ $ {A_u}]) $ 的母半概念。定理6 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,则$ ({(G,M,\tilde{I})}_{\text{SE-ISI}}, \leqslant ) $ 构成一个偏序集。其中“$ \leqslant $ ”由定义12所给出。定理7 在一个模糊形式背景
$(G,M,\widetilde I)$ 中,给定2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ,偏序集$((G,M,$ $ \tilde{I}{)}_{\text{SE-ISI}}, \leqslant ) $ 构成一个格,称之为SE-ISI模糊半概念格。其中,上确界“$ \vee $ ”和下确界“$ \wedge $ ”分别定义为(对$\forall (X,[{A_l},{A_u}]),(Y,[{B_l},{B_u}]) \in {(G,M,\widetilde I)_{{\text{SE-ISI}}}}$ )$$ (X,[{A_l},{A_u}]) \vee (Y,[{B_l},{B_u}]) = (X \cup Y,{(X \cup Y)^ \triangleright }) $$ $$ (X,[{A_l},{A_u}]) \wedge (Y,[{B_l},{B_u}]) = (X \cap Y,{(X \cap Y)^ \triangleright }) $$ 算法2 构造
${(G,M,\widetilde I)_{{\text{SE-ISI}}}}$ 输入 一个模糊形式背景
$(G,M,\widetilde I)$ ,2个阈值$\alpha $ 和$\beta $ 且满足$0 \leqslant \alpha < \beta \leqslant 1$ ;输出 所有SE-ISI模糊半概念
${(G,M,\widetilde I)_{{\text{SE-ISI}}}}$ 。1) Set
${(G,M,\widetilde I)_{{\text{SE-ISI}}}} = \varnothing $ ;2) for each
$X \in {{P}}(G)$ do3)
${A_l} = {X^{\underline * }}$ 且${A_u} = {X^{\overline * }}$ ;4)
${(G,M,\widetilde I)_{{\text{SE-ISI}}}} = {(G,M,\widetilde I)_{{\text{SE-ISI}}}} \cup (X,[{A_l},$ ${A_u}])$ ;5) end for
6) Return
${(G,M,\widetilde I)_{{\text{SE-ISI}}}}$ 。定理7保证了算法2的正确性。
与算法1的时间复杂度分析类似,算法2的时间复杂度为
$ O({2^{|G|}}) $ 。下面,通过一个实验案例对SE-ISI模糊半概念的相关定义和结论进行解释与验证。
例4(续例1) 在例1所示的模糊形式背景
$ ({G_1}, $ $ {M_1},\widetilde {{I_1}}) $ 中,阈值$\alpha = 0.70$ ,$\beta = 0.40$ 。根据定义11可知,$({x_1},[{a_1},{a_1}{a_2}])$ 是一个SE-ISI模糊半概念。这表示对于陈某来说,可以认为他(她)一定能胜任的是东北林区,可能能胜任的有东北林区和西南林区。下面,用算法2对具体案例进行实现:
首先,按照算法2的步骤1),可以得到初始值
$ {({G_1},{M_1},\widetilde {{I_1}})_{{\text{SE-ISI}}}} = \varnothing $ 。其次,按照算法2中步骤2)~5)的循环语句,例如可得到
$X = {x_4} \in {\text{P}}({G_1})$ 、${A_l} = {X^{\underline * }} = {a_1}$ 、$ {A_u} = {X^{\overline * }} = $ $ {a_1}{a_3} $ ,则有$ ({x_4},[{a_1},{a_1}{a_3}]) \in {({G_1},{M_1},\widetilde {{I_1}})_{{\text{SE-ISI}}}} $ 。再有,对于
${{P}}({G_1})$ 中的其余取值情况可依照上面的其次部分的循环过程进行实现。最后,按照算法2的步骤6),返回
$ ({G_1},{M_1}, $ $ \widetilde {{I_1}}{)_{{\text{SE-ISI}}}} $ 的值。因此,利用算法2可得到全体SE-ISI模糊半概念,其时间复杂度为
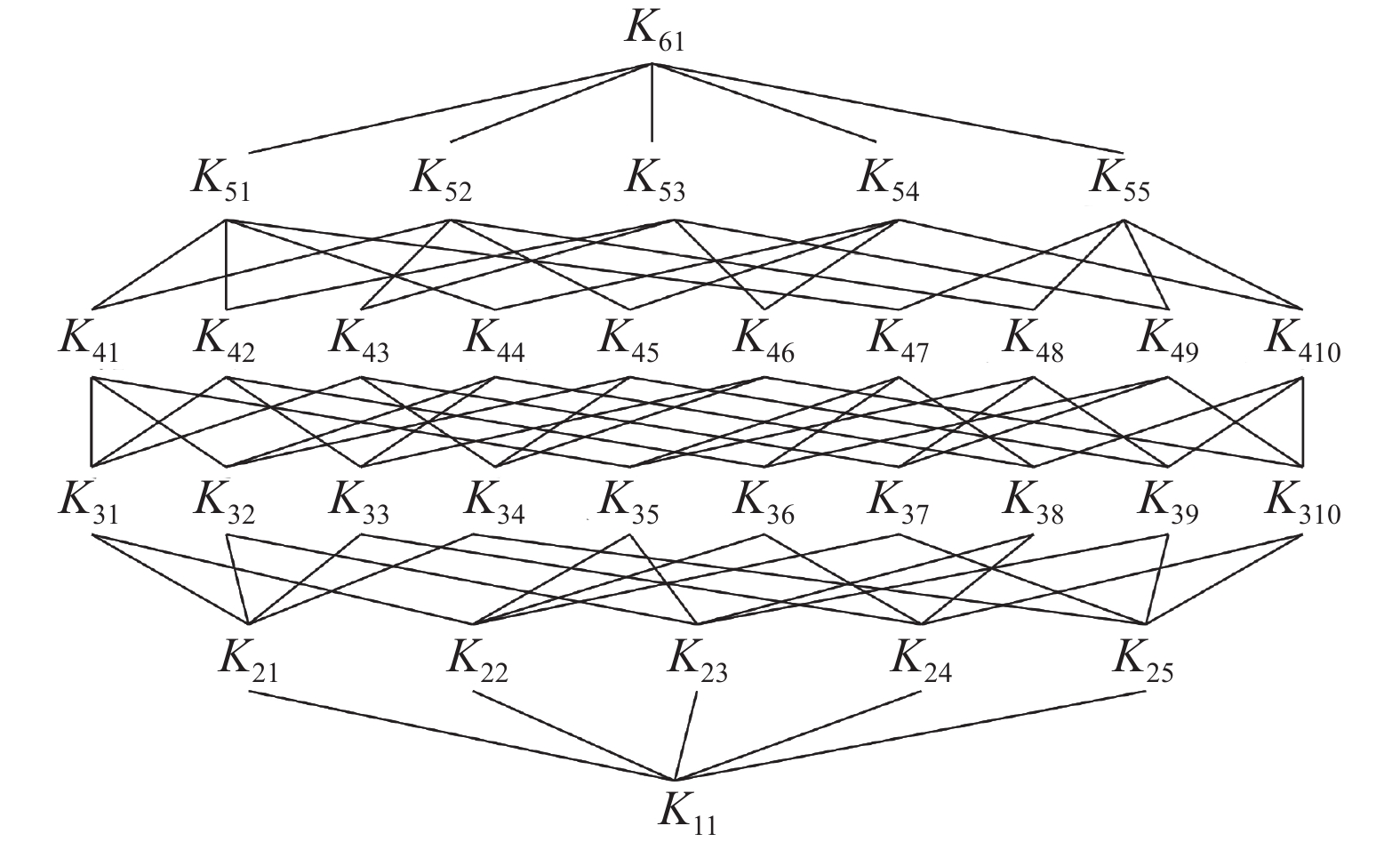
$ O({2^5}) $ 。所得相应实验结果见表6。表 6 SE-ISI模糊半概念Table 6 SE- ISI fuzzy semiconcepts标号 SE-ISI模糊半概念 标号 SE-ISI模糊半概念 ${K_{11}}$ $ (\varnothing ,[{M_1},{M_1}]) $ ${K_{41}}$ $ ({x_1}{x_2}{x_3},[\varnothing ,{a_2}]) $ ${K_{21}}$ $ ({x_1},[{a_1},{a_1}{a_2}]) $ ${K_{42}}$ $ ({x_1}{x_2}{x_4},[\varnothing ,{a_1}]) $ ${K_{22}}$ $ ({x_2},[{a_2},{a_1}{a_2}]) $ ${K_{43}}$ $ ({x_1}{x_2}{x_5},[\varnothing ,{a_2}]) $ ${K_{23}}$ $ ({x_3},[{a_2}{a_3},{a_2}{a_3}]) $ $ {K_{44}} $ $ ({x_1}{x_3}{x_4},[\varnothing ,\varnothing ]) $ ${K_{24}}$ $ ({x_4},[{a_1},{a_1}{a_3}]) $ $ {K_{45}} $ $ ({x_1}{x_3}{x_5},[\varnothing ,{a_2}]) $ ${K_{25}}$ $ ({x_5},[{a_2}{a_3},{a_2}{a_3}]) $ $ {K_{46}} $ $ ({x_1}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{31}}$ $ ({x_1}{x_2},[\varnothing ,{a_1}{a_2}]) $ $ {K_{47}} $ $ ({x_2}{x_3}{x_4},[\varnothing ,\varnothing ]) $ ${K_{32}}$ $ ({x_1}{x_3},[\varnothing ,{a_2}]) $ $ {K_{48}} $ $ ({x_2}{x_3}{x_5},[{a_2},{a_2}]) $ ${K_{33}}$ $ ({x_1}{x_4},[{a_1},{a_1}]) $ $ {K_{49}} $ $ ({x_2}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{34}}$ $ ({x_1}{x_5},[\varnothing ,{a_2}]) $ $ {K_{410}} $ $ ({x_3}{x_4}{x_5},[\varnothing ,{a_3}]) $ ${K_{35}}$ $ ({x_2}{x_3},[{a_2},{a_2}]) $ ${K_{51}}$ $ ({x_1}{x_2}{x_3}{x_4},[\varnothing ,\varnothing ]) $ ${K_{36}}$ $ ({x_2}{x_4},[\varnothing ,{a_1}]) $ ${K_{52}}$ $ ({x_1}{x_2}{x_3}{x_5},[\varnothing ,{a_2}]) $ ${K_{37}}$ $ ({x_2}{x_5},[{a_2},{a_2}]) $ ${K_{53}}$ $ ({x_1}{x_2}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{38}}$ $ ({x_3}{x_4},[\varnothing ,{a_3}]) $ ${K_{54}}$ $ ({x_1}{x_3}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{39}}$ $ ({x_3}{x_5},[{a_2}{a_3},{a_2}{a_3}]) $ ${K_{55}}$ $ ({x_2}{x_3}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{310}}$ $ ({x_4}{x_5},[\varnothing ,{a_3}]) $ ${K_{61}}$ $ ({G_1},[\varnothing ,\varnothing ]) $ 根据定理7,可得
$({G_1},{M_1},\widetilde {{I_1}})$ 下的SE-ISI模糊半概念格,如图2所示。下面将半概念[27-28]、模糊概念[15]和所讨论的ISE-SI模糊半概念、SE-ISI模糊半概念进行多方面的对比分析。
通过已有结论与本文所得结论,得到四方的定性对比如表7所示。从表7可以看出:
表 7 定性对比表Table 7 Qualitative comparative table名称 提取知识的表达形式 阈值数量 适用背景 提取知识的规则 提取知识的平台 半概念[27-28] $(X,A)$ 0 经典形式背景 $ X = {A^ * } $或$ {\text{ }}A = {X^ * } $ 格 模糊概念[15] $(X,A)$ 1 模糊形式背景 ${X^{{ * _\varepsilon }}} = A$且${A^{{ * _\varepsilon }}} = X$ 格 ISE-SI模糊半概念 $ ([{X_l},{X_u}],A) $ 2 模糊形式背景 ${A^ \triangleleft } = [{A^{\underline * }},{A^{\overline * }}] = [{X_l},{X_u}]$ 格 SE-ISI模糊半概念 $ (X,[{A_l},{A_u}]) $ 2 模糊形式背景 ${X^ \triangleright } = [{X^{\underline * }},{X^{\overline * }}] = [{A_l},{A_u}]$ 格 1) ISE-SI(SE-ISI)模糊半概念和模糊概念虽都是模糊形式背景下的二维数据,但模糊概念只由一个阈值所确定,ISE-SI(SE-ISI)模糊半概念则由2个阈值共同确定,事实上,这也是ISE-SI(SE-ISI)模糊半概念的外延(内涵)以区间集表示的原因。
2) ISE-SI(SE-ISI)模糊半概念、模糊概念和半概念均可借助各自对应的偏序关系构成格。不难发现,当ISE-SI(SE-ISI)模糊半概念中的2个阈值
$\alpha $ 和$\beta $ 相等时,得到的所有知识中就包含模糊概念所能提取到的所有知识;而当2个阈值$\alpha $ 和$\beta $ 相等且固定为$[0,1]$ 的某个数时,就能将模糊形式背景转化为经典形式背景,进而得到相应的半概念。可以看出本文所提出的思想在定性分析方面具备的优势有:
1) ISE-SI模糊半概念可挖掘出属性集中的所有属性被哪些对象可能共同拥有这类知识,SE-ISI模糊半概念可挖掘出对象集中的所有对象可能共同拥有哪些属性这类知识,而模糊概念无法办到。
2) 在实际问题的解决中,ISE-SI(SE-ISI)模糊半概念可以解决“单向”问题,而模糊概念只能解决“双向”问题。虽然ISE-SI(SE-ISI)模糊半概念结合了经典半概念,但ISE-SI(SE-ISI)模糊半概念可在模糊形式背景中进行相应知识提取。
此外,虽然文献[15, 27-28]中没有给出搜寻全体
$ \cup $ –半概念、$ \cap $ –半概念和模糊概念的方法,但可根据各自的定义和理论性质得到如下构造过程:1) 根据文献[27-28]中
$ \cup $ –半概念的定义:首先将集合
${(G,M,I)_ \cup }$ 设为空集,这个过程的时间复杂度为$ O(1) $ 。接着对
${{P}}(M)$ 中每一个集合$A$ ,利用算子*,得到对应$X$ 的值${A^ * }$ ,并把得到的所有$(X,A)$ 放到集合${(G,M,I)_ \cup }$ 中,这个过程的时间复杂度为$O({2^{|M|}})$ 。最后输出
${(G,M,I)_ \cup }$ 的值,这个过程的时间复杂度为$ O(1) $ 。因此,
$ \cup $ –半概念构造过程的时间复杂度为$O(1 + {2^{|M|}} + 1) = O({2^{|M|}})$ 。2) 根据文献[27-28]中
$ \cap $ –半概念的定义:首先将集合
${(G,M,I)_ \cap }$ 设为空集,这个过程的时间复杂度为$ O(1) $ 。接着对
${{P}}(G)$ 中每一个集合$X$ ,利用算子*,得到对应$A$ 的值${X^ * }$ ,并把得到的所有$(X,A)$ 放到集合${(G,M,I)_ \cap }$ 中,这个过程的时间复杂度为$O({2^{|G|}})$ 。最后输出
${(G,M,I)_ \cap }$ 的值,这个过程的时间复杂度为$ O(1) $ 。因此,
$ \cap $ –半概念构造过程的时间复杂度为$O(1 + {2^{|G|}} + 1) = O({2^{|G|}})$ 。3) 根据文献[15]中模糊概念的定义:
首先将集合
${(G,M,\widetilde I)_{{\text{FC1}}}}$ 和$ {(G,M,\widetilde I)_{{\text{FC}}}} $ 都设为空集,这个过程的时间复杂度为$ O(2) $ 。接着对
${{P}}(M)$ 中每一个集合$A$ ,利用算$子^{{ * _\varepsilon }} $ ,得到对应$X$ 的值$ {A^{{ * _\varepsilon }}} $ ,并把得到的所有$(X,A)$ 都放到集合${(G,M,\widetilde I)_{{\text{FC}}}}_{\text{1}}$ 中。然后对${(G,M,\widetilde I)_{{\text{FC}}}}_{\text{1}}$ 中每一个序对$(X,A)$ 进行条件判断:若$(X,A)$ 满足$A = $ ${X^{{ * _\varepsilon }}}$ ,则把$(X,A)$ 放到集合${(G,M,\widetilde I)_{{\text{FC}}}}$ 中;否则不进行任何操作。这个过程的时间复杂度为$O({2^{2|M|}})$ 。最后输出
${(G,M,\widetilde I)_{{\text{FC}}}}$ 的值,这个过程的时间复杂度为$ O(1) $ 。因此,模糊概念构造过程的时间复杂度为
$O(2 + {2^{2|M|}} + 1) = O({2^{2|M|}})$ 。同理,从
$P(G)$ 中每一个对象子集$X$ 出发,也可以经过类似步骤得到全体模糊概念。也就是说,相应的时间复杂度为$O(2 + {2^{2|G|}} + 1) = O({2^{2|G|}})$ 。综上所述,模糊概念构造过程的时间复杂度为
$\min \{ O({2^{2|M|}}),O({2^{2|G|}})\} $ 。对于上述3个构造过程1)~3),其相应实验案例背景见例1中的表2和表3,可得到它们分别对应的结果如下:
1) 通过表3所示的经典形式背景
$({G_1},{M_1},$ ${I_1})$ ,可得到全体$ \cup $ –半概念,有如下8个,即$$ \begin{gathered} {({G_1},{M_1},{I_1})_ \cup } = \{ ({G_1},\varnothing ),({x_1}{x_4},{a_1}),({x_2}{x_3}{x_5},{a_2}),({x_3}{x_5}, {a_3}),\\ (\varnothing ,{a_1}{a_2}),(\varnothing ,{a_1}{a_3}),({x_3}{x_5},{a_2}{a_3}),(\varnothing ,{M_1})\} \end{gathered}$$ 2) 通过表3所示的经典形式背景
$({G_1},{M_1},$ ${I_1})$ ,可得到全体$ \cap $ –半概念,有如下32个,即$$ \begin{gathered} {({G_1},{M_1},{I_1})_ \cap } = \{ (\varnothing ,{M_1}),({x_1},{a_1}),({x_2},{a_2}),({x_3},{a_2}{a_3}),({x_4}, {a_1}),\\ ({x_5},{a_2}{a_3}),({x_1}{x_2},\varnothing )({x_1}{x_3},\varnothing ),({x_1}{x_4},{a_1}),({x_1}{x_5},\varnothing ),({x_2} {x_3},{a_2}),\\ ({x_2}{x_4},\varnothing ),({x_2}{x_5},{a_2}), ({x_3}{x_4},\varnothing ),({x_3}{x_5},{a_2}{a_3}),({x_4}{x_5}, \varnothing ),\\ ({x_1}{x_2}{x_3},\varnothing ),({x_1}{x_2}{x_4},\varnothing ),({x_1}{x_2}{x_5},\varnothing ),({x_1}{x_3}{x_4},\varnothing ), ({x_1}{x_3} {x_5},\varnothing ),\\ ({x_1}{x_4}{x_5},\varnothing ),({x_2}{x_3}{x_4},\varnothing ),({x_2}{x_3}{x_5},{a_2}),({x_2}{x_4}{x_5},\varnothing ), ({x_3}{x_4}{x_5},\varnothing ),\\ ({x_1}{x_2}{x_3}{x_4},\varnothing ),({x_1}{x_2}{x_3}{x_5},\varnothing ),({x_1}{x_2}{x_4}{x_5},\varnothing ), ({x_1}{x_3}{x_4}{x_5},\varnothing ),\\ ({x_2}{x_3}{x_4}{x_5},\varnothing ),({G_1},\varnothing )\} \end{gathered}$$ 3) 通过表2所示的模糊形式背景
$({G_1},{M_1},$ $\widetilde {{I_1}})$ ,阈值取为$\beta $ ,可得到全体模糊概念,有如下5个,即$$ \begin{gathered} {({G_1},{M_1},\widetilde {{I_1}})_{{\text{FC}}}} = \{ (\varnothing ,{M_1}),({x_1}{x_4},{a_1}),({x_2}{x_3}{x_5}, {a_2}),\\ ({x_3}{x_5},{a_2}{a_3}),({G_1},\varnothing )\} \end{gathered} $$ 这些具体的结果也说明上面得到的3个结论是正确且可行的。
通过上面的分析并结合表5和表6,可得
$ \cup $ –半概念、$ \cap $ –半概念[27-28]、模糊概念[15]和ISE-SI模糊半概念、SE-ISI模糊半概念的定量对比,如表8所示。从表8可以看出:
1) 在时间复杂度和知识提取量上,构造
$ \cup $ –半概念与构造ISE-SI模糊半概念相等;构造$ \cap $ –半概念与构造SE-ISI模糊半概念相等。2) 模糊概念的知识提取量只占ISE-SI模糊半概念提取知识量的
$\dfrac{5}{8} \times 100\% = 62.5\% $ ,只占SE-ISI模糊半概念提取知识量的$\dfrac{5}{{32}} \times 100\% \approx 15.6\% $ 。可以看出本文所提出的思想在定量分析方面具备的优势有:
1) 当阈值
$\alpha = \beta $ 时,$ \cup $ –半概念($ \cap $ –半概念)一定是ISE-SI(SE-ISI)模糊半概念,反之也成立。例如,当$\alpha = \beta = 0.7$ 时,$ ({x_2}{x_3}{x_5},{a_2}) $ 是$ \cup $ –半概念,同时也是ISE-SI模糊半概念;$ ({x_1}{x_4},{a_1}) $ 是$ \cap $ –半概念,同时也是SE-ISI模糊半概念。然而,当阈值$\alpha \ne \beta $ 时,虽然$ \cup $ –半概念($ \cap $ –半概念)与ISE-SI(SE-ISI)模糊半概念在知识提取量上一样,但因ISE-SI(SE-ISI)模糊半概念的外延(内涵)是区间集形式,从而ISE-SI(SE-ISI)模糊半概念蕴含着更多的信息量。2) 在同一模糊形式背景中,模糊概念的知识提取量比ISE-SI(SE-ISI)模糊半概念的要小,故利用ISE-SI(SE-ISI)模糊半概念会提取到更丰富的知识。
下面,将说明ISE-SI(SE-ISI)模糊半概念相较半概念和模糊概念具备的独特研究意义:
1) 在例1的实验案例中,已经知道ISE-SI模糊半概念可提取出一定和可能能胜任该林区任务的护林员,而
$ \cup $ –半概念则只能提取出一定能胜任该林区任务的护林员,提取的信息量较少。2) 与ISE-SI模糊半概念对偶,SE-ISI模糊半概念的外延为集合形式,则会有针对性地关注对象子集所对应的属性区间集。这种情况在实际生活中同样具有很大的应用空间。比如在例1的实验案例中,若想提取出护林员一定能胜任的林区和可能能胜任的林区这类信息,那利用SE-ISI模糊半概念就可以达到这样的目的,而
$ \cap $ –半概念则只能提取出一定能胜任该林区任务的人员,提取的信息量较少。3) ISE-SI(SE-ISI)模糊半概念都是利用区间能表示不确定信息的特征,对模糊形式背景中所蕴含的知识进行深层次的挖掘和提取,并重点解决实际生活中常见的“单向”问题。然而,由于对象和属性之间的相互共有,导致模糊概念只能解决“双向”问题。比如在例1的实验案例中,
$({x_3}{x_5}, {a_2}{a_3})$ 是一个模糊概念,这表示护林员张某和李某一定能胜任的林区有西南和东南林区,而一定能胜任西南和东南林区的护林员也正好是张某和李某。也就是说,模糊概念还不能只提取出对象(属性)具有的属性(对象),满足的条件较为苛刻,适用范围也较窄。在提取知识的过程中,ISE-SI(SE-ISI)模糊半概念都受制于2个阈值的取定,从而还可通过控制阈值的大小来挖掘出实际所需的知识。
4. 结束语
本文利用单边区间集概念的思想并结合经典半概念理论,提出模糊形式背景下2种形式的单边区间集半概念,体现了单边区间的思想,但依然存在一些问题和不足之处:
1) 在模糊形式背景下展开的研究对具有随机性的数据不太适用。
2) 单边区间集模糊半概念提取的知识范围还需要进一步拓展。
3) 搜寻全体单边区间集模糊半概念算法的时间复杂度较高。
因此,针对上面的不足之处,将在后续研究中考虑以下3个方面的工作:
1) 面对一些同时具有模糊不确定性和随机不确定性的数据,传统的模糊形式背景已经不足以用来表达它们。因此,可尝试将随机不确定性引入到模糊形式背景,进而在新背景中继续研究单边区间集半概念的构造和性质。
2) 模糊形式背景只表达了对象拥有属性的程度。同样地,每个对象不拥有每个属性的程度也要在数据处理过程中考虑。因此,可尝试将犹豫模糊集、毕达哥拉斯模糊集与单边区间集概念以及经典半概念理论结合,进而挖掘出适用范围更广的知识表示。
3) 将寻找一些时间复杂度更小的算法来搜寻全体单边区间集模糊半概念,使构造过程更快捷。
-
表 1 评价统计表
Table 1 Evaluation statistics
护林员 东北林区 西南林区 东南林区 陈某 0.76 0.58 0.24 刘某 0.45 0.70 0.16 张某 0.13 0.87 0.74 王某 0.92 0.22 0.45 李某 0.08 0.95 0.80 表 2 相应的数学表达
Table 2 Corresponding mathematical expression
${G_1}$ ${a_1}$ ${a_2}$ ${a_3}$ ${x_1}$ 0.76 0.58 0.24 ${x_2}$ 0.45 0.70 0.16 ${x_3}$ 0.13 0.87 0.74 ${x_4}$ 0.92 0.22 0.45 ${x_5}$ 0.08 0.95 0.80 表 3 1个经典形式背景
$({G_1},{M_1},{I_1})$ Table 3 A classical formal context
$({G_1},{M_1},{I_1})$ ${G_1}$ ${a_1}$ ${a_2}$ ${a_3}$ ${x_1}$ 1 0 0 ${x_2}$ 0 1 0 ${x_3}$ 0 1 1 ${x_4}$ 1 0 0 ${x_5}$ 0 1 1 表 4 相关实验结果
Table 4 Related experimental results
$A$ ${A^{\underline * }}$ ${A^{ * }}$ $[{A^{\underline * }},{A^{ * }}]$ $\varnothing $ ${G_1}$ ${G_1}$ $[{G_1},{G_1}]$ ${a_1}$ ${x_1}{x_4}$ ${x_1}{x_2}{x_4}$ $[{x_1}{x_4},{x_1}{x_2}{x_4}]$ ${a_2}$ ${x_2}{x_3}{x_5}$ ${x_1}{x_2}{x_3}{x_5}$ $[{x_2}{x_3}{x_5},{x_1}{x_2}{x_3}{x_5}]$ ${a_3}$ ${x_3}{x_5}$ ${x_3}{x_4}{x_5}$ $[{x_3}{x_5},{x_3}{x_4}{x_5}]$ ${a_1}{a_2}$ $\varnothing $ ${x_1}{x_2}$ $[\varnothing ,{x_1}{x_2}]$ ${a_1}{a_3}$ $\varnothing $ ${x_4}$ $[\varnothing ,{x_4}]$ ${a_2}{a_3}$ ${x_3}{x_5}$ ${x_3}{x_5}$ $[{x_3}{x_5},{x_3}{x_5}]$ ${M_1}$ $\varnothing $ $\varnothing $ $[\varnothing ,\varnothing ]$ 表 5 ISE-SI模糊半概念
Table 5 ISE-SI fuzzy semiconcepts
标号 ISE-SI模糊半概念 标号 ISE-SI模糊半概念 ${O_{11}}$ $ ([{G_1},{G_1}],\varnothing ) $ ${O_{31}}$ $([\varnothing ,{x_1}{x_2}],{a_1}{a_2})$ ${O_{21}}$ $ ([{x_1}{x_4},{x_1}{x_2}{x_4}],{a_1}) $ ${O_{32}}$ $([\varnothing ,{x_4}],{a_1}{a_3})$ ${O_{22}}$ $ ([{x_2}{x_3}{x_5},{x_1}{x_2}{x_3}{x_5}],{a_2}) $ ${O_{33}}$ $([{x_3}{x_5},{x_3}{x_5}],{a_2}{a_3})$ ${O_{23}}$ $([{x_3}{x_5},{x_3}{x_4}{x_5}],{a_3})$ ${O_{41}}$ $([\varnothing ,\varnothing ],{M_1})$ 表 6 SE-ISI模糊半概念
Table 6 SE- ISI fuzzy semiconcepts
标号 SE-ISI模糊半概念 标号 SE-ISI模糊半概念 ${K_{11}}$ $ (\varnothing ,[{M_1},{M_1}]) $ ${K_{41}}$ $ ({x_1}{x_2}{x_3},[\varnothing ,{a_2}]) $ ${K_{21}}$ $ ({x_1},[{a_1},{a_1}{a_2}]) $ ${K_{42}}$ $ ({x_1}{x_2}{x_4},[\varnothing ,{a_1}]) $ ${K_{22}}$ $ ({x_2},[{a_2},{a_1}{a_2}]) $ ${K_{43}}$ $ ({x_1}{x_2}{x_5},[\varnothing ,{a_2}]) $ ${K_{23}}$ $ ({x_3},[{a_2}{a_3},{a_2}{a_3}]) $ $ {K_{44}} $ $ ({x_1}{x_3}{x_4},[\varnothing ,\varnothing ]) $ ${K_{24}}$ $ ({x_4},[{a_1},{a_1}{a_3}]) $ $ {K_{45}} $ $ ({x_1}{x_3}{x_5},[\varnothing ,{a_2}]) $ ${K_{25}}$ $ ({x_5},[{a_2}{a_3},{a_2}{a_3}]) $ $ {K_{46}} $ $ ({x_1}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{31}}$ $ ({x_1}{x_2},[\varnothing ,{a_1}{a_2}]) $ $ {K_{47}} $ $ ({x_2}{x_3}{x_4},[\varnothing ,\varnothing ]) $ ${K_{32}}$ $ ({x_1}{x_3},[\varnothing ,{a_2}]) $ $ {K_{48}} $ $ ({x_2}{x_3}{x_5},[{a_2},{a_2}]) $ ${K_{33}}$ $ ({x_1}{x_4},[{a_1},{a_1}]) $ $ {K_{49}} $ $ ({x_2}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{34}}$ $ ({x_1}{x_5},[\varnothing ,{a_2}]) $ $ {K_{410}} $ $ ({x_3}{x_4}{x_5},[\varnothing ,{a_3}]) $ ${K_{35}}$ $ ({x_2}{x_3},[{a_2},{a_2}]) $ ${K_{51}}$ $ ({x_1}{x_2}{x_3}{x_4},[\varnothing ,\varnothing ]) $ ${K_{36}}$ $ ({x_2}{x_4},[\varnothing ,{a_1}]) $ ${K_{52}}$ $ ({x_1}{x_2}{x_3}{x_5},[\varnothing ,{a_2}]) $ ${K_{37}}$ $ ({x_2}{x_5},[{a_2},{a_2}]) $ ${K_{53}}$ $ ({x_1}{x_2}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{38}}$ $ ({x_3}{x_4},[\varnothing ,{a_3}]) $ ${K_{54}}$ $ ({x_1}{x_3}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{39}}$ $ ({x_3}{x_5},[{a_2}{a_3},{a_2}{a_3}]) $ ${K_{55}}$ $ ({x_2}{x_3}{x_4}{x_5},[\varnothing ,\varnothing ]) $ ${K_{310}}$ $ ({x_4}{x_5},[\varnothing ,{a_3}]) $ ${K_{61}}$ $ ({G_1},[\varnothing ,\varnothing ]) $ 表 7 定性对比表
Table 7 Qualitative comparative table
名称 提取知识的表达形式 阈值数量 适用背景 提取知识的规则 提取知识的平台 半概念[27-28] $(X,A)$ 0 经典形式背景 $ X = {A^ * } $或$ {\text{ }}A = {X^ * } $ 格 模糊概念[15] $(X,A)$ 1 模糊形式背景 ${X^{{ * _\varepsilon }}} = A$且${A^{{ * _\varepsilon }}} = X$ 格 ISE-SI模糊半概念 $ ([{X_l},{X_u}],A) $ 2 模糊形式背景 ${A^ \triangleleft } = [{A^{\underline * }},{A^{\overline * }}] = [{X_l},{X_u}]$ 格 SE-ISI模糊半概念 $ (X,[{A_l},{A_u}]) $ 2 模糊形式背景 ${X^ \triangleright } = [{X^{\underline * }},{X^{\overline * }}] = [{A_l},{A_u}]$ 格 -
[1] WILLE R. Restructuring lattice theory: an approach based on hierarchies of concepts[M]Dordrecht: Springer, 1982: 445− 470. [2] GANTER B, WILLE R. Formal concept analysis: mathe- matical foundations[M]. Berlin: Springer, 1999: 78−98. [3] 毛华, 武秀. 三支概念的一种构建方法[J]. 智能系统学报, 2020, 15(3): 514–519. doi: 10.11992/tis.201904022 MAO Hua, WU Xiu. A new method for constructing three-way concept[J]. CAAI transactions on intelligent systems, 2020, 15(3): 514–519. doi: 10.11992/tis.201904022 [4] WANG Shengwen, LI Qingguo. A representation of L-domain by formal concept analysis[J]. Soft computing, 2022, 26(19): 9751–9760. doi: 10.1007/s00500-022-07326-y [5] 姬儒雅, 魏玲, 任睿思, 等. 毕达哥拉斯模糊三支概念格[J]. 山东大学学报(理学版), 2020, 55(11): 58–65. JI Ruya, WEI Ling, REN Ruisi, et al. Pythagorean fuzzy three-way concept lattice[J]. Journal of Shandong Univ- ersity (natural science edition), 2020, 55(11): 58–65. [6] 王太滨, 李德玉, 翟岩慧. 覆盖多粒度下的形式概念更新方法[J]. 计算机科学, 2023, 50(10): 18–27. doi: 10.11896/jsjkx.230600049 WANG Taibin, LI Deyu, ZHAI Yanhui. Method of updating formal concept under covering multi-granularity[J]. Computer science, 2023, 50(10): 18–27. doi: 10.11896/jsjkx.230600049 [7] YANG Dongqiang, YANG Xinran, JIA Hui, et al. Construction of fuzzy linguistic approximate concept lattice in an incomplete fuzzy linguistic formal context[J]. International journal of computational intelligence systems, 2022, 15(1): 154–169. [8] SHEMIS E, AMMAR M. A comprehensive review on updating concept lattices and its application in updating association rules[J]. Data mining and knowledge discovery, 2021, 11(2): 1–25. [9] 陈曜琦, 徐伟华, 蒋宗颖. 三支概念的恢复集[J]. 山东大学学报(理学版), 2023, 58(12): 52–62. CHEN Yaoqi, XU Weihua, JIANG Zongying. Recovery set of three-way concept[J]. Journal of Shandong University (natural science edition), 2023, 58(12): 52–62. [10] 魏玲, 赵思雨, 祁建军. 对称形式背景及其概念约简[J]. 西北大学学报(自然科学版), 2023, 53(5): 794–802. WEI Ling, ZHAO Siyu, QI Jianjun. Symmetric formal context and its concept reduct[J]. Journal of Northwest University (natural science edition), 2023, 53(5): 794–802. [11] 马文胜, 侯锡林. 形式概念分析中的同效关系与概念约简[J]. 计算机科学, 2023, 50(4): 63–76. doi: 10.11896/jsjkx.221000169 MA Wensheng, HOU Xilin. Same effect relation and concept reduction in formal concept analysis[J]. Computer science, 2023, 50(4): 63–76. doi: 10.11896/jsjkx.221000169 [12] LONG Binghan, XU Weihua, ZHANG Xiaoyan. Double threshold construction method for attribute-induced three- way concept lattice in incomplete fuzzy formal context[J]. The journal of engineering, 2020(13): 549–554. [13] ZHI Huilai, LI Jinhai. Granule description of incomplete data: a cognitive viewpoint[J]. Cognitive computation, 2022, 14: 2108–2119. doi: 10.1007/s12559-021-09918-6 [14] ZHI Huilai, LI Jinhai. Granule description based knowledge discovery from incomplete formal contexts via necessary attribute analysis[J]. Information sciences, 2019, 485: 347–361. doi: 10.1016/j.ins.2019.02.032 [15] 胡明涵, 张俐, 任飞亮. 模糊形式概念分析与模糊概念格[J]. 东北大学学报(自然科学版), 2007, 28(9): 1274–1277. doi: 10.3321/j.issn:1005-3026.2007.09.015 HU Minghan, ZHANG Li, REN Feiliang. Fuzzy formal concept analysis and fuzzy concept lattices[J]. Journal of Northeastern University(natural science edtion), 2007, 28(9): 1274–1277. doi: 10.3321/j.issn:1005-3026.2007.09.015 [16] SHAO Mingwen, LEUNG Yee, WANG Xizhao, et al. Granular reducts of formal fuzzy contexts[J]. Knowledge-based systems, 2016, 114(15): 156–166. [17] YAO Yiyu. Interval-set algebra for qualitative knowledge representation[C]//Procedding of ICCI’93: 5th International Conference on Computing and Information. Sudbury: IEEE, 1993: 370−374. [18] PAWLAK Z. Rough sets[J]. International journal of com- puter and information science, 1982, 11: 341–356. doi: 10.1007/BF01001956 [19] 梁美社, 米据生, 张少谱. 双论域上的广义直觉模糊概率粗糙集模型及其应用[J]. 智能系统学报, 2022, 17(3): 585–592. doi: 10.11992/tis.202106025 LIANG Meishe, MI Jusheng, ZHANG Shaopu. Generali- zed intuitionistic fuzzy probabilistic rough set models on two universes and their applications[J]. CAAI transact- ions on intelligent systems, 2022, 17(3): 585–592. doi: 10.11992/tis.202106025 [20] 徐伟华, 李金海, 魏玲, 等. 形式概念分析: 理论与应用[M]. 北京: 科学出版社, 2016: 69−88. XU Weihua, LI Jinhai, WEI Ling, et al. Formal concept analysis: theory and application[M]. Beijing: Science Pre- ss, 2016: 69−88. [21] MA Jianmin, CAI Mingjie. Concept acquisition approach of object-oriented concept lattices[J]. International journal of machine learning and cybernetics, 2017, 8(1): 123–134. doi: 10.1007/s13042-016-0576-1 [22] 郭庆春, 马建敏. 对偶区间集概念格上区间集协调集的判定方法[J]. 计算机科学, 2020, 47(3): 98–102. doi: 10.11896/jsjkx.190500098 GUO Qingchun, MA Jianmin. Judgment methods of interval-set consistent sets of dual interval-set concept lattices[J]. Computer science, 2020, 47(3): 98–102. doi: 10.11896/jsjkx.190500098 [23] 马建敏, 胡玲玲. 决策形式背景上区间集概念格的属性约简[J]. 模式识别与人工智能, 2018, 31(7): 581–590. MA Jianmin, HU Lingling. Attribute reductions of interval-Set concept lattices for decision formal contexts[J]. Pattern recognition and artificial intelligence, 2018, 31(7): 581–590. [24] REN Ruisi, WEI Ling, YAO Yiyu. An analysis of three types of partially-known formal concepts[J]. International journal of machine learning and cybernetics, 2018, 9: 1767–1783. doi: 10.1007/s13042-017-0743-z [25] YAO Yiyu. Interval sets and three-way concept analysis in incomplete contexts[J]. International journal of machine learning and cybernetics, 2017, 8: 3–20. doi: 10.1007/s13042-016-0568-1 [26] 王振, 魏玲. 基于单边区间集概念格的不完备形式背景的属性约简[J]. 计算机科学, 2018, 45(1): 73–78. WANG Zhen, WEI Ling. Attribute reduction of partially- known formal concept lattices for incomplete contexts[J]. Computer science, 2018, 45(1): 73–78. [27] MAO Hua, LIU Xiaoqin, WANG Gang. Two forms of three-way semiconcepts[J]. Journal of intelligent and fuzzy systems, 2021, 40(6): 10853–10864. doi: 10.3233/JIFS-201862 [28] VORMBROCK B, WILLE R. Semiconcept and proto- concept algebras: the basic theorems[M]. Berlin: Springer, 2005: 34-48. [29] 毛华, 牛振华, 马经泽, 等. 基于模糊三支区间集半概念知识提取方法研究[J]. 郑州大学学报(理学版), 2024, 56(1): 81–87. MAO Hua, NIU Zhenhua, MA Jingze, et al. Research on knowledge extraction method based on fuzzy three-way interval-Set semiconcept[J]. Journal of Zhengzhou University (natural science edition), 2024, 56(1): 81–87. [30] 毛华, 马经泽, 牛振华, 等. 三支半概念的广义结构及粗糙集近似算子[J]. 模糊系统与数学, 2022, 36(6): 89–101. MAO Hua, MA Jingze, NIU Zhenhua, et al. Generalized structures and rough set approximation operators of three- way semiconcepts[J]. Fuzzy systems and mathematics, 2022, 36(6): 89–101.

































































































































































































































































































































































































 下载:
下载: