Direct lift fully-automatic landing control of longitudinal carrier-based aircraft on basis of linear active disturbance rejection control
-
摘要: 舰载机的最终着舰过程受到强烈的舰尾流的干扰，为了抑制舰尾流扰动，本文提出一种基于径向基函数神经网络（radial basis functions neural network，RBFNN）结合线性自抗扰控制（liner active disturbance rejection control，LADRC）的创新设计方法，确保舰载机直接升力控制自动着舰系统的鲁棒性。LADRC将阵风扰动和系统不确定项作为总扰动，通过线性扩展状态观测器（liner extended state observer，LESO）对总扰动进行估计，并通过线性反馈控制律进行补偿，然后根据系统状态利用RBFNN在线调整LADRC控制器的参数，并构建Lyapunov函数以证明闭环系统的稳定性。舰载机跟踪理想下滑道的仿真结果表明，RBF-LADRC的抗干扰性、鲁棒性和跟踪精度均优于与之对比的控制方法。Abstract: The final landing process of an carrier-based aircraft is disturbed by strong carrier air-wake. In order to suppress the disturbance of carrier air-wake, an innovative design method based on radial basis functions neural network (RBFNN) combined with linear active disturbance rejection control (LADRC) is proposed to assure the robustness of direct lift automatic landing system of carrier-based aircraft. The LADRC takes the gust wind disturbance and internal uncertainty as the total disturbance, estimates the total disturbance by a linear extended state observer (LESO), and conducts compensation by a linear feedback control law, then the parameters of the LADRC controller are adjusted on line by using RBFNN according to the system state, Lyapunov functions are constructed to demonstrate the stability of the closed-loop system. Based on the simulation results of the carrier-based aircraft tracking the ideal slide path, it is shown that the anti-interference, robustness and tracking accuracy of RBF-LADRC are superior to other comparative control methods.
-
舰载机的着舰控制是飞行控制系统的一个重要研究内容，目的是提高着舰精度[1]。传统的舰载机采用油门控制下滑，俯仰杆控制迎角的控制方法。这种方法有很多缺点，如操纵通道的耦合，轨迹和姿态的耦合，以及着舰精度差等，因此提出了直接升力控制（direct lift control，DLC）用于舰载机着舰[2-3]。这种技术直接控制作用在飞机上的力，从而消除了轨迹和姿态运动的耦合。但是由于舰载机的最终着舰过程会受到强烈的舰尾流干扰，即使在DLC下，这些干扰也会大大影响着舰精度。如何使舰载机在干扰作用下快速准确地跟踪理想的下滑轨迹，是全自动着舰系统的关键问题。为了使直接升力控制自动着舰系统具有更好的抗干扰能力，需要引入先进的控制律来实现姿态稳定和理想下滑道跟踪。
对于DLC着舰控制系统的设计，许多专家设计了不同的方案。精密进近与着舰的增强引导综合控制技术就是利用DLC来提高舰载机下滑道跟踪性能。在飞机上的验证表明，舰载机着陆偏差被有效降低[4]。但是此设计的航母着陆系统仍然是一个人工控制系统，由飞行员发出引导指令。由于DLC系统的姿态和轨迹解耦性较差，因此设计了一种模糊动态逆控制器[5]，可以实现DLC，具有良好的鲁棒性，在动态响应方面优于常规动态逆控制器。然而，动态逆DLC着舰系统在很大程度上依赖于准确的飞机模型，当飞机模型数据不准确时，动态逆向控制器的性能会急剧下降。在文献[6]中，这种设计方法虽然可以保证DLC模式的实现，但在实现中需要根据不同的飞行状态求解合适的增益参数，因此很难实现飞行轨迹与姿态的真正解耦。H无穷控制策略被应用于飞行控制系统的设计，提高了系统的鲁棒性能[7-8]。然而，这种方法在处理高增益系统和设计高阶控制器时过于复杂。文献[9-10]将自适应模糊控制方法应用到飞行控制中，与传统控制方案相比，它提高了着舰精度。此方法解决了舰载机着舰模型中的强时变性、参数不确定性、复杂环境干扰等问题。然而，当模型发生重大变化时，自适应控制器的参数往往不能及时调整。因此，自抗扰控制（active disturbance rejection control，ADRC）得到了越来越多的关注。
ADRC已被成功地应用于许多领域。许多学者都给出了不同的设计方案，如非线性飞机模型姿态控制[11]、电力驱动速度控制[12]、解决高超音速飞行器控制系统中的耦合和干扰问题[13]以及无人驾驶飞机的可视化着陆系统[14]。然而，ADRC包含非线性函数和许多可调参数，这使得参数调整更加复杂。因此，文献[15]引入带宽的概念，将非线性ADRC转化为由线性扩张状态观测器（linear extended state observer，LESO）和比例−微分控制器（proportional-derivative controller，PD）组成的LADRC。LADRC大大简化了参数的设置，使得LADRC技术在各个领域得到了更广泛的应用。文献[16]为四旋翼无人机设计了一种滑模控制和LADRC相结合的控制方法，以解决在有干扰的情况下，无人机对参考信号的稳定跟踪。文献[17]介绍了一种自适应LADRC控制器，以实现强大的抗干扰性能并降低机电执行器的噪声敏感性。虽然LADRC具有上述优点，但当舰载机受到外部干扰和LESO估计误差的影响时，一组固定的反馈率参数使得控制效率不尽人意。径向基函数神经网络(radial basis function neural network, RBFNN)由于具有学习和自适应能力，可以有效控制复杂的不确定系统[18-20]。为了简化参数调整过程，增强控制器的抗干扰能力，使自动着舰控制系统在外界干扰下能快速稳定地沿理想下滑道飞行。本文提出了一种利用径向基函数神经网络对LADRC参数进行在线自动调整的新方法，并将该策略应用于直接升力控制自动着舰系统中。利用Lyapunov稳定性理论分析了控制系统的稳定性，并将仿真结果与传统的LADRC、比例−积分−微分控制器（proportional-integral-derivative controller，PID）控制方案、反向传播神经网络结合线性自抗扰控制（back propagation neural network combined with liner active disturbance rejection control，BP-LADRC）以及自适应滑膜控制进行了比较。结果表明，该方法能够快速、稳定地跟踪理想下滑道，并且对外部干扰具有良好的鲁棒性。
1. 着舰模型建立
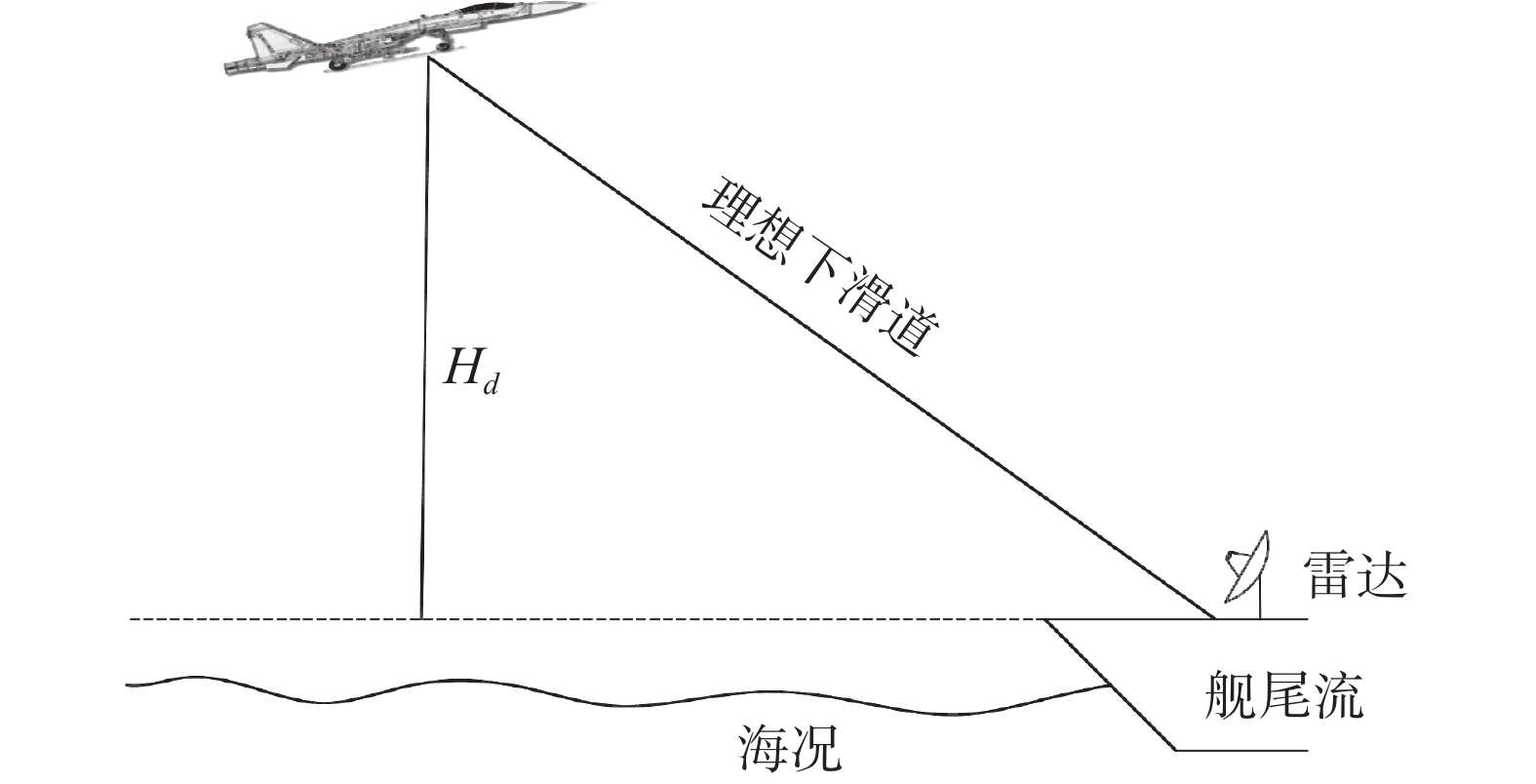
舰载机着舰如图1所示。本节介绍纵向飞机模型和舰尾流模型。
图 1 舰载机着舰阶段Fig. 1 Carrier-based aircraft landing phase
下载:
全尺寸图片
1.1 舰载机纵向非线性模型
舰载机的纵向飞行状态选择在没有大气干扰的情况下以70 m/s的恒定速度直线飞行，迎角为9.1°，襟翼偏转为20°，飞行轨迹角为−3.5°，3个控制效应器为升降舵
$ {\delta _e} $ 、襟翼$ {\delta _f} $ 和油门杆$ {\delta _{pl}} $ 。舰载机的纵向方程如下[21]。力方程：
$$ \dot V = \frac{{P\cos \alpha - D}}{m} - g\sin \gamma $$ (1) $$ \dot \gamma = \frac{{L + P\sin \alpha }}{{mV}} - \frac{g}{V}\cos \gamma $$ (2) 导航方程：
$$ \dot h = V\sin \gamma $$ (3) 力矩方程：
$$ \dot q = \frac{M}{{{I_{yy}}}} $$ 飞机的阻力、升力和俯仰力矩分别为
$$ D = 0.5\rho {V^2}S{C_D}\left( {\alpha ,{\delta _e},{\delta _c}} \right) $$ $$ L = 0.5\rho {V^2}S{C_L}\left( {\alpha ,{\delta _e},{\delta _c},{\delta _f}} \right) $$ $$ M = 0.5\rho {V^2}S\bar c{C_M}\left( {\alpha ,q,{\delta _e},{\delta _c},{\delta _f}} \right) $$ 式中：
$ V $ 为速度，$ \gamma $ 为飞行轨迹角，$ \alpha $ 为迎角，$ q $ 为俯仰角速率，$ \theta $ 为俯仰角，$ {C_M} $ 、$ {C_D} $ 和$ {C_L} $ 分别为俯仰力矩系数、升力系数和阻力系数，$ \rho $ 为空气密度，$ h $ 为高度，$ {I_{yy}} $ 为俯仰惯性力矩，$ P $ 为发动机推力，$ M $ 为俯仰力矩。1.2 舰尾流建模
采用美国军事标准MIL-F-8785C对舰尾流建模[22]。舰尾流由水平纵向部分
$ u $ 、水平横向部分$ v $ 和垂直部分$ w $ 等3个部分组成：$$ \left\{ {\begin{array}{l} {u = {u_1} + {u_2} + {u_3} + {u_4}} \\ {v = {v_1} + {v_4}} \\ {w = {w_1} + {w_2} + {w_3} + {w_4}} \end{array}} \right. $$ 式中：
$ {u_1} $ 、$ {v_1} $ 、$ w_{1} $ 为自由大气紊流分量，$ u_{2} $ 、$ w_{2} $ 为稳态分量，$ u_{3} $ 、$ w_{3} $ 为周期性分量，$ u_{4} $ 、$ v_{4} $ 、$ w_{4} $ 为随机性分量。1.3 舰载机在舰尾流扰动时的纵向线性模型
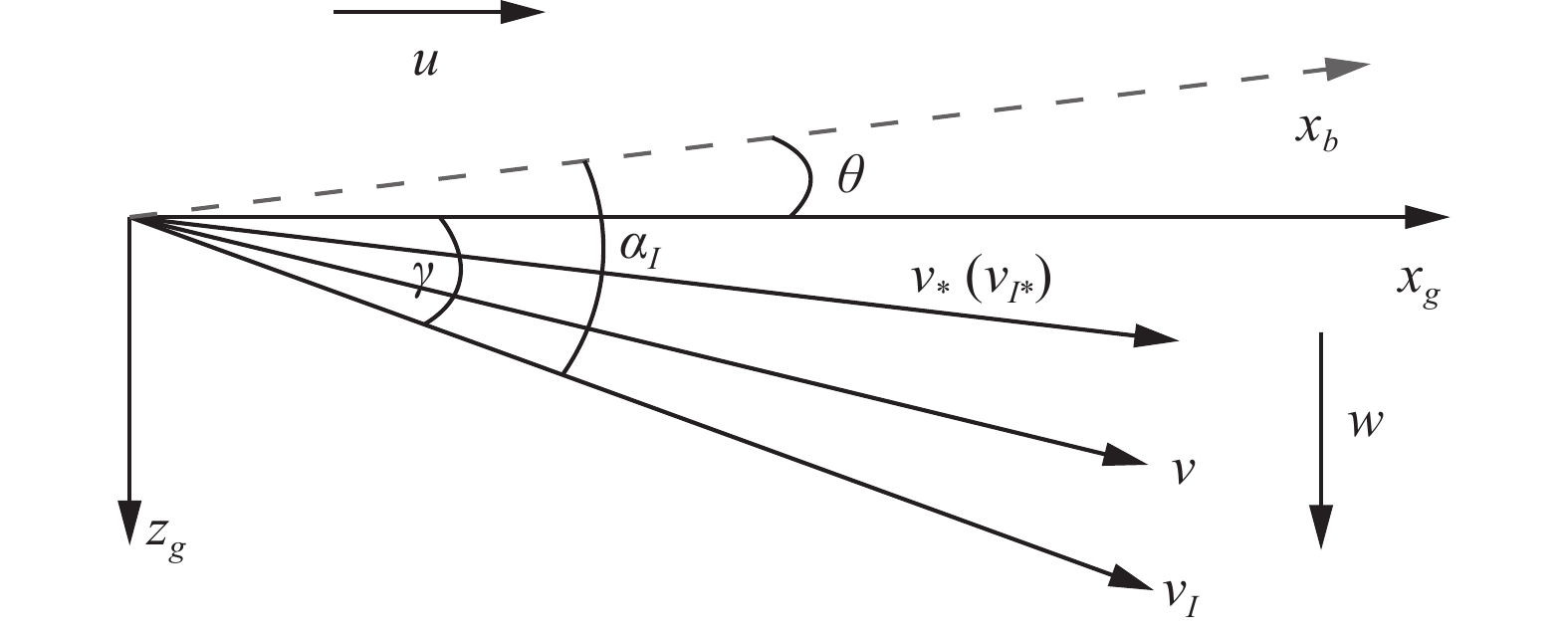
飞机在遇到阵风时，空气动力学会发生瞬变[23-25]。为了通过线性模型分析舰尾流对飞行状态的影响，根据以下思路对纵向线性模型进行扩展。本文只研究飞机纵向运动，因此可以忽略水平横向部分的影响。
如果
$ u > 0 $ ，在空气动力学上相当于空速的降低，关系为$$ {v_I} \approx v + u $$ 如果
$ w > 0 $ ，飞行状态立即发生变化，如图2所示，考虑到风速通常远小于飞行速度，$ v $ 和$ {v_I} $ 之间的角约等于$ w/{v_*} $ ，因此：
图 2 舰尾流中姿态和空速的关系Fig. 2 Relationship between attitude and airspeed in carrier air-wake下载:
全尺寸图片
$$ {\alpha _I} \approx \alpha + w/{v_*} $$ 假设风速参考值为零，因此
$ \Delta u = u $ ，$ \Delta w = w $ ；则带舰尾流扰动的飞机纵向线性模型为$$ \left\{ \begin{array}{l} {{{\boldsymbol{\dot x}}}_{\boldsymbol{w}}} = {\boldsymbol{A}}{{\boldsymbol{x}}_{\boldsymbol{w}}} + {\boldsymbol{Bu}} + {\boldsymbol{Ew}}\\ {{\boldsymbol{y}}_{\boldsymbol{w}}} = {\boldsymbol{C}}{{\boldsymbol{x}}_{\boldsymbol{w}}} + {\boldsymbol{Du}} + {\boldsymbol{Fw}} \end{array} \right.$$ 式中：
${{\boldsymbol{x}}_{\mathbf{w}}} = {\left[ {\begin{array}{*{20}{c}} {\Delta {v_I}}\quad{\Delta {\alpha _I}}\quad{\Delta q}\quad{\Delta \theta }\quad{\Delta h} \end{array}} \right]^{\text{T}}}$ ，${{\boldsymbol{y}}_{\boldsymbol{w}}} = \left[ {\Delta {v_I}}\quad {\Delta {\alpha _I}}\quad \right. \left.{\Delta q}\quad{\Delta \theta }\quad{\Delta h}\quad{{{\Delta {n_z}} \mathord{\left/ {\vphantom {{\Delta {n_z}} {{v_ * }}}} \right. } {{v_ * }}}}\quad{\Delta \gamma } \right]^{\text{T}}$ ，${\boldsymbol{w}} = {\left[ {\begin{array}{*{20}{c}} u\quad w \end{array}} \right]^{\text{T}}} $ ，${\boldsymbol{u}} = \left[ {\Delta {\delta _e}}\quad\right. \left.{\Delta {\delta _c}}\quad{\Delta {\delta _p}}\quad{\Delta {\delta _f}} \right]^{\text{T}}$ 。2. 控制器设计
2.1 通过RBF神经网络优化的LADRC
对于如下二阶系统：
$$ \left\{ {\begin{array}{l} {\ddot x = f + bu} \\ {y = x} \end{array}} \right. $$ 为了使输出跟踪参考信号，有必要设计二阶RBF-LADRC方案。下面将详细介绍该控制器的构造。
1）线性跟踪微分器。
线性跟踪微分器（linear tracking differentiator，LTD）的具体实现为
$$ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_{d_1}} = {x_{d_2}}} \\ {{{\dot x}_{d_2}} = - 2{r^2}\left( {{x_{d_1}} - {x_d}} \right) - 2r{x_{d_2}}} \end{array}} \right. $$ 式中：
$ {x_d} $ 为期望值；${x_{d_1}}$ 为软化后的期望值；${x_{d_2}}$ 为${x_{d_1}}$ 的微分信号；$ r $ 为快速因子，用于调整过渡过程的速度。2）线性扩展状态观测器。
将二阶系统中的总扰动视为扩展状态变量：
$$ \left\{ \begin{gathered} {{\dot x}_1} = {x_2} \\ {{\dot x}_2} = {x_3} + {b_0}u \\ {{\dot x}_3} = \dot f \\ \end{gathered} \right. $$ (4) 在式(4)的基础上建立一个三阶LESO为
$$\left\{ {\begin{array}{*{20}{l}} {e = {{\hat x}_1} - {x_1}}\\ {{{\dot {\hat x}}_1} = {{\hat x}_2} - {\beta _1}e}\\ {{{\dot {\hat x}}_2} = {{\hat x}_3} - {\beta _2}e + {b_0}u}\\ {{{\dot {\hat x}}_3} = - {\beta _3}e} \end{array}} \right. $$ (5) 式中：
$ {\hat x_1} $ 为对$ {x_1} $ 的精确估计；$ {\hat x_3} $ 为对整体扰动的估计；$ {\beta _i}(i = 1,2,3) $ 为观测器增益，$ {\beta _1} = 3{w_0} $ ，$ {\beta _2} = 3w_0^2 $ ，$ {\beta _3} = w_0^3 $ ，其中$ {w_0} $ 为观测器带宽[26]。3）线性状态误差反馈。
在LESO准确估计总扰动的情况下，设计控制器为
$$ u = {u_0} - \frac{{{{\hat x}_3}}}{{{b_0}}} $$ 忽略估计误差，将系统降为级联积分系统为
$$ \ddot x = (f - {{\textit{z}}_3}) + {u_0} \approx {u_0} $$ 由于LTD对参考信号的精确跟踪和对输出信号的精确估计，级联积分器系统可以很容易地由PD控制器控制：
$$ {u_0} = {k_{\rm{p}}}\left( {{x_{d_1}} - {{\hat x}_1}} \right) + {k_{\rm{d}}}\left( {{x_{d_2}} - {{\hat x}_2}} \right) $$ 为了简化参数设置，引入RBF神经网络对
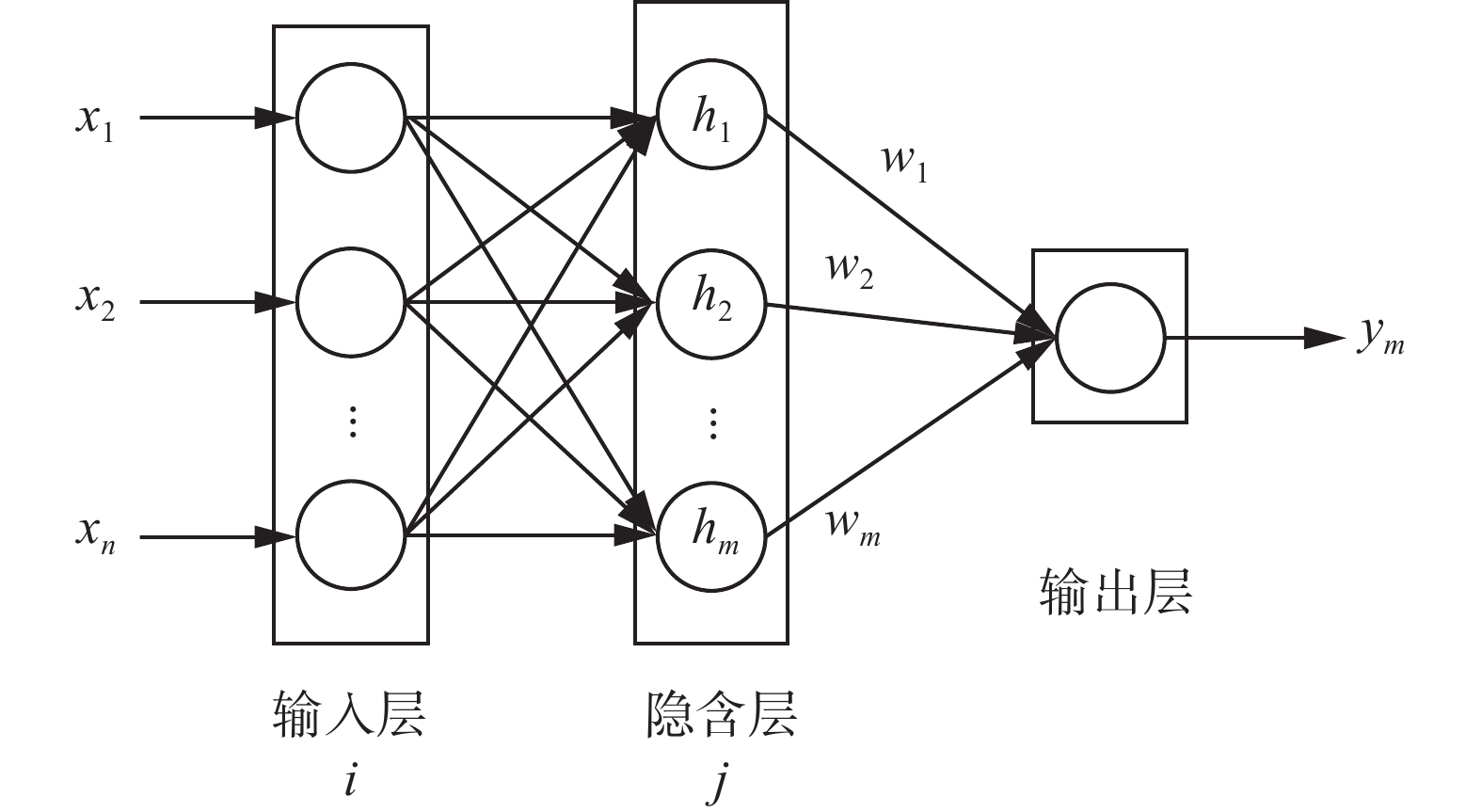
${k_{\rm{p}}}$ 和${k_{\rm{d}}}$ 进行实时调整。RBF神经网络是3层前馈网络，只有一个隐含层[27]，如图3所示。RBF神经网络模拟了人脑中局部调节的神经网络结构，已经证明RBF神经网络可以以任意的精度近似任何连续函数[28]。
图 3 RBF神经网络结构Fig. 3 RBF neural network structure diagram下载:
全尺寸图片
选择
${\boldsymbol{X}} = {[{{u}}({{k}})\;\;{{y}}({{k}})\;\;{{y}}({{k}} - 1)]^{\rm{T}}}$ 作为RBFNN的输入向量。RBFNN的性能指标函数为
$$ E(k) = \frac{1}{2}e^2{(k)} = \frac{1}{2}{\left( {y(k) - {y_m}(k)} \right)^2} $$ (6) 根据梯度下降法，输出权重向量、节点中心向量和节点基宽参数的迭代算法为
$$ \Delta {w_j}(k) = \eta \left( {y(k) - {y_m}(k)} \right){h_j} $$ $$ \Delta {b_j}(k) = \eta \left( {y(k) - {y_m}(k)} \right){\omega _j}{h_j}\frac{{{{\left\| {{\boldsymbol{X}} - {{\boldsymbol{C}}_j}} \right\|}^2}}}{{b_j^3}} $$ $$ {b_j}(k) = {b_j}(k - 1) + \Delta {b_j} + \alpha \left( {{b_j}(k - 1) - {b_j}(k - 2)} \right) $$ $$ \Delta {c_{ji}}(k) = \eta \left( {y(k) - {y_m}(k)} \right){\omega _j}\frac{{{x_i} - {c_{ji}}}}{{b_j^2}} $$ $$ {c_{ji}}(k) = {c_{ji}}(k - 1) + \Delta {c_{ji}}(k) + \alpha \left( {{c_{ji}}(k - 1) - {c_{ji}}(k - 2)} \right)$$ 式中：
$ \eta $ 为学习率，$ \alpha $ 为动量因子。RBFNN的Jacobian信息为
$$ \frac{{\partial y(k)}}{{\partial u(k)}} \approx \frac{{\partial {y_m}(k)}}{{\partial u(k)}} = \sum\limits_{j = 1}^m {{w_j}} {h_j}\frac{{{c_{ji}} - {x_1}}}{{b_j^2}} $$ 式中
$ {x_1} = u(k) $ 。梯度下降法被用来调整
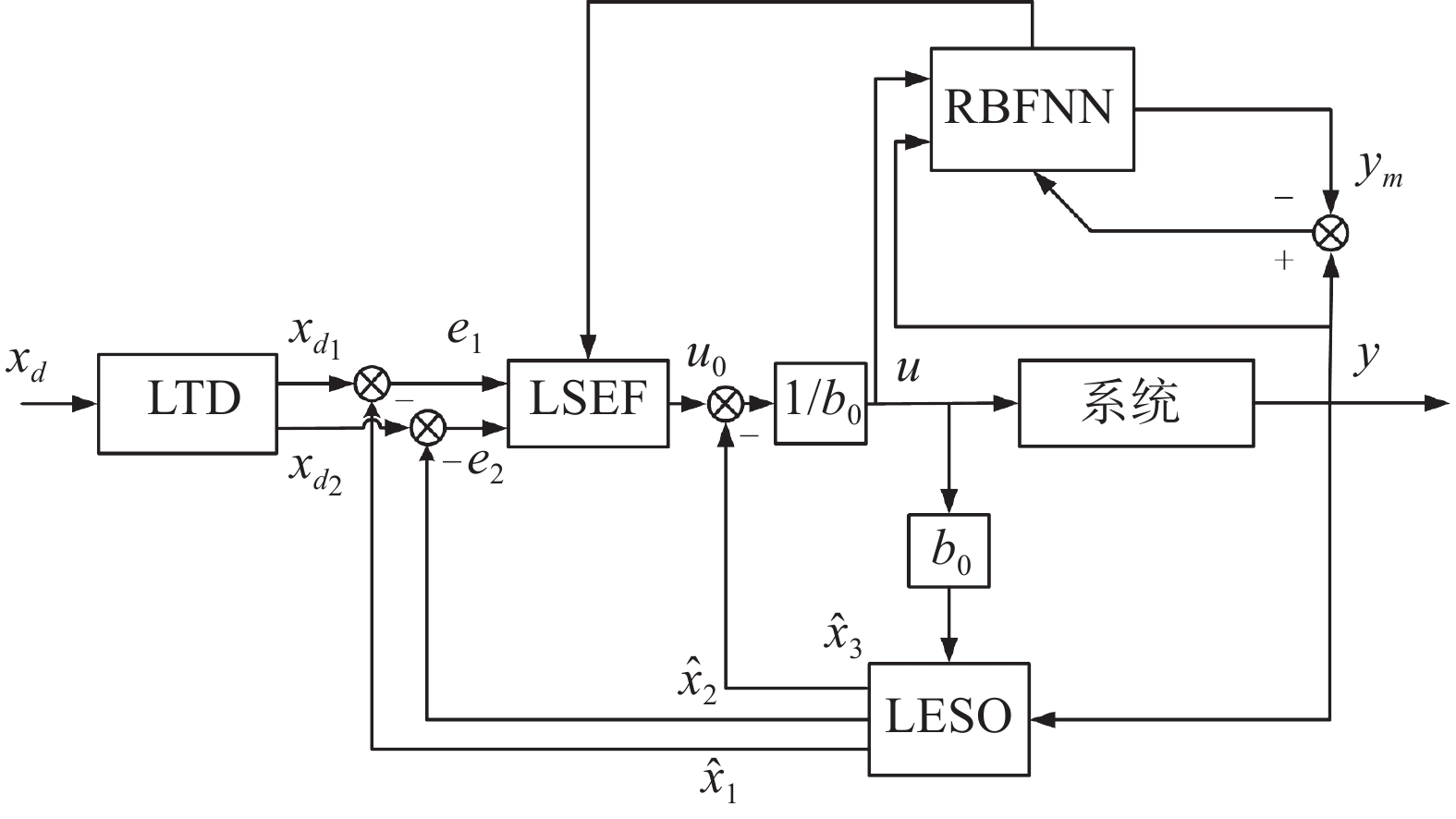
$ {k_p} $ 和$ {k_d}： $ $$ \Delta {k_p}(k) = - \eta \frac{{\partial E}}{{\partial {k_p}}} = - \eta \frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial u}}\frac{{\partial u}}{{\partial {k_p}}} = \eta e(k)\frac{{\partial y}}{{\partial u}} $$ $$ {k_p}(k) = {k_p}(k - 1) + \Delta {k_p}(k) $$ $$ \Delta {k_d}(k) = - \eta \frac{{\partial E}}{{\partial {k_d}}} = - \eta \frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial u}}\frac{{\partial u}}{{\partial {k_d}}} = \eta e(k)\frac{{\partial y}}{{\partial u}} $$ $$ {k_d}(k) = {k_d}(k - 1) + \Delta {k_d}(k) $$ 基于RBF神经网络的LADRC控制系统的结构如图4所示。
图 4 基于RBF神经网络的LADRC结构Fig. 4 Structure of RBF neural network based on LADRC下载:
全尺寸图片
2.2 稳定性分析
本节分析ESO收敛性和引入RBFNN后的闭环系统的稳定性。
ESO估计误差定义为
$$ \left\{ \begin{gathered} {\eta _1} = {x_1} - {{\hat x}_1} \\ {\eta _2} = {x_2} - {{\hat x}_2} \\ {\eta _3} = {f_0} - {{\hat x}_3} \\ \end{gathered} \right. $$ (7) 式(5)和式(7)结合起来，可以得到如下ESO估计误差形式：
$$ \left\{ \begin{gathered} {{\dot \eta }_1} = - {\beta _1}{\eta _1} + {\eta _2} \\ {{\dot \eta }_2}{\text{ }} = - {\beta _2}{\eta _1} + {\eta _3} \\ {{\dot \eta }_3}{\text{ }} = - {\beta _3}{\eta _1} + {{\dot f}_0} \\ \end{gathered} \right. $$ (8) 式(8)可以表示为
$$ \dot \xi = {\omega _0}{\boldsymbol{A}}\xi + {\boldsymbol{B}}\frac{{{{\dot f}_0}}}{{\omega _0^2}} $$ (9) 式中：
${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - 3}&1&0 \\ { - 3}&0&1 \\ { - 1}&0&0 \end{array}} \right]$ ，${\boldsymbol{B}} = \left[ {\begin{array}{*{20}{l}} 0 \\ 0 \\ 1 \end{array}} \right]$ ，$\xi = {\left[ {\begin{array}{*{20}{l}} {{\eta _1}}&{\dfrac{{{\eta _2}}}{{\omega_0}}}&{\dfrac{{{\eta _3}}}{{\omega {_0^2}}}} \end{array}} \right]^{\text{T}}}$ 。式(9)的解为
$$ \xi (t) = {{\rm{e}}^{{\omega _0}{\boldsymbol{A}}t}}{\mathbf{\xi }}(0) + \int_0^t {{{\rm{e}}^{{\omega _0}{\boldsymbol{A}}(t - \tau )}}} {\boldsymbol{B}}\frac{{{{\dot f}_0}}}{{\omega _{01}^2}}{\rm{d}}\tau $$ 设
$$ Q(t) = \int_0^t {{{\rm{e}}^{{\omega _0}A(t - \tau )}}} {\boldsymbol{B}}\frac{{{{\dot f}_0}}}{{\omega _0^2}}{\rm{d}}\tau $$ 式中：
$ {\dot f_0} $ 是有界的,$ |{\dot f_0}| \leqslant \tau $ ，$ \tau > 0 $ 。因此：$$ \left| {{{[Q(t)]}_i}} \right| \leqslant \frac{\tau }{{{\omega _0}}}\left[ {\left| {{{\left[ {{{\boldsymbol{A}}^{ - 1}}{\boldsymbol{B}}} \right]}_i}} \right| + \left| {{{\left[ {{{\boldsymbol{A}}^{ - 1}}{{\rm{e}}^{{\omega _0}{\boldsymbol{A}}t}}{\boldsymbol{B}}} \right]}_i}} \right|} \right] \leqslant \frac{{3\tau }}{{{\omega _0}^3}} + \frac{{4\tau }}{{{\omega _0}^6}} $$ 设
$ {\xi _{\max }}(0) = \left| {{\xi _1}(0)} \right| + \left| {{\xi _2}(0)} \right| + \left| {{\xi _3}(0)} \right| $ , 对于任意时间$ t \geqslant T > 0 $ ，i = 1, 2, 3，可以得到：$$ \left| {{{\left[ {{{\rm{e}}^{{\omega _0}At}}\xi (0)} \right]}_i}} \right| \leqslant \frac{{{\xi _{\max }}(0)}}{{\omega _0^3}} $$ 得到
$\left| {{\xi _i}(t)} \right| \leqslant \dfrac{{{\xi _{\max }}(0)}}{{\omega _0^3}} + \dfrac{{3\tau }}{{\omega _0^3}} + \dfrac{{4\tau }}{{\omega _0^6}}$ 。设
${E_{\max }}(0) = \left| {{E_1}(0)} \right| + \left| {{E_2}(0)} \right| + \left| {{E_3}(0)} \right|$ ，根据${\xi _i}(t) = {E_i}(t)/ \omega _{\,0}^{\,i - 1}$ ，可知：$$ \left| {{E_i}(t)} \right| \leqslant \frac{{{E_{\max }}(0)}}{{\omega _0^3}} + \frac{{3\tau }}{{\omega _0^{4 - i}}} + \frac{{4\tau }}{{\omega _0^{7 - i}}} = {\varepsilon _i} $$ 从上述分析可以看出，ESO的估计误差的上界随着观测器带宽的增加而单调地减少。
为了分析系统的闭环稳定性，构造Lyapunov函数为
$$ V(k) = \frac{1}{2}{\left( {y(k) - {y_m}(k)} \right)^2} = \frac{1}{2}{e^2}(k) $$ (10) 根据式(10)，得出Lyapunov函数的变化量为
$$ \Delta V(k) = V(k + 1) - V(k) = \frac{1}{2}\left[ {{e^2}(k + 1) - {e^2}(k)} \right] $$ (11) 权重的变化量为
$$ \Delta {w_j} = - {\eta _w}\frac{{\partial E}}{{\partial {w_j}}} = - {\eta _w}\frac{{\partial E}}{{\partial {y_m}}}\frac{{\partial {y_m}}}{{\partial {w_j}}} = {\eta _w}e{h_j} $$ $$ \Delta {b_j} = - {\eta _b}\frac{{\partial E}}{{\partial {b_j}}} = - {\eta _b}\frac{{\partial E}}{{\partial {y_m}}}\frac{{\partial {y_m}}}{{\partial {b_j}}} = {\eta _b}e{w_j}{h_j}\frac{{{{\left\| {{\boldsymbol{X}} - {{\boldsymbol{C}}_j}} \right\|}^2}}}{{b_j^3}} $$ $$ \Delta {c_j} = - {\eta _c}\frac{{\partial E}}{{\partial {c_j}}} = - {\eta _c}\frac{{\partial E}}{{\partial {y_m}}}\frac{{\partial {y_m}}}{{\partial {c_j}}} = {\eta _c}e{w_j}{h_j}\frac{{{x_i} - {c_{ji}}}}{{b_j^2}} $$ 设
${{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}(k) = \dfrac{{\partial {y_m}}}{{\partial {\boldsymbol{x}}}}$ ，其中${\boldsymbol{x}} = {\boldsymbol{w}}$ ，${\boldsymbol{b}}$ 和${\boldsymbol{c}}$ ，表示为$$ {{\boldsymbol{\varGamma }}_{\boldsymbol{w}}}(k) = \frac{{\partial {y_m}}}{{\partial {\boldsymbol{w}}}} = {\left[ {\frac{{\partial {y_m}}}{{\partial {w_1}}}\quad \frac{{\partial {y_m}}}{{\partial {w_2}}}\quad \cdots \quad \frac{{\partial {y_m}}}{{\partial {w_m}}}} \right]^{\text{T}}} $$ $$ {{\boldsymbol{\varGamma }}_{\boldsymbol{b}}}(k) = \frac{{\partial {y_m}}}{{\partial {\boldsymbol{b}}}} = {\left[ {\frac{{\partial {y_m}}}{{\partial {b_1}}}\quad \frac{{\partial {y_m}}}{{\partial {b_2}}}\quad \cdots \quad \frac{{\partial {y_m}}}{{\partial {b_m}}}} \right]^{\text{T}}} $$ $$ {{\boldsymbol{\varGamma }}_{\boldsymbol{c}}}(k) = \frac{{\partial {y_m}}}{{\partial {\boldsymbol{c}}}} = {\left[ {\frac{{\partial {y_m}}}{{\partial {c_1}}}\quad \frac{{\partial {y_m}}}{{\partial {c_2}}}\quad \cdots \quad \frac{{\partial {y_m}}}{{\partial {c_m}}}} \right]^{\text{T}}} $$ 其中：
$$ \left\{ {\begin{array}{l} {\dfrac{{\partial {y_m}}}{{\partial {w_j}}} = {h_j}} \\ {\dfrac{{\partial {y_m}}}{{\partial {b_j}}} = {w_j}{h_j}\dfrac{{{{\left\| {{\boldsymbol{X}} - {{\boldsymbol{C}}_j}} \right\|}^2}}}{{b_j^3}}} \\ {\dfrac{{\partial {y_m}}}{{\partial {c_j}}} = {w_j}{h_j}\dfrac{{{x_i} - {c_{ji}}}}{{b_j^2}}} \end{array}} \right. $$ 误差方程的线性化模型可以表示为
$$ e(k + 1){\text{ }} = e(k) + \Delta e(k) \cong e(k) + {\left[ {\frac{{\partial e(k)}}{{\partial {\boldsymbol{x}}}}} \right]^{\text{T}}}\Delta {\boldsymbol{x}} $$ (12) 使用式(6)可以得到：
$$ \frac{{\partial e(k)}}{{\partial {\boldsymbol{x}}}} = \frac{{\partial e(k)}}{{\partial {y_m}}}\frac{{\partial {y_m}}}{{\partial {\boldsymbol{x}}}} = - {{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}(k) $$ (13) 使用式(12)、(13)可以得到：
$$ e(k + 1) = e(k) - {\left[ {{{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}(k)} \right]^{\text{T}}}{\eta _{\text{x}}}e{{\boldsymbol{\varGamma }}_{\boldsymbol{X}}}(k) = e(k)\left[ {1 - {\eta _{\text{x}}}{{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}{{(k)}^{\text{T}}}{{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}(k)} \right] $$ (14) 根据式(11)、(14)，
$ \Delta V(k) $ 可以表示为$$ \Delta V(k) = \frac{1}{2}{e^2}(k){\eta _{{x}}}{\left\| {{{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}(k)} \right\|^2}\left[ {{\eta _{{x}}}{{\left\| {{{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}(k)} \right\|}^2} - 2} \right] $$ (15) 如果
$ {\eta _{{x}}} $ 选择为$$ 0 < {\eta _{{x}}} < \frac{2}{{{{\left\| {{{\boldsymbol{\varGamma }}_{\boldsymbol{x}}}(k)} \right\|}^2}}} $$ 则式(15)中的
$ \Delta V(k) $ 值将小于零。因此$ V > 0 $ 和$ \dot V < 0 $ ，根据 Lyapunov 稳定性定理，闭环系统渐近稳定。3. 直接升力自动着舰系统的设计
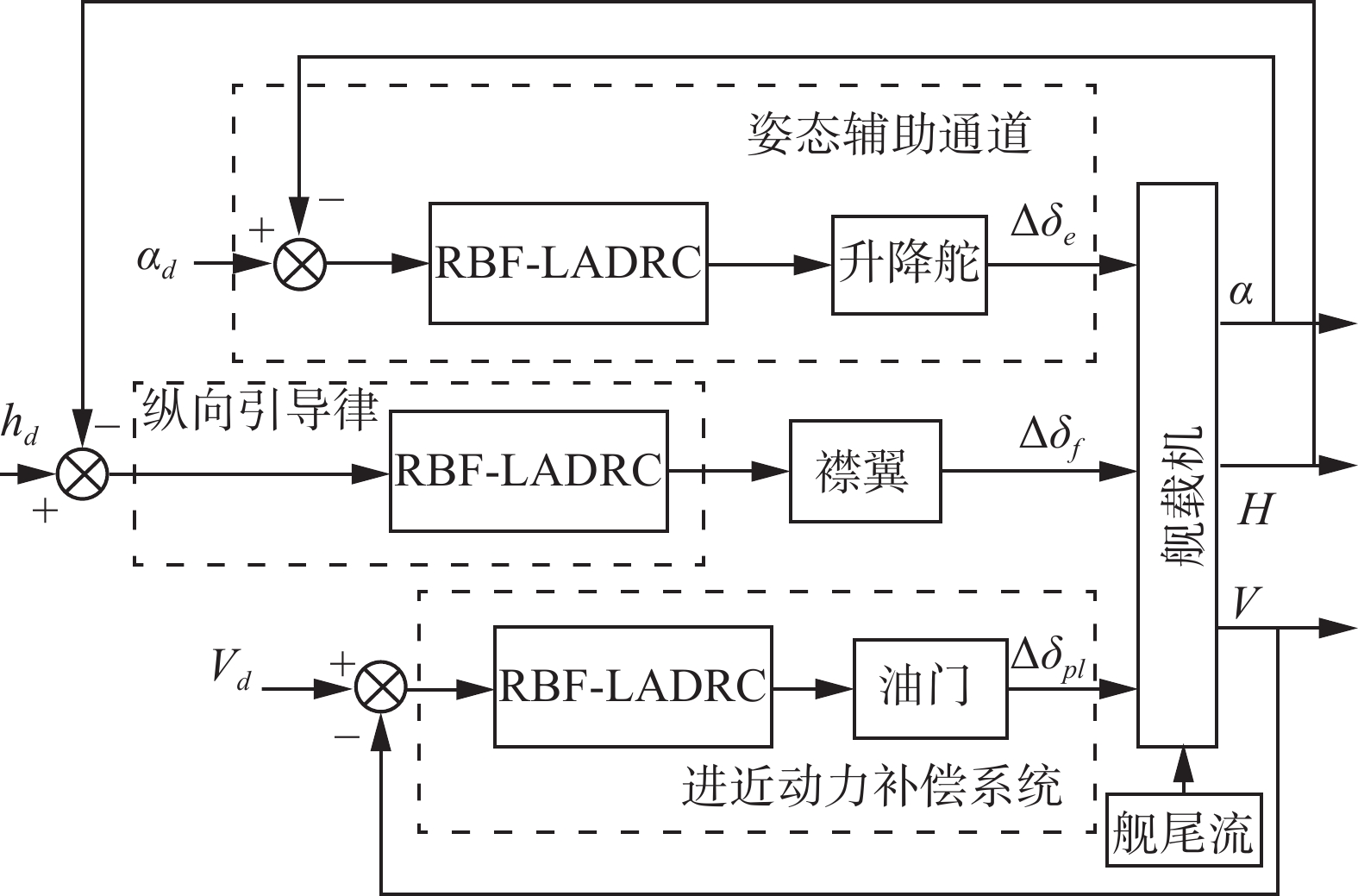
在本节中，基于RBF-LADRC的舰载机直接升力控制自动着舰系统的设计如图5所示。
图 5 基于RBF-LADRC的直接升力自动着舰系统示意Fig. 5 Diagram of the direct lift automatic landing system based on RBF-LADRC下载:
全尺寸图片
RBF-LADRC的设计将针对纵向引导律、姿态辅助控制通道和APCS进行。详细的设计过程将在下文中说明。
3.1 姿态辅助通道控制器设计方案
迎角、俯仰角和轨迹角之间的关系为
$$ \theta = \alpha + \gamma $$ (16) 将式(16)代入式(2)，可以得到方程：
$$ \dot \alpha = \frac{{L + P\sin \alpha }}{{mV}} - \frac{g}{V}\cos \gamma + \dot \theta $$ (17) 式(17)在参考点的线性化被扩展为以下方程：
$$ \Delta \dot \alpha = - \frac{1}{{m{V_*}}}\Delta L - \frac{{\Delta P\cos {\alpha _*} - {P_*}\Delta \alpha \sin {\alpha _*}}}{{m{V_*}}} - \frac{1}{{{V_*}}}g\Delta \gamma \sin {\gamma _*} + \Delta \dot \theta $$ (18) 升力的线性化为
$$ \Delta L = {L_v}_ * \Delta v + {L_\alpha }_ * \Delta \alpha + {L_{\delta e}}_ * \Delta {\delta _e} + {L_{\delta c}}_ * \Delta {\delta _c} + {L_f}_*\Delta {\delta _f} $$ (19) 将式(19)代入式(18)，式(18)变为
$$ \begin{array}{c} \Delta \dot \alpha = - \dfrac{1}{{mV}}\left[ {{L_v}_ * \Delta v + {L_\alpha }_ * \Delta \alpha + {L_{\delta e}}_ * \Delta {\delta _e} + {L_{\delta c}}_ * \Delta {\delta _c} + {L_f}_*\Delta {\delta _f}} \right] -\\ \dfrac{{\Delta P\cos {\alpha _*} - {P_*}\Delta \alpha \sin {\alpha _*}}}{{mV}} - \dfrac{1}{V}g\Delta \gamma \sin \gamma + \Delta \dot \theta \end{array} $$ (20) 设
$$ \begin{array}{c} {f_1} = - \dfrac{1}{{mV}}\left[ {{L_v}_ * \Delta v + {L_\alpha }_ * \Delta \alpha + {L_{\delta c}}_ * \Delta {\delta _c} + {L_f}_*\Delta {\delta _f}} \right]- \\ \dfrac{{\Delta P\cos {\alpha _*} - {P_*}\Delta \alpha \sin {\alpha _*}}}{{mV}} - \dfrac{1}{V}g\Delta \gamma \sin {\gamma _*} + \Delta \dot \theta \end{array} $$ $$ {b_1} = - \frac{1}{{mV}}{L_{\delta e}}_ * $$ 升降舵的传递函数是一个一阶惯性环节，所以式(20)变成了二阶形式：
$$ \Delta \ddot \alpha = {f_1} + {b_1}\Delta {\delta _e} $$ (21) 将迎角回路中的总扰动视为扩展的状态变量：
$$ \left\{ \begin{gathered} {{\dot \alpha }_1} = {\alpha _2} \\ {{\dot \alpha }_2} = {\alpha _3} + {b_1}{\delta _e} \\ {{\dot \alpha }_3} = {{\dot f}_1} \\ \end{gathered} \right. $$ (22) 在式(22)的基础上建立三阶LESO为
$$ \left\{ \begin{array}{l} e = {{\hat \alpha }_1} - {\alpha _1}\\ {{\dot {\hat \alpha }}_1} = {{\hat \alpha }_2} - {\beta _{01}}e\\ {{\dot {\hat \alpha }}_2} = {{\hat \alpha }_3} - {\beta _{02}}e + {b_1}{\delta _e}\\ {{\dot {\hat \alpha} }_3} = - {\beta _{03}}e \end{array} \right. $$ 定义迎角误差和迎角误差的微分，其中
$ {\alpha _{d_1}} $ 和$ {\alpha _{d_2}} $ 是期望迎角输入通过LTD后得到的跟踪和微分信号：$$ \left\{ {\begin{array}{*{20}{l}} {{e_1} = {\alpha _{d_1}} - {{\hat \alpha }_1}} \\ {{e_2} = {\alpha _{d_2}} - {{\hat \alpha }_2}} \end{array}} \right. $$ 将这2个误差进行线性组合，并对迎角控制回路的总干扰进行前馈补偿，得到最终的控制信号
$ u_1 $ 为$$ \left\{ {\begin{array}{*{20}{l}} {{u_1} = {k_{p_{_1}}}{e_1} + {k_{{d_1}}}{e_2}} \\ {{\delta _e} = {u_1} - \dfrac{{{{\hat \alpha }_3}}}{{{b_1}}}} \end{array}} \right. $$ 根据上述RBF-LADRC设计方法设计参数
$ {k_p} $ 和$ {k_d} $ ，采用梯度下降法调整$ {k_{{p_{_1}}}} $ 和$ {k_{{d_1}}} $ 。3.2 进近动力补偿系统控制器设计方案
进场动力补偿系统（approach power compensation system，APCS）用于自动调整油门以控制飞机的进场速度。
式(1)在参考点的线性化被扩展为
$$ \Delta \dot V = \frac{{\Delta P\cos {\alpha _*} - {P_*}\Delta \alpha \sin {\alpha _*}}}{m} - \frac{{\Delta D}}{m} - g\Delta \gamma \cos {\gamma _*} $$ (23) 推力的变化量为
$$ \Delta P = {(\frac{{\partial P}}{{\partial {\delta _p}}})_ * }\Delta {\delta _p} $$ (24) 将式(24)代入式(23)，可得：
$$ \Delta \dot V = \frac{{\cos {\alpha _*}}}{m}{(\frac{{\partial P}}{{\partial {\delta _p}}})_ * }\Delta {\delta _p} - \frac{{{P_*}\Delta \alpha \sin {\alpha _*}}}{m} - \frac{{\Delta D}}{m} - g\Delta \gamma \cos {\gamma _*} $$ (25) 令：
$$ {f_2} = - \frac{{{P_*}\Delta \alpha \sin {\alpha _*}}}{m} - \frac{{\Delta D}}{m} - g\Delta \gamma \cos {\gamma _*} $$ $$ {b_2} = \frac{{\cos {\alpha _*}}}{m}{(\frac{{\partial P}}{{\partial {\delta _p}}})_ * } $$ 油门杆作动器传递函数是一个一阶惯性环节，所以式(25)变成了如下的二阶形式：
$$ \Delta \ddot V = {b_2}\Delta {\delta _{pl}} + {f_2} $$ 建立三阶RBF-LADRC为
$$ \left\{ {\begin{array}{*{20}{l}} {e = {{\hat V}_1} - {V_1}}\\ {{{\dot {\hat V}}_1} = {{\hat V}_2} - {\beta _{11}}e}\\ {{{\dot {\hat V}}_2} = {{\hat V}_3} - {\beta _{12}}e + {b_2}{\delta _{pl}}}\\ {{{\dot {\hat V}}_3} = - {\beta _{13}}e}\\ {{e_1} = {V_{d1}} - {{\hat V}_1}}\\ {{e_2} = {V_{d2}} - {{\hat V}_2}}\\ {{u_2} = {k_{{p_2}}}{e_1} + {k_{{d_2}}}{e_2}}\\ {{\delta _{pl}} = {u_2} - \dfrac{{{{\hat V}_3}}}{{{b_2}}}} \end{array}} \right. $$ 根据上述RBF-LADRC设计方法设计参数
${k_{p_{_2}}}$ 和${k_{d_{_2}}}$ ，用梯度下降法来调整${k_{p_{_2}}}$ 和${k_{d_{_2}}}$ 。3.3 纵向引导律控制器设计方案
舰载机在着舰过程中受到舰尾流干扰。因此，可以使用RBF-LADRC的纵向引导律来有效抑制干扰。
式(3)在参考点的线性化被扩展为以下方程：
$$ \frac{{{\rm{d}}\Delta h}}{{{\rm{d}}t}} = \sin {\gamma _ * }\Delta v + {v_ * }\cos {\gamma _ * }\Delta \gamma $$ 令：
$$ f = \sin {\gamma _ * }\Delta v $$ $$ b = {v_ * }\cos {\gamma _ * } $$ $$ u = \Delta \gamma $$ 则此时式(26)可写为
$$ \Delta \dot h = f + bu $$ 将高度环路中的总扰动视为扩展状态，建立线性扩展状态观测器为
$$ \left\{ {\begin{array}{*{20}{l}} {e = {{\hat h}_1} - {h_1}}\\ {{{\dot {\hat h}}_1} = {{\hat h}_2} - {\beta _{21}}e + bu}\\ {{{\dot {\hat h}}_2} = - {\beta _{22}}e} \end{array}} \right.$$ 定义误差信号为
$$ {e}_{1}={h}_{d}-{\hat{h}}_{1} $$ 对这2个误差进行线性组合，并对高度控制回路的总扰动进行前馈补偿，得到最终控制信号
$ u $ 为$$ \left\{ {\begin{array}{*{20}{l}} {{u_3} = {k_{{p_3}}}{e_1}} \\ {u = {u_3} - \dfrac{{{{\hat h}_2}}}{{{b_3}}}} \end{array}} \right. $$ 根据上述RBF-LADRC设计方法，采用梯度下降法对参数
$ {k_{{p_3}}} $ 进行设计。4. 着舰仿真结果
当舰载机进入下滑道入口时，初始条件设定为：舰载机的飞行高度为
${h_0} = 114.3\;{\rm{m}}$ ，舰载机理想着陆点的参考高度为${h_c} = 21.1\;{\rm{m}}$ ，参考速度为${V_0} = 70\;{\rm{m}}/{\rm{s}}$ 。迎角控制在${\alpha _0} = {9.1 }$ °，轨迹角控制在${\gamma _0} = - {3.5}$ °。在仿真中，RBF-LADRC被应用于舰载机直接升力控制自动着舰系统以验证其着舰性能。此外，RBF-LADRC方案的着舰性能与传统的LADRC、PID、BP-LADRC以及自适应滑膜控制进行了比较。控制器参数设置为：三通道观测器带宽为
$ {w_1} = 10 $ ，$ {w_2} = 10 $ ，$ {w_3} = 3.5 $ ；RBF神经网络参数设置为学习率$ \eta = 0.25 $ ，动量因子$ \alpha = 0.05 $ ，$ m = 6 $ 。纵向线性小扰动方程的矩阵具体参数为
$$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{ - 0}}{{.067\;3}}}& {{{1}}{{.07}}}& 0& {{{ - 9}}{{.792}}}& {{{2}}{{.11}} \times {{10}^{ - 4}}} \\ {{{ - 0}}{{.004\;48}}}& {{{ - 0}}{{.422\;5}}}& 1& {0.008\;6}& {1.3 \times {{10}^{ - 5}}} \\ {2.05 \times {{10}^{ - 4}}}& {{{0}}{{.486}}}& {{{ - 0}}{{.159\;8}}}& {{{ - 4}}{{.7}} \times {{10}^{ - 4}}}& 0 \\ 0& 0& 1& 0& 0 \\ { - 0.061}& { - 69.87}& 0& {69.87}& 0 \end{array}} \right] $$ $$ {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{{ - 0}}{{.025\;78}}}&{{{ - 0}}{{.001\;197}}}&{{{0}}{{.107\;1}}} \\ {{{ - 0}}{{.001\;223}}}&{{{ - 8}}{{.9}} \times {{10}^{ - 5}}}&{{{ - 3}}{{.5}} \times {{10}^{ - 4}}} \\ {{{ - 0}}{{.021\;2}}}&{0.005\;13}&{1.14 \times {{10}^{ - 5}}} \\ 0&0&0 \\ 0&0&0 \end{array}\begin{array}{*{20}{c}} {{0}} \\ {{{6}}{{.84}} \times {{10}^{ - 4}}} \\ {{{0}}{{.003\;36}}} \\ 0 \\ 0 \end{array}} \right] $$ $$ {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0 \\ 0&1&0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&1&0 \\ 0&0&0&0&1 \\ {{\text{4}}{\text{.57}} \times {{10}^{ - 4}}}&{{\text{0}}{\text{.040\;2}}}&0&0&{{{ - 1}}{\text{.44}} \times {{10}^{ - 6}}} \\ 0&{{{ - 1}}}&0&1&0 \end{array}} \right] $$ $$ {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ {{\text{1}}{\text{.25}} \times {{10}^{ - 4}}}&{{\text{9}}{\text{.1}} \times {{10}^{ - 6}}}&0&{{{ - 6}}{\text{.9}} \times {{10}^{ - 5}}} \\ 0&0&0&0 \end{array}} \right] $$ $$ {\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.076}}}&{{{ - 0}}{\text{.14}}} \\ {{\text{0}}{\text{.004}}}&{{\text{0}}{\text{.006}}} \\ {{\text{0}}{\text{.000\;19}}}&{{{ - 0}}{\text{.007}}} \\ 0&0 \\ 0&0 \end{array}} \right] $$ $$ {\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&0 \\ 0&0 \\ 0&0 \\ 0&0 \\ {{{ - 5}}{\text{.45}} \times {{10}^{ - 4}}}&{{{ - 4}}{\text{.911}} \times {{10}^{ - 4}}} \\ 0&0 \end{array}} \right] $$ 4.1 LESO输出估计
从图6可以看出，通过LESO对三通道输出进行估计，精度高，响应快，有利于提高所提控制方案的抗干扰能力。
图 6 LESO对输出变化量的估计Fig. 6 Estimate of the output variation by LESO下载:
全尺寸图片
4.2 舰尾流扰动下着舰仿真结果与分析
1）稳定性比较。
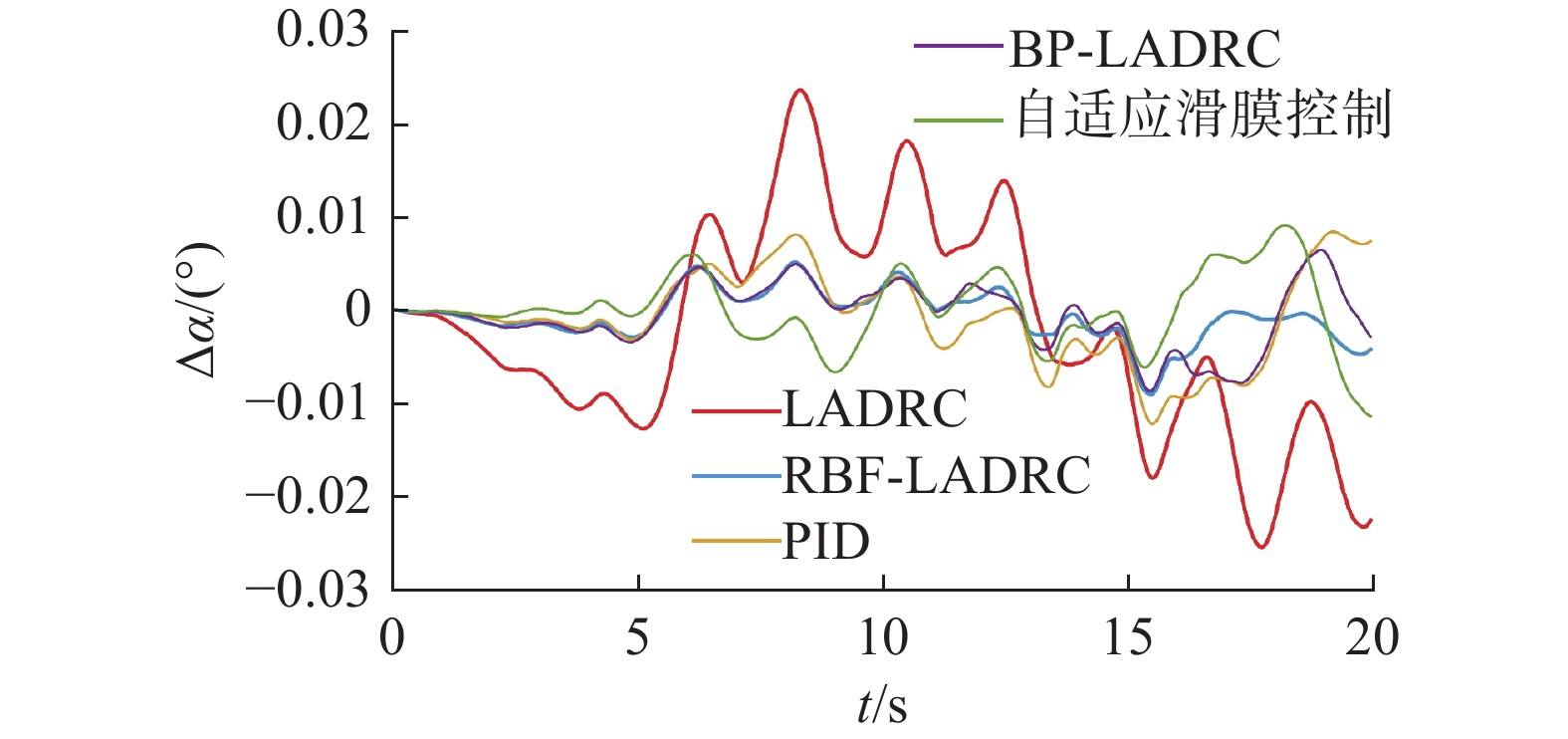
从图7可以看出，当不引入RBFNN时，传统LADRC的迎角偏差比较大。所提方法与PID相比，虽然偏差变化不明显，但迎角的波动明显减慢。通过对比分析，新设计方法下的迎角更加稳定。从图8可以看出，所提方法的速度扰动变化明显低于其他控制方法。相比之下，新设计方法的速度稳定性得到了较好的保持，并且可以有效地抑制舰尾流扰动。
图 7 迎角变化量对比Fig. 7 Comparison of the AOA variation下载:
全尺寸图片
图 8 速度变化量对比Fig. 8 Comparison of the velocity variation下载:
全尺寸图片
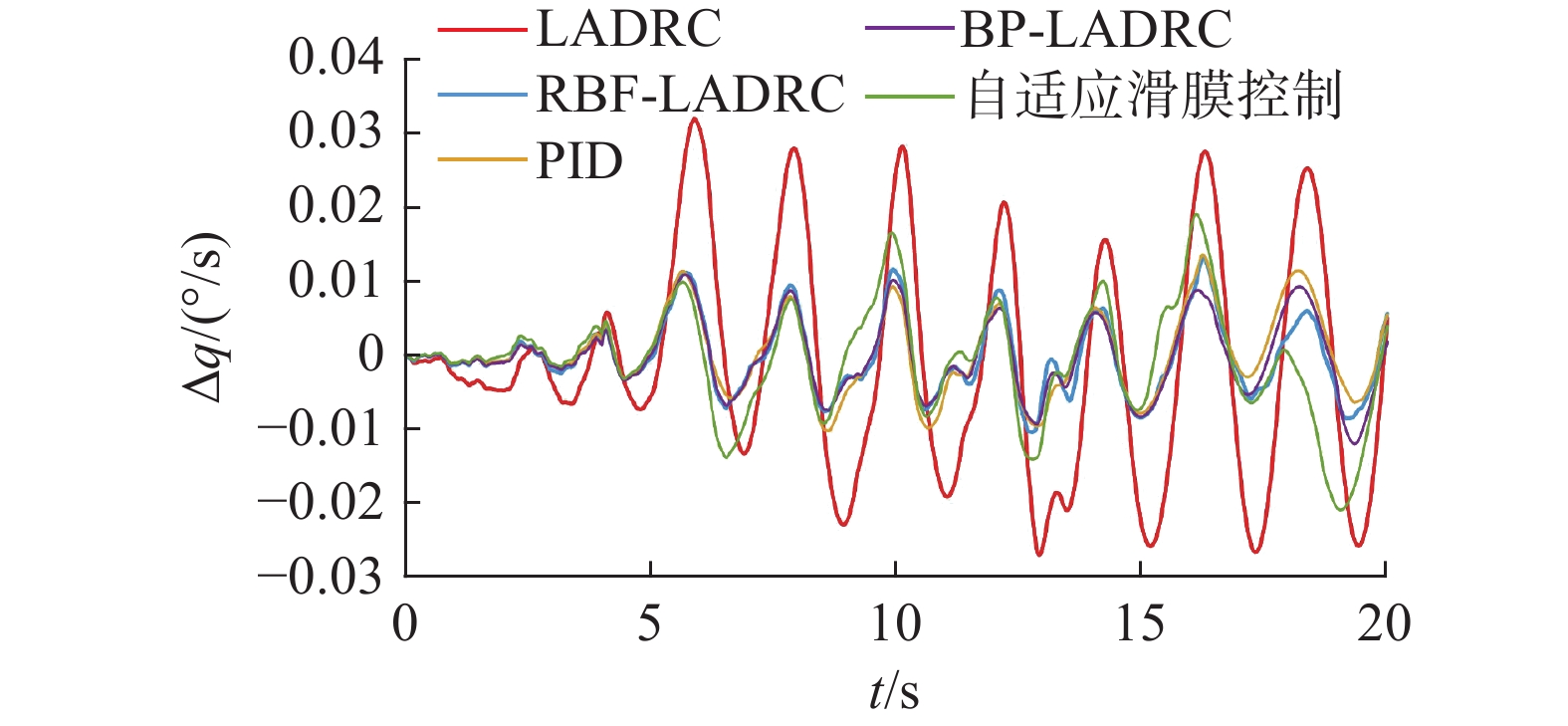
从图9和图10可以看出，引入RBFNN后，与传统的LADRC相比，所提方法的俯仰角偏差和俯仰率偏差波动明显减小，最大偏差值降低。相比之下，在RBF-LADRC方法下，舰载机的飞行姿态可以得到更好的保持。减少飞行姿态的偏差可以使航母飞机更平稳地降落，增强系统的稳定性。
图 9 俯仰角速率变化量对比Fig. 9 Comparison of the pitch angle rate variation下载:
全尺寸图片
图 10 俯仰角变化量对比Fig. 10 Comparison of the pitch angle variation下载:
全尺寸图片
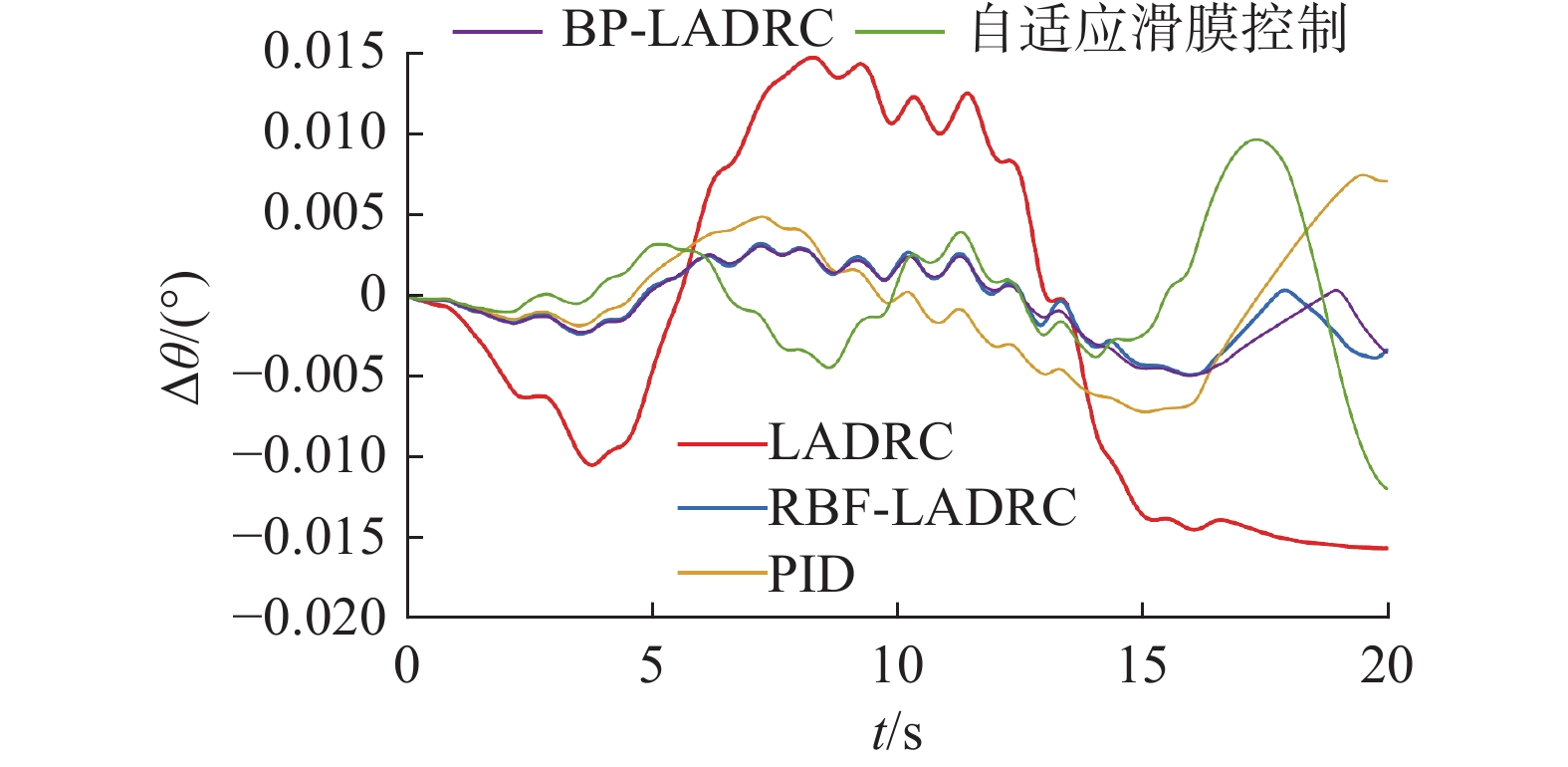
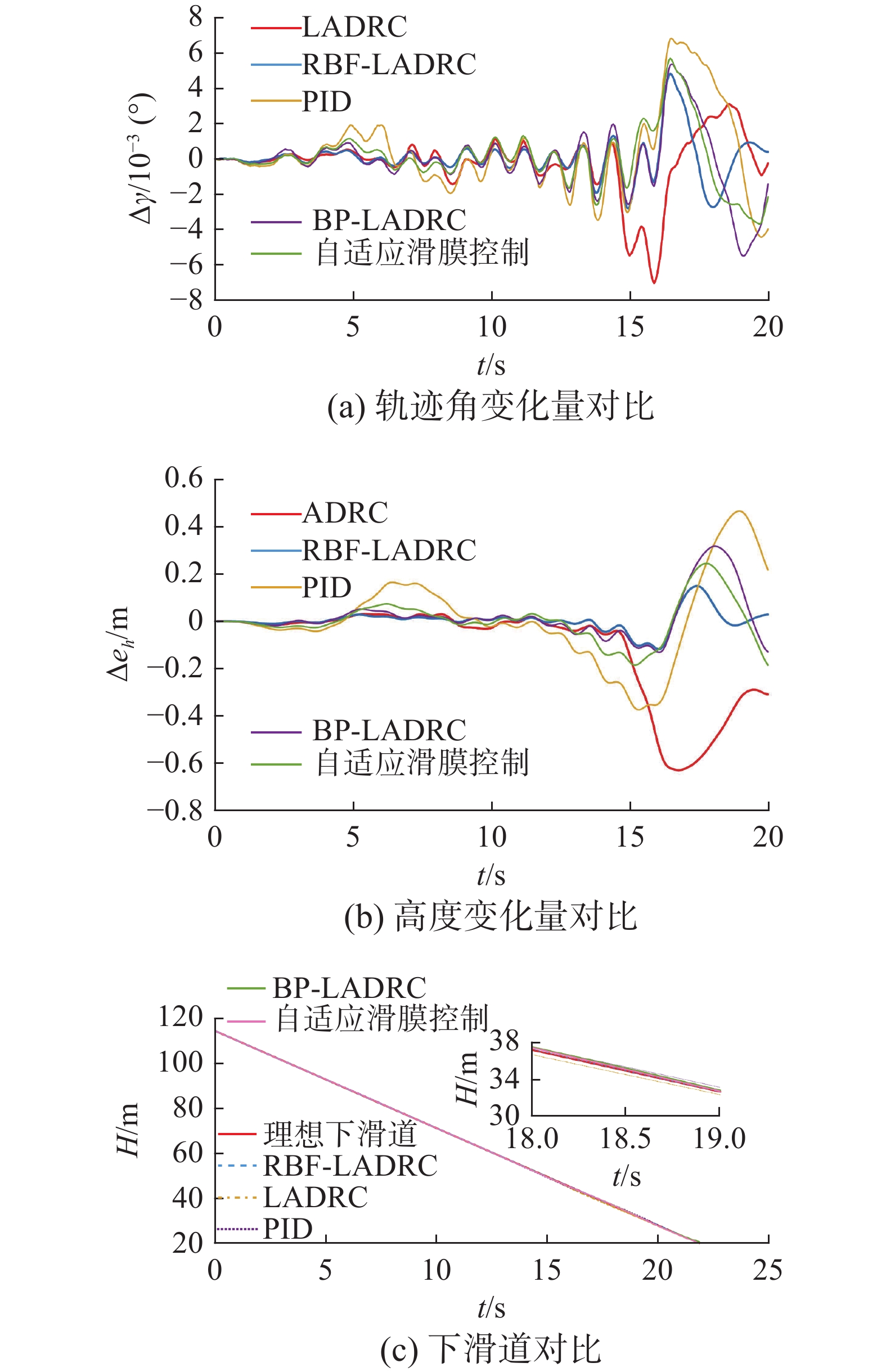
2）轨迹跟踪性能比较。
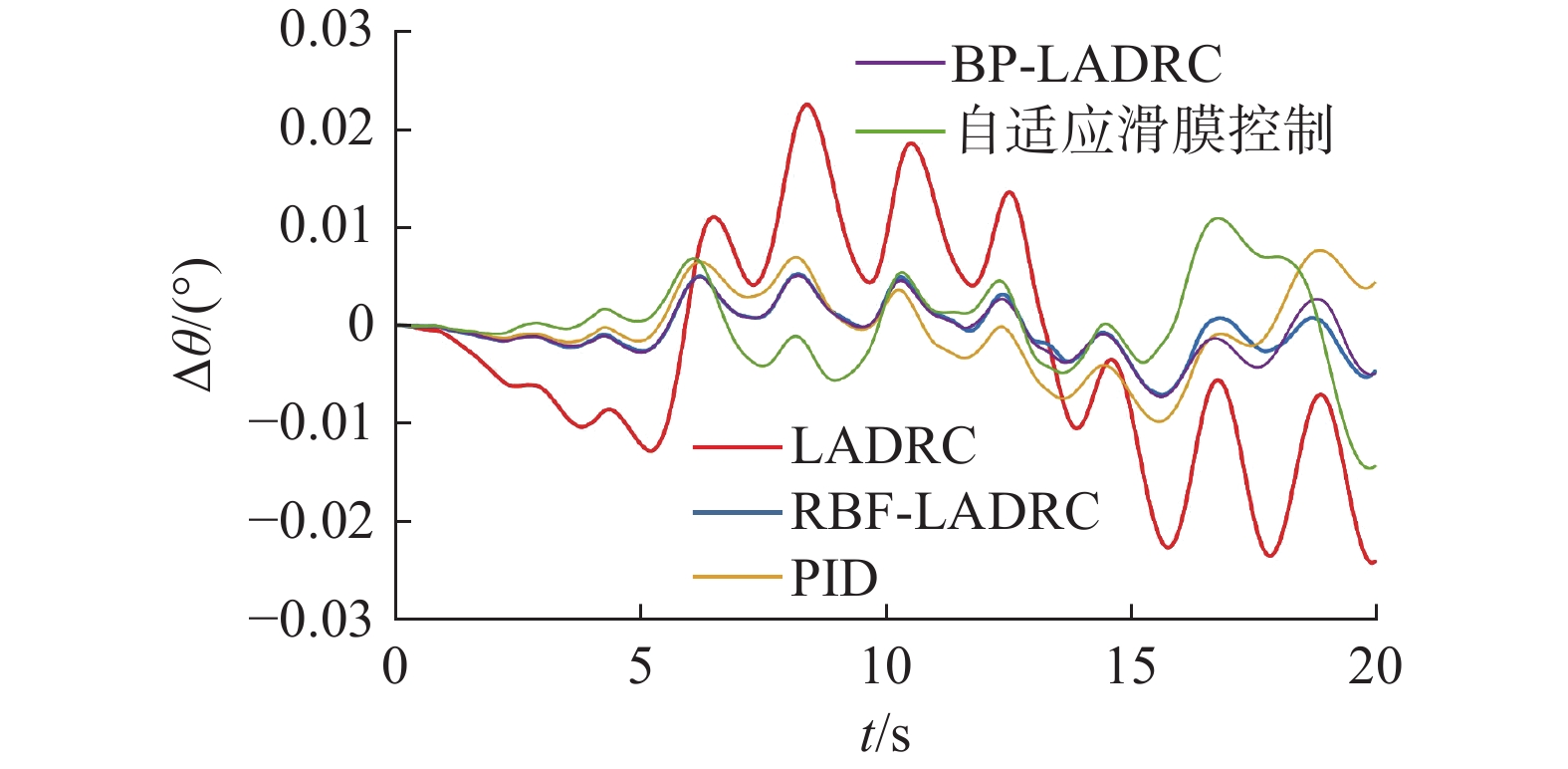
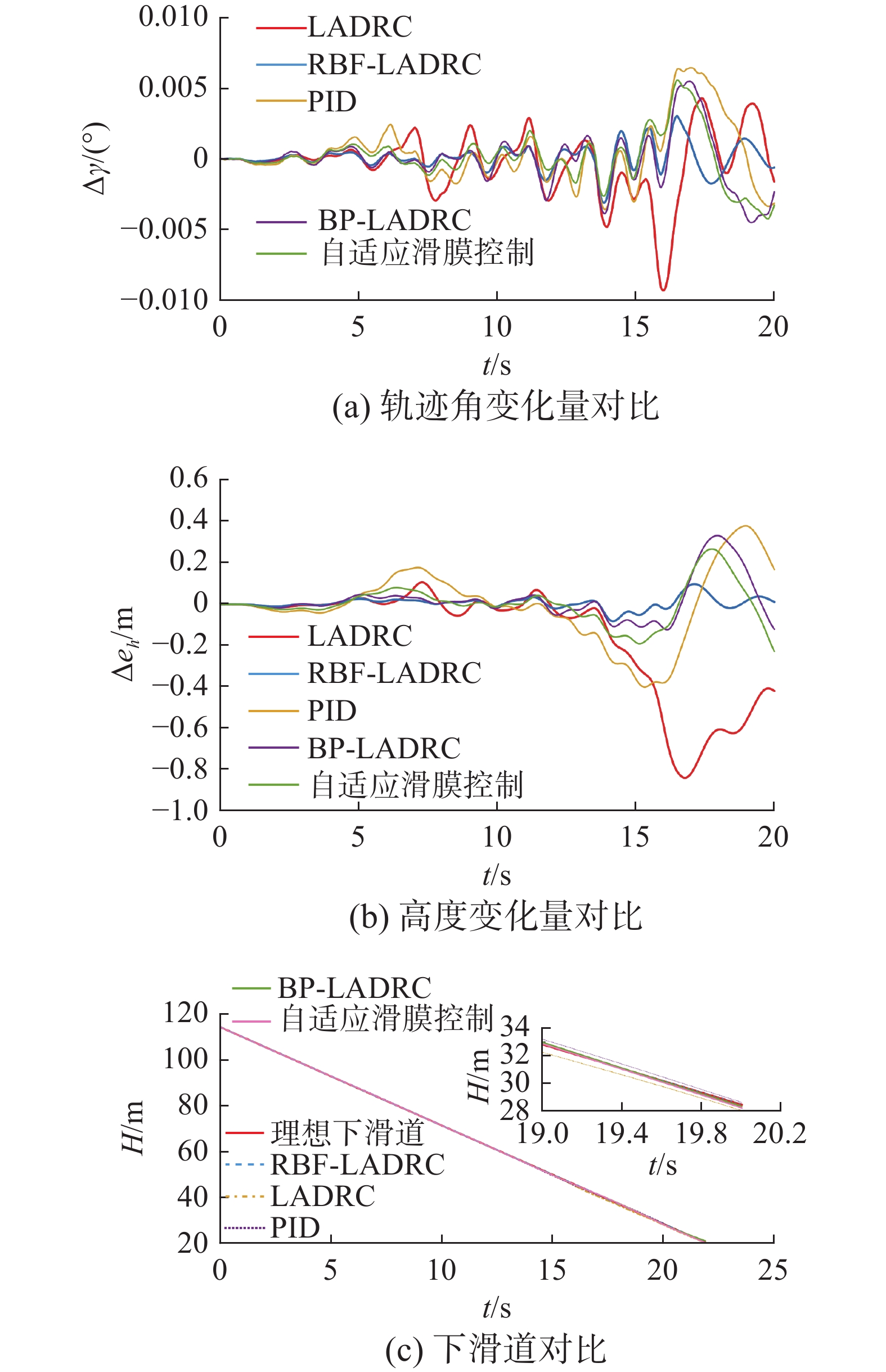
图11比较了所提方法与其他4种方法的轨迹角偏差，其中所提方法是指本文提出的RBF-LADRC控制器。比较分析表明，在舰尾流的影响下，RBF-LADRC能更好地保持轨迹角的稳定性。在自动着舰模式下，稳定的轨迹角表明此设计可以安全地完成着舰任务。图11给出了所提方法和其他4种方法的轨迹跟踪比较。高度偏差表示仿真结果与理想下滑道之间的偏差。可以看出，基于RBF-LADRC的舰载机直接升力自动着舰系统的跟踪误差在0.2 m以内。舰载机沿着理想的下滑路径着舰。通过稳定性比较部分可以看出，RBF-LADRC略优于BP-LADRC方法，但是轨迹跟踪性能仿真结果表明，所提出的基于RBF-LADRC的舰载机直接升力自动着舰系统在有舰尾流干扰的情况下能更好地跟踪理想下滑道。
图 11 飞行轨迹对比Fig. 11 Comparison of flight path下载:
全尺寸图片
4.3 执行器故障时着舰仿真结果与分析
为进一步验证本文设计的RBF-LADRC的鲁棒性，当执行器存在以下时变故障情况时进行仿真分析。发动机故障
${\delta _{pf}} = 10\sin \text{π} t/2.5$ (°)在$t = 4\;{\rm{s}}$ 处引入；升降舵故障$ {\delta _{ef}} = 8\sin \text{π} t/2.5$ (°)在$t = 5\;{\rm{s}}$ 引入。1）稳定性比较。
从图12~15可以看出，与其他方法相比，当飞机遭受干扰和时变故障时，所提出的方法的姿态角和速度更加稳定。
图 12 迎角变化量对比Fig. 12 Comparison of the AOA variation下载:
全尺寸图片
图 13 速度变化量对比Fig. 13 Comparison of the velocity variation下载:
全尺寸图片
图 14 俯仰角速率变化量对比Fig. 14 Comparison of the pitch angle rate variation下载:
全尺寸图片
图 15 俯仰角变化量对比Fig. 15 Comparison of the pitch angle variation下载:
全尺寸图片
2）轨迹跟踪性能比较。
从图16可以看出，所提出方法的轨迹角和高度变化均小于其他的控制方法，可以更好地跟踪理想下滑道的误差。
图 16 飞行轨迹对比Fig. 16 Comparison of flight path下载:
全尺寸图片
5. 结束语
1）本文设计了基于RBFNN结合线性自抗扰控制的舰载机直接升力自动着舰系统，能够较好地抑制舰尾流的扰动。对着舰系统进行仿真并与 PID 控制器和传统LADRC进行对比，结果表明该方法不仅抑制了舰尾流扰动，准确补偿了扰动造成的偏差，而且显著提高了系统的性能和鲁棒性，并能保持轨迹角的稳定性。
2）从仿真结果可以看出，所设计的控制方案是有效的，其设计思想和方法值得借鉴，如可应用于旋翼机、固定翼飞机、推力矢量飞机等。
3）未来将进一步研究如何利用该方法的鲁棒性和学习能力处理着舰系统的控制输入饱和、襟翼执行器故障等复杂控制问题。
-
图 1 舰载机着舰阶段
Fig. 1 Carrier-based aircraft landing phase
下载:
全尺寸图片
图 2 舰尾流中姿态和空速的关系
Fig. 2 Relationship between attitude and airspeed in carrier air-wake
下载:
全尺寸图片
图 3 RBF神经网络结构
Fig. 3 RBF neural network structure diagram
下载:
全尺寸图片
图 4 基于RBF神经网络的LADRC结构
Fig. 4 Structure of RBF neural network based on LADRC
下载:
全尺寸图片
图 5 基于RBF-LADRC的直接升力自动着舰系统示意
Fig. 5 Diagram of the direct lift automatic landing system based on RBF-LADRC
下载:
全尺寸图片
图 6 LESO对输出变化量的估计
Fig. 6 Estimate of the output variation by LESO
下载:
全尺寸图片
图 7 迎角变化量对比
Fig. 7 Comparison of the AOA variation
下载:
全尺寸图片
图 8 速度变化量对比
Fig. 8 Comparison of the velocity variation
下载:
全尺寸图片
图 9 俯仰角速率变化量对比
Fig. 9 Comparison of the pitch angle rate variation
下载:
全尺寸图片
图 10 俯仰角变化量对比
Fig. 10 Comparison of the pitch angle variation
下载:
全尺寸图片
图 11 飞行轨迹对比
Fig. 11 Comparison of flight path
下载:
全尺寸图片
图 12 迎角变化量对比
Fig. 12 Comparison of the AOA variation
下载:
全尺寸图片
图 13 速度变化量对比
Fig. 13 Comparison of the velocity variation
下载:
全尺寸图片
图 14 俯仰角速率变化量对比
Fig. 14 Comparison of the pitch angle rate variation
下载:
全尺寸图片
图 15 俯仰角变化量对比
Fig. 15 Comparison of the pitch angle variation
下载:
全尺寸图片
图 16 飞行轨迹对比
Fig. 16 Comparison of flight path
下载:
全尺寸图片
-
[1] PRICKETT A L, PARKES C J. Flight testing of the F/A-18E/F automatic carrier landing system[C]//2001 IEEE Aerospace Conference Proceedings (Cat. No. 01TH8542). Piscataway: IEEE, 2002: 2593−2612. [2] LUO Fei, ZHANG Junhong, LYU Pengfei, et al. Carrier-based aircraft precision landing using direct lift control based on incremental nonlinear dynamic inversion[J]. IEEE access, 2022, 10: 55709–55725. doi: 10.1109/ACCESS.2022.3175164 [3] DESALVO M, HEATHCOTE D, SMITH M J, et al. Direct lift control using distributed aerodynamic bleed[C]//Proceedings of the AIAA Scitech 2019 Forum. Reston, Virginia: AIAA, 2019: AIAA2019−0591. [4] 吴文海, 汪节, 高丽, 等. MAGIC CARPET着舰技术分析[J]. 系统工程与电子技术, 2018, 40(9): 2079–2091. doi: 10.3969/j.issn.1001-506X.2018.09.26 WU Wenhai, WANG Jie, GAO Li, et al. Analysis on MAGIC CARPET carrier landing technology[J]. Systems engineering and electronics, 2018, 40(9): 2079–2091. doi: 10.3969/j.issn.1001-506X.2018.09.26 [5] LIANG Hongyu, LI Zhengyang, SU Xichao, et al. Direct lift control of aircraft based on adaptive fuzzy dynamic inverse[C]//Proceedings of the 2019 4th International Conference on Robotics, Control and Automation. New York: ACM, 2019: 60−64. [6] ZHU Hongyuan, LIU Xiaoxiong, ZHANG Yuehang, et al. Design of carrier-based aircraft landing control law based on direct force[M]. Singapore: Springer, 2021: 1153−1163. [7] SUBRAHMANYAM M B. H-infinity design of F/A-18A automatic carrier landing system[J]. Journal of guidance, control, and dynamics, 1994, 17(1): 187–191. doi: 10.2514/3.21177 [8] URNES J M, HESS R K. Development of the F/A-18A automatic carrier landing system[J]. Journal of guidance, control, and dynamics, 1985, 8(3): 289–295. doi: 10.2514/3.19978 [9] 孙笑云, 江驹, 甄子洋, 等. 舰载飞机自适应模糊直接力着舰控制[J]. 西北工业大学学报, 2021, 39(2): 359–366. doi: 10.1051/jnwpu/20213920359 SUN Xiaoyun, JIANG Ju, ZHEN Ziyang, et al. Adaptive fuzzy direct lift control of aircraft carrier-based landing[J]. Journal of Northwestern Polytechnical University, 2021, 39(2): 359–366. doi: 10.1051/jnwpu/20213920359 [10] JAISWAL R, SHASTRY A, SWARNKAR S, et al. Adaptive longitudinal control of UAVs with direct lift control[J]. IFAC-Papersonline, 2016, 49(1): 296–301. doi: 10.1016/j.ifacol.2016.03.069 [11] ZHUANG Huixuan, SUN Qinglin, CHEN Zengqiang, et al. Back-stepping active disturbance rejection control for attitude control of aircraft systems based on extended state observer[J]. International journal of control, automation and systems, 2021, 19(6): 2134–2149. doi: 10.1007/s12555-019-1029-x [12] ZUO Yuefei, ZHU Xiaoyong, QUAN Li, et al. Active disturbance rejection controller for speed control of electrical drives using phase-locking loop observer[J]. IEEE transactions on industrial electronics, 2019, 66(3): 1748–1759. doi: 10.1109/TIE.2018.2838067 [13] WANG Fenfen, LIU Xubo, TIAN Haiming, et al. An improved auto-disturbance rejection control method for hypersonic vehicle control system[C]//2020 Chinese Control and Decision Conference . Piscataway: IEEE, 2020: 3410−3415. [14] WEI Bai, FENG Pan, BO Yangxing, et al. Visual landing system of UAV based on ADRC[C]//2017 29th Chinese Control and Decision Conference . Piscataway: IEEE, 2017: 7509−7514. [15] GAO Tongyue, WANG Dongdong, FEI Tao, et al. Attitude decoupling controller design of dual-ducted SUAV based on ADRC system[J]. Applied mechanics and materials, 2014, 536/537: 1143–1148. doi: 10.4028/www.scientific.net/AMM.536-537.1143 [16] WANG Zhaoji, ZHAO Tong. Based on robust sliding mode and linear active disturbance rejection control for attitude of quadrotor load UAV[J]. Nonlinear dynamics, 2022, 108(4): 3485–3503. doi: 10.1007/s11071-022-07349-y [17] LIU Chunqiang, LUO Guangzhao, DUAN Xiaoli, et al. Adaptive LADRC-based disturbance rejection method for electromechanical servo system[J]. IEEE transactions on industry applications, 2020, 56(1): 876–889. doi: 10.1109/TIA.2019.2955664 [18] YU Shiwei, LIU Lie, HAN Lianghua, et al. Research on ultra-high power laser curing based on RBF neural network[C]//2022 Global Conference on Robotics, Artificial Intelligence and Information Technology. Piscataway: IEEE, 2022: 290−293. [19] YANG Hongjun, LIU Jinkun. An adaptive RBF neural network control method for a class of nonlinear systems[J]. IEEE/CAA journal of automatica sinica, 2018, 5(2): 457–462. doi: 10.1109/JAS.2017.7510820 [20] HAN Honggui, LU Wei, HOU Ying, et al. An adaptive-PSO-based self-organizing RBF neural network[J]. IEEE transactions on neural networks and learning systems, 2018, 29(1): 104–117. doi: 10.1109/TNNLS.2016.2616413 [21] WANG Yangang, WANG Weijun, QU Xiangju. Multi-body dynamic system simulation of carrier-based aircraft ski-jump takeoff[J]. Chinese journal of aeronautics, 2013, 26(1): 104–111. doi: 10.1016/j.cja.2012.12.007 [22] ZHANG Wen, ZHANG Zhi, ZHU Qidan, et al. Dynamics model of carrier-based aircraft landing gears landed on dynamic deck[J]. Chinese journal of aeronautics, 2009, 22(4): 371–379. doi: 10.1016/S1000-9361(08)60113-2 [23] ZHEN Ziyang, JIANG Shuoying, MA Kun. Automatic carrier landing control for unmanned aerial vehicles based on preview control and particle filtering[J]. Aerospace science and technology, 2018, 81: 99–107. doi: 10.1016/j.ast.2018.07.039 [24] XIA Guihua, DONG Ran, XU Jiangtao, et al. Linearized model of carrier-based aircraft dynamics in final-approach air condition[J]. Journal of aircraft, 2016, 53(1): 33–47. doi: 10.2514/1.C033175 [25] KAHN A, EDWARDS D. Navigation, guidance and control for the CICADA expendable micro air vehicle[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2012: AIAA2012−4536. [26] FAST B, MIKLOSOVIC R, RADKE A. Active disturbance rejection control of a MEMS gyroscope[C]//2008 American Control Conference. Piscataway: IEEE, 2008: 3746−3750. [27] LAN Zebu. Applications of BP, convolutional and RBF networks[C]//2021 2nd International Conference on Computing and Data Science . Piscataway: IEEE, 2021: 543−547. [28] YANG Fangfang, GUO Chen, JIANG Yunbiao. RBF based integrated ADRC controller for a ship dynamic positioning system[M]. Singapore: Springer, 2017: 673−680.
