随着社会的发展，人类对海洋资源的探索更加深入，我们越来越需要清晰的水下图像来进行水下生物，水下操作系统的研究。然而，获取的水下图像往往降质十分严重，其中最主要的因素是水对于不同波长的光吸收率不同，红色光波长最长吸收最为严重，而蓝色光波长最短吸收最少，因此水下图像总是呈现出蓝绿色调，同时伴随着色偏和色彩不鲜明等问题。同时由于水中光线传播距离短，受到水分子、悬浮颗粒、藻类、微生物等的散射和吸收作用，光线的强度、频率和颜色均发生变化，从而导致水下图像总是模糊，充满了噪点。水下图像复原的方法可以被粗略的分为传统方法和基于深度学习的方法。早期人们尝试去通过调整像素值来提高视觉质量，例如动态像素的延展^[1]、像素点的自适应分配^[2]以及图像融合^[3]。尽管这些方法可以在一定程度上提高视觉质量，但它们忽略了水下成像机制，因此往往会导致过度增强或增强不足的问题，并且会导致伪影的产生。例如在一些水下场景中^[4]处理的效果并不总是很好。如今被广泛使用的是水下成像的物理模型，物理模型通过先验知识来评估水下成像模型的参数，这些基于先验知识的方法包括红通道先验^[5]、水下暗通道先验^[6]、最小信息先验^[7]等。尽管这些物理模型取得了不错的复原效果，但是其计算时间较长，同时其对水下成像公式中参数评估的准确性十分依赖于水下成像的类型，而且模型中的先验并不总是成立的，因此这类方法的泛化能力较差。神经网络模型的发展为水下图像处理提供了新的思路，随着Swin-Transformer^[8]、ConvNext^[9]等网络架构的提出，神经网络处理视觉任务获得了进一步的提升。但是与水下图像相对应的目标图像难以获取，现有的数据集中数据数量相比于其他任务如分类，语义分割等也十分稀少，这也限制了数据驱动模型的应用，为了解决数据集问题，文献[10-11]使用了生成对抗网络和水下图像生成公式来合成水下图像和清晰图像用于有监督学习。为了避免使用成对的训练数据，UcycleGAN^[12]使用了一个弱监督的水下图像修复网。

水下图像质量低主要体现在色偏和图像模糊两个方面，对于图像模糊的处理往往需要关注图像内物体的边缘细节，这是局部性的、像素级别的处理，而造成色偏的主要原因是水对于光的均匀吸收造成水下图像整体偏绿或偏蓝，这往往是全局性的与物体所处的位置无关。

考虑到以通用暗通道先验(generalization of the dark channel prior, GDCP)^[13]为代表的传统方法中物理先验知识的成功应用，本文提出了基于物理先验的特征融合水下图像恢复网络。首先考虑到水下图像的成像特点，将水下图像中局部空间信息和全局色彩信息进行分离，提取出保留像素空间位置关系的低通道数特征向量和宽、高均为1且只包含全局性色彩信息的高通道数特征向量。并且在空间信息提取模块中，通过空间注意力机制使模型专注于水下图像中某些局部信息，提高恢复图像中物体边缘细节的表现，减少模糊。在色彩信息提取模块中，考虑到不同成像条件对水下图像色彩的影响，通过引入通道注意力机制使模型专注于不同通道上色彩、对比度、亮度等全局信息的恢复，减少生成图像中的色偏，使生成图像尽可能地接近于陆地图像(GroudTruth)。提取出不同信息后，在解码器中逐步生成恢复图像，通过调制操作联合不同通道上的全局信息，使不同层级的解码器将不同尺度的色彩信息逐步融合进空间信息中。最后，在物理先验模块中，将水下光学成像模型IMF(image model function)嵌入到最终的生成器中，通过引入注意力机制，使网络在处理不同的水下图像时关注不同的成像机制，以综合利用神经网络和传统方法的优势。

1.   相关知识

1.1   水下图像生成

Jaffe-McGlamery模型^[11,14]是一种用于描述水下光学传输的经典模型，其假设水体是均质的，并考虑了散射、吸收和反射等因素对光线的影响，如图1所示。

图  1  水下图像成像过程

Fig.  1  Underwater image imaging process

下载: 全尺寸图片

该模型可抽象表达为

式中将水下获得的信号分为 $E_d $ 直接照射、 $E_f$ 前向散射和 $E_b$ 后向散射3个部分。 $(x,y)$ 表示图像中像素的坐标； $ E_T(x,y) $ 代表相机捕捉到的总光能量； $ E_d(x,y) $ 代表直接照射部分是指光线从物体表面反射并在未经散射的情况下到达相机的部分； $ E_f(x,y) $ 代表前向散射，是物体表面反射的光在到达相机这段距离上发生的散射； $ E_{b}(x, y) $ 代表后向散射部分，是指自然光到达物体表面之前被反射进相机的部分。

在水下环境中，光线很容易被吸收和散射，导致光线强度衰减快，前向散射能够传递的距离有限，因此前向散射所占比例较小。同时在水中水分子和悬浮颗粒的影响下，散射光线更容易向后方散射，这会进一步导致前向散射的减少，从而扩大后向散射所占比例，因此为了便于计算，我们常常忽略IMF中的前向散射部分，而使用简化后的Jaffe-McGlamery模型，该模型如下表示：

式中： $(x,y)$ 表示像素点在图像中的坐标, $c$ 代表红绿蓝(r、g、b)通道， $I_c(x,y)$ 表示相机直接拍摄的光强度， $t_c(x,y)$ 表示在水中介质传输率， $ J_{c}(x, y) t_{c}(x, y) $ 表示场景能量在水的吸收作用后剩余的部分， $ J_{c}(x, y) $ 表示未衰减的图像， $A_c$ 表示全局均匀环境光。

在水中， $t_c(x,y)$ 也被称为介质传输率，其值受到水下衰减系数和物体与相机间距离的影响，因此 $t_c(x,y)$ 可以通过以下关系式表示：

式中： $\,\beta _c$ 为不同通道的水下衰减系数，其由光的波长决定； $d(x)$ 表示目标的深度信息，即目标物体到相机的距离。

使用介质传输率和全局均匀环境光，可以得到未衰减图像的计算公式：

由于使用简化后的Jaffe-McGlamery模型会导致一些信息的丢失，同时为了保存一些深度信息，因此在实际应用中，设置 $t_0 = 0.1$ 作为下边界，同时裁剪 $J_c(x,y)$ 在13~255之间。

1.2   暗通道先验算法

单图像复原的通用暗通道先验GDCP算法^[13]提出了一种通用的基于物理先验的水下图像恢复方法，其通过水下图像的局部光强度估算介质传输率 $ {\tilde t_c} $ ，通过全局光强最高的点估计全局均匀背景光 ${A_c}$ ，最后通过式(4)得到恢复的水下图像。其具体表达式如下：

该公式通过点 $x$ 某一邻域内 ${\rm{r}}、{\rm{g}}、{\rm{b}}$ 三通道中光强的最小值估算不同通道的介质传输率。其中 $ y \in \Omega (x) $ 代表 $y$ 是始于 $x$ 邻域内的一个点。该公式的物理含义为点 $x$ 处的介质传输率是以 $x$ 为中心的某一区域内，r、g、b三通道中，像素值最小的点与均匀背景光 ${A_c}$ 的比值。为了计算 ${A_c}$ ，需要先计算暗通道先验的光强图 $I_{{\text{Dcp}}}^{{\rm{rgb}}}(x)$ ，其数学表达式如下：

该公式的物理含义为点 $x$ 处的暗通道先验光强是以 $x$ 为中心的某一邻域内， ${\rm{r}}、{\rm{g}}、{\rm{b}}$ 三通道中，像素值最小的点所对应的光强。

${A_c}$ 的数学表达式为

其中 ${P^{0.1\% }}$ 是 $I_{{\text{Dcp}}}^{{\rm{rgb}}}(x)$ 中前0.1%最大像素值点所构成的位置集。

该公式的物理含义为在 $I_{{\text{Dcp}}}^{{\rm{rgb}}}(x)$ 中前0.1%最大像素值点所构成的位置集中，对 ${\rm{r}}、{\rm{g}}、{\rm{b}}$ 三通道光强求和并找出其最大值，该值所对应的点处的光强即为均匀背景光。

最后将计算得到的 $ {\tilde t_{{\rm{rgb}}}}(x) $ 、 $ {A_c} $ 代入式(7)得到处理后得水下图像。

尽管GDCP算法取得了不错的恢复效果，但是由于物理参数很难估计准确，因此限制了该算法的应用。

2.   基于物理先验的深度特征融合网络

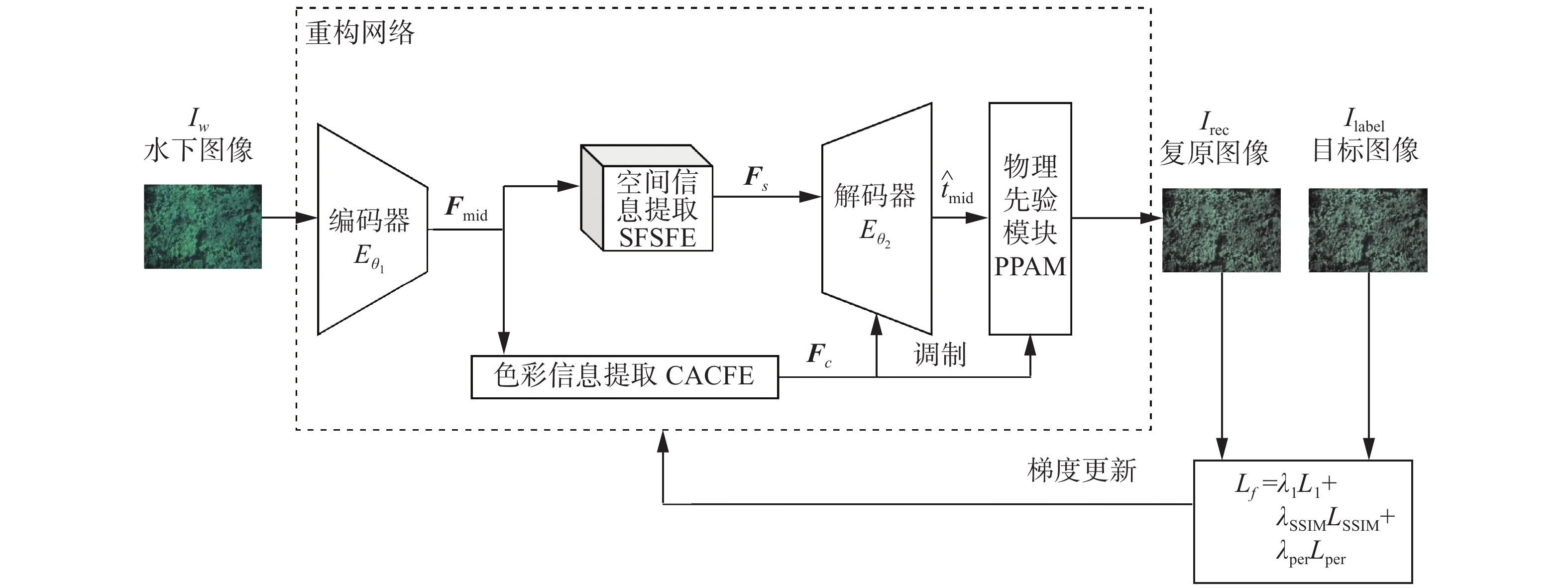
本文网络的整体流程如图2所示，受水下图像光学成像公式(式(1))和GDCP算法^[13]中利用背景光和色彩信息计算传输率的启发，本文提出通过数据驱动的深度学习方法，自适应地学习式(4)中的全局背景光 $A_c$ 和介质传输率图 ${\hat t_{{c}}}$ 。在解码器中充分利用局部空间信息和全局色彩信息估算传输率特征图 $\hat t_d$ ，再通过物理先验模块(physical priors, PPAM)中的调制卷积和物理先验知识分别生成基于数据的恢复图像 $I_g$ 和基于物理先验的恢复图像 $I_p$ ，最后通过PPAM模块中的混合注意力机制，将 $I_g$ 与 $I_p$ 进行深度特征级融合，并重建为最终的恢复图像 $I_{\text{rec}}$ 。

图  2  基于物理先验的深度特征融合水下图像恢复网络的整体流程

Fig.  2  Overall flow of underwater image restoration network based on physical prior deep feature fusion

下载: 全尺寸图片

恢复图象I_rec的具体数学表达式如下：

式中：PPAM、SFSFE、CACFE分别代表物理先验模块，空间注意力空间信息提取(spatial attention spatial feature extraction, SASFE)模块，通道注意力色彩信息提取(channel attention color information extraction, CACFE)模块； $ {{\boldsymbol{F}}_{{\text{mid}}}} $ 是中间特征向量； $ {\boldsymbol{F}}_s $ 是空间特征向量； $ {{\boldsymbol{F}}_c} $ 是色彩特征向量； $ {D_{{\theta _2}}} $ 是以 ${\theta _2}$ 为参数得解码器； $ {E_{{\theta _1}}} $ 是以 ${\theta _1}$ 为参数的编码器； ${I_w}$ 是水下图像；具体实现将在后文介绍。

由图2可知，本文网络的整体流程由5个部分组成，分别为编码器、解码器、SFSFE、CACFE、PPAM。

网络的输入为归一化至[−1,1]范围内的水下图像 ${I_w} \in {{\bf{R}}^{3 \times h \times w}}$ ，其中 $h$ 和 $w$ 分别代表水下图像的高和宽，本文中均取256。将 ${I_w}$ 送入编码器编码，编码器输出中间特征向量 ${{\boldsymbol{F}}_{{\text{mid}}}} = {E_{{\theta _1}}}({I_w})$ ， ${{\boldsymbol{F}}_{{\rm{mid}}}} \in {{\bf{R}}^{c \times {h_{{\text{mid}}}} \times {w_{{\text{mid}}}}}}$ 。其中 ${h_{{\text{mid}}}}$ 和 ${w_{{\text{mid}}}}$ 分别代表了 ${{\boldsymbol{F}}_{{\text{mid}}}}$ 的高和宽，本文中均为16， $c$ 代表通道数。然后 ${{\boldsymbol{F}}_{{\text{mid}}}}$ 经过SFSFE和CACFE分别得到空间特征向量 ${{\boldsymbol{F}}_s} \in {{\bf{R}}^{c \times {h_s} \times {w_s}}}$ 和色彩特征向量 ${{\boldsymbol{F}}_c} \in {{\bf{R}}^c}$ ；最后在解码器中通过调制操作将 ${{\boldsymbol{F}}_s}$ 与 ${{\boldsymbol{F}}_c}$ 融合，输出介质传输率向量 ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{t}}} _c} = {D_{{\theta _2}}}({{\boldsymbol{F}}_s}, M({{\boldsymbol{F}}_c})) \in {{\bf{R}}^{3 \times h \times w}}$ ， $M$ 是调制操作。下面对网络进行详细介绍。

2.1   编码器

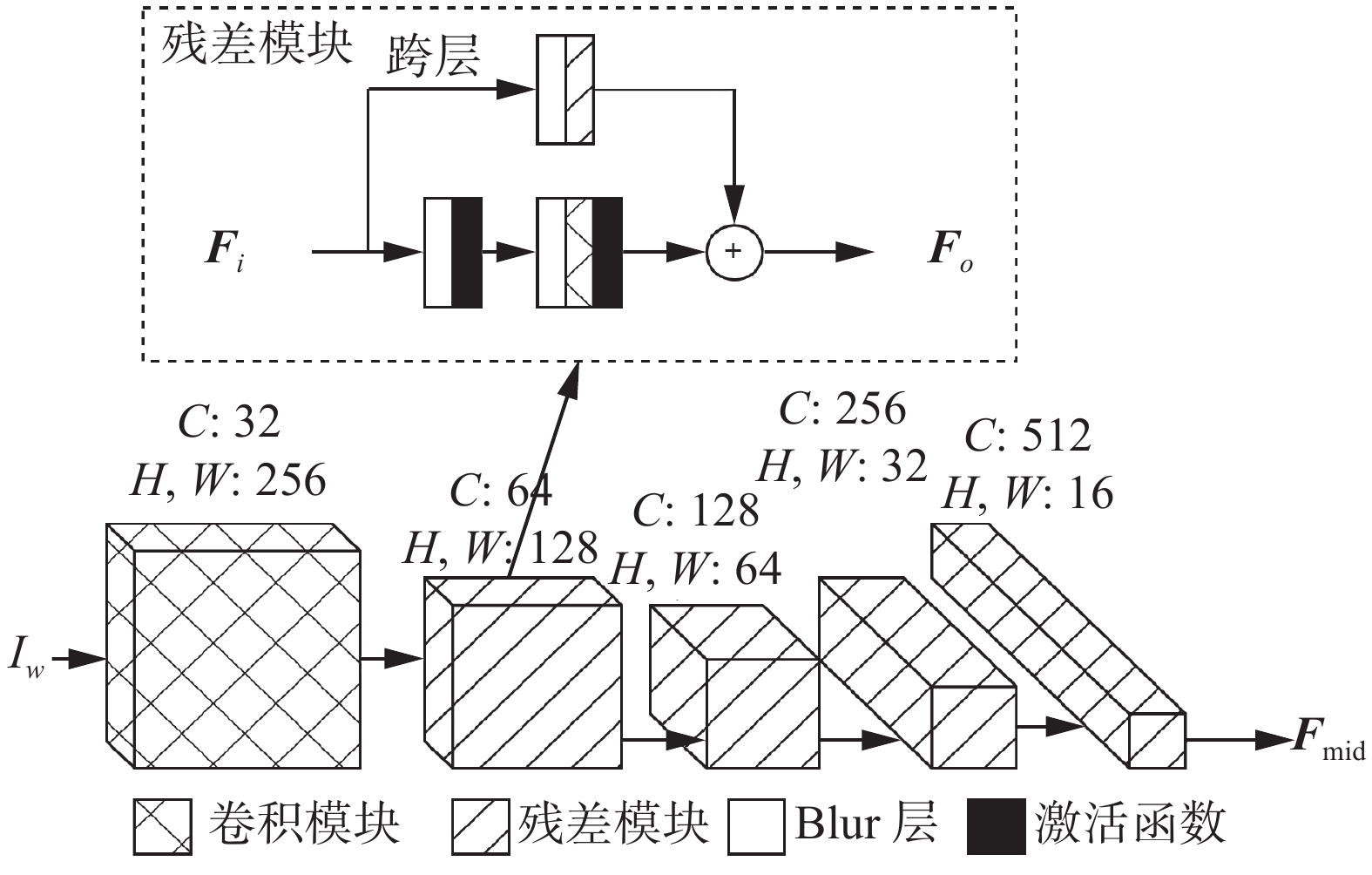
图3详细的展示了编码器结构，其由1个卷积模块和4个残差模块组成。

图  3  编码器结构

Fig.  3  Encoder structure

下载: 全尺寸图片

首先水下图像 ${I_w}$ 由一个卷积操作编码为一个水下特征向量 ${{\boldsymbol{F}}_w} = {\text{Conv}}({I_w}) \in {{\bf{R}}^{32 \times 256 \times 256}}$ ，得到的水下特征向量送入后续的残差模块，特征向量通道数由32逐渐增长至512，其增长因子是2，在通道数增长的同时，在每一个残差模块中，都对特征向量进行下采样，逐步提高神经网络的感受野，其下采样因子也为2，经过四个残差结构后，可以得到中间特征向量 ${{\boldsymbol{F}}_{{\text{mid}}}} = {E_{{\theta _1}}}({I_w}) \in {{\bf{R}}^{512 \times 16 \times 16}}$ 。

本文的编码器和解码器由残差模块作为基本单元组成，具体结构如图3中所示，每一个残差模块由3个卷积层2个激活层组成，使用残差模块的目的是提高数据的保真度并且可以避免梯度消失的问题^[15]，在每一个残差模块中，卷积层具有相同数量的滤波器。残差模块中所有的卷积层卷积核大小都为3，其步长均为1。残差模块的具体数学表达式如下：

式中： ${{\boldsymbol{F}}_o}$ 代表输出特征， ${{\boldsymbol{F}}_i}$ 代表输入特征， $ * $ 代表卷积操作， ${k^1}$ 、 ${k^2}$ 、 ${k^{{\rm{skip}}}}$ 分别代表第1层、第2层和跨层的卷积核参数， ${b^1}$ 、 ${b^2}$ 、 ${b^{{\rm{skip}}}}$ 分别代表第1层、第2层和跨层的卷积偏置值， $R( \cdot )$ 代表Relu激活函数， $B( \cdot )$ 代表Blur下采样操作。

在残差模块中使用了Blur^[16]进行下采样，这是因为使用Blur进行下采样可以降低图像中的高频信号，减少噪声和细节，从而避免神经网络学习到不必要的细节信息。此外，使用Blur进行下采样可以使图像保持平滑的特性，避免出现锯齿和马赛克等问题。最后，使用Blur进行下采样可以避免出现深度网络中的梯度消失问题，使得神经网络更加稳定和易于训练。

2.2   空间注意力空间特征提取模块

SFSFE由2个空间注意力模块所组成，空间注意力模块如图4所示。

图  4  空间注意力空间特征提取模块

Fig.  4  Spatial attention spatial feature extraction module

下载: 全尺寸图片

空间注意力模块输出的计算公式如下：

式中： ${{\boldsymbol{F}}_o}$ 为输出向量， ${\boldsymbol{F }}= {\text{Conv}}({{\boldsymbol{F}}_i})$ 代表输入特征经卷积操作后输出的特征图， ${f^{7 \times 7}}$ 是卷积核大小为7的卷积操作是图5中的第2个卷积操作， ${{\boldsymbol{F}}_{{\text{Avg}}}} = {\text{Avgpool}}({\boldsymbol{F}})$ 、 ${{\boldsymbol{F}}_{{\text{Max}}}} = {\text{Maxpool}}({\boldsymbol{F}})$ 分别代表在通道方向上的平均池化和最大池化后得到的特征图， ${{\boldsymbol{F}}_{{\text{cat}}}} = {\text{cat}}[{{\boldsymbol{F}}_{{\text{Avg}}}},{{\boldsymbol{F}}_{{\text{max}}}}]$ ，sig是sigmoid激活函数， $ \oplus $ 和 $ \otimes $ 分别代表了像素级别的加法和乘法。

图  5  通道注意力色彩信息提取模块

Fig.  5  Channel attention color information extraction module

下载: 全尺寸图片

第1个空间注意力模块不改变特征向量的通道数，在第2个注意力模块中，在通道方向上进行压缩，最终输出的空间信息特征向量 ${{\boldsymbol{F}}_s} \in {{\bf{R}}^{8 \times 16 \times 16}}$ 。

2.3   通道注意力色彩信息提取模块

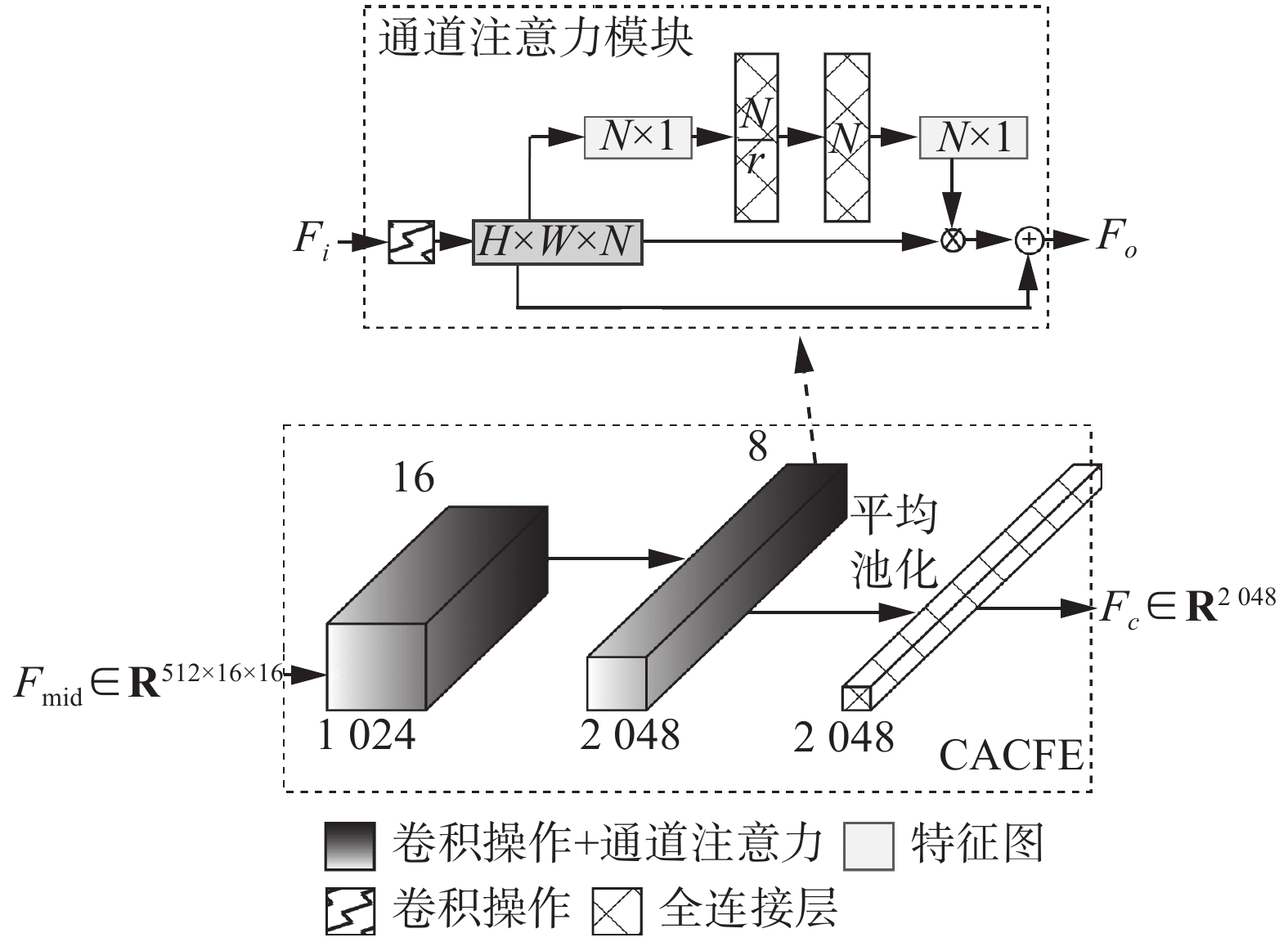
不同于GDCP^[13]直接使用局部光信息与全局均匀背景光估算介质传输率图 ${\hat {\boldsymbol{t}}_c} \in {{\bf{R}}^{3 \times 256 \times 256}}$ ，本文设计了CACFE模块以使用神经网络提取水下图像的全局色彩信息，以便在后续的模块中计算全局均匀背景光 ${A_c}$ 。

考虑到每个通道空间所包含的信息意义不同，因此提取色彩信息时每个通道应该具有不同的贡献。使用通道注意力模块提取水下图像的色彩信息。通道注意力模块如图5所示。

其输入特征是 ${{\boldsymbol{F}}_i} \in {{\bf{R}}^{N \times H \times W}}$ 的空间向量，其中 ${{\boldsymbol{F}}_i}$ 是输入特征图， $H$ 和 $W$ 分别代表特征图的高和宽。首先使用全局平均池化，从而得到一个信息描述符 $Z \in {{\bf{R}}^{N \times 1}}$ ，这是一个嵌入式的逐通道特征响应全局分布。第 $k$ 个 ${\textit{z}}$ 可以表述为

其中 $k \in [1,N]$ ，为了更好地利用通道之间的相互依赖性，使用了自门控机制来生成每个通道调制的权重集合。

其中： $\sigma $ 代表sigmoid激活函数， $\delta $ 代表Relu激活函数， $ * $ 代表卷积操作， $W_1$ 和 $W_2$ 分代表了2个卷积层的权重，其输出通道分别为 $\dfrac{N}{r}$ 和 $N$ ，其中 $r$ 等于16，其目的是为了减少运算量，加快程序的运行速度。同时，为了避免梯度消失和保持原有特征的特性，以残差的形式处理通道注意力的权重。

其中 ${{\boldsymbol{F}}_o} \in {{\bf{R}}^{c \times {H \mathord{\left/ {\vphantom {H 2}} \right. } 2} \times {W \mathord{\left/ {\vphantom {W 2}} \right. } 2}}}$ 是输出特征向量，其高宽通过卷积操作变为原来的1/2， $ \oplus $ 和 $ \otimes $ 分别代表了像素级别的加法和乘法。

色彩信息提取模块由两个通道注意力模块^[17]依次串联组成，考虑到色彩信息与空间信息无关，因此中间特征向量每通过一个通道注意力模块其宽高都会缩减为原来的1/2，在最后一个全连接层前使用全局平均池化替代下采样以消除空间信息，最终输出色彩信息特征向量 ${{\boldsymbol{F}}_c} \in {{\bf{R}}^{2\;048}}$ 。

2.4   解码器

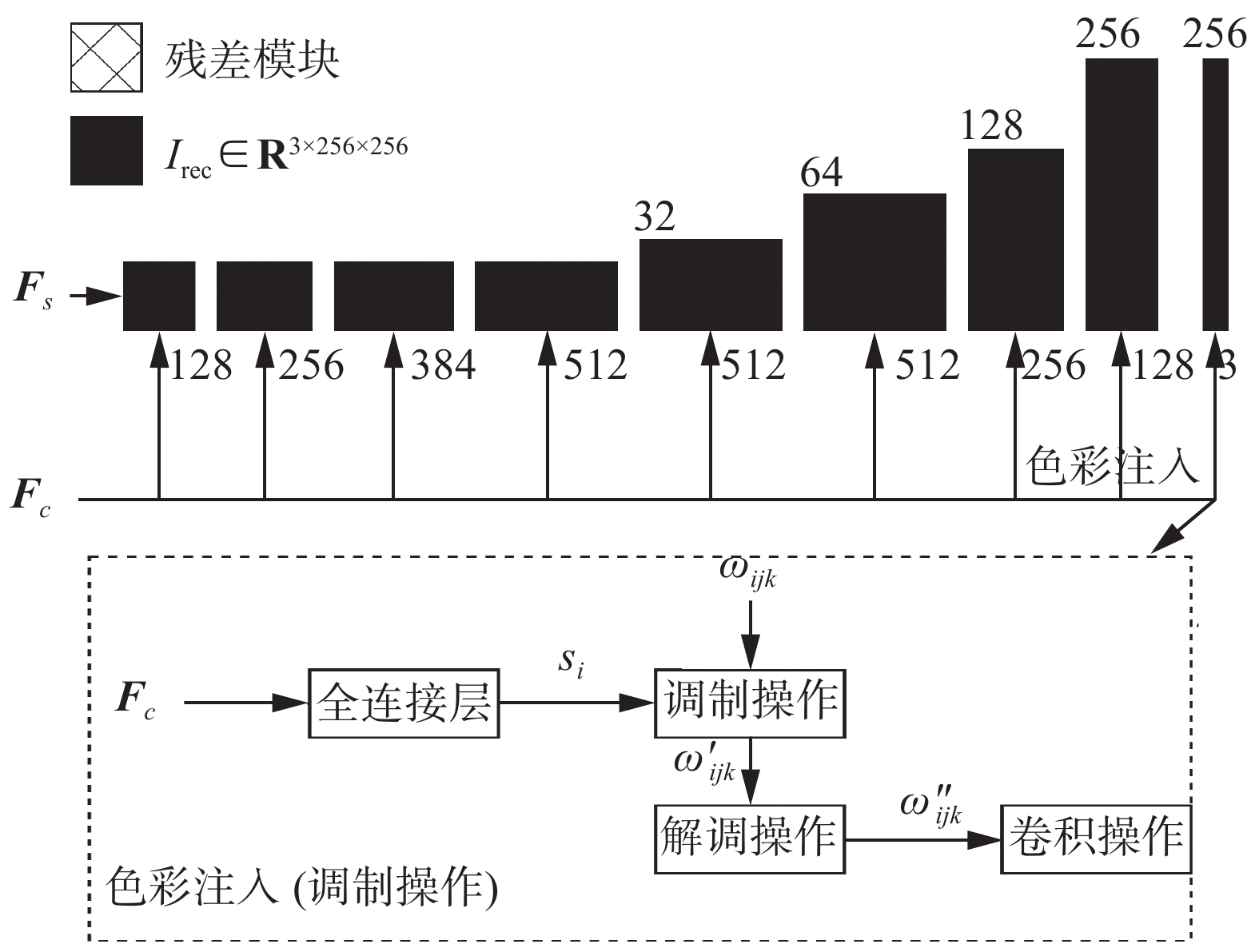
受GDCP^[13]算法中利用局部信息和全局色彩信息计算传输率图的启发，在解码器中将 ${{\boldsymbol{F}}_c}$ 与 ${{\boldsymbol{F}}_s}$ 相结合计算 ${\hat {\boldsymbol{t}}_c}$ ，以便在PPAM模块中利用式(4)生成一张基于物理先验的恢复图像。

如图6所示，本文的解码器共由9个残差模块组成，前4个残差模块只进行通道方向上的扩展并不进行上采样操作，受文献[18]的启发，本文使用调制操作，将色彩信息逐步融入进特征向量中。

图  6  解码器结构

Fig.  6  Decoder structure

下载: 全尺寸图片

简单来说调制操作是将学习到的调制向量映射到特定层的平均值和方差上，调制操作的数学表达式如下：

其中： $w$ 和 $w'$ 分别代表原始权重和调制权重，“·”代表元素相乘， ${s_i}$ 是通过全连接层所学到的与第i个输入特征图相对应的比例。本文中为色彩信息，j和k分别为特征图和卷积核的空间下标。经过调制和卷积操作后，输出向量的标准差为

为了将输出特征图恢复为单位标准差，本文需要解调操作，即将上述标准差再次嵌入到卷积权重中：

$\varepsilon $ 的作用是防止分母为0。

后5个残差模块在通道方向上不断的压缩，同时依旧使用Blur对图像进行上采样，在最后的残差模块中，生成传输率特征图 $ {\hat {\boldsymbol{t}}_c} \in {{\bf{R}}^{3 \times 256 \times 256}} $ 。

2.5   基于混合注意力机制的物理先验模块

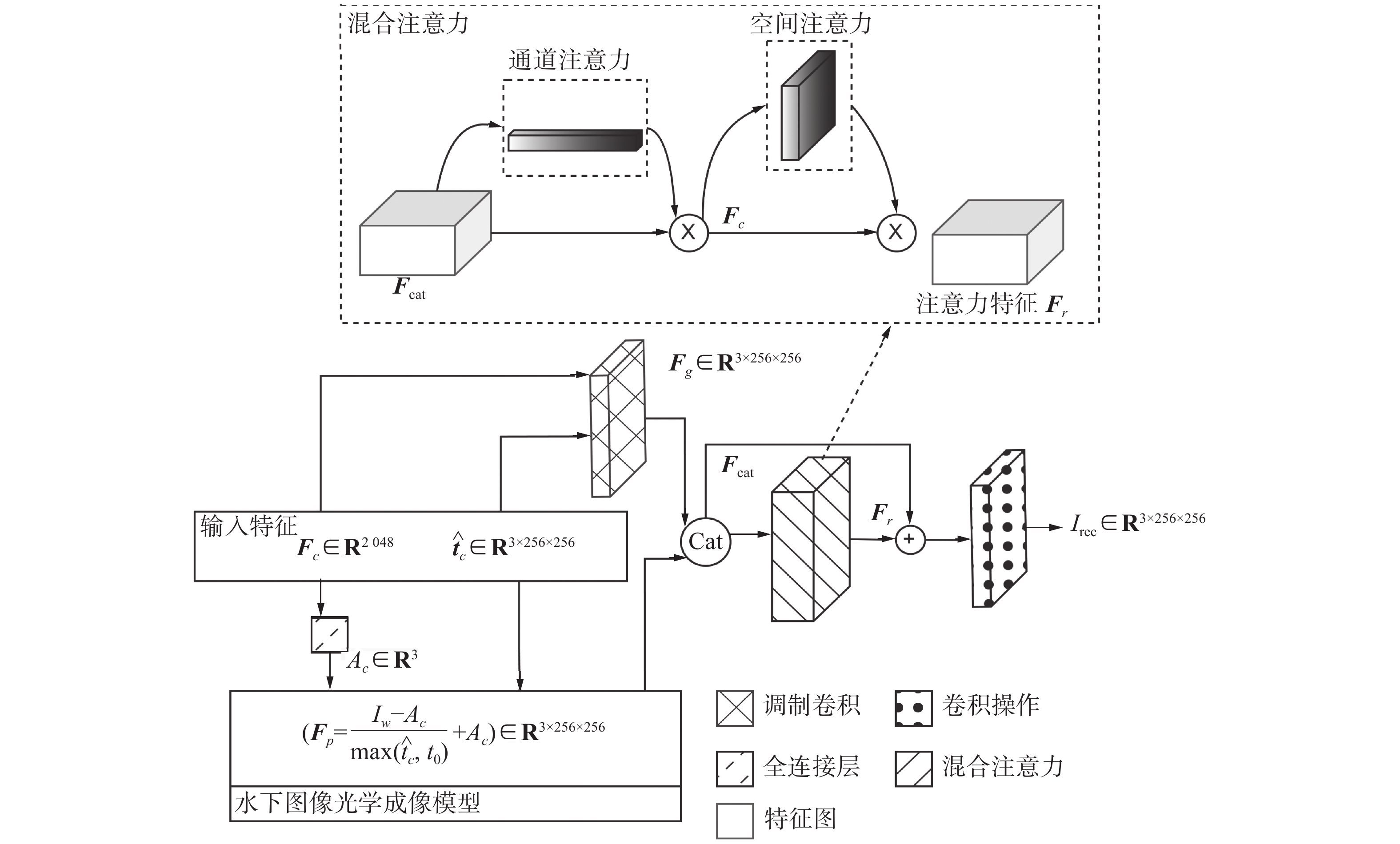
为了更好地利用已有的物理先验知识和深度神经网络的非线性学习能力，本文设计了物理先验模块。

如图7所示，在物理先验模块中，首先利用 ${\hat {\boldsymbol{t}}_c}$ 与 ${{\boldsymbol{F}}_c}$ 通过调制操作生成一张基于神经网络的恢复图像，称之为生成特征向量 ${\boldsymbol{F}}_g$ ；同时利用 ${\hat {\boldsymbol{t}}_c}$ 与 ${{\boldsymbol{F}}_c}$ 通过全连接层计算1.1中的式(4)中的参数并生成一张基于物理先验的恢复图像，称之为物理特征向量 ${\boldsymbol{F}}_p$ 。将生成特征向量和物理特征向量沿通道堆叠后，利用混合注意力机制生成的权重图，经过卷积操作后得到最终恢复的图像。

图  7  物理先验模块

Fig.  7  Physical prior module

下载: 全尺寸图片

其中 ${\boldsymbol{F}}_p$ 具体表达式如下：

其中： ${t_0}$ =0.1， ${A_c} = {\text{mlp}}({{\boldsymbol{F}}_c}) \in {{\bf{R}}^3}$ 是通过 ${\text{mlp}}$ 全连接层计算出的均匀背景光。

混合注意力流程如图7中所示，其具体数学表达式如下：

其中 $ M_s $ 和 $ M_c $ 分别代表空间注意力和通道注意力，具体实现见2.2、2.3节。PPAM的数学表达式如下：

其中 ${I_{{\text{rec}}}}$ 为恢复图像， ${\boldsymbol{F}}_{\text{cat}} = {\text{concat}}[{\boldsymbol{F}}_p,{\boldsymbol{F}}_g]$ 代表是将物理特征向量和生成特征向量沿通道方向堆叠后的堆叠特征图， ${\text{Conv}}$ 、 $ \oplus $ 分别为卷积操作、元素加法。

2.6   损失函数

为了训练本文网络，本文使用了3种损失函数的组合，分别为 $L_1$ 损失、SSIM^[19]损失、感知路径损失^[20]。

$L_1$ 损失，也被称为平均绝对误差（mean absolute error，MAE），是将每个样本的预测值与真实值之差的绝对值求和后再求平均值。

式中： $I_{{\rm{label}}}$ 和 $I_{\text{rec}}$ 分别代表了目标图像和复原图像在 $i$ 处的像素值， $n$ 为整张图像的像素点个数。

相比于 $L_2$ 损失， $L_1$ 损失对离群值更稳健，即数据集中存在的一些噪声点或异常值对损失的影响较小。并且 $L_1$ 损失更倾向于保留细节，在训练过程中易于优化，训练稳定，因此 $L_1$ 损失更适合于重构图像的任务^[21]。

同时，为了增强生成图像对于局部结构和细节的表现能力，提高原始图像与生成图像在亮度，对比度和结构上的相似性，本文也使用结构相似度SSIM^[19]作为损失函数的一部分。

式中：S代表结构相似度， $\mu_{\text{rec}}$ 和 $\mu_{\text{label}}$ 分别代表复原图像和目标图像的均值， $\sigma_{\text{rec}}$ 和 $\sigma_{\text{label}}$ 分别表示复原图像和目标图像的标准差， $\sigma_{\text{reclabel}}$ 表示两幅图像的协方差， $C_1$ 和 $C_2$ 是两个常数，用于避免分母为0的情况。

像素级别的差异有时并不一定能够反映人眼对图像质量的感知差异，因此引入了感知路径损失，其通过将图像转换为特征向量表示，并比较它们在特征空间中的相似度，可以更好地捕捉人眼对图像质量的感知，文献[22]的实验结果表明感知路径损失可以提高生成图像对于细节的表现能力和网络风格转换的能力。

本文中的感知路径损失是基于在ImageNet数据集上预训练的VGG-19网络来计算的，其具体表达式为

式中： $\varphi _j$ 表示VGG-19中的第j个卷积层， H、W分别代表图像的高和宽，m、n分别代表对应的像素点，本文使用特征提取层的输出之间的差值来衡量重构图像与真实图像之间的差值。

最终的整体损失函数为

式中： $\lambda $ 用于平衡不同损失之间的范围，最终设置 $\lambda_1 = 1$ ， $\lambda_{\text{SSIM}} = 1.1$ ， $\lambda_{\text{per}} = 0.1$ 。

3.   实验结果与分析

本文使用Adam优化器来训练网络，设置其学习率为0.0002， $\,\beta_1$ 为0.9， $\,\beta_2$ 为0.999。设置学习率每10个epoch缩小到原来的1/5，最终学习率固定在0.000001，设定batch size为8，将图片随机裁剪为256，随机使用水平翻转，垂直翻转等数据增强手段。

3.1   数据集

由于水下环境的复杂性和特殊性导致获取真实水下图像数据并进行标注是十分困难和昂贵的，因此现有的真实水下图像数据集中图像数量有限，成像条件单一。综上所述，本文使用文献[23-24]中的合成数据集进行模型预训练，并在Heron Island Coral Reef数据集（HICRD）^[25]上进行迁移训练，以下对数据集进行详细介绍。

3.1.1   合成数据集

如表1所示，文献[26]中给出了不同成像条件下的衰减系数，其中I、IA、IB、II和 III是开阔水域，1、3、5、7和9是沿海水域，1代表最干净，9代表最浑浊。

本文使用表1中的衰减系数，IMF图像公式和NYU-V2RGB-D^[27]数据集，按照文献[23-24]中所使用的方法合成了一个水下图像数据集。其中NYU-V2RGB-D数据集作为清晰图像的来源。首先随机生成深度系数 $d(x)$ ，其中 $x$ 代表位置坐标，然后使用生成的深度系数与数据集中的深度图像元素相乘，得到合成水下图像所需的深度图。最后我们生成背景光强度 $A_c$ ，得到所有参数后送入1.1节中的水下图像生成公式(式(2))中，得到合成的水下图像。

为每种水质类型生成5张合成图像，这样每张清晰图像都会有50张与之对应的水下图像。

3.1.2   真实数据集

Heron Island Coral Reef数据集（HICRD）^[25]包含了来自8个不同场地的原始水下图像，每个场地都有详细的元数据，包括水参数（漫反射衰减）、最大潜水深度和相机型号等信息。其中6个场地有详细的衰减系数。根据原始图像的深度信息和物体与相机之间的距离，具有相似深度、恒定距离和良好视觉质量的图像被标记为高质量。文献[25]中精确计算了未衰减的原始图像，并手工剔除了一些效果不尽如人意的图像，最终得到了一个包含6003张低质量水下图像、3673张高质量水下图像和2000张未衰减的原始图像的数据集。

3.2   合成数据集输出结果

如图8所示，本文使用UWCNN^[23]和UIE-DAL^[24]作为对比对象，UWCNN使用合成的数据集进行训练，针对不同的水质环境，训练不同模型，每次使用时需先根据水质类型选取对应的模型参数，由于类型I、IA、IB的衰减系数十分接近，为了简化训练过程，UWCNN合并了类型I、IA、IB因此共8个模型；UIE-DAL使用了对抗网络的思想，使用编码器获取剔除了水质环境因素的特征向量，使用该特征向量直接恢复目标图像，是一种通用模型。从对比图可知，UWCNN所恢复的图像在细节方面有所不足，但是其色彩表现稍好；UIE-DAL会在图像中添加伪影，使生成的图像偏红；本文模型在所有的水质类型中均可以做到对水下图像的恢复，特别是在类型5、7、9这样的极端环境中，其恢复效果要远好于UWCNN和UIE-DAL，但是在这样的极端环境当中，本文生成的图像与目标图像仍有较大差距，恢复图像中色彩信息表现不足。这是因为本文采用了空间信息和色彩信息相分离的生成结构，在极端环境下其色彩信息很少，因此恢复的图像总是缺乏色彩的。

图  8  合成数据集重构效果

Fig.  8  Reconstruction effect of composite dataset

下载: 全尺寸图片

通过对比类型7、Ⅱ、Ⅲ，可以发现经本文模型处理后的图像显著地减少了黄色和蓝色色偏。

相比于UWCNN^[23]和UIE-DAL^[24]，本文模型所生成的图像中伪影和色偏显著减少，并且本文的模型可以很好的保留图像中的细节部分，如在类型1、3中仍可看清床上的物品细节。

3.3   真实数据集输出结果

如图9所示，使用HICRD来测试本文的模型，图9(b)是由UIE-DAL的预训练模型生成，图9(c)是直接使用本文模型在合成数据集上训练的权重，图9(d)是本文模型在HICRD上进行迁移训练的结果。通过图9可以看出，本文模型在真实数据集上的泛化性显然好于UIE-DAL，尽管使用预训练模型时，大部分情况下，输出图像与目标图像有明显差异，输出图像的亮度显然高于目标图像，但这有可能是目标图像的不完全恢复所造成的，因为在第2行中，显然使用合成数据集训练的模型的输出结果更好，即更倾向于GroudTruth。这也从侧面证实了使用合成数据集进行训练的可靠性。

图  9  HICRD 重构效果

Fig.  9  Reconstruction effect of HICRD

下载: 全尺寸图片

通过生成图像与原图像之间的对比，发现生成图像的绿色色偏明显减少。不论使用何种模型，恢复图像的纹理细节表现显然好于水下图像，这证明了本文模型对于水下图像具有明显的增强效果，具有良好的泛化性，同时由于本文模型具有通用性，当在对应数据集上进行训练时，可以快速地逼近目标图像。

3.4   定量分析指标

使用SSIM和PSNR进行不同模型的定量对比。SSIM 是一个评估图像质量的指标，它考虑图像的结构信息和亮度信息，更能反映出人眼对图像细节和结构的敏感度，更接近于人类主观感受，其值范围从0到1，值越大，表示两幅图像越相似，具体公式见式(21)。

PSNR是最常用的评估图像质量的指标之一，表示生成图像与目标图像之间的差异大小，值越大，表示图像保真度、图像去噪的效果越好。

3.5   定量分析

表2给出了本文模型与当前主流模型在合成数据集上训练后的定量表现。从表2可以看出，随着成像条件变差，模型恢复效果也逐渐变差，在大多数的成像条件下，本文模型可以取得超越主流模型的性能表现，往往具有更高的SSIM值和PSNR值，在类型1成像条件下，尽管没有达到最大的SSIM值，但是其与UWCNN模型的差距非常小。

3.6   高级任务表现

水下图像处理是为了更好地执行后续的高级视觉任务，例如显著性目标检测。显著性目标检测（saliency object detection）是指在一张图片中自动识别出最显著、最引人注目的区域，即显著性区域，通常被认为是人眼在图片中第一时间注意到的区域。

图10给出了使用预训练模型BASNet^[30]在水下图像和复原图像上进行显著性目标检测的结果。从左至右分别为水下图像、复原图像、水下图像显著目标检测结果、复原图像显著目标检测结果。

图  10  重构图像显著目标检测表现

Fig.  10  Performance of significant target detection in reconstructed images

下载: 全尺寸图片

通过分析图10可以发现，复原图像显著目标检测效果远好于水下图像显著目标检测，例如在第1行中，使用复原图像可以更好地检测出水下蛙人的腿部和脚部细节；在第2行中，使用复原图像可以更好地检测出水下雕像的轮廓，并且可以检测出雕像手中的一些细节；在第3行中，原图像无法检测出的右下角石块在复原图像中可以被检测出；在第4行中，与原始水下图像相比复原图像可以检测出更多的人形雕塑。

4.   结束语

本文提出一种将物理先验知识和深度神经网络相结合的水下图像复原模型。受暗通道先验中使用RGB色彩信息计算传输率的启发，该模型分别提取水下图像的空间信息和色彩信息，再通过调制操作将色彩信息与空间信息融合以推断水下传输率，最后通过混合注意力机制将基于水下光学成像模型和调制卷积的复原特征图融合，生成最终的恢复图像。实验的结果表明，使用平均绝对误差损失，结构相似度损失和感知路径损失可以有效训练本文模型。本文模型在可以极大地改善水下图像的成像效果，减少图像中的模糊、色偏等问题，提高目标检测的检测效果。由于采用了信息分离的结构，本文模型具有良好的泛化性，适用于多种水下成像条件，特别是在极端的水下环境当中，本文模型仍可以恢复图像的部分细节。